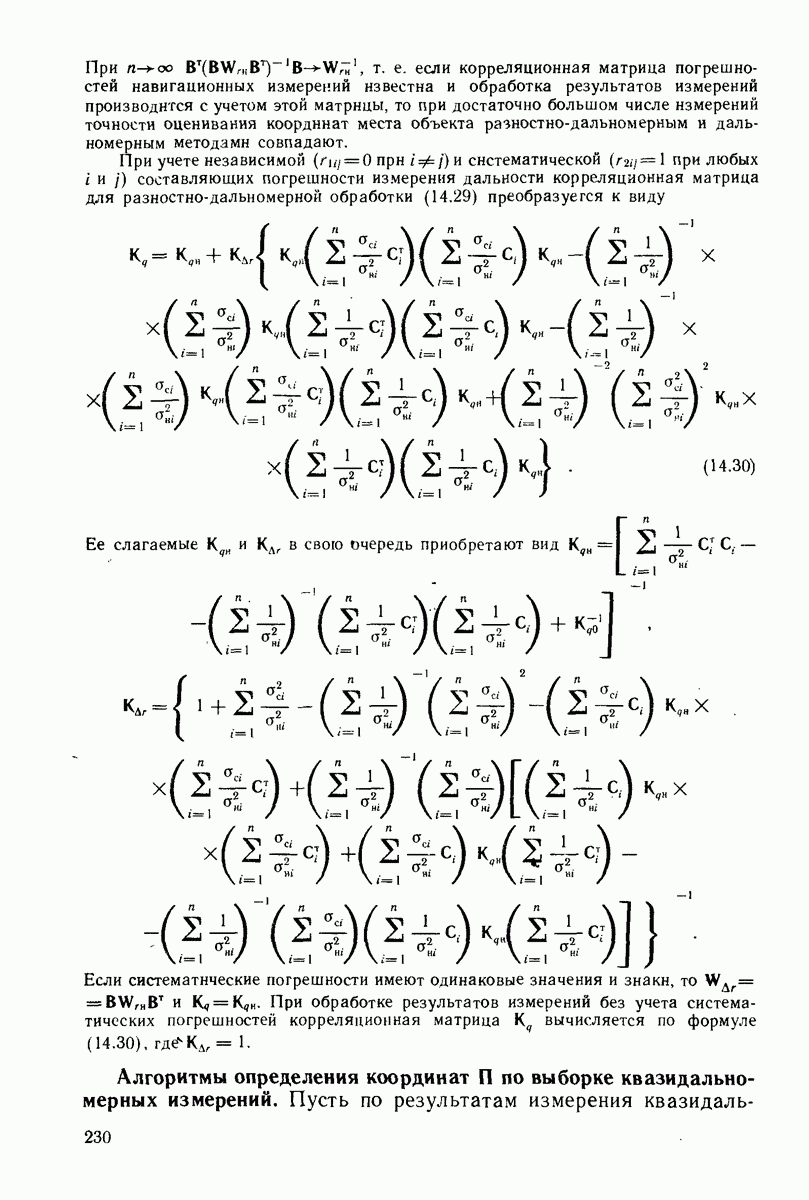| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
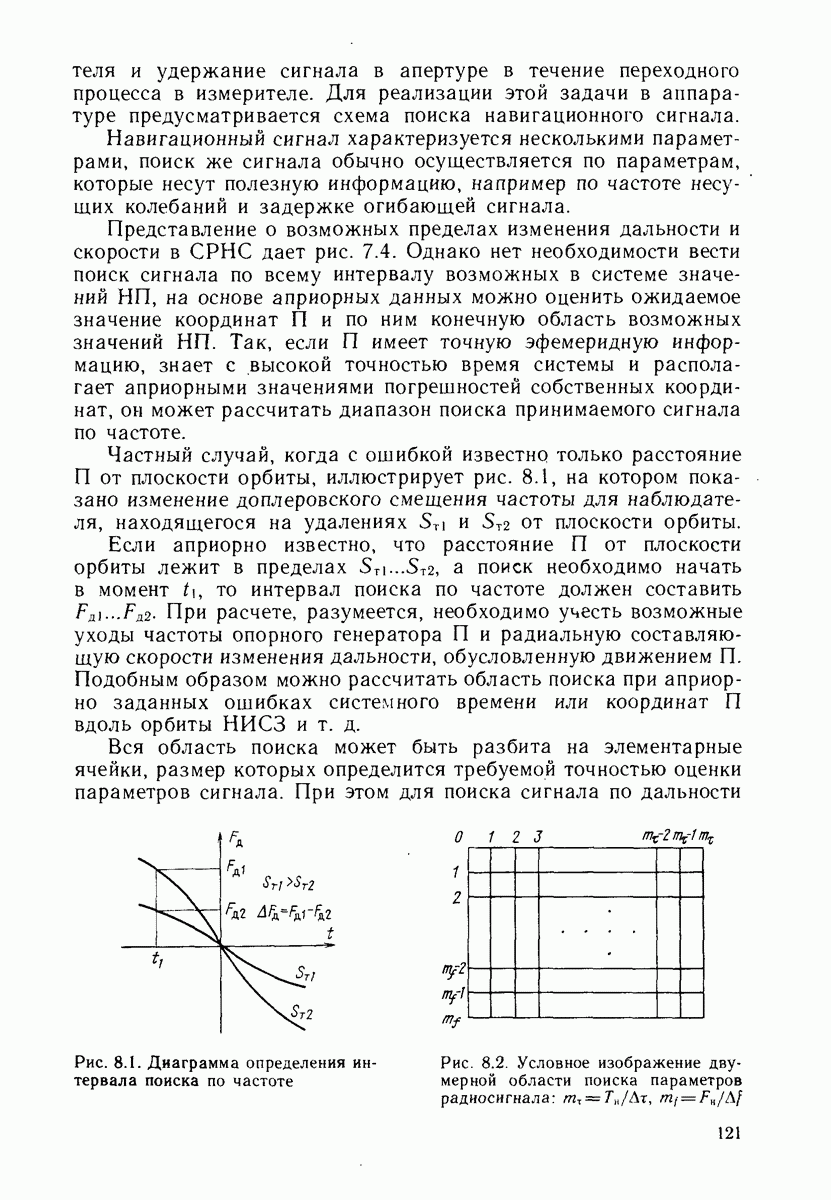
25.2. ВЫБОР ОПТИМАЛЬНОГО ПО КРИТЕРИЮ ТОЧНОСТИ СОЗВЕЗДИЯ НИСЗ
Рассмотрим способ получения обобщенных градиентов. Для исключения из обработки мешающего параметра  образуем разностно-дальномерные градиенты:
образуем разностно-дальномерные градиенты:

где  — чисто дальномерный градиент одного из квазидальномерных результатов измерений по одному из НИСЗ, принимаемому за ведущий;
— чисто дальномерный градиент одного из квазидальномерных результатов измерений по одному из НИСЗ, принимаемому за ведущий;  — дальномерные градиенты измерений по остальным ведомым НИСЗ. Обозначи
— дальномерные градиенты измерений по остальным ведомым НИСЗ. Обозначи  через
через  соответствующие погрешности измерений квазидальностей, полагаемые гауссовскими некоррелированными случайными величинами. Эти погрешности будут складываться из погрешностей измерений квазидальностей и фазирования генераторов НИСЗ. Корреляционная матрица погрешностей разностных измерений имеет вид
соответствующие погрешности измерений квазидальностей, полагаемые гауссовскими некоррелированными случайными величинами. Эти погрешности будут складываться из погрешностей измерений квазидальностей и фазирования генераторов НИСЗ. Корреляционная матрица погрешностей разностных измерений имеет вид

Приводя  к каноническому виду, можно представить матрицу
к каноническому виду, можно представить матрицу  виде суммы диад следующим образом:
виде суммы диад следующим образом:  Здесь
Здесь  введенные ранее формально обобщенные градиенты, определяемые теперь так:
введенные ранее формально обобщенные градиенты, определяемые теперь так:

Разностно-дальномерные градиенты  даются выражениями (25.10).
даются выражениями (25.10).
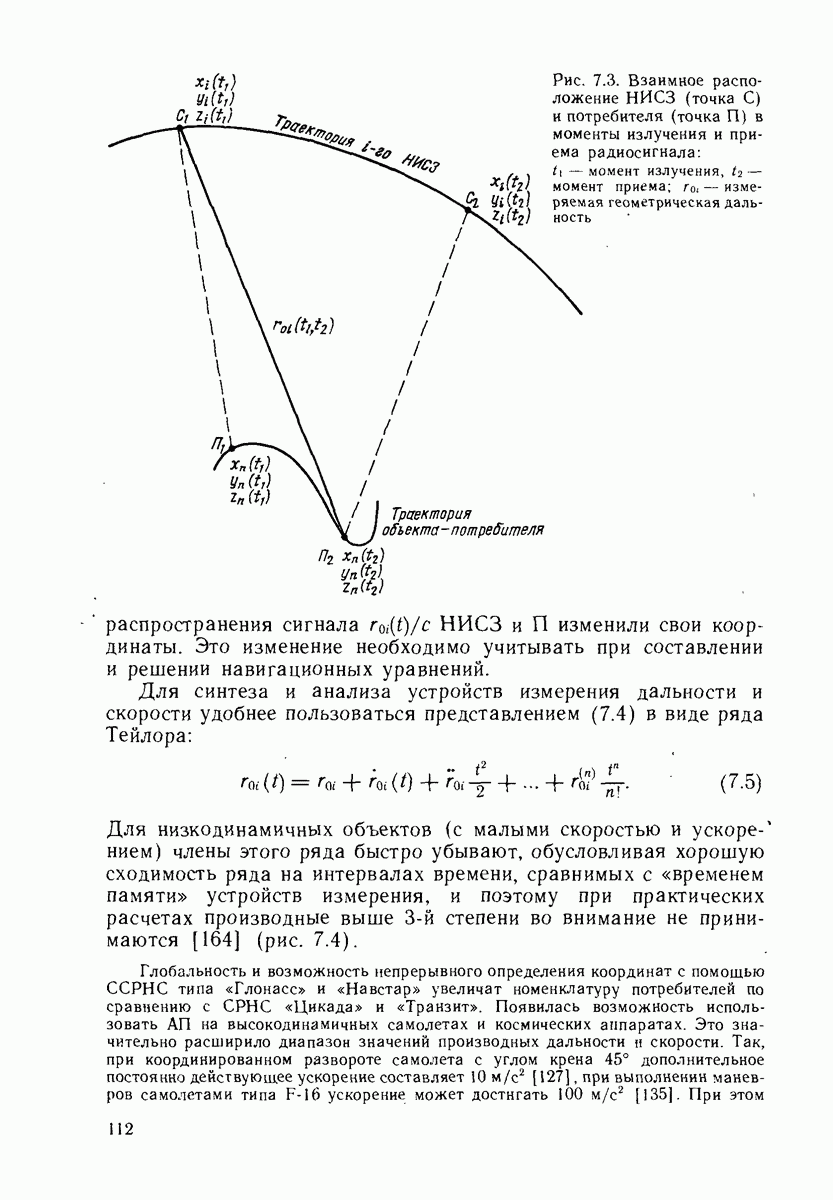
На рис. 25.1 показаны два НИСЗ и два дальномерных градиента  , соответствующие производимым по ним измерениям. Модуль градиента разностно-дальномерного измерения
, соответствующие производимым по ним измерениям. Модуль градиента разностно-дальномерного измерения  Угол 9 между дальномерными градиентами определяется в зависимости от геоцентрического угла X разнесения
Угол 9 между дальномерными градиентами определяется в зависимости от геоцентрического угла X разнесения

Рис. 25.1. Разностный градиент дальномерных измерений  градиенты дальномерных измерений
градиенты дальномерных измерений
НИСЗ и высоты  потребителя (П) над земной поверхностью из следующего уравнения:
потребителя (П) над земной поверхностью из следующего уравнения: 
Выбор оптимального созвездия НИСЗ для П, находящегося на высоте  эквивалентен такому выбору обобщенных градиентов, при котором корень из следа корреляционной матрицы погрешностей засечки
эквивалентен такому выбору обобщенных градиентов, при котором корень из следа корреляционной матрицы погрешностей засечки  достигает своего минимально возможного значения. Было показано, что
достигает своего минимально возможного значения. Было показано, что  При этом значения коэффициентов определяются через обобщенные градиенты
При этом значения коэффициентов определяются через обобщенные градиенты 

Итак, след корреляционной матрицы вектора погрешностей определяется выражением (25.9) через коэффициенты характеристического уравнения, определяемые зависимостями (25.12). При использовании квазидальномерных измерений обобщенные градиенты  суть линейные комбинации (25.11) разностно-дальномерных градиентов
суть линейные комбинации (25.11) разностно-дальномерных градиентов  с коэффициентами, являющимися компонентами собственных векторов корреляционной матрицы
с коэффициентами, являющимися компонентами собственных векторов корреляционной матрицы  погрешностей разностно-дальномерных измерений.
погрешностей разностно-дальномерных измерений.
Данное утверждение раскрывает общую структуру оценки точности навигационного определения, произведенного квазиметодом. При этом результат оказывается выраженным в простой и наглядной форме через обобщенные градиенты. В практических случаях более удобно использовать разностные градиенты вместо обобщенных.
Можно показать, что при определенных условиях при выборе оптимального созвездия критерий минимума следа можно заменить эквивалентом наиболее простого критерия. В частности, можно считать, что оптимизация выбора созвездия по минимуму  эквивалентна условию максимизации объема
эквивалентна условию максимизации объема  призмы, построенной на обобщенных градиентах, или, что то же, объема
призмы, построенной на обобщенных градиентах, или, что то же, объема  призмы, построенной на разностных градиентах
призмы, построенной на разностных градиентах 
Чтобы сделать результат очевидным, заметим, что для потенциально оптимального созвездия эллипсоид рассеивания должен быть осесимметричным  Обозначив через
Обозначив через  его полуоси, запишем критерии следа
его полуоси, запишем критерии следа  и объема V так:
и объема V так:

Отсюда при  и следует справедливость приведенного утверждения:
и следует справедливость приведенного утверждения:

Полученные результаты позволяют сделать важное заключение. Если единственным ограничением расположения НИСЗ является условие наблюдения, т. е. НИСЗ должны находиться в пределах области радионаблюдения с объекта  то потенциально оптимальное созвездие будет выглядеть следующим образом: один НИСЗ — в зените П, а три других равномерно распределены по границе конуса радиовидимости. Справедливость сказанного вытекает из того очевидного факта, что максимальный объем пирамиды, построенной на разностных градиентах, будет у правильной пирамиды, вписанной в сферический сегмент сферы радиовидимости П.
то потенциально оптимальное созвездие будет выглядеть следующим образом: один НИСЗ — в зените П, а три других равномерно распределены по границе конуса радиовидимости. Справедливость сказанного вытекает из того очевидного факта, что максимальный объем пирамиды, построенной на разностных градиентах, будет у правильной пирамиды, вписанной в сферический сегмент сферы радиовидимости П.
Потенциальная точность созвездия определится следующим образом. Обобщенные градиенты  оказываются в этом случае взаимно ортогональными, их модули соответственно:
оказываются в этом случае взаимно ортогональными, их модули соответственно:

причем  направлен по местной вертикали,
направлен по местной вертикали,  лежат в плоскости горизонта.
лежат в плоскости горизонта.
В этом случае полуоси корреляционного эллипсоида определяются особенно просто — они обратны 

где 9 — зенитный угол периферического НИСЗ, выражаемый через аналогичный геоцентрический угол радиус орбиты  и радиус Земли
и радиус Земли 

Полученный результат характеризует, очевидно, потенциальную точность навигационного определения.
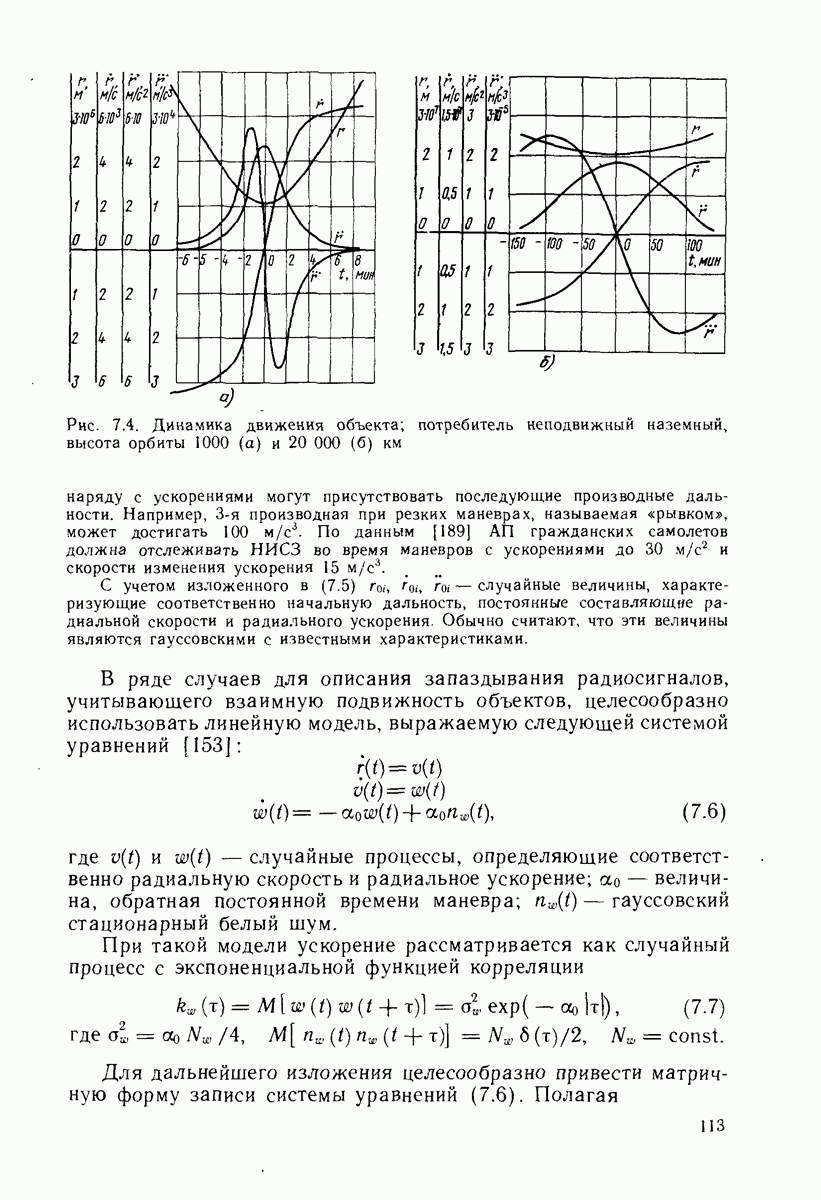
Сравнение критериев выбора рабочего созвездия по минимуму следа корреляционной матрицы и максимуму определителя. Полной точностной характеристикой выбранного созвездия служит корреляционный эллипсоид. Поэтому естественно рассмотреть трехмерное пространство, координаты которого будут соответствовать полуосям эллипсоида рассеяния. Постоянное значение критериальной функции задает в этом пространстве поверхность, на которой будут эквивалентными различные, созвездия, определяемые однозначно размерами полуосей соответствующих им эллипсоидов.
Пусть  нормированные значения полуосей корреляционного эллипсоида, тогда критерий следа корреляционной матрицы
нормированные значения полуосей корреляционного эллипсоида, тогда критерий следа корреляционной матрицы  будет изображаться в этом пространстве в виде сферы радиусом
будет изображаться в этом пространстве в виде сферы радиусом  С другой стороны, критерий определителя матрицы системы нормальных уравнений или эквивалентный ему критерий модуля определителя системы условных уравнений можно представить в виде
С другой стороны, критерий определителя матрицы системы нормальных уравнений или эквивалентный ему критерий модуля определителя системы условных уравнений можно представить в виде  Для сопоставления этих критериев необходимо установить связь значений отвечающих им критериальных функций из соображения, что оба критерия точно эквивалентны на биссектрисах координатных октантов.
Для сопоставления этих критериев необходимо установить связь значений отвечающих им критериальных функций из соображения, что оба критерия точно эквивалентны на биссектрисах координатных октантов.

Рис. 25.2. Сравнение результатов применения критериев следа корреляционной матрицы и определителя для выбора рабочего созвездия
Расхождение их в других точках пространства эллипсоидов  иллюстрируется рис. 25.2, где показаны сечения первых критериальных поверхностей, отвечающих различным значениям
иллюстрируется рис. 25.2, где показаны сечения первых критериальных поверхностей, отвечающих различным значениям  и сечения отвечающих этим же значениям вторых критериальных поверхностей V - плоскостью
и сечения отвечающих этим же значениям вторых критериальных поверхностей V - плоскостью  Рассмотрение этих зависимостей говорит о том, что для сильно вытянутых корреляционных эллипсоидов
Рассмотрение этих зависимостей говорит о том, что для сильно вытянутых корреляционных эллипсоидов  критерий определителя может давать результаты, заметно отличающиеся от результатов по критерию
критерий определителя может давать результаты, заметно отличающиеся от результатов по критерию  Следовательно, такой выбор приведет к заметному проигрышу в точности. Поэтому приближенная эквивалентность рассмотренных критериев имеет место при условии исключения сильно вытянутых корреляционных эллипсоидов, т. е. при выборе только хороших созвездий, что обычно и имеет место на практике.
Следовательно, такой выбор приведет к заметному проигрышу в точности. Поэтому приближенная эквивалентность рассмотренных критериев имеет место при условии исключения сильно вытянутых корреляционных эллипсоидов, т. е. при выборе только хороших созвездий, что обычно и имеет место на практике.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ ПЕРВЫЙ/ СТРУКТУРА И ФУНКЦИОНИРОВАНИЕ СЕТЕВЫХ СРНС
- 1.1. СТРУКТУРНАЯ СХЕМА СРНС
- 1.2. ОСОБЕННОСТИ СЕТЕВЫХ СРНС
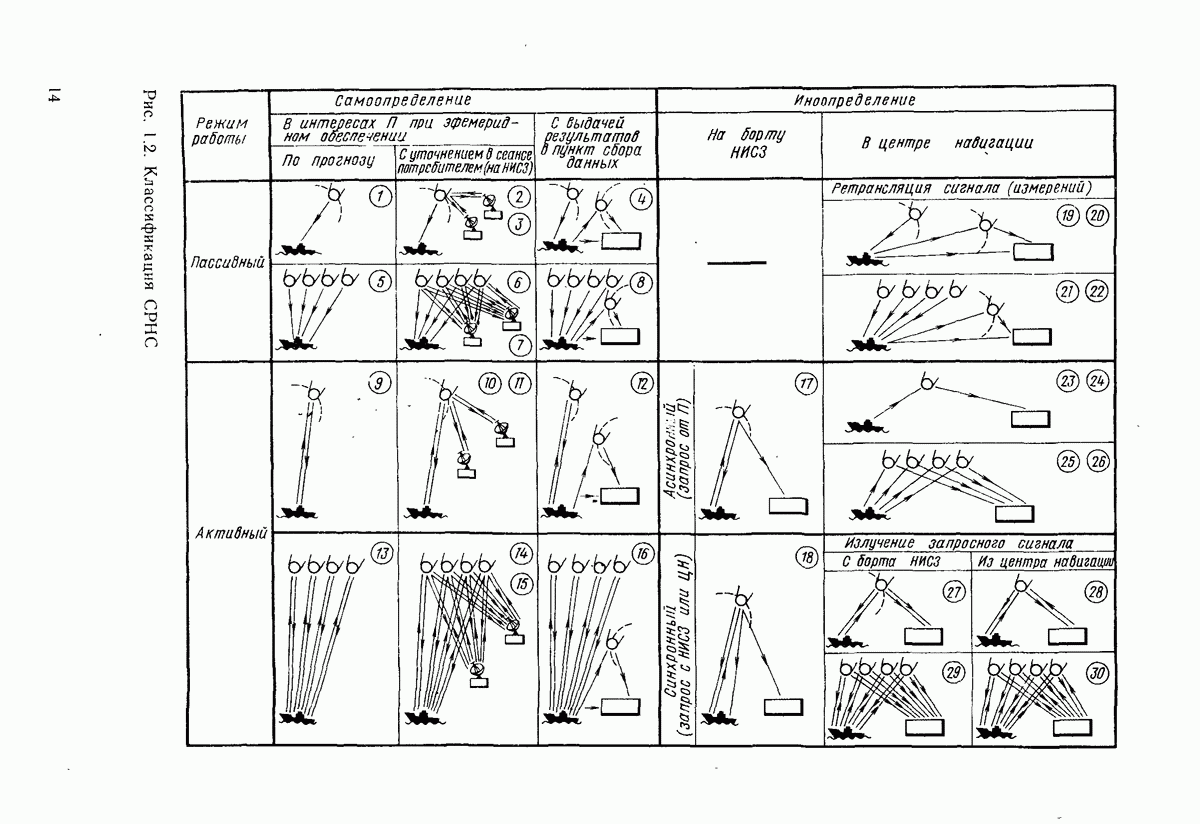
- 1.3. КЛАССИФИКАЦИЯ СРНС
- 1.4. СОГЛАСОВАНИЕ НАЧАЛ ОТСЧЕТА ПРОСТРАНСТВЕННЫХ И ВРЕМЕННОЙ КООРДИНАТ В ССРНС
- 1.5. ОБЩАЯ ХАРАКТЕРИСТИКА ЭЛЕМЕНТОВ ССРНС
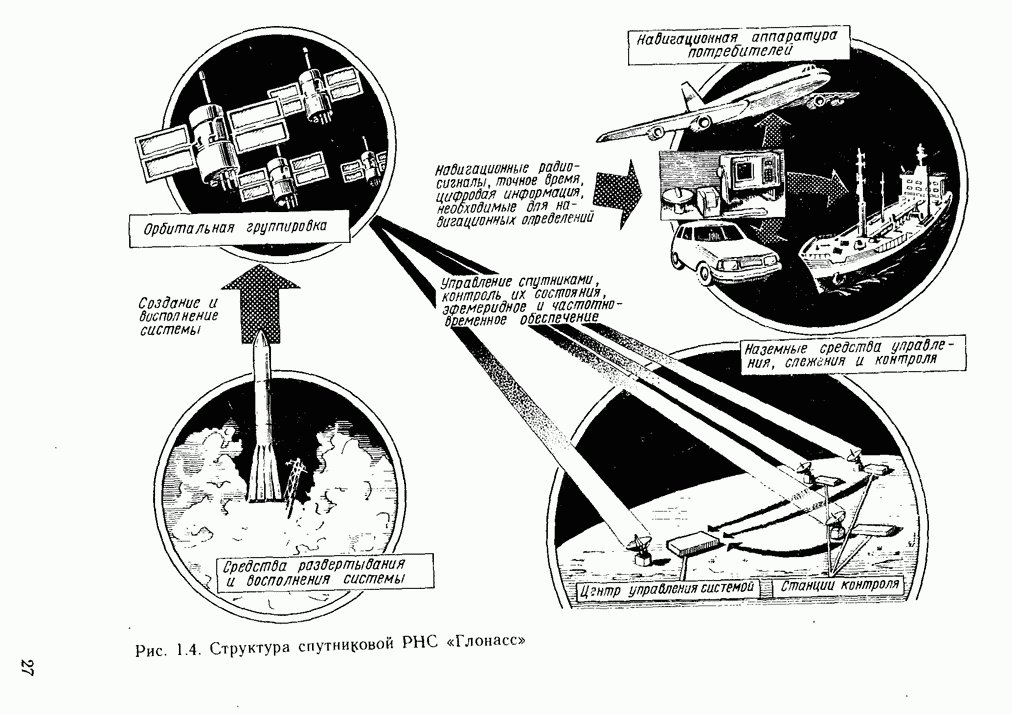
- 1.6. СОВЕТСКАЯ СЕТЕВАЯ СПУТНИКОВАЯ РНС «ГЛОНАСС»
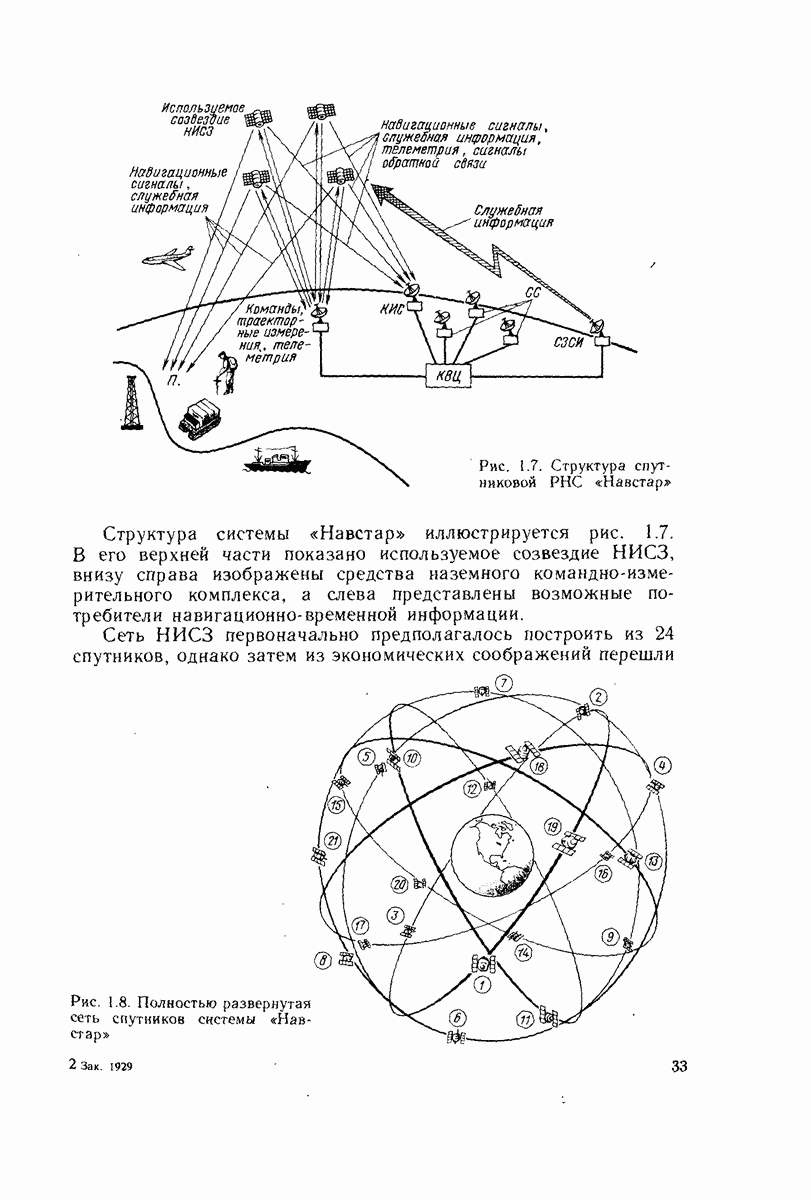
- 1.7. АМЕРИКАНСКАЯ СЕТЕВАЯ СПУТНИКОВАЯ РНС «НАВСТАР»
- 1.8. ИНФОРМАЦИОННЫЕ ЦЕНТРЫ СПУТНИКОВЫХ РНС
- ГЛАВА 2. ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА МЕТОДОВ ИЗМЕРЕНИЙ В ССРНС
- 2.2. НАВИГАЦИОННЫЕ ФУНКЦИИ
- 2.3. ГРАДИЕНТЫ ПОЛЕЙ НАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 2.4. ГРАДИЕНТНАЯ И ФУНДАМЕНТАЛЬНАЯ МАТРИЦЫ
- ГЛАВА 3. ОСНОВЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ В СРНС
- 3.1. КОНЕЧНЫЕ И ИТЕРАЦИОННЫЕ МЕТОДЫ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 3.2. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ОПРЕДЕЛЕНИЙ ПО ПОЛНОЙ ВЫБОРКЕ ИЗМЕРЕНИЙ
- 3.3. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ
- ГЛАВА 4. СИГНАЛЫ В СПУТНИКОВЫХ РНС
- 4.1. ОБЩИЕ ТРЕБОВАНИЯ К СИГНАЛАМ СРНС
- 4.2. СТАТИСТИЧЕСКАЯ МОДЕЛЬ РАДИОНАВИГАЦИОННОГО КАНАЛА СРНС
- 4.3. АНАЛИЗ ТРЕБОВАНИЙ, ПРЕДЪЯВЛЯЕМЫХ К СИГНАЛАМ СРНС
- 4.4. ТИПОВЫЕ СТРУКТУРЫ СОВМЕЩЕННЫХ СИГНАЛОВ ДЛЯ РАЗЛИЧНЫХ ВАРИАНТОВ ПАССИВНЫХ СРНС
- 4.5. ОСОБЕННОСТИ ВЫБОРА СТРУКТУРЫ СИГНАЛОВ В АКТИВНЫХ ВАРИАНТАХ СРНС
- ГЛАВА 5. ЭНЕРГЕТИКА НАВИГАЦИОННЫХ РАДИОЛИНИЙ
- 5.1. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К НАВИГАЦИОННЫМ РАДИОЛИНИЯМ
- 5.2. ОБЩАЯ ХАРАКТЕРИСТИКА ПРЯМОЙ И РЕТРАНСЛЯЦИОННОЙ РАДИОЛИНИЙ СРНС
- 5.3. УЧЕТ УСЛОВИЙ РАСПРОСТРАНЕНИЯ РАДИОВОЛН В СРНС
- 5.4. СПОСОБЫ УМЕНЬШЕНИЯ АТМОСФЕРНЫХ ПОГРЕШНОСТЕЙ ДАЛЬНОМЕРНОГО И ДОПЛЕРОВСКОГО ИЗМЕРЕНИЙ
- 5.5. ОСОБЕННОСТИ ЭНЕРГЕТИЧЕСКИХ РАСЧЕТОВ РАДИОЛИНИЙ В ЗАВИСИМОСТИ ОТ РАСПОЛОЖЕНИЯ ОБСЛУЖИВАЕМОГО СЛОЯ
- ГЛАВА 6. СПОСОБЫ РАЗДЕЛЕНИЯ СИГНАЛОВ
- 6.1. МЕТОДЫ УПЛОТНЕНИЯ И РАЗДЕЛЕНИЯ СИГНАЛОВ В СЕТЕВЫХ СРНС
- 6.2. ВЕРОЯТНОСТНОЕ РАЗДЕЛЕНИЕ СИГНАЛОВ СПУТНИКОВ ПРИ ИСПОЛЬЗОВАНИИ ШПС В ССРНС
- 6.3. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ШИРИНЫ ПОЛОСЫ ПРИНИМАЕМОГО ИЗЛУЧЕНИЯ В СЕТЕВЫХ СРНС
- 6.4. ОСОБЕННОСТИ РАЗДЕЛЕНИЯ СИГНАЛОВ В АКТИВНЫХ СРНС
- ГЛАВА 7. ПРИНЦИПЫ ПОСТРОЕНИЯ ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНОЙ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 7.1. ОБОБЩЕННАЯ СТРУКТУРНАЯ СХЕМА АП ССРНС
- 7.2. ИНФОРМАЦИОННЫЕ ПОТОКИ В АП
- 7.3. ИЗМЕРЯЕМЫЕ РАДИОНАВИГАЦИОННЫЕ ПАРАМЕТРЫ
- 7.4. ВИДЫ И МОДЕЛИ ПОМЕХ
- 7.5. ОСНОВЫ СТАТИСТИЧЕСКОГО СИНТЕЗА ИЗМЕРИТЕЛЕЙ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- ГЛАВА 8. УСТРОЙСТВА ПЕРВИЧНОЙ ОБРАБОТКИ РАДИОНАВИГАЦИОННОГО СИГНАЛА
- 8.1. НЕОБХОДИМОСТЬ ПОИСКА РАДИОНАВИГАЦИОННЫХ СИГНАЛОВ
- 8.2. СПОСОБЫ РЕШЕНИЯ ЗАДАЧИ ПОИСКА РАДИОСИГНАЛОВ НИСЗ
- 8.3. УСТРОЙСТВА ОЦЕНКИ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 8.4. ЦИФРОВАЯ РЕАЛИЗАЦИЯ УСТРОЙСТВ ПЕРВИЧНОЙ ОБРАБОТКИ
- 8.5. ОЦЕНКА ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 8.6. СПОСОБЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ АП
- ГЛАВА 9. РАЗНОВИДНОСТИ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 9.1. ОСОБЕННОСТИ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ РАЗЛИЧНЫХ ТИПОВ
- 9.2. ОДНОКАНАЛЬНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.3. МНОГОКАНАЛЬНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.4. МУЛЬТИПЛЕКСНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.5. АППАРАТУРА ПОТРЕБИТЕЛЕЙ ДЛЯ ОДНОВРЕМЕННОЙ РАБОТЫ ПО СИСТЕМАМ «ГЛОНАСС» и «НАВСТАР»
- 9.6. УНИФИКАЦИЯ АППАРАТУРНЫХ РЕШЕНИЙ
- ГЛАВА 10. КАДР НАВИГАЦИОННОГО СИГНАЛА
- 10.1. ОРГАНИЗАЦИЯ ОБРАБОТКИ ИЗМЕРЕНИЙ И ФОРМИРОВАНИЕ ЭФЕМЕРИДНОЙ ИНФОРМАЦИИ
- 10.2. МЕТОДОЛОГИЯ ВЫБОРА ЭЛЕМЕНТОВ КАДРА СИГНАЛА
- 10.3. УСЛОВИЯ РЕАЛИЗАЦИИ АЛГОРИТМОВ ПРОГНОЗИРОВАНИЯ ЭФЕМЕРИД НИСЗ
- 10.4. АЛГОРИТМЫ ПРОГНОЗИРОВАНИЯ ДВИЖЕНИЯ НИСЗ
- 10.5. СОСТАВ, ФОРМА ПРЕДСТАВЛЕНИЯ И ОБЪЕМ ИНФОРМАЦИИ, ПЕРЕДАВАЕМОЙ В КАДРЕ НАВИГАЦИОННОГО СИГНАЛА СИСТЕМЫ «НАВСТАР»
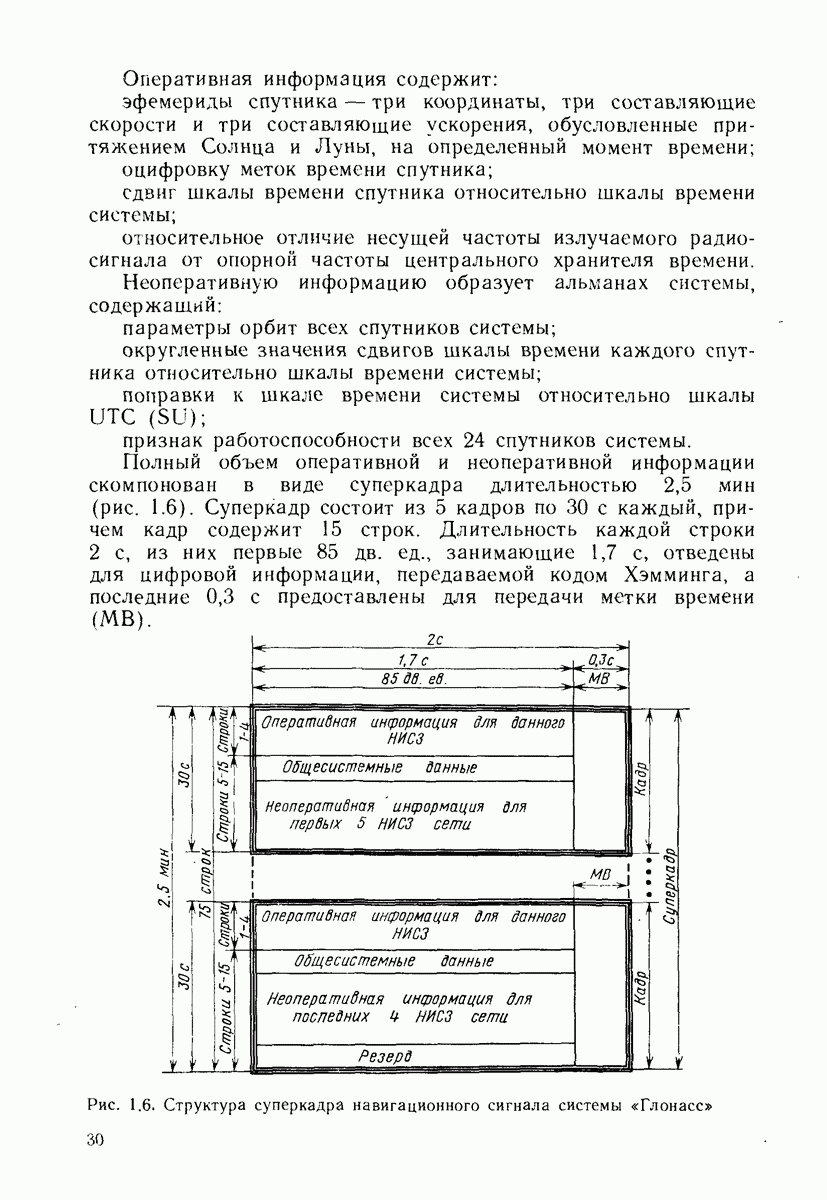
- 10.6. КАДР НАВИГАЦИОННОГО СИГНАЛА СИСТЕМЫ «ГЛОНАСС»
- ГЛАВА 11. СИНХРОНИЗАЦИЯ ВРЕМЕННЫХ ШКАЛ СИСТЕМЫ НИСЗ
- 11.1. ОБЩАЯ ХАРАКТЕРИСТИКА ХРАНИТЕЛЕЙ ВРЕМЕННЫХ ШКАЛ
- 11.2. МЕТОДЫ СВЕРКИ ВРЕМЕННЫХ ШКАЛ
- 11.3. КОРРЕКЦИЯ ВРЕМЕННЫХ ШКАЛ
- 11.4. СПОСОБЫ УЧЕТА В НАВИГАЦИОННОМ СЕАНСЕ СМЕЩЕНИЙ ВРЕМЕННЫХ ШКАЛ НИСЗ
- 11.5. СОГЛАСОВАНИЕ ШКАЛ ВРЕМЕНИ СИСТЕМ «ГЛОНАСС» И «НАВСТАР»
- 11.6. СИНХРОНИЗАЦИЯ ВРЕМЕННЫХ ШКАЛ СЕТИ НИСЗ НА ОСНОВЕ ВЗАИМНЫХ ВРЕМЕННЫХ ИЗМЕРЕНИЙ
- ГЛАВА 12. ОБЛАСТИ ИСПОЛЬЗОВАНИЯ СЕТЕВЫХ СПУТНИКОВЫХ РНС
- 12.1. ПРИМЕНЕНИЕ ССРНС — ОСНОВА КООРДИНАТНО-ВРЕМЕННОГО ОБЕСПЕЧЕНИЯ
- 12.2. ОПРЕДЕЛЕНИЕ КООРДИНАТ, ИХ ПРОИЗВОДНЫХ И НАВИГАЦИОННЫХ ЭЛЕМЕНТОВ НАЗЕМНЫХ И ПРИЗЕМНЫХ ОБЪЕКТОВ
- 12.3. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ДВИЖЕНИЯ ОКОЛОЗЕМНЫХ КА
- 12.4. ОПРЕДЕЛЕНИЕ ВЗАИМНЫХ КООРДИНАТ В ИНТЕРЕСАХ ПРЕДУПРЕЖДЕНИЯ СТОЛКНОВЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ И ГРУППОВОГО ИХ ВОЖДЕНИЯ
- 12.5. ВЫСОКОТОЧНАЯ ГЕОДЕЗИЧЕСКАЯ ПРИВЯЗКА
- 11.6. ОПРЕДЕЛЕНИЕ ОРИЕНТАЦИИ ОБЪЕКТОВ В ПРОСТРАНСТВЕ
- 12.7. СИНХРОНИЗАЦИЯ ИЗЛУЧЕНИЯ СТАНЦИИ С НАЗЕМНЫМ БАЗИРОВАНИЕМ
- 12.8. НАБЛЮДЕНИЕ ДЛЯ ОБЕСПЕЧЕНИЯ УПРАВЛЕНИЯ ДВИЖЕНИЕМ ПЕРЕМЕЩАЮЩИХСЯ ОБЪЕКТОВ
- 12.9. ЦЕЛЕУКАЗАНИЕ В СИСТЕМЕ ОБНАРУЖЕНИЯ ТЕРПЯЩИХ БЕДСТВИЕ
- РАЗДЕЛ ВТОРОЙ. ОСНОВЫ НАВИГАЦИОННОГО ИСПОЛЬЗОВАНИЯ ССРНС
- 13.1. ЗАДАЧА СИНТЕЗА АЛГОРИТМА НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 13.2. МОДЕЛЬ НАВИГАЦИОННЫХ ИЗМЕРЕНИЙ
- 13.3. МОДЕЛЬ ДИНАМИКИ ПОТРЕБИТЕЛЯ
- 13.4. ФАКТОРЫ, ВЛИЯЮЩИЕ НА ВЫБОР СПОСОБА ОБРАБОТКИ ИНФОРМАЦИИ В ССРНС
- ГЛАВА 14. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ ПО ВЫБОРКЕ ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.1. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ ПО ВЫБОРКЕ МИНИМАЛЬНОГО ОБЪЕМА ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.2. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ ПО ИЗБЫТОЧНОМУ ОБЪЕМУ ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.3. ОЦЕНКА СХОДИМОСТИ АЛГОРИТМОВ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ
- ГЛАВА 15. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ ПО ВЫБОРКЕ ИЗМЕРЕНИИ НАРАСТАЮЩЕГО ОБЪЕМА
- 15.1. РЕКУРРЕНТНЫЙ АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ МЕТОДОМ КАЛМАНА И ЕГО МОДИФИКАЦИИ ПРИ РАЗЛИЧНЫХ СОСТАВАХ ИЗМЕРЕНИЙ
- 15.2. СПОСОБЫ УСТРАНЕНИЯ РАСХОДИМОСТИ ФИЛЬТРОВ КАЛМАНА
- 15.3. РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ ГАУССОВСКОГО ФИЛЬТРА 2-ГО ПОРЯДКА
- 15.4. СРАВНЕНИЕ РЕКУРРЕНТНЫХ АЛГОРИТМОВ ПО РАЗМЕРАМ ОБЛАСТИ СХОДИМОСТИ
- ГЛАВА 16. СПОСОБЫ ОЦЕНКИ ТОЧНОСТИ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ
- 16.1. ПОКАЗАТЕЛИ ТОЧНОСТИ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 16.2. КОРРЕЛЯЦИОННАЯ МАТРИЦА ОШИБОК ОПРЕДЕЛЯЕМЫХ ПАРАМЕТРОВ
- 16.3. ИСТОЧНИКИ ОШИБОК НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 16.4. ОТОБРАЖЕНИЕ ТОЧНОСТНЫХ ХАРАКТЕРИСТИК И ИНТЕГРАЛЬНАЯ ОЦЕНКА ТОЧНОСТИ СРНС
- ГЛАВА 17. ВЫСОКОТОЧНОЕ СЛИЧЕНИЕ ШКАЛ ВРЕМЕНИ УДАЛЕННЫХ ПУНКТОВ ПО СИГНАЛАМ НИСЗ
- 17.1. МЕТОДЫ СИНХРОНИЗАЦИИ ШВ УДАЛЕННЫХ ПУНКТОВ
- 17.2. ОЦЕНКА ТОЧНОСТИ СВЕРКИ ШВ УДАЛЕННЫХ ПУНКТОВ ПО ВЫБОРКЕ ОДНОВРЕМЕННЫХ ПСЕВДОДАЛЬНОМЕРНЫХ ИЗМЕРЕНИЙ
- 17.3. ПОТЕНЦИАЛЬНАЯ ТОЧНОСТЬ СВЕРКИ ШВ ПУНКТА С ИЗВЕСТНЫМИ КООРДИНАТАМИ ПО ДАННЫМ ПСЕВДОДАЛЬНОМЕРНЫХ И РАДИАЛЬНЫХ ПСЕВДОСКОРОСТНЫХ ИЗМЕРЕНИЙ
- ГЛАВА 18. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ КООРДИНАТ ПРИ ОДНОМОМЕНТНЫХ ИЗМЕРЕНИЯХ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ НИСЗ
- 18.2. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПОВЕРХНОСТНЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ДВУХ НИСЗ
- 18.3. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПОВЕРХНОСТНЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ТРЕХ НИСЗ
- 18.4. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПРОСТРАНСТВЕННЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ЧЕТЫРЕХ НИСЗ
- 18.5. ТОЧНОСТНЫЕ СВОЙСТВА ДОПЛЕРОВСКИХ МЕТОДОВ В СЕТЕВЫХ СРНС В СРАВНЕНИИ С ДАЛЬНОМЕРНЫМИ
- ГЛАВА 19. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННЫХ КООРДИНАТ И ВЕКТОРА СКОРОСТИ ПО СЕТИ НИСЗ
- 19.2. РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ ГЕОМЕТРИЧЕСКИХ ФАКТОРОВ
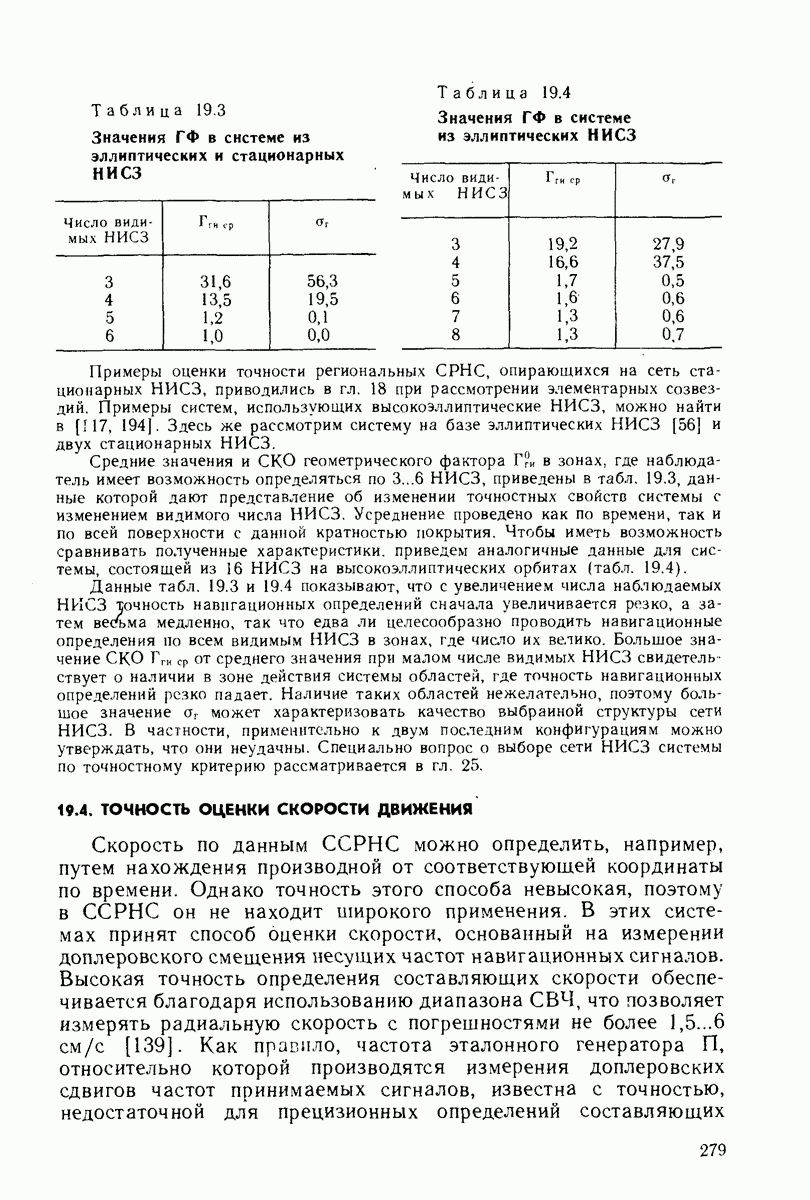
- 19.3. ТОЧНОСТЬ ОЦЕНКИ КООРДИНАТ И ВРЕМЕНИ
- 19.4. ТОЧНОСТЬ ОЦЕНКИ СКОРОСТИ ДВИЖЕНИЯ
- 19.5. ОЦЕНКА ТОЧНОСТИ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ КА
- ГЛАВА 20. ДИФФЕРЕНЦИАЛЬНЫЙ РЕЖИМ ССРНС
- 20.2. СТРУКТУРА ДИФФЕРЕНЦИАЛЬНОЙ ПОДСИСТЕМЫ
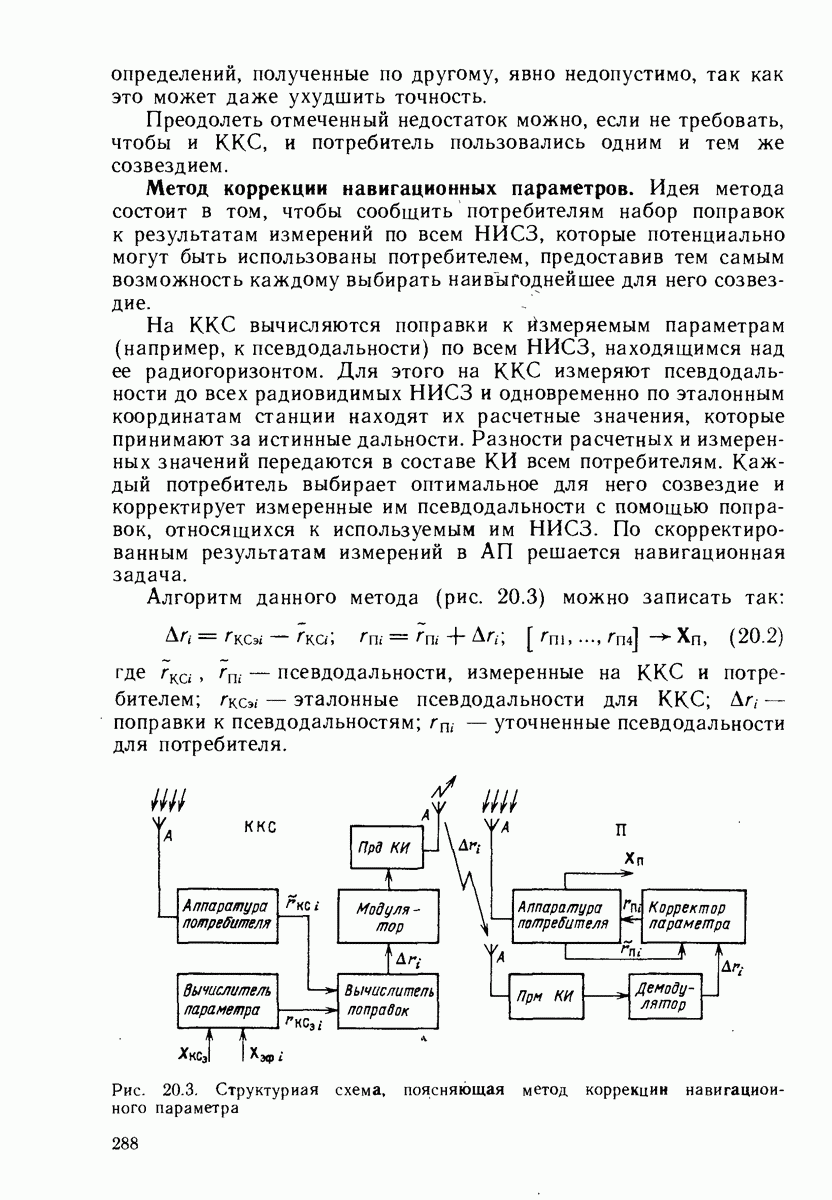
- 20.3. МЕТОДЫ ДИФФЕРЕНЦИАЛЬНЫХ ОПРЕДЕЛЕНИЙ
- 20.4. КОРРЕКТИРУЮЩАЯ ИНФОРМАЦИЯ
- 20.5. КАНАЛЫ ПЕРЕДАЧИ КОРРЕКТИРУЮЩЕЙ ИНФОРМАЦИИ
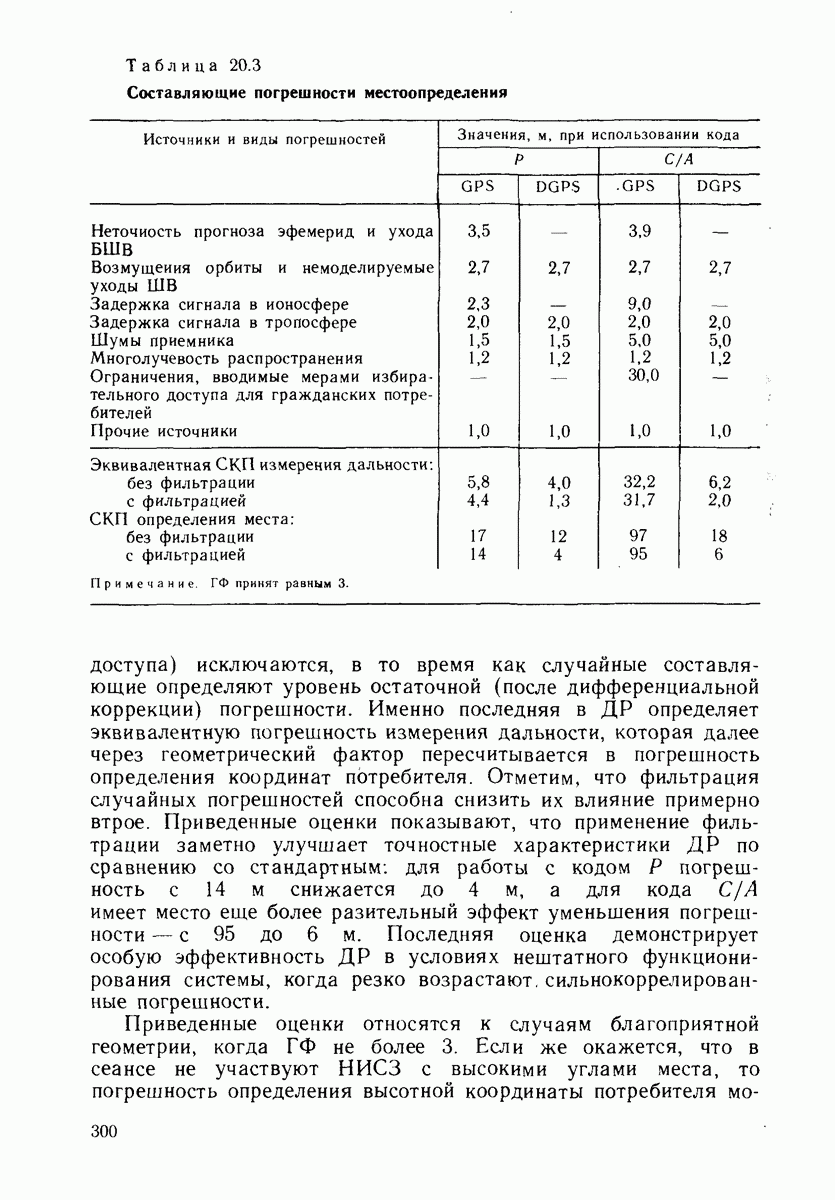
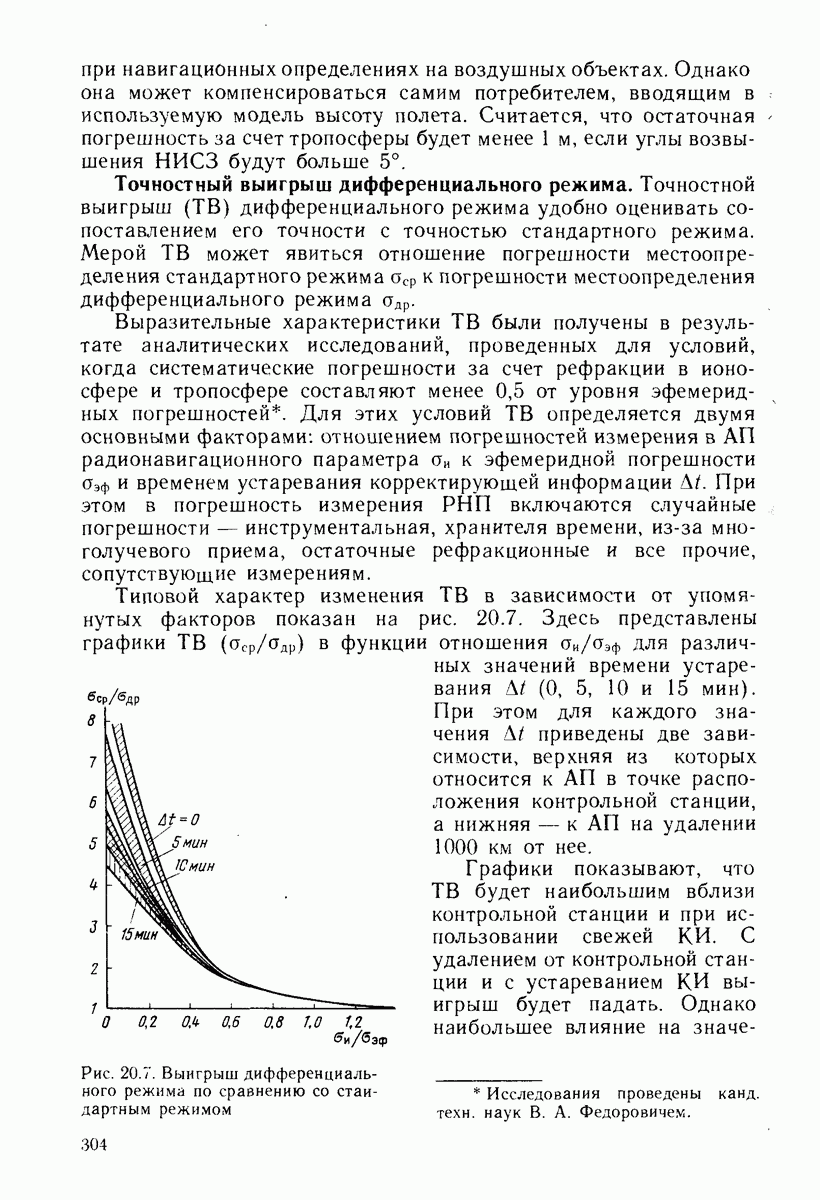
- 20.6. ТОЧНОСТНЫЕ ХАРАКТЕРИСТИКИ ДМ
- 20.7. ИЗМЕРЕНИЯ РНП ПО ФАЗЕ НЕСУЩИХ КОЛЕБАНИЙ
- 20.8. РЕЗУЛЬТАТЫ ИСПЫТАНИЙ. РЕАЛИЗАЦИЯ ДПС
- ГЛАВА 21. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ В АКТИВНОМ И ОТНОСИТЕЛЬНОМ РЕЖИМАХ
- 21.1. ТОЧНОСТНЫЕ ХАРАКТЕРИСТИКИ АКТИВНЫХ СРНС
- 21.2. ТОЧНОСТНЫЕ СВОЙСТВА СЕТЕВЫХ СРНС В ОТНОСИТЕЛЬНОМ РЕЖИМЕ
- ГЛАВА 22. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ БОРТОВОЙ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 22.1. АВТОМАТИЗАЦИЯ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ И ШТУРМАНСКИХ РАСЧЕТОВ
- 22.2. МЕТОДИЧЕСКИЕ ОСНОВЫ МАТЕМАТИЧЕСКОГО ОБЕСПЕЧЕНИЯ
- 22.3. ОСНОВНЫЕ ЗАДАЧИ ВТО
- 22.4. УПРАВЛЯЮЩИЙ АЛГОРИТМ
- 22.5. ВРЕМЕННАЯ ДИАГРАММА АЛГОРИТМА
- 22.6. ПРИНЦИПЫ ПРОЕКТИРОВАНИЯ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
- РАЗДЕЛ ТРЕТИЙ. КОМПЛЕКСНОЕ ПРОЕКТИРОВАНИЕ ССРНС
- 23.1. ОСНОВНЫЕ ЗАДАЧИ, РЕШАЕМЫЕ ПРИ КОМПЛЕКСНОМ ПРОЕКТИРОВАНИИ
- 23.2. ЭТАПЫ СОЗДАНИЯ ССРНС
- 23.3. ОСОБЕННОСТИ ПРОЕКТОВ СРНС РАЗЛИЧНОГО НАЗНАЧЕНИЯ
- ГЛАВА 24. СИНТЕЗ СТРУКТУРЫ СЕТИ НИСЗ ИЗ УСЛОВИИ ОБЕСПЕЧЕНИЯ ЗАДАННОЙ КРАТНОСТИ ПОКРЫТИЯ
- 24.2. ЗОНА РАДИОВИДИМОСТИ, ПОЛОСА ПОКРЫТИЯ И ОБЛАСТЬ ПЕРЕКРЫТИЯ
- 24.3. ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ СЕТИ НИСЗ, ОБЕСПЕЧИВАЮЩЕЙ ЗАДАННУЮ МИНИМАЛЬНУЮ КРАТНОСТЬ ПОКРЫТИЯ
- 24.4. НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ СЕТИ НИСЗ
- 24.5. СВОЙСТВА ЭКСТРЕМАЛЬНОЙ СЕТИ НИСЗ, ОБЕСПЕЧИВАЮЩЕЙ ЗАДАННУЮ МИНИМАЛЬНУЮ КРАТНОСТЬ ПОКРЫТИЯ
- 24.6. УСЛОВИЕ СТАБИЛЬНОСТИ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ СЕТИ НИСЗ
- ГЛАВА 25. СИНТЕЗ СТРУКТУРЫ СЕТИ НИСЗ ПО КРИТЕРИЮ ТОЧНОСТИ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 25.2. ВЫБОР ОПТИМАЛЬНОГО ПО КРИТЕРИЮ ТОЧНОСТИ СОЗВЕЗДИЯ НИСЗ
- 25.3. ПРИБЛИЖЕННЫМ УЧЕТ ПАРАЛЛАКСА МИНИМАЛЬНОГО СОЗВЕЗДИЯ
- 25.4. КАЧЕСТВЕННЫЙ АНАЛИЗ ЗОН ПОНИЖЕННОЙ ТОЧНОСТИ
- 25.5. УТОЧНЕНИЕ СТРУКТУРЫ СЕТИ НИСЗ ПО МИНИМАКСНОМУ КРИТЕРИЮ ТОЧНОСТИ
- 25.6. СРАВНЕНИЕ ССРНС «ГЛОНАСС» И «НАВСТАР»
- ГЛАВА 26. ОСНОВЫ КОМПЛЕКСНОГО ИСПОЛЬЗОВАНИЯ СРНС С ДРУГИМИ РАДИОНАВИГАЦИОННЫМИ И АВТОНОМНЫМИ НАВИГАЦИОННЫМИ СРЕДСТВАМИ
- 26.1. ОБЩИЕ ПРЕДПОСЫЛКИ И ВОЗМОЖНОСТИ СОВМЕСТНОГО ИСПОЛЬЗОВАНИЯ СПУТНИКОВЫХ РНС И ДРУГИХ НАВИГАЦИОННЫХ СРЕДСТВ
- 26.2. КОМБИНИРОВАННАЯ РАЗНОСТНО-ДАЛЬНОМЕРНАЯ РНС, СОСТОЯЩАЯ ИЗ НАЗЕМНЫХ СТАНЦИЙ И СТАЦИОНАРНОГО НИСЗ
- 26.3. КОМПЛЕКСНОЕ ИСПОЛЬЗОВАНИЕ НИЗКООРБИТАЛЬНОЙ СРНС И ФАЗОВОЙ СДВ РНС
- 26.4. КОМПЛЕКСИРОВАНИЕ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ НА УРОВНЕ ПЕРВИЧНОЙ ОБРАБОТКИ ИНФОРМАЦИИ
- ГЛАВА 27. КРИТЕРИИ ОЦЕНКИ ЭФФЕКТИВНОСТИ НАВИГАЦИОННОГО ИСПОЛЬЗОВАНИЯ СРНС
- 27.2. ОСОБЕННОСТИ ИССЛЕДОВАНИЯ ЭФФЕКТИВНОСТИ СПУТНИКОВЫХ РНС
- 27.3. ОБЩИЕ И ЧАСТНЫЕ КРИТЕРИИ ЭФФЕКТИВНОСТИ СРНС