| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
19.3. ТОЧНОСТЬ ОЦЕНКИ КООРДИНАТ И ВРЕМЕНИ
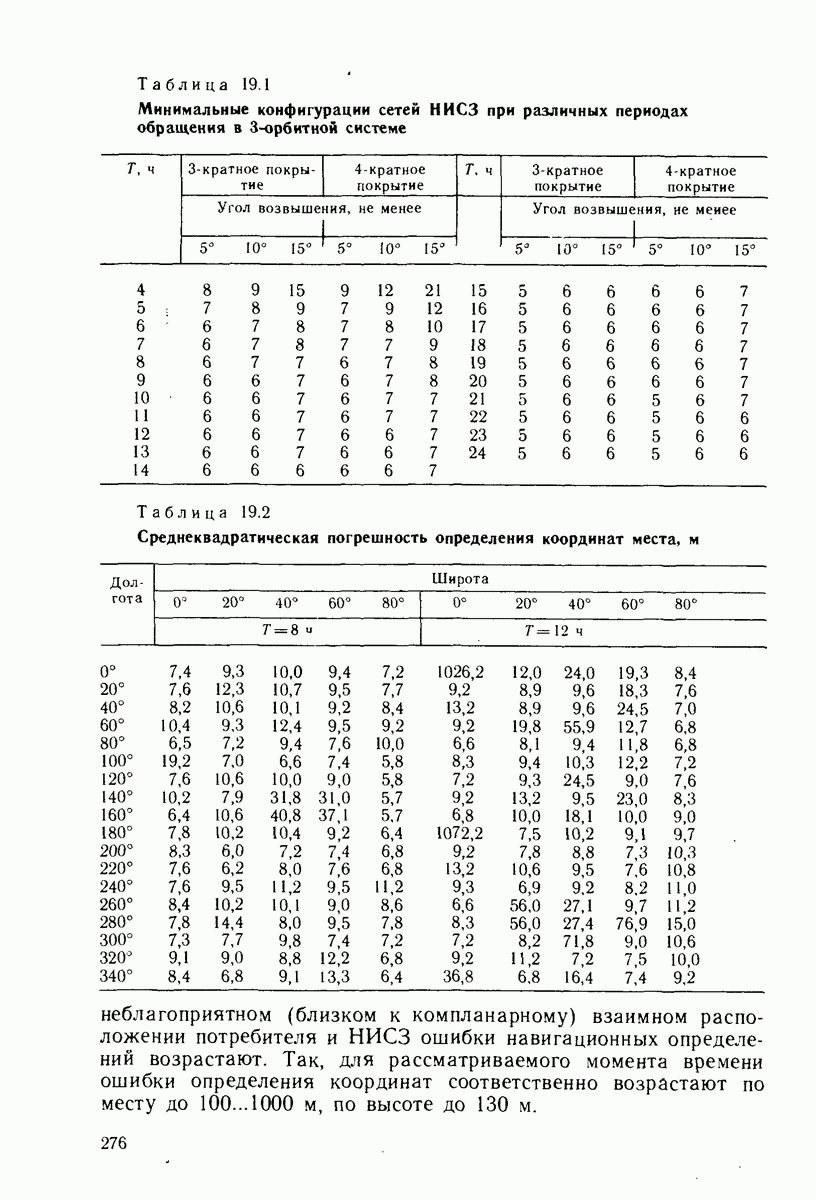
В качестве первого примера оценим точностные свойства двух из минимальных конфигураций ССРНС, т. е. таких, которые обеспечивают заданную кратность покрытия любой точки земного шара при минимальном числе равномерно разнесенных НИСЗ, обращающихся на заданном числе орбит. Математическое формулирование задачи отыскания состава минимальных систем не представляет сложностей и без ущерба для дальнейшего изложения может быть опущено. Результаты расчетов минимально необходимого числа НИСЗ на каждой из трех орбит, отвечающего сформулированным требованиям, приведены в табл. 19.1.
В табл. 19.2 для примера даны значения СКО определения координат места П, рассчитанные по (16.2), для глобальных СРНС с конфигурациями, приведенными в табл. 19.1 (при  -кратном покрытии), угол возвышения не менее 10°. Расчет точностей производился с использованием данных о погрешностях измерений и положений НИСЗ для системы «Навстар» (см. гл. 16).
-кратном покрытии), угол возвышения не менее 10°. Расчет точностей производился с использованием данных о погрешностях измерений и положений НИСЗ для системы «Навстар» (см. гл. 16).
Полученные результаты позволяют установить порядок значений возможных точностных характеристик ССРНС с минимальным числом НИСЗ. При обработке измерений от пяти и более НИСЗ в системе с  обеспечивается СКО определения места
обеспечивается СКО определения места  высоты
высоты  в системе на
в системе на  соответственно
соответственно  При обработке наблюдений четверок НИСЗ и
При обработке наблюдений четверок НИСЗ и
Таблица 19.1 (см. скан) Минимальные конфигурации сетей НИСЗ при различных периодах обращения в  -орбитной системе
-орбитной системе
Таблица 19.2 (см. скан) Среднеквадратическая погрешность определения координат места, 
неблагоприятном (близком к компланарному) взаимном расположении потребителя и НИСЗ ошибки навигационных определений возрастают. Так, для рассматриваемого момента времени ошибки определения координат соответственно возрастают по месту до  по высоте до
по высоте до 

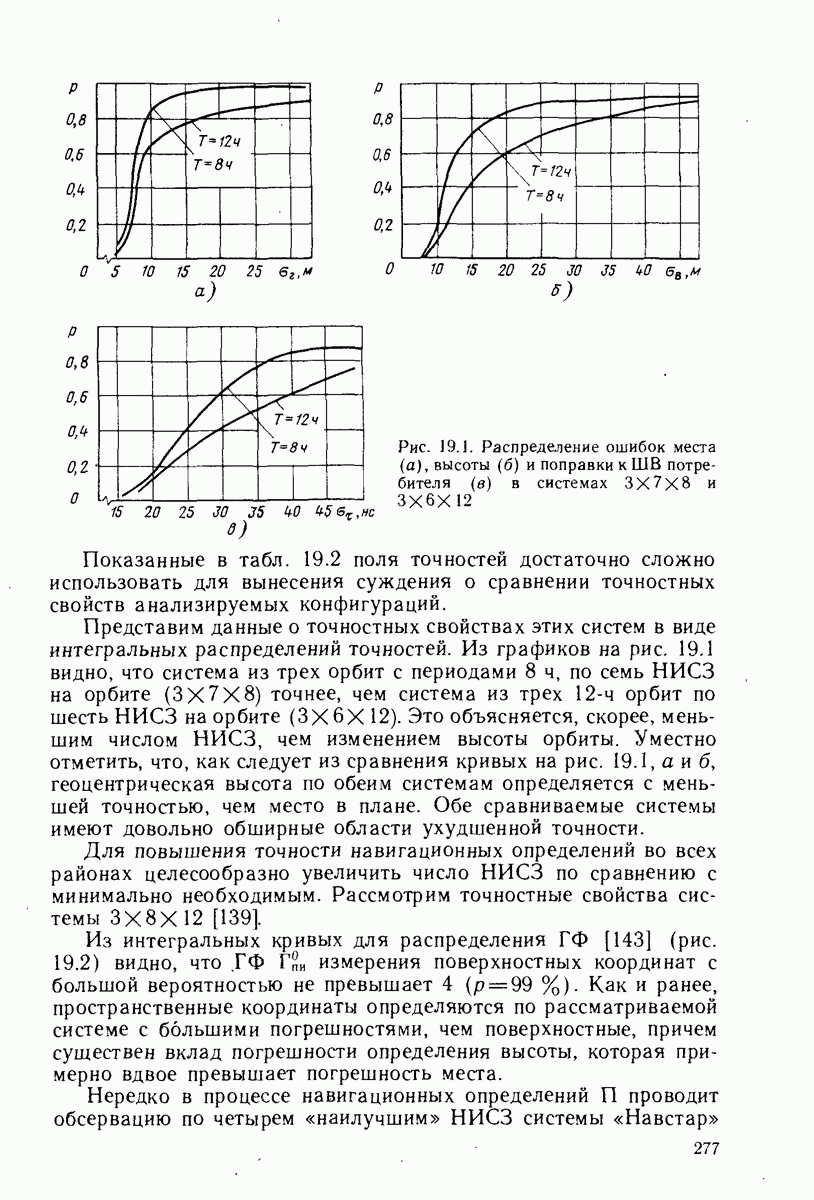
Рис. 19.1. Распределение ошибок места  высоты (б) и поправки к ШВ потребителя
высоты (б) и поправки к ШВ потребителя  в системах
в системах  и
и 
Показанные в табл. 19.2 поля точностей достаточно сложно использовать для вынесения суждения о сравнении точностных свойств анализируемых конфигураций.
Представим данные о точностных свойствах этих систем в виде интегральных распределений точностей. Из графиков на рис. 19.1 видно, что система из трех орбит с периодами  по семь НИСЗ на орбите
по семь НИСЗ на орбите  точнее, чем система из трех
точнее, чем система из трех  орбит по шесть НИСЗ на орбите
орбит по шесть НИСЗ на орбите  Это объясняется, скорее, меньшим числом НИСЗ, чем изменением высоты орбиты. Уместно отметить, что, как следует из сравнения кривых на рис. 19.1, а и б, геоцентрическая высота по обеим системам определяется с меньшей точностью, чем место в плане. Обе сравниваемые системы имеют довольно обширные области ухудшенной точности.
Это объясняется, скорее, меньшим числом НИСЗ, чем изменением высоты орбиты. Уместно отметить, что, как следует из сравнения кривых на рис. 19.1, а и б, геоцентрическая высота по обеим системам определяется с меньшей точностью, чем место в плане. Обе сравниваемые системы имеют довольно обширные области ухудшенной точности.
Для повышения точности навигационных определений во всех районах целесообразно увеличить число НИСЗ по сравнению с минимально необходимым. Рассмотрим точностные свойства системы  [139].
[139].
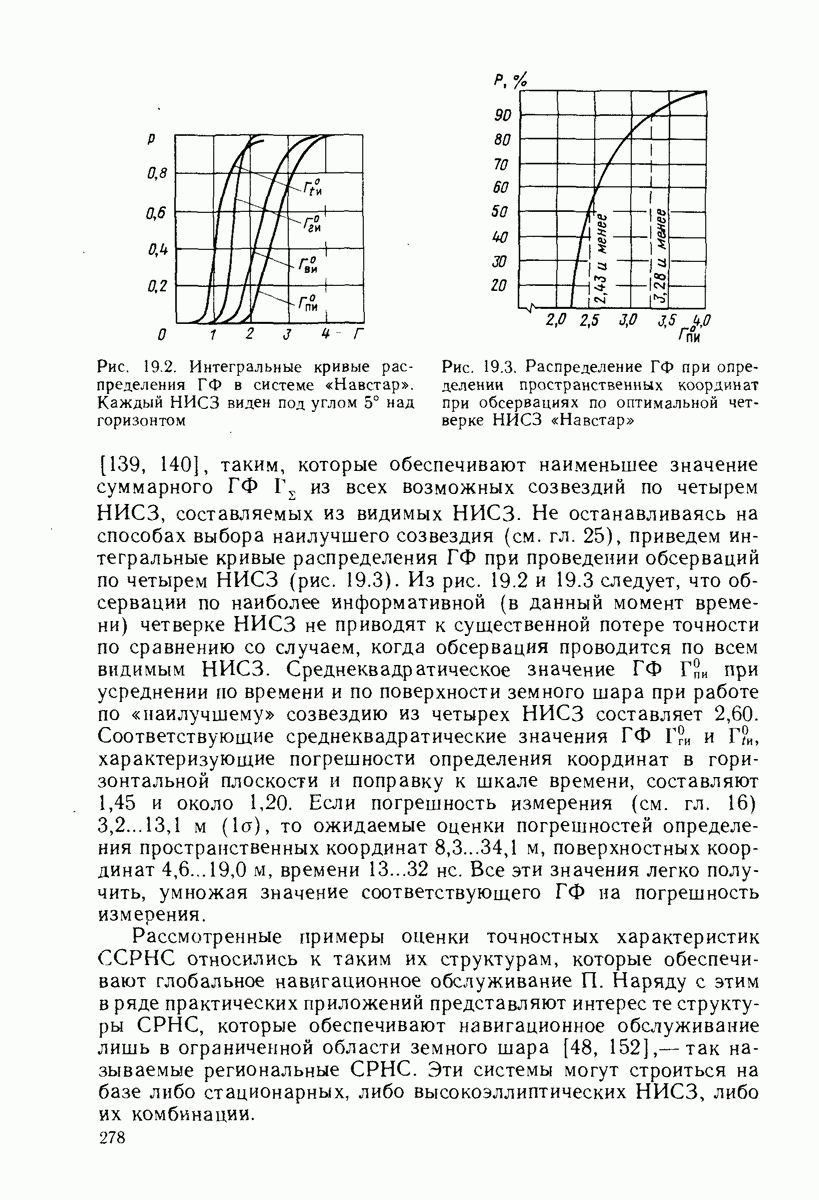
Из интегральных кривых для распределения ГФ [143] (рис. 19.2) видно, что  измерения поверхностных координат с большой вероятностью не превышает
измерения поверхностных координат с большой вероятностью не превышает  Как и ранее, пространственные координаты определяются по рассматриваемой системе с большими погрешностями, чем поверхностные, причем существен вклад погрешности определения высоты, которая примерно вдвое превышает погрешность места.
Как и ранее, пространственные координаты определяются по рассматриваемой системе с большими погрешностями, чем поверхностные, причем существен вклад погрешности определения высоты, которая примерно вдвое превышает погрешность места.
Нередко в процессе навигационных определений П проводит обсервацию по четырем «наилучшим» НИСЗ системы «Навстар»

Рис. 19.2. Интегральные кривые распределения ГФ в системе «Навстар». Каждый НИСЗ виден под углом 5° над горизонтом

Рис. 19.3. Распределение ГФ при определении пространственных координат при обсервациях по оптимальной четверке НИСЗ «Навстар»
[139, 140], таким, которые обеспечивают наименьшее значение суммарного  из всех возможных созвездий по четырем НИСЗ, составляемых из видимых НИСЗ. Не останавливаясь на способах выбора наилучшего созвездия (см. гл. 25), приведем интегральные кривые распределения ГФ при проведении обсерваций по четырем НИСЗ (рис. 19.3). Из рис. 19.2 и 19.3 следует, что обсервации по наиболее информативной (в данный момент времени) четверке НИСЗ не приводят к существенной потере точности по сравнению со случаем, когда обсервация проводится по всем видимым НИСЗ. Среднеквадрэтическое значение
из всех возможных созвездий по четырем НИСЗ, составляемых из видимых НИСЗ. Не останавливаясь на способах выбора наилучшего созвездия (см. гл. 25), приведем интегральные кривые распределения ГФ при проведении обсерваций по четырем НИСЗ (рис. 19.3). Из рис. 19.2 и 19.3 следует, что обсервации по наиболее информативной (в данный момент времени) четверке НИСЗ не приводят к существенной потере точности по сравнению со случаем, когда обсервация проводится по всем видимым НИСЗ. Среднеквадрэтическое значение  при усреднении по времени и по поверхности земного шара при работе по «наилучшему» созвездию из четырех НИСЗ составляет 2,60. Соответствующие среднеквадратические значения
при усреднении по времени и по поверхности земного шара при работе по «наилучшему» созвездию из четырех НИСЗ составляет 2,60. Соответствующие среднеквадратические значения  характеризующие погрешности определения координат в горизонтальной плоскости и поправку к шкале времени, составляют 1,45 и около 1,20. Если погрешность измерения (см. гл. 16)
характеризующие погрешности определения координат в горизонтальной плоскости и поправку к шкале времени, составляют 1,45 и около 1,20. Если погрешность измерения (см. гл. 16)  то ожидаемые оценки погрешностей определения пространственных координат
то ожидаемые оценки погрешностей определения пространственных координат  поверхностных координат
поверхностных координат  времени
времени  . Все эти значения легко получить, умножая значение соответствующего ГФ на погрешность измерения.
. Все эти значения легко получить, умножая значение соответствующего ГФ на погрешность измерения.
Рассмотренные примеры оценки точностных характеристик ССРНС относились к таким их структурам, которые обеспечивают глобальное навигационное обслуживание П. Наряду с этим в ряде практических приложений представляют интерес те структуры СРНС, которые обеспечивают навигационное обслуживание лишь в ограниченной области земного шара [48, 152], - так называемые региональные СРНС. Эти системы могут строиться на базе либо стационарных, либо высокоэллиптических НИСЗ, либо их комбинации.
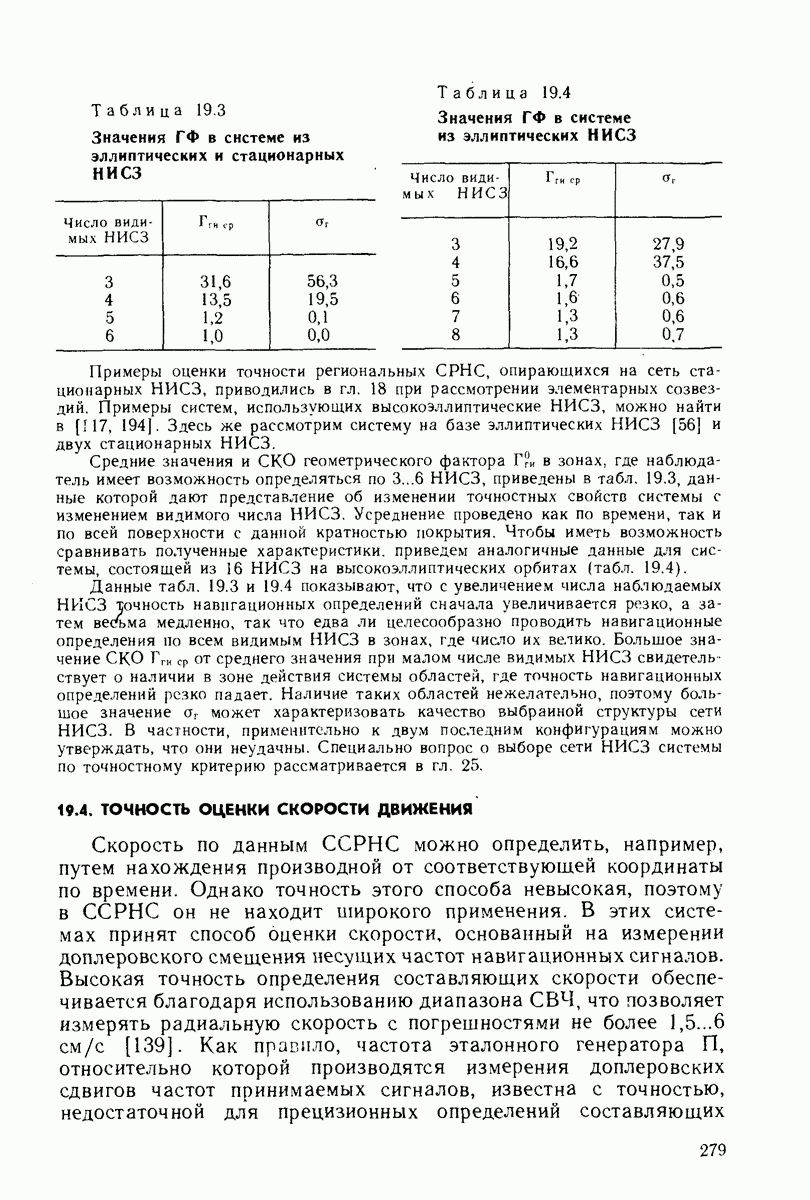
Таблица 19.3 (см. скан) Значения ГФ в системе из эллиптических и стационарных НИСЗ
Таблица 19.4 (см. скан) Значения ГФ в системе из эллиптических НИСЗ
Примеры оценки точности региональных СРНС, опирающихся на сеть стационарных НИСЗ, приводились в гл. 18 при рассмотрении элементарных созвездий. Примеры систем, использующих высокоэллиптические НИСЗ, можно найти в [117, 194]. Здесь же рассмотрим систему на базе эллиптических НИСЗ [56] и двух стационарных НИСЗ.
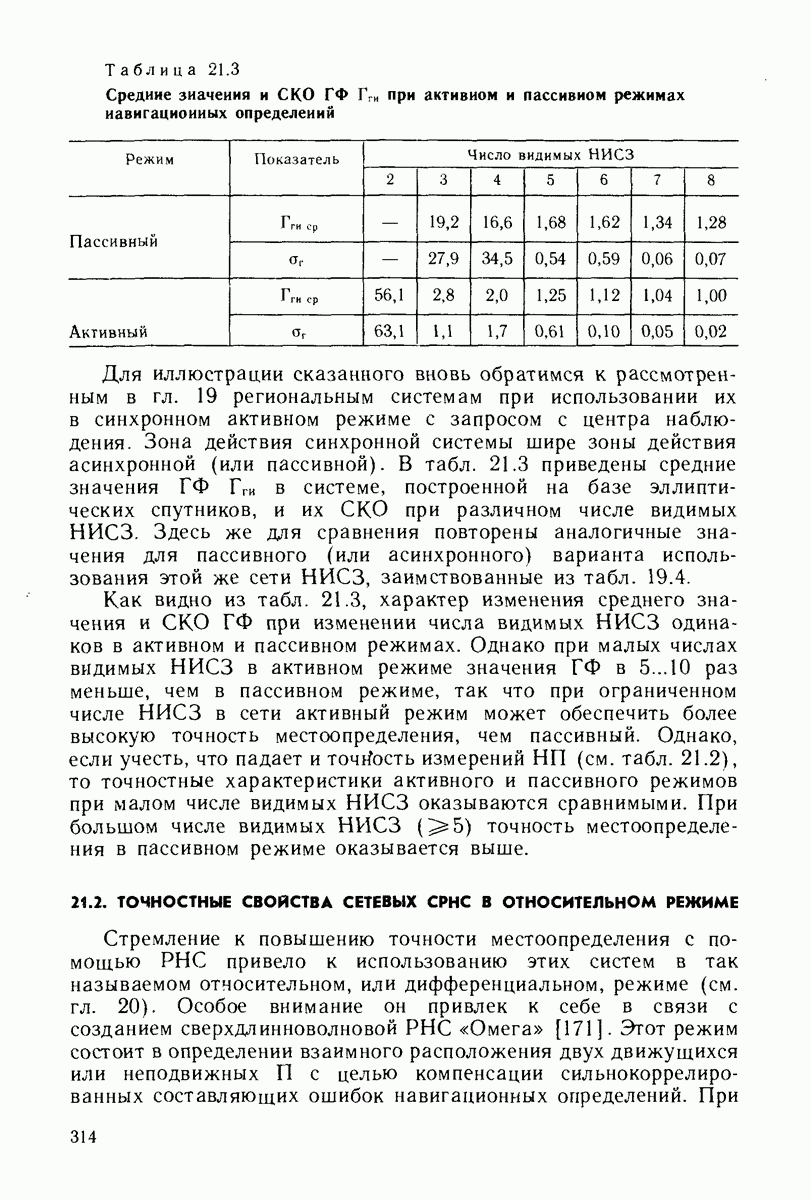
Средние значения и СКО геометрического фактора  в зонах, где наблюдатель имеет возможность определяться по
в зонах, где наблюдатель имеет возможность определяться по  приведены в табл. 19.3, данные которой дают представление об изменении точностных свойств системы с изменением видимого числа НИСЗ. Усреднение проведено как по времени, так и по всей поверхности с данной кратностью покрытия. Чтобы иметь возможность сравнивать полученные характеристики, приведем аналогичные данные для системы, состоящей из
приведены в табл. 19.3, данные которой дают представление об изменении точностных свойств системы с изменением видимого числа НИСЗ. Усреднение проведено как по времени, так и по всей поверхности с данной кратностью покрытия. Чтобы иметь возможность сравнивать полученные характеристики, приведем аналогичные данные для системы, состоящей из  на высокоэллиптических орбитах (табл. 19.4).
на высокоэллиптических орбитах (табл. 19.4).
Данные табл. 19.3 и 19.4 показывают, что с увеличением числа наблюдаемых НИСЗ точность навнгационных определений сначала увеличивается резко, а затем  медленно, так что едва ли целесообразно проводить навигационные определения по всем видимым НИСЗ в зонах, где число их велико. Большое значение
медленно, так что едва ли целесообразно проводить навигационные определения по всем видимым НИСЗ в зонах, где число их велико. Большое значение  от среднего значения при малом числе видимых НИСЗ свидетельствует о наличии в зоне действия системы областей, где точность навигационных определений резко падает. Наличие таких областей нежелательно, поэтому большое значение
от среднего значения при малом числе видимых НИСЗ свидетельствует о наличии в зоне действия системы областей, где точность навигационных определений резко падает. Наличие таких областей нежелательно, поэтому большое значение  может характеризовать качество выбранной структуры сети НИСЗ. В частности, применительно к двум последним конфигурациям можно утверждать, что они неудачны. Специально вопрос о выборе сети НИСЗ системы по точностному критерию рассматривается в гл. 25.
может характеризовать качество выбранной структуры сети НИСЗ. В частности, применительно к двум последним конфигурациям можно утверждать, что они неудачны. Специально вопрос о выборе сети НИСЗ системы по точностному критерию рассматривается в гл. 25.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ ПЕРВЫЙ/ СТРУКТУРА И ФУНКЦИОНИРОВАНИЕ СЕТЕВЫХ СРНС
- 1.1. СТРУКТУРНАЯ СХЕМА СРНС
- 1.2. ОСОБЕННОСТИ СЕТЕВЫХ СРНС
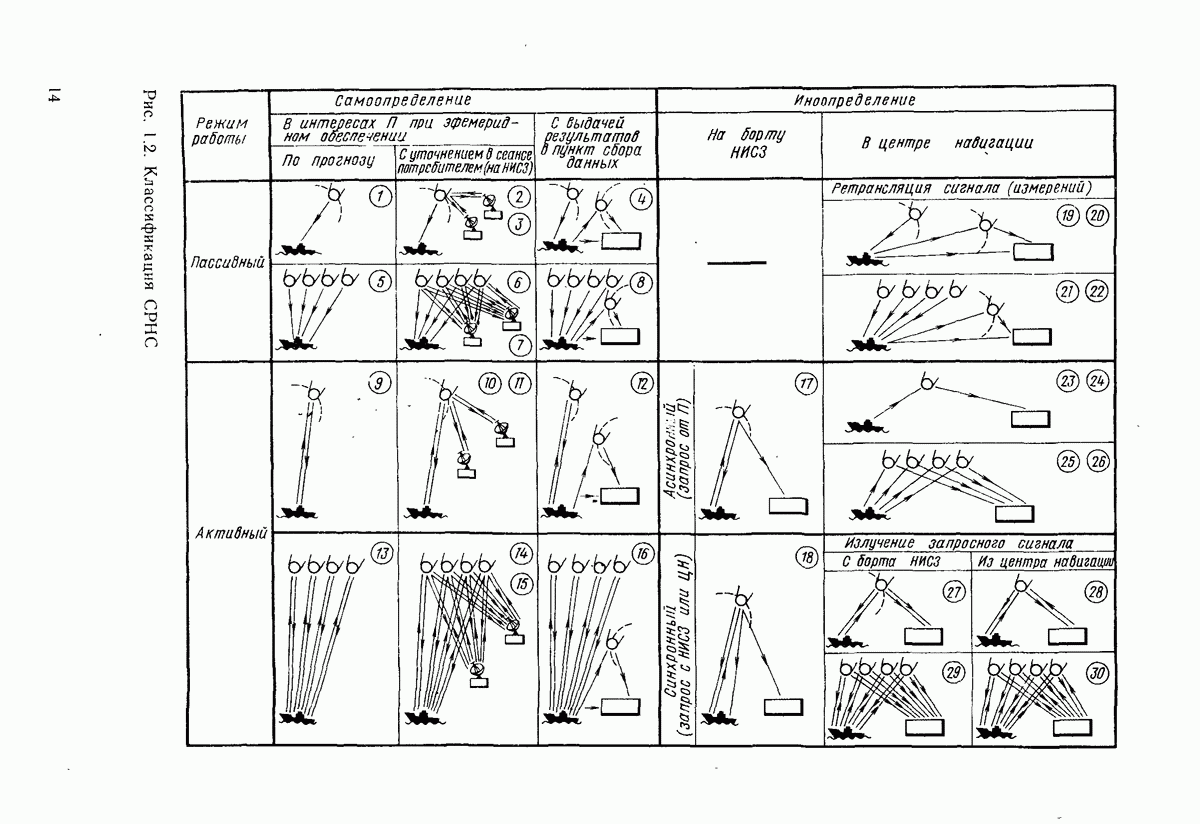
- 1.3. КЛАССИФИКАЦИЯ СРНС
- 1.4. СОГЛАСОВАНИЕ НАЧАЛ ОТСЧЕТА ПРОСТРАНСТВЕННЫХ И ВРЕМЕННОЙ КООРДИНАТ В ССРНС
- 1.5. ОБЩАЯ ХАРАКТЕРИСТИКА ЭЛЕМЕНТОВ ССРНС
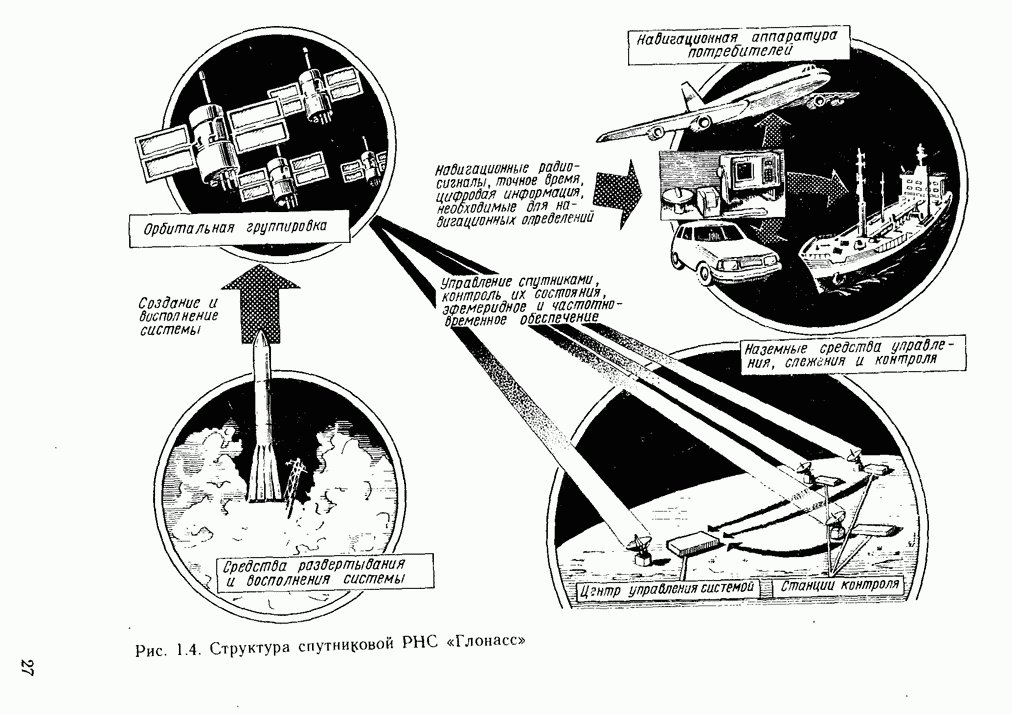
- 1.6. СОВЕТСКАЯ СЕТЕВАЯ СПУТНИКОВАЯ РНС «ГЛОНАСС»
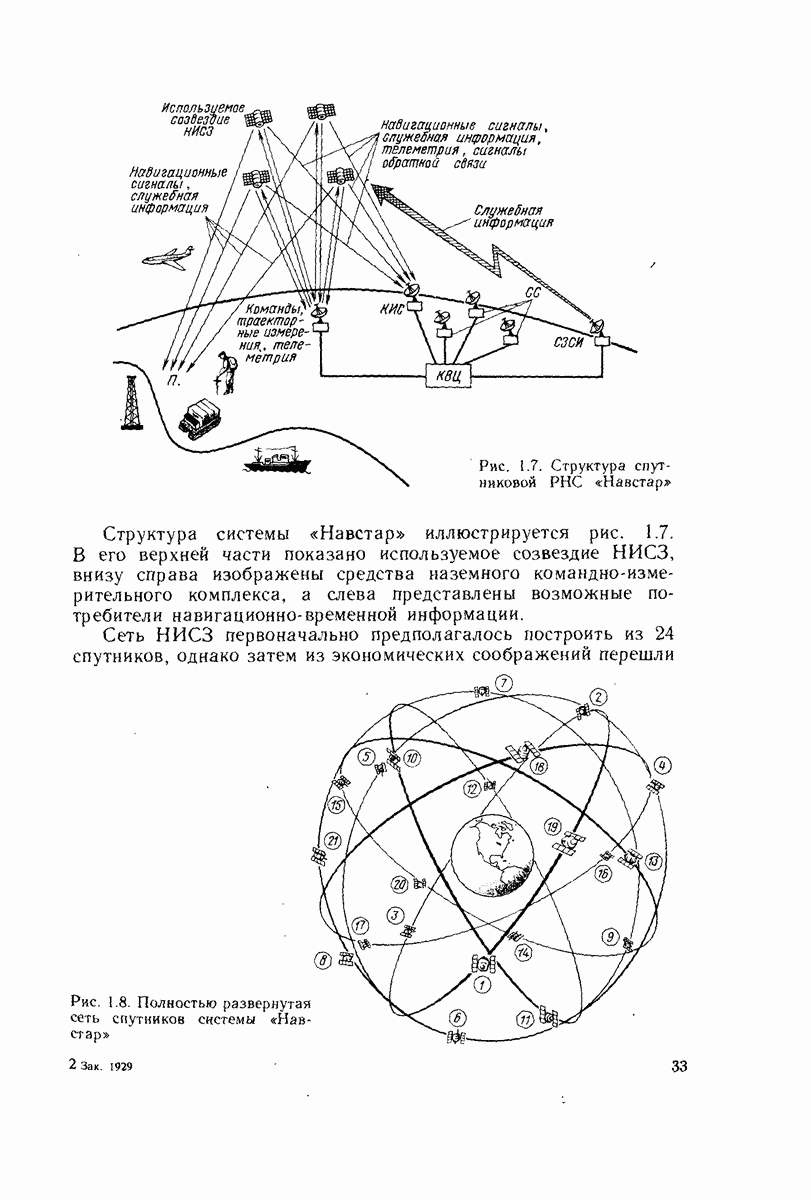
- 1.7. АМЕРИКАНСКАЯ СЕТЕВАЯ СПУТНИКОВАЯ РНС «НАВСТАР»
- 1.8. ИНФОРМАЦИОННЫЕ ЦЕНТРЫ СПУТНИКОВЫХ РНС
- ГЛАВА 2. ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА МЕТОДОВ ИЗМЕРЕНИЙ В ССРНС
- 2.2. НАВИГАЦИОННЫЕ ФУНКЦИИ
- 2.3. ГРАДИЕНТЫ ПОЛЕЙ НАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 2.4. ГРАДИЕНТНАЯ И ФУНДАМЕНТАЛЬНАЯ МАТРИЦЫ
- ГЛАВА 3. ОСНОВЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ В СРНС
- 3.1. КОНЕЧНЫЕ И ИТЕРАЦИОННЫЕ МЕТОДЫ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 3.2. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ОПРЕДЕЛЕНИЙ ПО ПОЛНОЙ ВЫБОРКЕ ИЗМЕРЕНИЙ
- 3.3. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ
- ГЛАВА 4. СИГНАЛЫ В СПУТНИКОВЫХ РНС
- 4.1. ОБЩИЕ ТРЕБОВАНИЯ К СИГНАЛАМ СРНС
- 4.2. СТАТИСТИЧЕСКАЯ МОДЕЛЬ РАДИОНАВИГАЦИОННОГО КАНАЛА СРНС
- 4.3. АНАЛИЗ ТРЕБОВАНИЙ, ПРЕДЪЯВЛЯЕМЫХ К СИГНАЛАМ СРНС
- 4.4. ТИПОВЫЕ СТРУКТУРЫ СОВМЕЩЕННЫХ СИГНАЛОВ ДЛЯ РАЗЛИЧНЫХ ВАРИАНТОВ ПАССИВНЫХ СРНС
- 4.5. ОСОБЕННОСТИ ВЫБОРА СТРУКТУРЫ СИГНАЛОВ В АКТИВНЫХ ВАРИАНТАХ СРНС
- ГЛАВА 5. ЭНЕРГЕТИКА НАВИГАЦИОННЫХ РАДИОЛИНИЙ
- 5.1. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К НАВИГАЦИОННЫМ РАДИОЛИНИЯМ
- 5.2. ОБЩАЯ ХАРАКТЕРИСТИКА ПРЯМОЙ И РЕТРАНСЛЯЦИОННОЙ РАДИОЛИНИЙ СРНС
- 5.3. УЧЕТ УСЛОВИЙ РАСПРОСТРАНЕНИЯ РАДИОВОЛН В СРНС
- 5.4. СПОСОБЫ УМЕНЬШЕНИЯ АТМОСФЕРНЫХ ПОГРЕШНОСТЕЙ ДАЛЬНОМЕРНОГО И ДОПЛЕРОВСКОГО ИЗМЕРЕНИЙ
- 5.5. ОСОБЕННОСТИ ЭНЕРГЕТИЧЕСКИХ РАСЧЕТОВ РАДИОЛИНИЙ В ЗАВИСИМОСТИ ОТ РАСПОЛОЖЕНИЯ ОБСЛУЖИВАЕМОГО СЛОЯ
- ГЛАВА 6. СПОСОБЫ РАЗДЕЛЕНИЯ СИГНАЛОВ
- 6.1. МЕТОДЫ УПЛОТНЕНИЯ И РАЗДЕЛЕНИЯ СИГНАЛОВ В СЕТЕВЫХ СРНС
- 6.2. ВЕРОЯТНОСТНОЕ РАЗДЕЛЕНИЕ СИГНАЛОВ СПУТНИКОВ ПРИ ИСПОЛЬЗОВАНИИ ШПС В ССРНС
- 6.3. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ШИРИНЫ ПОЛОСЫ ПРИНИМАЕМОГО ИЗЛУЧЕНИЯ В СЕТЕВЫХ СРНС
- 6.4. ОСОБЕННОСТИ РАЗДЕЛЕНИЯ СИГНАЛОВ В АКТИВНЫХ СРНС
- ГЛАВА 7. ПРИНЦИПЫ ПОСТРОЕНИЯ ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНОЙ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 7.1. ОБОБЩЕННАЯ СТРУКТУРНАЯ СХЕМА АП ССРНС
- 7.2. ИНФОРМАЦИОННЫЕ ПОТОКИ В АП
- 7.3. ИЗМЕРЯЕМЫЕ РАДИОНАВИГАЦИОННЫЕ ПАРАМЕТРЫ
- 7.4. ВИДЫ И МОДЕЛИ ПОМЕХ
- 7.5. ОСНОВЫ СТАТИСТИЧЕСКОГО СИНТЕЗА ИЗМЕРИТЕЛЕЙ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- ГЛАВА 8. УСТРОЙСТВА ПЕРВИЧНОЙ ОБРАБОТКИ РАДИОНАВИГАЦИОННОГО СИГНАЛА
- 8.1. НЕОБХОДИМОСТЬ ПОИСКА РАДИОНАВИГАЦИОННЫХ СИГНАЛОВ
- 8.2. СПОСОБЫ РЕШЕНИЯ ЗАДАЧИ ПОИСКА РАДИОСИГНАЛОВ НИСЗ
- 8.3. УСТРОЙСТВА ОЦЕНКИ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 8.4. ЦИФРОВАЯ РЕАЛИЗАЦИЯ УСТРОЙСТВ ПЕРВИЧНОЙ ОБРАБОТКИ
- 8.5. ОЦЕНКА ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 8.6. СПОСОБЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ АП
- ГЛАВА 9. РАЗНОВИДНОСТИ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 9.1. ОСОБЕННОСТИ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ РАЗЛИЧНЫХ ТИПОВ
- 9.2. ОДНОКАНАЛЬНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.3. МНОГОКАНАЛЬНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.4. МУЛЬТИПЛЕКСНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.5. АППАРАТУРА ПОТРЕБИТЕЛЕЙ ДЛЯ ОДНОВРЕМЕННОЙ РАБОТЫ ПО СИСТЕМАМ «ГЛОНАСС» и «НАВСТАР»
- 9.6. УНИФИКАЦИЯ АППАРАТУРНЫХ РЕШЕНИЙ
- ГЛАВА 10. КАДР НАВИГАЦИОННОГО СИГНАЛА
- 10.1. ОРГАНИЗАЦИЯ ОБРАБОТКИ ИЗМЕРЕНИЙ И ФОРМИРОВАНИЕ ЭФЕМЕРИДНОЙ ИНФОРМАЦИИ
- 10.2. МЕТОДОЛОГИЯ ВЫБОРА ЭЛЕМЕНТОВ КАДРА СИГНАЛА
- 10.3. УСЛОВИЯ РЕАЛИЗАЦИИ АЛГОРИТМОВ ПРОГНОЗИРОВАНИЯ ЭФЕМЕРИД НИСЗ
- 10.4. АЛГОРИТМЫ ПРОГНОЗИРОВАНИЯ ДВИЖЕНИЯ НИСЗ
- 10.5. СОСТАВ, ФОРМА ПРЕДСТАВЛЕНИЯ И ОБЪЕМ ИНФОРМАЦИИ, ПЕРЕДАВАЕМОЙ В КАДРЕ НАВИГАЦИОННОГО СИГНАЛА СИСТЕМЫ «НАВСТАР»
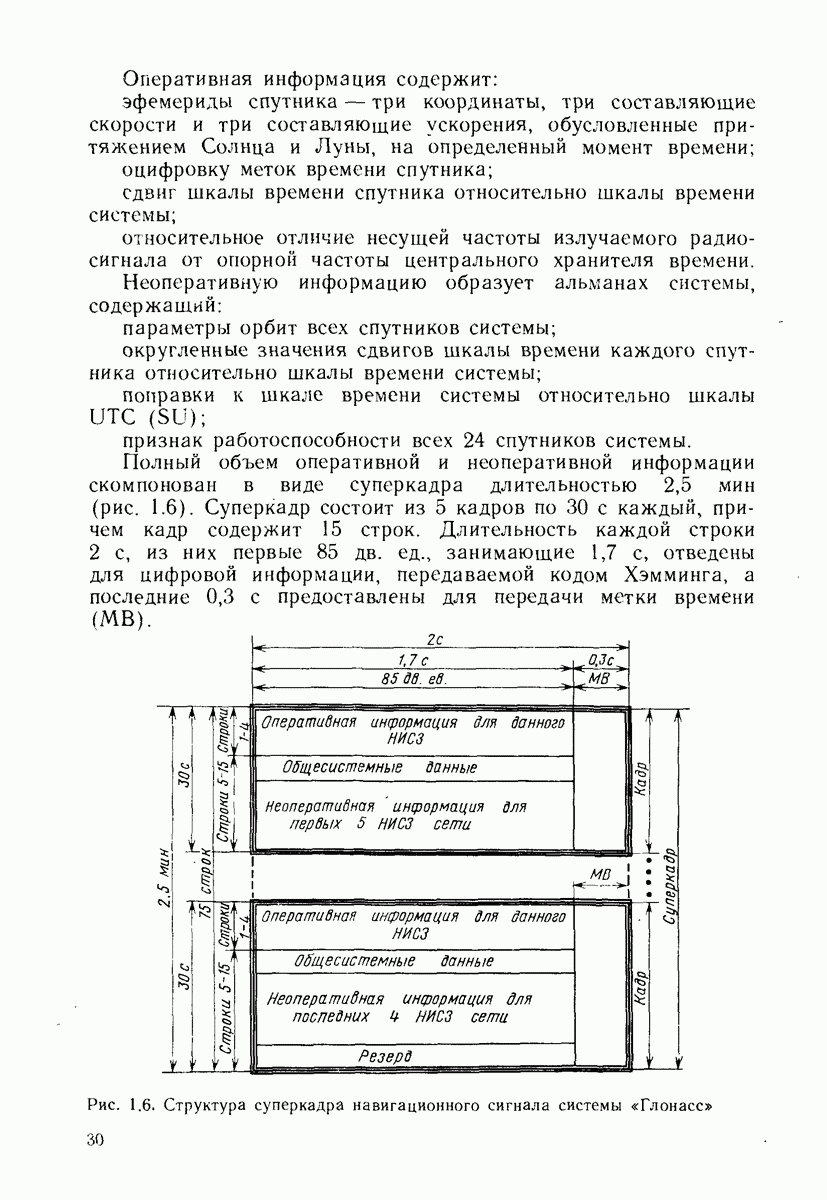
- 10.6. КАДР НАВИГАЦИОННОГО СИГНАЛА СИСТЕМЫ «ГЛОНАСС»
- ГЛАВА 11. СИНХРОНИЗАЦИЯ ВРЕМЕННЫХ ШКАЛ СИСТЕМЫ НИСЗ
- 11.1. ОБЩАЯ ХАРАКТЕРИСТИКА ХРАНИТЕЛЕЙ ВРЕМЕННЫХ ШКАЛ
- 11.2. МЕТОДЫ СВЕРКИ ВРЕМЕННЫХ ШКАЛ
- 11.3. КОРРЕКЦИЯ ВРЕМЕННЫХ ШКАЛ
- 11.4. СПОСОБЫ УЧЕТА В НАВИГАЦИОННОМ СЕАНСЕ СМЕЩЕНИЙ ВРЕМЕННЫХ ШКАЛ НИСЗ
- 11.5. СОГЛАСОВАНИЕ ШКАЛ ВРЕМЕНИ СИСТЕМ «ГЛОНАСС» И «НАВСТАР»
- 11.6. СИНХРОНИЗАЦИЯ ВРЕМЕННЫХ ШКАЛ СЕТИ НИСЗ НА ОСНОВЕ ВЗАИМНЫХ ВРЕМЕННЫХ ИЗМЕРЕНИЙ
- ГЛАВА 12. ОБЛАСТИ ИСПОЛЬЗОВАНИЯ СЕТЕВЫХ СПУТНИКОВЫХ РНС
- 12.1. ПРИМЕНЕНИЕ ССРНС — ОСНОВА КООРДИНАТНО-ВРЕМЕННОГО ОБЕСПЕЧЕНИЯ
- 12.2. ОПРЕДЕЛЕНИЕ КООРДИНАТ, ИХ ПРОИЗВОДНЫХ И НАВИГАЦИОННЫХ ЭЛЕМЕНТОВ НАЗЕМНЫХ И ПРИЗЕМНЫХ ОБЪЕКТОВ
- 12.3. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ДВИЖЕНИЯ ОКОЛОЗЕМНЫХ КА
- 12.4. ОПРЕДЕЛЕНИЕ ВЗАИМНЫХ КООРДИНАТ В ИНТЕРЕСАХ ПРЕДУПРЕЖДЕНИЯ СТОЛКНОВЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ И ГРУППОВОГО ИХ ВОЖДЕНИЯ
- 12.5. ВЫСОКОТОЧНАЯ ГЕОДЕЗИЧЕСКАЯ ПРИВЯЗКА
- 11.6. ОПРЕДЕЛЕНИЕ ОРИЕНТАЦИИ ОБЪЕКТОВ В ПРОСТРАНСТВЕ
- 12.7. СИНХРОНИЗАЦИЯ ИЗЛУЧЕНИЯ СТАНЦИИ С НАЗЕМНЫМ БАЗИРОВАНИЕМ
- 12.8. НАБЛЮДЕНИЕ ДЛЯ ОБЕСПЕЧЕНИЯ УПРАВЛЕНИЯ ДВИЖЕНИЕМ ПЕРЕМЕЩАЮЩИХСЯ ОБЪЕКТОВ
- 12.9. ЦЕЛЕУКАЗАНИЕ В СИСТЕМЕ ОБНАРУЖЕНИЯ ТЕРПЯЩИХ БЕДСТВИЕ
- РАЗДЕЛ ВТОРОЙ. ОСНОВЫ НАВИГАЦИОННОГО ИСПОЛЬЗОВАНИЯ ССРНС
- 13.1. ЗАДАЧА СИНТЕЗА АЛГОРИТМА НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 13.2. МОДЕЛЬ НАВИГАЦИОННЫХ ИЗМЕРЕНИЙ
- 13.3. МОДЕЛЬ ДИНАМИКИ ПОТРЕБИТЕЛЯ
- 13.4. ФАКТОРЫ, ВЛИЯЮЩИЕ НА ВЫБОР СПОСОБА ОБРАБОТКИ ИНФОРМАЦИИ В ССРНС
- ГЛАВА 14. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ ПО ВЫБОРКЕ ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.1. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ ПО ВЫБОРКЕ МИНИМАЛЬНОГО ОБЪЕМА ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.2. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ ПО ИЗБЫТОЧНОМУ ОБЪЕМУ ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.3. ОЦЕНКА СХОДИМОСТИ АЛГОРИТМОВ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ
- ГЛАВА 15. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ ПО ВЫБОРКЕ ИЗМЕРЕНИИ НАРАСТАЮЩЕГО ОБЪЕМА
- 15.1. РЕКУРРЕНТНЫЙ АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ МЕТОДОМ КАЛМАНА И ЕГО МОДИФИКАЦИИ ПРИ РАЗЛИЧНЫХ СОСТАВАХ ИЗМЕРЕНИЙ
- 15.2. СПОСОБЫ УСТРАНЕНИЯ РАСХОДИМОСТИ ФИЛЬТРОВ КАЛМАНА
- 15.3. РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ ГАУССОВСКОГО ФИЛЬТРА 2-ГО ПОРЯДКА
- 15.4. СРАВНЕНИЕ РЕКУРРЕНТНЫХ АЛГОРИТМОВ ПО РАЗМЕРАМ ОБЛАСТИ СХОДИМОСТИ
- ГЛАВА 16. СПОСОБЫ ОЦЕНКИ ТОЧНОСТИ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ
- 16.1. ПОКАЗАТЕЛИ ТОЧНОСТИ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 16.2. КОРРЕЛЯЦИОННАЯ МАТРИЦА ОШИБОК ОПРЕДЕЛЯЕМЫХ ПАРАМЕТРОВ
- 16.3. ИСТОЧНИКИ ОШИБОК НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 16.4. ОТОБРАЖЕНИЕ ТОЧНОСТНЫХ ХАРАКТЕРИСТИК И ИНТЕГРАЛЬНАЯ ОЦЕНКА ТОЧНОСТИ СРНС
- ГЛАВА 17. ВЫСОКОТОЧНОЕ СЛИЧЕНИЕ ШКАЛ ВРЕМЕНИ УДАЛЕННЫХ ПУНКТОВ ПО СИГНАЛАМ НИСЗ
- 17.1. МЕТОДЫ СИНХРОНИЗАЦИИ ШВ УДАЛЕННЫХ ПУНКТОВ
- 17.2. ОЦЕНКА ТОЧНОСТИ СВЕРКИ ШВ УДАЛЕННЫХ ПУНКТОВ ПО ВЫБОРКЕ ОДНОВРЕМЕННЫХ ПСЕВДОДАЛЬНОМЕРНЫХ ИЗМЕРЕНИЙ
- 17.3. ПОТЕНЦИАЛЬНАЯ ТОЧНОСТЬ СВЕРКИ ШВ ПУНКТА С ИЗВЕСТНЫМИ КООРДИНАТАМИ ПО ДАННЫМ ПСЕВДОДАЛЬНОМЕРНЫХ И РАДИАЛЬНЫХ ПСЕВДОСКОРОСТНЫХ ИЗМЕРЕНИЙ
- ГЛАВА 18. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ КООРДИНАТ ПРИ ОДНОМОМЕНТНЫХ ИЗМЕРЕНИЯХ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ НИСЗ
- 18.2. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПОВЕРХНОСТНЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ДВУХ НИСЗ
- 18.3. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПОВЕРХНОСТНЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ТРЕХ НИСЗ
- 18.4. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПРОСТРАНСТВЕННЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ЧЕТЫРЕХ НИСЗ
- 18.5. ТОЧНОСТНЫЕ СВОЙСТВА ДОПЛЕРОВСКИХ МЕТОДОВ В СЕТЕВЫХ СРНС В СРАВНЕНИИ С ДАЛЬНОМЕРНЫМИ
- ГЛАВА 19. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННЫХ КООРДИНАТ И ВЕКТОРА СКОРОСТИ ПО СЕТИ НИСЗ
- 19.2. РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ ГЕОМЕТРИЧЕСКИХ ФАКТОРОВ
- 19.3. ТОЧНОСТЬ ОЦЕНКИ КООРДИНАТ И ВРЕМЕНИ
- 19.4. ТОЧНОСТЬ ОЦЕНКИ СКОРОСТИ ДВИЖЕНИЯ
- 19.5. ОЦЕНКА ТОЧНОСТИ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ КА
- ГЛАВА 20. ДИФФЕРЕНЦИАЛЬНЫЙ РЕЖИМ ССРНС
- 20.2. СТРУКТУРА ДИФФЕРЕНЦИАЛЬНОЙ ПОДСИСТЕМЫ
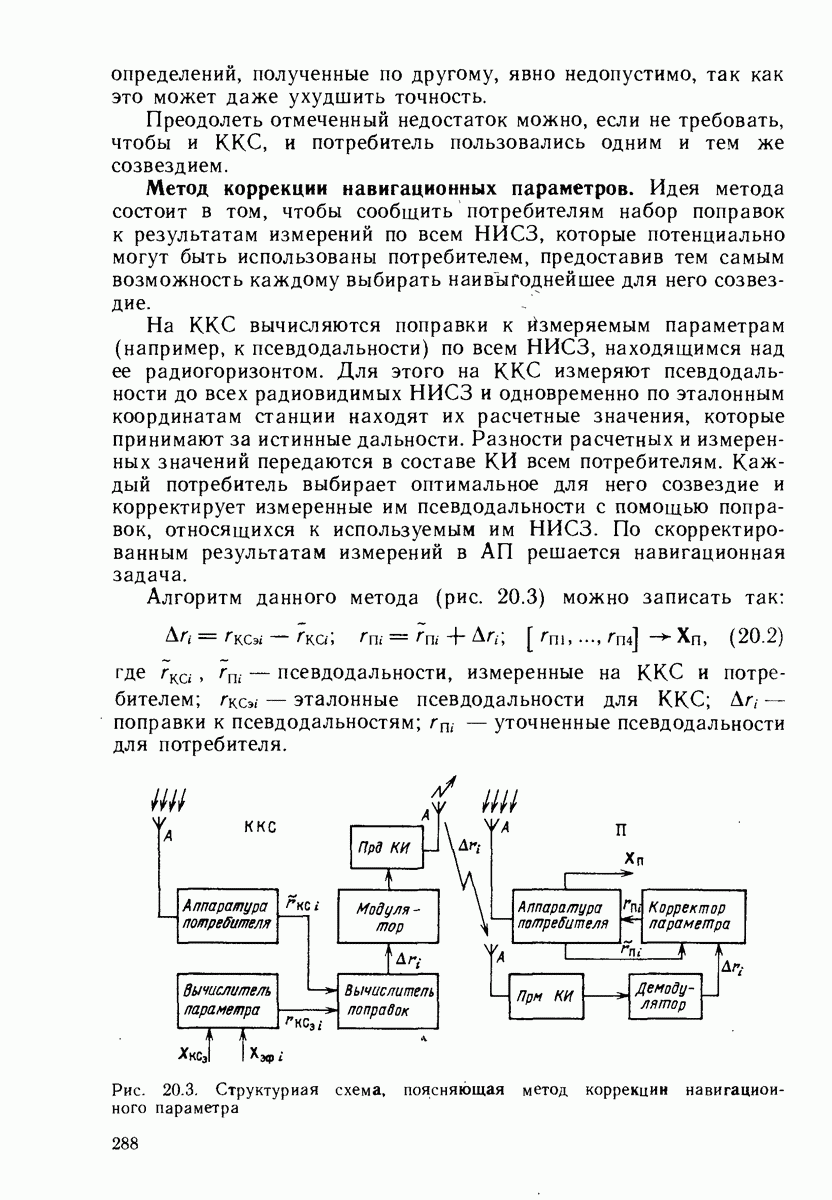
- 20.3. МЕТОДЫ ДИФФЕРЕНЦИАЛЬНЫХ ОПРЕДЕЛЕНИЙ
- 20.4. КОРРЕКТИРУЮЩАЯ ИНФОРМАЦИЯ
- 20.5. КАНАЛЫ ПЕРЕДАЧИ КОРРЕКТИРУЮЩЕЙ ИНФОРМАЦИИ
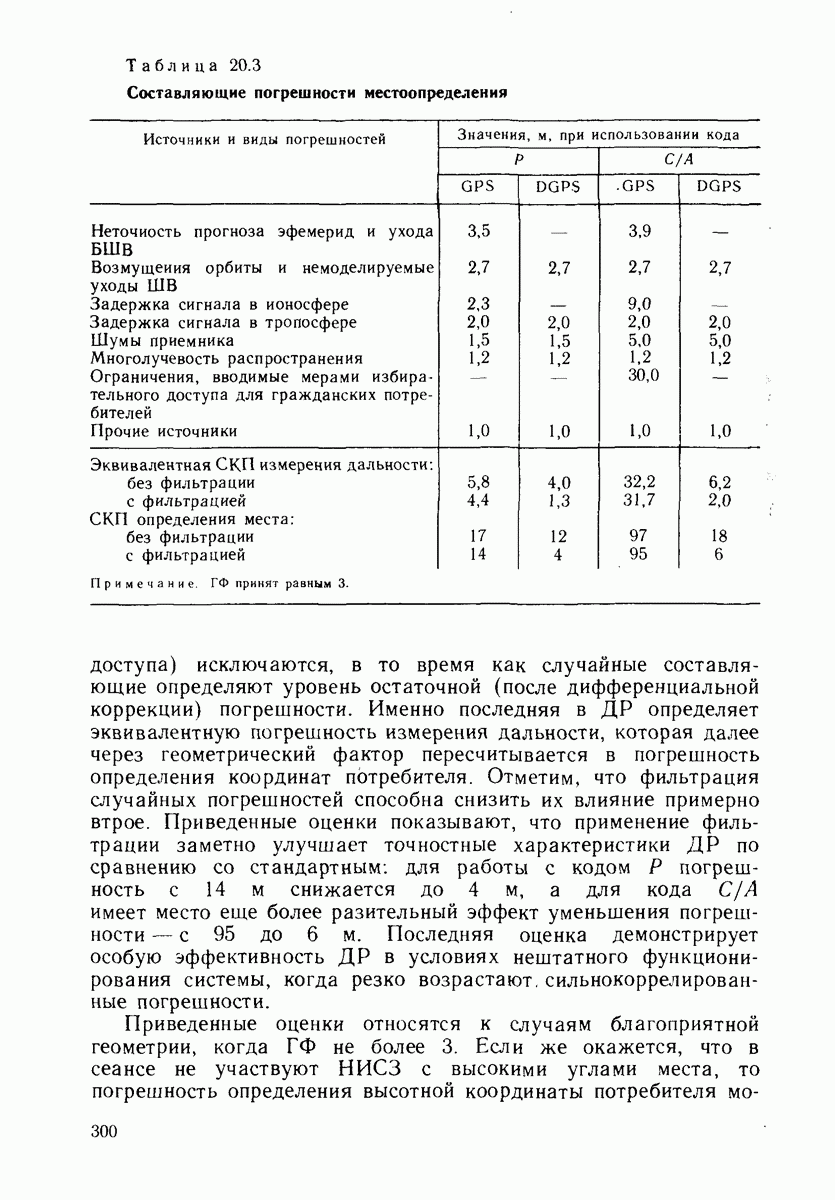
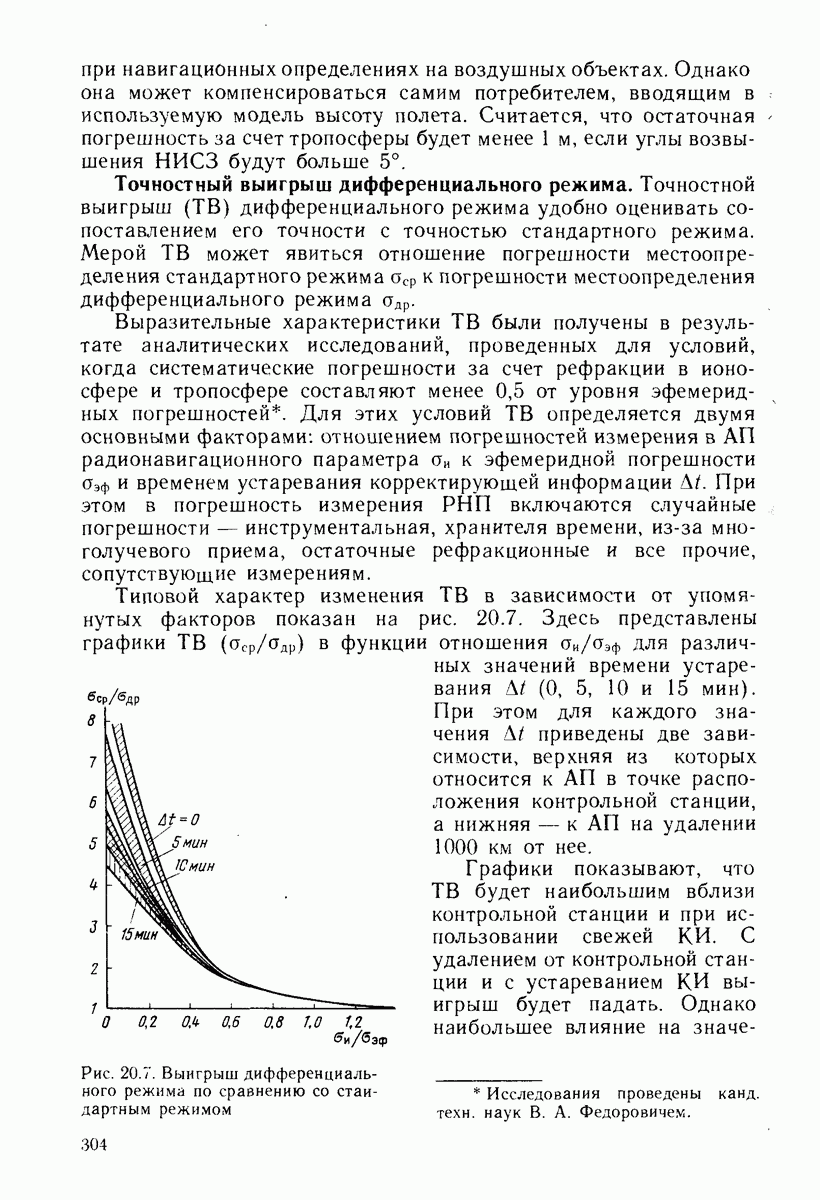
- 20.6. ТОЧНОСТНЫЕ ХАРАКТЕРИСТИКИ ДМ
- 20.7. ИЗМЕРЕНИЯ РНП ПО ФАЗЕ НЕСУЩИХ КОЛЕБАНИЙ
- 20.8. РЕЗУЛЬТАТЫ ИСПЫТАНИЙ. РЕАЛИЗАЦИЯ ДПС
- ГЛАВА 21. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ В АКТИВНОМ И ОТНОСИТЕЛЬНОМ РЕЖИМАХ
- 21.1. ТОЧНОСТНЫЕ ХАРАКТЕРИСТИКИ АКТИВНЫХ СРНС
- 21.2. ТОЧНОСТНЫЕ СВОЙСТВА СЕТЕВЫХ СРНС В ОТНОСИТЕЛЬНОМ РЕЖИМЕ
- ГЛАВА 22. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ БОРТОВОЙ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 22.1. АВТОМАТИЗАЦИЯ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ И ШТУРМАНСКИХ РАСЧЕТОВ
- 22.2. МЕТОДИЧЕСКИЕ ОСНОВЫ МАТЕМАТИЧЕСКОГО ОБЕСПЕЧЕНИЯ
- 22.3. ОСНОВНЫЕ ЗАДАЧИ ВТО
- 22.4. УПРАВЛЯЮЩИЙ АЛГОРИТМ
- 22.5. ВРЕМЕННАЯ ДИАГРАММА АЛГОРИТМА
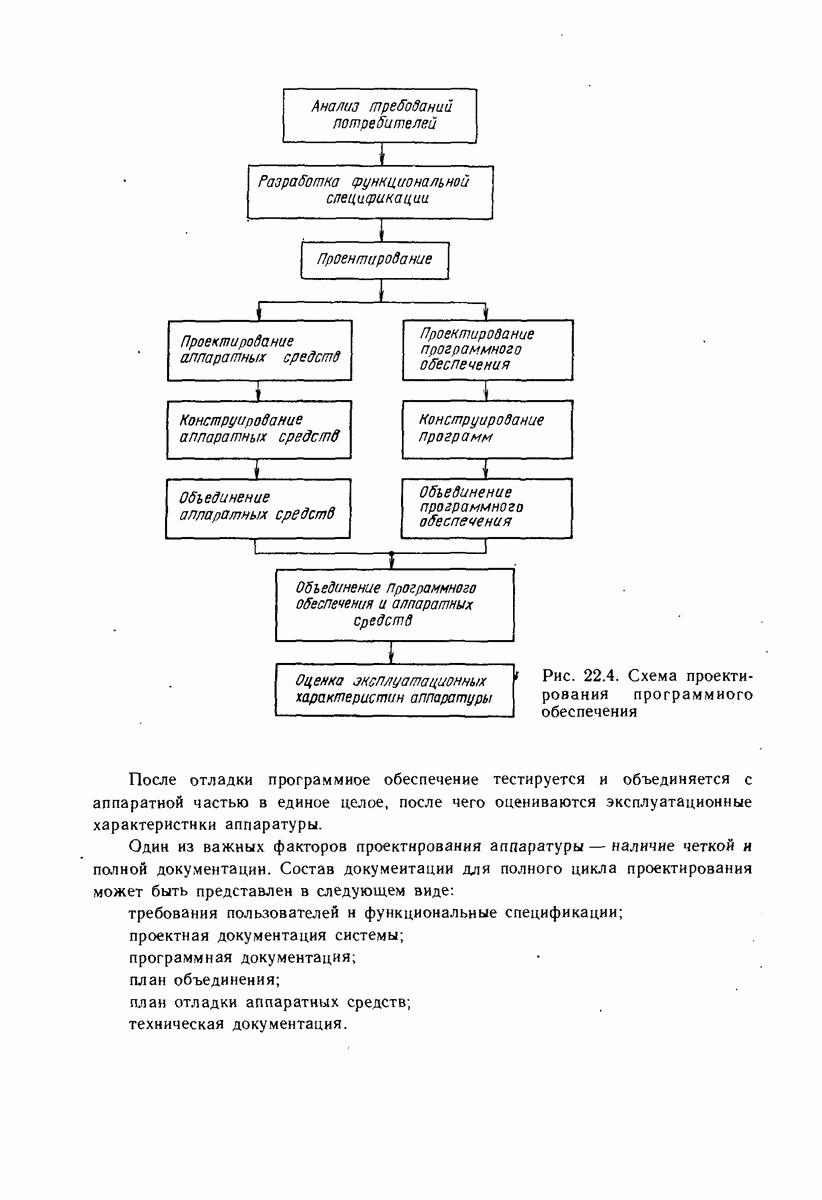
- 22.6. ПРИНЦИПЫ ПРОЕКТИРОВАНИЯ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
- РАЗДЕЛ ТРЕТИЙ. КОМПЛЕКСНОЕ ПРОЕКТИРОВАНИЕ ССРНС
- 23.1. ОСНОВНЫЕ ЗАДАЧИ, РЕШАЕМЫЕ ПРИ КОМПЛЕКСНОМ ПРОЕКТИРОВАНИИ
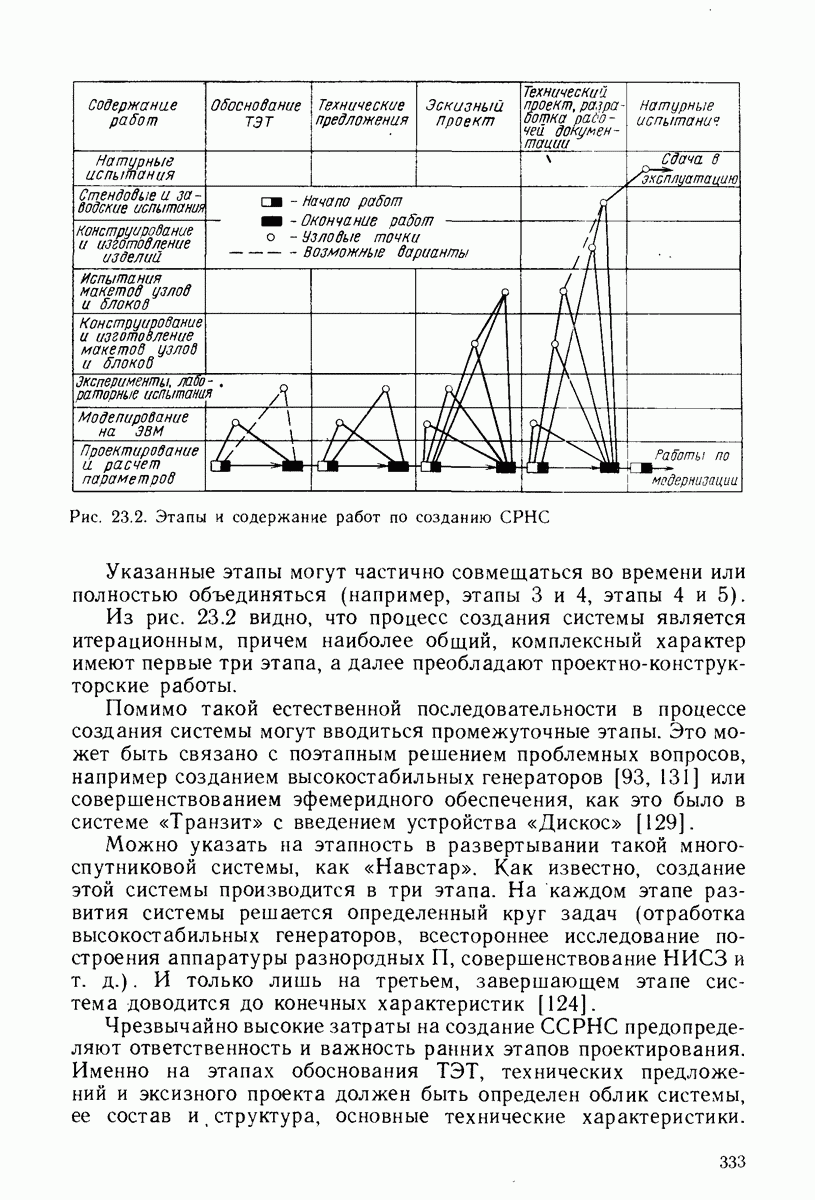
- 23.2. ЭТАПЫ СОЗДАНИЯ ССРНС
- 23.3. ОСОБЕННОСТИ ПРОЕКТОВ СРНС РАЗЛИЧНОГО НАЗНАЧЕНИЯ
- ГЛАВА 24. СИНТЕЗ СТРУКТУРЫ СЕТИ НИСЗ ИЗ УСЛОВИИ ОБЕСПЕЧЕНИЯ ЗАДАННОЙ КРАТНОСТИ ПОКРЫТИЯ
- 24.2. ЗОНА РАДИОВИДИМОСТИ, ПОЛОСА ПОКРЫТИЯ И ОБЛАСТЬ ПЕРЕКРЫТИЯ
- 24.3. ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ СЕТИ НИСЗ, ОБЕСПЕЧИВАЮЩЕЙ ЗАДАННУЮ МИНИМАЛЬНУЮ КРАТНОСТЬ ПОКРЫТИЯ
- 24.4. НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ СЕТИ НИСЗ
- 24.5. СВОЙСТВА ЭКСТРЕМАЛЬНОЙ СЕТИ НИСЗ, ОБЕСПЕЧИВАЮЩЕЙ ЗАДАННУЮ МИНИМАЛЬНУЮ КРАТНОСТЬ ПОКРЫТИЯ
- 24.6. УСЛОВИЕ СТАБИЛЬНОСТИ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ СЕТИ НИСЗ
- ГЛАВА 25. СИНТЕЗ СТРУКТУРЫ СЕТИ НИСЗ ПО КРИТЕРИЮ ТОЧНОСТИ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 25.2. ВЫБОР ОПТИМАЛЬНОГО ПО КРИТЕРИЮ ТОЧНОСТИ СОЗВЕЗДИЯ НИСЗ
- 25.3. ПРИБЛИЖЕННЫМ УЧЕТ ПАРАЛЛАКСА МИНИМАЛЬНОГО СОЗВЕЗДИЯ
- 25.4. КАЧЕСТВЕННЫЙ АНАЛИЗ ЗОН ПОНИЖЕННОЙ ТОЧНОСТИ
- 25.5. УТОЧНЕНИЕ СТРУКТУРЫ СЕТИ НИСЗ ПО МИНИМАКСНОМУ КРИТЕРИЮ ТОЧНОСТИ
- 25.6. СРАВНЕНИЕ ССРНС «ГЛОНАСС» И «НАВСТАР»
- ГЛАВА 26. ОСНОВЫ КОМПЛЕКСНОГО ИСПОЛЬЗОВАНИЯ СРНС С ДРУГИМИ РАДИОНАВИГАЦИОННЫМИ И АВТОНОМНЫМИ НАВИГАЦИОННЫМИ СРЕДСТВАМИ
- 26.1. ОБЩИЕ ПРЕДПОСЫЛКИ И ВОЗМОЖНОСТИ СОВМЕСТНОГО ИСПОЛЬЗОВАНИЯ СПУТНИКОВЫХ РНС И ДРУГИХ НАВИГАЦИОННЫХ СРЕДСТВ
- 26.2. КОМБИНИРОВАННАЯ РАЗНОСТНО-ДАЛЬНОМЕРНАЯ РНС, СОСТОЯЩАЯ ИЗ НАЗЕМНЫХ СТАНЦИЙ И СТАЦИОНАРНОГО НИСЗ
- 26.3. КОМПЛЕКСНОЕ ИСПОЛЬЗОВАНИЕ НИЗКООРБИТАЛЬНОЙ СРНС И ФАЗОВОЙ СДВ РНС
- 26.4. КОМПЛЕКСИРОВАНИЕ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ НА УРОВНЕ ПЕРВИЧНОЙ ОБРАБОТКИ ИНФОРМАЦИИ
- ГЛАВА 27. КРИТЕРИИ ОЦЕНКИ ЭФФЕКТИВНОСТИ НАВИГАЦИОННОГО ИСПОЛЬЗОВАНИЯ СРНС
- 27.2. ОСОБЕННОСТИ ИССЛЕДОВАНИЯ ЭФФЕКТИВНОСТИ СПУТНИКОВЫХ РНС
- 27.3. ОБЩИЕ И ЧАСТНЫЕ КРИТЕРИИ ЭФФЕКТИВНОСТИ СРНС