| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.2. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ОПРЕДЕЛЕНИЙ ПО ПОЛНОЙ ВЫБОРКЕ ИЗМЕРЕНИЙ
Рассмотрим основы статистической обработки полной выборки результатов измерений применительно к процедуре метода наименьших квадратов. Ради упрощения будем считать, что определяются всего три параметра — сферические координаты  неподвижного П. Навигационные параметры, измеряемые по сигналам НИСЗ, обозначим
неподвижного П. Навигационные параметры, измеряемые по сигналам НИСЗ, обозначим  их расчетные значения
их расчетные значения  а общее число измерений
а общее число измерений  Пространственное положение НИСЗ задается геоцентрическими координатами
Пространственное положение НИСЗ задается геоцентрическими координатами  Координаты
Координаты  обозначим соответственно
обозначим соответственно  .
.
Общее выражение навигационной функции для измерений в момент  имеет вид
имеет вид

Конкретное выражение определяется, естественно, видом  например, для дальномерного метода измерений будет записываться в виде (2.2)
например, для дальномерного метода измерений будет записываться в виде (2.2)

Если имеются результаты  измерений:
измерений:  то может быть составлена система уравнений
то может быть составлена система уравнений

в которой различные строки могут относиться как к измерениям по одному и тому же НИСЗ, но в разные моменты времени, так и к измерениям по различным НИСЗ (одновременным или разновременным).
Для линеаризации системы (3.2) в окрестностях расчетных значений определяемых параметров вычисляют значения  либо с помощью априорной информации, либо с помощью решения каких-то трех совместных уравнений системы (3.2), что позволяет рассчитывать значения измеряемых параметров
либо с помощью априорной информации, либо с помощью решения каких-то трех совместных уравнений системы (3.2), что позволяет рассчитывать значения измеряемых параметров  Тогда получается система уравнений для расчетных значений:
Тогда получается система уравнений для расчетных значений:

Разность измеренных и расчетных параметров можно выразить через поправки  к приближенным значениям координат
к приближенным значениям координат  и далее обработку вести до получения наилучшей оценки этих поправок с использованием всей наличной измерительной информации. Тогда можно записать
и далее обработку вести до получения наилучшей оценки этих поправок с использованием всей наличной измерительной информации. Тогда можно записать

Линеаризация проводится путем разложения системы уравнений (3.4) в ряд Тейлора по степеням поправок 6; с удержанием первых членов разложения. После этого получится следующая система уравнений:

Входящие в систему (3.5) частные производные  функции
функции  по координатам, отвечающим приближенно известному месту, являются постоянными для сеанса измерений. Матрица частных производных
по координатам, отвечающим приближенно известному месту, являются постоянными для сеанса измерений. Матрица частных производных  имеет большое значение для оценки свойств методов навигации (см. § 2.4). Введем для этой матрицы размерностью
имеет большое значение для оценки свойств методов навигации (см. § 2.4). Введем для этой матрицы размерностью  следующее обозначение:
следующее обозначение:

Воспользуемся далее понятиями градиентной и фундаментальной матриц (2.9) и (2.10) и для условий данного рассмотрения запишем

Заметим, что число столбцов матрицы  совпадает с числом строк матрицы
совпадает с числом строк матрицы  что дает основание образовать произведение этих матриц. Выполнив матричное перемножение, убедимся, что полученная матрица и есть матрица (3.6) коэффициентов системы линейных уравнений (3.5). В этой матрице каждый элемент представляет собой трехчлен вида (2.8). К примеру элемент с индексами
что дает основание образовать произведение этих матриц. Выполнив матричное перемножение, убедимся, что полученная матрица и есть матрица (3.6) коэффициентов системы линейных уравнений (3.5). В этой матрице каждый элемент представляет собой трехчлен вида (2.8). К примеру элемент с индексами  развертывается как
развертывается как

Итак, имеет место соотношение

Последние преобразования показали достаточную компактность записи. Именно поэтому в алгоритмах обработки измерительной информации в настоящее время широко употребляется матричный способ описания. Можно и всю систему уравнений (3.5) записать в виде компактного матричного соотношения.
Введем столбцовую матрицу А поправок  к уточняемым координатам
к уточняемым координатам

а также матрицу-столбец  из разностей измеренного и расчетного значений НП
из разностей измеренного и расчетного значений НП

Тогда в результате перемножения матриц С размерности  размерности (3X1) можно получить матрицу-столбец размерности
размерности (3X1) можно получить матрицу-столбец размерности  которая полностью совпадает с матрицей правых частей системы уравнений (3,5). В то же время по определению матрицей
которая полностью совпадает с матрицей правых частей системы уравнений (3,5). В то же время по определению матрицей  размерности
размерности  описывается совокупность левых частей системы рассматриваемых уравнений. Поэтому система исходных линеаризованных уравнений представится в матричной записи как
описывается совокупность левых частей системы рассматриваемых уравнений. Поэтому система исходных линеаризованных уравнений представится в матричной записи как

Обратим внимание на то, что в системе (3.5) различные уравнения могут иметь неодинаковые размерности, поскольку разности  могут соответствовать различным измерениям навигационных параметров, а среди однородных параметров найдутся неравноточные, относящиеся к измерениям по
могут соответствовать различным измерениям навигационных параметров, а среди однородных параметров найдутся неравноточные, относящиеся к измерениям по
различным НИСЗ. Ради придания системе (3.5) однородности целесообразно привести все разности  к безразмерному виду. Для этого левые и правые части системы (3.5) домножаются на весовые коэффициенты, имеющие размерность, обратную размерности
к безразмерному виду. Для этого левые и правые части системы (3.5) домножаются на весовые коэффициенты, имеющие размерность, обратную размерности 

где  дисперсия погрешностей измерения НП, а
дисперсия погрешностей измерения НП, а  некоторый масштабирующий коэффициент. В результате, учитывая обозначения (3.10), получаем безразмерную систему уравнений
некоторый масштабирующий коэффициент. В результате, учитывая обозначения (3.10), получаем безразмерную систему уравнений

которую именуют системой условных уравнений.
Если из весовых коэффициентов  образовать диагональную матрицу
образовать диагональную матрицу 

то выполненное домножение левых и правых частей системы уравнений на весовые коэффициенты можно представить как матричные операции умножения, приводящие к матричному виду системы условных уравнений:

Далее к системе условных уравнений применяют процедуру метода наименьших квадратов, основанную на следующих соображениях. Система (3.12) является системой  уравнений с тремя неизвестными. Если только эти
уравнений с тремя неизвестными. Если только эти  уравнений независимы, то какая-то совокупность трех поправок
уравнений независимы, то какая-то совокупность трех поправок  , не может удовлетворить этой системе и при подстановке
, не может удовлетворить этой системе и при подстановке  , в соответствующие уравнения левые и правые их части окажутся неравными, появится невязка этих частей. Обозначив разницу (невязку) через
, в соответствующие уравнения левые и правые их части окажутся неравными, появится невязка этих частей. Обозначив разницу (невязку) через  получим новую запись
получим новую запись

Ее матричным эквивалентом явится выражение

в котором использовано представление о совокупности невязок как матрице-столбце размерности 

Важным обстоятельством является то, что невязки предполагаются случайными величинами. Метод наименьших квадратов позволяет найти такие наилучшие поправки к координатам  при которых сумма квадратов невязок
при которых сумма квадратов невязок  минимальна:
минимальна:

Сказанному можно дать геометрическое истолкование, которое сохраняет наглядность при малой мерности пространства определяемых параметров и малом числе измерений. Примем поэтому  и выполним следующее построение (рис. 3.1).
и выполним следующее построение (рис. 3.1).
В пространстве  относительно точки с априорными координатами
относительно точки с априорными координатами  Но) построим ортогональный базис поправок
Но) построим ортогональный базис поправок  оси которого параллельны соответственно осям
оси которого параллельны соответственно осям  и
и  Тогда система трех линейных уравнений вида (3.5), отвечающих трем результатам измерений,
Тогда система трех линейных уравнений вида (3.5), отвечающих трем результатам измерений,  формально-геометрически может интерпретироваться как совокупность трех прямых
формально-геометрически может интерпретироваться как совокупность трех прямых  касательных к линиям положения в окрестности априорного места
касательных к линиям положения в окрестности априорного места  Но). Эти линии отстоят от начала координат на расстояния, равные разностям измеренных и расчетных значений параметров
Но). Эти линии отстоят от начала координат на расстояния, равные разностям измеренных и расчетных значений параметров  причем в случае безошибочных измерений все они пересекались бы в одной точке — истинном месте П. Влияние ошибок приводит к тому, что пересечениями этих прямых образуется треугольная область
причем в случае безошибочных измерений все они пересекались бы в одной точке — истинном месте П. Влияние ошибок приводит к тому, что пересечениями этих прямых образуется треугольная область  возможного нахождения объекта. Оптимизация решения, предусматриваемая методом наименьших квадратов, состоит в отыскании точки, наивыгоднейшим образом удаленной от всех трех касательных, чему соответствует минимальность суммы квадратов невязок
возможного нахождения объекта. Оптимизация решения, предусматриваемая методом наименьших квадратов, состоит в отыскании точки, наивыгоднейшим образом удаленной от всех трех касательных, чему соответствует минимальность суммы квадратов невязок  Эта точка дает оценки искомым поправкам
Эта точка дает оценки искомым поправкам 

Рис. 3.1. Геометрическое истолкование оптимизации по методу наименьших квадратов

Рис. 3.2. Ортогональное проектирование  вектора
вектора  в пространстве измерений
в пространстве измерений
Геометрическое толкование выражений (3.14), (3.14) удобно дать в пространстве измерений. Для этого построим координатный базис в осях разностей  Для рассматриваемого случая матрица (3.6), имея размерность (3X2), может распасться на два вектора
Для рассматриваемого случая матрица (3.6), имея размерность (3X2), может распасться на два вектора

которые можно истолковать как своеобразные базисные векторы пространства частных производных  заданные в пространстве измерений. Сориентировав по этим векторам произведения
заданные в пространстве измерений. Сориентировав по этим векторам произведения  можно путем суммирования получить в данном базисе вектор матричного произведения
можно путем суммирования получить в данном базисе вектор матричного произведения  В то же время в базисе
В то же время в базисе  вектор измерений
вектор измерений  фиксируется так, что разность
фиксируется так, что разность  дает вектор
дает вектор  который в соответствии с (3.14) представляет собой вектор невязок. Можно показать, что вектор невязок
который в соответствии с (3.14) представляет собой вектор невязок. Можно показать, что вектор невязок  будет ортогонален любому вектору
будет ортогонален любому вектору  из базисного подпространства параметров подпространства, заданного векторами
из базисного подпространства параметров подпространства, заданного векторами  Значит, при оптимизации методом наименьших квадратов проводится ортогональное проектирование вектора измерений
Значит, при оптимизации методом наименьших квадратов проводится ортогональное проектирование вектора измерений  на подпространство параметров. Дальнейшее разложение этой проекции
на подпространство параметров. Дальнейшее разложение этой проекции  по базисным осям
по базисным осям  пространства определяемых параметров дает оценки искомых поправок
пространства определяемых параметров дает оценки искомых поправок 
Аналитически минимизация суммы квадратов невязок связана со следующими вычислениями. Условие (3.16) распадается на три условия:

Вычислим в соответствии с (3.17) значения частных производных функционала V по поправкам  Дифференцирование V по первой поправке
Дифференцирование V по первой поправке  дает
дает

откуда следует, что

Аналогично этому дифференцирование функционала V по поправкам  и 63 дает выражения, подобные (3.18), с той разницей, что в повторяющемся в каждом члене сомножителе
и 63 дает выражения, подобные (3.18), с той разницей, что в повторяющемся в каждом члене сомножителе
производные будут браться соответственно по  Совокупность всех полученных в результате дифференцирований выражений даст систему трех уравнений с тремя неизвестными
Совокупность всех полученных в результате дифференцирований выражений даст систему трех уравнений с тремя неизвестными  Если коэффициенты при неизвестных обозначить через
Если коэффициенты при неизвестных обозначить через  а коэффициенты при правых частях уравнений через
а коэффициенты при правых частях уравнений через  то полученную систему, именуемую системой нормальных уравнений, можно записать в следующем виде:
то полученную систему, именуемую системой нормальных уравнений, можно записать в следующем виде:

где

Выражения (3.19) — (3.21) представляют собой принципиальный алгоритм обработки результатов измерений  для определения поправок
для определения поправок  к априорно известным пространственным координатам
к априорно известным пространственным координатам  Таким образом, при решении навигационных задач методом наименьших квадратов по существу решается система линейных нормальных уравнений (3.19), коэффициенты которой
Таким образом, при решении навигационных задач методом наименьших квадратов по существу решается система линейных нормальных уравнений (3.19), коэффициенты которой  на первом итерационном цикле вычисляются по априорным данным, а коэффициенты
на первом итерационном цикле вычисляются по априорным данным, а коэффициенты  на том же цикле — как по априорным сведениям, так и по результатам измерений. Начальными значениями координат для каждого последующего цикла принимают начальные значения предыдущего цикла, исправленные на величины оцененных поправок.
на том же цикле — как по априорным сведениям, так и по результатам измерений. Начальными значениями координат для каждого последующего цикла принимают начальные значения предыдущего цикла, исправленные на величины оцененных поправок.
Для выражения коэффициентов  и 64 в литературе часто применяется введенная Гауссом символика, избавляющая от необходимости пользоваться знаком суммирования по индексу числа измерений:
и 64 в литературе часто применяется введенная Гауссом символика, избавляющая от необходимости пользоваться знаком суммирования по индексу числа измерений:

Коэффициенты  системы нормальных уравнений используют при оценке точностных свойств навигационных методов. Как было отмечено в § 2.4, градиентная и фундаментальная матрицы отражают видовые и общие свойства методов измерений, а совокупность коэффициентов
системы нормальных уравнений используют при оценке точностных свойств навигационных методов. Как было отмечено в § 2.4, градиентная и фундаментальная матрицы отражают видовые и общие свойства методов измерений, а совокупность коэффициентов  выражается как раз через элементы этих матриц (см. гл. 16).
выражается как раз через элементы этих матриц (см. гл. 16).
Образуем матричное произведение двух матриц:  и С (3.6), что для уточняемой системы координат дает
и С (3.6), что для уточняемой системы координат дает

Проведем транспонирование полученного произведения  в результате получим
в результате получим

Оказывается, что совокупность коэффициентов  является ни чем иным, как произведением транспонированной матрицы (3.23) на исходную (3.22). Запишем это произведение в виде матрицы размерности (3X3):
является ни чем иным, как произведением транспонированной матрицы (3.23) на исходную (3.22). Запишем это произведение в виде матрицы размерности (3X3):

Обозначим матрицу коэффициентов системы нормальных уравнений через  Тогда из сопоставления (3.20) и (3.24) следует матричное равенство
Тогда из сопоставления (3.20) и (3.24) следует матричное равенство

Заметим, что весовая матрица  была определена как (3.13) ради придания системе условных уравнений безразмерных свойств. Но поскольку
была определена как (3.13) ради придания системе условных уравнений безразмерных свойств. Но поскольку  диагональная матрица, ее вид при транспонировании не меняется, а следовательно, произведение
диагональная матрица, ее вид при транспонировании не меняется, а следовательно, произведение  дает также диагональную матрицу
дает также диагональную матрицу  элементы которой являются квадратами элементов матрицы
элементы которой являются квадратами элементов матрицы 

Ввиду этого

Обратившись к правым частям системы  обнаружим, что их матрица получается в результате перемножения матриц
обнаружим, что их матрица получается в результате перемножения матриц  размерности
размерности  :
:

Обозначив матрицу правых частей через В, запишем очевидное равенство 
Таким образом, система нормальных уравнений в матричном виде

или сокращенно

Полученная выше матрица коэффициентов  имеет размерность (3X3), что связано с трехмерным характером решаемой навигационной задачи. В случае определения шестимерного вектора состояния П составляется система 6 нормальных уравнений и матрица А будет иметь размерность (6X6).
имеет размерность (3X3), что связано с трехмерным характером решаемой навигационной задачи. В случае определения шестимерного вектора состояния П составляется система 6 нормальных уравнений и матрица А будет иметь размерность (6X6).
Вопросы решения системы нормальных уравнений, сходимости итерационных решений, а также особенности решений при использовании иных критериев оптимальности рассмотрены подробно в гл. 13 и 14. Здесь же уместно остановиться на том, как элементы матрицы А используются для оценки точности навигационных определений.
Упомянем, что один из способов решения системы (3.26) связан с обращением матрицы А. Дело в том, что, умножая левую и правую части системы (3.27) слева на обратную матрицу  можно получить в явном виде решение для поправок:
можно получить в явном виде решение для поправок: 
Приняв для простоты число результатов измерений равным числу определяемых параметров  будем иметь дело с квадратными матрицами
будем иметь дело с квадратными матрицами  и
и  Тогда, применив правила обращения матриц к соотношению (3.25), увидим, что матрица
Тогда, применив правила обращения матриц к соотношению (3.25), увидим, что матрица  выражается через обращенные матрицы
выражается через обращенные матрицы  Выясним, какой смысл имеет
Выясним, какой смысл имеет  для чего вспомним, что матрица
для чего вспомним, что матрица  диагональная, а при обращении таких матриц их элементы переходят в обратные величины. Стало быть, элементы матрицы
диагональная, а при обращении таких матриц их элементы переходят в обратные величины. Стало быть, элементы матрицы  с точностью до коэффициента представляют собой дисперсии измерений
с точностью до коэффициента представляют собой дисперсии измерений  частном случае равноточных измерений все диагональные элементы будут равны между собой и определятся дисперсией измерителя).
частном случае равноточных измерений все диагональные элементы будут равны между собой и определятся дисперсией измерителя).
С другой стороны, матрица  имеет смысл корреляционной матрицы погрешностей определения искомых параметров
имеет смысл корреляционной матрицы погрешностей определения искомых параметров  диагональные элементы которой суть дисперсии определяемых параметров.
диагональные элементы которой суть дисперсии определяемых параметров.
Для наглядности сочтем, что определяемые параметры образуют ортогональный базис. Тогда результирующая погрешность пространственного местоопределения выразится через след корреляционной матрицы 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ ПЕРВЫЙ/ СТРУКТУРА И ФУНКЦИОНИРОВАНИЕ СЕТЕВЫХ СРНС
- 1.1. СТРУКТУРНАЯ СХЕМА СРНС
- 1.2. ОСОБЕННОСТИ СЕТЕВЫХ СРНС
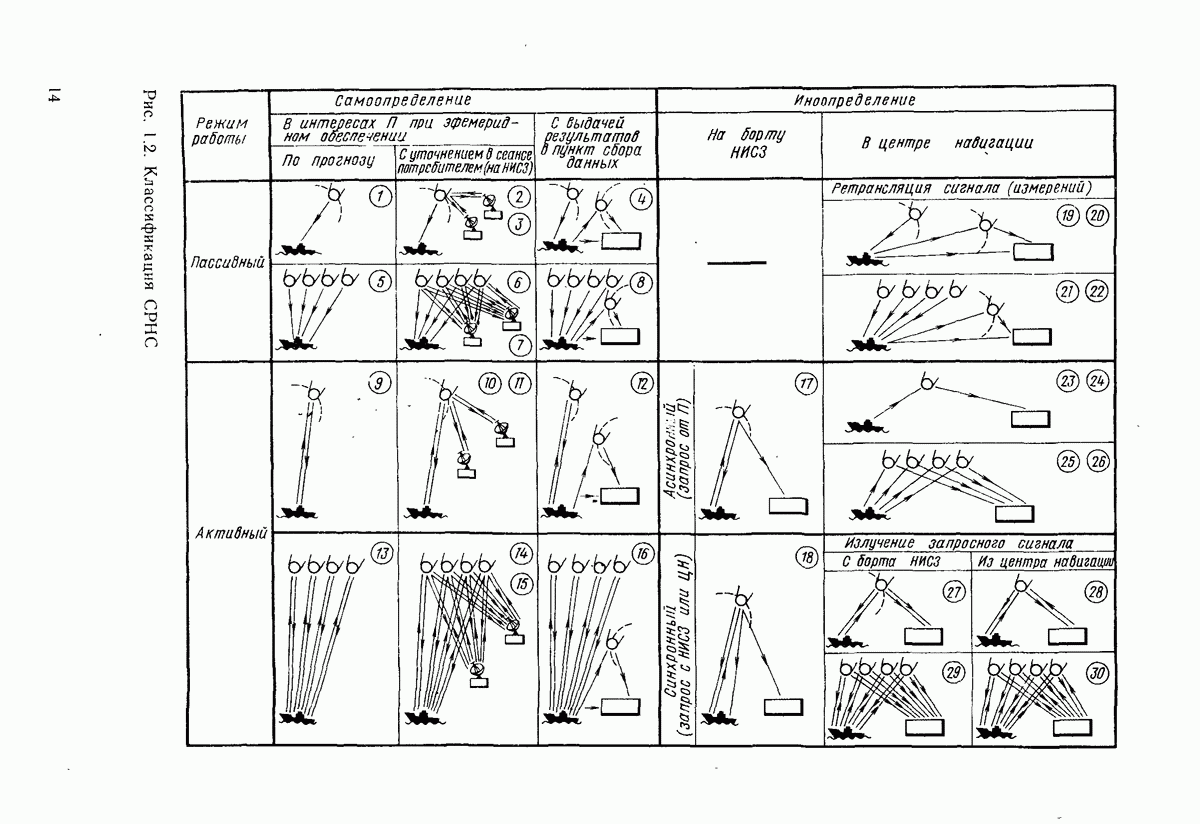
- 1.3. КЛАССИФИКАЦИЯ СРНС
- 1.4. СОГЛАСОВАНИЕ НАЧАЛ ОТСЧЕТА ПРОСТРАНСТВЕННЫХ И ВРЕМЕННОЙ КООРДИНАТ В ССРНС
- 1.5. ОБЩАЯ ХАРАКТЕРИСТИКА ЭЛЕМЕНТОВ ССРНС
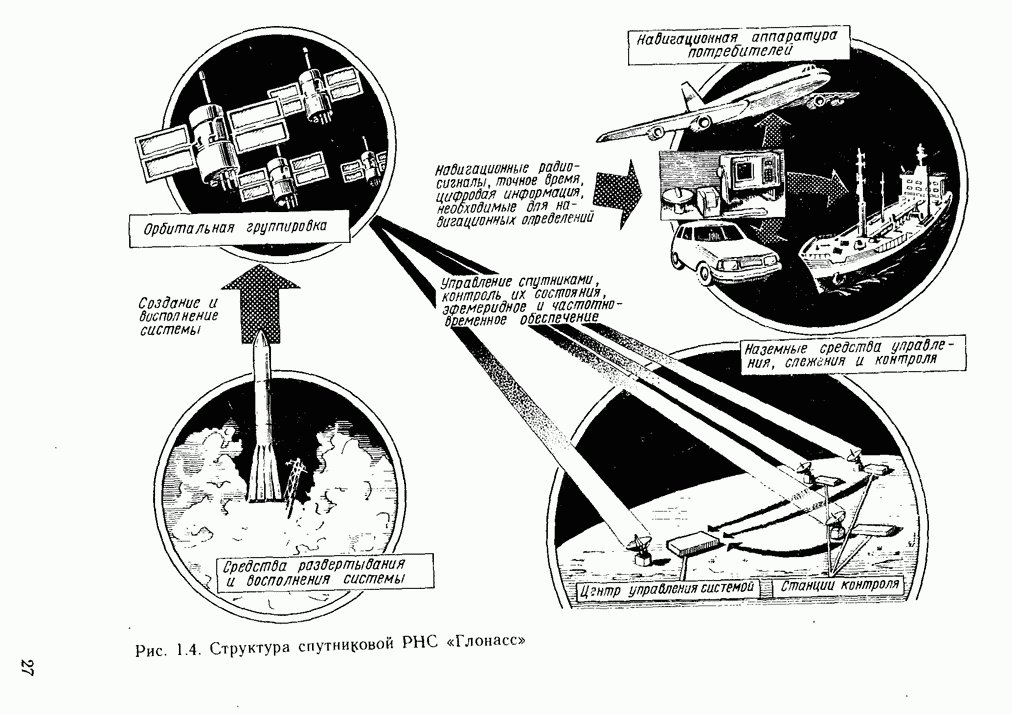
- 1.6. СОВЕТСКАЯ СЕТЕВАЯ СПУТНИКОВАЯ РНС «ГЛОНАСС»
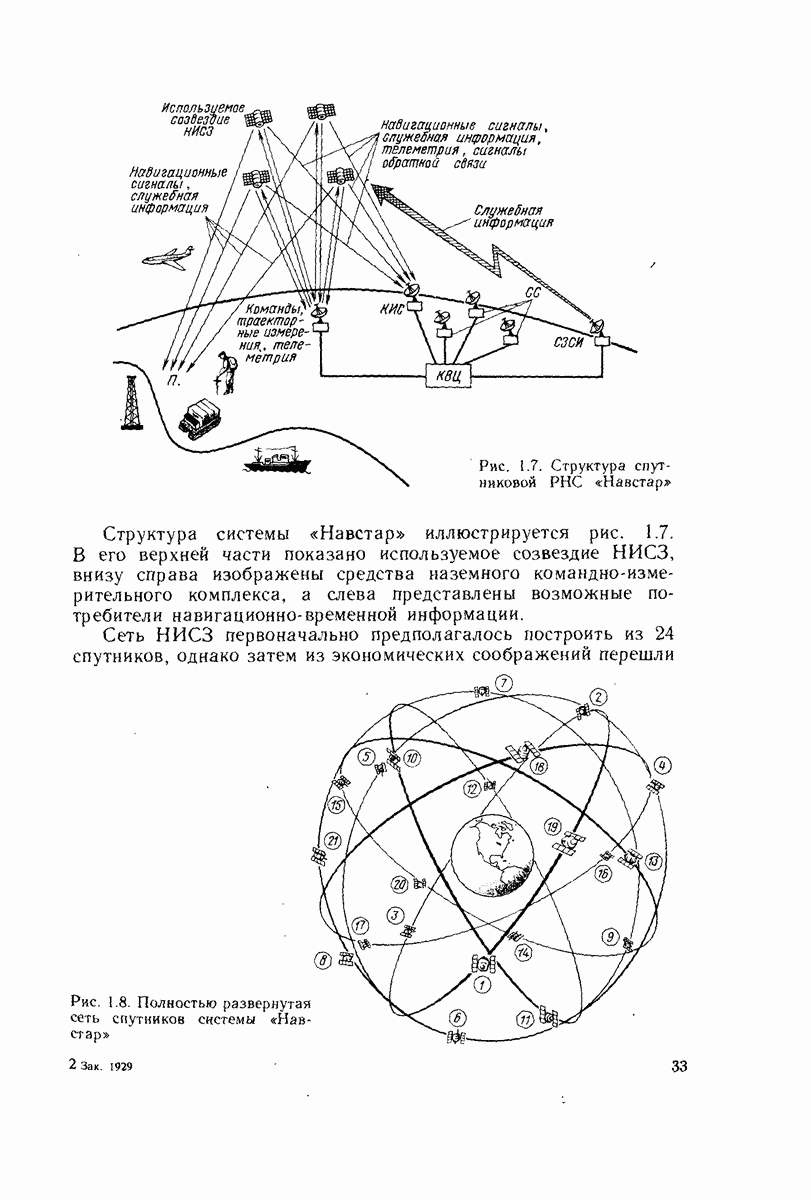
- 1.7. АМЕРИКАНСКАЯ СЕТЕВАЯ СПУТНИКОВАЯ РНС «НАВСТАР»
- 1.8. ИНФОРМАЦИОННЫЕ ЦЕНТРЫ СПУТНИКОВЫХ РНС
- ГЛАВА 2. ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА МЕТОДОВ ИЗМЕРЕНИЙ В ССРНС
- 2.2. НАВИГАЦИОННЫЕ ФУНКЦИИ
- 2.3. ГРАДИЕНТЫ ПОЛЕЙ НАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 2.4. ГРАДИЕНТНАЯ И ФУНДАМЕНТАЛЬНАЯ МАТРИЦЫ
- ГЛАВА 3. ОСНОВЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ В СРНС
- 3.1. КОНЕЧНЫЕ И ИТЕРАЦИОННЫЕ МЕТОДЫ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 3.2. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ОПРЕДЕЛЕНИЙ ПО ПОЛНОЙ ВЫБОРКЕ ИЗМЕРЕНИЙ
- 3.3. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ
- ГЛАВА 4. СИГНАЛЫ В СПУТНИКОВЫХ РНС
- 4.1. ОБЩИЕ ТРЕБОВАНИЯ К СИГНАЛАМ СРНС
- 4.2. СТАТИСТИЧЕСКАЯ МОДЕЛЬ РАДИОНАВИГАЦИОННОГО КАНАЛА СРНС
- 4.3. АНАЛИЗ ТРЕБОВАНИЙ, ПРЕДЪЯВЛЯЕМЫХ К СИГНАЛАМ СРНС
- 4.4. ТИПОВЫЕ СТРУКТУРЫ СОВМЕЩЕННЫХ СИГНАЛОВ ДЛЯ РАЗЛИЧНЫХ ВАРИАНТОВ ПАССИВНЫХ СРНС
- 4.5. ОСОБЕННОСТИ ВЫБОРА СТРУКТУРЫ СИГНАЛОВ В АКТИВНЫХ ВАРИАНТАХ СРНС
- ГЛАВА 5. ЭНЕРГЕТИКА НАВИГАЦИОННЫХ РАДИОЛИНИЙ
- 5.1. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К НАВИГАЦИОННЫМ РАДИОЛИНИЯМ
- 5.2. ОБЩАЯ ХАРАКТЕРИСТИКА ПРЯМОЙ И РЕТРАНСЛЯЦИОННОЙ РАДИОЛИНИЙ СРНС
- 5.3. УЧЕТ УСЛОВИЙ РАСПРОСТРАНЕНИЯ РАДИОВОЛН В СРНС
- 5.4. СПОСОБЫ УМЕНЬШЕНИЯ АТМОСФЕРНЫХ ПОГРЕШНОСТЕЙ ДАЛЬНОМЕРНОГО И ДОПЛЕРОВСКОГО ИЗМЕРЕНИЙ
- 5.5. ОСОБЕННОСТИ ЭНЕРГЕТИЧЕСКИХ РАСЧЕТОВ РАДИОЛИНИЙ В ЗАВИСИМОСТИ ОТ РАСПОЛОЖЕНИЯ ОБСЛУЖИВАЕМОГО СЛОЯ
- ГЛАВА 6. СПОСОБЫ РАЗДЕЛЕНИЯ СИГНАЛОВ
- 6.1. МЕТОДЫ УПЛОТНЕНИЯ И РАЗДЕЛЕНИЯ СИГНАЛОВ В СЕТЕВЫХ СРНС
- 6.2. ВЕРОЯТНОСТНОЕ РАЗДЕЛЕНИЕ СИГНАЛОВ СПУТНИКОВ ПРИ ИСПОЛЬЗОВАНИИ ШПС В ССРНС
- 6.3. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ШИРИНЫ ПОЛОСЫ ПРИНИМАЕМОГО ИЗЛУЧЕНИЯ В СЕТЕВЫХ СРНС
- 6.4. ОСОБЕННОСТИ РАЗДЕЛЕНИЯ СИГНАЛОВ В АКТИВНЫХ СРНС
- ГЛАВА 7. ПРИНЦИПЫ ПОСТРОЕНИЯ ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНОЙ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 7.1. ОБОБЩЕННАЯ СТРУКТУРНАЯ СХЕМА АП ССРНС
- 7.2. ИНФОРМАЦИОННЫЕ ПОТОКИ В АП
- 7.3. ИЗМЕРЯЕМЫЕ РАДИОНАВИГАЦИОННЫЕ ПАРАМЕТРЫ
- 7.4. ВИДЫ И МОДЕЛИ ПОМЕХ
- 7.5. ОСНОВЫ СТАТИСТИЧЕСКОГО СИНТЕЗА ИЗМЕРИТЕЛЕЙ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- ГЛАВА 8. УСТРОЙСТВА ПЕРВИЧНОЙ ОБРАБОТКИ РАДИОНАВИГАЦИОННОГО СИГНАЛА
- 8.1. НЕОБХОДИМОСТЬ ПОИСКА РАДИОНАВИГАЦИОННЫХ СИГНАЛОВ
- 8.2. СПОСОБЫ РЕШЕНИЯ ЗАДАЧИ ПОИСКА РАДИОСИГНАЛОВ НИСЗ
- 8.3. УСТРОЙСТВА ОЦЕНКИ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 8.4. ЦИФРОВАЯ РЕАЛИЗАЦИЯ УСТРОЙСТВ ПЕРВИЧНОЙ ОБРАБОТКИ
- 8.5. ОЦЕНКА ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 8.6. СПОСОБЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ АП
- ГЛАВА 9. РАЗНОВИДНОСТИ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 9.1. ОСОБЕННОСТИ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ РАЗЛИЧНЫХ ТИПОВ
- 9.2. ОДНОКАНАЛЬНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.3. МНОГОКАНАЛЬНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.4. МУЛЬТИПЛЕКСНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.5. АППАРАТУРА ПОТРЕБИТЕЛЕЙ ДЛЯ ОДНОВРЕМЕННОЙ РАБОТЫ ПО СИСТЕМАМ «ГЛОНАСС» и «НАВСТАР»
- 9.6. УНИФИКАЦИЯ АППАРАТУРНЫХ РЕШЕНИЙ
- ГЛАВА 10. КАДР НАВИГАЦИОННОГО СИГНАЛА
- 10.1. ОРГАНИЗАЦИЯ ОБРАБОТКИ ИЗМЕРЕНИЙ И ФОРМИРОВАНИЕ ЭФЕМЕРИДНОЙ ИНФОРМАЦИИ
- 10.2. МЕТОДОЛОГИЯ ВЫБОРА ЭЛЕМЕНТОВ КАДРА СИГНАЛА
- 10.3. УСЛОВИЯ РЕАЛИЗАЦИИ АЛГОРИТМОВ ПРОГНОЗИРОВАНИЯ ЭФЕМЕРИД НИСЗ
- 10.4. АЛГОРИТМЫ ПРОГНОЗИРОВАНИЯ ДВИЖЕНИЯ НИСЗ
- 10.5. СОСТАВ, ФОРМА ПРЕДСТАВЛЕНИЯ И ОБЪЕМ ИНФОРМАЦИИ, ПЕРЕДАВАЕМОЙ В КАДРЕ НАВИГАЦИОННОГО СИГНАЛА СИСТЕМЫ «НАВСТАР»
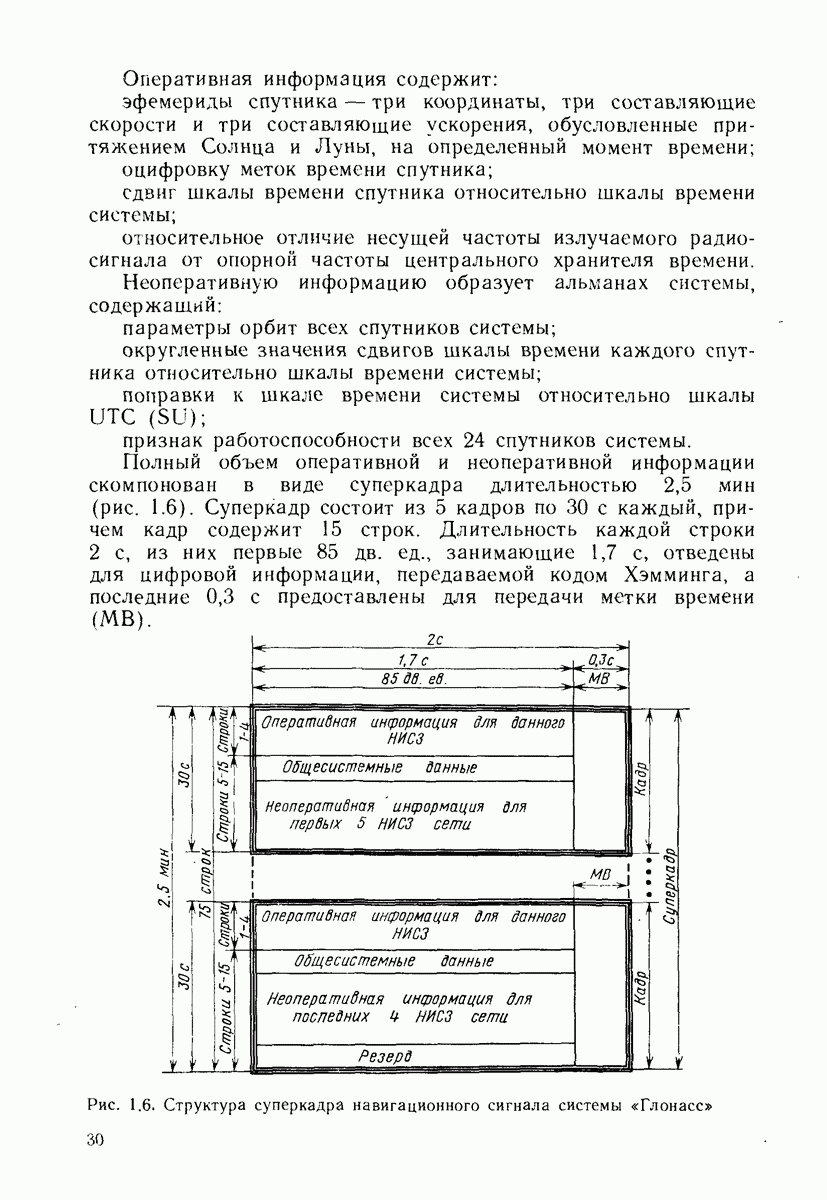
- 10.6. КАДР НАВИГАЦИОННОГО СИГНАЛА СИСТЕМЫ «ГЛОНАСС»
- ГЛАВА 11. СИНХРОНИЗАЦИЯ ВРЕМЕННЫХ ШКАЛ СИСТЕМЫ НИСЗ
- 11.1. ОБЩАЯ ХАРАКТЕРИСТИКА ХРАНИТЕЛЕЙ ВРЕМЕННЫХ ШКАЛ
- 11.2. МЕТОДЫ СВЕРКИ ВРЕМЕННЫХ ШКАЛ
- 11.3. КОРРЕКЦИЯ ВРЕМЕННЫХ ШКАЛ
- 11.4. СПОСОБЫ УЧЕТА В НАВИГАЦИОННОМ СЕАНСЕ СМЕЩЕНИЙ ВРЕМЕННЫХ ШКАЛ НИСЗ
- 11.5. СОГЛАСОВАНИЕ ШКАЛ ВРЕМЕНИ СИСТЕМ «ГЛОНАСС» И «НАВСТАР»
- 11.6. СИНХРОНИЗАЦИЯ ВРЕМЕННЫХ ШКАЛ СЕТИ НИСЗ НА ОСНОВЕ ВЗАИМНЫХ ВРЕМЕННЫХ ИЗМЕРЕНИЙ
- ГЛАВА 12. ОБЛАСТИ ИСПОЛЬЗОВАНИЯ СЕТЕВЫХ СПУТНИКОВЫХ РНС
- 12.1. ПРИМЕНЕНИЕ ССРНС — ОСНОВА КООРДИНАТНО-ВРЕМЕННОГО ОБЕСПЕЧЕНИЯ
- 12.2. ОПРЕДЕЛЕНИЕ КООРДИНАТ, ИХ ПРОИЗВОДНЫХ И НАВИГАЦИОННЫХ ЭЛЕМЕНТОВ НАЗЕМНЫХ И ПРИЗЕМНЫХ ОБЪЕКТОВ
- 12.3. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ДВИЖЕНИЯ ОКОЛОЗЕМНЫХ КА
- 12.4. ОПРЕДЕЛЕНИЕ ВЗАИМНЫХ КООРДИНАТ В ИНТЕРЕСАХ ПРЕДУПРЕЖДЕНИЯ СТОЛКНОВЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ И ГРУППОВОГО ИХ ВОЖДЕНИЯ
- 12.5. ВЫСОКОТОЧНАЯ ГЕОДЕЗИЧЕСКАЯ ПРИВЯЗКА
- 11.6. ОПРЕДЕЛЕНИЕ ОРИЕНТАЦИИ ОБЪЕКТОВ В ПРОСТРАНСТВЕ
- 12.7. СИНХРОНИЗАЦИЯ ИЗЛУЧЕНИЯ СТАНЦИИ С НАЗЕМНЫМ БАЗИРОВАНИЕМ
- 12.8. НАБЛЮДЕНИЕ ДЛЯ ОБЕСПЕЧЕНИЯ УПРАВЛЕНИЯ ДВИЖЕНИЕМ ПЕРЕМЕЩАЮЩИХСЯ ОБЪЕКТОВ
- 12.9. ЦЕЛЕУКАЗАНИЕ В СИСТЕМЕ ОБНАРУЖЕНИЯ ТЕРПЯЩИХ БЕДСТВИЕ
- РАЗДЕЛ ВТОРОЙ. ОСНОВЫ НАВИГАЦИОННОГО ИСПОЛЬЗОВАНИЯ ССРНС
- 13.1. ЗАДАЧА СИНТЕЗА АЛГОРИТМА НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 13.2. МОДЕЛЬ НАВИГАЦИОННЫХ ИЗМЕРЕНИЙ
- 13.3. МОДЕЛЬ ДИНАМИКИ ПОТРЕБИТЕЛЯ
- 13.4. ФАКТОРЫ, ВЛИЯЮЩИЕ НА ВЫБОР СПОСОБА ОБРАБОТКИ ИНФОРМАЦИИ В ССРНС
- ГЛАВА 14. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ ПО ВЫБОРКЕ ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.1. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ ПО ВЫБОРКЕ МИНИМАЛЬНОГО ОБЪЕМА ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.2. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ ПО ИЗБЫТОЧНОМУ ОБЪЕМУ ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.3. ОЦЕНКА СХОДИМОСТИ АЛГОРИТМОВ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ
- ГЛАВА 15. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ ПО ВЫБОРКЕ ИЗМЕРЕНИИ НАРАСТАЮЩЕГО ОБЪЕМА
- 15.1. РЕКУРРЕНТНЫЙ АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ МЕТОДОМ КАЛМАНА И ЕГО МОДИФИКАЦИИ ПРИ РАЗЛИЧНЫХ СОСТАВАХ ИЗМЕРЕНИЙ
- 15.2. СПОСОБЫ УСТРАНЕНИЯ РАСХОДИМОСТИ ФИЛЬТРОВ КАЛМАНА
- 15.3. РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ ГАУССОВСКОГО ФИЛЬТРА 2-ГО ПОРЯДКА
- 15.4. СРАВНЕНИЕ РЕКУРРЕНТНЫХ АЛГОРИТМОВ ПО РАЗМЕРАМ ОБЛАСТИ СХОДИМОСТИ
- ГЛАВА 16. СПОСОБЫ ОЦЕНКИ ТОЧНОСТИ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ
- 16.1. ПОКАЗАТЕЛИ ТОЧНОСТИ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 16.2. КОРРЕЛЯЦИОННАЯ МАТРИЦА ОШИБОК ОПРЕДЕЛЯЕМЫХ ПАРАМЕТРОВ
- 16.3. ИСТОЧНИКИ ОШИБОК НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 16.4. ОТОБРАЖЕНИЕ ТОЧНОСТНЫХ ХАРАКТЕРИСТИК И ИНТЕГРАЛЬНАЯ ОЦЕНКА ТОЧНОСТИ СРНС
- ГЛАВА 17. ВЫСОКОТОЧНОЕ СЛИЧЕНИЕ ШКАЛ ВРЕМЕНИ УДАЛЕННЫХ ПУНКТОВ ПО СИГНАЛАМ НИСЗ
- 17.1. МЕТОДЫ СИНХРОНИЗАЦИИ ШВ УДАЛЕННЫХ ПУНКТОВ
- 17.2. ОЦЕНКА ТОЧНОСТИ СВЕРКИ ШВ УДАЛЕННЫХ ПУНКТОВ ПО ВЫБОРКЕ ОДНОВРЕМЕННЫХ ПСЕВДОДАЛЬНОМЕРНЫХ ИЗМЕРЕНИЙ
- 17.3. ПОТЕНЦИАЛЬНАЯ ТОЧНОСТЬ СВЕРКИ ШВ ПУНКТА С ИЗВЕСТНЫМИ КООРДИНАТАМИ ПО ДАННЫМ ПСЕВДОДАЛЬНОМЕРНЫХ И РАДИАЛЬНЫХ ПСЕВДОСКОРОСТНЫХ ИЗМЕРЕНИЙ
- ГЛАВА 18. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ КООРДИНАТ ПРИ ОДНОМОМЕНТНЫХ ИЗМЕРЕНИЯХ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ НИСЗ
- 18.2. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПОВЕРХНОСТНЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ДВУХ НИСЗ
- 18.3. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПОВЕРХНОСТНЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ТРЕХ НИСЗ
- 18.4. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПРОСТРАНСТВЕННЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ЧЕТЫРЕХ НИСЗ
- 18.5. ТОЧНОСТНЫЕ СВОЙСТВА ДОПЛЕРОВСКИХ МЕТОДОВ В СЕТЕВЫХ СРНС В СРАВНЕНИИ С ДАЛЬНОМЕРНЫМИ
- ГЛАВА 19. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННЫХ КООРДИНАТ И ВЕКТОРА СКОРОСТИ ПО СЕТИ НИСЗ
- 19.2. РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ ГЕОМЕТРИЧЕСКИХ ФАКТОРОВ
- 19.3. ТОЧНОСТЬ ОЦЕНКИ КООРДИНАТ И ВРЕМЕНИ
- 19.4. ТОЧНОСТЬ ОЦЕНКИ СКОРОСТИ ДВИЖЕНИЯ
- 19.5. ОЦЕНКА ТОЧНОСТИ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ КА
- ГЛАВА 20. ДИФФЕРЕНЦИАЛЬНЫЙ РЕЖИМ ССРНС
- 20.2. СТРУКТУРА ДИФФЕРЕНЦИАЛЬНОЙ ПОДСИСТЕМЫ
- 20.3. МЕТОДЫ ДИФФЕРЕНЦИАЛЬНЫХ ОПРЕДЕЛЕНИЙ
- 20.4. КОРРЕКТИРУЮЩАЯ ИНФОРМАЦИЯ
- 20.5. КАНАЛЫ ПЕРЕДАЧИ КОРРЕКТИРУЮЩЕЙ ИНФОРМАЦИИ
- 20.6. ТОЧНОСТНЫЕ ХАРАКТЕРИСТИКИ ДМ
- 20.7. ИЗМЕРЕНИЯ РНП ПО ФАЗЕ НЕСУЩИХ КОЛЕБАНИЙ
- 20.8. РЕЗУЛЬТАТЫ ИСПЫТАНИЙ. РЕАЛИЗАЦИЯ ДПС
- ГЛАВА 21. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ В АКТИВНОМ И ОТНОСИТЕЛЬНОМ РЕЖИМАХ
- 21.1. ТОЧНОСТНЫЕ ХАРАКТЕРИСТИКИ АКТИВНЫХ СРНС
- 21.2. ТОЧНОСТНЫЕ СВОЙСТВА СЕТЕВЫХ СРНС В ОТНОСИТЕЛЬНОМ РЕЖИМЕ
- ГЛАВА 22. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ БОРТОВОЙ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 22.1. АВТОМАТИЗАЦИЯ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ И ШТУРМАНСКИХ РАСЧЕТОВ
- 22.2. МЕТОДИЧЕСКИЕ ОСНОВЫ МАТЕМАТИЧЕСКОГО ОБЕСПЕЧЕНИЯ
- 22.3. ОСНОВНЫЕ ЗАДАЧИ ВТО
- 22.4. УПРАВЛЯЮЩИЙ АЛГОРИТМ
- 22.5. ВРЕМЕННАЯ ДИАГРАММА АЛГОРИТМА
- 22.6. ПРИНЦИПЫ ПРОЕКТИРОВАНИЯ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
- РАЗДЕЛ ТРЕТИЙ. КОМПЛЕКСНОЕ ПРОЕКТИРОВАНИЕ ССРНС
- 23.1. ОСНОВНЫЕ ЗАДАЧИ, РЕШАЕМЫЕ ПРИ КОМПЛЕКСНОМ ПРОЕКТИРОВАНИИ
- 23.2. ЭТАПЫ СОЗДАНИЯ ССРНС
- 23.3. ОСОБЕННОСТИ ПРОЕКТОВ СРНС РАЗЛИЧНОГО НАЗНАЧЕНИЯ
- ГЛАВА 24. СИНТЕЗ СТРУКТУРЫ СЕТИ НИСЗ ИЗ УСЛОВИИ ОБЕСПЕЧЕНИЯ ЗАДАННОЙ КРАТНОСТИ ПОКРЫТИЯ
- 24.2. ЗОНА РАДИОВИДИМОСТИ, ПОЛОСА ПОКРЫТИЯ И ОБЛАСТЬ ПЕРЕКРЫТИЯ
- 24.3. ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ СЕТИ НИСЗ, ОБЕСПЕЧИВАЮЩЕЙ ЗАДАННУЮ МИНИМАЛЬНУЮ КРАТНОСТЬ ПОКРЫТИЯ
- 24.4. НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ СЕТИ НИСЗ
- 24.5. СВОЙСТВА ЭКСТРЕМАЛЬНОЙ СЕТИ НИСЗ, ОБЕСПЕЧИВАЮЩЕЙ ЗАДАННУЮ МИНИМАЛЬНУЮ КРАТНОСТЬ ПОКРЫТИЯ
- 24.6. УСЛОВИЕ СТАБИЛЬНОСТИ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ СЕТИ НИСЗ
- ГЛАВА 25. СИНТЕЗ СТРУКТУРЫ СЕТИ НИСЗ ПО КРИТЕРИЮ ТОЧНОСТИ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 25.2. ВЫБОР ОПТИМАЛЬНОГО ПО КРИТЕРИЮ ТОЧНОСТИ СОЗВЕЗДИЯ НИСЗ
- 25.3. ПРИБЛИЖЕННЫМ УЧЕТ ПАРАЛЛАКСА МИНИМАЛЬНОГО СОЗВЕЗДИЯ
- 25.4. КАЧЕСТВЕННЫЙ АНАЛИЗ ЗОН ПОНИЖЕННОЙ ТОЧНОСТИ
- 25.5. УТОЧНЕНИЕ СТРУКТУРЫ СЕТИ НИСЗ ПО МИНИМАКСНОМУ КРИТЕРИЮ ТОЧНОСТИ
- 25.6. СРАВНЕНИЕ ССРНС «ГЛОНАСС» И «НАВСТАР»
- ГЛАВА 26. ОСНОВЫ КОМПЛЕКСНОГО ИСПОЛЬЗОВАНИЯ СРНС С ДРУГИМИ РАДИОНАВИГАЦИОННЫМИ И АВТОНОМНЫМИ НАВИГАЦИОННЫМИ СРЕДСТВАМИ
- 26.1. ОБЩИЕ ПРЕДПОСЫЛКИ И ВОЗМОЖНОСТИ СОВМЕСТНОГО ИСПОЛЬЗОВАНИЯ СПУТНИКОВЫХ РНС И ДРУГИХ НАВИГАЦИОННЫХ СРЕДСТВ
- 26.2. КОМБИНИРОВАННАЯ РАЗНОСТНО-ДАЛЬНОМЕРНАЯ РНС, СОСТОЯЩАЯ ИЗ НАЗЕМНЫХ СТАНЦИЙ И СТАЦИОНАРНОГО НИСЗ
- 26.3. КОМПЛЕКСНОЕ ИСПОЛЬЗОВАНИЕ НИЗКООРБИТАЛЬНОЙ СРНС И ФАЗОВОЙ СДВ РНС
- 26.4. КОМПЛЕКСИРОВАНИЕ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ НА УРОВНЕ ПЕРВИЧНОЙ ОБРАБОТКИ ИНФОРМАЦИИ
- ГЛАВА 27. КРИТЕРИИ ОЦЕНКИ ЭФФЕКТИВНОСТИ НАВИГАЦИОННОГО ИСПОЛЬЗОВАНИЯ СРНС
- 27.2. ОСОБЕННОСТИ ИССЛЕДОВАНИЯ ЭФФЕКТИВНОСТИ СПУТНИКОВЫХ РНС
- 27.3. ОБЩИЕ И ЧАСТНЫЕ КРИТЕРИИ ЭФФЕКТИВНОСТИ СРНС