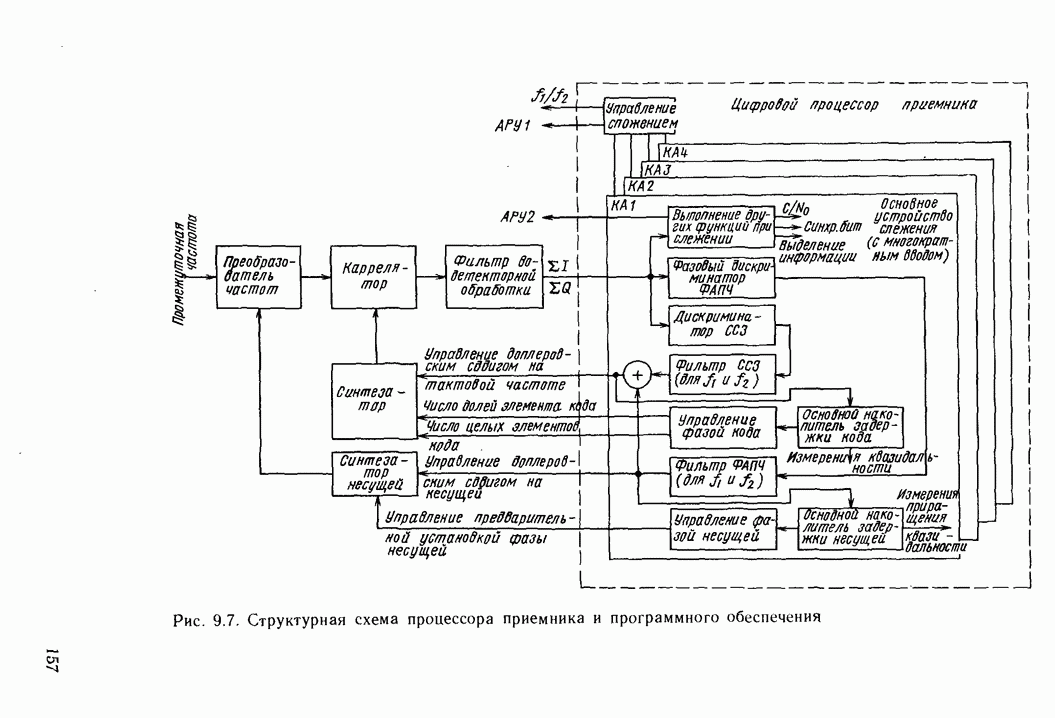
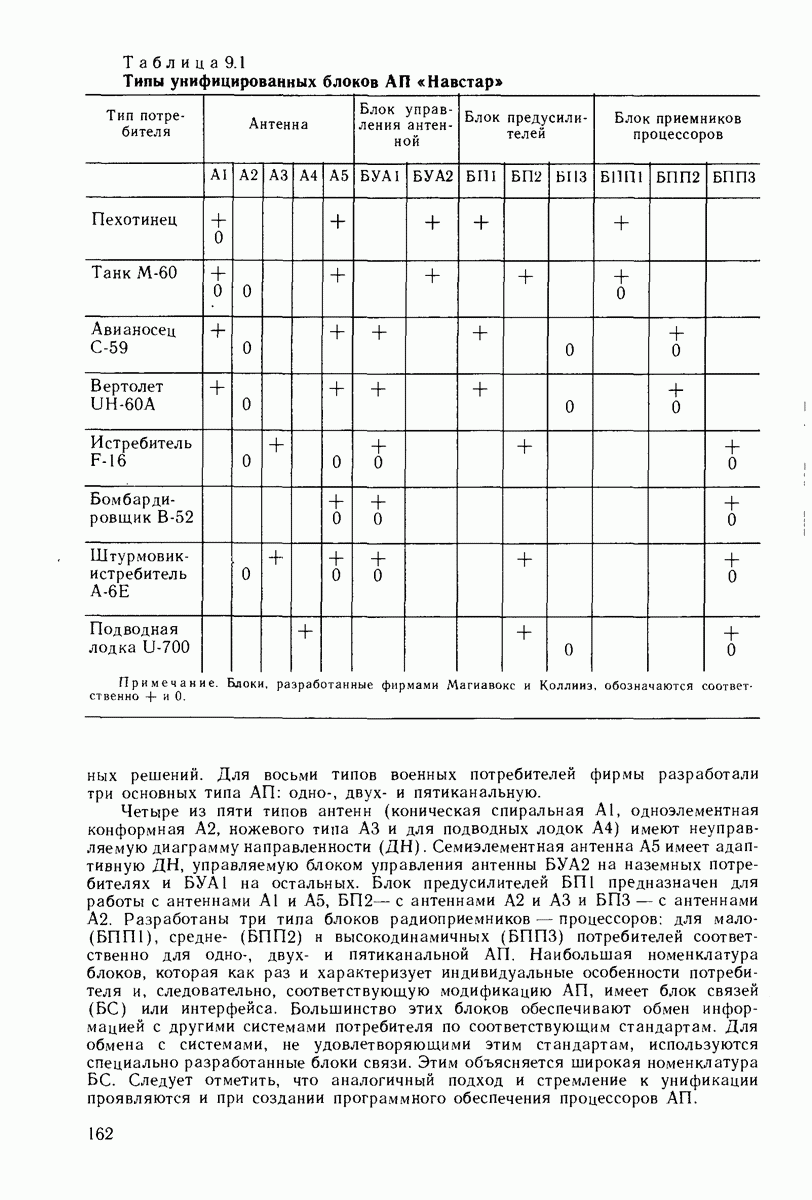
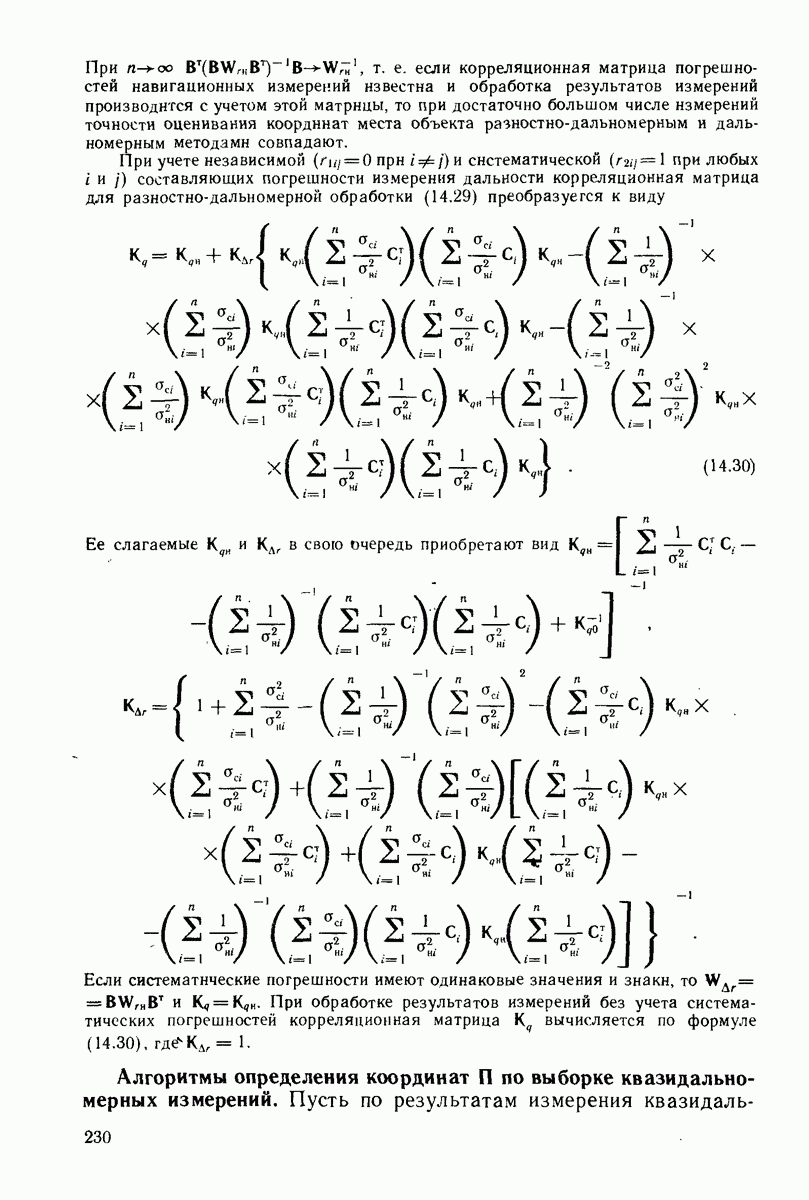| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
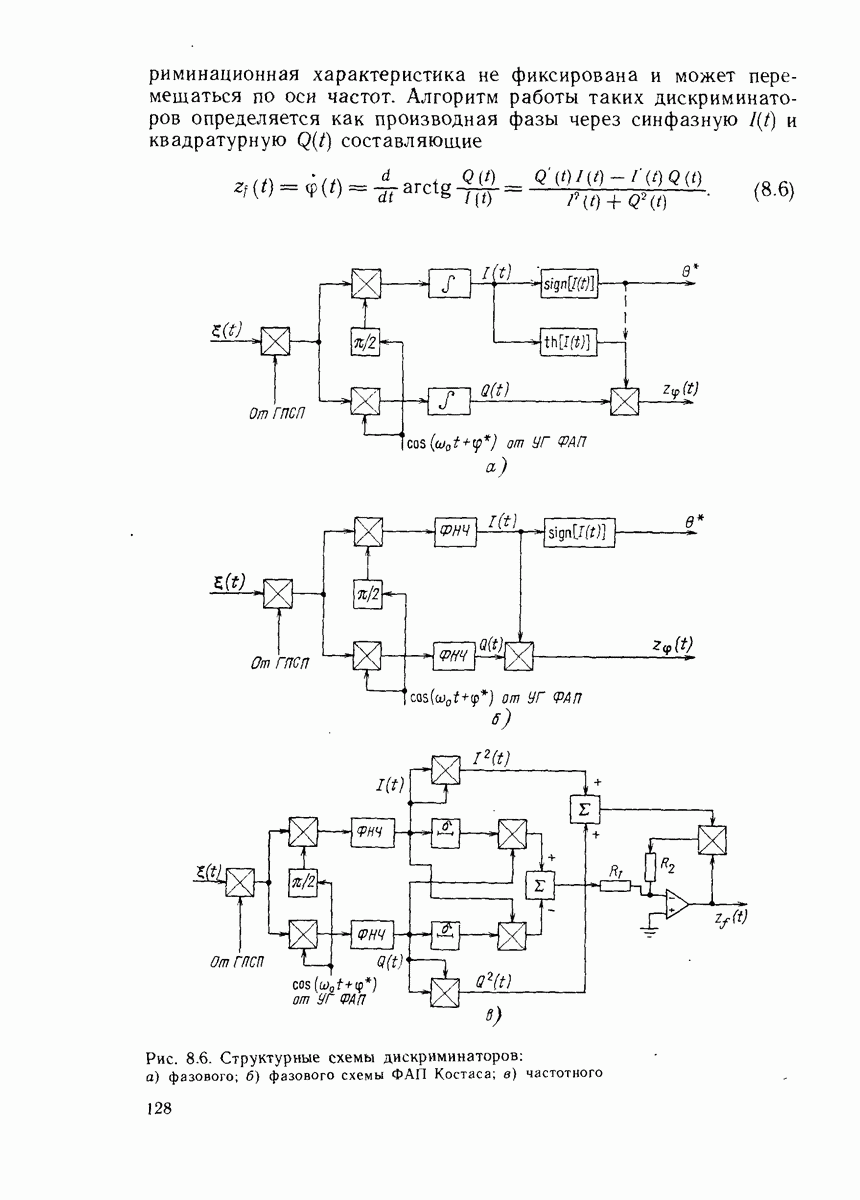
15.3. РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ ГАУССОВСКОГО ФИЛЬТРА 2-ГО ПОРЯДКА
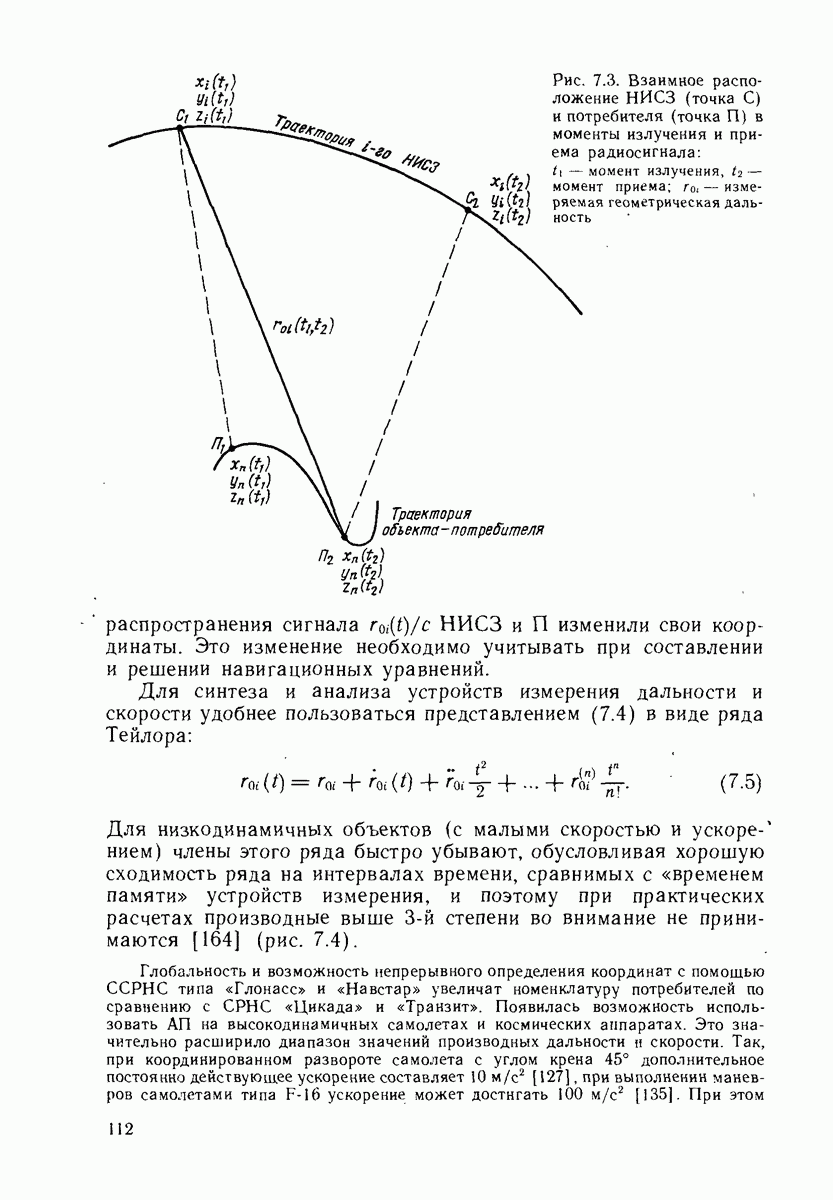
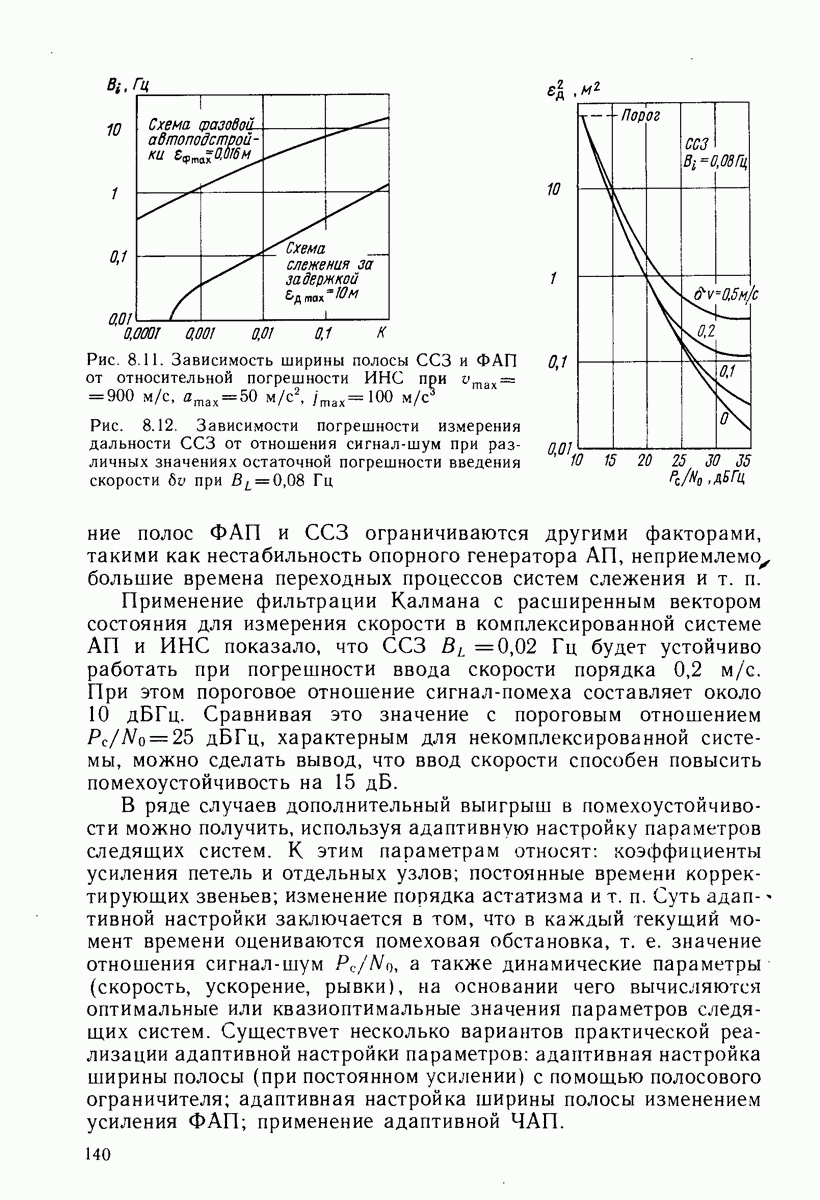
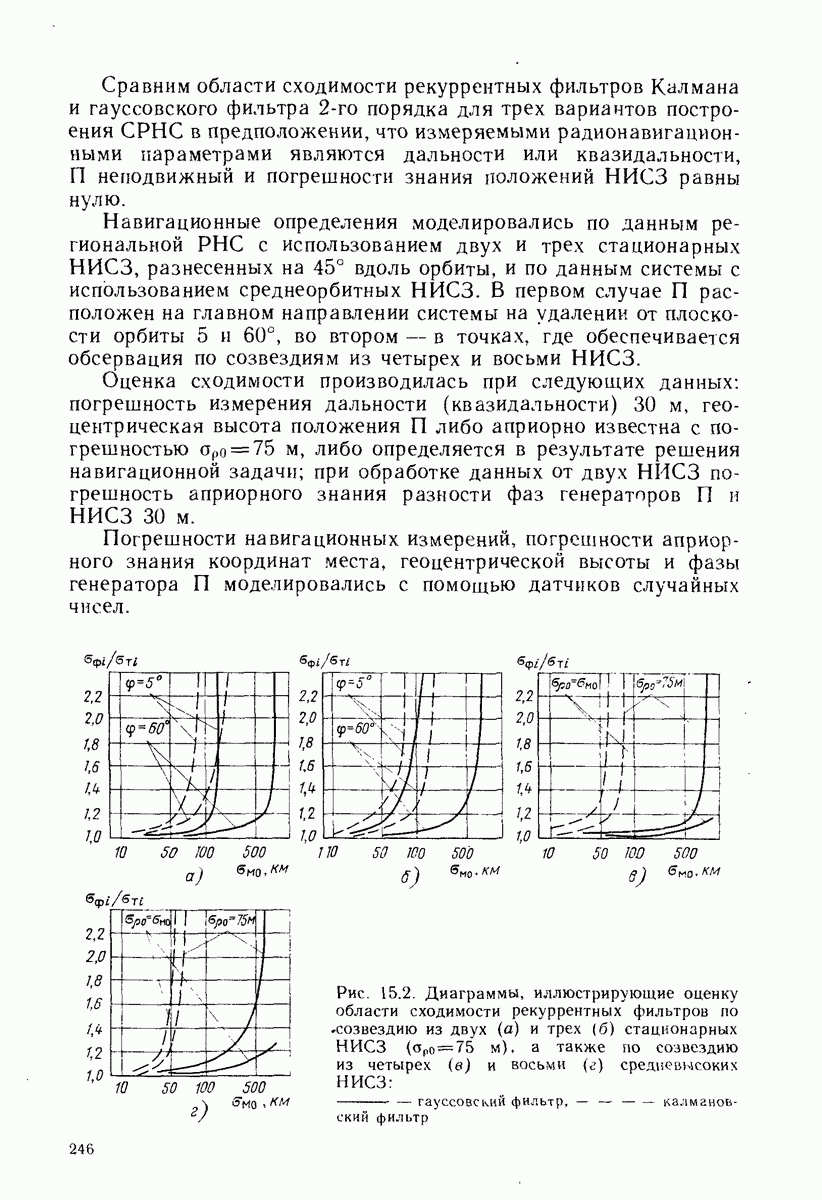
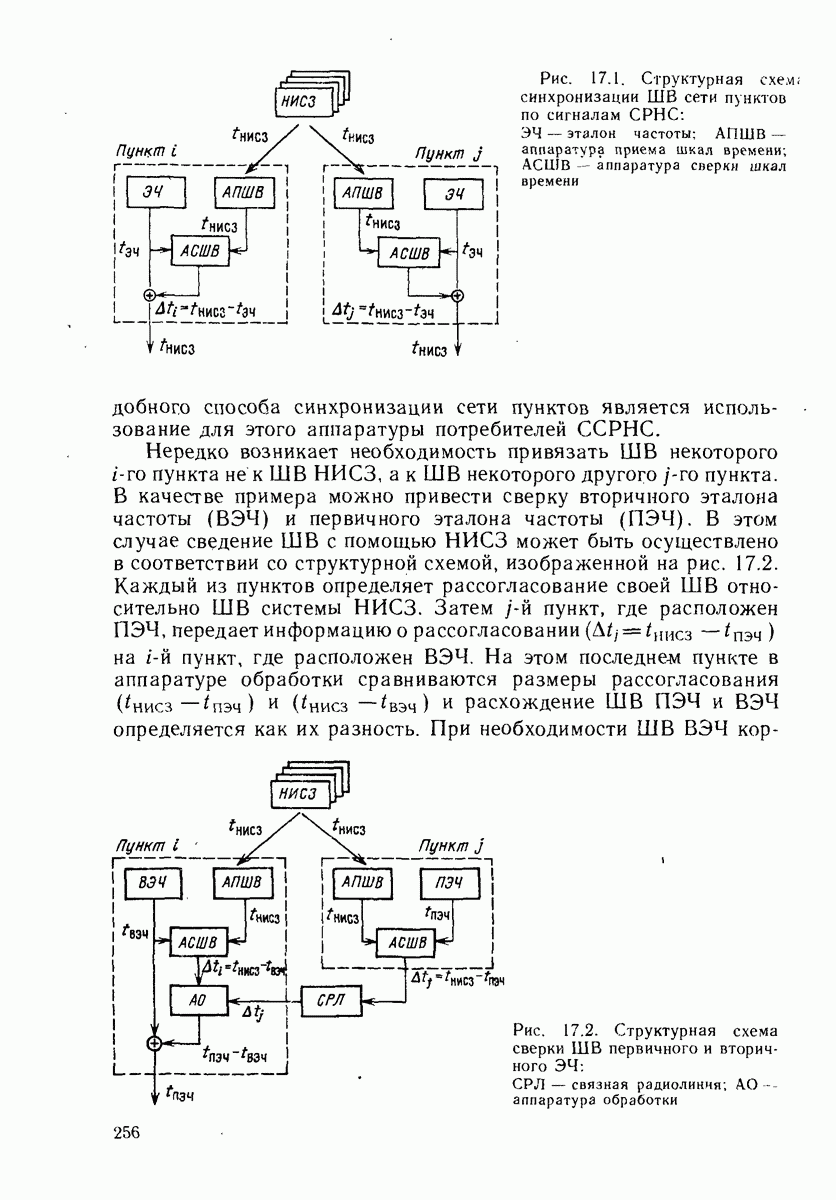
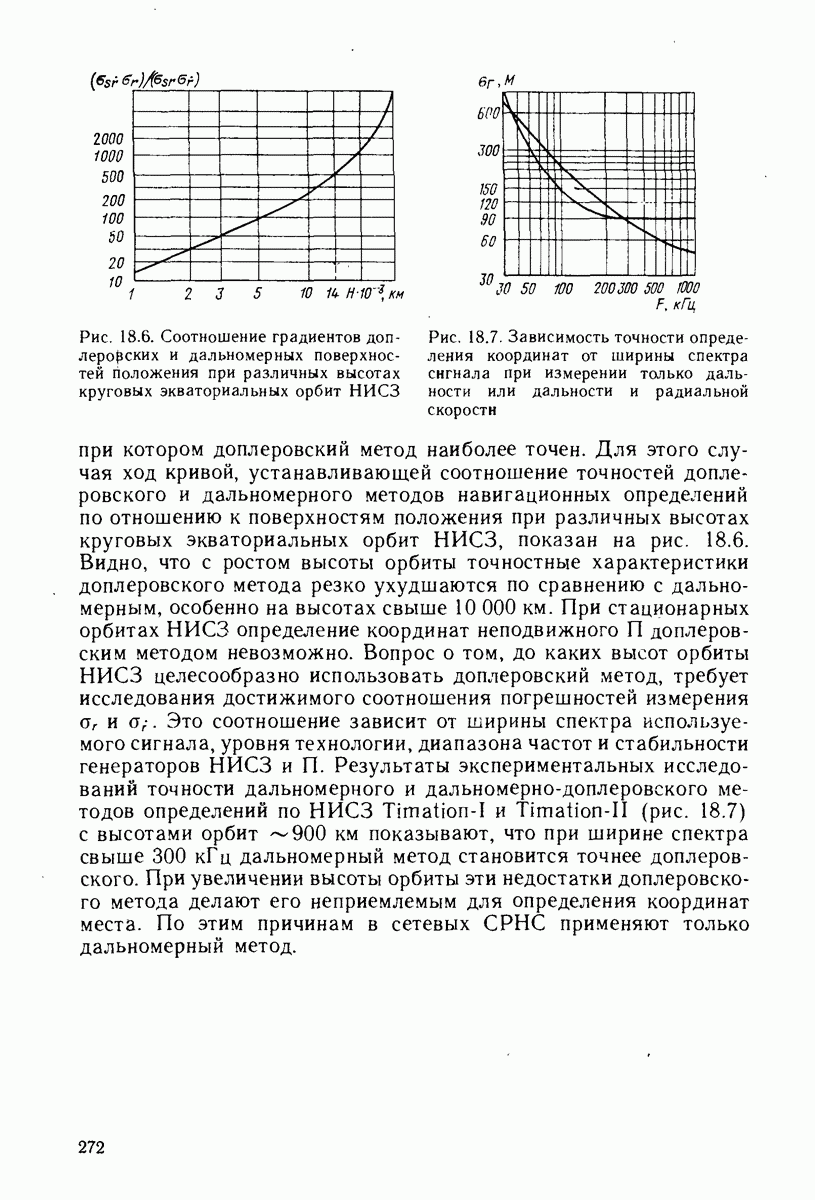
Применительно к дальномерным СРНС неточность задания математической модели канала измерения может проявляться в том, что при определенных априорных погрешностях координат П пренебрежение нелинейностью в функции измерения дальности приводит к расходимости рекуррентного фильтра.
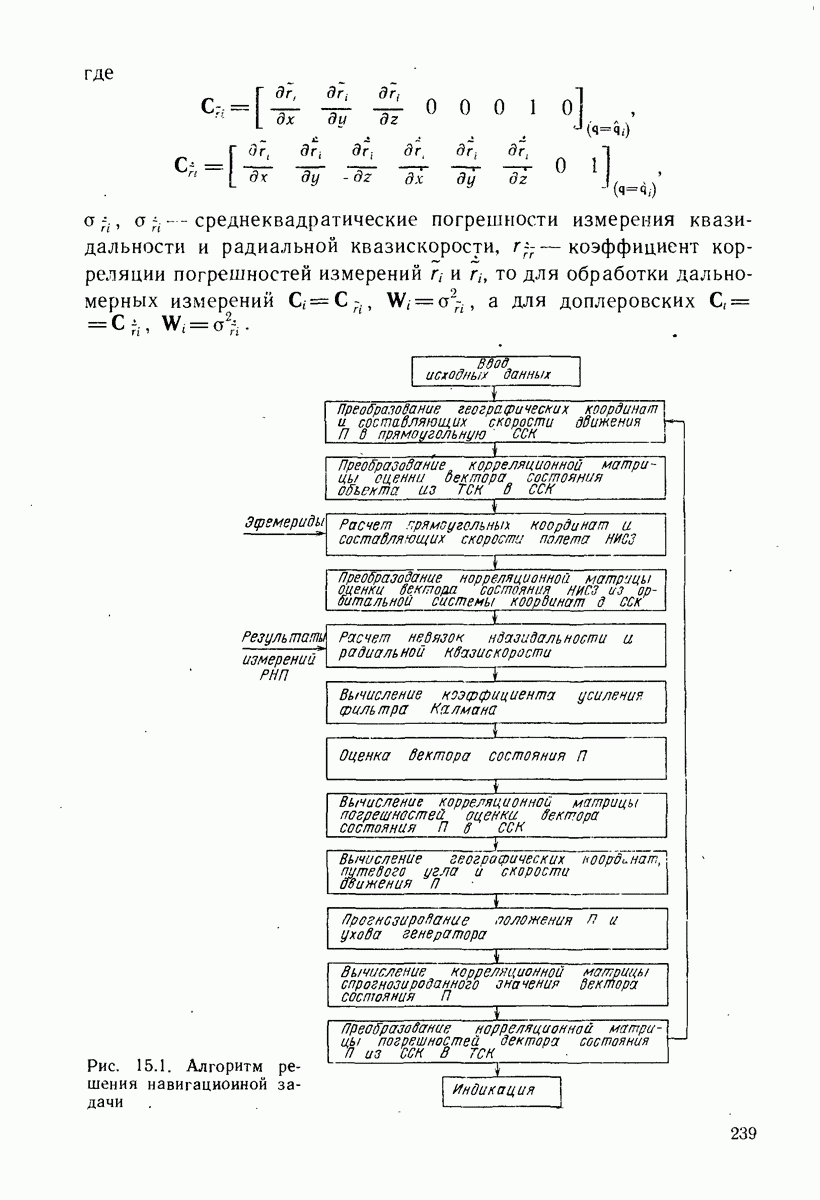
Рассмотрим рекуррентный метод решения навигационной задачи применительно к неподвижному П при нулевых погрешностях положений НИСЗ. При этих условиях уравнения фильтра Калмана (15.4)-(15.8) примут вид

Одно из основных допущений, сделанное при выводе этих выражений, состояло в использовании линеаризованного уравнения канала измерения. Применение метода линеаризации правомерно только тогда, когда диапазон изменения аргументов навигационной функции достаточно мал. На практике это условие не всегда может выполняться, - и тогда пренебрежение нелинейными членами разложения приводит к несоответствию между вычисленными значениями корреляционной матрицы  и истинными погрешностями навигационных определений, что нарушает оптимальность обработки последующих результатов измерений и вызывает расходимость рекуррентных алгоритмов. Один из наиболее естественных способов сохранения оптимальности обработки состоит в учете при разложении нелинейной функции
и истинными погрешностями навигационных определений, что нарушает оптимальность обработки последующих результатов измерений и вызывает расходимость рекуррентных алгоритмов. Один из наиболее естественных способов сохранения оптимальности обработки состоит в учете при разложении нелинейной функции  в ряд Тейлора не только линейных, но и некоторых последующих членов разложения более высокого порядка:
в ряд Тейлора не только линейных, но и некоторых последующих членов разложения более высокого порядка:

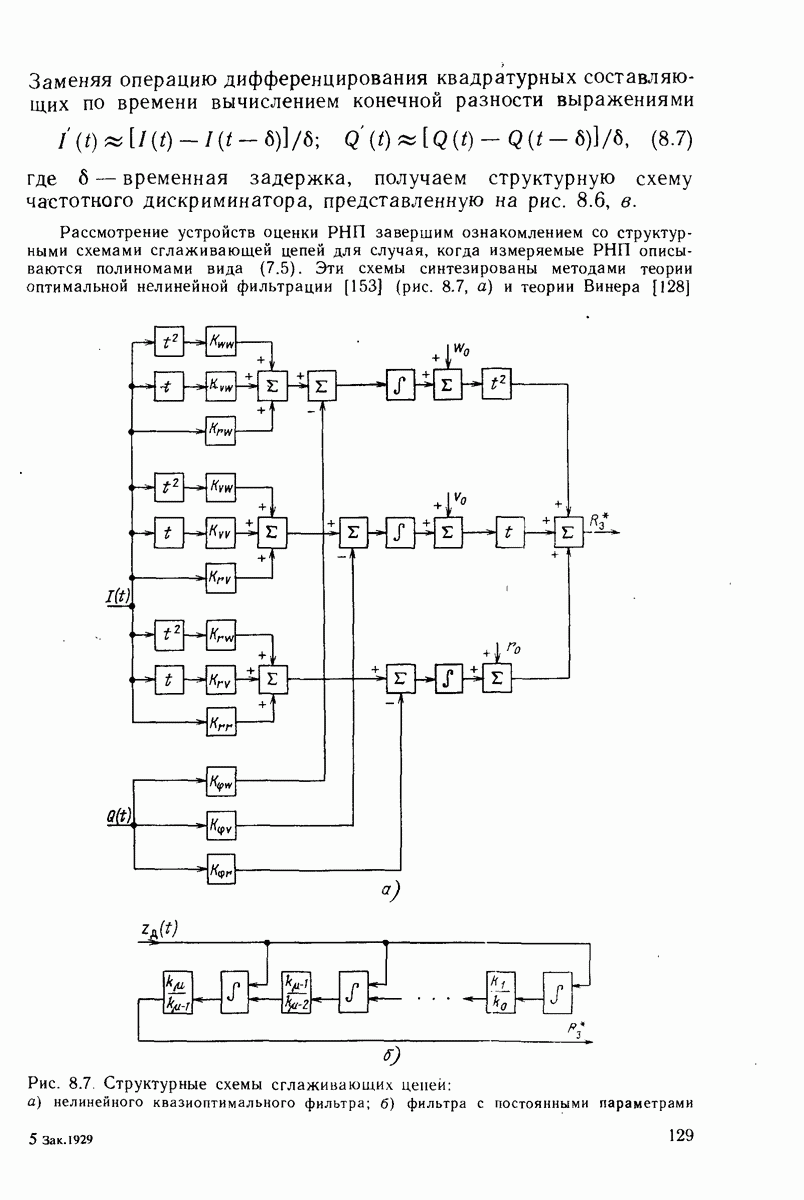
где 
Если в (15.20) сохранить члены разложения до квадратичного включительно, то условное математическое ожидание  и априорное значение дисперсии
и априорное значение дисперсии  примут вид
примут вид

где  след матрицы. Последние члены в (15.21) и (15.22) представляют собой поправки на нелинейность функции.
след матрицы. Последние члены в (15.21) и (15.22) представляют собой поправки на нелинейность функции.
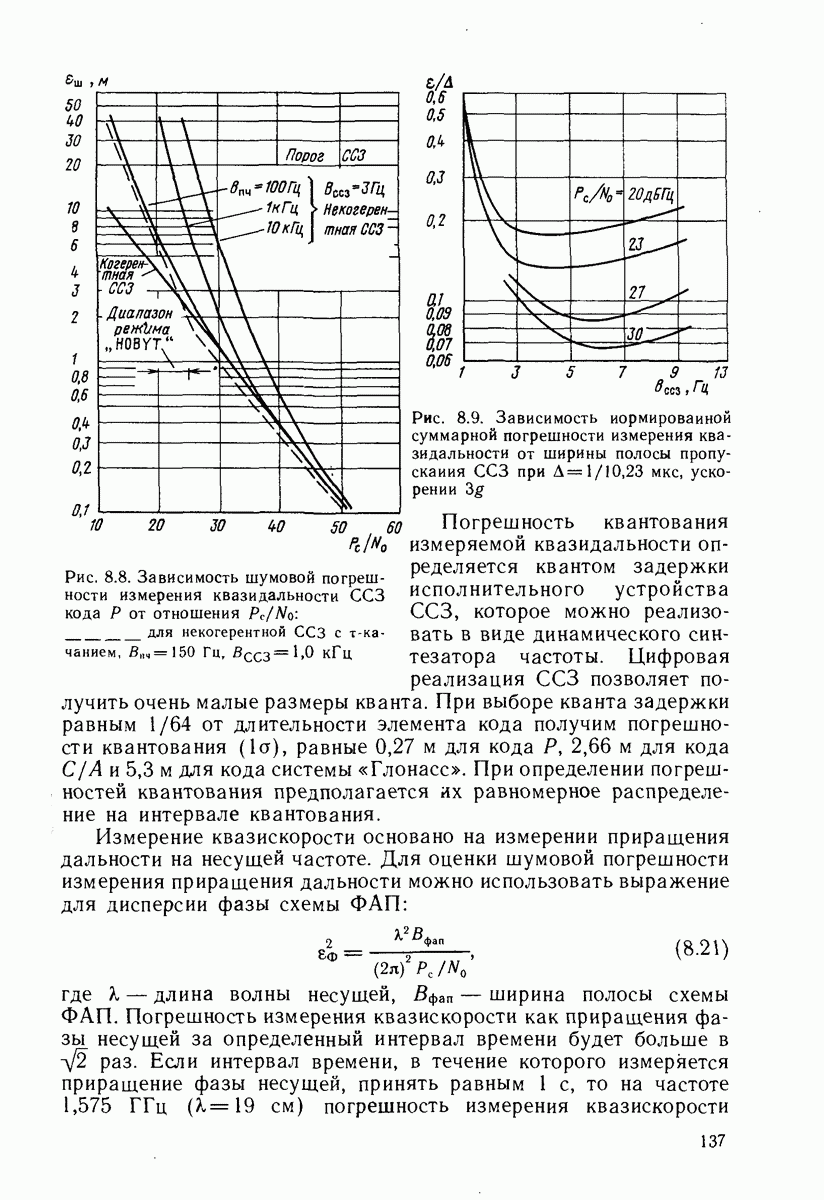
Чтобы уравнения (15.15) — (15.19) можно было использовать для решения навигационной задачи, необходимо выполнение неравенства

Если погрешности априорного знания координат места П характеризуются матрицей

то для дальномерных СРНС

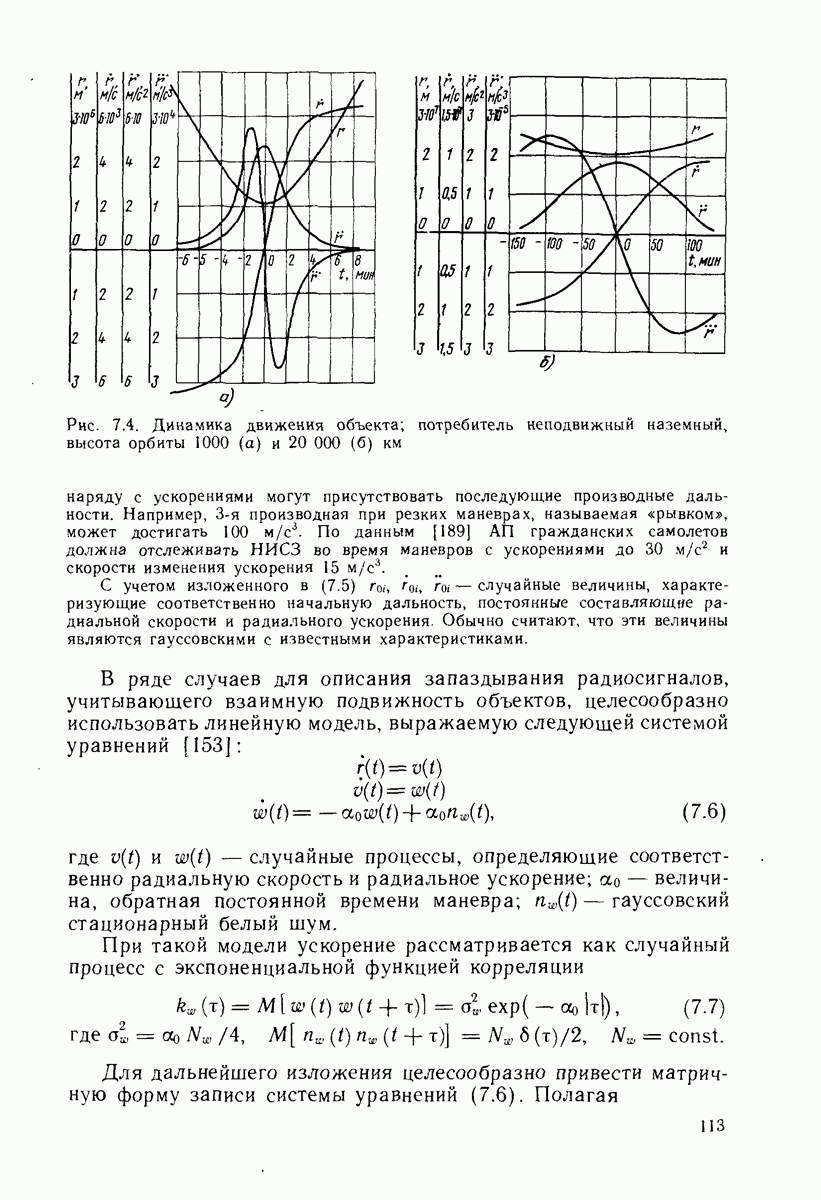
Допустимая погрешность априорного знания координат места,  которой погрешности линеаризации не приводят к расходимости фильтра, зависит от дальности
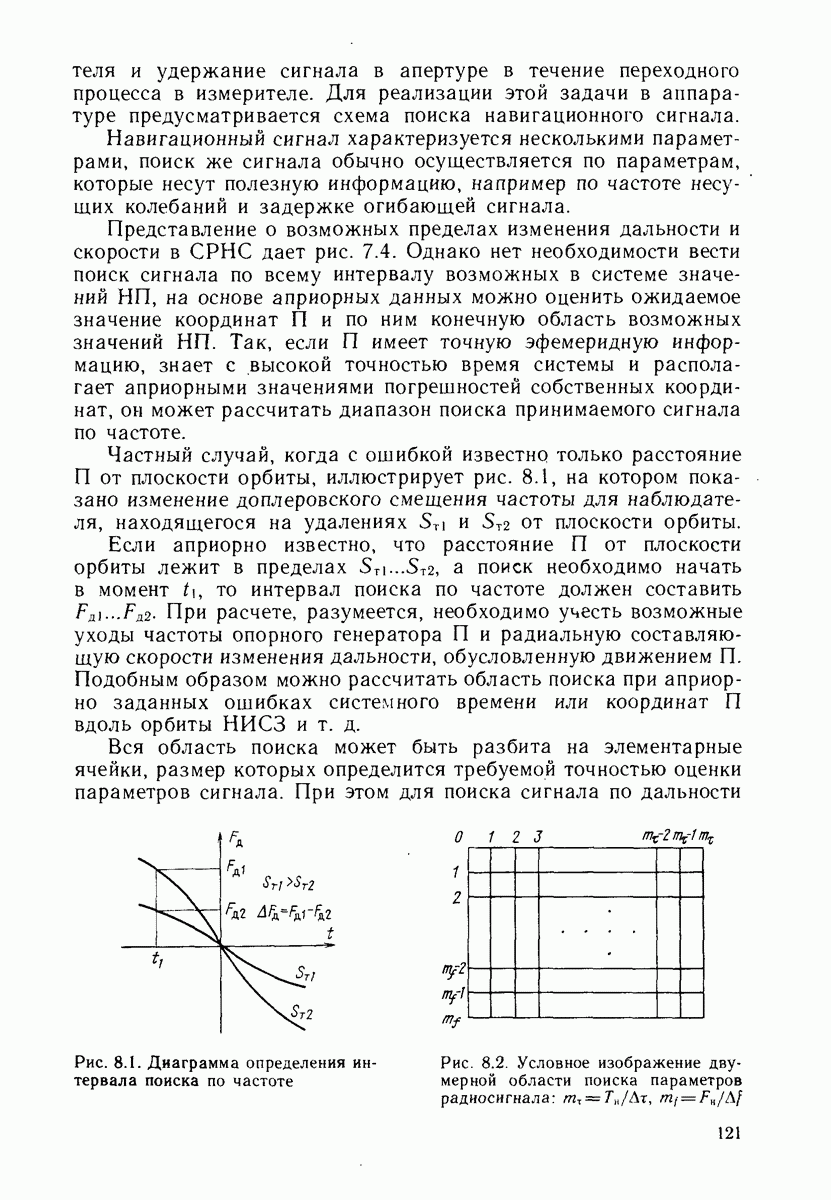
которой погрешности линеаризации не приводят к расходимости фильтра, зависит от дальности  (от высоты орбиты и положения П относительно НИСЗ) и погрешностей навигационных измерений. Эта величина в первом приближении характеризует размеры области сходимости фильтра и при
(от высоты орбиты и положения П относительно НИСЗ) и погрешностей навигационных измерений. Эта величина в первом приближении характеризует размеры области сходимости фильтра и при  определяется из неравенства
определяется из неравенства  При
При  для НС на стационарных орбитах
для НС на стационарных орбитах  а для систем, использующих НИСЗ с периодом обращения
а для систем, использующих НИСЗ с периодом обращения 
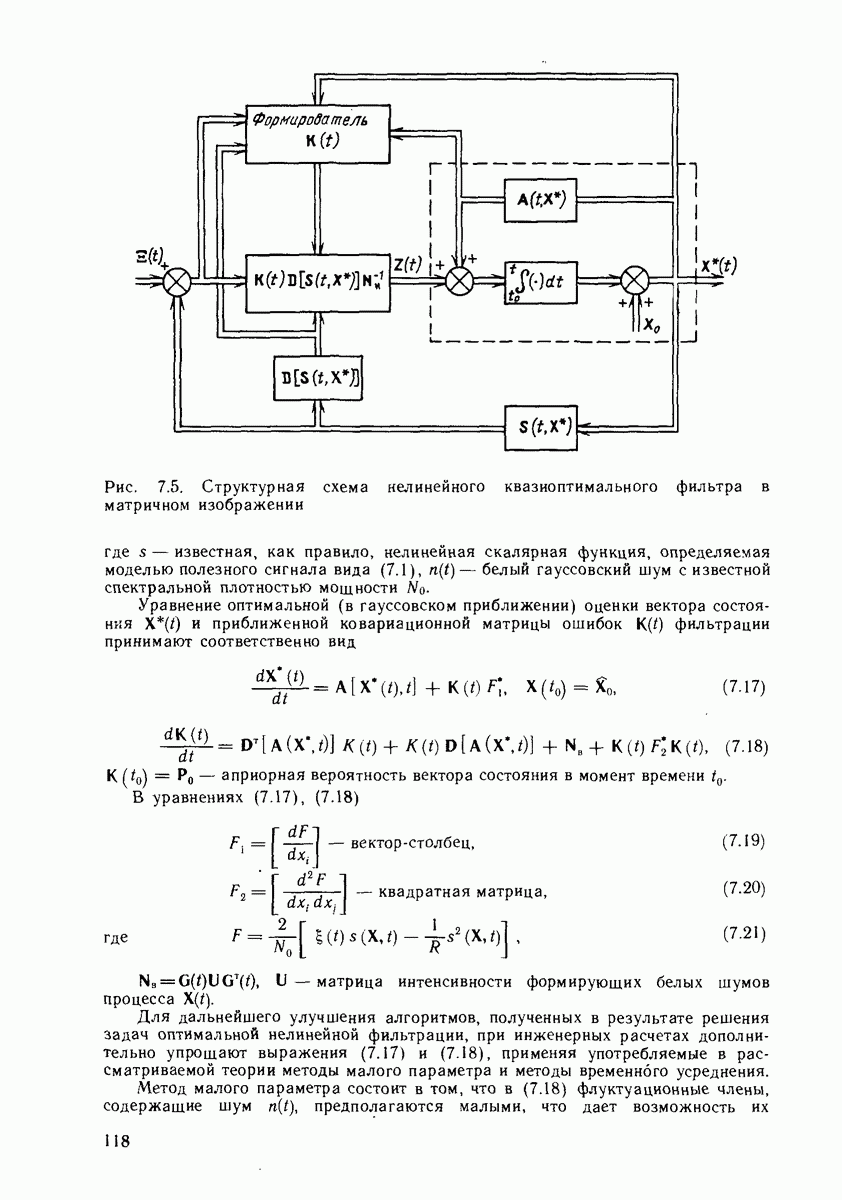
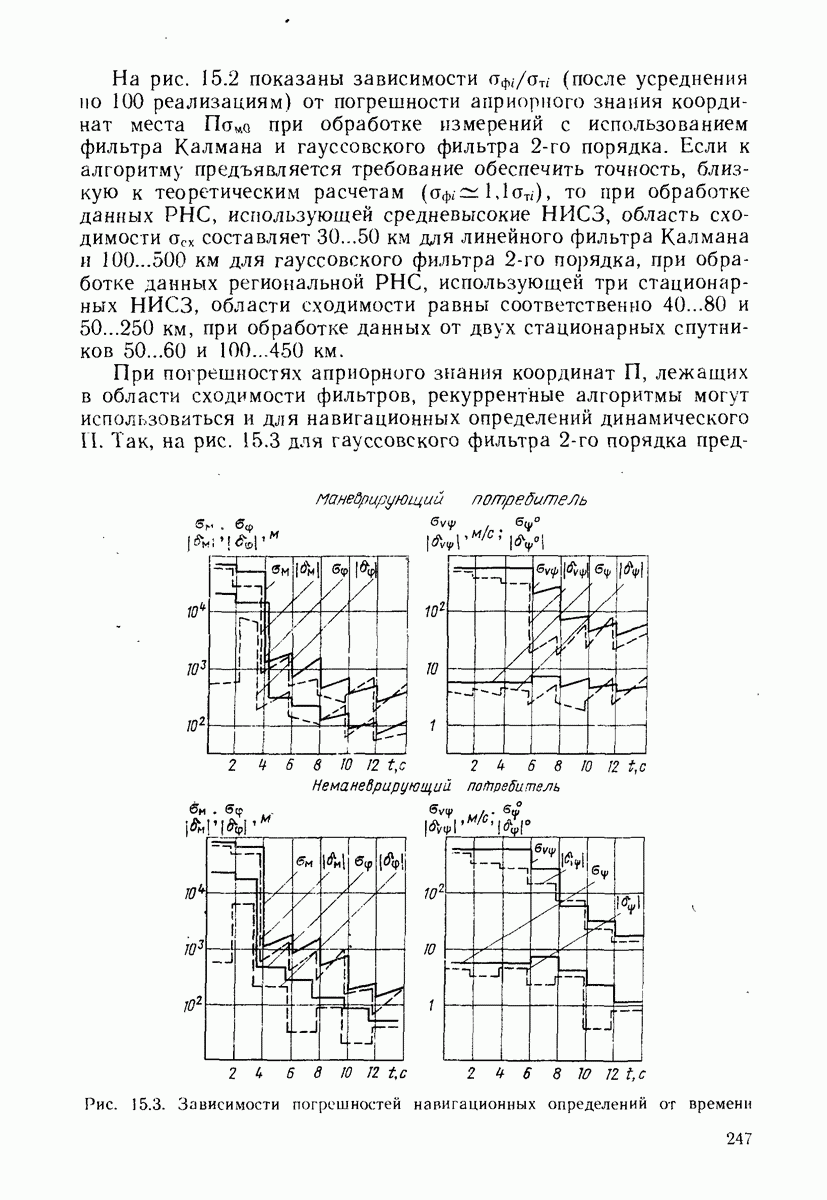
Чтобы расширить область сходимости, можно учитывать квадратичную нелинейность путем введения соответствующего смещения и увеличения априорной дисперсии погрешностей
навигационных измерений согласно уравнениям (15.21), (15.22). Рекуррентные фильтры, учитывающие квадратичную нелинейность, называют гауссовскими фильтрами 2-го порядка [88]. Для обработки дальномерных измерений такой фильтр имеет вид

Эти уравнения отличаются от обычно используемых уравнений (15.15) — (15.19) двумя слагаемыми, учитывающими погрешности линеаризации. По мере повышения точности навигационных определений добавочные слагаемые уменьшаются и гауссовский фильтр 2-го порядка преобразуется в фильтр Калмана.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- РАЗДЕЛ ПЕРВЫЙ/ СТРУКТУРА И ФУНКЦИОНИРОВАНИЕ СЕТЕВЫХ СРНС
- 1.1. СТРУКТУРНАЯ СХЕМА СРНС
- 1.2. ОСОБЕННОСТИ СЕТЕВЫХ СРНС
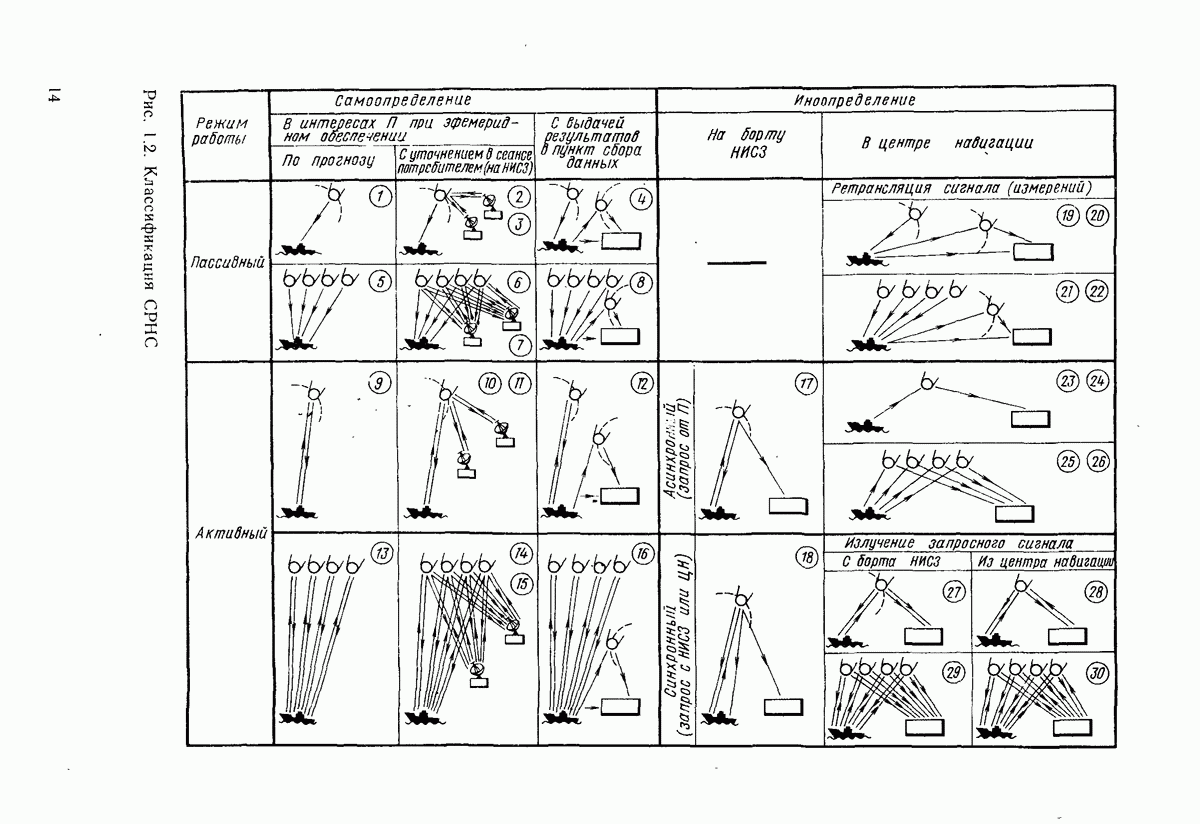
- 1.3. КЛАССИФИКАЦИЯ СРНС
- 1.4. СОГЛАСОВАНИЕ НАЧАЛ ОТСЧЕТА ПРОСТРАНСТВЕННЫХ И ВРЕМЕННОЙ КООРДИНАТ В ССРНС
- 1.5. ОБЩАЯ ХАРАКТЕРИСТИКА ЭЛЕМЕНТОВ ССРНС
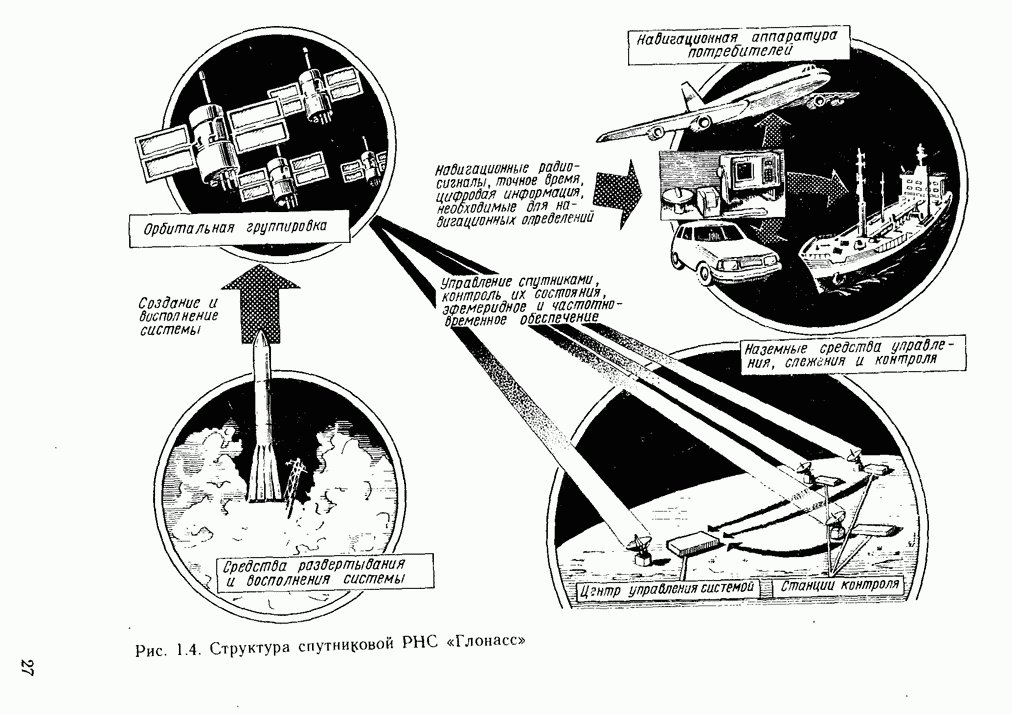
- 1.6. СОВЕТСКАЯ СЕТЕВАЯ СПУТНИКОВАЯ РНС «ГЛОНАСС»
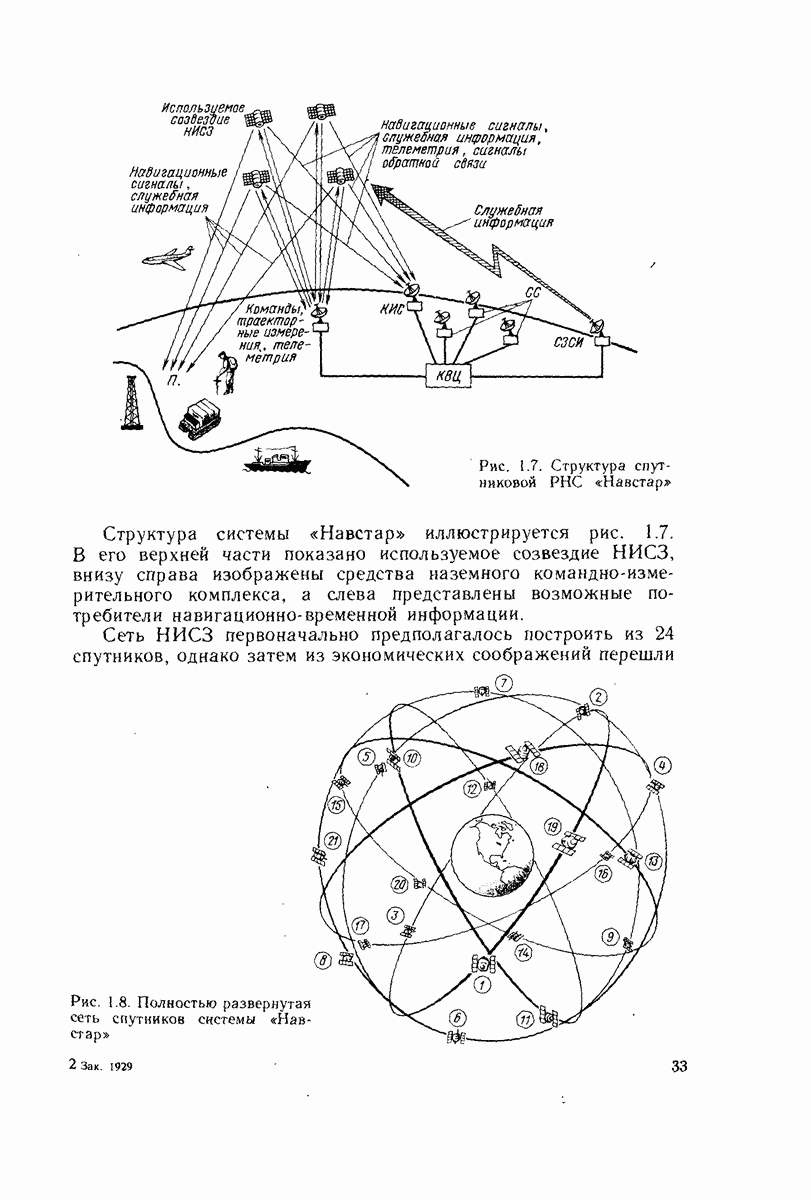
- 1.7. АМЕРИКАНСКАЯ СЕТЕВАЯ СПУТНИКОВАЯ РНС «НАВСТАР»
- 1.8. ИНФОРМАЦИОННЫЕ ЦЕНТРЫ СПУТНИКОВЫХ РНС
- ГЛАВА 2. ГЕОМЕТРИЧЕСКИЕ СВОЙСТВА МЕТОДОВ ИЗМЕРЕНИЙ В ССРНС
- 2.2. НАВИГАЦИОННЫЕ ФУНКЦИИ
- 2.3. ГРАДИЕНТЫ ПОЛЕЙ НАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 2.4. ГРАДИЕНТНАЯ И ФУНДАМЕНТАЛЬНАЯ МАТРИЦЫ
- ГЛАВА 3. ОСНОВЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ В СРНС
- 3.1. КОНЕЧНЫЕ И ИТЕРАЦИОННЫЕ МЕТОДЫ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 3.2. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ОПРЕДЕЛЕНИЙ ПО ПОЛНОЙ ВЫБОРКЕ ИЗМЕРЕНИЙ
- 3.3. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ
- ГЛАВА 4. СИГНАЛЫ В СПУТНИКОВЫХ РНС
- 4.1. ОБЩИЕ ТРЕБОВАНИЯ К СИГНАЛАМ СРНС
- 4.2. СТАТИСТИЧЕСКАЯ МОДЕЛЬ РАДИОНАВИГАЦИОННОГО КАНАЛА СРНС
- 4.3. АНАЛИЗ ТРЕБОВАНИЙ, ПРЕДЪЯВЛЯЕМЫХ К СИГНАЛАМ СРНС
- 4.4. ТИПОВЫЕ СТРУКТУРЫ СОВМЕЩЕННЫХ СИГНАЛОВ ДЛЯ РАЗЛИЧНЫХ ВАРИАНТОВ ПАССИВНЫХ СРНС
- 4.5. ОСОБЕННОСТИ ВЫБОРА СТРУКТУРЫ СИГНАЛОВ В АКТИВНЫХ ВАРИАНТАХ СРНС
- ГЛАВА 5. ЭНЕРГЕТИКА НАВИГАЦИОННЫХ РАДИОЛИНИЙ
- 5.1. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К НАВИГАЦИОННЫМ РАДИОЛИНИЯМ
- 5.2. ОБЩАЯ ХАРАКТЕРИСТИКА ПРЯМОЙ И РЕТРАНСЛЯЦИОННОЙ РАДИОЛИНИЙ СРНС
- 5.3. УЧЕТ УСЛОВИЙ РАСПРОСТРАНЕНИЯ РАДИОВОЛН В СРНС
- 5.4. СПОСОБЫ УМЕНЬШЕНИЯ АТМОСФЕРНЫХ ПОГРЕШНОСТЕЙ ДАЛЬНОМЕРНОГО И ДОПЛЕРОВСКОГО ИЗМЕРЕНИЙ
- 5.5. ОСОБЕННОСТИ ЭНЕРГЕТИЧЕСКИХ РАСЧЕТОВ РАДИОЛИНИЙ В ЗАВИСИМОСТИ ОТ РАСПОЛОЖЕНИЯ ОБСЛУЖИВАЕМОГО СЛОЯ
- ГЛАВА 6. СПОСОБЫ РАЗДЕЛЕНИЯ СИГНАЛОВ
- 6.1. МЕТОДЫ УПЛОТНЕНИЯ И РАЗДЕЛЕНИЯ СИГНАЛОВ В СЕТЕВЫХ СРНС
- 6.2. ВЕРОЯТНОСТНОЕ РАЗДЕЛЕНИЕ СИГНАЛОВ СПУТНИКОВ ПРИ ИСПОЛЬЗОВАНИИ ШПС В ССРНС
- 6.3. СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ШИРИНЫ ПОЛОСЫ ПРИНИМАЕМОГО ИЗЛУЧЕНИЯ В СЕТЕВЫХ СРНС
- 6.4. ОСОБЕННОСТИ РАЗДЕЛЕНИЯ СИГНАЛОВ В АКТИВНЫХ СРНС
- ГЛАВА 7. ПРИНЦИПЫ ПОСТРОЕНИЯ ИЗМЕРИТЕЛЬНО-ВЫЧИСЛИТЕЛЬНОЙ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 7.1. ОБОБЩЕННАЯ СТРУКТУРНАЯ СХЕМА АП ССРНС
- 7.2. ИНФОРМАЦИОННЫЕ ПОТОКИ В АП
- 7.3. ИЗМЕРЯЕМЫЕ РАДИОНАВИГАЦИОННЫЕ ПАРАМЕТРЫ
- 7.4. ВИДЫ И МОДЕЛИ ПОМЕХ
- 7.5. ОСНОВЫ СТАТИСТИЧЕСКОГО СИНТЕЗА ИЗМЕРИТЕЛЕЙ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- ГЛАВА 8. УСТРОЙСТВА ПЕРВИЧНОЙ ОБРАБОТКИ РАДИОНАВИГАЦИОННОГО СИГНАЛА
- 8.1. НЕОБХОДИМОСТЬ ПОИСКА РАДИОНАВИГАЦИОННЫХ СИГНАЛОВ
- 8.2. СПОСОБЫ РЕШЕНИЯ ЗАДАЧИ ПОИСКА РАДИОСИГНАЛОВ НИСЗ
- 8.3. УСТРОЙСТВА ОЦЕНКИ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 8.4. ЦИФРОВАЯ РЕАЛИЗАЦИЯ УСТРОЙСТВ ПЕРВИЧНОЙ ОБРАБОТКИ
- 8.5. ОЦЕНКА ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ РАДИОНАВИГАЦИОННЫХ ПАРАМЕТРОВ
- 8.6. СПОСОБЫ ПОВЫШЕНИЯ ПОМЕХОУСТОЙЧИВОСТИ АП
- ГЛАВА 9. РАЗНОВИДНОСТИ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 9.1. ОСОБЕННОСТИ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ РАЗЛИЧНЫХ ТИПОВ
- 9.2. ОДНОКАНАЛЬНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.3. МНОГОКАНАЛЬНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.4. МУЛЬТИПЛЕКСНАЯ АППАРАТУРА ПОТРЕБИТЕЛЕЙ
- 9.5. АППАРАТУРА ПОТРЕБИТЕЛЕЙ ДЛЯ ОДНОВРЕМЕННОЙ РАБОТЫ ПО СИСТЕМАМ «ГЛОНАСС» и «НАВСТАР»
- 9.6. УНИФИКАЦИЯ АППАРАТУРНЫХ РЕШЕНИЙ
- ГЛАВА 10. КАДР НАВИГАЦИОННОГО СИГНАЛА
- 10.1. ОРГАНИЗАЦИЯ ОБРАБОТКИ ИЗМЕРЕНИЙ И ФОРМИРОВАНИЕ ЭФЕМЕРИДНОЙ ИНФОРМАЦИИ
- 10.2. МЕТОДОЛОГИЯ ВЫБОРА ЭЛЕМЕНТОВ КАДРА СИГНАЛА
- 10.3. УСЛОВИЯ РЕАЛИЗАЦИИ АЛГОРИТМОВ ПРОГНОЗИРОВАНИЯ ЭФЕМЕРИД НИСЗ
- 10.4. АЛГОРИТМЫ ПРОГНОЗИРОВАНИЯ ДВИЖЕНИЯ НИСЗ
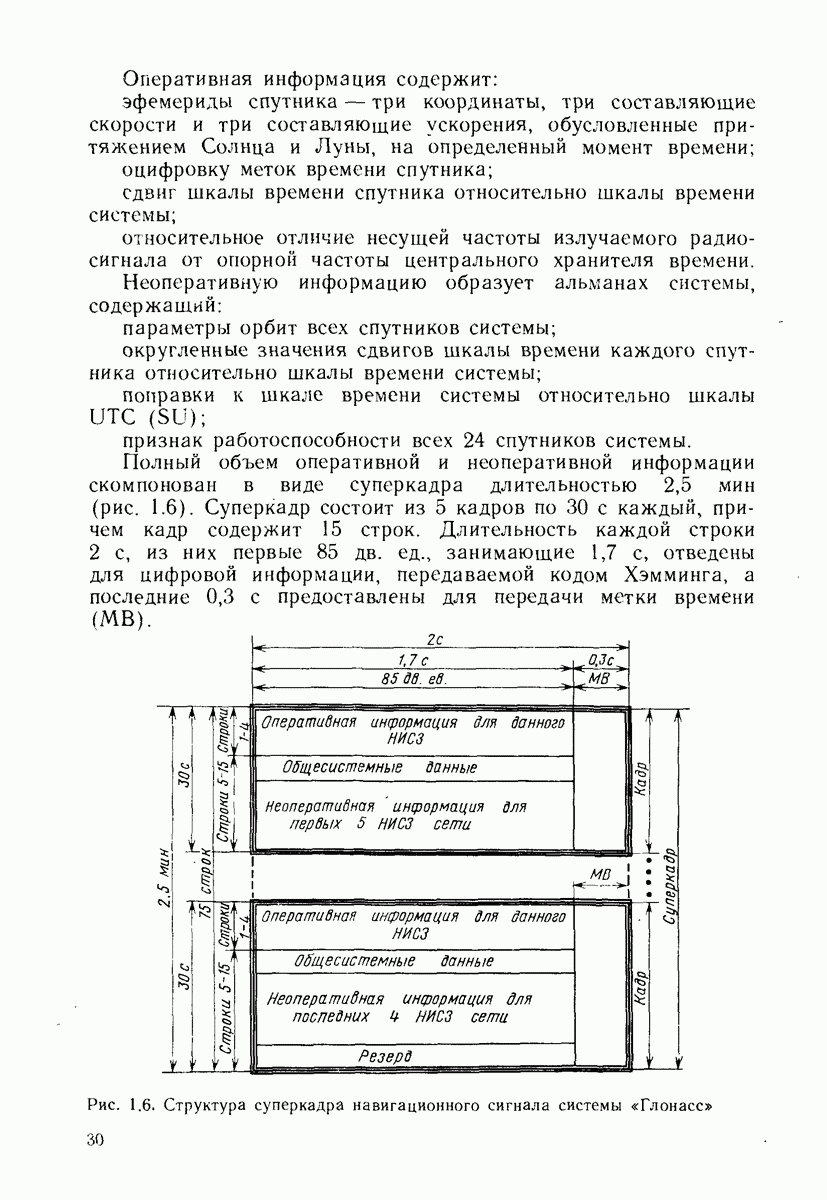
- 10.5. СОСТАВ, ФОРМА ПРЕДСТАВЛЕНИЯ И ОБЪЕМ ИНФОРМАЦИИ, ПЕРЕДАВАЕМОЙ В КАДРЕ НАВИГАЦИОННОГО СИГНАЛА СИСТЕМЫ «НАВСТАР»
- 10.6. КАДР НАВИГАЦИОННОГО СИГНАЛА СИСТЕМЫ «ГЛОНАСС»
- ГЛАВА 11. СИНХРОНИЗАЦИЯ ВРЕМЕННЫХ ШКАЛ СИСТЕМЫ НИСЗ
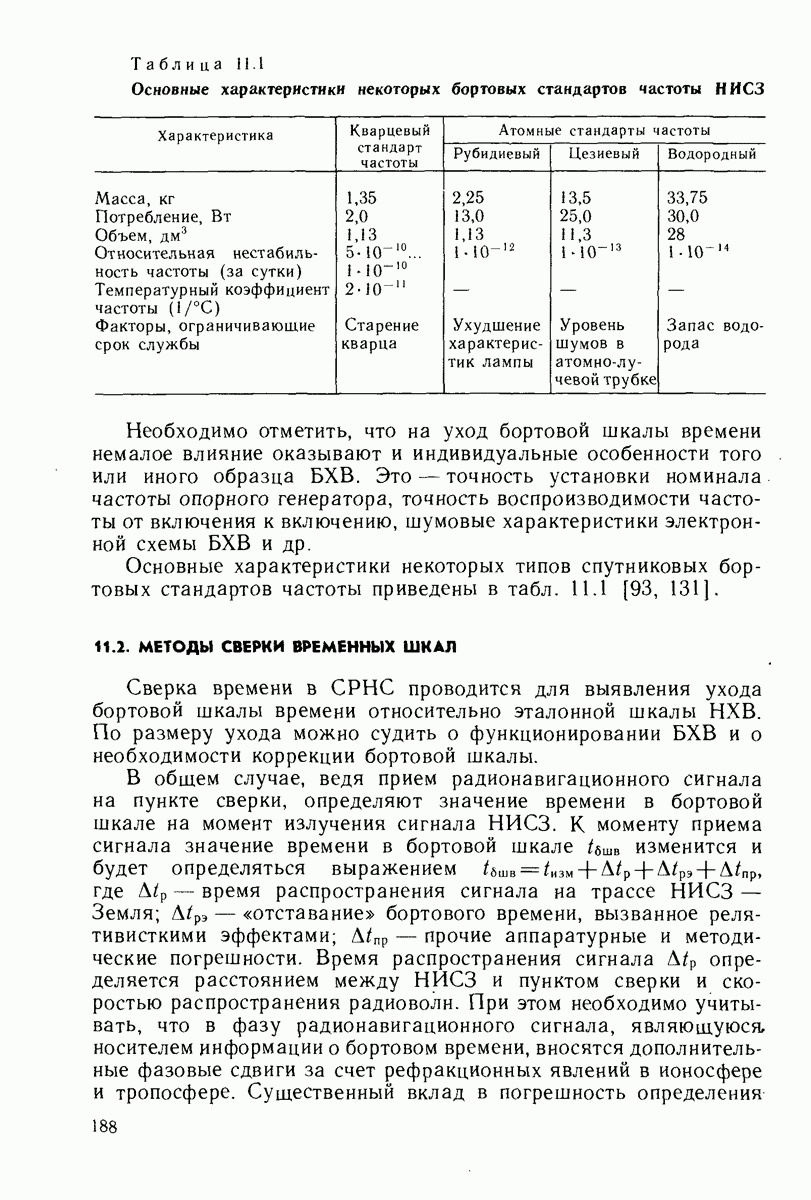
- 11.1. ОБЩАЯ ХАРАКТЕРИСТИКА ХРАНИТЕЛЕЙ ВРЕМЕННЫХ ШКАЛ
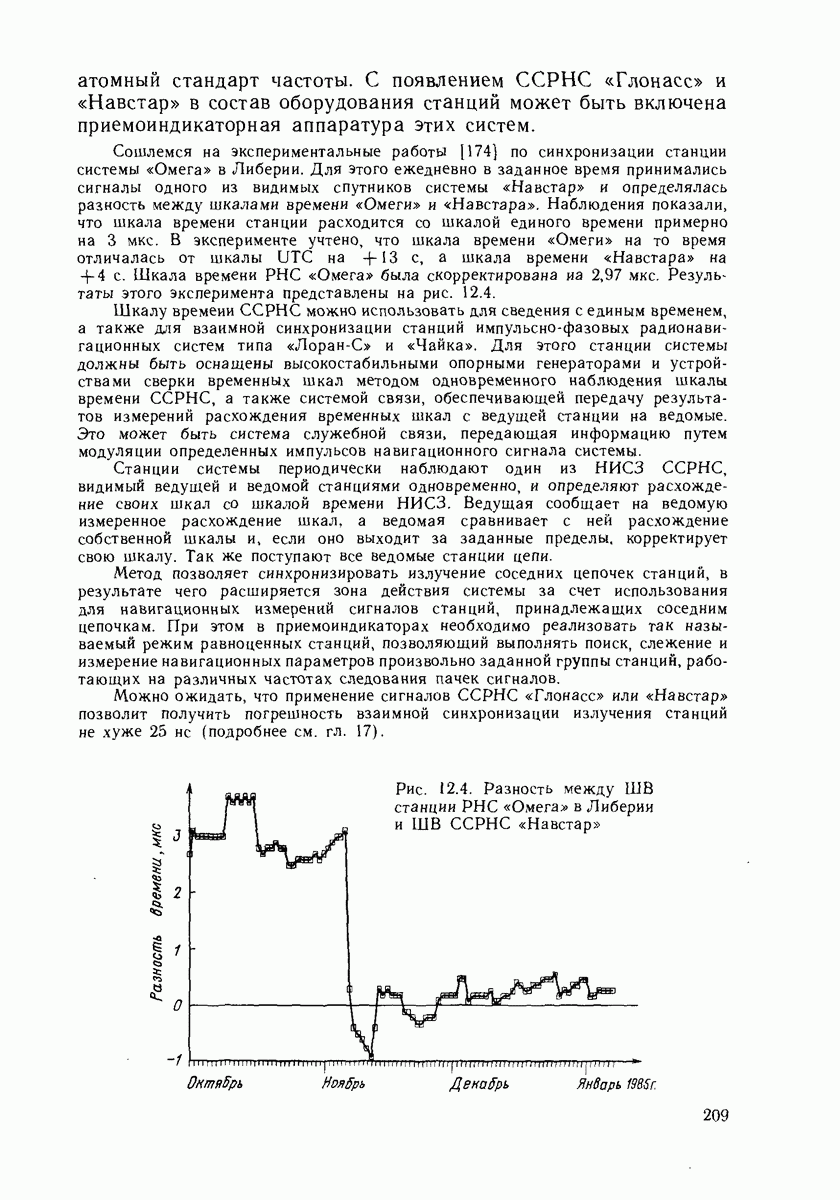
- 11.2. МЕТОДЫ СВЕРКИ ВРЕМЕННЫХ ШКАЛ
- 11.3. КОРРЕКЦИЯ ВРЕМЕННЫХ ШКАЛ
- 11.4. СПОСОБЫ УЧЕТА В НАВИГАЦИОННОМ СЕАНСЕ СМЕЩЕНИЙ ВРЕМЕННЫХ ШКАЛ НИСЗ
- 11.5. СОГЛАСОВАНИЕ ШКАЛ ВРЕМЕНИ СИСТЕМ «ГЛОНАСС» И «НАВСТАР»
- 11.6. СИНХРОНИЗАЦИЯ ВРЕМЕННЫХ ШКАЛ СЕТИ НИСЗ НА ОСНОВЕ ВЗАИМНЫХ ВРЕМЕННЫХ ИЗМЕРЕНИЙ
- ГЛАВА 12. ОБЛАСТИ ИСПОЛЬЗОВАНИЯ СЕТЕВЫХ СПУТНИКОВЫХ РНС
- 12.1. ПРИМЕНЕНИЕ ССРНС — ОСНОВА КООРДИНАТНО-ВРЕМЕННОГО ОБЕСПЕЧЕНИЯ
- 12.2. ОПРЕДЕЛЕНИЕ КООРДИНАТ, ИХ ПРОИЗВОДНЫХ И НАВИГАЦИОННЫХ ЭЛЕМЕНТОВ НАЗЕМНЫХ И ПРИЗЕМНЫХ ОБЪЕКТОВ
- 12.3. ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ДВИЖЕНИЯ ОКОЛОЗЕМНЫХ КА
- 12.4. ОПРЕДЕЛЕНИЕ ВЗАИМНЫХ КООРДИНАТ В ИНТЕРЕСАХ ПРЕДУПРЕЖДЕНИЯ СТОЛКНОВЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ И ГРУППОВОГО ИХ ВОЖДЕНИЯ
- 12.5. ВЫСОКОТОЧНАЯ ГЕОДЕЗИЧЕСКАЯ ПРИВЯЗКА
- 11.6. ОПРЕДЕЛЕНИЕ ОРИЕНТАЦИИ ОБЪЕКТОВ В ПРОСТРАНСТВЕ
- 12.7. СИНХРОНИЗАЦИЯ ИЗЛУЧЕНИЯ СТАНЦИИ С НАЗЕМНЫМ БАЗИРОВАНИЕМ
- 12.8. НАБЛЮДЕНИЕ ДЛЯ ОБЕСПЕЧЕНИЯ УПРАВЛЕНИЯ ДВИЖЕНИЕМ ПЕРЕМЕЩАЮЩИХСЯ ОБЪЕКТОВ
- 12.9. ЦЕЛЕУКАЗАНИЕ В СИСТЕМЕ ОБНАРУЖЕНИЯ ТЕРПЯЩИХ БЕДСТВИЕ
- РАЗДЕЛ ВТОРОЙ. ОСНОВЫ НАВИГАЦИОННОГО ИСПОЛЬЗОВАНИЯ ССРНС
- 13.1. ЗАДАЧА СИНТЕЗА АЛГОРИТМА НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 13.2. МОДЕЛЬ НАВИГАЦИОННЫХ ИЗМЕРЕНИЙ
- 13.3. МОДЕЛЬ ДИНАМИКИ ПОТРЕБИТЕЛЯ
- 13.4. ФАКТОРЫ, ВЛИЯЮЩИЕ НА ВЫБОР СПОСОБА ОБРАБОТКИ ИНФОРМАЦИИ В ССРНС
- ГЛАВА 14. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ ПО ВЫБОРКЕ ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.1. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ ПО ВЫБОРКЕ МИНИМАЛЬНОГО ОБЪЕМА ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.2. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ ПО ИЗБЫТОЧНОМУ ОБЪЕМУ ОДНОВРЕМЕННЫХ ИЗМЕРЕНИЙ
- 14.3. ОЦЕНКА СХОДИМОСТИ АЛГОРИТМОВ РЕШЕНИЯ НАВИГАЦИОННОЙ ЗАДАЧИ
- ГЛАВА 15. АЛГОРИТМЫ РЕШЕНИЯ НАВИГАЦИОННЫХ ЗАДАЧ ПО ВЫБОРКЕ ИЗМЕРЕНИИ НАРАСТАЮЩЕГО ОБЪЕМА
- 15.1. РЕКУРРЕНТНЫЙ АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ МЕТОДОМ КАЛМАНА И ЕГО МОДИФИКАЦИИ ПРИ РАЗЛИЧНЫХ СОСТАВАХ ИЗМЕРЕНИЙ
- 15.2. СПОСОБЫ УСТРАНЕНИЯ РАСХОДИМОСТИ ФИЛЬТРОВ КАЛМАНА
- 15.3. РЕКУРРЕНТНЫЕ СООТНОШЕНИЯ ГАУССОВСКОГО ФИЛЬТРА 2-ГО ПОРЯДКА
- 15.4. СРАВНЕНИЕ РЕКУРРЕНТНЫХ АЛГОРИТМОВ ПО РАЗМЕРАМ ОБЛАСТИ СХОДИМОСТИ
- ГЛАВА 16. СПОСОБЫ ОЦЕНКИ ТОЧНОСТИ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ
- 16.1. ПОКАЗАТЕЛИ ТОЧНОСТИ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 16.2. КОРРЕЛЯЦИОННАЯ МАТРИЦА ОШИБОК ОПРЕДЕЛЯЕМЫХ ПАРАМЕТРОВ
- 16.3. ИСТОЧНИКИ ОШИБОК НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 16.4. ОТОБРАЖЕНИЕ ТОЧНОСТНЫХ ХАРАКТЕРИСТИК И ИНТЕГРАЛЬНАЯ ОЦЕНКА ТОЧНОСТИ СРНС
- ГЛАВА 17. ВЫСОКОТОЧНОЕ СЛИЧЕНИЕ ШКАЛ ВРЕМЕНИ УДАЛЕННЫХ ПУНКТОВ ПО СИГНАЛАМ НИСЗ
- 17.1. МЕТОДЫ СИНХРОНИЗАЦИИ ШВ УДАЛЕННЫХ ПУНКТОВ
- 17.2. ОЦЕНКА ТОЧНОСТИ СВЕРКИ ШВ УДАЛЕННЫХ ПУНКТОВ ПО ВЫБОРКЕ ОДНОВРЕМЕННЫХ ПСЕВДОДАЛЬНОМЕРНЫХ ИЗМЕРЕНИЙ
- 17.3. ПОТЕНЦИАЛЬНАЯ ТОЧНОСТЬ СВЕРКИ ШВ ПУНКТА С ИЗВЕСТНЫМИ КООРДИНАТАМИ ПО ДАННЫМ ПСЕВДОДАЛЬНОМЕРНЫХ И РАДИАЛЬНЫХ ПСЕВДОСКОРОСТНЫХ ИЗМЕРЕНИЙ
- ГЛАВА 18. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ КООРДИНАТ ПРИ ОДНОМОМЕНТНЫХ ИЗМЕРЕНИЯХ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ НИСЗ
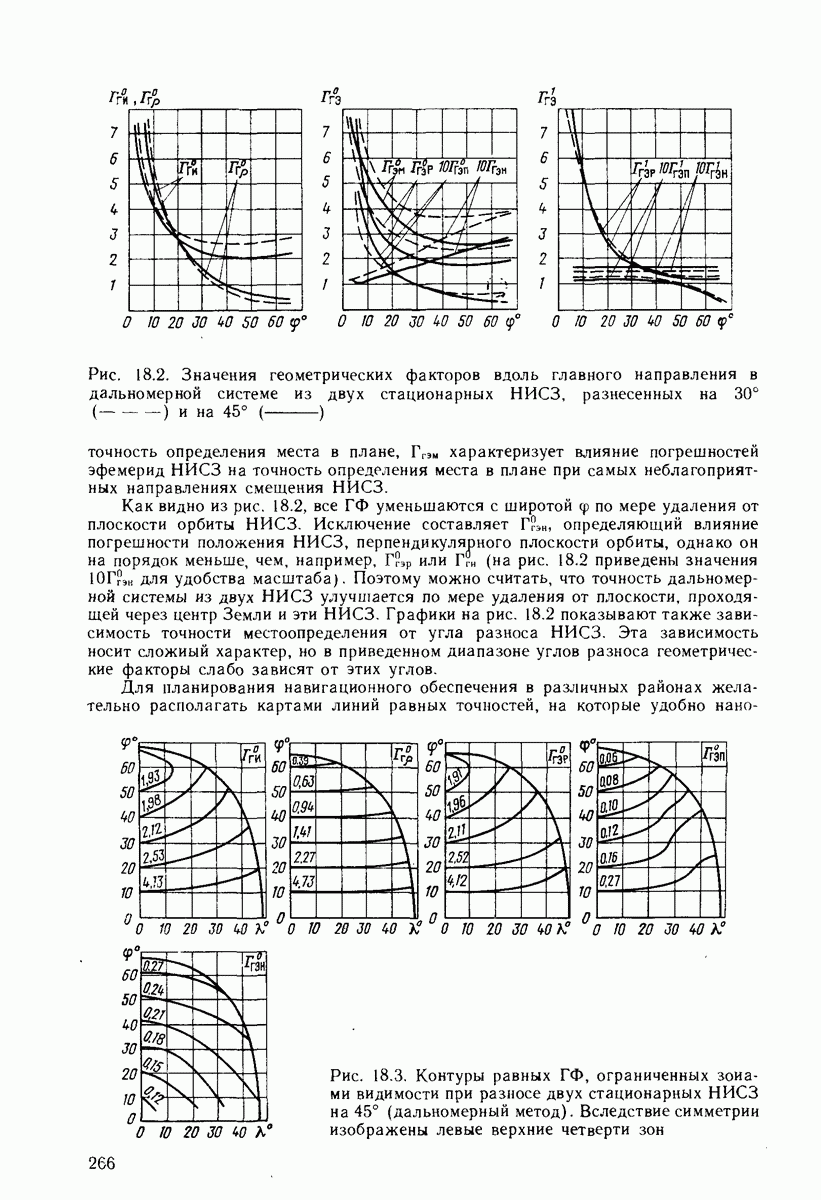
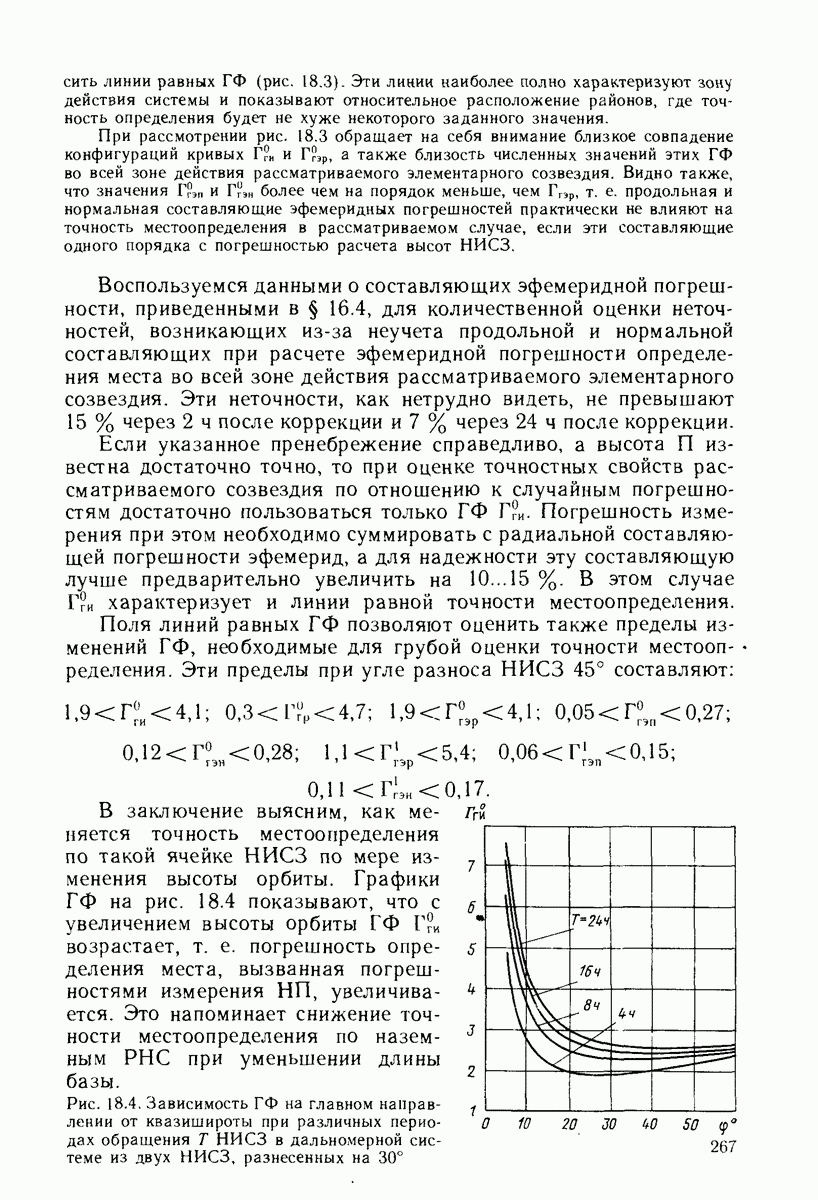
- 18.2. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПОВЕРХНОСТНЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ДВУХ НИСЗ
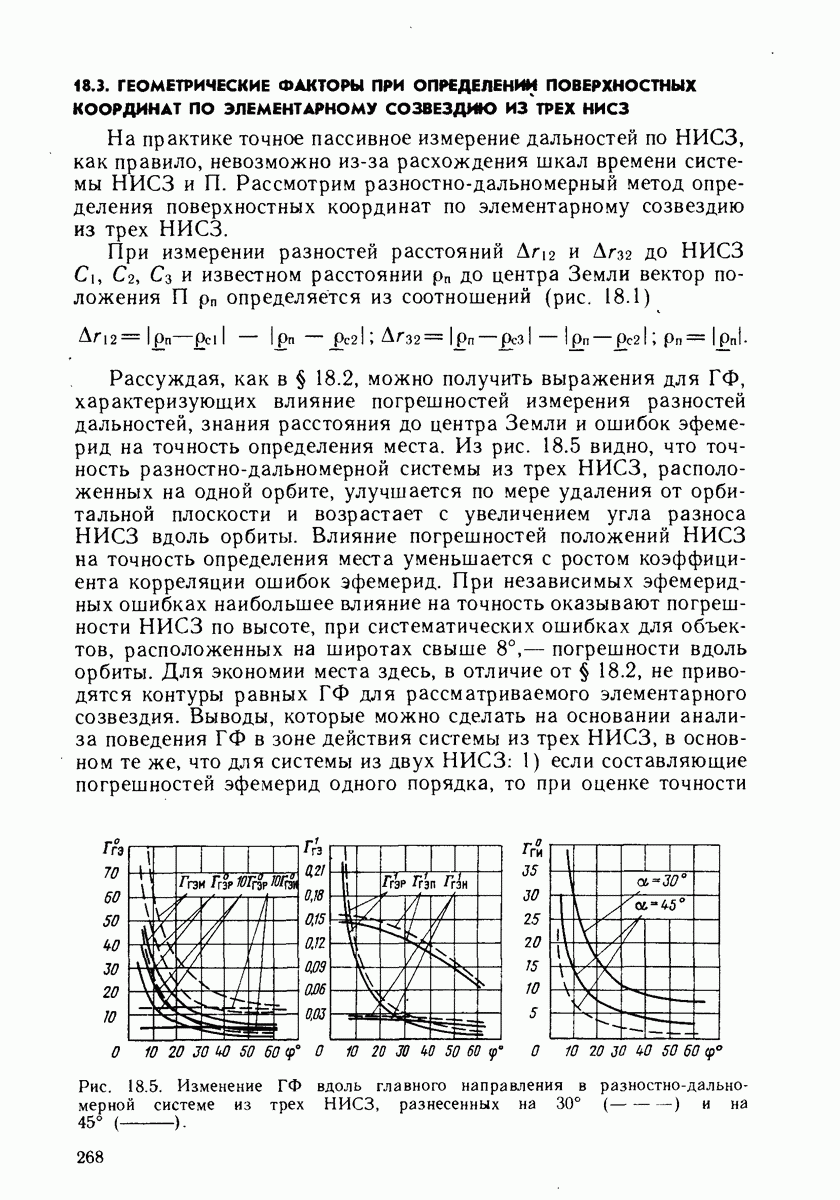
- 18.3. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПОВЕРХНОСТНЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ТРЕХ НИСЗ
- 18.4. ГЕОМЕТРИЧЕСКИЕ ФАКТОРЫ ПРИ ОПРЕДЕЛЕНИИ ПРОСТРАНСТВЕННЫХ КООРДИНАТ ПО ЭЛЕМЕНТАРНОМУ СОЗВЕЗДИЮ ИЗ ЧЕТЫРЕХ НИСЗ
- 18.5. ТОЧНОСТНЫЕ СВОЙСТВА ДОПЛЕРОВСКИХ МЕТОДОВ В СЕТЕВЫХ СРНС В СРАВНЕНИИ С ДАЛЬНОМЕРНЫМИ
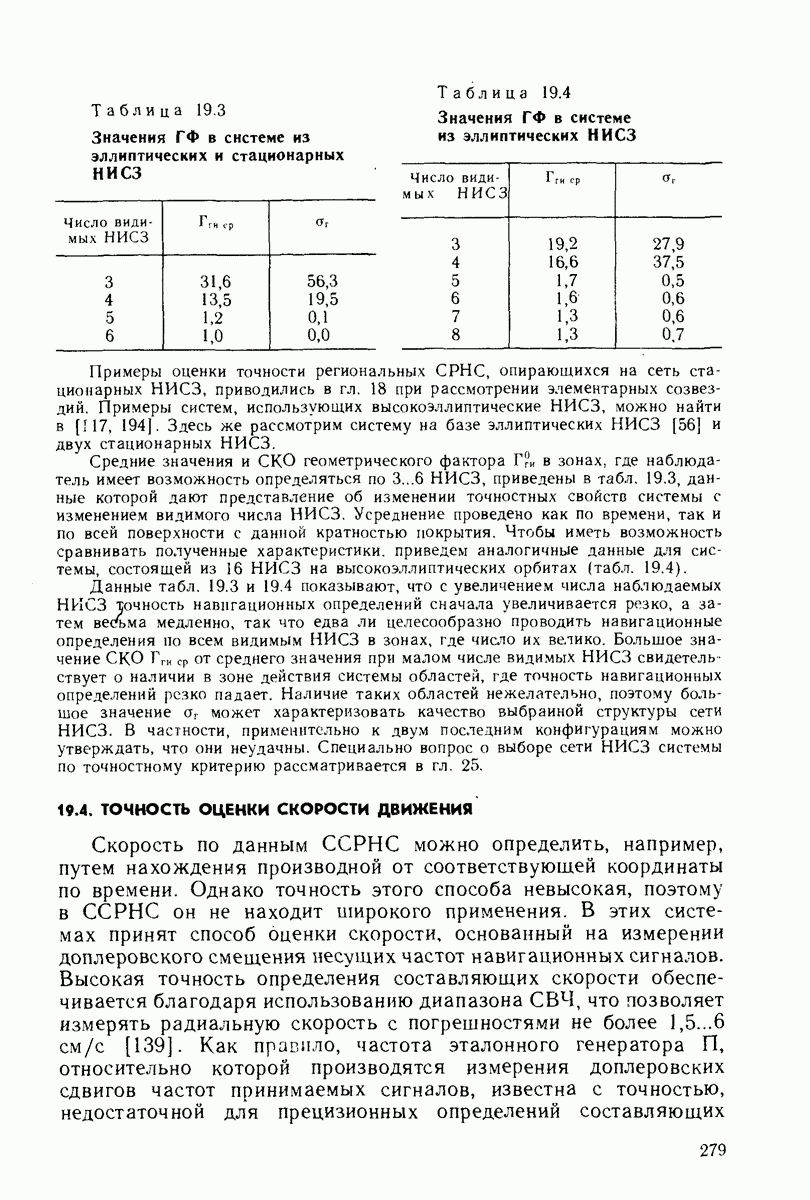
- ГЛАВА 19. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПРОСТРАНСТВЕННЫХ КООРДИНАТ И ВЕКТОРА СКОРОСТИ ПО СЕТИ НИСЗ
- 19.2. РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ ГЕОМЕТРИЧЕСКИХ ФАКТОРОВ
- 19.3. ТОЧНОСТЬ ОЦЕНКИ КООРДИНАТ И ВРЕМЕНИ
- 19.4. ТОЧНОСТЬ ОЦЕНКИ СКОРОСТИ ДВИЖЕНИЯ
- 19.5. ОЦЕНКА ТОЧНОСТИ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ КА
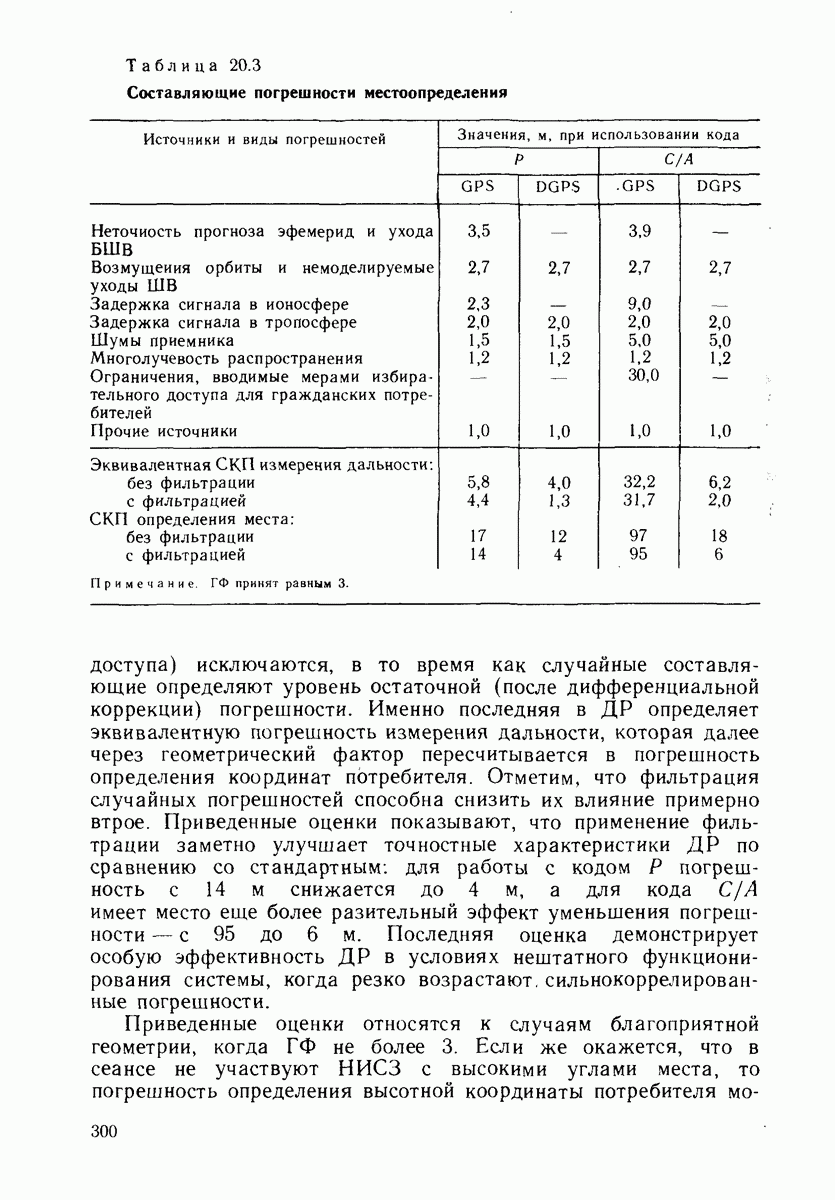
- ГЛАВА 20. ДИФФЕРЕНЦИАЛЬНЫЙ РЕЖИМ ССРНС
- 20.2. СТРУКТУРА ДИФФЕРЕНЦИАЛЬНОЙ ПОДСИСТЕМЫ
- 20.3. МЕТОДЫ ДИФФЕРЕНЦИАЛЬНЫХ ОПРЕДЕЛЕНИЙ
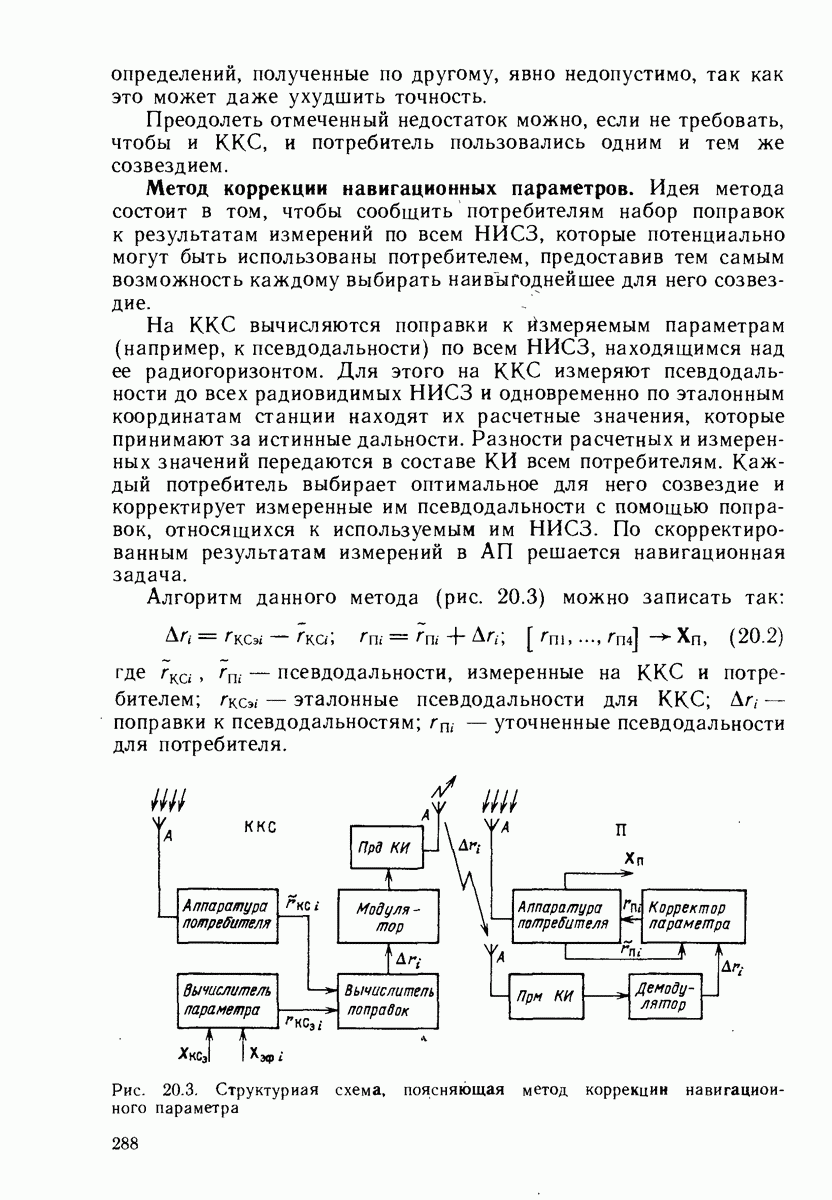
- 20.4. КОРРЕКТИРУЮЩАЯ ИНФОРМАЦИЯ
- 20.5. КАНАЛЫ ПЕРЕДАЧИ КОРРЕКТИРУЮЩЕЙ ИНФОРМАЦИИ
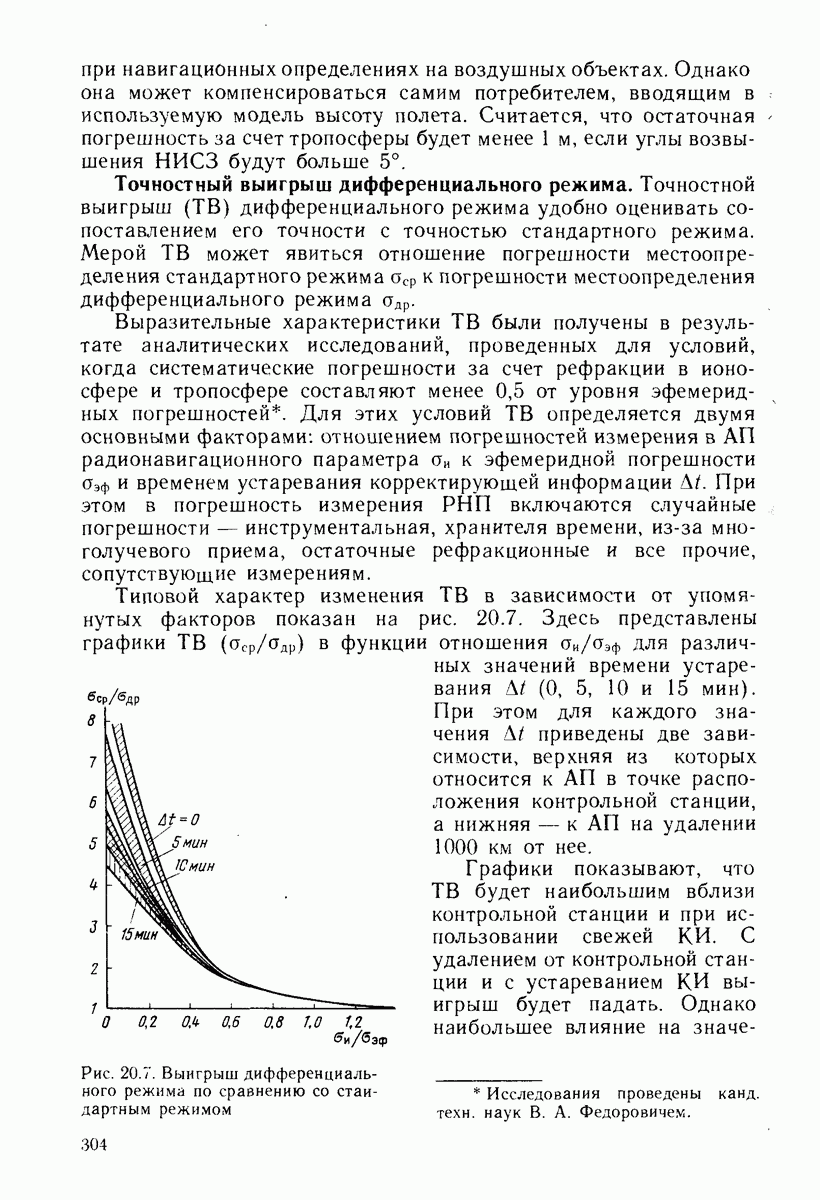
- 20.6. ТОЧНОСТНЫЕ ХАРАКТЕРИСТИКИ ДМ
- 20.7. ИЗМЕРЕНИЯ РНП ПО ФАЗЕ НЕСУЩИХ КОЛЕБАНИЙ
- 20.8. РЕЗУЛЬТАТЫ ИСПЫТАНИЙ. РЕАЛИЗАЦИЯ ДПС
- ГЛАВА 21. ТОЧНОСТЬ ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ В АКТИВНОМ И ОТНОСИТЕЛЬНОМ РЕЖИМАХ
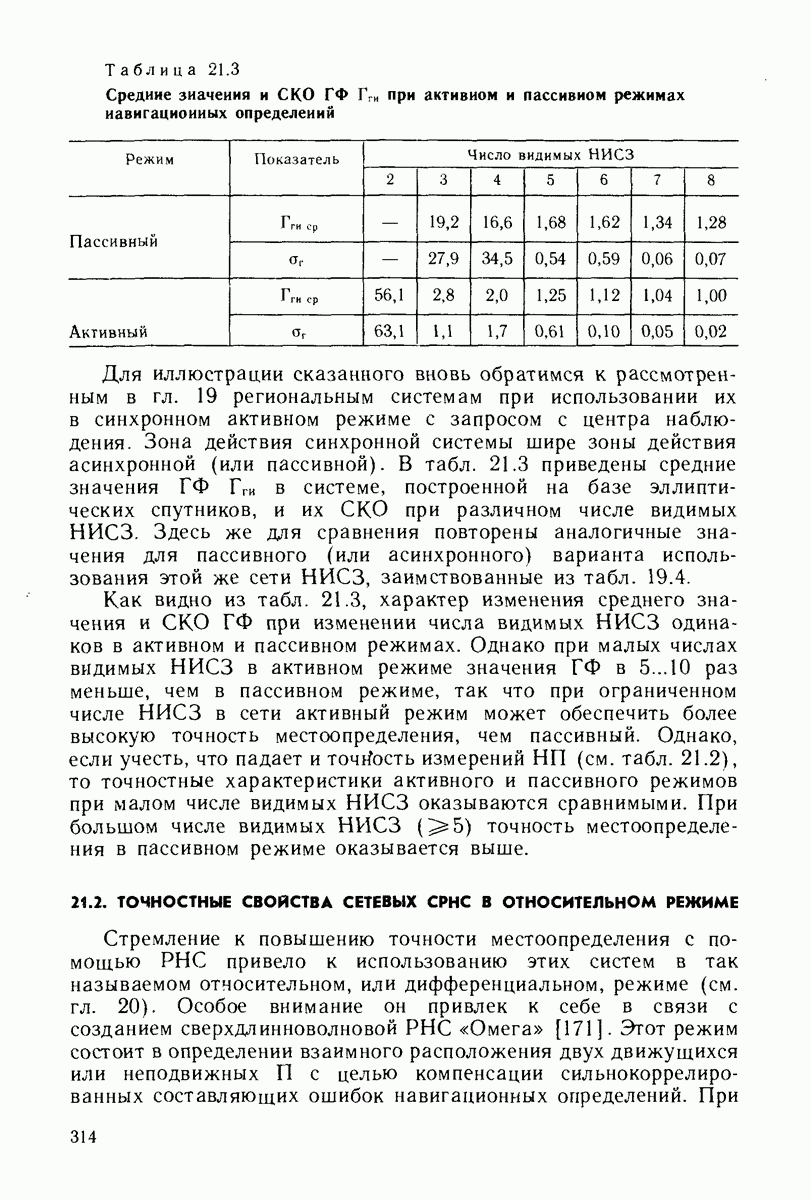
- 21.1. ТОЧНОСТНЫЕ ХАРАКТЕРИСТИКИ АКТИВНЫХ СРНС
- 21.2. ТОЧНОСТНЫЕ СВОЙСТВА СЕТЕВЫХ СРНС В ОТНОСИТЕЛЬНОМ РЕЖИМЕ
- ГЛАВА 22. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ БОРТОВОЙ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ
- 22.1. АВТОМАТИЗАЦИЯ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ И ШТУРМАНСКИХ РАСЧЕТОВ
- 22.2. МЕТОДИЧЕСКИЕ ОСНОВЫ МАТЕМАТИЧЕСКОГО ОБЕСПЕЧЕНИЯ
- 22.3. ОСНОВНЫЕ ЗАДАЧИ ВТО
- 22.4. УПРАВЛЯЮЩИЙ АЛГОРИТМ
- 22.5. ВРЕМЕННАЯ ДИАГРАММА АЛГОРИТМА
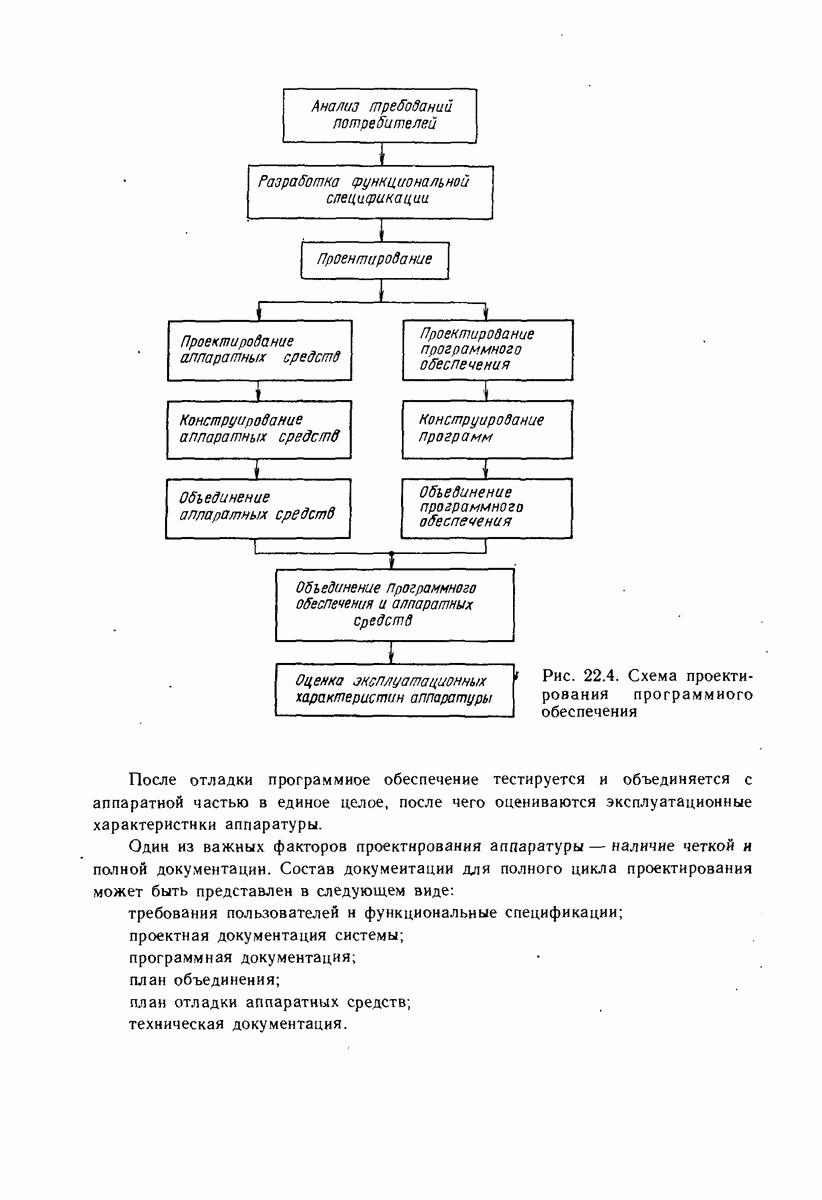
- 22.6. ПРИНЦИПЫ ПРОЕКТИРОВАНИЯ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ
- РАЗДЕЛ ТРЕТИЙ. КОМПЛЕКСНОЕ ПРОЕКТИРОВАНИЕ ССРНС
- 23.1. ОСНОВНЫЕ ЗАДАЧИ, РЕШАЕМЫЕ ПРИ КОМПЛЕКСНОМ ПРОЕКТИРОВАНИИ
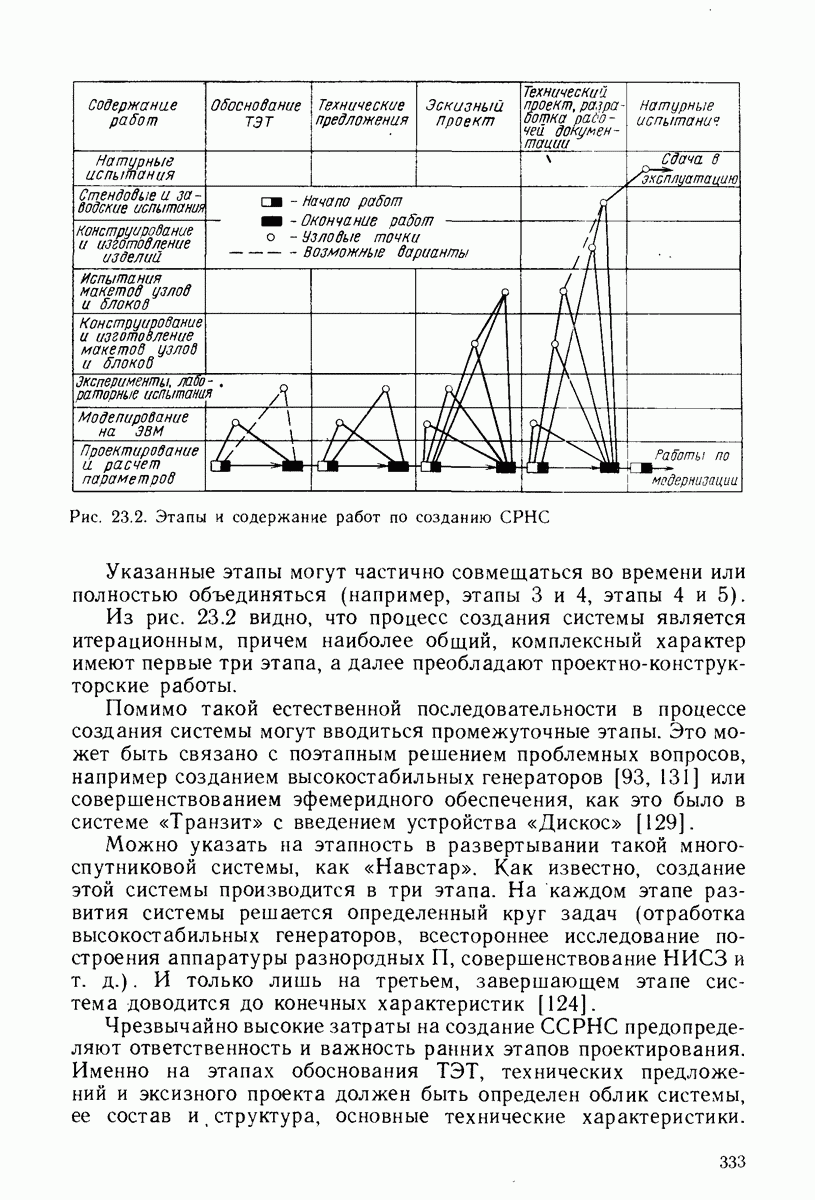
- 23.2. ЭТАПЫ СОЗДАНИЯ ССРНС
- 23.3. ОСОБЕННОСТИ ПРОЕКТОВ СРНС РАЗЛИЧНОГО НАЗНАЧЕНИЯ
- ГЛАВА 24. СИНТЕЗ СТРУКТУРЫ СЕТИ НИСЗ ИЗ УСЛОВИИ ОБЕСПЕЧЕНИЯ ЗАДАННОЙ КРАТНОСТИ ПОКРЫТИЯ
- 24.2. ЗОНА РАДИОВИДИМОСТИ, ПОЛОСА ПОКРЫТИЯ И ОБЛАСТЬ ПЕРЕКРЫТИЯ
- 24.3. ДОСТАТОЧНЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ СЕТИ НИСЗ, ОБЕСПЕЧИВАЮЩЕЙ ЗАДАННУЮ МИНИМАЛЬНУЮ КРАТНОСТЬ ПОКРЫТИЯ
- 24.4. НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМАЛЬНОСТИ СЕТИ НИСЗ
- 24.5. СВОЙСТВА ЭКСТРЕМАЛЬНОЙ СЕТИ НИСЗ, ОБЕСПЕЧИВАЮЩЕЙ ЗАДАННУЮ МИНИМАЛЬНУЮ КРАТНОСТЬ ПОКРЫТИЯ
- 24.6. УСЛОВИЕ СТАБИЛЬНОСТИ ПРОСТРАНСТВЕННОЙ КОНФИГУРАЦИИ СЕТИ НИСЗ
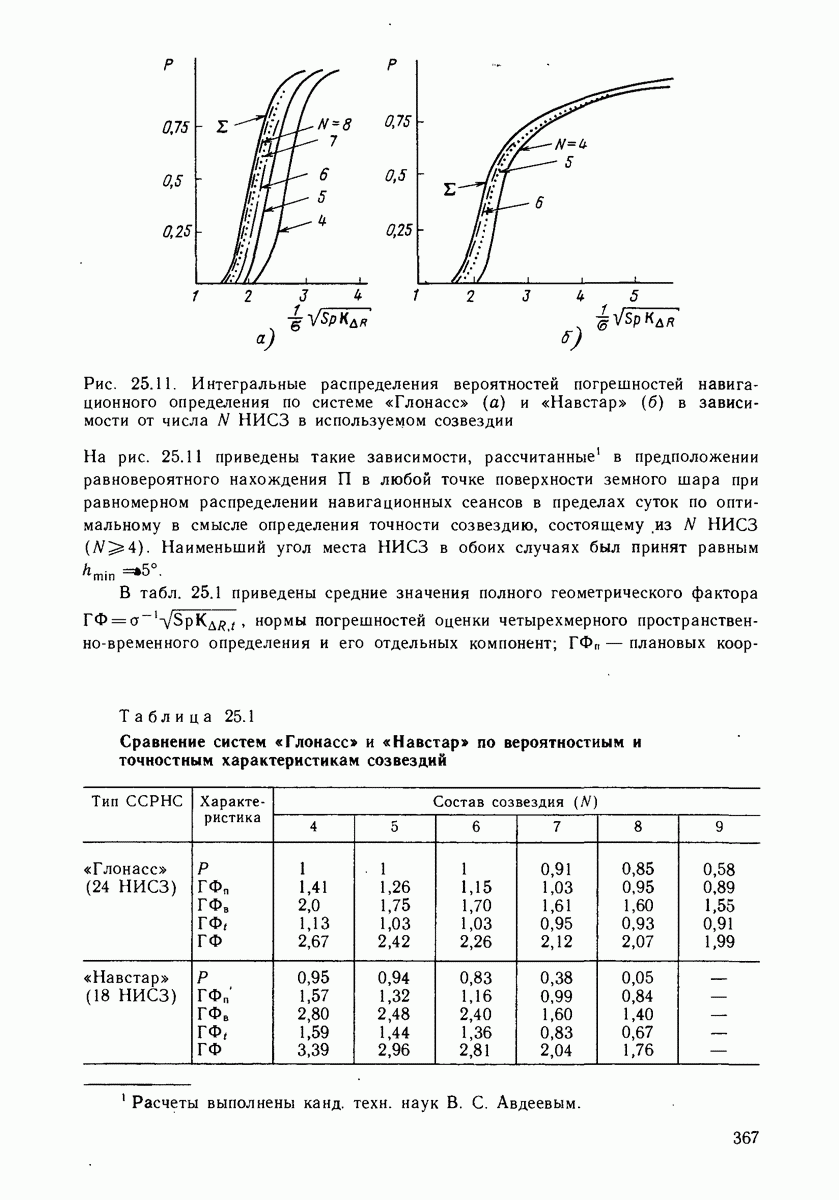
- ГЛАВА 25. СИНТЕЗ СТРУКТУРЫ СЕТИ НИСЗ ПО КРИТЕРИЮ ТОЧНОСТИ НАВИГАЦИОННЫХ ОПРЕДЕЛЕНИЙ
- 25.2. ВЫБОР ОПТИМАЛЬНОГО ПО КРИТЕРИЮ ТОЧНОСТИ СОЗВЕЗДИЯ НИСЗ
- 25.3. ПРИБЛИЖЕННЫМ УЧЕТ ПАРАЛЛАКСА МИНИМАЛЬНОГО СОЗВЕЗДИЯ
- 25.4. КАЧЕСТВЕННЫЙ АНАЛИЗ ЗОН ПОНИЖЕННОЙ ТОЧНОСТИ
- 25.5. УТОЧНЕНИЕ СТРУКТУРЫ СЕТИ НИСЗ ПО МИНИМАКСНОМУ КРИТЕРИЮ ТОЧНОСТИ
- 25.6. СРАВНЕНИЕ ССРНС «ГЛОНАСС» И «НАВСТАР»
- ГЛАВА 26. ОСНОВЫ КОМПЛЕКСНОГО ИСПОЛЬЗОВАНИЯ СРНС С ДРУГИМИ РАДИОНАВИГАЦИОННЫМИ И АВТОНОМНЫМИ НАВИГАЦИОННЫМИ СРЕДСТВАМИ
- 26.1. ОБЩИЕ ПРЕДПОСЫЛКИ И ВОЗМОЖНОСТИ СОВМЕСТНОГО ИСПОЛЬЗОВАНИЯ СПУТНИКОВЫХ РНС И ДРУГИХ НАВИГАЦИОННЫХ СРЕДСТВ
- 26.2. КОМБИНИРОВАННАЯ РАЗНОСТНО-ДАЛЬНОМЕРНАЯ РНС, СОСТОЯЩАЯ ИЗ НАЗЕМНЫХ СТАНЦИЙ И СТАЦИОНАРНОГО НИСЗ
- 26.3. КОМПЛЕКСНОЕ ИСПОЛЬЗОВАНИЕ НИЗКООРБИТАЛЬНОЙ СРНС И ФАЗОВОЙ СДВ РНС
- 26.4. КОМПЛЕКСИРОВАНИЕ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ НА УРОВНЕ ПЕРВИЧНОЙ ОБРАБОТКИ ИНФОРМАЦИИ
- ГЛАВА 27. КРИТЕРИИ ОЦЕНКИ ЭФФЕКТИВНОСТИ НАВИГАЦИОННОГО ИСПОЛЬЗОВАНИЯ СРНС
- 27.2. ОСОБЕННОСТИ ИССЛЕДОВАНИЯ ЭФФЕКТИВНОСТИ СПУТНИКОВЫХ РНС
- 27.3. ОБЩИЕ И ЧАСТНЫЕ КРИТЕРИИ ЭФФЕКТИВНОСТИ СРНС