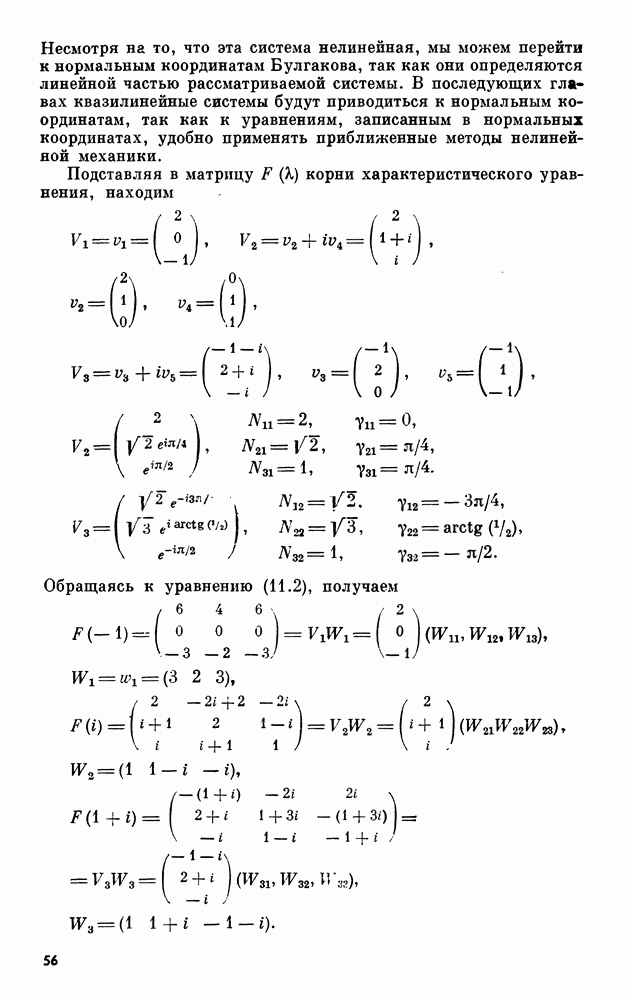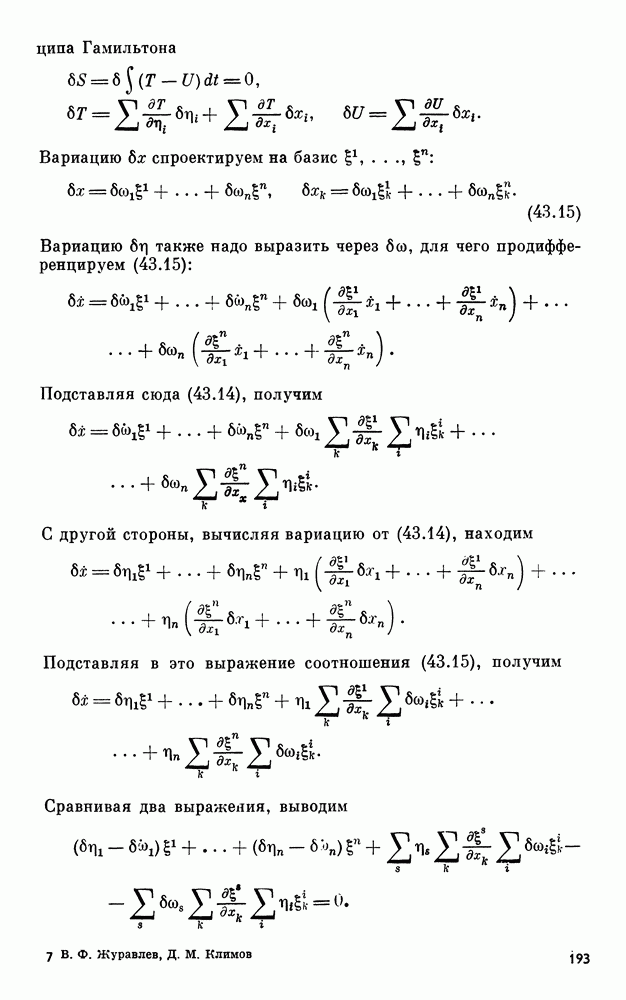| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
19. Математические основы метода осреднения
Приведенные в предыдущем разделе рассуждения, основанные на введении понятия эволюции при помощи оператора сглаживания, оправдывают рассмотренную приближенную процедуру, но не обосновывают ее. Между тем потребность в обосновании диктуется не только стремлением к формально-математической завершенности решения. При невыполнении строгих условий применимости метода могут возникнуть погрешности, грубо искажающие наше представление о существе исследуемого явления. В рассмотренном выше примере осциллятора с кубическим демпфированием полученное приближенное решение (18.15) правильно описывает характер затухания колебаний в системе, если  . Если же перед параметром 8 в уравнении осциллятора стоит знак «минус», то решение (18.15) в этом случае принимает вид
. Если же перед параметром 8 в уравнении осциллятора стоит знак «минус», то решение (18.15) в этом случае принимает вид

Оно уходит за конечное время в бесконечность при любых не равных нулю начальных условиях. В действительности же для точного уравнения существует множество не нулевых начальных условий, для которых решение уходит в бесконечность за бесконечное время. Таким образом, приближенное решение даже качественно не соответствует точному.
Приводимые ниже теоремы устанавливают четкие границы применимости метода осреднения и позволяют избежать подобных неприятностей.
Основной результат теории составляет теорема Н. Н. Боголюбова. Мы приведем полностью доказательство этой теоремы, поскольку техника доказательства [62] является, во-первых, типичной для такого рода результатов, во-вторых, конструктивной,
т. е. она позволяет строить эффективные оценки точности для конкретных задач.
Будут сравниваться две начальные задачи Коши:

На систему 1, правая часть которой определена в некоторой области  переменных
переменных  (область
(область  — открытая, связная область в
— открытая, связная область в  -мерном пространстве) и для
-мерном пространстве) и для  накладываются следующие условия:
накладываются следующие условия:
а)  — измеримая по
— измеримая по  функция при любых фиксированных
функция при любых фиксированных  частности, кусочно-непрерывная функция, множество точек разрыва которой не имеет точек сгущения);
частности, кусочно-непрерывная функция, множество точек разрыва которой не имеет точек сгущения);
б) можно найти такие две ни от чего не зависящие константы М и  что
что  для любых значений переменных из области определения (под
для любых значений переменных из области определения (под
нормой понимается евклидова норма 
в) предел  существует равномерно относительно и из
существует равномерно относительно и из  и
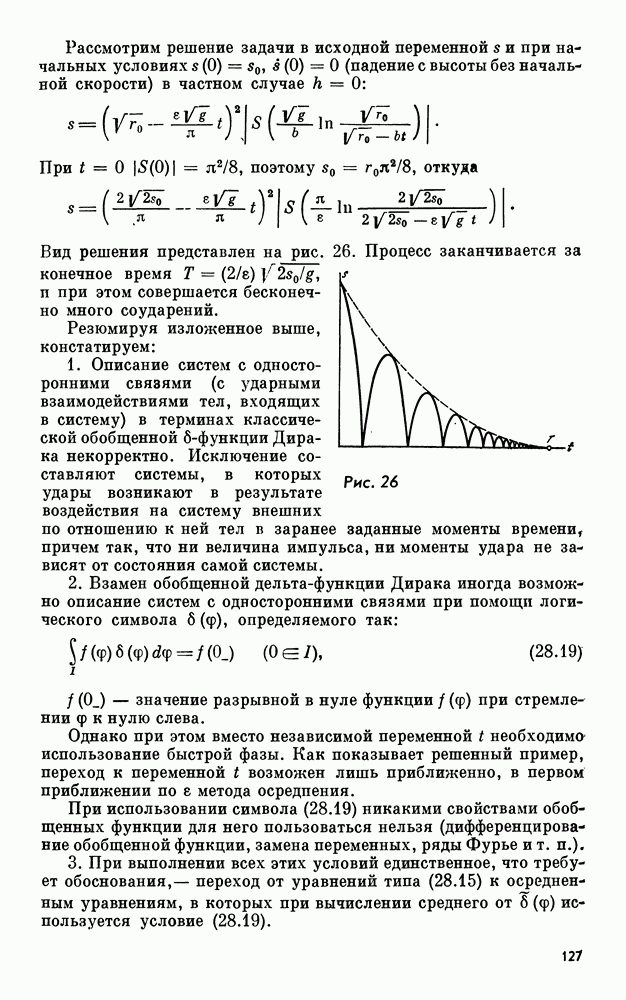
и  из
из 
Прежде чем формулировать и доказывать теорему Боголюбова, прокомментируем условия, накладываемые на правые части изучаемой системы I.
Самые слабые условия накладываются на аналитические свойства зависимости правых частей от времени. Под условие измеримости подходят кусочно-непрерывные функции, что в подавляющем большинстве случаев исчерпывает потребности практики.
Может показаться излишне обременительным первое из условий б) (ограниченность X в области определения). Например, функция  определена для
определена для  и неограничена в
и неограничена в  Однако для выяснения близости найденного решения системы II к соответствующему, но не найденному решению системы I свойства правых частей достаточно рассматривать не во всей области их определения, а лишь в малой окрестности (трубке) решения приближенной системы, в которой и следует вычислять константы
Однако для выяснения близости найденного решения системы II к соответствующему, но не найденному решению системы I свойства правых частей достаточно рассматривать не во всей области их определения, а лишь в малой окрестности (трубке) решения приближенной системы, в которой и следует вычислять константы  Второе из условий, называемое условием Липшица, более жесткое. Оно выполнено заведомо если функция
Второе из условий, называемое условием Липшица, более жесткое. Оно выполнено заведомо если функция  дифференцируема по
дифференцируема по  в области определения, и не выполнено, если эта функция разрывна по х. Обобщение доказываемой ниже теоремы на случай разрывных по х функций (кусочно-непрерывных с изолированными поверхностями разрыва) не представляет больших затруднений. Требуется только дополнительно накладывать условие, что траектория не скользит по поверхности разрыва или вблизи нее, а протыкает ее с ненулевым углом наклона. В конкретных задачах теории колебаний
в области определения, и не выполнено, если эта функция разрывна по х. Обобщение доказываемой ниже теоремы на случай разрывных по х функций (кусочно-непрерывных с изолированными поверхностями разрыва) не представляет больших затруднений. Требуется только дополнительно накладывать условие, что траектория не скользит по поверхности разрыва или вблизи нее, а протыкает ее с ненулевым углом наклона. В конкретных задачах теории колебаний
выполнение этого условия бывает очевидно по самому смыслу изучаемого процесса.
Если функция  периодична по
периодична по  то в условии в) предел заведомо существует, однако проверка этого условия всегда необходима, поскольку может не выполниться требование равномерности этого предела по параметру
то в условии в) предел заведомо существует, однако проверка этого условия всегда необходима, поскольку может не выполниться требование равномерности этого предела по параметру  . Например, это имеет место для скалярного уравнения
. Например, это имеет место для скалярного уравнения  правая часть которого периодична. Ее среднее существует и равно нулю, но рассматриваемый предел
правая часть которого периодична. Ее среднее существует и равно нулю, но рассматриваемый предел  неравномерен по
неравномерен по  из интервала
из интервала  Поэтому для этого примера формируемая ниже теорема неверна.
Поэтому для этого примера формируемая ниже теорема неверна.
Теорема 1. Если решение и  начальной задачи Коши для системы II определено для
начальной задачи Коши для системы II определено для  и принадлежит области
и принадлежит области  вместе со своей
вместе со своей  -окрестностью, то для любого наперед заданного числа
-окрестностью, то для любого наперед заданного числа  можно найти
можно найти  такое, что
такое, что

При

Если правая часть системы периодична  , то оценка (19.1) может быть существенно улучшена:
, то оценка (19.1) может быть существенно улучшена:

Доказательство. Левша (Гронуолла). Пусть скалярные и непрерывные при  функции
функции  неотрицательны. Если для них выполнено неравенство
неотрицательны. Если для них выполнено неравенство 

где С — положительное число, то верным для них будет и следующее неравенство: 

на том же интервале времени.
Доказательство леммы. Из неравенства, входящего в условие леммы, получаем

Умножая на неотрицательную функцию  найдем
найдем

Так как

то, интегрируя последнее соотношение в пределах от нуля до  будем иметь
будем иметь

или

откуда, вспоминая исходное неравенство, и получаем

Лемма доказана.
Доказательство теоремы. Перейдем от систем I и II к эквивалентным им интегральным уравнениям, после чего вычтем из первой вторую: 

В подынтегральном выражении добавим и вычтем функцию  после чего оценим это соотношение по норме, пользуясь свойствами нормы и условием б):
после чего оценим это соотношение по норме, пользуясь свойствами нормы и условием б):

где  Полученное неравенство удовлетворяет условиям леммы Гронуолла, поэтому
Полученное неравенство удовлетворяет условиям леммы Гронуолла, поэтому
можно написать

где

Оценка величины  зависит от того, является ли X периодической функцией
зависит от того, является ли X периодической функцией  или нет. Начнем с непериодического случая. Предварительно заметим, что в любом случае функции
или нет. Начнем с непериодического случая. Предварительно заметим, что в любом случае функции  удовлетворяют условию б) с константами
удовлетворяют условию б) с константами

Если и  — стационарное решение начальной задачи Коши II, то, полагая
— стационарное решение начальной задачи Коши II, то, полагая  , в силу условия в) теоремы имеем
, в силу условия в) теоремы имеем

Обозначим  существует и стремится к нулю вместе сев силу предположения о равномерности предела по
существует и стремится к нулю вместе сев силу предположения о равномерности предела по  и по
и по  . Таким образом, для стационарного решения
. Таким образом, для стационарного решения  при
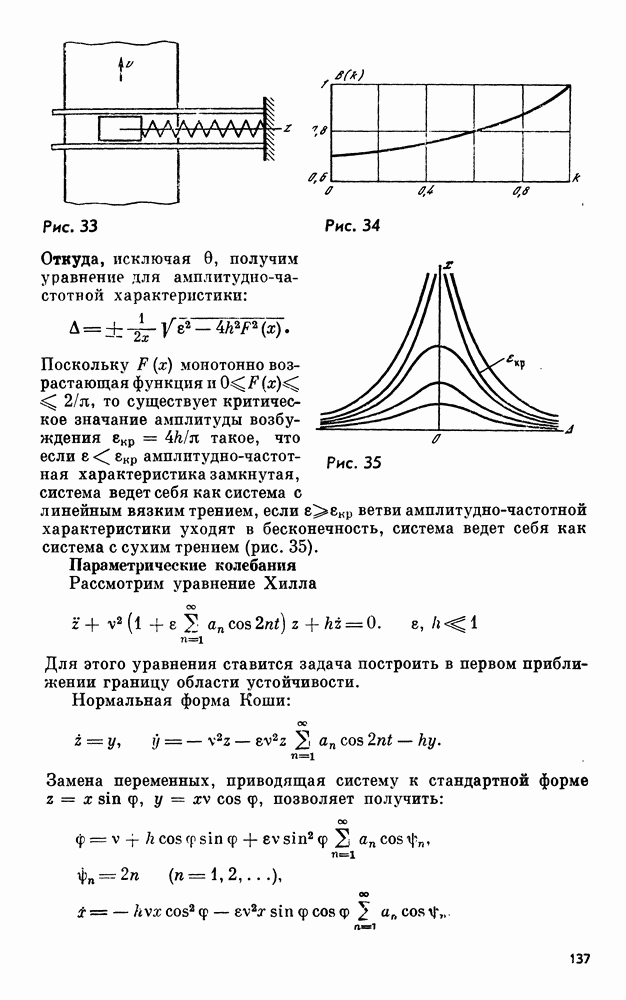
при  . Покажем, что общий случай сводится к стационарному. Разобьем интервал
. Покажем, что общий случай сводится к стационарному. Разобьем интервал  на
на  равных интервалов (рис. 7) и запишем
равных интервалов (рис. 7) и запишем

где 
По только что доказанному

Остается оценить


Рис. 7

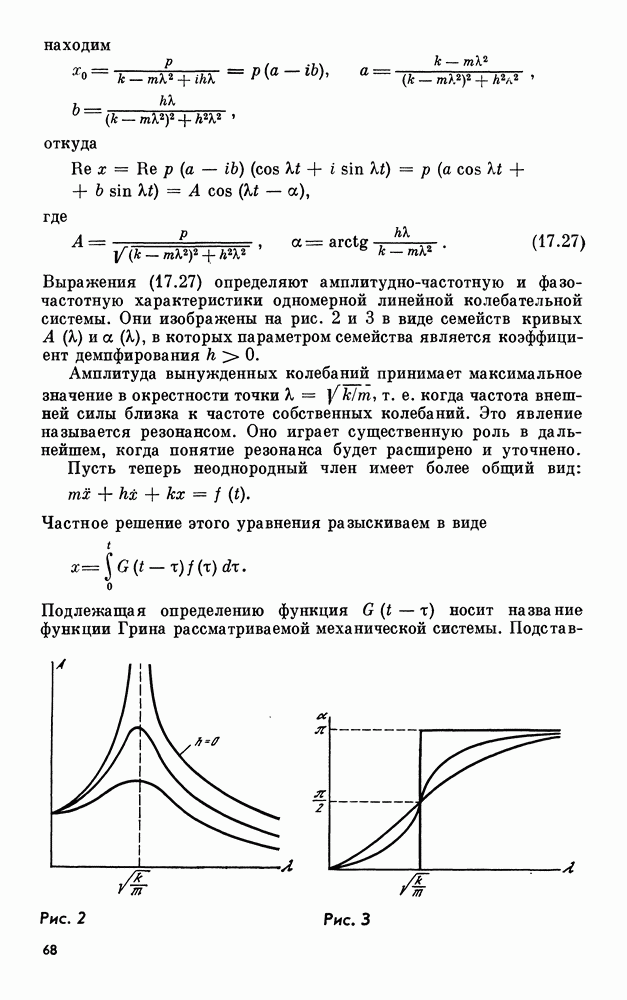
Рис. 8
Норма разности  оценивается исходя из начальной задачи Коши:
оценивается исходя из начальной задачи Коши:

откуда

что дает

Или окончательно имеем 

Очевидно, что  следует выбрать так, чтобы правая часть этого соотношения была минимальной: Откуда и следует оценка (19.1).
следует выбрать так, чтобы правая часть этого соотношения была минимальной: Откуда и следует оценка (19.1).
Рассмотрим теперь периодический случай. Пусть Т — период и  Тогда
Тогда

Поскольку

то

Как и в предыдущем случае,  . Поэтому
. Поэтому 

Учитывая, что  получим неравенство (19.2).
получим неравенство (19.2).
Теорема доказана.
Рассмотрим пример применения сформулированной теоремы. В примере с осциллятором с кубическим демпфированием

Решение осредненной системы (18.13) с начальными условиями:  имеет вид
имеет вид

Область  в которой определена система (18.11) и которая фигурирует в теореме, совпадает со всей плоскостью
в которой определена система (18.11) и которая фигурирует в теореме, совпадает со всей плоскостью  При построении оценок точности выгодно брать область
При построении оценок точности выгодно брать область  как можна меньшей. Достаточно взять лишь
как можна меньшей. Достаточно взять лишь  -окрестность решения (19.4). Такая область изображена на рис. 8.
-окрестность решения (19.4). Такая область изображена на рис. 8.
Все условия теоремы в этой области выполнены, следует только подсчитать константы М и X, фигурирующие в оценке (19.2). Имеем

Подставляя выражения для М и К в соотношение (19.2), получаем

Такая оценка будет верна, если неизвестное точное решение  на рассматриваемом интервале времени
на рассматриваемом интервале времени  лежит в области
лежит в области 
То максимальное значение  , при котором это можно гарантировать, и есть фигурирующее в теореме
, при котором это можно гарантировать, и есть фигурирующее в теореме  Очевидно, оно может быть найдено из условия равенства оценки нормы
Очевидно, оно может быть найдено из условия равенства оценки нормы  величине
величине 

Пусть нам задан параметр  и интервал времени, на котором рассматривается решение
и интервал времени, на котором рассматривается решение  Тогда число
Тогда число  Из соотношения (19.5) получаем, что
Из соотношения (19.5) получаем, что  Это дает нам
Это дает нам  Подставляя их в оценку (19.2), получаем
Подставляя их в оценку (19.2), получаем  для
для 
В случае, когда имеется отрицательное кубическое демпфирование, решение и  не ограничено. Неограниченной оказывается и область
не ограничено. Неограниченной оказывается и область  . В неограниченной области правые части (18.11) также неограничены, т. е. теорема 1 не дает никаких гарантий точности, поскольку
. В неограниченной области правые части (18.11) также неограничены, т. е. теорема 1 не дает никаких гарантий точности, поскольку 
Если рассматриваемое решение осредненной системы асимптотически устойчиво, то оценки типа (19.1), (19.2) оказываются справедливыми на бесконечном интервале времени. Этот факт был установлен К. Банфи [61].
Предметом интереса в теории колебаний часто является не начальная задача Коши для систем вида (18.7), а стационарные режимы, которые для исходных уравнений (18.7) обычно определяют периодический процесс. Метод осреднения позволяет не только доказать существование и найти такой процесс, но и изучить его устойчивость. При обосновании решения задачи в такой постановке приходится сравнивать не частные решения точной и осредненной систем с одинаковыми начальными условиями, а стационарные режимы в этих системах, которые, вообще говоря, удовлетворяют различным начальным условиям. Соответствие между такими решениями устанавливает теорема 2.
Теорема 2. Имеются две системы I и II:

Пусть Т — период функции  по
по  не зависящий от
не зависящий от 

Пусть  — стационарное решение системы II, т. е.
— стационарное решение системы II, т. е.  для которого матрица
для которого матрица  невырожденна. Тогда для всех достаточно малых
невырожденна. Тогда для всех достаточно малых  системы I существует периодическое решение с периодом Г, которое при
системы I существует периодическое решение с периодом Г, которое при  стремится к
стремится к  Если, кроме того, собственные числа X этой матрицы, определяемые характеристическим уравнением
Если, кроме того, собственные числа X этой матрицы, определяемые характеристическим уравнением

имеют отрицательные вещественные части (стационарное решение системы II асимптотически устойчиво), то это периодическое решение системы I асимптотически устойчиво.
Для справедливости теоремы требуется существование непрерывных частных производных первого порядка по  функции
функции  в окрестности точки
в окрестности точки  а также непрерывность этой функции по
а также непрерывность этой функции по  и ее непрерывность (достаточно и измеримости) по
и ее непрерывность (достаточно и измеримости) по  Таким образом, теорема 2 позволяет из существования и устойчивости стационарного режима в осредненной системе (что, как правило, представляет собой достаточно простую задачу) выводить существование и устойчивость периодического решения в точной системе. Полное доказательство теоремы приведено в [11].
Таким образом, теорема 2 позволяет из существования и устойчивости стационарного режима в осредненной системе (что, как правило, представляет собой достаточно простую задачу) выводить существование и устойчивость периодического решения в точной системе. Полное доказательство теоремы приведено в [11].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава первая. ЛИНЕЙНЫЕ СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- 2. Блочные матрицы
- 3. Матрицы Кейли
- 4. Полиномиальные матрицы
- 5. Собственные движения линейной системы с линейными элементарными делителями
- 6. Общий случай собственных движений линейной системы
- 7. Приведение общего решения линейной системы к действительной форме
- 8. Список правил построения общего решения однородной системы линейных дифференциальных уравнений
- 9. Примеры собственных движений линейных систем
- 10. Общий случай вынужденных движений линейных систем
- 11. Метод вариации постоянных Лагранжа в форме Булгакова
- 12. Список правил построения общего решения неоднородной системы линейных дифференциальных уравнений
- 13. Примеры построения общего решения неоднородных систем линейных уравнений
- 14. Метод нормальных координат Булгакова
- 15. Список правил перехода к нормальным координатам Булгакова
- 16. Пример использования нормальных координат Булгакова
- 17. Механические колебательные системы. Спектральные свойства
- Глава вторя. НЕЛИНЕЙНЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ, МЕТОД ОСРЕДНЕНИЯ
- 18. Одночастотные системы. Первая стандартная форма
- 19. Математические основы метода осреднения
- 20. Построение высших приближений. Понятие об асимптотическом ряде
- 21. Введение малого параметра. Осреднение функций
- 22. Многочастотные системы. Резонанс
- 23. Квазилинейные системы
- 24. Существенно нелинейные системы
- 25. Лагранжев формализм
- 26. Метод осреднения в гироскопических системах
- 27. Осреднение в системах с ударными взаимодействиями
- 28. Об использовании обобщенных функций в задачах с ударными взаимодействиями
- 29. Метод двух масштабов
- 30. Примеры типичных постановок задач, решаемых методом осреднения
- Глава третья. ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП ЛИ
- 32. Группа Ли. Примеры
- 33. Инфинитезимальный оператор группы. Алгебра Ли
- 34. Однопараметрические группы. Теорема единственности
- 35. Уравнение Лиувилля. Инварианты. Собственные функции
- 36. Линейные уравнения с частными производными
- 37. Замена переменных. Канонические координаты
- 38. Формула Хаусдорфа. Группы симметрий
- 39. Принцип суперпозиции решений и разделение движений в нелинейных системах
- 40. Продолжение оператора. Дифференциальные и интегральные инварианты
- 41. Уравнения, допускающие заданную группу
- 42. Симметрии уравнений в частных производных
- 43. Примеры
- Глава четвертая АСИМПТОТИЧЕСКИЕ МЕТОДЫ, ОСНОВАННЫЕ НА ПОНЯТИИ ГРУППЫ ЛИ
- 45. Метод Хори
- 46. Одночастотный метод осреднения на основе формулы Хаусдорфа
- 47. Многочастотные системы
- 48. Метод нормальной формы
- 49. Применение одночленных групп к построению нормальной формы
- 50. Метод касательных (оскулирующих) приближений
- Глава пятая. ТЕОРИЯ КОЛЕБАНИЙ В ЗАДАЧАХ ТЕХНИКИ
- 51. Существенно нелинейные вынужденные колебания гироскопа в кардановом подвесе
- 52. Вынужденные колебания гироскопа в окрестности неизолированного положения равновесия
- 53. Явление самосинхронизации в скоростных гироскопических опорах
- 54. Об устойчивости стационарных движений плоского тела в поле центральной силы
- 55. Эффект инертности упругих волн в симметричных упругих телах
- 56. Прецессия стоячих волн во вращающемся упругом растяжимом кольце
- 57. Пространственная прецессия стоячих волн во вращающемся сферически симметричном упругом теле
- 58. Вынужденные колебания системы с двумя ударными парами
- 59. Ударный проглотитель колебаний
- 60. Виброударная система с ограниченным возбуждением
- 61. Волчок Лагранжа на подвижном основании. Ядерный магнитный резонанс
- ЛИТЕРАТУРА