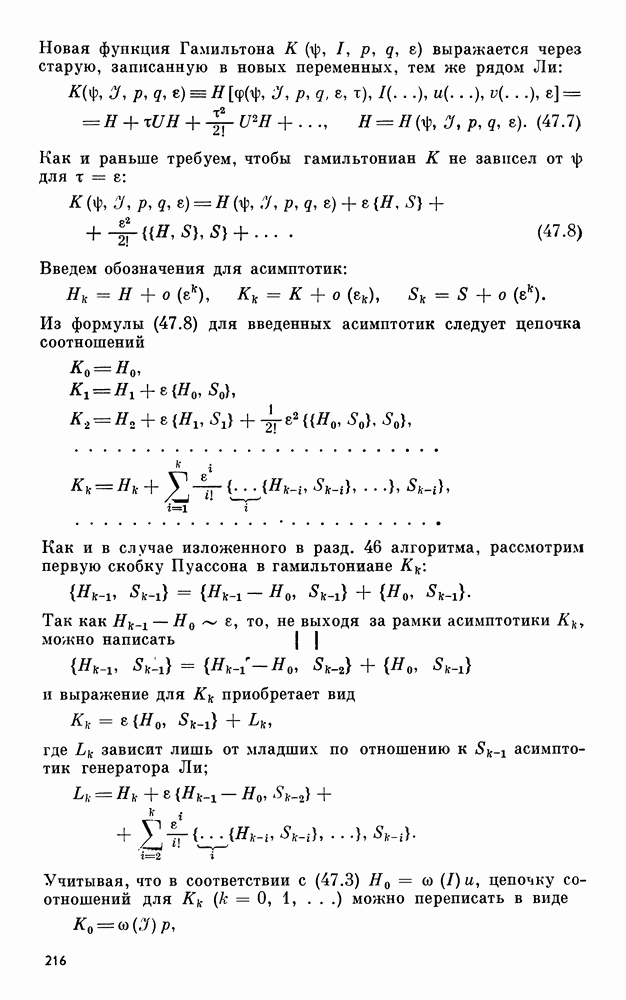| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
43. Примеры
Пример 1. Группы симметрий уравнений классической механики:

Прежде всего заметим следующее. В механике сила  обычно рассматривается зависящей от времени, координаты х и скорости
обычно рассматривается зависящей от времени, координаты х и скорости
х. Однако всякие такие зависимости отражают некоторые подробности конкретно выбранной задачи. При построении групп симметрий уравнений механики, отражающих наиболее общие свойства этих уравнений, никакими конкретными зависимостями силы от аргументов интересоваться не нужно. Поэтому мы и будем полагать силу постоянной.
Искомая группа симметрий действует в пространстве переменных 

Уравнение (43.1) должно быть инвариантным относительно дважды продолженной группы с оператором:

где  (скорость),
(скорость),  (ускорение).
(ускорение).
Уравнение (43.1) в пространстве переменных  определяет гиперплоскость
определяет гиперплоскость

Условие ее инвариантности есть

что в данном случае дает

В соответствии с (40.7) и (40.4) в используемых в этом примере обозначениях

Следовательно, условие инвариантности есть

Так как функция  не зависит от
не зависит от  то полученное уравнение распадается на два:
то полученное уравнение распадается на два:

Подставим в эти уравнения  из (43.4):
из (43.4):

Поскольку функции  не зависят от у, то эти уравнения, в свою очередь, распадаются:
не зависят от у, то эти уравнения, в свою очередь, распадаются:

Из этих уравнений видно, что  есть линейная функция
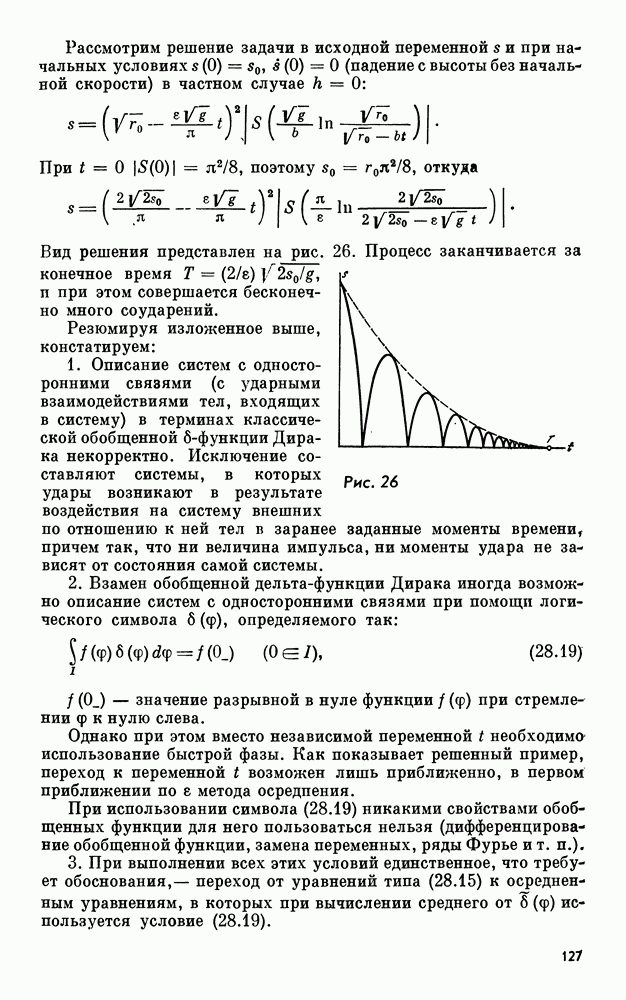
есть линейная функция  :
:

но тогда  , следовательно,
, следовательно,  также есть линейная функция
также есть линейная функция  :
:

причем  в силу
в силу  , наконец, из условия
, наконец, из условия  находим
находим 
Общее выражение для оператора  получается таким:
получается таким:

где

 — произвольные постоянные.
— произвольные постоянные.
Первые два оператора определяют трансляции, третий — группу неоднородных растяжений (изменение масштабов) и четвертый — группу Галилея.
Рассмотрен одномерный случай. Пространственный случай рассматривается аналогично. Необходимо только предварительно получить аналоги формул (40.7) и (40.4), определяющих продолжение оператора для пространственного случая.
Базис операторов в пространственном случае следующий:

Алгебра симметрий уравнений классической механики восьмимерна. Заметим, что операторы группы вращений не входят в эту алгебру. Уравнения Ньютона не инвариантны по отношению к поворотам. Преобразования группы вращений изменяют уравнения Ньютона, однако обе части этих уравнений (ускорения и силы) изменяются по одному и тому же закону, и это отражается в несколько ином понятии — ковариантности [19].
Пример 2. Релятивистская механика. Построение уравнений релятивистской механики основывается на трех аксиомах:
A. Аксиома инерциальной координатной системы: существует система координат  в которой любая свободная материальная точка описывает прямую.
в которой любая свободная материальная точка описывает прямую.
Б. Аксиома относительности: в любых инерциальных системах уравнения Максвелла в пустоте имеют одинаковый вид:

B. Аксиома динамики: в любых инерциальных системах закон движения материальной точки выражается дифференциальным уравнением второго порядка, имеющим пределом уравнение Ньютона при с 

где  и
и  — параметры предельного уравнения, т. е. масса и сила.
— параметры предельного уравнения, т. е. масса и сила.
Для нахождения релятивистских уравнений динамики необходимо выяснить, как связаны друг с другом инерциальные системы в силу условия инвариантности уравнений Максвелла, т. е. необходимо найти группу симметрий этих уравнений. Из уравнения Максвелла последовательно получаем

(без ограничения общности 
Рассмотрим для простоты одномерный случай (там, где неодномерность будет существенной, это будет указано):

По-прежнему исходим из условия (42.11), в котором операторы А и  имеют теперь вид
имеют теперь вид

(Поскольку нас интересуют лишь преобразования независимых переменных, то 
В результате чего определяющие уравнения для нахождения коэффициентов искомого оператора  получаются в виде
получаются в виде

Из  следует
следует

Следовательно, независимы только три соотношения:

где  — произвольная функция.
— произвольная функция.
Имеем систему трех уравнений для нахождения двух функций Произвольную функцию к  надо выбирать так, чтобы эта система была совместной. Имеет место следующий (легко проверяемый) факт. Если к
надо выбирать так, чтобы эта система была совместной. Имеет место следующий (легко проверяемый) факт. Если к  некоторая функция, при которой существует решение (43.6)
некоторая функция, при которой существует решение (43.6)

то заведомо будет существовать решение этой системы, если в качестве к взять любую из этих функций, т. е.  или
или  Этот факт определяет рекуррентный алгоритм построения бесконечномерной алгебры симметрий уравнения (43.5).
Этот факт определяет рекуррентный алгоритм построения бесконечномерной алгебры симметрий уравнения (43.5).
Начнем со случая  Из уравнений (43.6) имеем
Из уравнений (43.6) имеем

где  — произвольные константы. Таким образом, находим следующие три оператора симметрий:
— произвольные константы. Таким образом, находим следующие три оператора симметрий:

Для продолжения процесса к может быть выбрано в одном из следующих видов:

Для  из (43.6) легко следует
из (43.6) легко следует

 — новые произвольные постоянные. То есть отличным от найденных будет только оператор
— новые произвольные постоянные. То есть отличным от найденных будет только оператор

Положим теперь  следует
следует  из
из  следует
следует  Уравнение
Уравнение  влечет
влечет

В силу независимости С от  и В от х это уравнение распадается на два:
и В от х это уравнение распадается на два:

где а — произвольная константа. Откуда

Следовательно,

т. е. к найденным операторам добавляется новый:

Совершенно аналогично находим: для 

для 

Начиная с операторов  новые операторы симметрий можно получать, вычисляя коммутаторы. Из бесконечномерной алгебры симметрий необходимо оставить лишь те операторы, которые не нарушают аксиомы А, т. е. прямые преобразованиями группы должны переходить в прямые. Последним свойством обладает лишь проективная группа. Поэтому решением задачи нахождения всех преобразований, переводящих инерциальные системы в инерциальные и не изменяющих уравнения (43.5), будет пересечение алгебры проективной группы (см. разд. 33, п. G) с алгеброй симметрий волнового уравнения. Это пересечение есть четырехмерная алгебра с базисом
новые операторы симметрий можно получать, вычисляя коммутаторы. Из бесконечномерной алгебры симметрий необходимо оставить лишь те операторы, которые не нарушают аксиомы А, т. е. прямые преобразованиями группы должны переходить в прямые. Последним свойством обладает лишь проективная группа. Поэтому решением задачи нахождения всех преобразований, переводящих инерциальные системы в инерциальные и не изменяющих уравнения (43.5), будет пересечение алгебры проективной группы (см. разд. 33, п. G) с алгеброй симметрий волнового уравнения. Это пересечение есть четырехмерная алгебра с базисом

Таким образом, единственной группой, отличной от трансляций и однородных растяжений, удовлетворяющей поставленным условиям, является группа, определяемая оператором:

Это и есть группа Лоренца.
Преобразование координат  их индуцирует преобразование скоростей и ускорений (продолжение группы). Продолженный оператор по формулам (40.8), (40.7), (40.4) имеет вид
их индуцирует преобразование скоростей и ускорений (продолжение группы). Продолженный оператор по формулам (40.8), (40.7), (40.4) имеет вид

Для построения самой группы решаем уравнения

где правые части составлены из компонент оператора (43.8). Первые два уравнения дают

Из третьего находим

Последним соотношением удобно воспользоваться, чтобы придать каноническому параметру  механический смысл. Пусть относительно неподвижной системы отсчета
механический смысл. Пусть относительно неподвижной системы отсчета  система
система  движется по пространственной координате со скоростью
движется по пространственной координате со скоростью  Тогда для начала координат системы
Тогда для начала координат системы  что дает
что дает

Подставляя это выражение для  в (43.9) и (43.10), получим
в (43.9) и (43.10), получим

Это и есть полные выражения для дважды продолженной группы Лоренца. Первые два соотношения — обычные преобразования Лоренца, третье — закон преобразования скоростей, четвертое — закон преобразования ускорений.
Закон преобразования скоростей часто неточно называется законом сложения скоростей. Он может рассматриваться лишь как частный случай последнего, когда одна из складываемых скоростей — переменная  а другая — постоянная
а другая — постоянная 
Построим инварианты группы (43.11). Исходим из уравнения

Откуда следуют три инварианта:

Инвариант  в теории относительности носит название интервала. Интегральные инварианты. Исходим из уравнения
в теории относительности носит название интервала. Интегральные инварианты. Исходим из уравнения

откуда следует 

т. е. интегральный инвариант группы Лоренца имеет вид

где  — произвольная функция инвариантов (43.12).
— произвольная функция инвариантов (43.12).
В частности, инвариант 

в теории относительности получил название собственного времени частицы, движущейся со скоростью х.
После того как найдены инварианты, можно приступить к нахождению обобщения для уравнений Ньютона. По постулату В это уравнение должно иметь одинаковый вид в любой инерциальной системе координат. Иными словами, оно должно быть инвариантным относительно построенной группы Лоренца. Общий вид уравнений второго порядка, инвариантных относительно заданной группы, в соответствии с (41.9) есть

В силу однородности пространства (допустимость группы трансляций) зависимости от  быть не может, так как
быть не может, так как  не являются инвариантами трансляций, потому уравнение динамики приобретает вид
не являются инвариантами трансляций, потому уравнение динамики приобретает вид  Используя найденное выше выражение для
Используя найденное выше выражение для  получим (возвращаясь к измерению с в принятых масштабах):
получим (возвращаясь к измерению с в принятых масштабах):

Из условия

находим 
Для получения трехмерного случая перепишем (43.13) в виде

Если система допускает лагранжево описание, то лагранжиан должен удовлетворять уравнению

откуда находим

Трехмерное обобщение, учитывающее инвариантность лагранжиана относительно поворотов, есть

Заметим, что действие по Гамильтону

есть интегральный инвариант, поэтому пространственные уравнения релятивистской механики должны иметь вид

Поскольку при записи уравнений Лагранжа в новых переменных  происходит также и перепроектирование их на новые оси, то закон преобразования левых частей написанных уравнений навязывает тот же закон и для преобразования правых частей. В трехмерном случае при переходе от одной инерциальной системы к другой, стоящие в правых частях силы изменяются. Для одномерного случая это не так, сила
происходит также и перепроектирование их на новые оси, то закон преобразования левых частей написанных уравнений навязывает тот же закон и для преобразования правых частей. В трехмерном случае при переходе от одной инерциальной системы к другой, стоящие в правых частях силы изменяются. Для одномерного случая это не так, сила  одна и та же во всех системах координат и представляет собой обычную ньютонову силу. В одномерном случае уравнение механики инвариантно по отношению к лоренцевой группе, в трехмерном оно лишь ковариантно.
одна и та же во всех системах координат и представляет собой обычную ньютонову силу. В одномерном случае уравнение механики инвариантно по отношению к лоренцевой группе, в трехмерном оно лишь ковариантно.
Пример 3. Уравнения механики Пуанкаре.
Пусть имеется механическая система, Т — ее кинетическая энергия,  — потенциальная энергия.
— потенциальная энергия.
Пусть  — локальные лагранжевы координаты этой системы;
— локальные лагранжевы координаты этой системы;  — скорости.
— скорости.
Пусть, наконец, в области определения системы действует локальная группа Ли, обладающая свойством транзитивности (группа транзитивна, если для любых двух точек пространства положений существует преобразование из группы, переводящее одну точку в другую).
Группа транзитивна тогда и только тогда, когда она содержит  линейно несвязанных операторов:
линейно несвязанных операторов:

векторы

образуют в пространстве х базис, по которому можно разложить скорость:

Выберем в качестве фазовых переменных системы переменные

Подставляя (43.14) в  получим
получим  (для простоты новую функцию обозначили той же буквой). Исходим из
(для простоты новую функцию обозначили той же буквой). Исходим из

(кликните для просмотра скана)

(кликните для просмотра скана)
Частным случаем уравнений являются, очевидно, уравнения Лагранжа.
В динамике твердого тела роль переменных  могут играть компоненты вектора угловой скорости в проекции на оси тела. В этом случае уравнения Пуанкаре переходят в уравнения Эйлера.
могут играть компоненты вектора угловой скорости в проекции на оси тела. В этом случае уравнения Пуанкаре переходят в уравнения Эйлера.
Пример 4. Теорема Нётер. Если функция Лагранжа механической системы  инвариантна относительно группы
инвариантна относительно группы

где  — локальные координаты, то механическая система имеет первый интеграл
— локальные координаты, то механическая система имеет первый интеграл

Доказательство. Для того чтобы записать условие инвариантности лагранжиана, необходимо построить продолжение оператора группы на скорости. С этой целью будем полагать, что группа действует в расширенном координатном пространстве  добавив преобразование временив
добавив преобразование временив  Тогда оператор первого продолжения получается по формулам разд. 31 таким:
Тогда оператор первого продолжения получается по формулам разд. 31 таким:

Условие инвариантности лагранжиана есть

Из уравнений Лагранжа имеем 

Подставляя в условие инвариантности, получим

или

что и требовалось.
Замечание 1. Эта теорема легко обобщается на неголономные системы. В самом деле, пусть неголономная связь имеет вид

где  — зависят от координат и времени.
— зависят от координат и времени.
К условиям теоремы Нётер в этом случае следует добавить естественное требование  бесконечно малые преобразования группы должны принадлежать виртуальным перемещениям системы. В данном случае из уравнений Лагранжа следует
бесконечно малые преобразования группы должны принадлежать виртуальным перемещениям системы. В данном случае из уравнений Лагранжа следует

После подстановки этого выражения в условие инвариантности приходим к тому же результату благодаря введенному дополнительному требованию.
Замечание 2. Обобщение теоремы Нётер. Если существует группа (в отличие от предыдущего, время преобразуется тоже):

для которой действие по Гамильтону

есть интегральный инвариант, то у системы есть интеграл

где Н — функция Гамильтона,  обобщенные импульсы:
обобщенные импульсы:

Доказательство. Условие интегрального инварианта (40.12) запишется

Учитывая (40.4), перепишем это равенство:

Так как имеет место

то это дает

Или иначе:

Откуда и следует приведенное утверждение.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава первая. ЛИНЕЙНЫЕ СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- 2. Блочные матрицы
- 3. Матрицы Кейли
- 4. Полиномиальные матрицы
- 5. Собственные движения линейной системы с линейными элементарными делителями
- 6. Общий случай собственных движений линейной системы
- 7. Приведение общего решения линейной системы к действительной форме
- 8. Список правил построения общего решения однородной системы линейных дифференциальных уравнений
- 9. Примеры собственных движений линейных систем
- 10. Общий случай вынужденных движений линейных систем
- 11. Метод вариации постоянных Лагранжа в форме Булгакова
- 12. Список правил построения общего решения неоднородной системы линейных дифференциальных уравнений
- 13. Примеры построения общего решения неоднородных систем линейных уравнений
- 14. Метод нормальных координат Булгакова
- 15. Список правил перехода к нормальным координатам Булгакова
- 16. Пример использования нормальных координат Булгакова
- 17. Механические колебательные системы. Спектральные свойства
- Глава вторя. НЕЛИНЕЙНЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ, МЕТОД ОСРЕДНЕНИЯ
- 18. Одночастотные системы. Первая стандартная форма
- 19. Математические основы метода осреднения
- 20. Построение высших приближений. Понятие об асимптотическом ряде
- 21. Введение малого параметра. Осреднение функций
- 22. Многочастотные системы. Резонанс
- 23. Квазилинейные системы
- 24. Существенно нелинейные системы
- 25. Лагранжев формализм
- 26. Метод осреднения в гироскопических системах
- 27. Осреднение в системах с ударными взаимодействиями
- 28. Об использовании обобщенных функций в задачах с ударными взаимодействиями
- 29. Метод двух масштабов
- 30. Примеры типичных постановок задач, решаемых методом осреднения
- Глава третья. ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП ЛИ
- 32. Группа Ли. Примеры
- 33. Инфинитезимальный оператор группы. Алгебра Ли
- 34. Однопараметрические группы. Теорема единственности
- 35. Уравнение Лиувилля. Инварианты. Собственные функции
- 36. Линейные уравнения с частными производными
- 37. Замена переменных. Канонические координаты
- 38. Формула Хаусдорфа. Группы симметрий
- 39. Принцип суперпозиции решений и разделение движений в нелинейных системах
- 40. Продолжение оператора. Дифференциальные и интегральные инварианты
- 41. Уравнения, допускающие заданную группу
- 42. Симметрии уравнений в частных производных
- 43. Примеры
- Глава четвертая АСИМПТОТИЧЕСКИЕ МЕТОДЫ, ОСНОВАННЫЕ НА ПОНЯТИИ ГРУППЫ ЛИ
- 45. Метод Хори
- 46. Одночастотный метод осреднения на основе формулы Хаусдорфа
- 47. Многочастотные системы
- 48. Метод нормальной формы
- 49. Применение одночленных групп к построению нормальной формы
- 50. Метод касательных (оскулирующих) приближений
- Глава пятая. ТЕОРИЯ КОЛЕБАНИЙ В ЗАДАЧАХ ТЕХНИКИ
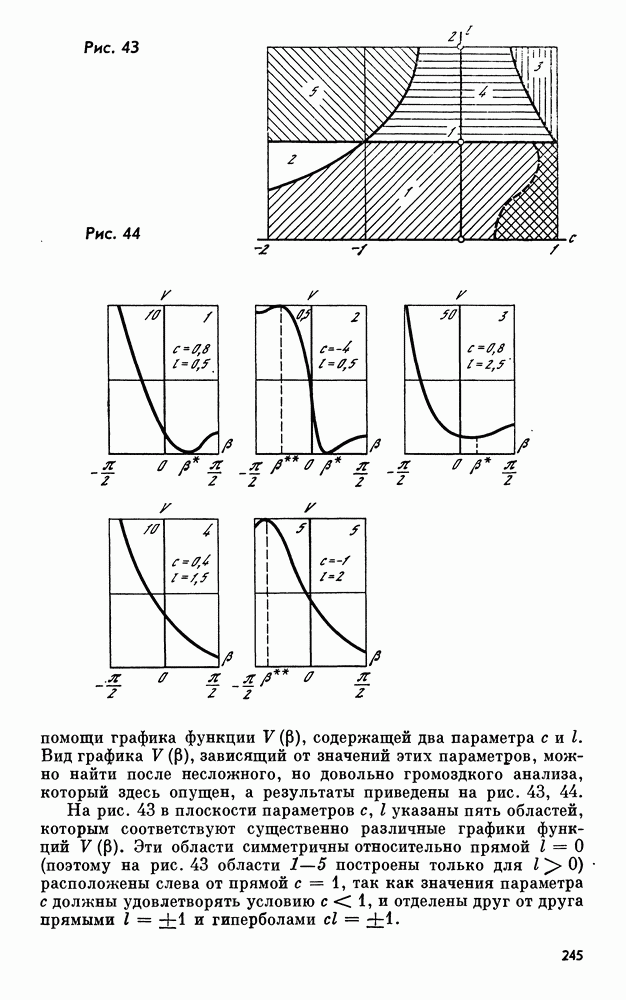
- 51. Существенно нелинейные вынужденные колебания гироскопа в кардановом подвесе
- 52. Вынужденные колебания гироскопа в окрестности неизолированного положения равновесия
- 53. Явление самосинхронизации в скоростных гироскопических опорах
- 54. Об устойчивости стационарных движений плоского тела в поле центральной силы
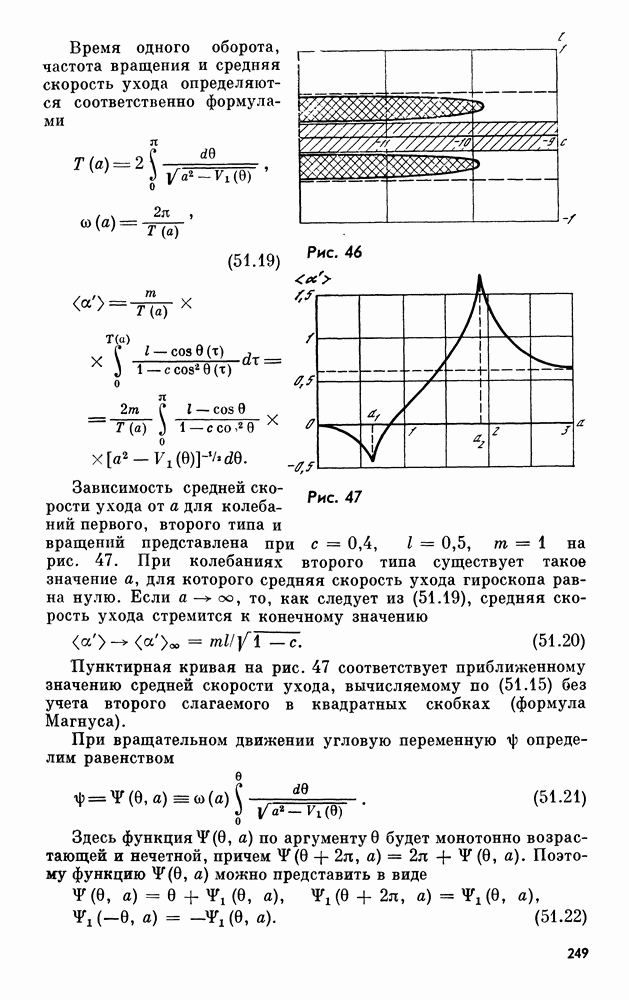
- 55. Эффект инертности упругих волн в симметричных упругих телах
- 56. Прецессия стоячих волн во вращающемся упругом растяжимом кольце
- 57. Пространственная прецессия стоячих волн во вращающемся сферически симметричном упругом теле
- 58. Вынужденные колебания системы с двумя ударными парами
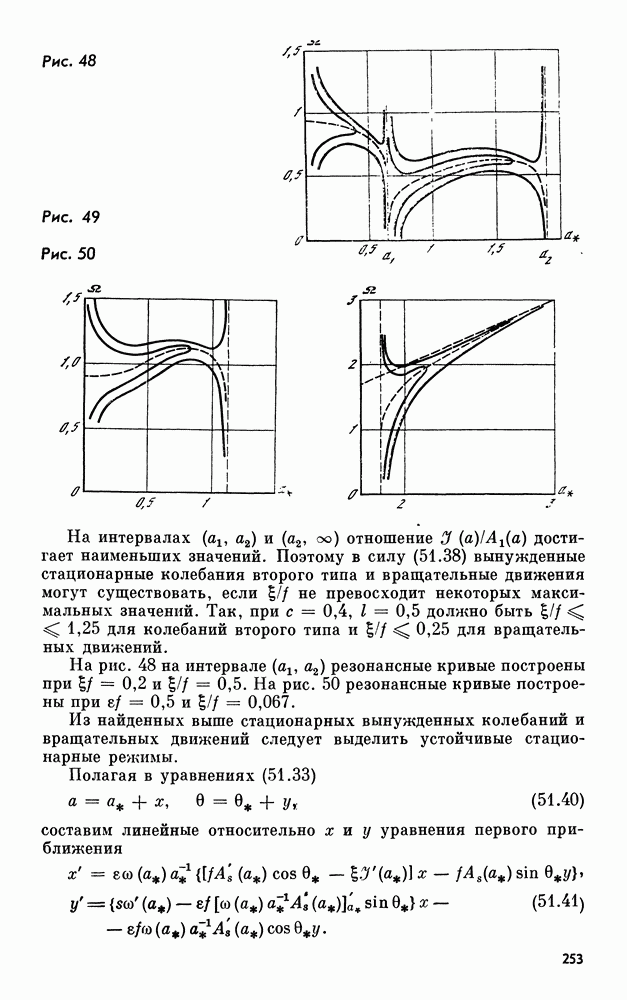
- 59. Ударный проглотитель колебаний
- 60. Виброударная система с ограниченным возбуждением
- 61. Волчок Лагранжа на подвижном основании. Ядерный магнитный резонанс
- ЛИТЕРАТУРА