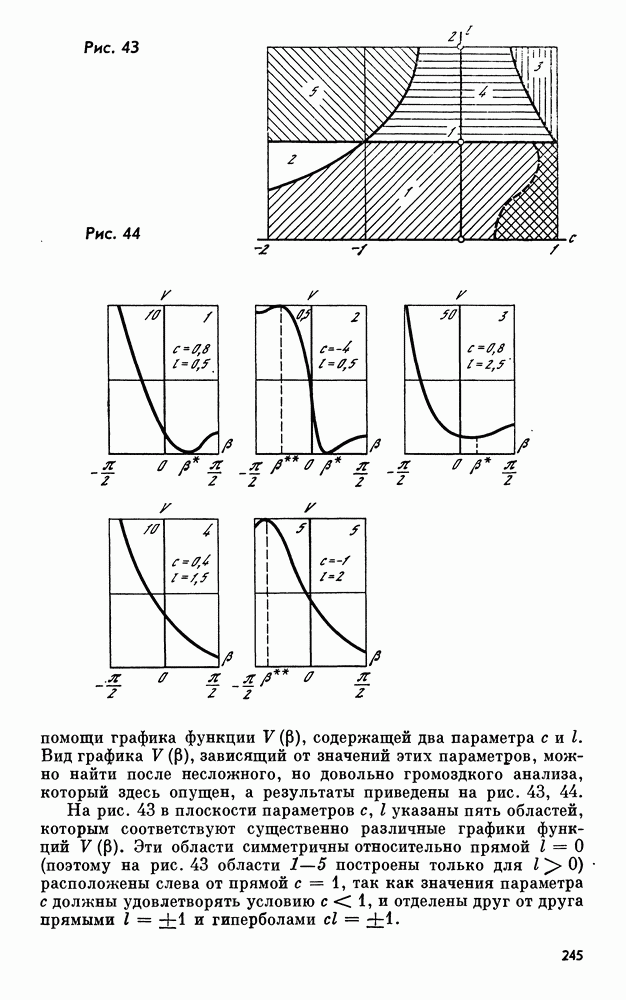
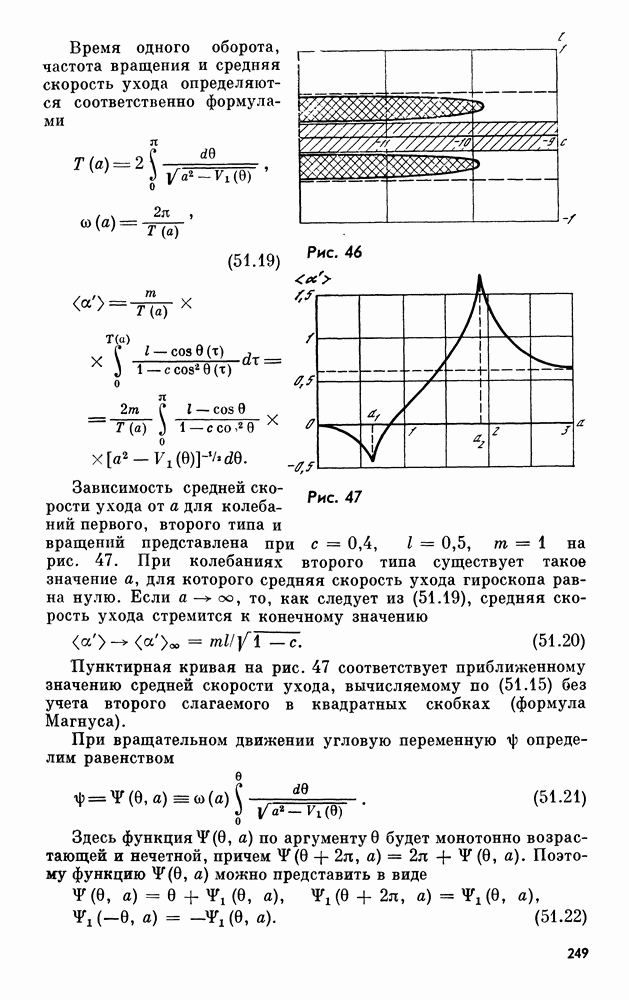
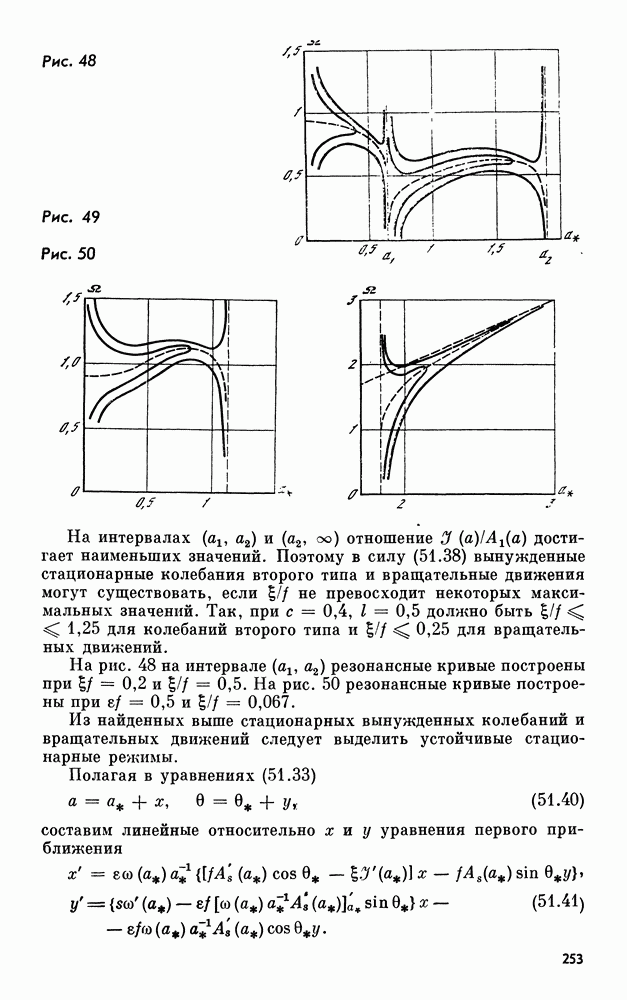
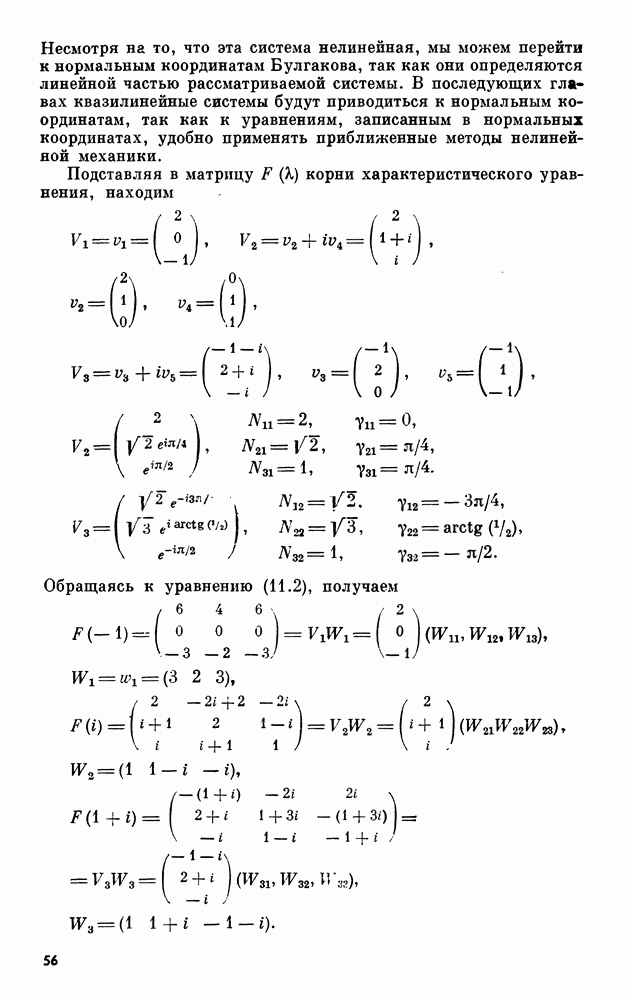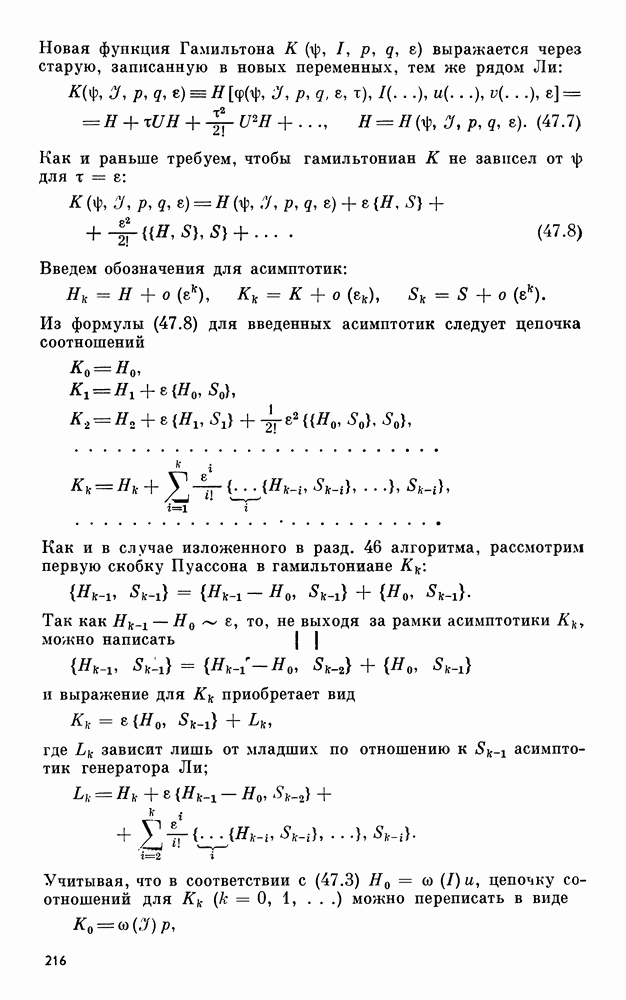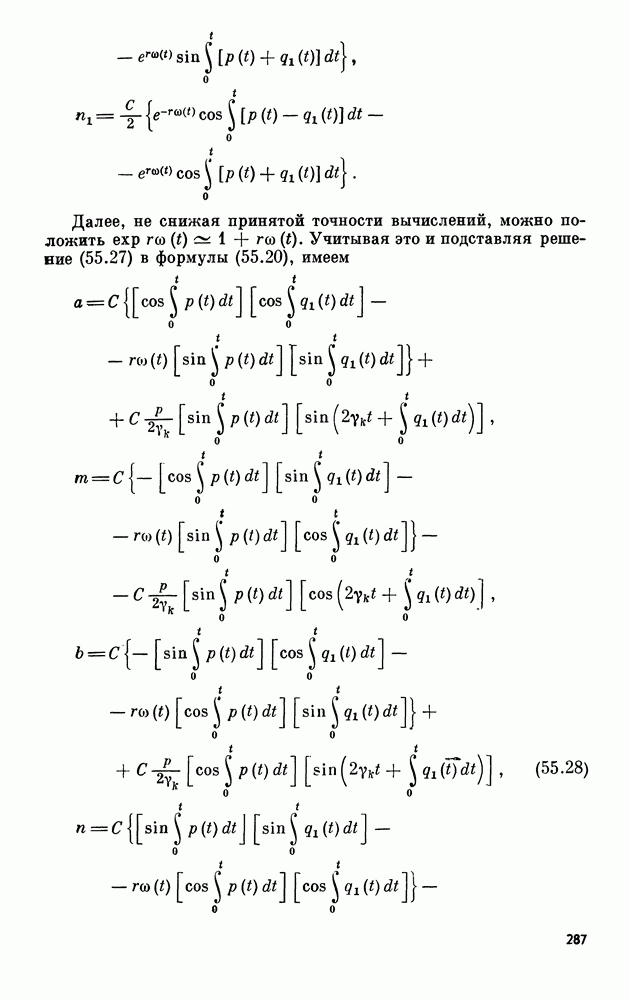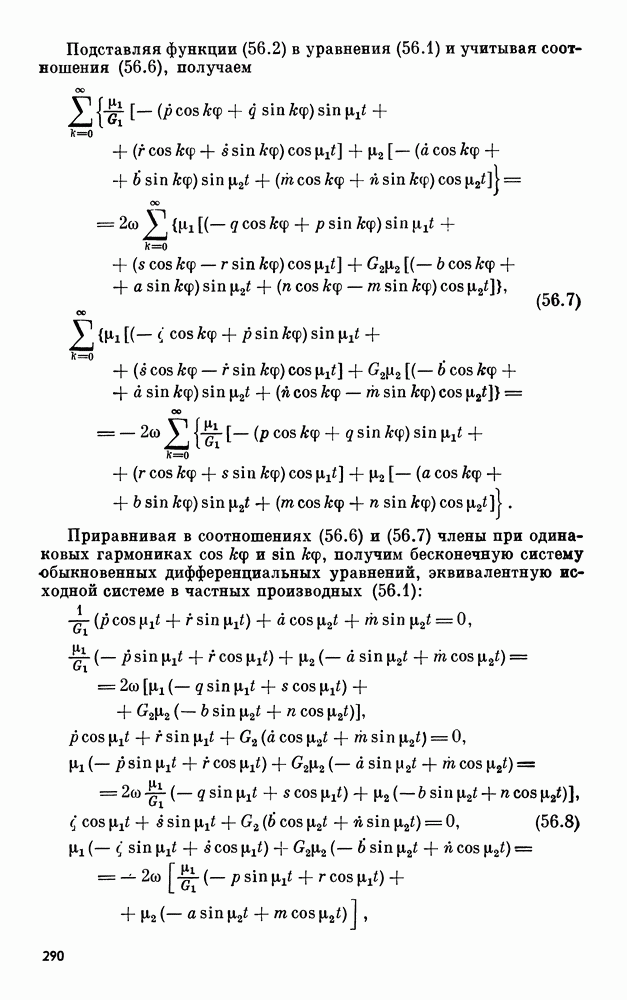| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
35. Уравнение Лиувилля. Инварианты. Собственные функции
Пусть группа задана через канонический параметр 

и ой эквивалентна по доказанному система

Вернемся к вопросу о преобразовании с помощью этой группы некоторой функции  :
:

Определим производную этой функции по  :
:

Или в силу (35.1)

где  — оператор группы.
— оператор группы.
Уравнение

называется уравнением Лиувилля.
Найдем связь преобразованной функции  с исходной функцией
с исходной функцией  и оператором преобразования
и оператором преобразования 
Ряд Тейлора для 

Здесь

а из (35.2) имеем

Обозначив  получим
получим

т. е.

к! гак далее. В результате получаем искомую связь в виде

Этот ряд называется рядом Ли. Он может быть записан еще в такой форме:

Выражение (35.3) служит определением операторной экспоненты (35.4). Дифференцируя (35.3) по  имеем
имеем

Иными словами, имеет место правило

С другой стороны, полученное представление позволяет переписать уравнение Лнувилля в эквивалентной форме:

Здесь уже оператор  зависит от старых переменных:
зависит от старых переменных:

Дополнив начальным условием  получаем начальную задачу Коши для уравнения в частных производных (35.5) относительно искомой функции
получаем начальную задачу Коши для уравнения в частных производных (35.5) относительно искомой функции  эквивалентную системе нелинейных дифференциальных уравнений (35.1). Эквивалентность понимается в следующем смысле. Если известно общее решение системы (35.1):
эквивалентную системе нелинейных дифференциальных уравнений (35.1). Эквивалентность понимается в следующем смысле. Если известно общее решение системы (35.1):  то решение (35.5) есть
то решение (35.5) есть

Обратно, если известно решение указанной начальной задачи для  то, выбрав в качестве
то, выбрав в качестве  вначале
вначале  затем
затем  получим общее решение (35.1).
получим общее решение (35.1).
Указанная эквивалентность позволяет заменить изучение нелинейной системы (35.1) часто более удобным изучением линейного уравнения (35.5).
Из (35.3) для частного вида функции  следуют формулы, восстанавливающие группу по ее оператору:
следуют формулы, восстанавливающие группу по ее оператору:

которые представляют собой также запись решения системы дифференциальных уравнений (35.1) с начальными условиями  форме рядов по
форме рядов по  .
.
Пример. Восстановить группу вращений по ее оператору  то можно сделать, решив начальную задачу Коши:
то можно сделать, решив начальную задачу Коши:

Пользуемся рядами Ли (35.6). Последовательно находим

откуда имеем

Определение. Функция  называется инвариантом группы, если она не изменяется группой:
называется инвариантом группы, если она не изменяется группой:

Ряд Ли (35.3) показывает, что, для того чтобы аналитическая функция своих переменных была инвариантом группы, необходимо и достаточно, чтобы она была корнем оператора группы:

Свойство инварианта. Пусть  — инвариант,
— инвариант,  — произвольная функция. Тогда
— произвольная функция. Тогда

т. е. инвариант группы играет роль константы для ее оператора.
Определение. Функция  называется собственной функцией оператора, если
называется собственной функцией оператора, если

где  — инвариант, называемый в данном случае собственным значением.
— инвариант, называемый в данном случае собственным значением.
Если  — собственная функция оператора, то она преобразуется соответствующей этому оператору группой так:
— собственная функция оператора, то она преобразуется соответствующей этому оператору группой так:

где  - инвариант группы при любом фиксированном
- инвариант группы при любом фиксированном  Это следует из (35.3) и (35.8).
Это следует из (35.3) и (35.8).
Очевидно следующее свойство собственных функций оператора. Если  — собственная функция, соответствующая собственному значению
— собственная функция, соответствующая собственному значению  аналогично этому
аналогично этому  то
то

 — также собственная функция, соответствующая собственному значению
— также собственная функция, соответствующая собственному значению 
Пример. Группа винтов в 

Ее оператор  Инвариантом группы является функция
Инвариантом группы является функция

В этом можно убедиться двумя способами. Во-первых,

и, во-вторых, из условия  имеем
имеем

Инвариантное семейство кривых. Если функция  есть инвариант группы, то, приравнивая ее произвольной постоянной
есть инвариант группы, то, приравнивая ее произвольной постоянной  , получим семейство кривых в плоскости
, получим семейство кривых в плоскости  каждая из которых группой не изменяется, т. е. каждая кривая преобразуется сама в себя. Иными словами, любая кривая такого семейства является инвариантной кривой.
каждая из которых группой не изменяется, т. е. каждая кривая преобразуется сама в себя. Иными словами, любая кривая такого семейства является инвариантной кривой.
Представляет интерес несколько иная ситуация. Пусть задано некоторое семейство кривых  Причем функция
Причем функция  инвариантом группы не является. Таким образом, преобразования группы изменяют кривые семейства. Нас будет интересовать случай, когда при таком изменении они будут переходить в другие кривые того же семейства. Такое семейство и будет называться инвариантным.
инвариантом группы не является. Таким образом, преобразования группы изменяют кривые семейства. Нас будет интересовать случай, когда при таком изменении они будут переходить в другие кривые того же семейства. Такое семейство и будет называться инвариантным.
Пример. Семейство прямых, исходящих из начала координат,  является инвариантным семейством группы вращения.
является инвариантным семейством группы вращения.
Найдем условие, которому должна удовлетворять функция со  чтобы она определяла инвариантное семейство.
чтобы она определяла инвариантное семейство.
Пусть  — два представления одного и того же семейства. Каждая кривая одного представления конгруэнтна некоторой кривой другого. Это значит, что для каждого
— два представления одного и того же семейства. Каждая кривая одного представления конгруэнтна некоторой кривой другого. Это значит, что для каждого
значения С первого представления найдется такое значение к второго, что оба представления определяют одну и ту же кривую. То есть к есть функция  Но тогда
Но тогда  . Таким образом, условие инвариантности семейства
. Таким образом, условие инвариантности семейства  состоит в следующем:
состоит в следующем:

Раскладывая (35.10) в ряд по  найдем
найдем

Сравнивая этот ряд с рядом Ли (35.3), находим необходимое условие инвариантности семейства в виде

Это условие является и достаточным, поскольку, если оно выполнено, то

и так далее. Это условие можно представить в более удобной форме, если избавиться от произвола в выборе функции  Будем искать из него не
Будем искать из него не  , а некоторую функцию от этой функции:
, а некоторую функцию от этой функции:  . Поскольку
. Поскольку  определяет то же семейство, то
определяет то же семейство, то

Откуда следует

Пользуясь произволом в выборе  положим
положим  Это приводит к условию
Это приводит к условию

которое и будем считать основным для нахождения инвариантного семейства кривых.
Инвариантная кривая. Рассмотрим условия инвариантности одной отдельно взятой кривой в плоскости х, у:

Эта кривая называется инвариантной кривой группы, если она не изменяется при действии любого преобразования из группы. При этом кривая может оставаться неизменной в двух случаях. Во-первых, если остается неподвижной каждая точка кривой и, во-вторых, если каждая точка кривой преобразуется в точку, принадлежащую этой же кривой. Первый случай реализуется, если равен нулю сам оператор группы на этой кривой, т. е.

Во втором случае должно быть выполнено условие (35.7), однако уже не для любых х и у, а в точках самой кривой:

Пример. Инвариантной кривой, целиком составленной из инвариантных точек, для группы, порождаемой оператором

будет прямая 
Пример. Инвариантной кривой второго типа для оператора

является окружность 
Действительно,

обращается в нуль на этой окружности.
Аналогичные понятия (инвариантные кривые, инвариантные поверхности) имеют место в пространстве  измерений.
измерений.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава первая. ЛИНЕЙНЫЕ СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- 2. Блочные матрицы
- 3. Матрицы Кейли
- 4. Полиномиальные матрицы
- 5. Собственные движения линейной системы с линейными элементарными делителями
- 6. Общий случай собственных движений линейной системы
- 7. Приведение общего решения линейной системы к действительной форме
- 8. Список правил построения общего решения однородной системы линейных дифференциальных уравнений
- 9. Примеры собственных движений линейных систем
- 10. Общий случай вынужденных движений линейных систем
- 11. Метод вариации постоянных Лагранжа в форме Булгакова
- 12. Список правил построения общего решения неоднородной системы линейных дифференциальных уравнений
- 13. Примеры построения общего решения неоднородных систем линейных уравнений
- 14. Метод нормальных координат Булгакова
- 15. Список правил перехода к нормальным координатам Булгакова
- 16. Пример использования нормальных координат Булгакова
- 17. Механические колебательные системы. Спектральные свойства
- Глава вторя. НЕЛИНЕЙНЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ, МЕТОД ОСРЕДНЕНИЯ
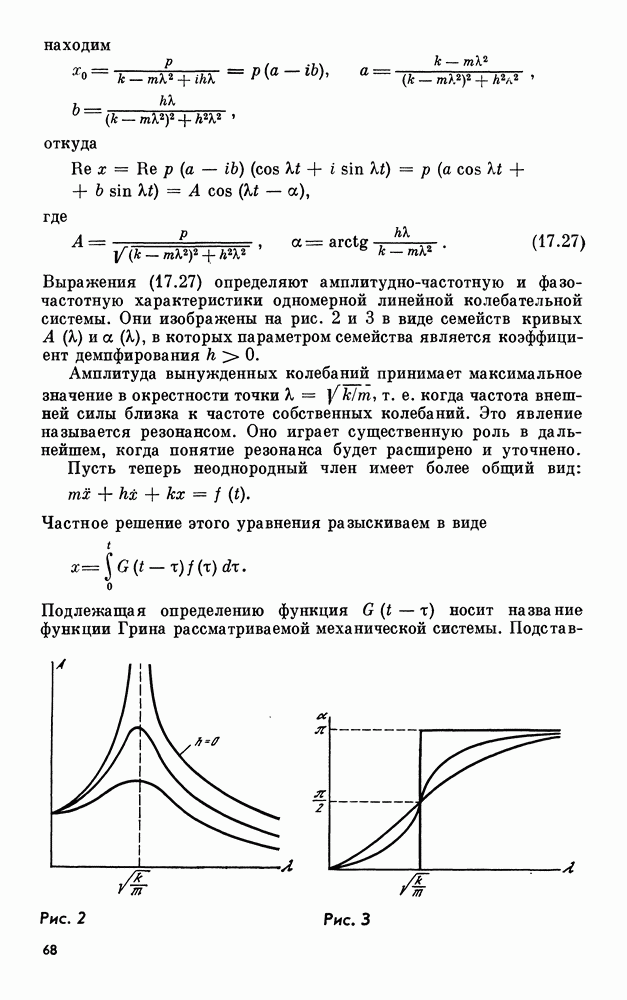
- 18. Одночастотные системы. Первая стандартная форма
- 19. Математические основы метода осреднения
- 20. Построение высших приближений. Понятие об асимптотическом ряде
- 21. Введение малого параметра. Осреднение функций
- 22. Многочастотные системы. Резонанс
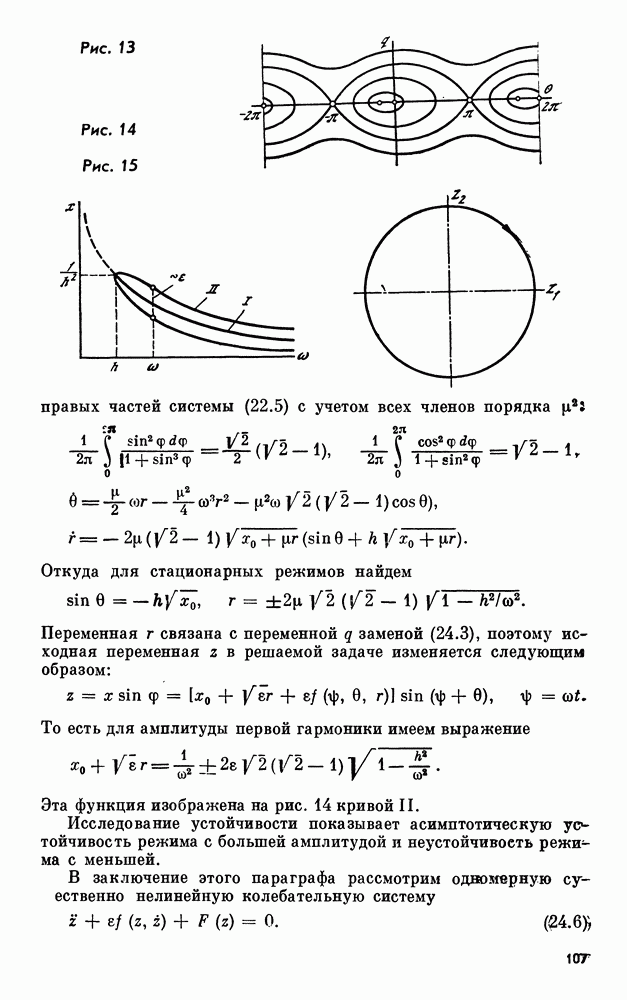
- 23. Квазилинейные системы
- 24. Существенно нелинейные системы
- 25. Лагранжев формализм
- 26. Метод осреднения в гироскопических системах
- 27. Осреднение в системах с ударными взаимодействиями
- 28. Об использовании обобщенных функций в задачах с ударными взаимодействиями
- 29. Метод двух масштабов
- 30. Примеры типичных постановок задач, решаемых методом осреднения
- Глава третья. ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП ЛИ
- 32. Группа Ли. Примеры
- 33. Инфинитезимальный оператор группы. Алгебра Ли
- 34. Однопараметрические группы. Теорема единственности
- 35. Уравнение Лиувилля. Инварианты. Собственные функции
- 36. Линейные уравнения с частными производными
- 37. Замена переменных. Канонические координаты
- 38. Формула Хаусдорфа. Группы симметрий
- 39. Принцип суперпозиции решений и разделение движений в нелинейных системах
- 40. Продолжение оператора. Дифференциальные и интегральные инварианты
- 41. Уравнения, допускающие заданную группу
- 42. Симметрии уравнений в частных производных
- 43. Примеры
- Глава четвертая АСИМПТОТИЧЕСКИЕ МЕТОДЫ, ОСНОВАННЫЕ НА ПОНЯТИИ ГРУППЫ ЛИ
- 45. Метод Хори
- 46. Одночастотный метод осреднения на основе формулы Хаусдорфа
- 47. Многочастотные системы
- 48. Метод нормальной формы
- 49. Применение одночленных групп к построению нормальной формы
- 50. Метод касательных (оскулирующих) приближений
- Глава пятая. ТЕОРИЯ КОЛЕБАНИЙ В ЗАДАЧАХ ТЕХНИКИ
- 51. Существенно нелинейные вынужденные колебания гироскопа в кардановом подвесе
- 52. Вынужденные колебания гироскопа в окрестности неизолированного положения равновесия
- 53. Явление самосинхронизации в скоростных гироскопических опорах
- 54. Об устойчивости стационарных движений плоского тела в поле центральной силы
- 55. Эффект инертности упругих волн в симметричных упругих телах
- 56. Прецессия стоячих волн во вращающемся упругом растяжимом кольце
- 57. Пространственная прецессия стоячих волн во вращающемся сферически симметричном упругом теле
- 58. Вынужденные колебания системы с двумя ударными парами
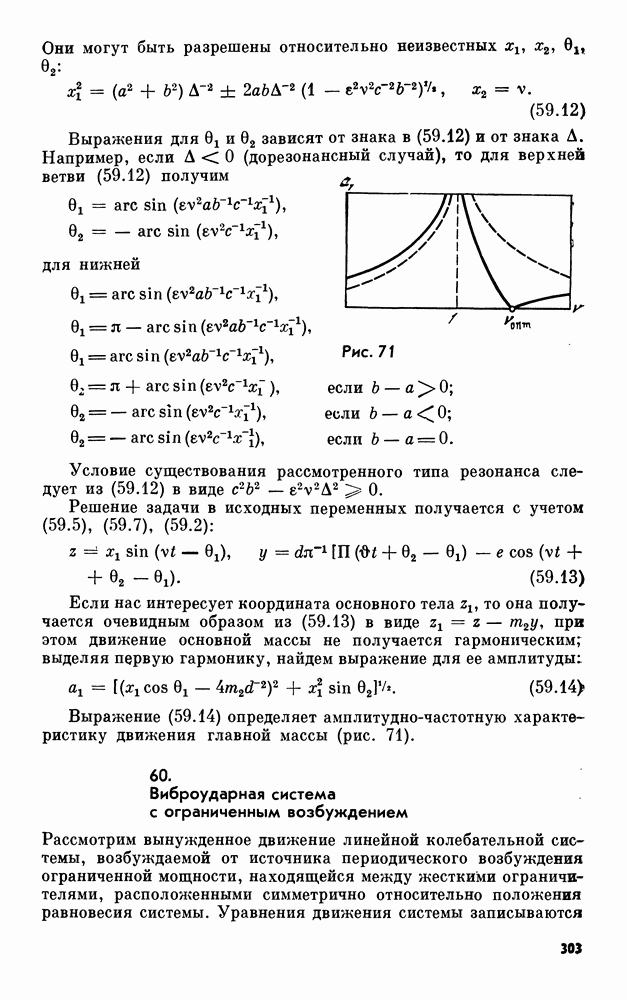
- 59. Ударный проглотитель колебаний
- 60. Виброударная система с ограниченным возбуждением
- 61. Волчок Лагранжа на подвижном основании. Ядерный магнитный резонанс
- ЛИТЕРАТУРА