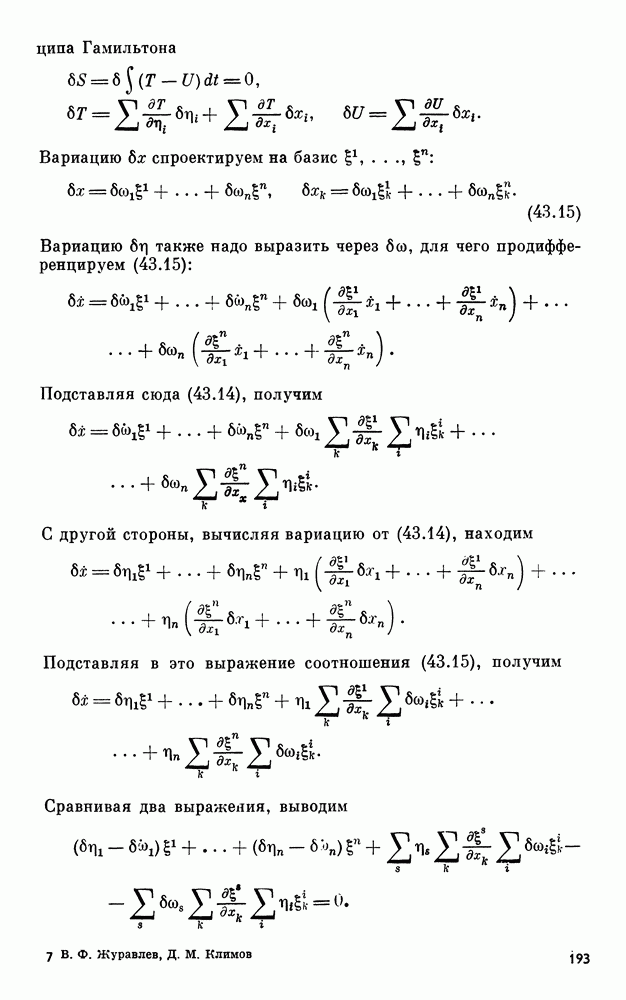| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
38. Формула Хаусдорфа. Группы симметрий
В разд. 35 было выяснено, как преобразуется функция, заданная в плоскости (или в некоторой ее области) однопараметрической группой преобразований. Результат был представлен в двух формах: уравнение Лиувилля (35.2) или (35.5) и ряд Ли (35.3). В обеих формах приведенные соотношения связывали выражение рассматриваемой функции в старых координатах, ее выражение в новых координатах и оператор группы преобразований старых координат в новые.
В настоящем разделе рассматривается аналогичная задача, однако объектом преобразования является уже не функция, а система дифференциальных уравнений

Пусть задана группа преобразований 

Требуется выяснить, как изменятся уравнения (38.1) при этих преобразованиях. В терминах операторов групп задача формулируется так. Уравнения (38.1) порождают однопараметрическую группу с оператором

Группа преобразований (38.2) определяется оператором

В новых переменных уравнения (38.1) принимают вид

и им соответствует оператор

Необходимо установить связь между операторами 
Решение этой задачи и дается формулой Хаусдорфа, к выводу которой мы приступаем. Запишем преобразование группы  а также и им обратные в виде рядов Ли (35.6):
а также и им обратные в виде рядов Ли (35.6):

Напомним, что в этих выражениях в случае прямого преобразования  имеет вид (38.4), а в случае обратного в этом операторе вместо старых переменных следует писать новые:
имеет вид (38.4), а в случае обратного в этом операторе вместо старых переменных следует писать новые:

Используя формулы (37.2), (37.3), перейдем в операторе (38.6) обратно от новых переменных  , и к старым переменным
, и к старым переменным  в результате чего получим
в результате чего получим

Компоненты оператора  являются функциями и и
являются функциями и и  Заменяя в них
Заменяя в них  по формулам (38.7), приходим к компонентам исходного оператора
по формулам (38.7), приходим к компонентам исходного оператора

Эти выражения не зависят от  поэтому
поэтому

откуда

Первый и второй члены этого соотношения получены дифференцированием по явно входящему т. Третий член представляет собой дифференцирование по  функции, зависящей от и и у, которые в свою очередь зависят от
функции, зависящей от и и у, которые в свою очередь зависят от  по формуле (38.7). Такая производная определяется формулой Лиувилля (35.2).
по формуле (38.7). Такая производная определяется формулой Лиувилля (35.2).
В результате получаем

К этому уравнению следует добавить начальное условие

чтобы получить искомую связь между 
Уравнение (38.8), определяющее преобразованный оператор
А, является аналогом уравнения Лиувилля, определяющего преобразованную функцию. Соотношение (38.8) раскрывает смысл второго названия для коммутатора — производный оператор: коммутатор есть в буквальном смысле слова производная оператора А по параметру группы, определяемой оператором  Приведенная начальная задача Коши для операторного уравнения (38.8) решается при помощи разложения
Приведенная начальная задача Коши для операторного уравнения (38.8) решается при помощи разложения  в ряд Тейлора по
в ряд Тейлора по 

Из (38.8)

Для нахождения второй производной дифференцируем (38.8):  Если бы оператор
Если бы оператор  получался из какого-то оператора В в результате преобразования группы с оператором (7, то мы имели бы право, как и в (38.8), написать
получался из какого-то оператора В в результате преобразования группы с оператором (7, то мы имели бы право, как и в (38.8), написать

Покажем, что это действительно так. В качестве оператора В можно взять  . В силу инвариантности коммутатора по отношению к заменам переменных (см. разд. 33) имеем
. В силу инвариантности коммутатора по отношению к заменам переменных (см. разд. 33) имеем  Однако очевидно
Однако очевидно  что и доказывает справедливость (38.9). Остальные производные определяются аналогично.
что и доказывает справедливость (38.9). Остальные производные определяются аналогично.
В результате приходим к формуле Хаусдорфа

Из этой формулы следует, что если

то  т. е. преобразования (38.2) не изменяют оператора (или уравнений (38.1).
т. е. преобразования (38.2) не изменяют оператора (или уравнений (38.1).
Группа (38.2) называется в этом случае группой симметрий уравнений (38.1). Или говорят, что уравнения (38.1) допускают группу (38.2).
Для того чтобы такой факт имел место, условие (38.11) является, как это следует из (38.10), необходимым и достаточным.
Так как уравнения (38.1) преобразованиями группы симметрий не изменяются, то это означает, что любые решения этих уравнений группой симметрий переводятся в решения этих же уравнений. Этот факт может служить определением группы симметрий. Если же обратиться к эквивалентному системе (38.1) уравнению др  Лиувилля
Лиувилля  , то любое решение этого уравнения
, то любое решение этого уравнения  будет переводиться оператором группы симметрий
будет переводиться оператором группы симметрий  в решение этого же уравнения
в решение этого же уравнения  Все введенные понятия и полученные формулы никак с размерностью пространства не связаны и справедливы для произвольной размерности. Полезность установления симметрий дифференциальной системы демонстрирует следующая теорема.
Все введенные понятия и полученные формулы никак с размерностью пространства не связаны и справедливы для произвольной размерности. Полезность установления симметрий дифференциальной системы демонстрирует следующая теорема.
Теорема. Пусть задана система

Если известна группа симметрий этой системы, оператор которой 

т. e.  , где А — оператор системы (38.12), то система (38.12) может быть понижена в порядке.
, где А — оператор системы (38.12), то система (38.12) может быть понижена в порядке.
Дока зательство. Укажем алгоритм понижения порядка. Группа, порождаемая оператором (38.13), предполагается известной, это означает, в частности, что известна полная система инвариантов этой группы, так что известны ее канонические координаты

в которых оператор (38.13) имеет простейший вид:

но тогда условие  переходит в условие
переходит в условие

Последний коммутатор сводится в силу (33.5) к дифференцированию компонент оператора 1 по Равенство нулю означает при этом, что в новых переменных оператор А (а следовательно, и преобразованная система (38.12)) не зависит от переменной  . Теорема доказана.
. Теорема доказана.
Пример. Понизить порядок уравнения:

Вначале приведем это уравнение к виду (38.12):

Группа симметрий этого уравнения очевидна. Она связана с изменением масштаба измерения переменной у. Это группа растяжений

Следовательно, операторы  имеют вид
имеют вид

Легко убедиться, что в этом случае  Разыскиваем канонические координаты группы
Разыскиваем канонические координаты группы

откуда  Находим выражение оператора 4 в новых переменных:
Находим выражение оператора 4 в новых переменных:

Или, выражая  через
через 

Иными словами, в новых переменных исходная дифференциальная система имеет вид

т. е. задача сводится к интегрированию уравнения Риккати.
Заметим, что приведенный способ понижения порядка требует знания канонических координат группы симметрий. Однако есть случаи, когда для этого достаточно лишь знания оператора группы. Например, это возможно, когда размерность системы равна двум.
Рассмотрим этот случай. Пусть имеем систему

с оператором

И пусть известен оператор ее группы симметрий

про который будем дополнительно предполагать, что он является линейно несвязанным (условие линейной несвязанности является более жестким, чем условие линейной независимости, и определяется так: операторы  называются линейно несвязанными, если не существует таких
называются линейно несвязанными, если не существует таких  не всех тождественно равных нулю, что
не всех тождественно равных нулю, что

В отличие от определения линейной независимости здесь коэффициенты X могут зависеть от переменных  с оператором А. Пусть далее
с оператором А. Пусть далее

— первый интеграл рассматриваемой системы. Это значит, что имеет место)

Поскольку группа симметрий сохраняет систему, то она должна переводить интегральные кривые в интегральные кривые, т. е. семейство (38.15) должно быть инвариантным семейством группы. В соответствии с (35.11) это дает  . Или
. Или

Разрешая эту линейную систему, найдем

Откуда первый интеграл исходной системы находится квадратурой

Аналогичный результат имеет место и в случае произвольной размерности. В [56] он сформулирован так:
Теорема. Если система (38.12) допускает  -параметрическую разрешимую группу
-параметрическую разрешимую группу  операторы которой
операторы которой  вместе с оператором А составляют линейно несвязанную систему, то уравнения (38.12) интегрируются в квадратурах.
вместе с оператором А составляют линейно несвязанную систему, то уравнения (38.12) интегрируются в квадратурах.
Термин «разрешимая группа» как раз и происходит от возможности использования таких групп для интегрирования в квадратурах систем обыкновенных дифференциальных уравнений. Не приводя точного определения понятия «разрешимая группа», приведем критерий, позволяющий устанавливать наличие этого свойства:  -параметрическая группа разрешима тогда и только тогда, когда ее структурные константы (33.6) связаны условием
-параметрическая группа разрешима тогда и только тогда, когда ее структурные константы (33.6) связаны условием

( — суммирование (Картан)).
— суммирование (Картан)).
Напомним, как вычисляются криволинейные интегралы, к которым сводятся получаемые указанным способом квадратуры. Рассматривая изменение переменных интегрирования вдоль прямой:

напишем

Интегрирование вдоль прямой выбирается исключительно ради простоты. Поскольку подынтегральная функция в криволинейном интеграле есть полный дифференциал, то сам интеграл от пути интегрирования не зависит, а зависит только от начальной и конечной точки.
Пример. Найти потенциал для векторного поля  Поскольку
Поскольку  то такой потенциал существует и равен
то такой потенциал существует и равен 
Пользуясь указанным приемом, находим

Расширение понятия группы симметрий. Вернемся к системе

Пусть известна группа преобразований (38.2) с оператором (38.4), таким, что имеет место

Используя формулу Хаусдорфа (38.10), выясним, как в этом случае изменяются уравнения (38.16).
Последовательно находим

и так далее. Следовательно, формула Хаусдорфа дает

Таким образом, уравнения (38.16) преобразуются к виду

Хотя уравнения и изменились, но фазовые траектории остались теми же:

Группа, удовлетворяющая условию (38.17), также называется группой симметрий. Такая группа переводит интегральные кривые системы (38.16) в ее же интегральные кривые.
Теорема. Если система (38.16) допускает группу симметрий в расширенном смысле, то эта система может быть понижена в порядке.
Доказательство проводится, как и ранее, посредством перехода к каноническим координатам группы, в которых система (38.16) после приведения ее к форме (38.18) оказывается не зависящей от одной переменной.
Замечание. Этот результат не зависит от размерности пространства и, как и ранее, в случае плоскости для интегрирования в квадратурах достаточно знания лишь оператора группы. Пример. Уравнение Блазиуса:

Требуется понизить порядок.
Приводам предварительно это уравнение к нормальной форме Коши автономной системы:

Оператор этой системы таков:

Ищем группу симметрий при помощи изменения масштаба 

Откуда видно, что правая часть приобретает общий скалярный множитель, если 
Следовательно, однопараметрическая группа стшетрий (в расширенном смысле) имеет вид

или

Оператор этой группы

Коммутатор операторов  в этом примере равен
в этом примере равен

Для понижения порядка системы достаточно перейти от переменных, в которых она записана, к переменным, являющимся каноническими координатами ее группы симметрий 

Эта система представляет собой полную запись условий, которым должны удовлетворять канонические координаты, однако при практических вычислениях выписывать два нижних уравнения не требуется, поскольку все необходимые интегралы получаются уже из первого уравнения:

Обратная замена:

Осталось найти вид оператора Л в новых переменных:

Следовательно, исходные уравнения в новых переменных получают вид

В этом примере видно, в чем состоит отличие случая, когда  от случая, когда
от случая, когда  . В первом случае при переходе к каноническим координатам система теряет зависимость от одной из переменных, во втором — зависимость от одной из Беременных присутствует лишь в виде общего скалярного множителя при всей правой части (в этом примере
. В первом случае при переходе к каноническим координатам система теряет зависимость от одной из переменных, во втором — зависимость от одной из Беременных присутствует лишь в виде общего скалярного множителя при всей правой части (в этом примере  что не мешает понижению порядка:
что не мешает понижению порядка:

Уравнение (38.17) позволяет поставить следующую задачу. Система (38.16) задана, требуется найти ее группу симметрий. В этом случае (38.17) представляет собой систему уравнений для нахождения коэффициентов  неизвестного оператора
неизвестного оператора  Эта система имеет следующий вид:
Эта система имеет следующий вид:

Эта линейная система относительно неизвестных функций  называется определяющей системой. Она относится к следующему типу систем:
называется определяющей системой. Она относится к следующему типу систем:

Легко показать, что такие системы эквивалентны одному уравнению такого же вида, как и рассмотренные в разд. 36.
Если  решений этого уравнения, для которых
решений этого уравнения, для которых  тогда найденные из них
тогда найденные из них  есть решения исходной системы.
есть решения исходной системы.
Отметим важное свойство определяющей системы. Множество операторов, удовлетворяющих этой системе, образует алгебру. Это означает, что если некоторый оператор  есть оператор группы симметрий уравнений (38.16) и некоторый другой оператор V — также оператор группы симметрий, т. е.
есть оператор группы симметрий уравнений (38.16) и некоторый другой оператор V — также оператор группы симметрий, т. е.  То оператор
То оператор  также есть оператор группы симметрий.
также есть оператор группы симметрий.
В самом деле:

т. е.

Однако в силу тождества Якоби имеем

Поэтому

Но это и означает, что  есть оператор симметрий.
есть оператор симметрий.
Примеры решения определяющих уравнений с целью нахождения алгебры симметрий будут рассмотрены в разд. 42 и 43.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава первая. ЛИНЕЙНЫЕ СИСТЕМЫ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- 2. Блочные матрицы
- 3. Матрицы Кейли
- 4. Полиномиальные матрицы
- 5. Собственные движения линейной системы с линейными элементарными делителями
- 6. Общий случай собственных движений линейной системы
- 7. Приведение общего решения линейной системы к действительной форме
- 8. Список правил построения общего решения однородной системы линейных дифференциальных уравнений
- 9. Примеры собственных движений линейных систем
- 10. Общий случай вынужденных движений линейных систем
- 11. Метод вариации постоянных Лагранжа в форме Булгакова
- 12. Список правил построения общего решения неоднородной системы линейных дифференциальных уравнений
- 13. Примеры построения общего решения неоднородных систем линейных уравнений
- 14. Метод нормальных координат Булгакова
- 15. Список правил перехода к нормальным координатам Булгакова
- 16. Пример использования нормальных координат Булгакова
- 17. Механические колебательные системы. Спектральные свойства
- Глава вторя. НЕЛИНЕЙНЫЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ, МЕТОД ОСРЕДНЕНИЯ
- 18. Одночастотные системы. Первая стандартная форма
- 19. Математические основы метода осреднения
- 20. Построение высших приближений. Понятие об асимптотическом ряде
- 21. Введение малого параметра. Осреднение функций
- 22. Многочастотные системы. Резонанс
- 23. Квазилинейные системы
- 24. Существенно нелинейные системы
- 25. Лагранжев формализм
- 26. Метод осреднения в гироскопических системах
- 27. Осреднение в системах с ударными взаимодействиями
- 28. Об использовании обобщенных функций в задачах с ударными взаимодействиями
- 29. Метод двух масштабов
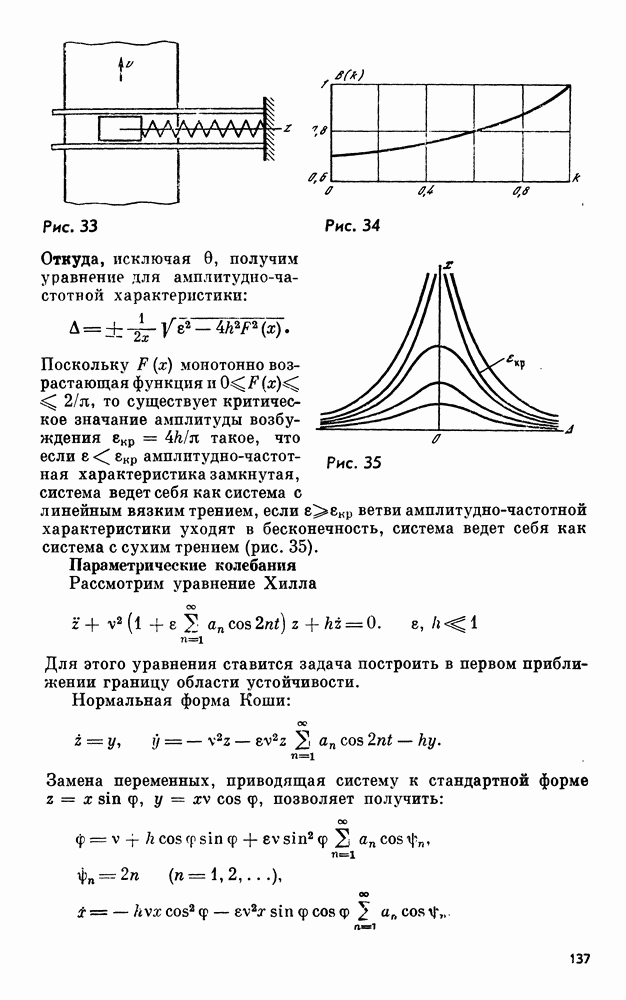
- 30. Примеры типичных постановок задач, решаемых методом осреднения
- Глава третья. ЭЛЕМЕНТЫ ТЕОРИИ ГРУПП ЛИ
- 32. Группа Ли. Примеры
- 33. Инфинитезимальный оператор группы. Алгебра Ли
- 34. Однопараметрические группы. Теорема единственности
- 35. Уравнение Лиувилля. Инварианты. Собственные функции
- 36. Линейные уравнения с частными производными
- 37. Замена переменных. Канонические координаты
- 38. Формула Хаусдорфа. Группы симметрий
- 39. Принцип суперпозиции решений и разделение движений в нелинейных системах
- 40. Продолжение оператора. Дифференциальные и интегральные инварианты
- 41. Уравнения, допускающие заданную группу
- 42. Симметрии уравнений в частных производных
- 43. Примеры
- Глава четвертая АСИМПТОТИЧЕСКИЕ МЕТОДЫ, ОСНОВАННЫЕ НА ПОНЯТИИ ГРУППЫ ЛИ
- 45. Метод Хори
- 46. Одночастотный метод осреднения на основе формулы Хаусдорфа
- 47. Многочастотные системы
- 48. Метод нормальной формы
- 49. Применение одночленных групп к построению нормальной формы
- 50. Метод касательных (оскулирующих) приближений
- Глава пятая. ТЕОРИЯ КОЛЕБАНИЙ В ЗАДАЧАХ ТЕХНИКИ
- 51. Существенно нелинейные вынужденные колебания гироскопа в кардановом подвесе
- 52. Вынужденные колебания гироскопа в окрестности неизолированного положения равновесия
- 53. Явление самосинхронизации в скоростных гироскопических опорах
- 54. Об устойчивости стационарных движений плоского тела в поле центральной силы
- 55. Эффект инертности упругих волн в симметричных упругих телах
- 56. Прецессия стоячих волн во вращающемся упругом растяжимом кольце
- 57. Пространственная прецессия стоячих волн во вращающемся сферически симметричном упругом теле
- 58. Вынужденные колебания системы с двумя ударными парами
- 59. Ударный проглотитель колебаний
- 60. Виброударная система с ограниченным возбуждением
- 61. Волчок Лагранжа на подвижном основании. Ядерный магнитный резонанс
- ЛИТЕРАТУРА