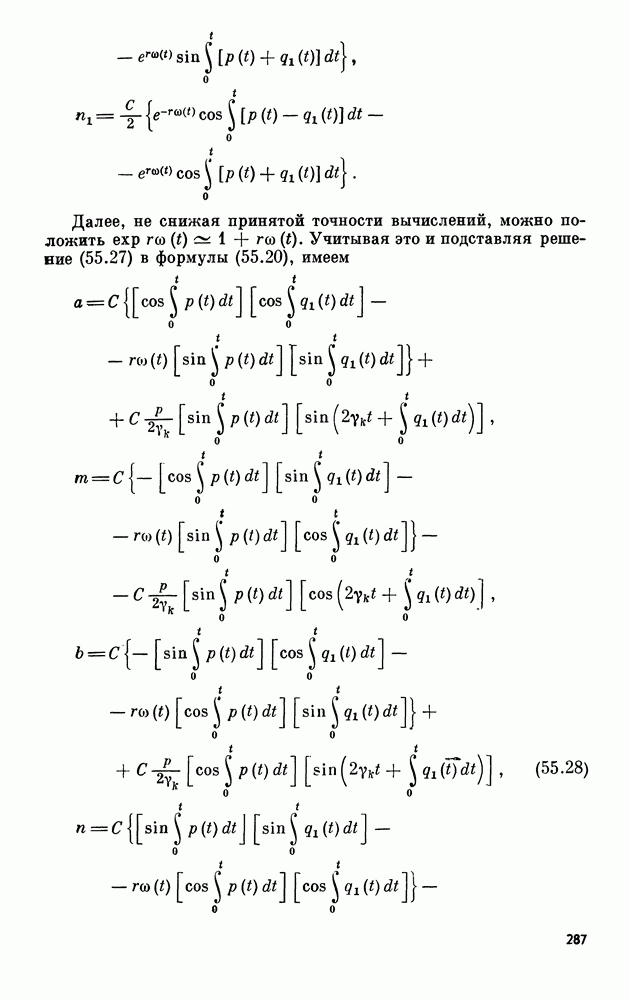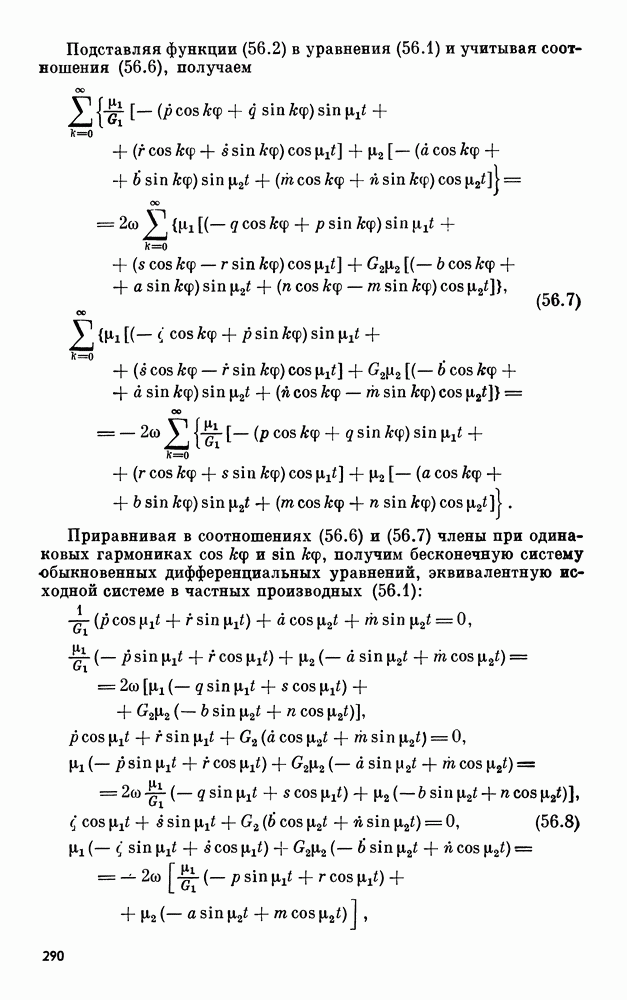17. Механические колебательные системы. Спектральные свойства

Уравнения движения консервативных линейных механических систем представляют собой частный вид уравнений (5.4), обычно записываемый в форме

где А и С — симметрические, положительно определенные матрицы.

Разыскиваем решение системы (17.1) в виде

где — неизвестный постоянный вектор; — неизвестные скаляры (частота и начальная фаза). Для нахождения получается система

Система линейных однородных уравнений (17.2) разрешима с если и только если

Это характеристическое уравнение порядка относительно неизвестной X называется уравнением частот.

Теорема. Уравнение частот имеет только вещественные и положительные корни.

Доказательство. Пусть X — комплексный корень и ему соответствует комплексное решение Умножим (17.2) слева на эрмитово сопряженный вектор т. е. транспонированный и с комплексно сопряженными элементами:

Получаем

откуда находим

Поскольку система вещественная, то имеется и комплексно сопряженный корень , с комплексно сопряженным решением

Проделывая аналогичную выкладку, получаем

В силу симметричности матриц А и С

т. е. — вещественное, а в силу положительной определенности форм

Следовательно, уравнение частот имеет положительных корней и им соответствует вещественных векторов:

Теорема. Если среди корней уравнения частот нет кратных, то собственные векторы являются Л-ортогоналъными, т. е.

Доказательство. Из уравнения (17.2) имеем

Умножая первое скалярно на а второе на получаем

Вычитая одно из другого:

откуда, если

Векторы А-ортогональны. Если то

Нормируя вектор свойство (17.4) можно записать так: — символ Кронекера при если

Следствие. Векторы линейно независимы. Действительно, если , то

откуда следует, что

— противоречие.

Следовательно, общее решение системы (17.1) есть

Векторы носят название амплитудных векторов. Колебания с чистым тоном, из которых составляется общее решение

называются главными колебаниями системы.

Для перехода к нормальным координатам в системе (17.1) используется матрица перехода, составленная из амплитудных векторов, т. е. переход осуществляется по формуле

где

Подставляя это преобразование в (17.1) и умножая полученную систему слева на получим

Однако в силу — единичная матрица, а в силу того, что

имеем

так что система (17.5) имеет вид

Координаты и называются нормальными.

Все вышесказанное получено в предположении отсутствия кратных корней в уравнениях частот. Все остается справедливым и в случае кратных частот (следует из известной в алгебре теоремы о приведении пары форм к главным осям). При решении уравнений (17.2) для кратного корня размерность пространства решений равна кратности корня. Выбор независимых решений из этого пространства осуществляется с использованием процедуры ортогонализации.

Системами вида (17.1) не исчерпывается класс линейных колебательных систем, поскольку добавление гироскопических сил не меняет положительности корней уравнений частот.

Будем рассматривать линейную гироскопическую систему общего вида

где А — матрица кинетической энергии; С — матрица потенциальной энергии; обе симметрические и положительно определенные; Г — кососимметрическая матрица: .

Будем для системы (17.6) интересоваться поведением собственных частот при изменении матриц . Свойства собственных частот этой системы в случае были рассмотрены Рэлеем [25, 50].

Пусть Нетрудно показать, что уравнение частот и в этом случае имеет положительные корни, следовательно, частное решение системы (17.6) можно искать в виде

Подставляя это решение в (17.6), получим

Как и ранее, для существования ненулевого решения требуется

Если — корень этого уравнения, то и также корень. Решения уравнения (17.8) относительно являются теперь уже комплексными: Разделяя в (17.8) вещественную и мнимую части, получим

В этой системе уже все три матрицы симметрические. Наряду с механической системой (17.6) можно рассматривать механическую систему вдвое большей размерности, которая уже не является гироскопической и матрица потенциальной энергии которой отрицательно определена:

Разыскивая ее решение в виде приходим к уравнениям (17.10).

Некоторые свойства решений (17.10) устанавливает следующая лемма.

Лемма 1. Пусть — некоторый корень уравнения (17.9), а — решение системы (17.10), соответствующее этому корню. Тогда существует такое решение системы (17.10) для что имеют место следующие равенства:

Доказательство. Покажем, что всем условиям удовлетворяет вектор (Е — единичная матрица):

Подставим это выражение в уравнение (17.10), в котором положим после чего умножим слева на матрицу Е. В результате получим

Нетрудно видеть, что

Получаем уравнение для вектора которое им обращается в тождество. Итак, указанное выражение для действительно есть решение уравнения (17.10) при Проверим свойство 1. Имеем в силу (17.12). Свойство 2 проверяется аналогично.

Характеристическая функция. Умножим (17.10) скалярно на

Перенося член в правую часть и возводя обе части уравнения в квадрат, получим

Если — решение системы (17.10) для то, решая квадратное уравнение (17.14), получим выражение для квадрата этого корня: Если же — произвольный вектор, то оно определяет неявную функцию к Будем называть эту функцию характеристической функцией системы (17.6) или (17.11).

Лемма 2. Решения алгебраической системы (17.10) и только они являются критическими точками функции

Доказательство. Продифференцируем соотношение (17.13) по считая

Покажем, что выражение в квадратных скобках отлично от нуля для Пусть это не так, тогда найдется значение , такое, что

Подставляя это значение в соотношение (17.13), получим

что невозможно в силу положительной определенности Г и V. Следовательно, обращается в нуль только для тех которые являются решениями системы (17.10). С другой стороны, из (17.13) видно, что в силу положительной определенности , если . Поэтому обращается в нуль там же, где и

Лемма 3. Функция (каждая из ее ветвей) — монотонно возрастающая функция потенциальной энергии, т. е. если имеются две механические системы с одинаковыми и с , такими, что для любого , то и

Доказательство. Введем обозначения

Из (17.14) найдем

Дифференцируя, получим для так как

Характеристическая поверхность. Будем считать, что в определена метрика при помощи квадратичной формы

Рассмотрим в этом пространстве гиперповерхность П, определяемую уравнением

Подставляя отсюда в (17.14), получим для этой поверхности следующее уравнение:

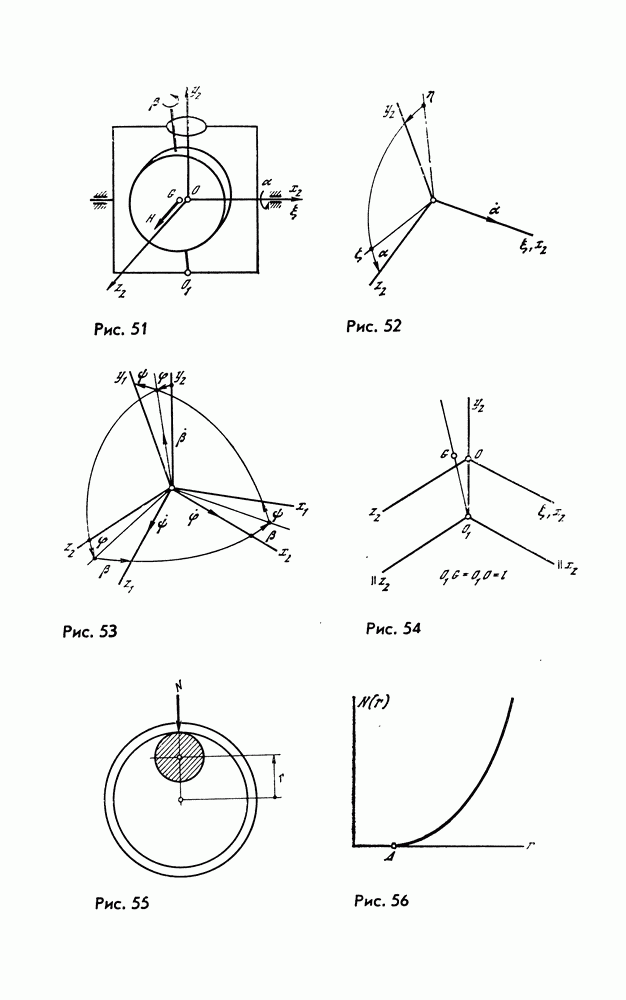
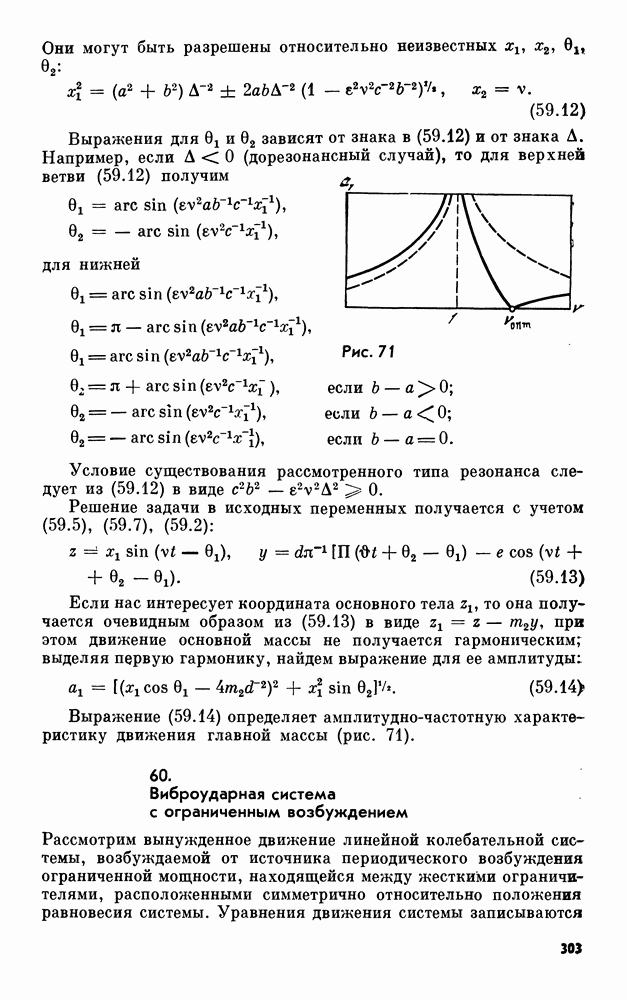
Уравнение (17.18) определяет замкнутую поверхность восьмого порядка. Луч, выпущенный из начала координат в любом направлении, пересекает ее в двух точках, соответствующих разным знакам в (17.16).

Лемма 4. Вектор удовлетворяющий (17.10) и имеющий длину где — соответствующее этому вектору значение частоты, принадлежит П.

Доказательство. Подставляя в (17.17) и имея в виду что для одной из ветвей получаем тождество. Длину такого вектора будем называть главной полуосью поверхности. Будем различать в дальнейшем две ветви поверхности П: ветвь, соответствующую верхнему знаку в (17.16), обозначим ветвь, соответствующую нижнему знаку, — Аналогичные обозначения введем и для ветвей

Лемма Поверхности имеют одну и ту же систему главных полуосей.

Дока зательство. Рассматривая (17.16) и опираясь на лемму 1, получим Отсюда линейно-независимая система решений (17.10), состоящая из векторов, может быть разбита на две подсистемы:

такие, что откуда и вытекает утверждаемый факт.

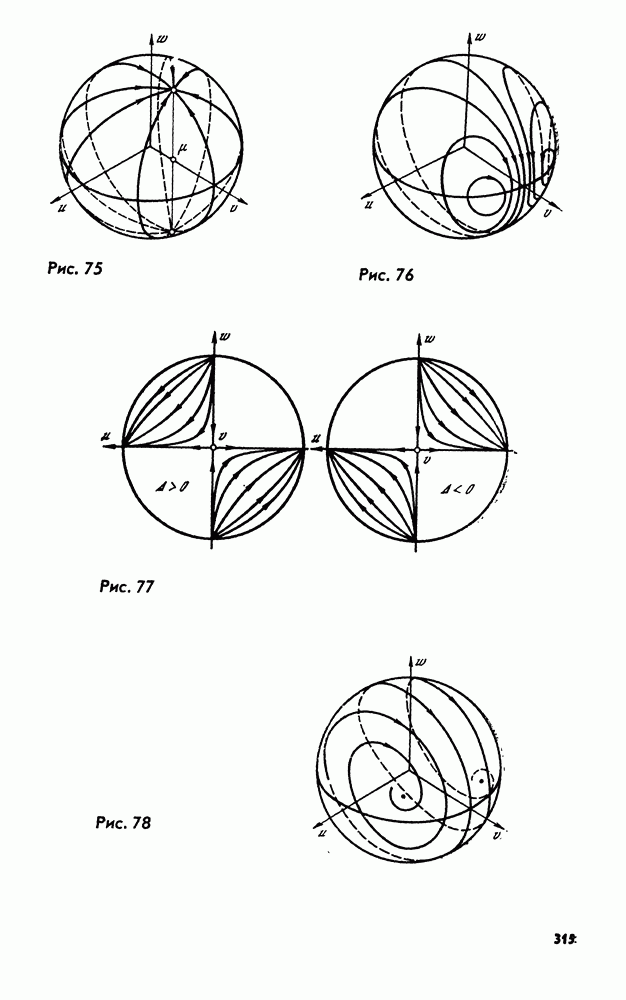
Будем считать, что для введенной в лемме 5 системы векторов (17.19) соответствующие характеристические числа расположены в порядке возрастания их модулей: Введем обозначения для главных полуосей:

Очевидно,

Поскольку каждая из ветвей обладает одной и той же системой полуосей (17.20), в дальнейшем достаточно рассмотреть одну из них. Рассмотрим для определенности Покажем, что главные полуоси обладают экстремальными свойствами.

Пусть подпространство, определяемое векторами как базисными. Норма этих векторов меньше или равна .

Лемма для

Доказательство. Рассмотрим механическую систему (17.11), на которую наложена дополнительно связь Она эквивалентна механической системе с числом степеней свободы, для которой формы равны ограничению соответствующих форм системы без связи на Следовательно, и ограничение характеристической функции к на будет равно характеристической функции системы со связью. У такой функции ровно критических точек. С другой стороны, векторы, составившие линейную оболочку очевидно, останутся критическими для ограничения характеристической функции на а так как их , то они и только они удовлетворяют необходимым условиям экстремума функции к для При этом — абсолютный минимум функции к на откуда в силу — абсолютный максимум нормы радиус-вектора поверхности на

Рассмотрим сечение поверхности некоторым подпространством Введем обозначение для

Лемма 7. Для любого

Доказательство. Пусть — подпространство, фигурирующее в лемме 6. Поскольку суммарная размерность больше то эти подпространства пересекаются. Пусть тогда в силу леммы 6, с другой стороны, так как откуда . При этом очевидно, что так как верхняя грань достигается на подпространстве, являющемся линейной оболочкой .

Теорема о поведении собственных частот при изменении жесткости. Пусть даны две механические системы вида (17.6), имеющие одинаковые матрицы кинетической энергии и гироскопических

сил. Матрицы потенциальной энергии . Систему будем называть более жесткой, если ее потенциальная энергия больше: при любом .

Теорема. При увеличении жесткости системы (17.6), где А и С положительно определены, произвольная кососимметрическая матрица, все собственные частоты могут только возрасти.

Доказательство. Из неравенства следует неравенство откуда в силу леммы 3 для всех . Это означает в силу (17.17), что лежит целиком внутри Рассмотрим сечение поверхностей подпространством Очевидно, следовательно, но откуда Используя равенство получим ( — произвольно).

Следствие 1. При доказанная теорема переходит в теорему Рэлея.

Следствие 2. Будем называть систему обладающей большей массой, если для любого ее кинетическая энергия больше: Имеет место следующая теорема: при увеличении массы системы все собственные частоты ее могут только уменьшиться.

Для доказательства достаточно показать аналогично лемме 3 монотонное убывание при любом фиксированном с увеличением кинетической энергии.

Следствие 3. Требование положительной определенности С может быть заменено требованием неотрицательности: при любом В самом деле, утверждение теоремы верно, когда некоторые из собственных чисел матрицы С сколь угодно малы. В силу непрерывной зависимости корней характеристического уравнения от его коэффициентов утверждение теоремы верно и в пределе, т. е. для случая, когда некоторое количество собственных чисел матрицы С нулевые.

Замечание. Доказанная теорема носит глобальный характер. Локальный результат, когда поведение частот изучается при малой вариации матрицы С, уже мог следовать из лемм 2 и 3.

Поведение собственных частот при изменении гироскопических сил. Перепишем систему (17.6) в виде

где выделен скалярный параметр Н, определяющий норму матрицы гироскопических сил. Представляет интерес изучение поведения собственных частот системы при

Введем следующие определения.

Прецессионной системой, определяемой системой (17.21), называется следующая система:

Нутационной системой, определяемой (17.21), называется система

Теорема. Если в системе (17.21) С — положительно определена и , то собственные частоты делятся на две группы: при Частоты первой группы при этом стремятся к частотам нутационной системы, а частоты второй группы — к частотам прецессионной системы.

Доказательство. Прежде всего заметим, что условие может быть выполнено только для систем, имеющих четную размерность, т. е. . Действительно,

и если — нечетно, то это возможно лишь когда Если то ровно корней образует группу а) и столько же — группу б).

Покажем это. Сделаем замену времени

и обозначим Получим уравнение частот в виде

Рассматриваем это уравнение как неявную функцию, определяющую со При получается уравнение частот нутационной системы (в измененном времени), корни которого обозначим так:

Нулевых корней не больше чем поскольку Рассмотрим ненулевые корни. По теореме о неявных функциях в случае отсутствия кратных корней среди (17.25) корни (17.24) можно получить в виде

Точками обозначены члены высшего порядка малости по а, т. е. частное решение имеет вид

откуда и следует первая группа частот

Если среди ненулевых корней (17.25) имеется кратный кратности то разложение корня уравнения (17.24) в окрестности кратного корня осуществляется по степеням величины Результат оказывается тем же, хотя скорость стремления корней полной системы к корням нутационной будет меньше.

Для рассмотрения второй группы частот выполняется иная замена времени: после чего уравнение частот получается в виде

Рис. 1

При получается уравнение частот прецессионной системы. Аналогично предыдущему в случае отсутствия кратных частот у прецессионной системы имеем

Откуда и следует вторая группа частот (после возвращения к исходному времени):

Случай кратных корней трактуется таким же образом, как и в предыдущем рассуждении.

Теорема доказана.

Если в условии теоремы (для нечетномерных систем так будет всегда), то помимо указанных двух групп частот будет еще третья, частоты которой имеют конечные, отличные от нуля пределы при

Суммируя все случаи, приходим к заключению. Если С — положительно определена, то при частоты системы (17.21) ведут себя следующим образом: часть частот, называемых прецессионными, стремится к нулю: часть частот, называемых нутационными, стремится к бесконечности: , часть частот, называемых маятниковыми, стремится к конечным, не равным нулю пределам: Число маятниковых частот равно разности между размерностью системы и рангом матрицы Г. Типичное поведение частот гироскопической системы изображено на рис. 1.

Вынужденные колебания линейных механических систем. Решение задачи о вынужденных колебаниях может быть получено с использованием общих результатов, приведенных в разд. 12. Однако в частных случаях бывает удобно пользоваться более простыми приемами, приводимыми ниже.

Рассмотрим вначале линейный одномерный осциллятор

для которого требуется построить частное периодическое решение, имеющее тот же период, что и период неоднородного члена. В силу принципа суперпозиции интересующее нас решение будет представлять собой вещественную часть соответствующего частного решения следующего уравнения:

Разыскивая решение этого уравнения в виде

находим

откуда

где

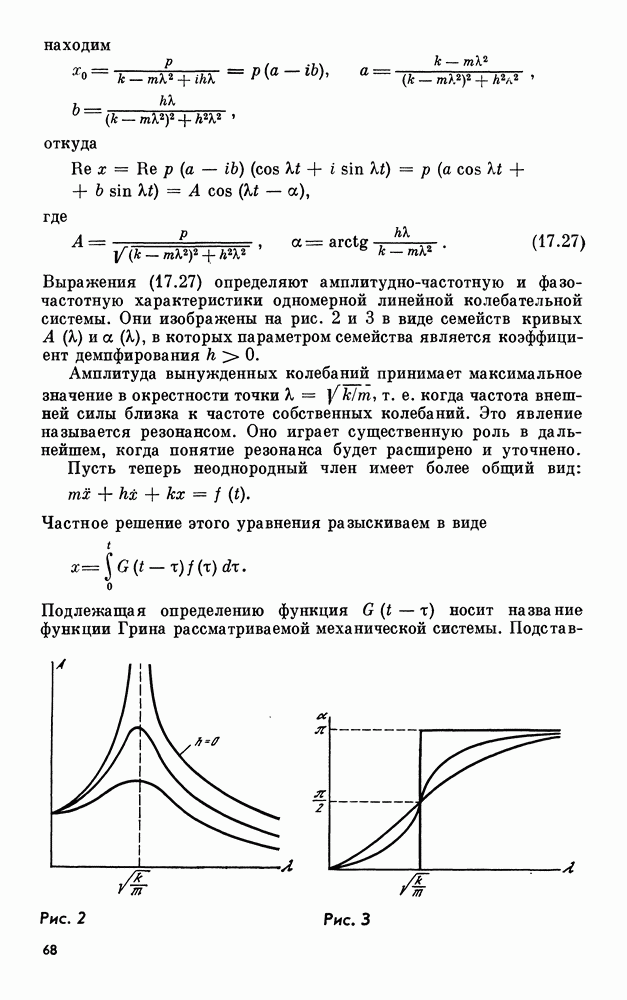
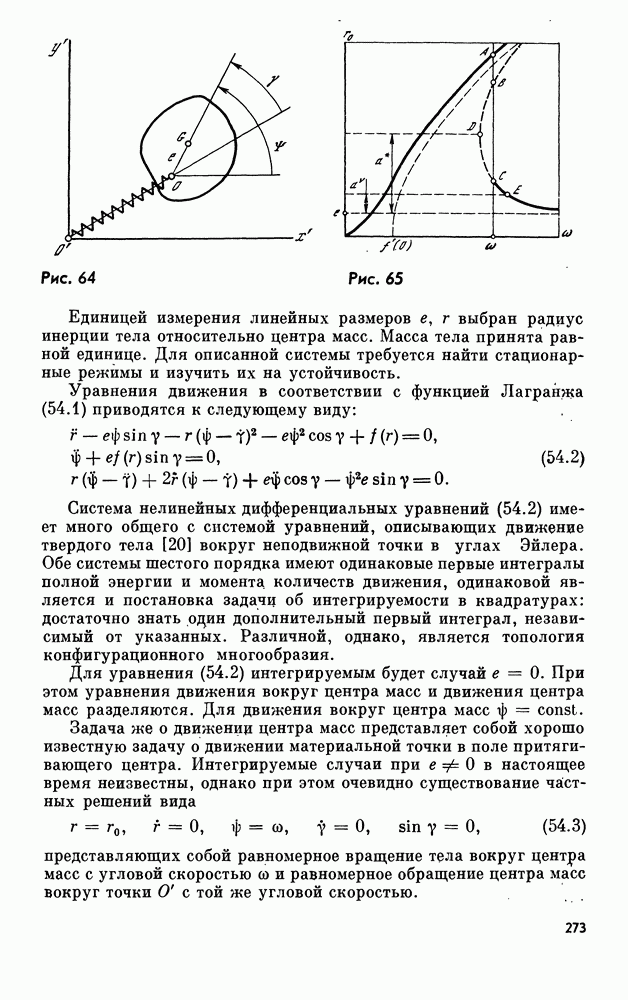
Выражения (17.27) определяют амплитудно-частотную и фазочастотную характеристики одномерной линейной колебательной системы. Они изображены на рис. 2 и 3 в виде семейств кривых в которых параметром семейства является коэффициент демпфирования

Амплитуда вынужденных колебаний принимает максимальное значение в окрестности точки т. е. когда частота внешней силы близка к частоте собственных колебаний. Это явление называется резонансом. Оно играет существенную роль в дальнейшем, когда понятие резонанса будет расширено и уточнено. Пусть теперь неоднородный член имеет более общий вид:

Частное решение этого уравнения разыскиваем в виде

Подлежащая определению функция носит название функции Грина рассматриваемой механической системы.

Рис. 2

Рис. 3

Подставляя это решение в уравнение, найдем

Для того чтобы это соотношение выполнялось тождественно, достаточно положить

Таким образом, функция Грина удовлетворяет указанной начальной задаче Коши для соответствующего однородного уравнения и, следовательно, имеет вид

Таким образом, частное решение при произвольном свободном члене имеет вид

Это частное решение, как следует из изложенного, удовлетворяет нулевым начальным условиям: . Произвольное число степеней свободы

Будем полагать, что гармоническая внешняя сила приложена по обобщенной координате, т. е. имеет вид

Переходя к нормальным координатам вместо (17.5) получим

или в покоординатной форме:

Решение этой системы имеет вид

Рис. 4

Рис. 5

Или же, возвращаясь к старым координатам, найдем

Коэффициенты показывающие, как возбуждение по координате влияет на движение по 5-й, называются гармоническими коэффициентами влияния. Они, очевидно, являются симметрическими: что выражает так называемый принцип взаимности. Если то в выражении для числители всех слагаемых положительны и график зависимости сочетающий в себе понятия амплитудно-частотной и фазочастотной характеристик одномерной системы, имеет вид, изображенный на рис. 4. График показывает, что всегда имеется ровно резонансов и ровно точек на оси частот, при которых амплитуда колебаний возбуждаемой массы равна нулю. Такое явление называется явлением динамического поглощения колебаний, или антирезонансом. Если же к то в силу - ортогональности амплитудных векторов (17.4) числители слагаемых, входящих в выражение обязательно имеют разные знаки. Число антирезонансов может быть меньше чем (их может не быть совсем), и график например, имеет такой вид, как изображен на рис. 5.

Диссипа тивные системы:

Поступаем так же, как и в случае одномерной системы, т. е. заменим написанное уравнение следующим:

Частное периодическое решение исходного уравнения получается как вещественная часть соответствующего решения написанного:

Для вектора амплитуд I получается система алгебраических уравнений

Решая ее по правилу Крамера, получаем для компоненты вектора I:

где А — определитель системы (17.28), а — алгебраическое дополнение элемента этого определителя, стоящего в пересечении строки и столбца. Искомое решение исходной системы имеет вид

Функция

определяет амплитудно-частотную характеристику колебаний по 5-й координате при возбуждении по