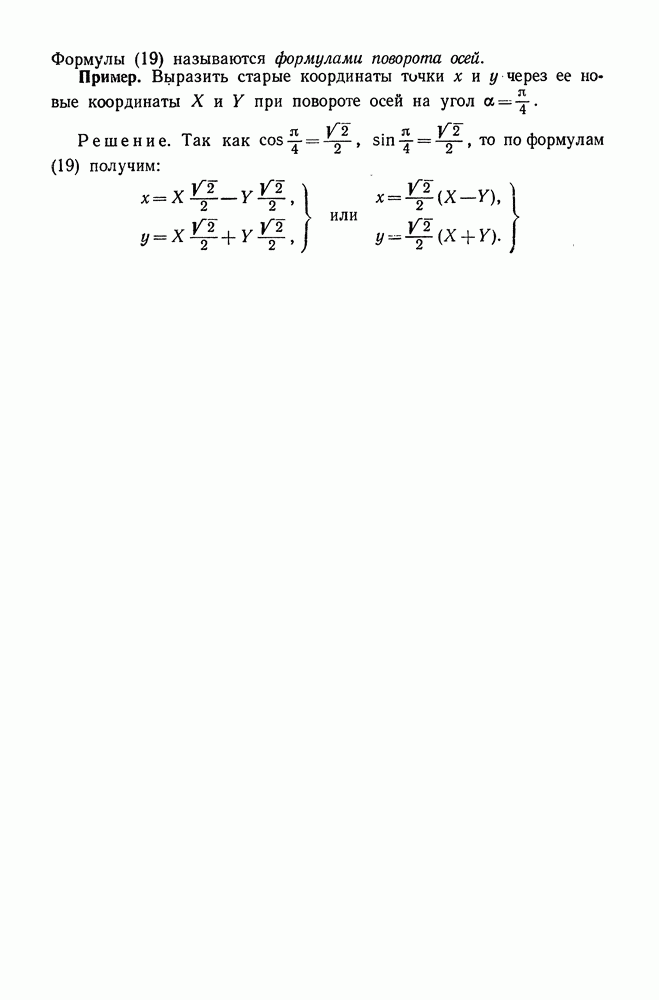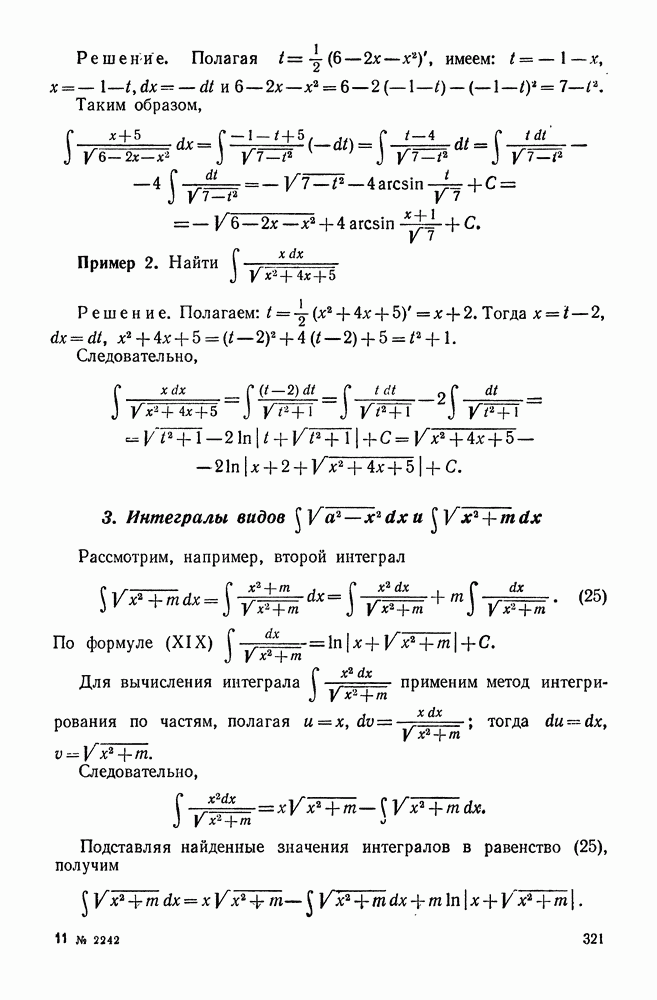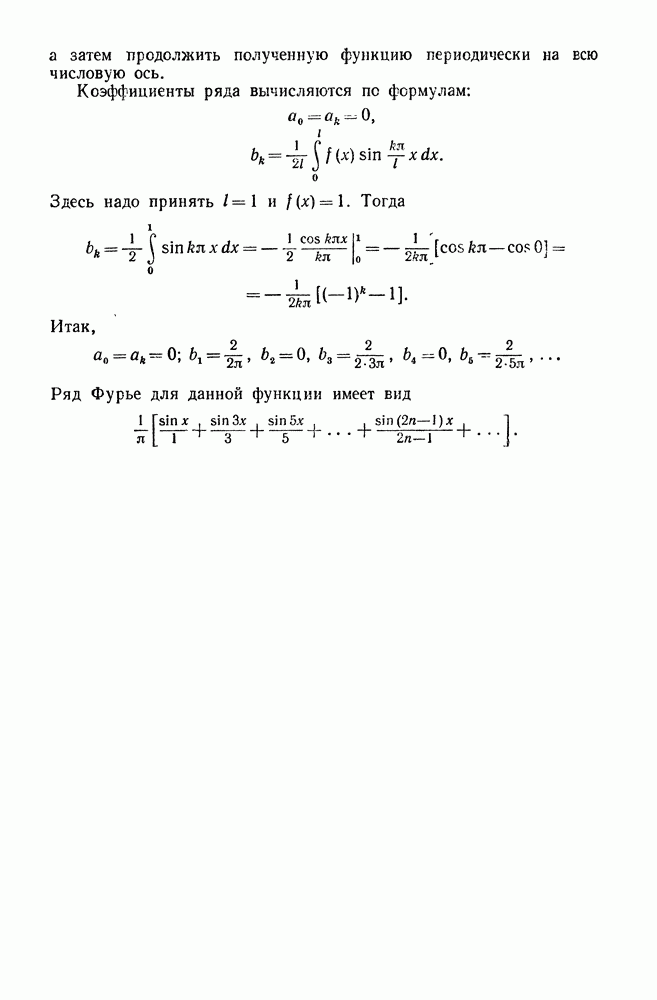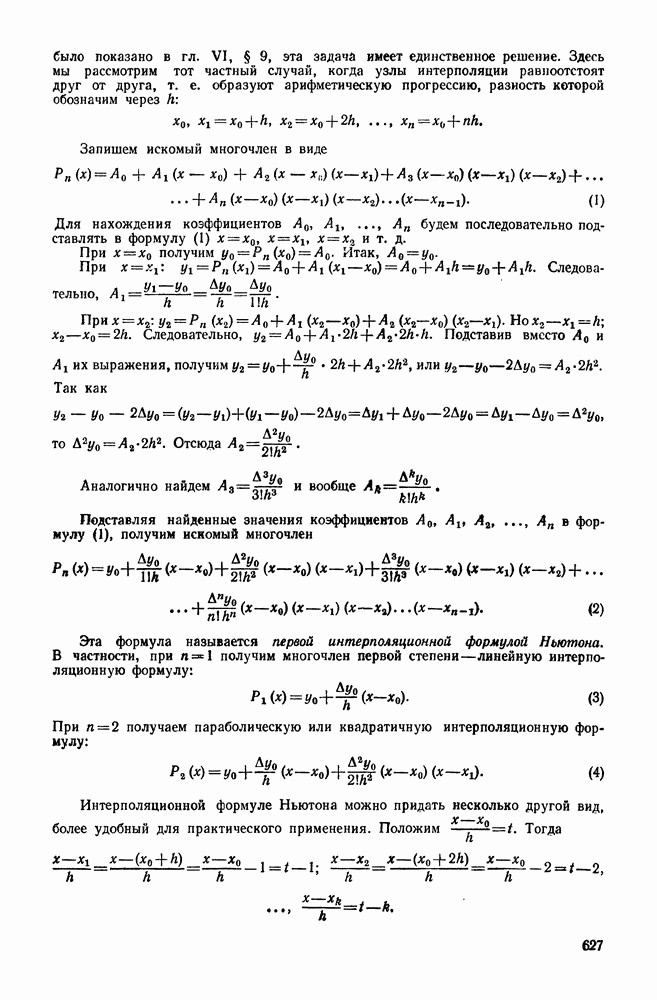| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
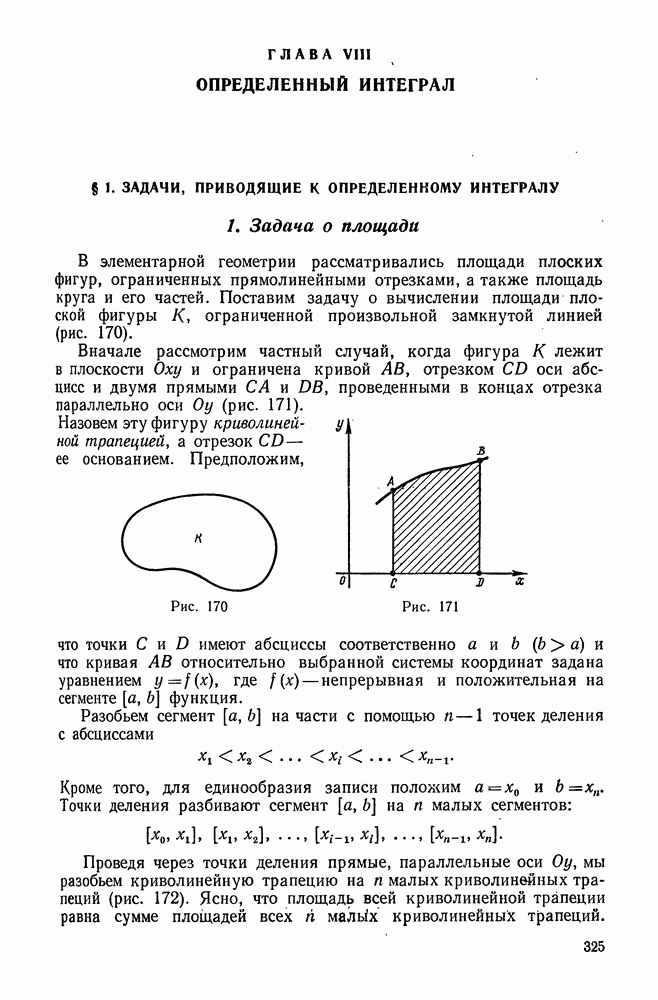
7. Криволинейный интеграл по длине дуги
В предыдущих пунктах мы рассматривали криволинейный интеграл от вектор-функции (криволинейный интеграл по координатам). Однако некоторые задачи приводят к криволинейному интегралу другого рода. Рассмотрим в плоскости  кривую АВ длины
кривую АВ длины  . Пусть вдоль этой кривой распределена масса с линейной плотностью
. Пусть вдоль этой кривой распределена масса с линейной плотностью  . Определим массу
. Определим массу  кривой. Для этого разобьем кривую АВ точками деления
кривой. Для этого разобьем кривую АВ точками деления  на
на  частей, обозначая для единообразия точки А и В соответственно через
частей, обозначая для единообразия точки А и В соответственно через  Обозначим через
Обозначим через  массу дуги
массу дуги  длины
длины  Ясно, что,
Ясно, что,  Подсчитаем приближенно массу дуги
Подсчитаем приближенно массу дуги  . Пусть
. Пусть  произвольная точка дуги
произвольная точка дуги  . Считая, что плотность в каждой точке дуги
. Считая, что плотность в каждой точке дуги  такая же, как в точке
такая же, как в точке  получим приближенное значение массы:
получим приближенное значение массы:  Суммируя, найдем приближенное значение массы
Суммируя, найдем приближенное значение массы 

За точное значение массы кривой АВ примем предел суммы (57) при условии, что все  . Итак,
. Итак,

К подобного рода суммам и их пределам приводят и другие задачи. Отвлекаясь от конкретного содержания приведенной задачи, рассмотрим непрерывную функиию  , определенную в точках дуги АВ. Составленная для нее сумма вида (57) называется интегральной суммой. Предел интегральной суммы (57) при условии, что все
, определенную в точках дуги АВ. Составленная для нее сумма вида (57) называется интегральной суммой. Предел интегральной суммы (57) при условии, что все  называете я криволинейным интегралом от функции
называете я криволинейным интегралом от функции  по длине дуги АВ и обозначается символом
по длине дуги АВ и обозначается символом  или
или 
Итак

Таким образом, масса дуги равна криволинейному интегралу от плотности по длине этой дуги:

Следует обратить внимание на то, что, в отличие от криволинейного интеграла по координатам, криволинейный интеграл по длине дуги не зависит от выбора направления на кривой.
Можно показать, что вычисление криволинейного интеграла по длине дуги сводится к вычислению определенного интеграла.
Если дуга АВ задана уравнением  то
то

Подынтегральное выражение в правой части равенства (60) получается из подынтегрального выражения в левой части заменой  и дифференциала дуги
и дифференциала дуги  на его выражение в декартовых координатах
на его выражение в декартовых координатах 
Пример. Найти массу дуги кривой  между точками с абсциссами
между точками с абсциссами  , если плотность
, если плотность  .
.
Решение. Применяя формулы (59) и (60), получим

Замечание. Часто криволинейный интеграл по длине дуги называют криволинейным интегралом первого рода, а криволинейный интеграл от вектор-функции — криволинейным интегралом второго рода.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. МЕТОД КООРДИНАТ. ПОНЯТИЕ ФУНКЦИИ
- § 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КООРДИНАТЫ ТОЧКИ НА ПРЯМОЙ
- 2. Геометрическое изображение действительных чисел. Координаты точки на прямой
- 3. Абсолютная величина действительного числа
- 4. Расстояние между двумя точками на прямой
- § 2. КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
- 2. Расстояние между двумя точками на плоскости
- 3. Деление отрезка в данном отношении
- 4. Координаты точки в пространстве
- 5. Расстояние между двумя точками в пространстве
- § 3. УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ
- 2. Полярные координаты
- 3. Зависимость между декартовыми и полярными координатами
- § 4. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ
- 2. Понятие функции
- 3. График функции
- 4. Способы задания функций
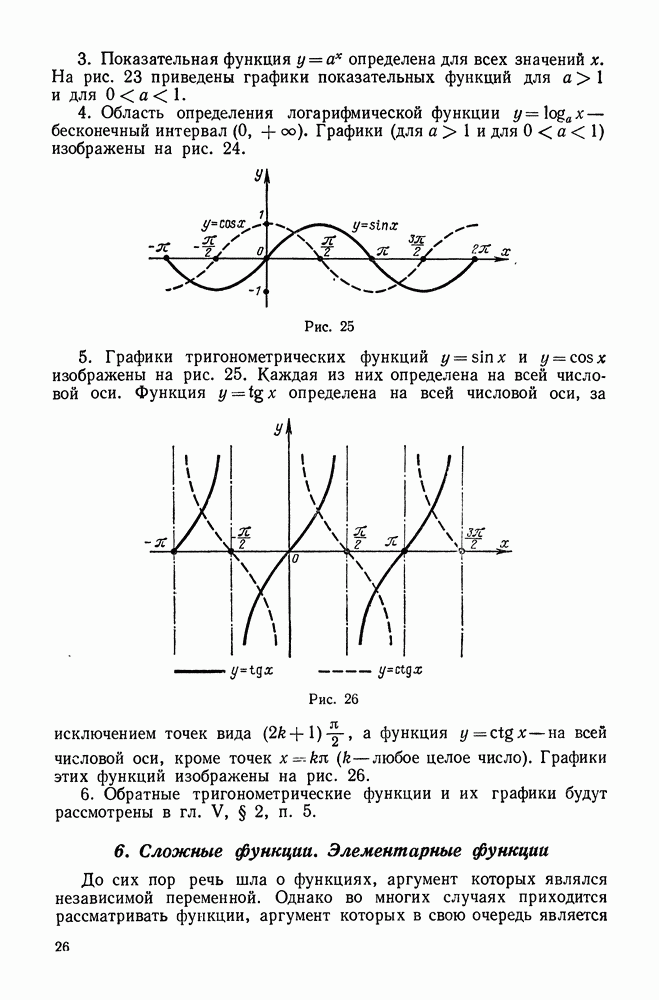
- 5. Основные элементарные функции и их графики
- 6. Сложные функции. Элементарные функции
- 7. Целые и дробно-рациональные функции
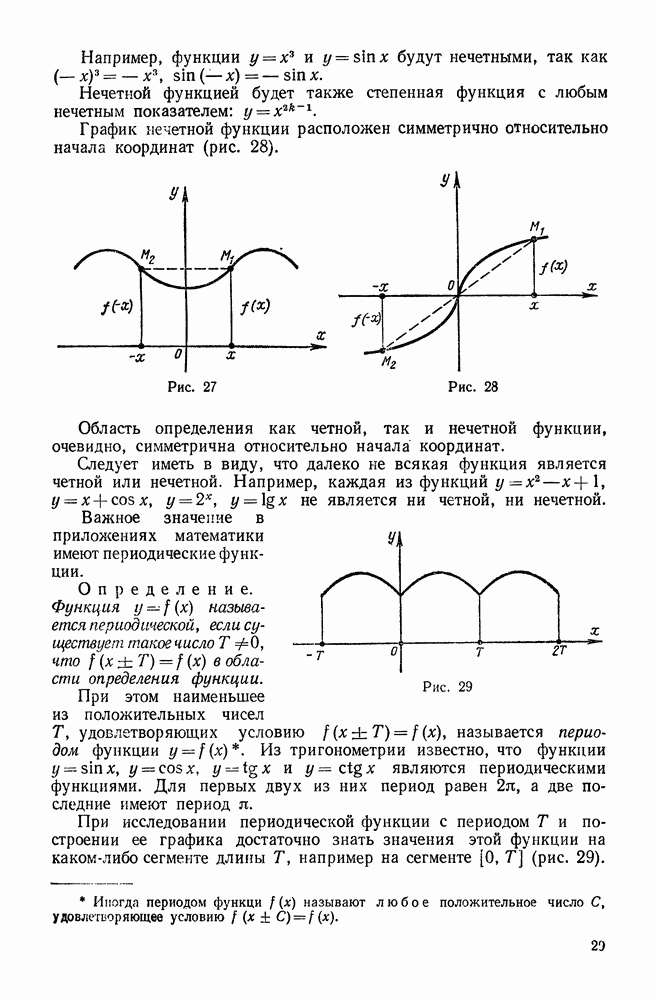
- 8. Функции четные и нечетные. Периодические функции
- § 5. УРАВНЕНИЕ ЛИНИИ
- 2. Нахождение уравнения линии по ее геометрическим свойствам
- § 6 ПРЕОБРАЗОВАНИЕ КООРДИНАТ
- 2. Поворот осей координат
- ГЛАВА II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- § 1. ПРЯМАЯ
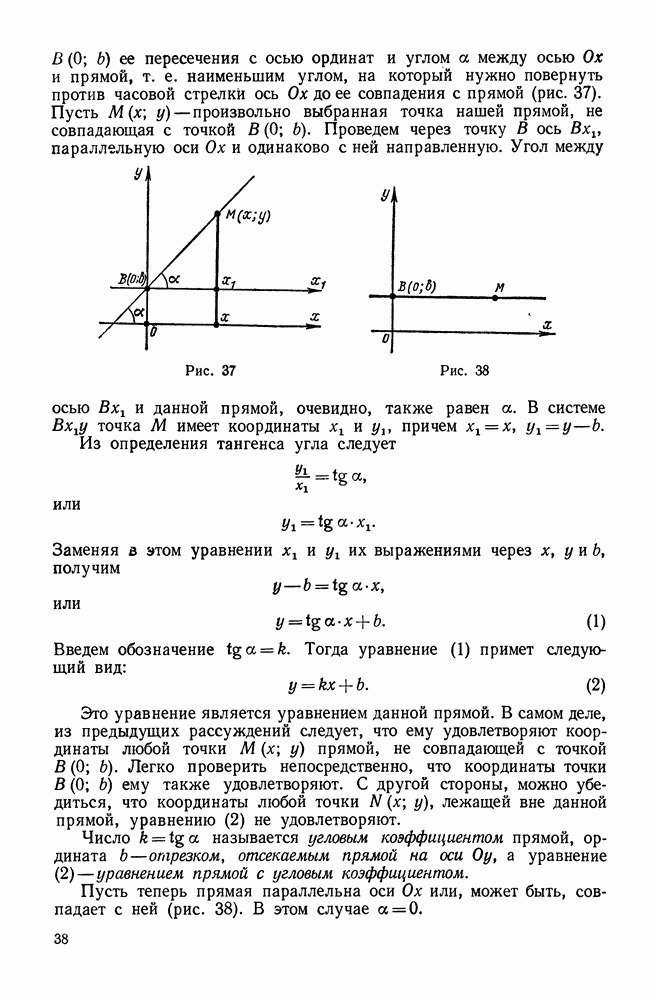
- 2. Уравнение прямой с угловым коэффициентом
- 3. Уравнение прямой, параллельной оси ординат
- 4. Общее уравнение прямой и его частные случаи
- 5. Точка пересечения прямых. Построение прямой по ее уравнению
- 6. Вычисление угла между двумя прямыми. Условия параллельности и перпендикулярности двух прямых
- 7. Уравнение прямой, проходящей через данную точку в заданном направлении
- 8. Пучок прямых
- 9. Уравнение прямой, проходящей через две данные точки
- 10. Расстояние от точки до прямой
- § 2. КРИВЫЕ ВТОРОГО ПОРЯДКА
- 2. Окружность
- 3. Эллипс
- 4. Гипербола
- 5. Парабола
- 6. Окружность, эллипс, гипербола и парабола как конические сечения
- 7. Упрощение уравнения кривой второго порядка. График квадратного трехчлена
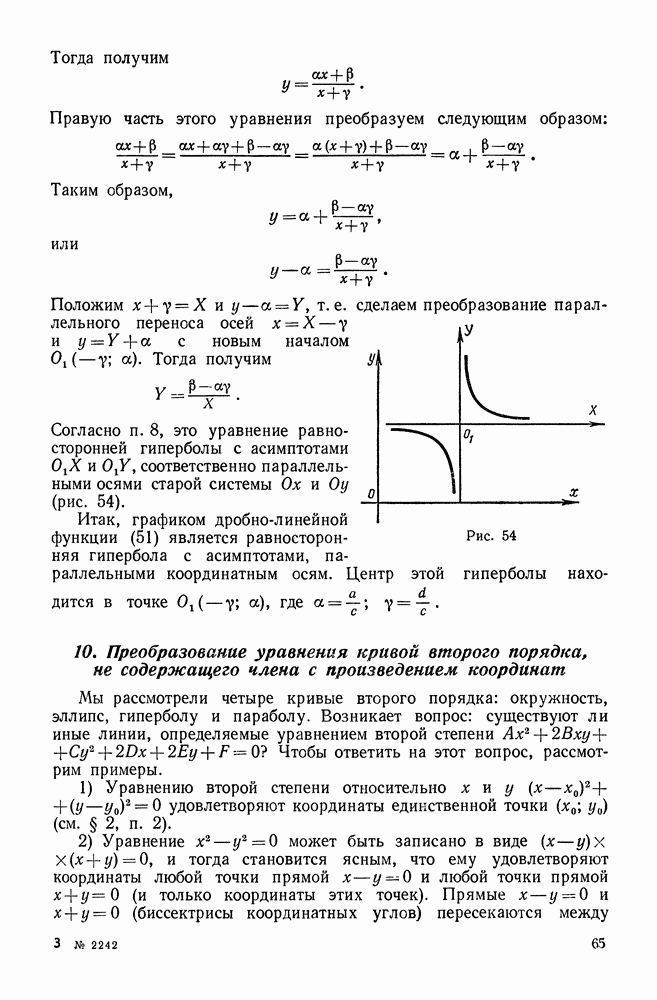
- 8. Уравнение равносторонней гиперболы, асимптоты которой приняты за оси координат
- 9. График дробно-линейной функции
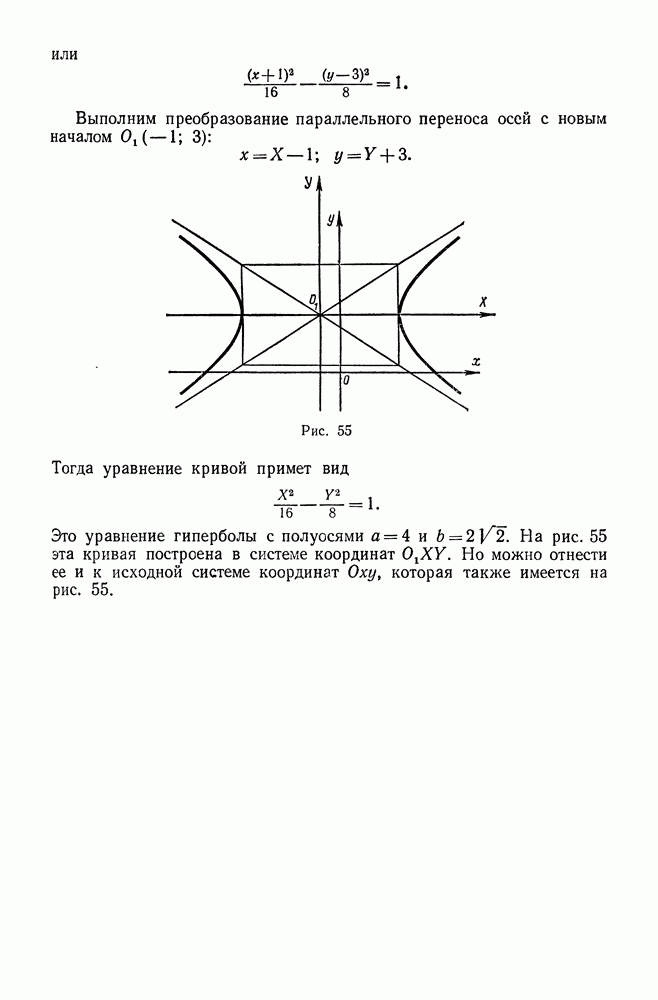
- 10. Преобразование уравнения кривой второго порядка, не содержащего члена с произведением координат
- ГЛАВА III. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ
- § 1. ЭЛЕМЕНТЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ
- 2. Определитель третьего порядка
- 3. Понятие об определителях высших порядков
- § 2. СИСТЕМЫ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ
- 2. Однородная система двух уравнений первой степени с тремя неизвестными
- 3. Система трех уравнений первой степени с тремя неизвестными
- 4. Однородная система трех уравнений первой степени с тремя неизвестными
- § 3. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- 2. Линейные операции над векторами
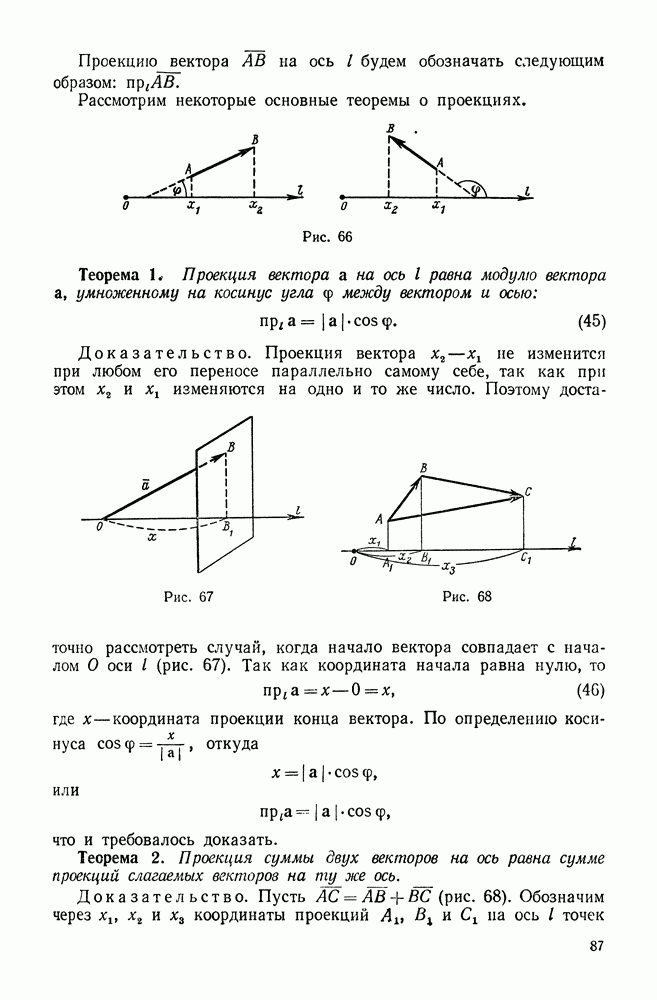
- 4. Проекция вектора на ось и составляются вектора по оси
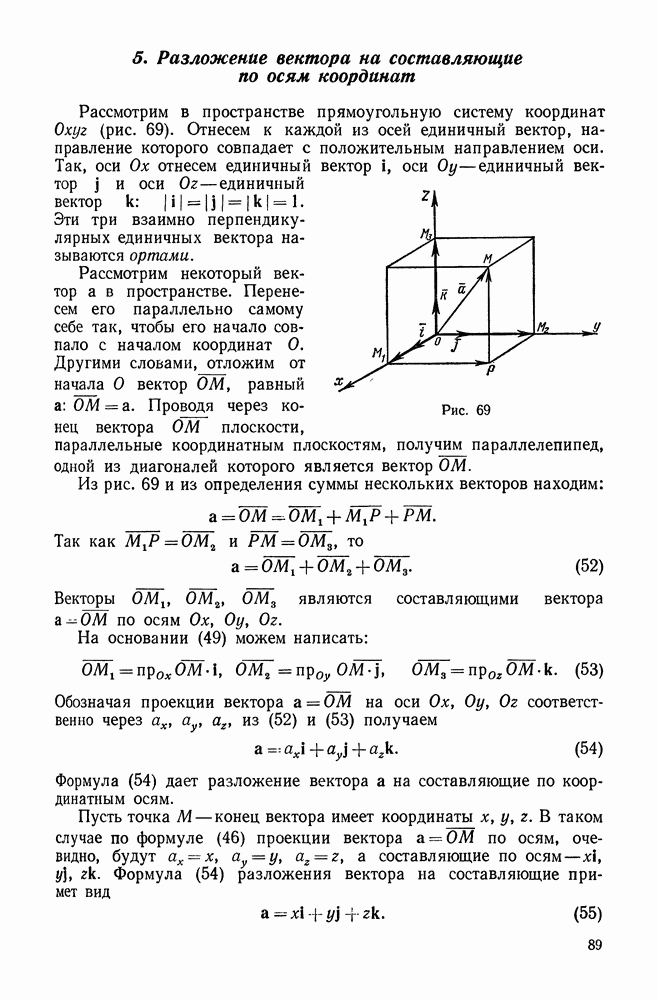
- 5. Разложение вектора на составляющие по осям координат
- 6. Направляющие косинусы вектора
- 7. Условие коллинеарности двух векторов
- 8. Скалярное произведение
- 9. Выражение скалярного произведения через проекции перемножаемых векторов
- 10. Косинус угла между двумя векторами
- 11. Векторное произведение
- 12. Выражение векторного произведения через проекции перемножаемых векторов
- 13. Смешанное произведение трех векторов
- 14. Геометрический смысл смешанного произведения
- 15. Условие компланарности трех векторов
- § 4. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 2. Равенство матриц. Действия над матрицами
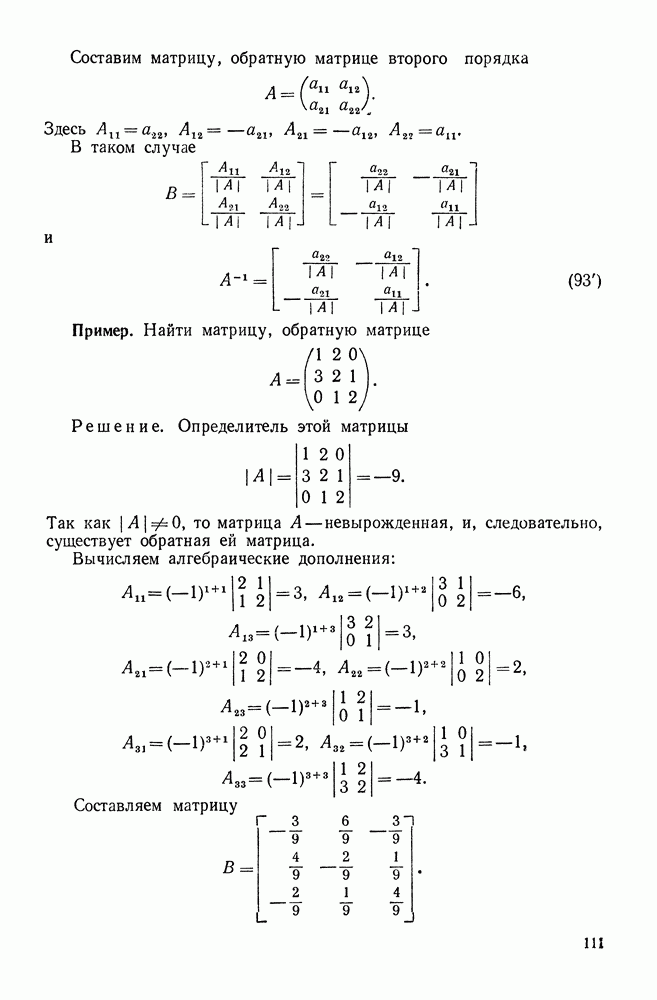
- 3. Обратная матрица
- 4. Матричная запись и матричное решение системы уравнений первой степени
- § 5. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ
- 2. Преобразование координат
- 3. Приведение квадратичной формы к каноническому виду
- 4. Упрощение общего уравнения кривой второго порядка
- ГЛАВА IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- § 1. ПЛОСКОСТЬ
- 2. Нормальный вектор плоскости. Уравнение плоскости, проходящей через данную точку
- 3. Общее уравнение плоскости и его частные случаи
- 4. Построение плоскости по ее уравнению
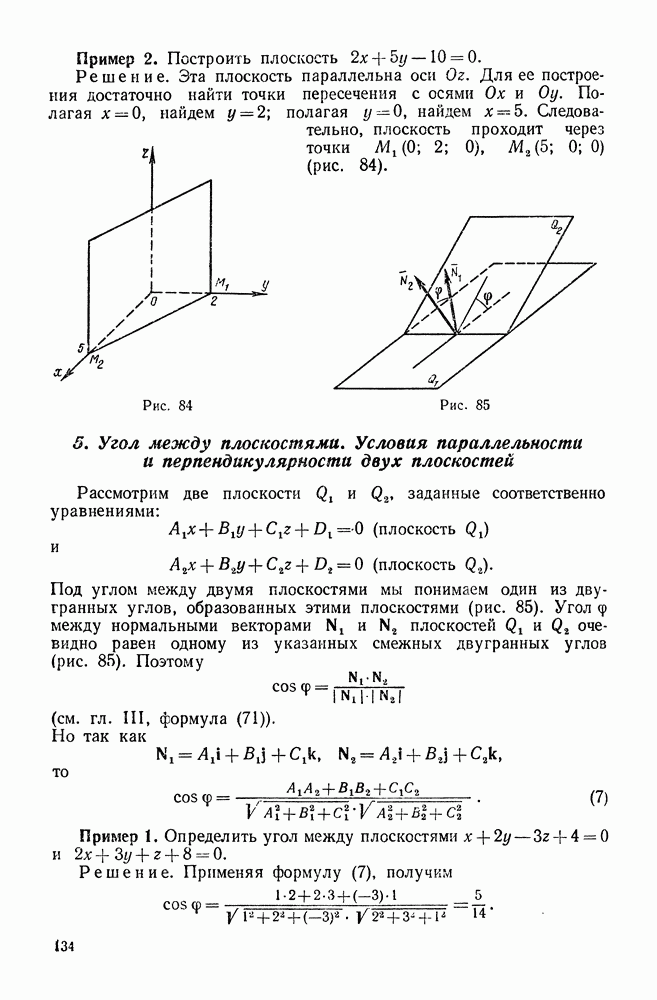
- 5. Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей
- 6. Точка пересечения трех плоскостей
- § 2. ПРЯМАЯ В ПРОСТРАНСТВЕ
- 2. Общие уравнения прямой
- 3. Векторное уравнение прямой. Параметрические уравнения прямой
- 4. Канонические уравнения прямой
- 5. Уравнения прямой, проходящей через две точки
- 6. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых
- § 3. Прямая и плоскость в пространстве
- 2. Точка пересечения прямой с плоскостью
- 3. Расстояние от точки до плоскости
- 4. Пучок плоскостей
- § 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
- 2. Цилиндрические поверхности
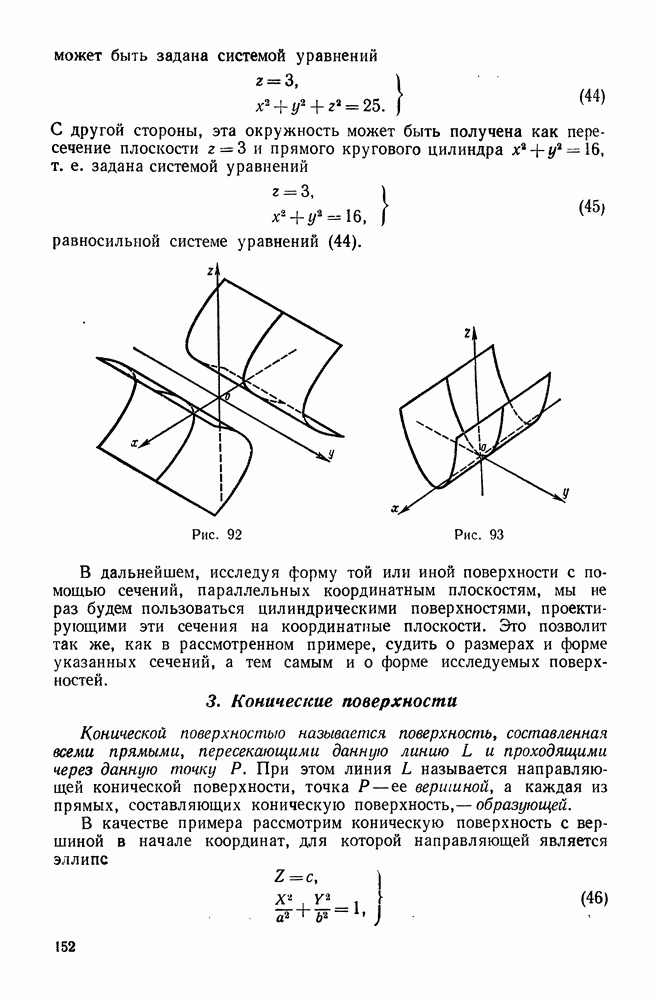
- 3. Конические поверхности
- 4. Поверхность вращения
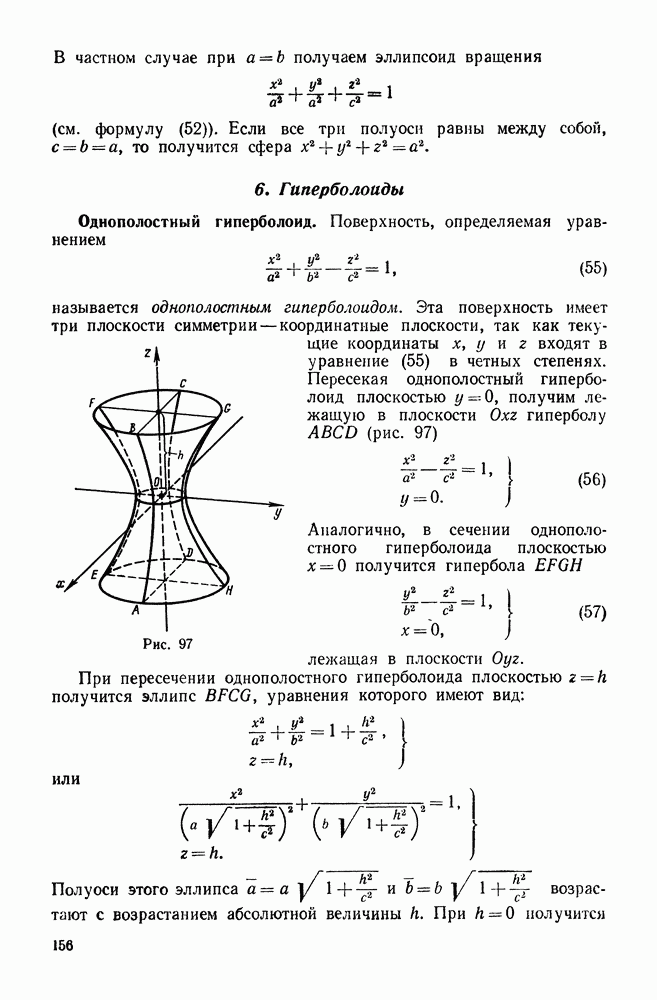
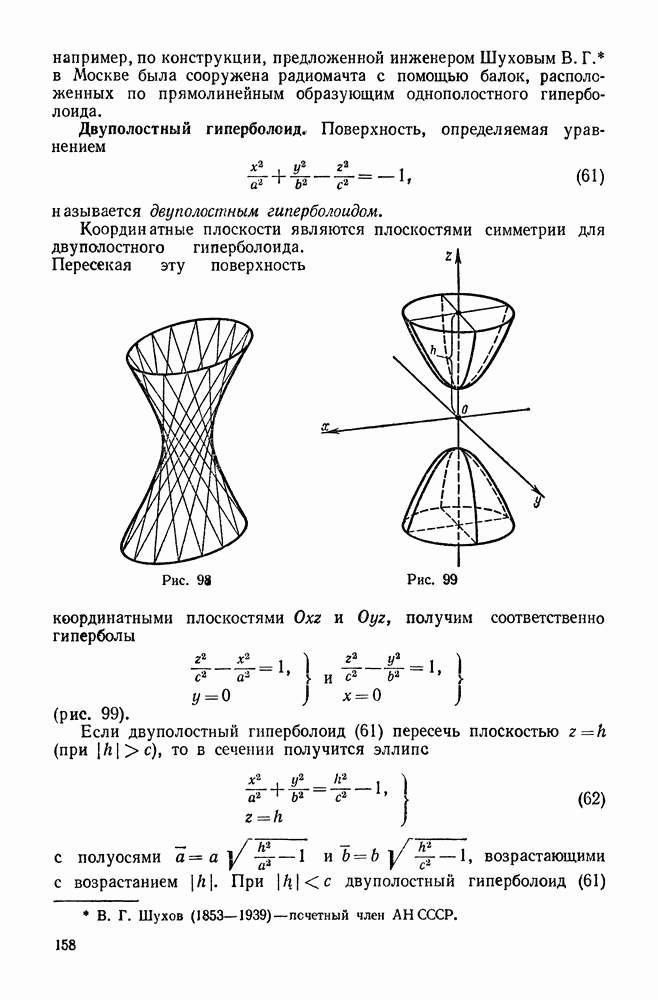
- 6. Гиперболоиды
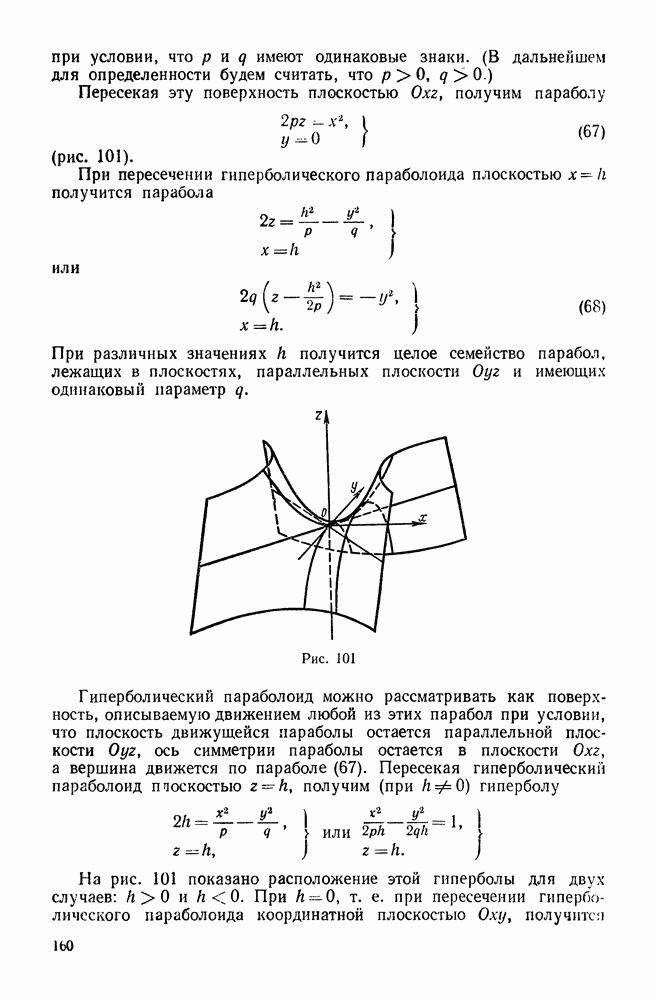
- 7. Параболоиды
- ГЛАВА V. ТЕОРИЯ ПРЕДЕЛОВ
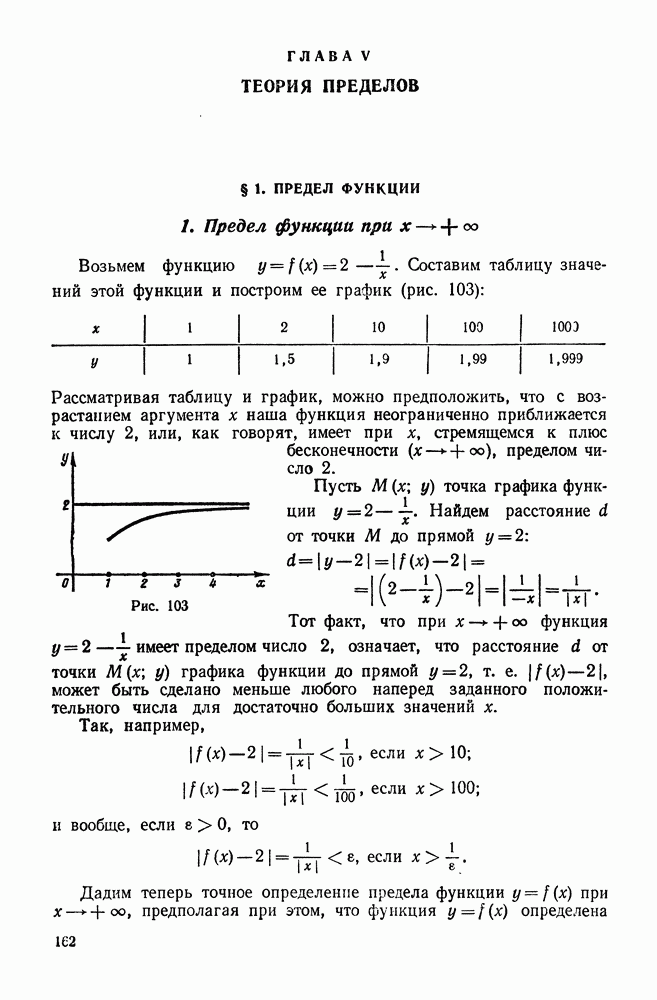
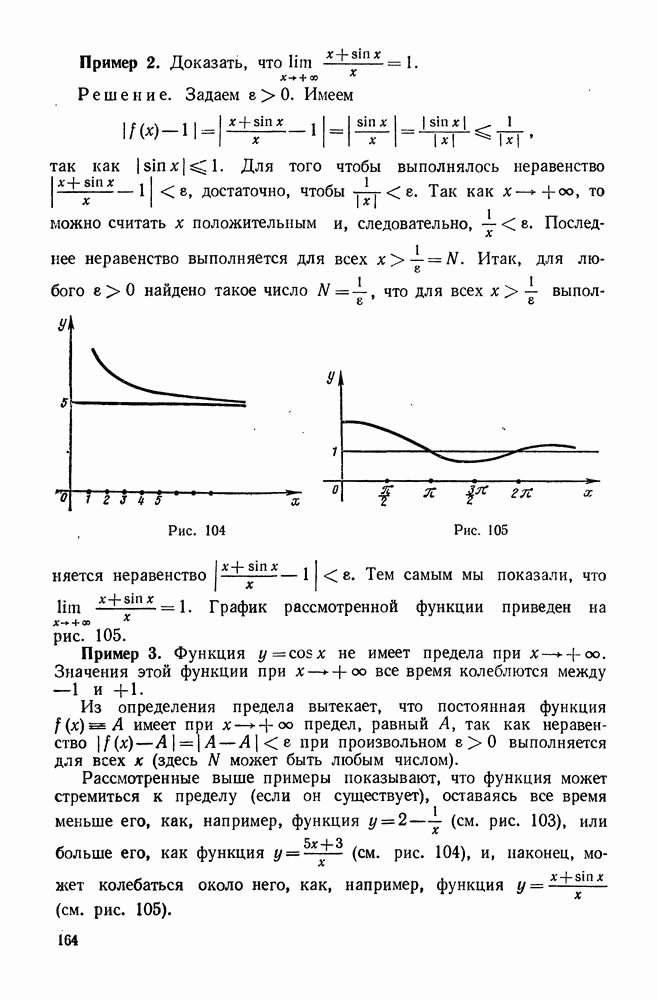
- § 1. ПРЕДЕЛ ФУНКЦИИ
- 2. Предел функции при х -> -оо
- 3. Предел функции при х->х0
- 4. Бесконечно малые функции. Ограниченные функции
- 5. Бесконечно большие функции и их связь с бесконечно малыми функциями
- 6. Основные теоремы о пределах
- 7. Предел функции при x -> 0
- 8. Последовательность. Число e
- 9. Натуральные логарифмы
- 10. Сравнение бесконечно малых функций
- § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 2. Операции над непрерывными функциями. Непрерывность элементарных функций
- 3. Свойства функций, непрерывных на сегменте
- 4. Понятие об обратной функции
- 5. Обратные тригонометрические функции
- 6. Показательная и логарифмическая функции
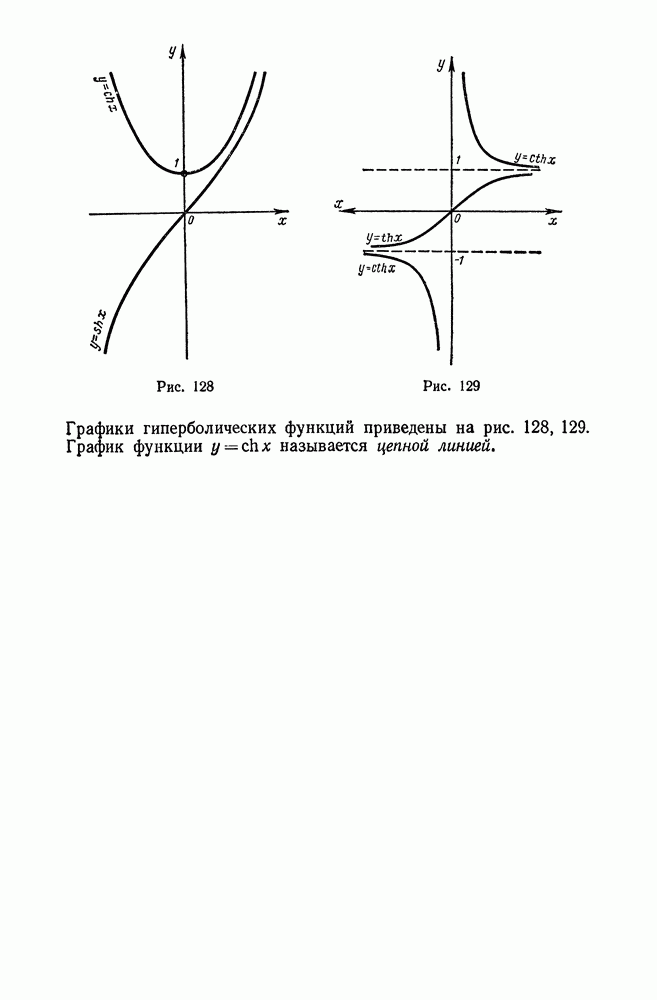
- 7. Понятие о гиперболических функциях
- ГЛАВА VI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
- 1. Приращение аргумента и приращение функции
- 2. Определение непрерывности функции с помощью понятии приращения аргумента и приращения функции
- 3. Задачи, приводящие к понятию производной
- 4. Определение производной и ее механический смысл
- 5. Дифференцируемость функции
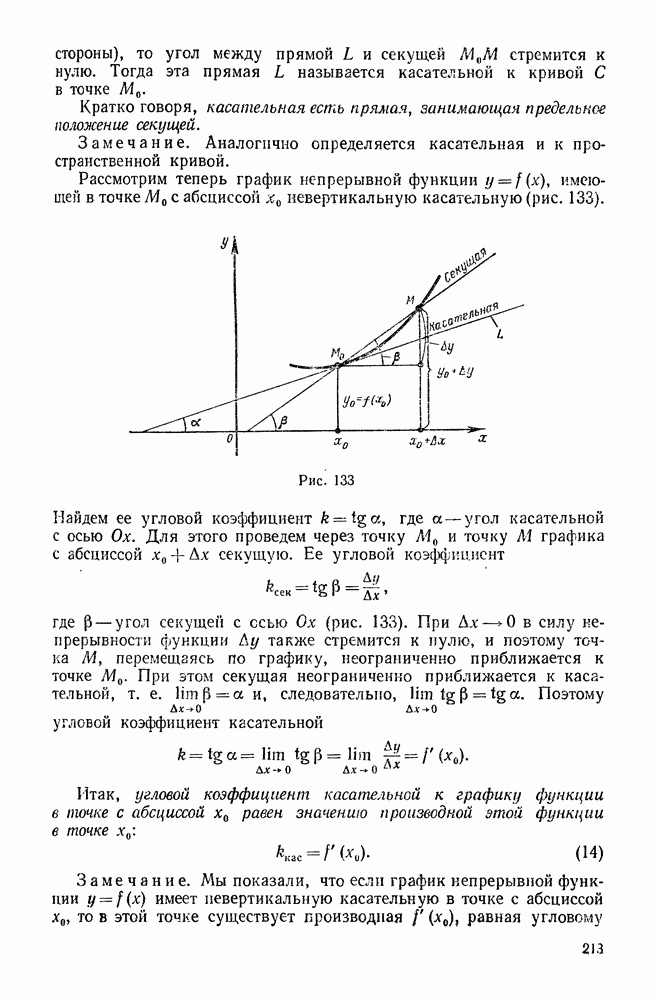
- 6. Геометрический смысл производной
- 7. Производные некоторых основных элементарных функций
- 8. Основные правила дифференцирования
- 9. Производная обратной функции
- 10. Производные обратных тригонометрических функций
- 11. Производная сложной функции
- § 12. Производные гиперболических функций
- 13. Производная степенной функции с любым показателем
- 14. Сводная таблица формул дифференцирования
- 15. Неявные функции и их дифференцирование
- 16. Уравнения касательной а нормали к кривой
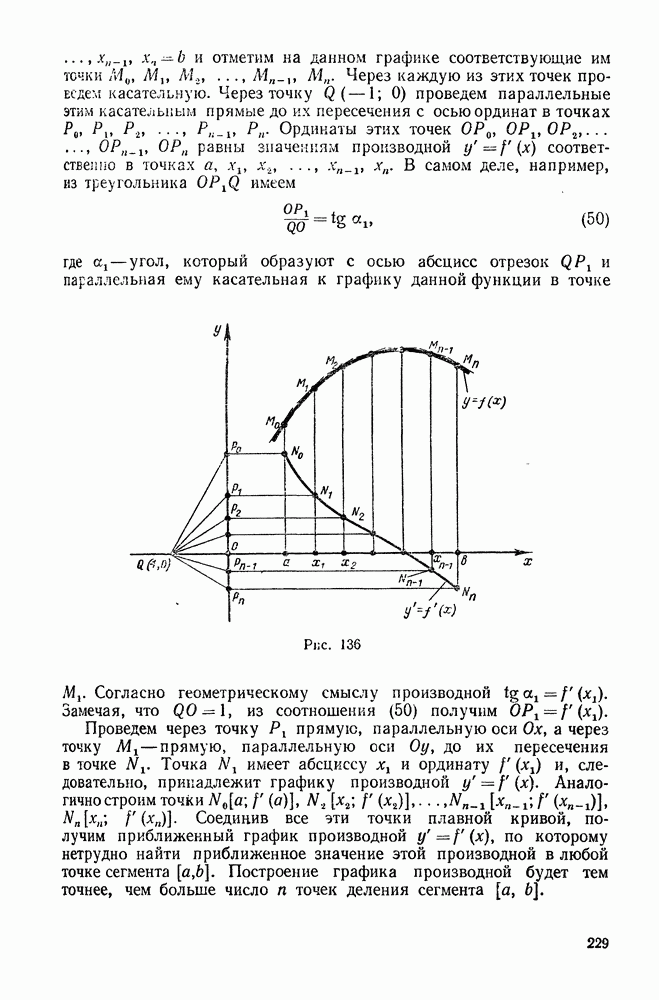
- 17. Графическое дифференцирование
- § 2. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
- 1. Нахождение производных высших порядков
- 2. Механический смысл второй производной
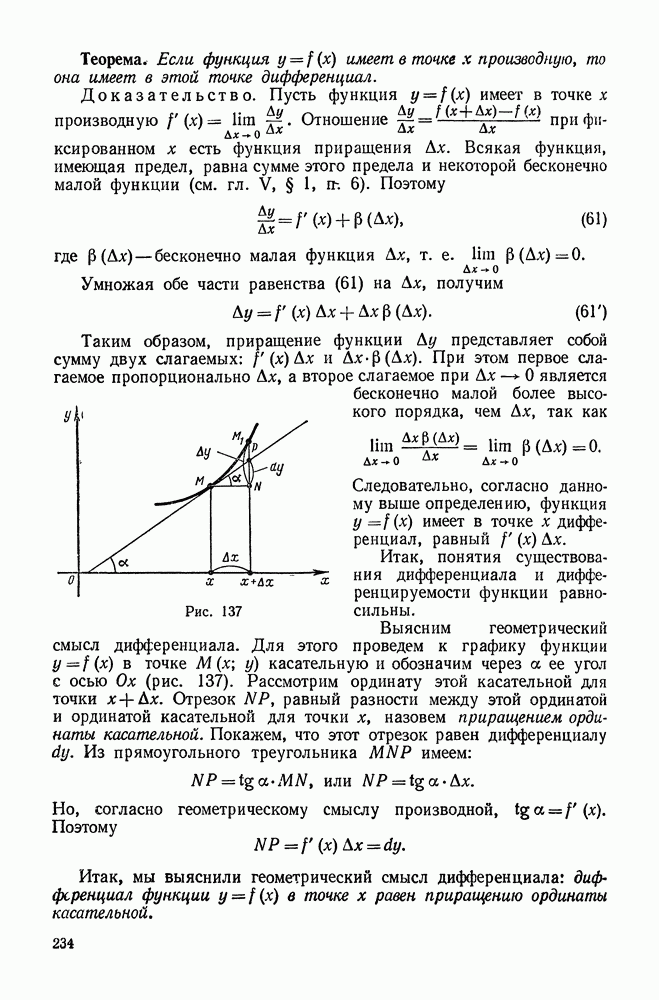
- § 3. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
- 2. Производная как отношение дифференциалов
- 3. Дифференциал суммы, произведения и частного функций
- 4. Дифференциал сложной функции. Инвариантность формы дифференциала
- 5. Применение дифференциала к приближенным вычислениям
- 6. Дифференциалы высших порядков
- § 4. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ, И ИХ ДИФФЕРЕНЦИРОВАНИЕ
- 2. Дифференцирование функций, заданных параметрически
- § 5. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
- 2. Векторная функция скалярного аргумента и ее производная
- 3. Уравнения касательной прямой и нормальной плоскости к пространственной кривой
- 4. Механический смысл первой и второй производных векторной функции скалярного аргумента
- § 6. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
- 2. Теорема Ролля
- 3. Теорема Лагранжа
- 4. Правило Лопиталя
- § 7. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ
- 2. Максимум и минимум функции
- 3. Достаточный признак существования экстремума, основанный на знаке второй производной
- 4. Отыскание наибольшего и наименьшего значений функции
- 5. Применение теории максимума и минимума к решению задач
- 6. Выпуклость и вогнутость графика функции. Точки перегиба
- 7. Асимптоты графика функции
- 8. Общая схема исследования функции и построение ее графика
- § 8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
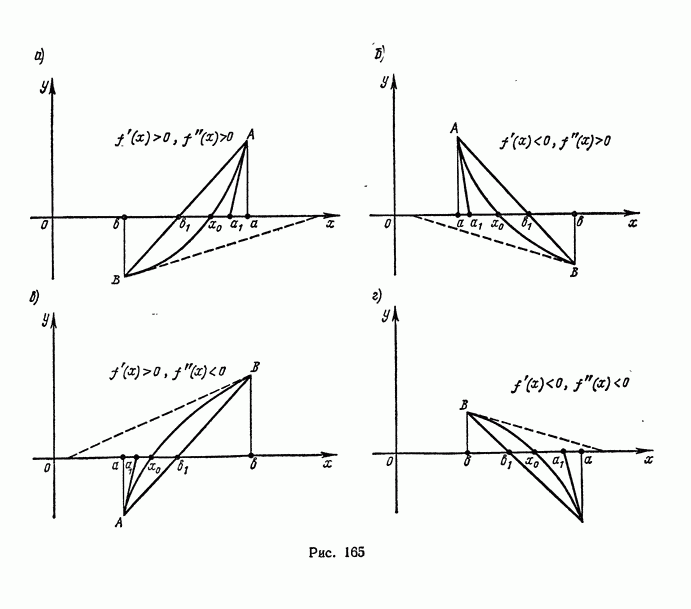
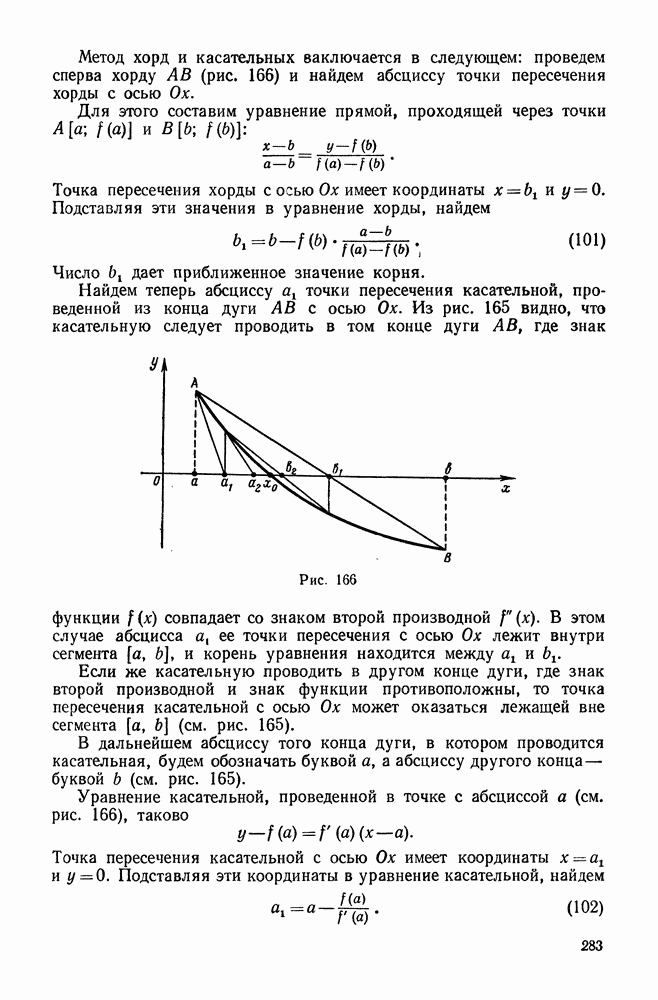
- 2. Уточнение найденных значений корней методом хорд и касательных
- § 9. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА
- ГЛАВА VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА
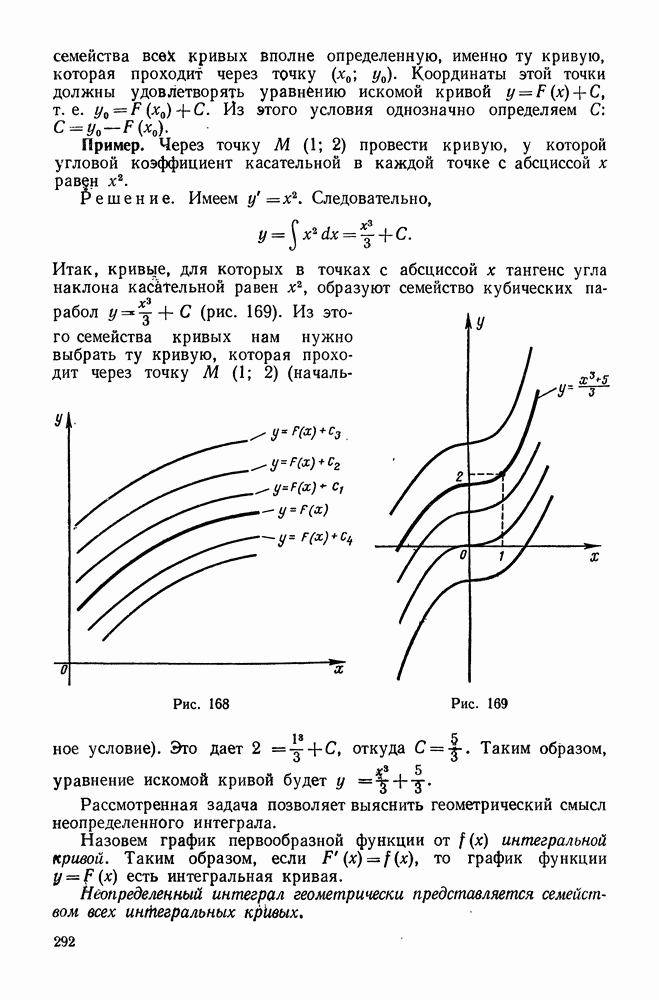
- 2. Геометрический смысл неопределенного интеграла
- 3. Таблица основных интегралов
- 4. Основные свойства неопределенного интеграла
- § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
- 2. Интегрирование методом замены переменной
- 3. Интегрирование по частям
- § 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- 2. Рациональные дроби. Выделение правильной рациональной дроби
- 3. Интегрирование простейших рациональных дробей
- 4. Разложение правильной рациональной дроби на простейшие дроби
- 5. Метод неопределенных коэффициентов
- 6. Интегрирование рациональных дробей
- § 4. Интегрирование тригонометрических функций
- 2. Рациональные функции двух переменных
- 3. Интегралы вида
- § 5. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
- 2. Интеграл вида
- 3. Интегралы видов
- 4. Интегралы вида
- § 6. ОБЩИЕ ЗАМЕЧАНИЯ О МЕТОДАХ ИНТЕГРИРОВАНИЯ. ИНТЕГРАЛЫ, НЕ БЕРУЩИЕСЯ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
- 2. Понятие об интегралах, не берущихся в элементарных функциях
- ГЛАВА VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ОПРЕДЕЛЕННОМУ ИНТЕГРАЛУ
- 2. Задача о работе переменной силы
- § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- 2. Свойства определенного интеграла
- 3. Производная интеграла по переменной верхней границе
- 4. Формула Ньютона—Лейбница
- 5. Замена переменной в определенном интеграле
- 6. Интегрирование по частям в определенном интеграле
- § 3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 2. Вычисление площади в полярных координатах
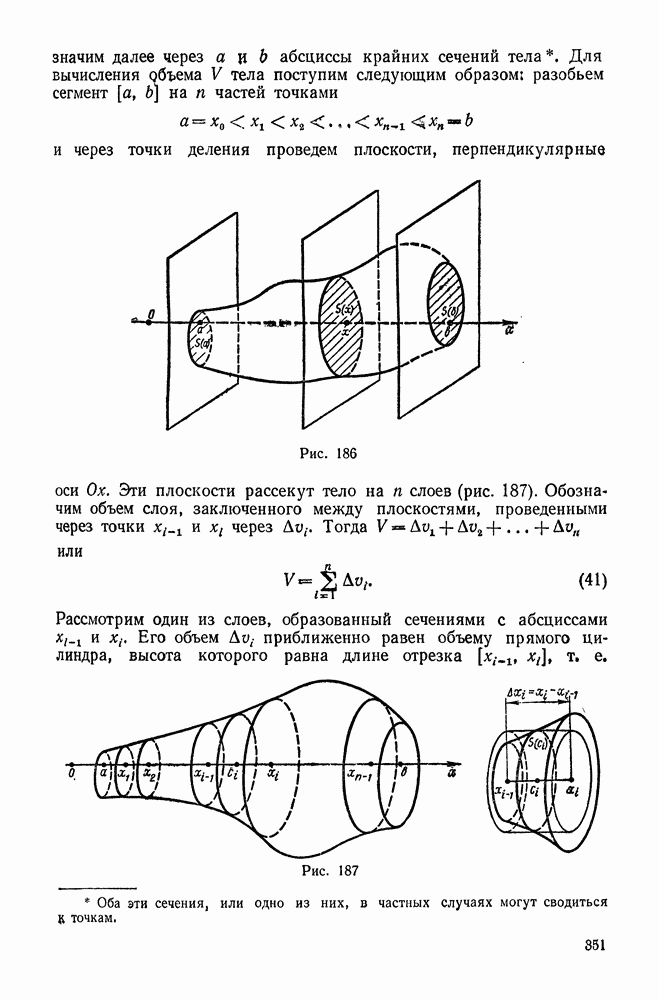
- 3. Вычисление объема тела по известным поперечным сечениям
- 4. Объем тела вращения
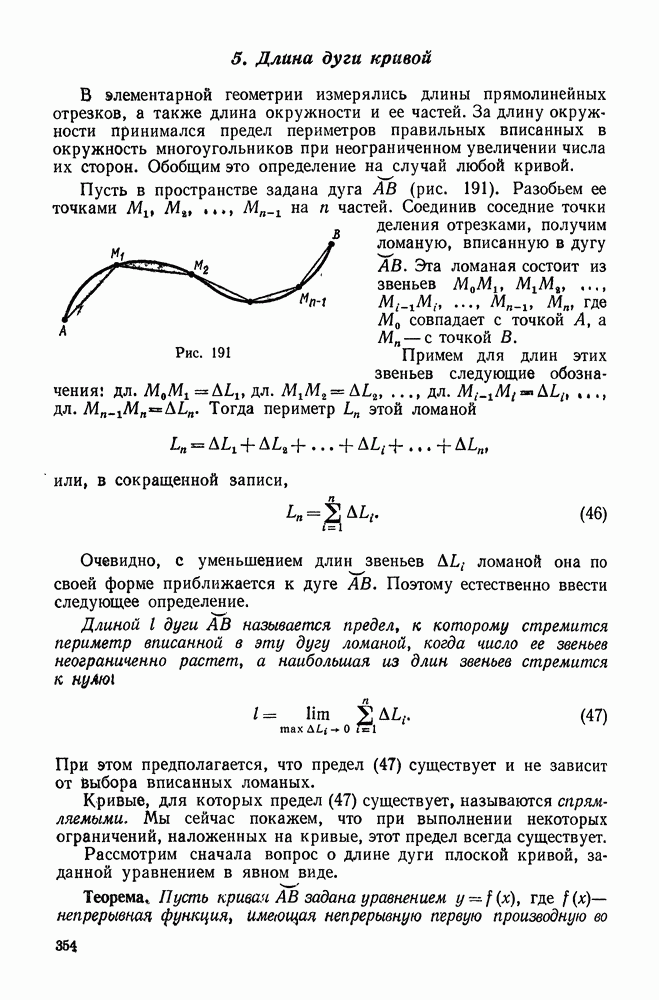
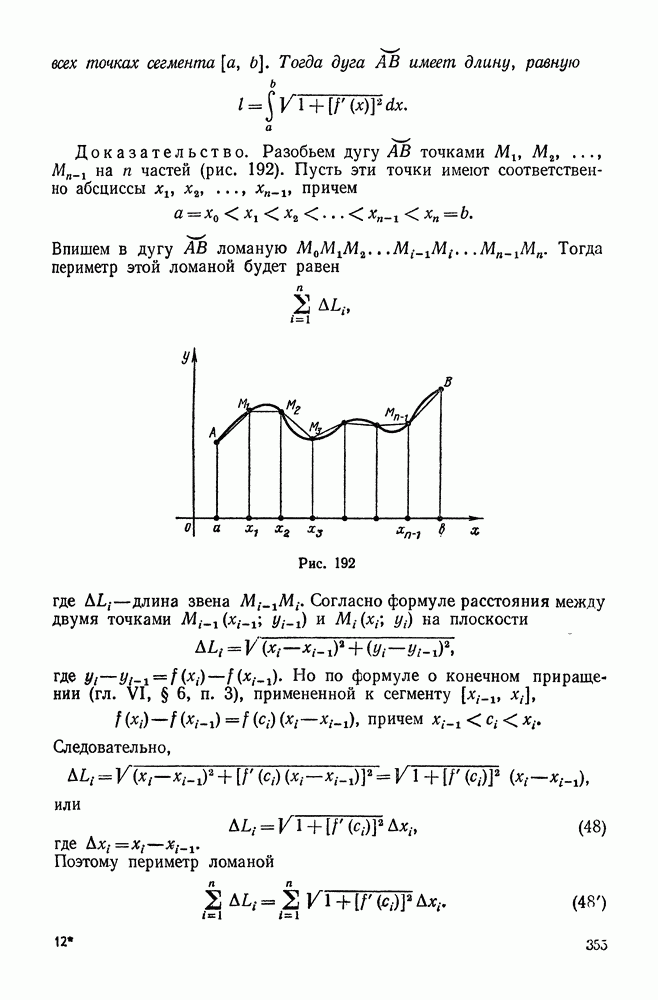
- 5. Длина дуги кривой
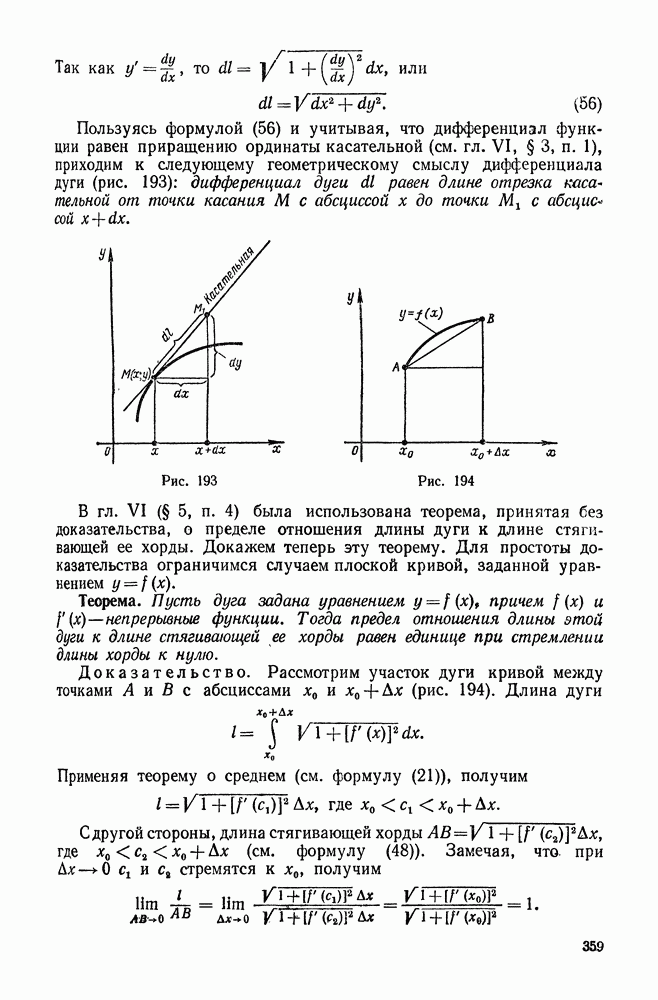
- 6. Дифференциал дуги
- 7. Площадь поверхности вращения
- 8. Общие замечания о решении задач методом интегральных сумм
- § 4. КРИВИЗНА ПЛОСКОЙ КРИВОЙ
- 2. Вычисление кривизны
- 3. Радиус кривизны. Круг кривизны. Центр кривизны
- 4. Эволюта и эвольвента
- § 5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- 2. Интегралы от разрывных функций
- 3. Признаки сходимости несобственных интегралов
- § 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
- 2. Метод трапеций
- 3. Метод параболических трапеций (метод Симпсона)
- ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 2. График функции двух переменных
- 3. Функции трех и большего числа переменных
- § 2. Предел функции нескольких переменных. Непрерывность функции. Точки разрыва
- 2. Непрерывность функции нескольких переменных
- 3. Понятие области
- 4. Точки разрыва
- 5. Свойства функций, непрерывных в ограниченной замкнутой области
- § 3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ
- 2. Геометрический смысл частных производных функции двух переменных
- 3. Частные производные высших порядков
- § 4. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 2. Полный дифференциал функции
- 3. Приложение полного дифференциала к приближенным вычислениям
- § 5. Дифференцирование сложных и неявных функций
- 2. Инвариантность формы полного дифференциала
- 3. Дифференцирование неявных функций
- § 6. СКАЛЯРНОЕ ПОЛЕ
- 2. Производная по направлению
- 3. Градиент
- 4. Касательная плоскость а нормаль к поверхности
- 5. Геометрический смысл полного дифференциала функции двух переменных
- § 7. ЭКСТРЕМУМ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ
- 2. Наибольшее и наименьшее значения функции двух переменных
- ГЛАВА X. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- § 1. ДВОЙНОЙ ИНТЕГРАЛ
- 2. Двойной интеграл. Теорема существования
- 3. Свойства двойного интеграла
- 4. Вычисление двойного интеграла в декартовых координатах
- 5. Вычисление двойного интеграла в полярных координатах
- 6. Приложения двойного интеграла
- § 2. ТРОЙНОЙ ИНТЕГРАЛ
- 2. Тройной интеграл и его свойства
- 3. Вычисление тройного интеграла в декартовых координатах
- 4. Вычисление тройного интеграла в цилиндрических координатах
- 5. Приложения тройного интеграла
- § 3. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
- 2. Задача о работе. Криволинейный интеграл
- 3. Вычисление криволинейного интеграла
- 4. Формула Остроградского — Грина
- 5. Независимость криволинейного интеграла от пути интегрирования
- 6. Отыскание первообразной по полному дифференциалу
- 7. Криволинейный интеграл по длине дуги
- ГЛАВА XI. РЯДЫ
- § 1. ЧИСЛОВЫЕ РЯДЫ
- 2. Геометрическая прогрессия
- 3. Простейшие свойства числовых рядов
- 4. Необходимый признак сходимости ряда
- 5. Достаточные признаки сходимости знакоположительных рядов
- 6. Знакопеременные ряды
- 7. Остаток ряда и его оценка
- § 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
- 2. Правильно сходящиеся функциональные ряды и их свойства
- § 3. СТЕПЕННЫЕ РЯДЫ
- 2. Свойства степенных рядов
- 3. Ряды по степеням разности х-а
- 4. Разложение функций в степенные ряды. Ряд Тейлора
- 5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена
- § 4. ПРИЛОЖЕНИЕ РЯДОВ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
- 2. Приближенное вычисление интегралов
- § 5. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. СТЕПЕННЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 2. Числовые ряды с комплексными членами
- 3. Степенные ряды в комплексной области
- § 6. РЯДЫ ФУРЬЕ
- 2. Ряд Фурье
- 3. Сходимость ряда Фурье
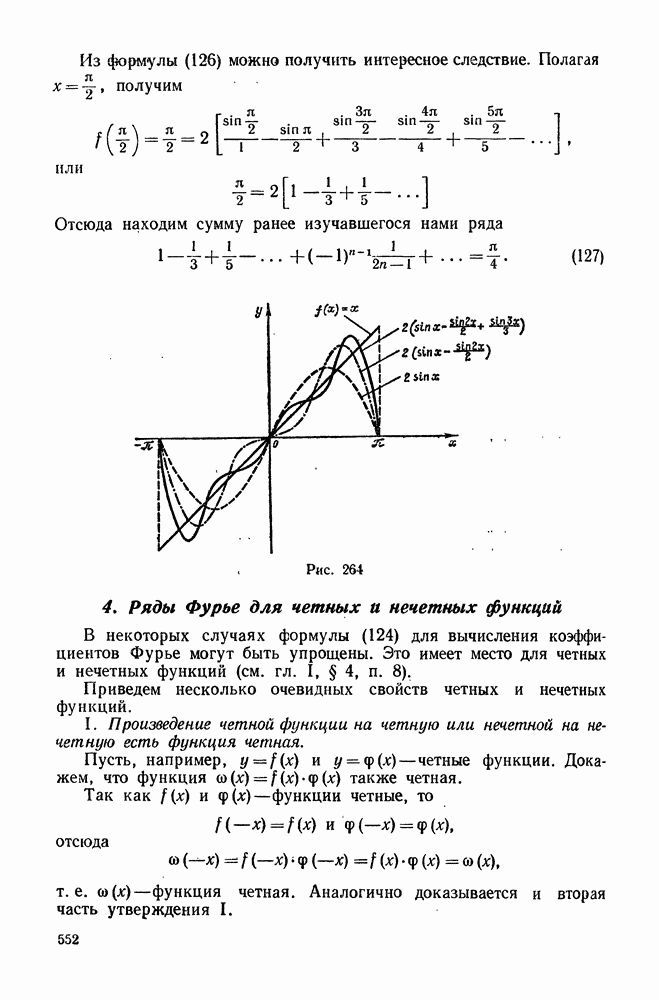
- 4. Ряды Фурье для четных и нечетных функций
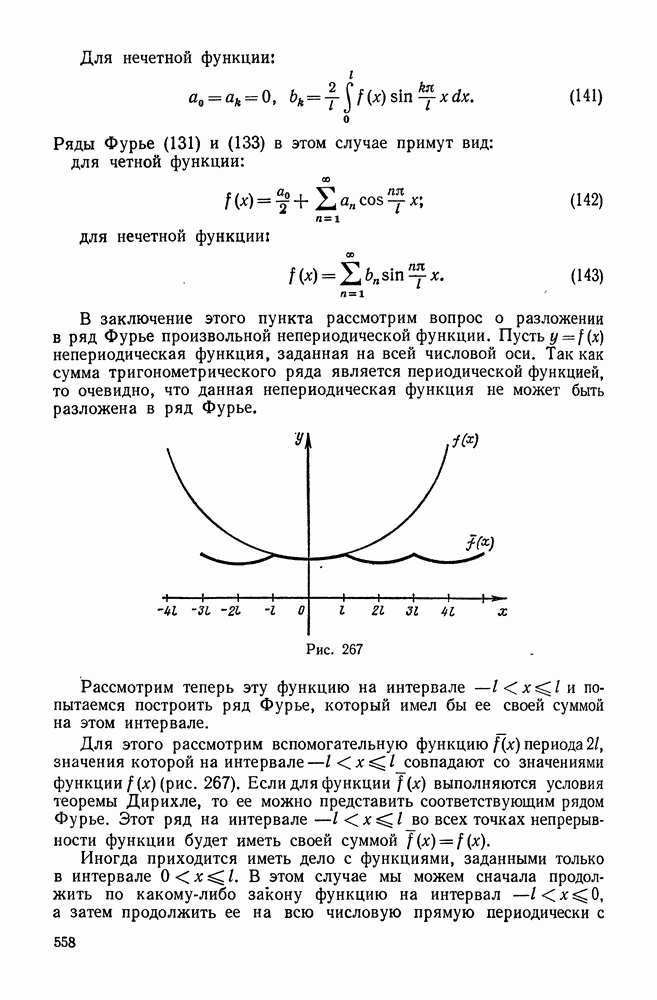
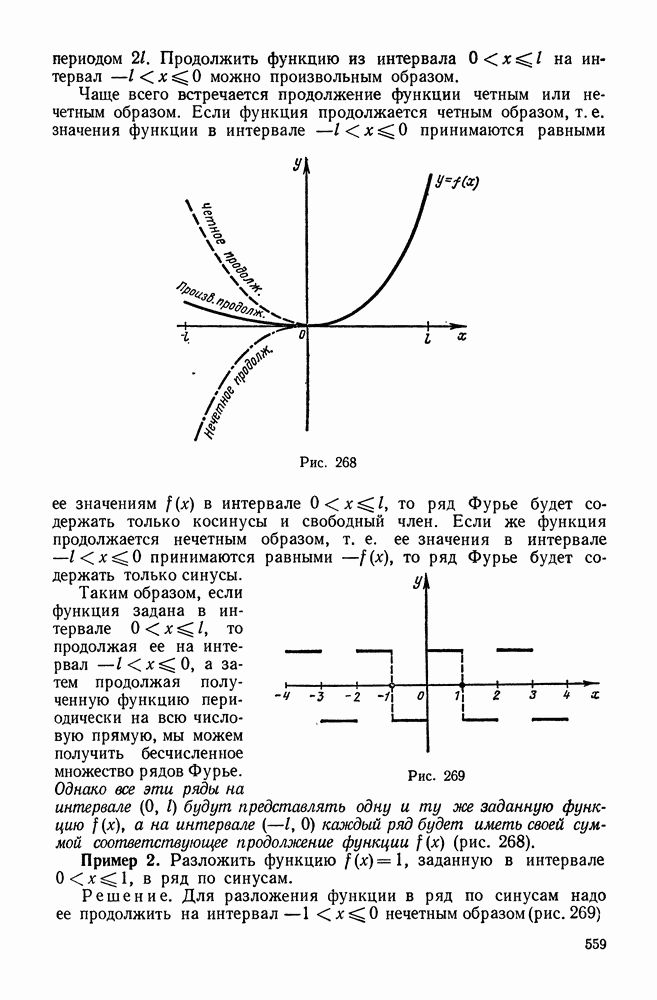
- 5. Разложение в ряд Фурье функций с периодом 2l
- ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- 2. Дифференциальные уравнения первого порядка
- 3. Уравнения с разделяющимися переменными
- 4. Однородные уравнения
- 5. Линейные уравнения
- 6. Уравнение в полных дифференциалах
- 7. Особые решения
- 8. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- 2. Простейшие уравнения второго порядка, допускающие понижение порядка
- 3. Понятие о дифференциальных уравнениях высших порядков
- § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- 2. Линейные однородные дифференциальные уравнения второго порядка
- 3. Линейные неоднородные дифференциальные уравнения второго порядка
- 4. Метод вариации произвольных постоянных
- § 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- 2. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
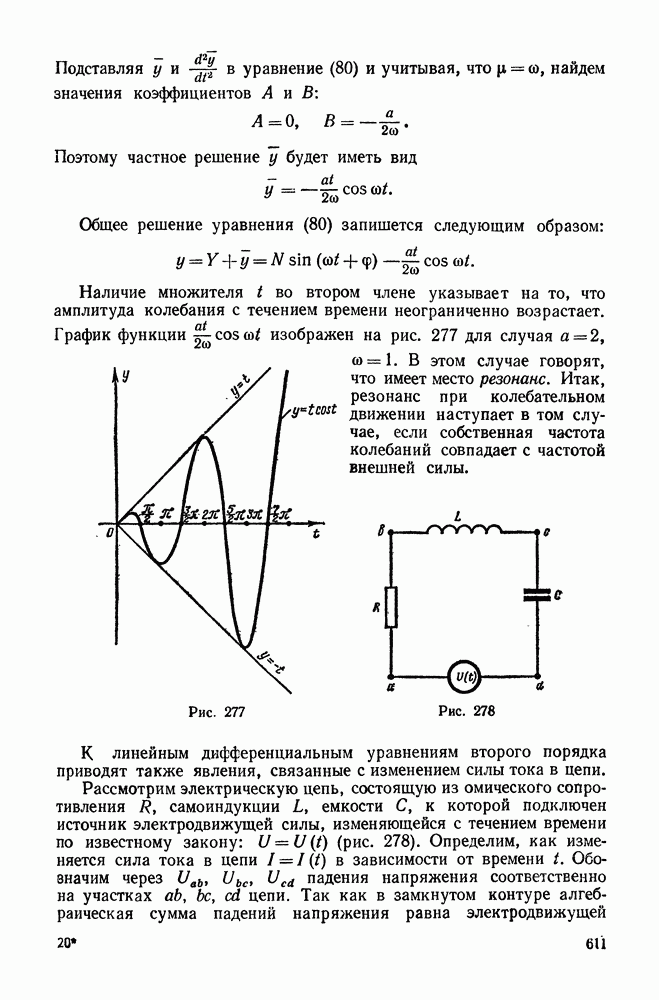
- 3. Приложение линейных дифференциальных уравнений второго порядка к изучению механических и электрических колебаний
- § 5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
- 2. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами
- § 6. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ
- § 7. ПОНЯТИЕ О СИСТЕМАХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 2. Системы линейных дифференциальных уравнений с постоянными коэффициентами
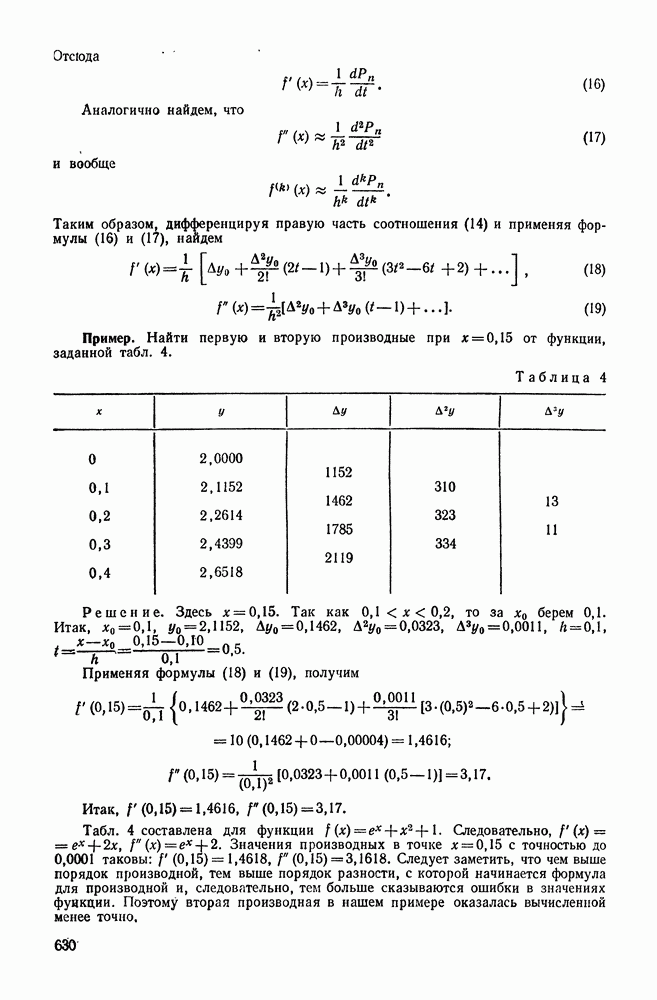
- ПРИЛОЖЕНИЕ 1. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА
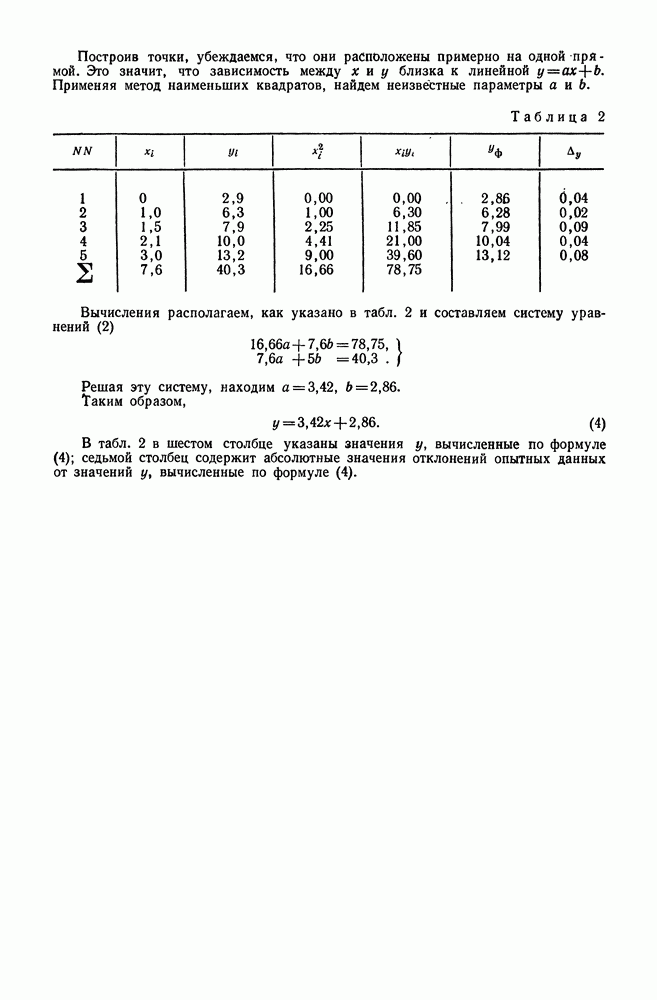
- ПРИЛОЖЕНИЕ 2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ