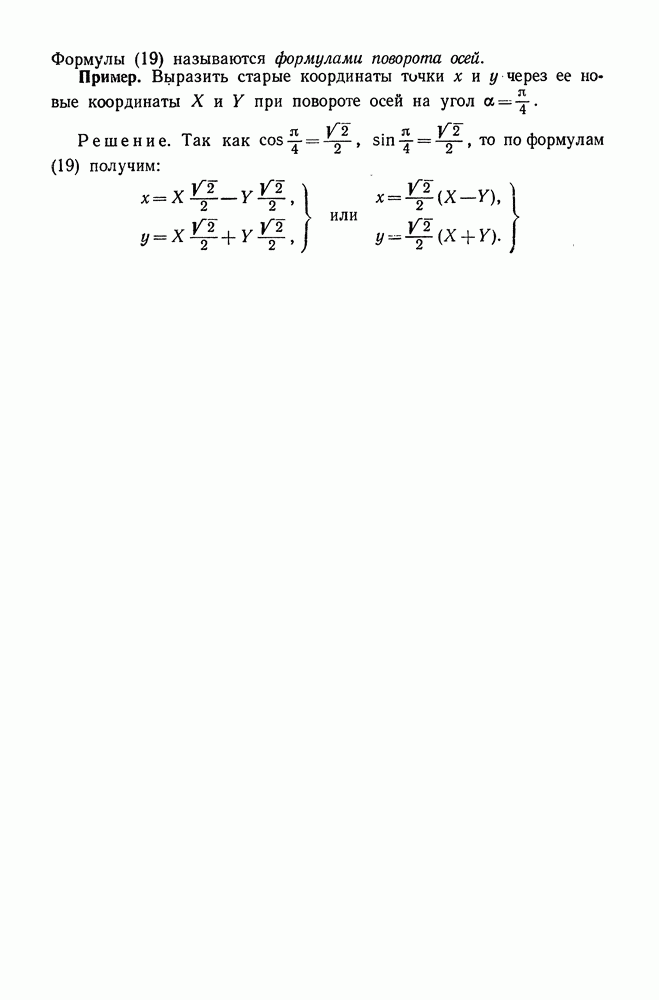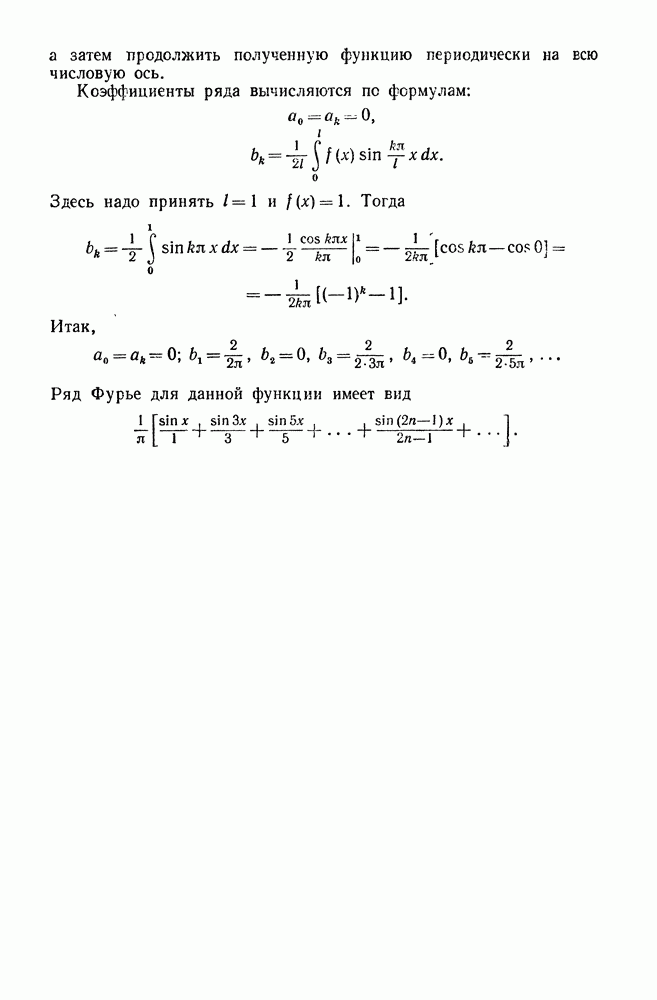| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
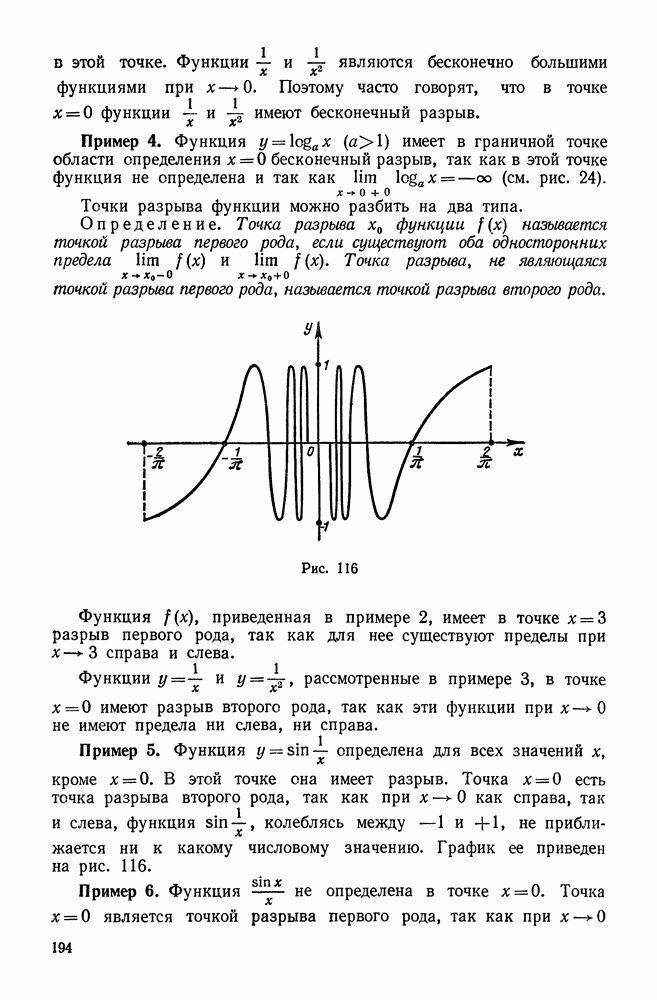
116
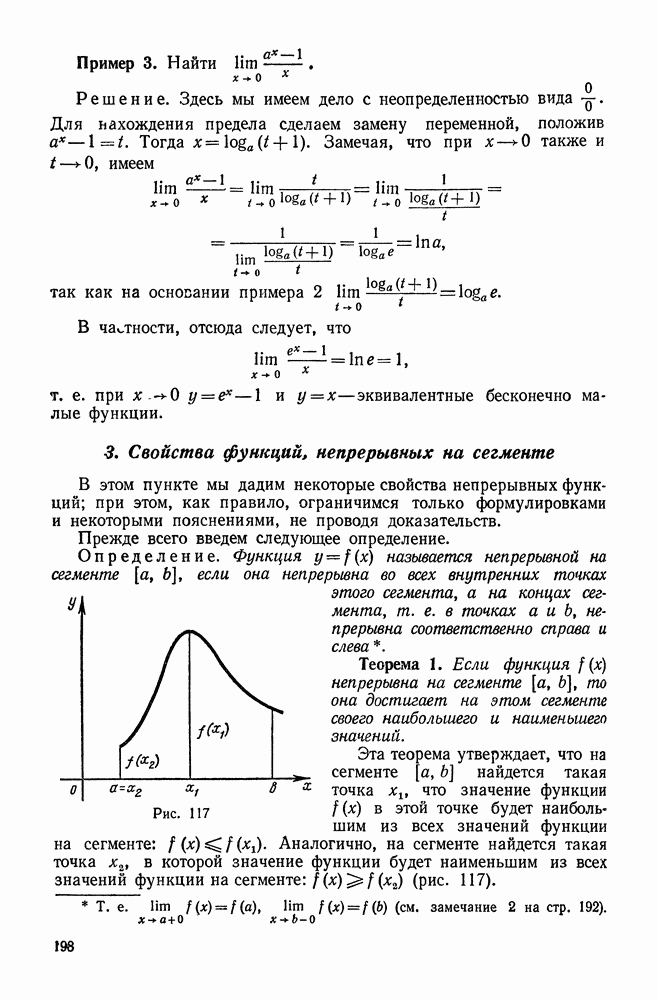
117
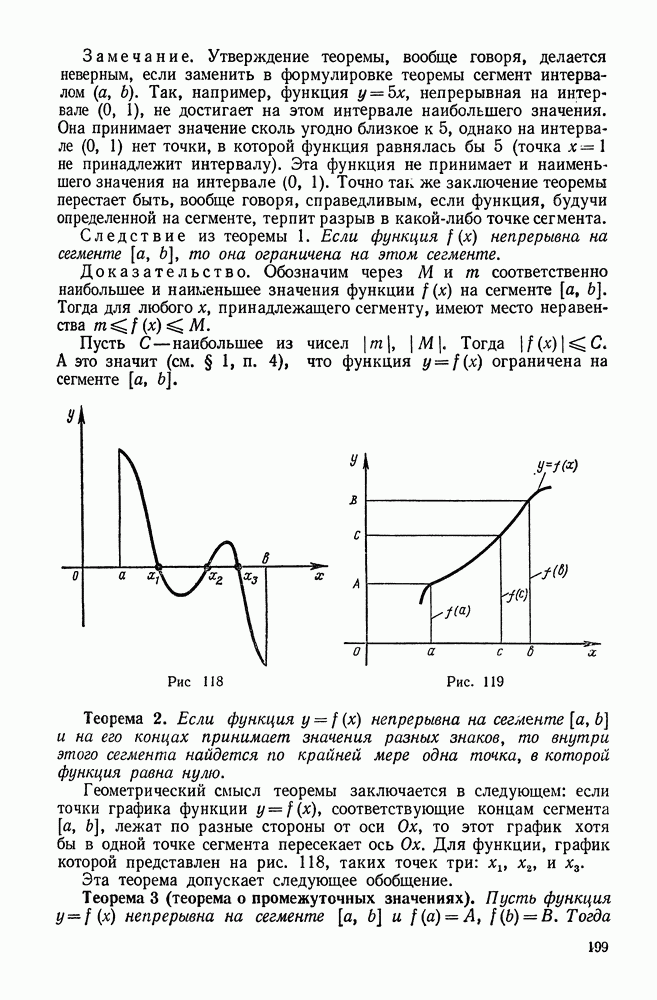
118
119
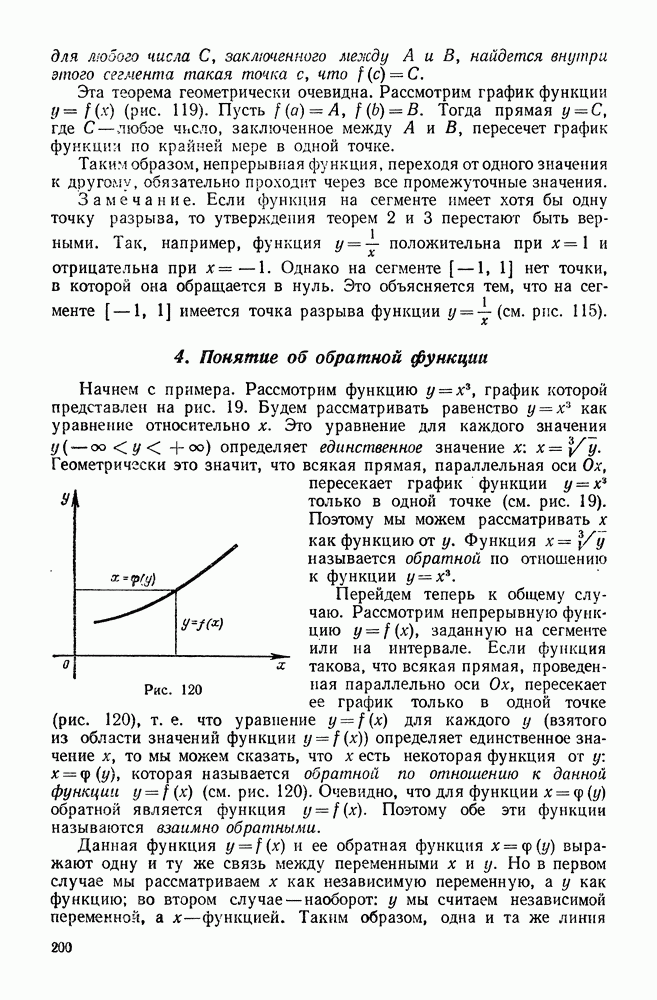
120
121
122
123
124
125
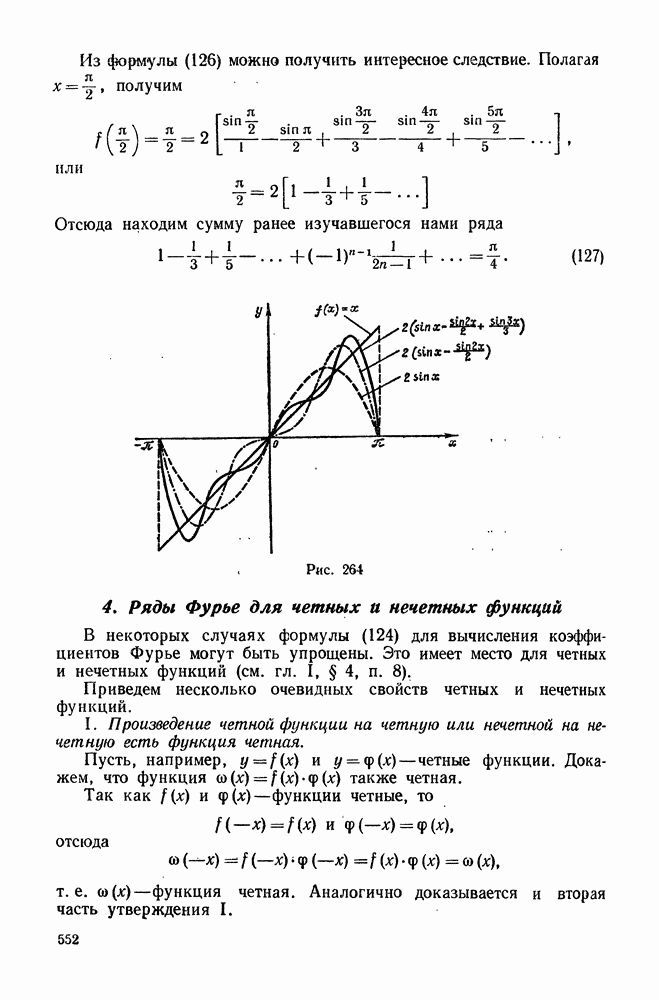
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
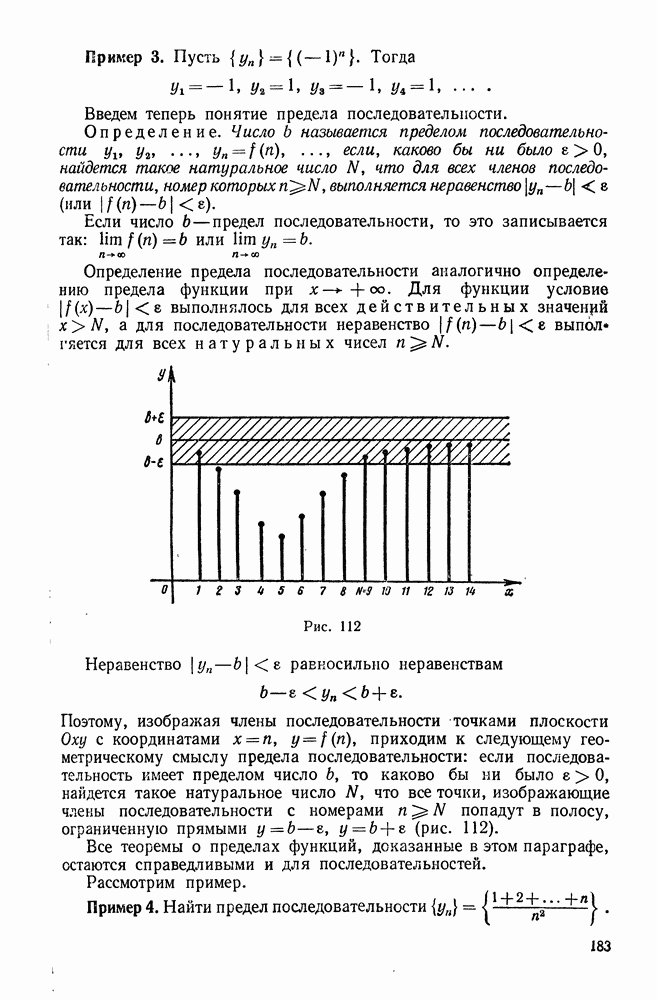
183
184
185
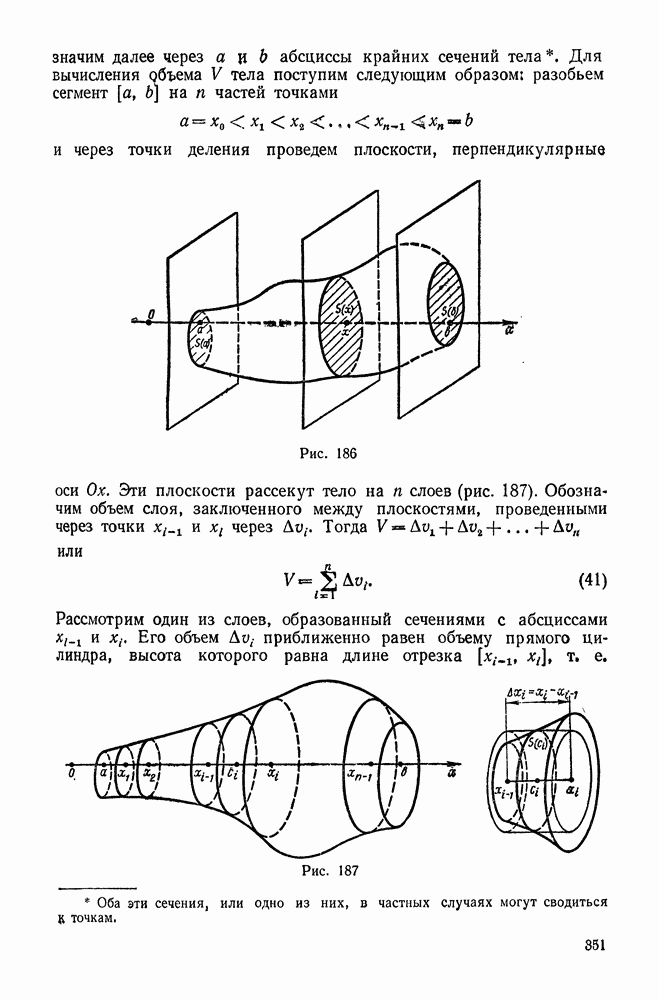
186
187
188
189
190
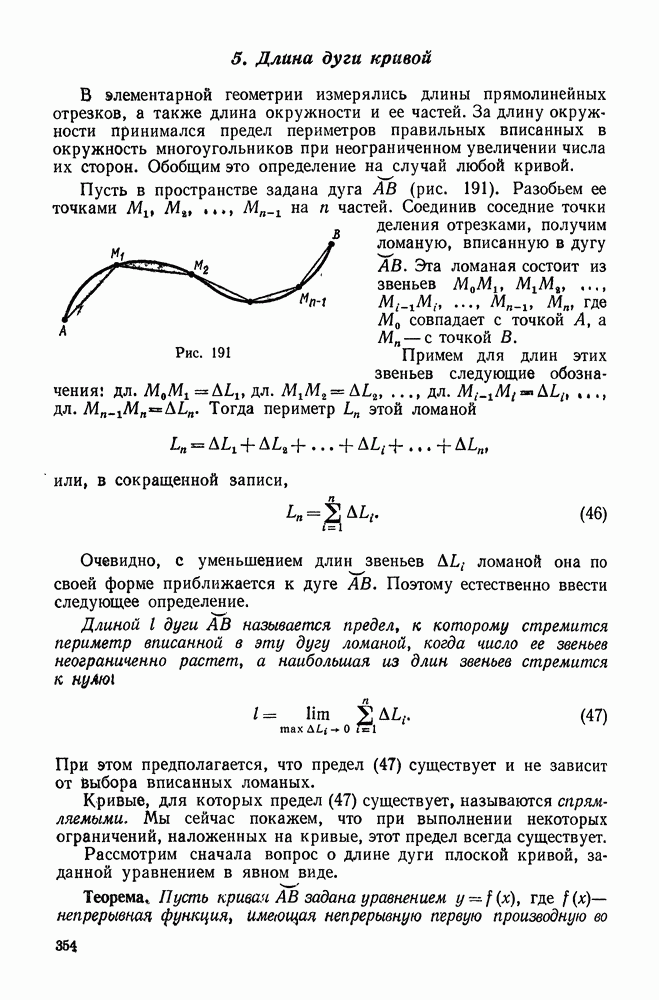
191
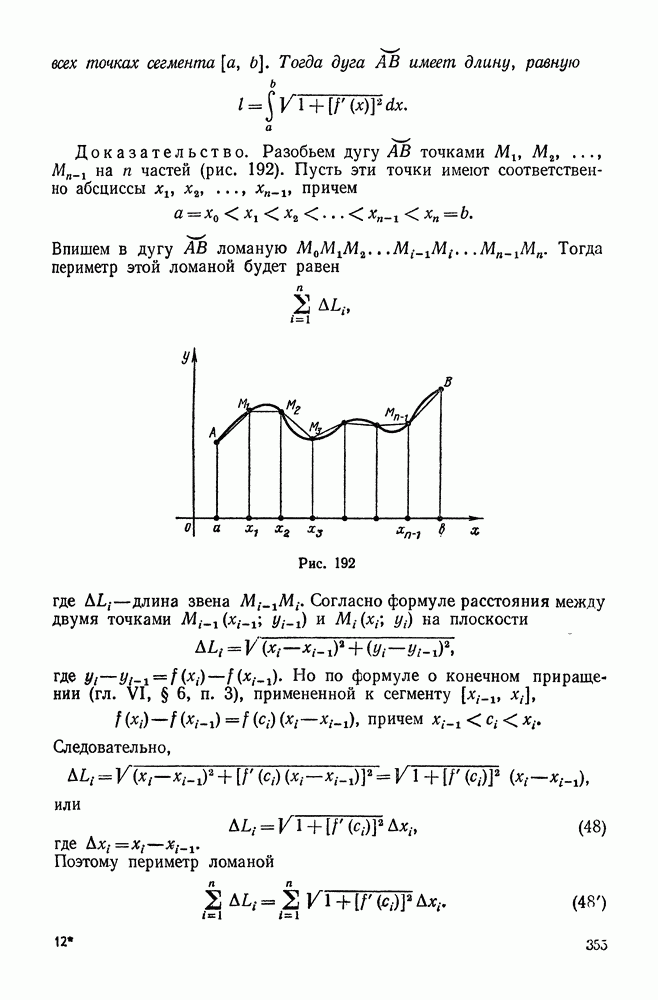
192
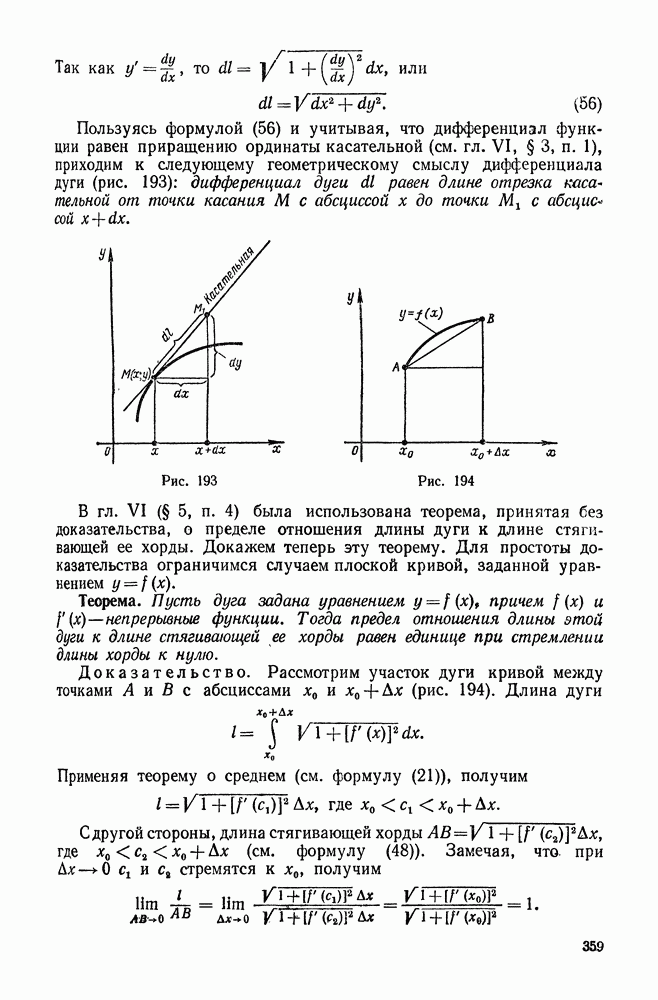
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
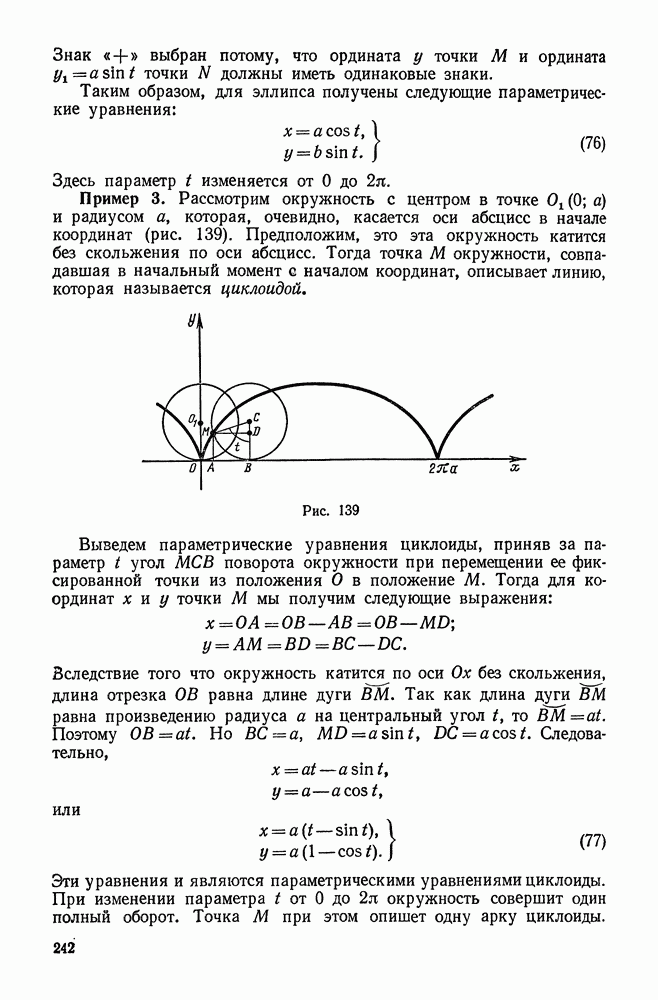
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
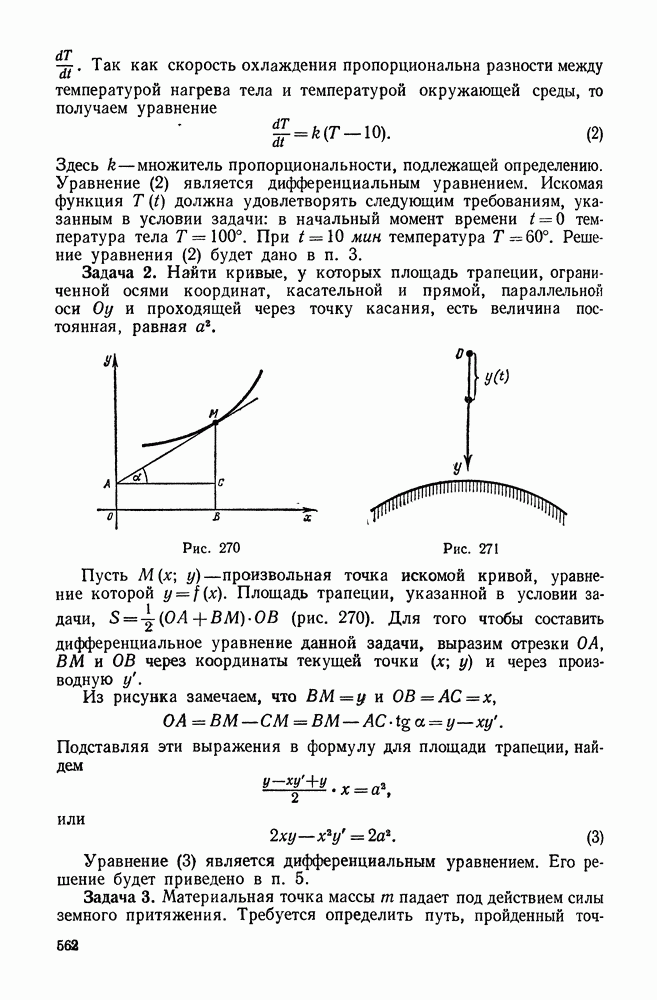
270
271
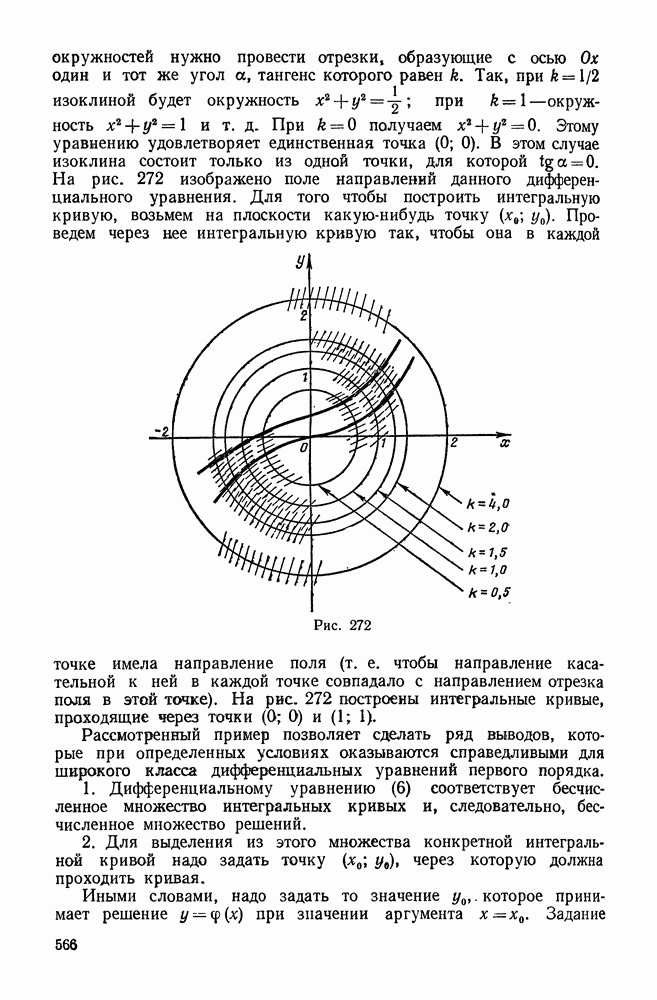
272
273
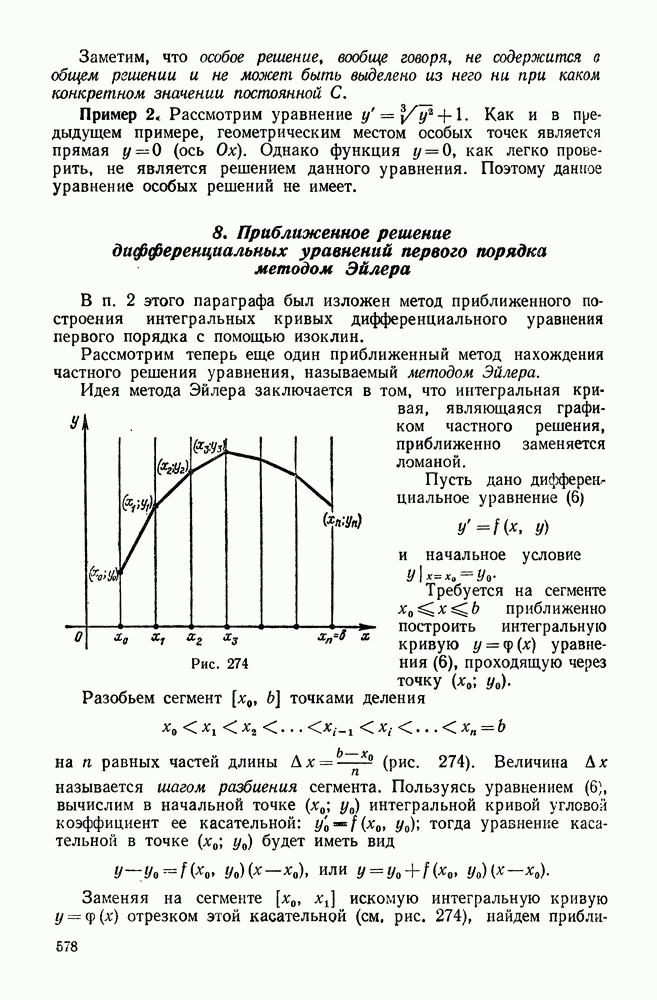
274
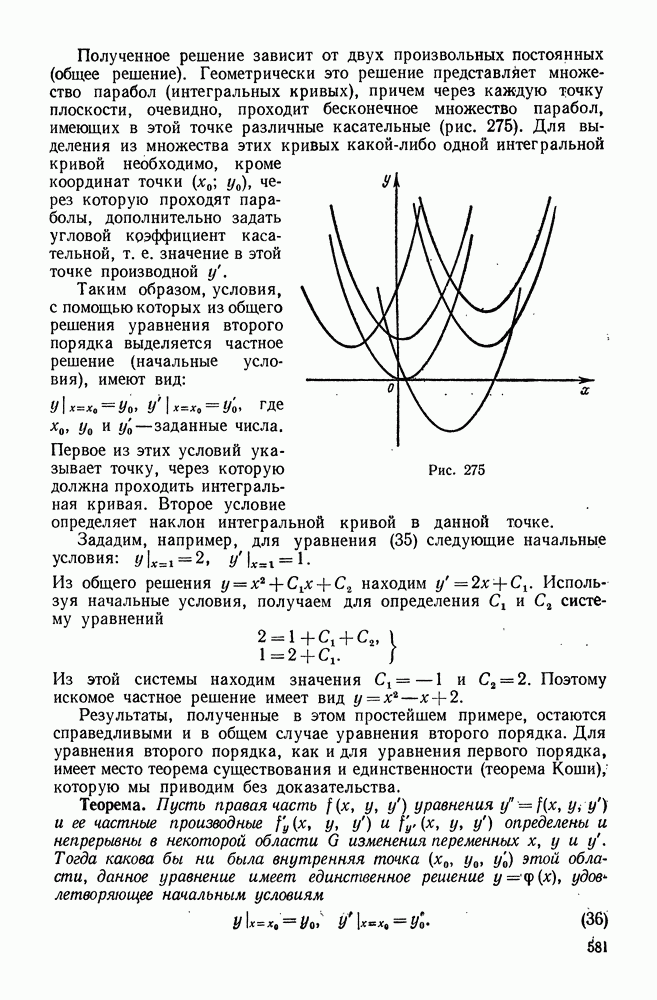
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
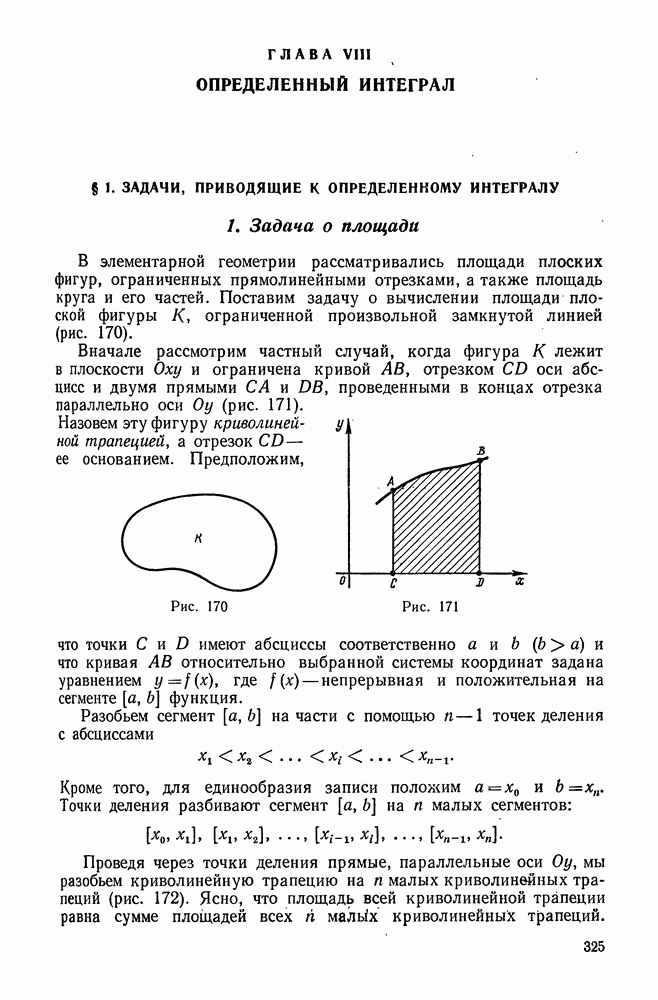
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
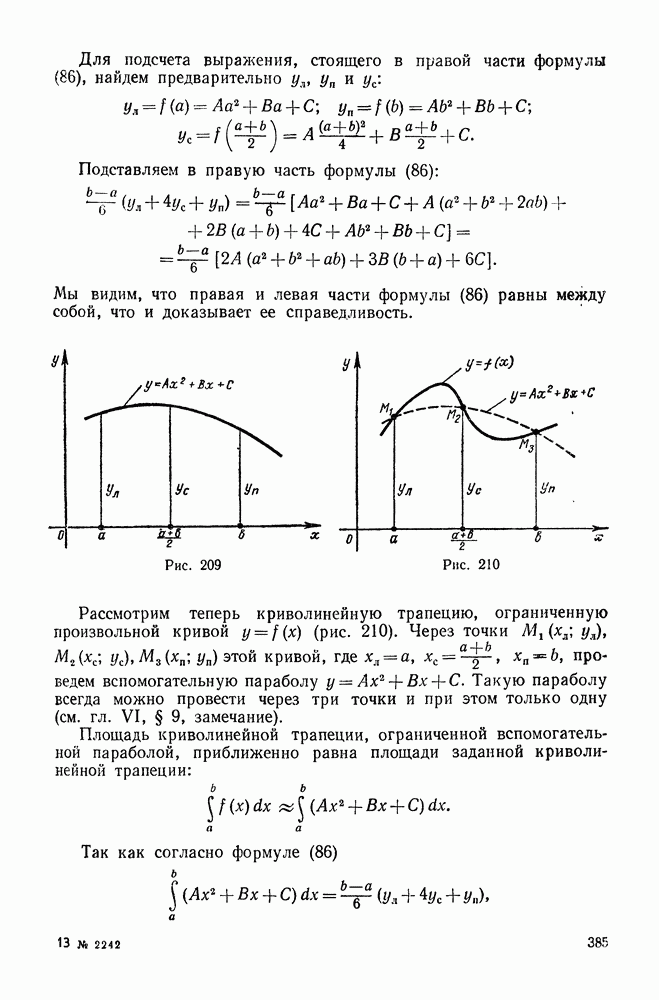
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
430
431
432
433
434
435
436
437
438
439
440
441
442
443
444
445
446
447
448
449
450
451
452
453
454
455
456
457
458
459
460
461
462
463
464
465
466
467
468
469
470
471
472
473
474
475
476
477
478
479
480
481
482
483
484
485
486
487
488
489
490
491
492
493
494
495
496
497
498
499
500
501
502
503
504
505
506
507
508
509
510
511
512
513
514
515
516
517
518
519
520
521
522
523
524
525
526
527
528
529
530
531
532
533
534
535
536
537
538
539
540
541
542
543
544
545
546
547
548
549
550
551
552
553
554
555
556
557
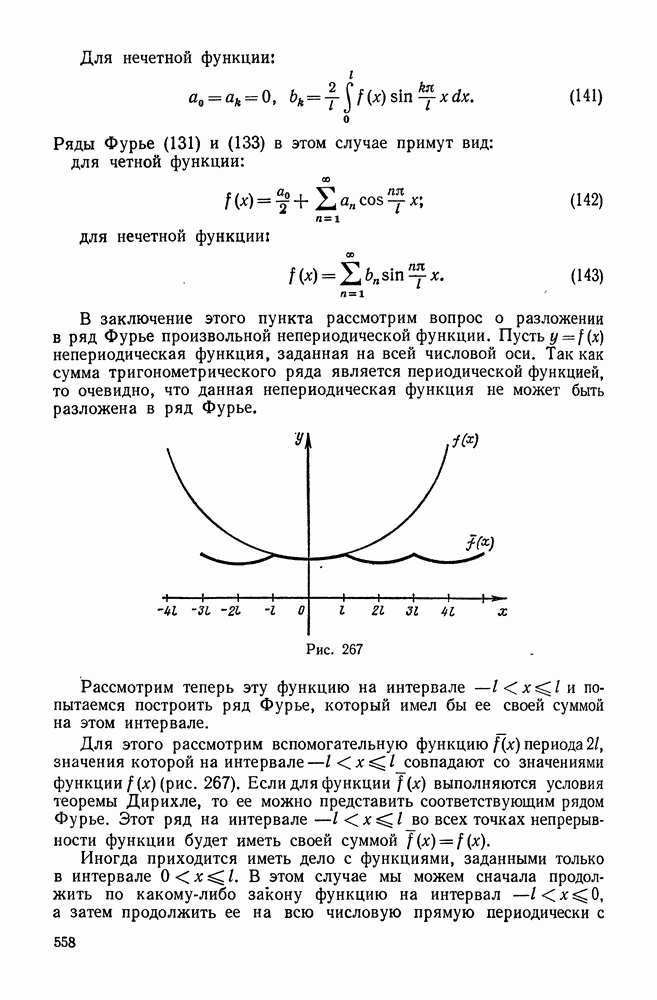
558
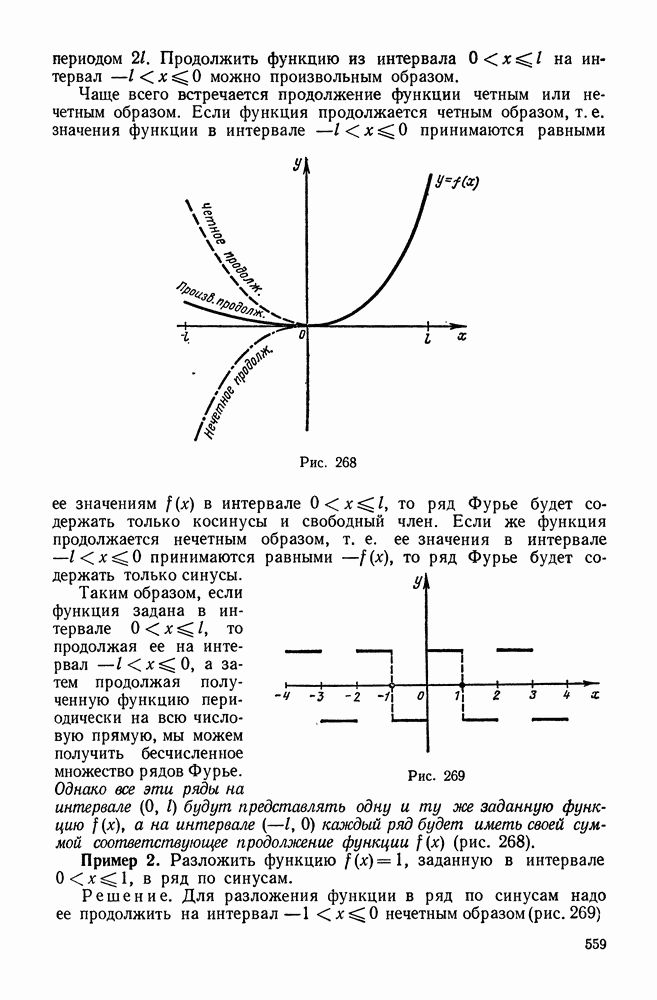
559
560
561
562
563
564
565
566
567
568
569
570
571
572
573
574
575
576
577
578
579
580
581
582
583
584
585
586
587
588
589
590
591
592
593
594
595
596
597
598
599
600
601
602
603
604
605
606
607
608
609
610
611
612
613
614
615
616
617
618
619
620
621
622
623
624
625
626
627
628
629
630
631
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
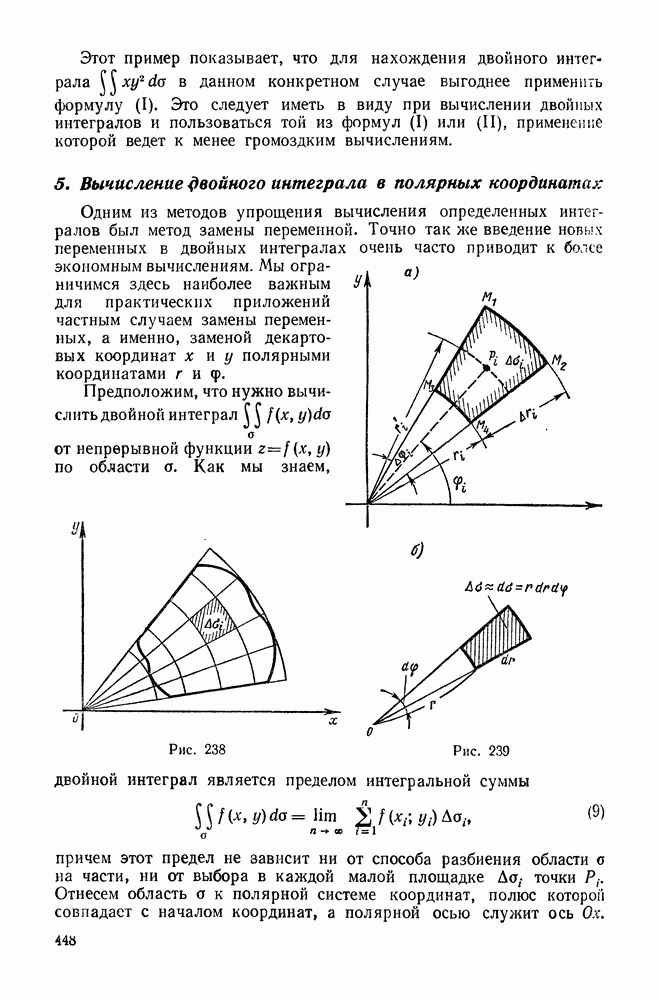
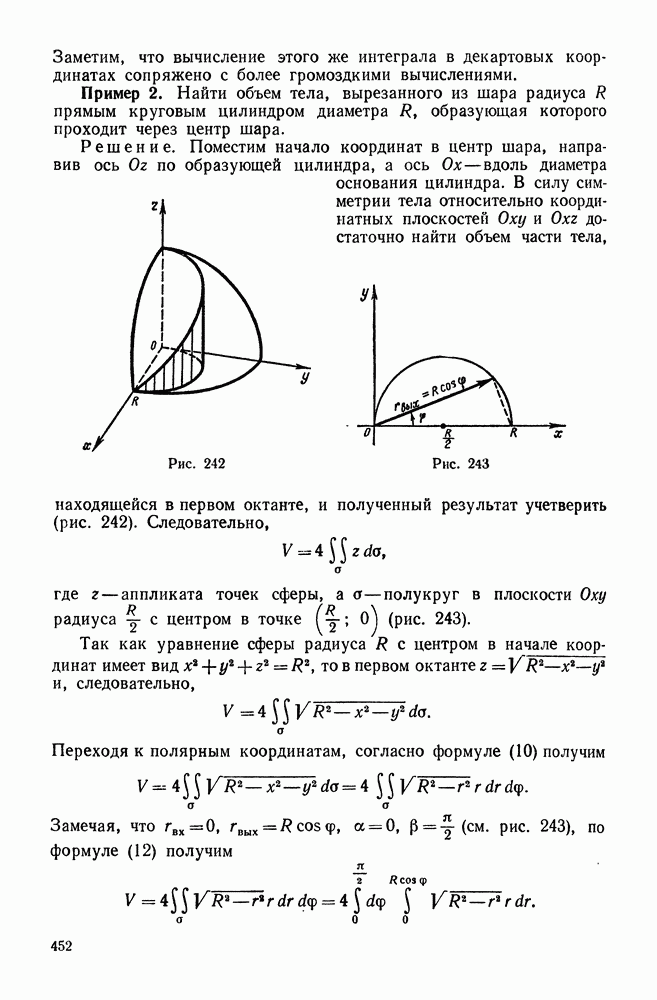
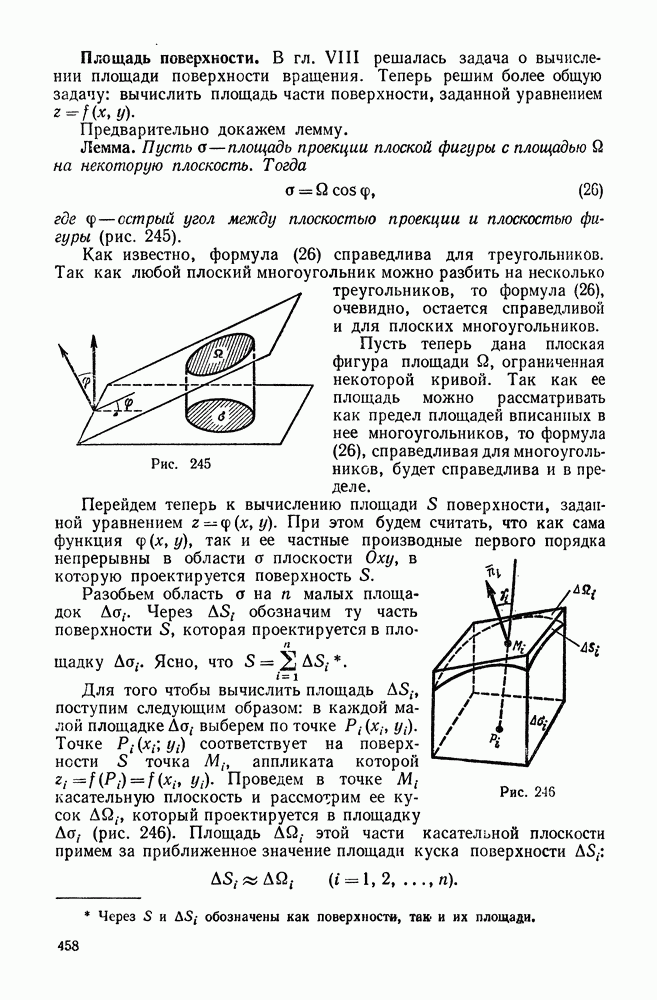
4. Вычисление двойного интеграла в декартовых координатах
Вычисление двойного интеграла как предела интегральной суммы, так же как и в случае определенного интеграла, связано обычно с большими трудностями. Чтобы их избежать, вычисление двойного интеграла сводят к последовательному вычислению двух определенных интегралов. Покажем, как это делается. Для простоты при выводе ограничимся случаем, когда в области интегрирования а подынтегральная функция  . Такое предположение позволяет нам рассматривать двойной интеграл как объем цилиндрического тела.
. Такое предположение позволяет нам рассматривать двойной интеграл как объем цилиндрического тела.
Итак, требуется вычислить двойной интеграл  от непрерывной функции
от непрерывной функции  .
.
Предположим сперва, что область интегрирования а ограничена двумя непрерывными кривыми  и двумя прямыми
и двумя прямыми  причем для всех значений
причем для всех значений  заключенных между а и
заключенных между а и  имеет место неравенство
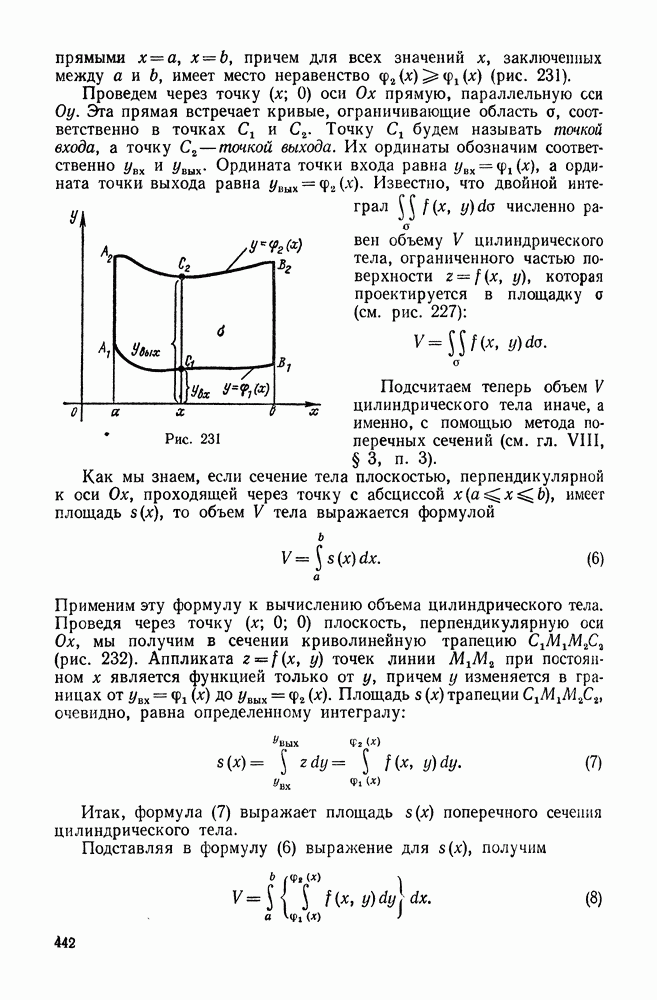
имеет место неравенство  (рис. 231).
(рис. 231).
Проведем через точку  оси
оси  прямую, параллельную
прямую, параллельную  Эта прямая встречает кривые, ограничивающие область а, соответственно в точках
Эта прямая встречает кривые, ограничивающие область а, соответственно в точках  Точку
Точку  будем называть точкой входа, а точку
будем называть точкой входа, а точку  — точкой выхода. Их ординаты обозначим соответственно
— точкой выхода. Их ординаты обозначим соответственно  и увых. Ордината точки входа равна
и увых. Ордината точки входа равна  а ордината точки выхода равна
а ордината точки выхода равна  Известно, что двойной интеграл
Известно, что двойной интеграл  численно равен объему V цилиндрического тела, ограниченного частью поверхности
численно равен объему V цилиндрического тела, ограниченного частью поверхности  , которая проектируется в площадку а (см. рис. 227):
, которая проектируется в площадку а (см. рис. 227):


Рис. 231
Подсчитаем теперь объем У цилиндрического тела иначе, а именно, с помощью метода поперечных сечений (см. гл. VIII, § 3, п. 3).
Как мы знаем, если сечение тела плоскостью, перпендикулярной к оси Ох, проходящей через точку с абсциссой  имеет площадь
имеет площадь  , то объем V тела выражается формулой
, то объем V тела выражается формулой

Применим эту формулу к вычислению объема цилиндрического тела. Проведя через точку  плоскость, перпендикулярную оси
плоскость, перпендикулярную оси  мы получим в сечении криволинейную трапецию
мы получим в сечении криволинейную трапецию  (рис. 232). Аппликата
(рис. 232). Аппликата  точек линии МХМ при постоянном
точек линии МХМ при постоянном  является функцией только от
является функцией только от  причем у изменяется в границах от
причем у изменяется в границах от  до увых
до увых  Площадь
Площадь  трапеции очевидно, равна определенному интегралу:
трапеции очевидно, равна определенному интегралу:

Итак, формула (7) выражает площадь  поперечного сечения цилиндрического тела.
поперечного сечения цилиндрического тела.
Подставляя в формулу (6) выражение для  получим
получим

Но так как, с другой стороны, объем V цилиндрического тела равен двойному интегралу  то имеем
то имеем

или

Эта и есть искомая формула.

Рис. 232
Поясним смысл формулы (I). Для того чтобы вычислить двойной интеграл  нужно сперва вычислить определенный интеграл
нужно сперва вычислить определенный интеграл  считая
считая  постоянным (или, как говорят, вычислить внутренний интеграл).
постоянным (или, как говорят, вычислить внутренний интеграл).
Нижней границей интегрирования является ордината точки входа  а верхней границей интегрирования является ордината точки выхода увых
а верхней границей интегрирования является ордината точки выхода увых  соответствующие данному фиксированному значению
соответствующие данному фиксированному значению  Результат вычисления этого интеграла является функцией только от
Результат вычисления этого интеграла является функцией только от  Интегрируя теперь эту функцию в границах от а до b, получим значение двойного интеграла. Сделаем следующие замечания.
Интегрируя теперь эту функцию в границах от а до b, получим значение двойного интеграла. Сделаем следующие замечания.
Замечание 1.
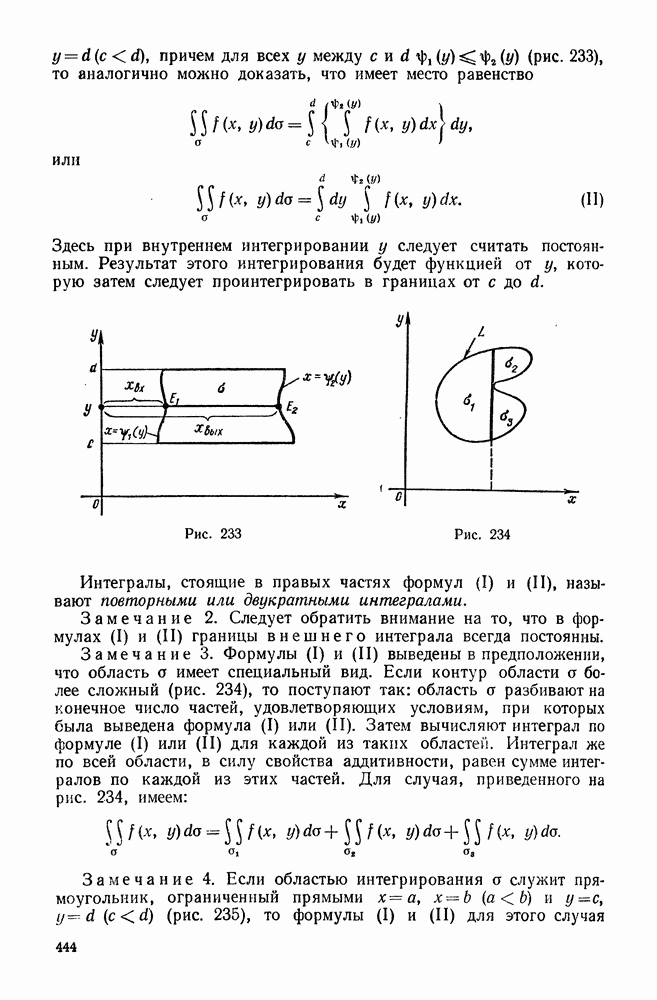
Если область о ограничена двумя кривыми  двумя горизонтальными прямыми
двумя горизонтальными прямыми  причем для всех у между
причем для всех у между  (рис 233), то аналогично можно доказать, что имеет место равенство
(рис 233), то аналогично можно доказать, что имеет место равенство

или

Здесь при внутреннем интегрировании у следует считать постоянным. Результат этого интегрирования будет функцией от у, которую затем следует проинтегрировать в границах от с до d.

Рис. 233

Рис. 234
Интегралы, стоящие в правых частях формул (I) и (II), называют повторными или двукратными интегралами.
Замечание 2. Следует обратить внимание на то, что в формулах (I) и (II) границы внешнего интеграла всегда постоянны.
Замечание 3. Формулы (I) и (II) выведены в предположении, что область а имеет специальный вид. Если контур области а более сложный (рис. 234), то поступают так: область  разбивают на конечное число частей, удовлетворяющих условиям, при которых была выведена формула (I) или (II). Затем вычисляют интеграл по формуле (I) или (II) для каждой из таких областей. Интеграл же по всей области, в силу свойства аддитивности, равен сумме интегралов по каждой из этих частей. Для случая, приведенного на рис. 234, имеем:
разбивают на конечное число частей, удовлетворяющих условиям, при которых была выведена формула (I) или (II). Затем вычисляют интеграл по формуле (I) или (II) для каждой из таких областей. Интеграл же по всей области, в силу свойства аддитивности, равен сумме интегралов по каждой из этих частей. Для случая, приведенного на рис. 234, имеем:

Замечание 4.
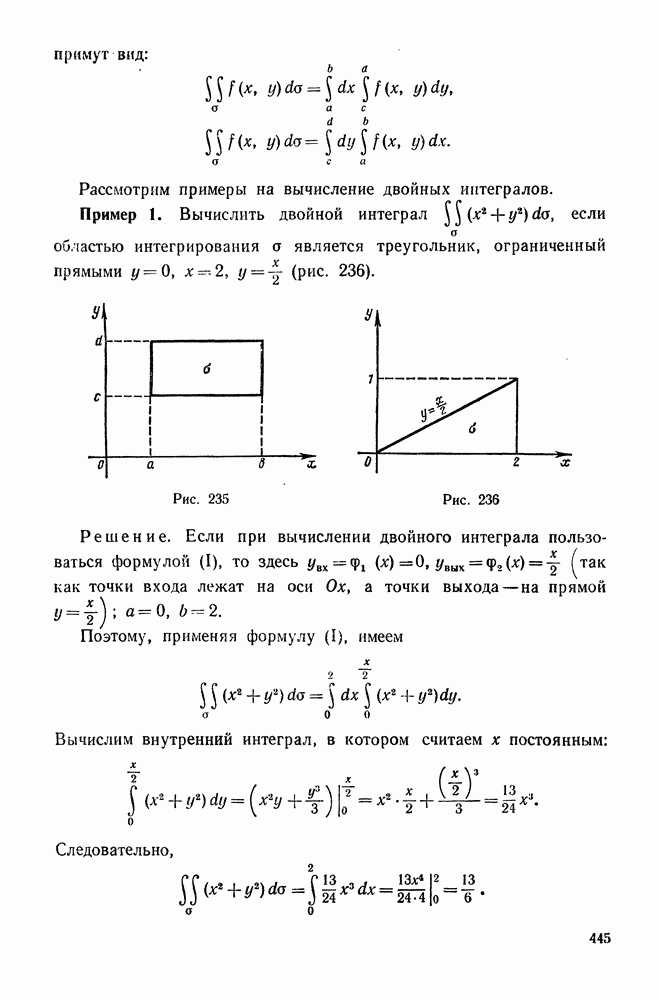
Если областью интегрирования а служит прямоугольник, ограниченный прямыми  (рис. 235), то формулы (I) и (II) для этого случая примут вид:
(рис. 235), то формулы (I) и (II) для этого случая примут вид:

Рассмотрим примеры на вычисление двойных интегралов. Пример 1. Вычислить двойной интеграл  если областью интегрирования а является треугольник, ограниченный прямыми
если областью интегрирования а является треугольник, ограниченный прямыми  (рис. 236).
(рис. 236).

Рис. 235

Рис. 236
Решение. Если при вычислении двойного интеграла пользоваться формулой (I), то здесь  как точки входа лежат на оси Ох, а точки выхода — на прямой
как точки входа лежат на оси Ох, а точки выхода — на прямой 
Поэтому, применяя формулу (I), имеем

Вычислим внутренний интеграл, в котором считаем  постоянным:
постоянным:

Следовательно,

Применяя для вычисления двойного интеграла  формулу (II), получим, конечно, тот же результат. Замечая, что в этом случае
формулу (II), получим, конечно, тот же результат. Замечая, что в этом случае  (так как точка входа лежит на прямой
(так как точка входа лежит на прямой  или
или  , а точка выхода на прямой
, а точка выхода на прямой  (см. рис. 236), получим
(см. рис. 236), получим

Так как

то

Если принять во внимание геометрический смысл двойного интеграла, то  дает объем V цилиндрического тела, ограниченного сверху частью параболоида вращения
дает объем V цилиндрического тела, ограниченного сверху частью параболоида вращения  которая проектируется на плоскость
которая проектируется на плоскость  в треугольник
в треугольник  .
.

Рис. 237
Пример 2. Вычислить двойной интеграл  если область интегрирсвания а ограничена линиями
если область интегрирсвания а ограничена линиями  (рис. 237).
(рис. 237).
Решение. Применим для вычисления двойного интеграла формулу (I). Здесь  . Поэтому
. Поэтому

Вычислим внутренний интеграл, в котором считаем я постоянным:

Следовательно,

Если при вычислении двойного интеграла  пользоваться формулой (II), то придется область интегрирования а разбить на две части
пользоваться формулой (II), то придется область интегрирования а разбить на две части  и (см. рис. 237), так как линия ОАВ, на которой расположены точки выхода на отдельных участках, задается различными уравнениями. По свойству аддитивности
и (см. рис. 237), так как линия ОАВ, на которой расположены точки выхода на отдельных участках, задается различными уравнениями. По свойству аддитивности

Применяем формулу (II) к каждому из интегралов, стоящих в правой части последнего равенства:

так как  Вычисляем внутренний интеграл, помня, что у — постоянно:
Вычисляем внутренний интеграл, помня, что у — постоянно:

Следовательно,

Аналогично находим

Следовательно,

Таким образом, окончательно,

Этот пример показывает, что для нахождения двойного интеграла  в данном конкретном случае выгоднее применить формулу (I). Это следует иметь в виду при вычислении двойных интегралов и пользоваться той из формул (I) или (II), применение которой ведет к менее громоздким вычислениям.
в данном конкретном случае выгоднее применить формулу (I). Это следует иметь в виду при вычислении двойных интегралов и пользоваться той из формул (I) или (II), применение которой ведет к менее громоздким вычислениям.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. МЕТОД КООРДИНАТ. ПОНЯТИЕ ФУНКЦИИ
- § 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КООРДИНАТЫ ТОЧКИ НА ПРЯМОЙ
- 2. Геометрическое изображение действительных чисел. Координаты точки на прямой
- 3. Абсолютная величина действительного числа
- 4. Расстояние между двумя точками на прямой
- § 2. КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
- 2. Расстояние между двумя точками на плоскости
- 3. Деление отрезка в данном отношении
- 4. Координаты точки в пространстве
- 5. Расстояние между двумя точками в пространстве
- § 3. УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ
- 2. Полярные координаты
- 3. Зависимость между декартовыми и полярными координатами
- § 4. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ
- 2. Понятие функции
- 3. График функции
- 4. Способы задания функций
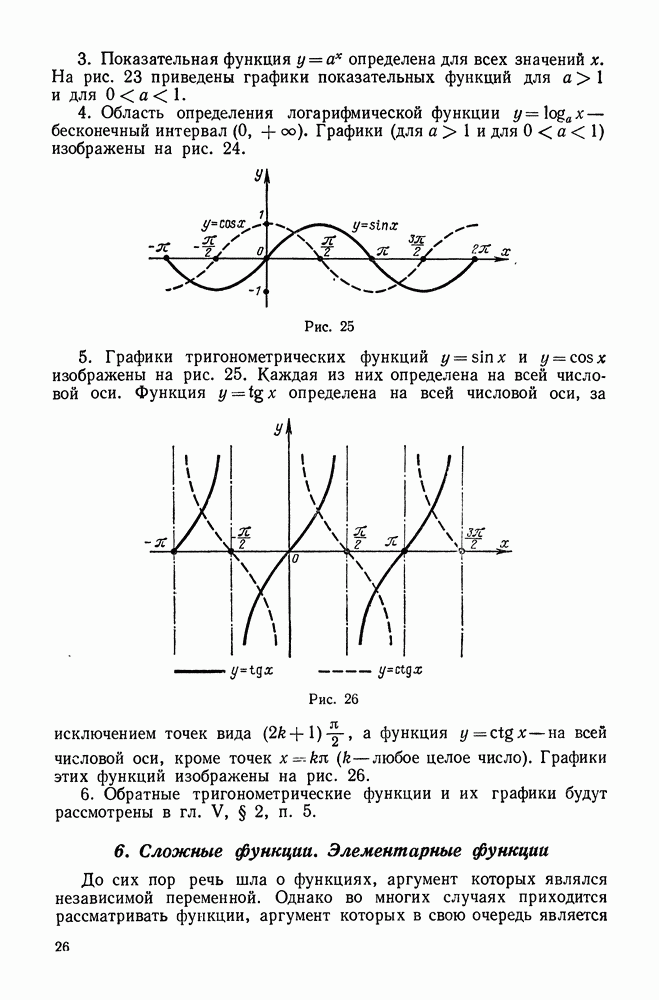
- 5. Основные элементарные функции и их графики
- 6. Сложные функции. Элементарные функции
- 7. Целые и дробно-рациональные функции
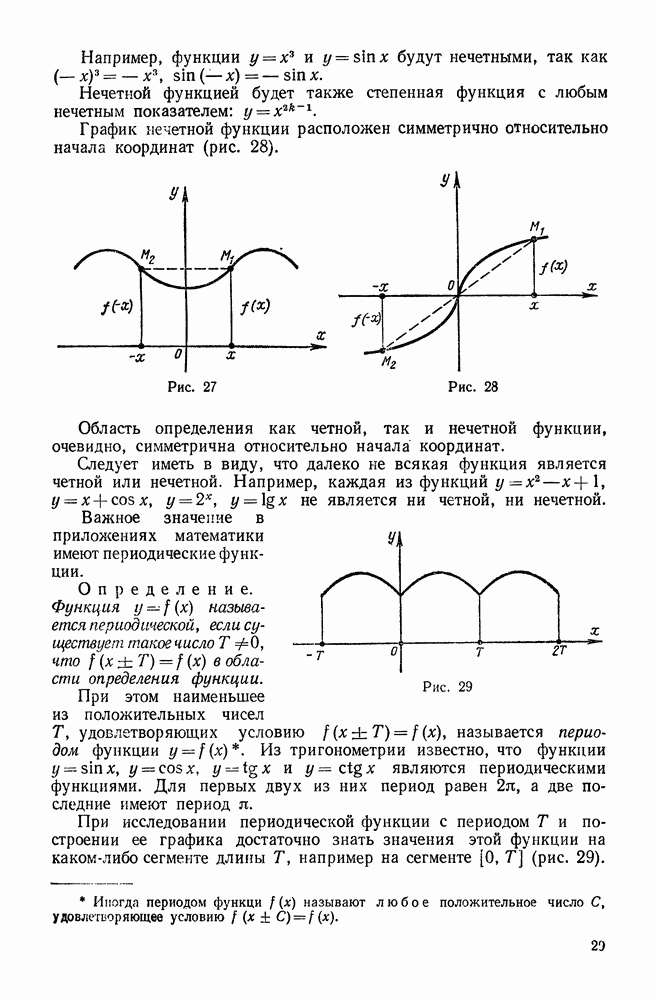
- 8. Функции четные и нечетные. Периодические функции
- § 5. УРАВНЕНИЕ ЛИНИИ
- 2. Нахождение уравнения линии по ее геометрическим свойствам
- § 6 ПРЕОБРАЗОВАНИЕ КООРДИНАТ
- 2. Поворот осей координат
- ГЛАВА II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- § 1. ПРЯМАЯ
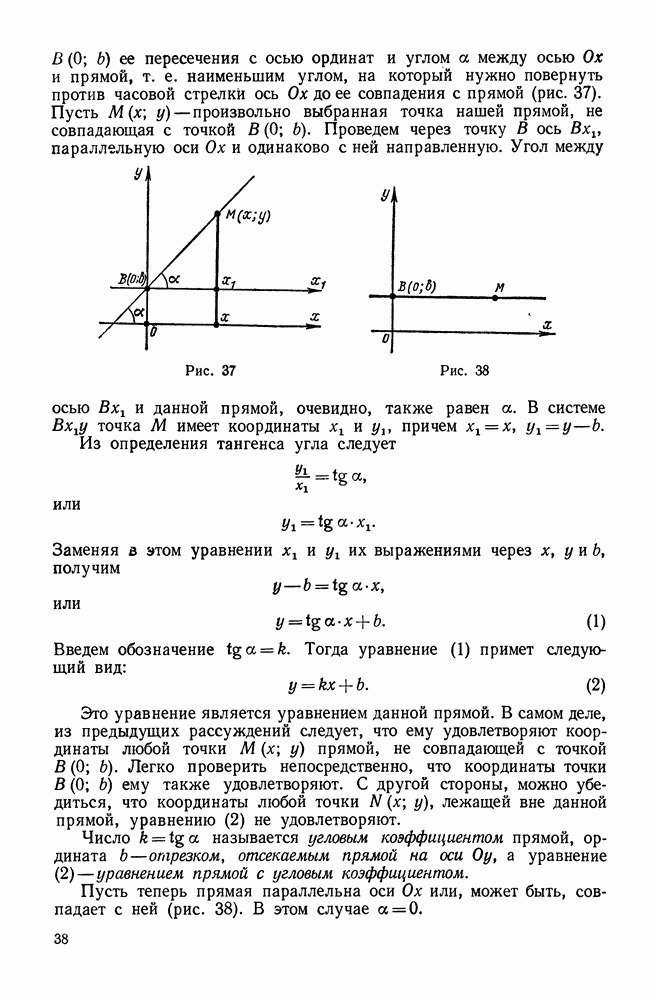
- 2. Уравнение прямой с угловым коэффициентом
- 3. Уравнение прямой, параллельной оси ординат
- 4. Общее уравнение прямой и его частные случаи
- 5. Точка пересечения прямых. Построение прямой по ее уравнению
- 6. Вычисление угла между двумя прямыми. Условия параллельности и перпендикулярности двух прямых
- 7. Уравнение прямой, проходящей через данную точку в заданном направлении
- 8. Пучок прямых
- 9. Уравнение прямой, проходящей через две данные точки
- 10. Расстояние от точки до прямой
- § 2. КРИВЫЕ ВТОРОГО ПОРЯДКА
- 2. Окружность
- 3. Эллипс
- 4. Гипербола
- 5. Парабола
- 6. Окружность, эллипс, гипербола и парабола как конические сечения
- 7. Упрощение уравнения кривой второго порядка. График квадратного трехчлена
- 8. Уравнение равносторонней гиперболы, асимптоты которой приняты за оси координат
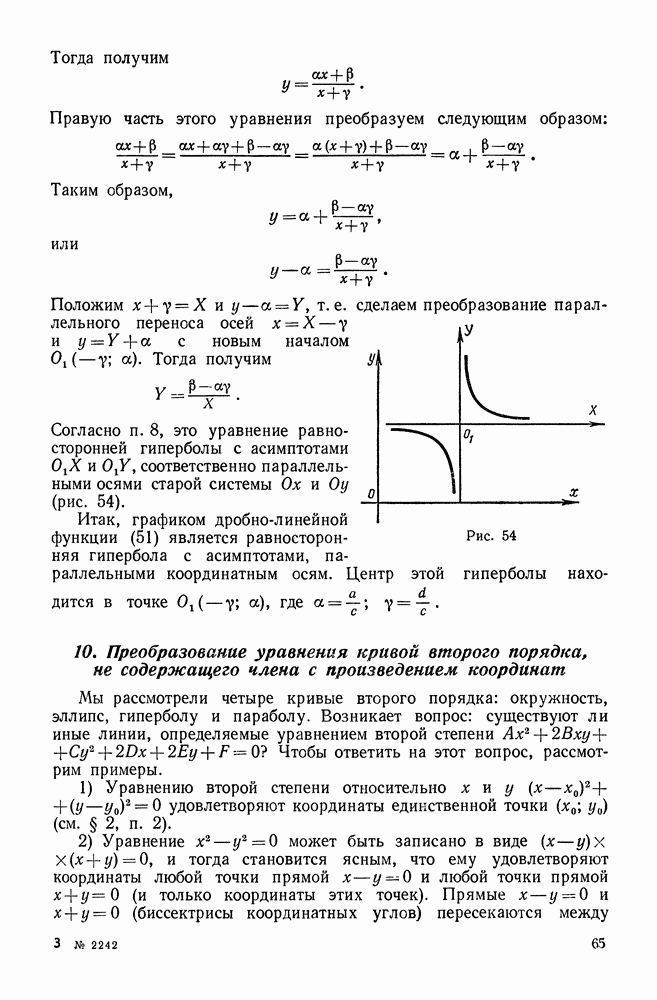
- 9. График дробно-линейной функции
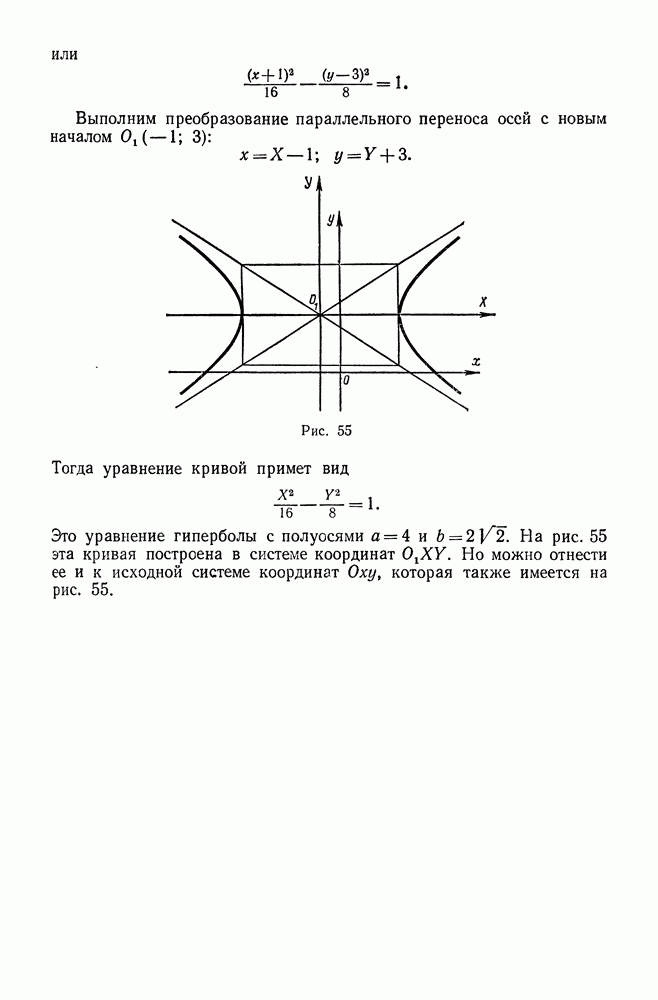
- 10. Преобразование уравнения кривой второго порядка, не содержащего члена с произведением координат
- ГЛАВА III. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ
- § 1. ЭЛЕМЕНТЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ
- 2. Определитель третьего порядка
- 3. Понятие об определителях высших порядков
- § 2. СИСТЕМЫ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ
- 2. Однородная система двух уравнений первой степени с тремя неизвестными
- 3. Система трех уравнений первой степени с тремя неизвестными
- 4. Однородная система трех уравнений первой степени с тремя неизвестными
- § 3. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- 2. Линейные операции над векторами
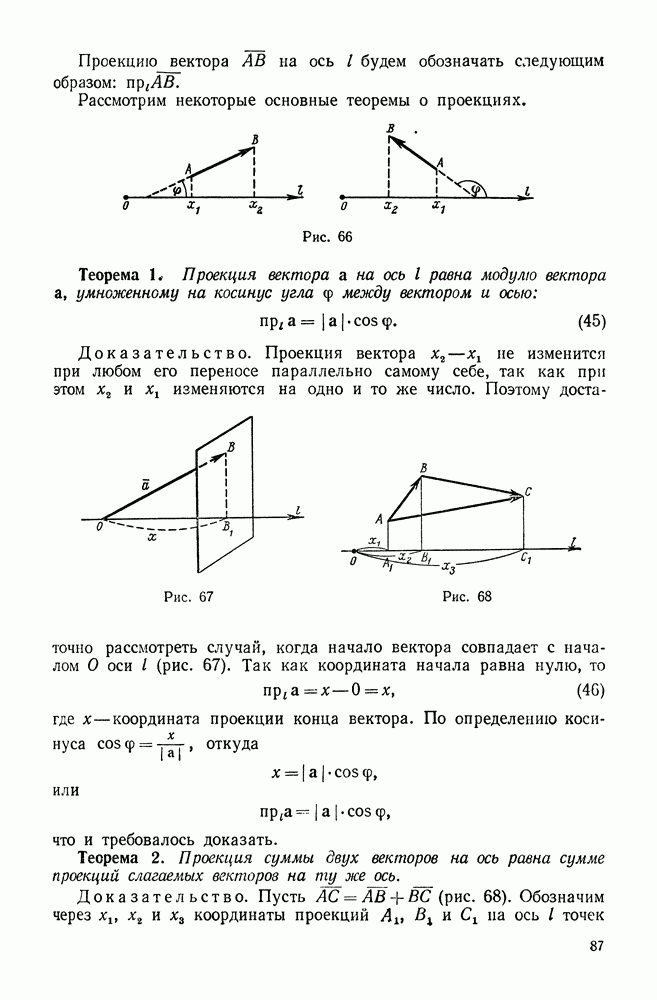
- 4. Проекция вектора на ось и составляются вектора по оси
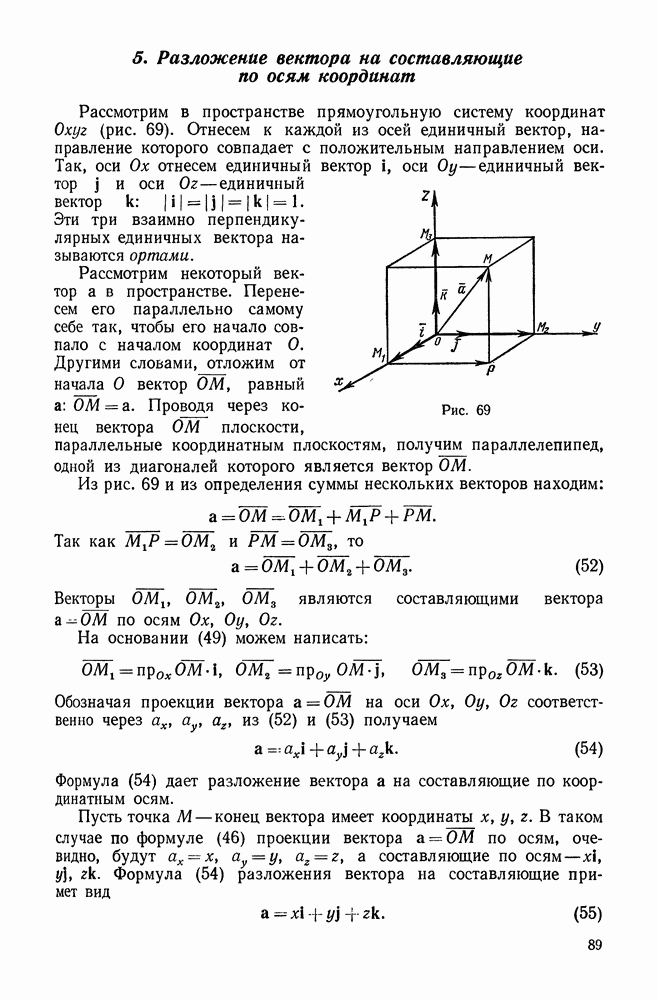
- 5. Разложение вектора на составляющие по осям координат
- 6. Направляющие косинусы вектора
- 7. Условие коллинеарности двух векторов
- 8. Скалярное произведение
- 9. Выражение скалярного произведения через проекции перемножаемых векторов
- 10. Косинус угла между двумя векторами
- 11. Векторное произведение
- 12. Выражение векторного произведения через проекции перемножаемых векторов
- 13. Смешанное произведение трех векторов
- 14. Геометрический смысл смешанного произведения
- 15. Условие компланарности трех векторов
- § 4. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 2. Равенство матриц. Действия над матрицами
- 3. Обратная матрица
- 4. Матричная запись и матричное решение системы уравнений первой степени
- § 5. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ
- 2. Преобразование координат
- 3. Приведение квадратичной формы к каноническому виду
- 4. Упрощение общего уравнения кривой второго порядка
- ГЛАВА IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- § 1. ПЛОСКОСТЬ
- 2. Нормальный вектор плоскости. Уравнение плоскости, проходящей через данную точку
- 3. Общее уравнение плоскости и его частные случаи
- 4. Построение плоскости по ее уравнению
- 5. Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей
- 6. Точка пересечения трех плоскостей
- § 2. ПРЯМАЯ В ПРОСТРАНСТВЕ
- 2. Общие уравнения прямой
- 3. Векторное уравнение прямой. Параметрические уравнения прямой
- 4. Канонические уравнения прямой
- 5. Уравнения прямой, проходящей через две точки
- 6. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых
- § 3. Прямая и плоскость в пространстве
- 2. Точка пересечения прямой с плоскостью
- 3. Расстояние от точки до плоскости
- 4. Пучок плоскостей
- § 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
- 2. Цилиндрические поверхности
- 3. Конические поверхности
- 4. Поверхность вращения
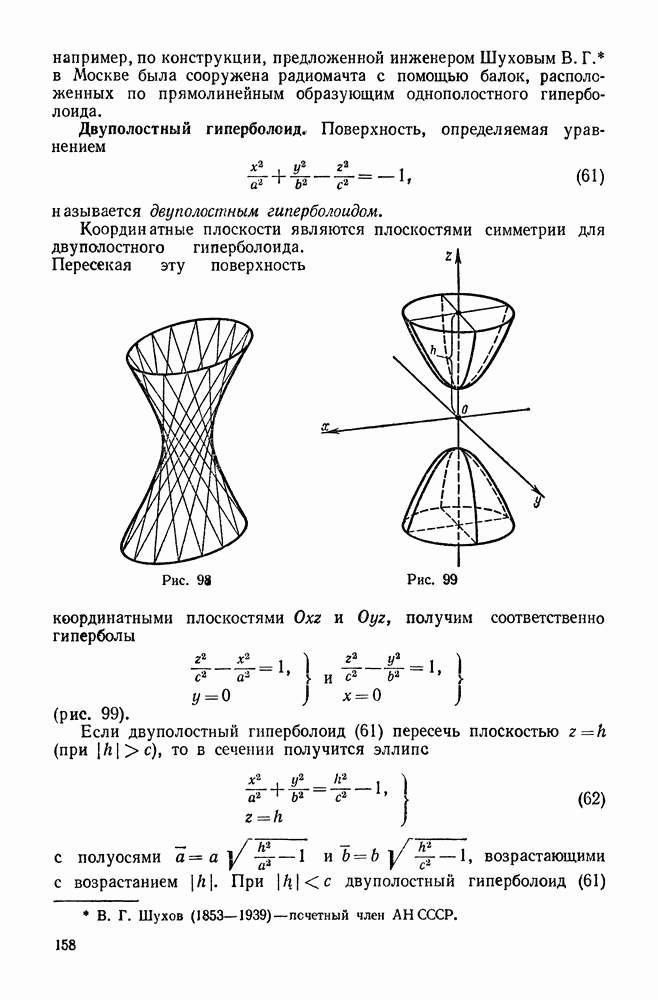
- 6. Гиперболоиды
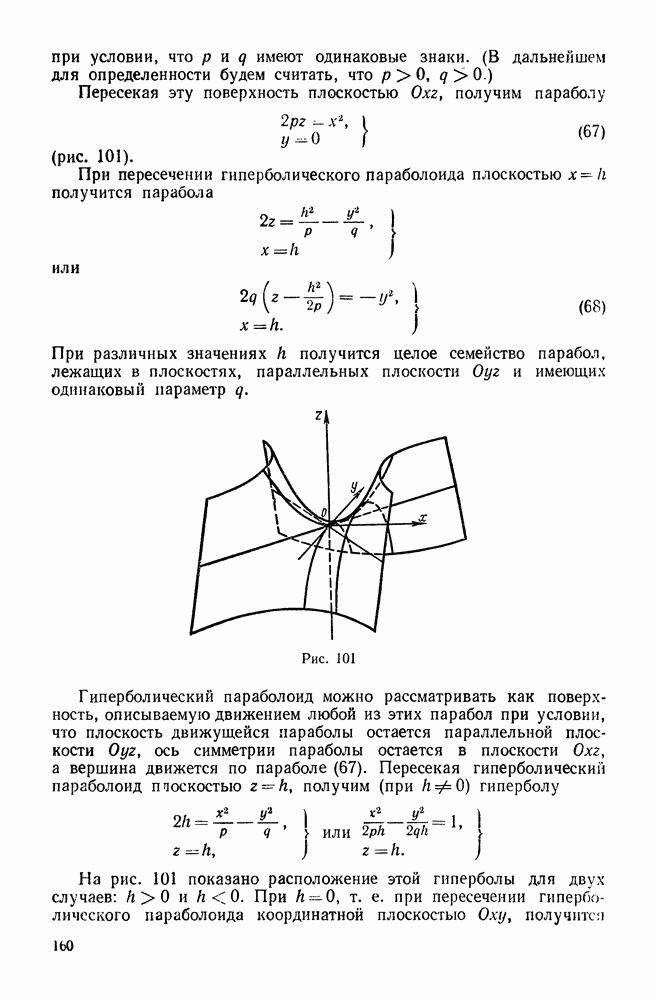
- 7. Параболоиды
- ГЛАВА V. ТЕОРИЯ ПРЕДЕЛОВ
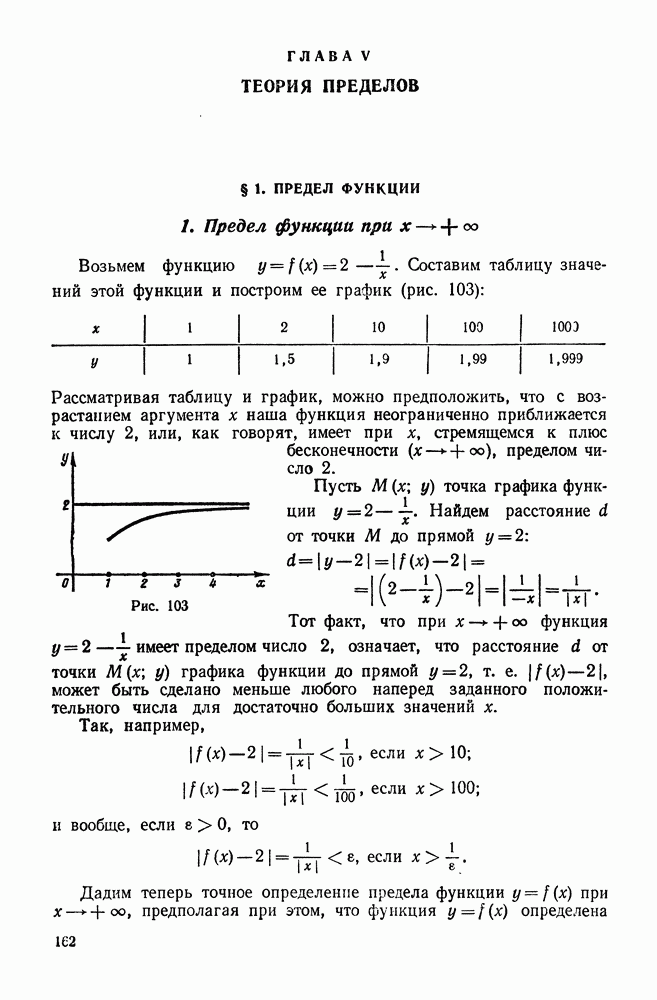
- § 1. ПРЕДЕЛ ФУНКЦИИ
- 2. Предел функции при х -> -оо
- 3. Предел функции при х->х0
- 4. Бесконечно малые функции. Ограниченные функции
- 5. Бесконечно большие функции и их связь с бесконечно малыми функциями
- 6. Основные теоремы о пределах
- 7. Предел функции при x -> 0
- 8. Последовательность. Число e
- 9. Натуральные логарифмы
- 10. Сравнение бесконечно малых функций
- § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 2. Операции над непрерывными функциями. Непрерывность элементарных функций
- 3. Свойства функций, непрерывных на сегменте
- 4. Понятие об обратной функции
- 5. Обратные тригонометрические функции
- 6. Показательная и логарифмическая функции
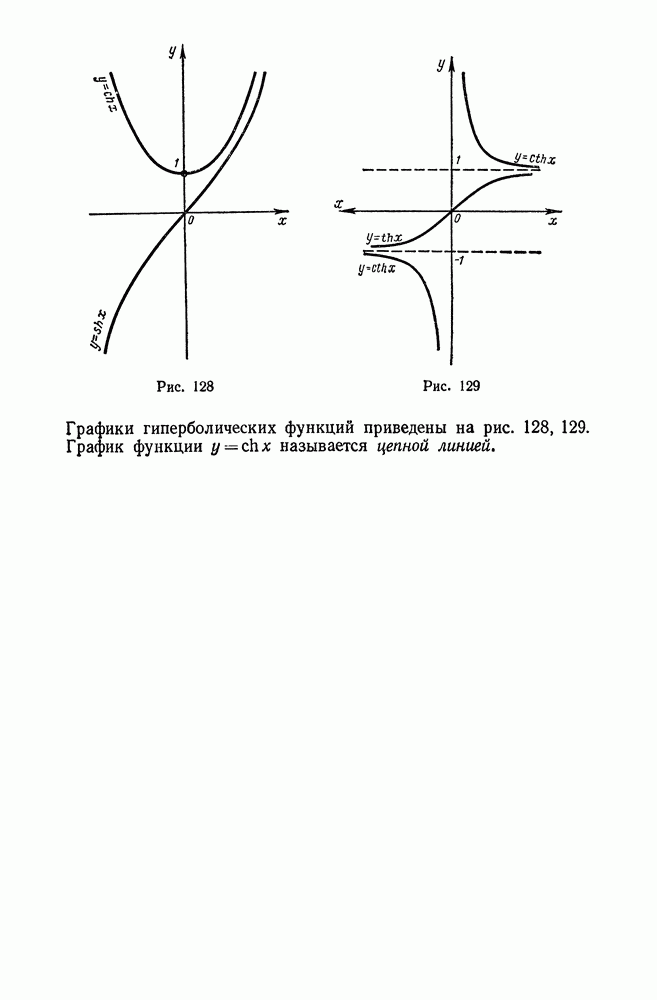
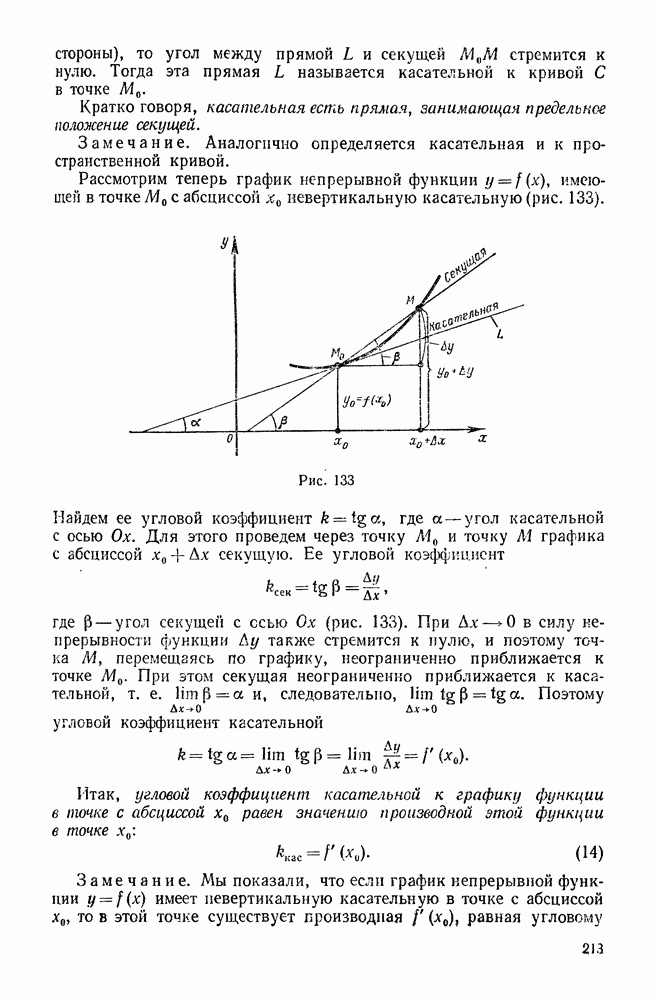
- 7. Понятие о гиперболических функциях
- ГЛАВА VI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
- 1. Приращение аргумента и приращение функции
- 2. Определение непрерывности функции с помощью понятии приращения аргумента и приращения функции
- 3. Задачи, приводящие к понятию производной
- 4. Определение производной и ее механический смысл
- 5. Дифференцируемость функции
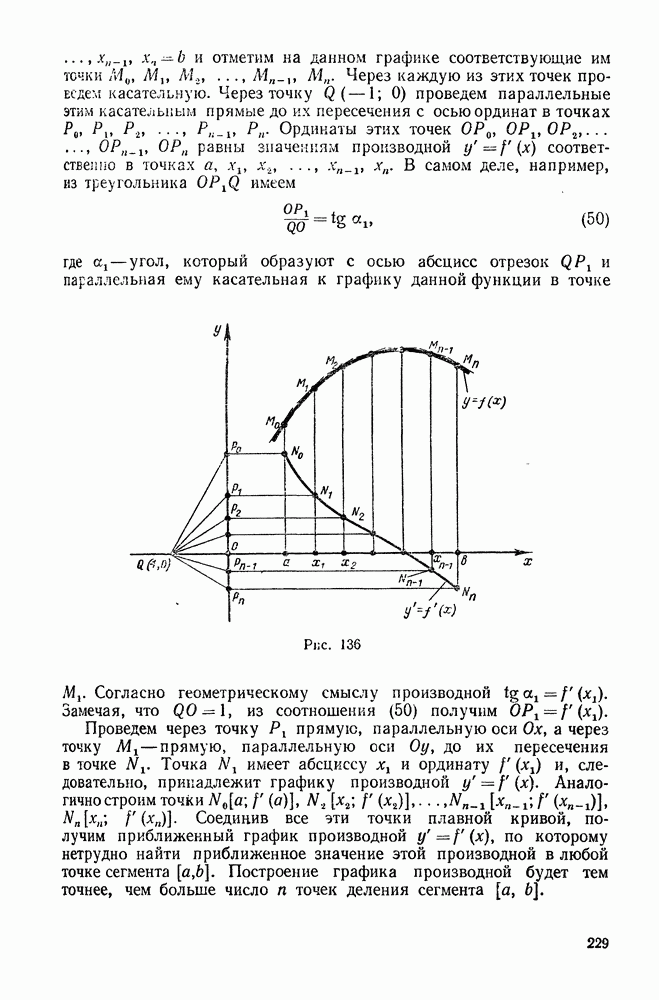
- 6. Геометрический смысл производной
- 7. Производные некоторых основных элементарных функций
- 8. Основные правила дифференцирования
- 9. Производная обратной функции
- 10. Производные обратных тригонометрических функций
- 11. Производная сложной функции
- § 12. Производные гиперболических функций
- 13. Производная степенной функции с любым показателем
- 14. Сводная таблица формул дифференцирования
- 15. Неявные функции и их дифференцирование
- 16. Уравнения касательной а нормали к кривой
- 17. Графическое дифференцирование
- § 2. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
- 1. Нахождение производных высших порядков
- 2. Механический смысл второй производной
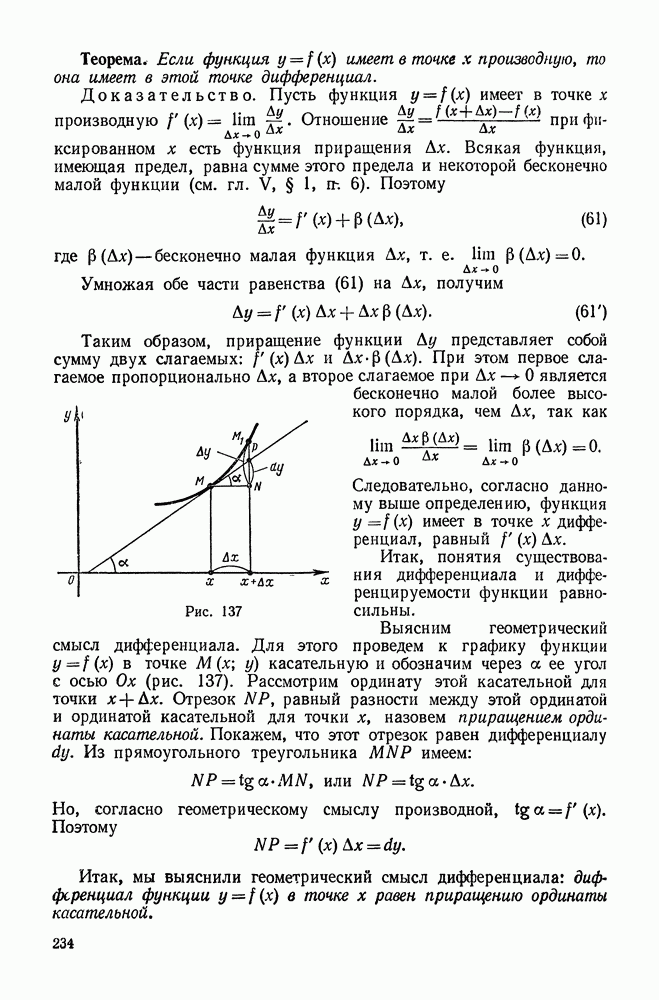
- § 3. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
- 2. Производная как отношение дифференциалов
- 3. Дифференциал суммы, произведения и частного функций
- 4. Дифференциал сложной функции. Инвариантность формы дифференциала
- 5. Применение дифференциала к приближенным вычислениям
- 6. Дифференциалы высших порядков
- § 4. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ, И ИХ ДИФФЕРЕНЦИРОВАНИЕ
- 2. Дифференцирование функций, заданных параметрически
- § 5. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
- 2. Векторная функция скалярного аргумента и ее производная
- 3. Уравнения касательной прямой и нормальной плоскости к пространственной кривой
- 4. Механический смысл первой и второй производных векторной функции скалярного аргумента
- § 6. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
- 2. Теорема Ролля
- 3. Теорема Лагранжа
- 4. Правило Лопиталя
- § 7. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ
- 2. Максимум и минимум функции
- 3. Достаточный признак существования экстремума, основанный на знаке второй производной
- 4. Отыскание наибольшего и наименьшего значений функции
- 5. Применение теории максимума и минимума к решению задач
- 6. Выпуклость и вогнутость графика функции. Точки перегиба
- 7. Асимптоты графика функции
- 8. Общая схема исследования функции и построение ее графика
- § 8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
- 2. Уточнение найденных значений корней методом хорд и касательных
- § 9. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА
- ГЛАВА VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА
- 2. Геометрический смысл неопределенного интеграла
- 3. Таблица основных интегралов
- 4. Основные свойства неопределенного интеграла
- § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
- 2. Интегрирование методом замены переменной
- 3. Интегрирование по частям
- § 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- 2. Рациональные дроби. Выделение правильной рациональной дроби
- 3. Интегрирование простейших рациональных дробей
- 4. Разложение правильной рациональной дроби на простейшие дроби
- 5. Метод неопределенных коэффициентов
- 6. Интегрирование рациональных дробей
- § 4. Интегрирование тригонометрических функций
- 2. Рациональные функции двух переменных
- 3. Интегралы вида
- § 5. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
- 2. Интеграл вида
- 3. Интегралы видов
- 4. Интегралы вида
- § 6. ОБЩИЕ ЗАМЕЧАНИЯ О МЕТОДАХ ИНТЕГРИРОВАНИЯ. ИНТЕГРАЛЫ, НЕ БЕРУЩИЕСЯ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
- 2. Понятие об интегралах, не берущихся в элементарных функциях
- ГЛАВА VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ОПРЕДЕЛЕННОМУ ИНТЕГРАЛУ
- 2. Задача о работе переменной силы
- § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- 2. Свойства определенного интеграла
- 3. Производная интеграла по переменной верхней границе
- 4. Формула Ньютона—Лейбница
- 5. Замена переменной в определенном интеграле
- 6. Интегрирование по частям в определенном интеграле
- § 3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 2. Вычисление площади в полярных координатах
- 3. Вычисление объема тела по известным поперечным сечениям
- 4. Объем тела вращения
- 5. Длина дуги кривой
- 6. Дифференциал дуги
- 7. Площадь поверхности вращения
- 8. Общие замечания о решении задач методом интегральных сумм
- § 4. КРИВИЗНА ПЛОСКОЙ КРИВОЙ
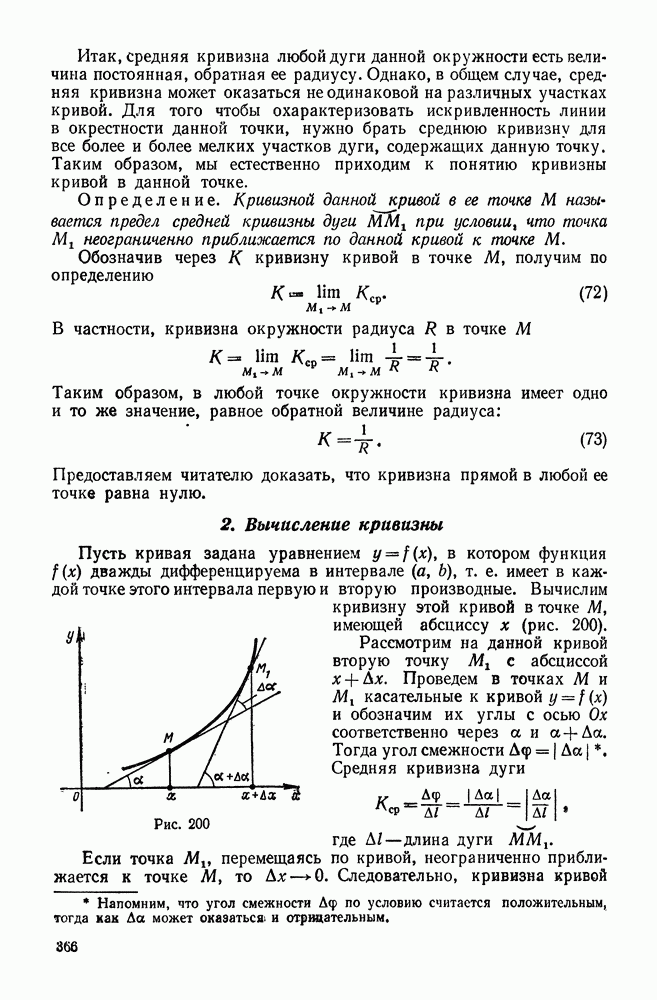
- 2. Вычисление кривизны
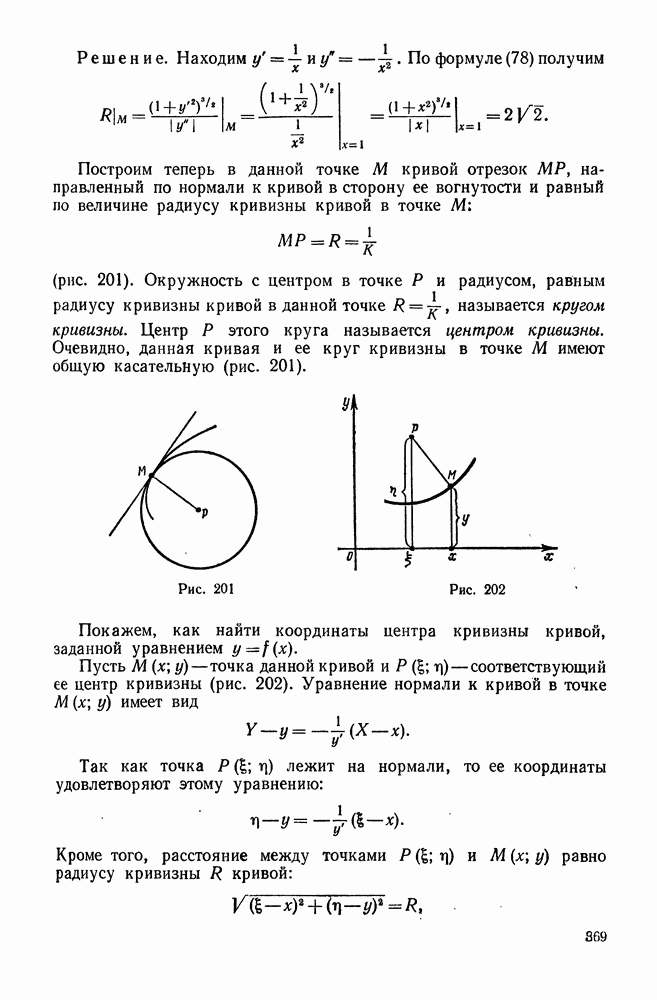
- 3. Радиус кривизны. Круг кривизны. Центр кривизны
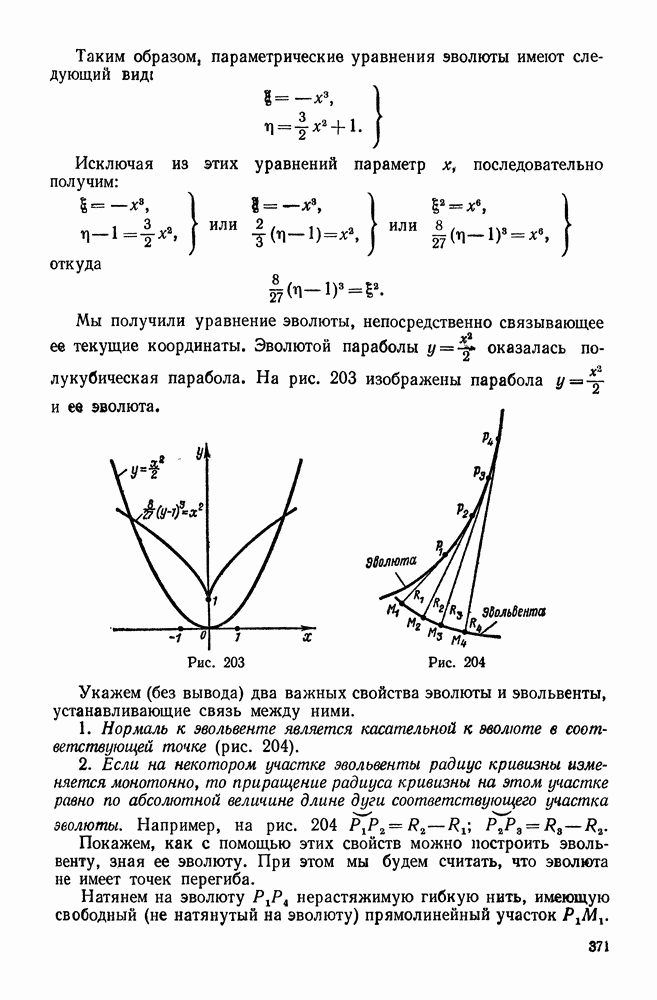
- 4. Эволюта и эвольвента
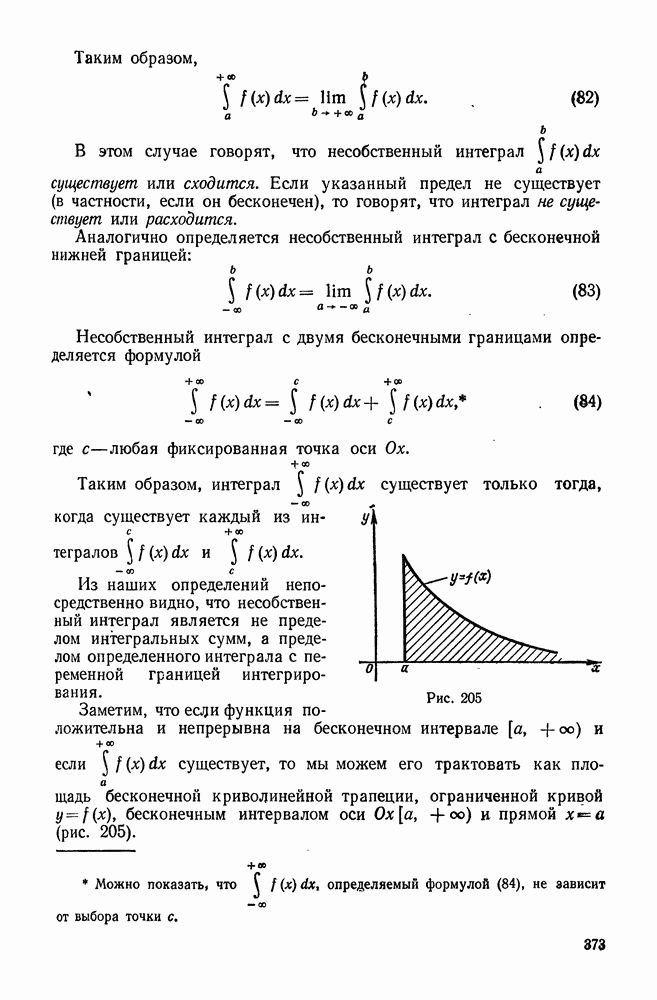
- § 5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
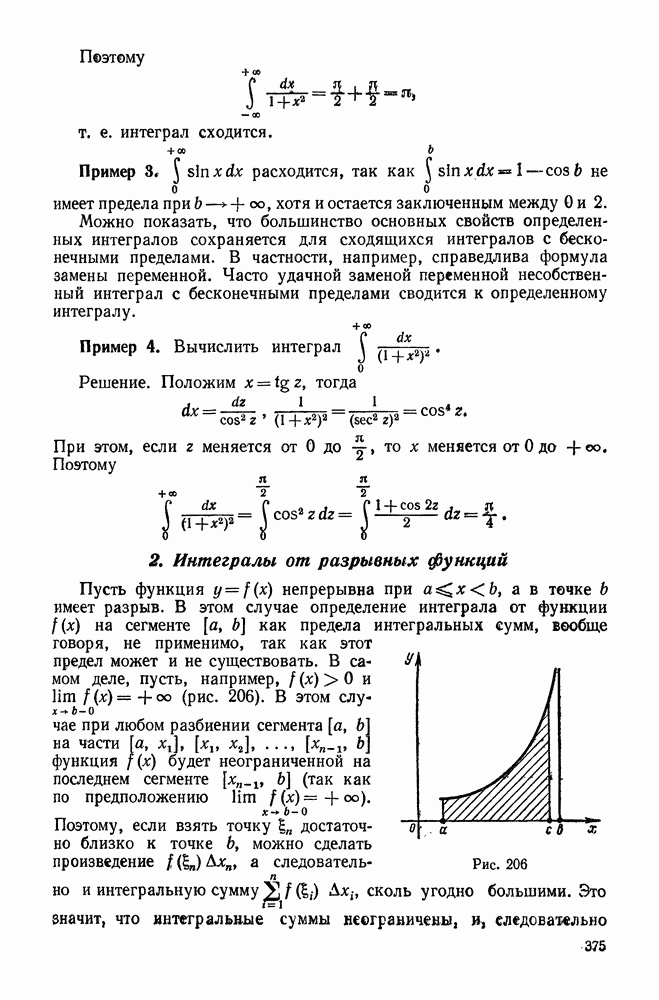
- 2. Интегралы от разрывных функций
- 3. Признаки сходимости несобственных интегралов
- § 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
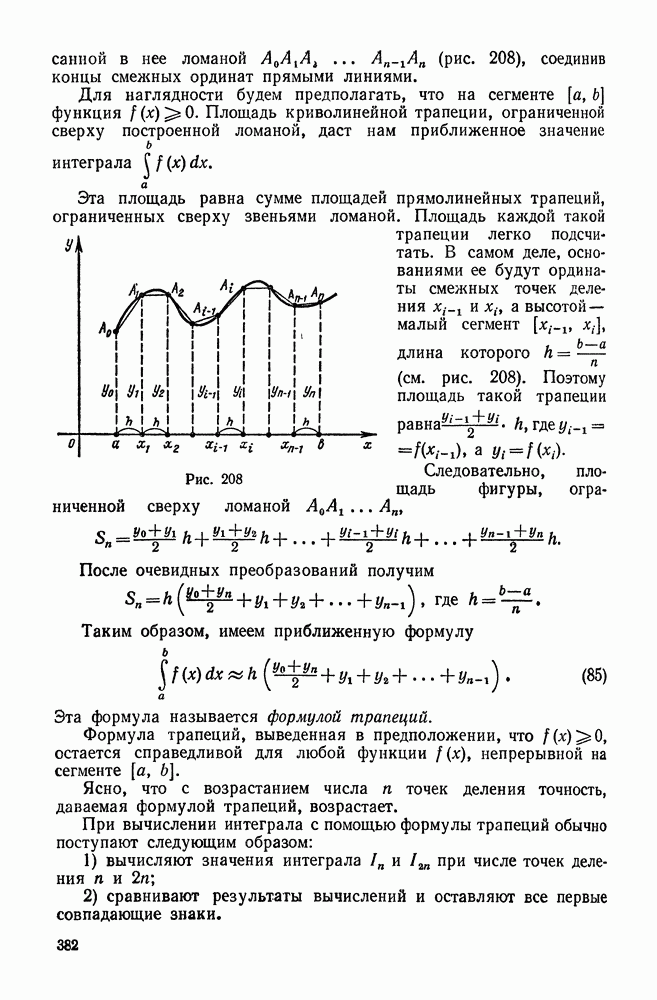
- 2. Метод трапеций
- 3. Метод параболических трапеций (метод Симпсона)
- ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 2. График функции двух переменных
- 3. Функции трех и большего числа переменных
- § 2. Предел функции нескольких переменных. Непрерывность функции. Точки разрыва
- 2. Непрерывность функции нескольких переменных
- 3. Понятие области
- 4. Точки разрыва
- 5. Свойства функций, непрерывных в ограниченной замкнутой области
- § 3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ
- 2. Геометрический смысл частных производных функции двух переменных
- 3. Частные производные высших порядков
- § 4. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 2. Полный дифференциал функции
- 3. Приложение полного дифференциала к приближенным вычислениям
- § 5. Дифференцирование сложных и неявных функций
- 2. Инвариантность формы полного дифференциала
- 3. Дифференцирование неявных функций
- § 6. СКАЛЯРНОЕ ПОЛЕ
- 2. Производная по направлению
- 3. Градиент
- 4. Касательная плоскость а нормаль к поверхности
- 5. Геометрический смысл полного дифференциала функции двух переменных
- § 7. ЭКСТРЕМУМ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ
- 2. Наибольшее и наименьшее значения функции двух переменных
- ГЛАВА X. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- § 1. ДВОЙНОЙ ИНТЕГРАЛ
- 2. Двойной интеграл. Теорема существования
- 3. Свойства двойного интеграла
- 4. Вычисление двойного интеграла в декартовых координатах
- 5. Вычисление двойного интеграла в полярных координатах
- 6. Приложения двойного интеграла
- § 2. ТРОЙНОЙ ИНТЕГРАЛ
- 2. Тройной интеграл и его свойства
- 3. Вычисление тройного интеграла в декартовых координатах
- 4. Вычисление тройного интеграла в цилиндрических координатах
- 5. Приложения тройного интеграла
- § 3. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
- 2. Задача о работе. Криволинейный интеграл
- 3. Вычисление криволинейного интеграла
- 4. Формула Остроградского — Грина
- 5. Независимость криволинейного интеграла от пути интегрирования
- 6. Отыскание первообразной по полному дифференциалу
- 7. Криволинейный интеграл по длине дуги
- ГЛАВА XI. РЯДЫ
- § 1. ЧИСЛОВЫЕ РЯДЫ
- 2. Геометрическая прогрессия
- 3. Простейшие свойства числовых рядов
- 4. Необходимый признак сходимости ряда
- 5. Достаточные признаки сходимости знакоположительных рядов
- 6. Знакопеременные ряды
- 7. Остаток ряда и его оценка
- § 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
- 2. Правильно сходящиеся функциональные ряды и их свойства
- § 3. СТЕПЕННЫЕ РЯДЫ
- 2. Свойства степенных рядов
- 3. Ряды по степеням разности х-а
- 4. Разложение функций в степенные ряды. Ряд Тейлора
- 5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена
- § 4. ПРИЛОЖЕНИЕ РЯДОВ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
- 2. Приближенное вычисление интегралов
- § 5. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. СТЕПЕННЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 2. Числовые ряды с комплексными членами
- 3. Степенные ряды в комплексной области
- § 6. РЯДЫ ФУРЬЕ
- 2. Ряд Фурье
- 3. Сходимость ряда Фурье
- 4. Ряды Фурье для четных и нечетных функций
- 5. Разложение в ряд Фурье функций с периодом 2l
- ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- 2. Дифференциальные уравнения первого порядка
- 3. Уравнения с разделяющимися переменными
- 4. Однородные уравнения
- 5. Линейные уравнения
- 6. Уравнение в полных дифференциалах
- 7. Особые решения
- 8. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- 2. Простейшие уравнения второго порядка, допускающие понижение порядка
- 3. Понятие о дифференциальных уравнениях высших порядков
- § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- 2. Линейные однородные дифференциальные уравнения второго порядка
- 3. Линейные неоднородные дифференциальные уравнения второго порядка
- 4. Метод вариации произвольных постоянных
- § 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- 2. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- 3. Приложение линейных дифференциальных уравнений второго порядка к изучению механических и электрических колебаний
- § 5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
- 2. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами
- § 6. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ
- § 7. ПОНЯТИЕ О СИСТЕМАХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 2. Системы линейных дифференциальных уравнений с постоянными коэффициентами
- ПРИЛОЖЕНИЕ 1. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА
- ПРИЛОЖЕНИЕ 2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ