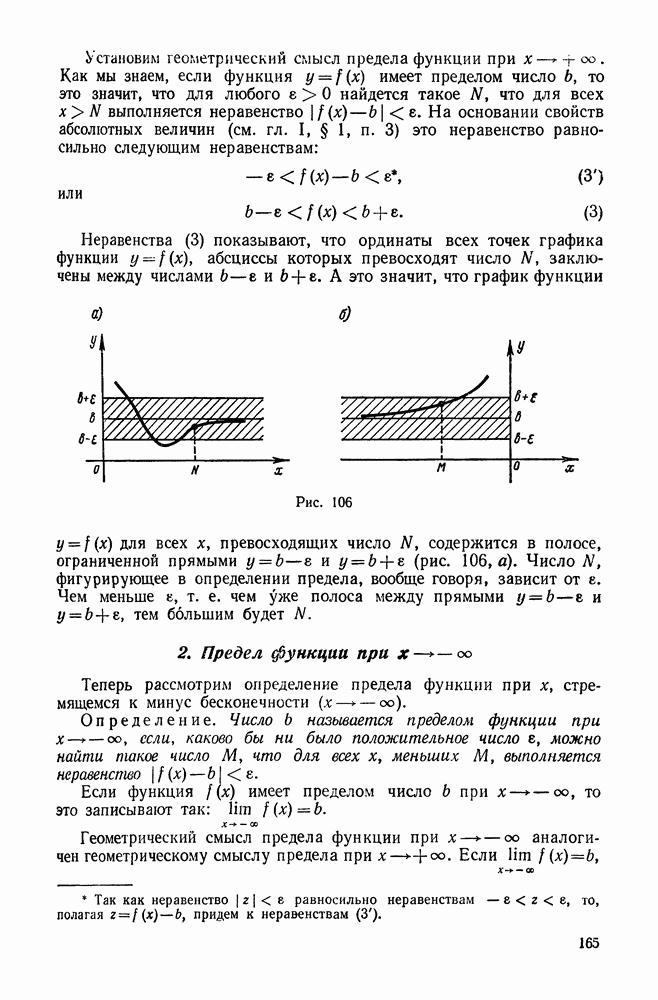
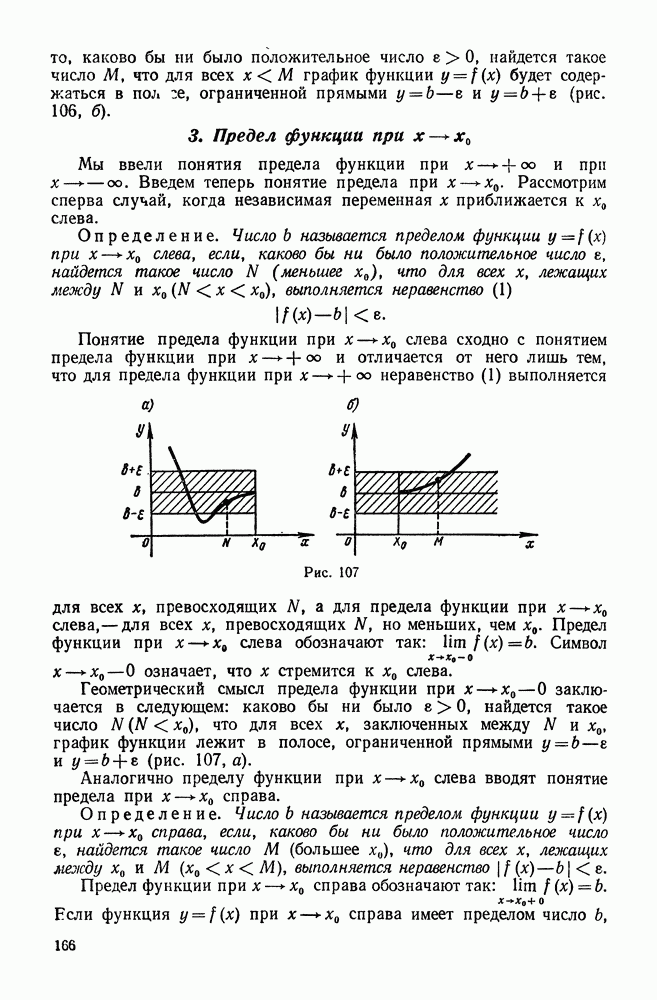
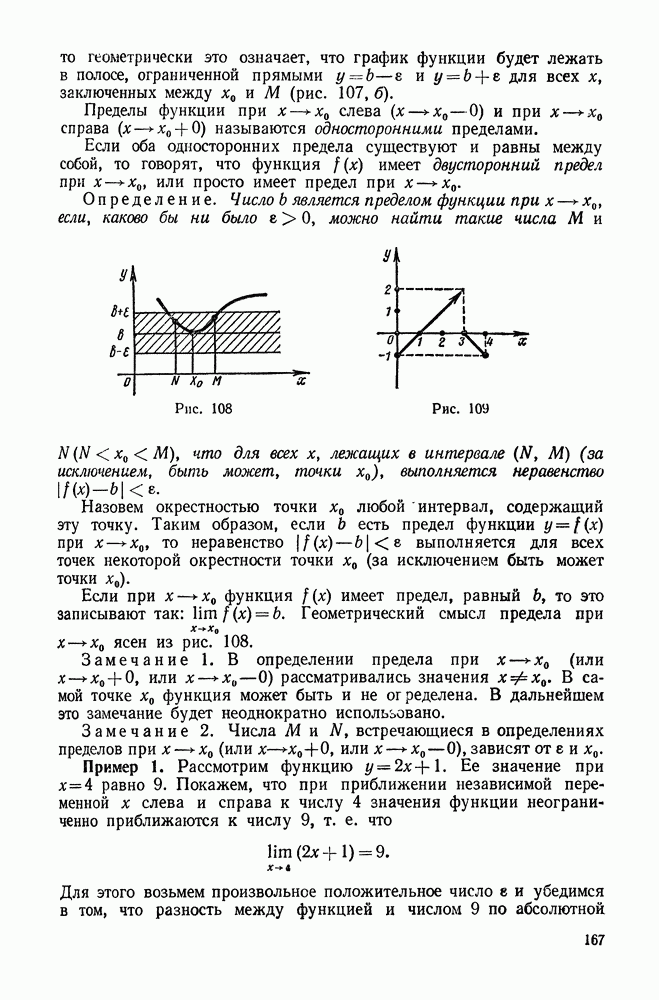
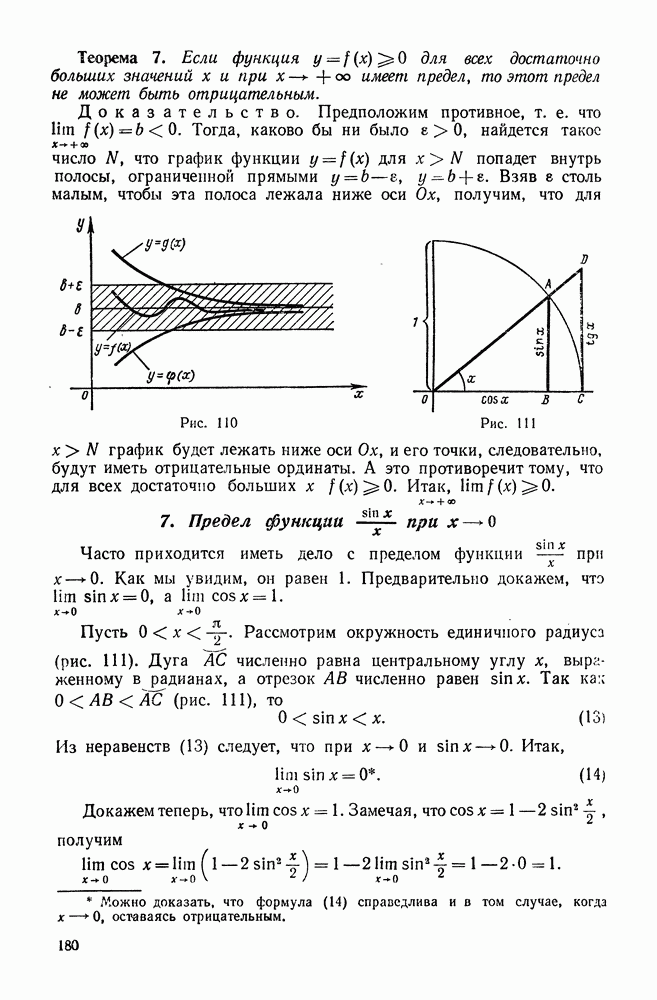
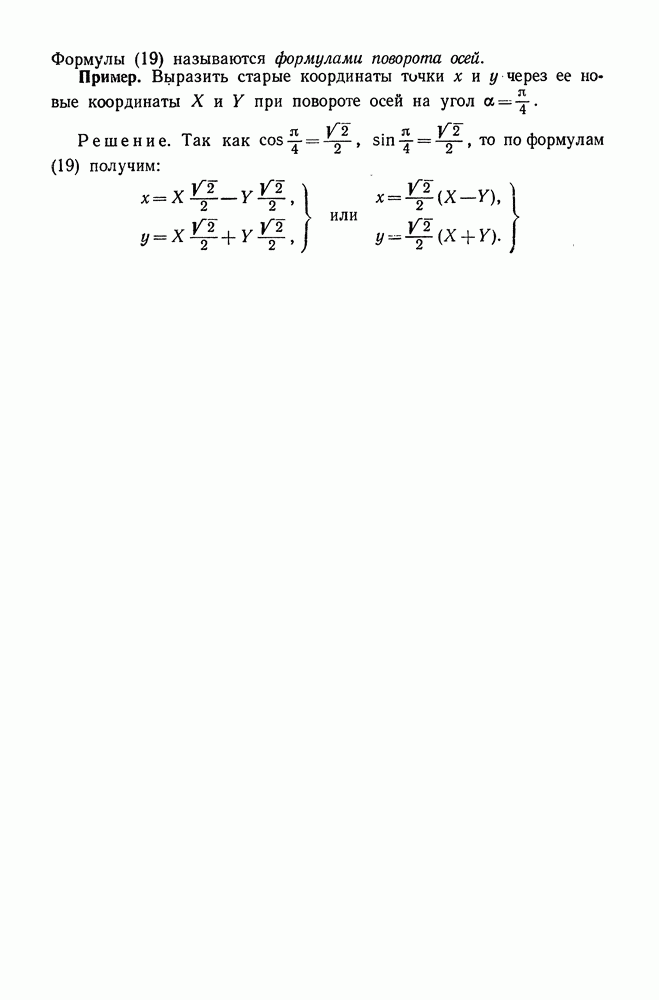| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
6. Знакопеременные ряды
До сих пор мы изучали только ряды, все члены которых были положительными  . Теперь мы перейдем к рассмотрению рядов, содержащих как положительные, так и отрицательные члены. Такие ряды называются знакопеременными.
. Теперь мы перейдем к рассмотрению рядов, содержащих как положительные, так и отрицательные члены. Такие ряды называются знакопеременными.
В качестве примера знакопеременного ряда приведем ряд

Изучение знакопеременных рядов мы начнем с частного случая, так называемых знакочередующихся рядов, т. е. рядов, в которых за каждым положительным членом следует отрицательный и за каждым отрицательным членом следует положительный.
Обозначая через  — абсолютные величины членов ряда и считая, что первый член положителен, знакочередующийся ряд запишем следующим образом:
— абсолютные величины членов ряда и считая, что первый член положителен, знакочередующийся ряд запишем следующим образом:

Для знакочередующихся рядов имеет место достаточный признак сходимости Лейбница.
Признак Лейбница. Если в знакочередующемся ряде (34) абсолютные величины членов убывают:

и общий член ряда стремится к нулю:  , то ряд сходится и его сумма не превосходит первого члена ряда.
, то ряд сходится и его сумма не превосходит первого члена ряда.
Доказательство. Рассмотрим частичную сумму четного числа членов ряда

Сгруппируем члены попарно:

Так как по условию абсолютные величины членов ряда убывают, то все разности в скобках положительны и, следовательно, сумма  положительна и возрастает при увеличении
положительна и возрастает при увеличении  .
.
Запишем теперь  группируя члены иным образом:
группируя члены иным образом:

Сумма в квадратных скобках будет также положительной. Поэтому для любого значения  . Таким образом, последовательность четных частичных сумм
. Таким образом, последовательность четных частичных сумм  возрастает с увеличением
возрастает с увеличением  , оставаясь при этом ограниченной. Следовательно,
, оставаясь при этом ограниченной. Следовательно,  имеет предел
имеет предел 
При этом, так как  то ясно, что
то ясно, что  Рассмотрим теперь сумму нечетного числа членов:
Рассмотрим теперь сумму нечетного числа членов:

При  имеем
имеем

так как по условию  и, следовательно,
и, следовательно,  .
.
Таким образом, частичные суммы как четного, так и нечетного числа членов имеют общий предел S. Это означает, что вообще  , т. е. ряд сходится. При этом, как видно из доказательства, сумма ряда S не превосходит первого члена ряда.
, т. е. ряд сходится. При этом, как видно из доказательства, сумма ряда S не превосходит первого члена ряда.
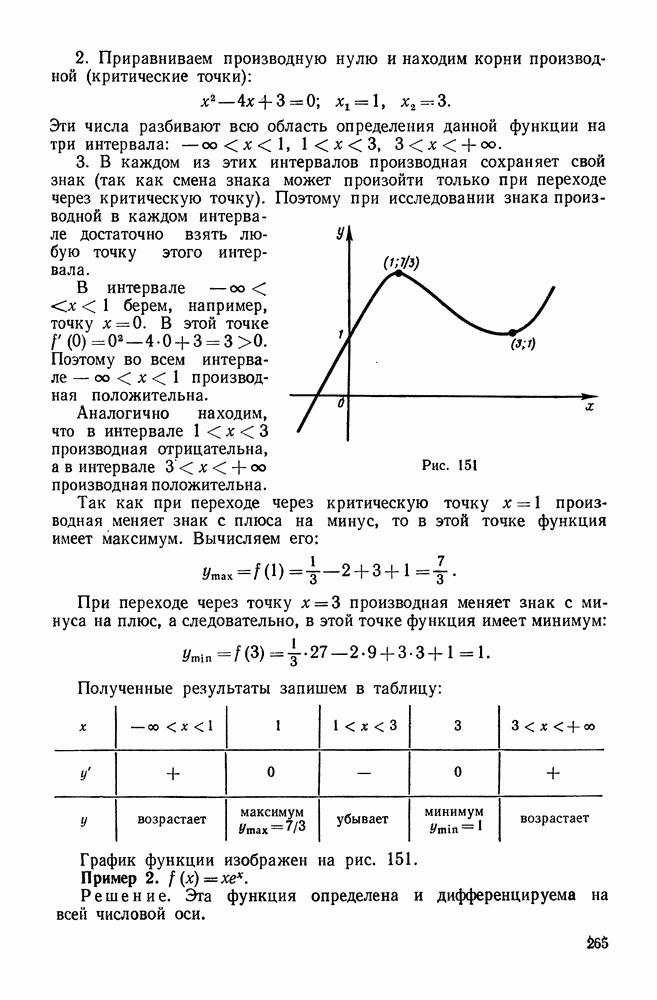
Пример 1. Исследовать, сходится или расходится ряд

Решение. Этот ряд удовлетворяет условиям признака Лейбница:

Следовательно, ряд сходится.
Перейдем теперь к рассмотрению общего случая знакопеременного ряда. Будем предполагать, что в ряде

числа  могут быть как положительными, так и отрицательными.
могут быть как положительными, так и отрицательными.
Для таких рядов имеет место следующий достаточный признак сходимости знакопеременного ряда.
Теорема. Если для знакопеременного ряда

сходится ряд, составленный из абсолютных величин его членов

то данный знакопеременный ряд также сходится.
Доказательство. Рассмотрим вспомогательный ряд, составленный из членов рядов (37) и (38):

Имеем:

Таким образом, члены ряда (39) либо равны членам сходящегося ряда (38), либо меньше их. Поэтому ряд (39) сходится на основании признака сравнения (см. п. 5, теорему 1 и сноску на стр. 501).
Умножив все члены сходящегося ряда (38) на  получим сходящийся ряд
получим сходящийся ряд

(см. п. 3, теорема 1). Рассмотрим теперь ряд, являющийся разностью сходящихся рядов (39) и (40)

Этот ряд сходится на основании теоремы 2 п. 3.
Но ряд (37) получается из последнего ряда умножением всех его членов на 2:

Следовательно, ряд (37) также сходится (п. 3, теорема 1).
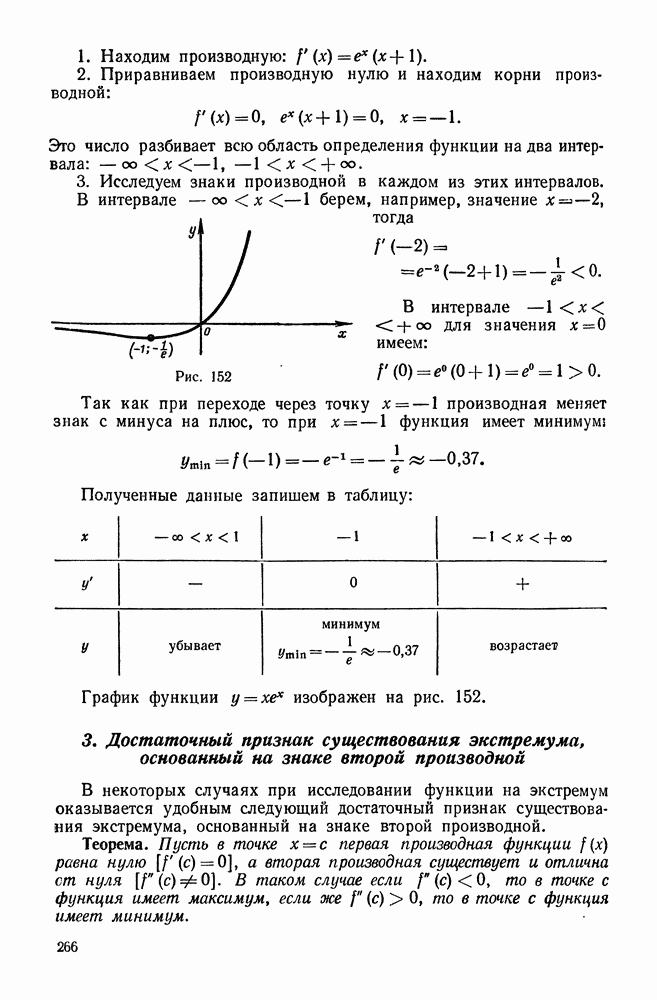
Пример 2. Исследовать на сходимость знакопеременный ряд (33)

Решение. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда

Этот ряд сходится, как обобщенный гармонический ряд с показателем  . Следовательно, на основании доказанного признака сходится и данный ряд (33).
. Следовательно, на основании доказанного признака сходится и данный ряд (33).
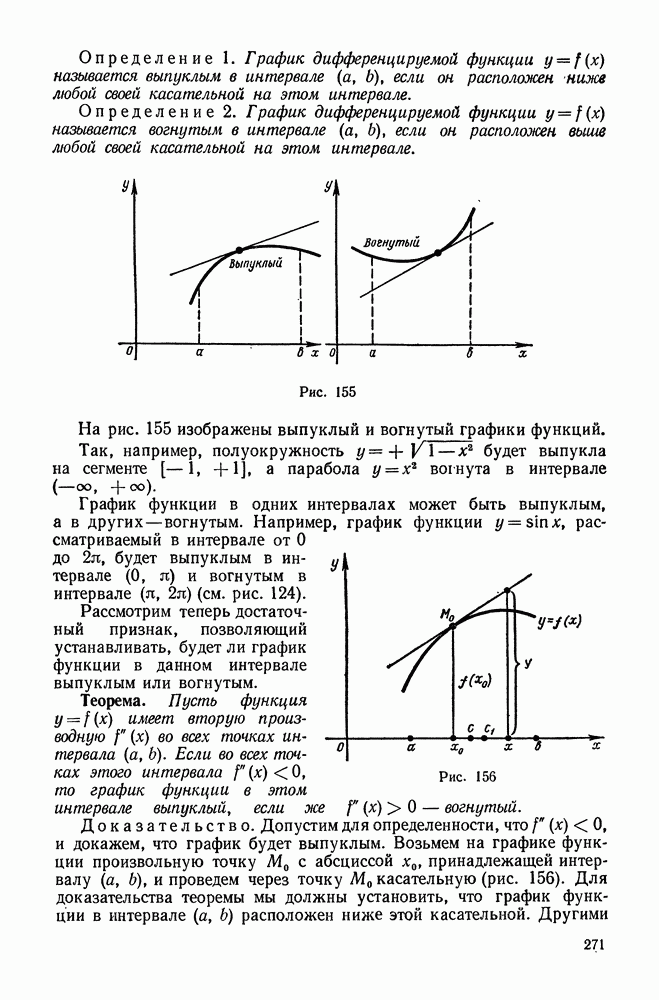
Этот признак является достаточным, но не необходимым. Это значит, что существуют знакопеременные ряды, которые сходятся, в то время как ряды, составленные из абсолютных величин их членов, расходятся.
Действительно рассмотрим ряд

который, очевидно, сходится по признаку Лейбница. Между тем, ряд

составленный из абсолютных величин членов данного ряда  является гармоническим и, следовательно, расходится.
является гармоническим и, следовательно, расходится.
Хотя рассмотренные выше ряды (33) и (42) оба сходятся, однако характер их сходимости различен.
Ряд (33) сходится одновременно с рядом (41), составленным из абсолютных величин его членов, тогда как ряд (43), составленный из абсолютных величин сходящегося ряда (42), расходится.
В связи с этим введем следующие определения.
Определение. Знакопеременный ряд  абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов
абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов 
На основании достаточного признака сходимости знакопеременного ряда всякий абсолютно сходящийся ряд будет сходящимся.
Определение. Знакопеременный ряд  называется неабсолютно сходящимся, если он сходится, а ряд, составленный из абсолютных величин его членов
называется неабсолютно сходящимся, если он сходится, а ряд, составленный из абсолютных величин его членов  их
их  расходится.
расходится.
Возвращаясь к рассмотренным выше примерам, можем сказать, что ряд (33) является абсолютно сходящимся, а ряд ( - неабсолютно сходящимся.
- неабсолютно сходящимся.
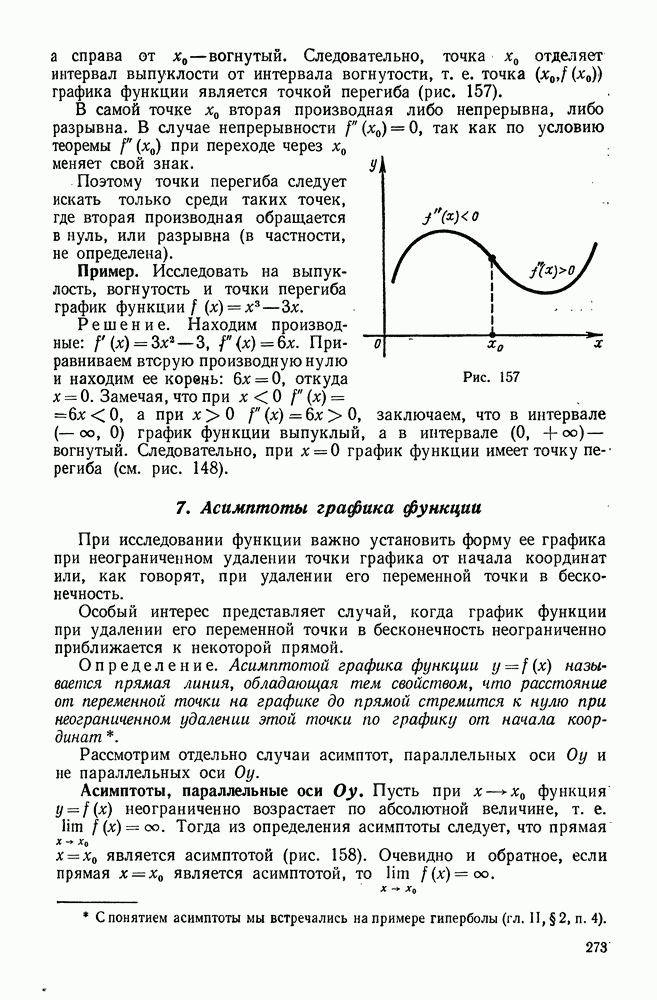
Среди знакопеременных рядов абсолютно сходящиеся ряды занимают особое место. Это объясняется тем, что на такие ряды переносятся основные свойства конечных сумм. Особое значение имеет свойство переместительности, которым обладают только абсолютно сходящиеся ряды.
Это свойство, которое мы приводим без доказательства, формулируется следующим образом.
Сумма абсолютно сходящегося ряда не меняется от любой перестановки его членов.
Наоборот, в неабсолютно сходящемся ряде нельзя переставлять члены, так как в случае их перестановки может измениться сумма ряда и даже получиться расходящийся ряд.
Говоря о перестановке членов, мы подразумеваем, что меняем местами бесконечное множество членов, так как, переставляя два, три, четыре или любое конечное число членов, мы, очевидно, не изменим суммы ряда.
Рассмотрим в качестве примера неабсолютно сходящийся ряд (42)

сумму которого обозначим через 
Переставим члены этого ряда, поместив после каждого положительного члена два отрицательных. Получим ряд

Обозначим частичные суммы ряда (42) через  и ряда (42) через
и ряда (42) через  Тогда
Тогда

Итак,  и вообще, как можно показать,
и вообще, как можно показать,  Так как
Так как  то
то  .
.
Итак, последовательность частичных сумм ряда (42) с номерами, кратными трем, имеет своим пределом у S. Можно показать, что этот же предел  имеют последовательности всех частичных сумм
имеют последовательности всех частичных сумм  .
.
Таким образом,  существует и, значит, ряд (42) сходится. При этом его сумма составляет половину суммы ряда (42), из которого он получен перестановкой членов.
существует и, значит, ряд (42) сходится. При этом его сумма составляет половину суммы ряда (42), из которого он получен перестановкой членов.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА I. МЕТОД КООРДИНАТ. ПОНЯТИЕ ФУНКЦИИ
- § 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КООРДИНАТЫ ТОЧКИ НА ПРЯМОЙ
- 2. Геометрическое изображение действительных чисел. Координаты точки на прямой
- 3. Абсолютная величина действительного числа
- 4. Расстояние между двумя точками на прямой
- § 2. КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
- 2. Расстояние между двумя точками на плоскости
- 3. Деление отрезка в данном отношении
- 4. Координаты точки в пространстве
- 5. Расстояние между двумя точками в пространстве
- § 3. УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ
- 2. Полярные координаты
- 3. Зависимость между декартовыми и полярными координатами
- § 4. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ
- 2. Понятие функции
- 3. График функции
- 4. Способы задания функций
- 5. Основные элементарные функции и их графики
- 6. Сложные функции. Элементарные функции
- 7. Целые и дробно-рациональные функции
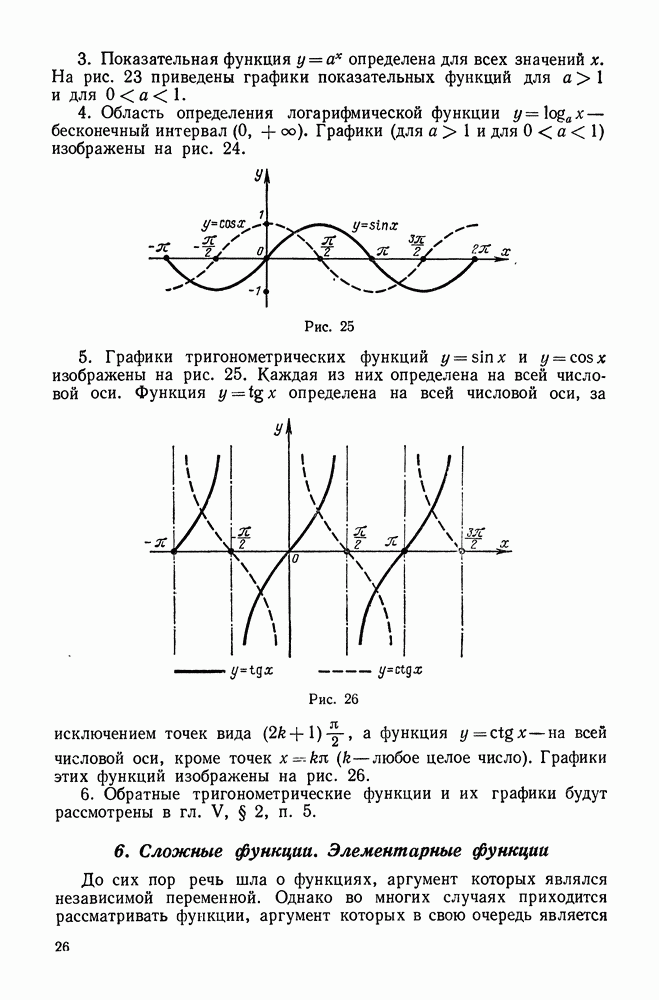
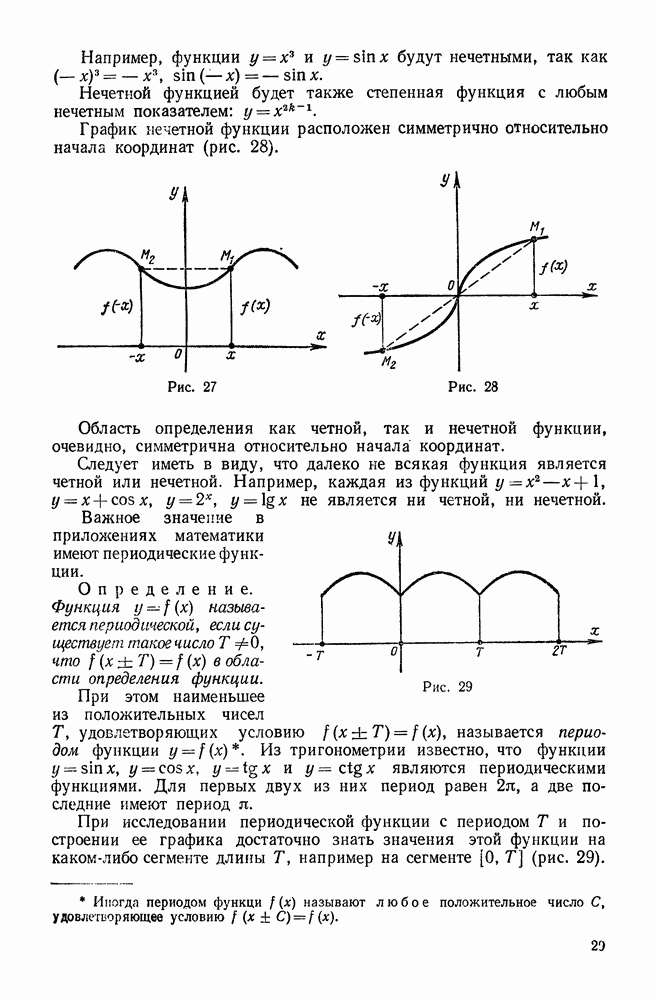
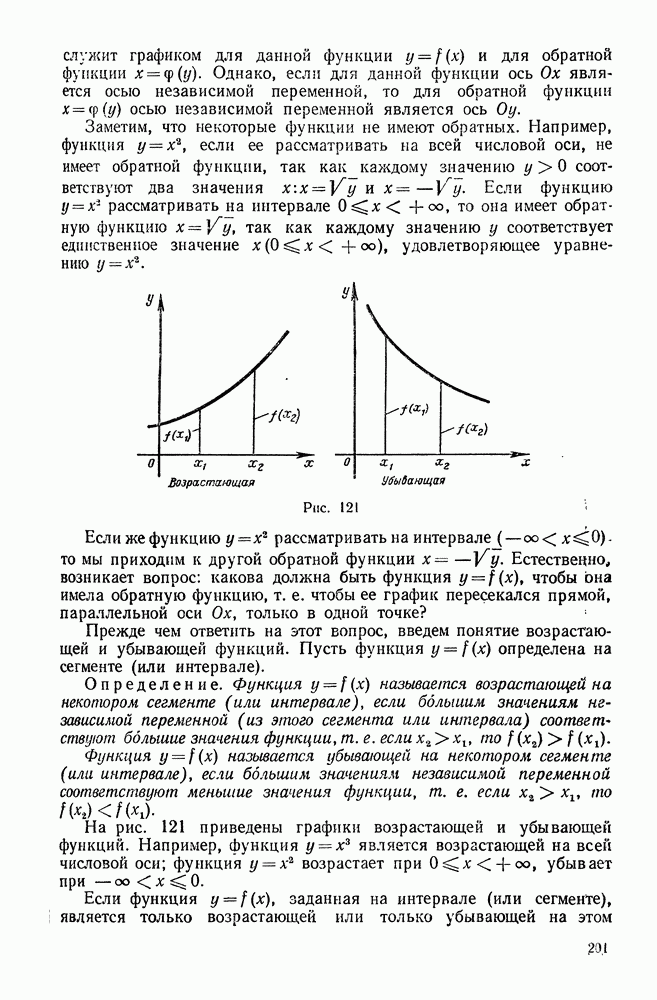
- 8. Функции четные и нечетные. Периодические функции
- § 5. УРАВНЕНИЕ ЛИНИИ
- 2. Нахождение уравнения линии по ее геометрическим свойствам
- § 6 ПРЕОБРАЗОВАНИЕ КООРДИНАТ
- 2. Поворот осей координат
- ГЛАВА II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- § 1. ПРЯМАЯ
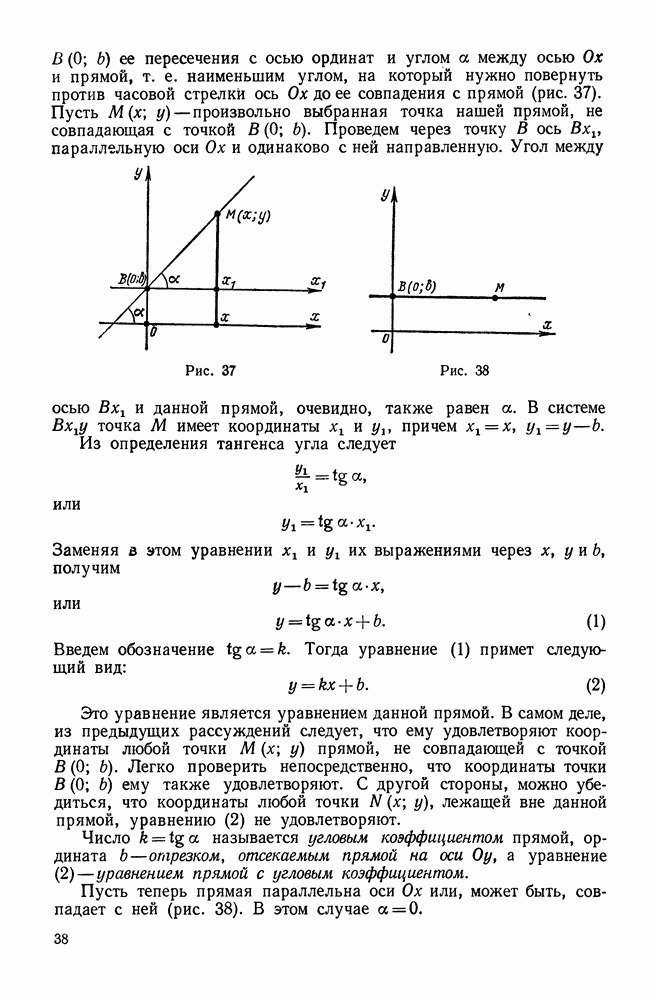
- 2. Уравнение прямой с угловым коэффициентом
- 3. Уравнение прямой, параллельной оси ординат
- 4. Общее уравнение прямой и его частные случаи
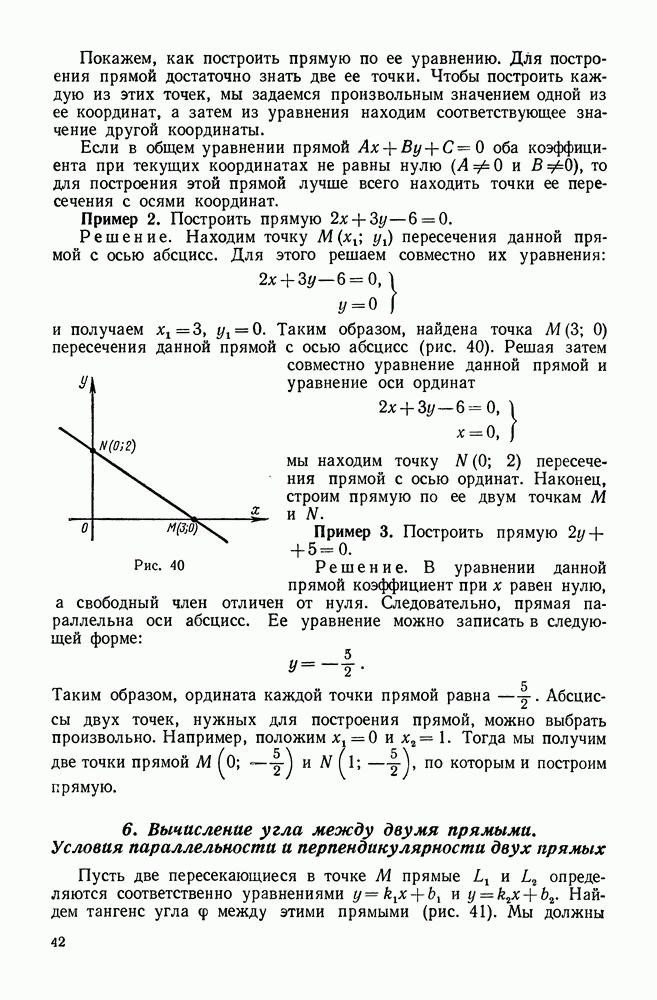
- 5. Точка пересечения прямых. Построение прямой по ее уравнению
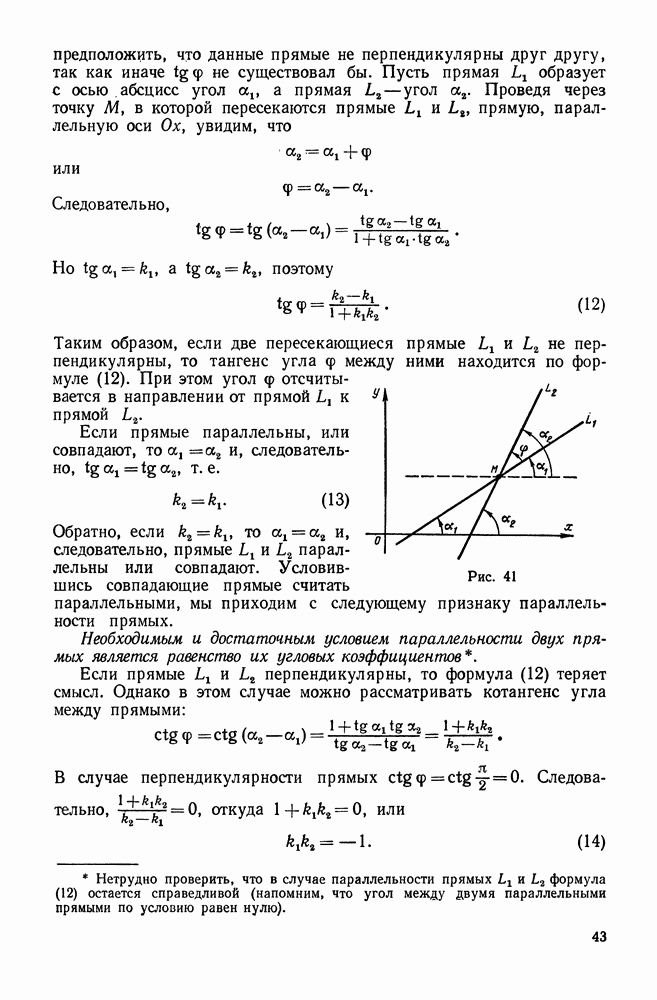
- 6. Вычисление угла между двумя прямыми. Условия параллельности и перпендикулярности двух прямых
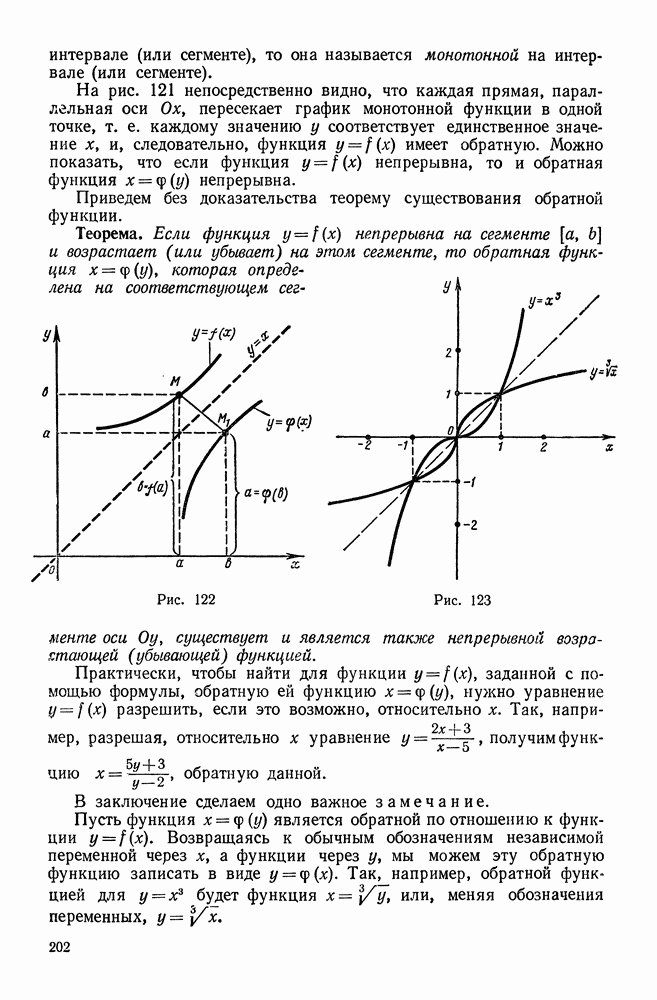
- 7. Уравнение прямой, проходящей через данную точку в заданном направлении
- 8. Пучок прямых
- 9. Уравнение прямой, проходящей через две данные точки
- 10. Расстояние от точки до прямой
- § 2. КРИВЫЕ ВТОРОГО ПОРЯДКА
- 2. Окружность
- 3. Эллипс
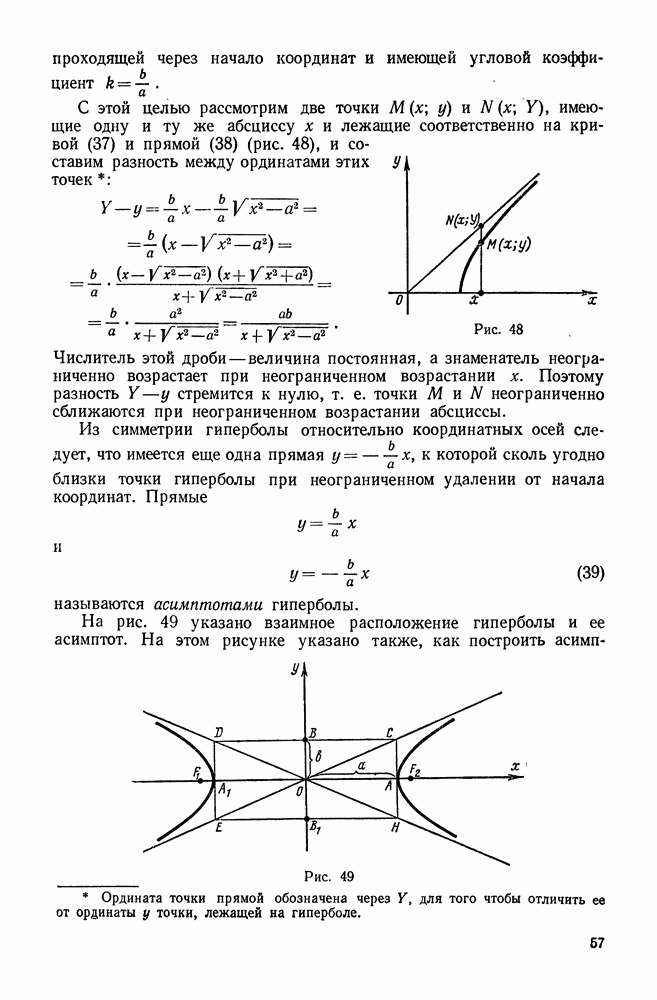
- 4. Гипербола
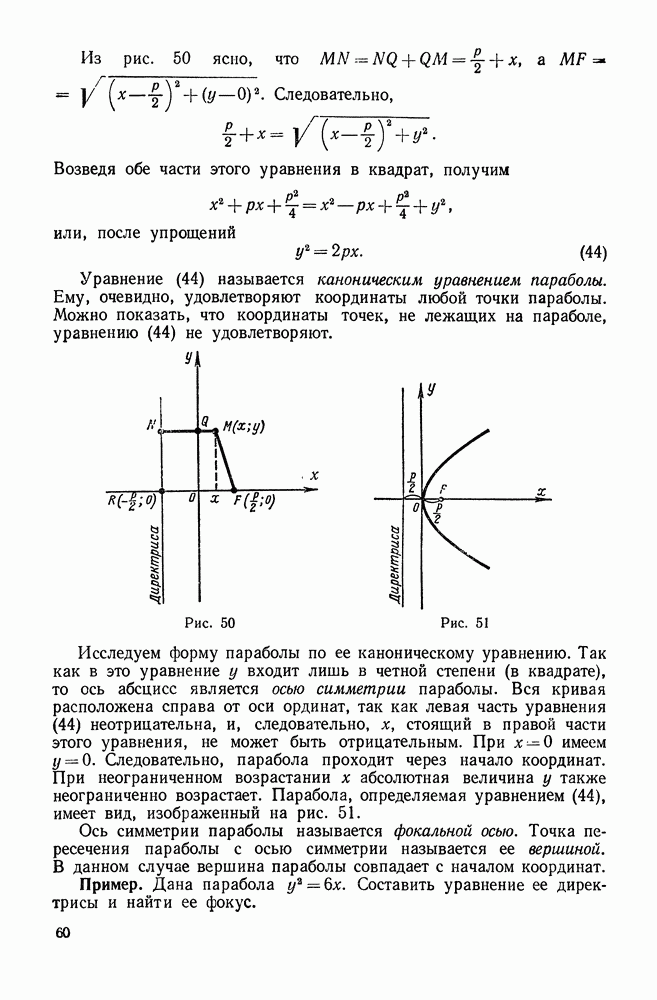
- 5. Парабола
- 6. Окружность, эллипс, гипербола и парабола как конические сечения
- 7. Упрощение уравнения кривой второго порядка. График квадратного трехчлена
- 8. Уравнение равносторонней гиперболы, асимптоты которой приняты за оси координат
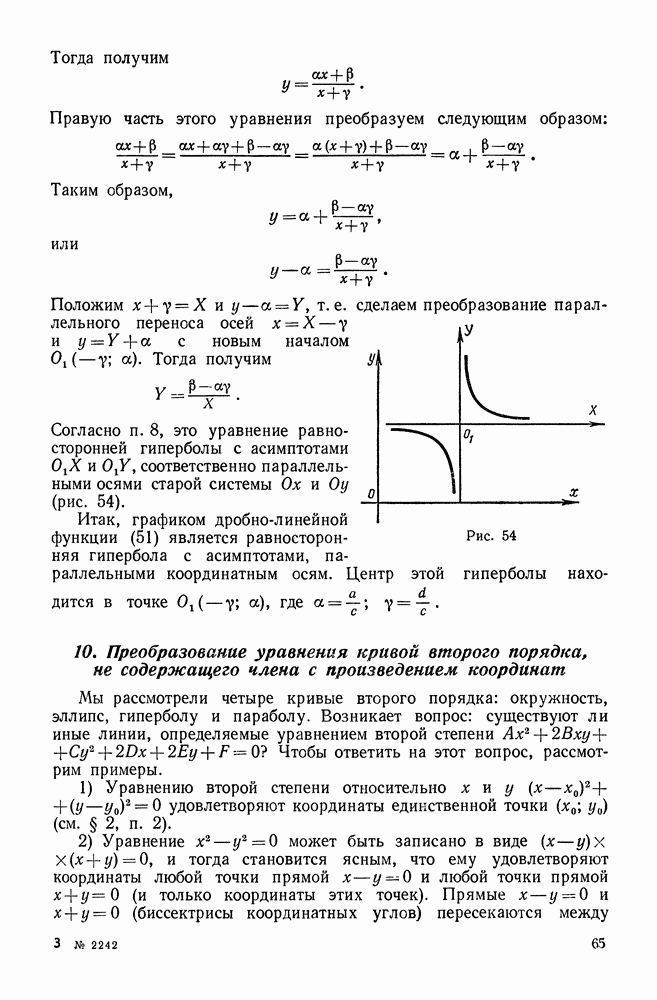
- 9. График дробно-линейной функции
- 10. Преобразование уравнения кривой второго порядка, не содержащего члена с произведением координат
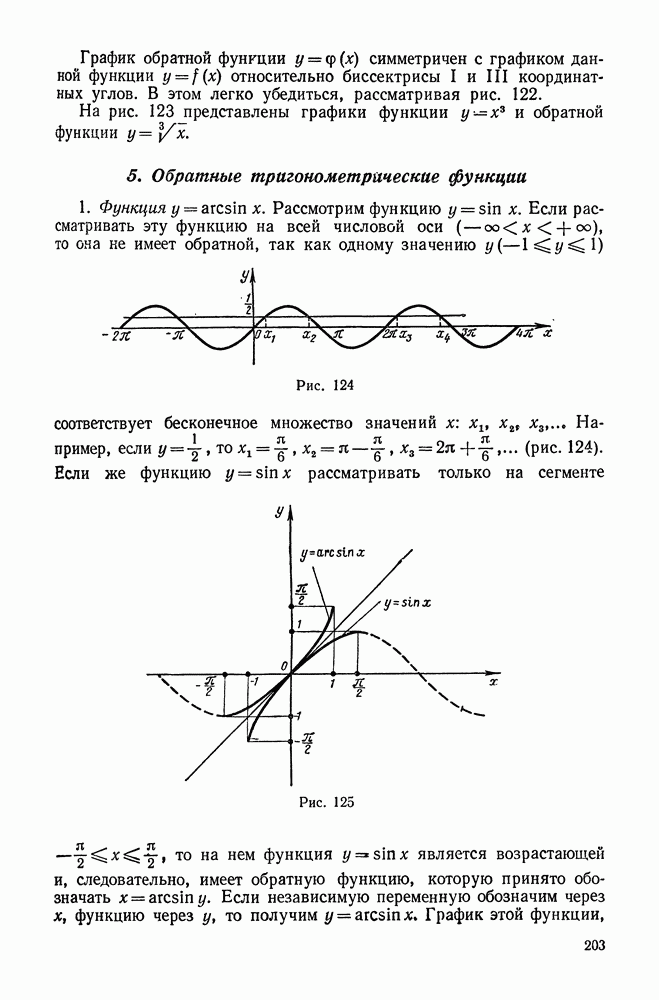
- ГЛАВА III. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ
- § 1. ЭЛЕМЕНТЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ
- 2. Определитель третьего порядка
- 3. Понятие об определителях высших порядков
- § 2. СИСТЕМЫ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ
- 2. Однородная система двух уравнений первой степени с тремя неизвестными
- 3. Система трех уравнений первой степени с тремя неизвестными
- 4. Однородная система трех уравнений первой степени с тремя неизвестными
- § 3. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
- 2. Линейные операции над векторами
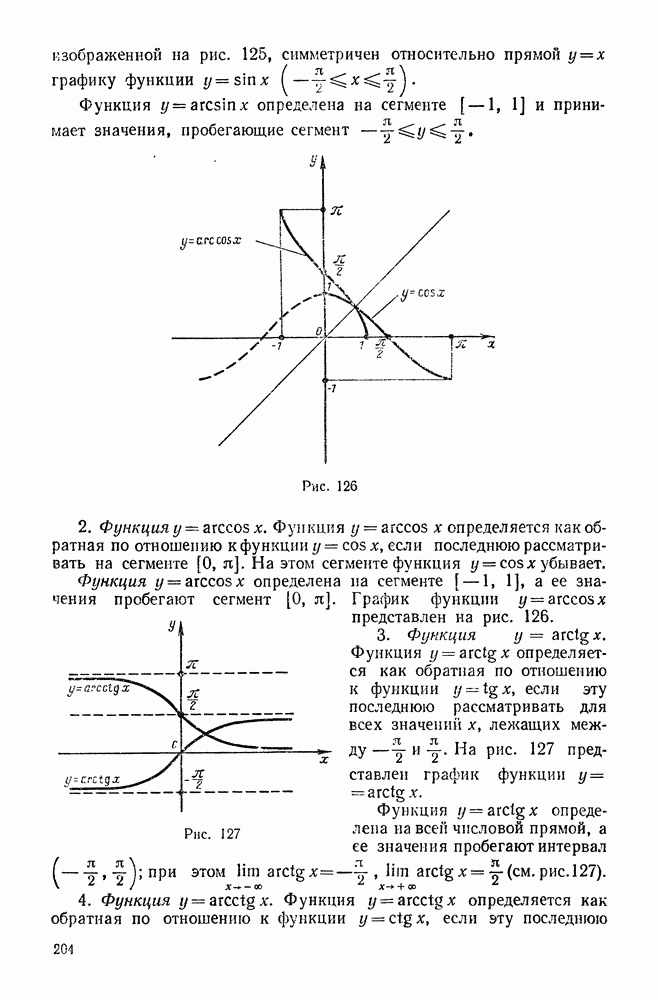
- 4. Проекция вектора на ось и составляются вектора по оси
- 5. Разложение вектора на составляющие по осям координат
- 6. Направляющие косинусы вектора
- 7. Условие коллинеарности двух векторов
- 8. Скалярное произведение
- 9. Выражение скалярного произведения через проекции перемножаемых векторов
- 10. Косинус угла между двумя векторами
- 11. Векторное произведение
- 12. Выражение векторного произведения через проекции перемножаемых векторов
- 13. Смешанное произведение трех векторов
- 14. Геометрический смысл смешанного произведения
- 15. Условие компланарности трех векторов
- § 4. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 2. Равенство матриц. Действия над матрицами
- 3. Обратная матрица
- 4. Матричная запись и матричное решение системы уравнений первой степени
- § 5. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ
- 2. Преобразование координат
- 3. Приведение квадратичной формы к каноническому виду
- 4. Упрощение общего уравнения кривой второго порядка
- ГЛАВА IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
- § 1. ПЛОСКОСТЬ
- 2. Нормальный вектор плоскости. Уравнение плоскости, проходящей через данную точку
- 3. Общее уравнение плоскости и его частные случаи
- 4. Построение плоскости по ее уравнению
- 5. Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей
- 6. Точка пересечения трех плоскостей
- § 2. ПРЯМАЯ В ПРОСТРАНСТВЕ
- 2. Общие уравнения прямой
- 3. Векторное уравнение прямой. Параметрические уравнения прямой
- 4. Канонические уравнения прямой
- 5. Уравнения прямой, проходящей через две точки
- 6. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых
- § 3. Прямая и плоскость в пространстве
- 2. Точка пересечения прямой с плоскостью
- 3. Расстояние от точки до плоскости
- 4. Пучок плоскостей
- § 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
- 2. Цилиндрические поверхности
- 3. Конические поверхности
- 4. Поверхность вращения
- 6. Гиперболоиды
- 7. Параболоиды
- ГЛАВА V. ТЕОРИЯ ПРЕДЕЛОВ
- § 1. ПРЕДЕЛ ФУНКЦИИ
- 2. Предел функции при х -> -оо
- 3. Предел функции при х->х0
- 4. Бесконечно малые функции. Ограниченные функции
- 5. Бесконечно большие функции и их связь с бесконечно малыми функциями
- 6. Основные теоремы о пределах
- 7. Предел функции при x -> 0
- 8. Последовательность. Число e
- 9. Натуральные логарифмы
- 10. Сравнение бесконечно малых функций
- § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 2. Операции над непрерывными функциями. Непрерывность элементарных функций
- 3. Свойства функций, непрерывных на сегменте
- 4. Понятие об обратной функции
- 5. Обратные тригонометрические функции
- 6. Показательная и логарифмическая функции
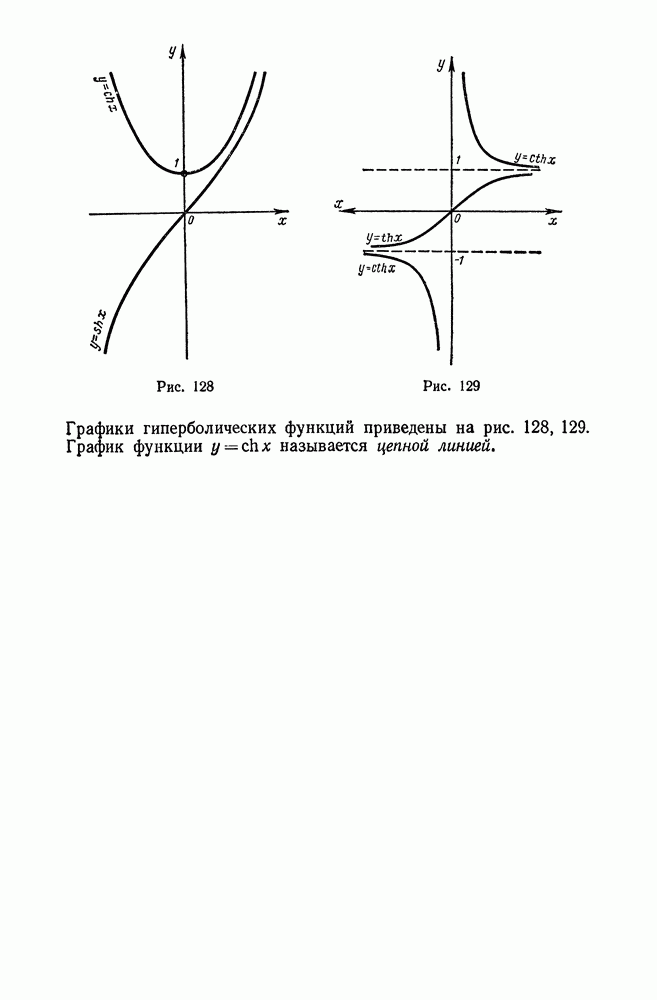
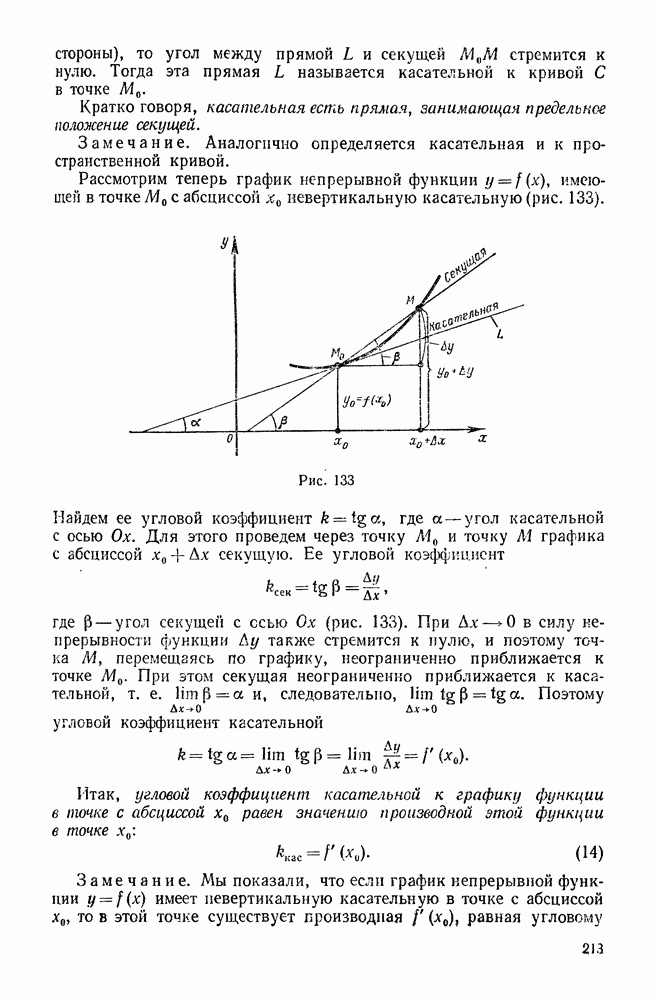
- 7. Понятие о гиперболических функциях
- ГЛАВА VI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
- 1. Приращение аргумента и приращение функции
- 2. Определение непрерывности функции с помощью понятии приращения аргумента и приращения функции
- 3. Задачи, приводящие к понятию производной
- 4. Определение производной и ее механический смысл
- 5. Дифференцируемость функции
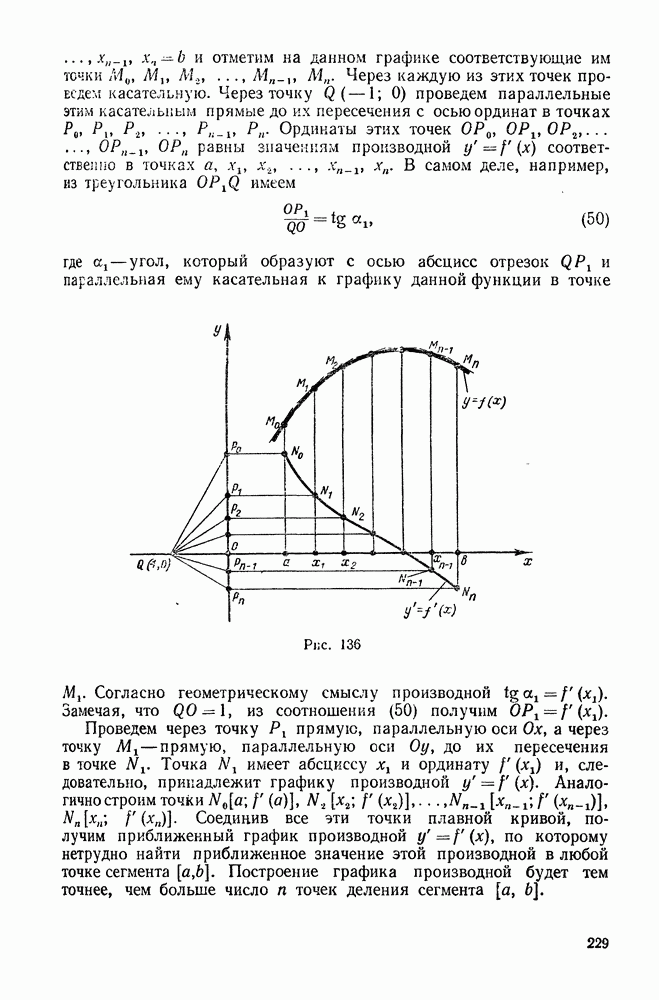
- 6. Геометрический смысл производной
- 7. Производные некоторых основных элементарных функций
- 8. Основные правила дифференцирования
- 9. Производная обратной функции
- 10. Производные обратных тригонометрических функций
- 11. Производная сложной функции
- § 12. Производные гиперболических функций
- 13. Производная степенной функции с любым показателем
- 14. Сводная таблица формул дифференцирования
- 15. Неявные функции и их дифференцирование
- 16. Уравнения касательной а нормали к кривой
- 17. Графическое дифференцирование
- § 2. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
- 1. Нахождение производных высших порядков
- 2. Механический смысл второй производной
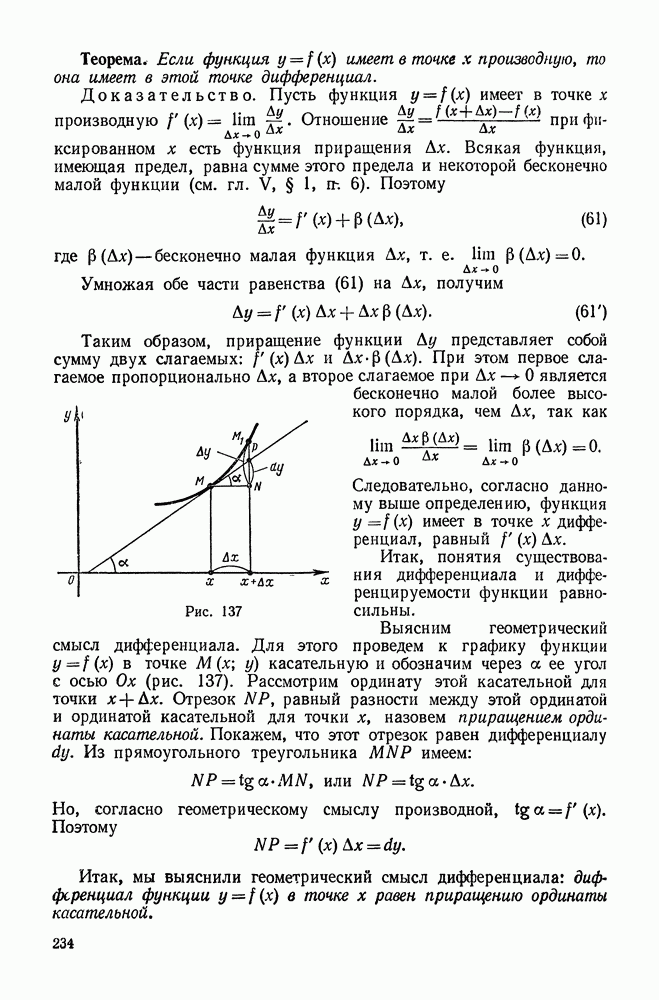
- § 3. ДИФФЕРЕНЦИАЛ ФУНКЦИИ
- 2. Производная как отношение дифференциалов
- 3. Дифференциал суммы, произведения и частного функций
- 4. Дифференциал сложной функции. Инвариантность формы дифференциала
- 5. Применение дифференциала к приближенным вычислениям
- 6. Дифференциалы высших порядков
- § 4. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ, И ИХ ДИФФЕРЕНЦИРОВАНИЕ
- 2. Дифференцирование функций, заданных параметрически
- § 5. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА
- 2. Векторная функция скалярного аргумента и ее производная
- 3. Уравнения касательной прямой и нормальной плоскости к пространственной кривой
- 4. Механический смысл первой и второй производных векторной функции скалярного аргумента
- § 6. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ
- 2. Теорема Ролля
- 3. Теорема Лагранжа
- 4. Правило Лопиталя
- § 7. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ
- 2. Максимум и минимум функции
- 3. Достаточный признак существования экстремума, основанный на знаке второй производной
- 4. Отыскание наибольшего и наименьшего значений функции
- 5. Применение теории максимума и минимума к решению задач
- 6. Выпуклость и вогнутость графика функции. Точки перегиба
- 7. Асимптоты графика функции
- 8. Общая схема исследования функции и построение ее графика
- § 8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ
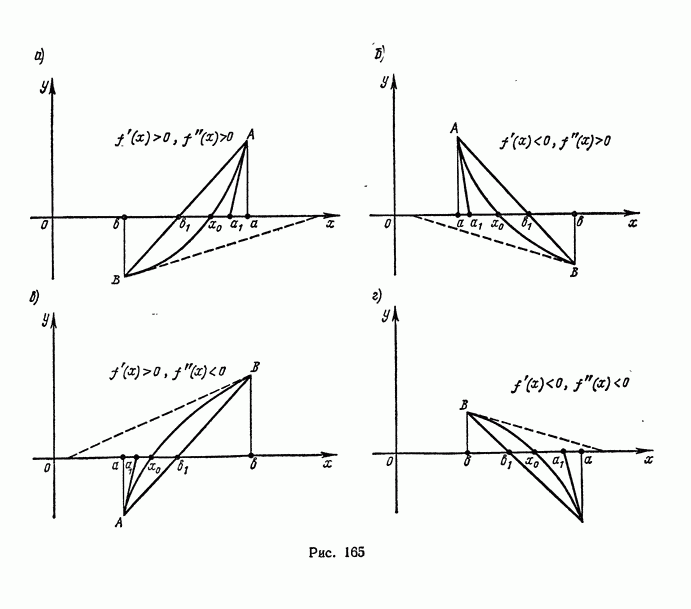
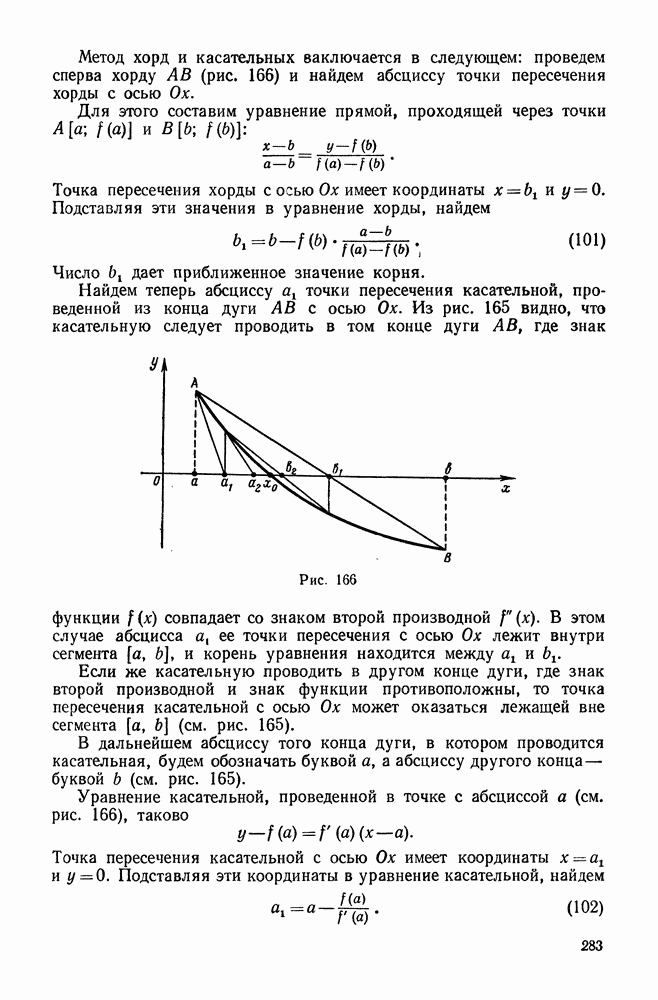
- 2. Уточнение найденных значений корней методом хорд и касательных
- § 9. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА
- ГЛАВА VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА
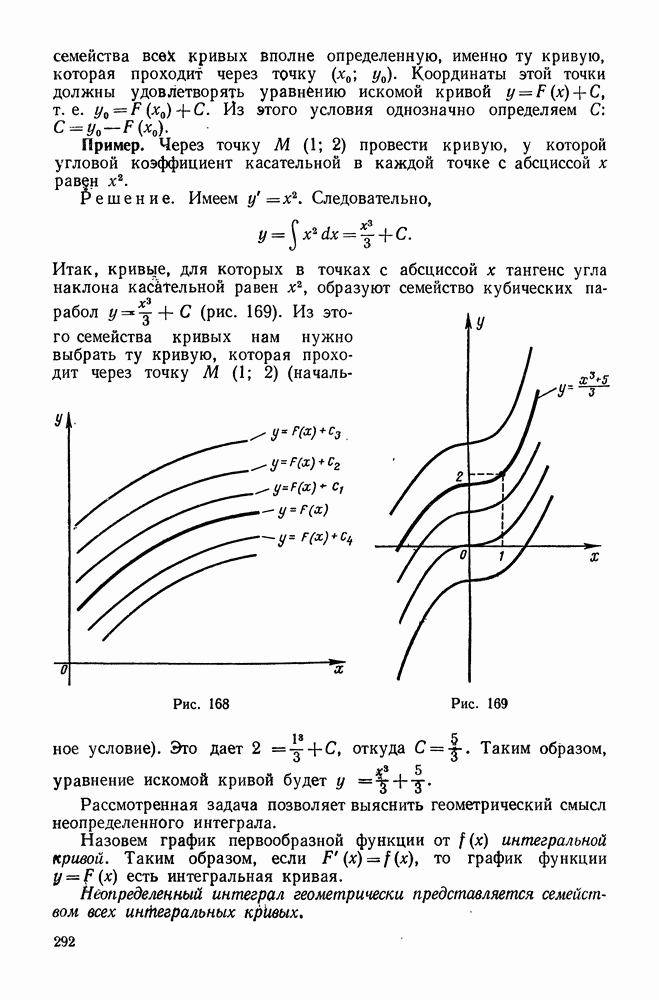
- 2. Геометрический смысл неопределенного интеграла
- 3. Таблица основных интегралов
- 4. Основные свойства неопределенного интеграла
- § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
- 2. Интегрирование методом замены переменной
- 3. Интегрирование по частям
- § 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- 2. Рациональные дроби. Выделение правильной рациональной дроби
- 3. Интегрирование простейших рациональных дробей
- 4. Разложение правильной рациональной дроби на простейшие дроби
- 5. Метод неопределенных коэффициентов
- 6. Интегрирование рациональных дробей
- § 4. Интегрирование тригонометрических функций
- 2. Рациональные функции двух переменных
- 3. Интегралы вида
- § 5. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ
- 2. Интеграл вида
- 3. Интегралы видов
- 4. Интегралы вида
- § 6. ОБЩИЕ ЗАМЕЧАНИЯ О МЕТОДАХ ИНТЕГРИРОВАНИЯ. ИНТЕГРАЛЫ, НЕ БЕРУЩИЕСЯ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ
- 2. Понятие об интегралах, не берущихся в элементарных функциях
- ГЛАВА VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- § 1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ОПРЕДЕЛЕННОМУ ИНТЕГРАЛУ
- 2. Задача о работе переменной силы
- § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
- 2. Свойства определенного интеграла
- 3. Производная интеграла по переменной верхней границе
- 4. Формула Ньютона—Лейбница
- 5. Замена переменной в определенном интеграле
- 6. Интегрирование по частям в определенном интеграле
- § 3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
- 2. Вычисление площади в полярных координатах
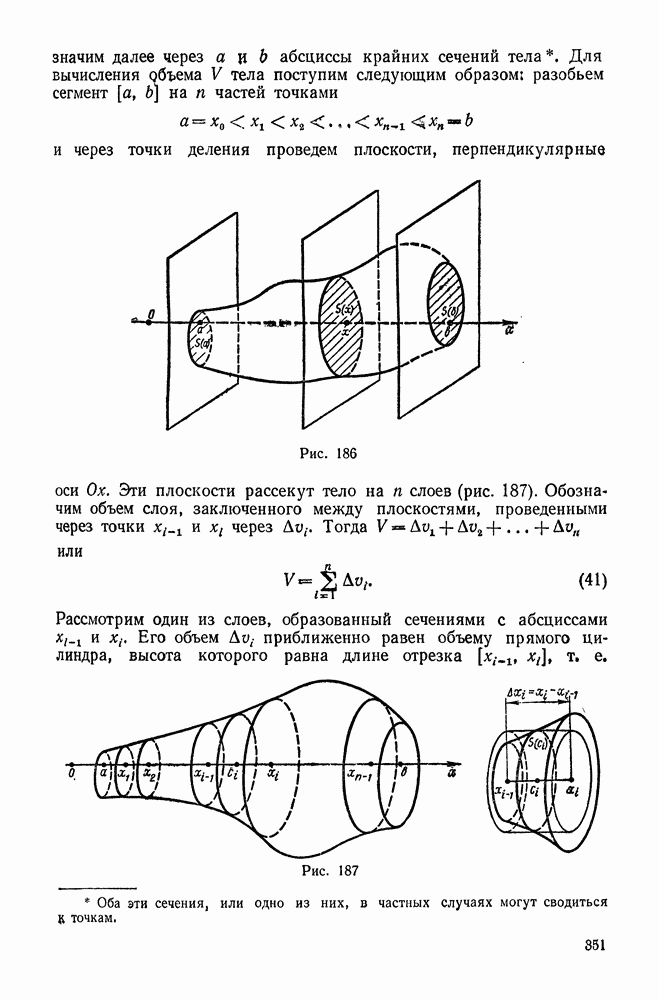
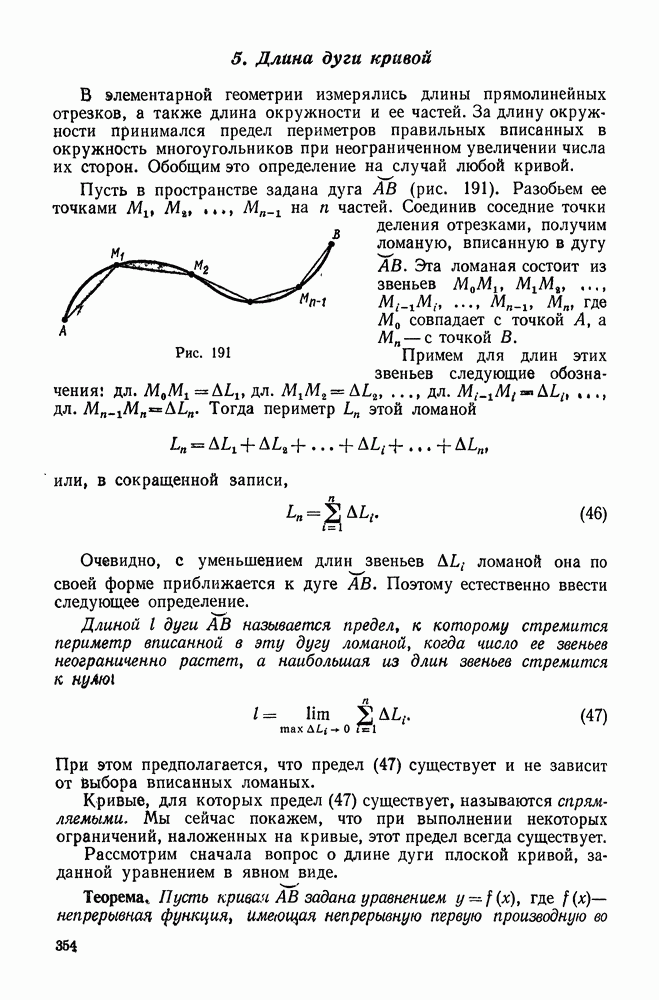
- 3. Вычисление объема тела по известным поперечным сечениям
- 4. Объем тела вращения
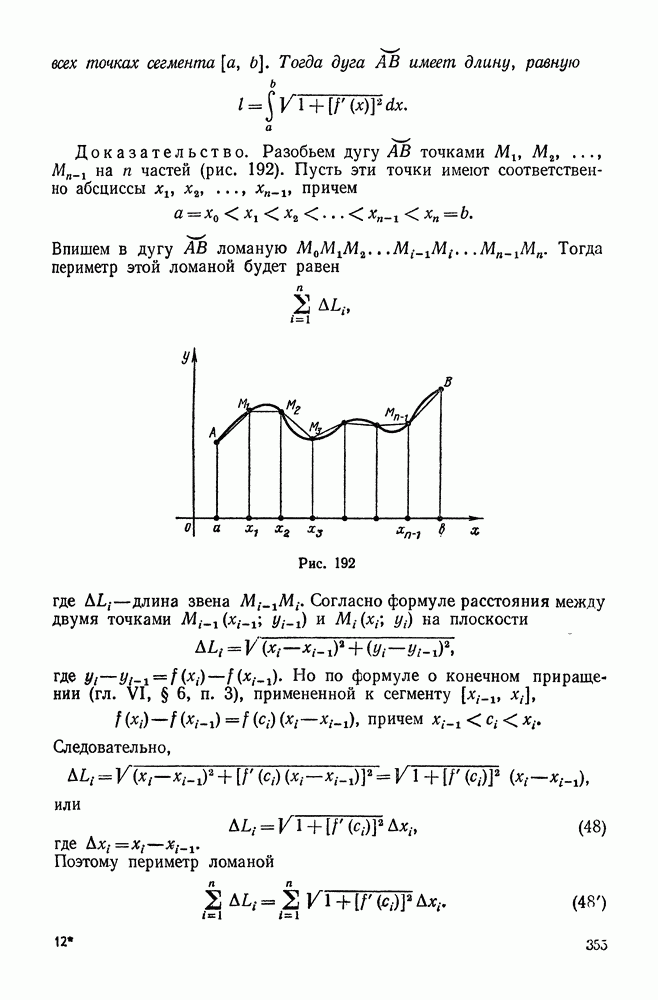
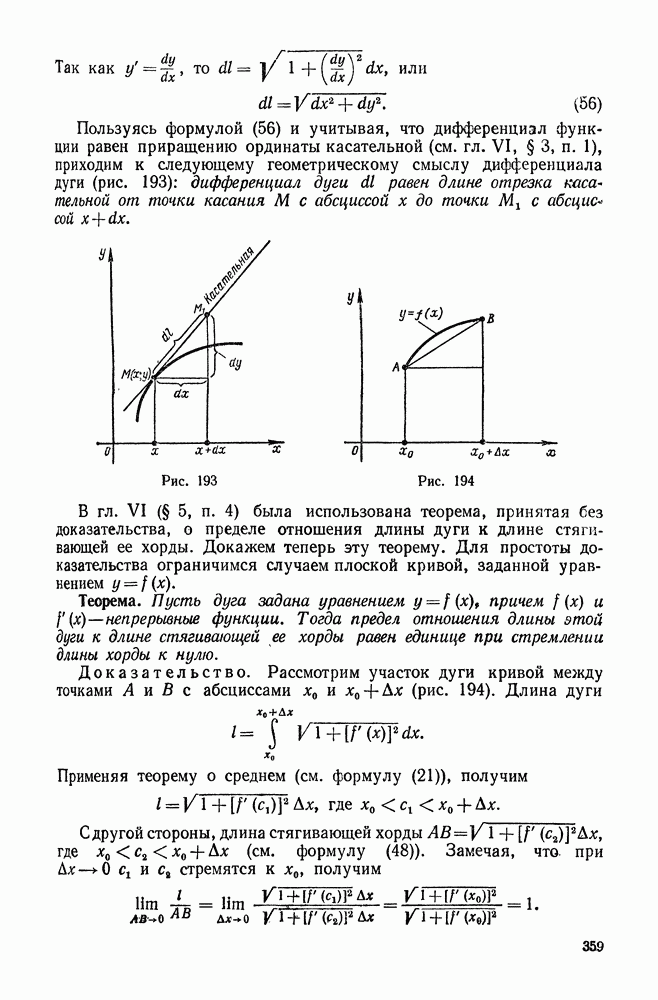
- 5. Длина дуги кривой
- 6. Дифференциал дуги
- 7. Площадь поверхности вращения
- 8. Общие замечания о решении задач методом интегральных сумм
- § 4. КРИВИЗНА ПЛОСКОЙ КРИВОЙ
- 2. Вычисление кривизны
- 3. Радиус кривизны. Круг кривизны. Центр кривизны
- 4. Эволюта и эвольвента
- § 5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
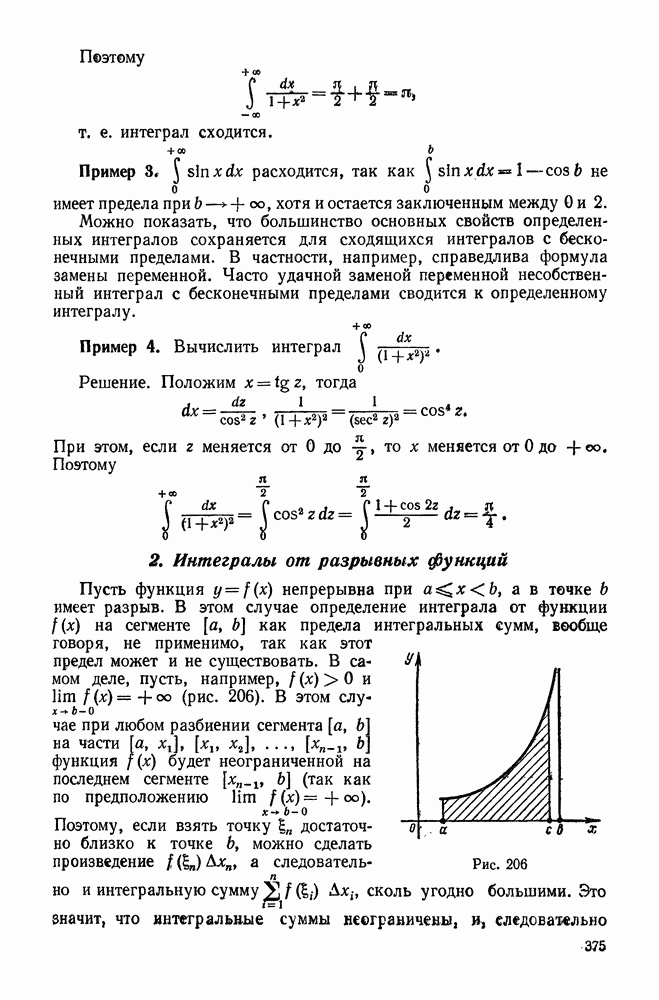
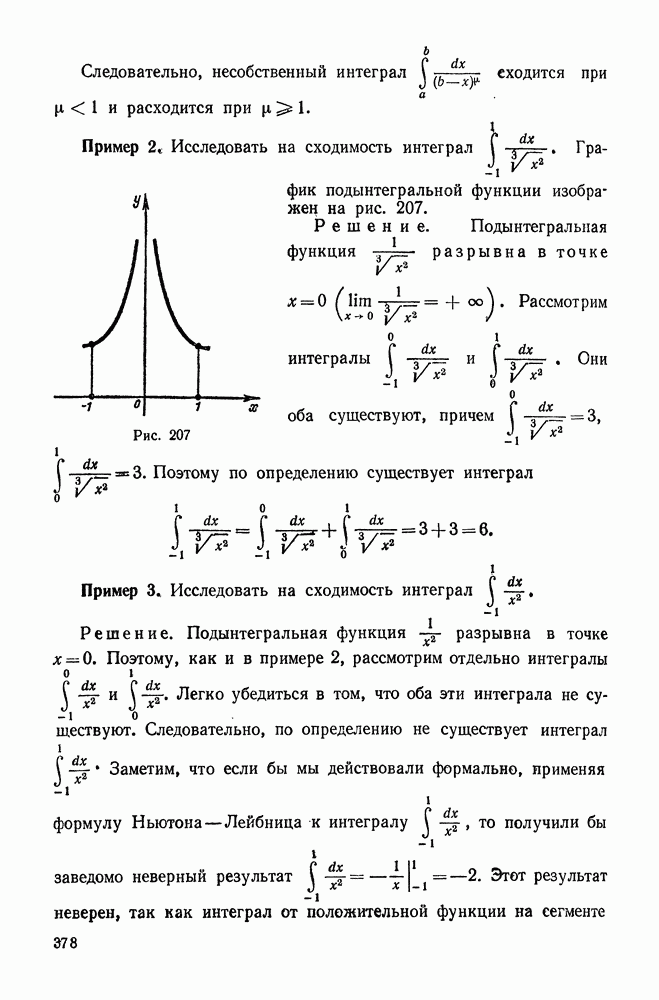
- 2. Интегралы от разрывных функций
- 3. Признаки сходимости несобственных интегралов
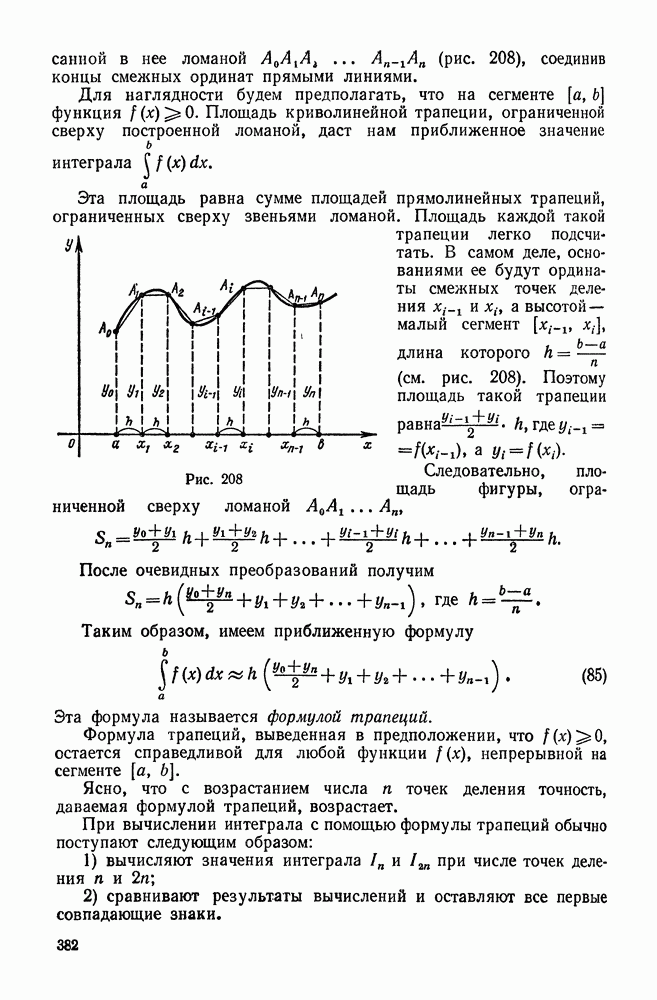
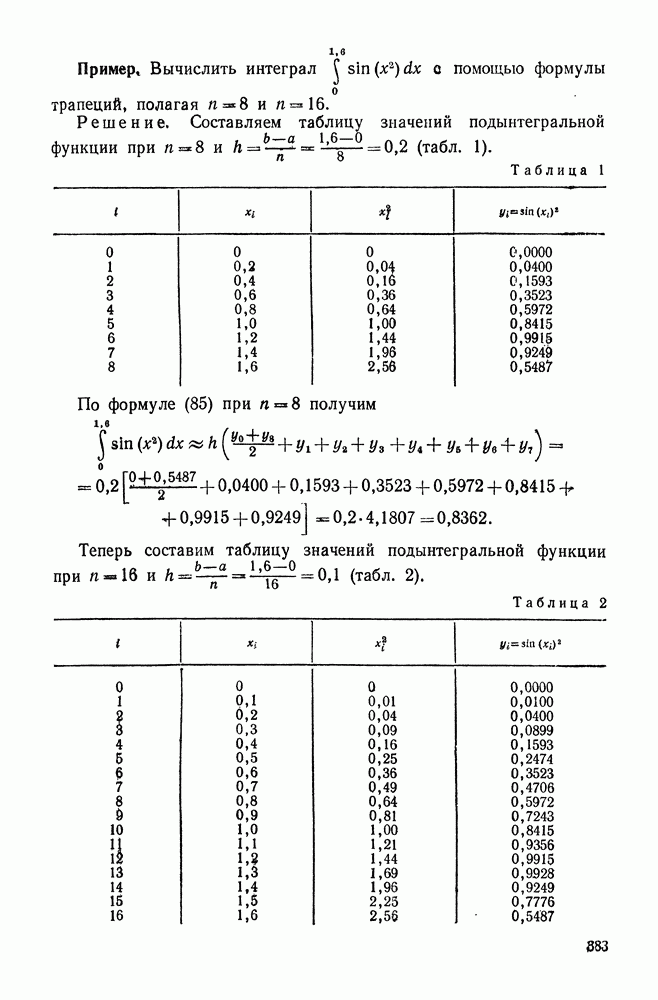
- § 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
- 2. Метод трапеций
- 3. Метод параболических трапеций (метод Симпсона)
- ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- § 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 2. График функции двух переменных
- 3. Функции трех и большего числа переменных
- § 2. Предел функции нескольких переменных. Непрерывность функции. Точки разрыва
- 2. Непрерывность функции нескольких переменных
- 3. Понятие области
- 4. Точки разрыва
- 5. Свойства функций, непрерывных в ограниченной замкнутой области
- § 3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ
- 2. Геометрический смысл частных производных функции двух переменных
- 3. Частные производные высших порядков
- § 4. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
- 2. Полный дифференциал функции
- 3. Приложение полного дифференциала к приближенным вычислениям
- § 5. Дифференцирование сложных и неявных функций
- 2. Инвариантность формы полного дифференциала
- 3. Дифференцирование неявных функций
- § 6. СКАЛЯРНОЕ ПОЛЕ
- 2. Производная по направлению
- 3. Градиент
- 4. Касательная плоскость а нормаль к поверхности
- 5. Геометрический смысл полного дифференциала функции двух переменных
- § 7. ЭКСТРЕМУМ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ
- 2. Наибольшее и наименьшее значения функции двух переменных
- ГЛАВА X. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- § 1. ДВОЙНОЙ ИНТЕГРАЛ
- 2. Двойной интеграл. Теорема существования
- 3. Свойства двойного интеграла
- 4. Вычисление двойного интеграла в декартовых координатах
- 5. Вычисление двойного интеграла в полярных координатах
- 6. Приложения двойного интеграла
- § 2. ТРОЙНОЙ ИНТЕГРАЛ
- 2. Тройной интеграл и его свойства
- 3. Вычисление тройного интеграла в декартовых координатах
- 4. Вычисление тройного интеграла в цилиндрических координатах
- 5. Приложения тройного интеграла
- § 3. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
- 2. Задача о работе. Криволинейный интеграл
- 3. Вычисление криволинейного интеграла
- 4. Формула Остроградского — Грина
- 5. Независимость криволинейного интеграла от пути интегрирования
- 6. Отыскание первообразной по полному дифференциалу
- 7. Криволинейный интеграл по длине дуги
- ГЛАВА XI. РЯДЫ
- § 1. ЧИСЛОВЫЕ РЯДЫ
- 2. Геометрическая прогрессия
- 3. Простейшие свойства числовых рядов
- 4. Необходимый признак сходимости ряда
- 5. Достаточные признаки сходимости знакоположительных рядов
- 6. Знакопеременные ряды
- 7. Остаток ряда и его оценка
- § 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
- 2. Правильно сходящиеся функциональные ряды и их свойства
- § 3. СТЕПЕННЫЕ РЯДЫ
- 2. Свойства степенных рядов
- 3. Ряды по степеням разности х-а
- 4. Разложение функций в степенные ряды. Ряд Тейлора
- 5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена
- § 4. ПРИЛОЖЕНИЕ РЯДОВ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ
- 2. Приближенное вычисление интегралов
- § 5. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. СТЕПЕННЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ
- 2. Числовые ряды с комплексными членами
- 3. Степенные ряды в комплексной области
- § 6. РЯДЫ ФУРЬЕ
- 2. Ряд Фурье
- 3. Сходимость ряда Фурье
- 4. Ряды Фурье для четных и нечетных функций
- 5. Разложение в ряд Фурье функций с периодом 2l
- ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
- § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
- 2. Дифференциальные уравнения первого порядка
- 3. Уравнения с разделяющимися переменными
- 4. Однородные уравнения
- 5. Линейные уравнения
- 6. Уравнение в полных дифференциалах
- 7. Особые решения
- 8. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- 2. Простейшие уравнения второго порядка, допускающие понижение порядка
- 3. Понятие о дифференциальных уравнениях высших порядков
- § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
- 2. Линейные однородные дифференциальные уравнения второго порядка
- 3. Линейные неоднородные дифференциальные уравнения второго порядка
- 4. Метод вариации произвольных постоянных
- § 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
- 2. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- 3. Приложение линейных дифференциальных уравнений второго порядка к изучению механических и электрических колебаний
- § 5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
- 2. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами
- § 6. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ
- § 7. ПОНЯТИЕ О СИСТЕМАХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 2. Системы линейных дифференциальных уравнений с постоянными коэффициентами
- ПРИЛОЖЕНИЕ 1. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА
- ПРИЛОЖЕНИЕ 2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ