| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
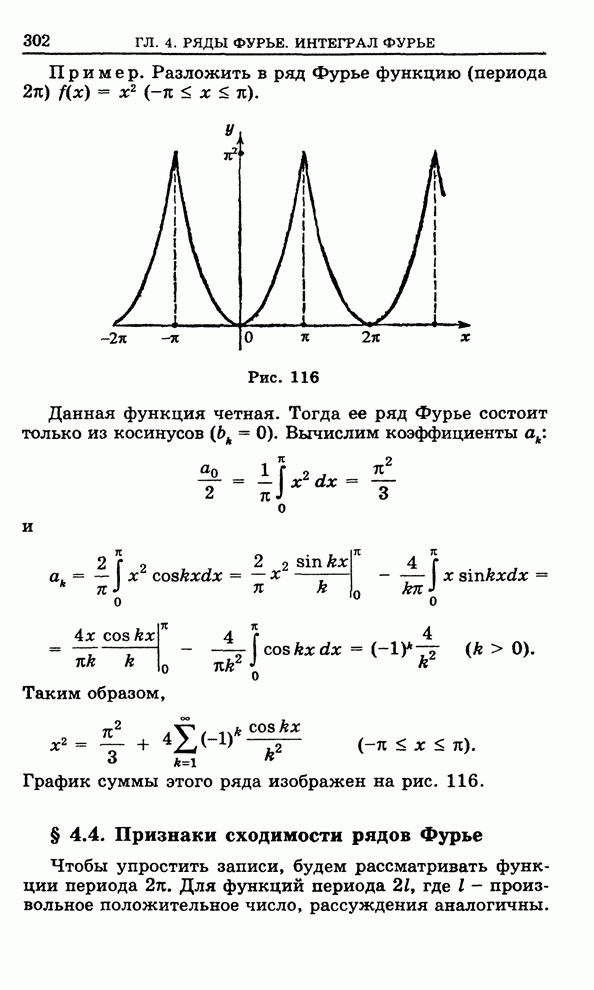
§ 5.7. Малые колебания струны
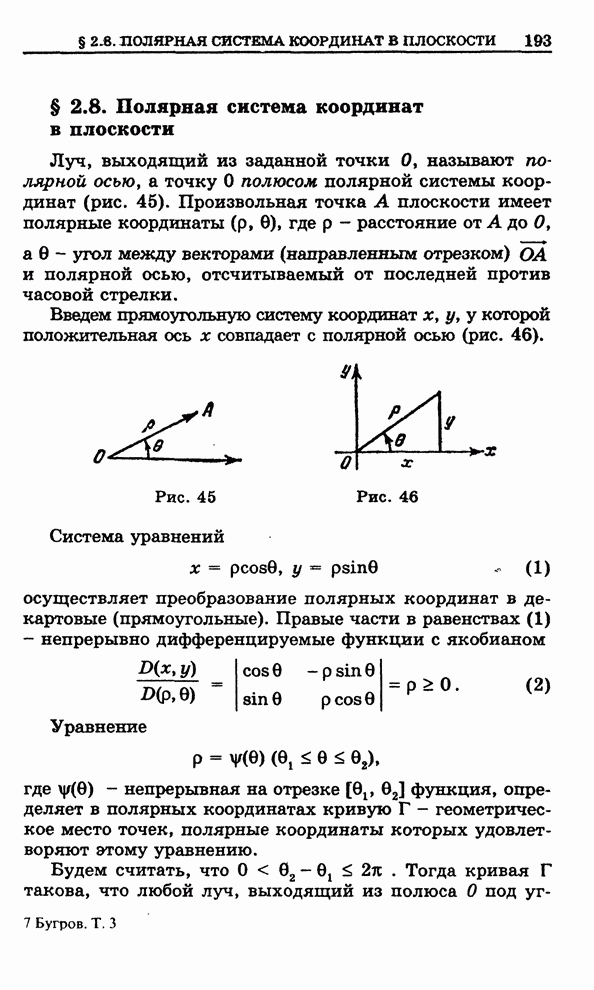
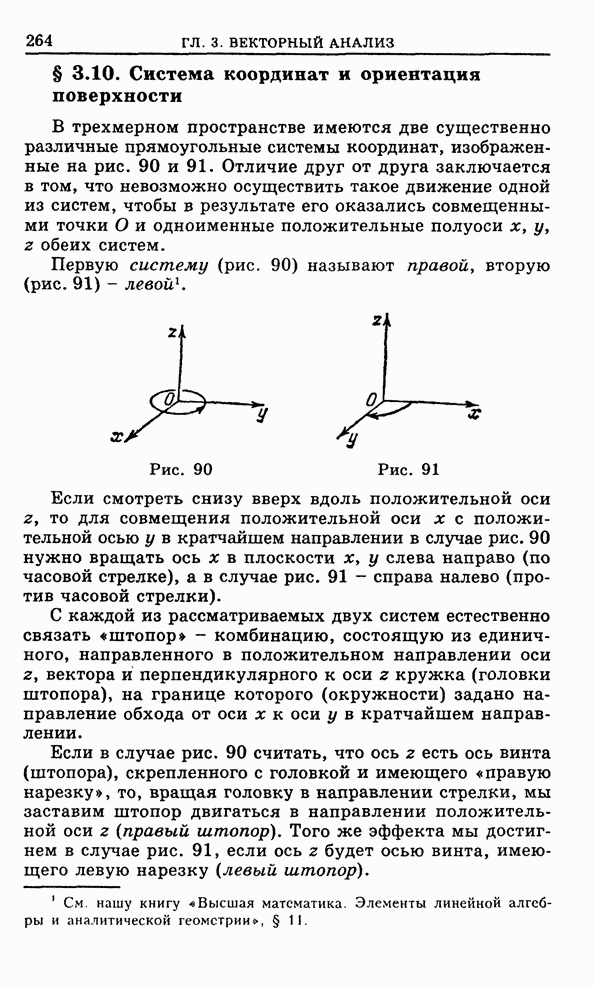
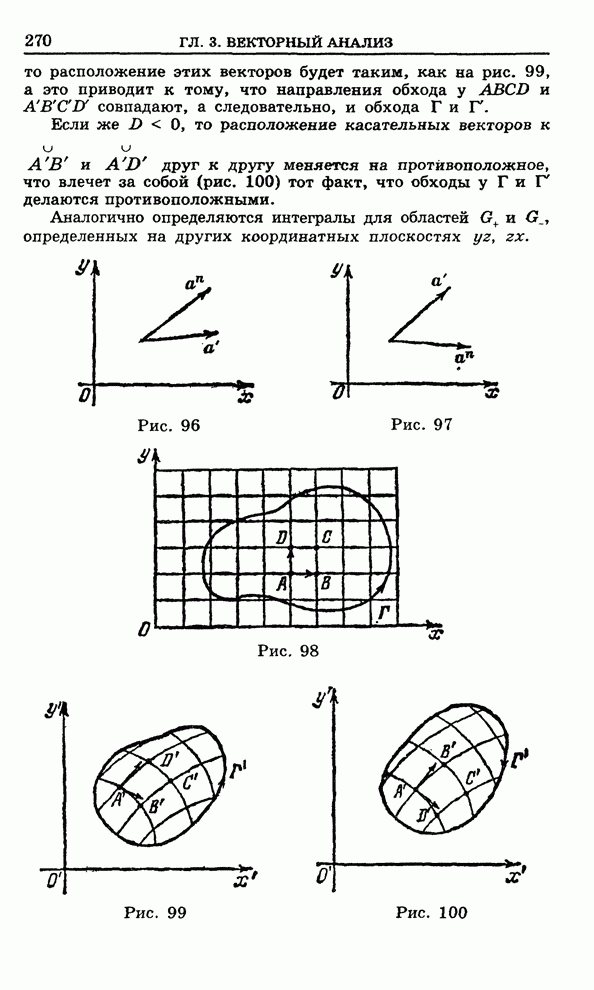
Струной называется тонкая нить, работающая на растяжение, но не на изгиб. Если ненатянутую струну мять, она не сопротивляется, однако если ее растягивать, то в ней возникают напряжения.
Пусть
концы куска натянутой струны закреплены в точках ![]() ,
, ![]() оси
оси ![]() . Будем считать, что величина
возникающего в ней напряжения равна числу
. Будем считать, что величина
возникающего в ней напряжения равна числу ![]() . Плотность струны будем считать
равной числу
. Плотность струны будем считать
равной числу ![]() на
всем ее протяжении. В момент времени
на
всем ее протяжении. В момент времени ![]() выведем нашу струну из равновесия,
например оттянем пальцем и предоставим ей свободно колебаться (дрожать) – совершать
малые колебания.
выведем нашу струну из равновесия,
например оттянем пальцем и предоставим ей свободно колебаться (дрожать) – совершать
малые колебания.

Рис. 125
Отклонение
струны в любой ее точке, имеющей абсциссу ![]() , в момент времени
, в момент времени ![]() обозначим через
обозначим через
![]()
![]() .
.
Выведем
дифференциальное уравнение, которому удовлетворяет функция ![]() .
.
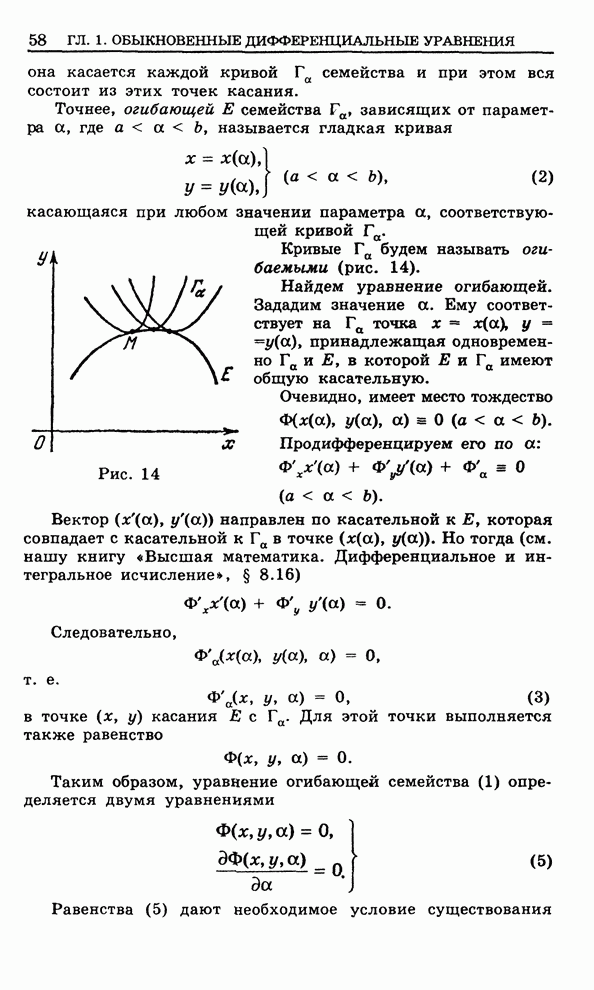
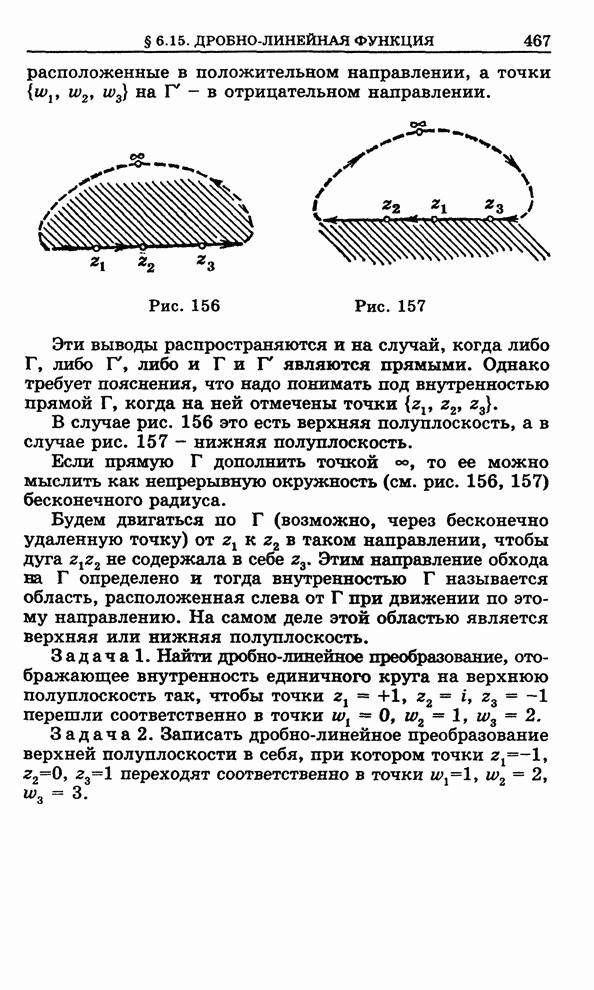
На рис.
125 изображен график нашей струны в момент времени ![]() .
.
На
элемент ее, соответствующий отрезку ![]() , действуют две силы натяжения
, действуют две силы натяжения ![]() и
и ![]() . Скалярная величина
каждой из этих сил равна
. Скалярная величина
каждой из этих сил равна ![]() :
:
![]() .
.
Сила ![]() приложена к точке
приложена к точке ![]() , имеющей абсциссу
, имеющей абсциссу ![]() , направлена по
касательной к струне в этой точке и образует с положительным направлением оси
, направлена по
касательной к струне в этой точке и образует с положительным направлением оси ![]() угол
угол ![]() , тангенс которого
равен
, тангенс которого
равен
![]() .
.
Так как струна совершает малые колебания, то можно считать приближенно
![]() .
.
Таким образом,
![]() .
.
Проекция
силы ![]() на
ось
на
ось ![]() ,
очевидно, равна
,
очевидно, равна
![]() .
.
Проекция
же силы ![]() на
ось
на
ось ![]() ,
очевидно, равна
,
очевидно, равна
![]() .
.
Сумма этих проекций равна
![]() .
.
Мы
пренебрегаем бесконечно малыми более высокого порядка, чем ![]() , потому что рассматриваем,
как говорят, малые колебания струны.
, потому что рассматриваем,
как говорят, малые колебания струны.
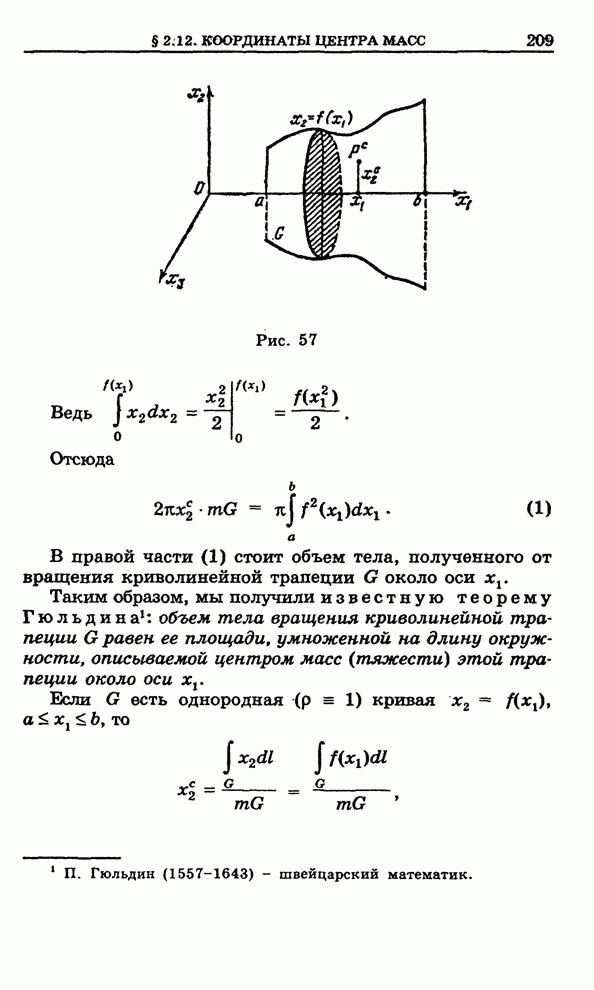
С другой стороны, произведение массы на ускорение рассматриваемого элемента струны равно
![]() .
.
Поэтому на основании закона Ньютона
![]() .
.
Сокращая
на ![]() ,
получим дифференциальное уравнение колебаний струны:
,
получим дифференциальное уравнение колебаний струны:
![]()
![]() . (1)
. (1)
Теперь математическую задачу, к которой приводит изучение свободных колебаний струны, можно сформулировать так: требуется решить линейное дифференциальное уравнение с частными производными второго порядка (1) при начальных условиях
![]() ,
,
![]() (2)
(2)
и при краевых условиях
![]() . (3)
. (3)
Начальные
условия (2) показывают, в каком положении находилась струна в начальный момент
времени и какова скорость каждой ее точки при ![]() . Функции
. Функции ![]() и
и ![]() - заданные функции.
- заданные функции.
Краевые
условия (3) показывают, что концы струны закреплены в точках ![]() и
и ![]() .
.
Решение поставленной задачи можно провести методом Фурье (так же как в § 5.5). Ищем сначала решение уравнения (1) в виде произведения
![]() , (4)
, (4)
удовлетворяющее граничным условиям
![]() (5)
(5)
для всех
![]() . Но
тогда
. Но
тогда
![]() ,
,
потому
что иначе было бы ![]() и
и ![]() .
.
Подставляя произведение (4) в (1), получим
![]() ,
,
или
![]() .
.
Но
функция от ![]() может
равняться функции от
может
равняться функции от ![]() , только если обе они равны
постоянному числу, которое мы обозначим через
, только если обе они равны
постоянному числу, которое мы обозначим через ![]() :
:
![]() .
.
В результате получаем два обыкновенных дифференциальных уравнения
![]() ,
,
![]() , (6)
, (6)
![]() . (7)
. (7)
Уравнение
(6) надо решить с краевыми условиями ![]() , т. е. надо решить для этого
уравнения проблему Штурма-Лиувилля (см. § 5.5). Как показано в § 5.5, решением
этой проблемы являются числа (собственные значения)
, т. е. надо решить для этого
уравнения проблему Штурма-Лиувилля (см. § 5.5). Как показано в § 5.5, решением
этой проблемы являются числа (собственные значения)
![]()
![]()
и соответствующие им нетривиальные функции (собственные функции)
![]()
![]() ,
,
удовлетворяющие при этих числах условиям (5).
Общее
решение уравнения (7) при найденных ![]() имеет вид
имеет вид
![]()
![]() .
.
Следовательно, все решения дифференциального уравнения (1) вида (4), удовлетворяющие граничным условиям (5), можно записать в виде
![]()
![]() ,
,
где
постоянные ![]() ,
,
![]() для
каждого
для
каждого ![]() могут
быть взяты произвольно. Но тогда и любые суммы
могут
быть взяты произвольно. Но тогда и любые суммы

суть решения уравнения (1), удовлетворяющие граничным условиям (5). Вместе с этими суммами обладают этим свойством и суммы бесконечных рядов
 , (8)
, (8)
если
числа ![]() и
и ![]() достаточно быстро
стремятся к нулю, чтобы эти ряды можно было два раза почленно дифференцировать.
достаточно быстро
стремятся к нулю, чтобы эти ряды можно было два раза почленно дифференцировать.
Теперь в
нашем распоряжении имеется большой запас функций ![]() , удовлетворяющих уравнению (1) и граничным
условиям (3), - они определяются формулой (8), где числа
, удовлетворяющих уравнению (1) и граничным
условиям (3), - они определяются формулой (8), где числа ![]() ,
, ![]() - произвольные, лишь бы
выполнялись указанные условия сходимости.
- произвольные, лишь бы
выполнялись указанные условия сходимости.
Чтобы
найти решение поставленной задачи, удовлетворяющее начальным условиям (2),
дифференцируем (8) по ![]() :
:
 (9)
(9)
и
приравниваем (8) и (9) при ![]() заданным функциям
заданным функциям ![]() и
и ![]() :
:
 ,
,
 . (10)
. (10)
Отсюда
 ,
,
 . (11)
. (11)
Если
функции ![]() и
и
![]() непрерывные
на
непрерывные
на ![]() , то
этого достаточно, чтобы можно было вычислить числа
, то
этого достаточно, чтобы можно было вычислить числа ![]() ,
, ![]() по формулам (11) и ряды
(10) будут сходиться к этим функциям во всяком случае в смысле среднего
квадратического (см. § 4.10). Конечно, если функции
по формулам (11) и ряды
(10) будут сходиться к этим функциям во всяком случае в смысле среднего
квадратического (см. § 4.10). Конечно, если функции ![]() и
и ![]() не только непрерывны, но и
имеют непрерывные производные (достаточно третьего порядка), то сумма ряда (8)
уже заведомо будет иметь вторые непрерывные производные.
не только непрерывны, но и
имеют непрерывные производные (достаточно третьего порядка), то сумма ряда (8)
уже заведомо будет иметь вторые непрерывные производные.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. Обыкновенные дифференциальные уравнения
- 1.1. Задача, приводящая к дифференциальному уравнению
- 1.2. Общие понятия
- 1.2.1. Понятие обыкновенного дифференциального уравнения
- 1.2.2. Дифференциальное уравнение первого порядка
- 1.2.3. Задача Коши
- 1.2.4. Примеры дифференциальных уравнений первого порядка
- 1.2.5. Общий интеграл дифференциального уравнения первого порядка
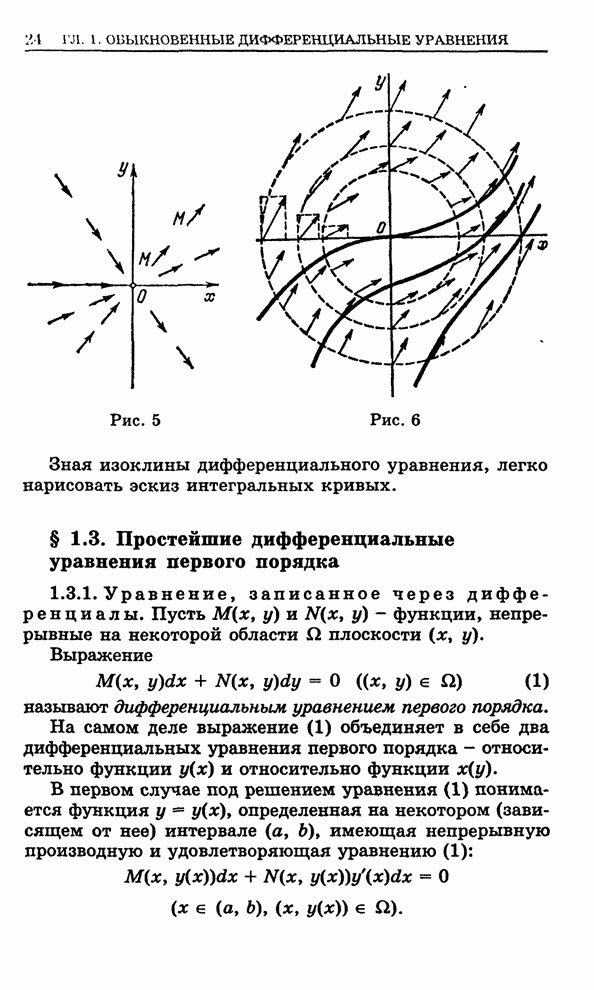
- 1.2.6. Поле направлений
- 1.3. Простейшие дифференциальные уравнения первого порядка
- 1.3.1. Уравнение, записанное через дифференциалы
- 1.3.2. Уравнения с разделенными переменными
- 1.3.3. Уравнения с разделяющимися переменными
- 1.3.4. Однородные уравнения
- 1.3.5. Линейное уравнение
- 1.3.6. Уравнение Бернулли
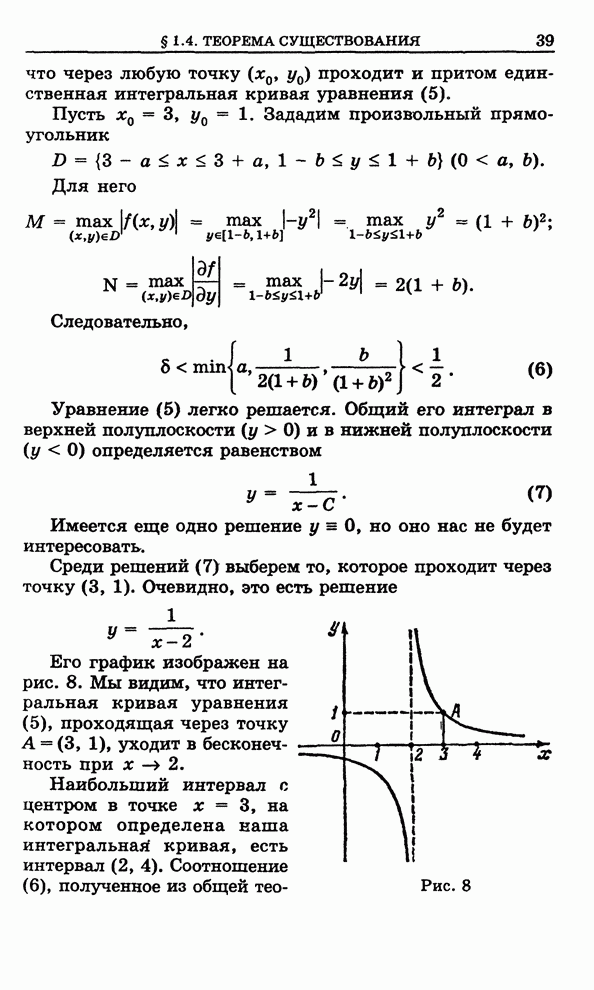
- 1.4. Теорема существования решения дифференциального уравнения первого порядка
- 1.5. Метрическое пространство
- 1.5.1. Понятие метрического пространства
- 1.5.2. Полное метрическое пространство
- 1.5.3. Принцип сжатых отображений
- 1.5.4. Приближенное значение корня функции
- 1.5.5. Метод Ньютона
- 1.6. Доказательство теоремы существования решения диффереацнального уравнения первого порядка
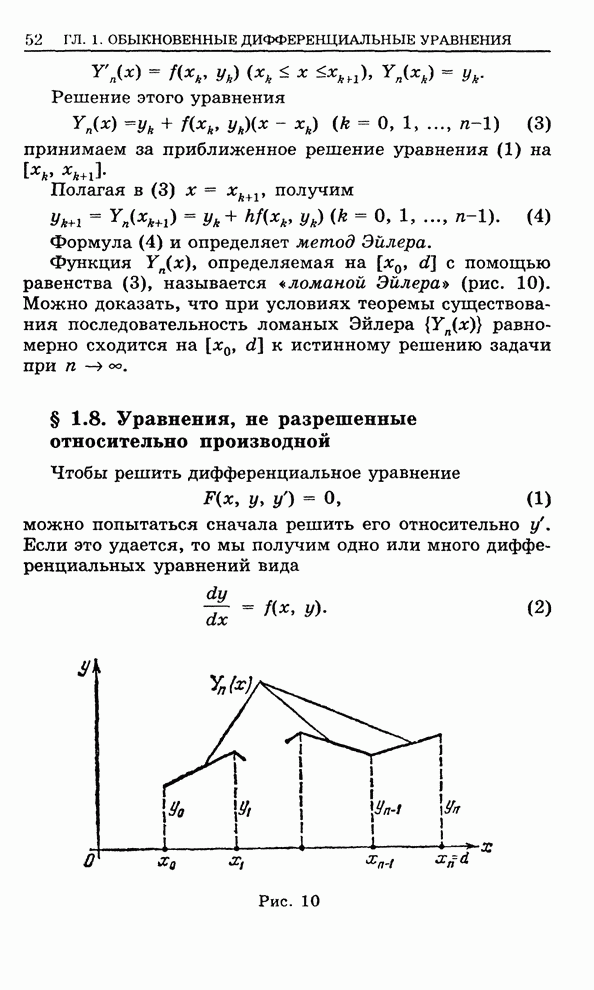
- 1.7. Метод Эйлера приближенного решения дифференциального уравнения первого порядка
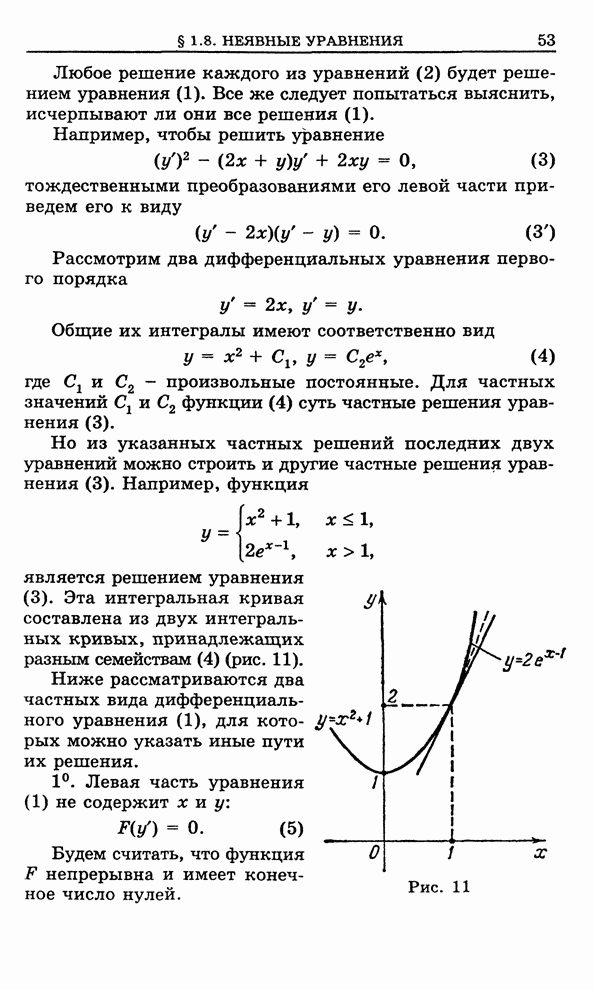
- 1.8. Уравнения, не разрешенные относительно производной
- 1.9. Особые решения
- 1.10. Огибающая семейства кривых
- 1.11. Дифференциальное уравнение второго порядка
- 1.12. Система из двух дифференциальных уравнений первого порядка
- 1.13. Дифференциальное уравнение n-го порядка
- 1.14. Понижение порядка дифференциального уравнения
- 1.15. Линейные уравнения высшего порядка
- 1.15.1. Понятие линейного уравнения высшего порядка
- 1.15.2. Фундаментальная система решений уравнения
- 1.15.3. Определитель Вронского
- 1.15.4. Структура общего решения
- 1.16. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- 1.16.1. Методы решения
- 1.16.2. Уравнение Эйлера
- 1.17. Метод вариации постоянных
- 1.18. Частное решение неоднородного уравнения с постоянными коэффициентами. Приложения
- 1.18.1. Методы нахождения частных решений
- 1.18.2. Дифференциальное уравнение колебания пружины
- 1.19. Системы дифференциальных уравнений. Фазовое пространство
- 1.20. Линейная однородная система дифференциальных уравнений
- 1.21. Общее решение линейной однородной системы дифференциальных уравнений с постоянными коэффициентами
- 1.22. Сведение системы уравнений к одному уравнению
- 1.23. Неоднородная система линейных дифференциальных уравнений с постоянными коэффициентами
- 1.24. Интегрирование дифференциальных уравнений с помощью степенных рядов
- 1.25. Элементы теории устойчивости
- 1.26. Классификация точек покоя
- Глава 2. Кратные интегралы
- 2.1. Введение
- 2.2. Сведения из теории меры Жордана
- 2.3. Свойства кратных интегралов. Теоремы существования
- 2.4. Сведение кратного интеграла к повторным
- 2.5. Доказательство существования интеграла от непрерывной функции
- 2.6. Замена переменных. Простейший случай
- 2.7. Замена переменных. Общий случай
- 2.8. Полярная система координат в плоскости
- 2.9. Полярная система координат в пространстве
- 2.10. Цилиндрические координаты
- 2.11. Площадь поверхности
- 2.12. Координаты центра масс
- 2.13. Несобственные интегралы
- 2.14. Несобственный интеграл с особенностями вдоль линии
- 2.15. Несобственный интеграл, зависящий от параметра
- Глава 3. Векторный анализ
- 3.1. Кусочно-гладкая ориентированная кривая
- 3.2. Криволинейный интеграл первого рода
- 3.3. Интеграл от вектора вдоль кривой
- 3.3.1. Поле вектора
- 3.3.2. Криволинейный интеграл от вектора вдоль кривой
- 3.3.3. Свойства криволинейных интегралов второго рода
- 3.4. Поле потенциала
- 3.4.1. Понятие потенциала и его свойства
- 3.4.2. Доказательство свойств потенциала
- 3.4.3. Ротор вектора
- 3.5. Дифференциальное уравнение в полных дифференциалах
- 3.6. Ориентация плоской области
- 3.7. Формула Грина
- 3.8. Интеграл по поверхности первого рода
- 3.9. Ориентация поверхности
- 3.10. Система координат и ориентация поверхности
- 3.11. Интеграл по ориентированной плоской области
- 3.12. Поток вектора через ориентированную поверхность
- 3.13. Дивергенция. Теорема Гаусса—Остроградского
- 3.14. Соленоидальное поле
- 3.15. Формула Стокса
- Глава 4. Ряды Фурье. Интеграл Фурье
- 4.1. Тригонометрические ряды
- 4.2. Сходимость тригонометрических рядов
- 4.3. Ряд Фурье
- 4.4. Признаки сходимости рядов Фурье
- 4.5. Ортогональные свойства тригонометрических функций
- 4.6. Коэффициенты Фурье
- 4.7. Оценка коэффициентов Фурье
- 4.8. Пространство функций со скалярным произведением
- 4.9. Ортогональная система функций
- 4.10. Полнота тригонометрических функций
- 4.11. Комплексная форма ряда Фурье
- 4.12. Понятие интеграла Фурье. Повторный интеграл Фурье
- 4.13. Косинус- и синус- преобразования Фурье
- 4.14. Примеры
- 4.15. Приближение интеграла Фурье
- 4.16. Сумма Фейера
- 4.17. Полнота систем функций в С и L2’
- 4.18. Сведения из теории кратных рядов Фурье
- Глава 5. Уравнения математической физики
- 5.1. Температура тела
- 5.2. Задача Дирихле
- 5.3. Задача Дирихле для круга
- 5.4. Задача Дирихле для полуплоскости
- 5.5. Уравнение теплопроводности в стержне
- 5.6. Теплопроводность для бесконечного стержня
- 5.7. Малые колебания струны
- 5.8. Колебание бесконечной струны. Формула Даламбера
- 5.9. Колебание круглой мембраны
- 5.10. Общая задача Штурма-Лиувилля
- 5.11. Интеграл энергии (Дирихле)
- 5.12. Применение преобразований Фурье
- Глава 6. Теория функций комплексного переменного
- 6.1. Понятие функции комплексного переменного
- 6.2. Производная функция комплексного переменного
- 6.3. Условия Даламбера-Эйлера (Коши-Римана)
- 6.4. Гармонические функции
- 6.5. Обратная функция
- 6.6. Интегрирование функций комплексного переменного
- 6.7. Формула Коши
- 6.8. Интеграл типа Коши
- 6.9. Степенной ряд
- 6.10. Ряд Лорана
- 6.11. Классификация изолированных особых точек. Вычеты
- 6.12. Классификация особых точек на бесконечности
- 6.13. Теорема о вычетах
- 6.14. Вычисление интегралов при помощи вычетов
- 6.15. Линейная функция. Дробно-линейная функция
- Глава 7. Операционное исчисление
- 7.1. Изображение Лапласа
- 7.2. Изображение простейших функций и свойства изображений
- 7.3. Приложения операционного исчисления
- 7.3.1. Операторное уравнение
- 7.3.2. Решение систем дифференциальных уравнений
- 7.3.3. Вычисление интегралов
- Глава 8. Обобщенные функции
- 8.1. Понятие обобщенной функции
- 8.2. Операции над обобщенными функциями
- 8.3. Преобразование Фурье обобщенных функций