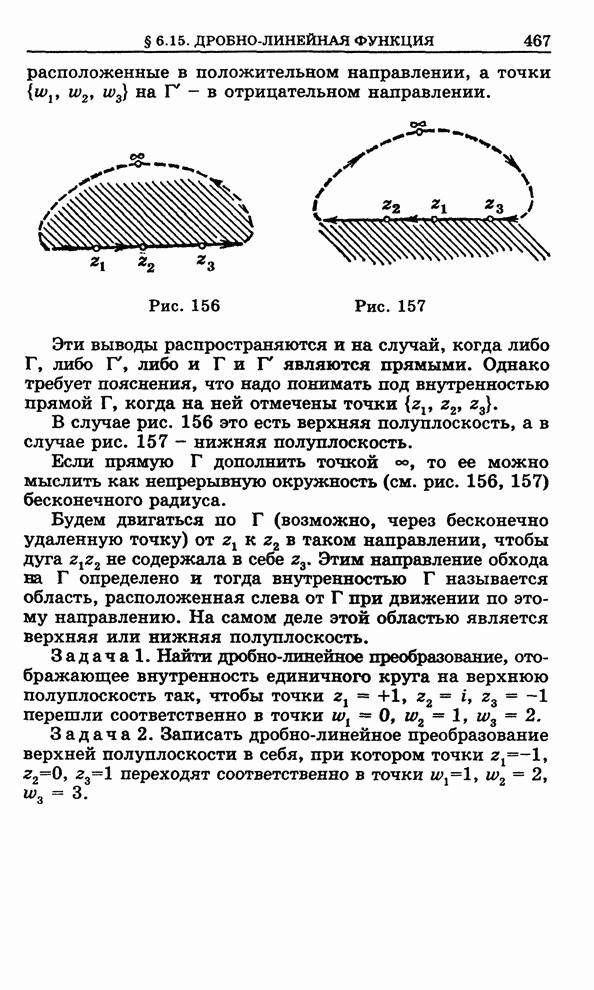
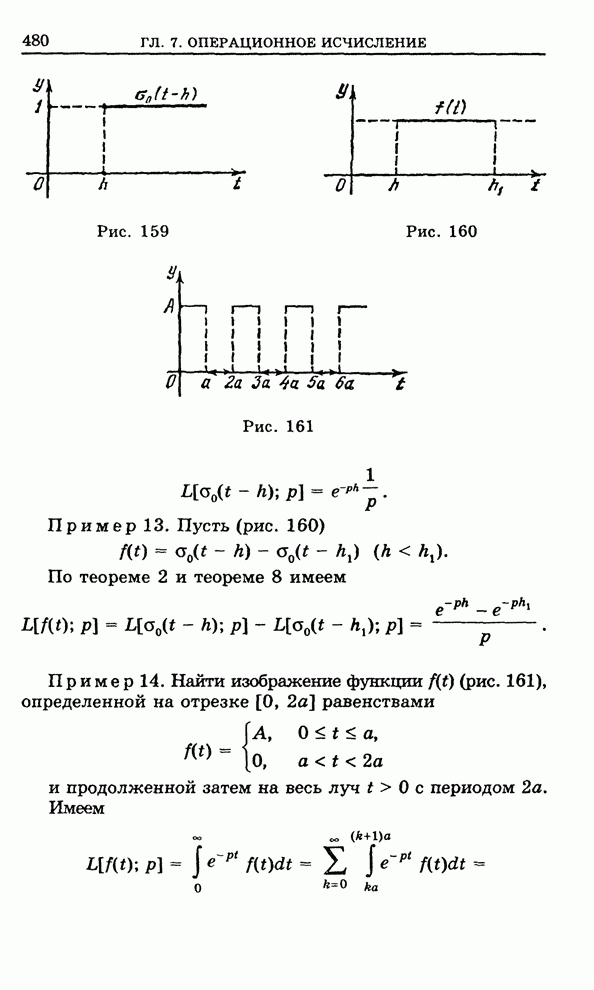
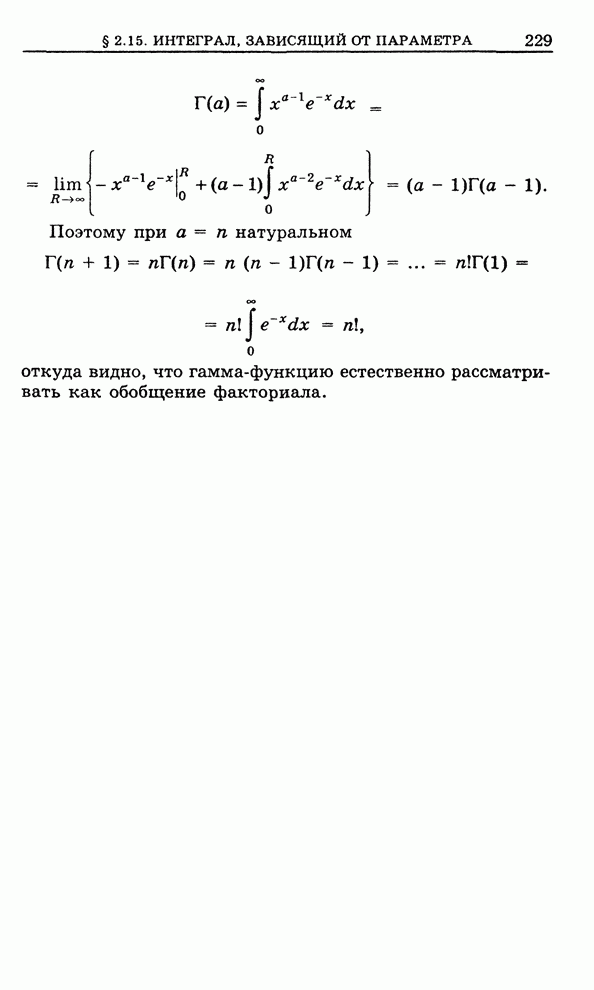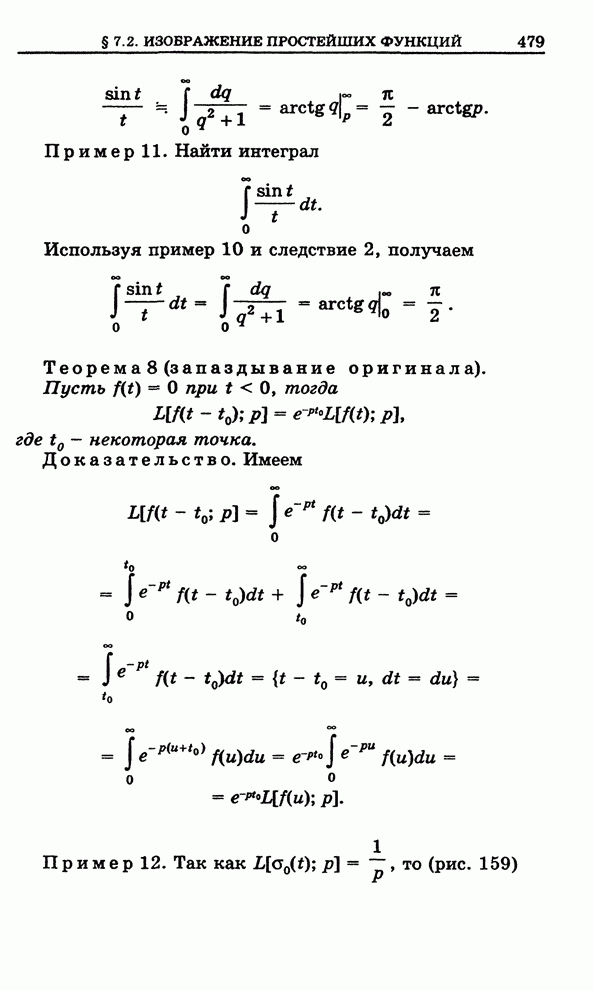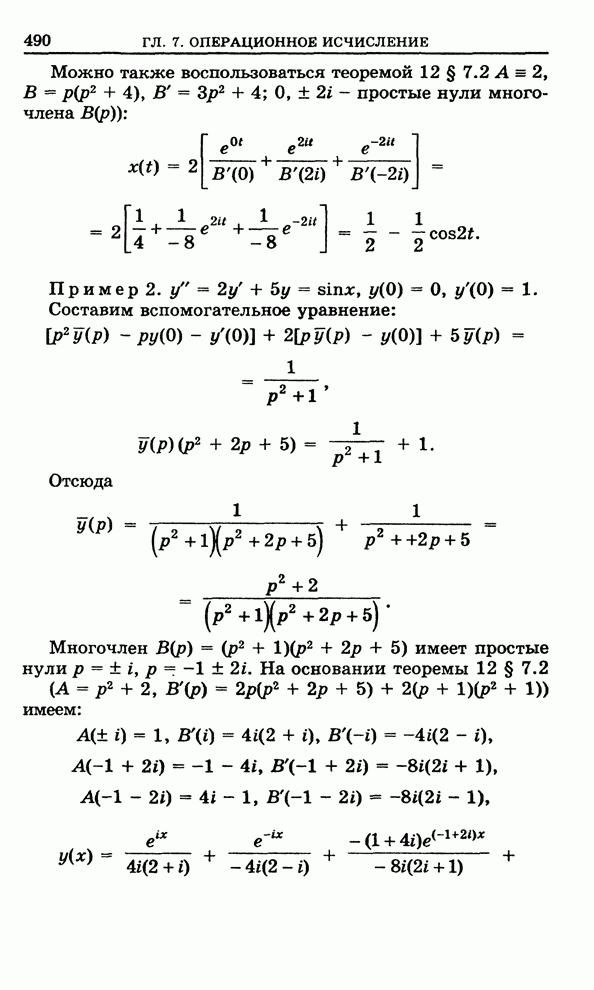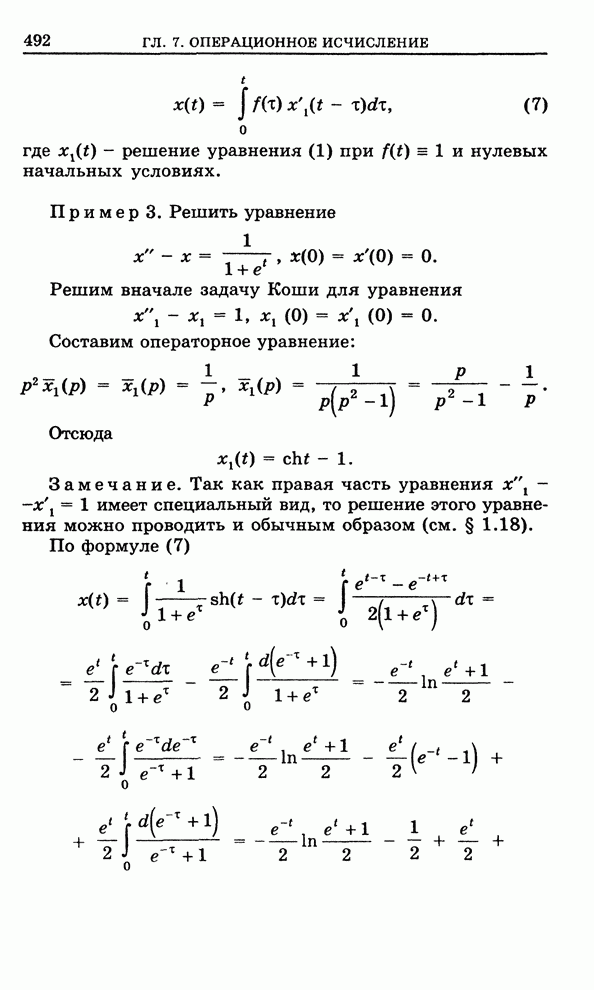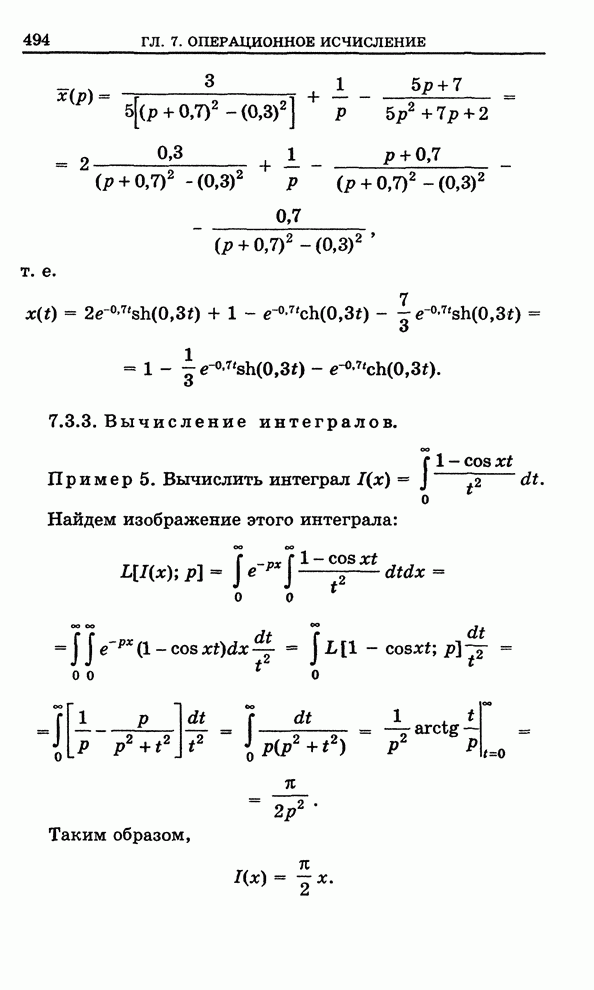| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 1.6. Доказательство теоремы существования решения диффереацнального уравнения первого порядка
Пусть задано уравнение
![]() (1)
(1)
где функция ![]() непрерывна на
прямоугольнике
непрерывна на
прямоугольнике
![]()
и имеет
ограниченную частную производную ![]() , удовлетворяющую неравенству
, удовлетворяющую неравенству ![]() .
.
Нам надо
доказать, что на отрезке ![]() существует и притом единственное
решение
существует и притом единственное
решение ![]() дифференциального
уравнения (1), удовлетворяющее условию
дифференциального
уравнения (1), удовлетворяющее условию
![]() (2)
(2)
где
![]() (3)
(3)
При этом ![]() непрерывно
дифференцируема на
непрерывно
дифференцируема на ![]() . Дифференциальное уравнение (1) с
условием (2) эквивалентно следующему интегральному уравнению:
. Дифференциальное уравнение (1) с
условием (2) эквивалентно следующему интегральному уравнению:
 (4)
(4)
В самом деле,
пусть непрерывная функция ![]() является решением (4), тогда
дифференцируя тождество (4), получим
является решением (4), тогда
дифференцируя тождество (4), получим
![]() и, очевидно,
и, очевидно, ![]() .
.
Таким образом,
функция ![]() удовлетворяет
уравнению (1) с условием (2).
удовлетворяет
уравнению (1) с условием (2).
Обратно, пусть ![]() является решением
(1):
является решением
(1):
![]() .
.
Тогда,
интегрируя это тождество в пределах от ![]() до
до ![]() , получим
, получим

или

т. е. ![]() является решением
(4).
является решением
(4).
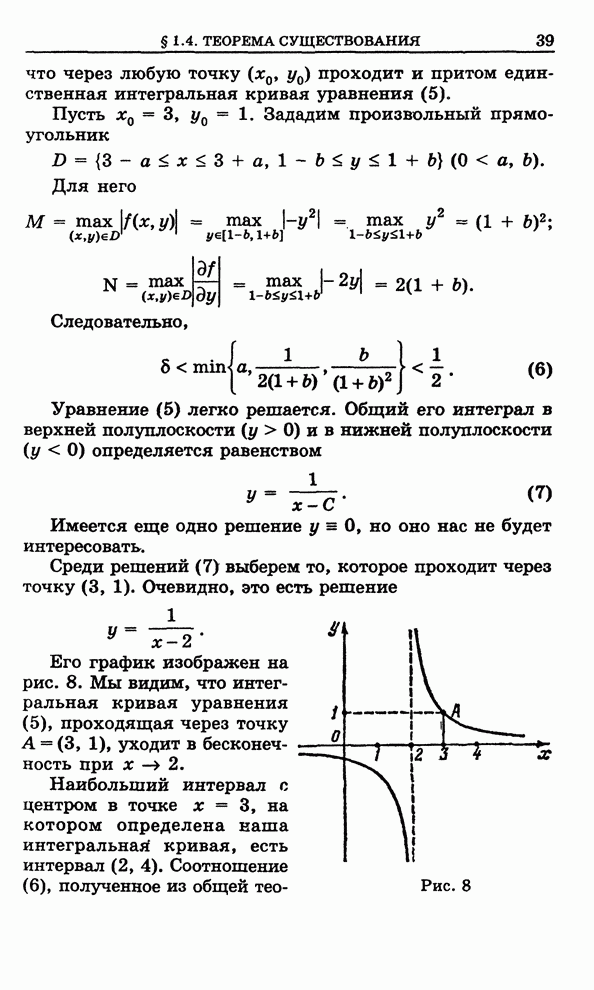
В дальнейшем мы будем исследовать уравнение (4).
Обозначим через ![]() множество
непрерывных функций
множество
непрерывных функций ![]() , заданных на отрезке
, заданных на отрезке ![]() и удовлетворяющих
на нем неравенству
и удовлетворяющих
на нем неравенству ![]() .
.
В ![]() введем расстояние
введем расстояние
![]() .
.
Таким образом, ![]() , есть метрическое
пространство. Это полное пространство. В самом деле, если последовательность
функций
, есть метрическое
пространство. Это полное пространство. В самом деле, если последовательность
функций ![]() удовлетворяет
в смысле введенной метрики условию Коши (является фундаментальной последовательностью),
то, как мы знаем, эта последовательность сходится равномерно на отрезке
удовлетворяет
в смысле введенной метрики условию Коши (является фундаментальной последовательностью),
то, как мы знаем, эта последовательность сходится равномерно на отрезке ![]() к некоторой
непрерывной на этом отрезке функции
к некоторой
непрерывной на этом отрезке функции ![]() (см. § 1.5).
(см. § 1.5).
Для функций ![]() выполняется
неравенство
выполняется
неравенство
![]() ,
,
которое после
перехода к пределу при ![]() сохраняется:
сохраняется:
![]() .
.
Но тогда ![]() , что показывает,
что
, что показывает,
что ![]() -
полное пространство.
-
полное пространство.
Равенство
 , (5)
, (5)
приводит в
соответствие каждой функции ![]() некоторую функцию
некоторую функцию ![]() . В самом деле, есть
. В самом деле, есть ![]() , то
, то ![]() есть непрерывная функция,
график которой принадлежит к прямоугольнику
есть непрерывная функция,
график которой принадлежит к прямоугольнику
![]() ,
,
поэтому в силу
непрерывности ![]() на
на
![]() , правая
часть равенства (5) есть непрерывная функция от
, правая
часть равенства (5) есть непрерывная функция от ![]() , т. е.
, т. е. ![]() есть непрерывная функция на
есть непрерывная функция на ![]() . Далее
. Далее
 ,
,
что показывает,
что ![]() .
.
Итак, мы можем считать, что равенство (5) определяет оператор
![]() ,
,
отображающий
полное пространство ![]() , в полное пространство
, в полное пространство ![]() . Этот оператор
сжимающий, потому что, если
. Этот оператор
сжимающий, потому что, если
![]() ,
,
то
 (6)
(6)
где число ![]() удовлетворяет
неравенству
удовлетворяет
неравенству ![]() ,
потому что по условию
,
потому что по условию ![]() . Из (6) следует, что
. Из (6) следует, что
![]() .
.
Но тогда, как мы
знаем, в ![]() (см.
§ 1.5) существует единственная функция (неподвижная точка)
(см.
§ 1.5) существует единственная функция (неподвижная точка) ![]() , для которой
, для которой
![]() ,
,
иначе говоря, которая удовлетворяет уравнению (4), а, следовательно, уравнению (1) и условию (2).
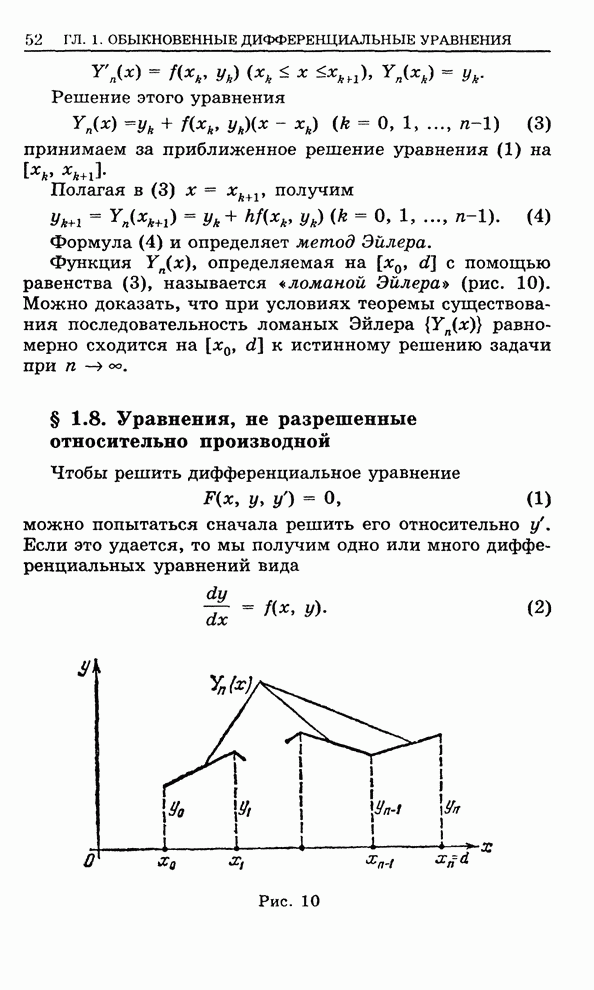
Применяя метод итераций, можно получить приближенное решение уравнения (1):
 , (7)
, (7)
где ![]() .
.
На основании формулы (10) § 1.5 оценка приближения имеет вид
![]() .
.
Существуют и другие приближенные методы решения задачи Коши.
Весьма простым является метод Эйлера (см. § 1.7).
Остается еще
доказать, что если ![]() имеет непрерывные производные по
имеет непрерывные производные по ![]() и
и ![]() до
до ![]() -го порядка на
-го порядка на ![]() , то указанное
решение
, то указанное
решение ![]() уравнения
(1) имеет непрерывные производные по
уравнения
(1) имеет непрерывные производные по ![]() до
до ![]() -го порядка на
-го порядка на ![]() .
.
В самом деле, имеет место тождество
![]() . (8)
. (8)
Так как функция ![]() удовлетворяет
дифференциальному уравнению (1), то она всюду на
удовлетворяет
дифференциальному уравнению (1), то она всюду на ![]() имеет производную по
имеет производную по ![]() и потому непрерывна.
Далее по условию
и потому непрерывна.
Далее по условию ![]() непрерывна
по
непрерывна
по ![]() и
и ![]() на
на ![]() , поэтому правая
часть (8) непрерывна по
, поэтому правая
часть (8) непрерывна по ![]() на
на ![]() . Значит,
. Значит, ![]() также непрерывна на
также непрерывна на ![]() .
.
Если ![]() , то правая часть
(8) имеет непрерывную производную по переменной
, то правая часть
(8) имеет непрерывную производную по переменной ![]() , значит, и левая часть тождества имеет
непрерывную производную по
, значит, и левая часть тождества имеет
непрерывную производную по ![]() . Следовательно, функция
. Следовательно, функция ![]() имеет непрерывную
производную второго порядка. Из тождества (8) находим
имеет непрерывную
производную второго порядка. Из тождества (8) находим
![]() . (9)
. (9)
Применяя к
тождеству (9) те же рассуждения, что и выше, найдем, что при ![]() функция
функция ![]() имеет непрерывную
производную третьего порядка на
имеет непрерывную
производную третьего порядка на ![]() и т.д.
и т.д.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. Обыкновенные дифференциальные уравнения
- 1.1. Задача, приводящая к дифференциальному уравнению
- 1.2. Общие понятия
- 1.2.1. Понятие обыкновенного дифференциального уравнения
- 1.2.2. Дифференциальное уравнение первого порядка
- 1.2.3. Задача Коши
- 1.2.4. Примеры дифференциальных уравнений первого порядка
- 1.2.5. Общий интеграл дифференциального уравнения первого порядка
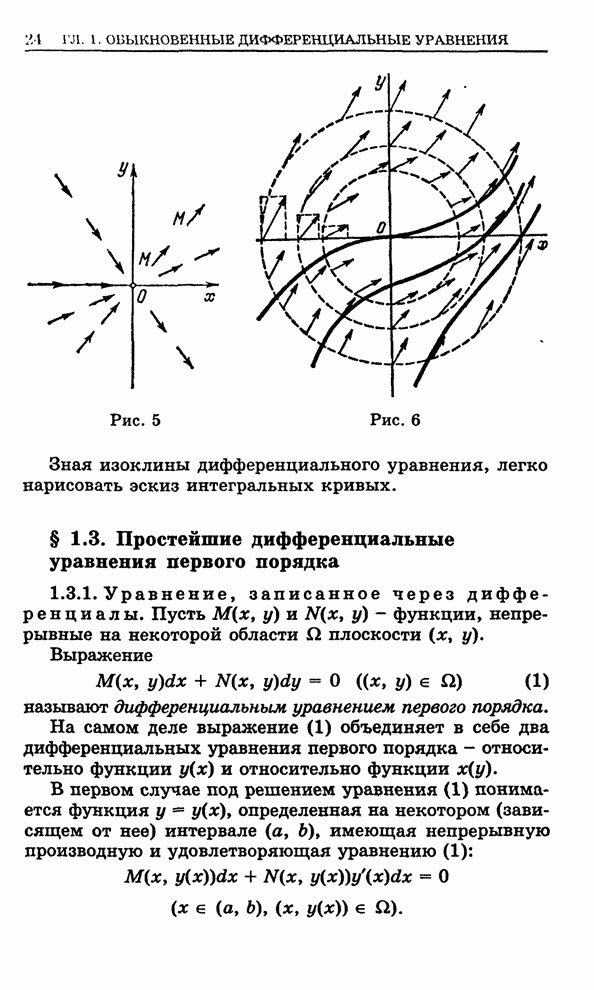
- 1.2.6. Поле направлений
- 1.3. Простейшие дифференциальные уравнения первого порядка
- 1.3.1. Уравнение, записанное через дифференциалы
- 1.3.2. Уравнения с разделенными переменными
- 1.3.3. Уравнения с разделяющимися переменными
- 1.3.4. Однородные уравнения
- 1.3.5. Линейное уравнение
- 1.3.6. Уравнение Бернулли
- 1.4. Теорема существования решения дифференциального уравнения первого порядка
- 1.5. Метрическое пространство
- 1.5.1. Понятие метрического пространства
- 1.5.2. Полное метрическое пространство
- 1.5.3. Принцип сжатых отображений
- 1.5.4. Приближенное значение корня функции
- 1.5.5. Метод Ньютона
- 1.6. Доказательство теоремы существования решения диффереацнального уравнения первого порядка
- 1.7. Метод Эйлера приближенного решения дифференциального уравнения первого порядка
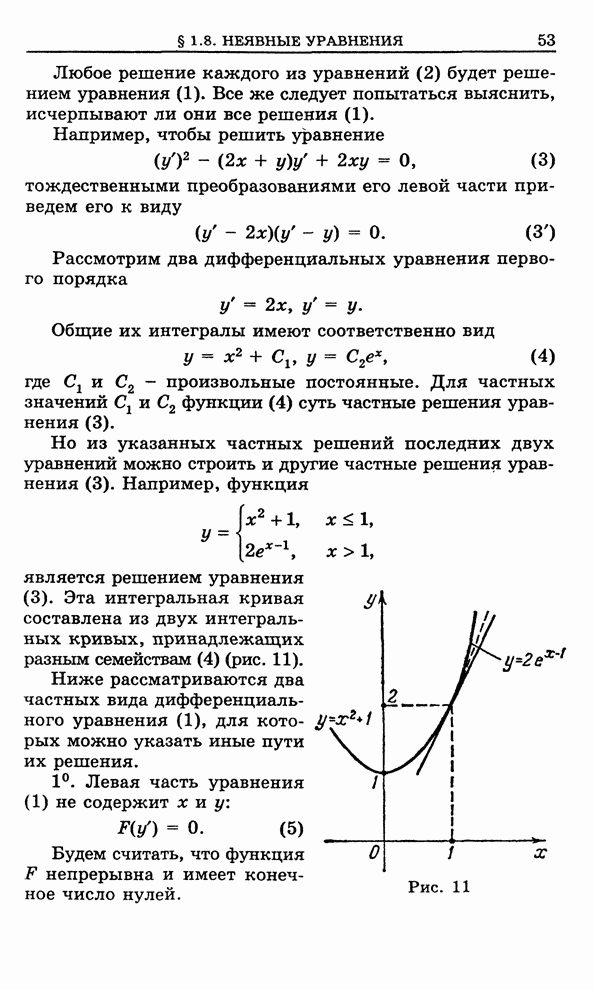
- 1.8. Уравнения, не разрешенные относительно производной
- 1.9. Особые решения
- 1.10. Огибающая семейства кривых
- 1.11. Дифференциальное уравнение второго порядка
- 1.12. Система из двух дифференциальных уравнений первого порядка
- 1.13. Дифференциальное уравнение n-го порядка
- 1.14. Понижение порядка дифференциального уравнения
- 1.15. Линейные уравнения высшего порядка
- 1.15.1. Понятие линейного уравнения высшего порядка
- 1.15.2. Фундаментальная система решений уравнения
- 1.15.3. Определитель Вронского
- 1.15.4. Структура общего решения
- 1.16. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- 1.16.1. Методы решения
- 1.16.2. Уравнение Эйлера
- 1.17. Метод вариации постоянных
- 1.18. Частное решение неоднородного уравнения с постоянными коэффициентами. Приложения
- 1.18.1. Методы нахождения частных решений
- 1.18.2. Дифференциальное уравнение колебания пружины
- 1.19. Системы дифференциальных уравнений. Фазовое пространство
- 1.20. Линейная однородная система дифференциальных уравнений
- 1.21. Общее решение линейной однородной системы дифференциальных уравнений с постоянными коэффициентами
- 1.22. Сведение системы уравнений к одному уравнению
- 1.23. Неоднородная система линейных дифференциальных уравнений с постоянными коэффициентами
- 1.24. Интегрирование дифференциальных уравнений с помощью степенных рядов
- 1.25. Элементы теории устойчивости
- 1.26. Классификация точек покоя
- Глава 2. Кратные интегралы
- 2.1. Введение
- 2.2. Сведения из теории меры Жордана
- 2.3. Свойства кратных интегралов. Теоремы существования
- 2.4. Сведение кратного интеграла к повторным
- 2.5. Доказательство существования интеграла от непрерывной функции
- 2.6. Замена переменных. Простейший случай
- 2.7. Замена переменных. Общий случай
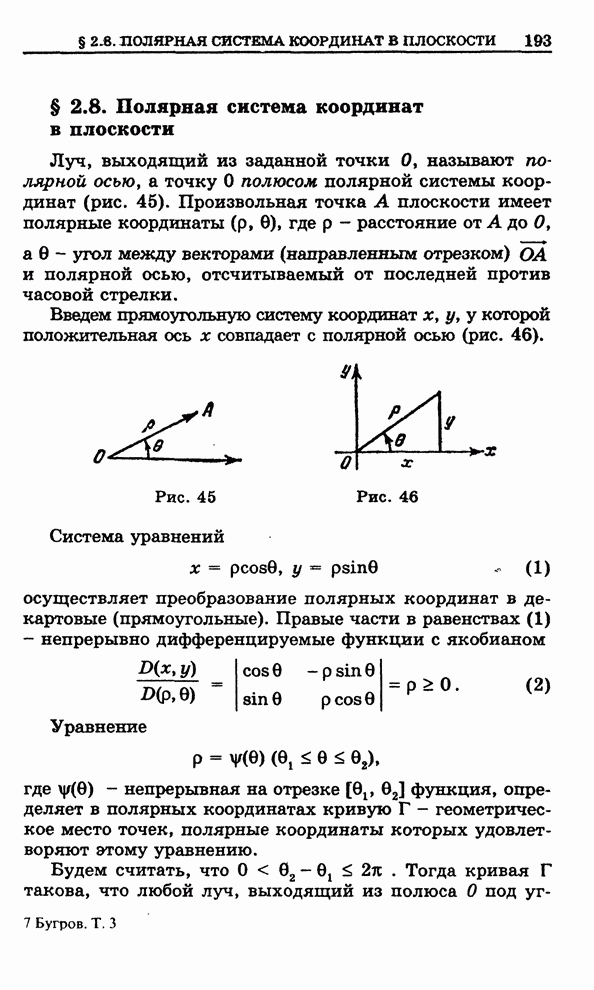
- 2.8. Полярная система координат в плоскости
- 2.9. Полярная система координат в пространстве
- 2.10. Цилиндрические координаты
- 2.11. Площадь поверхности
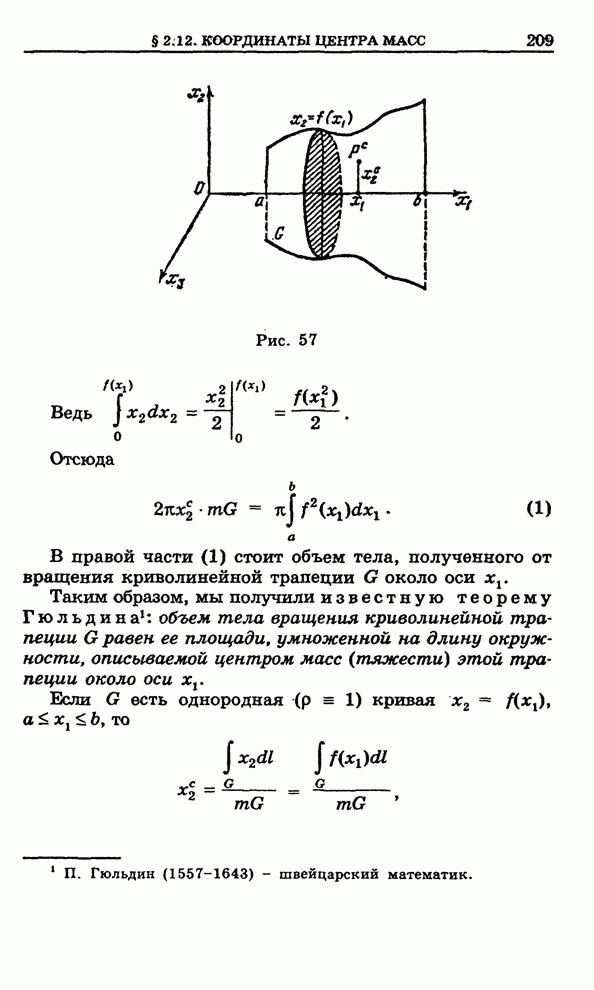
- 2.12. Координаты центра масс
- 2.13. Несобственные интегралы
- 2.14. Несобственный интеграл с особенностями вдоль линии
- 2.15. Несобственный интеграл, зависящий от параметра
- Глава 3. Векторный анализ
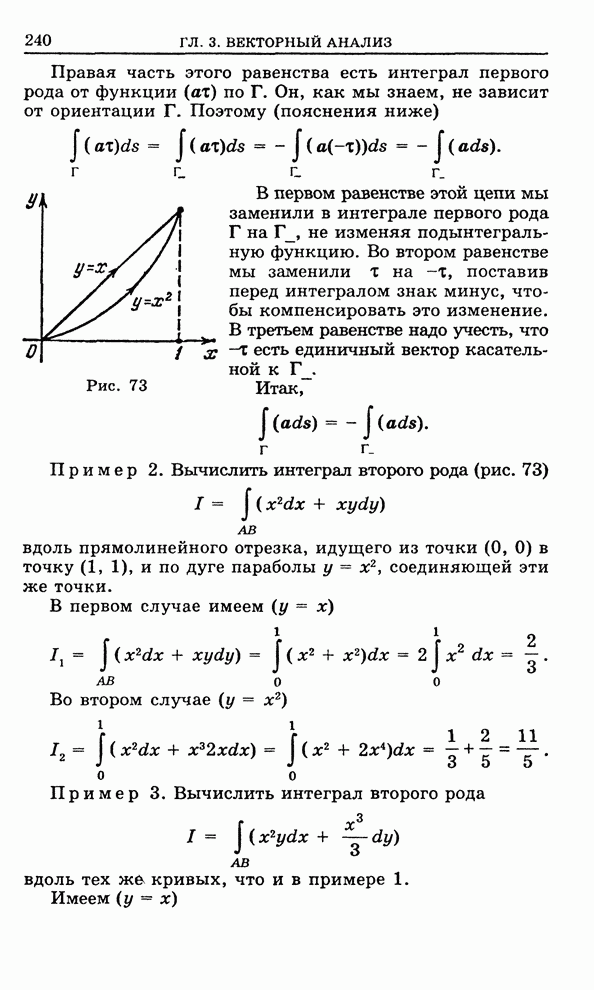
- 3.1. Кусочно-гладкая ориентированная кривая
- 3.2. Криволинейный интеграл первого рода
- 3.3. Интеграл от вектора вдоль кривой
- 3.3.1. Поле вектора
- 3.3.2. Криволинейный интеграл от вектора вдоль кривой
- 3.3.3. Свойства криволинейных интегралов второго рода
- 3.4. Поле потенциала
- 3.4.1. Понятие потенциала и его свойства
- 3.4.2. Доказательство свойств потенциала
- 3.4.3. Ротор вектора
- 3.5. Дифференциальное уравнение в полных дифференциалах
- 3.6. Ориентация плоской области
- 3.7. Формула Грина
- 3.8. Интеграл по поверхности первого рода
- 3.9. Ориентация поверхности
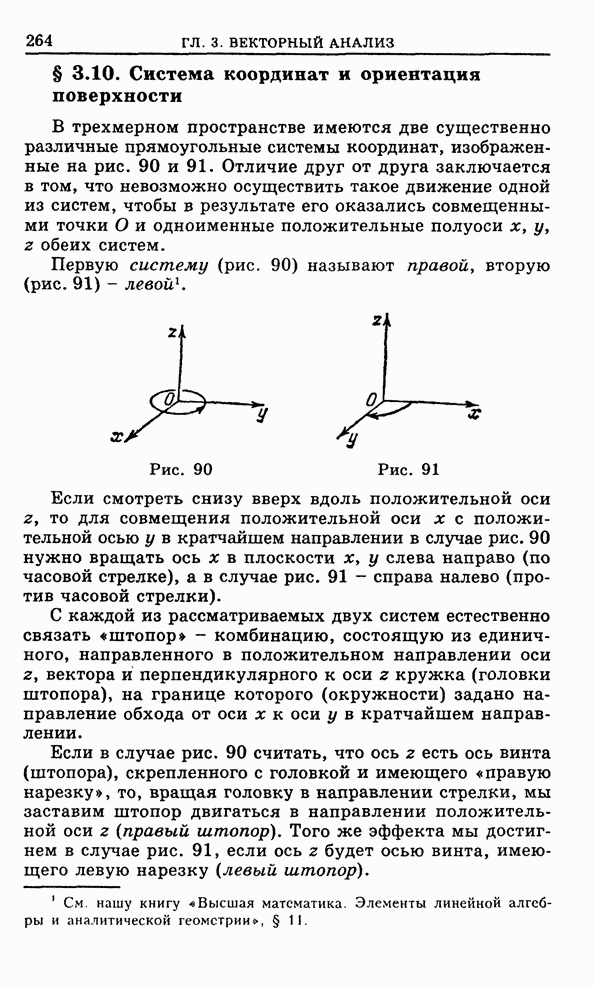
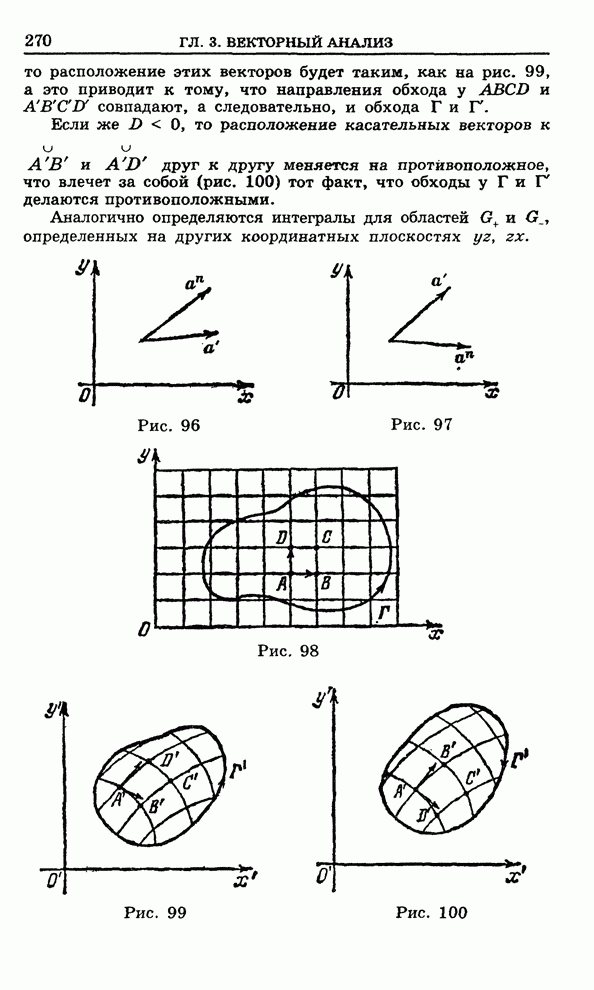
- 3.10. Система координат и ориентация поверхности
- 3.11. Интеграл по ориентированной плоской области
- 3.12. Поток вектора через ориентированную поверхность
- 3.13. Дивергенция. Теорема Гаусса—Остроградского
- 3.14. Соленоидальное поле
- 3.15. Формула Стокса
- Глава 4. Ряды Фурье. Интеграл Фурье
- 4.1. Тригонометрические ряды
- 4.2. Сходимость тригонометрических рядов
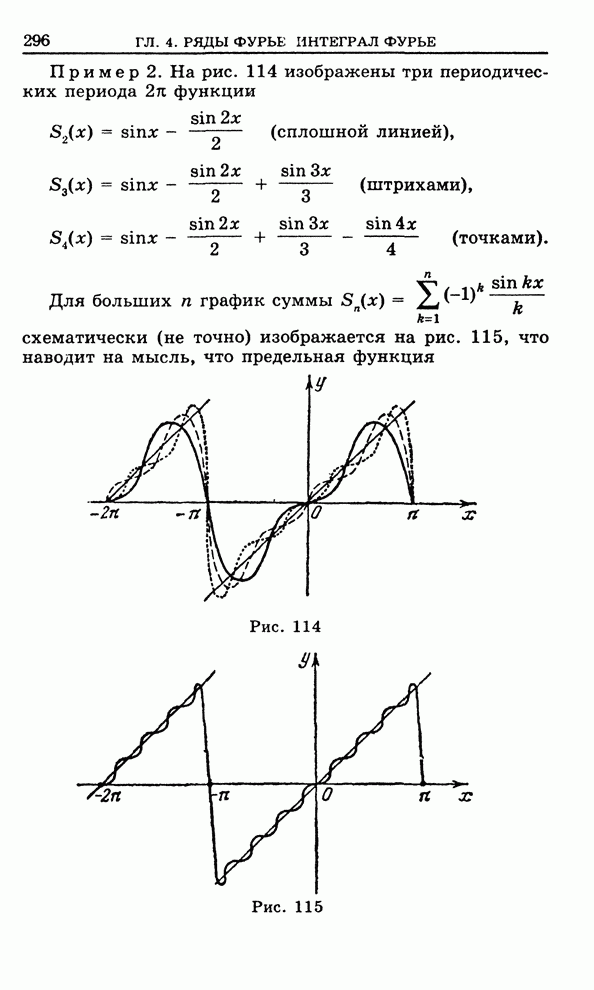
- 4.3. Ряд Фурье
- 4.4. Признаки сходимости рядов Фурье
- 4.5. Ортогональные свойства тригонометрических функций
- 4.6. Коэффициенты Фурье
- 4.7. Оценка коэффициентов Фурье
- 4.8. Пространство функций со скалярным произведением
- 4.9. Ортогональная система функций
- 4.10. Полнота тригонометрических функций
- 4.11. Комплексная форма ряда Фурье
- 4.12. Понятие интеграла Фурье. Повторный интеграл Фурье
- 4.13. Косинус- и синус- преобразования Фурье
- 4.14. Примеры
- 4.15. Приближение интеграла Фурье
- 4.16. Сумма Фейера
- 4.17. Полнота систем функций в С и L2’
- 4.18. Сведения из теории кратных рядов Фурье
- Глава 5. Уравнения математической физики
- 5.1. Температура тела
- 5.2. Задача Дирихле
- 5.3. Задача Дирихле для круга
- 5.4. Задача Дирихле для полуплоскости
- 5.5. Уравнение теплопроводности в стержне
- 5.6. Теплопроводность для бесконечного стержня
- 5.7. Малые колебания струны
- 5.8. Колебание бесконечной струны. Формула Даламбера
- 5.9. Колебание круглой мембраны
- 5.10. Общая задача Штурма-Лиувилля
- 5.11. Интеграл энергии (Дирихле)
- 5.12. Применение преобразований Фурье
- Глава 6. Теория функций комплексного переменного
- 6.1. Понятие функции комплексного переменного
- 6.2. Производная функция комплексного переменного
- 6.3. Условия Даламбера-Эйлера (Коши-Римана)
- 6.4. Гармонические функции
- 6.5. Обратная функция
- 6.6. Интегрирование функций комплексного переменного
- 6.7. Формула Коши
- 6.8. Интеграл типа Коши
- 6.9. Степенной ряд
- 6.10. Ряд Лорана
- 6.11. Классификация изолированных особых точек. Вычеты
- 6.12. Классификация особых точек на бесконечности
- 6.13. Теорема о вычетах
- 6.14. Вычисление интегралов при помощи вычетов
- 6.15. Линейная функция. Дробно-линейная функция
- Глава 7. Операционное исчисление
- 7.1. Изображение Лапласа
- 7.2. Изображение простейших функций и свойства изображений
- 7.3. Приложения операционного исчисления
- 7.3.1. Операторное уравнение
- 7.3.2. Решение систем дифференциальных уравнений
- 7.3.3. Вычисление интегралов
- Глава 8. Обобщенные функции
- 8.1. Понятие обобщенной функции
- 8.2. Операции над обобщенными функциями
- 8.3. Преобразование Фурье обобщенных функций