| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2.4. Сведение кратного интеграла к повторным
Рассмотрим интеграл
![]() , (1)
, (1)
где функция ![]() задана на
прямоугольнике
задана на
прямоугольнике
![]() , (2)
, (2)
т. е. на
множестве точек ![]() ,
где
,
где
![]() .
.
Здесь
интегрирование производится по переменной ![]() . Но подынтегральная функция зависит не
только от
. Но подынтегральная функция зависит не
только от ![]() ,
но и от
,
но и от ![]() , поэтому
интеграл (1) есть функция
, поэтому
интеграл (1) есть функция ![]() от
от ![]() .
.
Говорят, что интеграл
(1) есть функция от параметра ![]() .
.
Теорема 1. Если
функция ![]() непрерывна
на прямоугольнике
непрерывна
на прямоугольнике ![]() ,
то функция
,
то функция ![]() непрерывна
на отрезке
непрерывна
на отрезке ![]() .
.
Доказательство. Имеем
![]() .
.
Так как функция ![]() непрерывна на
замкнутом ограниченном множестве
непрерывна на
замкнутом ограниченном множестве ![]() , то она равномерно непрерывна на
, то она равномерно непрерывна на ![]() . Следовательно, для
любого
. Следовательно, для
любого ![]() найдется
найдется
![]() такое,
что
такое,
что
![]()
для всех ![]() , лишь бы
, лишь бы ![]() . Но тогда
. Но тогда
![]() ,
,
и теорема доказана.
Теорема 2. При условиях теоремы 1 существует повторный интеграл
![]() .
(3)
.
(3)
В самом деле,
непрерывная на отрезке ![]() функция
функция ![]() интегрируема на нем.
интегрируема на нем.
Теорема 3. При условиях теоремы 1 справедливы равенства
![]() . (4)
. (4)
Первый член цепи
(4) есть кратный интеграл от непрерывной функции на замкнутом множестве ![]() с кусочно-гладкой
границей. Он существует (см. ниже § 2.5). Повторные интегралы, представляющие
собой второй и третий члены цепи равенства (4), тоже существуют по теореме 2.
с кусочно-гладкой
границей. Он существует (см. ниже § 2.5). Повторные интегралы, представляющие
собой второй и третий члены цепи равенства (4), тоже существуют по теореме 2.
Данная теорема
утверждает равенство этих трех интегралов. Тем самым вычисление кратного
интеграла сводится к вычислению одномерных интегралов по каждой переменной ![]() в отдельности.
в отдельности.
Доказательство.
Разделим стороны ![]() на
на
![]() равных
частей:
равных
частей:
![]() ,
,
![]() ,
,
и через точки деления
проведем прямые, параллельные соответственно оси ![]() в оси
в оси ![]() . Этим
. Этим ![]() разделится на равные прямоугольники
разделится на равные прямоугольники ![]() :
:

и
 (5)
(5)
Мы применили
сначала к интегралу ![]() по
по ![]() от функции
от функции  теорему о среднем, а затем к
интегралу
теорему о среднем, а затем к
интегралу  ту
же теорему.
ту
же теорему.
Мы доказали, что
повторный интеграл в левой части (5) можно рассматривать как интегральную сумму
кратного интеграла ![]() соответствующую разбиению
соответствующую разбиению ![]() на части
на части ![]() при некоторых
точках
при некоторых
точках ![]() .
.
Перейдем теперь
к пределу в равенстве (5) при ![]() . Левая часть (5) при этом есть
определенное (не зависящее от
. Левая часть (5) при этом есть
определенное (не зависящее от ![]() ) число, а правая часть стремится при
) число, а правая часть стремится при ![]() к кратному
интегралу от
к кратному
интегралу от ![]() по
по
![]() (если
кратный интеграл существует, то любая интегральная сумма стремится к этому
интегралу).
(если
кратный интеграл существует, то любая интегральная сумма стремится к этому
интегралу).
Поэтому
 ,
,
и мы доказали первое равенство (4). Равенство второго повторного интеграла с кратным интегралом доказывается аналогично.
Рассмотрим в
плоскости ![]() область
область
![]() ,
ограниченную гладкими кривыми (рис. 35)
,
ограниченную гладкими кривыми (рис. 35)

Рис. 35
![]() ,
,
где
![]() .
.
Пусть на
замыкании ![]() области
области
![]() задана
произвольная непрерывная функция
задана
произвольная непрерывная функция ![]() . Чтобы вычислить кратный интеграл от
. Чтобы вычислить кратный интеграл от ![]() по области
по области ![]() (или, что все
равно, по
(или, что все
равно, по ![]() ),
применяют следующий метод: сначала интегрируют функцию
),
применяют следующий метод: сначала интегрируют функцию ![]() по переменной
по переменной ![]() от
от ![]() до
до ![]() , считая
, считая ![]() постоянным, а затем
результат интегрируют по
постоянным, а затем
результат интегрируют по ![]() : на отрезке
: на отрезке ![]() :
:
 (6)
(6)
В случае, когда ![]() есть прямоугольник
со сторонами, параллельными осям координат, равенство (6) было выше обосновано
(см. теорему 3). Теми же рассуждениями можно было бы обосновать (6) и в общем
случае.
есть прямоугольник
со сторонами, параллельными осям координат, равенство (6) было выше обосновано
(см. теорему 3). Теми же рассуждениями можно было бы обосновать (6) и в общем
случае.
Пример 1. Вычислить площадь эллипса
![]() .
.
Мы называем
эллипсом множество точек ![]() , для которых
, для которых ![]() , так же как множество точек
, так же как множество точек ![]() , для которых
, для которых ![]() . Подобную вольность
мы будем позволять себе, называя эллипсоидом как множество точек
. Подобную вольность
мы будем позволять себе, называя эллипсоидом как множество точек ![]() , для которых
, для которых ![]() , так и множество
точек
, так и множество
точек ![]() ,
удовлетворяющих уравнению
,
удовлетворяющих уравнению
![]() .
.
Решение. Область
![]() , о
которой идет речь, ограничена снизу кривой
, о
которой идет речь, ограничена снизу кривой
![]()
и сверху кривой
![]() .
.
Искомая площадь равна

Пример 2. Вычислить
площадь фигуры ![]() ,
ограниченной параболой
,
ограниченной параболой ![]() и прямой
и прямой ![]() (рис. 36).
(рис. 36).
Имеем
 .
.

Рис. 36
Метод вычисления кратных интегралов сведением их к одномерным применяется в пространствах любых измерений. Покажем это на примерах.
Пример З.
Требуется вычислить объем ![]() эллипсоида
эллипсоида
![]() .
.
Решим
относительно ![]() уравнение
уравнение
![]() .
.
Получим две непрерывные функции
 .
.
Они определены
на множестве ![]() точек
точек
![]() , удовлетворяющих
неравенству
, удовлетворяющих
неравенству
![]() .
.
Объем или
трехмерная мера ![]() равен
кратному интегралу
равен
кратному интегралу
![]() .
.
Чтобы его
вычислить, надо для любой точки ![]() проинтегрировать единичную функцию
(равную 1) по
проинтегрировать единичную функцию
(равную 1) по ![]() от
от
 до
до  . Результат,
зависящий от
. Результат,
зависящий от ![]() ,
затем надо проинтегрировать по всем
,
затем надо проинтегрировать по всем ![]() :
:

Последнее равенство в этой цепи следует из формулы (6). Дальнейшие вычисления требуют владения техникой интегрирования:


Далее
 .
.
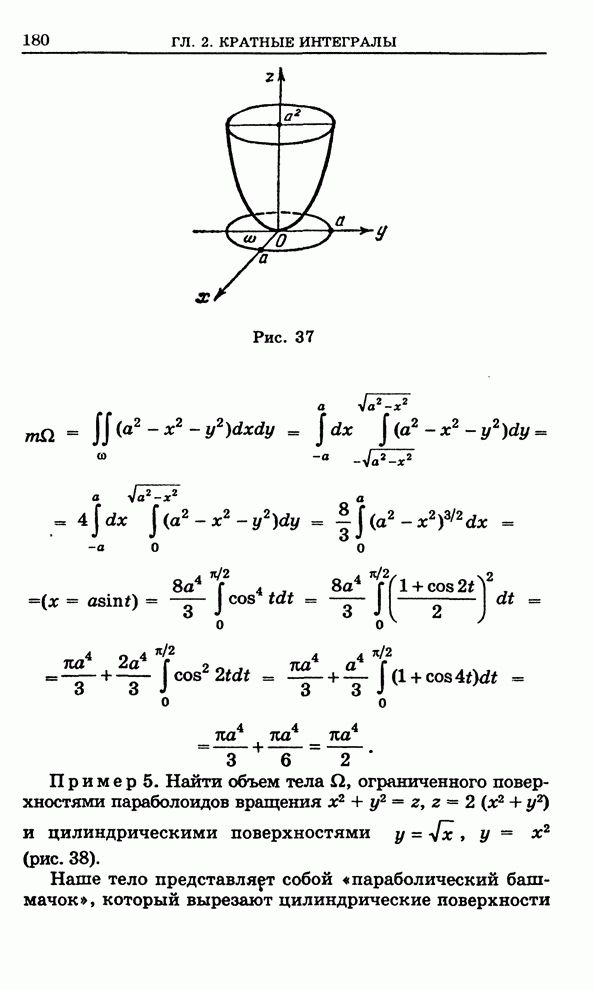
Пример 4. Найти
объем части параболоида вращения ![]() :
: ![]() (рис. 37).
(рис. 37).
Так же как в примере 3, имеем
 ,
,
где ![]() - множество точек
- множество точек ![]() , удовлетворяющих
неравенству
, удовлетворяющих
неравенству ![]() ,
т. е. это круг радиуса
,
т. е. это круг радиуса ![]() . Далее имеем
. Далее имеем

Рис. 37

Пример 5. Найти
объем тела ![]() ,
ограниченного поверхностями параболоидов вращения
,
ограниченного поверхностями параболоидов вращения ![]() и цилиндрическими
поверхностями
и цилиндрическими
поверхностями ![]() (рис.
38).
(рис.
38).
Наше тело
представляет собой «параболический башмачок», который вырезают цилиндрические
поверхности ![]() и
и
![]() между
параболоидами вращения. Снизу башмачок ограничен куском поверхности
между
параболоидами вращения. Снизу башмачок ограничен куском поверхности ![]() , а сверху куском
поверхности параболоида вращения
, а сверху куском
поверхности параболоида вращения ![]() . Проекция этого тела
. Проекция этого тела ![]() на плоскость
на плоскость ![]() дает множество
дает множество ![]() , состоящее из точек
, состоящее из точек
![]() , координаты
которых удовлетворяют неравенствам:
, координаты
которых удовлетворяют неравенствам: ![]() .
.

Рис. 38
Поэтому

Вернемся снова к интегралу (1), зависящему от параметра.
Теорема 4. Если
функция ![]() непрерывна
и имеет непрерывную производную
непрерывна
и имеет непрерывную производную ![]() на прямоугольнике
на прямоугольнике
![]() ,
,
то функция

имеет
производную на отрезке ![]() , причем
, причем
 . (7)
. (7)
Доказательство. Мы должны доказать, что
 . (8)
. (8)
Имеем, применяя теорему Лагранжа
 .
.
Поэтому

при ![]() , где
, где ![]() зависящее от
зависящее от ![]() достаточно мало.
Дело в том, что функция
достаточно мало.
Дело в том, что функция ![]() непрерывная на
непрерывная на ![]() , равномерно-непрерывная на
, равномерно-непрерывная на ![]() , т. е. для
, т. е. для ![]() :
:
![]()
для любых ![]() .
.
Таким образом, равенство (8), а с ним и (7) доказано. Рассмотрим теперь более общий, чем (1) интеграл
 , (9)
, (9)
где ![]() и
и ![]() - непрерывные на
отрезке
- непрерывные на
отрезке ![]() функции,
удовлетворяющие неравенствам
функции,
удовлетворяющие неравенствам
![]() ,
,
а ![]() непрерывна для всех
точек
непрерывна для всех
точек ![]() , удовлетворяющих
неравенствам
, удовлетворяющих
неравенствам
![]() .
.
Покажем, что при
указанных условиях функция ![]() непрерывна на
непрерывна на ![]() .
.
В самом деле,
заменим в интеграле (9) переменную интегрирования ![]() на другую переменную
на другую переменную ![]() при помощи
равенства
при помощи
равенства
![]() . (10)
. (10)
При ![]() , при
, при ![]() (
(![]() фиксировано, и его
мы считаем постоянным при замене переменной). Следовательно,
фиксировано, и его
мы считаем постоянным при замене переменной). Следовательно,
 . (11)
. (11)
Здесь множитель ![]() есть непрерывная
функция от
есть непрерывная
функция от ![]() ,
а под знаком интеграла стоит непрерывная функция от точки
,
а под знаком интеграла стоит непрерывная функция от точки ![]() , принадлежащей
прямоугольнику
, принадлежащей
прямоугольнику ![]() .
Поэтому сам интеграл - непрерывная функция на
.
Поэтому сам интеграл - непрерывная функция на ![]() согласно теореме 1. Функция
согласно теореме 1. Функция ![]() будет непрерывной
на
будет непрерывной
на ![]() , как
произведение двух непрерывных функций.
, как
произведение двух непрерывных функций.
Теорема 5. Если
функция ![]() непрерывна
вместе со своей частной производной
непрерывна
вместе со своей частной производной ![]() , на
, на
![]() ,
,
а функции ![]() непрерывны на
непрерывны на ![]() , то функция (9) имеет
производную, вычисляемую по формуле
, то функция (9) имеет
производную, вычисляемую по формуле
 . (12)
. (12)
Доказательство. Введем вспомогательную функцию
 ,
,
заданную на
множестве ![]() .
.
Согласно теореме 4
 .
.
Используя правило дифференцирования интеграла с переменным пределом интегрирования, имеем
![]() .
.
Далее ![]() , поэтому по
правилу дифференцирования сложной функции получаем
, поэтому по
правилу дифференцирования сложной функции получаем

что и требовалось доказать.
Пример 6. Найти производную от функции
 .
.
Согласно (12) получаем
 .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. Обыкновенные дифференциальные уравнения
- 1.1. Задача, приводящая к дифференциальному уравнению
- 1.2. Общие понятия
- 1.2.1. Понятие обыкновенного дифференциального уравнения
- 1.2.2. Дифференциальное уравнение первого порядка
- 1.2.3. Задача Коши
- 1.2.4. Примеры дифференциальных уравнений первого порядка
- 1.2.5. Общий интеграл дифференциального уравнения первого порядка
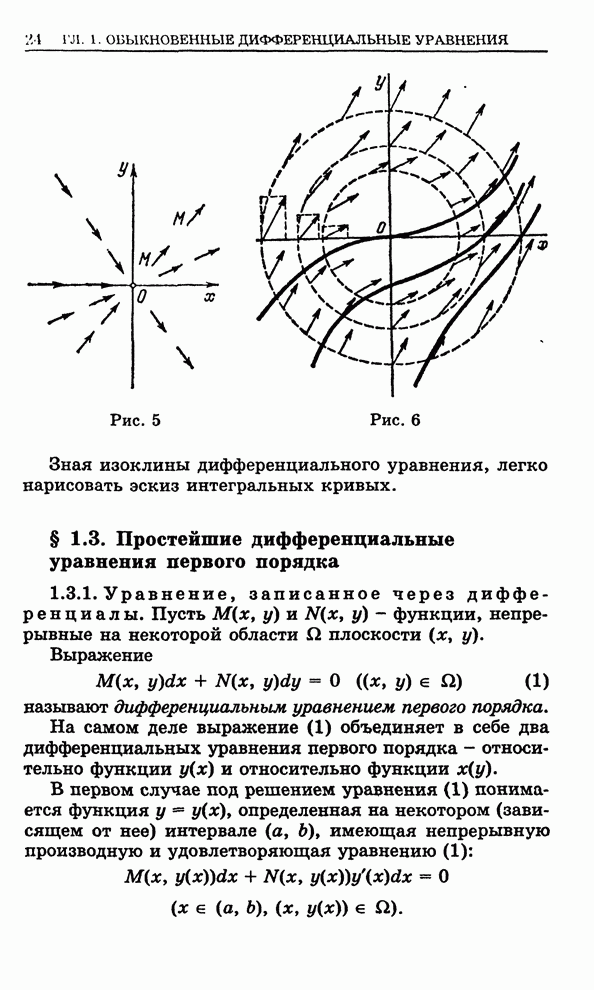
- 1.2.6. Поле направлений
- 1.3. Простейшие дифференциальные уравнения первого порядка
- 1.3.1. Уравнение, записанное через дифференциалы
- 1.3.2. Уравнения с разделенными переменными
- 1.3.3. Уравнения с разделяющимися переменными
- 1.3.4. Однородные уравнения
- 1.3.5. Линейное уравнение
- 1.3.6. Уравнение Бернулли
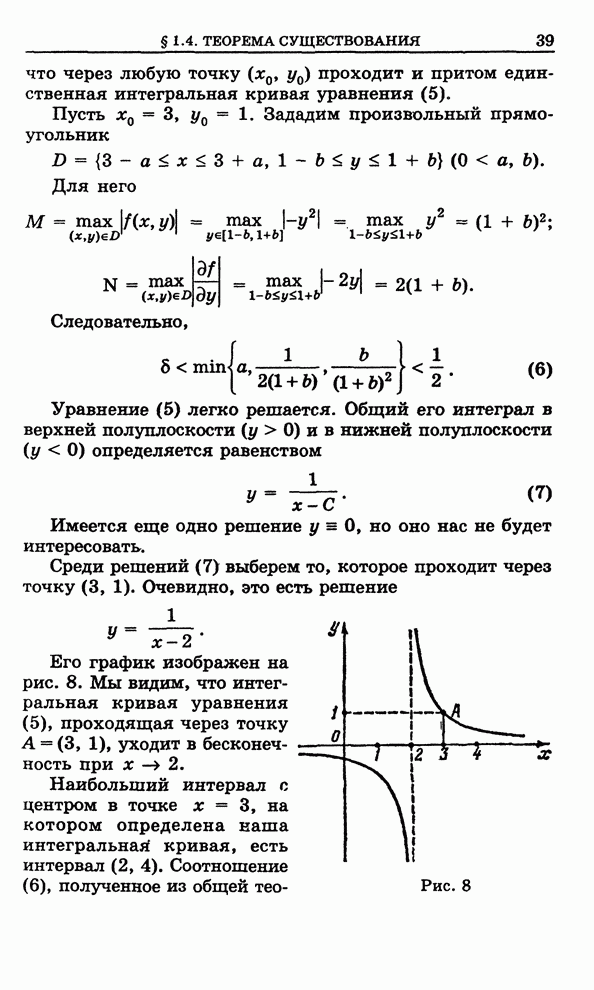
- 1.4. Теорема существования решения дифференциального уравнения первого порядка
- 1.5. Метрическое пространство
- 1.5.1. Понятие метрического пространства
- 1.5.2. Полное метрическое пространство
- 1.5.3. Принцип сжатых отображений
- 1.5.4. Приближенное значение корня функции
- 1.5.5. Метод Ньютона
- 1.6. Доказательство теоремы существования решения диффереацнального уравнения первого порядка
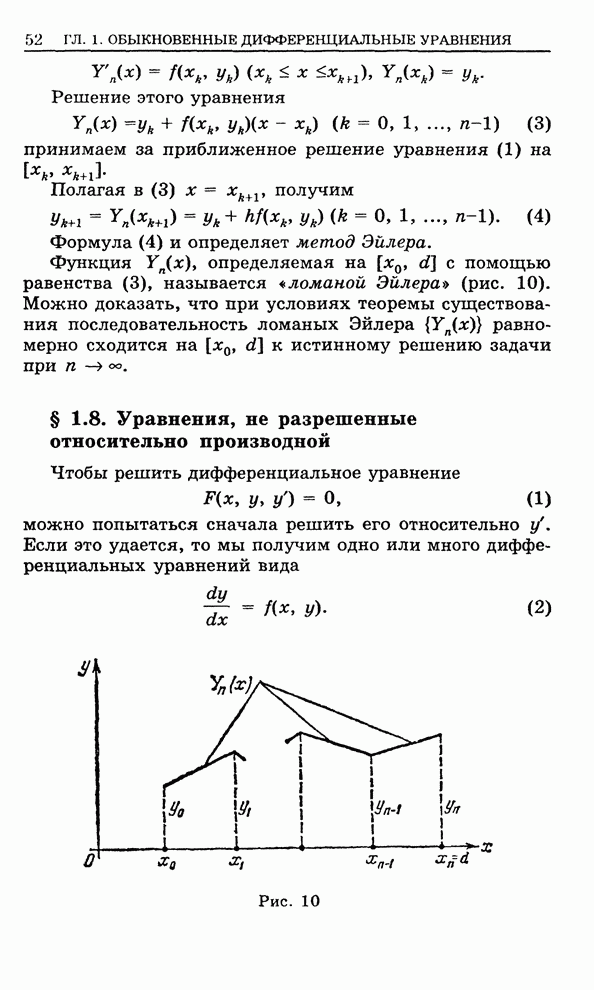
- 1.7. Метод Эйлера приближенного решения дифференциального уравнения первого порядка
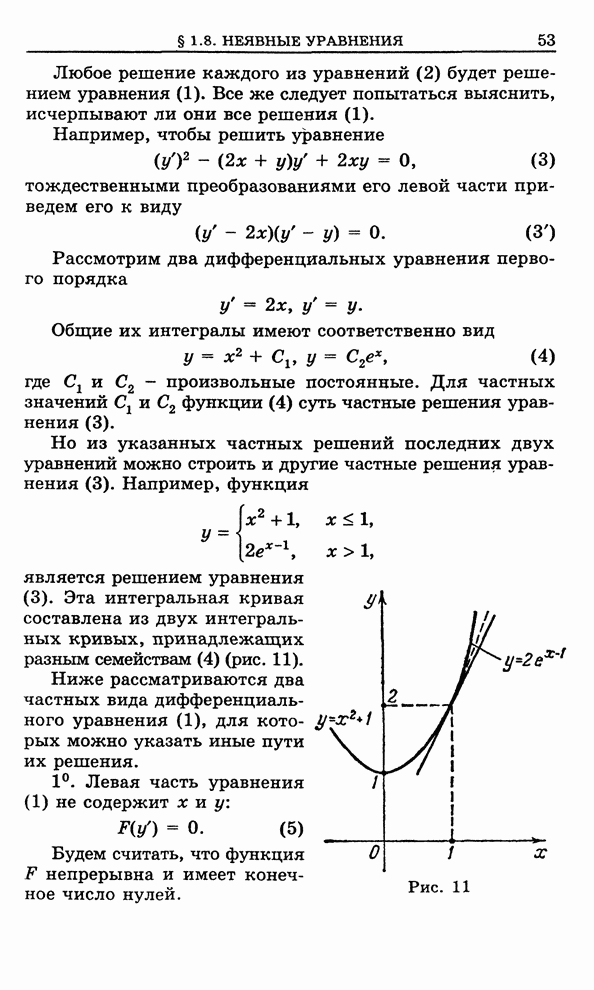
- 1.8. Уравнения, не разрешенные относительно производной
- 1.9. Особые решения
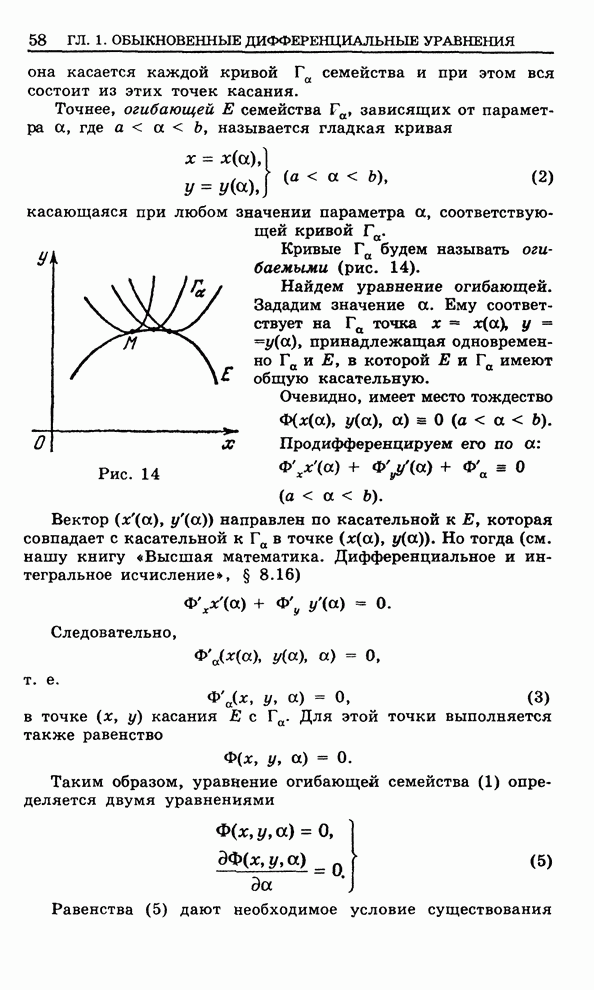
- 1.10. Огибающая семейства кривых
- 1.11. Дифференциальное уравнение второго порядка
- 1.12. Система из двух дифференциальных уравнений первого порядка
- 1.13. Дифференциальное уравнение n-го порядка
- 1.14. Понижение порядка дифференциального уравнения
- 1.15. Линейные уравнения высшего порядка
- 1.15.1. Понятие линейного уравнения высшего порядка
- 1.15.2. Фундаментальная система решений уравнения
- 1.15.3. Определитель Вронского
- 1.15.4. Структура общего решения
- 1.16. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- 1.16.1. Методы решения
- 1.16.2. Уравнение Эйлера
- 1.17. Метод вариации постоянных
- 1.18. Частное решение неоднородного уравнения с постоянными коэффициентами. Приложения
- 1.18.1. Методы нахождения частных решений
- 1.18.2. Дифференциальное уравнение колебания пружины
- 1.19. Системы дифференциальных уравнений. Фазовое пространство
- 1.20. Линейная однородная система дифференциальных уравнений
- 1.21. Общее решение линейной однородной системы дифференциальных уравнений с постоянными коэффициентами
- 1.22. Сведение системы уравнений к одному уравнению
- 1.23. Неоднородная система линейных дифференциальных уравнений с постоянными коэффициентами
- 1.24. Интегрирование дифференциальных уравнений с помощью степенных рядов
- 1.25. Элементы теории устойчивости
- 1.26. Классификация точек покоя
- Глава 2. Кратные интегралы
- 2.1. Введение
- 2.2. Сведения из теории меры Жордана
- 2.3. Свойства кратных интегралов. Теоремы существования
- 2.4. Сведение кратного интеграла к повторным
- 2.5. Доказательство существования интеграла от непрерывной функции
- 2.6. Замена переменных. Простейший случай
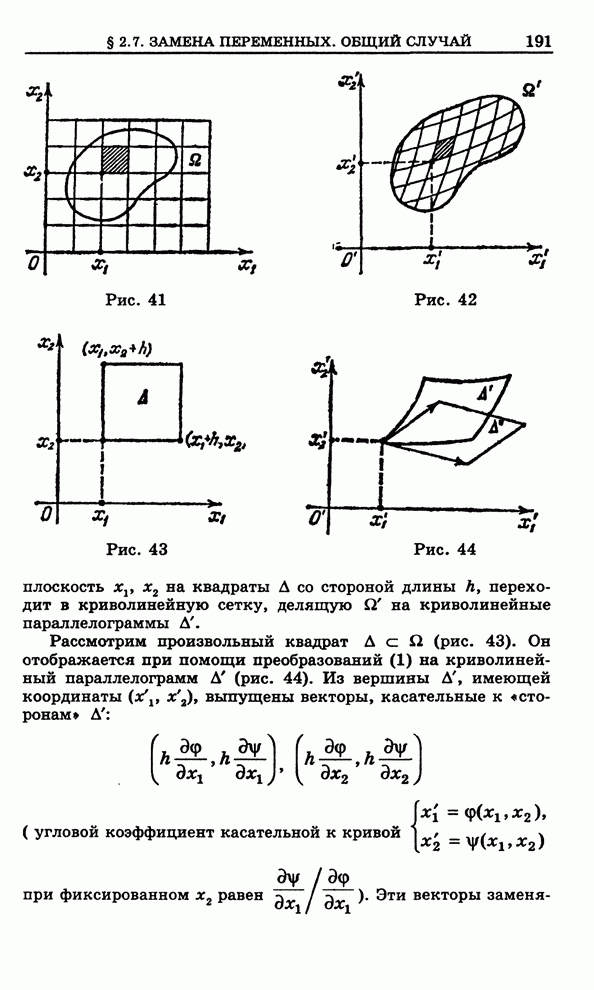
- 2.7. Замена переменных. Общий случай
- 2.8. Полярная система координат в плоскости
- 2.9. Полярная система координат в пространстве
- 2.10. Цилиндрические координаты
- 2.11. Площадь поверхности
- 2.12. Координаты центра масс
- 2.13. Несобственные интегралы
- 2.14. Несобственный интеграл с особенностями вдоль линии
- 2.15. Несобственный интеграл, зависящий от параметра
- Глава 3. Векторный анализ
- 3.1. Кусочно-гладкая ориентированная кривая
- 3.2. Криволинейный интеграл первого рода
- 3.3. Интеграл от вектора вдоль кривой
- 3.3.1. Поле вектора
- 3.3.2. Криволинейный интеграл от вектора вдоль кривой
- 3.3.3. Свойства криволинейных интегралов второго рода
- 3.4. Поле потенциала
- 3.4.1. Понятие потенциала и его свойства
- 3.4.2. Доказательство свойств потенциала
- 3.4.3. Ротор вектора
- 3.5. Дифференциальное уравнение в полных дифференциалах
- 3.6. Ориентация плоской области
- 3.7. Формула Грина
- 3.8. Интеграл по поверхности первого рода
- 3.9. Ориентация поверхности
- 3.10. Система координат и ориентация поверхности
- 3.11. Интеграл по ориентированной плоской области
- 3.12. Поток вектора через ориентированную поверхность
- 3.13. Дивергенция. Теорема Гаусса—Остроградского
- 3.14. Соленоидальное поле
- 3.15. Формула Стокса
- Глава 4. Ряды Фурье. Интеграл Фурье
- 4.1. Тригонометрические ряды
- 4.2. Сходимость тригонометрических рядов
- 4.3. Ряд Фурье
- 4.4. Признаки сходимости рядов Фурье
- 4.5. Ортогональные свойства тригонометрических функций
- 4.6. Коэффициенты Фурье
- 4.7. Оценка коэффициентов Фурье
- 4.8. Пространство функций со скалярным произведением
- 4.9. Ортогональная система функций
- 4.10. Полнота тригонометрических функций
- 4.11. Комплексная форма ряда Фурье
- 4.12. Понятие интеграла Фурье. Повторный интеграл Фурье
- 4.13. Косинус- и синус- преобразования Фурье
- 4.14. Примеры
- 4.15. Приближение интеграла Фурье
- 4.16. Сумма Фейера
- 4.17. Полнота систем функций в С и L2’
- 4.18. Сведения из теории кратных рядов Фурье
- Глава 5. Уравнения математической физики
- 5.1. Температура тела
- 5.2. Задача Дирихле
- 5.3. Задача Дирихле для круга
- 5.4. Задача Дирихле для полуплоскости
- 5.5. Уравнение теплопроводности в стержне
- 5.6. Теплопроводность для бесконечного стержня
- 5.7. Малые колебания струны
- 5.8. Колебание бесконечной струны. Формула Даламбера
- 5.9. Колебание круглой мембраны
- 5.10. Общая задача Штурма-Лиувилля
- 5.11. Интеграл энергии (Дирихле)
- 5.12. Применение преобразований Фурье
- Глава 6. Теория функций комплексного переменного
- 6.1. Понятие функции комплексного переменного
- 6.2. Производная функция комплексного переменного
- 6.3. Условия Даламбера-Эйлера (Коши-Римана)
- 6.4. Гармонические функции
- 6.5. Обратная функция
- 6.6. Интегрирование функций комплексного переменного
- 6.7. Формула Коши
- 6.8. Интеграл типа Коши
- 6.9. Степенной ряд
- 6.10. Ряд Лорана
- 6.11. Классификация изолированных особых точек. Вычеты
- 6.12. Классификация особых точек на бесконечности
- 6.13. Теорема о вычетах
- 6.14. Вычисление интегралов при помощи вычетов
- 6.15. Линейная функция. Дробно-линейная функция
- Глава 7. Операционное исчисление
- 7.1. Изображение Лапласа
- 7.2. Изображение простейших функций и свойства изображений
- 7.3. Приложения операционного исчисления
- 7.3.1. Операторное уравнение
- 7.3.2. Решение систем дифференциальных уравнений
- 7.3.3. Вычисление интегралов
- Глава 8. Обобщенные функции
- 8.1. Понятие обобщенной функции
- 8.2. Операции над обобщенными функциями
- 8.3. Преобразование Фурье обобщенных функций