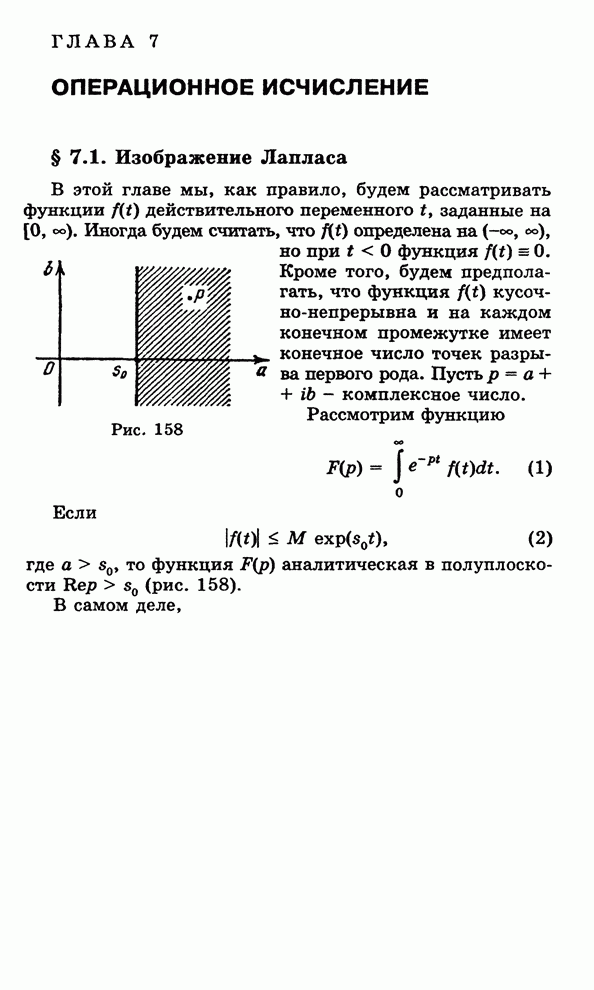
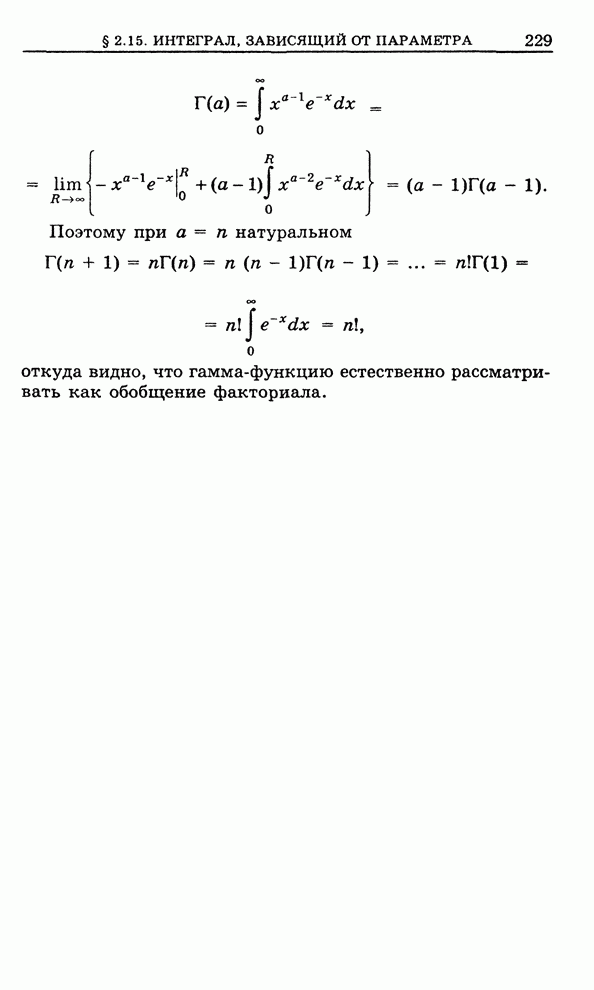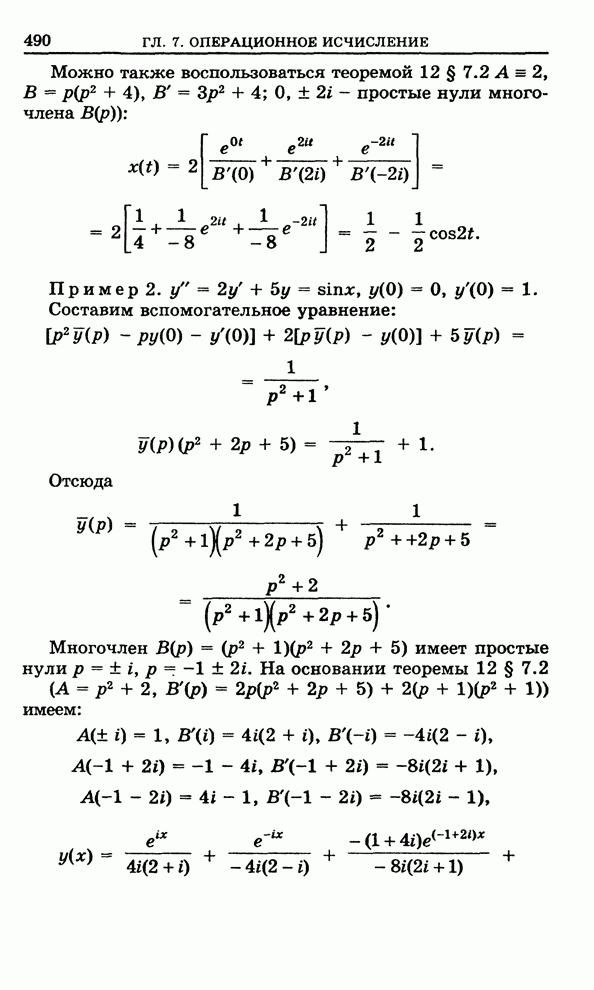| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§3.7. Формула Грина
Для
достаточно общих плоских областей ![]() с положительно ориентированной
границей
с положительно ориентированной
границей ![]() справедлива
формула
справедлива
формула
 , (1)
, (1)
называется
формулой Грина. Здесь предполагается, что ![]() непрерывны на замыкании
непрерывны на замыкании ![]() области
области ![]() .
.
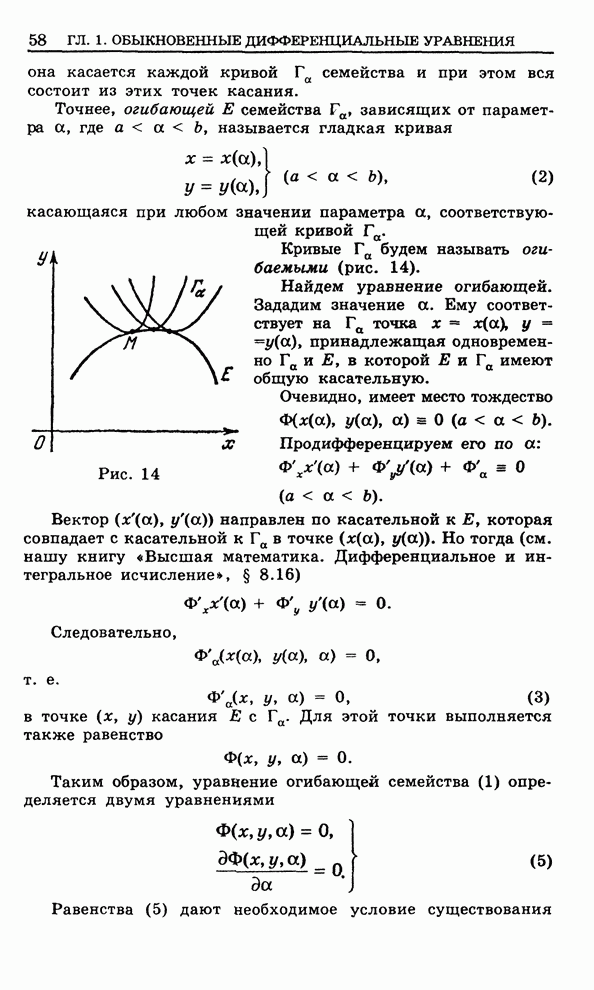
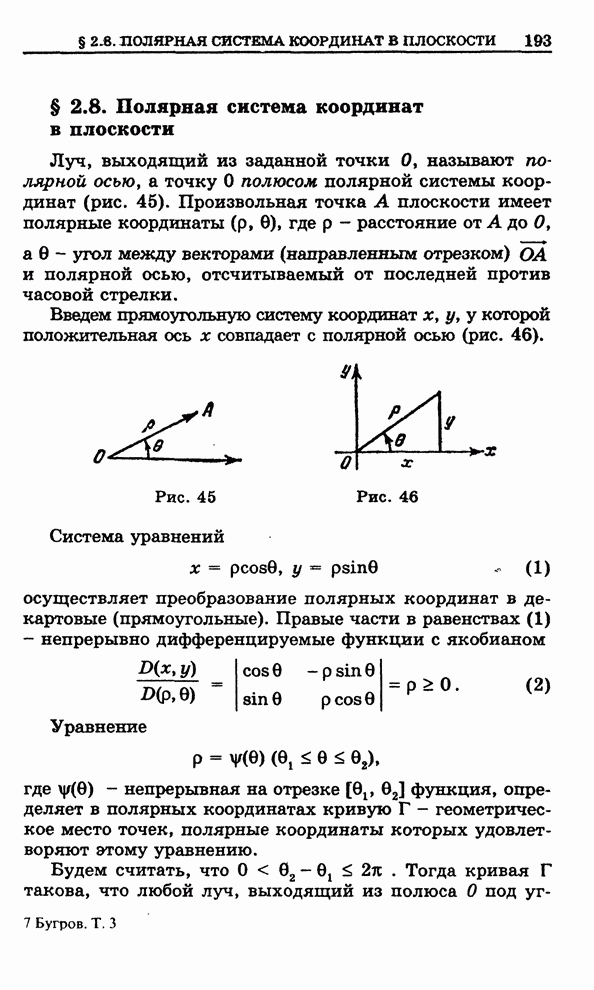
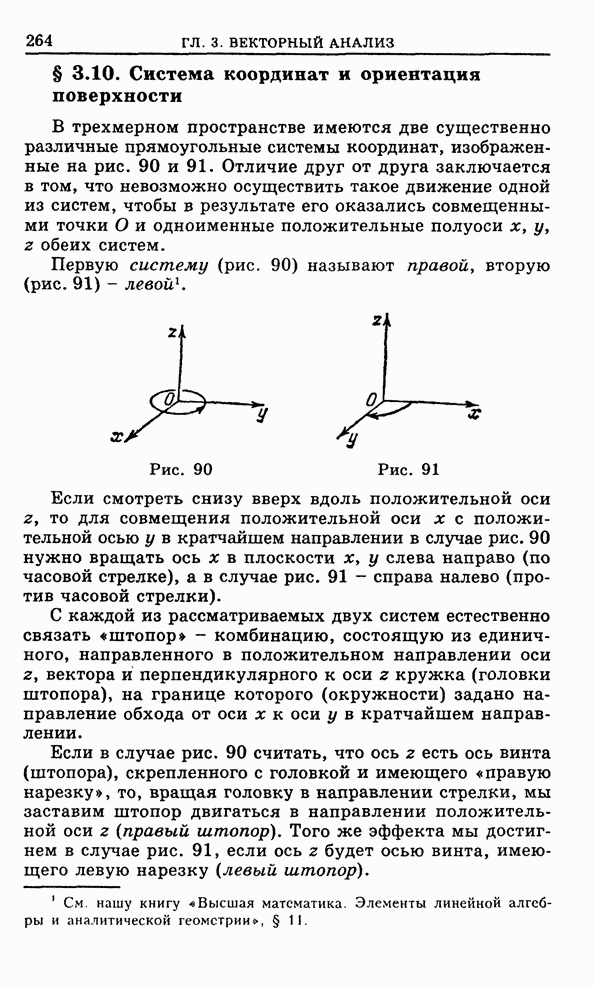
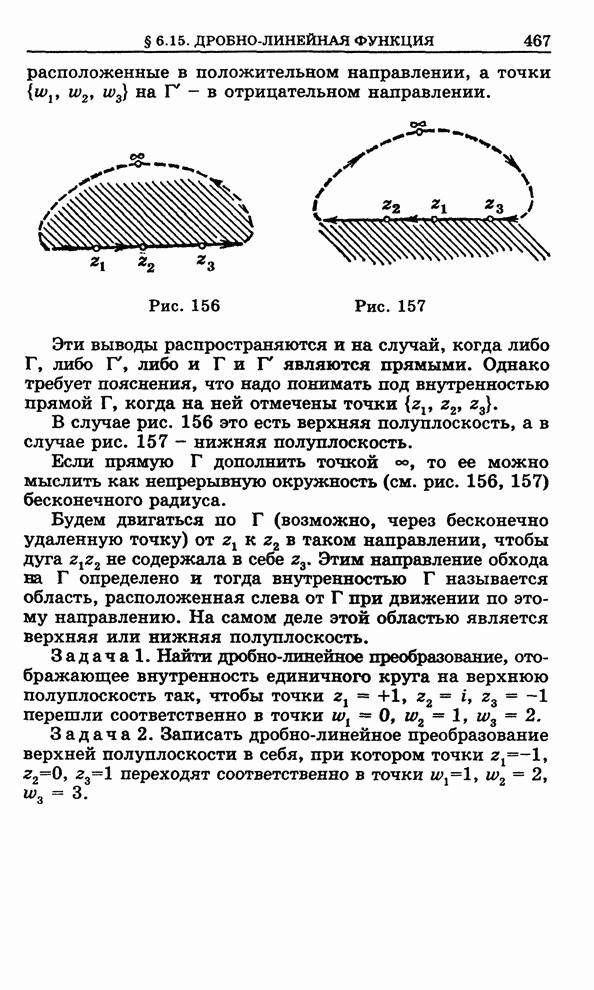
Начнем
с того, что рассмотрим плоскую область ![]() , изображенную на рис.84, которую мы будем
называть элементарной
, изображенную на рис.84, которую мы будем
называть элементарной ![]() -областью. Снизу и сверху
-областью. Снизу и сверху ![]() ограничена
кусочно-гладкими кривыми, имеющими соответственно уравнения
ограничена
кусочно-гладкими кривыми, имеющими соответственно уравнения


Рис. 84
С
боков ![]() ограничена
отрезками прямых параллельных оси ординат. Отметим, что эти отрезки могут
вырождаться в точку.
ограничена
отрезками прямых параллельных оси ординат. Отметим, что эти отрезки могут
вырождаться в точку.
Граница
![]() области
области ![]() состоит из четырех
частей:
состоит из четырех
частей:
![]() .
.
Для
такой области ![]() имеют
равенства (пояснения ниже, ориентировано положительно)
имеют
равенства (пояснения ниже, ориентировано положительно)

Поясним
последнее равенство. Кривая ![]() имеет параметрические уравнения (с
параметром
имеет параметрические уравнения (с
параметром ![]() )
)
![]() .
.
При
этом значению ![]() соответствует
точка
соответствует
точка ![]() , а
значению
, а
значению ![]() -
точка
-
точка ![]() . Кривая
. Кривая
![]() определяется
уравнениями
определяется
уравнениями
![]() .
.
Значению
![]() соответствует
точка
соответствует
точка ![]() и
значению
и
значению ![]() -
точка
-
точка ![]() . Наконец,
отрезок
. Наконец,
отрезок ![]() имеет
уравнения
имеет
уравнения ![]() (с
параметром
(с
параметром ![]() ).
Вдоль этого отрезка
).
Вдоль этого отрезка ![]() , поэтому на самом деле
, поэтому на самом деле
![]() .
.
Аналогично
интеграл по отрезку ![]() равен нулю:
равен нулю:
![]() .
.
Итак, мы определили, что
![]() . (2)
. (2)
Эта
формула распространяется на любую область![]() , которую можно разрезать на конечное
число элементарных
, которую можно разрезать на конечное
число элементарных ![]() -областей. Такую область будем называть
просто
-областей. Такую область будем называть
просто ![]() -областью.
-областью.
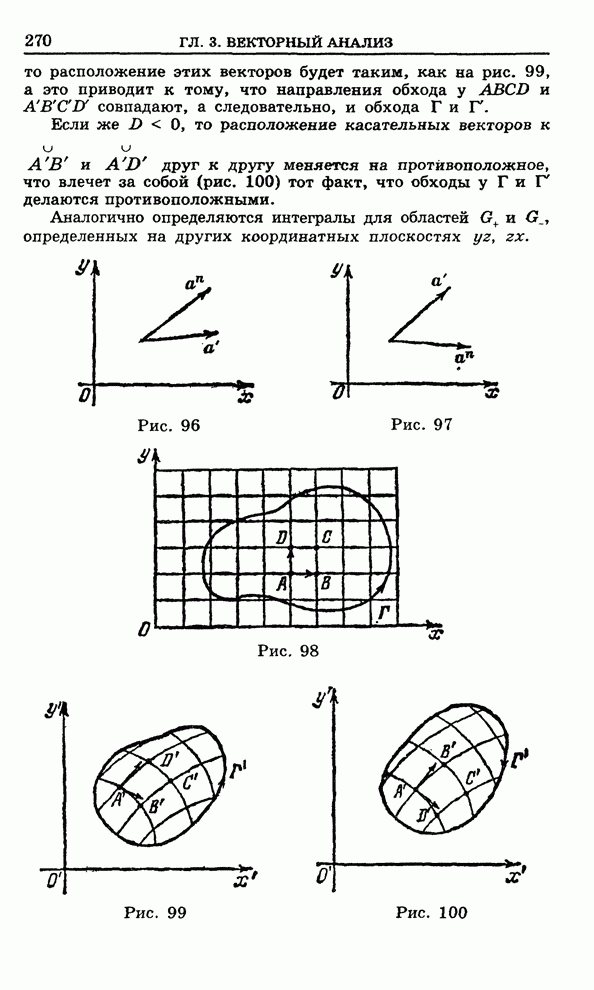
В
самом деле, пусть  ,
где
,
где ![]() -
элементарные
-
элементарные ![]() -области
с границей
-области
с границей ![]() ,
которые будем считать ориентированными положительно (рис.85). Тогда (пояснения
ниже)
,
которые будем считать ориентированными положительно (рис.85). Тогда (пояснения
ниже)
 . (3)
. (3)
Пояснения требует третье равенство.
Здесь
важно отметить, что, если два контура ![]() , и
, и ![]() имеют общий кусок
имеют общий кусок ![]() , то он как часть
, то он как часть ![]() и как часть
и как часть ![]() ориентирован
противоположно, и потому криволинейные интегралы от
ориентирован
противоположно, и потому криволинейные интегралы от ![]() по
по ![]() в обоих случаях отличаются
лишь знаком
в обоих случаях отличаются
лишь знаком ![]() их
сумма равна нулю. Если учесть это, то сумма
их
сумма равна нулю. Если учесть это, то сумма ![]() в цепи (3) сведется к сумме
криволинейных интегралов по кускам
в цепи (3) сведется к сумме
криволинейных интегралов по кускам ![]() , принадлежащим к
, принадлежащим к ![]() , равной интегралу по контуру
, равной интегралу по контуру
![]() .
.

Рис. 85 Рис.86
По
аналогии можно ввести понятие элементарной ![]() -области. В этом случае
-области. В этом случае ![]() ограничена слева и
справа кусочно-гладкими кривыми (рис. 86)
ограничена слева и
справа кусочно-гладкими кривыми (рис. 86)
![]() .
.
Сверху
и снизу ![]() ограничена
отрезками прямых параллельных оси
ограничена
отрезками прямых параллельных оси ![]() .
.
Можно
также сказать, что элементарная ![]() -область определяется так же, как
элементарная
-область определяется так же, как
элементарная ![]() -область,
только роль
-область,
только роль ![]() теперь
играет
теперь
играет ![]() .
.
Для
элементарной ![]() -области
-области
![]() получаем
(пояснения ниже)
получаем
(пояснения ниже)
 (4)
(4)
так как ![]() на отрезках
на отрезках ![]() и
и ![]() , то и
, то и
![]() .
.
Формула
(4) также распространяется на любую область ![]() , которую можно разрезать на конечное
число элементарных
, которую можно разрезать на конечное
число элементарных ![]() -областей. Такую область будем называть
просто
-областей. Такую область будем называть
просто ![]() -областью.
-областью.
Итак, мы доказали предложение:
Теорема
1. Если область ![]() является
одновременно
является
одновременно ![]() -
и
-
и ![]() -областью,
то для нее имеет место формула Грина.
-областью,
то для нее имеет место формула Грина.
Для
доказательства достаточно вычесть из равенства (4) равенство (3), которые
справедливы для области ![]() , обладающей указанными свойствами.
, обладающей указанными свойствами.
Примерами
областей, одновременно являющихся ![]() - и
- и ![]() -областями, могут служить область
-областями, могут служить область

и эллипс
![]() .
.
Более
того, эти области являются элементарными ![]() - и
- и ![]() -областями.
-областями.
Замечание
1. Можно доказать более общее утверждение. Если область ![]() ограничена произвольным
замкнутым кусочно-гладким самонепересекающимся контуром
ограничена произвольным
замкнутым кусочно-гладким самонепересекающимся контуром ![]() , то для нее верна формула
Грина (1).
, то для нее верна формула
Грина (1).
Следствие.
Если плоская область ![]() односвязна и на ней задан непрерывно
дифференцируемый вектор
односвязна и на ней задан непрерывно
дифференцируемый вектор
![]() ,
,
для которого
![]() ,
,
то ![]() имеет на
имеет на ![]() потенциал (т. е.
имеет место в плоском случае теорема 3 § 3.4).
потенциал (т. е.
имеет место в плоском случае теорема 3 § 3.4).
В
самом деле, зададим произвольный самонепересекающийся непрерывный
кусочно-гладкий контур ![]() , ориентированный положительно (рис.
87).
, ориентированный положительно (рис.
87).
Он
служит границей некоторой области ![]() . Согласно теореме (формуле) Грина (см.
замечание 1)
. Согласно теореме (формуле) Грина (см.
замечание 1)
 ,
,

Рис. 87
и так как ![]() - произвольный
замкнутый самонепересекающийся контур, то на основании теоремы 1 § 3.4 вектор
- произвольный
замкнутый самонепересекающийся контур, то на основании теоремы 1 § 3.4 вектор ![]() имеет потенциал на
имеет потенциал на ![]() .
.
Замечание
2. Так как двойной интеграл от единичной функции по области ![]() равен площади (мере) области
равен площади (мере) области
![]() , то,
выбирая функции
, то,
выбирая функции ![]() и
и
![]() так,
чтобы
так,
чтобы ![]() , мы
получим различные выражения площади области
, мы
получим различные выражения площади области ![]() через криволинейный интеграл:
через криволинейный интеграл:
![]() .
.
В
частности, при ![]() получаем
получаем
![]() . (5)
. (5)
Пример. Вычислить площадь, ограниченную эллипсом
![]() .
.
Согласно формуле (5) имеем
 .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. Обыкновенные дифференциальные уравнения
- 1.1. Задача, приводящая к дифференциальному уравнению
- 1.2. Общие понятия
- 1.2.1. Понятие обыкновенного дифференциального уравнения
- 1.2.2. Дифференциальное уравнение первого порядка
- 1.2.3. Задача Коши
- 1.2.4. Примеры дифференциальных уравнений первого порядка
- 1.2.5. Общий интеграл дифференциального уравнения первого порядка
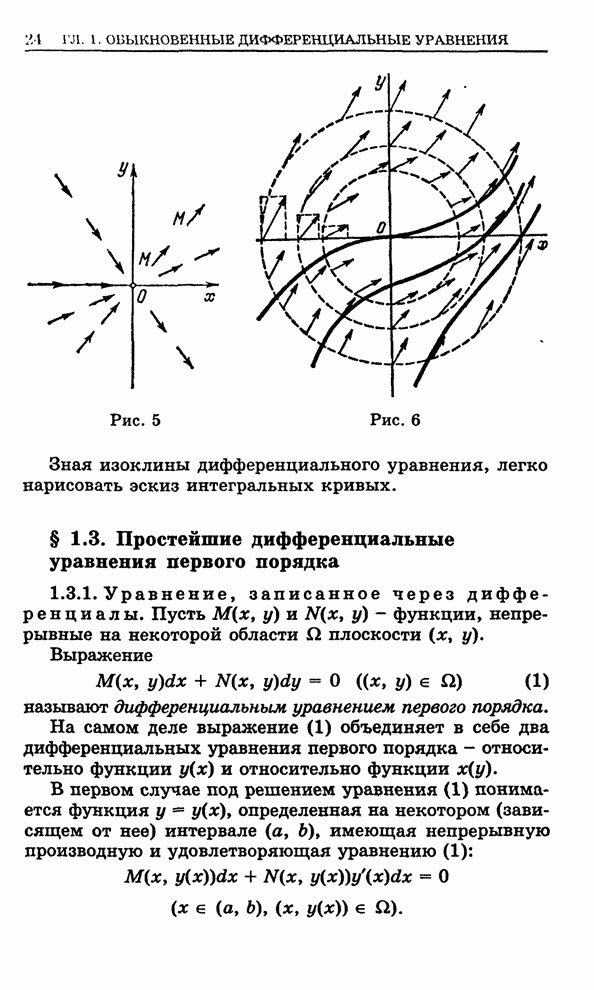
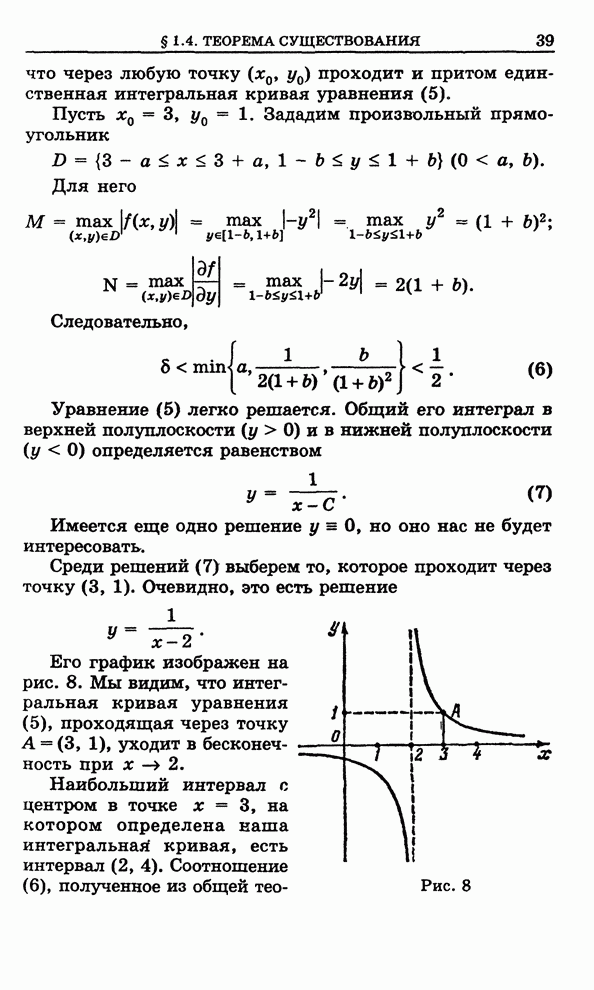
- 1.2.6. Поле направлений
- 1.3. Простейшие дифференциальные уравнения первого порядка
- 1.3.1. Уравнение, записанное через дифференциалы
- 1.3.2. Уравнения с разделенными переменными
- 1.3.3. Уравнения с разделяющимися переменными
- 1.3.4. Однородные уравнения
- 1.3.5. Линейное уравнение
- 1.3.6. Уравнение Бернулли
- 1.4. Теорема существования решения дифференциального уравнения первого порядка
- 1.5. Метрическое пространство
- 1.5.1. Понятие метрического пространства
- 1.5.2. Полное метрическое пространство
- 1.5.3. Принцип сжатых отображений
- 1.5.4. Приближенное значение корня функции
- 1.5.5. Метод Ньютона
- 1.6. Доказательство теоремы существования решения диффереацнального уравнения первого порядка
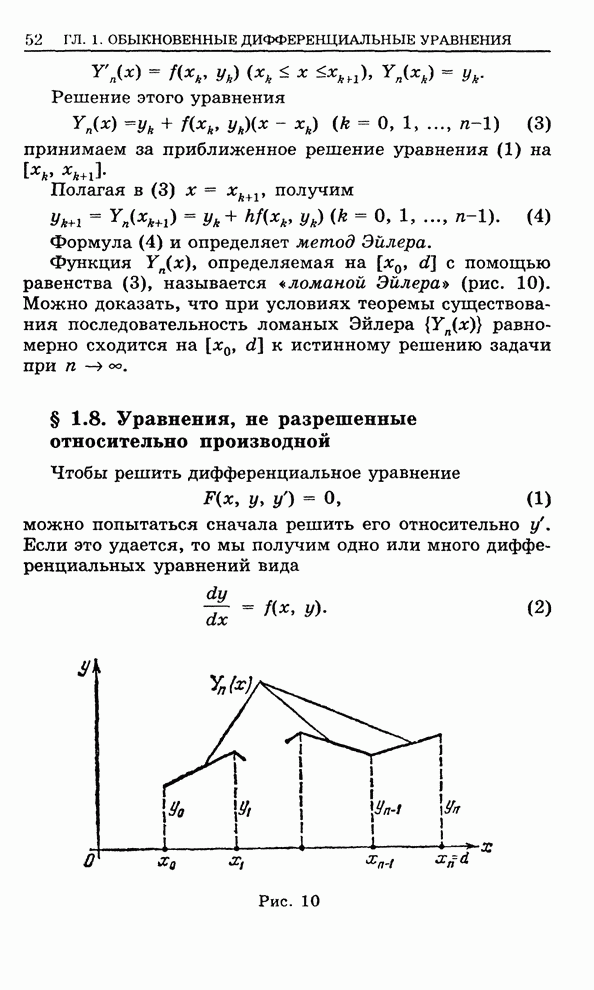
- 1.7. Метод Эйлера приближенного решения дифференциального уравнения первого порядка
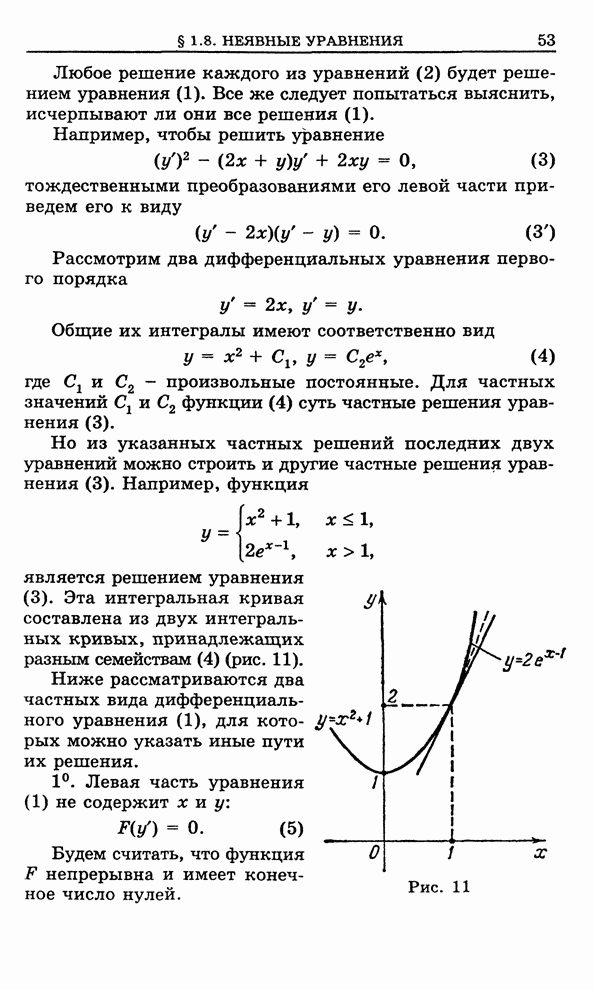
- 1.8. Уравнения, не разрешенные относительно производной
- 1.9. Особые решения
- 1.10. Огибающая семейства кривых
- 1.11. Дифференциальное уравнение второго порядка
- 1.12. Система из двух дифференциальных уравнений первого порядка
- 1.13. Дифференциальное уравнение n-го порядка
- 1.14. Понижение порядка дифференциального уравнения
- 1.15. Линейные уравнения высшего порядка
- 1.15.1. Понятие линейного уравнения высшего порядка
- 1.15.2. Фундаментальная система решений уравнения
- 1.15.3. Определитель Вронского
- 1.15.4. Структура общего решения
- 1.16. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- 1.16.1. Методы решения
- 1.16.2. Уравнение Эйлера
- 1.17. Метод вариации постоянных
- 1.18. Частное решение неоднородного уравнения с постоянными коэффициентами. Приложения
- 1.18.1. Методы нахождения частных решений
- 1.18.2. Дифференциальное уравнение колебания пружины
- 1.19. Системы дифференциальных уравнений. Фазовое пространство
- 1.20. Линейная однородная система дифференциальных уравнений
- 1.21. Общее решение линейной однородной системы дифференциальных уравнений с постоянными коэффициентами
- 1.22. Сведение системы уравнений к одному уравнению
- 1.23. Неоднородная система линейных дифференциальных уравнений с постоянными коэффициентами
- 1.24. Интегрирование дифференциальных уравнений с помощью степенных рядов
- 1.25. Элементы теории устойчивости
- 1.26. Классификация точек покоя
- Глава 2. Кратные интегралы
- 2.1. Введение
- 2.2. Сведения из теории меры Жордана
- 2.3. Свойства кратных интегралов. Теоремы существования
- 2.4. Сведение кратного интеграла к повторным
- 2.5. Доказательство существования интеграла от непрерывной функции
- 2.6. Замена переменных. Простейший случай
- 2.7. Замена переменных. Общий случай
- 2.8. Полярная система координат в плоскости
- 2.9. Полярная система координат в пространстве
- 2.10. Цилиндрические координаты
- 2.11. Площадь поверхности
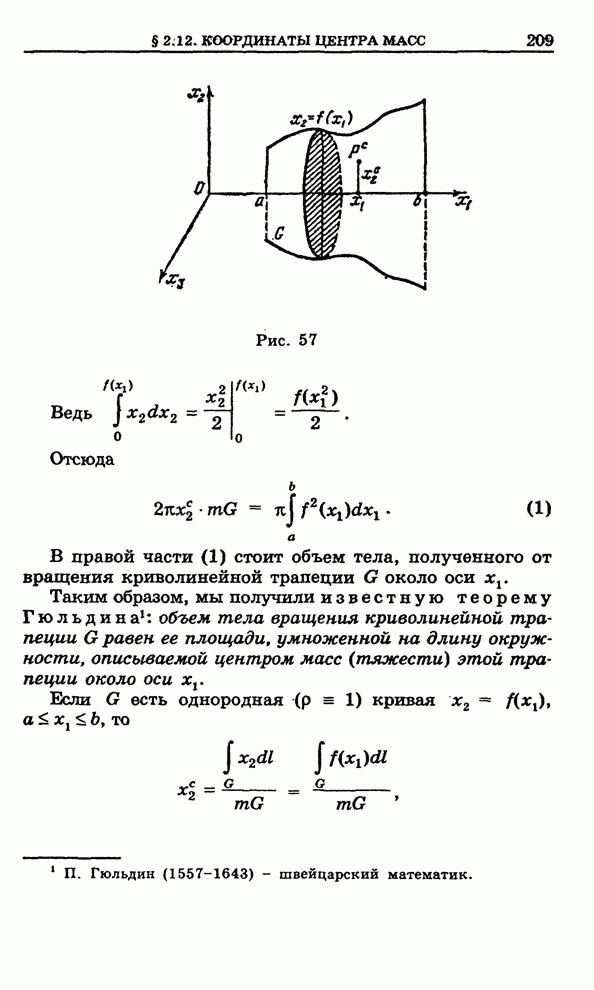
- 2.12. Координаты центра масс
- 2.13. Несобственные интегралы
- 2.14. Несобственный интеграл с особенностями вдоль линии
- 2.15. Несобственный интеграл, зависящий от параметра
- Глава 3. Векторный анализ
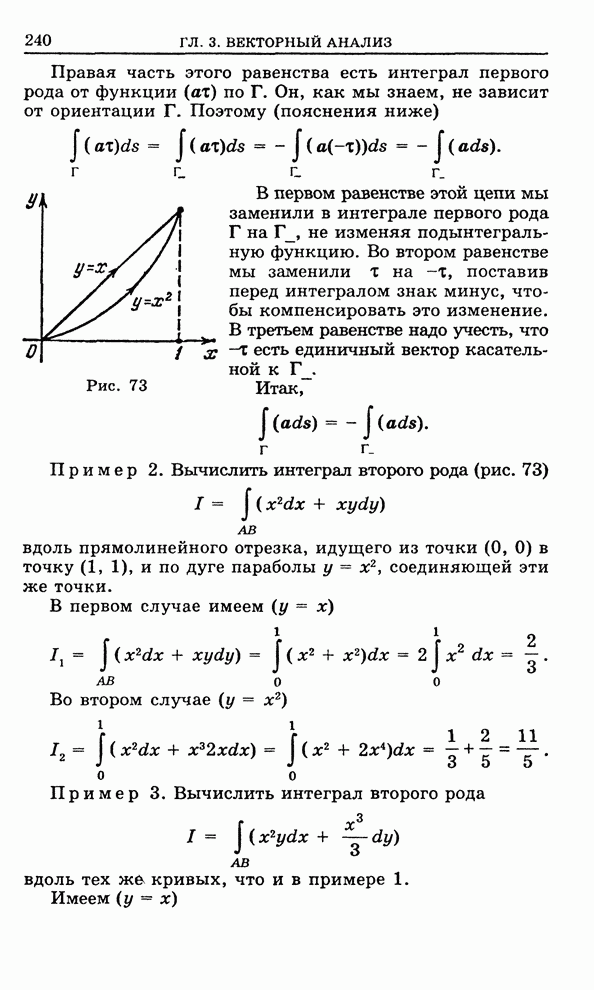
- 3.1. Кусочно-гладкая ориентированная кривая
- 3.2. Криволинейный интеграл первого рода
- 3.3. Интеграл от вектора вдоль кривой
- 3.3.1. Поле вектора
- 3.3.2. Криволинейный интеграл от вектора вдоль кривой
- 3.3.3. Свойства криволинейных интегралов второго рода
- 3.4. Поле потенциала
- 3.4.1. Понятие потенциала и его свойства
- 3.4.2. Доказательство свойств потенциала
- 3.4.3. Ротор вектора
- 3.5. Дифференциальное уравнение в полных дифференциалах
- 3.6. Ориентация плоской области
- 3.7. Формула Грина
- 3.8. Интеграл по поверхности первого рода
- 3.9. Ориентация поверхности
- 3.10. Система координат и ориентация поверхности
- 3.11. Интеграл по ориентированной плоской области
- 3.12. Поток вектора через ориентированную поверхность
- 3.13. Дивергенция. Теорема Гаусса—Остроградского
- 3.14. Соленоидальное поле
- 3.15. Формула Стокса
- Глава 4. Ряды Фурье. Интеграл Фурье
- 4.1. Тригонометрические ряды
- 4.2. Сходимость тригонометрических рядов
- 4.3. Ряд Фурье
- 4.4. Признаки сходимости рядов Фурье
- 4.5. Ортогональные свойства тригонометрических функций
- 4.6. Коэффициенты Фурье
- 4.7. Оценка коэффициентов Фурье
- 4.8. Пространство функций со скалярным произведением
- 4.9. Ортогональная система функций
- 4.10. Полнота тригонометрических функций
- 4.11. Комплексная форма ряда Фурье
- 4.12. Понятие интеграла Фурье. Повторный интеграл Фурье
- 4.13. Косинус- и синус- преобразования Фурье
- 4.14. Примеры
- 4.15. Приближение интеграла Фурье
- 4.16. Сумма Фейера
- 4.17. Полнота систем функций в С и L2’
- 4.18. Сведения из теории кратных рядов Фурье
- Глава 5. Уравнения математической физики
- 5.1. Температура тела
- 5.2. Задача Дирихле
- 5.3. Задача Дирихле для круга
- 5.4. Задача Дирихле для полуплоскости
- 5.5. Уравнение теплопроводности в стержне
- 5.6. Теплопроводность для бесконечного стержня
- 5.7. Малые колебания струны
- 5.8. Колебание бесконечной струны. Формула Даламбера
- 5.9. Колебание круглой мембраны
- 5.10. Общая задача Штурма-Лиувилля
- 5.11. Интеграл энергии (Дирихле)
- 5.12. Применение преобразований Фурье
- Глава 6. Теория функций комплексного переменного
- 6.1. Понятие функции комплексного переменного
- 6.2. Производная функция комплексного переменного
- 6.3. Условия Даламбера-Эйлера (Коши-Римана)
- 6.4. Гармонические функции
- 6.5. Обратная функция
- 6.6. Интегрирование функций комплексного переменного
- 6.7. Формула Коши
- 6.8. Интеграл типа Коши
- 6.9. Степенной ряд
- 6.10. Ряд Лорана
- 6.11. Классификация изолированных особых точек. Вычеты
- 6.12. Классификация особых точек на бесконечности
- 6.13. Теорема о вычетах
- 6.14. Вычисление интегралов при помощи вычетов
- 6.15. Линейная функция. Дробно-линейная функция
- Глава 7. Операционное исчисление
- 7.1. Изображение Лапласа
- 7.2. Изображение простейших функций и свойства изображений
- 7.3. Приложения операционного исчисления
- 7.3.1. Операторное уравнение
- 7.3.2. Решение систем дифференциальных уравнений
- 7.3.3. Вычисление интегралов
- Глава 8. Обобщенные функции
- 8.1. Понятие обобщенной функции
- 8.2. Операции над обобщенными функциями
- 8.3. Преобразование Фурье обобщенных функций