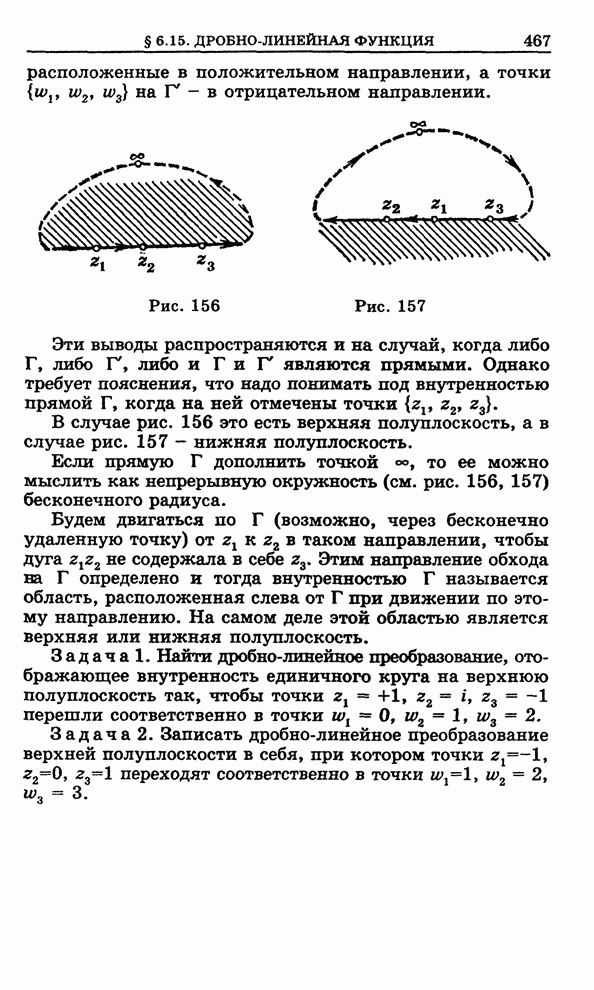
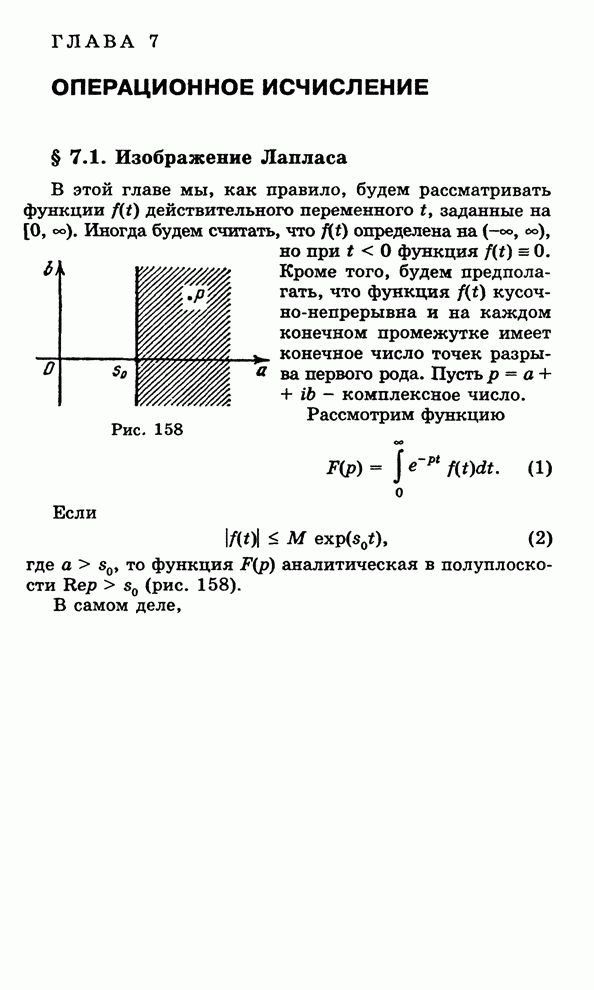
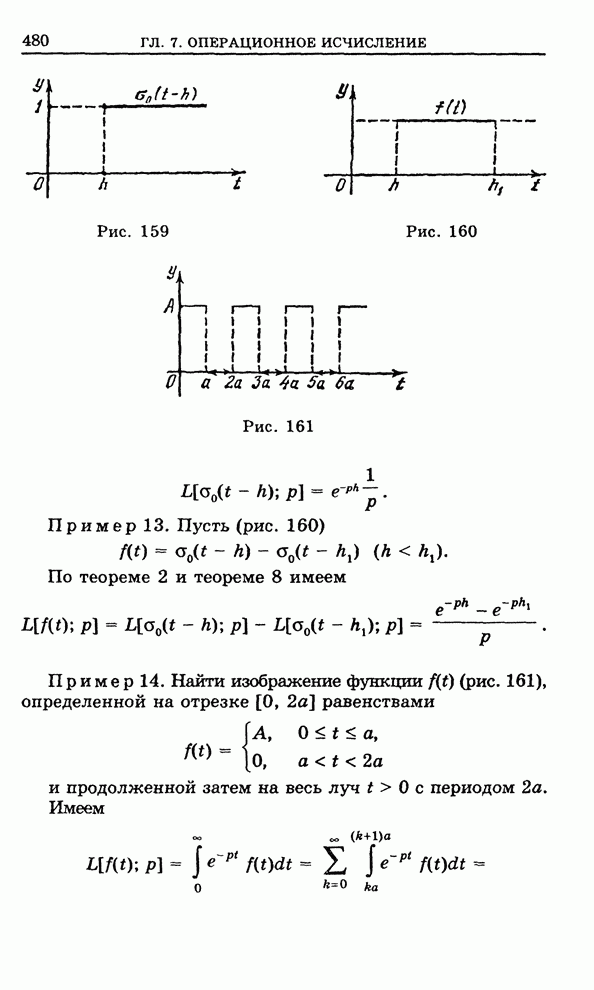
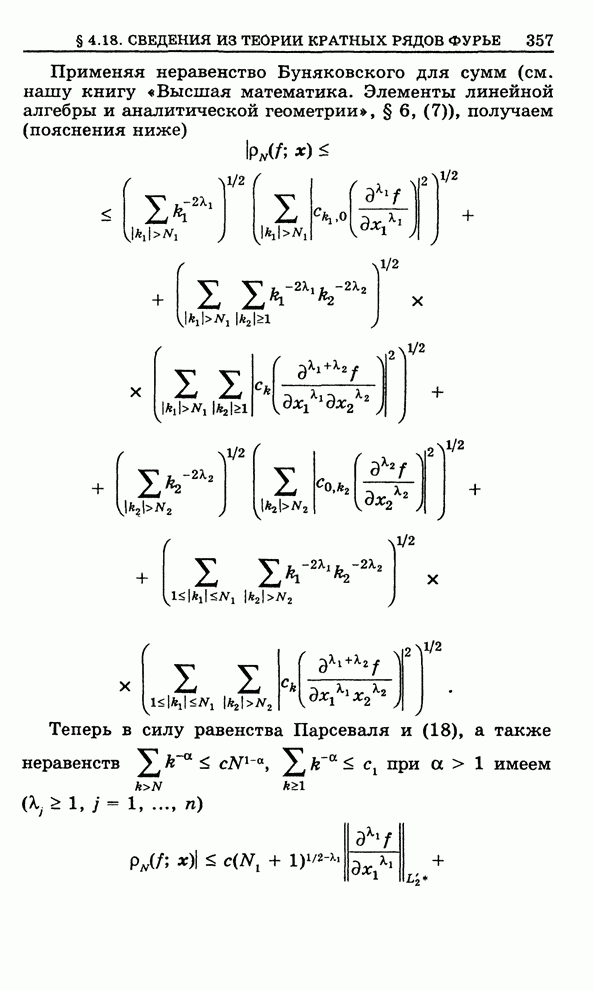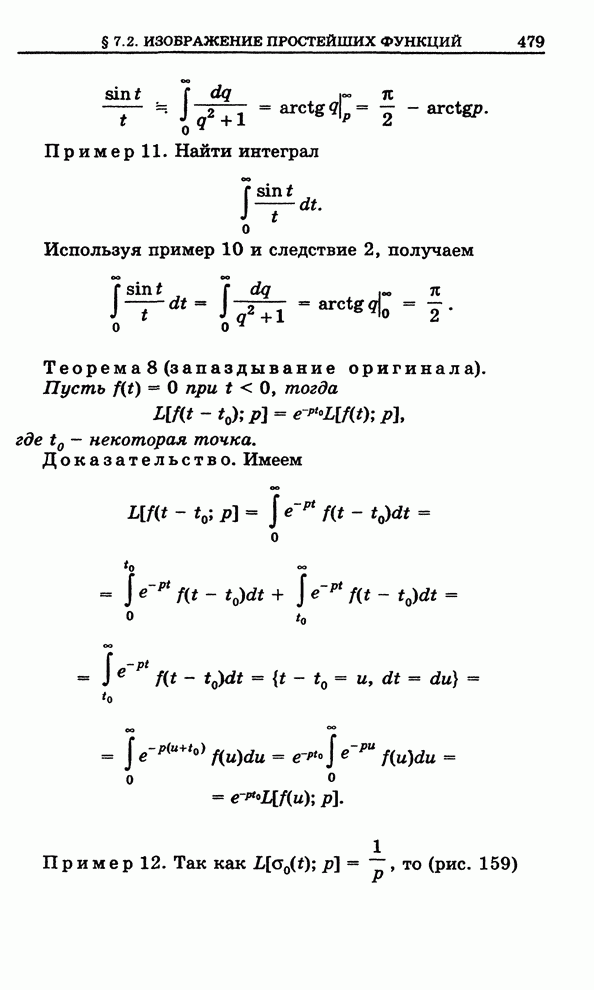| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
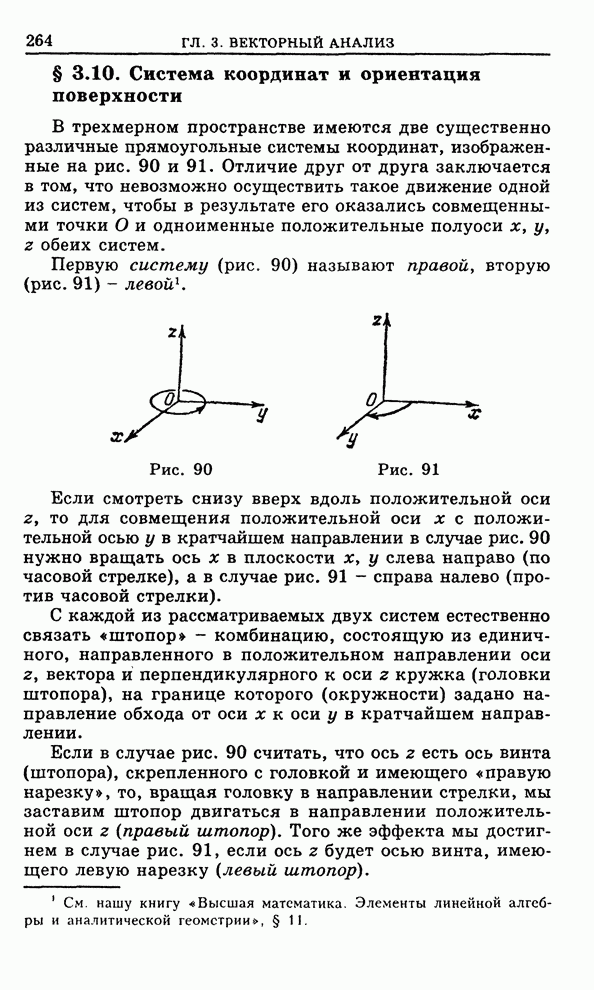
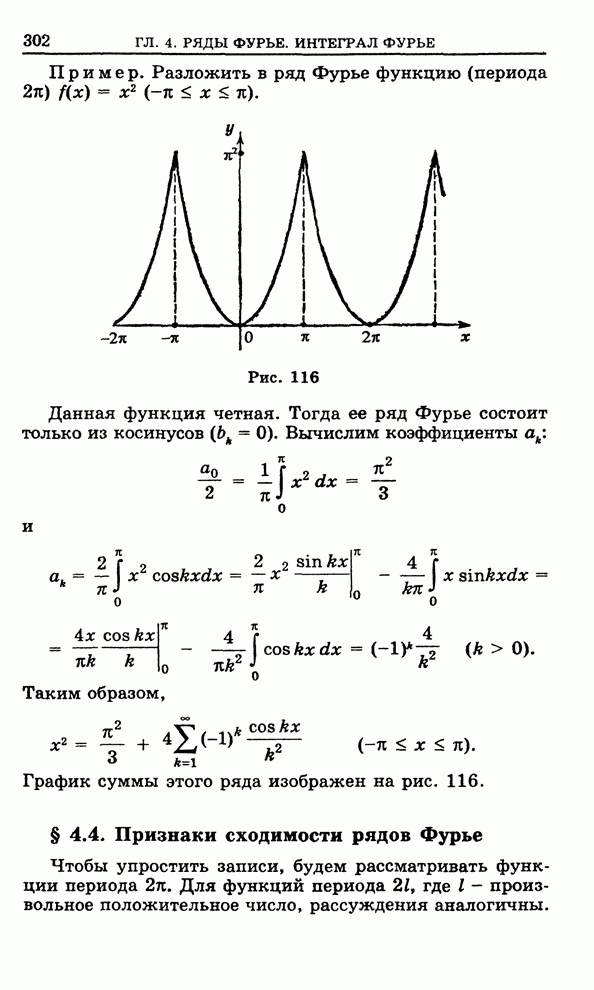
§ 1.9. Особые решения
Пусть дано дифференциальное уравнение
![]() . (1)
. (1)
Если в
окрестности точки ![]() плоскости
плоскости
![]() выполняются
условия теоремы существования и единственности,
то через нее проходит и притом только одна интегральная кривая.
выполняются
условия теоремы существования и единственности,
то через нее проходит и притом только одна интегральная кривая.
Если условия теоремы существования не
соблюдаются, то тут могут быть различные случаи. Через точку ![]() все же может
проходить одна интегральная кривая или несколько или бесконечное множество, или
же нет интегральной кривой, которая
проходила бы через точку
все же может
проходить одна интегральная кривая или несколько или бесконечное множество, или
же нет интегральной кривой, которая
проходила бы через точку ![]() . Интересен тот случай, когда дифференциальное уравнение (1) имеет
особое решение.
. Интересен тот случай, когда дифференциальное уравнение (1) имеет
особое решение.
Решение дифференциального уравнения первого порядка называется особым, если соответствующая интегральная кривая обладает тем свойством, что через любую ее точку проходит, кроме нее, еще и другая касающаяся ее интегральная кривая данного уравнения.
Нередко приходится иметь дело с дифференциальными
уравнениями вида (1), где функция ![]() непрерывна на некоторой области
непрерывна на некоторой области ![]() , а ее частная
производная
, а ее частная
производная ![]() конечна
и непрерывна не всюду на
конечна
и непрерывна не всюду на ![]() . Имеются на
. Имеются на ![]() такие точки, где
такие точки, где ![]() . В каждой такой
точке, вообще говоря, нарушаются условия существования и единственности решения
дифференциального уравнения (1), а если такие точки образуют гладкие линии, то
последние могут представлять особые решения дифференциального уравнения.
. В каждой такой
точке, вообще говоря, нарушаются условия существования и единственности решения
дифференциального уравнения (1), а если такие точки образуют гладкие линии, то
последние могут представлять особые решения дифференциального уравнения.
П р и м е р 1. Рассмотрим простейшее уравнение
Бернулли ![]() .
Здесь
.
Здесь ![]() - непрерывная
функция на верхней полуплоскости. Функция
- непрерывная
функция на верхней полуплоскости. Функция ![]() при
при ![]() не ограничена в окрестности
не ограничена в окрестности ![]() . Функция
. Функция ![]() является решением
уравнения. Для начального условия
является решением
уравнения. Для начального условия ![]() есть еще одно решение
есть еще одно решение
![]() ,
,
удовлетворяющее
этому уравнению и проходящее через точку ![]() . Касательная к этой кривой в точке
. Касательная к этой кривой в точке ![]() , очевидно, есть ось
, очевидно, есть ось
![]() . Поэтому
. Поэтому ![]() есть особое
решение.
есть особое
решение.
Пример 2. ![]() .
.
Здесь ![]() и при
и при ![]() эта функция не ограничена
в окрестности
эта функция не ограничена
в окрестности ![]() .
Однако
.
Однако ![]() не
является решением уравнения. Решение уравнения, например при
не
является решением уравнения. Решение уравнения, например при ![]() , определяется неявно
равенством
, определяется неявно
равенством ![]() ,
т. е. через каждую точку
,
т. е. через каждую точку ![]() проходит единственная интегральная
кривая
проходит единственная интегральная
кривая ![]() .
.
Пример 3.
Функции ![]() при
любом
при
любом ![]() (рис.
13) являются решениями уравнения
(рис.
13) являются решениями уравнения ![]() . Функция
. Функция ![]() является особым решением данного
уравнения.
является особым решением данного
уравнения.

Рис. 13
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. Обыкновенные дифференциальные уравнения
- 1.1. Задача, приводящая к дифференциальному уравнению
- 1.2. Общие понятия
- 1.2.1. Понятие обыкновенного дифференциального уравнения
- 1.2.2. Дифференциальное уравнение первого порядка
- 1.2.3. Задача Коши
- 1.2.4. Примеры дифференциальных уравнений первого порядка
- 1.2.5. Общий интеграл дифференциального уравнения первого порядка
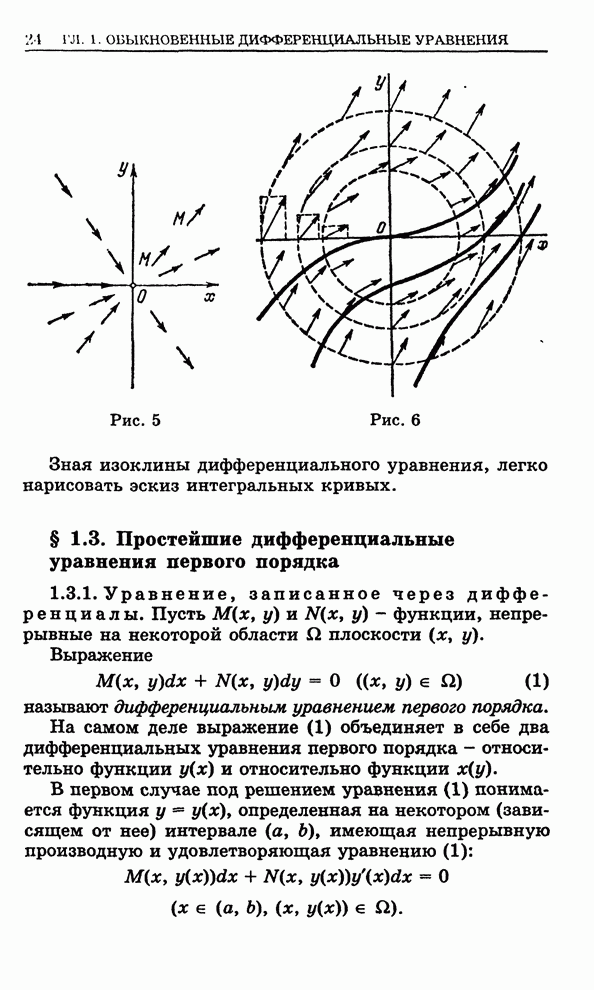
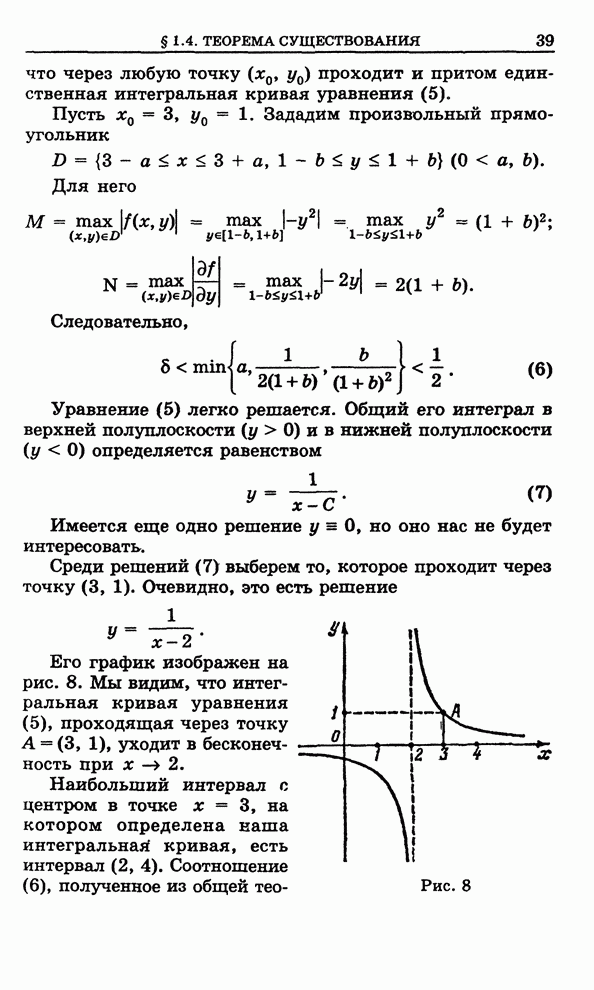
- 1.2.6. Поле направлений
- 1.3. Простейшие дифференциальные уравнения первого порядка
- 1.3.1. Уравнение, записанное через дифференциалы
- 1.3.2. Уравнения с разделенными переменными
- 1.3.3. Уравнения с разделяющимися переменными
- 1.3.4. Однородные уравнения
- 1.3.5. Линейное уравнение
- 1.3.6. Уравнение Бернулли
- 1.4. Теорема существования решения дифференциального уравнения первого порядка
- 1.5. Метрическое пространство
- 1.5.1. Понятие метрического пространства
- 1.5.2. Полное метрическое пространство
- 1.5.3. Принцип сжатых отображений
- 1.5.4. Приближенное значение корня функции
- 1.5.5. Метод Ньютона
- 1.6. Доказательство теоремы существования решения диффереацнального уравнения первого порядка
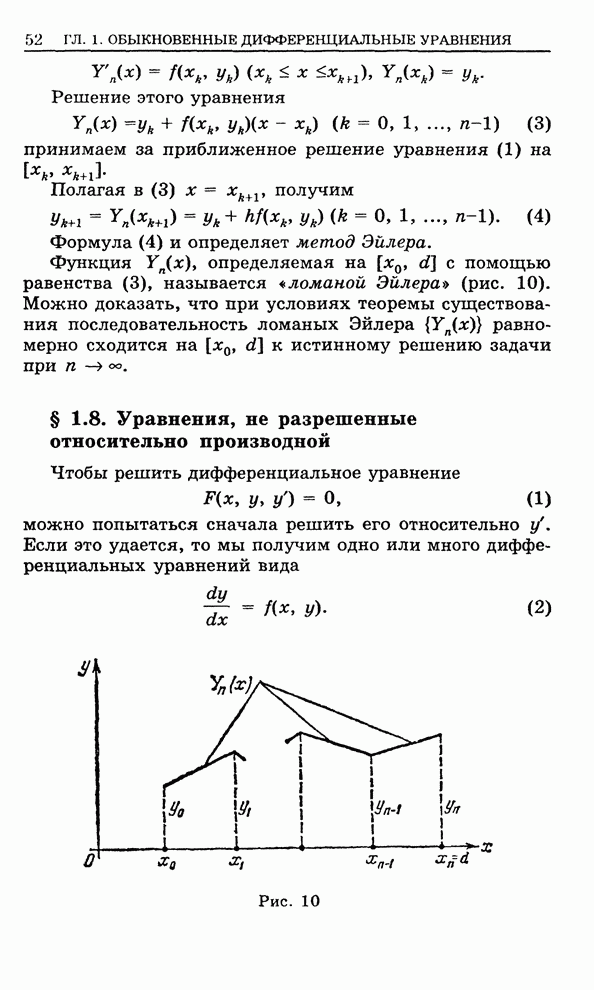
- 1.7. Метод Эйлера приближенного решения дифференциального уравнения первого порядка
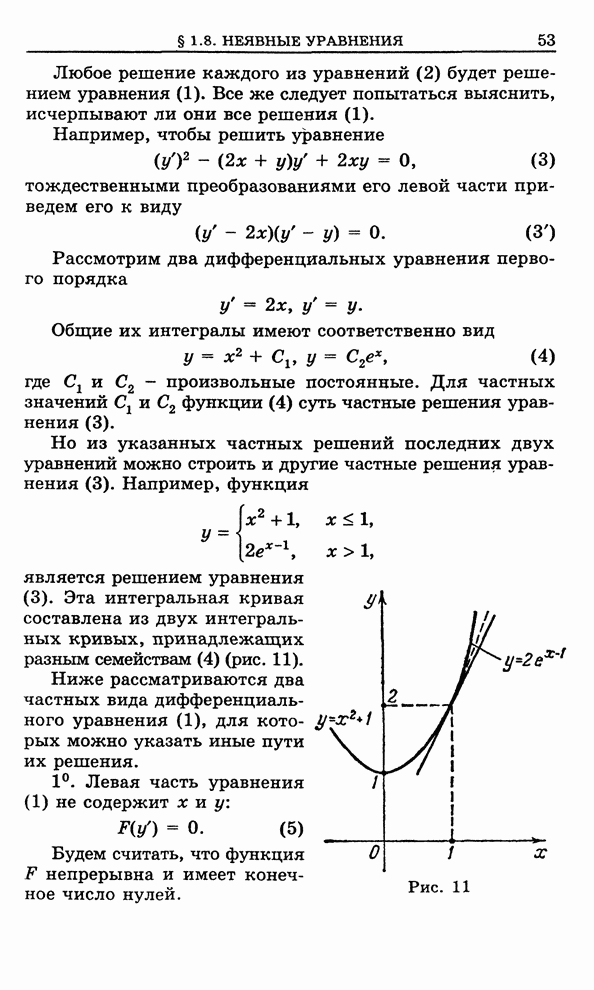
- 1.8. Уравнения, не разрешенные относительно производной
- 1.9. Особые решения
- 1.10. Огибающая семейства кривых
- 1.11. Дифференциальное уравнение второго порядка
- 1.12. Система из двух дифференциальных уравнений первого порядка
- 1.13. Дифференциальное уравнение n-го порядка
- 1.14. Понижение порядка дифференциального уравнения
- 1.15. Линейные уравнения высшего порядка
- 1.15.1. Понятие линейного уравнения высшего порядка
- 1.15.2. Фундаментальная система решений уравнения
- 1.15.3. Определитель Вронского
- 1.15.4. Структура общего решения
- 1.16. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- 1.16.1. Методы решения
- 1.16.2. Уравнение Эйлера
- 1.17. Метод вариации постоянных
- 1.18. Частное решение неоднородного уравнения с постоянными коэффициентами. Приложения
- 1.18.1. Методы нахождения частных решений
- 1.18.2. Дифференциальное уравнение колебания пружины
- 1.19. Системы дифференциальных уравнений. Фазовое пространство
- 1.20. Линейная однородная система дифференциальных уравнений
- 1.21. Общее решение линейной однородной системы дифференциальных уравнений с постоянными коэффициентами
- 1.22. Сведение системы уравнений к одному уравнению
- 1.23. Неоднородная система линейных дифференциальных уравнений с постоянными коэффициентами
- 1.24. Интегрирование дифференциальных уравнений с помощью степенных рядов
- 1.25. Элементы теории устойчивости
- 1.26. Классификация точек покоя
- Глава 2. Кратные интегралы
- 2.1. Введение
- 2.2. Сведения из теории меры Жордана
- 2.3. Свойства кратных интегралов. Теоремы существования
- 2.4. Сведение кратного интеграла к повторным
- 2.5. Доказательство существования интеграла от непрерывной функции
- 2.6. Замена переменных. Простейший случай
- 2.7. Замена переменных. Общий случай
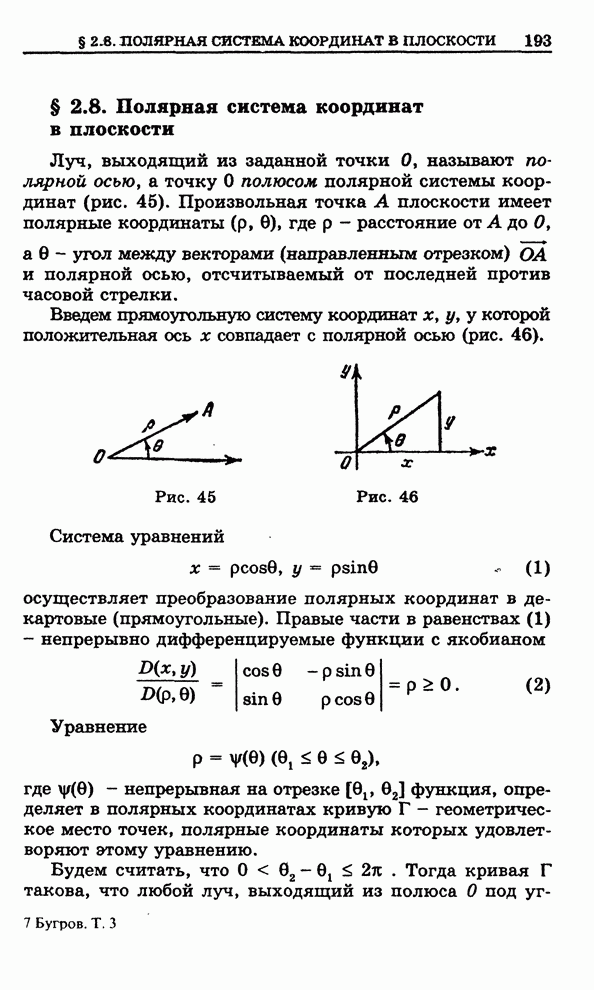
- 2.8. Полярная система координат в плоскости
- 2.9. Полярная система координат в пространстве
- 2.10. Цилиндрические координаты
- 2.11. Площадь поверхности
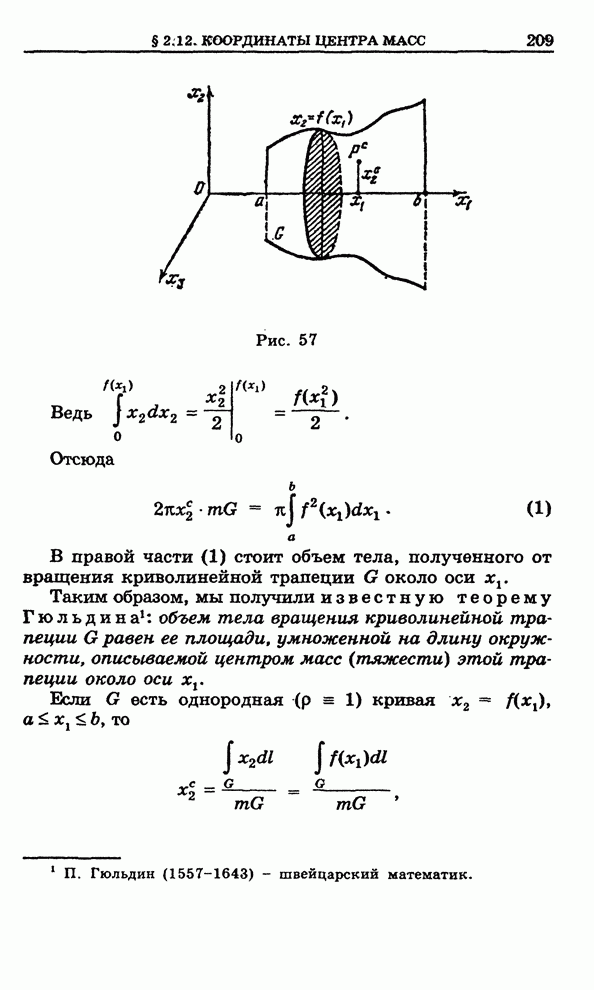
- 2.12. Координаты центра масс
- 2.13. Несобственные интегралы
- 2.14. Несобственный интеграл с особенностями вдоль линии
- 2.15. Несобственный интеграл, зависящий от параметра
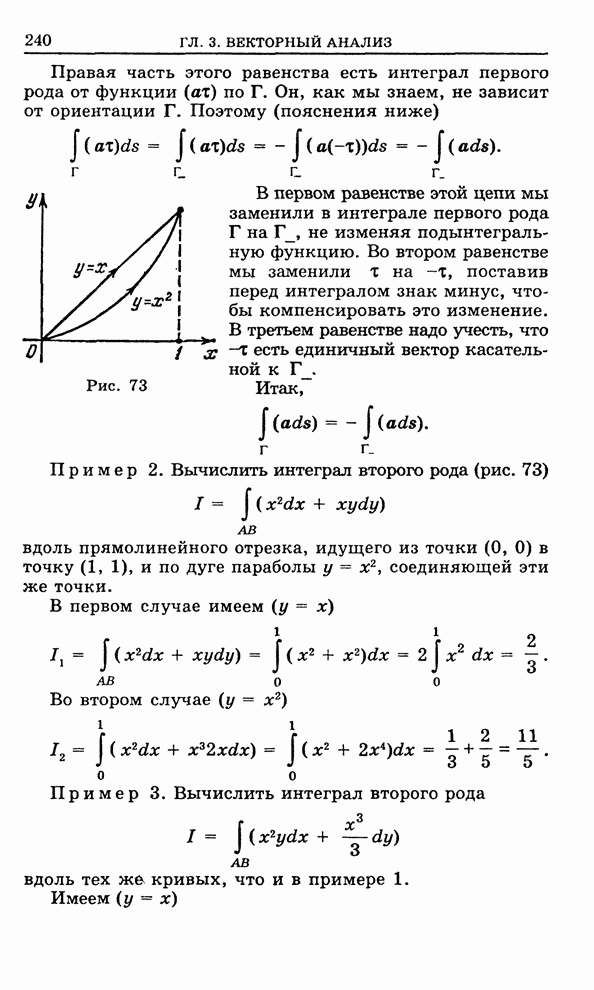
- Глава 3. Векторный анализ
- 3.1. Кусочно-гладкая ориентированная кривая
- 3.2. Криволинейный интеграл первого рода
- 3.3. Интеграл от вектора вдоль кривой
- 3.3.1. Поле вектора
- 3.3.2. Криволинейный интеграл от вектора вдоль кривой
- 3.3.3. Свойства криволинейных интегралов второго рода
- 3.4. Поле потенциала
- 3.4.1. Понятие потенциала и его свойства
- 3.4.2. Доказательство свойств потенциала
- 3.4.3. Ротор вектора
- 3.5. Дифференциальное уравнение в полных дифференциалах
- 3.6. Ориентация плоской области
- 3.7. Формула Грина
- 3.8. Интеграл по поверхности первого рода
- 3.9. Ориентация поверхности
- 3.10. Система координат и ориентация поверхности
- 3.11. Интеграл по ориентированной плоской области
- 3.12. Поток вектора через ориентированную поверхность
- 3.13. Дивергенция. Теорема Гаусса—Остроградского
- 3.14. Соленоидальное поле
- 3.15. Формула Стокса
- Глава 4. Ряды Фурье. Интеграл Фурье
- 4.1. Тригонометрические ряды
- 4.2. Сходимость тригонометрических рядов
- 4.3. Ряд Фурье
- 4.4. Признаки сходимости рядов Фурье
- 4.5. Ортогональные свойства тригонометрических функций
- 4.6. Коэффициенты Фурье
- 4.7. Оценка коэффициентов Фурье
- 4.8. Пространство функций со скалярным произведением
- 4.9. Ортогональная система функций
- 4.10. Полнота тригонометрических функций
- 4.11. Комплексная форма ряда Фурье
- 4.12. Понятие интеграла Фурье. Повторный интеграл Фурье
- 4.13. Косинус- и синус- преобразования Фурье
- 4.14. Примеры
- 4.15. Приближение интеграла Фурье
- 4.16. Сумма Фейера
- 4.17. Полнота систем функций в С и L2’
- 4.18. Сведения из теории кратных рядов Фурье
- Глава 5. Уравнения математической физики
- 5.1. Температура тела
- 5.2. Задача Дирихле
- 5.3. Задача Дирихле для круга
- 5.4. Задача Дирихле для полуплоскости
- 5.5. Уравнение теплопроводности в стержне
- 5.6. Теплопроводность для бесконечного стержня
- 5.7. Малые колебания струны
- 5.8. Колебание бесконечной струны. Формула Даламбера
- 5.9. Колебание круглой мембраны
- 5.10. Общая задача Штурма-Лиувилля
- 5.11. Интеграл энергии (Дирихле)
- 5.12. Применение преобразований Фурье
- Глава 6. Теория функций комплексного переменного
- 6.1. Понятие функции комплексного переменного
- 6.2. Производная функция комплексного переменного
- 6.3. Условия Даламбера-Эйлера (Коши-Римана)
- 6.4. Гармонические функции
- 6.5. Обратная функция
- 6.6. Интегрирование функций комплексного переменного
- 6.7. Формула Коши
- 6.8. Интеграл типа Коши
- 6.9. Степенной ряд
- 6.10. Ряд Лорана
- 6.11. Классификация изолированных особых точек. Вычеты
- 6.12. Классификация особых точек на бесконечности
- 6.13. Теорема о вычетах
- 6.14. Вычисление интегралов при помощи вычетов
- 6.15. Линейная функция. Дробно-линейная функция
- Глава 7. Операционное исчисление
- 7.1. Изображение Лапласа
- 7.2. Изображение простейших функций и свойства изображений
- 7.3. Приложения операционного исчисления
- 7.3.1. Операторное уравнение
- 7.3.2. Решение систем дифференциальных уравнений
- 7.3.3. Вычисление интегралов
- Глава 8. Обобщенные функции
- 8.1. Понятие обобщенной функции
- 8.2. Операции над обобщенными функциями
- 8.3. Преобразование Фурье обобщенных функций