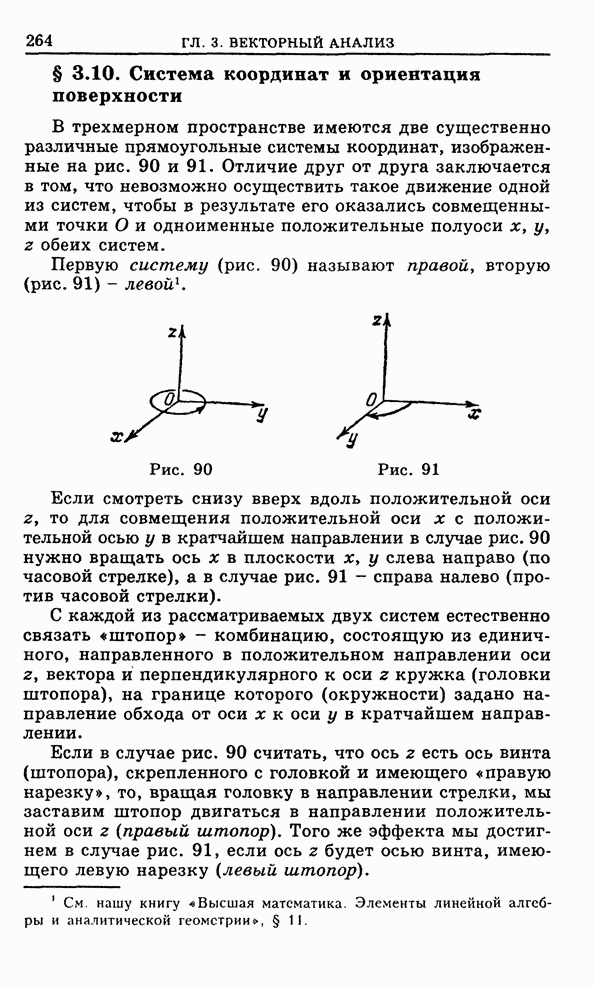
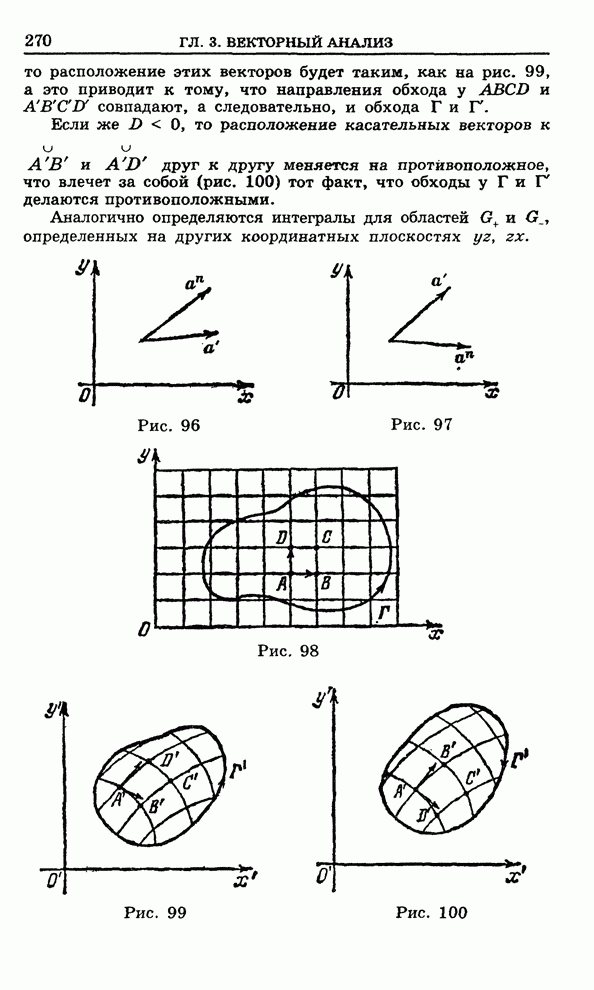
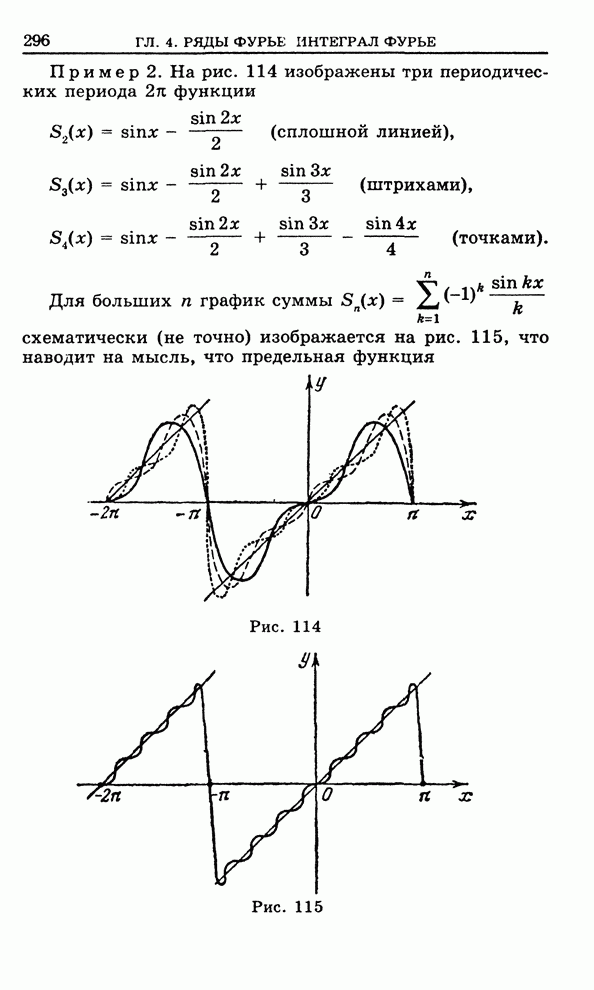
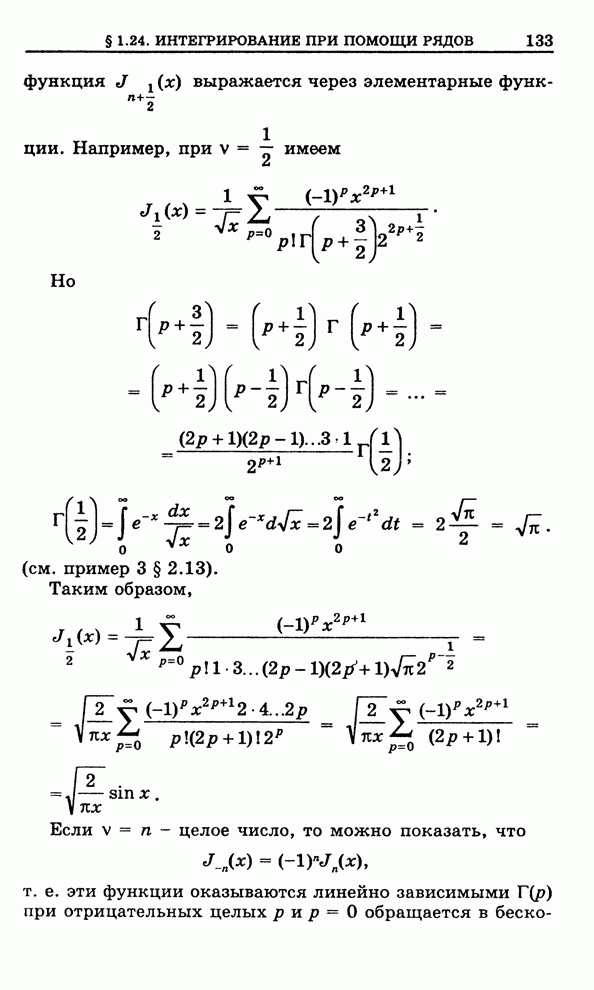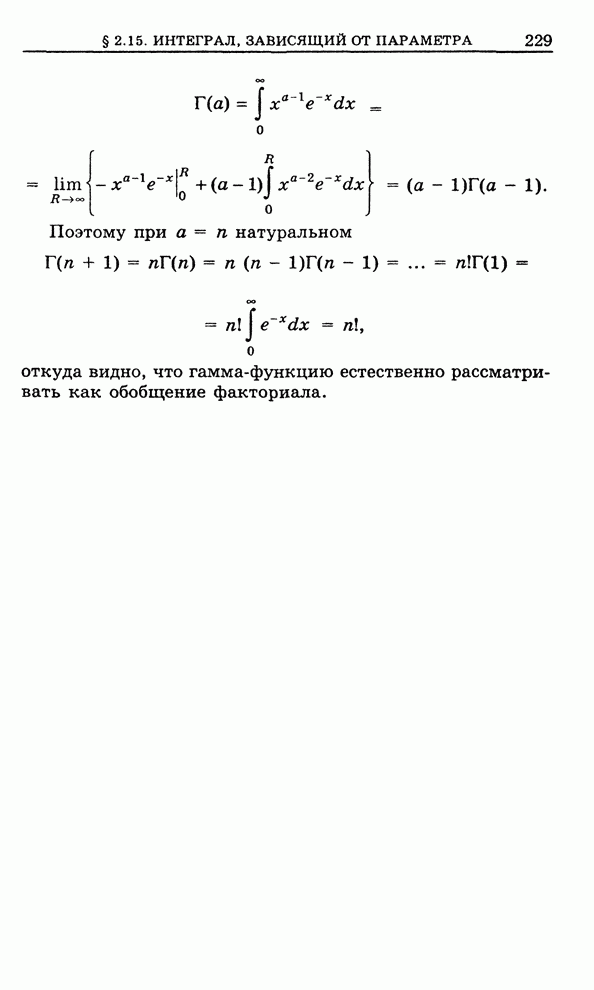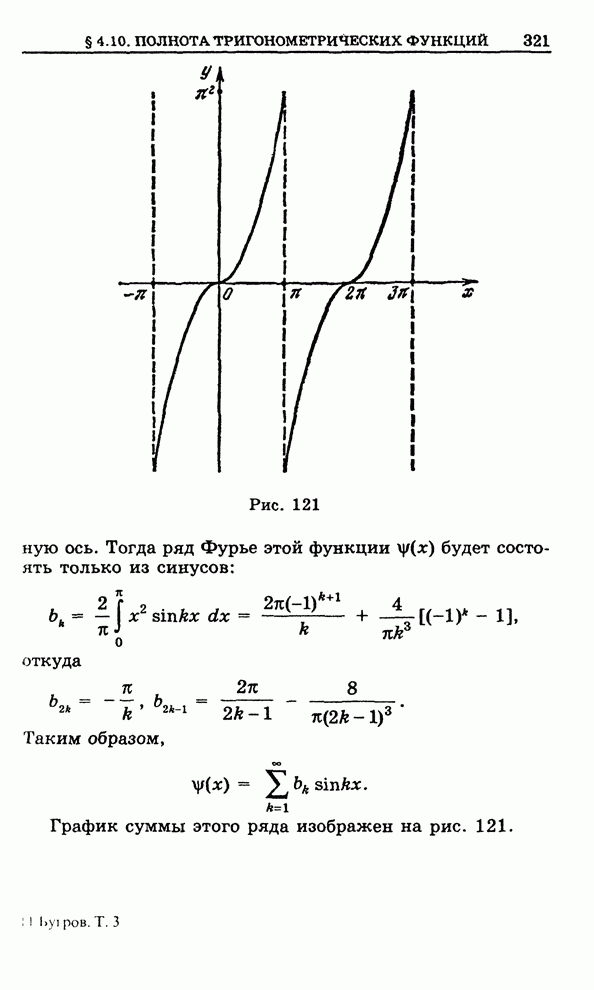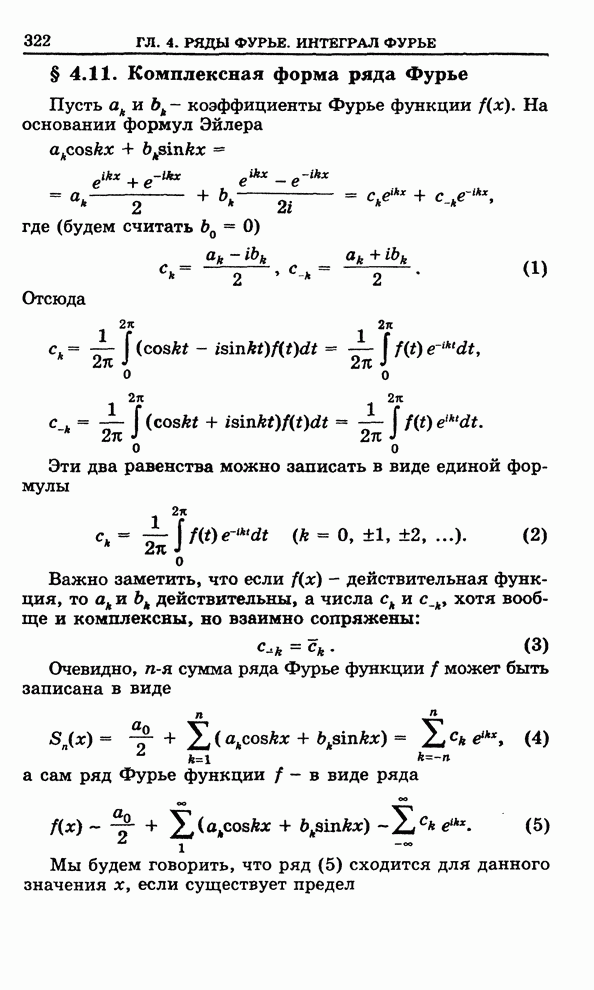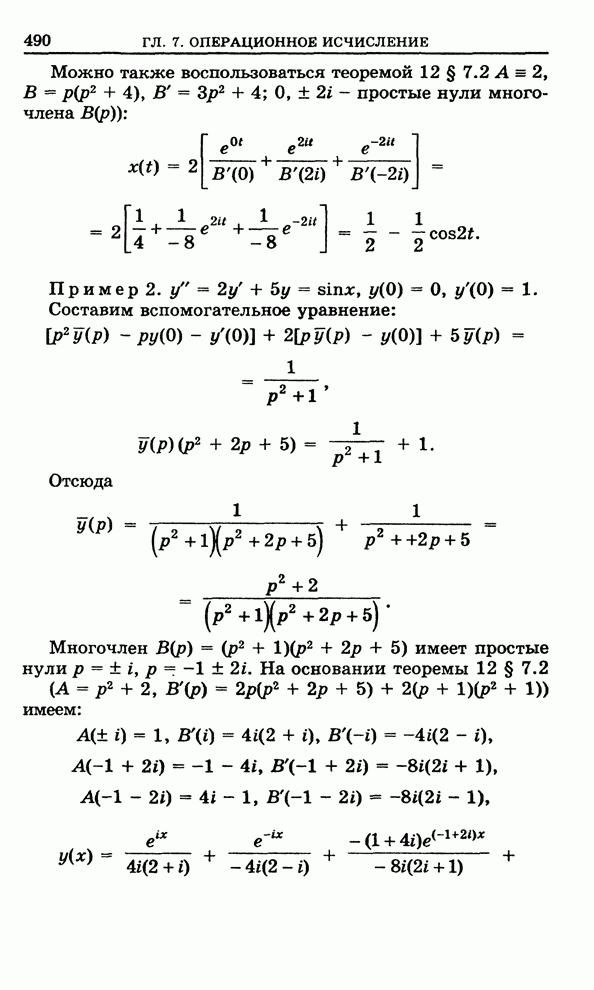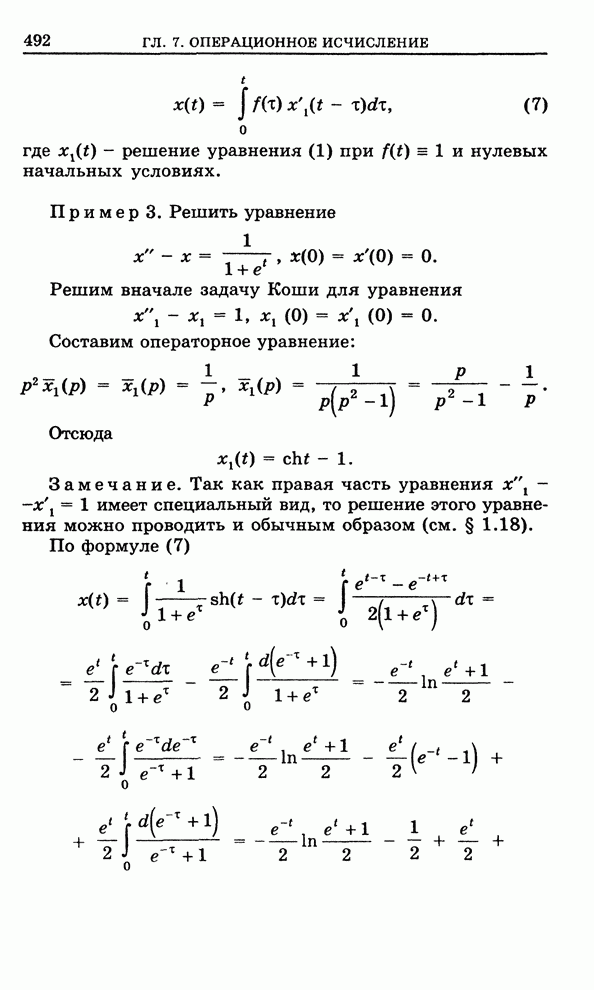| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 1.24. Интегрирование дифференциальных уравнений с помощью степенных рядов.
В этом параграфе рассматривается два примера решения линейных дифференциальных уравнений второго порядка с помощью степенных рядов. Коэффициентами их являются некоторые многочлены.
Второй пример посвящен важному в математике и ее приложениях дифференциальному уравнению Бесселя. Решения уравнения Бесселя, составляющие его фундаментальную систему функций, не являются элементарными функциями. Но они, как мы увидим, разлагаются в степенные ряды, коэффициенты которых вычисляются довольно просто.
Пример 1. ![]() .
.
В данном
случае ![]() ,
т.е. является многочленом первой степени относительно
,
т.е. является многочленом первой степени относительно ![]() . Будем искать решения в виде
ряда
. Будем искать решения в виде
ряда
 . (1)
. (1)
В силу
начального условия ![]() получаем, что
получаем, что ![]() . Из условия
. Из условия ![]() , получаем
, получаем ![]() . Дифференцируя
формально данный ряд почленно два раза и подставляя в уравнение, получаем
. Дифференцируя
формально данный ряд почленно два раза и подставляя в уравнение, получаем
 . (2)
. (2)
Сравнивая
коэффициенты при одинаковых степенях ![]() в левой и правой частях (2), получим:
в левой и правой частях (2), получим:
![]()
![]() , откуда
, откуда ![]()
![]() , откуда
, откуда ![]()
![]() , откуда
, откуда ![]()
![]() , откуда
, откуда ![]()
![]()
![]() , откуда
, откуда ![]()
![]()
Так как у нас ![]() , то все
коэффициенты
, то все
коэффициенты
![]() .
.
Далее
 .
.
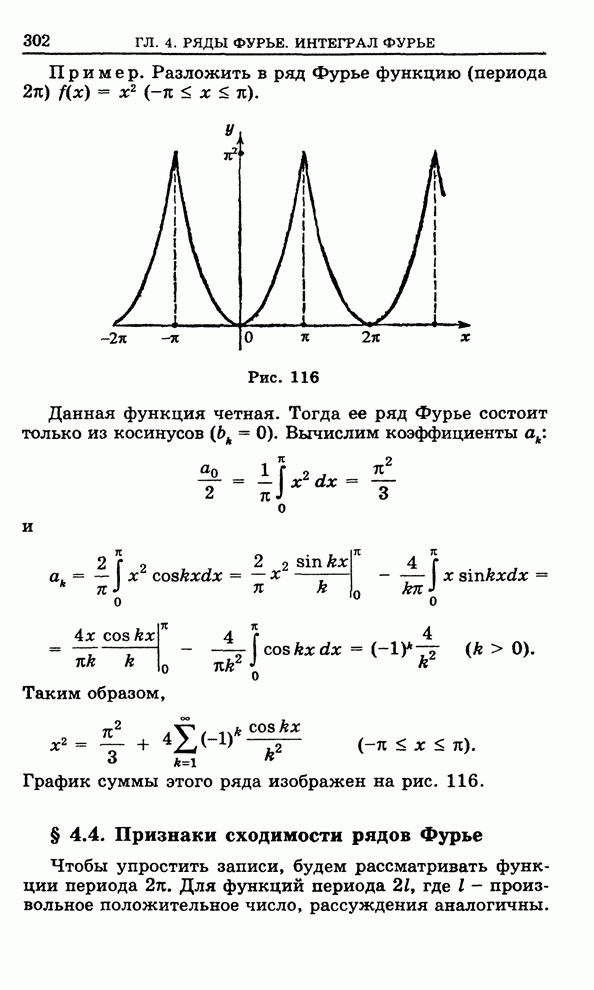
Итак,
 . (3)
. (3)
По признаку
Даламбера радиус сходимости этого ряда равен бесконечности. Следовательно, все
наши операции были законными и сумма ряда при всех значениях ![]() является решением
уравнения.
является решением
уравнения.
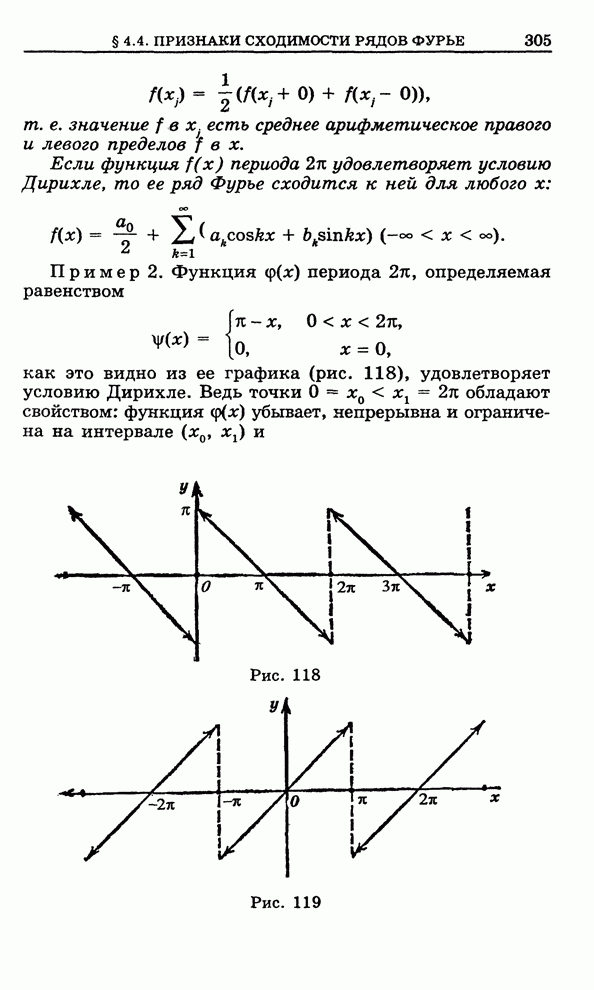
Пример 2. Уравнение Бесселя:
![]() . (4)
. (4)
К этому уравнению сводятся многие задачи математической физики.
Будем искать частное решение (4) в виде обобщенного степенного ряда
 . (5)
. (5)
Дифференцируя (5) два раза почленно и подставляя в (4), получим
 ,
,
 .
.
Сравнивая
коэффициенты при одинаковых степенях ![]() , получаем
, получаем
 (6)
(6)
Коэффициент ![]() при низшей степени
при низшей степени ![]() будем считать
отличным от нуля, тогда первое уравнение в (6) дает
будем считать
отличным от нуля, тогда первое уравнение в (6) дает
![]() .
.
Пусть пока ![]() . Тогда из второго
уравнения (6) получаем
. Тогда из второго
уравнения (6) получаем ![]() , т.е.
, т.е. ![]() , а, следовательно, и все коэффициенты
с нечетными номерами равны нулю
, а, следовательно, и все коэффициенты
с нечетными номерами равны нулю ![]() . Далее
. Далее
 (7)
(7)
При ![]() (
(![]() - не целое) таким
же образом получаем
- не целое) таким
же образом получаем
 .
.
Таким образом,
при ![]() решение
уравнения (4) запишется так:
решение
уравнения (4) запишется так:
 . (8)
. (8)
Введем функцию (см. ниже § 2.15, пример 3)
 ,
,
называемую гамма-функцией Эйлера.
Легко проверить, что ![]() и что для целых
и что для целых ![]() ,
, ![]() .
.
Для
отрицательных ![]() ,
,
![]() определяется
по-другому, но свойство
определяется
по-другому, но свойство ![]() сохраняется. Если выбрать произвольное
постоянное
сохраняется. Если выбрать произвольное
постоянное ![]() ,
то (8) запишется
,
то (8) запишется
 . (9)
. (9)
При ![]() (
(![]() - не целое),
выбирая постоянное
- не целое),
выбирая постоянное ![]() , аналогично получим
, аналогично получим
 . (10)
. (10)
Функции ![]() и
и ![]() называются
функциями Бесселя первого рода порядка
называются
функциями Бесселя первого рода порядка ![]() и
и ![]() соответственно.
соответственно.
Ряд (9)
сходится для всех ![]() ,
а ряд (10)
,
а ряд (10) ![]() и
оба они допускают двукратное почленное дифференцирование, следовательно,
и
оба они допускают двукратное почленное дифференцирование, следовательно, ![]() и
и ![]() - решения уравнения
Бесселя (4).
- решения уравнения
Бесселя (4).
Если ![]() - не целое число,
то функции
- не целое число,
то функции ![]() и
и
![]() линейно независимы,
так как их ряды начинаются с различных степеней
линейно независимы,
так как их ряды начинаются с различных степеней ![]() и линейная комбинация
и линейная комбинация
![]()
только при ![]() . Поэтому общее решение (4) в
этом случае имеет вид
. Поэтому общее решение (4) в
этом случае имеет вид
![]() .
.
Интересно
отметить, что при ![]() (
(![]() - целое число)
функция
- целое число)
функция ![]() выражается
через элементарные функции. Например, при
выражается
через элементарные функции. Например, при ![]() имеем
имеем
 .
.
Но

 .
.
(см. пример 3 § 2.13).
Таким образом,

 .
.
Если ![]() - целое число, то
можно показать, что
- целое число, то
можно показать, что
![]() ,
,
т.е. эти функции оказывается
линейно зависимыми ![]() при отрицательных целых
при отрицательных целых ![]() и
и ![]() обращается в
бесконечность. Поэтому за второе линейно независимое решение надо брать какую
то другую функцию. Обычно берут функцию Бесселя второго рода
обращается в
бесконечность. Поэтому за второе линейно независимое решение надо брать какую
то другую функцию. Обычно берут функцию Бесселя второго рода ![]() . Эта функция
является некоторой комбинацией функций
. Эта функция
является некоторой комбинацией функций ![]() и
и ![]() :
:

![]()
(![]() - не целое и стремится к
- не целое и стремится к ![]() ).
).
Замечание 1.
Таким образом, общее решение уравнения (4) при ![]() натуральном имеет вид
натуральном имеет вид
![]() ,
,
где ![]() - произвольные постоянные. Заметим, что
функция
- произвольные постоянные. Заметим, что
функция ![]() не
ограничена в окрестности
не
ограничена в окрестности ![]() . Например,
. Например,
 ,
,
где ![]() - постоянная Эйлера
- постоянная Эйлера ![]() .
.
Поэтому любое
решение уравнения (4), ограниченное в окрестности ![]() , имеет вид
, имеет вид ![]() , т.е. для него
, т.е. для него ![]() .
.
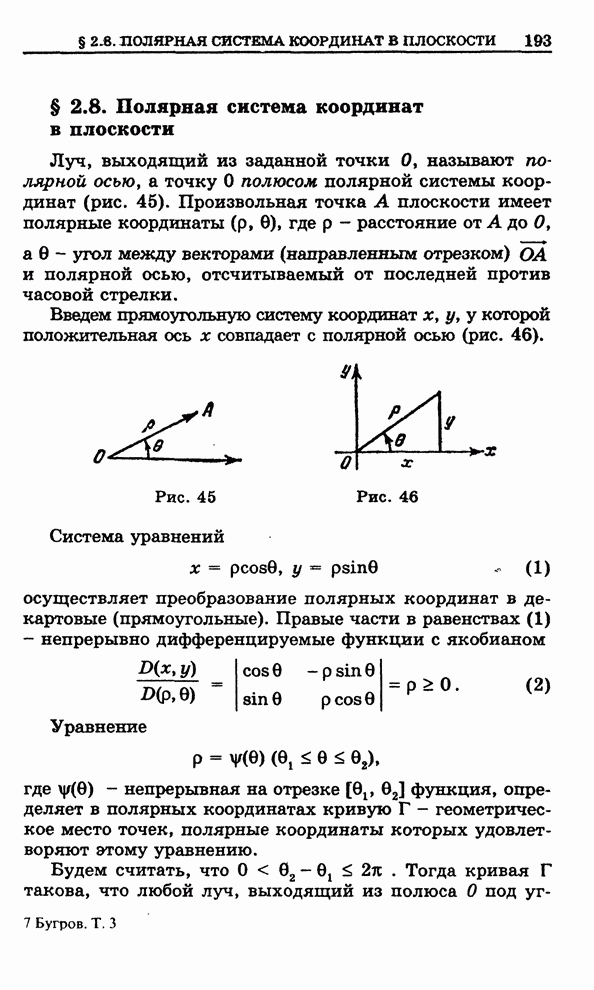
Приведем
графики функций Бесселя (рис.17) ![]() (четной) и
(четной) и ![]() (нечетной).
(нечетной).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. Обыкновенные дифференциальные уравнения
- 1.1. Задача, приводящая к дифференциальному уравнению
- 1.2. Общие понятия
- 1.2.1. Понятие обыкновенного дифференциального уравнения
- 1.2.2. Дифференциальное уравнение первого порядка
- 1.2.3. Задача Коши
- 1.2.4. Примеры дифференциальных уравнений первого порядка
- 1.2.5. Общий интеграл дифференциального уравнения первого порядка
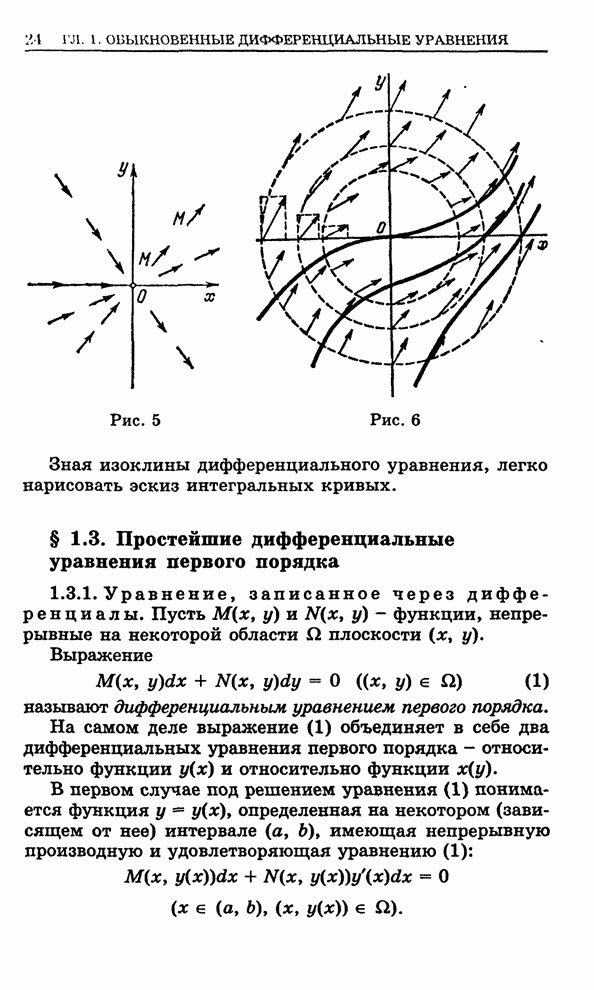
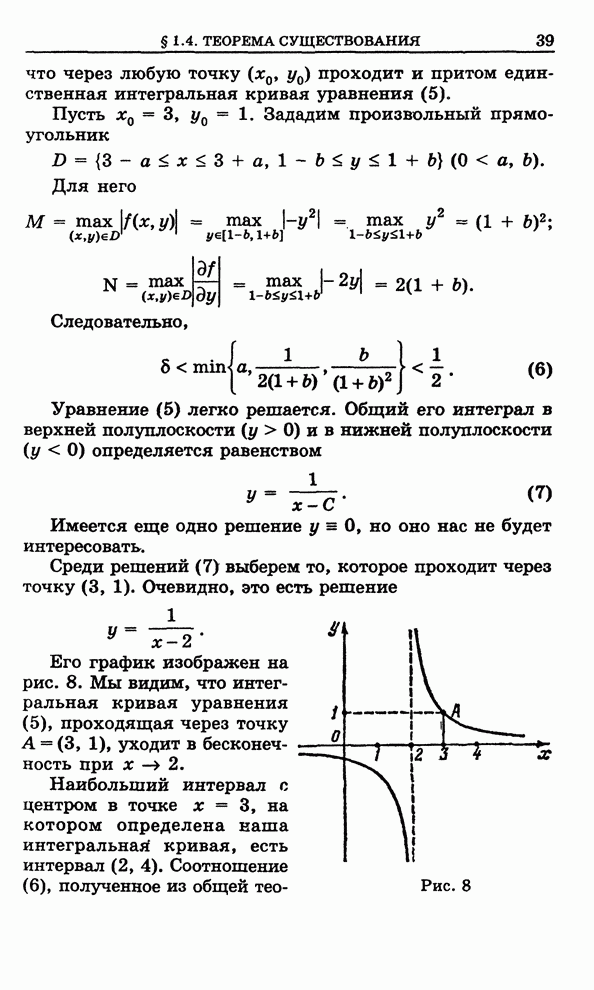
- 1.2.6. Поле направлений
- 1.3. Простейшие дифференциальные уравнения первого порядка
- 1.3.1. Уравнение, записанное через дифференциалы
- 1.3.2. Уравнения с разделенными переменными
- 1.3.3. Уравнения с разделяющимися переменными
- 1.3.4. Однородные уравнения
- 1.3.5. Линейное уравнение
- 1.3.6. Уравнение Бернулли
- 1.4. Теорема существования решения дифференциального уравнения первого порядка
- 1.5. Метрическое пространство
- 1.5.1. Понятие метрического пространства
- 1.5.2. Полное метрическое пространство
- 1.5.3. Принцип сжатых отображений
- 1.5.4. Приближенное значение корня функции
- 1.5.5. Метод Ньютона
- 1.6. Доказательство теоремы существования решения диффереацнального уравнения первого порядка
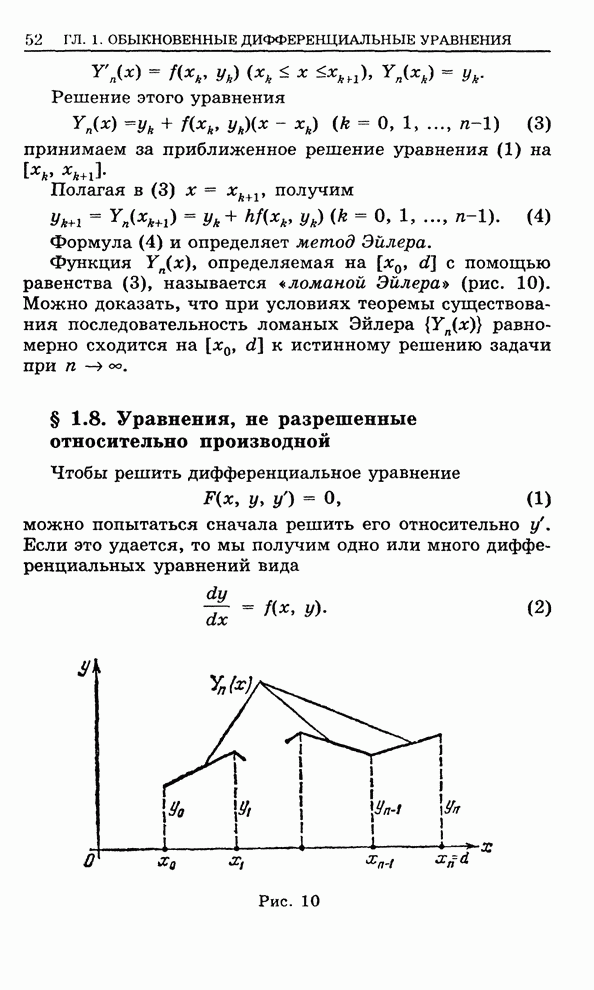
- 1.7. Метод Эйлера приближенного решения дифференциального уравнения первого порядка
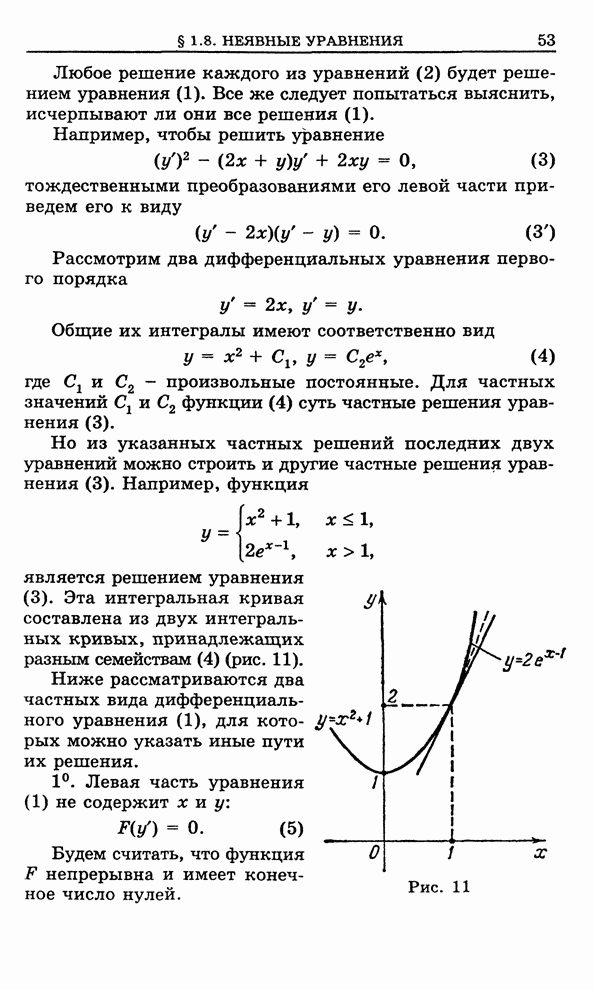
- 1.8. Уравнения, не разрешенные относительно производной
- 1.9. Особые решения
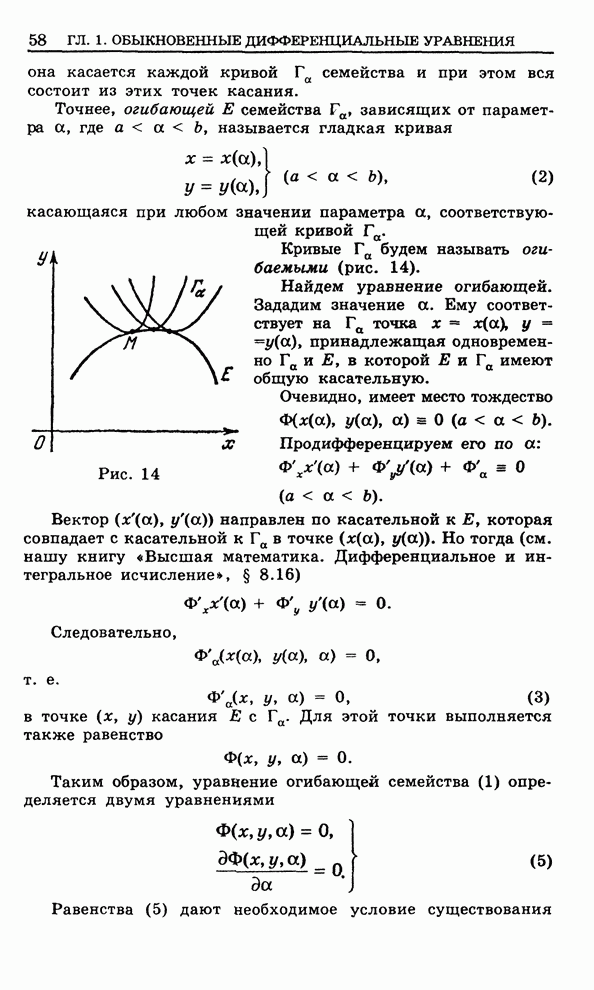
- 1.10. Огибающая семейства кривых
- 1.11. Дифференциальное уравнение второго порядка
- 1.12. Система из двух дифференциальных уравнений первого порядка
- 1.13. Дифференциальное уравнение n-го порядка
- 1.14. Понижение порядка дифференциального уравнения
- 1.15. Линейные уравнения высшего порядка
- 1.15.1. Понятие линейного уравнения высшего порядка
- 1.15.2. Фундаментальная система решений уравнения
- 1.15.3. Определитель Вронского
- 1.15.4. Структура общего решения
- 1.16. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- 1.16.1. Методы решения
- 1.16.2. Уравнение Эйлера
- 1.17. Метод вариации постоянных
- 1.18. Частное решение неоднородного уравнения с постоянными коэффициентами. Приложения
- 1.18.1. Методы нахождения частных решений
- 1.18.2. Дифференциальное уравнение колебания пружины
- 1.19. Системы дифференциальных уравнений. Фазовое пространство
- 1.20. Линейная однородная система дифференциальных уравнений
- 1.21. Общее решение линейной однородной системы дифференциальных уравнений с постоянными коэффициентами
- 1.22. Сведение системы уравнений к одному уравнению
- 1.23. Неоднородная система линейных дифференциальных уравнений с постоянными коэффициентами
- 1.24. Интегрирование дифференциальных уравнений с помощью степенных рядов
- 1.25. Элементы теории устойчивости
- 1.26. Классификация точек покоя
- Глава 2. Кратные интегралы
- 2.1. Введение
- 2.2. Сведения из теории меры Жордана
- 2.3. Свойства кратных интегралов. Теоремы существования
- 2.4. Сведение кратного интеграла к повторным
- 2.5. Доказательство существования интеграла от непрерывной функции
- 2.6. Замена переменных. Простейший случай
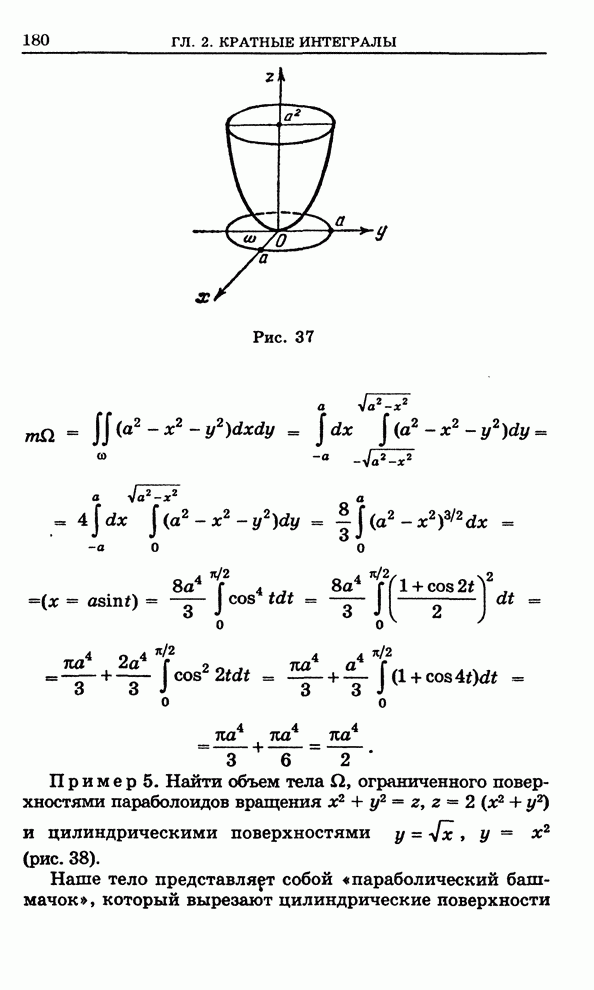
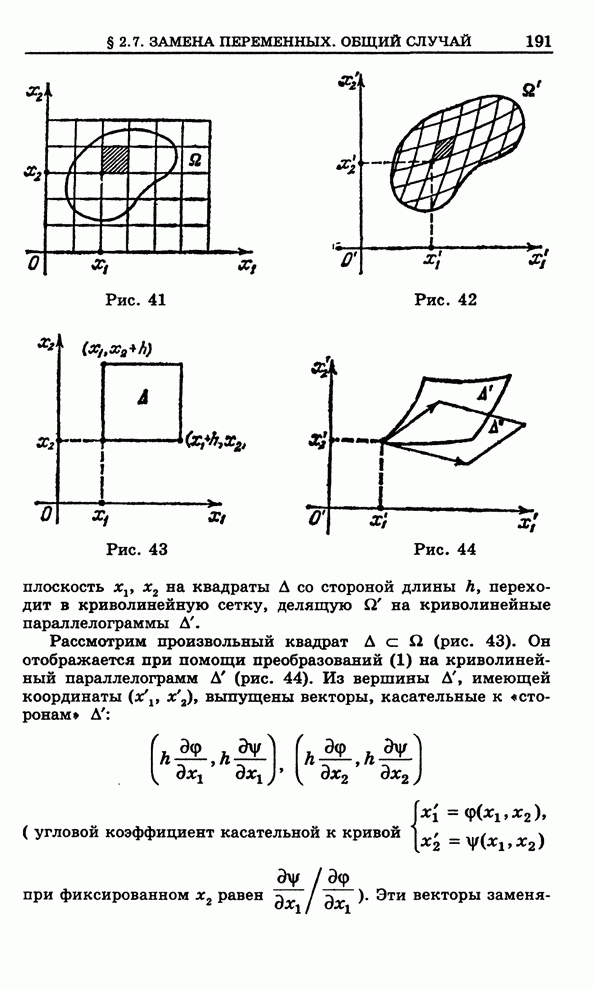
- 2.7. Замена переменных. Общий случай
- 2.8. Полярная система координат в плоскости
- 2.9. Полярная система координат в пространстве
- 2.10. Цилиндрические координаты
- 2.11. Площадь поверхности
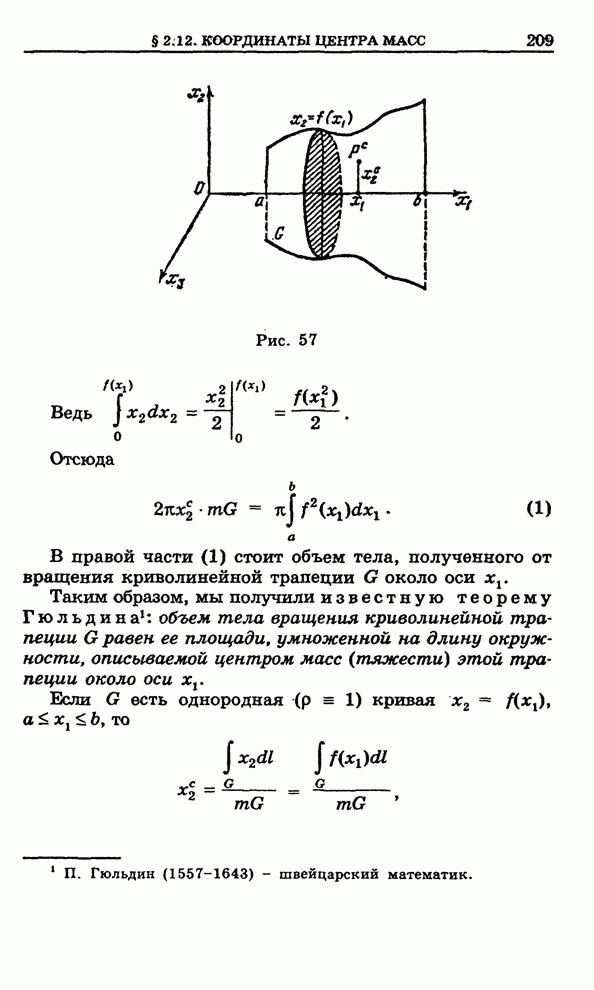
- 2.12. Координаты центра масс
- 2.13. Несобственные интегралы
- 2.14. Несобственный интеграл с особенностями вдоль линии
- 2.15. Несобственный интеграл, зависящий от параметра
- Глава 3. Векторный анализ
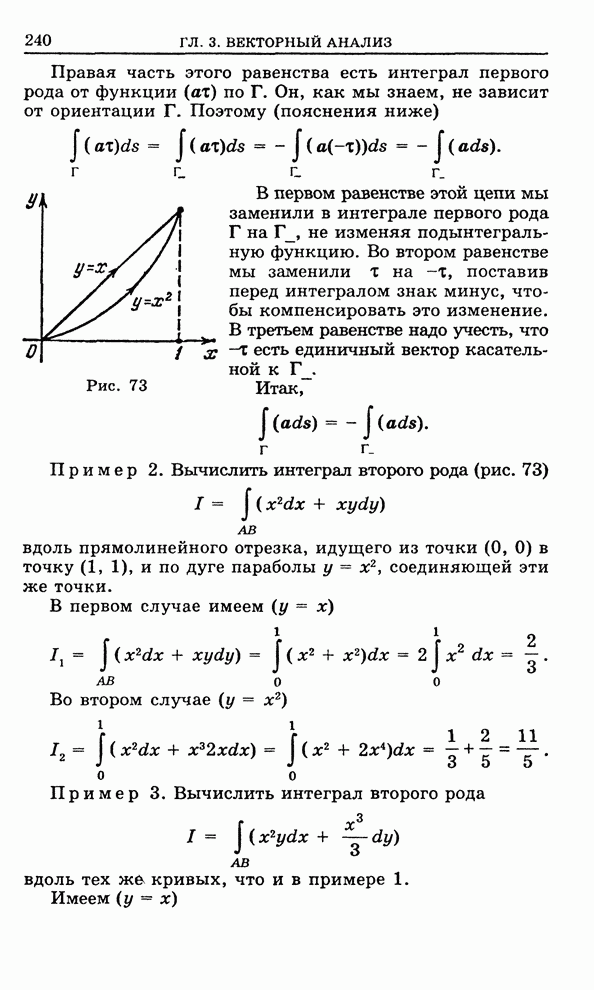
- 3.1. Кусочно-гладкая ориентированная кривая
- 3.2. Криволинейный интеграл первого рода
- 3.3. Интеграл от вектора вдоль кривой
- 3.3.1. Поле вектора
- 3.3.2. Криволинейный интеграл от вектора вдоль кривой
- 3.3.3. Свойства криволинейных интегралов второго рода
- 3.4. Поле потенциала
- 3.4.1. Понятие потенциала и его свойства
- 3.4.2. Доказательство свойств потенциала
- 3.4.3. Ротор вектора
- 3.5. Дифференциальное уравнение в полных дифференциалах
- 3.6. Ориентация плоской области
- 3.7. Формула Грина
- 3.8. Интеграл по поверхности первого рода
- 3.9. Ориентация поверхности
- 3.10. Система координат и ориентация поверхности
- 3.11. Интеграл по ориентированной плоской области
- 3.12. Поток вектора через ориентированную поверхность
- 3.13. Дивергенция. Теорема Гаусса—Остроградского
- 3.14. Соленоидальное поле
- 3.15. Формула Стокса
- Глава 4. Ряды Фурье. Интеграл Фурье
- 4.1. Тригонометрические ряды
- 4.2. Сходимость тригонометрических рядов
- 4.3. Ряд Фурье
- 4.4. Признаки сходимости рядов Фурье
- 4.5. Ортогональные свойства тригонометрических функций
- 4.6. Коэффициенты Фурье
- 4.7. Оценка коэффициентов Фурье
- 4.8. Пространство функций со скалярным произведением
- 4.9. Ортогональная система функций
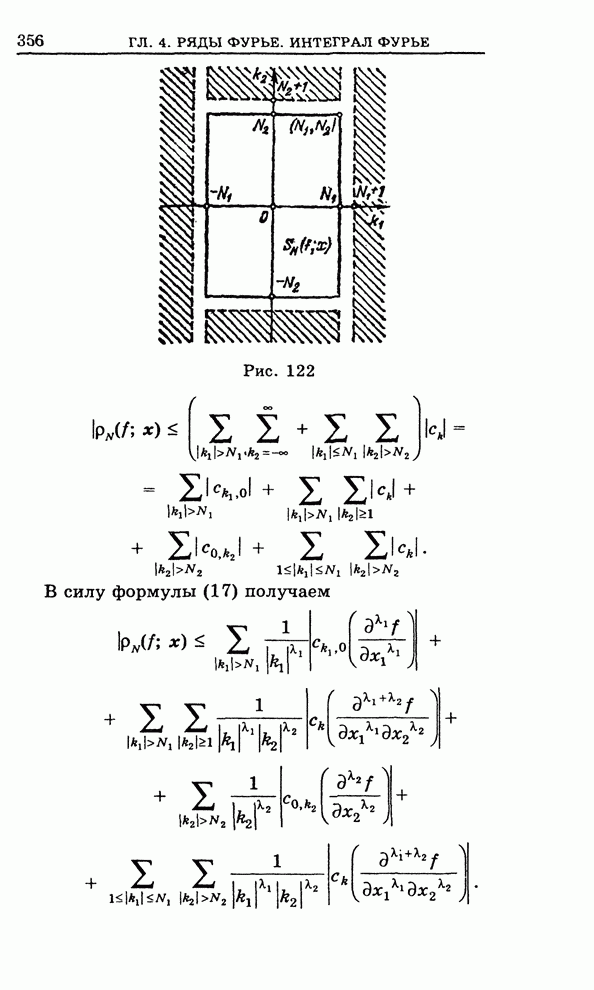
- 4.10. Полнота тригонометрических функций
- 4.11. Комплексная форма ряда Фурье
- 4.12. Понятие интеграла Фурье. Повторный интеграл Фурье
- 4.13. Косинус- и синус- преобразования Фурье
- 4.14. Примеры
- 4.15. Приближение интеграла Фурье
- 4.16. Сумма Фейера
- 4.17. Полнота систем функций в С и L2’
- 4.18. Сведения из теории кратных рядов Фурье
- Глава 5. Уравнения математической физики
- 5.1. Температура тела
- 5.2. Задача Дирихле
- 5.3. Задача Дирихле для круга
- 5.4. Задача Дирихле для полуплоскости
- 5.5. Уравнение теплопроводности в стержне
- 5.6. Теплопроводность для бесконечного стержня
- 5.7. Малые колебания струны
- 5.8. Колебание бесконечной струны. Формула Даламбера
- 5.9. Колебание круглой мембраны
- 5.10. Общая задача Штурма-Лиувилля
- 5.11. Интеграл энергии (Дирихле)
- 5.12. Применение преобразований Фурье
- Глава 6. Теория функций комплексного переменного
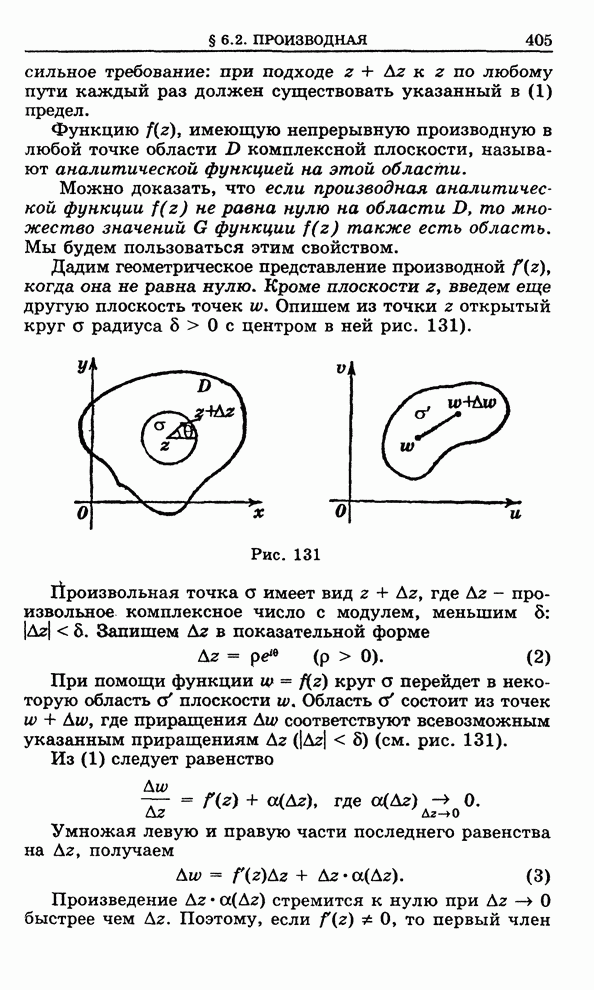
- 6.1. Понятие функции комплексного переменного
- 6.2. Производная функция комплексного переменного
- 6.3. Условия Даламбера-Эйлера (Коши-Римана)
- 6.4. Гармонические функции
- 6.5. Обратная функция
- 6.6. Интегрирование функций комплексного переменного
- 6.7. Формула Коши
- 6.8. Интеграл типа Коши
- 6.9. Степенной ряд
- 6.10. Ряд Лорана
- 6.11. Классификация изолированных особых точек. Вычеты
- 6.12. Классификация особых точек на бесконечности
- 6.13. Теорема о вычетах
- 6.14. Вычисление интегралов при помощи вычетов
- 6.15. Линейная функция. Дробно-линейная функция
- Глава 7. Операционное исчисление
- 7.1. Изображение Лапласа
- 7.2. Изображение простейших функций и свойства изображений
- 7.3. Приложения операционного исчисления
- 7.3.1. Операторное уравнение
- 7.3.2. Решение систем дифференциальных уравнений
- 7.3.3. Вычисление интегралов
- Глава 8. Обобщенные функции
- 8.1. Понятие обобщенной функции
- 8.2. Операции над обобщенными функциями
- 8.3. Преобразование Фурье обобщенных функций