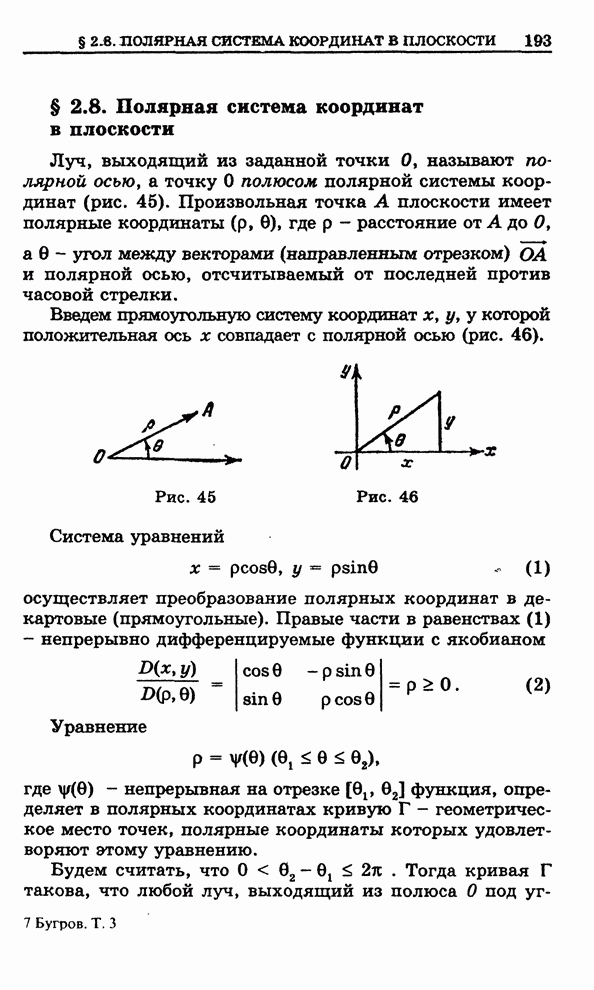
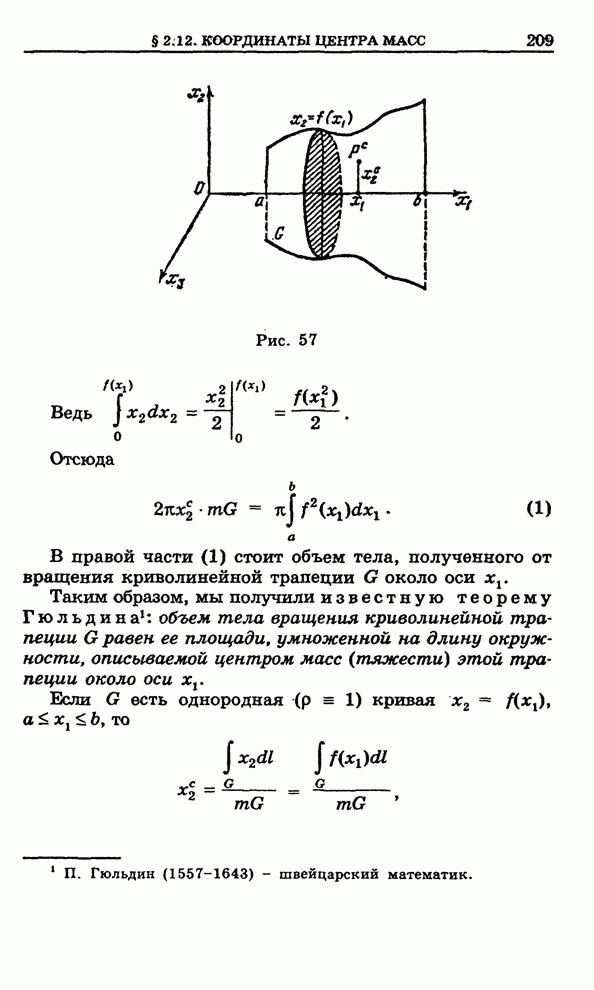
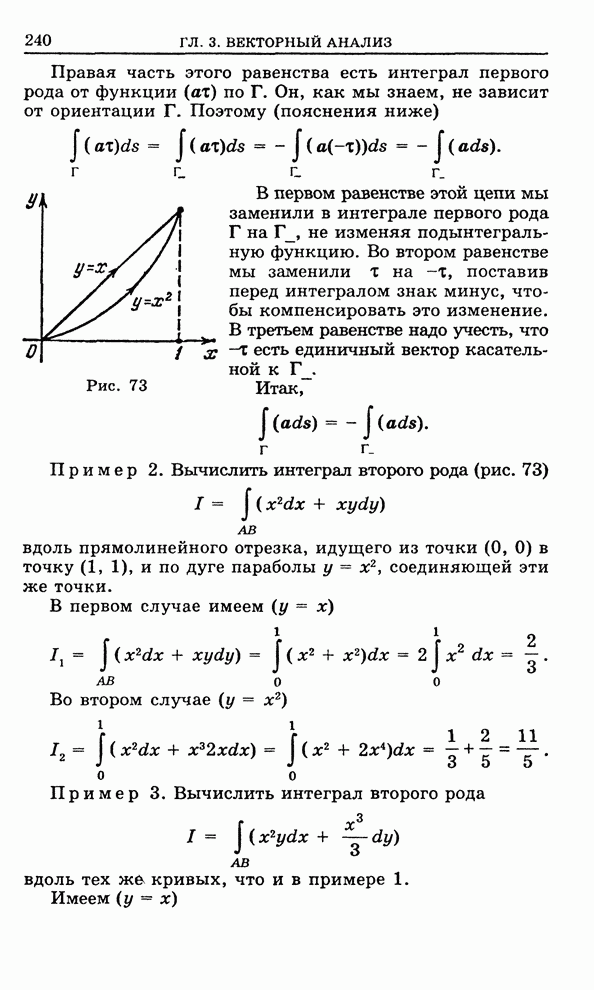
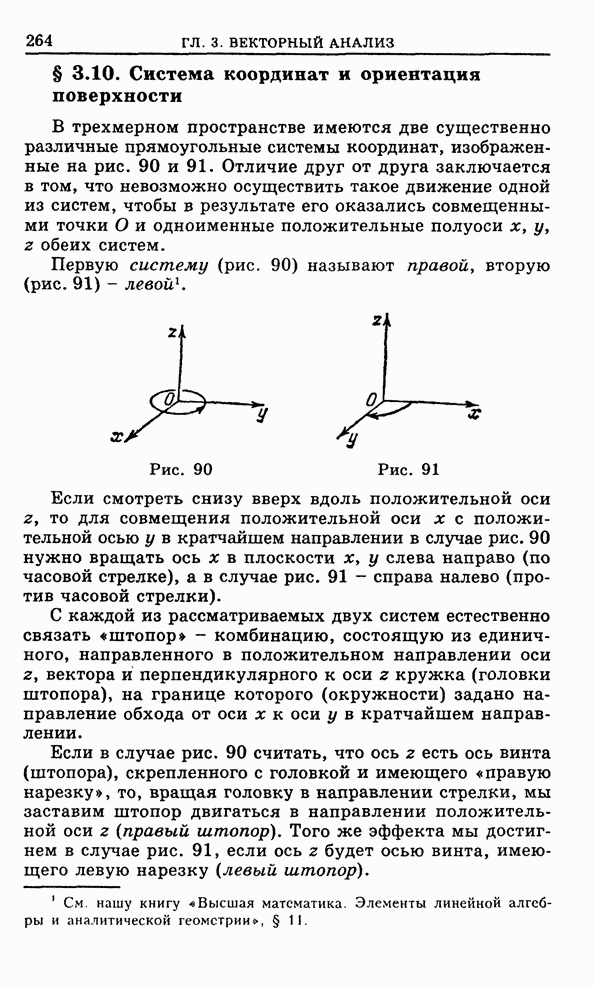
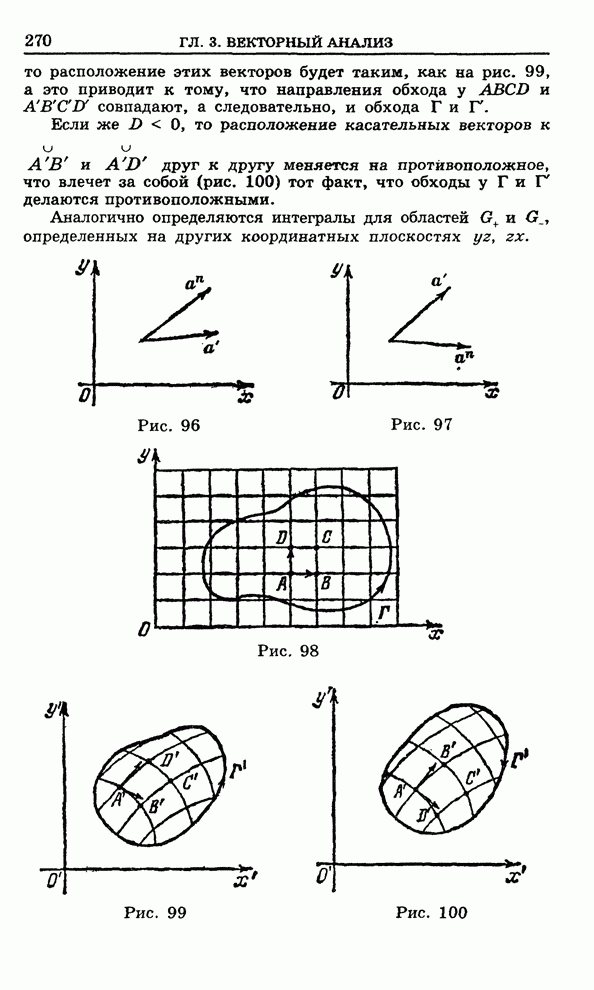
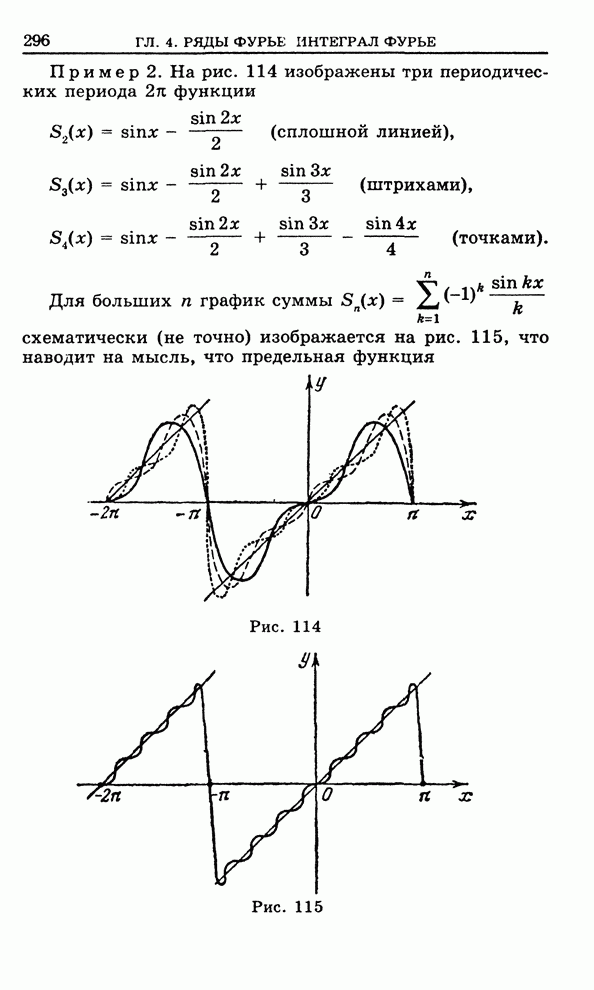
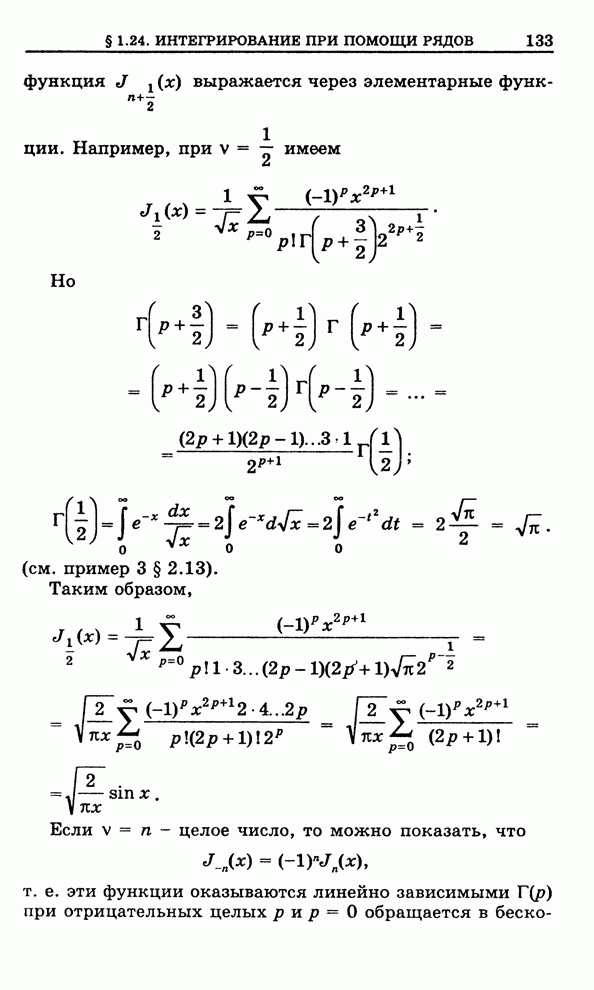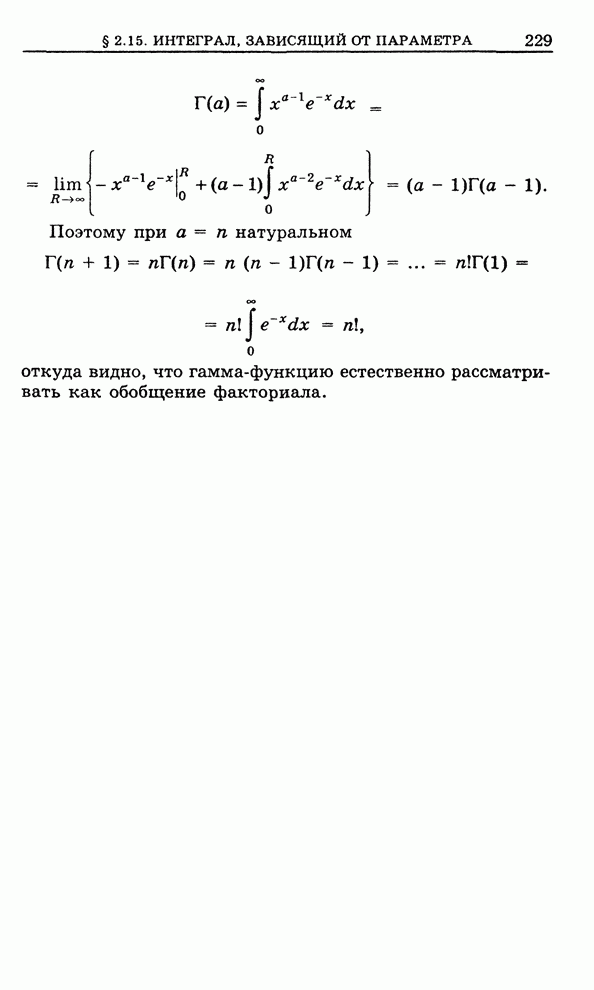| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2.2. Сведения из теории меры Жордана
Ограничимся
рассмотрением двумерных множеств. В плоскости зададим прямоугольную систему
координат ![]() .
Зададим натуральное число
.
Зададим натуральное число ![]() и две системы прямых
и две системы прямых
![]() ,
,
определяющих в
плоскости прямоугольную сетку, состоящую из квадратов со стороной ![]() . Такую сетку мы
будем называть
. Такую сетку мы
будем называть ![]() -
сеткой (рис. 29). Ясно, что при переходе от
-
сеткой (рис. 29). Ясно, что при переходе от ![]() к
к ![]() каждый квадрат
каждый квадрат ![]() - сетки (
- сетки ( ![]() ) разрезается на
четыре равных квадратика. Последние образуют уже
) разрезается на
четыре равных квадратика. Последние образуют уже ![]() сетку.
сетку.
В плоскости
зададим произвольное ограниченное множество ![]() и для данного
и для данного ![]() введем два множества
введем два множества ![]() и
и ![]() ,. Первое из них
,. Первое из них ![]() есть сумма
(теоретико-множественная) квадратиков
есть сумма
(теоретико-множественная) квадратиков ![]() - сетки (
- сетки (![]() ), каждый из которых полностью
принадлежит к
), каждый из которых полностью
принадлежит к ![]() (на
рис. 29 заштрихованная часть). Будем называть
(на
рис. 29 заштрихованная часть). Будем называть ![]() внутренней фигурой множества
внутренней фигурой множества ![]() (определяемой
данной
(определяемой
данной ![]() -
сеткой). Может случиться, что
-
сеткой). Может случиться, что ![]() есть пустое множество, т. е. нет ни
одного квадратика, который бы полностью принадлежал к
есть пустое множество, т. е. нет ни
одного квадратика, который бы полностью принадлежал к ![]() . Это имеет место, например,
если
. Это имеет место, например,
если ![]() есть
множество, состоящее из конечного числа точек, или если это есть кусок гладкой
кривой.
есть
множество, состоящее из конечного числа точек, или если это есть кусок гладкой
кривой.

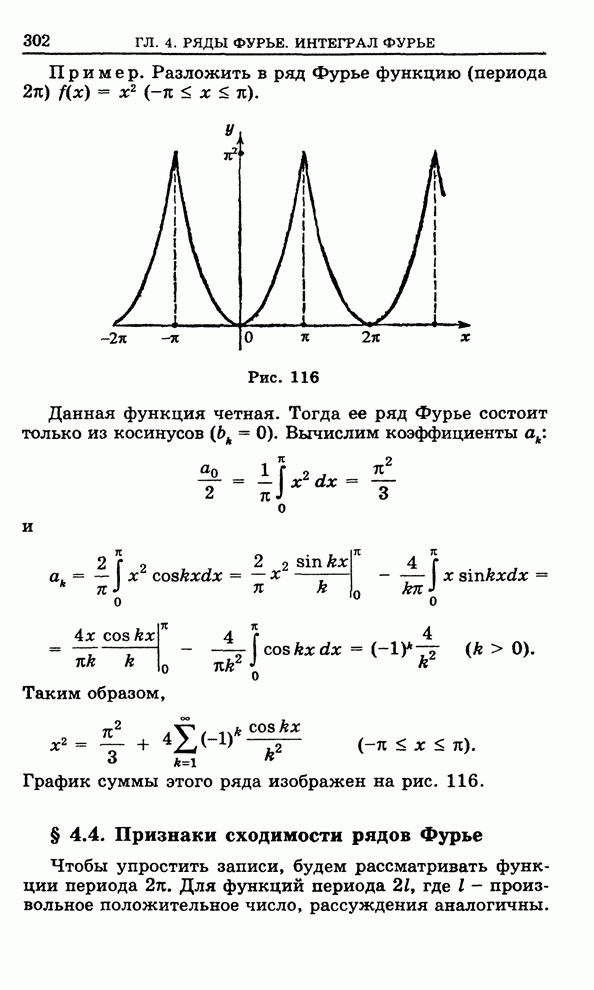
Рис. 29
Второе множество ![]() мы называем внешней
фигурой множества
мы называем внешней
фигурой множества ![]() (определяемой
данной
(определяемой
данной ![]() -
сеткой). Оно есть сумма квадратиков
-
сеткой). Оно есть сумма квадратиков ![]() - сетки, каждый из которых содержит в
себе хотя бы одну точку
- сетки, каждый из которых содержит в
себе хотя бы одну точку ![]() . Очевидно,
. Очевидно,
![]() ,
,
и площади фигур ![]() которые мы будем
обозначать через
которые мы будем
обозначать через ![]() удовлетворяют
неравенству
удовлетворяют
неравенству
![]() .
.
Если ![]() - пустое множество,
то считают
- пустое множество,
то считают ![]() .
Нетрудно видеть, что
.
Нетрудно видеть, что
![]() ,
,
откуда
![]() .
.
Таким образом,
![]()
каковы бы ни
были натуральные числа ![]() и
и ![]() .
.
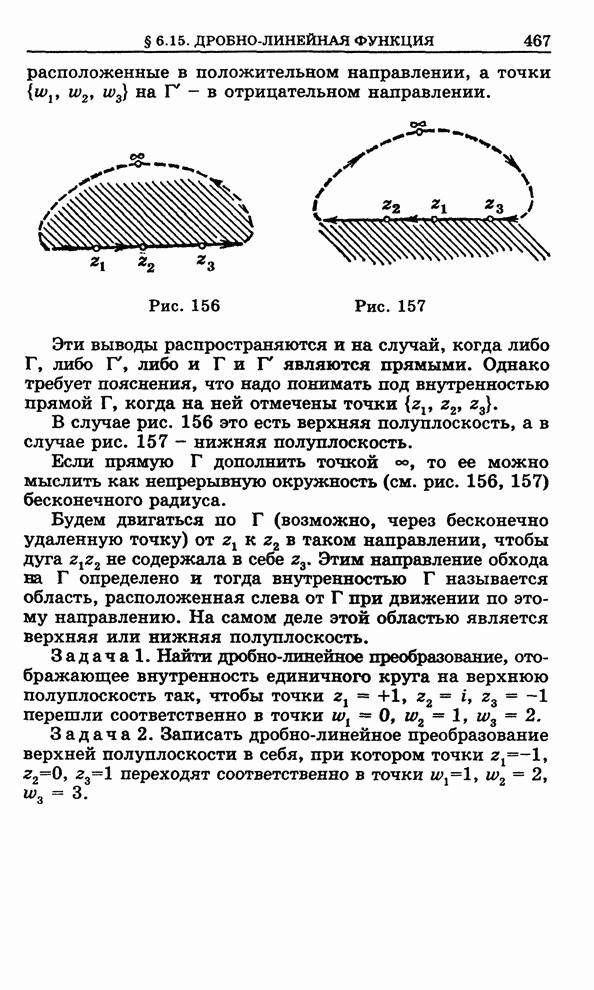
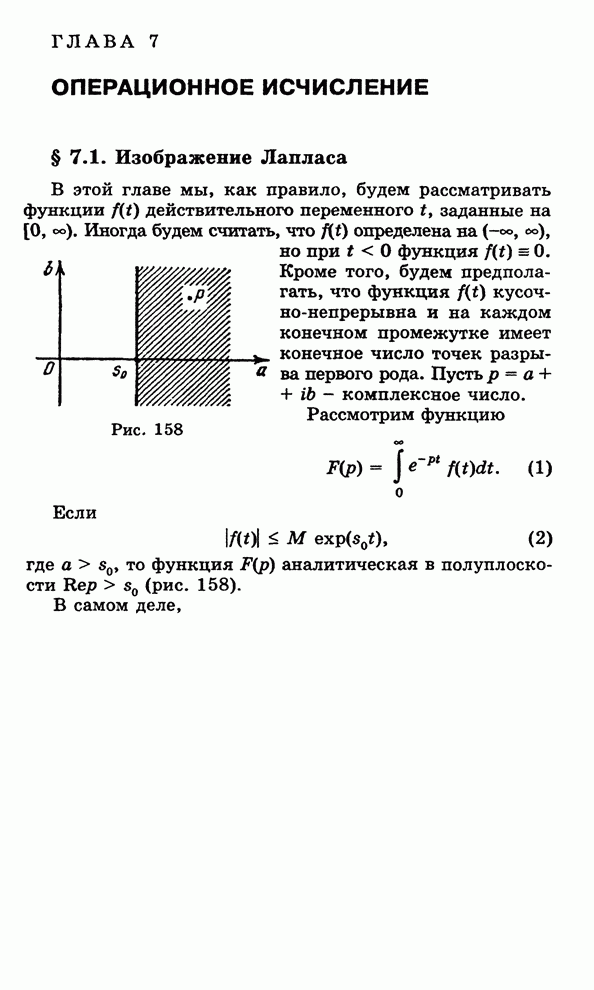
Если
зафиксировать ![]() ,
то получится, что числа
,
то получится, что числа ![]() при неограниченном возрастании
при неограниченном возрастании ![]() не убывают,
оставаясь не большими числа
не убывают,
оставаясь не большими числа ![]() . Это показывает, что существует предел
. Это показывает, что существует предел
![]() .
.
Его называют внутренней
мерой множества ![]() и
обозначают так:
и
обозначают так:
![]() .
.
Это вполне
определенное число, не зависящее от ![]() . Мы получили неравенство
. Мы получили неравенство
![]() ,
,
где числа ![]() монотонно не
возрастают при неограниченном возрастании
монотонно не
возрастают при неограниченном возрастании ![]() . Но тогда существует предел
. Но тогда существует предел
![]() ,
,
который называют
внешней мерой Жордана множества ![]() и обозначают через
и обозначают через ![]() .
.
Итак, произвольное
ограниченное множество ![]() плоскости имеет внутреннюю и внешнюю
меры
плоскости имеет внутреннюю и внешнюю
меры ![]() и
и ![]() . Это
неотрицательные числа, удовлетворяющие неравенству
. Это
неотрицательные числа, удовлетворяющие неравенству ![]() .
.
Если на самом
деле имеет место равенство, то ![]() называют измеримым по Жордану в
двумерном смысле и число
называют измеримым по Жордану в
двумерном смысле и число
![]()
называют двумерной
мерой ![]() по
Жордану.
по
Жордану.
Меру Жордана мы будем называть
также и просто мерой. Итак, множество ![]() измеримо (по Жордану), если для него
измеримо (по Жордану), если для него
![]() . (1)
. (1)
Обозначим через ![]() границу множества
границу множества ![]() . Чтобы получить
совокупность квадратиков сетки, покрывающих
. Чтобы получить
совокупность квадратиков сетки, покрывающих ![]() или, как мы будем говорить, чтобы
получить фигуру, покрывающую
или, как мы будем говорить, чтобы
получить фигуру, покрывающую ![]() (см. рис. 29), надо из фигуры
(см. рис. 29), надо из фигуры ![]() , вычесть в
теоретико-множественном смысле фигуру
, вычесть в
теоретико-множественном смысле фигуру ![]() и замкнуть полученное множество
и замкнуть полученное множество
![]() .
.
Очевидно,
площадь (двумерная мера) ![]() равна
равна
![]() .
.
Из (1) следует:
![]() . (2)
. (2)
Обратно, из равенства
![]() ,
(3)
,
(3)
учитывая, что
пределы ![]() и
и
![]() существуют,
следует равенство (1), т. е. измеримость
существуют,
следует равенство (1), т. е. измеримость ![]() .
.
Заметим, что
предел (3) есть внешняя мера ![]() , т. е.
, т. е.
![]() .
.
Но ![]() , поэтому и
, поэтому и
![]() .
.
Мы доказали
важное утверждение: для того, чтобы множество ![]() плоскости было измеримым по Жордану,
необходимо и достаточно, чтобы мера его границы равнялась нулю (
плоскости было измеримым по Жордану,
необходимо и достаточно, чтобы мера его границы равнялась нулю (![]() ).
).
Ниже будет
показано, что кусочно-гладкая кривая имеет, двумерную меру нуль. Но тогда
область ![]() , имеющая
кусочно-гладкую границу, измерима в двумерном смысле по Жордану.
, имеющая
кусочно-гладкую границу, измерима в двумерном смысле по Жордану.
Рассмотрим примеры.
Пример 1. Множество ![]() , состоящее из одной
точки, имеет двумерную меру нуль
, состоящее из одной
точки, имеет двумерную меру нуль ![]() . Точка может принадлежать самое
большее к четырем квадратикам
. Точка может принадлежать самое
большее к четырем квадратикам ![]() -сетки, их общая площадь стремится к
нулю при
-сетки, их общая площадь стремится к
нулю при ![]() и,
следовательно,
и,
следовательно, ![]() ,
но
,
но ![]() ,
поэтому
,
поэтому ![]() .
.
Пример 2. Непрерывная
кривая ![]() (рис.
30)
(рис.
30) ![]() имеет
двумерную меру нуль
имеет
двумерную меру нуль ![]() .
.

Рис. 30
В самом деле, вследствие
равномерной непрерывности ![]() на
на ![]() для любого
для любого ![]() найдется
найдется ![]() такое, что
такое, что ![]() для всех
для всех ![]() , удовлетворяющих неравенству
, удовлетворяющих неравенству ![]() . Найденное
. Найденное ![]() можно уменьшить,
как мы хотим. Будем считать, что
можно уменьшить,
как мы хотим. Будем считать, что ![]() . Зададим
. Зададим ![]() -сетку с
-сетку с
![]()
и рассмотрим
какой-либо столбик из квадратов сетки, содержащих в себе точки ![]() . Его высота не
превышает
. Его высота не
превышает ![]() (на
рис. 30 при
(на
рис. 30 при ![]() выделенный
столбик включает четыре квадратика
выделенный
столбик включает четыре квадратика ![]() - сетки, содержащих точки
- сетки, содержащих точки ![]() и
и ![]() ), а площадь не
превышает
), а площадь не
превышает
![]() ,
,
где ![]() - длина некоторого
отрезка, содержащего в себе отрезок
- длина некоторого
отрезка, содержащего в себе отрезок ![]() .
.
Это показывает,
что общая площадь ![]() квадратиков,
покрывающих кривую
квадратиков,
покрывающих кривую ![]() , при достаточно большом
, при достаточно большом ![]() может быть сделана
меньшей наперед заданного как угодно малого положительного, и, следовательно,
внешняя мера
может быть сделана
меньшей наперед заданного как угодно малого положительного, и, следовательно,
внешняя мера ![]() ,
тем более внутренняя, равна нулю. Но тогда
,
тем более внутренняя, равна нулю. Но тогда
![]() .
.
Так как сумма конечного числа множеств, имеющих меру нуль, очевидно, имеет меру нуль, то из примера 1 следует, что двумерная мера множества, состоящего из конечного числа точек равна нулю.
А из примера 2 следует, что гладкая кривая
![]() (4)
(4)
имеет двумерную меру нуль (рис. 31).
Дело в том, что
если ![]() -
гладкая кривая, то отрезок
-
гладкая кривая, то отрезок ![]() можно разделить на конечное число
отрезков точками
можно разделить на конечное число
отрезков точками
![]()

Рис. 31 Рис.32
так, что на
каждом частичном отрезке ![]() одно из двух уравнений (4) можно
разрешить относительно
одно из двух уравнений (4) можно
разрешить относительно ![]() и подставить во второе. В результате
получим, что соответствующий кусок
и подставить во второе. В результате
получим, что соответствующий кусок ![]() кривой
кривой ![]() описывается либо уравнением вида
описывается либо уравнением вида
![]() ,
,
либо уравнением вида
![]()
где функции ![]() и
и ![]() непрерывны на
соответствующих отрезках.
непрерывны на
соответствующих отрезках.
Но тогда, как мы знаем из примера 2,
![]() .
.
Поэтому, так как
![]() есть
сумма конечного числа кусков
есть
сумма конечного числа кусков ![]() .
.
 ,
,
каждый из
которых имеет меру нуль, то ![]() .
.
Отметим, что
если два множества ![]() и
и ![]() измеримы, то измеримы также их сумма
измеримы, то измеримы также их сумма ![]() , разность
, разность ![]() и пересечение
и пересечение ![]() .
.
В самом деле,
обозначим через ![]() границу
множества
границу
множества![]() . На рис. 32 изображены два множества
. На рис. 32 изображены два множества ![]() и
и ![]() . Очевидно,
. Очевидно,
 (5)
(5)
Если ![]() и
и ![]() измеримы, то
измеримы, то ![]() , но тогда и меры
левых частей (5) равны нулю, что показывает, что множества
, но тогда и меры
левых частей (5) равны нулю, что показывает, что множества ![]() и
и ![]() ,
, ![]() ,
,![]() измеримы.
измеримы.

Рис.33
Здесь мы
воспользовались очевидным свойством меры. Если множество ![]() имеет меру нуль, то и любое
его подмножество имеет меру нуль.
имеет меру нуль, то и любое
его подмножество имеет меру нуль.
Наконец, если ![]() и
и ![]() - измеримые
множества, пересекающиеся разве что по своим границам, то
- измеримые
множества, пересекающиеся разве что по своим границам, то
![]() . (6)
. (6)
В самом деле, очевидно (рис. 33)
![]() ,
,
и так как

то, очевидно,
![]() ,
,
что доказывает (6).
Отметим, что
если область ![]() измерима,
то ее мера Жордана равна мере ее замыкания:
измерима,
то ее мера Жордана равна мере ее замыкания:
![]() .
.
В самом деле, ![]() где
где ![]() - граница
- граница ![]() и
и ![]() , где
, где ![]() .
.
Пример 3.
Множество ![]() ,
состоящее из всех рациональных чисел отрезка
,
состоящее из всех рациональных чисел отрезка ![]() , не измеримо по Жордану:
, не измеримо по Жордану: ![]() .
.
В трехмерном
случае теория меры Жордана аналогична. Теперь вводится прямоугольная система
координат ![]() и
три семейства параллельных плоскостей
и
три семейства параллельных плоскостей

делящих
пространство на кубики с ребром ![]() .
.
Такое разбиение
пространства мы снова называем ![]() -сеткой (трехмерной).
-сеткой (трехмерной).
Пусть ![]() есть ограниченное
множество точек, принадлежащих пространству. Обозначим через
есть ограниченное
множество точек, принадлежащих пространству. Обозначим через ![]() внутреннюю фигуру
множества
внутреннюю фигуру
множества ![]() -
совокупность кубиков сетки, полностью принадлежащих
-
совокупность кубиков сетки, полностью принадлежащих ![]() , и через
, и через ![]() ,- внешнюю фигуру множества
,- внешнюю фигуру множества ![]() - совокупность
кубиков сетки, каждый из которых содержит хотя бы одну точку
- совокупность
кубиков сетки, каждый из которых содержит хотя бы одну точку ![]() .
.
Снова заключаем, что

откуда следует:

и
![]() ,
,
каковы бы ни
были натуральные ![]() и
и
![]() . Отсюда
вытекает существование пределов
. Отсюда
вытекает существование пределов
![]() .
.
Первый предел в
этом неравенстве называется внутренней (трехмерной) мерой ![]() :
:
![]() ,
,
а второй - внешней
мерой ![]() :
:
![]() .
.
Таким образом,
![]() .
.
Если
![]() ,
,
то множество ![]() называют измеримым
в трехмерном смысле по Жордану и число
называют измеримым
в трехмерном смысле по Жордану и число ![]() называют его трехмерной мерой.
называют его трехмерной мерой.
Рассуждениями, подобными тем, которые велись в связи с равенствами (1), (2), (3), доказывается, что множество измеримо в трехмерном смысле тогда и только тогда, когда его граница имеет трехмерную меру нуль.
Мы не будем формулировать дальнейшие свойства измеримых в трехмерном смысле множеств. Они аналогичны отмеченным выше свойствам множеств, измеримых в двумерном смысле.
Остановимся
только на объяснении того, что кусочно-гладкая поверхность имеет трехмерную
меру нуль. Такая поверхность состоит из конечного числа кусков ![]() , пересекающихся
разве что по своим краям, каждый из которых при соответствующем переобозначении
координат определяется уравнением
, пересекающихся
разве что по своим краям, каждый из которых при соответствующем переобозначении
координат определяется уравнением
![]() ,
,
где ![]() - замыкание
некоторой ограниченной в плоскости
- замыкание
некоторой ограниченной в плоскости ![]() области.
области.
Зададим ![]() и подберем
и подберем ![]() так, чтобы
так, чтобы
![]()
для всех точек ![]() , находящихся на
расстоянии друг от друга
, находящихся на
расстоянии друг от друга
![]() .
.
Считаем ![]() и берем
и берем ![]() - сетку с
- сетку с ![]() . Рассматриваем
какой-либо столбик из кубиков сетки, содержащих в себе точки
. Рассматриваем
какой-либо столбик из кубиков сетки, содержащих в себе точки ![]() . Его высота не
превышает
. Его высота не
превышает ![]() ,
а объем не превышает
,
а объем не превышает![]() . Общий объем всех таких столбиков,
покрывающих
. Общий объем всех таких столбиков,
покрывающих ![]() ,
не превышает
,
не превышает
![]() . (7)
. (7)
Здесь ![]() есть площадь
квадрата
есть площадь
квадрата ![]() ,
покрывающего множество
,
покрывающего множество ![]() . Правая часть (7) может быть взята как
угодно малой, что доказывает, что трехмерная мера
. Правая часть (7) может быть взята как
угодно малой, что доказывает, что трехмерная мера ![]() .
.
Можно ввести по
аналогии понятие ![]() -мерной
меры для множеств пространства
-мерной
меры для множеств пространства ![]() и показать, что гладкая поверхность в
и показать, что гладкая поверхность в ![]() имеет
имеет ![]() -мерную меру нуль.
-мерную меру нуль.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. Обыкновенные дифференциальные уравнения
- 1.1. Задача, приводящая к дифференциальному уравнению
- 1.2. Общие понятия
- 1.2.1. Понятие обыкновенного дифференциального уравнения
- 1.2.2. Дифференциальное уравнение первого порядка
- 1.2.3. Задача Коши
- 1.2.4. Примеры дифференциальных уравнений первого порядка
- 1.2.5. Общий интеграл дифференциального уравнения первого порядка
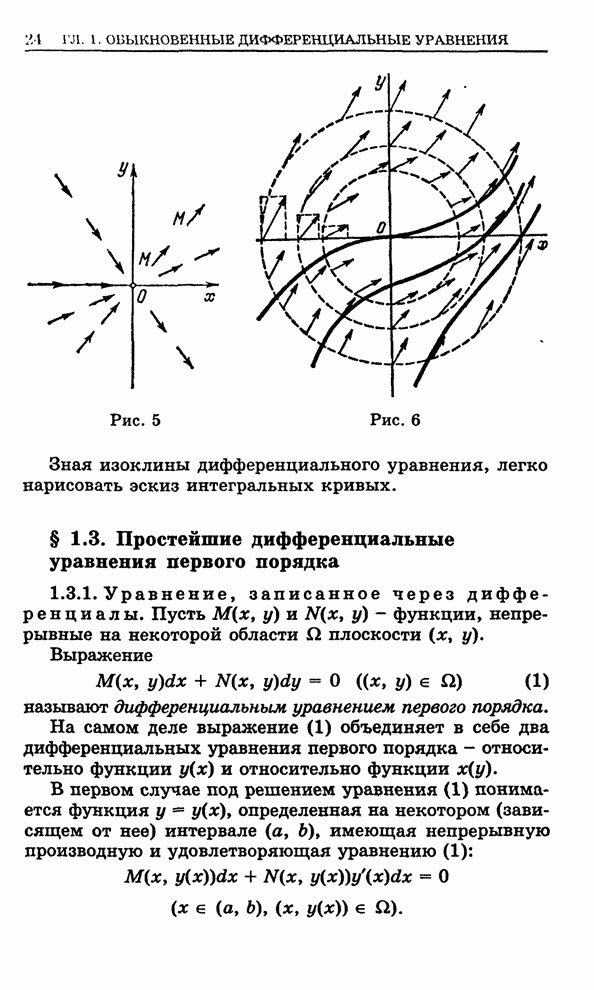
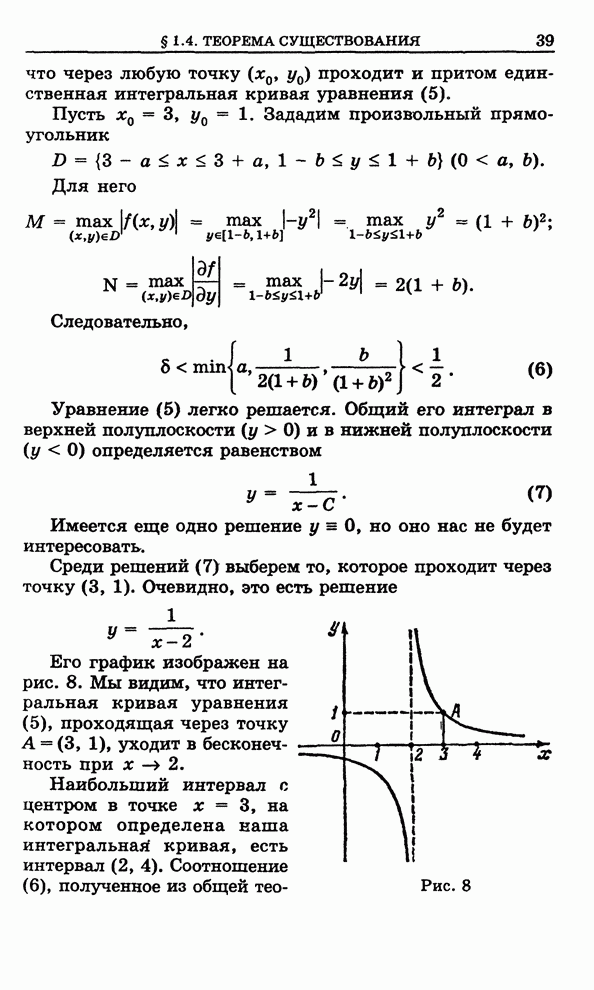
- 1.2.6. Поле направлений
- 1.3. Простейшие дифференциальные уравнения первого порядка
- 1.3.1. Уравнение, записанное через дифференциалы
- 1.3.2. Уравнения с разделенными переменными
- 1.3.3. Уравнения с разделяющимися переменными
- 1.3.4. Однородные уравнения
- 1.3.5. Линейное уравнение
- 1.3.6. Уравнение Бернулли
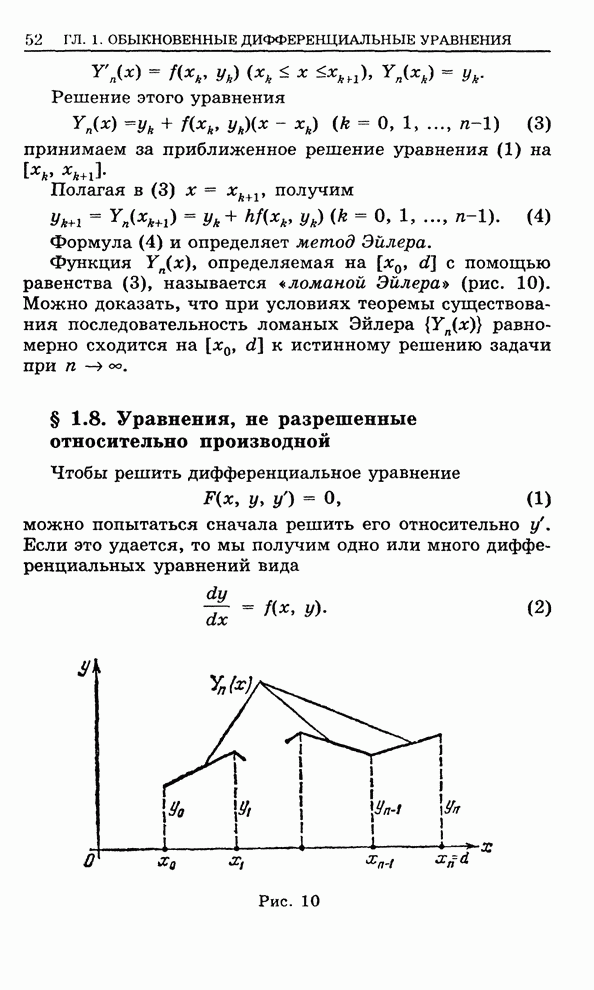
- 1.4. Теорема существования решения дифференциального уравнения первого порядка
- 1.5. Метрическое пространство
- 1.5.1. Понятие метрического пространства
- 1.5.2. Полное метрическое пространство
- 1.5.3. Принцип сжатых отображений
- 1.5.4. Приближенное значение корня функции
- 1.5.5. Метод Ньютона
- 1.6. Доказательство теоремы существования решения диффереацнального уравнения первого порядка
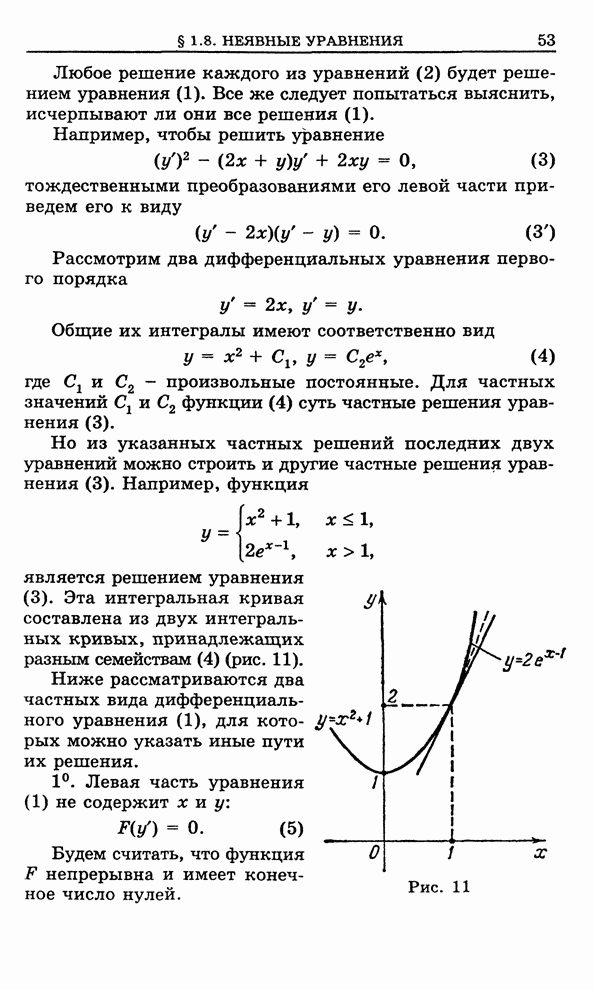
- 1.7. Метод Эйлера приближенного решения дифференциального уравнения первого порядка
- 1.8. Уравнения, не разрешенные относительно производной
- 1.9. Особые решения
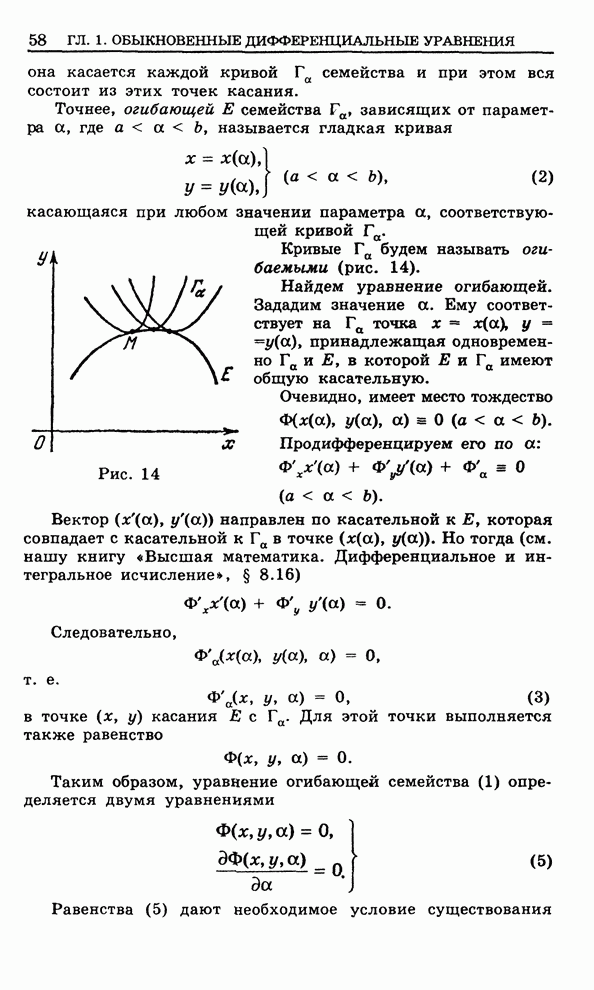
- 1.10. Огибающая семейства кривых
- 1.11. Дифференциальное уравнение второго порядка
- 1.12. Система из двух дифференциальных уравнений первого порядка
- 1.13. Дифференциальное уравнение n-го порядка
- 1.14. Понижение порядка дифференциального уравнения
- 1.15. Линейные уравнения высшего порядка
- 1.15.1. Понятие линейного уравнения высшего порядка
- 1.15.2. Фундаментальная система решений уравнения
- 1.15.3. Определитель Вронского
- 1.15.4. Структура общего решения
- 1.16. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- 1.16.1. Методы решения
- 1.16.2. Уравнение Эйлера
- 1.17. Метод вариации постоянных
- 1.18. Частное решение неоднородного уравнения с постоянными коэффициентами. Приложения
- 1.18.1. Методы нахождения частных решений
- 1.18.2. Дифференциальное уравнение колебания пружины
- 1.19. Системы дифференциальных уравнений. Фазовое пространство
- 1.20. Линейная однородная система дифференциальных уравнений
- 1.21. Общее решение линейной однородной системы дифференциальных уравнений с постоянными коэффициентами
- 1.22. Сведение системы уравнений к одному уравнению
- 1.23. Неоднородная система линейных дифференциальных уравнений с постоянными коэффициентами
- 1.24. Интегрирование дифференциальных уравнений с помощью степенных рядов
- 1.25. Элементы теории устойчивости
- 1.26. Классификация точек покоя
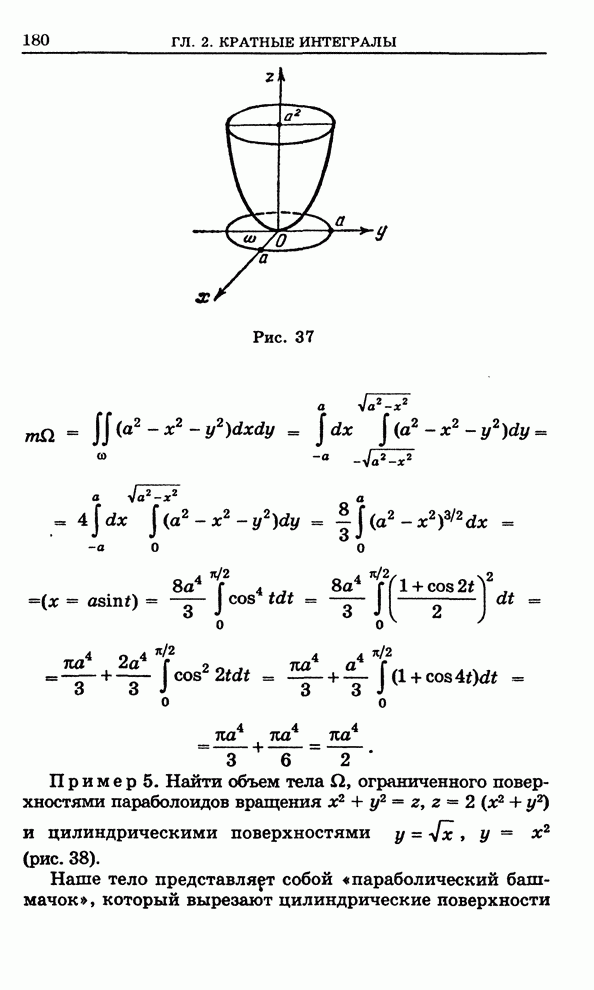
- Глава 2. Кратные интегралы
- 2.1. Введение
- 2.2. Сведения из теории меры Жордана
- 2.3. Свойства кратных интегралов. Теоремы существования
- 2.4. Сведение кратного интеграла к повторным
- 2.5. Доказательство существования интеграла от непрерывной функции
- 2.6. Замена переменных. Простейший случай
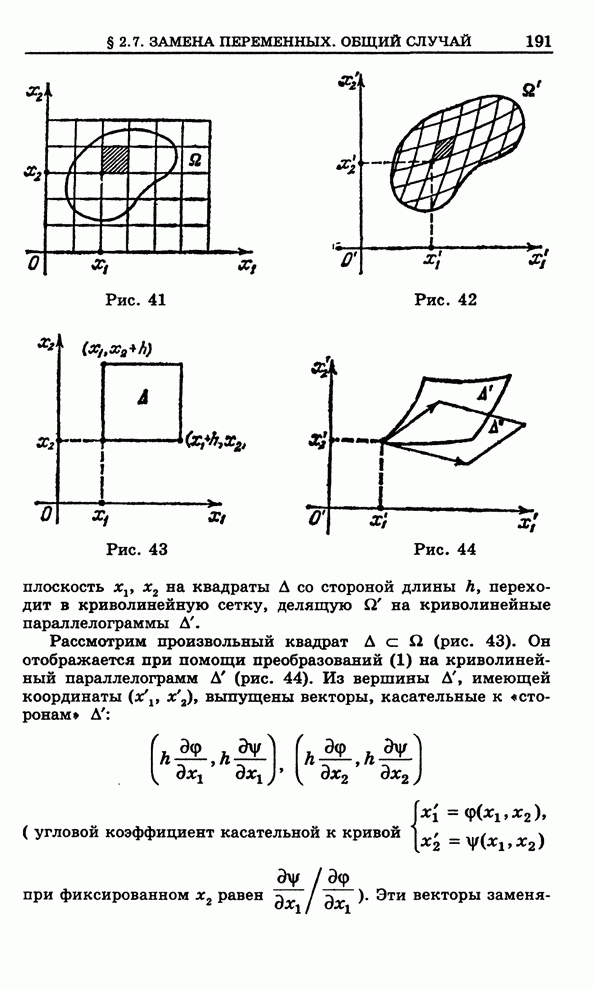
- 2.7. Замена переменных. Общий случай
- 2.8. Полярная система координат в плоскости
- 2.9. Полярная система координат в пространстве
- 2.10. Цилиндрические координаты
- 2.11. Площадь поверхности
- 2.12. Координаты центра масс
- 2.13. Несобственные интегралы
- 2.14. Несобственный интеграл с особенностями вдоль линии
- 2.15. Несобственный интеграл, зависящий от параметра
- Глава 3. Векторный анализ
- 3.1. Кусочно-гладкая ориентированная кривая
- 3.2. Криволинейный интеграл первого рода
- 3.3. Интеграл от вектора вдоль кривой
- 3.3.1. Поле вектора
- 3.3.2. Криволинейный интеграл от вектора вдоль кривой
- 3.3.3. Свойства криволинейных интегралов второго рода
- 3.4. Поле потенциала
- 3.4.1. Понятие потенциала и его свойства
- 3.4.2. Доказательство свойств потенциала
- 3.4.3. Ротор вектора
- 3.5. Дифференциальное уравнение в полных дифференциалах
- 3.6. Ориентация плоской области
- 3.7. Формула Грина
- 3.8. Интеграл по поверхности первого рода
- 3.9. Ориентация поверхности
- 3.10. Система координат и ориентация поверхности
- 3.11. Интеграл по ориентированной плоской области
- 3.12. Поток вектора через ориентированную поверхность
- 3.13. Дивергенция. Теорема Гаусса—Остроградского
- 3.14. Соленоидальное поле
- 3.15. Формула Стокса
- Глава 4. Ряды Фурье. Интеграл Фурье
- 4.1. Тригонометрические ряды
- 4.2. Сходимость тригонометрических рядов
- 4.3. Ряд Фурье
- 4.4. Признаки сходимости рядов Фурье
- 4.5. Ортогональные свойства тригонометрических функций
- 4.6. Коэффициенты Фурье
- 4.7. Оценка коэффициентов Фурье
- 4.8. Пространство функций со скалярным произведением
- 4.9. Ортогональная система функций
- 4.10. Полнота тригонометрических функций
- 4.11. Комплексная форма ряда Фурье
- 4.12. Понятие интеграла Фурье. Повторный интеграл Фурье
- 4.13. Косинус- и синус- преобразования Фурье
- 4.14. Примеры
- 4.15. Приближение интеграла Фурье
- 4.16. Сумма Фейера
- 4.17. Полнота систем функций в С и L2’
- 4.18. Сведения из теории кратных рядов Фурье
- Глава 5. Уравнения математической физики
- 5.1. Температура тела
- 5.2. Задача Дирихле
- 5.3. Задача Дирихле для круга
- 5.4. Задача Дирихле для полуплоскости
- 5.5. Уравнение теплопроводности в стержне
- 5.6. Теплопроводность для бесконечного стержня
- 5.7. Малые колебания струны
- 5.8. Колебание бесконечной струны. Формула Даламбера
- 5.9. Колебание круглой мембраны
- 5.10. Общая задача Штурма-Лиувилля
- 5.11. Интеграл энергии (Дирихле)
- 5.12. Применение преобразований Фурье
- Глава 6. Теория функций комплексного переменного
- 6.1. Понятие функции комплексного переменного
- 6.2. Производная функция комплексного переменного
- 6.3. Условия Даламбера-Эйлера (Коши-Римана)
- 6.4. Гармонические функции
- 6.5. Обратная функция
- 6.6. Интегрирование функций комплексного переменного
- 6.7. Формула Коши
- 6.8. Интеграл типа Коши
- 6.9. Степенной ряд
- 6.10. Ряд Лорана
- 6.11. Классификация изолированных особых точек. Вычеты
- 6.12. Классификация особых точек на бесконечности
- 6.13. Теорема о вычетах
- 6.14. Вычисление интегралов при помощи вычетов
- 6.15. Линейная функция. Дробно-линейная функция
- Глава 7. Операционное исчисление
- 7.1. Изображение Лапласа
- 7.2. Изображение простейших функций и свойства изображений
- 7.3. Приложения операционного исчисления
- 7.3.1. Операторное уравнение
- 7.3.2. Решение систем дифференциальных уравнений
- 7.3.3. Вычисление интегралов
- Глава 8. Обобщенные функции
- 8.1. Понятие обобщенной функции
- 8.2. Операции над обобщенными функциями
- 8.3. Преобразование Фурье обобщенных функций