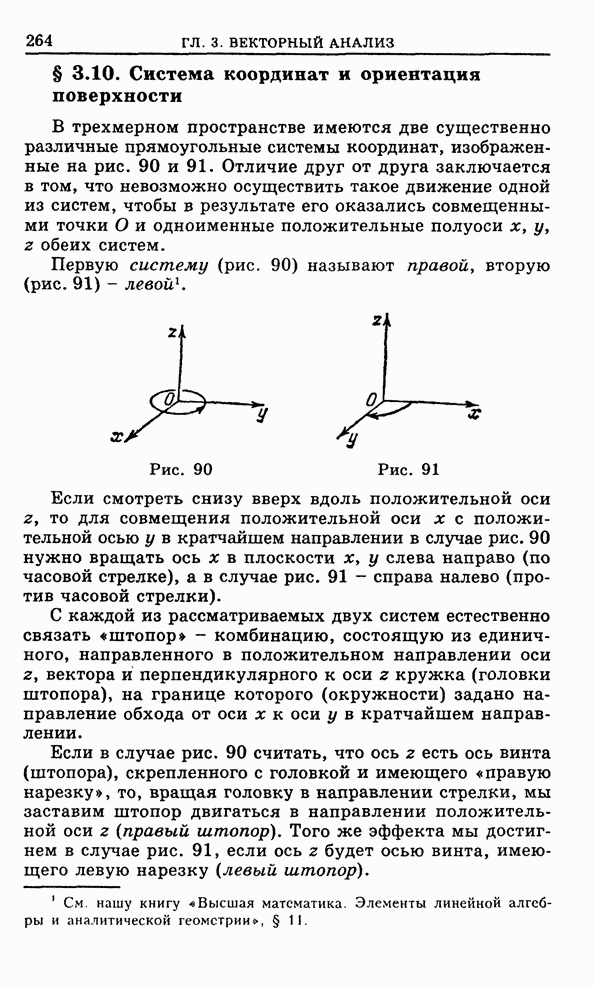
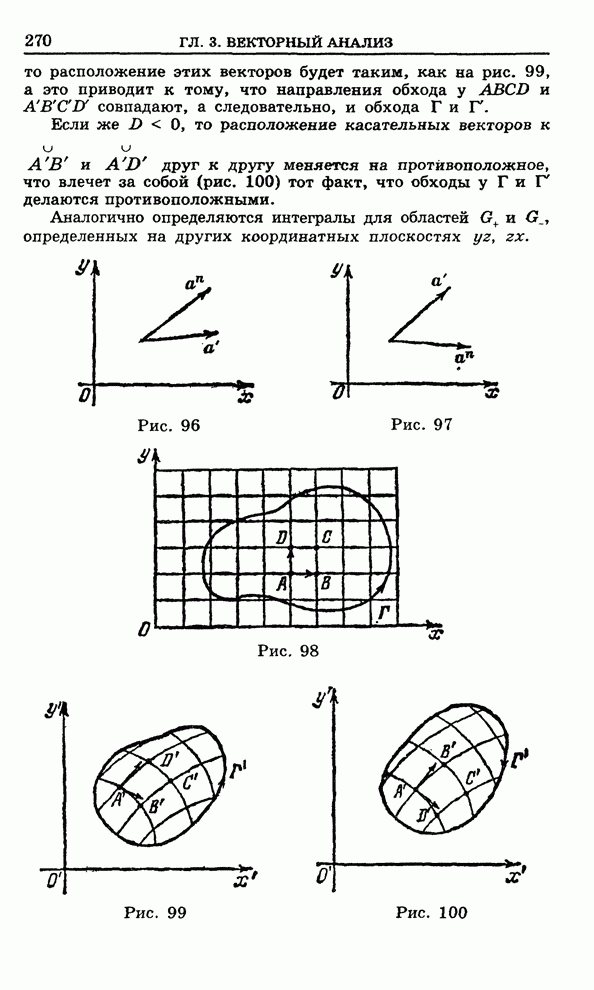
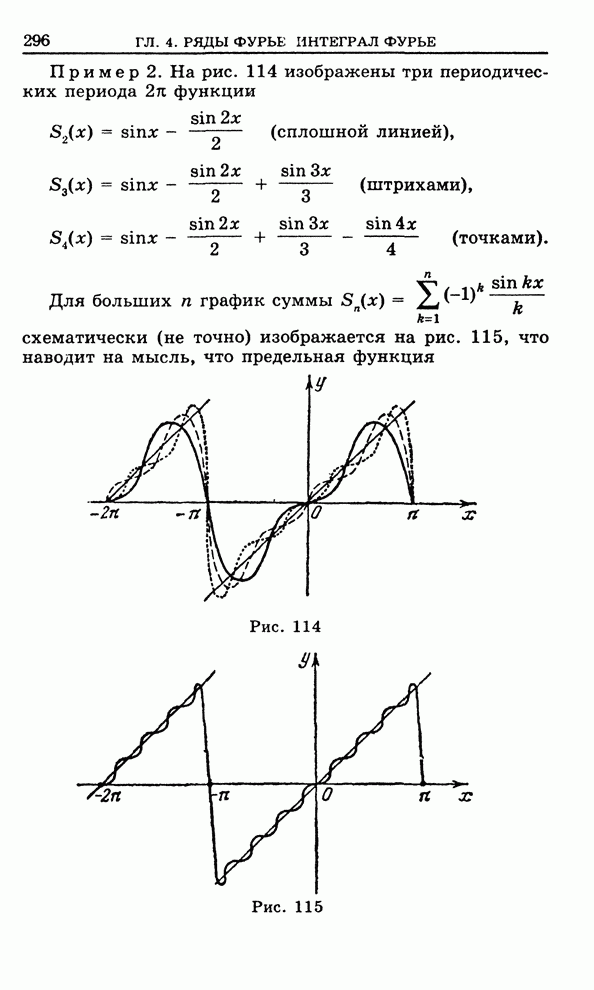
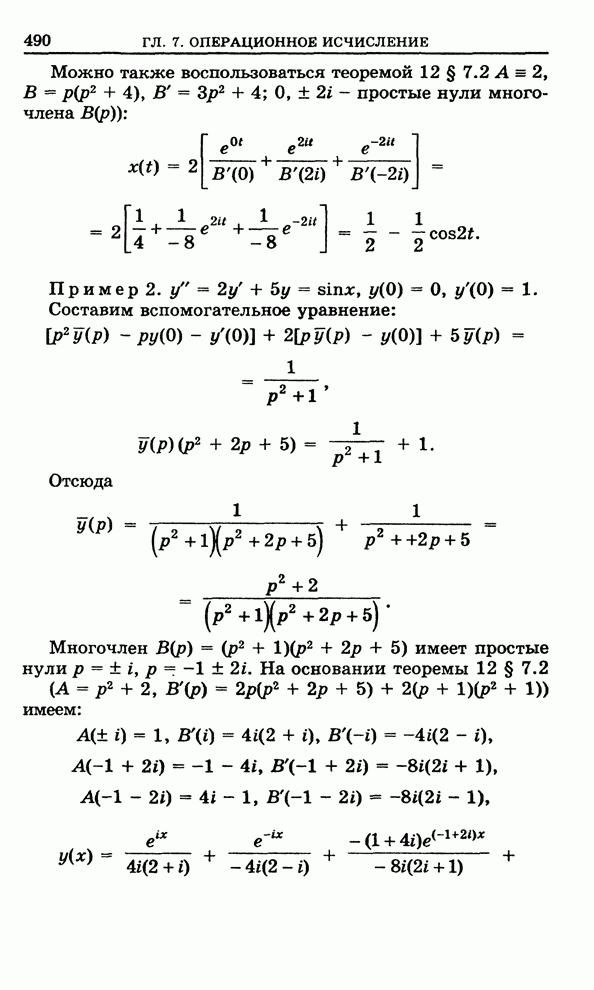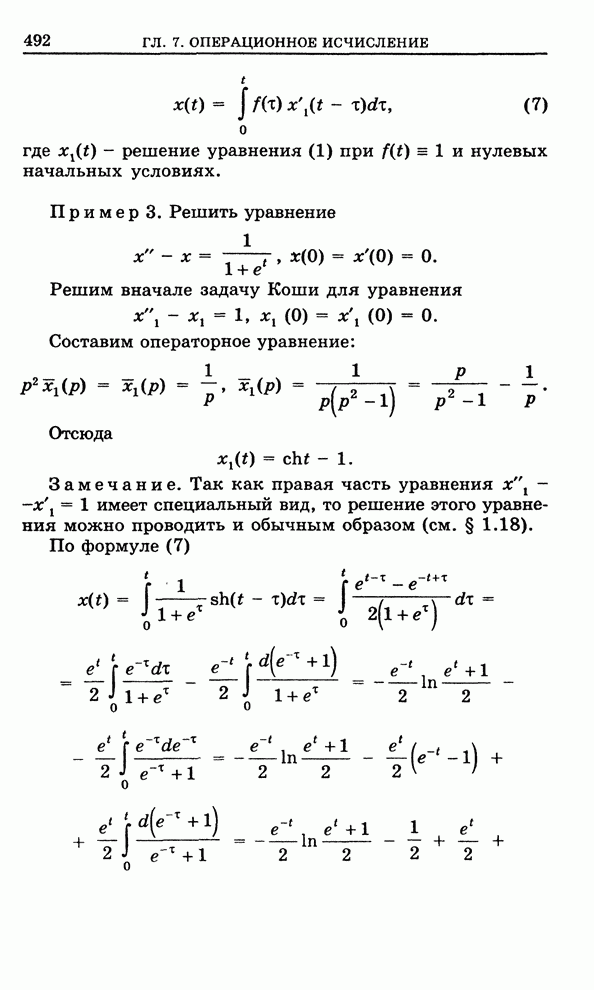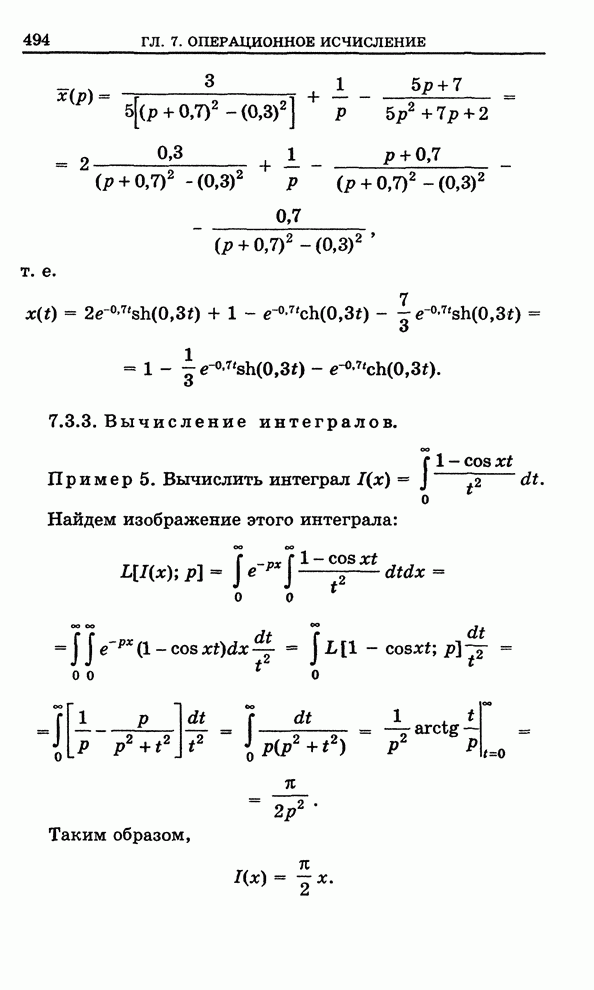| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 6.3. Условия Даламбера-Эйлера (Коши-Римана)
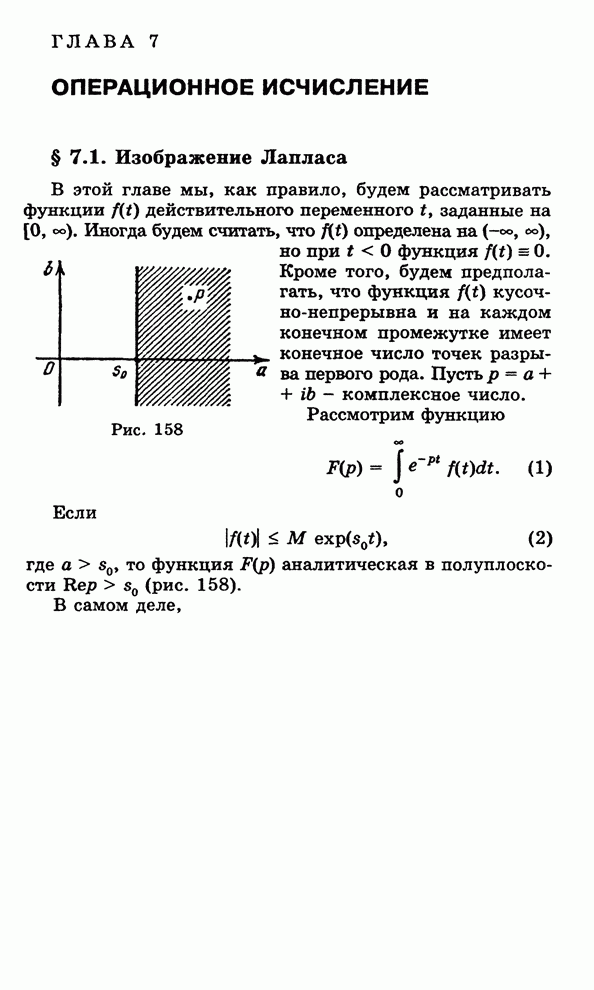
Рассмотрим комплексную функцию
![]()
![]() ,
,
определенную
на области ![]() комплексной
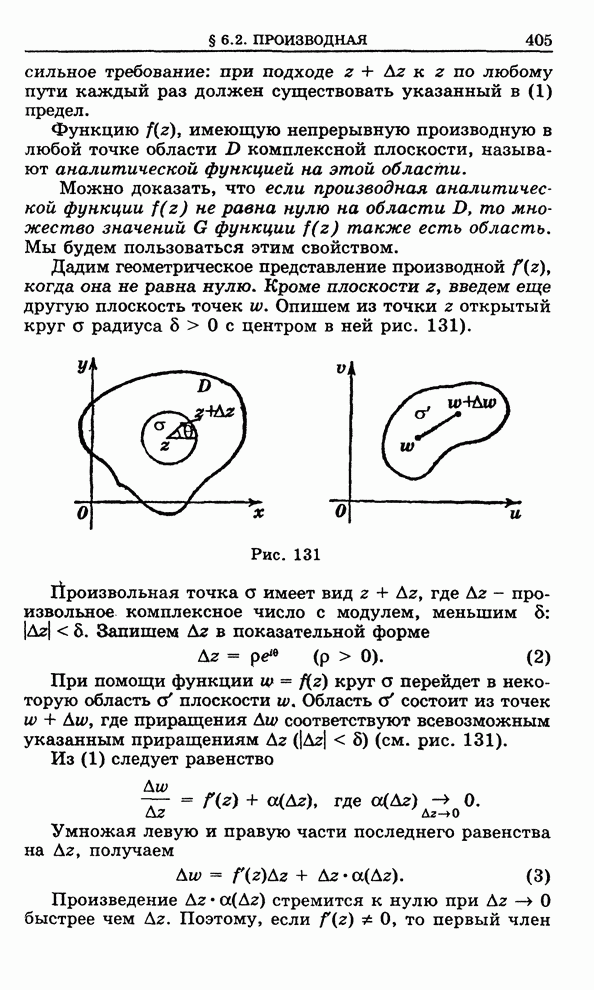
плоскости. Пусть она имеет производную в точке
комплексной
плоскости. Пусть она имеет производную в точке ![]()
![]() ,
,
![]()
![]() .
.
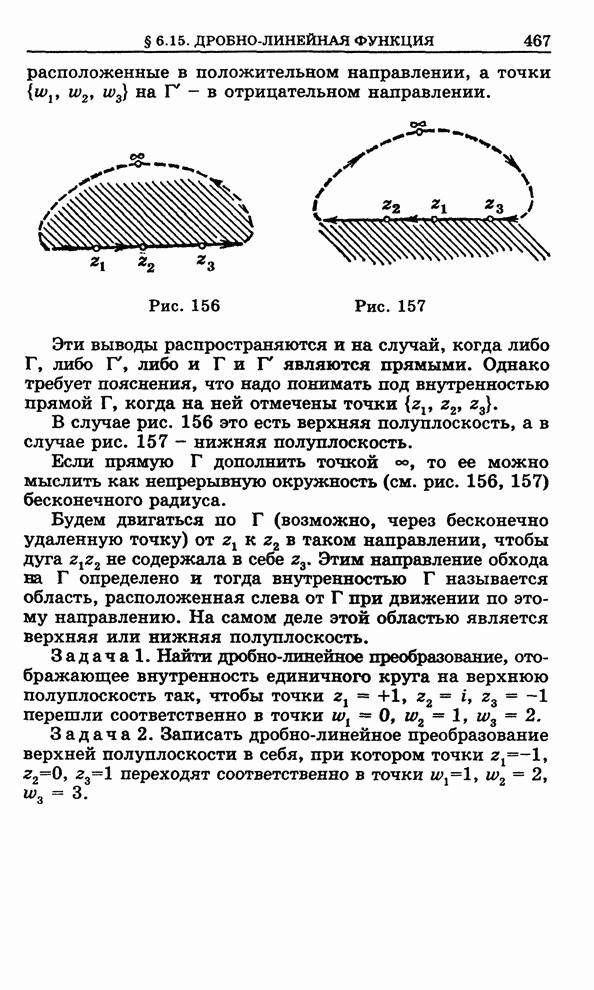
Таким образом, при любом способе
стремления ![]() к
нулю должен существовать предел (1), равный одному и тому же комплексному
числу
к
нулю должен существовать предел (1), равный одному и тому же комплексному
числу ![]() . В
частности, это должно иметь место, если a)
. В
частности, это должно иметь место, если a) ![]() и
и ![]() или, если б)
или, если б) ![]() и
и ![]() .
.
В первом случае (см. § 6.1, (3))
![]()
![]()
![]()
![]() .
.
Во втором случае
![]()
![]()
![]()
![]() . (2)
. (2)
Но тогда должны выполняться равенства
![]() ,
,
![]() ,
,
которые обычно называют условиями Коши-Римана. Некоторое время думали, что именно Коши и Риман впервые получили эти условия. Теперь выяснилось, что они были известны еще Эйлеру и Даламберу.
Итак, нами доказана
Теорема 1. Если функция
![]()
имеет
производную в точке
![]() , то
ее действительные компоненты
, то
ее действительные компоненты ![]() и
и ![]() имеют в точке
имеют в точке ![]() частные
производные первого порядка, удовлетворяющие условию Коши-Римана.
частные
производные первого порядка, удовлетворяющие условию Коши-Римана.
Теорему 1 можно обратить, правда
при добавочном предположении, что частные производные от ![]() и
и ![]() непрерывны.
непрерывны.
Теорема 2. Если функции ![]() и
и ![]() имеют в точке
имеют в точке
![]() непрерывные
частные производные, удовлетворяющие условиям Коши-Римана, то функция комплексной
переменной
непрерывные
частные производные, удовлетворяющие условиям Коши-Римана, то функция комплексной
переменной ![]() имеет
в точке
имеет
в точке ![]() производную.
производную.
Доказательство. Пусть функции ![]() и
и ![]() имеют непрерывные
частные производные в точке
имеют непрерывные
частные производные в точке ![]() . Тогда они дифференцируемы в этой
точке, т. е. их приращения, соответствующие приращениям
. Тогда они дифференцируемы в этой
точке, т. е. их приращения, соответствующие приращениям ![]() ,
, ![]() , могут быть записаны в
виде
, могут быть записаны в
виде
![]()
![]() ,
,
![]()
![]() ,
,
где
![]() ,
, ![]() и
и ![]()
![]() - бесконечно малые
функции высшего порядка малости чем
- бесконечно малые
функции высшего порядка малости чем ![]() , т. е.
, т. е. ![]()
![]() . Поэтому, учитывая, что
. Поэтому, учитывая, что ![]()
![]() , имеем (в силу
(2))
, имеем (в силу
(2))


![]() ,
,
потому
что ![]() .
Символ
.
Символ ![]() означает
бесконечно малую функцию при
означает
бесконечно малую функцию при ![]() . Таким образом,
. Таким образом,
![]()
т.
е. функция ![]() имеет
в точке
имеет
в точке ![]() производную,
равную
производную,
равную
![]() . (3)
. (3)
Используя условия (2), можно
получить и другие формы для выражения производной ![]() . Теорема доказана.
. Теорема доказана.
Если учесть, что существование
производной ![]() на
области
на
области ![]() автоматически
влечет за собой ее непрерывность на
автоматически
влечет за собой ее непрерывность на ![]() , то из теорем 1 и 2 вытекает
следующая
, то из теорем 1 и 2 вытекает
следующая
Теорема 3. Для того чтобы функция
![]()
была
аналитической на области
![]() плоскости
плоскости
![]() , необходимо
и достаточно, чтобы частные производные первого порядка функций
, необходимо
и достаточно, чтобы частные производные первого порядка функций ![]() и
и ![]() были непрерывны
на
были непрерывны
на ![]() и
выполнялись условия Коши - Римана
и
выполнялись условия Коши - Римана
![]() ,
,
![]() ,
, ![]() .
.
Функции ![]() и
и ![]() называют сопряженными
друг к другу на
называют сопряженными
друг к другу на ![]() .
.
Пример 1. Функции ![]() ,
, ![]() ,
, ![]() не являются
аналитическими на плоскости
не являются
аналитическими на плоскости ![]() . Ведь каждая из них может быть
записана в виде
. Ведь каждая из них может быть
записана в виде ![]() ,
где
,
где ![]() и
и ![]() - действительные
функции, очевидно, не удовлетворяющие условиям Коши - Римана.
- действительные
функции, очевидно, не удовлетворяющие условиям Коши - Римана.
Пример 2. Проверить выполнение
условий Коши - Римана для действительной и мнимой частей функции ![]() .
.
В примере 1 § 6.2 мы показали, что
![]() ,
,
![]() .
.
Отсюда
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Таким образом,
![]() ,
,
![]()
![]() ,
,
т. е. условия Коши - Римана выполнены.
Так как частные производные
первого порядка от функций ![]() и
и ![]() непрерывны для любых точек
непрерывны для любых точек ![]() , то функция
, то функция ![]() аналитична на всей
комплексной плоскости.
аналитична на всей
комплексной плоскости.
Задача. Записать функции ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (
(![]() - натуральное) в
виде
- натуральное) в
виде
![]() ,
,
где ![]() ,
, ![]() , и убедиться в том, что они удовлетворяют
условиям Коши - Римана.
, и убедиться в том, что они удовлетворяют
условиям Коши - Римана.
Замечание. Если функцию ![]() представить в виде
представить в виде
![]() ,
,
где
![]() -
модуль, а
-
модуль, а ![]() -
аргумент функции
-
аргумент функции ![]() ,
то условия Коши - Римана имеют вид
,
то условия Коши - Римана имеют вид
![]() ,
,
![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. Обыкновенные дифференциальные уравнения
- 1.1. Задача, приводящая к дифференциальному уравнению
- 1.2. Общие понятия
- 1.2.1. Понятие обыкновенного дифференциального уравнения
- 1.2.2. Дифференциальное уравнение первого порядка
- 1.2.3. Задача Коши
- 1.2.4. Примеры дифференциальных уравнений первого порядка
- 1.2.5. Общий интеграл дифференциального уравнения первого порядка
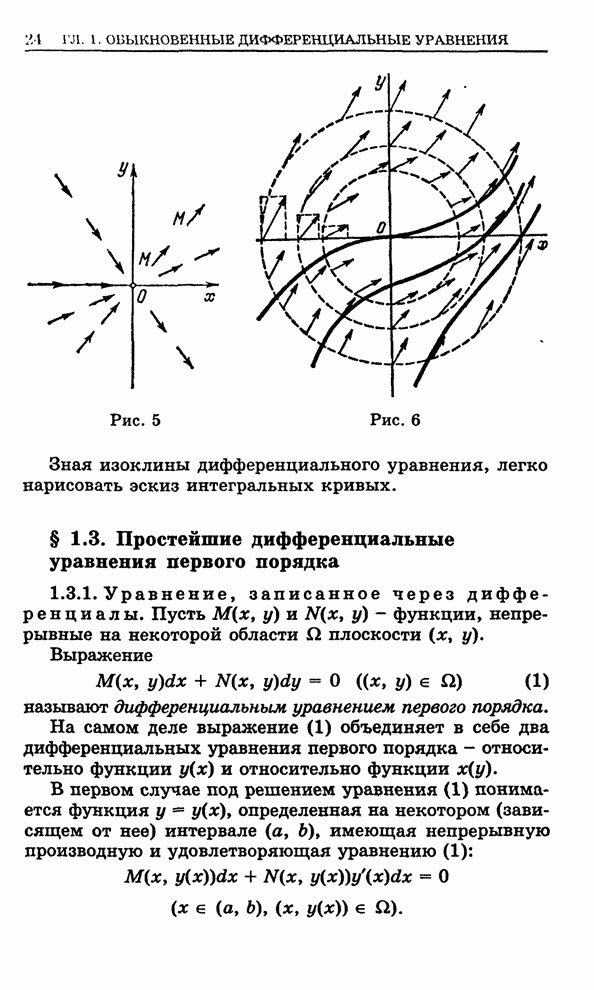
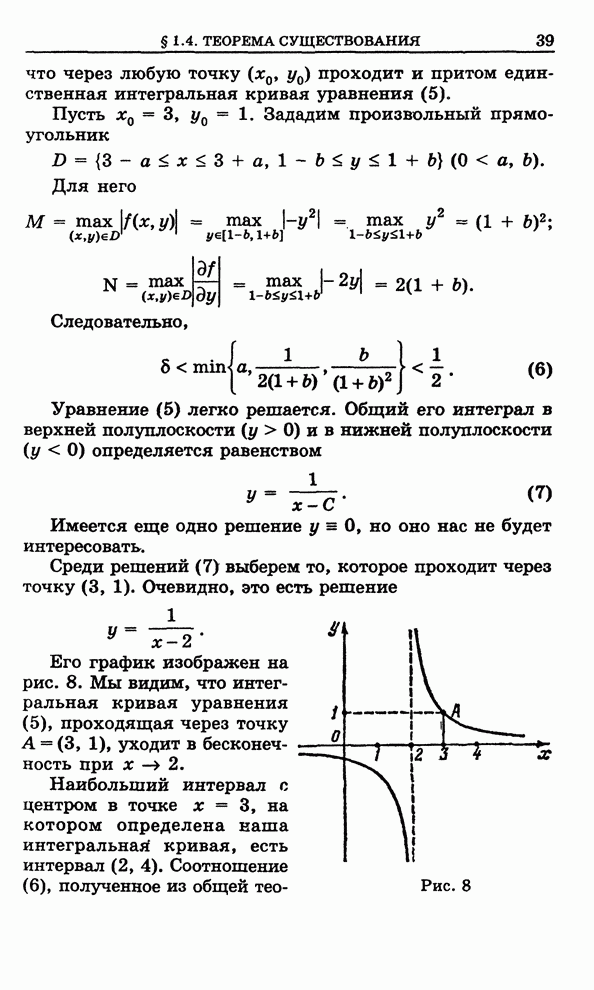
- 1.2.6. Поле направлений
- 1.3. Простейшие дифференциальные уравнения первого порядка
- 1.3.1. Уравнение, записанное через дифференциалы
- 1.3.2. Уравнения с разделенными переменными
- 1.3.3. Уравнения с разделяющимися переменными
- 1.3.4. Однородные уравнения
- 1.3.5. Линейное уравнение
- 1.3.6. Уравнение Бернулли
- 1.4. Теорема существования решения дифференциального уравнения первого порядка
- 1.5. Метрическое пространство
- 1.5.1. Понятие метрического пространства
- 1.5.2. Полное метрическое пространство
- 1.5.3. Принцип сжатых отображений
- 1.5.4. Приближенное значение корня функции
- 1.5.5. Метод Ньютона
- 1.6. Доказательство теоремы существования решения диффереацнального уравнения первого порядка
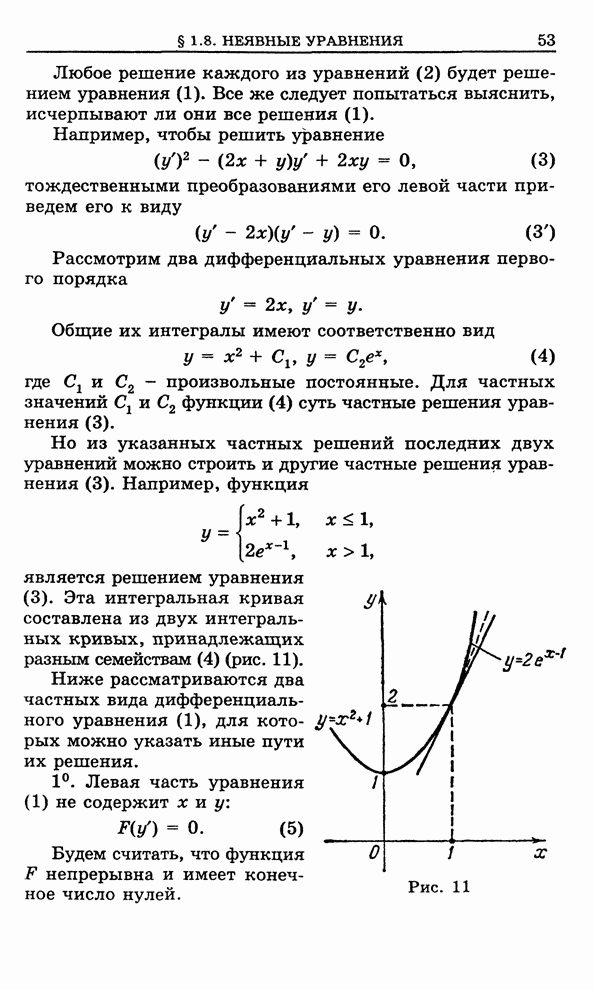
- 1.7. Метод Эйлера приближенного решения дифференциального уравнения первого порядка
- 1.8. Уравнения, не разрешенные относительно производной
- 1.9. Особые решения
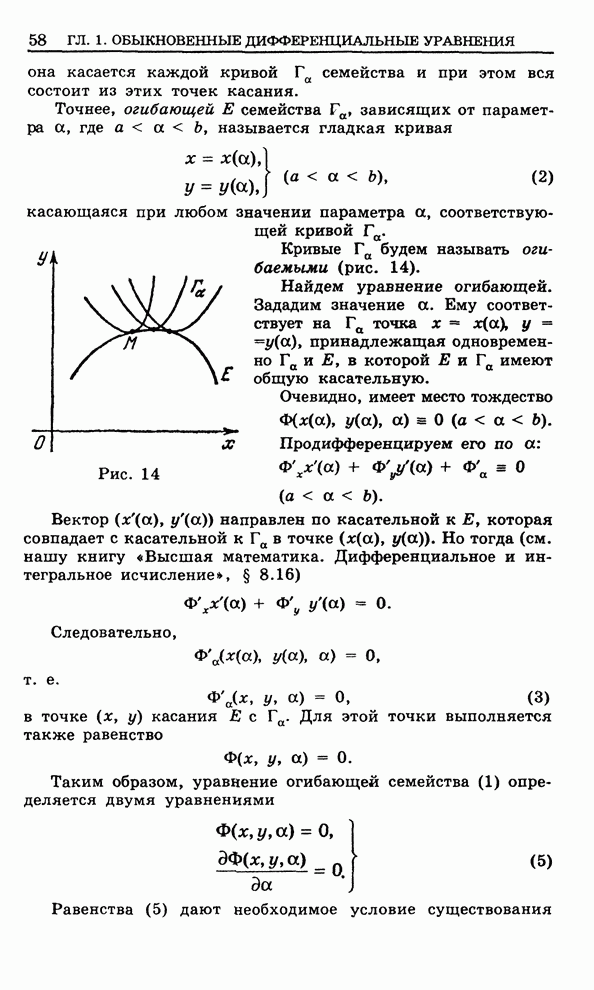
- 1.10. Огибающая семейства кривых
- 1.11. Дифференциальное уравнение второго порядка
- 1.12. Система из двух дифференциальных уравнений первого порядка
- 1.13. Дифференциальное уравнение n-го порядка
- 1.14. Понижение порядка дифференциального уравнения
- 1.15. Линейные уравнения высшего порядка
- 1.15.1. Понятие линейного уравнения высшего порядка
- 1.15.2. Фундаментальная система решений уравнения
- 1.15.3. Определитель Вронского
- 1.15.4. Структура общего решения
- 1.16. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- 1.16.1. Методы решения
- 1.16.2. Уравнение Эйлера
- 1.17. Метод вариации постоянных
- 1.18. Частное решение неоднородного уравнения с постоянными коэффициентами. Приложения
- 1.18.1. Методы нахождения частных решений
- 1.18.2. Дифференциальное уравнение колебания пружины
- 1.19. Системы дифференциальных уравнений. Фазовое пространство
- 1.20. Линейная однородная система дифференциальных уравнений
- 1.21. Общее решение линейной однородной системы дифференциальных уравнений с постоянными коэффициентами
- 1.22. Сведение системы уравнений к одному уравнению
- 1.23. Неоднородная система линейных дифференциальных уравнений с постоянными коэффициентами
- 1.24. Интегрирование дифференциальных уравнений с помощью степенных рядов
- 1.25. Элементы теории устойчивости
- 1.26. Классификация точек покоя
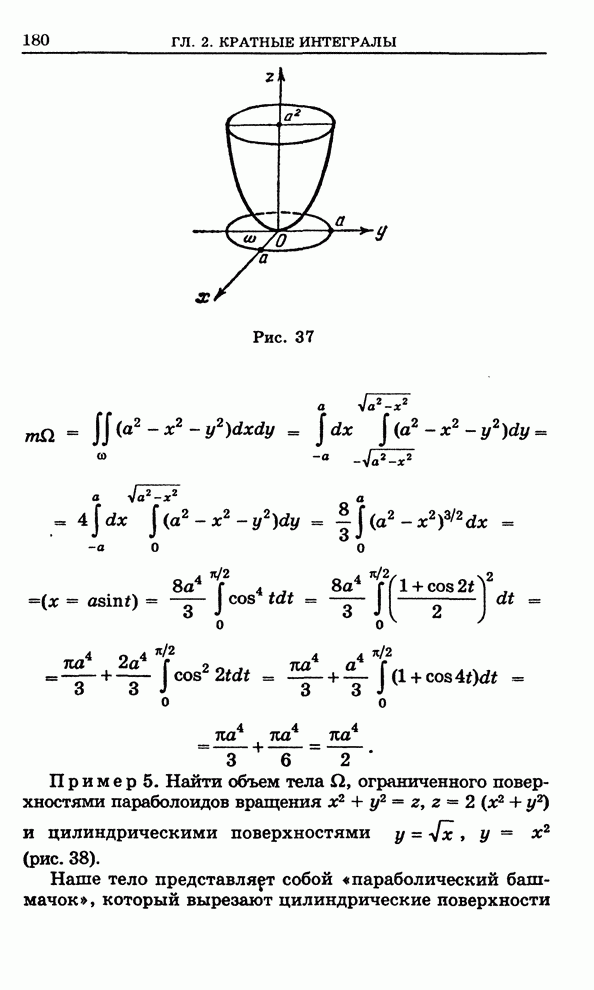
- Глава 2. Кратные интегралы
- 2.1. Введение
- 2.2. Сведения из теории меры Жордана
- 2.3. Свойства кратных интегралов. Теоремы существования
- 2.4. Сведение кратного интеграла к повторным
- 2.5. Доказательство существования интеграла от непрерывной функции
- 2.6. Замена переменных. Простейший случай
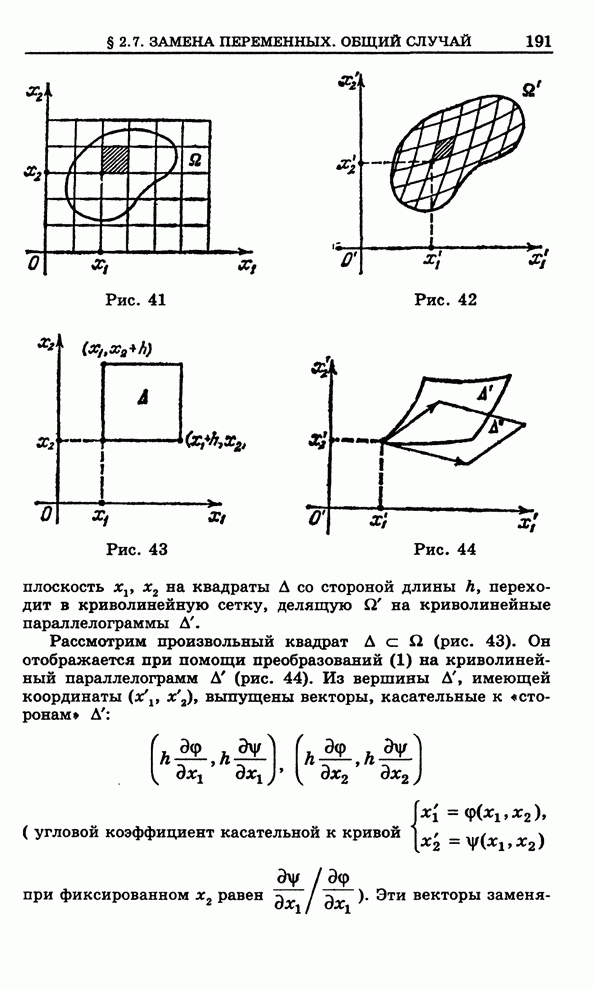
- 2.7. Замена переменных. Общий случай
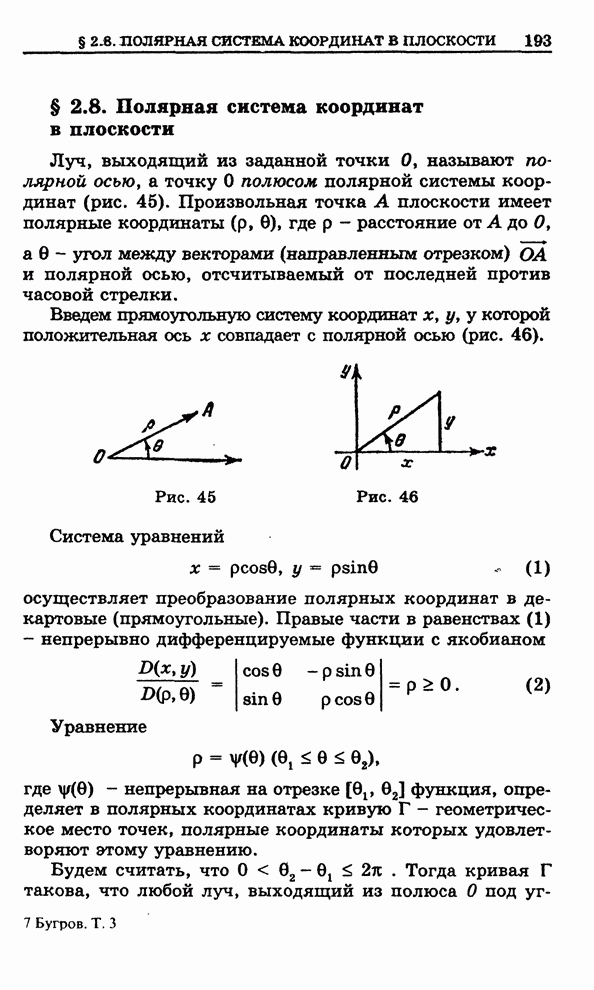
- 2.8. Полярная система координат в плоскости
- 2.9. Полярная система координат в пространстве
- 2.10. Цилиндрические координаты
- 2.11. Площадь поверхности
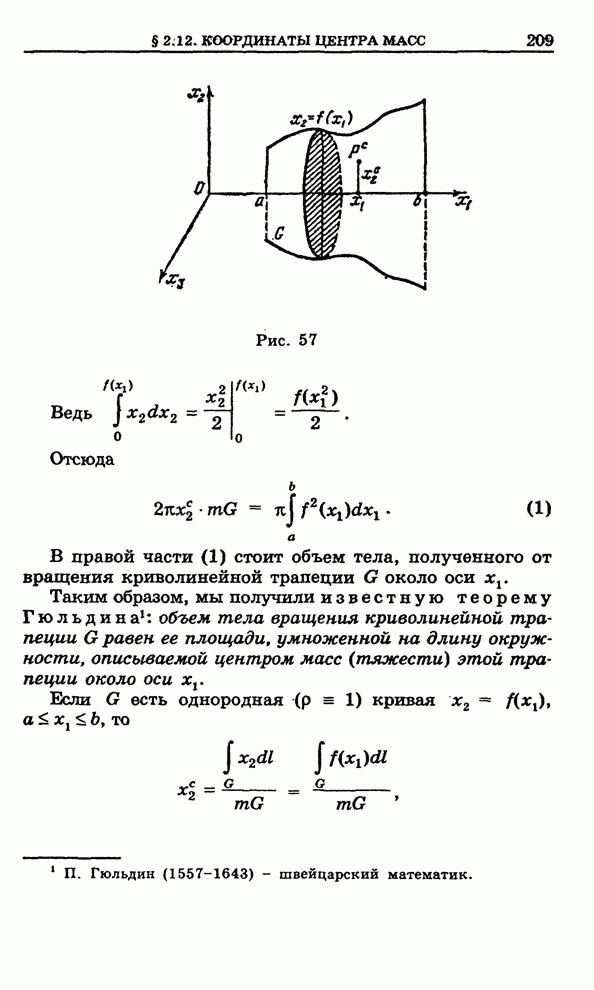
- 2.12. Координаты центра масс
- 2.13. Несобственные интегралы
- 2.14. Несобственный интеграл с особенностями вдоль линии
- 2.15. Несобственный интеграл, зависящий от параметра
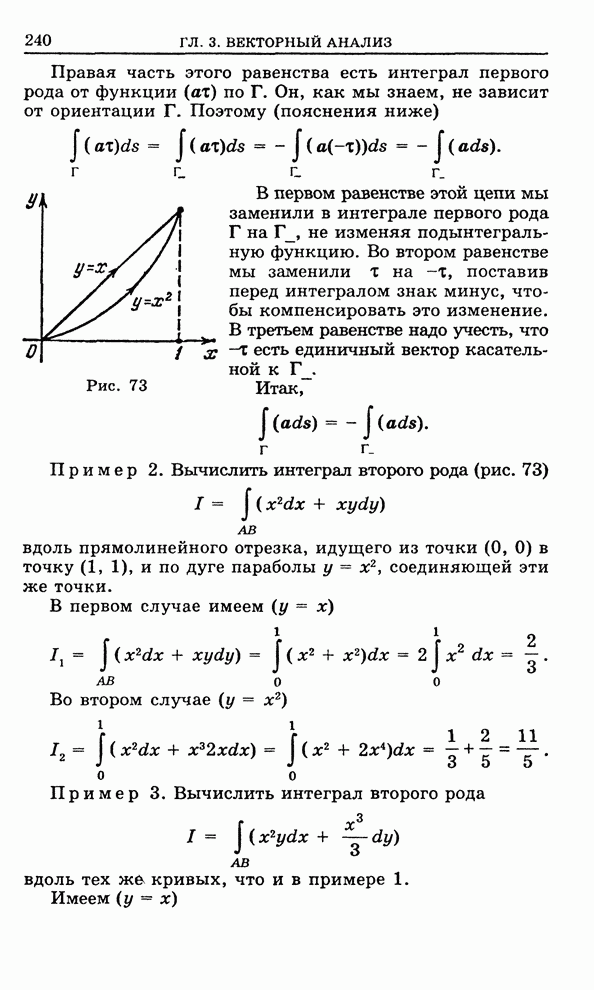
- Глава 3. Векторный анализ
- 3.1. Кусочно-гладкая ориентированная кривая
- 3.2. Криволинейный интеграл первого рода
- 3.3. Интеграл от вектора вдоль кривой
- 3.3.1. Поле вектора
- 3.3.2. Криволинейный интеграл от вектора вдоль кривой
- 3.3.3. Свойства криволинейных интегралов второго рода
- 3.4. Поле потенциала
- 3.4.1. Понятие потенциала и его свойства
- 3.4.2. Доказательство свойств потенциала
- 3.4.3. Ротор вектора
- 3.5. Дифференциальное уравнение в полных дифференциалах
- 3.6. Ориентация плоской области
- 3.7. Формула Грина
- 3.8. Интеграл по поверхности первого рода
- 3.9. Ориентация поверхности
- 3.10. Система координат и ориентация поверхности
- 3.11. Интеграл по ориентированной плоской области
- 3.12. Поток вектора через ориентированную поверхность
- 3.13. Дивергенция. Теорема Гаусса—Остроградского
- 3.14. Соленоидальное поле
- 3.15. Формула Стокса
- Глава 4. Ряды Фурье. Интеграл Фурье
- 4.1. Тригонометрические ряды
- 4.2. Сходимость тригонометрических рядов
- 4.3. Ряд Фурье
- 4.4. Признаки сходимости рядов Фурье
- 4.5. Ортогональные свойства тригонометрических функций
- 4.6. Коэффициенты Фурье
- 4.7. Оценка коэффициентов Фурье
- 4.8. Пространство функций со скалярным произведением
- 4.9. Ортогональная система функций
- 4.10. Полнота тригонометрических функций
- 4.11. Комплексная форма ряда Фурье
- 4.12. Понятие интеграла Фурье. Повторный интеграл Фурье
- 4.13. Косинус- и синус- преобразования Фурье
- 4.14. Примеры
- 4.15. Приближение интеграла Фурье
- 4.16. Сумма Фейера
- 4.17. Полнота систем функций в С и L2’
- 4.18. Сведения из теории кратных рядов Фурье
- Глава 5. Уравнения математической физики
- 5.1. Температура тела
- 5.2. Задача Дирихле
- 5.3. Задача Дирихле для круга
- 5.4. Задача Дирихле для полуплоскости
- 5.5. Уравнение теплопроводности в стержне
- 5.6. Теплопроводность для бесконечного стержня
- 5.7. Малые колебания струны
- 5.8. Колебание бесконечной струны. Формула Даламбера
- 5.9. Колебание круглой мембраны
- 5.10. Общая задача Штурма-Лиувилля
- 5.11. Интеграл энергии (Дирихле)
- 5.12. Применение преобразований Фурье
- Глава 6. Теория функций комплексного переменного
- 6.1. Понятие функции комплексного переменного
- 6.2. Производная функция комплексного переменного
- 6.3. Условия Даламбера-Эйлера (Коши-Римана)
- 6.4. Гармонические функции
- 6.5. Обратная функция
- 6.6. Интегрирование функций комплексного переменного
- 6.7. Формула Коши
- 6.8. Интеграл типа Коши
- 6.9. Степенной ряд
- 6.10. Ряд Лорана
- 6.11. Классификация изолированных особых точек. Вычеты
- 6.12. Классификация особых точек на бесконечности
- 6.13. Теорема о вычетах
- 6.14. Вычисление интегралов при помощи вычетов
- 6.15. Линейная функция. Дробно-линейная функция
- Глава 7. Операционное исчисление
- 7.1. Изображение Лапласа
- 7.2. Изображение простейших функций и свойства изображений
- 7.3. Приложения операционного исчисления
- 7.3.1. Операторное уравнение
- 7.3.2. Решение систем дифференциальных уравнений
- 7.3.3. Вычисление интегралов
- Глава 8. Обобщенные функции
- 8.1. Понятие обобщенной функции
- 8.2. Операции над обобщенными функциями
- 8.3. Преобразование Фурье обобщенных функций