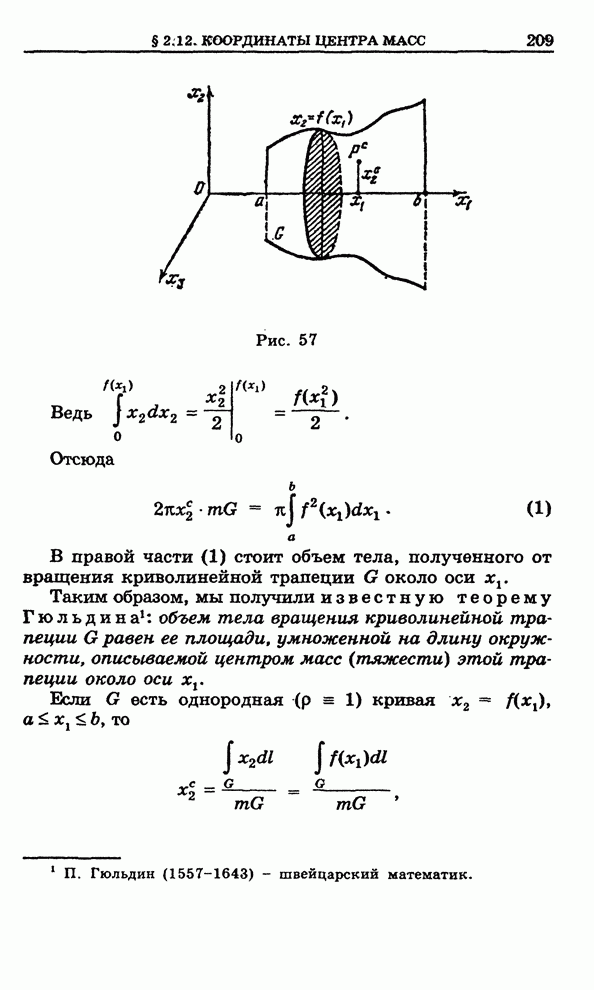
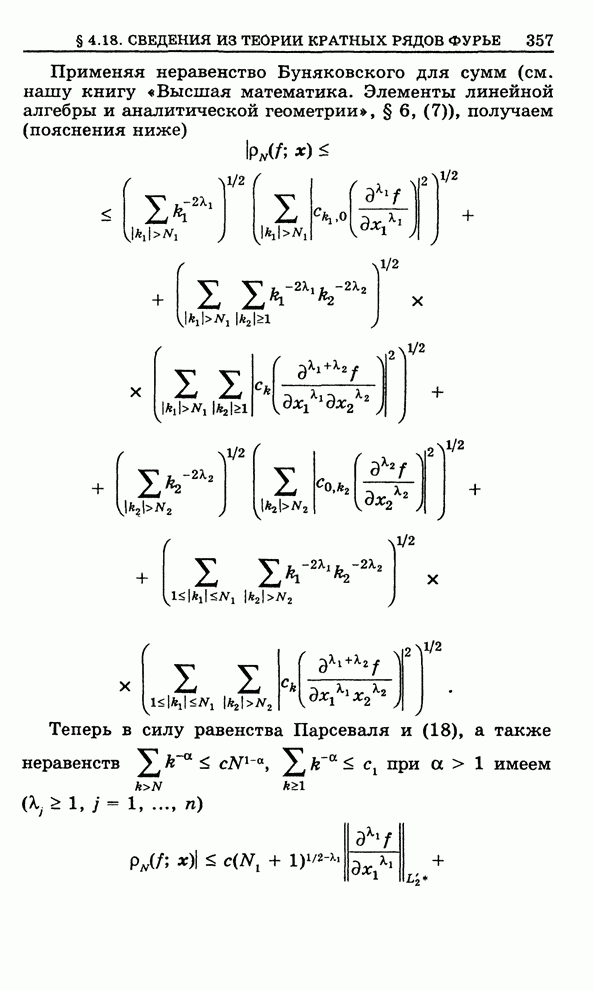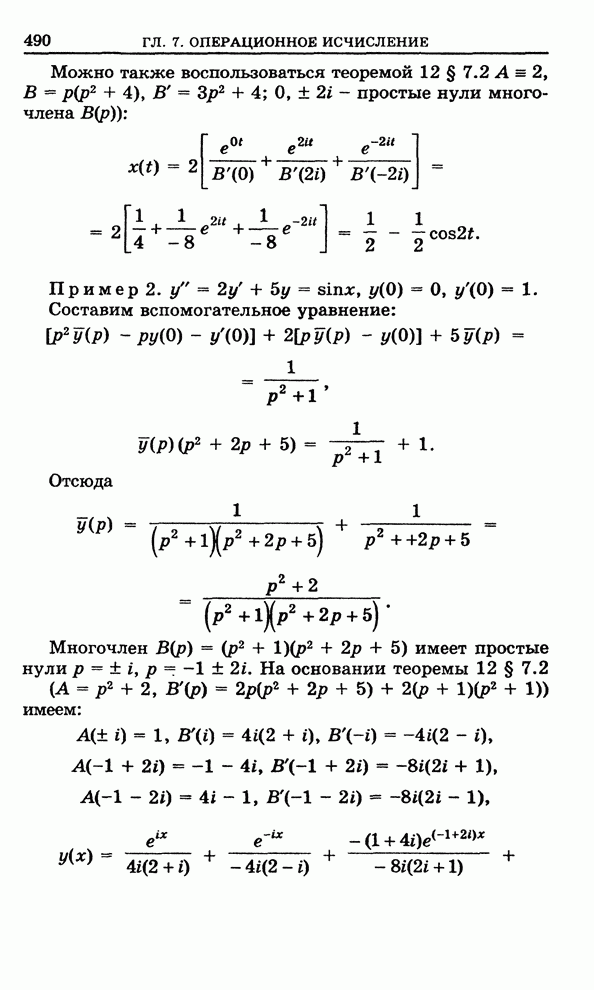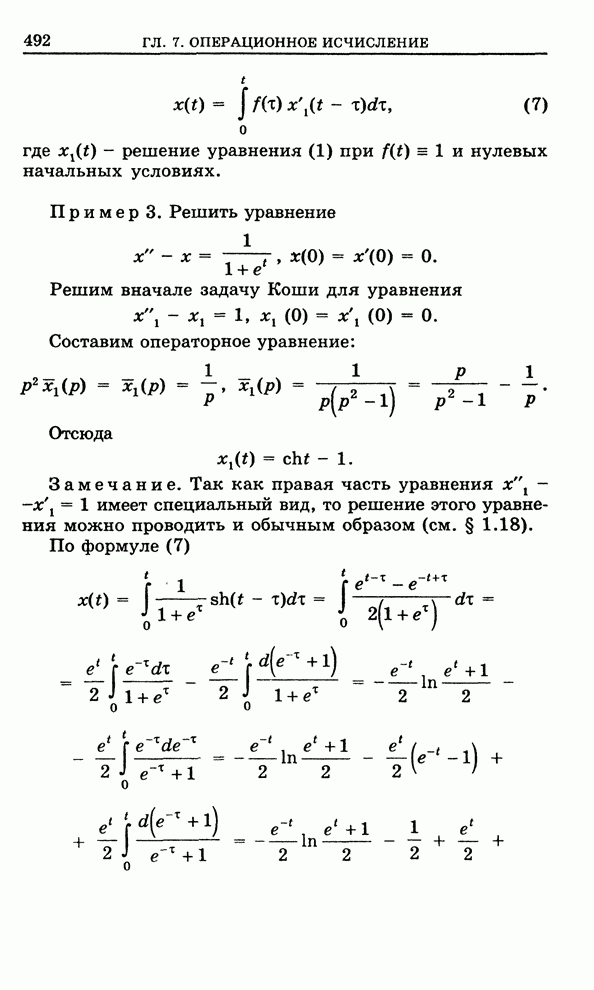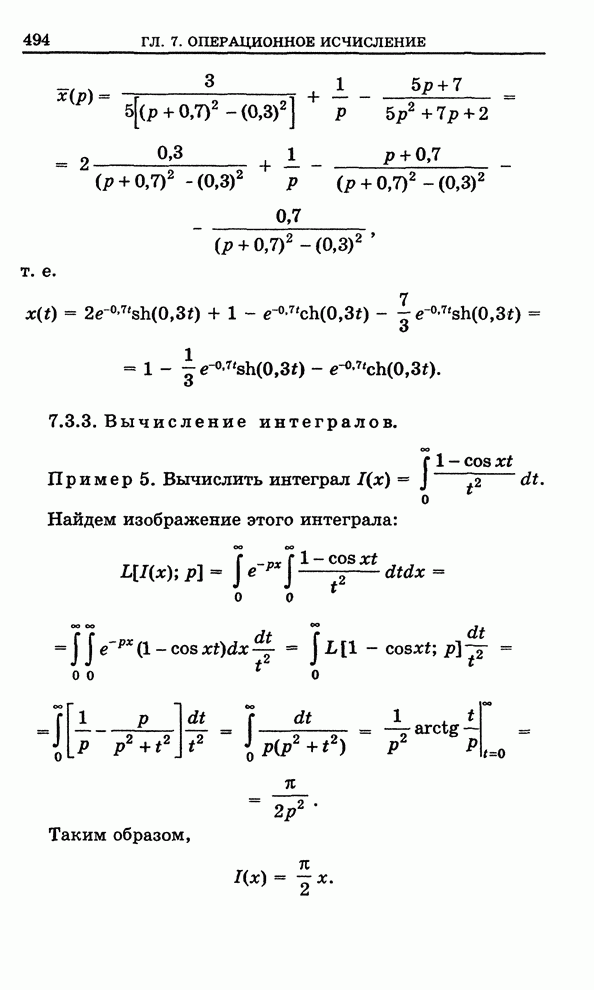| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6.2. Производная функция комплексного переменного
Пусть задана однозначная функция ![]() на области
на области ![]() (открытом связном
множестве) комплексной плоскости
(открытом связном
множестве) комплексной плоскости ![]() .
.
Производной от функции ![]() в точке
в точке ![]() называется предел
называется предел
![]() (1)
(1)
когда
![]() любым
образом стремится к нулю.
любым
образом стремится к нулю.
Далеко не всякая функция
комплексного переменного имеет производную. Существование предела (1) – очень сильное
требование: при подходе ![]() к
к ![]() по любому пути каждый раз должен
существовать указанный в (1) предел.
по любому пути каждый раз должен
существовать указанный в (1) предел.
Функцию ![]() , имеющую непрерывную
производную в любой точке области
, имеющую непрерывную
производную в любой точке области ![]() комплексной плоскости, называют аналитической
функцией на этой области.
комплексной плоскости, называют аналитической
функцией на этой области.
Можно доказать, что если
производная аналитической функции ![]() не равна нулю на области
не равна нулю на области ![]() , то множество
значений
, то множество
значений ![]() функции
функции
![]() также
есть область. Мы будем пользоваться этим свойством.
также
есть область. Мы будем пользоваться этим свойством.
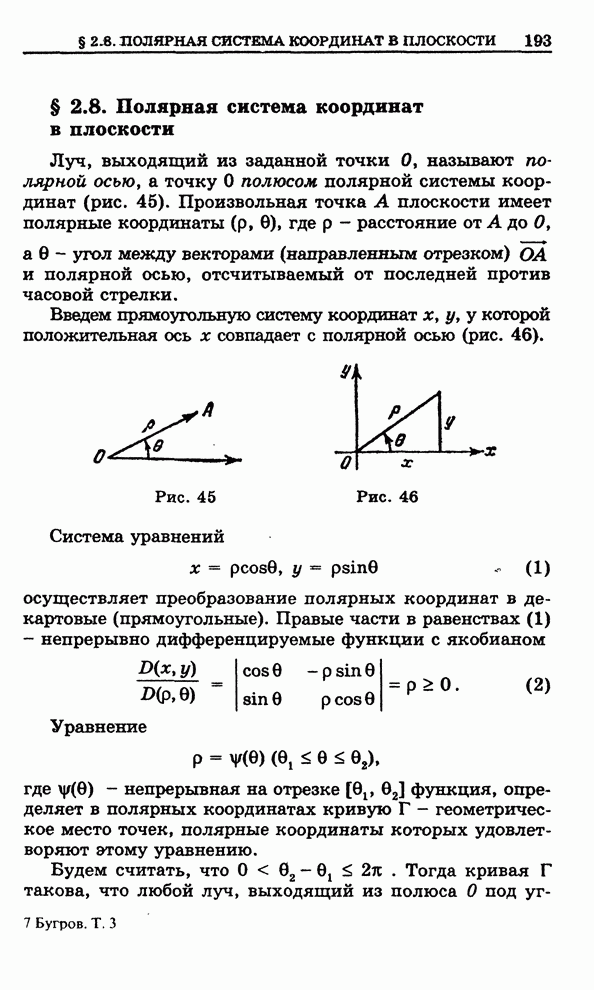
Дадим геометрическое
представление производной ![]() , когда она не равна нулю. Кроме плоскости
, когда она не равна нулю. Кроме плоскости ![]() , введем еще другую
плоскость точек
, введем еще другую
плоскость точек ![]() .
Опишем из точки
.
Опишем из точки ![]() открытый
круг
открытый
круг ![]() радиуса
радиуса
![]() с
центром в ней (рис. 131).
с
центром в ней (рис. 131).

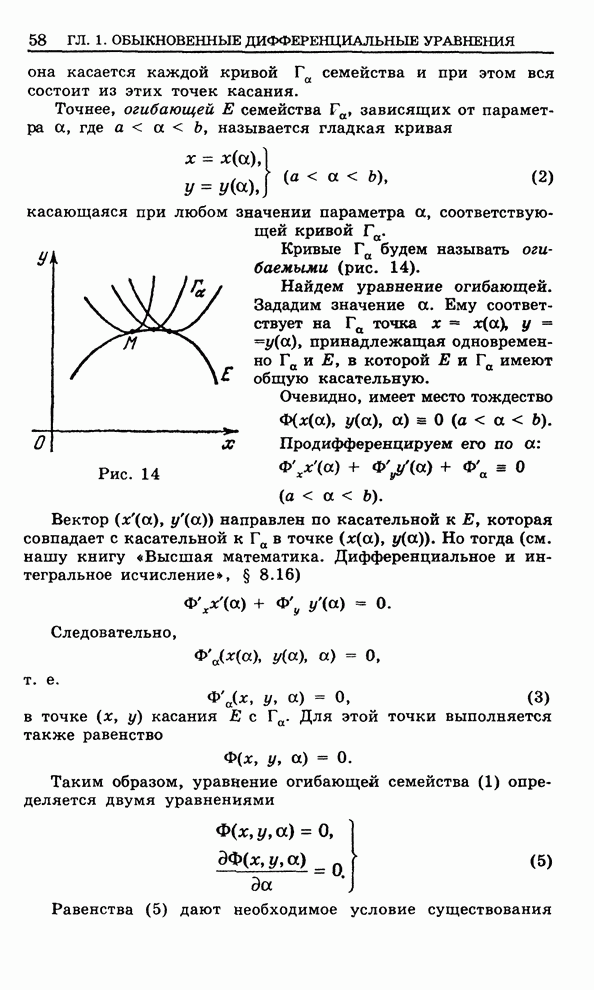
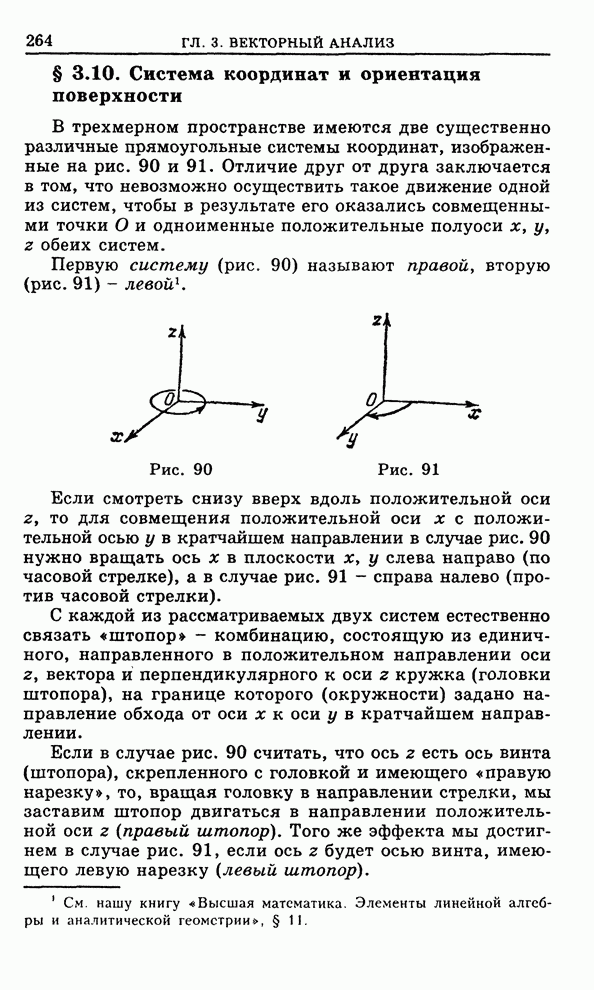
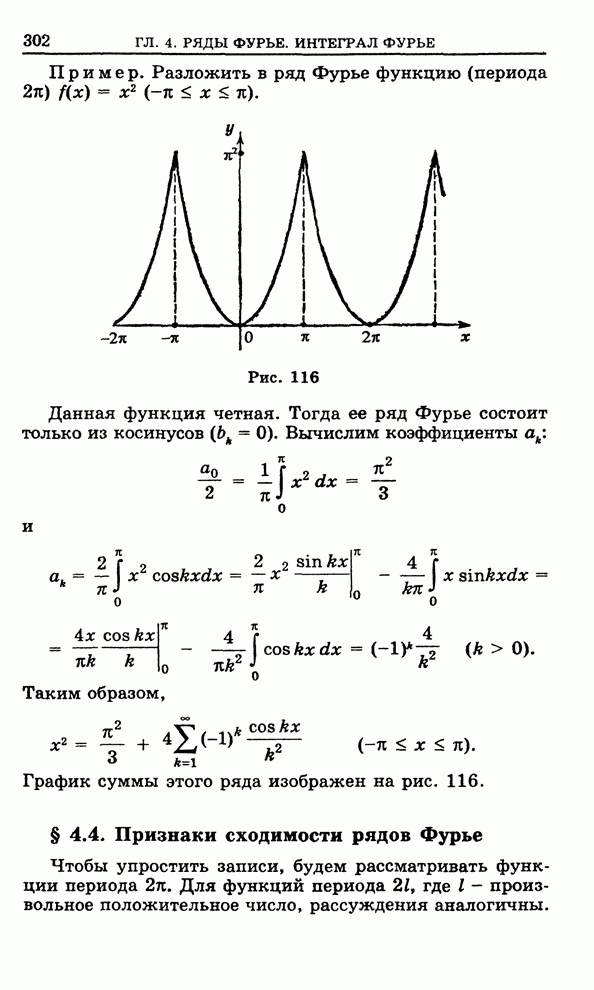
Рис. 131
Произвольная точка ![]() имеет вид
имеет вид ![]() , где
, где ![]() - произвольное
комплексное число с модулем, меньшим
- произвольное
комплексное число с модулем, меньшим ![]() . Запишем
. Запишем ![]() в показательной форме
в показательной форме
![]()
![]() . (2)
. (2)
При помощи функции ![]() круг
круг ![]() перейдет в некоторую
область
перейдет в некоторую
область ![]() плоскости
плоскости
![]() . Область
. Область
![]() состоит
из точек
состоит
из точек ![]() ,
где приращения
,
где приращения ![]() соответствуют
всевозможным указанным приращениям
соответствуют
всевозможным указанным приращениям ![]() (см. рис. 131).
(см. рис. 131).
Из (1) следует равенство
![]() ,
где
,
где ![]() .
.
Умножая левую и правую части
последнего равенства на ![]() , получаем
, получаем
![]() . (3)
. (3)
Произведение ![]() стремится к нулю при
стремится к нулю при ![]() быстрее чем
быстрее чем ![]() . Поэтому, если
. Поэтому, если ![]() , то первый член правой
части (3) является главным. Приближенно, с точностью до бесконечно
малых высшего порядка (по сравнению с
, то первый член правой
части (3) является главным. Приближенно, с точностью до бесконечно
малых высшего порядка (по сравнению с ![]() ), при достаточно малых
), при достаточно малых ![]() можно написать
можно написать
![]() .
.
Число ![]() запишем в показательной
форме
запишем в показательной
форме
![]()
![]() . (4)
. (4)
Поэтому, учитывая (2), получим
![]()
![]() .
.
Мы видим, что модуль ![]() , с точностью до
бесконечно малой высшего порядка, в
, с точностью до
бесконечно малой высшего порядка, в ![]() раз больше модуля
раз больше модуля ![]() :
:
![]() ,
,
а
аргумент ![]() (тоже
с точностью до бесконечно малой высшего порядка) получается из аргумента
(тоже
с точностью до бесконечно малой высшего порядка) получается из аргумента ![]() прибавлением к
нему числа
прибавлением к
нему числа ![]() (рис.
132):
(рис.
132):
![]() .
.
Таким образом, для того чтобы
представить себе, куда перешли точки ![]() с
с ![]() при помощи функции
при помощи функции ![]() надо 1) повернуть
круг
надо 1) повернуть
круг ![]() на
угол
на
угол ![]() и
2) растянуть его в
и
2) растянуть его в ![]() раз. Каждая точка
раз. Каждая точка ![]() ,
, ![]() , при помощи этих двух
операций перейдет в некоторую точку, которую надо еще сдвинуть на величину
, при помощи этих двух
операций перейдет в некоторую точку, которую надо еще сдвинуть на величину ![]() - бесконечно малую
высшего порядка чем
- бесконечно малую
высшего порядка чем ![]() .
.
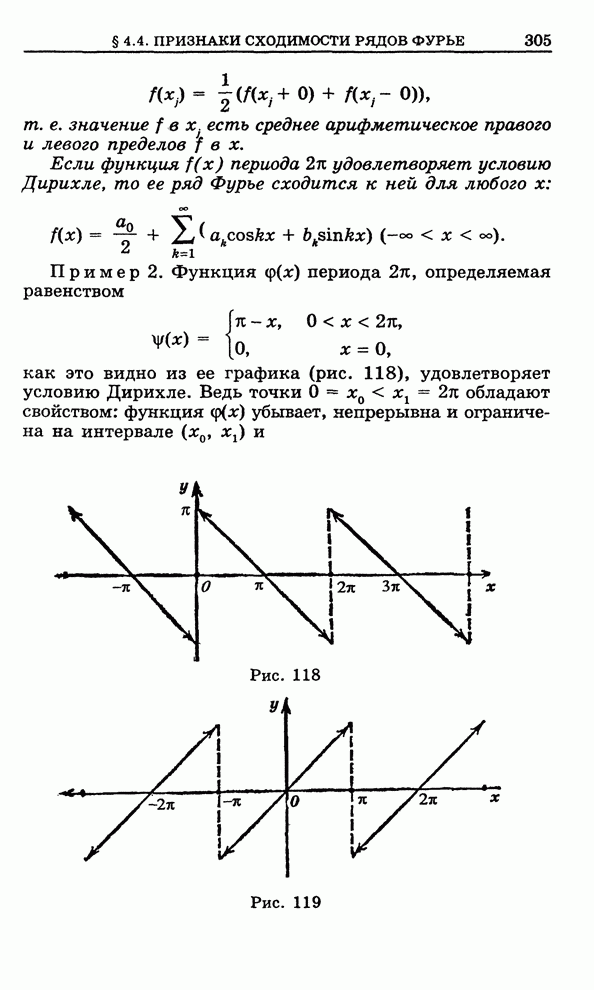
Пусть ![]() и
и ![]() - гладкие кривые, выходящие
из точки
- гладкие кривые, выходящие
из точки ![]() .
Касательные к ним образуют с осью
.
Касательные к ним образуют с осью ![]() углы соответственно
углы соответственно ![]() (отсчитываемые от
оси
(отсчитываемые от
оси ![]() против
часовой стрелки). Образы этих кривых
против
часовой стрелки). Образы этих кривых ![]() на плоскости
на плоскости ![]() (рис. 133) при помощи
функции
(рис. 133) при помощи
функции ![]() имеют
касательные в точке
имеют
касательные в точке ![]() , образующие с осью абсцисс
соответственно углы
, образующие с осью абсцисс
соответственно углы ![]() (которые отсчитываются тоже против
часовой стрелки).
(которые отсчитываются тоже против
часовой стрелки).

Рис. 132
При этом (в силу свойства 1))
![]() ,
,
![]() ,
,
откуда следует свойство
![]() ,
,
выражающее,
как говорят, что данное отображение сохраняет углы и притом с
сохранением направления отсчета (если ![]() , то
, то ![]() ).
).

Рис. 133
Кроме того, как мы видели выше,
данное отображение осуществляет в каждой точке ![]() , где
, где ![]() , растяжение, не зависящее от
направления.
, растяжение, не зависящее от
направления.
Отображение, обладающее (с точностью до бесконечно малых высшего порядка) свойством сохранения углов (с сохранением направления отсчета) и свойством постоянства растяжений, называется конформным отображением.
Из вышеизложенного следует, что отображение
с помощью аналитической функции ![]() является конформным во всех
точках, где
является конформным во всех
точках, где ![]() .
.
Замечание 1. Если функция ![]() комплексной
переменной
комплексной
переменной ![]() имеет
всюду на области
имеет
всюду на области ![]() производную
производную ![]() , то
автоматически эта производная непрерывна всюду на
, то
автоматически эта производная непрерывна всюду на ![]() , т. е.
, т. е. ![]() аналитическая
на
аналитическая
на ![]() .
Этим утверждением мы будем пользоваться, хотя доказывать его не будем.
.
Этим утверждением мы будем пользоваться, хотя доказывать его не будем.
Замечание 2. Из равенства (3)
следует, что если функция ![]() имеет производную в точке
имеет производную в точке ![]() , то она непрерывна
в этой точке (т. е.
, то она непрерывна
в этой точке (т. е. ![]() при
при ![]() ).
).
Производная от функции ![]() порядка
порядка ![]() обозначается через
обозначается через
![]() и
определяется по индукции
и
определяется по индукции
![]()
![]() .
.
Зная, что у аналитической на
области ![]() функции
функции
![]() производная
непрерывна на
производная
непрерывна на ![]() ,
нам будет в дальнейшем нетрудно заключить, что
,
нам будет в дальнейшем нетрудно заключить, что ![]() имеет на
имеет на ![]() непрерывные производные
любого порядка
непрерывные производные
любого порядка
![]() .
.
Употребляют еще такую
терминологию: функция ![]() называется аналитической в точке
называется аналитической в точке
![]() , если
она аналитическая на некоторой окрестности этой точки. Наконец, говорят, что
функция
, если
она аналитическая на некоторой окрестности этой точки. Наконец, говорят, что
функция ![]() аналитическая
на замыкании
аналитическая
на замыкании ![]() области
области
![]() , если
существует область
, если
существует область ![]() , содержащая в себе
, содержащая в себе ![]()
![]() , на которой
, на которой ![]() аналитическая.
аналитическая.
Приведем основные свойства производных функций комплексного переменного, аналогичные соответствующим свойствам производных для функций действительного переменного, которые и доказываются аналогично:
![]() , (5)
, (5)
![]() , (6)
, (6)

![]() , (7)
, (7)
![]() . (8)
. (8)
Формулу (8) надо понимать так:
если ![]() есть
функция
есть
функция ![]() комплексного
переменного
комплексного
переменного ![]() ,
имеющая производную
,
имеющая производную ![]() , a
, a ![]() - функция от комплексной переменной
- функция от комплексной переменной ![]() , имеющая
производную
, имеющая
производную ![]() ,
то производная сложной функции
,
то производная сложной функции
![]()
вычисляется по формуле (8).
Ниже мы приводим некоторые элементарные функции комплексного переменного.
Степенная функция
![]() ,
,
![]() -
целое.
-
целое.
Эта функция имеет производную, вычисляемую по формуле
![]()
![]() .
.
При ![]() ее удобно вычислить как предел
ее удобно вычислить как предел
![]() ,
,
применяя формулу бинома Ньютона.
При ![]() теперь можно воспользоваться формулой
(7).
теперь можно воспользоваться формулой
(7).
Функция ![]() при
при ![]() аналитическая на всей
плоскости
аналитическая на всей
плоскости ![]() ,
а при
,
а при ![]() на
всей плоскости с выколотой из нее точкой
на
всей плоскости с выколотой из нее точкой ![]() .
.
Функции ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Первые три из этих функций определены в нашей книге «Высшая математика. Дифференциальное и интегральное исчисление», § 9.13, как суммы степенных рядов:
![]() ,
,
![]() ,
,
![]() .
.
Радиус сходимости каждого из этих
рядов равен ![]() .
Поэтому производные от этих функций могут быть получены для любого
.
Поэтому производные от этих функций могут быть получены для любого ![]() почленным
дифференцированием соответствующих рядов:
почленным
дифференцированием соответствующих рядов:
![]() .
.
![]() .
.
![]() .
.
Формулы для тригонометрических функций суммы комплексных аргументов остаются такими же, как и в случае действительного переменного.
Функция ![]() определяется по формуле
определяется по формуле
![]() .
.
Ее производная равна
![]()
![]() ,
,
что следует из формулы (7).
Функция ![]() (
(![]() ) может быть определена по формуле
) может быть определена по формуле
![]() .
.
Ее производная вычисляется на основании формулы (8) о производной сложной функции:
![]() .
.
Гиперболические функции ![]() ,
, ![]() ,
, ![]() определяются формулами
определяются формулами
![]() ,
,
![]() ,
, ![]() .
.
Отсюда следует, что
![]() ,
,
![]() . (9)
. (9)
Заменяя в (9) ![]() на
на ![]() , получаем
, получаем
![]() ,
,
![]() . (10)
. (10)
Отметим еще легко проверяемую формулу
![]() .
.
Формулы сложения для гиперболических функций легко получить из (9) и (10) соответствующих формул для тригонометрических функций от комплексного переменного. Например:
![]()
![]()
![]() .
.
Производные от этих функций вычисляются на основании формул (5), (7), (8):
 ,
,
![]() ,
,
![]()
![]() .
.
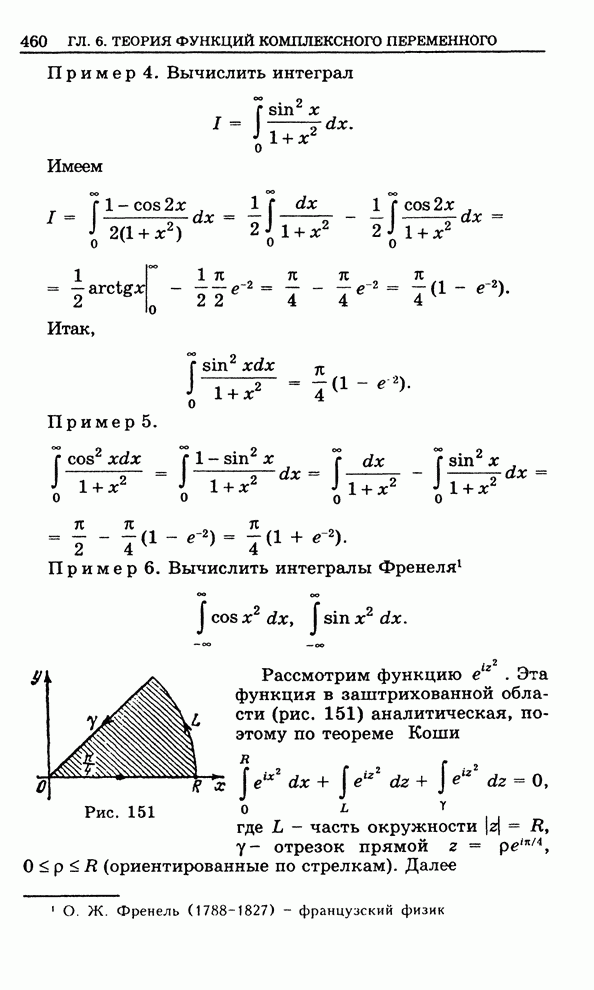
Пример. Выделить действительную и
мнимую части у функции ![]() и найти нули этой функции.
и найти нули этой функции.
Пусть ![]() ,
, ![]() .
.
Имеем ![]() .
.
Таким образом, ![]() ,
, ![]() .
.
Чтобы найти нули функции ![]() , мы должны приравнять
нулю ее действительную и мнимую части:
, мы должны приравнять
нулю ее действительную и мнимую части:
![]()
Решим эту систему. Так как ![]() для любого действительного
для любого действительного
![]() , то из
первого уравнения получаем
, то из
первого уравнения получаем ![]() .
.
Из второго уравнения при ![]() получаем, что
получаем, что ![]() . При
действительных
. При
действительных ![]() косинус
и синус не обращаются одновременно в нуль, поэтому при
косинус
и синус не обращаются одновременно в нуль, поэтому при ![]() система решений не имеет.
Если же
система решений не имеет.
Если же ![]() ,
то
,
то ![]() и
второе уравнение удовлетворяется при любых
и
второе уравнение удовлетворяется при любых ![]() . Таким образом, нули функции
. Таким образом, нули функции ![]() расположены на
действительной оси
расположены на
действительной оси ![]() и совпадают с нулями
и совпадают с нулями ![]() .
.
Замечание 3. Из этого утверждения
следует, что нули функции ![]() совпадают с нулями функции
совпадают с нулями функции ![]() , где
, где ![]() .
.
Замечание 4. Отметим еще § 6.15, посвященный линейной и дробно-линейной функциям; его можно читать и непосредственно после настоящего § 6.2.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. Обыкновенные дифференциальные уравнения
- 1.1. Задача, приводящая к дифференциальному уравнению
- 1.2. Общие понятия
- 1.2.1. Понятие обыкновенного дифференциального уравнения
- 1.2.2. Дифференциальное уравнение первого порядка
- 1.2.3. Задача Коши
- 1.2.4. Примеры дифференциальных уравнений первого порядка
- 1.2.5. Общий интеграл дифференциального уравнения первого порядка
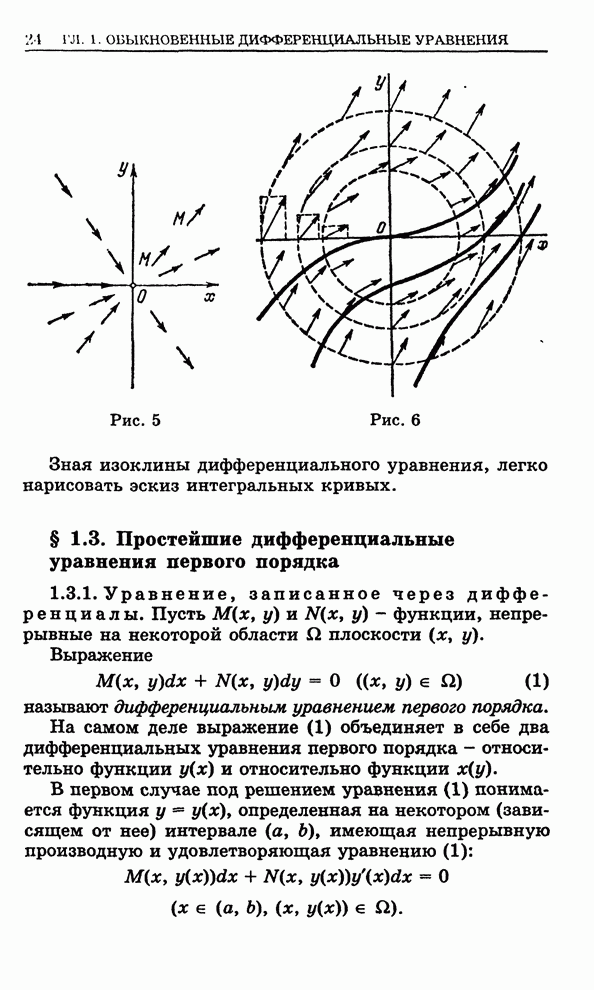
- 1.2.6. Поле направлений
- 1.3. Простейшие дифференциальные уравнения первого порядка
- 1.3.1. Уравнение, записанное через дифференциалы
- 1.3.2. Уравнения с разделенными переменными
- 1.3.3. Уравнения с разделяющимися переменными
- 1.3.4. Однородные уравнения
- 1.3.5. Линейное уравнение
- 1.3.6. Уравнение Бернулли
- 1.4. Теорема существования решения дифференциального уравнения первого порядка
- 1.5. Метрическое пространство
- 1.5.1. Понятие метрического пространства
- 1.5.2. Полное метрическое пространство
- 1.5.3. Принцип сжатых отображений
- 1.5.4. Приближенное значение корня функции
- 1.5.5. Метод Ньютона
- 1.6. Доказательство теоремы существования решения диффереацнального уравнения первого порядка
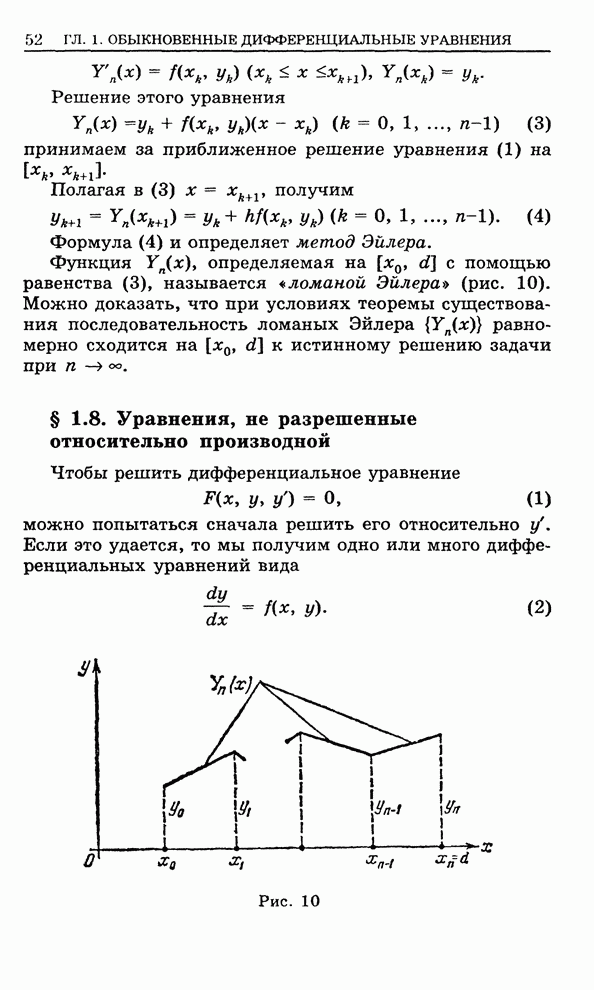
- 1.7. Метод Эйлера приближенного решения дифференциального уравнения первого порядка
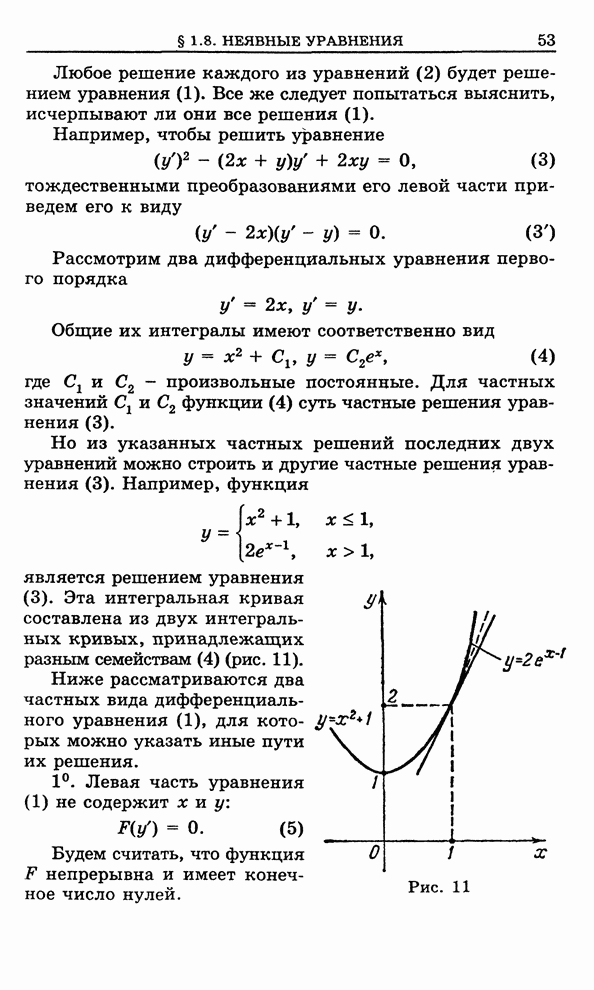
- 1.8. Уравнения, не разрешенные относительно производной
- 1.9. Особые решения
- 1.10. Огибающая семейства кривых
- 1.11. Дифференциальное уравнение второго порядка
- 1.12. Система из двух дифференциальных уравнений первого порядка
- 1.13. Дифференциальное уравнение n-го порядка
- 1.14. Понижение порядка дифференциального уравнения
- 1.15. Линейные уравнения высшего порядка
- 1.15.1. Понятие линейного уравнения высшего порядка
- 1.15.2. Фундаментальная система решений уравнения
- 1.15.3. Определитель Вронского
- 1.15.4. Структура общего решения
- 1.16. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- 1.16.1. Методы решения
- 1.16.2. Уравнение Эйлера
- 1.17. Метод вариации постоянных
- 1.18. Частное решение неоднородного уравнения с постоянными коэффициентами. Приложения
- 1.18.1. Методы нахождения частных решений
- 1.18.2. Дифференциальное уравнение колебания пружины
- 1.19. Системы дифференциальных уравнений. Фазовое пространство
- 1.20. Линейная однородная система дифференциальных уравнений
- 1.21. Общее решение линейной однородной системы дифференциальных уравнений с постоянными коэффициентами
- 1.22. Сведение системы уравнений к одному уравнению
- 1.23. Неоднородная система линейных дифференциальных уравнений с постоянными коэффициентами
- 1.24. Интегрирование дифференциальных уравнений с помощью степенных рядов
- 1.25. Элементы теории устойчивости
- 1.26. Классификация точек покоя
- Глава 2. Кратные интегралы
- 2.1. Введение
- 2.2. Сведения из теории меры Жордана
- 2.3. Свойства кратных интегралов. Теоремы существования
- 2.4. Сведение кратного интеграла к повторным
- 2.5. Доказательство существования интеграла от непрерывной функции
- 2.6. Замена переменных. Простейший случай
- 2.7. Замена переменных. Общий случай
- 2.8. Полярная система координат в плоскости
- 2.9. Полярная система координат в пространстве
- 2.10. Цилиндрические координаты
- 2.11. Площадь поверхности
- 2.12. Координаты центра масс
- 2.13. Несобственные интегралы
- 2.14. Несобственный интеграл с особенностями вдоль линии
- 2.15. Несобственный интеграл, зависящий от параметра
- Глава 3. Векторный анализ
- 3.1. Кусочно-гладкая ориентированная кривая
- 3.2. Криволинейный интеграл первого рода
- 3.3. Интеграл от вектора вдоль кривой
- 3.3.1. Поле вектора
- 3.3.2. Криволинейный интеграл от вектора вдоль кривой
- 3.3.3. Свойства криволинейных интегралов второго рода
- 3.4. Поле потенциала
- 3.4.1. Понятие потенциала и его свойства
- 3.4.2. Доказательство свойств потенциала
- 3.4.3. Ротор вектора
- 3.5. Дифференциальное уравнение в полных дифференциалах
- 3.6. Ориентация плоской области
- 3.7. Формула Грина
- 3.8. Интеграл по поверхности первого рода
- 3.9. Ориентация поверхности
- 3.10. Система координат и ориентация поверхности
- 3.11. Интеграл по ориентированной плоской области
- 3.12. Поток вектора через ориентированную поверхность
- 3.13. Дивергенция. Теорема Гаусса—Остроградского
- 3.14. Соленоидальное поле
- 3.15. Формула Стокса
- Глава 4. Ряды Фурье. Интеграл Фурье
- 4.1. Тригонометрические ряды
- 4.2. Сходимость тригонометрических рядов
- 4.3. Ряд Фурье
- 4.4. Признаки сходимости рядов Фурье
- 4.5. Ортогональные свойства тригонометрических функций
- 4.6. Коэффициенты Фурье
- 4.7. Оценка коэффициентов Фурье
- 4.8. Пространство функций со скалярным произведением
- 4.9. Ортогональная система функций
- 4.10. Полнота тригонометрических функций
- 4.11. Комплексная форма ряда Фурье
- 4.12. Понятие интеграла Фурье. Повторный интеграл Фурье
- 4.13. Косинус- и синус- преобразования Фурье
- 4.14. Примеры
- 4.15. Приближение интеграла Фурье
- 4.16. Сумма Фейера
- 4.17. Полнота систем функций в С и L2’
- 4.18. Сведения из теории кратных рядов Фурье
- Глава 5. Уравнения математической физики
- 5.1. Температура тела
- 5.2. Задача Дирихле
- 5.3. Задача Дирихле для круга
- 5.4. Задача Дирихле для полуплоскости
- 5.5. Уравнение теплопроводности в стержне
- 5.6. Теплопроводность для бесконечного стержня
- 5.7. Малые колебания струны
- 5.8. Колебание бесконечной струны. Формула Даламбера
- 5.9. Колебание круглой мембраны
- 5.10. Общая задача Штурма-Лиувилля
- 5.11. Интеграл энергии (Дирихле)
- 5.12. Применение преобразований Фурье
- Глава 6. Теория функций комплексного переменного
- 6.1. Понятие функции комплексного переменного
- 6.2. Производная функция комплексного переменного
- 6.3. Условия Даламбера-Эйлера (Коши-Римана)
- 6.4. Гармонические функции
- 6.5. Обратная функция
- 6.6. Интегрирование функций комплексного переменного
- 6.7. Формула Коши
- 6.8. Интеграл типа Коши
- 6.9. Степенной ряд
- 6.10. Ряд Лорана
- 6.11. Классификация изолированных особых точек. Вычеты
- 6.12. Классификация особых точек на бесконечности
- 6.13. Теорема о вычетах
- 6.14. Вычисление интегралов при помощи вычетов
- 6.15. Линейная функция. Дробно-линейная функция
- Глава 7. Операционное исчисление
- 7.1. Изображение Лапласа
- 7.2. Изображение простейших функций и свойства изображений
- 7.3. Приложения операционного исчисления
- 7.3.1. Операторное уравнение
- 7.3.2. Решение систем дифференциальных уравнений
- 7.3.3. Вычисление интегралов
- Глава 8. Обобщенные функции
- 8.1. Понятие обобщенной функции
- 8.2. Операции над обобщенными функциями
- 8.3. Преобразование Фурье обобщенных функций