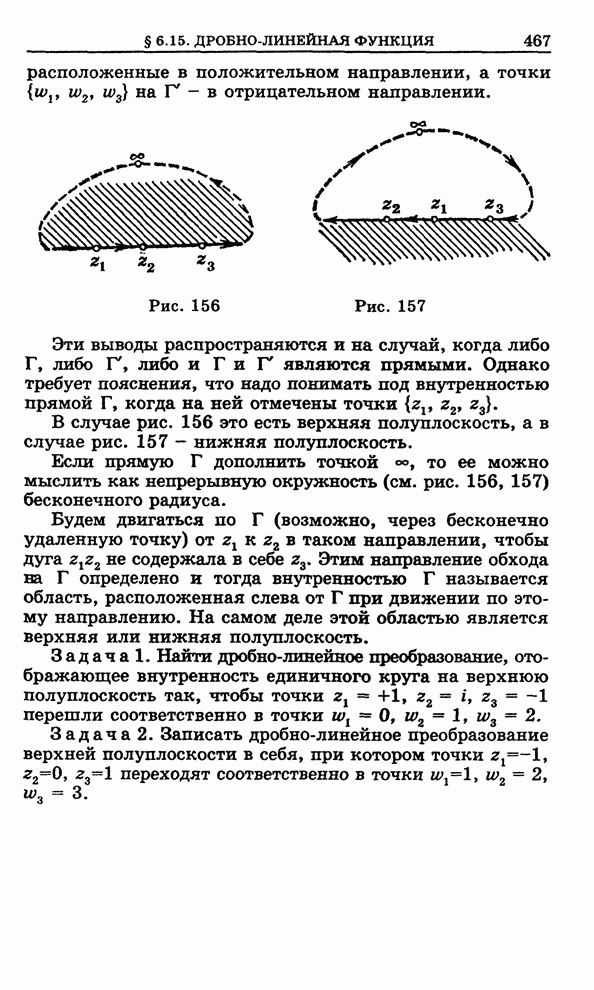
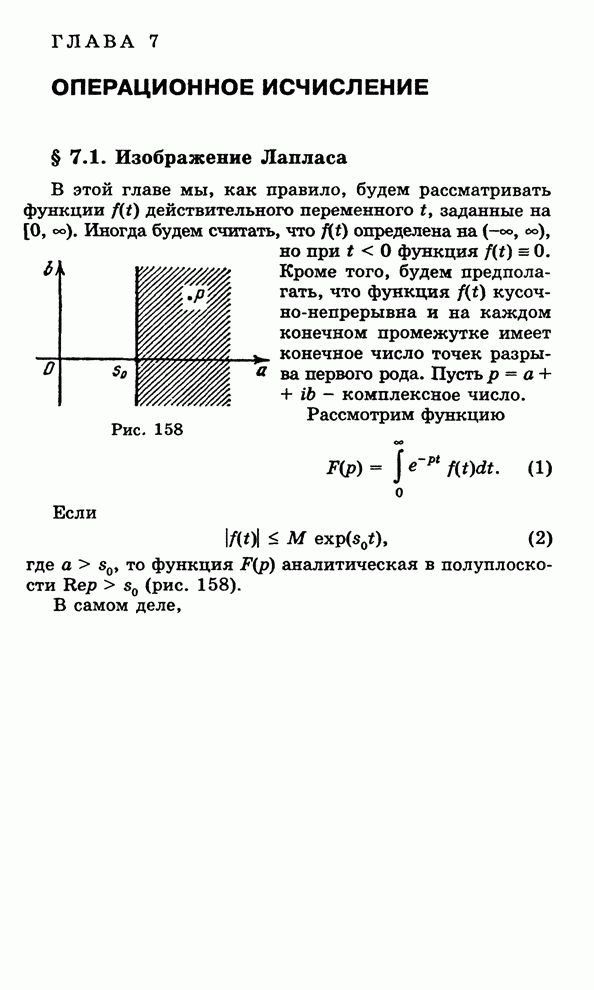
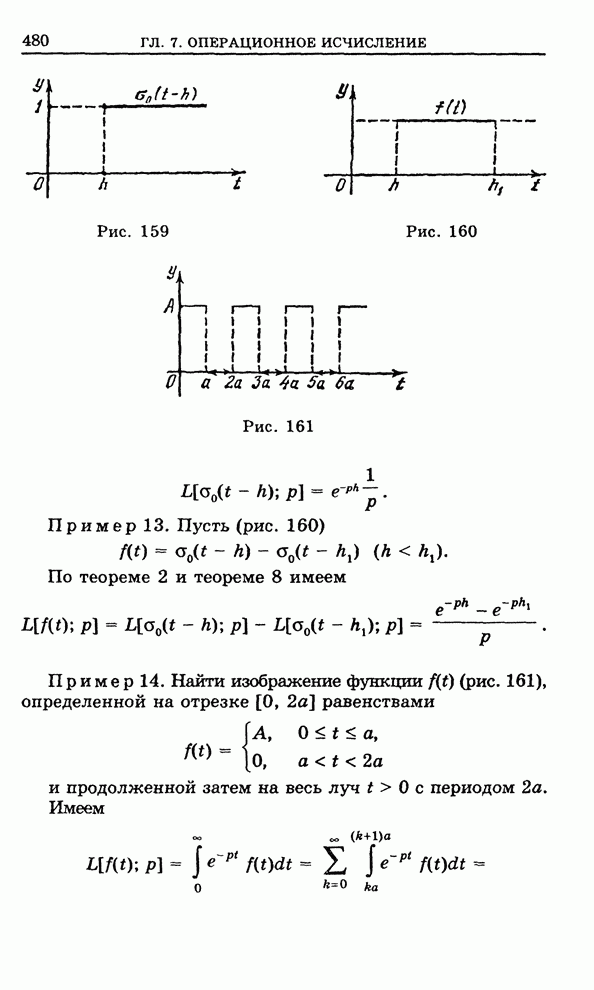
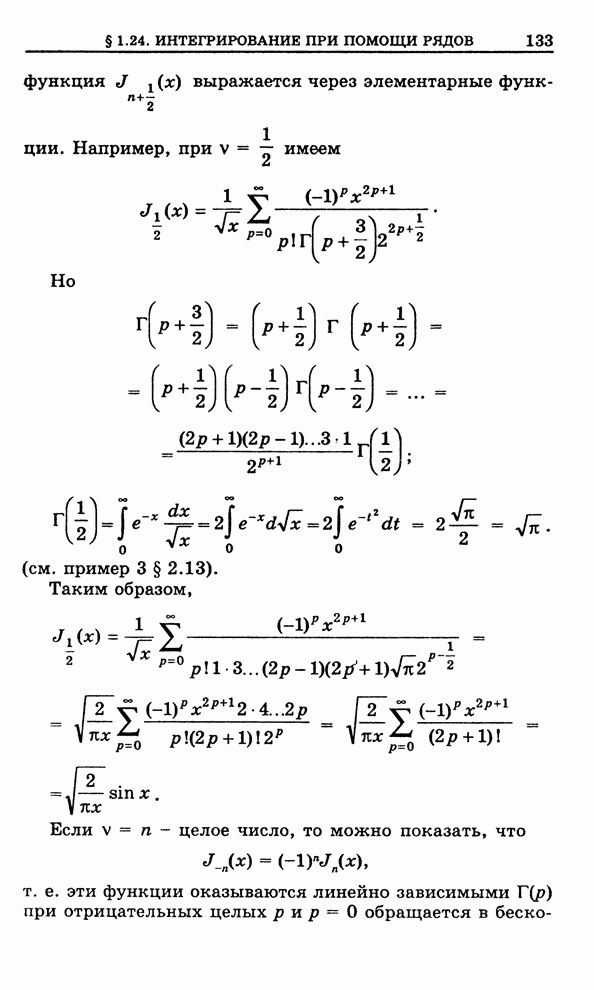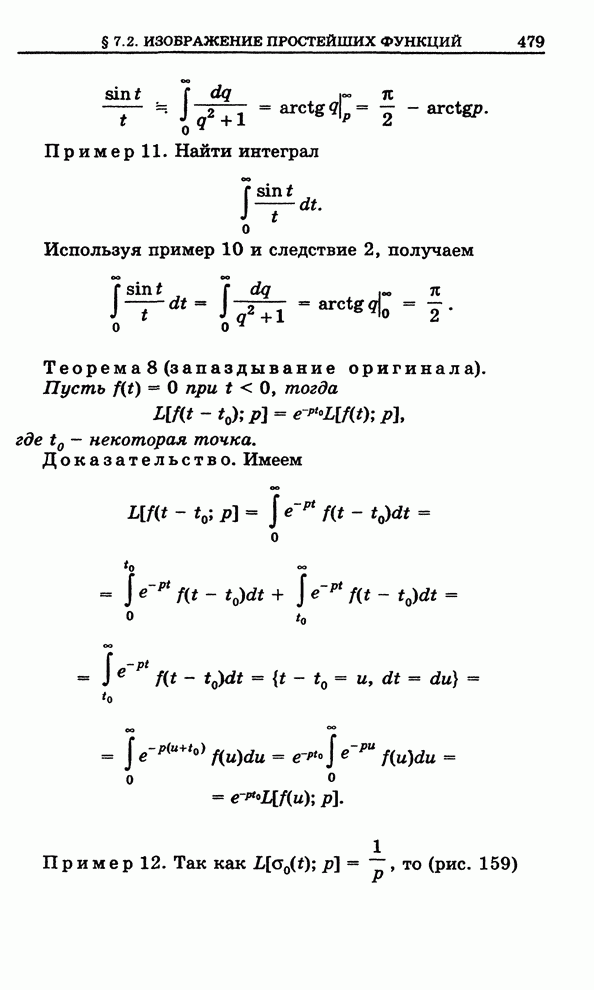| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
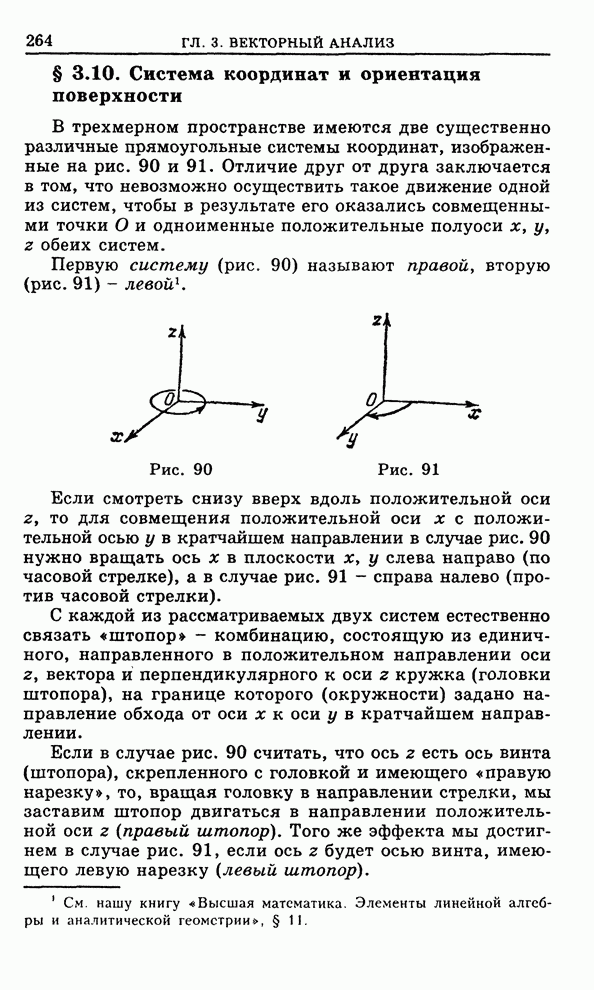
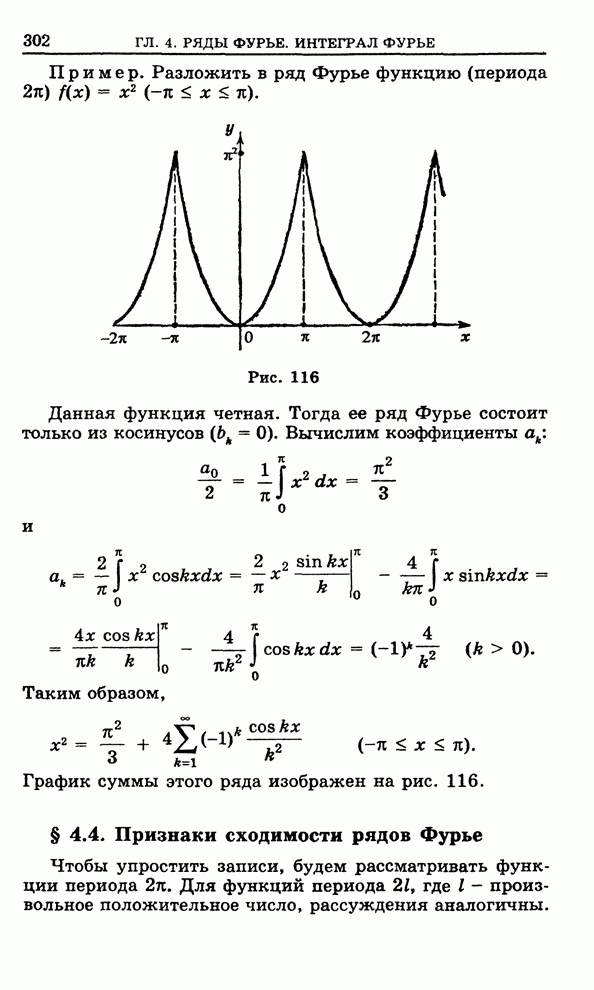
ГЛАВА 6 ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
§ 6.1. Понятие функции комплексного переменного
Понятие комплексного числа было
рассмотрено в нашей книге «Высшая математика. Дифференциальное и интегральное
исчисление», глава 5. Там же были рассмотрены многочлены ![]() от комплексного
переменного. Многочлен является простейшим примером функции комплексного
переменного.
от комплексного
переменного. Многочлен является простейшим примером функции комплексного
переменного.
Комплексные числа мы условились изображать точками плоскости, где задана прямоугольная система координат.
Дадим понятие функции от комплексного переменного.
Пусть даны две плоскости
комплексных чисел ![]() и
и ![]() (рис. 129). Рассмотрим некоторое
множество
(рис. 129). Рассмотрим некоторое
множество

Рис. 129
точек
![]() в
плоскости
в
плоскости ![]() и
множество
и
множество ![]() в
плоскости
в
плоскости ![]() .
Если каждому числу
.
Если каждому числу ![]() по некоторому закону поставлено в
соответствие определенное комплексное число
по некоторому закону поставлено в
соответствие определенное комплексное число ![]() , то говорят, что на множестве
, то говорят, что на множестве ![]() задана
однозначная функция комплексного переменного, отображающая множество
задана
однозначная функция комплексного переменного, отображающая множество ![]() в множество
в множество
![]() .
Символически это обозначают так:
.
Символически это обозначают так:
![]()
Множество ![]() называют областью
определения функции
называют областью
определения функции ![]() . Если каждая точка множества
. Если каждая точка множества ![]() является значением
функции, то говорят, что
является значением
функции, то говорят, что ![]() - область значений этой функции или образ
множества
- область значений этой функции или образ
множества ![]() при
помощи функции
при
помощи функции ![]() .
В этом случае говорят еще, что функция
.
В этом случае говорят еще, что функция ![]() отображает
отображает ![]() на
на ![]() .
.
Функцию ![]() можно записать в виде
можно записать в виде
![]()
![]() ,
,
где
![]() ,
,
![]()
![]() ,
,
-
действительные функции от переменных ![]() .
.
Если каждому ![]() соответствует несколько
разных значений
соответствует несколько
разных значений ![]() ,
то функция
,
то функция ![]() называется
многозначной.
называется
многозначной.
Понятия предела и непрерывности функции комплексного переменного вводятся аналогично, как это делается для функции действительного переменного, необходимо лишь всюду вместо абсолютной величины писать модуль комплексного числа.
Говорят, что функция
![]()
имеет
предел в точке ![]() ,
равный числу
,
равный числу ![]() ,
если
,
если
![]() . (1)
. (1)
В этом случае пишут
![]() .
.
На языке функций ![]() и
и ![]() свойство (1)
записывается в виде равенства
свойство (1)
записывается в виде равенства
![]() (2)
(2)
или, что все равно, в виде двух равенств
![]() ,
, ![]() . (3)
. (3)
Для комплексных функций ![]() и
и ![]() имеют место
свойства, аналогичные соответствующим свойствам действительных функций:
имеют место
свойства, аналогичные соответствующим свойствам действительных функций:
 (4)
(4)
Как обычно, формулы (4) надо понимать в том смысле, что если пределы, стоящие в их правых частях, существуют, то существуют также пределы, стоящие в их левых частях, и выполняется соответствующее равенство.
Функция ![]() называется непрерывной
в точке
называется непрерывной
в точке ![]() ,
если для нее выполняется свойство
,
если для нее выполняется свойство
![]() ,
,
![]() ,
, ![]() . (5)
. (5)
Таким образом, непрерывная в
точке ![]() функция
должна быть определена в окрестности этой точки, в том числе и в ней самой и
должно выполняться равенство (5). Равенство (5) эквивалентно двум равенствам:
функция
должна быть определена в окрестности этой точки, в том числе и в ней самой и
должно выполняться равенство (5). Равенство (5) эквивалентно двум равенствам:
![]() ,
,
![]() .
.
Следовательно, непрерывность ![]() в точке
в точке ![]() эквивалентна
непрерывности функций
эквивалентна
непрерывности функций ![]() и
и ![]() в точке
в точке ![]() .
.
Из свойств (4) следует, что
сумма, разность, произведение и частное непрерывных в точке ![]() комплексных функций
комплексных функций
![]() и
и ![]() есть непрерывная
функция в этой точке. В случае частного надо в этой формулировке считать, что
есть непрерывная
функция в этой точке. В случае частного надо в этой формулировке считать, что ![]() .
.
Пример 1. Функция ![]() задана на всей
комплексной плоскости. Ее значения – неотрицательные числа. Эта функция
непрерывна во всех точках комплексной плоскости:
задана на всей
комплексной плоскости. Ее значения – неотрицательные числа. Эта функция
непрерывна во всех точках комплексной плоскости:
![]()
![]() .
.
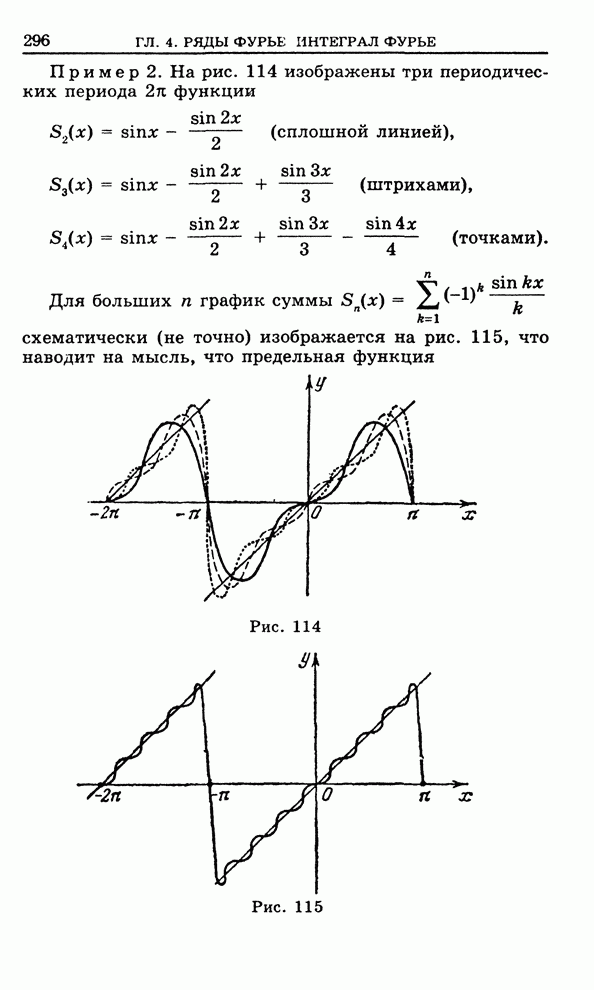
Пример 2.
![]()
![]() . (6)
. (6)
Эта функция многозначная
(бесконечнозначная); ![]() - главное значение аргумента
- главное значение аргумента ![]() .
.
Пример 3. Функция ![]() . Она непрерывна:
. Она непрерывна:
![]()
![]() .
.

Рис. 130
Но тогда и функция ![]()
![]() непрерывна как произведение
конечного числа непрерывных функций.
непрерывна как произведение
конечного числа непрерывных функций.
Множество комплексных чисел ![]() будем называть областью,
если
будем называть областью,
если ![]() ,
как множество точек плоскости, открыто и связно.
,
как множество точек плоскости, открыто и связно.
Область ![]() называется односвязной,
если любая непрерывная замкнутая самонепересекающаяся кривая, проведенная в
называется односвязной,
если любая непрерывная замкнутая самонепересекающаяся кривая, проведенная в ![]() , ограничивает
некоторую область
, ограничивает
некоторую область ![]() , целиком принадлежащую
, целиком принадлежащую ![]() . Область, не
обладающую этим свойством, будем называть многосвязной.
. Область, не
обладающую этим свойством, будем называть многосвязной.
Пример 4. Кольцо ![]() - многосвязная
(двусвязная) область. Кривая
- многосвязная
(двусвязная) область. Кривая ![]() (рис. 130) принадлежит кольцу, но
ограничивает область, не входящую целиком в него.
(рис. 130) принадлежит кольцу, но
ограничивает область, не входящую целиком в него.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. Обыкновенные дифференциальные уравнения
- 1.1. Задача, приводящая к дифференциальному уравнению
- 1.2. Общие понятия
- 1.2.1. Понятие обыкновенного дифференциального уравнения
- 1.2.2. Дифференциальное уравнение первого порядка
- 1.2.3. Задача Коши
- 1.2.4. Примеры дифференциальных уравнений первого порядка
- 1.2.5. Общий интеграл дифференциального уравнения первого порядка
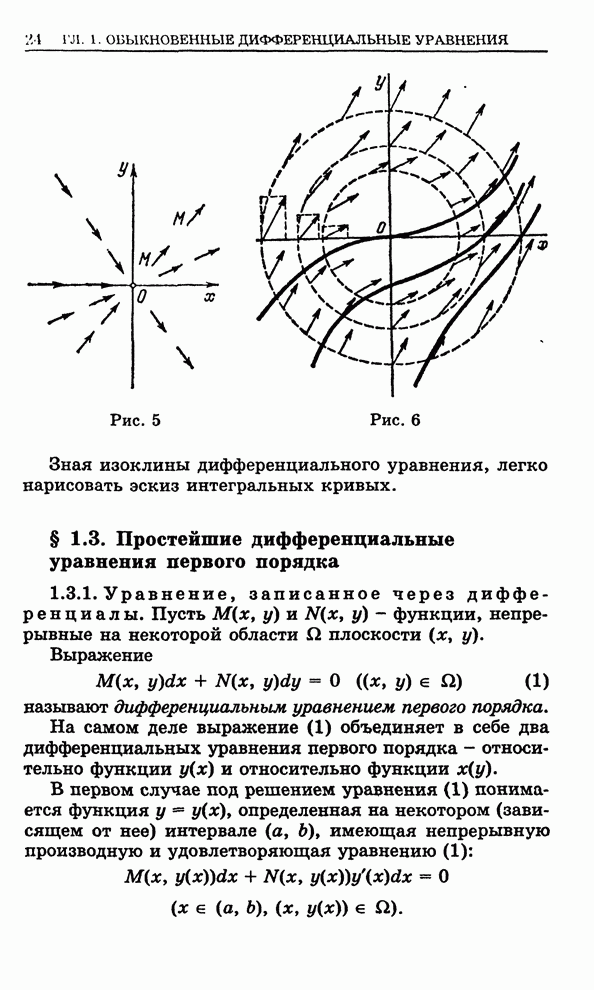
- 1.2.6. Поле направлений
- 1.3. Простейшие дифференциальные уравнения первого порядка
- 1.3.1. Уравнение, записанное через дифференциалы
- 1.3.2. Уравнения с разделенными переменными
- 1.3.3. Уравнения с разделяющимися переменными
- 1.3.4. Однородные уравнения
- 1.3.5. Линейное уравнение
- 1.3.6. Уравнение Бернулли
- 1.4. Теорема существования решения дифференциального уравнения первого порядка
- 1.5. Метрическое пространство
- 1.5.1. Понятие метрического пространства
- 1.5.2. Полное метрическое пространство
- 1.5.3. Принцип сжатых отображений
- 1.5.4. Приближенное значение корня функции
- 1.5.5. Метод Ньютона
- 1.6. Доказательство теоремы существования решения диффереацнального уравнения первого порядка
- 1.7. Метод Эйлера приближенного решения дифференциального уравнения первого порядка
- 1.8. Уравнения, не разрешенные относительно производной
- 1.9. Особые решения
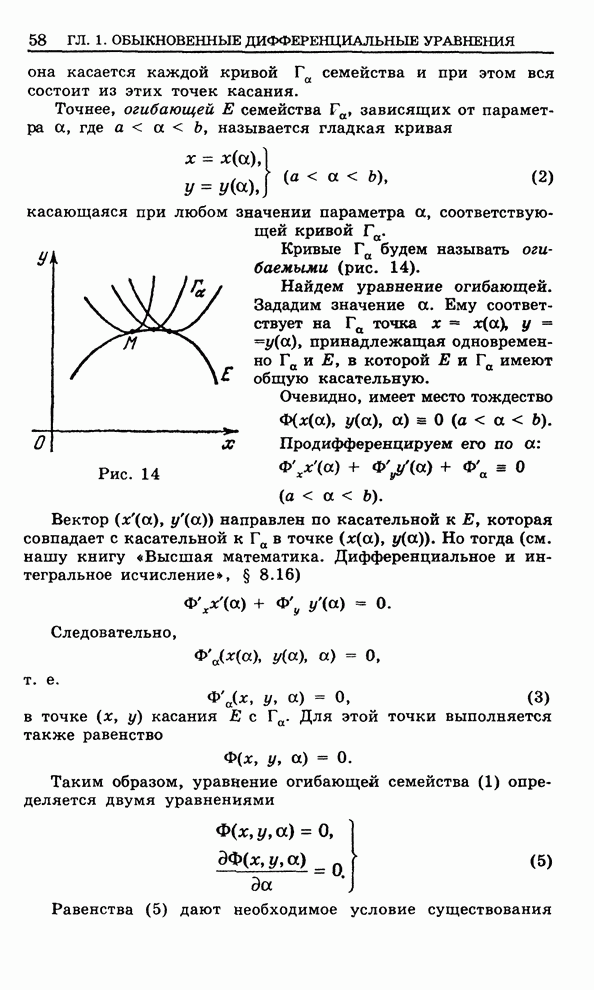
- 1.10. Огибающая семейства кривых
- 1.11. Дифференциальное уравнение второго порядка
- 1.12. Система из двух дифференциальных уравнений первого порядка
- 1.13. Дифференциальное уравнение n-го порядка
- 1.14. Понижение порядка дифференциального уравнения
- 1.15. Линейные уравнения высшего порядка
- 1.15.1. Понятие линейного уравнения высшего порядка
- 1.15.2. Фундаментальная система решений уравнения
- 1.15.3. Определитель Вронского
- 1.15.4. Структура общего решения
- 1.16. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- 1.16.1. Методы решения
- 1.16.2. Уравнение Эйлера
- 1.17. Метод вариации постоянных
- 1.18. Частное решение неоднородного уравнения с постоянными коэффициентами. Приложения
- 1.18.1. Методы нахождения частных решений
- 1.18.2. Дифференциальное уравнение колебания пружины
- 1.19. Системы дифференциальных уравнений. Фазовое пространство
- 1.20. Линейная однородная система дифференциальных уравнений
- 1.21. Общее решение линейной однородной системы дифференциальных уравнений с постоянными коэффициентами
- 1.22. Сведение системы уравнений к одному уравнению
- 1.23. Неоднородная система линейных дифференциальных уравнений с постоянными коэффициентами
- 1.24. Интегрирование дифференциальных уравнений с помощью степенных рядов
- 1.25. Элементы теории устойчивости
- 1.26. Классификация точек покоя
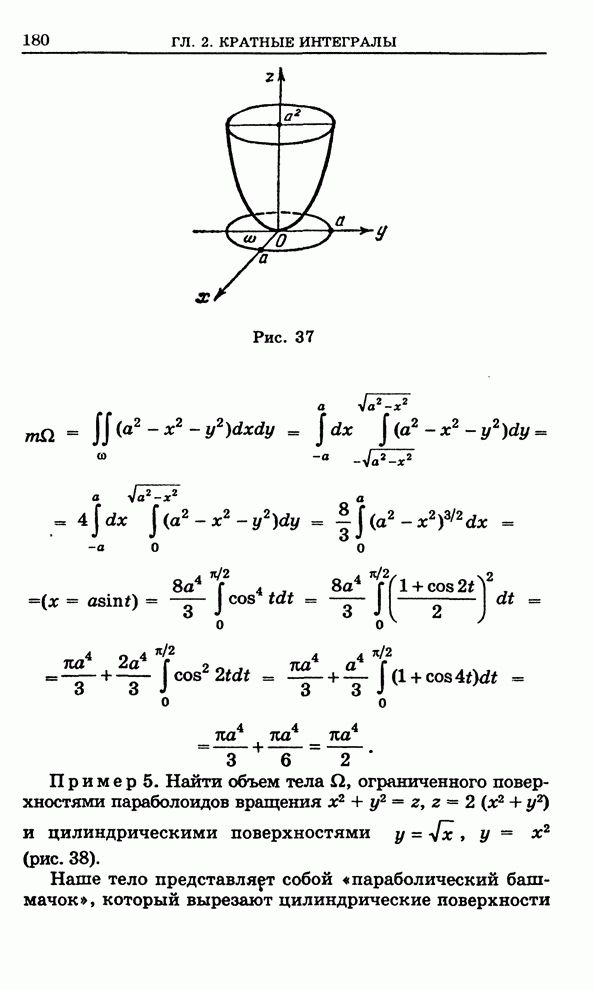
- Глава 2. Кратные интегралы
- 2.1. Введение
- 2.2. Сведения из теории меры Жордана
- 2.3. Свойства кратных интегралов. Теоремы существования
- 2.4. Сведение кратного интеграла к повторным
- 2.5. Доказательство существования интеграла от непрерывной функции
- 2.6. Замена переменных. Простейший случай
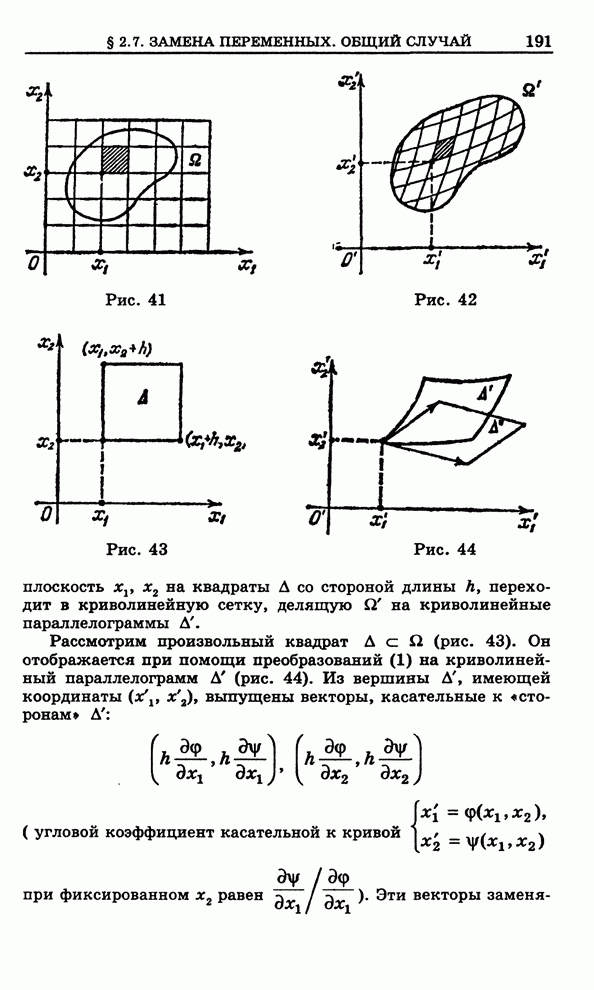
- 2.7. Замена переменных. Общий случай
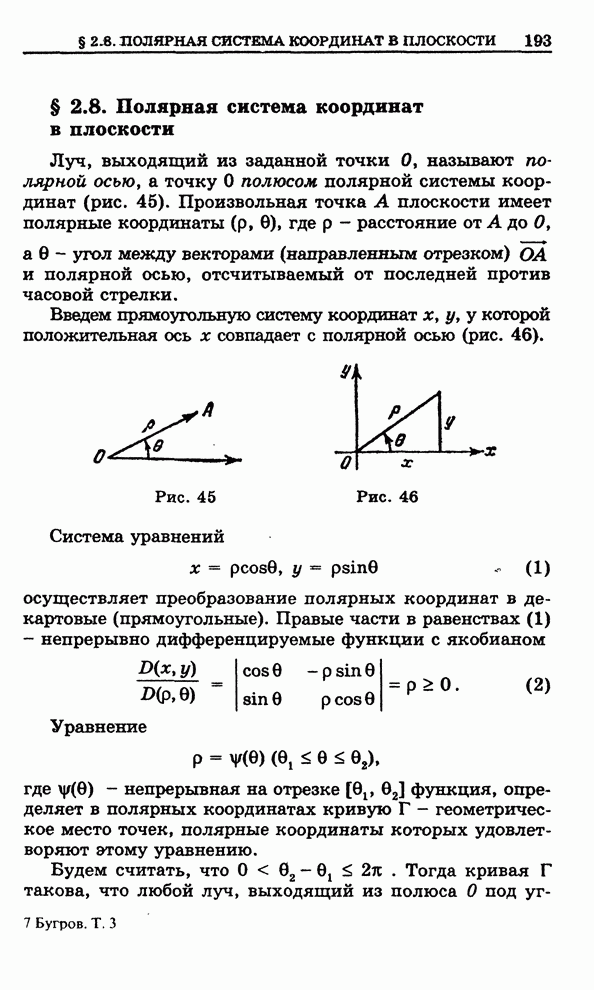
- 2.8. Полярная система координат в плоскости
- 2.9. Полярная система координат в пространстве
- 2.10. Цилиндрические координаты
- 2.11. Площадь поверхности
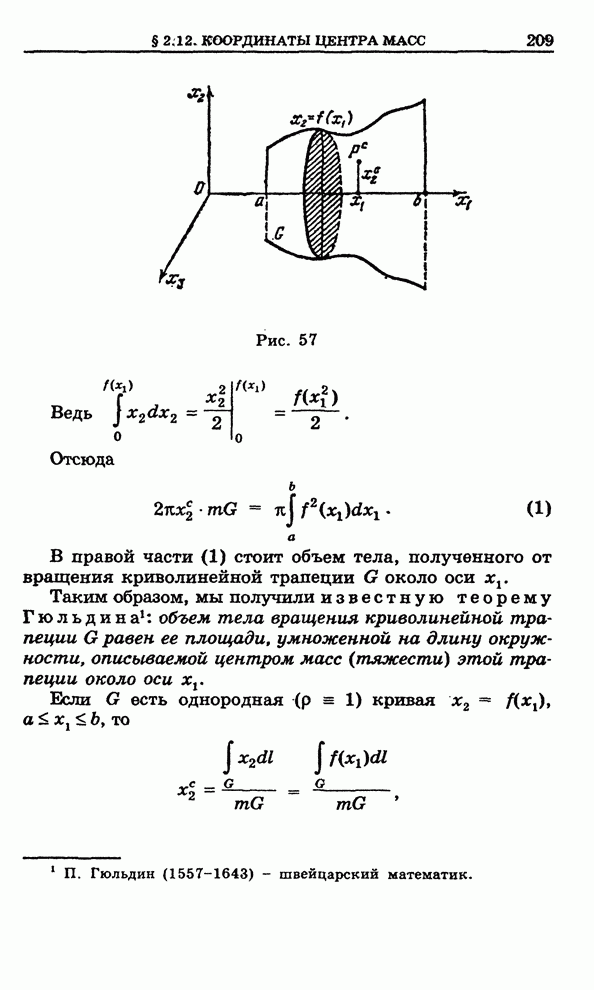
- 2.12. Координаты центра масс
- 2.13. Несобственные интегралы
- 2.14. Несобственный интеграл с особенностями вдоль линии
- 2.15. Несобственный интеграл, зависящий от параметра
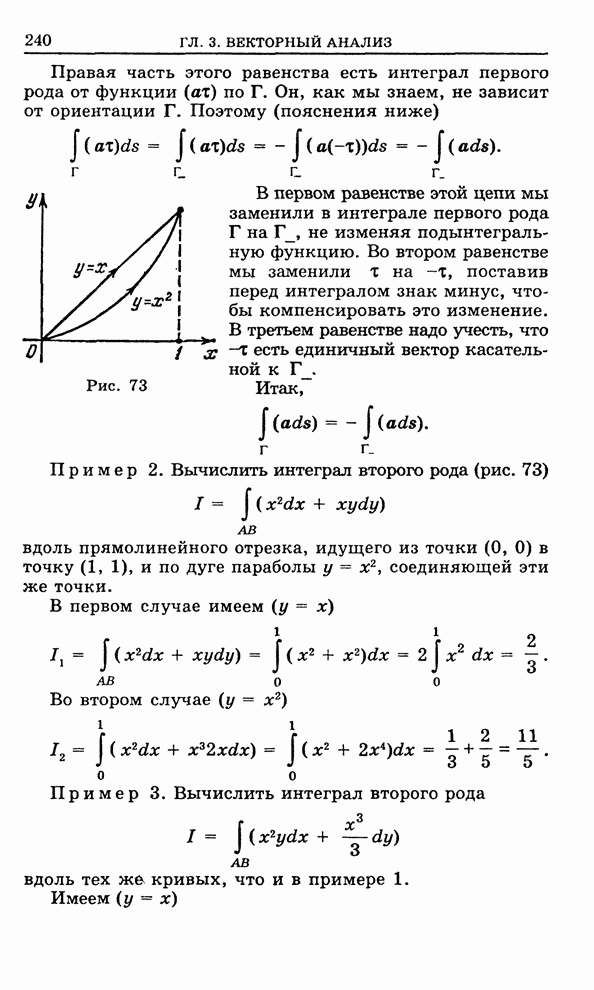
- Глава 3. Векторный анализ
- 3.1. Кусочно-гладкая ориентированная кривая
- 3.2. Криволинейный интеграл первого рода
- 3.3. Интеграл от вектора вдоль кривой
- 3.3.1. Поле вектора
- 3.3.2. Криволинейный интеграл от вектора вдоль кривой
- 3.3.3. Свойства криволинейных интегралов второго рода
- 3.4. Поле потенциала
- 3.4.1. Понятие потенциала и его свойства
- 3.4.2. Доказательство свойств потенциала
- 3.4.3. Ротор вектора
- 3.5. Дифференциальное уравнение в полных дифференциалах
- 3.6. Ориентация плоской области
- 3.7. Формула Грина
- 3.8. Интеграл по поверхности первого рода
- 3.9. Ориентация поверхности
- 3.10. Система координат и ориентация поверхности
- 3.11. Интеграл по ориентированной плоской области
- 3.12. Поток вектора через ориентированную поверхность
- 3.13. Дивергенция. Теорема Гаусса—Остроградского
- 3.14. Соленоидальное поле
- 3.15. Формула Стокса
- Глава 4. Ряды Фурье. Интеграл Фурье
- 4.1. Тригонометрические ряды
- 4.2. Сходимость тригонометрических рядов
- 4.3. Ряд Фурье
- 4.4. Признаки сходимости рядов Фурье
- 4.5. Ортогональные свойства тригонометрических функций
- 4.6. Коэффициенты Фурье
- 4.7. Оценка коэффициентов Фурье
- 4.8. Пространство функций со скалярным произведением
- 4.9. Ортогональная система функций
- 4.10. Полнота тригонометрических функций
- 4.11. Комплексная форма ряда Фурье
- 4.12. Понятие интеграла Фурье. Повторный интеграл Фурье
- 4.13. Косинус- и синус- преобразования Фурье
- 4.14. Примеры
- 4.15. Приближение интеграла Фурье
- 4.16. Сумма Фейера
- 4.17. Полнота систем функций в С и L2’
- 4.18. Сведения из теории кратных рядов Фурье
- Глава 5. Уравнения математической физики
- 5.1. Температура тела
- 5.2. Задача Дирихле
- 5.3. Задача Дирихле для круга
- 5.4. Задача Дирихле для полуплоскости
- 5.5. Уравнение теплопроводности в стержне
- 5.6. Теплопроводность для бесконечного стержня
- 5.7. Малые колебания струны
- 5.8. Колебание бесконечной струны. Формула Даламбера
- 5.9. Колебание круглой мембраны
- 5.10. Общая задача Штурма-Лиувилля
- 5.11. Интеграл энергии (Дирихле)
- 5.12. Применение преобразований Фурье
- Глава 6. Теория функций комплексного переменного
- 6.1. Понятие функции комплексного переменного
- 6.2. Производная функция комплексного переменного
- 6.3. Условия Даламбера-Эйлера (Коши-Римана)
- 6.4. Гармонические функции
- 6.5. Обратная функция
- 6.6. Интегрирование функций комплексного переменного
- 6.7. Формула Коши
- 6.8. Интеграл типа Коши
- 6.9. Степенной ряд
- 6.10. Ряд Лорана
- 6.11. Классификация изолированных особых точек. Вычеты
- 6.12. Классификация особых точек на бесконечности
- 6.13. Теорема о вычетах
- 6.14. Вычисление интегралов при помощи вычетов
- 6.15. Линейная функция. Дробно-линейная функция
- Глава 7. Операционное исчисление
- 7.1. Изображение Лапласа
- 7.2. Изображение простейших функций и свойства изображений
- 7.3. Приложения операционного исчисления
- 7.3.1. Операторное уравнение
- 7.3.2. Решение систем дифференциальных уравнений
- 7.3.3. Вычисление интегралов
- Глава 8. Обобщенные функции
- 8.1. Понятие обобщенной функции
- 8.2. Операции над обобщенными функциями
- 8.3. Преобразование Фурье обобщенных функций