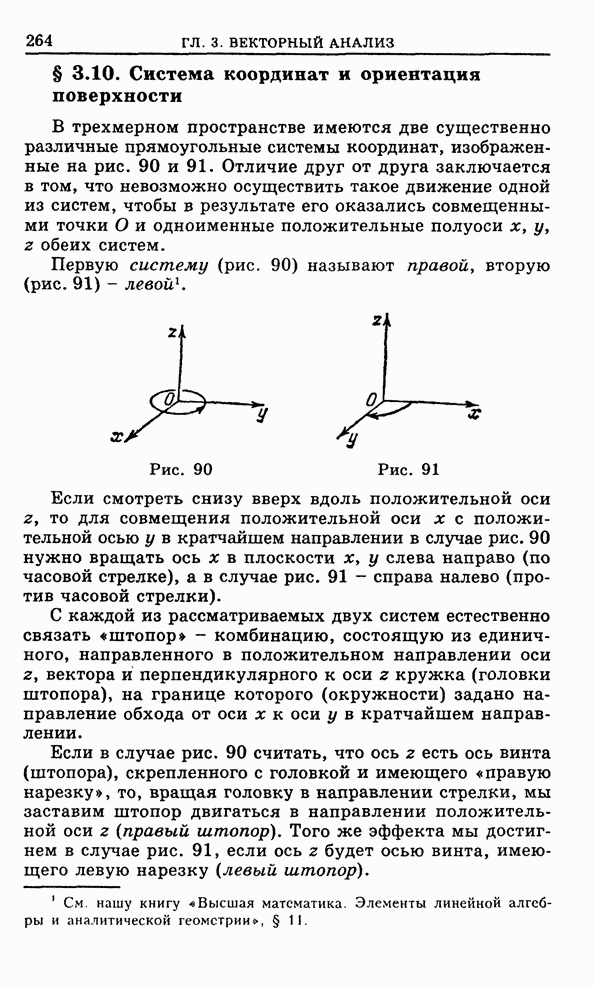
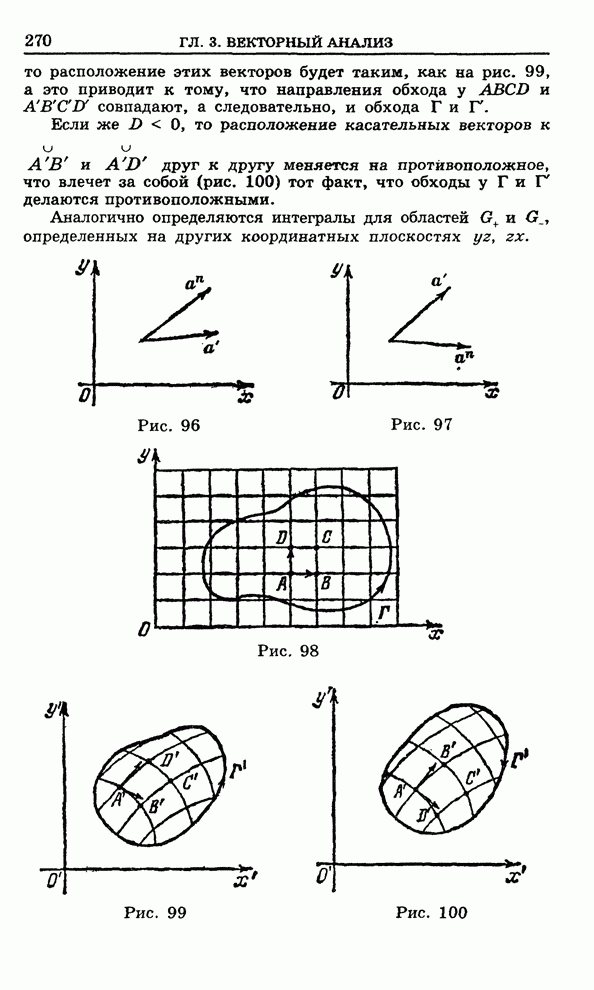
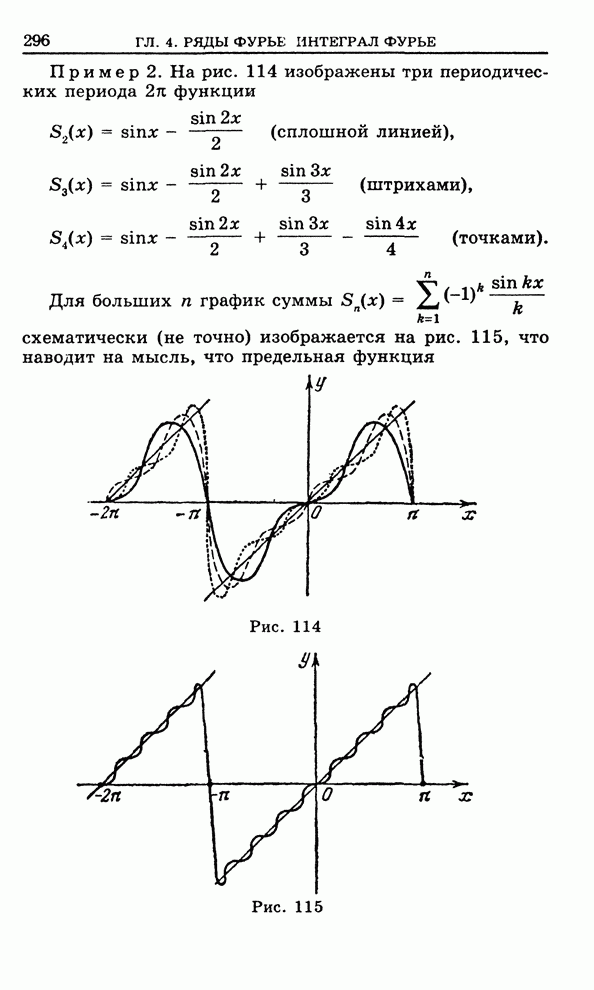
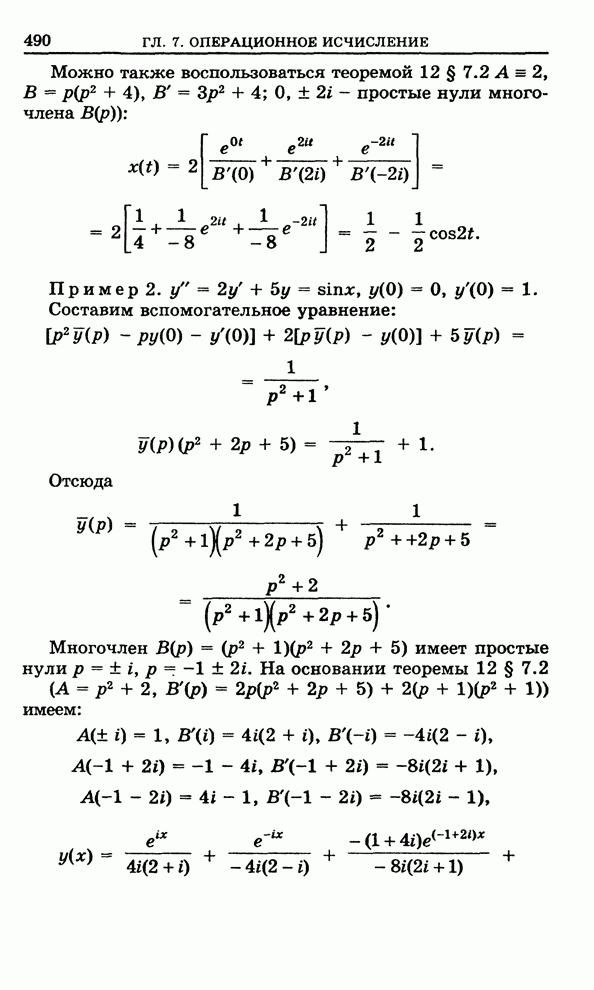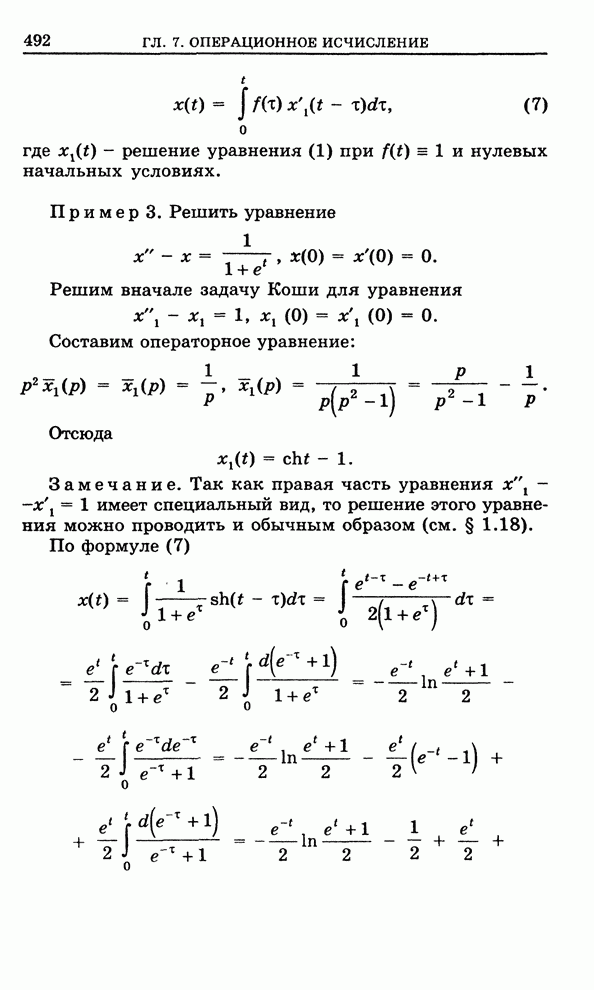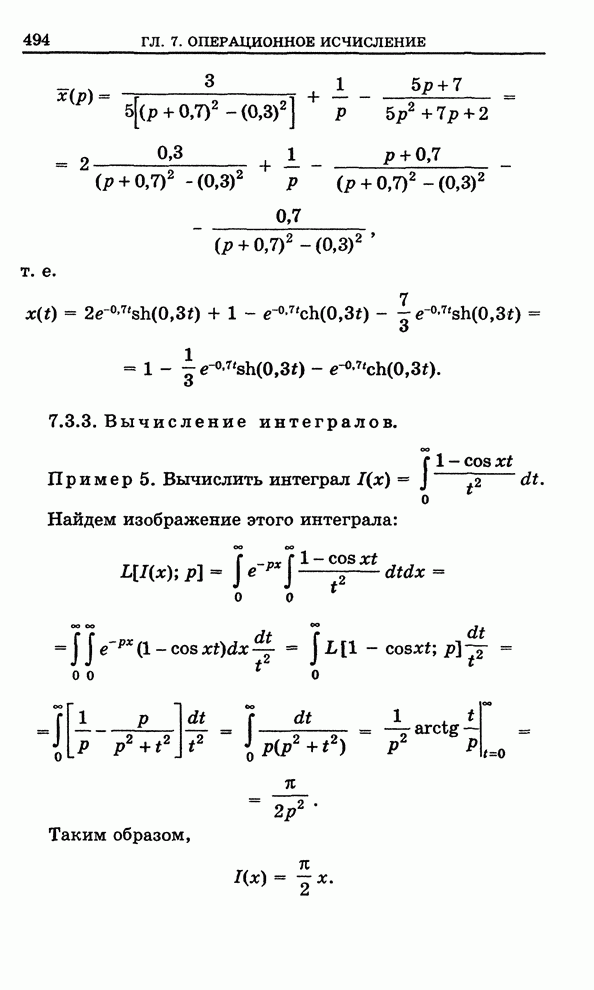| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 6.14. Вычисление интегралов при помощи вычетов
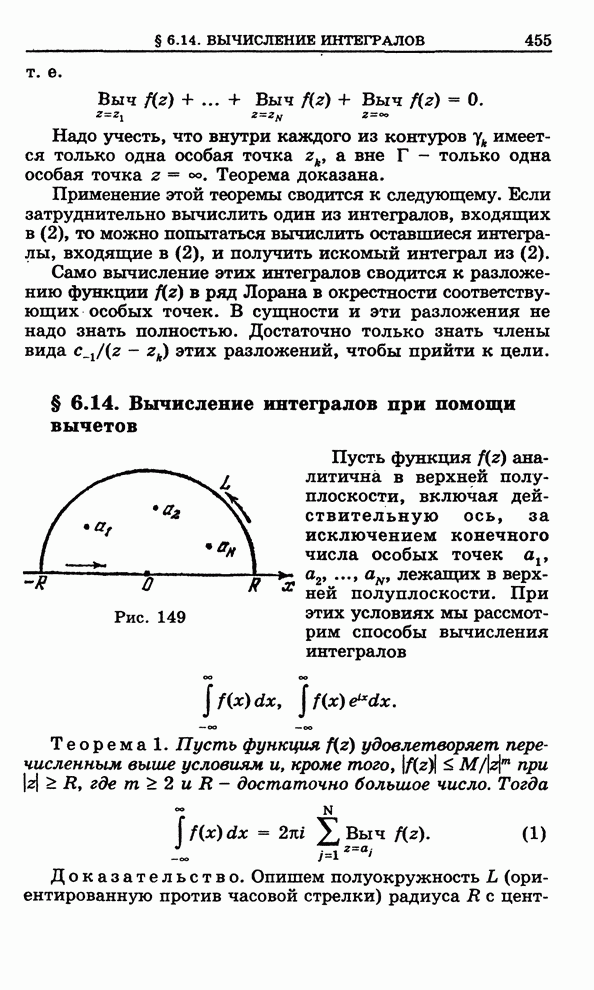
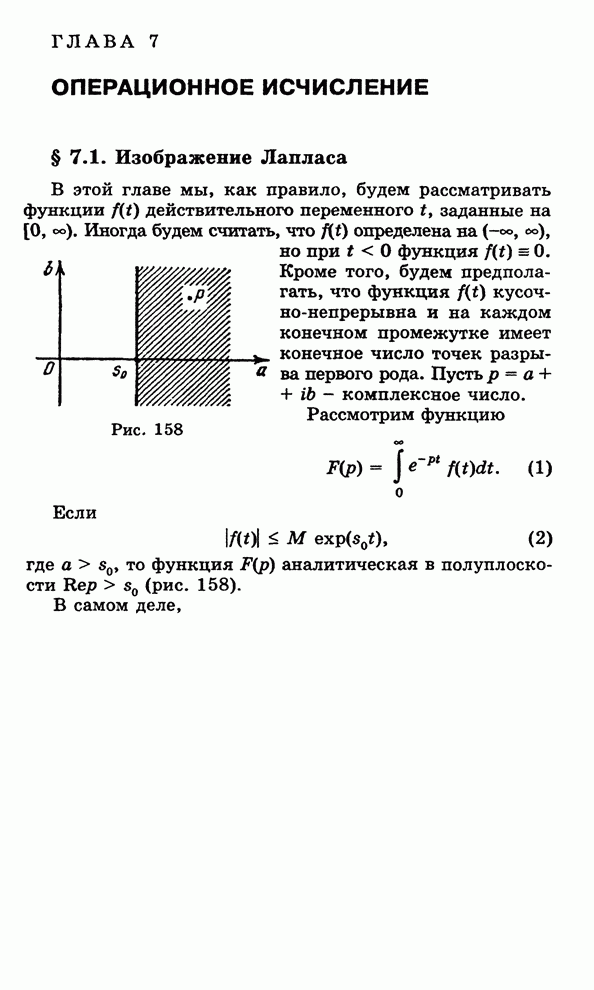
Пусть функция ![]() аналитична в верхней полуплоскости,
включая действительную ось, за исключением конечного числа особых точек
аналитична в верхней полуплоскости,
включая действительную ось, за исключением конечного числа особых точек ![]() , лежащих в верхней
полуплоскости. При этих условиях мы рассмотрим способы вычисления интегралов
, лежащих в верхней
полуплоскости. При этих условиях мы рассмотрим способы вычисления интегралов
 ,
,
 .
.
Теорема 1. Пусть функция ![]() удовлетворяет
перечисленным выше условиям и, кроме того,
удовлетворяет
перечисленным выше условиям и, кроме того, ![]() при
при ![]() , где
, где ![]() и
и ![]() - достаточно
большое число. Тогда
- достаточно
большое число. Тогда
 . (1)
. (1)
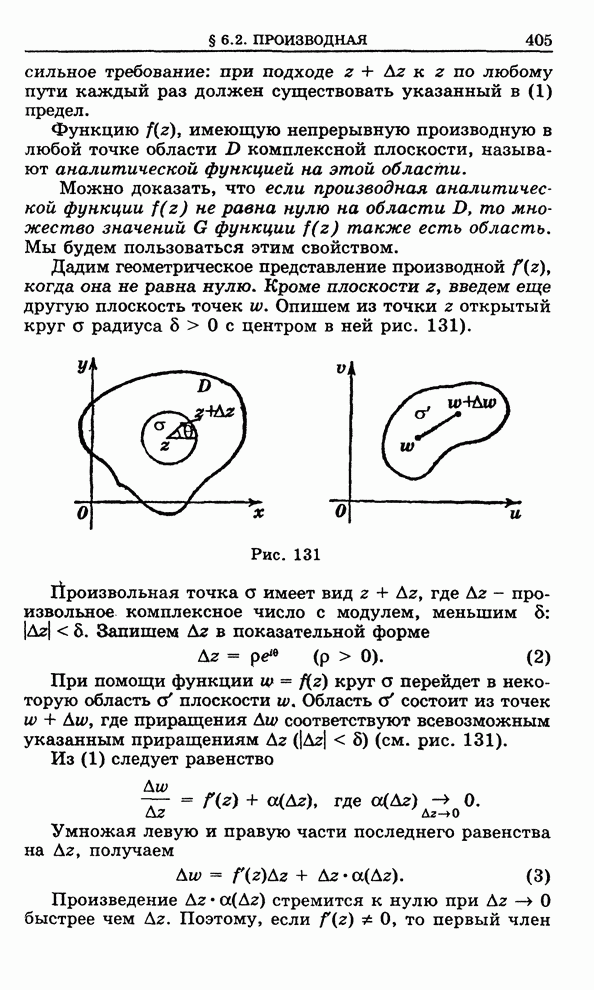
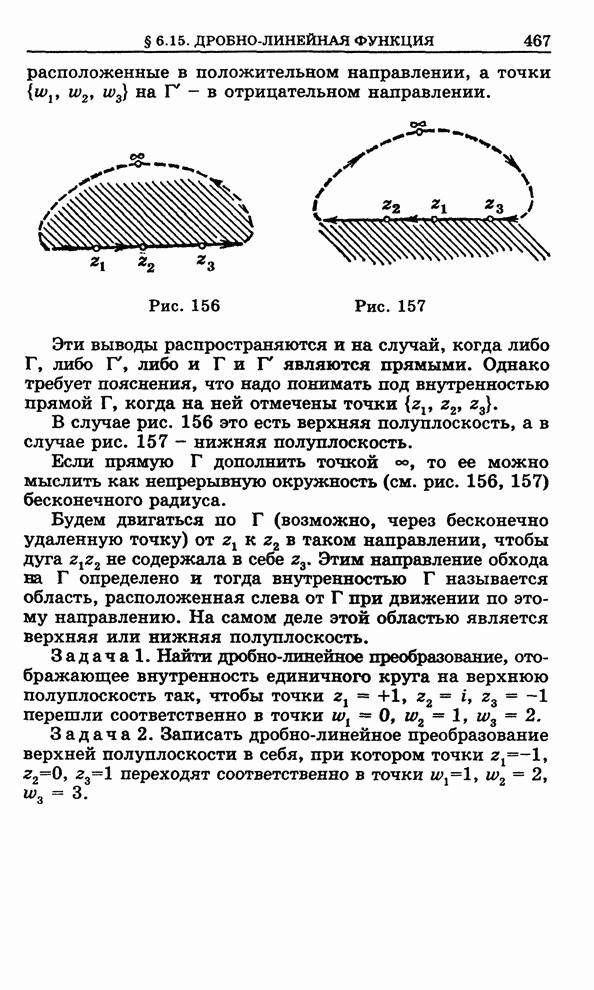
Доказательство. Опишем
полуокружность ![]() (ориентированную
против часовой стрелки) радиуса
(ориентированную
против часовой стрелки) радиуса ![]() с центром в точке
с центром в точке ![]() так, чтобы все особые точки
функции
так, чтобы все особые точки
функции ![]() попали
внутрь
попали
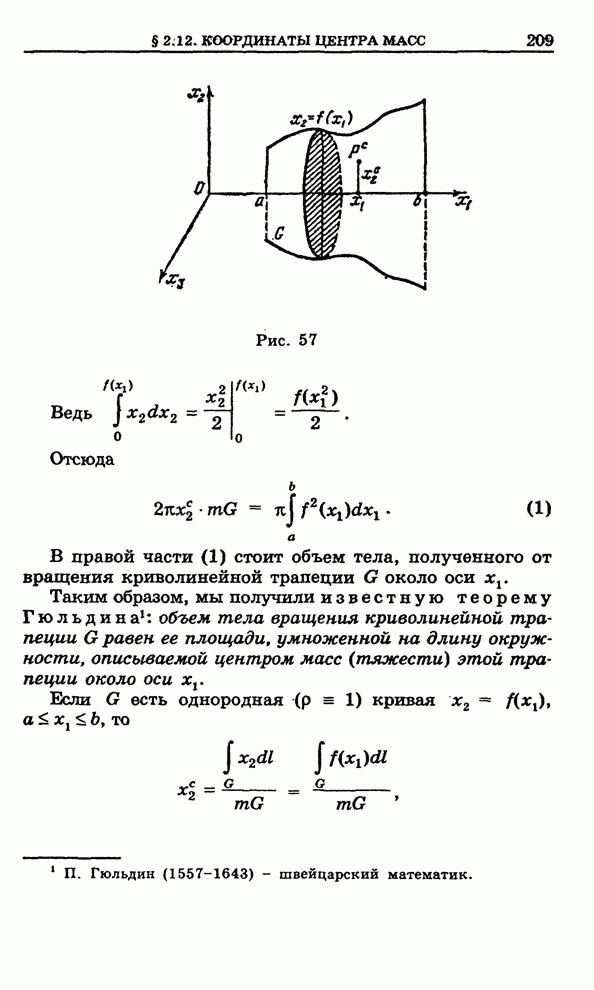
внутрь ![]() (рис.
149). В силу теоремы 1 § 6.13
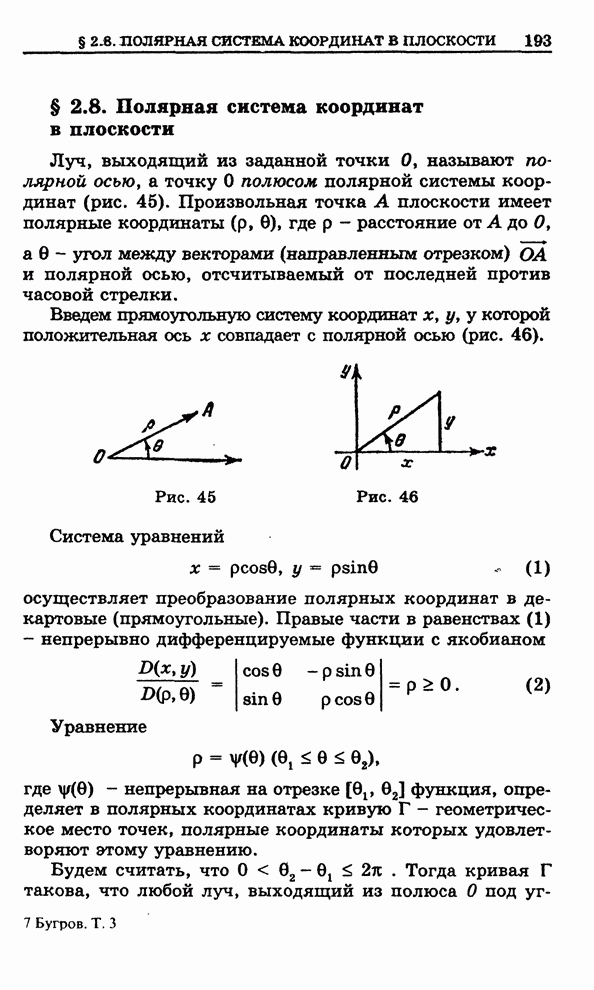
(рис.
149). В силу теоремы 1 § 6.13
 . (2)
. (2)

Рис. 149
Так как ![]() при
при ![]() , то
, то
 ,
,
![]()
![]() .
.
Переходя к пределу в равенстве
(2) при ![]() ,
получим (1).
,
получим (1).
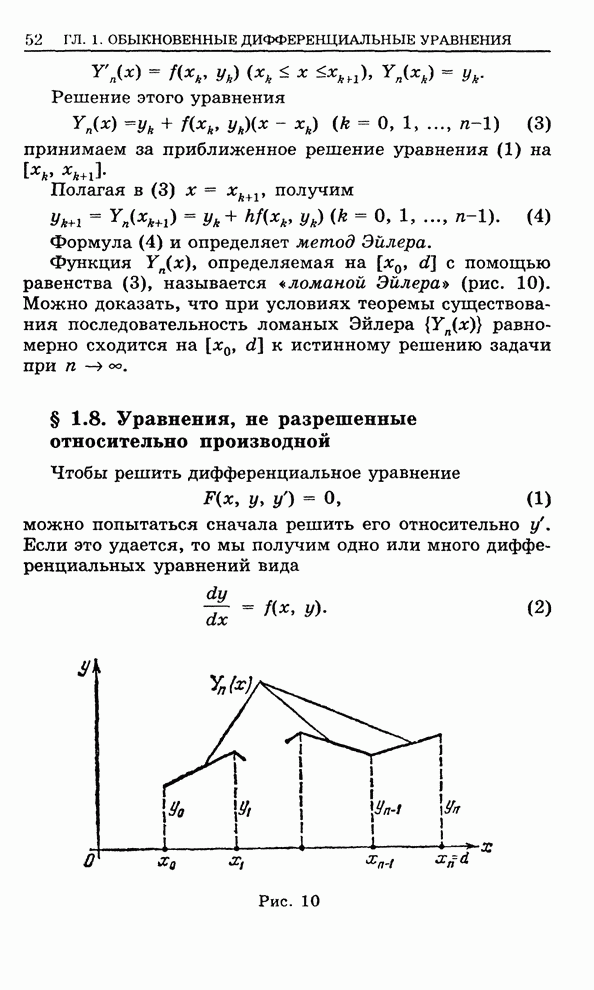
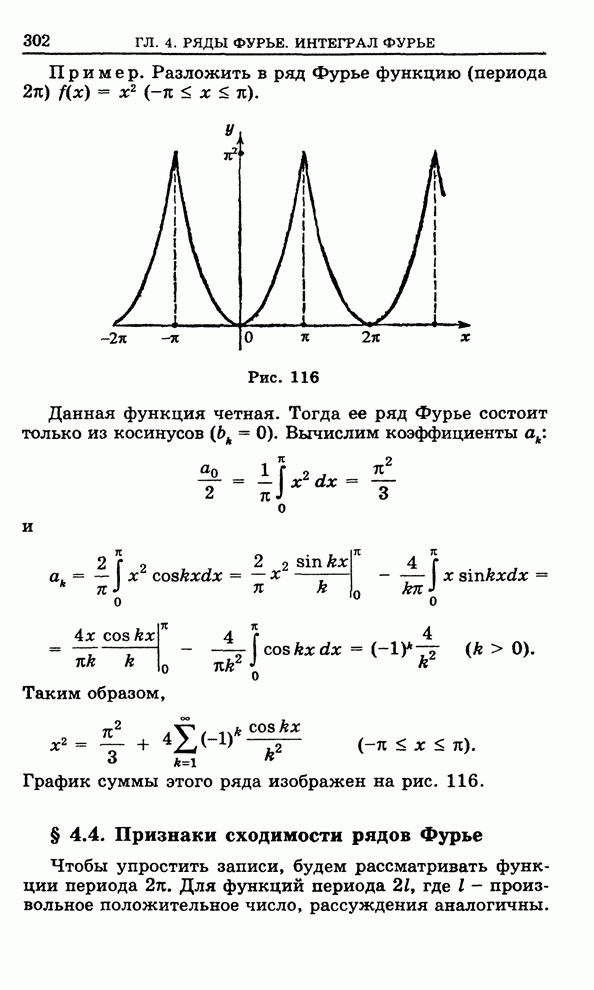
Пример 1. Вычислить интеграл  .
.
Функция ![]() аналитична в верхней
полуплоскости, за исключением точек
аналитична в верхней
полуплоскости, за исключением точек
![]() ,
,
![]() ,
,
в
которых она имеет простые полюсы. Кроме того, ![]() (
(![]() ). Найдем вычеты функции
). Найдем вычеты функции ![]() в точках
в точках ![]() . По формуле (16) §
6.11
. По формуле (16) §
6.11
![]()
![]() ,
,
где
![]() . Имеем
. Имеем ![]() ,
, ![]() ,
, ![]() . Отсюда
. Отсюда
![]() ,
,
![]() .
.
По формуле (1) получаем

![]() .
.
Теорема 2. Пусть функция ![]() удовлетворяет условиям,
отмеченным в начале параграфа и
удовлетворяет условиям,
отмеченным в начале параграфа и ![]() равномерно относительно
равномерно относительно ![]() . Тогда
. Тогда
 . (3)
. (3)
Доказательство. Так же как при доказательстве теоремы 1, имеем
 (4)
(4)
(функция
![]() имеет те
же особенности, что и
имеет те
же особенности, что и ![]() ).
).
Нам нужно доказать, что при ![]() интеграл
интеграл ![]() стремится к нулю.
Имеем
стремится к нулю.
Имеем

 .
.
В силу условия теоремы ![]() при
при ![]() для всех
для всех ![]() (
(![]() ) и достаточно
большого
) и достаточно
большого ![]() .
Поэтому (
.
Поэтому (![]() при
при ![]() )
)



![]() .
.
Переходя к пределу в (4), при ![]() получаем (3).
получаем (3).
Если функция ![]() имеет особенности на
действительной оси, то специальным построением контура интегрирования можно
вычислить соответствующие интегралы, если они существуют.
имеет особенности на
действительной оси, то специальным построением контура интегрирования можно
вычислить соответствующие интегралы, если они существуют.
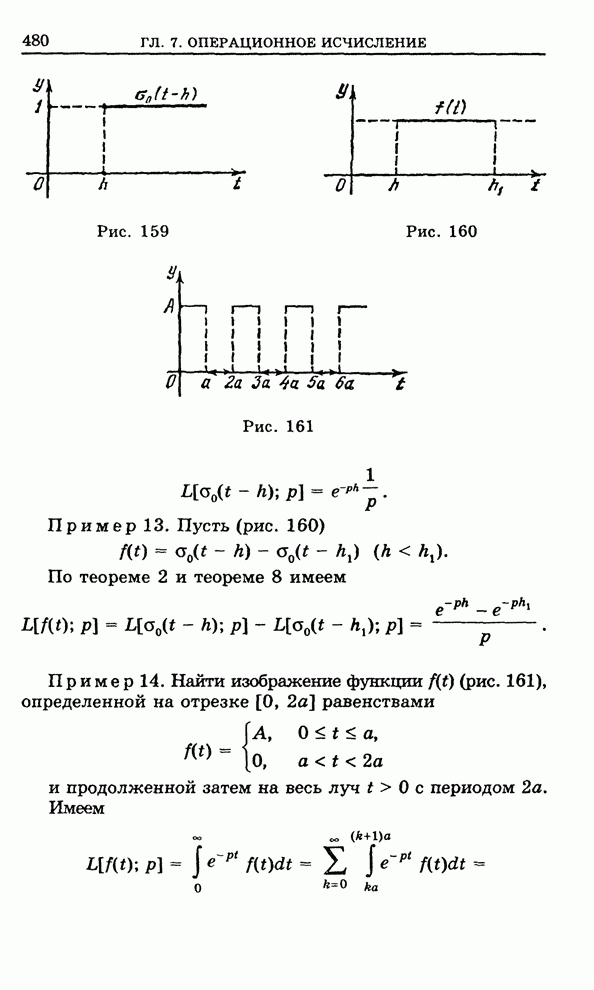
П р и м е р 2. Пусть ![]() . Эта функция имеет
простой полюс на действительной оси
. Эта функция имеет
простой полюс на действительной оси
в
точке ![]() .
Далее,
.
Далее, ![]() равномерно
относительно
равномерно
относительно ![]() .
.
Построим контур интегрирования,
как на рис. 150. Обход контура осуществляется по стрелкам, указанным на этом
рисунке. В заштрихованной части функция ![]() аналитическая при любом
аналитическая при любом ![]() и любом
и любом ![]() , поэтому по
теореме Коши (полуокружность
, поэтому по
теореме Коши (полуокружность ![]() ориентирована против часовой стрелки)
ориентирована против часовой стрелки)
 . (5)
. (5)

Рис. 150
Как и выше, легко показать, что ![]() .
.
Далее

 .
.
Таким образом, равенство (5) в
пределе, при ![]() и
и
![]() ,
принимает вид
,
принимает вид

 ,
,
т. e.
 .
.
Так как функция ![]() четная, то
четная, то
 .
.
Замечание. Если под знаком
интеграла есть сомножитель ![]() или
или ![]() , то часто удобно рассматривать интеграл
от функции, где
, то часто удобно рассматривать интеграл
от функции, где ![]() или
или
![]() заменены
на
заменены
на ![]() . Это
объясняется тем, что
. Это
объясняется тем, что ![]() и
и ![]() неограниченно возрастают при
неограниченно возрастают при ![]() , а
, а ![]() при
при ![]() (
(![]() ). Поэтому поведение
функции
). Поэтому поведение
функции ![]() будет
другое, чем у функции
будет
другое, чем у функции ![]() . Затем, получив значение интеграла
. Затем, получив значение интеграла  , выделяя
действительную и мнимую части, мы найдем
, выделяя
действительную и мнимую части, мы найдем  и
и  .
.
Пример 3. Вычислить интеграл

![]() .
.
Рассмотрим функцию ![]() . Эта функция
аналитична в верхней полуплоскости, кроме точки
. Эта функция
аналитична в верхней полуплоскости, кроме точки ![]() . Функция
. Функция ![]() при
при ![]() равномерно относительно
равномерно относительно ![]() . Поэтому по
теореме 2
. Поэтому по
теореме 2
 .
.
Выделяя действительную часть, получим
 ,
,
 .
.
Пример 4. Вычислить интеграл
 .
.
Имеем

 .
.
Итак,
 .
.
Пример 5.

![]() .
.
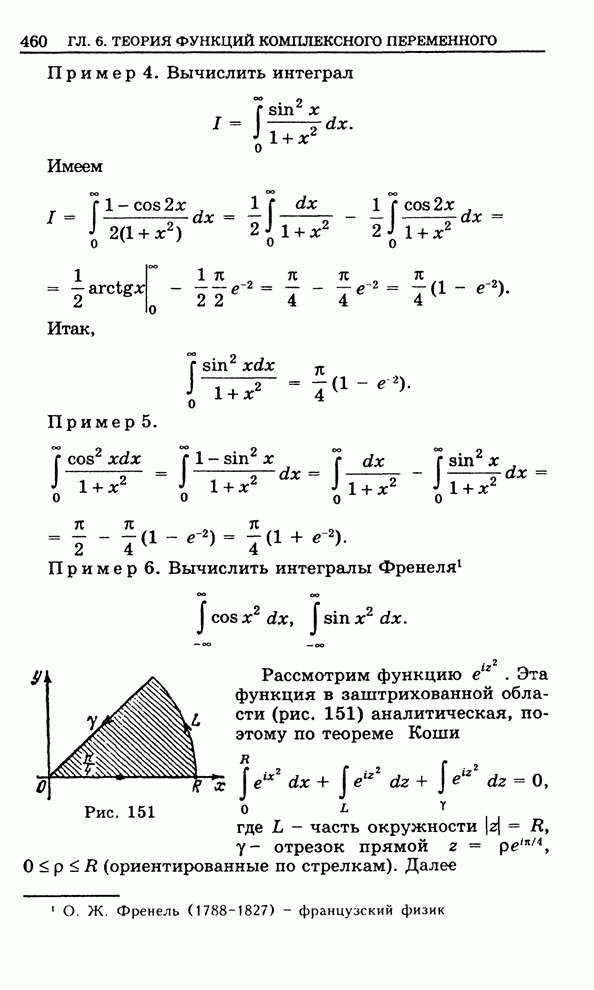
Пример 6. Вычислить интегралы Френеля
 ,
,
 .
.
Рассмотрим функцию ![]() . Эта функция в
заштрихованной области (рис. 151) аналитическая, поэтому по теореме Коши
. Эта функция в
заштрихованной области (рис. 151) аналитическая, поэтому по теореме Коши
 ,
,
где
![]() - часть
окружности
- часть
окружности ![]() ,
,
![]() -
отрезок прямой
-
отрезок прямой ![]() ,
,
![]() (ориентированные
по стрелкам).
(ориентированные
по стрелкам).

Рис. 151
Далее

 ;
;



 ,
,
![]() .
.
Итак, в пределе при ![]() получаем (см.
пример 3 §2.13)
получаем (см.
пример 3 §2.13)
 .
Выделяя действительную и мнимую части, получаем
.
Выделяя действительную и мнимую части, получаем
 ,
,
 ,
,
т. е.
 .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. Обыкновенные дифференциальные уравнения
- 1.1. Задача, приводящая к дифференциальному уравнению
- 1.2. Общие понятия
- 1.2.1. Понятие обыкновенного дифференциального уравнения
- 1.2.2. Дифференциальное уравнение первого порядка
- 1.2.3. Задача Коши
- 1.2.4. Примеры дифференциальных уравнений первого порядка
- 1.2.5. Общий интеграл дифференциального уравнения первого порядка
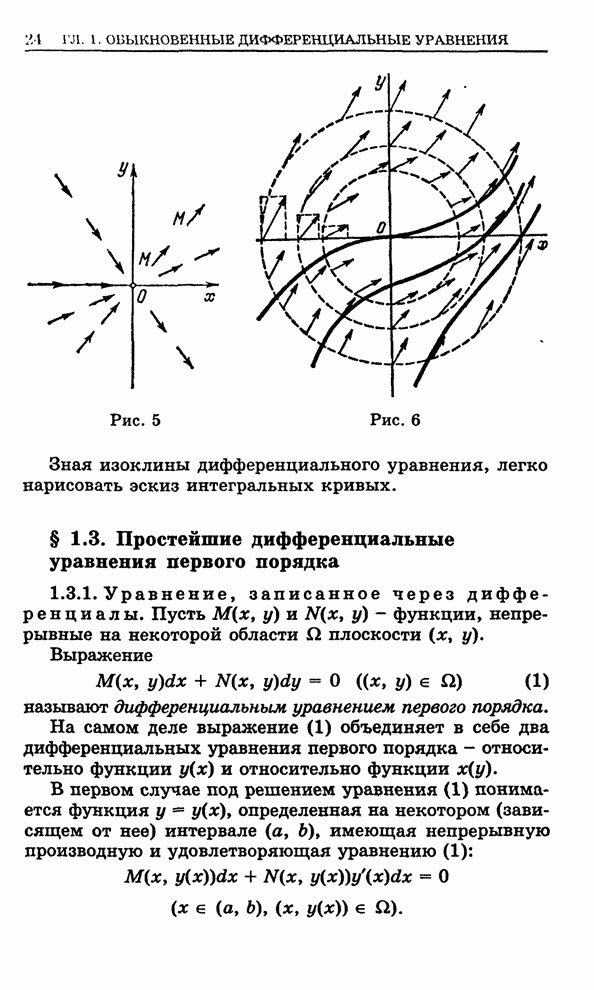
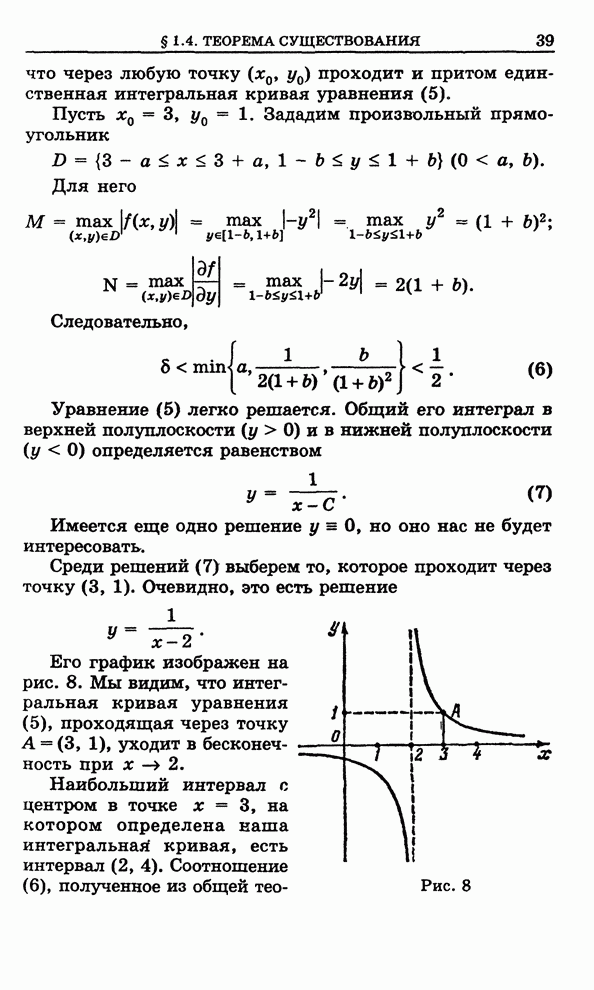
- 1.2.6. Поле направлений
- 1.3. Простейшие дифференциальные уравнения первого порядка
- 1.3.1. Уравнение, записанное через дифференциалы
- 1.3.2. Уравнения с разделенными переменными
- 1.3.3. Уравнения с разделяющимися переменными
- 1.3.4. Однородные уравнения
- 1.3.5. Линейное уравнение
- 1.3.6. Уравнение Бернулли
- 1.4. Теорема существования решения дифференциального уравнения первого порядка
- 1.5. Метрическое пространство
- 1.5.1. Понятие метрического пространства
- 1.5.2. Полное метрическое пространство
- 1.5.3. Принцип сжатых отображений
- 1.5.4. Приближенное значение корня функции
- 1.5.5. Метод Ньютона
- 1.6. Доказательство теоремы существования решения диффереацнального уравнения первого порядка
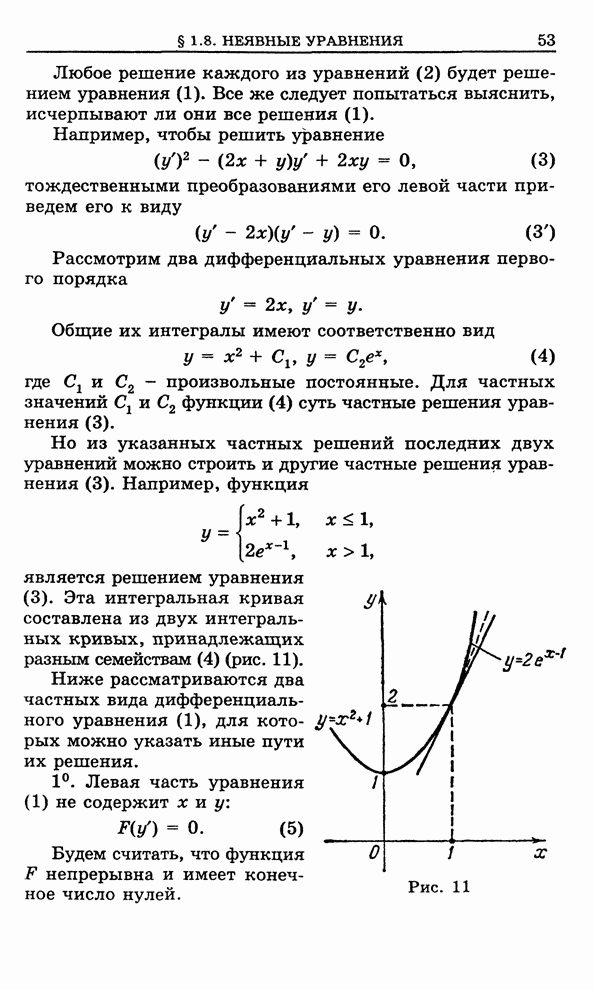
- 1.7. Метод Эйлера приближенного решения дифференциального уравнения первого порядка
- 1.8. Уравнения, не разрешенные относительно производной
- 1.9. Особые решения
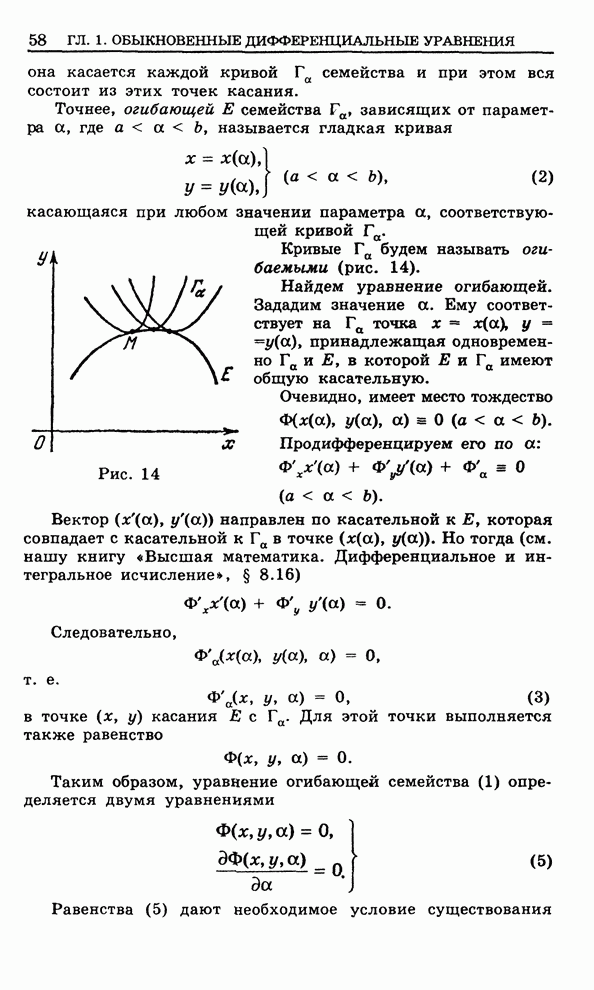
- 1.10. Огибающая семейства кривых
- 1.11. Дифференциальное уравнение второго порядка
- 1.12. Система из двух дифференциальных уравнений первого порядка
- 1.13. Дифференциальное уравнение n-го порядка
- 1.14. Понижение порядка дифференциального уравнения
- 1.15. Линейные уравнения высшего порядка
- 1.15.1. Понятие линейного уравнения высшего порядка
- 1.15.2. Фундаментальная система решений уравнения
- 1.15.3. Определитель Вронского
- 1.15.4. Структура общего решения
- 1.16. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- 1.16.1. Методы решения
- 1.16.2. Уравнение Эйлера
- 1.17. Метод вариации постоянных
- 1.18. Частное решение неоднородного уравнения с постоянными коэффициентами. Приложения
- 1.18.1. Методы нахождения частных решений
- 1.18.2. Дифференциальное уравнение колебания пружины
- 1.19. Системы дифференциальных уравнений. Фазовое пространство
- 1.20. Линейная однородная система дифференциальных уравнений
- 1.21. Общее решение линейной однородной системы дифференциальных уравнений с постоянными коэффициентами
- 1.22. Сведение системы уравнений к одному уравнению
- 1.23. Неоднородная система линейных дифференциальных уравнений с постоянными коэффициентами
- 1.24. Интегрирование дифференциальных уравнений с помощью степенных рядов
- 1.25. Элементы теории устойчивости
- 1.26. Классификация точек покоя
- Глава 2. Кратные интегралы
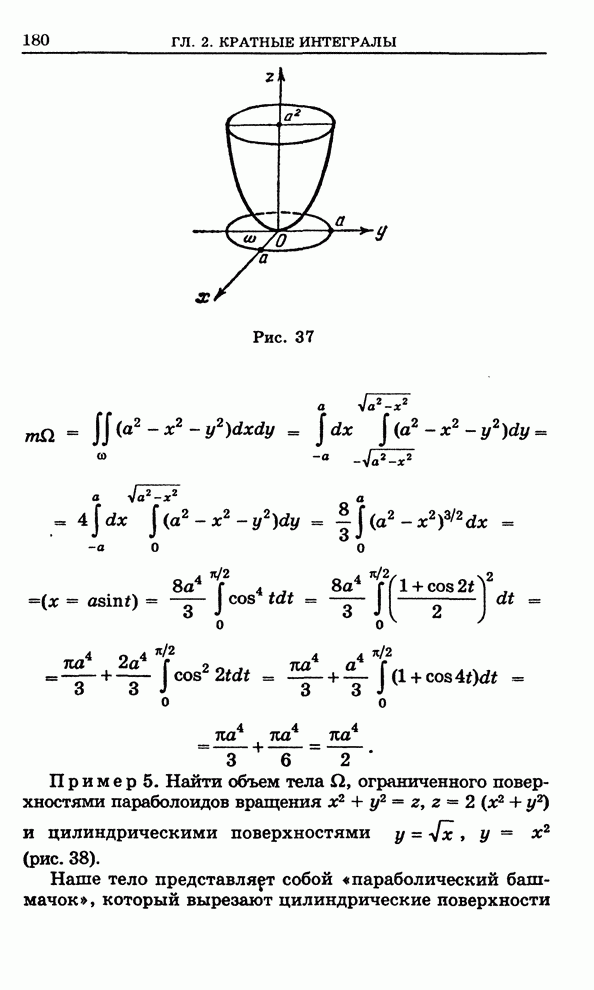
- 2.1. Введение
- 2.2. Сведения из теории меры Жордана
- 2.3. Свойства кратных интегралов. Теоремы существования
- 2.4. Сведение кратного интеграла к повторным
- 2.5. Доказательство существования интеграла от непрерывной функции
- 2.6. Замена переменных. Простейший случай
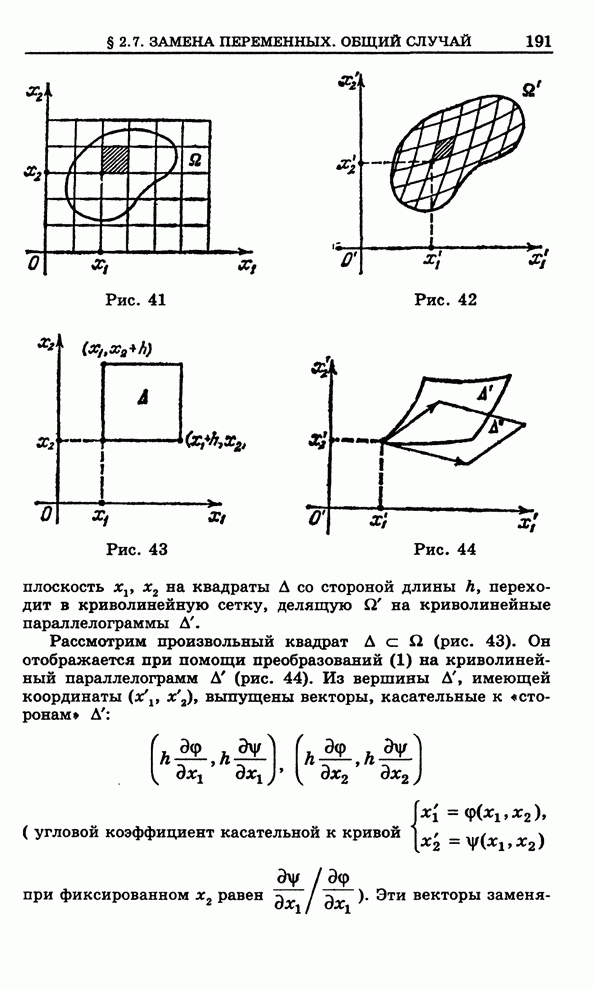
- 2.7. Замена переменных. Общий случай
- 2.8. Полярная система координат в плоскости
- 2.9. Полярная система координат в пространстве
- 2.10. Цилиндрические координаты
- 2.11. Площадь поверхности
- 2.12. Координаты центра масс
- 2.13. Несобственные интегралы
- 2.14. Несобственный интеграл с особенностями вдоль линии
- 2.15. Несобственный интеграл, зависящий от параметра
- Глава 3. Векторный анализ
- 3.1. Кусочно-гладкая ориентированная кривая
- 3.2. Криволинейный интеграл первого рода
- 3.3. Интеграл от вектора вдоль кривой
- 3.3.1. Поле вектора
- 3.3.2. Криволинейный интеграл от вектора вдоль кривой
- 3.3.3. Свойства криволинейных интегралов второго рода
- 3.4. Поле потенциала
- 3.4.1. Понятие потенциала и его свойства
- 3.4.2. Доказательство свойств потенциала
- 3.4.3. Ротор вектора
- 3.5. Дифференциальное уравнение в полных дифференциалах
- 3.6. Ориентация плоской области
- 3.7. Формула Грина
- 3.8. Интеграл по поверхности первого рода
- 3.9. Ориентация поверхности
- 3.10. Система координат и ориентация поверхности
- 3.11. Интеграл по ориентированной плоской области
- 3.12. Поток вектора через ориентированную поверхность
- 3.13. Дивергенция. Теорема Гаусса—Остроградского
- 3.14. Соленоидальное поле
- 3.15. Формула Стокса
- Глава 4. Ряды Фурье. Интеграл Фурье
- 4.1. Тригонометрические ряды
- 4.2. Сходимость тригонометрических рядов
- 4.3. Ряд Фурье
- 4.4. Признаки сходимости рядов Фурье
- 4.5. Ортогональные свойства тригонометрических функций
- 4.6. Коэффициенты Фурье
- 4.7. Оценка коэффициентов Фурье
- 4.8. Пространство функций со скалярным произведением
- 4.9. Ортогональная система функций
- 4.10. Полнота тригонометрических функций
- 4.11. Комплексная форма ряда Фурье
- 4.12. Понятие интеграла Фурье. Повторный интеграл Фурье
- 4.13. Косинус- и синус- преобразования Фурье
- 4.14. Примеры
- 4.15. Приближение интеграла Фурье
- 4.16. Сумма Фейера
- 4.17. Полнота систем функций в С и L2’
- 4.18. Сведения из теории кратных рядов Фурье
- Глава 5. Уравнения математической физики
- 5.1. Температура тела
- 5.2. Задача Дирихле
- 5.3. Задача Дирихле для круга
- 5.4. Задача Дирихле для полуплоскости
- 5.5. Уравнение теплопроводности в стержне
- 5.6. Теплопроводность для бесконечного стержня
- 5.7. Малые колебания струны
- 5.8. Колебание бесконечной струны. Формула Даламбера
- 5.9. Колебание круглой мембраны
- 5.10. Общая задача Штурма-Лиувилля
- 5.11. Интеграл энергии (Дирихле)
- 5.12. Применение преобразований Фурье
- Глава 6. Теория функций комплексного переменного
- 6.1. Понятие функции комплексного переменного
- 6.2. Производная функция комплексного переменного
- 6.3. Условия Даламбера-Эйлера (Коши-Римана)
- 6.4. Гармонические функции
- 6.5. Обратная функция
- 6.6. Интегрирование функций комплексного переменного
- 6.7. Формула Коши
- 6.8. Интеграл типа Коши
- 6.9. Степенной ряд
- 6.10. Ряд Лорана
- 6.11. Классификация изолированных особых точек. Вычеты
- 6.12. Классификация особых точек на бесконечности
- 6.13. Теорема о вычетах
- 6.14. Вычисление интегралов при помощи вычетов
- 6.15. Линейная функция. Дробно-линейная функция
- Глава 7. Операционное исчисление
- 7.1. Изображение Лапласа
- 7.2. Изображение простейших функций и свойства изображений
- 7.3. Приложения операционного исчисления
- 7.3.1. Операторное уравнение
- 7.3.2. Решение систем дифференциальных уравнений
- 7.3.3. Вычисление интегралов
- Глава 8. Обобщенные функции
- 8.1. Понятие обобщенной функции
- 8.2. Операции над обобщенными функциями
- 8.3. Преобразование Фурье обобщенных функций