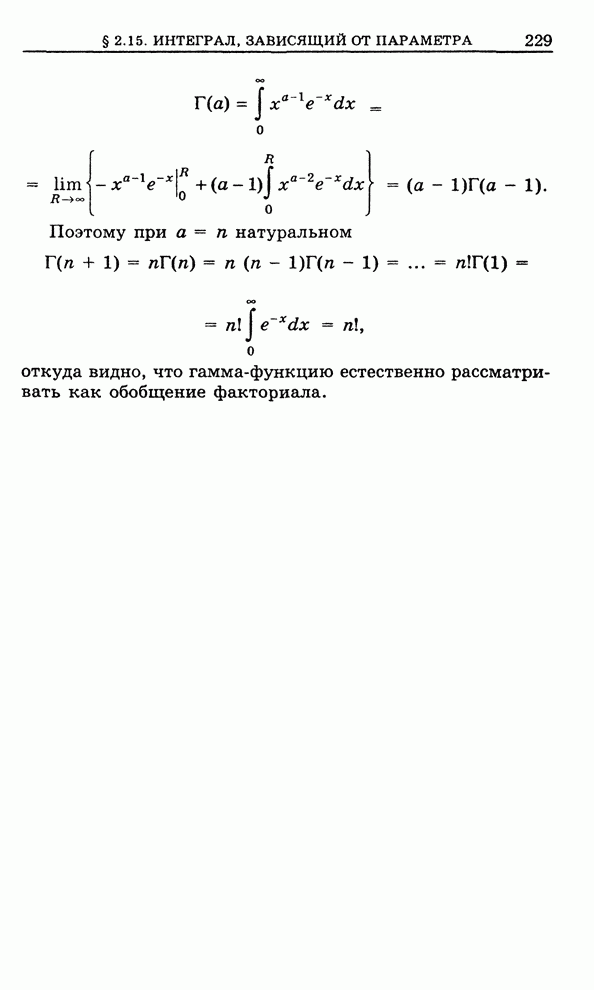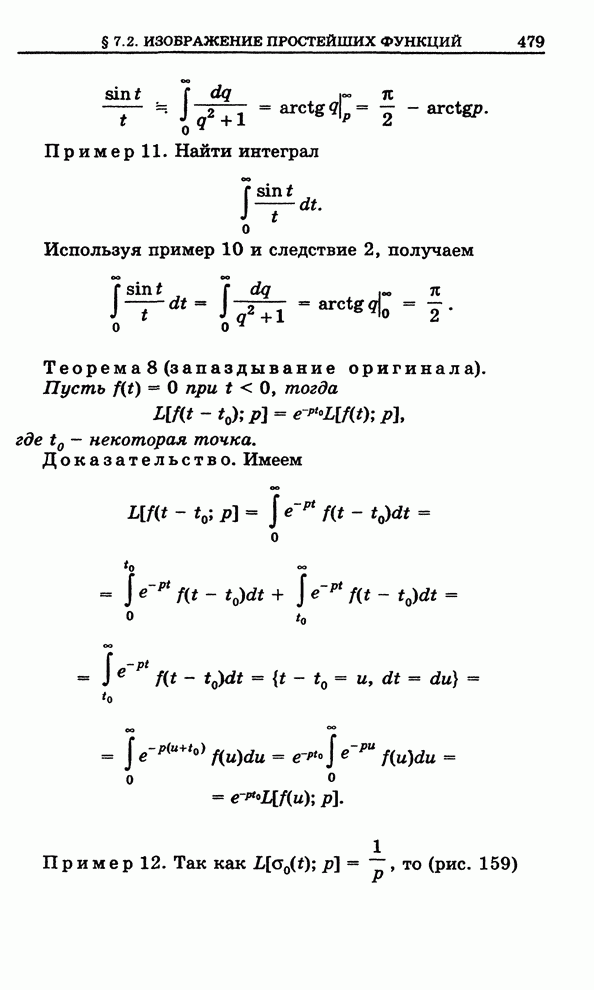| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
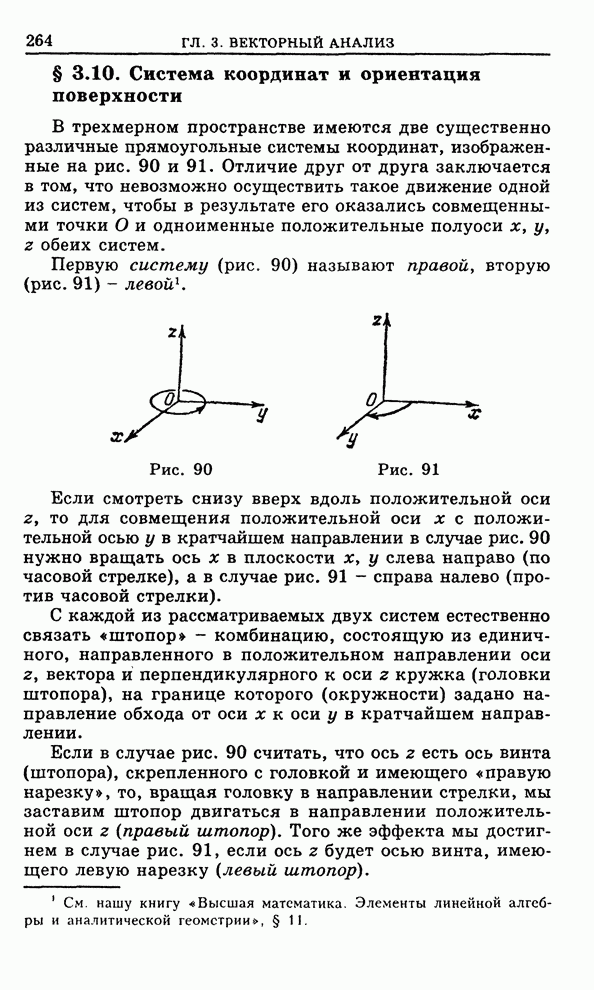
1.2.5. Общий интеграл дифференциального уравнения первого порядка.
Дадим определение общего интеграла дифференциального уравнения первого порядка.
Пусть задано дифференциальное уравнение первого порядка
![]() , (2)
, (2)
где функция ![]() и ее частные
производные
и ее частные
производные ![]() и
и
![]() непрерывны
на области
непрерывны
на области ![]() точек
точек
![]() трехмерного
пространства.
трехмерного
пространства.
Общим интегралом дифференциального уравнения (2) называется равенство
![]() , (9)
, (9)
где функция ![]() непрерывно
дифференцируема на некоторой области точек
непрерывно
дифференцируема на некоторой области точек ![]() и обладает следующим свойством: если
продифференцировать равенство (9) по
и обладает следующим свойством: если
продифференцировать равенство (9) по ![]() , считая формально, что
, считая формально, что ![]() :
:
![]() , (10)
, (10)
и исключить ![]() из уравнений (9) и (10), то
получим дифференциальное уравнение, эквивалентное уравнению (2).
из уравнений (9) и (10), то
получим дифференциальное уравнение, эквивалентное уравнению (2).
Называют еще уравнение (2)
дифференциальным уравнением семейства
функций (9), зависящих от параметра ![]() .
.
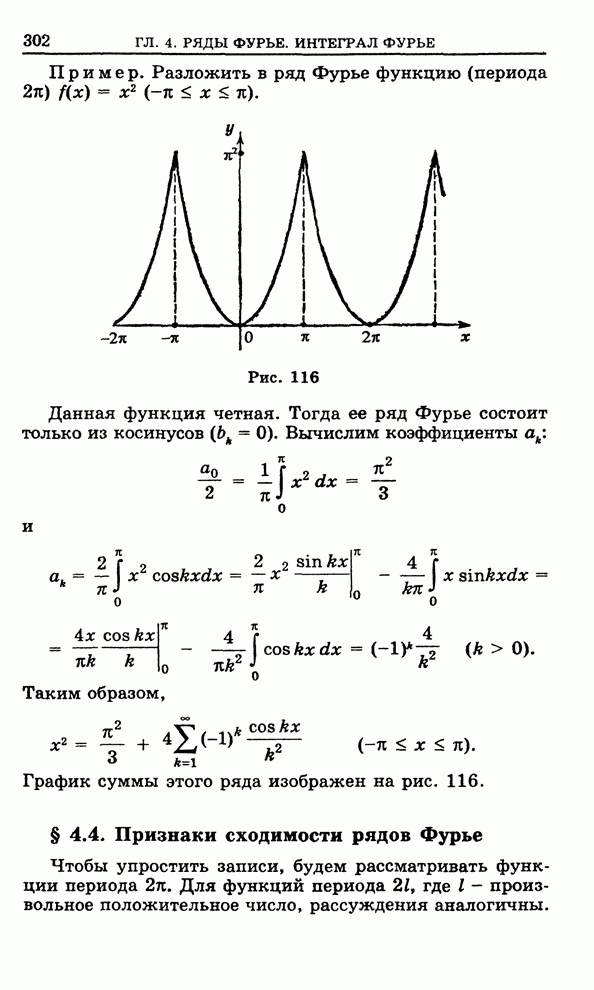
Пример 3. Рассмотрим семейство функций.
![]() , (11)
, (11)
зависящих от
произвольного параметра ![]() .
.
Продифференцируем
(11) по ![]() :
:
![]() (12)
(12)
и возведем полученное равенство в куб:
![]() . (13)
. (13)
Легко видеть, что мы получили дифференциальное уравнение, эквивалентное уравнению (12). Но тогда из (11) и (13) следует дифференциальное уравнение
![]() (14)
(14)
Легко проверить,
что любая функция (11) удовлетворяет этому уравнению. Впрочем, этот факт уже
следует из того, что дифференциальное
уравнение (14) есть результат исключения параметра ![]() из равенств (11) и (13).
из равенств (11) и (13).
Мы доказали, что
равенство (11), содержащее произвольный параметр ![]() , есть общий интеграл дифференциального
уравнения (14).
, есть общий интеграл дифференциального
уравнения (14).
В дальнейшем мы
будем изучать некоторые типы дифференциальных уравнений первого порядка и будем
указывать методы их решения, которые приведут к семействам решений, зависящих от одного параметра ![]() . Обычно эти семейства и будут
общими интегралами соответствующих дифференциальных уравнений.
. Обычно эти семейства и будут
общими интегралами соответствующих дифференциальных уравнений.
Возникает вопрос, содержит ли общий интеграл
данного дифференциального уравнения первого порядка при любых значениях
параметра ![]() все
решения этого уравнения. Вообще говоря, это не так. Но это заведомо имеет
место, если общий интеграл дифференциального уравнения первого порядка можно
записать в разрешенном относительно
все
решения этого уравнения. Вообще говоря, это не так. Но это заведомо имеет
место, если общий интеграл дифференциального уравнения первого порядка можно
записать в разрешенном относительно ![]() виде
виде
![]() , (15)
, (15)
и при этом левая часть уравнения (15) есть непрерывно дифференцируемая функция. Именно, справедлива теорема.
Теорема 1. Пусть задано дифференциальное уравнение
![]() , (2')
, (2')
где функция ![]() вместе с ее частными
производными
вместе с ее частными
производными ![]() ,
,
![]() непрерывна
на области
непрерывна
на области ![]() пространства
пространства
![]() , и пусть
равенство (15) есть его общий интеграл, где
, и пусть
равенство (15) есть его общий интеграл, где
![]() -
непрерывно дифференцируемая на некоторой области плоскости
-
непрерывно дифференцируемая на некоторой области плоскости ![]() функция.
функция.
Тогда, если
![]() ,
,
есть непрерывно дифференцируемое на ![]() решение уравнения (15)
при некотором значении
решение уравнения (15)
при некотором значении ![]() , то оно обязательно есть решение
дифференциального уравнения (2') и обратно, всякое решение дифференциального уравнения (2') удовлетворяет уравнению (15) на
интервале, где оно задано, при некоторой постоянной
, то оно обязательно есть решение
дифференциального уравнения (2') и обратно, всякое решение дифференциального уравнения (2') удовлетворяет уравнению (15) на
интервале, где оно задано, при некоторой постоянной ![]() .
.
Доказательство. Пусть ![]() , есть непрерывно дифференцируемое решение уравнения (15) при постоянной
, есть непрерывно дифференцируемое решение уравнения (15) при постоянной
![]() :
:
![]() .
.
Продифференцируем
это тождество по ![]() :
:
![]() .
(16)
.
(16)
Это показывает, что функция ![]() есть решение дифференциального
уравнения
есть решение дифференциального
уравнения
![]() , (17)
, (17)
а следовательно,
и решение дифференциального уравнения (2'), которое эквивалентно на ![]() уравнению (17) (согласно
определению общего интеграла).
уравнению (17) (согласно
определению общего интеграла).
Обратно, пусть ![]() , есть решение дифференциального
уравнения (2'), следовательно, и уравнения (17), т. е. пусть выполняется
тождество (16), которое можно записать так:
, есть решение дифференциального
уравнения (2'), следовательно, и уравнения (17), т. е. пусть выполняется
тождество (16), которое можно записать так:
![]() .
.
Интегрируя его от ![]() до
до ![]() , где
, где ![]() , получим
, получим

т. е. функция ![]() удовлетворяет на
удовлетворяет на ![]() уравнению
уравнению ![]() .
.
Замечание к примеру 2. Общий интеграл дифференциального уравнения
![]() (6')
(6')
в разрешенной
относительно ![]() форме
(см. (7)) имеет вид
форме
(см. (7)) имеет вид
![]() (18)
(18)
Так как левая
часть этого уравнения имеет непрерывные частные производные на всей плоскости ![]() , то на основании
теоремы 1 общий интеграл (18) содержит при различных постоянных
, то на основании
теоремы 1 общий интеграл (18) содержит при различных постоянных ![]() все решения
дифференциального уравнения (6').
все решения
дифференциального уравнения (6').
Чтобы решить
задачу Коши для дифференциального уравнения (6') при начальном условии ![]() , подставляем
, подставляем ![]() в (18) и находим
в (18) и находим ![]() :
:
![]()
Решение задачи Коши имеет вид
![]()
или
![]() .
.
Замечание к примеру 3. Дифференциальное уравнение в этом примере можно записать в виде
![]() , (19)
, (19)
где функция
![]()
непрерывно
дифференцируемая на всем пространстве ![]() , которое обозначим через
, которое обозначим через ![]() .
.
Мы знаем уже, что общий интеграл этого уравнения имеет вид
![]()
![]() . (11)
. (11)
Если решить
уравнение (11) относительно ![]() , то получим
, то получим
![]() .
(11')
.
(11')
Частная
производная по ![]() от
функции
от
функции ![]() не
существует на оси
не
существует на оси ![]() ,
поэтому условие теоремы 1 не выполняется. Но
тогда нельзя гарантировать, что любое решение дифференциального уравнения
(19) входит в его общий интеграл при некотором
,
поэтому условие теоремы 1 не выполняется. Но
тогда нельзя гарантировать, что любое решение дифференциального уравнения
(19) входит в его общий интеграл при некотором ![]() .
.
На рис. 2
изображено семейство кубических парабол (11) для различных значений ![]() . Каждая из этих
парабол есть интегральная кривая дифференциального уравнения (19). Но имеются
еще и другие интегральные кривые, например кривая, изображенная на рис. 2
жирной линией:
. Каждая из этих
парабол есть интегральная кривая дифференциального уравнения (19). Но имеются
еще и другие интегральные кривые, например кривая, изображенная на рис. 2
жирной линией:

Итак,
дифференциальное уравнение (19) имеет
определенный на всей плоскости ![]() общий интеграл (11), но он не
содержит в себе при различных значениях
общий интеграл (11), но он не
содержит в себе при различных значениях ![]() все решения этого уравнения. Имеется
бесконечное множество решений, соответствующих парам чисел
все решения этого уравнения. Имеется
бесконечное множество решений, соответствующих парам чисел ![]() , где
, где ![]() , которые не получаются из
семейства (11) при некотором значении
, которые не получаются из
семейства (11) при некотором значении ![]()

Рис.2
Однако если дифференциальное уравнение (19)
рассматривать для положительных ![]() , т. е. считать, что функция
, т. е. считать, что функция ![]() задана на
полупространстве
задана на
полупространстве ![]() ,
которое мы обозначим
,
которое мы обозначим ![]() , то общий интеграл
, то общий интеграл

определяется функцией ![]() , непрерывно дифференцируемой
на
, непрерывно дифференцируемой
на ![]() . Поэтому
в данном случае применима теорема 1, и общий интеграл содержит в себе при
различных
. Поэтому
в данном случае применима теорема 1, и общий интеграл содержит в себе при
различных ![]() все
решения дифференциального уравнения, принадлежащие к верхней полуплоскости
все
решения дифференциального уравнения, принадлежащие к верхней полуплоскости
![]() .
.
Подобный факт
имеет место и для области ![]() точек
точек ![]() , где
, где ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. Обыкновенные дифференциальные уравнения
- 1.1. Задача, приводящая к дифференциальному уравнению
- 1.2. Общие понятия
- 1.2.1. Понятие обыкновенного дифференциального уравнения
- 1.2.2. Дифференциальное уравнение первого порядка
- 1.2.3. Задача Коши
- 1.2.4. Примеры дифференциальных уравнений первого порядка
- 1.2.5. Общий интеграл дифференциального уравнения первого порядка
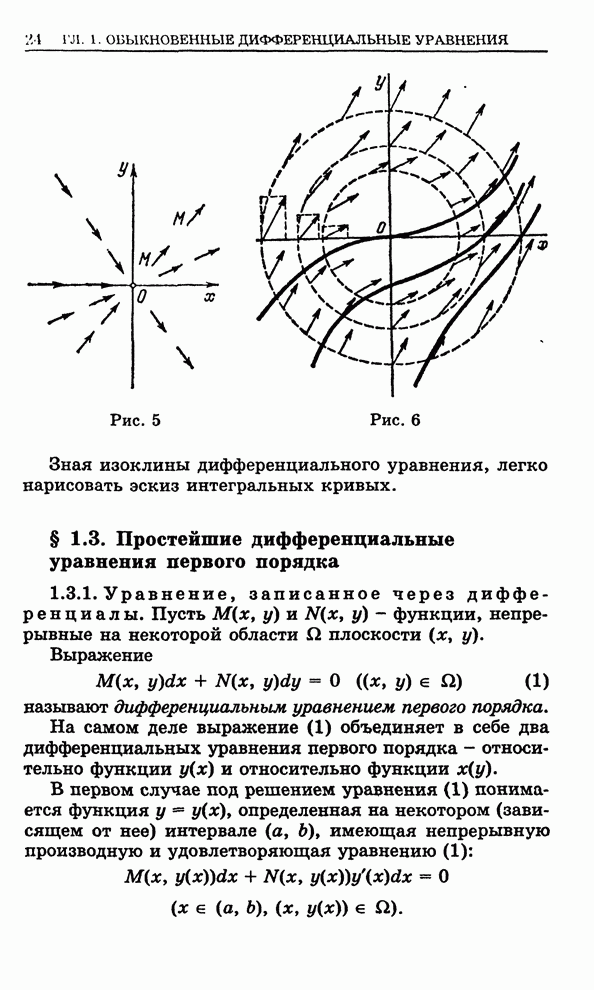
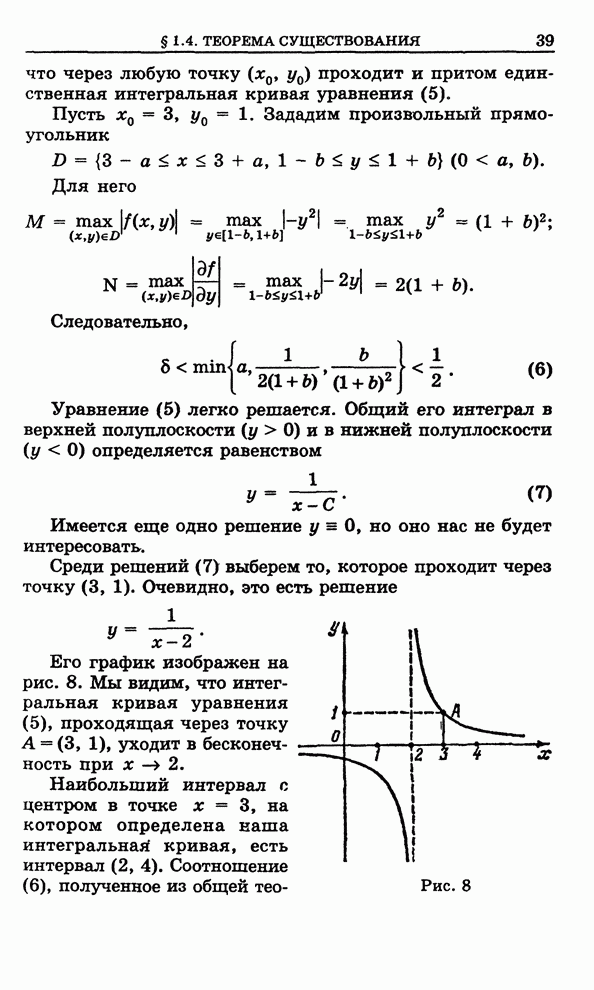
- 1.2.6. Поле направлений
- 1.3. Простейшие дифференциальные уравнения первого порядка
- 1.3.1. Уравнение, записанное через дифференциалы
- 1.3.2. Уравнения с разделенными переменными
- 1.3.3. Уравнения с разделяющимися переменными
- 1.3.4. Однородные уравнения
- 1.3.5. Линейное уравнение
- 1.3.6. Уравнение Бернулли
- 1.4. Теорема существования решения дифференциального уравнения первого порядка
- 1.5. Метрическое пространство
- 1.5.1. Понятие метрического пространства
- 1.5.2. Полное метрическое пространство
- 1.5.3. Принцип сжатых отображений
- 1.5.4. Приближенное значение корня функции
- 1.5.5. Метод Ньютона
- 1.6. Доказательство теоремы существования решения диффереацнального уравнения первого порядка
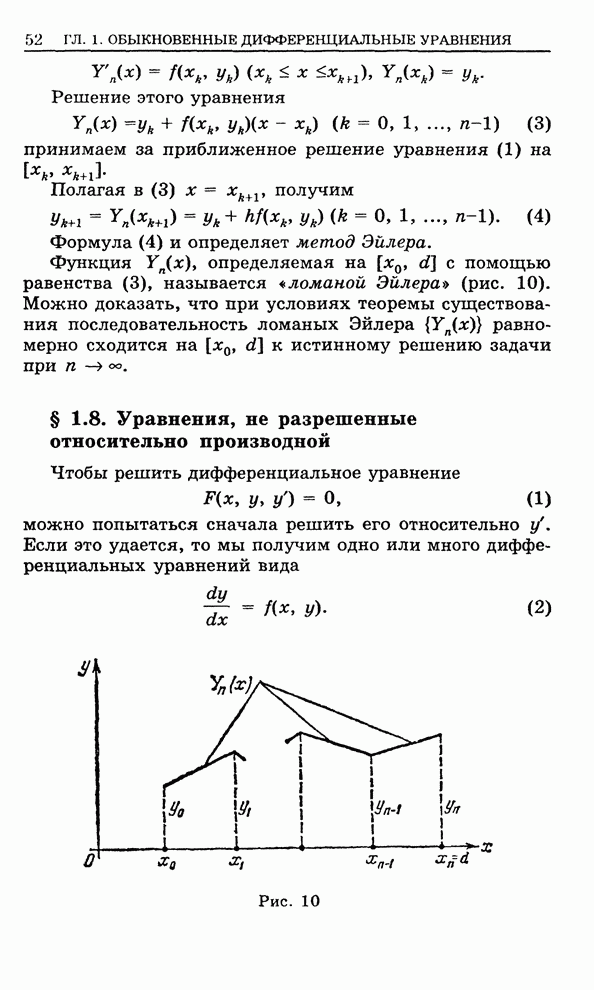
- 1.7. Метод Эйлера приближенного решения дифференциального уравнения первого порядка
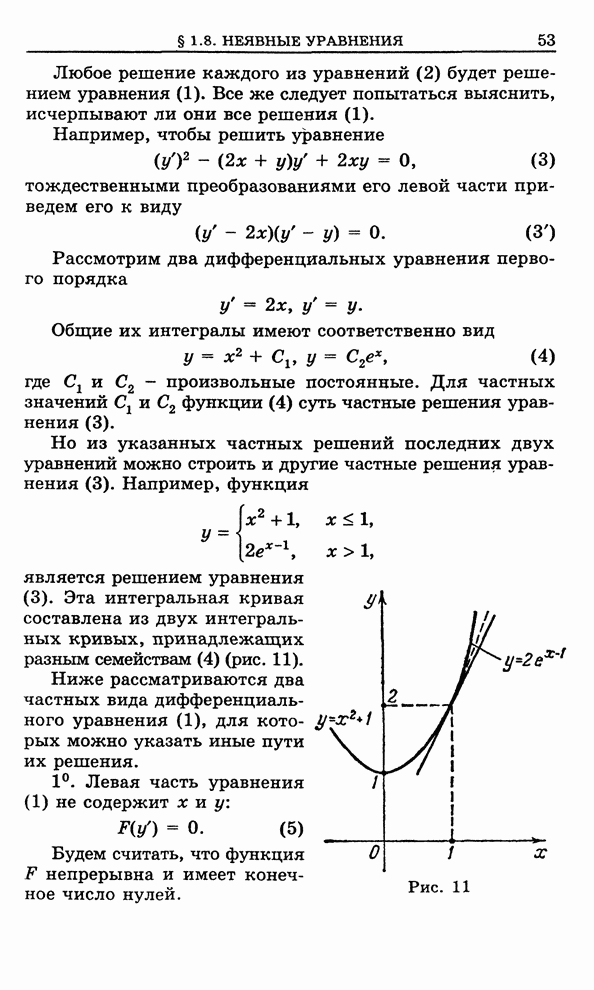
- 1.8. Уравнения, не разрешенные относительно производной
- 1.9. Особые решения
- 1.10. Огибающая семейства кривых
- 1.11. Дифференциальное уравнение второго порядка
- 1.12. Система из двух дифференциальных уравнений первого порядка
- 1.13. Дифференциальное уравнение n-го порядка
- 1.14. Понижение порядка дифференциального уравнения
- 1.15. Линейные уравнения высшего порядка
- 1.15.1. Понятие линейного уравнения высшего порядка
- 1.15.2. Фундаментальная система решений уравнения
- 1.15.3. Определитель Вронского
- 1.15.4. Структура общего решения
- 1.16. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- 1.16.1. Методы решения
- 1.16.2. Уравнение Эйлера
- 1.17. Метод вариации постоянных
- 1.18. Частное решение неоднородного уравнения с постоянными коэффициентами. Приложения
- 1.18.1. Методы нахождения частных решений
- 1.18.2. Дифференциальное уравнение колебания пружины
- 1.19. Системы дифференциальных уравнений. Фазовое пространство
- 1.20. Линейная однородная система дифференциальных уравнений
- 1.21. Общее решение линейной однородной системы дифференциальных уравнений с постоянными коэффициентами
- 1.22. Сведение системы уравнений к одному уравнению
- 1.23. Неоднородная система линейных дифференциальных уравнений с постоянными коэффициентами
- 1.24. Интегрирование дифференциальных уравнений с помощью степенных рядов
- 1.25. Элементы теории устойчивости
- 1.26. Классификация точек покоя
- Глава 2. Кратные интегралы
- 2.1. Введение
- 2.2. Сведения из теории меры Жордана
- 2.3. Свойства кратных интегралов. Теоремы существования
- 2.4. Сведение кратного интеграла к повторным
- 2.5. Доказательство существования интеграла от непрерывной функции
- 2.6. Замена переменных. Простейший случай
- 2.7. Замена переменных. Общий случай
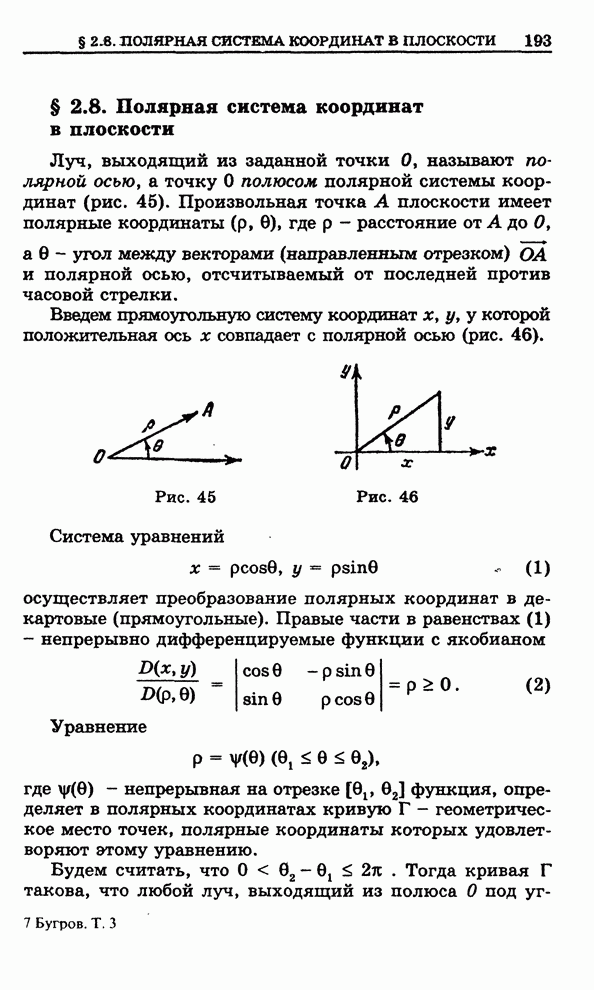
- 2.8. Полярная система координат в плоскости
- 2.9. Полярная система координат в пространстве
- 2.10. Цилиндрические координаты
- 2.11. Площадь поверхности
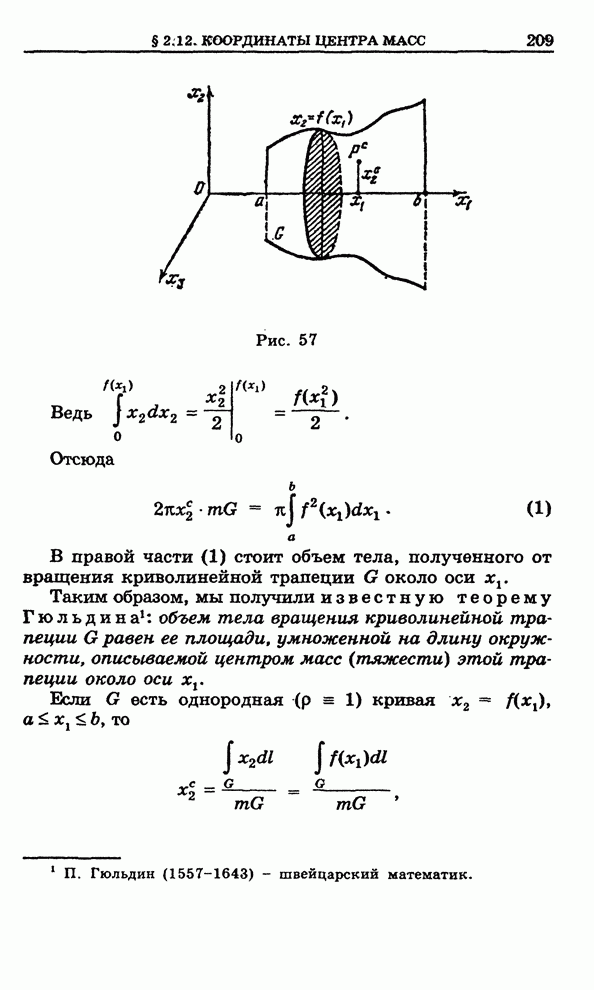
- 2.12. Координаты центра масс
- 2.13. Несобственные интегралы
- 2.14. Несобственный интеграл с особенностями вдоль линии
- 2.15. Несобственный интеграл, зависящий от параметра
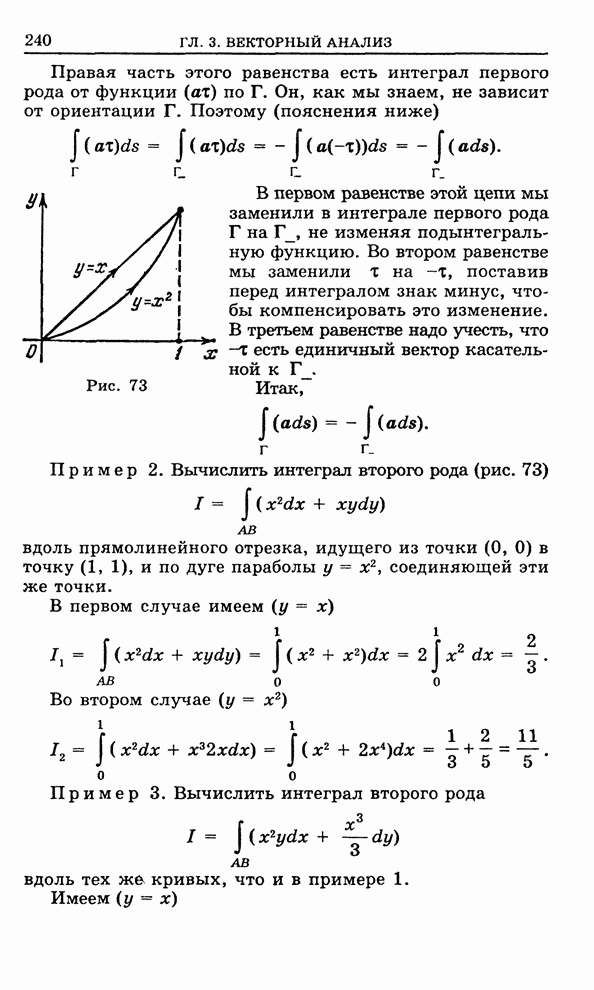
- Глава 3. Векторный анализ
- 3.1. Кусочно-гладкая ориентированная кривая
- 3.2. Криволинейный интеграл первого рода
- 3.3. Интеграл от вектора вдоль кривой
- 3.3.1. Поле вектора
- 3.3.2. Криволинейный интеграл от вектора вдоль кривой
- 3.3.3. Свойства криволинейных интегралов второго рода
- 3.4. Поле потенциала
- 3.4.1. Понятие потенциала и его свойства
- 3.4.2. Доказательство свойств потенциала
- 3.4.3. Ротор вектора
- 3.5. Дифференциальное уравнение в полных дифференциалах
- 3.6. Ориентация плоской области
- 3.7. Формула Грина
- 3.8. Интеграл по поверхности первого рода
- 3.9. Ориентация поверхности
- 3.10. Система координат и ориентация поверхности
- 3.11. Интеграл по ориентированной плоской области
- 3.12. Поток вектора через ориентированную поверхность
- 3.13. Дивергенция. Теорема Гаусса—Остроградского
- 3.14. Соленоидальное поле
- 3.15. Формула Стокса
- Глава 4. Ряды Фурье. Интеграл Фурье
- 4.1. Тригонометрические ряды
- 4.2. Сходимость тригонометрических рядов
- 4.3. Ряд Фурье
- 4.4. Признаки сходимости рядов Фурье
- 4.5. Ортогональные свойства тригонометрических функций
- 4.6. Коэффициенты Фурье
- 4.7. Оценка коэффициентов Фурье
- 4.8. Пространство функций со скалярным произведением
- 4.9. Ортогональная система функций
- 4.10. Полнота тригонометрических функций
- 4.11. Комплексная форма ряда Фурье
- 4.12. Понятие интеграла Фурье. Повторный интеграл Фурье
- 4.13. Косинус- и синус- преобразования Фурье
- 4.14. Примеры
- 4.15. Приближение интеграла Фурье
- 4.16. Сумма Фейера
- 4.17. Полнота систем функций в С и L2’
- 4.18. Сведения из теории кратных рядов Фурье
- Глава 5. Уравнения математической физики
- 5.1. Температура тела
- 5.2. Задача Дирихле
- 5.3. Задача Дирихле для круга
- 5.4. Задача Дирихле для полуплоскости
- 5.5. Уравнение теплопроводности в стержне
- 5.6. Теплопроводность для бесконечного стержня
- 5.7. Малые колебания струны
- 5.8. Колебание бесконечной струны. Формула Даламбера
- 5.9. Колебание круглой мембраны
- 5.10. Общая задача Штурма-Лиувилля
- 5.11. Интеграл энергии (Дирихле)
- 5.12. Применение преобразований Фурье
- Глава 6. Теория функций комплексного переменного
- 6.1. Понятие функции комплексного переменного
- 6.2. Производная функция комплексного переменного
- 6.3. Условия Даламбера-Эйлера (Коши-Римана)
- 6.4. Гармонические функции
- 6.5. Обратная функция
- 6.6. Интегрирование функций комплексного переменного
- 6.7. Формула Коши
- 6.8. Интеграл типа Коши
- 6.9. Степенной ряд
- 6.10. Ряд Лорана
- 6.11. Классификация изолированных особых точек. Вычеты
- 6.12. Классификация особых точек на бесконечности
- 6.13. Теорема о вычетах
- 6.14. Вычисление интегралов при помощи вычетов
- 6.15. Линейная функция. Дробно-линейная функция
- Глава 7. Операционное исчисление
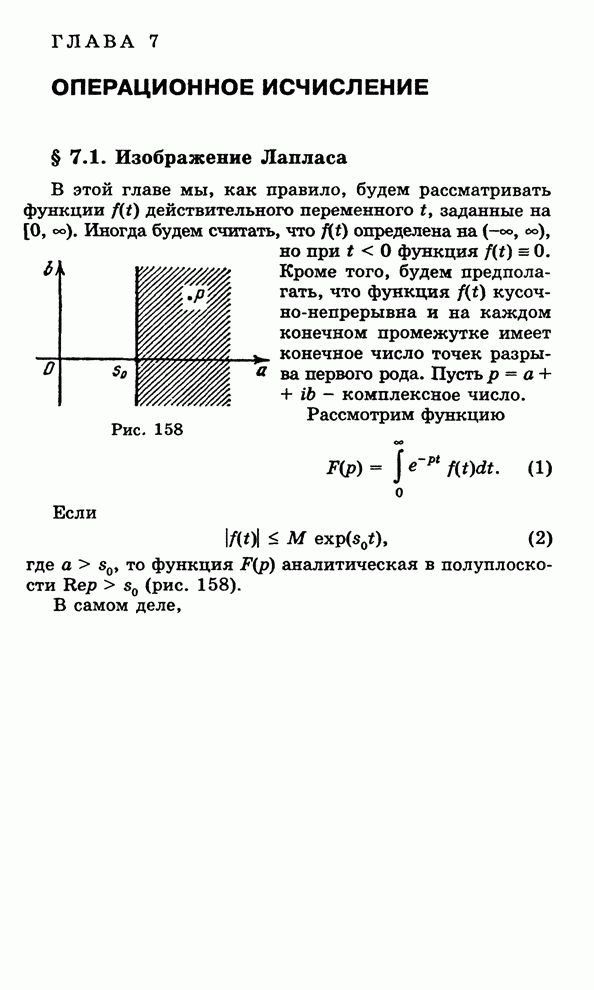
- 7.1. Изображение Лапласа
- 7.2. Изображение простейших функций и свойства изображений
- 7.3. Приложения операционного исчисления
- 7.3.1. Операторное уравнение
- 7.3.2. Решение систем дифференциальных уравнений
- 7.3.3. Вычисление интегралов
- Глава 8. Обобщенные функции
- 8.1. Понятие обобщенной функции
- 8.2. Операции над обобщенными функциями
- 8.3. Преобразование Фурье обобщенных функций