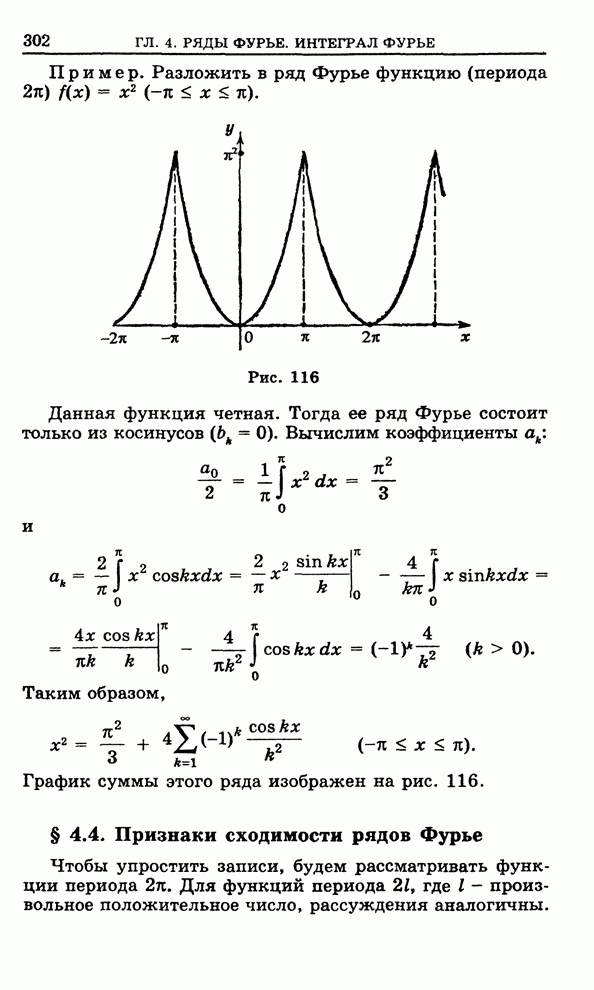
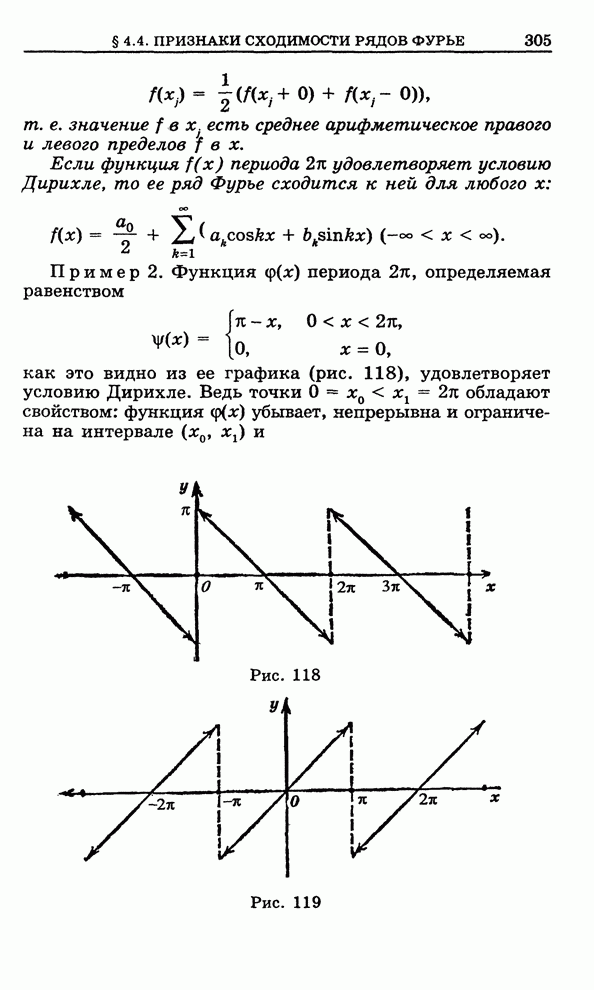
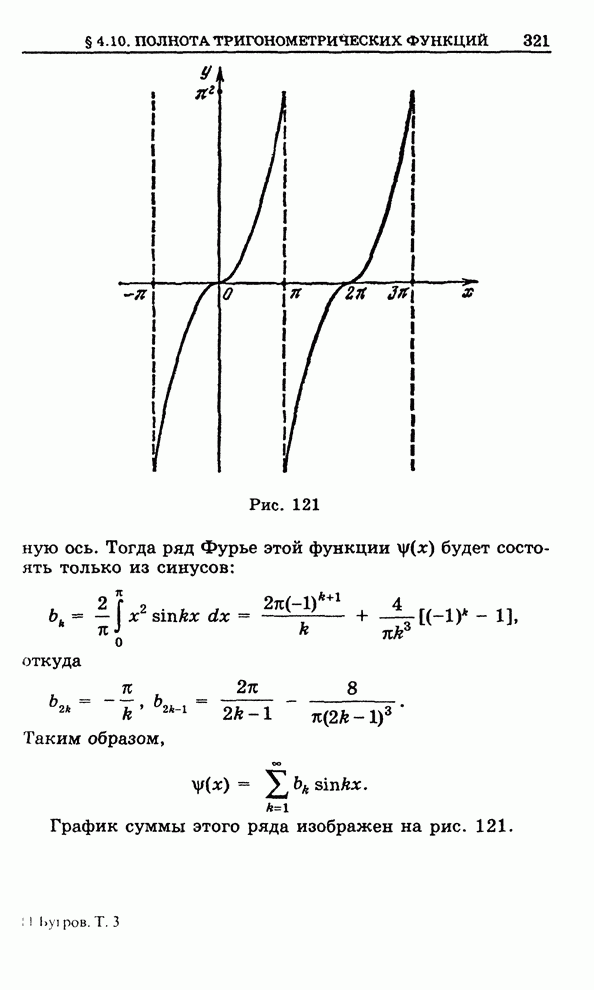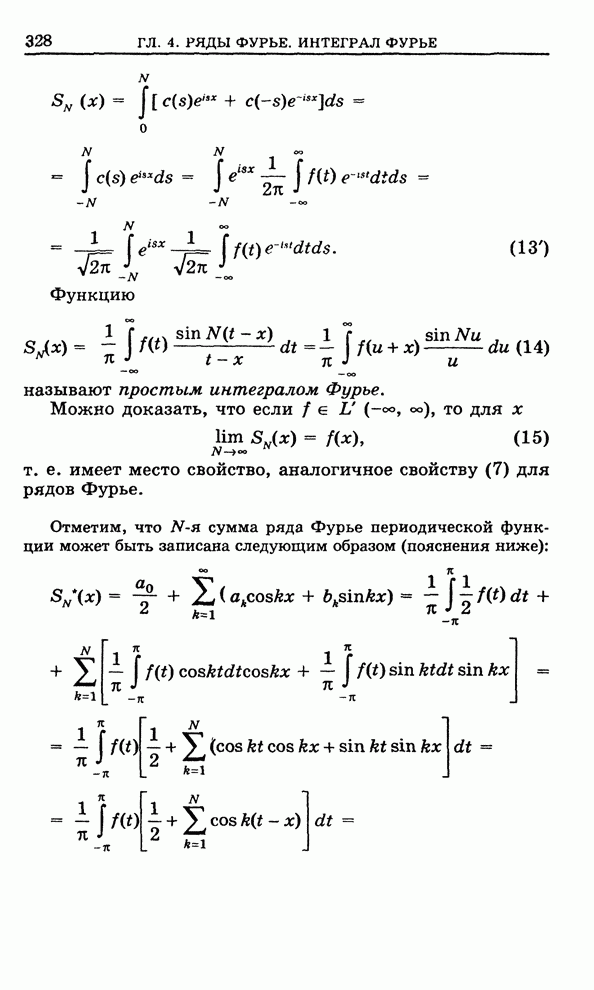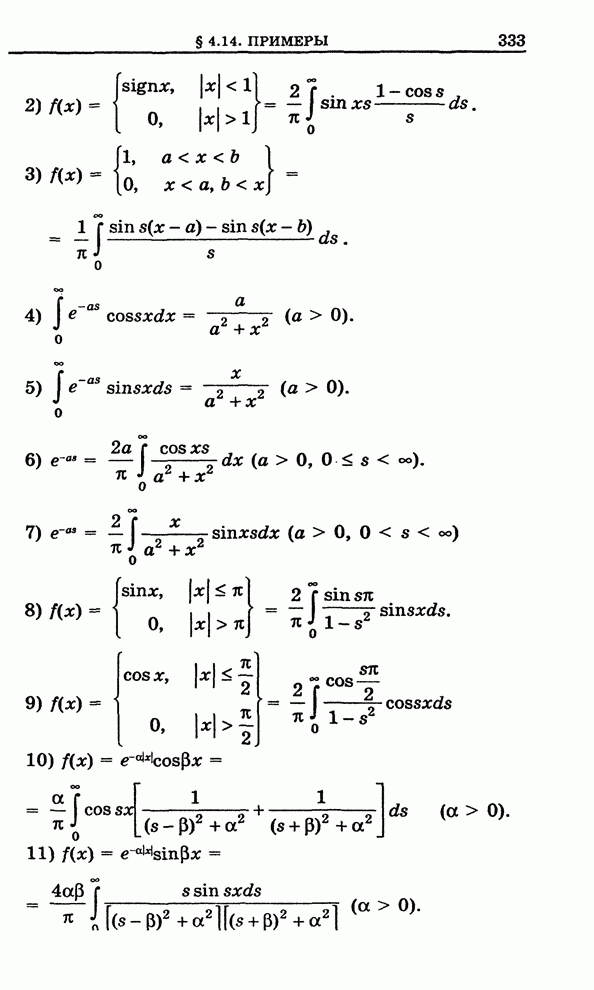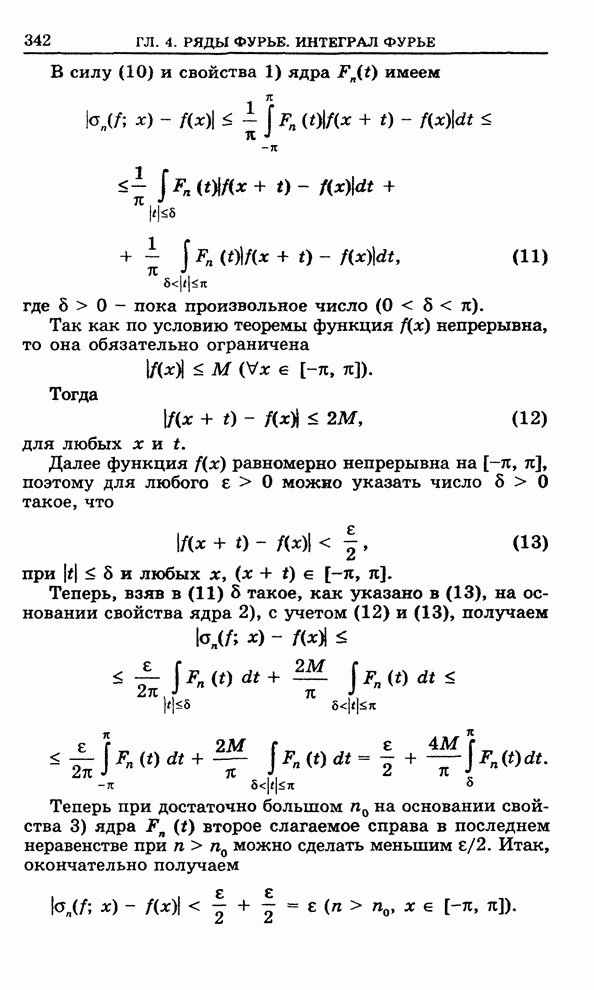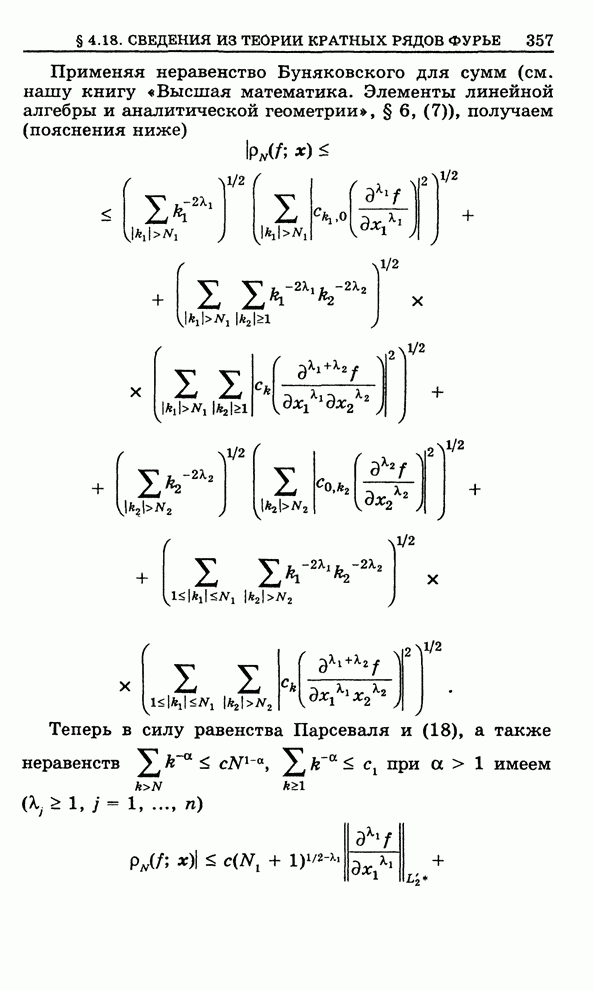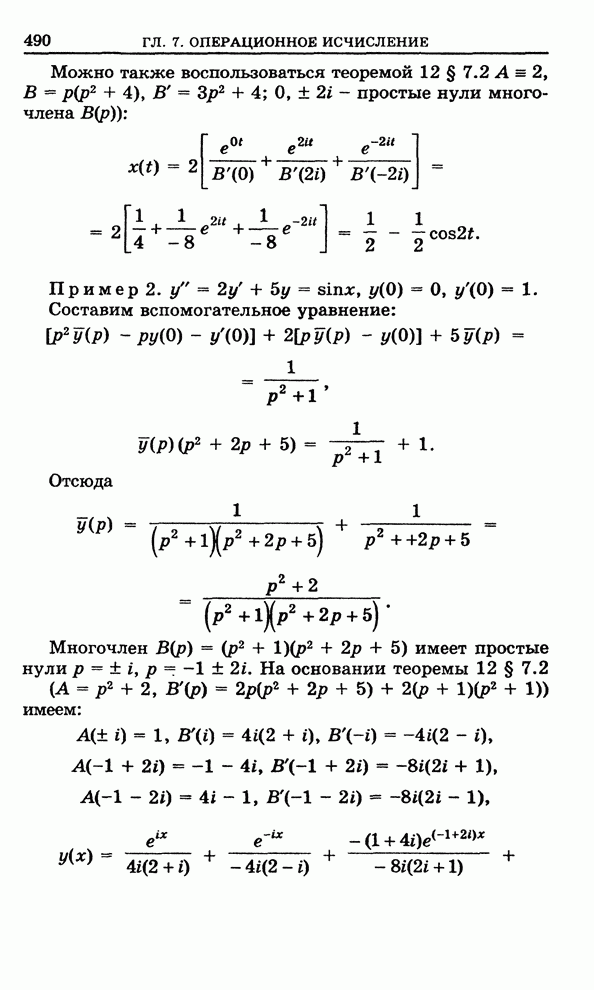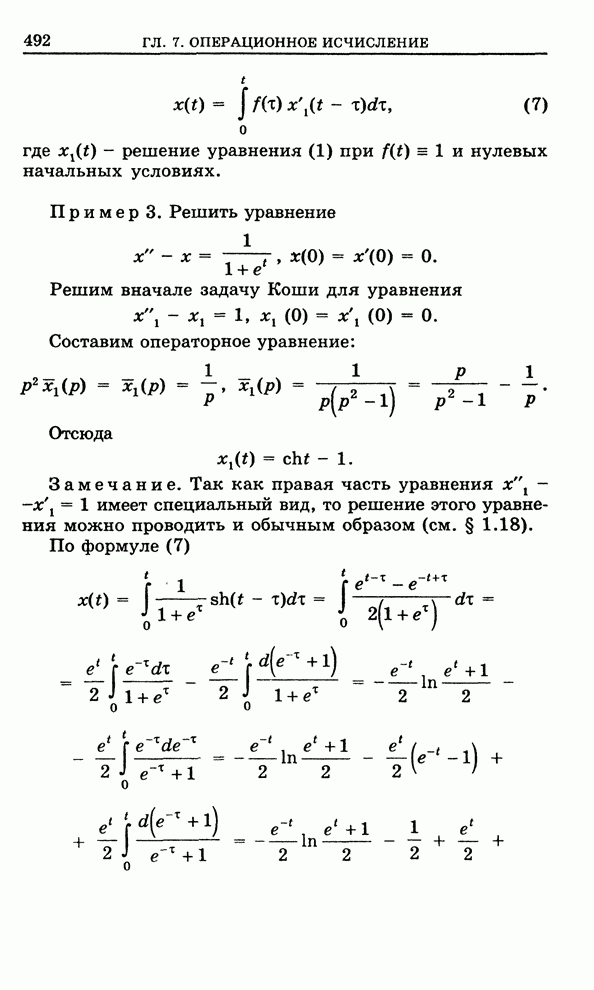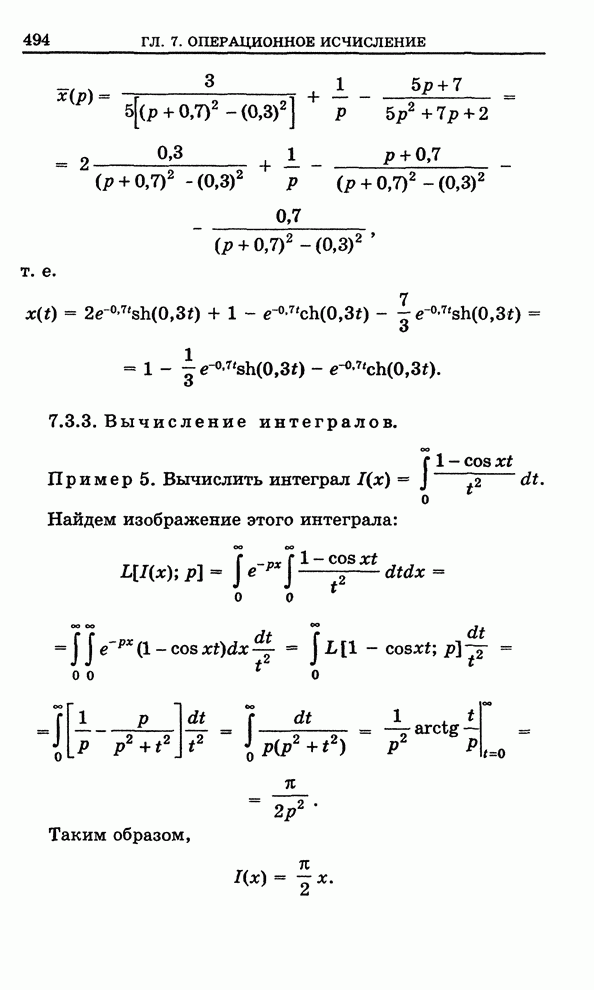| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 6.15. Линейная функция. Дробно-линейная функция
Целая линейная функция. Рассмотрим три функции
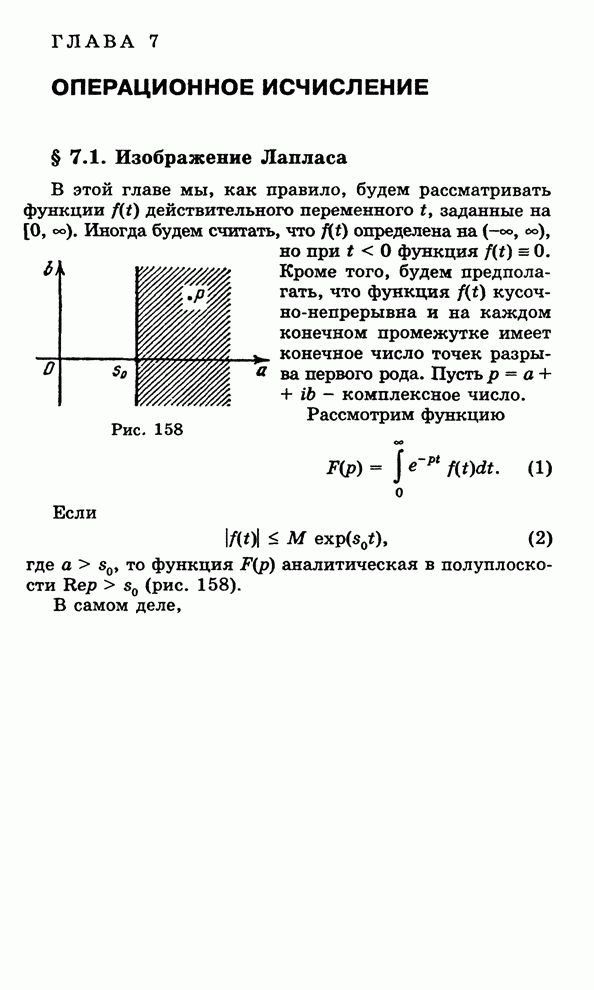
![]() , (1)
, (1)
![]() , (2)
, (2)
![]() , (3)
, (3)
где
![]() -
постоянное комплексное число,
-
постоянное комплексное число, ![]() ,
, ![]() - произвольное действительное число.
- произвольное действительное число.
Все три функции (1), (2), (3)
отображают плоскость ![]() на всю плоскость
на всю плоскость ![]() .
.

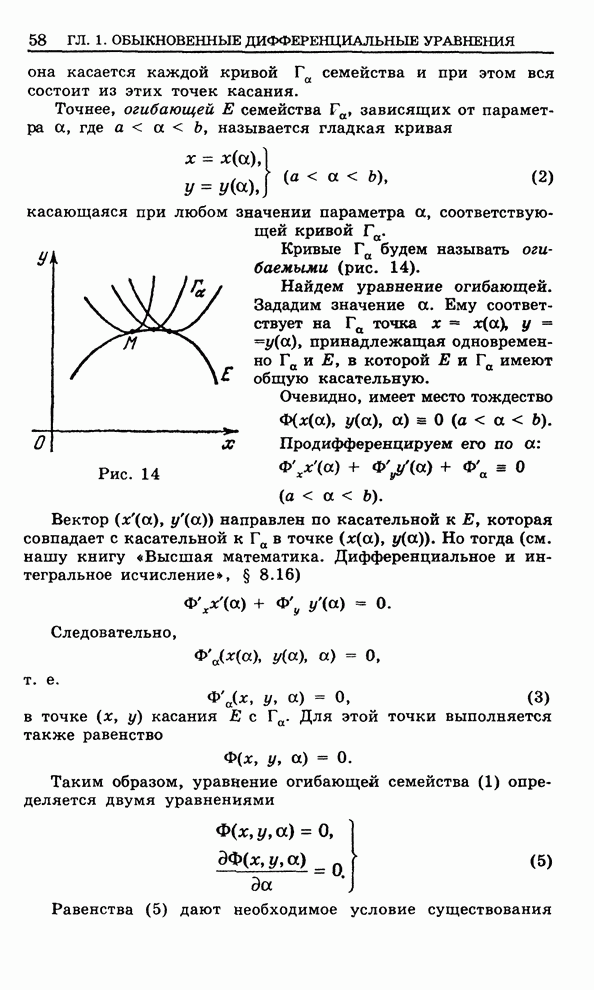
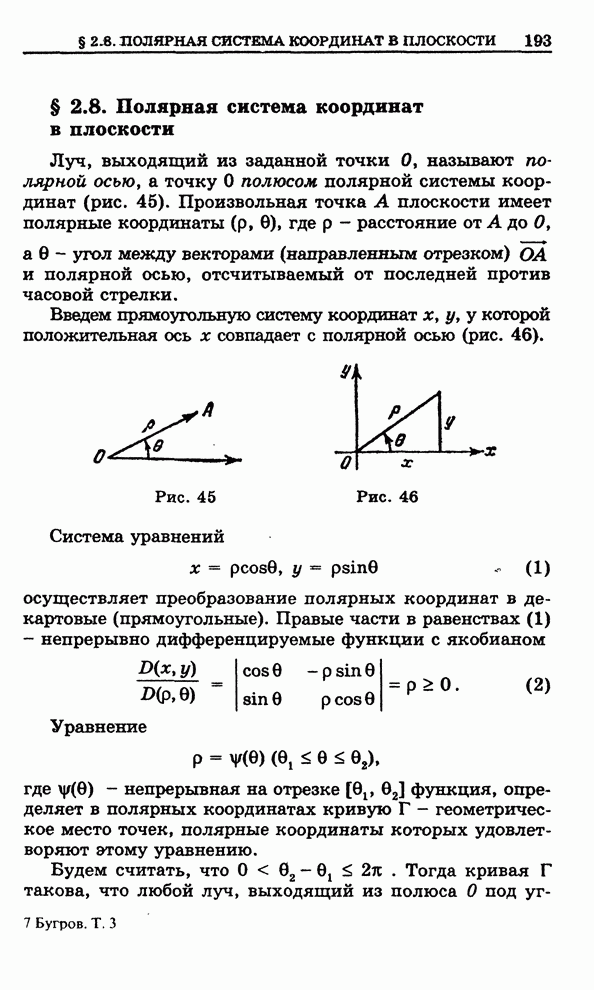
Рис. 152

Рис. 153

Рис. 154
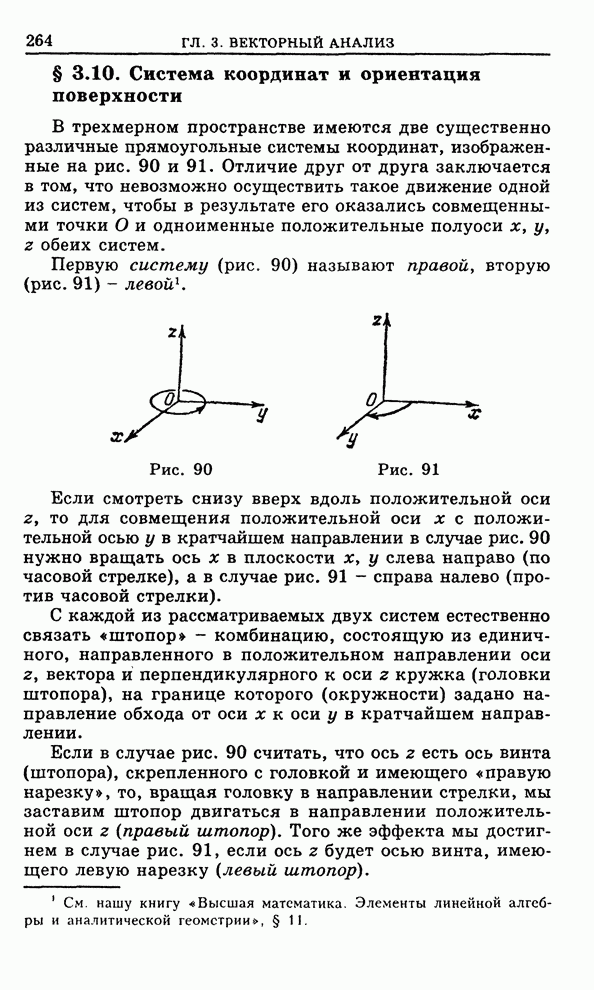
Функция (1) осуществляет сдвиг
плоскости ![]() на
вектор
на
вектор ![]() (рис.
152).
(рис.
152).
Функция (2) ![]() осуществляет растяжение
(при
осуществляет растяжение
(при ![]() ) и
сжатие (при
) и
сжатие (при ![]() )
плоскости
)
плоскости ![]() в
в
![]() раз:
раз: ![]() ,
, ![]() . На рис. 153
показан случай
. На рис. 153
показан случай ![]() .
.
Функция (3) осуществляет поворот
плоскости ![]() вокруг
нулевой точки на угол
вокруг
нулевой точки на угол ![]() (рис. 154).
(рис. 154).
Функции (1), (2), (3) имеют соответственно производные
![]() ,
,
![]() ,
, ![]() ,
,
не равные нулю и потому они осуществляют конформные отображения.
Все эти три функции являются частными случаями более общей целой линейной функции
![]()
![]() , (4)
, (4)
где
![]() и
и ![]() - постоянные
комплексные числа.
- постоянные
комплексные числа.
Осуществляемое ею отображение можно записать в виде
![]() ,
,
где
![]() ,
, ![]() .
.
Отсюда следует, что она сводится к (1), (2), (3):
![]() ,
,
![]() ,
, ![]() .
.
Иначе говоря, преобразование
плоскости ![]() ,
осуществляемое функцией (4), сводится к переносу (на вектор
,
осуществляемое функцией (4), сводится к переносу (на вектор ![]() ), затем к повороту
плоскости (на угол
), затем к повороту
плоскости (на угол ![]() ) и затем к растяжению или сжатию
плоскости в
) и затем к растяжению или сжатию
плоскости в ![]() раз.
раз.
Функция ![]() . Полагая
. Полагая ![]() ,
, ![]() , имеем
, имеем
![]() ,
,
![]() , (5)
, (5)
где
второе равенство надо понимать с точностью до ![]()
![]() .
.
Отсюда видно, что окружность ![]() переходит в себя,
точнее каждая ее точка переходит в точку, симметричную относительно
действительной оси.
переходит в себя,
точнее каждая ее точка переходит в точку, симметричную относительно
действительной оси.
Отметим, что если окружность ![]() проходится в
направлении против часовой стрелки, то отображенная окружность
проходится в
направлении против часовой стрелки, то отображенная окружность ![]() проходится по
часовой стрелке.
проходится по
часовой стрелке.
Преобразование (5) удобно разбить на два преобразования:
![]() ,
,
![]() ; (6)
; (6)
![]() ,
,
![]() . (7)
. (7)
Преобразование (6) называется инверсией относительно единичной окружности.
При инверсии относительно
единичной окружности точки ![]() и
и ![]() , лежащие на луче, составляющем угол
, лежащие на луче, составляющем угол ![]() с осью
с осью ![]() , переходят в
точки, лежащие на этом же луче, и притом так, что
, переходят в
точки, лежащие на этом же луче, и притом так, что
![]() .
.
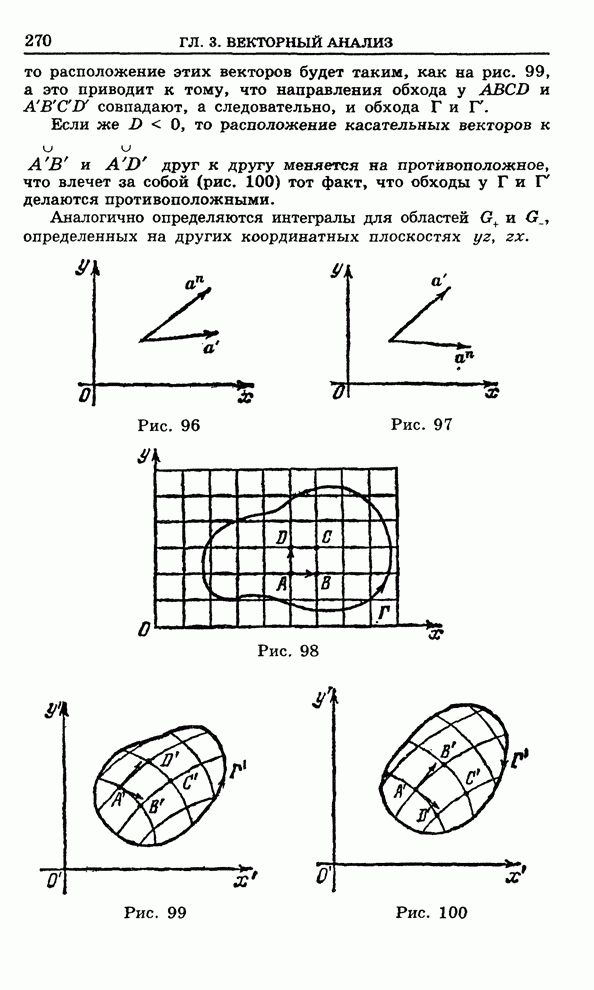
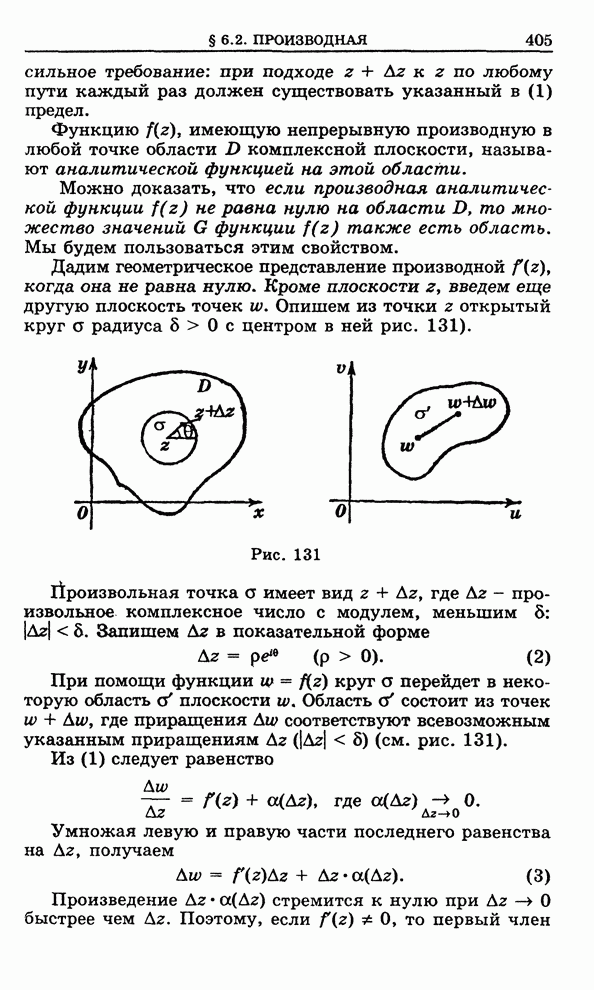
Построение точки ![]() по известной точке
по известной точке
![]() видно
из рис. 155, где рассмотрен случай, когда
видно
из рис. 155, где рассмотрен случай, когда ![]() лежит вне окружности
лежит вне окружности ![]() . Из точки
. Из точки ![]() проводим
касательную к окружности
проводим
касательную к окружности ![]() ,
, ![]() - точка касания,
- точка касания, ![]() . Из подобия треугольников
(
. Из подобия треугольников
(![]() и
и ![]() )
)
![]() ,
,
![]() ,
, ![]() .
.

Рис. 155
Если точка ![]() находится внутри окружности
находится внутри окружности
![]() , то
восстанавливаем из нее перпендикуляр к
, то
восстанавливаем из нее перпендикуляр к ![]() до пересечения с окружностью в точке
до пересечения с окружностью в точке
![]() . Через
последнюю проводим касательную к окружности до пересечения с лучом
. Через
последнюю проводим касательную к окружности до пересечения с лучом ![]() . Точка пересечения
и будет точкой
. Точка пересечения
и будет точкой ![]() .
.
Точки ![]() и
и ![]() называют взаимно
симметричными относительно окружности
называют взаимно
симметричными относительно окружности ![]() .
.
Отображая теперь (по (7)) точку ![]() зеркально относительно
действительной оси, мы получаем точку
зеркально относительно
действительной оси, мы получаем точку
![]() .
.
Из формулы ![]() видно, что при
видно, что при ![]() точка
точка ![]() имеет
неограниченно возрастающий модуль, поэтому удобно считать, что при помощи этой
формулы точке
имеет
неограниченно возрастающий модуль, поэтому удобно считать, что при помощи этой
формулы точке ![]() соответствует
«бесконечно удаленная точка», которую обозначают символом
соответствует
«бесконечно удаленная точка», которую обозначают символом ![]() .
.
Итак, функция ![]() отображает плоскость
отображает плоскость ![]() на плоскость
на плоскость ![]() при помощи
преобразования инверсии относительно окружности
при помощи
преобразования инверсии относительно окружности ![]() и зеркального отображения
относительно оси
и зеркального отображения
относительно оси ![]() .
При этом точка
.
При этом точка ![]() переходит
в точку
переходит
в точку ![]() ,
а точка
,
а точка ![]() -
в точку
-
в точку ![]() .
.
Далее ![]() при любых
при любых ![]() с
с ![]() , поэтому
отображение с помощью функции
, поэтому
отображение с помощью функции ![]()
![]() конформно.
конформно.
Дробно-линейная функция
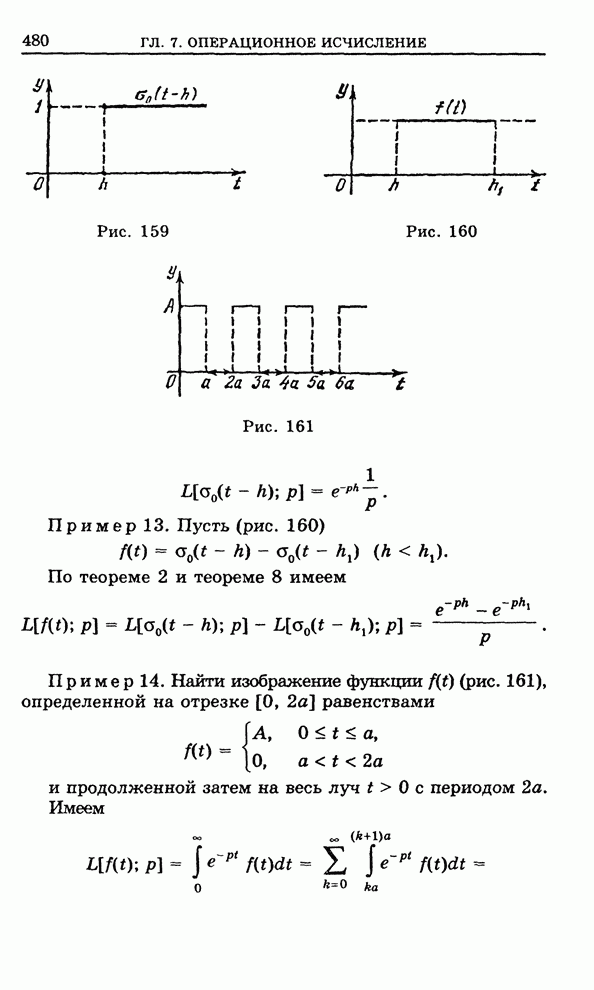
![]() . (8)
. (8)
Будем считать, что ![]() . Очевидно, что
точка
. Очевидно, что
точка ![]()
![]() переходит в точку
переходит в точку ![]() .
.
Функцию ![]() , выделяя ее целую часть,
можно представить в виде
, выделяя ее целую часть,
можно представить в виде
![]() , (9)
, (9)
откуда видно, что
![]()
![]() ,
,
т. е. отображение с помощью функции (8) конформно.
Из равенства (9) видно, что данное отображение состоит из рассмотренных выше отображений:
![]() ,
, ![]() ,
, ![]() .
.
Если считать прямую линию за окружность бесконечного радиуса, то при преобразовании (9) окружность переходит в окружность (круговое свойство).
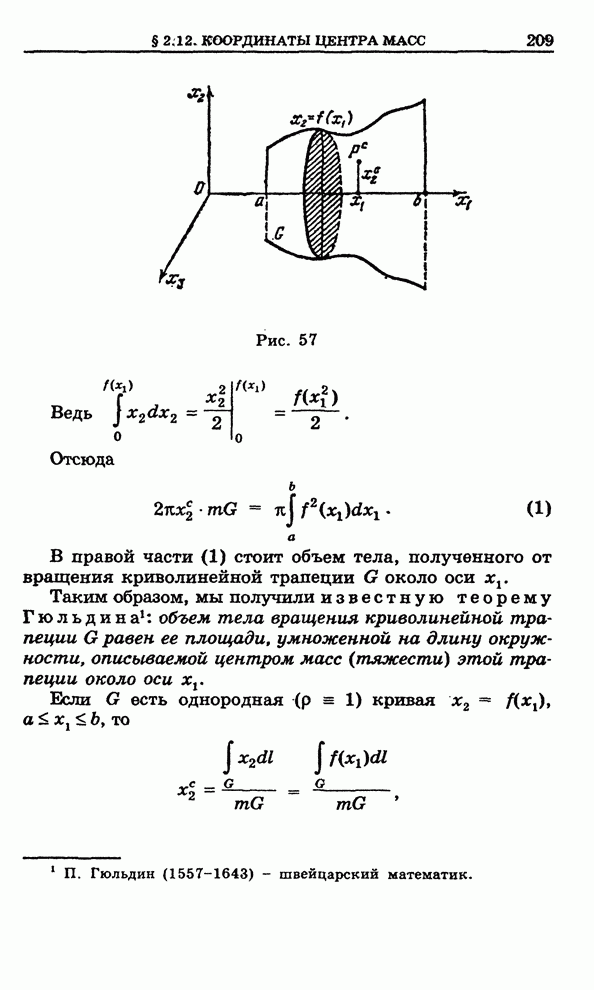
Из геометрических соображений
ясно, что при параллельном переносе, растяжении и вращении окружность
переходит в окружность. Больше того, внутренность отображаемой окружности
переходит на внутренность отображенной окружности. Поэтому достаточно
проверить круговое свойство для преобразования ![]() . Уравнение окружности в плоскости
. Уравнение окружности в плоскости ![]() , как нам известно,
имеет вид
, как нам известно,
имеет вид
![]()
или
![]()
![]()
или
![]()
![]() . (10)
. (10)
В рассматриваемом случае ![]() ,
, ![]() . Следовательно,
уравнение (10) переходит в уравнение
. Следовательно,
уравнение (10) переходит в уравнение
![]()
или в уравнение
![]()
![]() ,
,
которое
описывает некоторую окружность в плоскости ![]() .
.
В частности, при ![]() получаем прямую
линию, т. е. окружность, проходящая через начало координат в плоскости
получаем прямую
линию, т. е. окружность, проходящая через начало координат в плоскости ![]() , переходит в
прямую в плоскости
, переходит в
прямую в плоскости ![]() .
.
Отметим, что отображение с помощью функции (9) может переводить внутренность отображаемой окружности как на внутренность, так и на внешность отображенной окружности.
Функция (9) в принципе зависит от
трех параметров, за которые можно взять отношение чисел ![]() к одному из них (не равному
0).
к одному из них (не равному
0).
Поэтому, чтобы определить преобразование (9), надо задать три условия. Обычно задают три пары соответствующих точек:
![]()
![]() .
.
Легко подсчитать, что
![]() ,
,
 .
.
Отсюда
![]() . (11)
. (11)
Это и есть преобразование (9),
переводящее точки ![]() в
в ![]()
![]() .
.
Пусть заданы две окружности ![]() и
и ![]() соответственно в
плоскостях
соответственно в
плоскостях ![]() и
и
![]() .
Требуется найти дробно-линейное отображение, переводящее
.
Требуется найти дробно-линейное отображение, переводящее ![]() на
на ![]() и внутренность
и внутренность ![]() на внутренность
на внутренность ![]() .
.
На ![]() и
и ![]() соответственно зададим произвольные
тройки точек
соответственно зададим произвольные
тройки точек ![]() и
и
![]() ,
следующие в положительном направлении, т. е. против часовой стрелки. Тогда преобразование
(11) и будет решением поставленной задачи.
,
следующие в положительном направлении, т. е. против часовой стрелки. Тогда преобразование
(11) и будет решением поставленной задачи.
В самом деле, оно отображает
точки ![]() соответственно
в точки
соответственно
в точки ![]()
![]() и, очевидно,
окружность
и, очевидно,
окружность ![]() на
на
![]() (в силу
кругового свойства).
(в силу
кругового свойства).
Тот факт, что в данном случае
внутренность ![]() переходит
на внутренность
переходит
на внутренность ![]() ,
следует из конформности отображения, осуществляемого дробно-линейной функцией.
,
следует из конформности отображения, осуществляемого дробно-линейной функцией.
В данном случае окружности ![]() ,
, ![]() имеют положительную
ориентацию (проходятся против часовой стрелки). В силу конформности отображения
внутренняя нормаль к
имеют положительную
ориентацию (проходятся против часовой стрелки). В силу конформности отображения
внутренняя нормаль к ![]() (например, в точке
(например, в точке ![]() ) переходит в дугу
окружности (перпендикулярной
) переходит в дугу
окружности (перпендикулярной ![]() в точке
в точке ![]() ), которая находится внутри
), которая находится внутри ![]() , а это и обеспечивает
отображение внутренности
, а это и обеспечивает
отображение внутренности ![]() на внутренность
на внутренность ![]() .
.
Если же нужно найти
дробно-линейное преобразование, отображающее ![]() на
на ![]() и внутренность
и внутренность ![]() на внешность
на внешность ![]() , то в формуле (11)
надо взять точки
, то в формуле (11)
надо взять точки ![]() на
на
![]() , расположенные
в положительном направлении, а точки
, расположенные
в положительном направлении, а точки ![]() на
на ![]() - в отрицательном направлении.
- в отрицательном направлении.

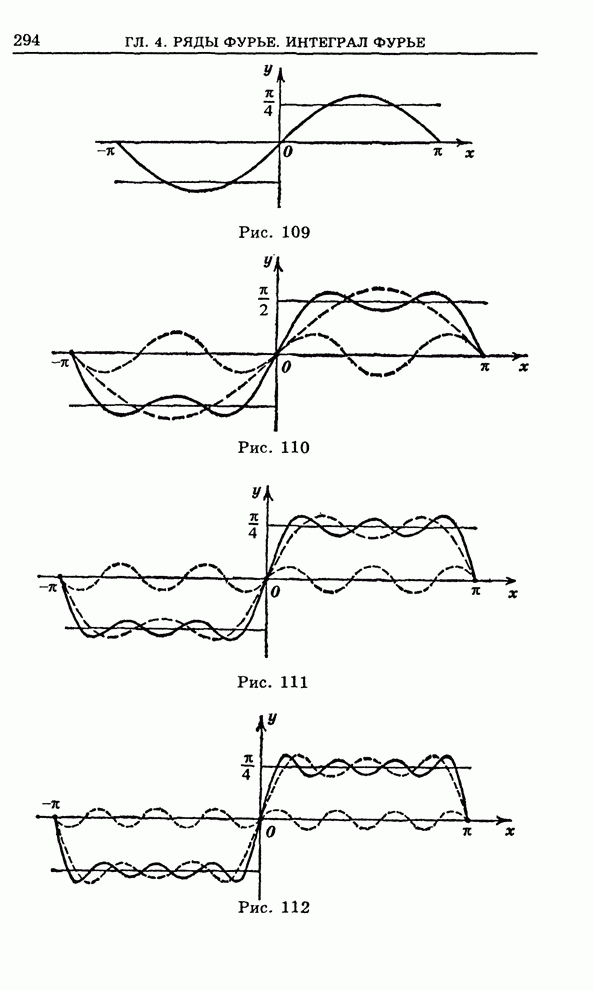
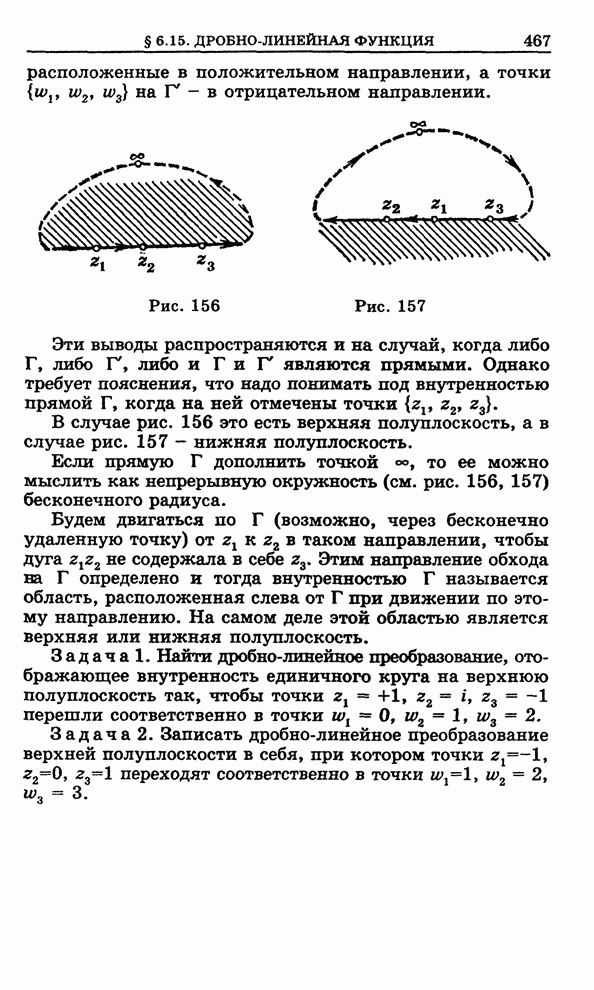
Рис. 156

Рис. 157
Эти выводы распространяются и на
случай, когда либо ![]() , либо
, либо ![]() , либо и
, либо и ![]() и
и ![]() являются прямыми. Однако требует
пояснения, что надо понимать под внутренностью прямой
являются прямыми. Однако требует
пояснения, что надо понимать под внутренностью прямой ![]() , когда на ней отмечены
точки
, когда на ней отмечены
точки ![]() .
.
В случае рис. 156 это есть верхняя полуплоскость, а в случае рис. 157 - нижняя полуплоскость.
Если прямую ![]() дополнить точкой
дополнить точкой ![]() , то ее можно
мыслить как непрерывную окружность (см. рис. 156, 157) бесконечного радиуса.
, то ее можно
мыслить как непрерывную окружность (см. рис. 156, 157) бесконечного радиуса.
Будем двигаться по ![]() (возможно, через
бесконечно удаленную точку) от
(возможно, через
бесконечно удаленную точку) от ![]() к
к ![]() в таком направлении, чтобы дуга
в таком направлении, чтобы дуга ![]() не содержала в
себе
не содержала в
себе ![]() .
Этим направление обхода на
.
Этим направление обхода на ![]() определено и тогда внутренностью
определено и тогда внутренностью ![]() называется
область, расположенная слева от
называется
область, расположенная слева от ![]() при движении по этому направлению.
На самом деле этой областью является верхняя или нижняя полуплоскость.
при движении по этому направлению.
На самом деле этой областью является верхняя или нижняя полуплоскость.
3адача 1. Найти дробно-линейное
преобразование, отображающее внутренность единичного круга на верхнюю
полуплоскость так, чтобы точки ![]() ,
, ![]() ,
, ![]() перешли соответственно в точки
перешли соответственно в точки ![]() ,
, ![]() ,
, ![]() .
.
Задача 2. Записать
дробно-линейное преобразование верхней полуплоскости в себя, при котором точки ![]() ,
, ![]() ,
, ![]() переходят
соответственно в точки
переходят
соответственно в точки ![]() ,
, ![]() ,
, ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. Обыкновенные дифференциальные уравнения
- 1.1. Задача, приводящая к дифференциальному уравнению
- 1.2. Общие понятия
- 1.2.1. Понятие обыкновенного дифференциального уравнения
- 1.2.2. Дифференциальное уравнение первого порядка
- 1.2.3. Задача Коши
- 1.2.4. Примеры дифференциальных уравнений первого порядка
- 1.2.5. Общий интеграл дифференциального уравнения первого порядка
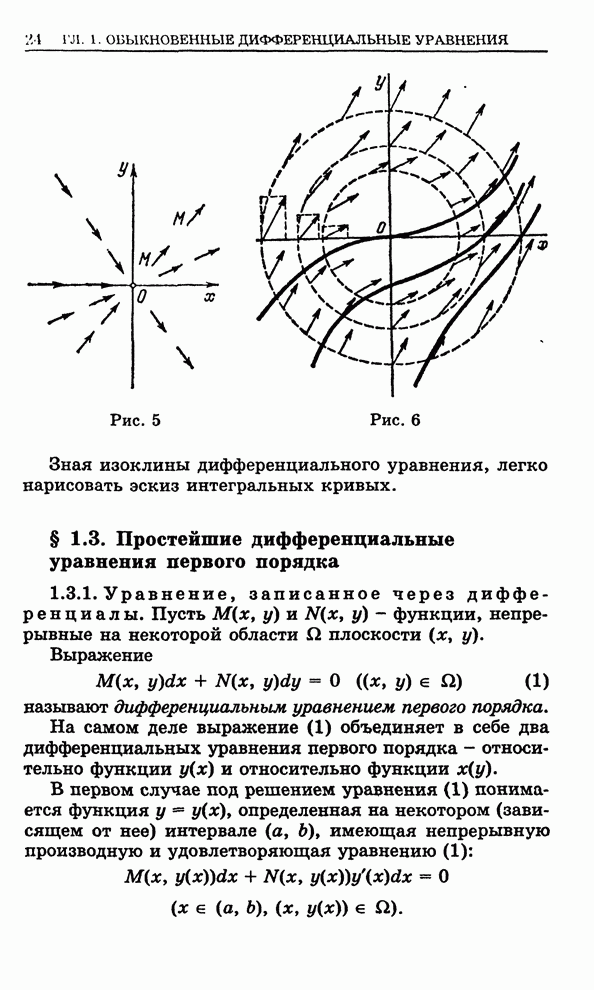
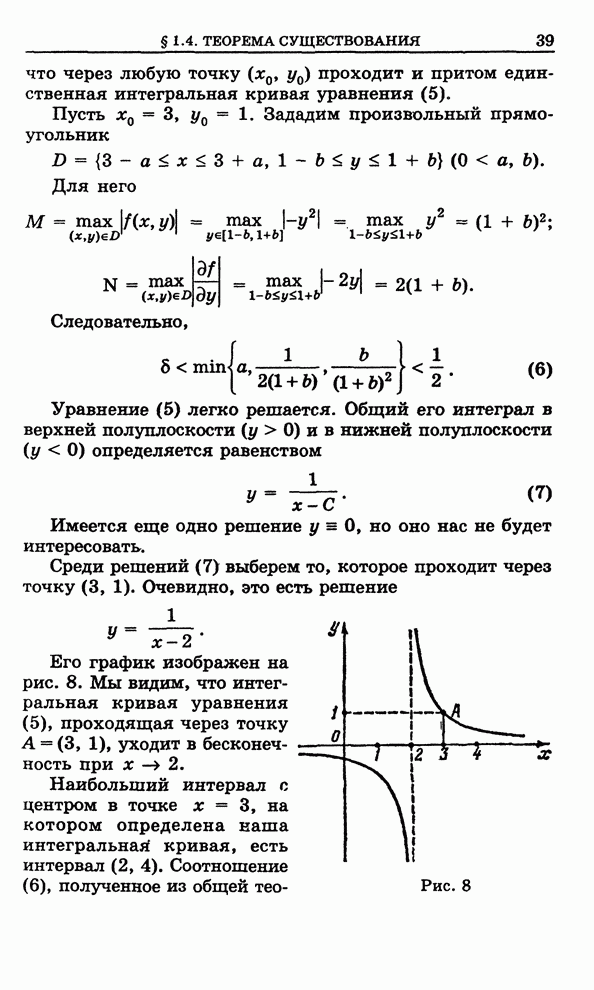
- 1.2.6. Поле направлений
- 1.3. Простейшие дифференциальные уравнения первого порядка
- 1.3.1. Уравнение, записанное через дифференциалы
- 1.3.2. Уравнения с разделенными переменными
- 1.3.3. Уравнения с разделяющимися переменными
- 1.3.4. Однородные уравнения
- 1.3.5. Линейное уравнение
- 1.3.6. Уравнение Бернулли
- 1.4. Теорема существования решения дифференциального уравнения первого порядка
- 1.5. Метрическое пространство
- 1.5.1. Понятие метрического пространства
- 1.5.2. Полное метрическое пространство
- 1.5.3. Принцип сжатых отображений
- 1.5.4. Приближенное значение корня функции
- 1.5.5. Метод Ньютона
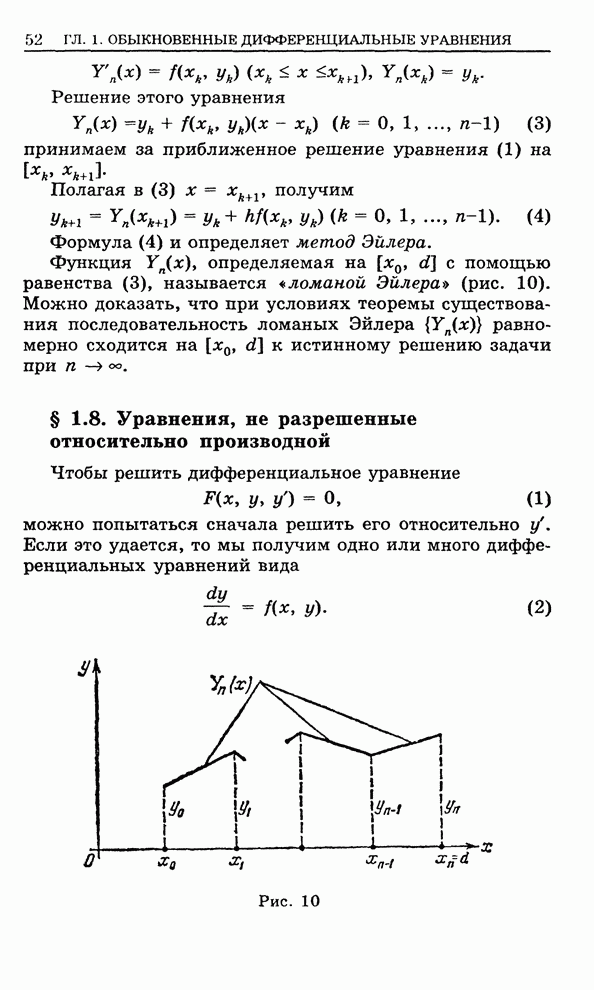
- 1.6. Доказательство теоремы существования решения диффереацнального уравнения первого порядка
- 1.7. Метод Эйлера приближенного решения дифференциального уравнения первого порядка
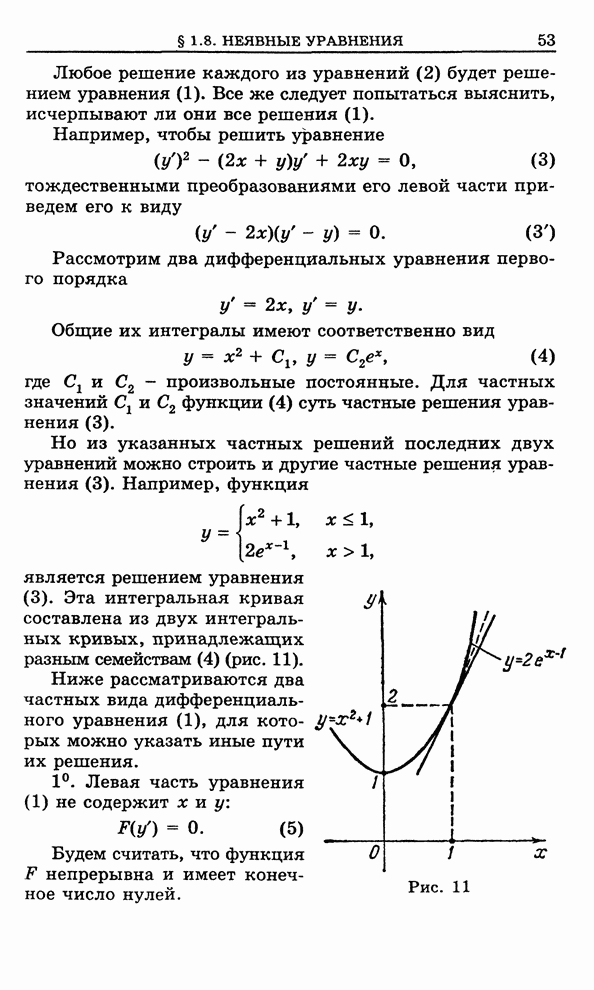
- 1.8. Уравнения, не разрешенные относительно производной
- 1.9. Особые решения
- 1.10. Огибающая семейства кривых
- 1.11. Дифференциальное уравнение второго порядка
- 1.12. Система из двух дифференциальных уравнений первого порядка
- 1.13. Дифференциальное уравнение n-го порядка
- 1.14. Понижение порядка дифференциального уравнения
- 1.15. Линейные уравнения высшего порядка
- 1.15.1. Понятие линейного уравнения высшего порядка
- 1.15.2. Фундаментальная система решений уравнения
- 1.15.3. Определитель Вронского
- 1.15.4. Структура общего решения
- 1.16. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- 1.16.1. Методы решения
- 1.16.2. Уравнение Эйлера
- 1.17. Метод вариации постоянных
- 1.18. Частное решение неоднородного уравнения с постоянными коэффициентами. Приложения
- 1.18.1. Методы нахождения частных решений
- 1.18.2. Дифференциальное уравнение колебания пружины
- 1.19. Системы дифференциальных уравнений. Фазовое пространство
- 1.20. Линейная однородная система дифференциальных уравнений
- 1.21. Общее решение линейной однородной системы дифференциальных уравнений с постоянными коэффициентами
- 1.22. Сведение системы уравнений к одному уравнению
- 1.23. Неоднородная система линейных дифференциальных уравнений с постоянными коэффициентами
- 1.24. Интегрирование дифференциальных уравнений с помощью степенных рядов
- 1.25. Элементы теории устойчивости
- 1.26. Классификация точек покоя
- Глава 2. Кратные интегралы
- 2.1. Введение
- 2.2. Сведения из теории меры Жордана
- 2.3. Свойства кратных интегралов. Теоремы существования
- 2.4. Сведение кратного интеграла к повторным
- 2.5. Доказательство существования интеграла от непрерывной функции
- 2.6. Замена переменных. Простейший случай
- 2.7. Замена переменных. Общий случай
- 2.8. Полярная система координат в плоскости
- 2.9. Полярная система координат в пространстве
- 2.10. Цилиндрические координаты
- 2.11. Площадь поверхности
- 2.12. Координаты центра масс
- 2.13. Несобственные интегралы
- 2.14. Несобственный интеграл с особенностями вдоль линии
- 2.15. Несобственный интеграл, зависящий от параметра
- Глава 3. Векторный анализ
- 3.1. Кусочно-гладкая ориентированная кривая
- 3.2. Криволинейный интеграл первого рода
- 3.3. Интеграл от вектора вдоль кривой
- 3.3.1. Поле вектора
- 3.3.2. Криволинейный интеграл от вектора вдоль кривой
- 3.3.3. Свойства криволинейных интегралов второго рода
- 3.4. Поле потенциала
- 3.4.1. Понятие потенциала и его свойства
- 3.4.2. Доказательство свойств потенциала
- 3.4.3. Ротор вектора
- 3.5. Дифференциальное уравнение в полных дифференциалах
- 3.6. Ориентация плоской области
- 3.7. Формула Грина
- 3.8. Интеграл по поверхности первого рода
- 3.9. Ориентация поверхности
- 3.10. Система координат и ориентация поверхности
- 3.11. Интеграл по ориентированной плоской области
- 3.12. Поток вектора через ориентированную поверхность
- 3.13. Дивергенция. Теорема Гаусса—Остроградского
- 3.14. Соленоидальное поле
- 3.15. Формула Стокса
- Глава 4. Ряды Фурье. Интеграл Фурье
- 4.1. Тригонометрические ряды
- 4.2. Сходимость тригонометрических рядов
- 4.3. Ряд Фурье
- 4.4. Признаки сходимости рядов Фурье
- 4.5. Ортогональные свойства тригонометрических функций
- 4.6. Коэффициенты Фурье
- 4.7. Оценка коэффициентов Фурье
- 4.8. Пространство функций со скалярным произведением
- 4.9. Ортогональная система функций
- 4.10. Полнота тригонометрических функций
- 4.11. Комплексная форма ряда Фурье
- 4.12. Понятие интеграла Фурье. Повторный интеграл Фурье
- 4.13. Косинус- и синус- преобразования Фурье
- 4.14. Примеры
- 4.15. Приближение интеграла Фурье
- 4.16. Сумма Фейера
- 4.17. Полнота систем функций в С и L2’
- 4.18. Сведения из теории кратных рядов Фурье
- Глава 5. Уравнения математической физики
- 5.1. Температура тела
- 5.2. Задача Дирихле
- 5.3. Задача Дирихле для круга
- 5.4. Задача Дирихле для полуплоскости
- 5.5. Уравнение теплопроводности в стержне
- 5.6. Теплопроводность для бесконечного стержня
- 5.7. Малые колебания струны
- 5.8. Колебание бесконечной струны. Формула Даламбера
- 5.9. Колебание круглой мембраны
- 5.10. Общая задача Штурма-Лиувилля
- 5.11. Интеграл энергии (Дирихле)
- 5.12. Применение преобразований Фурье
- Глава 6. Теория функций комплексного переменного
- 6.1. Понятие функции комплексного переменного
- 6.2. Производная функция комплексного переменного
- 6.3. Условия Даламбера-Эйлера (Коши-Римана)
- 6.4. Гармонические функции
- 6.5. Обратная функция
- 6.6. Интегрирование функций комплексного переменного
- 6.7. Формула Коши
- 6.8. Интеграл типа Коши
- 6.9. Степенной ряд
- 6.10. Ряд Лорана
- 6.11. Классификация изолированных особых точек. Вычеты
- 6.12. Классификация особых точек на бесконечности
- 6.13. Теорема о вычетах
- 6.14. Вычисление интегралов при помощи вычетов
- 6.15. Линейная функция. Дробно-линейная функция
- Глава 7. Операционное исчисление
- 7.1. Изображение Лапласа
- 7.2. Изображение простейших функций и свойства изображений
- 7.3. Приложения операционного исчисления
- 7.3.1. Операторное уравнение
- 7.3.2. Решение систем дифференциальных уравнений
- 7.3.3. Вычисление интегралов
- Глава 8. Обобщенные функции
- 8.1. Понятие обобщенной функции
- 8.2. Операции над обобщенными функциями
- 8.3. Преобразование Фурье обобщенных функций