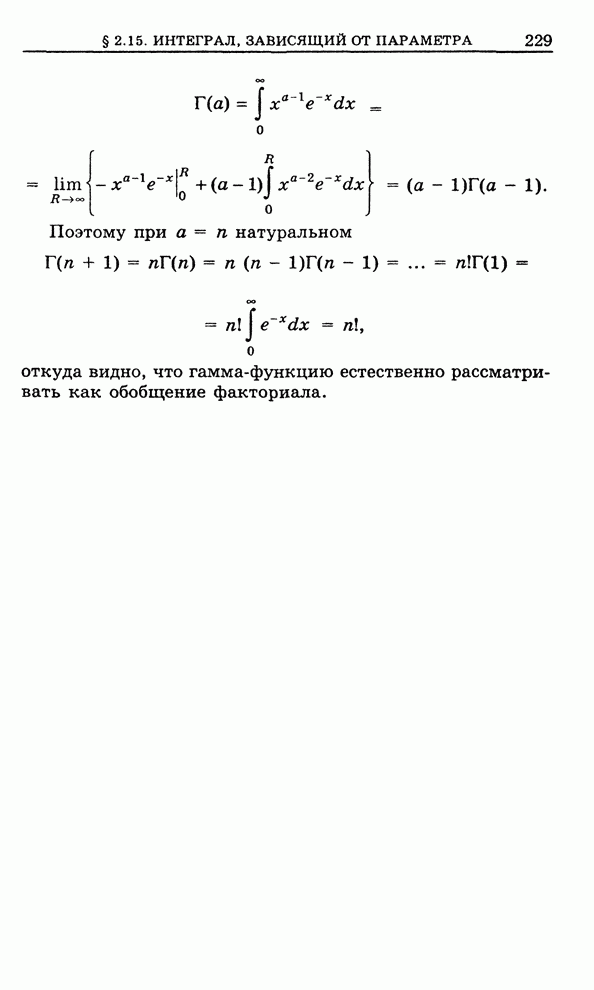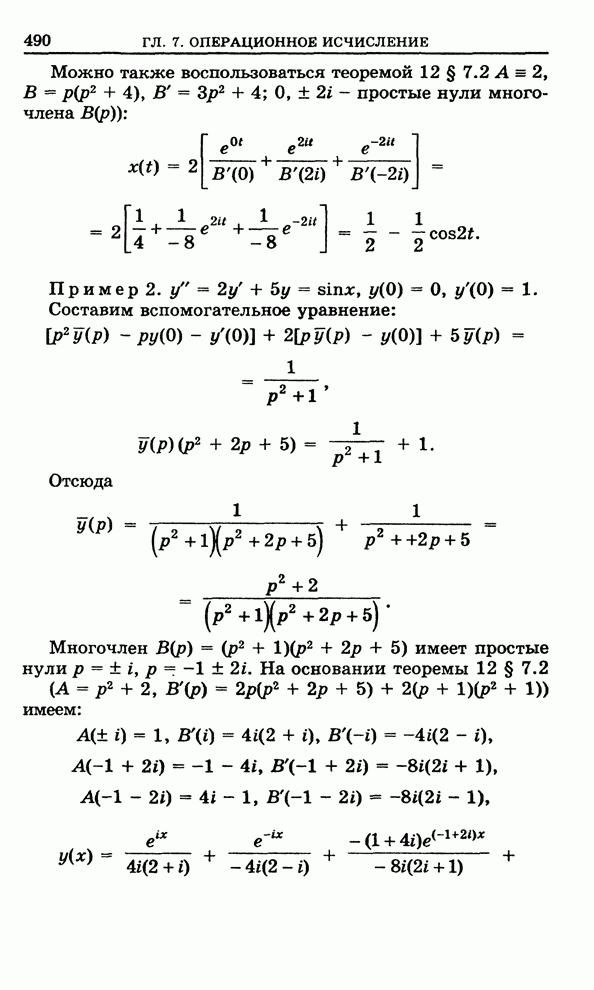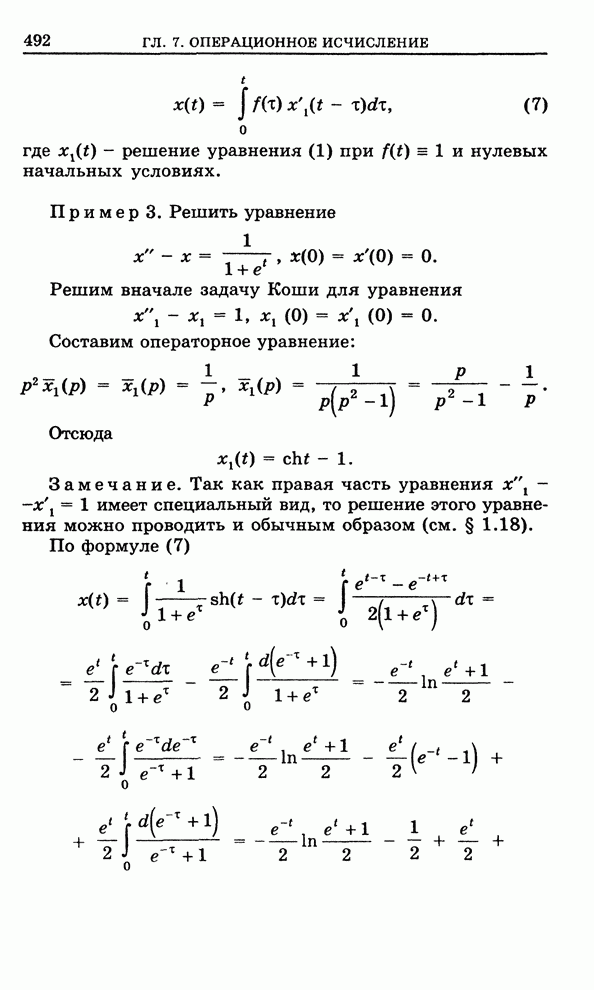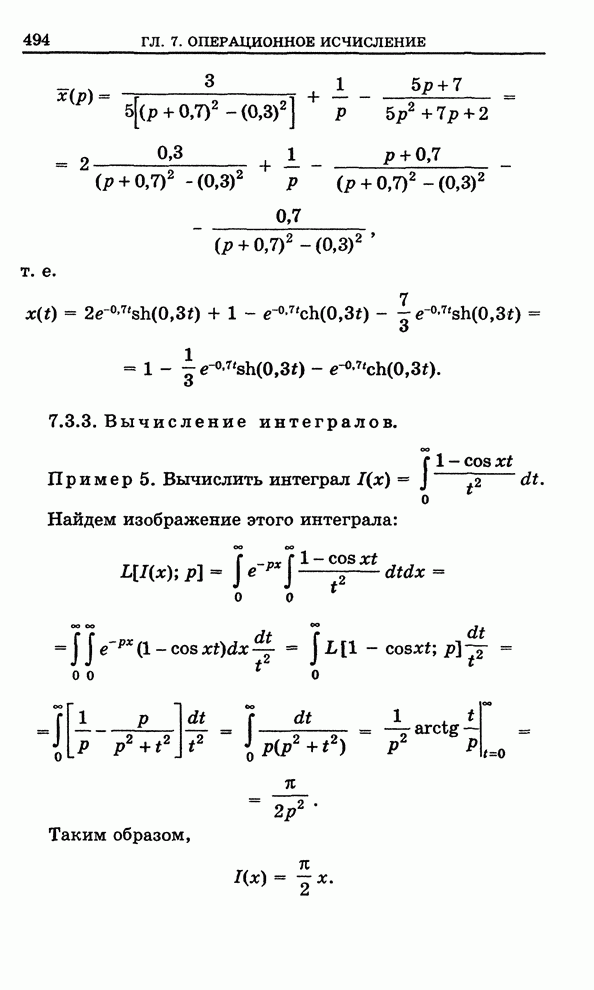| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ГЛАВА 2 КРАТНЫЕ ИНТЕГРАЛЫ
§ 2.1. Введение
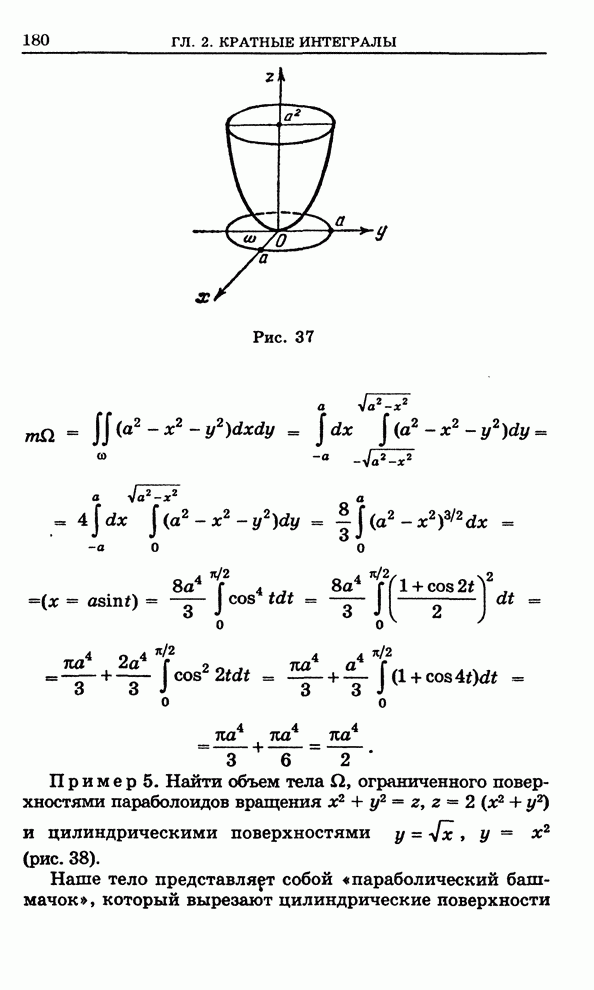
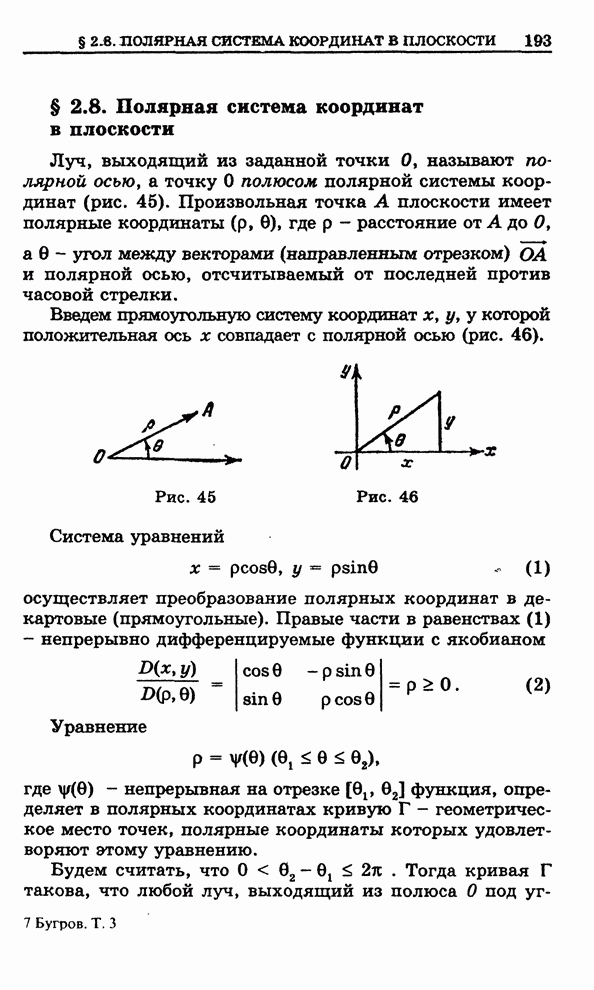
Пусть в
трехмерном пространстве, в котором определена прямоугольная система координат ![]() , задана непрерывная
поверхность
, задана непрерывная
поверхность
![]() ,
,
где ![]() есть ограниченное
(двумерное) множество, для которого возможно определить понятие его площади
(двумерной меры, см. ниже § 2.2). В качестве
есть ограниченное
(двумерное) множество, для которого возможно определить понятие его площади
(двумерной меры, см. ниже § 2.2). В качестве ![]() может быть взят круг, прямоугольник,
эллипс и т. д. Будем считать, что функция
может быть взят круг, прямоугольник,
эллипс и т. д. Будем считать, что функция ![]() положительная, и поставим задачу:
требуется определить объем тела, ограниченного сверху нашей поверхностью, снизу
плоскостью
положительная, и поставим задачу:
требуется определить объем тела, ограниченного сверху нашей поверхностью, снизу
плоскостью ![]() и
с боков цилиндрической поверхностью, проходящей через границу у плоского
множества
и
с боков цилиндрической поверхностью, проходящей через границу у плоского
множества ![]() ,
с образующей параллельной оси
,
с образующей параллельной оси ![]() .
.
Искомый объем
естественно определить следующим образом. Разделим ![]() на конечное число частей
на конечное число частей
![]() ,
(1)
,
(1)
перекрывающихся между собой разве
что по своим границам. Однако эти части должны быть такими, чтобы можно было
определить их площади (двумерные меры), которые мы обозначим соответственно
через ![]() .
.
Введем понятие диаметра множества ![]() - это есть точная
верхняя грань
- это есть точная
верхняя грань ![]() .
.
В каждой части ![]() выберем по
произвольной точке
выберем по
произвольной точке ![]() и составим сумму
и составим сумму
 , (2)
, (2)
которую
естественно считать приближенным выражением искомого объема ![]() . Надо думать, что
приближение
. Надо думать, что
приближение ![]() будет
тем более точным, чем меньшими будут диаметры
будет
тем более точным, чем меньшими будут диаметры ![]() частей
частей ![]() . Поэтому естественно объем нашего тела
определить как предел суммы (2)
. Поэтому естественно объем нашего тела
определить как предел суммы (2)
 , (3)
, (3)
когда
максимальный диаметр частичных множеств разбиения (1) стремится к нулю, если,
конечно, этот предел существует и равен одному и тому же числу независимо от
способа последовательного разбиения ![]() .
.
Можно отвлечься
от задачи о нахождении объема тела и смотреть на выражение (3) как на некоторую
операцию, которая производится над функцией ![]() , определенной на
, определенной на ![]() . Эта операция называется операцией
двойного интегрирования по Риману функции
. Эта операция называется операцией
двойного интегрирования по Риману функции ![]() на множестве
на множестве ![]() , а ее результат - определенным
двойным интегралом (Римана) от
, а ее результат - определенным
двойным интегралом (Римана) от ![]() на
на ![]() , обозначаемым так:
, обозначаемым так:
 .
.
Пусть теперь в
трехмерном пространстве, где определена прямоугольная система координат ![]() , задано тело
, задано тело ![]() (множество) с
неравномерно распределенной в нем массой с плотностью распределения
(множество) с
неравномерно распределенной в нем массой с плотностью распределения ![]() . Требуется
определить общую массу тела
. Требуется
определить общую массу тела ![]() . Чтобы решить эту задачу, естественно
произвести разбиение
. Чтобы решить эту задачу, естественно
произвести разбиение ![]() на части
на части ![]() , объемы (трехмерные меры) которых (в
предположении, что они существуют) пусть будут
, объемы (трехмерные меры) которых (в
предположении, что они существуют) пусть будут ![]() , выбрать произвольным образом в каждой
части по точке
, выбрать произвольным образом в каждой
части по точке ![]() и
считать, что искомая масса равна
и
считать, что искомая масса равна
 . (4)
. (4)
Снова на
выражение (4) можно смотреть как на определенную операцию над функцией ![]() , заданной теперь на
трехмерном множестве
, заданной теперь на
трехмерном множестве ![]() . Эта операция на этот раз называется операцией
тройного интегрирования (по Риману), а результат ее - определенным тройным
интегралом (Римана), обозначаемым так:
. Эта операция на этот раз называется операцией
тройного интегрирования (по Риману), а результат ее - определенным тройным
интегралом (Римана), обозначаемым так:
 .
.
В этом же духе
определяется понятие ![]() -кратного интеграла Римана.
-кратного интеграла Римана.
Мы увидим, что
часть теории кратного интегрирования, содержащая теоремы существования и
теоремы об аддитивных свойствах интеграла, может быть изложена совершенно
аналогично как в одномерном, так и в ![]() -мерном случае. Однако в теории кратных
интегралов возникают трудности, которых не было у нас при изложении теории
однократных интегралов.
-мерном случае. Однако в теории кратных
интегралов возникают трудности, которых не было у нас при изложении теории
однократных интегралов.

Рис.26 Рис.27
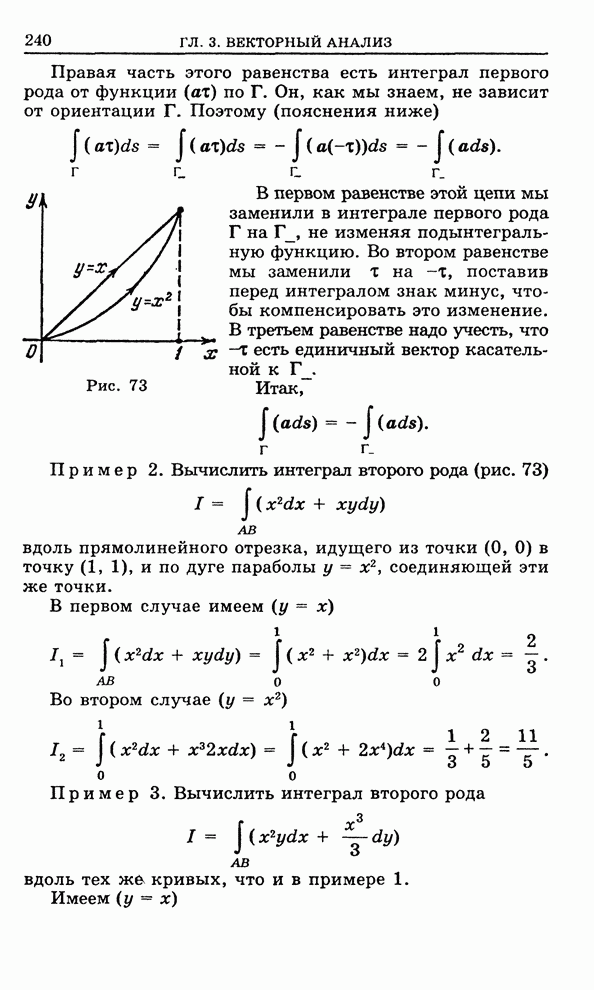
Дело в том, что
однократный интеграл Римана мы определили для очень простого множества -
отрезка ![]() , который
дробился снова на отрезки. Никаких трудностей в определении длины (одномерной
меры) отрезков не возникало. Между тем в случае двойных и вообще
, который
дробился снова на отрезки. Никаких трудностей в определении длины (одномерной
меры) отрезков не возникало. Между тем в случае двойных и вообще ![]() -кратных интегралов
область интегрирования
-кратных интегралов
область интегрирования ![]() приходится делить на части с
криволинейными границами, и возникает вопрос об общем определении понятия
площади или вообще
приходится делить на части с
криволинейными границами, и возникает вопрос об общем определении понятия
площади или вообще ![]() - мерной меры этих частей.
- мерной меры этих частей.
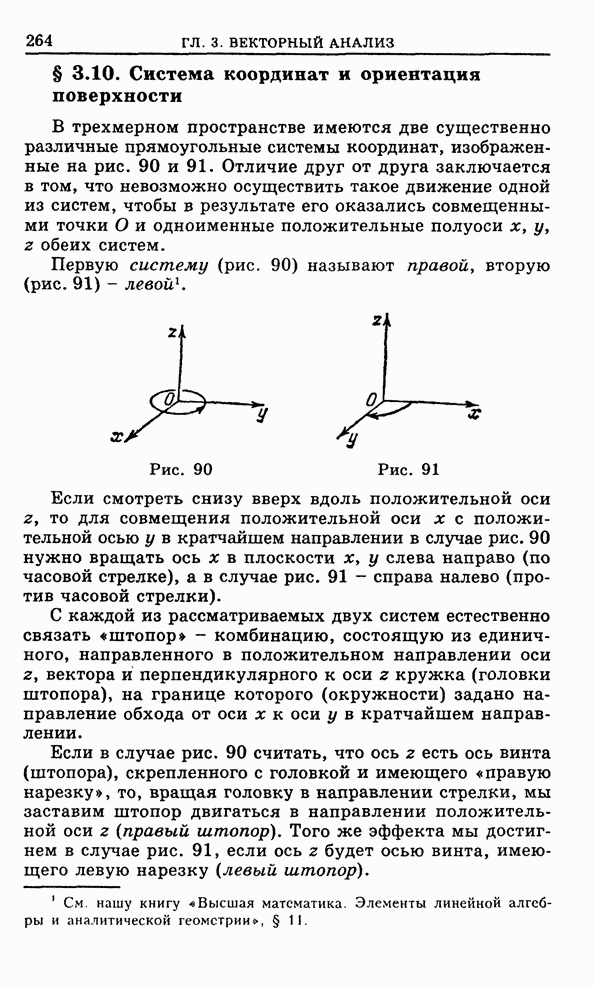
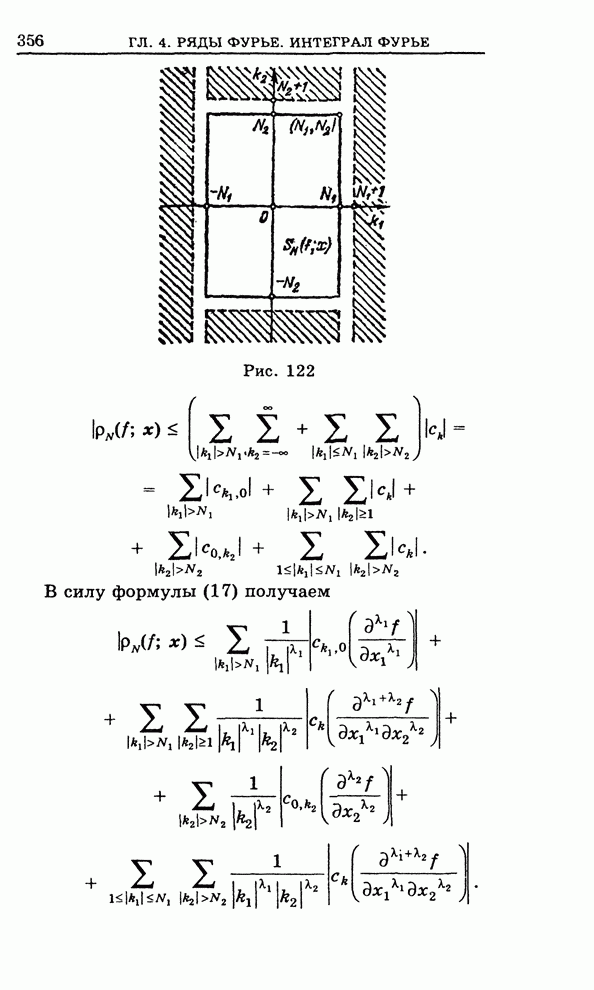
В двумерном случае мы будем иметь дело с ограниченными областями, имеющими гладкую границу (рис. 26) или кусочно-гладкую границу (рис. 27), т. е. состоящую из конечного числа гладких кусков (линий).
Эти области в свою очередь приходится делить на части, имеющие кусочно-гладкую границу.
Каждой такой
области ![]() и
некоторым другим множествам можно привести в соответствие положительное число
и
некоторым другим множествам можно привести в соответствие положительное число ![]() , называемое площадью
или двумерной мерой Жордана (общее определение двумерной меры Жордана дано в §
2.2).
, называемое площадью
или двумерной мерой Жордана (общее определение двумерной меры Жордана дано в §
2.2).
При этом выполняются свойства:
1) Если ![]() - прямоугольник с
основанием
- прямоугольник с
основанием ![]() и
высотой
и
высотой ![]() , то
, то
![]() .
.
2) Если ![]() и
и
![]() имеют
меры
имеют
меры ![]() , то
, то ![]() .
.
3) Если область ![]() разрезана при помощи кусочно-гладкой
кривой на две части
разрезана при помощи кусочно-гладкой
кривой на две части ![]() и
и ![]() , то
, то
![]() .
.
Существуют множества двумерной меры нуль такие, как точка, отрезок, гладкая или кусочно-гладкая кривая.
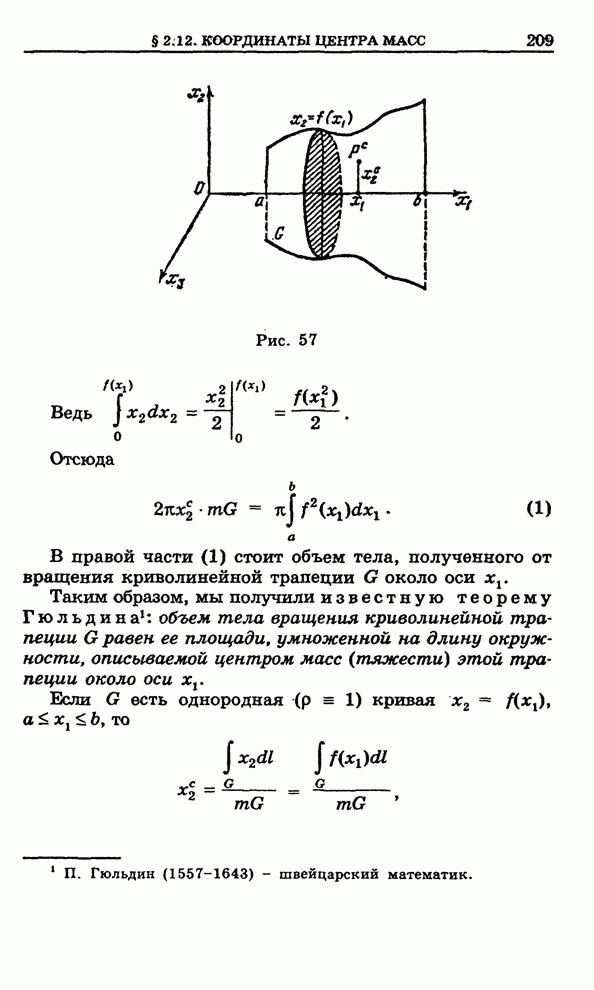
В трехмерном случае нас будут интересовать области, имеющие в качестве своей границы кусочно-гладкие поверхности. Про такие области будем говорить, что они имеют кусочно-гладкую границу. Шар, эллипсоид, куб могут служить примерами таких областей.
Поверхность называется гладкой, если в любой ее точке к ней можно провести касательную плоскость, непрерывно изменяющуюся вместе с этой точкой. Поверхность называется кусочно-гладкой, если ее можно разрезать на конечное число гладких кусков. По линиям разрезов касательные плоскости к поверхности могут и не существовать.
Для трехмерных
ограниченных областей ![]() с кусочно-гладкими границами можно
определить их объем (трехмерную меру), т. е. положительное число
с кусочно-гладкими границами можно
определить их объем (трехмерную меру), т. е. положительное число ![]() , удовлетворяющее
свойствам:
, удовлетворяющее
свойствам:
1) Если ![]() -
прямоугольный параллелепипед с ребрами
-
прямоугольный параллелепипед с ребрами ![]() , то
, то ![]() .
.
2) Если, ![]() и
и
![]() имеют
меры
имеют
меры ![]() , то
, то
![]() .
.
3) Если область ![]() разрезана при
помощи кусочно-гладкой поверхности на части
разрезана при
помощи кусочно-гладкой поверхности на части ![]() и
и ![]() , то
, то
![]() .
.
Есть множества трехмерной меры нуль. Такими являются точка, отрезок, прямоугольник (плоский), гладкая или кусочно-гладкая поверхность.
По аналогии
можно рассматривать ![]() -мерные области
-мерные области ![]() с кусочно-гладкой границей и
для них определить
с кусочно-гладкой границей и
для них определить ![]() -мерную меру -
-мерную меру - ![]() , обладающую свойствами,
подобными свойствам 1), 2), 3).
, обладающую свойствами,
подобными свойствам 1), 2), 3).
Прямоугольник ![]() в
в ![]() определяется как
множество точек
определяется как
множество точек ![]() ,
координаты которых удовлетворяют неравенствам
,
координаты которых удовлетворяют неравенствам
![]() .
.
Мера (![]() -мерная)
-мерная) ![]() определяется как
произведение:
определяется как
произведение:
![]() .
.
Примером гладкой
поверхности ![]() может
быть множество точек
может
быть множество точек ![]() , удовлетворяющих уравнению
, удовлетворяющих уравнению
![]() ,
,
где ![]() может иметь одно из
значений
может иметь одно из
значений ![]() .
При этом
.
При этом ![]() есть
непрерывно дифференцируемая функция на замыкании некоторой
есть
непрерывно дифференцируемая функция на замыкании некоторой ![]() -мерной ограниченной области
-мерной ограниченной области ![]() точек
точек ![]() .
.
Кусочно-гладкая
поверхность в ![]() по
определению состоит из конечного числа гладких кусков (поверхностей),
пересекающихся между собой разве что по их краям.
по
определению состоит из конечного числа гладких кусков (поверхностей),
пересекающихся между собой разве что по их краям.
Повторим определение кратного интеграла, не прибегая к задачам геометрического или физического содержания.
Пусть в ![]() -мерном пространстве
-мерном пространстве
![]() задана
ограниченная область
задана
ограниченная область ![]() с кусочно-гладкой границей
с кусочно-гладкой границей ![]() и на
и на ![]() (или
(или ![]() ) задана функция
) задана функция
![]() .
.
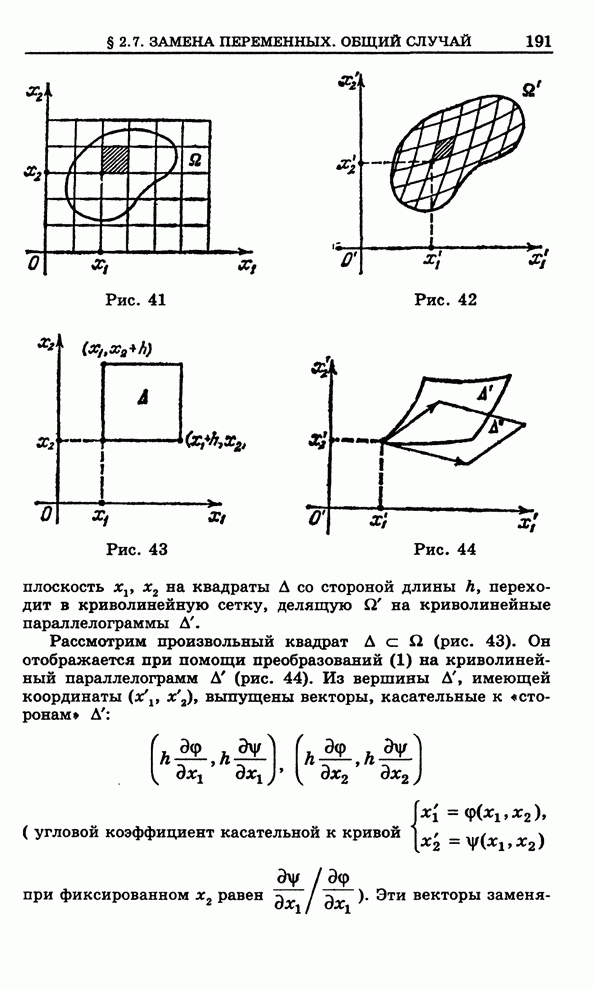
Разрежем ![]() на части
на части ![]() , пересекающиеся
разве что по своим границам, которые будем считать кусочно-гладкими. Для
краткости будем говорить, что мы произвели разбиение
, пересекающиеся
разве что по своим границам, которые будем считать кусочно-гладкими. Для
краткости будем говорить, что мы произвели разбиение ![]() множества
множества ![]() .
.
Выберем в каждой
части ![]() по
произвольной точке
по
произвольной точке ![]() и составим сумму
и составим сумму
 ,
,
которую будем
называть интегральной суммой Римана функции ![]() отвечающей разбиению
отвечающей разбиению ![]() . Предел суммы
. Предел суммы
 , (5)
, (5)
когда
максимальный диаметр частичных множеств ![]() стремится к нулю, называется кратным
интегралом от функции
стремится к нулю, называется кратным
интегралом от функции ![]() на
на ![]() (или по
(или по ![]() ).
).
Подчеркнем, что
предел (5) называется кратным интегралом функции ![]() , если он не зависит от выбора точек
, если он не зависит от выбора точек ![]() в
в ![]() и не зависит от
способов разбиения
и не зависит от
способов разбиения ![]() области
области ![]() .
.
Сделаем несколько замечаний.
Замечание 1.
Будем ли мы вычислять предел (5) для области ![]() или для ее замыкания
или для ее замыкания ![]() , не имеет значения.
Это связано с тем, что
, не имеет значения.
Это связано с тем, что ![]() , где
, где ![]() - граница
- граница ![]() , предположенная
кусочно-гладкой. А кусочно-гладкая граница имеет
, предположенная
кусочно-гладкой. А кусочно-гладкая граница имеет ![]() - мерную меру нуль (
- мерную меру нуль (![]() , см. ниже § 2.2).
, см. ниже § 2.2).
Замечание 2.
Если предел (5), т.е. кратный интеграл ![]() существует, то функция
существует, то функция ![]() ограничена на
ограничена на ![]() . Это доказывается
так же, как в случае одномерного определенного интеграла.
. Это доказывается
так же, как в случае одномерного определенного интеграла.

Рис. 28
Замечание 3. Если ![]() , то сумма мер тех
частиц
, то сумма мер тех
частиц ![]() ,
которые непосредственно прилегают к кусочно-гладкой границе
,
которые непосредственно прилегают к кусочно-гладкой границе ![]() , тоже стремится к нулю
, тоже стремится к нулю
![]() .
.
Здесь двойной
штрих при ![]()
![]() обозначает, что
сумма распространена на те части
обозначает, что
сумма распространена на те части ![]() , которые прилегают к
, которые прилегают к ![]() .
.
Например, если
область ![]() разрезать
на части при помощи квадратной сетки, как на рис. 28, то соответствующее
разбиение можно записать в виде
разрезать
на части при помощи квадратной сетки, как на рис. 28, то соответствующее
разбиение можно записать в виде
![]() ,
,
где сумма ![]() распространена на
полные квадратики (попавшие в
распространена на
полные квадратики (попавшие в ![]() ), а сумма
), а сумма ![]() - на неполные квадратики.
Важно, что мера второй суммы стремится к нулю при неограниченном стремлении
диаметра диагонали квадратиков сетки к нулю:
- на неполные квадратики.
Важно, что мера второй суммы стремится к нулю при неограниченном стремлении
диаметра диагонали квадратиков сетки к нулю:
![]() .
.
Замечание 4. Из предыдущих замечаний следует, что
![]() .
.
Это показывает, что интеграл (5) можно определить так же, как предел суммы
![]() ,
,
распространенной
только на такие части ![]() разбиения, которые не прилегают к
разбиения, которые не прилегают к ![]() .
.
Замечания 1, 2, 3, 4 мы формально не обосновываем. Впрочем, они легко вытекают из приводимого ниже § 2.2.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. Обыкновенные дифференциальные уравнения
- 1.1. Задача, приводящая к дифференциальному уравнению
- 1.2. Общие понятия
- 1.2.1. Понятие обыкновенного дифференциального уравнения
- 1.2.2. Дифференциальное уравнение первого порядка
- 1.2.3. Задача Коши
- 1.2.4. Примеры дифференциальных уравнений первого порядка
- 1.2.5. Общий интеграл дифференциального уравнения первого порядка
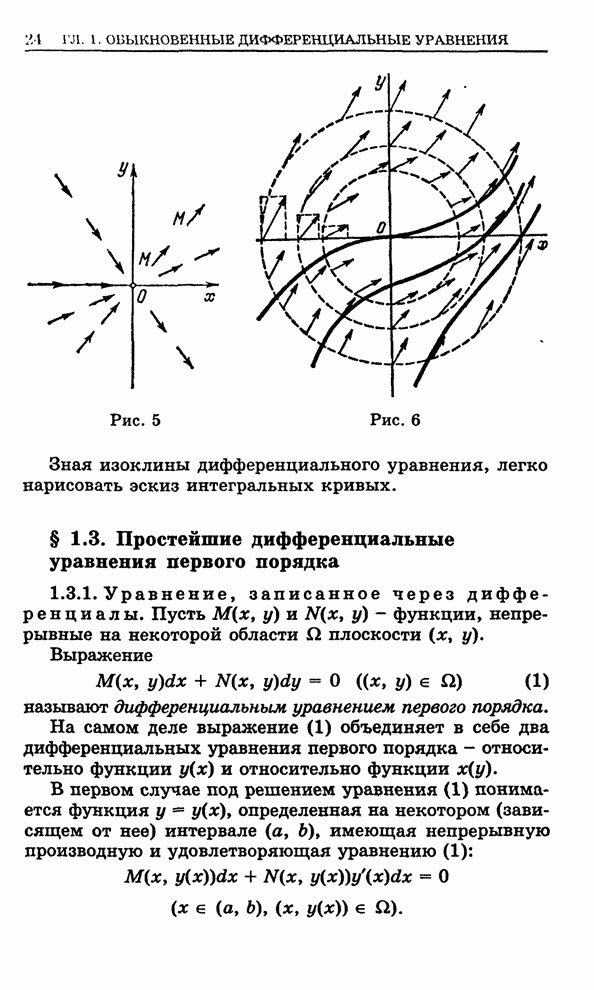
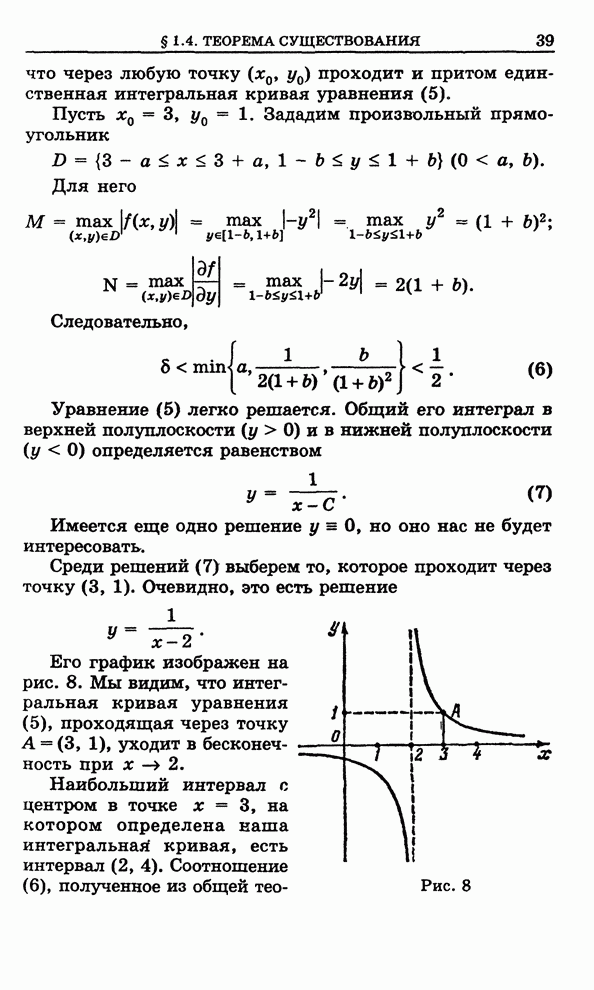
- 1.2.6. Поле направлений
- 1.3. Простейшие дифференциальные уравнения первого порядка
- 1.3.1. Уравнение, записанное через дифференциалы
- 1.3.2. Уравнения с разделенными переменными
- 1.3.3. Уравнения с разделяющимися переменными
- 1.3.4. Однородные уравнения
- 1.3.5. Линейное уравнение
- 1.3.6. Уравнение Бернулли
- 1.4. Теорема существования решения дифференциального уравнения первого порядка
- 1.5. Метрическое пространство
- 1.5.1. Понятие метрического пространства
- 1.5.2. Полное метрическое пространство
- 1.5.3. Принцип сжатых отображений
- 1.5.4. Приближенное значение корня функции
- 1.5.5. Метод Ньютона
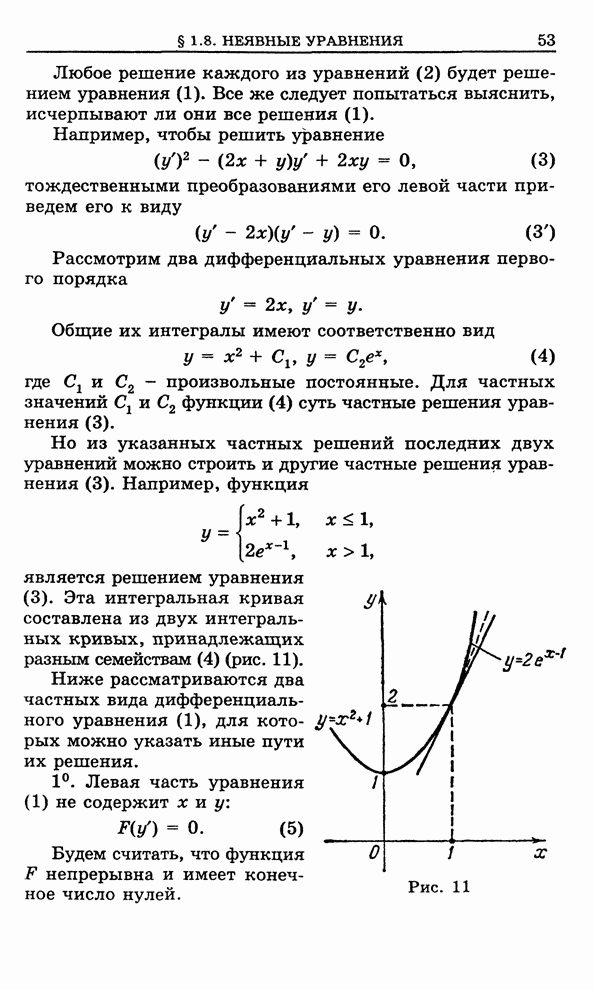
- 1.6. Доказательство теоремы существования решения диффереацнального уравнения первого порядка
- 1.7. Метод Эйлера приближенного решения дифференциального уравнения первого порядка
- 1.8. Уравнения, не разрешенные относительно производной
- 1.9. Особые решения
- 1.10. Огибающая семейства кривых
- 1.11. Дифференциальное уравнение второго порядка
- 1.12. Система из двух дифференциальных уравнений первого порядка
- 1.13. Дифференциальное уравнение n-го порядка
- 1.14. Понижение порядка дифференциального уравнения
- 1.15. Линейные уравнения высшего порядка
- 1.15.1. Понятие линейного уравнения высшего порядка
- 1.15.2. Фундаментальная система решений уравнения
- 1.15.3. Определитель Вронского
- 1.15.4. Структура общего решения
- 1.16. Линейные однородные уравнения n-го порядка с постоянными коэффициентами
- 1.16.1. Методы решения
- 1.16.2. Уравнение Эйлера
- 1.17. Метод вариации постоянных
- 1.18. Частное решение неоднородного уравнения с постоянными коэффициентами. Приложения
- 1.18.1. Методы нахождения частных решений
- 1.18.2. Дифференциальное уравнение колебания пружины
- 1.19. Системы дифференциальных уравнений. Фазовое пространство
- 1.20. Линейная однородная система дифференциальных уравнений
- 1.21. Общее решение линейной однородной системы дифференциальных уравнений с постоянными коэффициентами
- 1.22. Сведение системы уравнений к одному уравнению
- 1.23. Неоднородная система линейных дифференциальных уравнений с постоянными коэффициентами
- 1.24. Интегрирование дифференциальных уравнений с помощью степенных рядов
- 1.25. Элементы теории устойчивости
- 1.26. Классификация точек покоя
- Глава 2. Кратные интегралы
- 2.1. Введение
- 2.2. Сведения из теории меры Жордана
- 2.3. Свойства кратных интегралов. Теоремы существования
- 2.4. Сведение кратного интеграла к повторным
- 2.5. Доказательство существования интеграла от непрерывной функции
- 2.6. Замена переменных. Простейший случай
- 2.7. Замена переменных. Общий случай
- 2.8. Полярная система координат в плоскости
- 2.9. Полярная система координат в пространстве
- 2.10. Цилиндрические координаты
- 2.11. Площадь поверхности
- 2.12. Координаты центра масс
- 2.13. Несобственные интегралы
- 2.14. Несобственный интеграл с особенностями вдоль линии
- 2.15. Несобственный интеграл, зависящий от параметра
- Глава 3. Векторный анализ
- 3.1. Кусочно-гладкая ориентированная кривая
- 3.2. Криволинейный интеграл первого рода
- 3.3. Интеграл от вектора вдоль кривой
- 3.3.1. Поле вектора
- 3.3.2. Криволинейный интеграл от вектора вдоль кривой
- 3.3.3. Свойства криволинейных интегралов второго рода
- 3.4. Поле потенциала
- 3.4.1. Понятие потенциала и его свойства
- 3.4.2. Доказательство свойств потенциала
- 3.4.3. Ротор вектора
- 3.5. Дифференциальное уравнение в полных дифференциалах
- 3.6. Ориентация плоской области
- 3.7. Формула Грина
- 3.8. Интеграл по поверхности первого рода
- 3.9. Ориентация поверхности
- 3.10. Система координат и ориентация поверхности
- 3.11. Интеграл по ориентированной плоской области
- 3.12. Поток вектора через ориентированную поверхность
- 3.13. Дивергенция. Теорема Гаусса—Остроградского
- 3.14. Соленоидальное поле
- 3.15. Формула Стокса
- Глава 4. Ряды Фурье. Интеграл Фурье
- 4.1. Тригонометрические ряды
- 4.2. Сходимость тригонометрических рядов
- 4.3. Ряд Фурье
- 4.4. Признаки сходимости рядов Фурье
- 4.5. Ортогональные свойства тригонометрических функций
- 4.6. Коэффициенты Фурье
- 4.7. Оценка коэффициентов Фурье
- 4.8. Пространство функций со скалярным произведением
- 4.9. Ортогональная система функций
- 4.10. Полнота тригонометрических функций
- 4.11. Комплексная форма ряда Фурье
- 4.12. Понятие интеграла Фурье. Повторный интеграл Фурье
- 4.13. Косинус- и синус- преобразования Фурье
- 4.14. Примеры
- 4.15. Приближение интеграла Фурье
- 4.16. Сумма Фейера
- 4.17. Полнота систем функций в С и L2’
- 4.18. Сведения из теории кратных рядов Фурье
- Глава 5. Уравнения математической физики
- 5.1. Температура тела
- 5.2. Задача Дирихле
- 5.3. Задача Дирихле для круга
- 5.4. Задача Дирихле для полуплоскости
- 5.5. Уравнение теплопроводности в стержне
- 5.6. Теплопроводность для бесконечного стержня
- 5.7. Малые колебания струны
- 5.8. Колебание бесконечной струны. Формула Даламбера
- 5.9. Колебание круглой мембраны
- 5.10. Общая задача Штурма-Лиувилля
- 5.11. Интеграл энергии (Дирихле)
- 5.12. Применение преобразований Фурье
- Глава 6. Теория функций комплексного переменного
- 6.1. Понятие функции комплексного переменного
- 6.2. Производная функция комплексного переменного
- 6.3. Условия Даламбера-Эйлера (Коши-Римана)
- 6.4. Гармонические функции
- 6.5. Обратная функция
- 6.6. Интегрирование функций комплексного переменного
- 6.7. Формула Коши
- 6.8. Интеграл типа Коши
- 6.9. Степенной ряд
- 6.10. Ряд Лорана
- 6.11. Классификация изолированных особых точек. Вычеты
- 6.12. Классификация особых точек на бесконечности
- 6.13. Теорема о вычетах
- 6.14. Вычисление интегралов при помощи вычетов
- 6.15. Линейная функция. Дробно-линейная функция
- Глава 7. Операционное исчисление
- 7.1. Изображение Лапласа
- 7.2. Изображение простейших функций и свойства изображений
- 7.3. Приложения операционного исчисления
- 7.3.1. Операторное уравнение
- 7.3.2. Решение систем дифференциальных уравнений
- 7.3.3. Вычисление интегралов
- Глава 8. Обобщенные функции
- 8.1. Понятие обобщенной функции
- 8.2. Операции над обобщенными функциями
- 8.3. Преобразование Фурье обобщенных функций