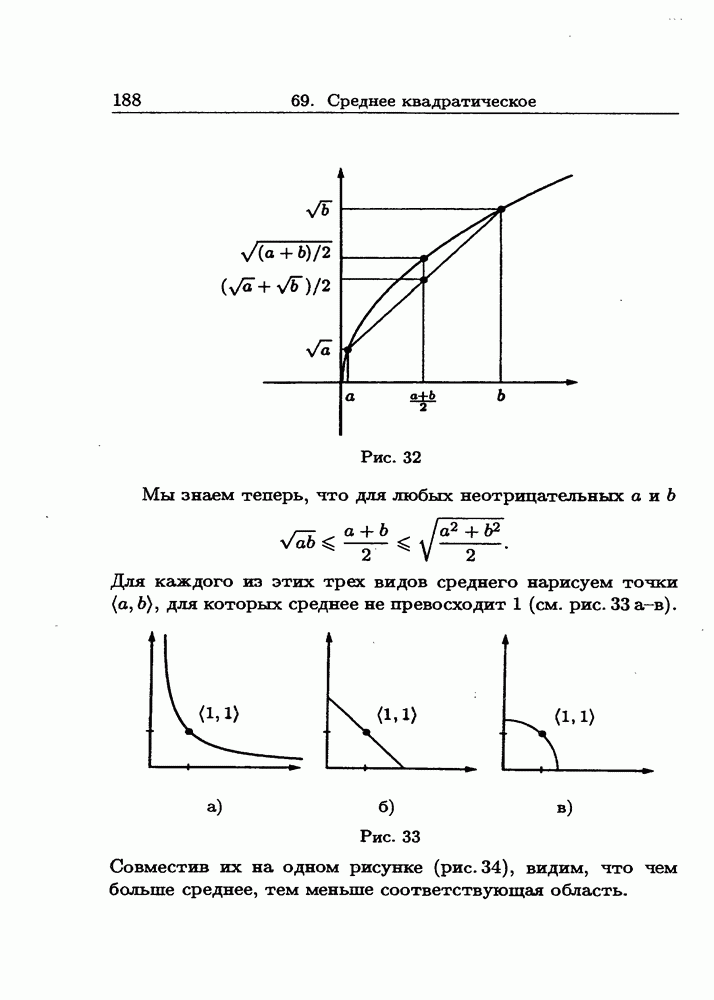
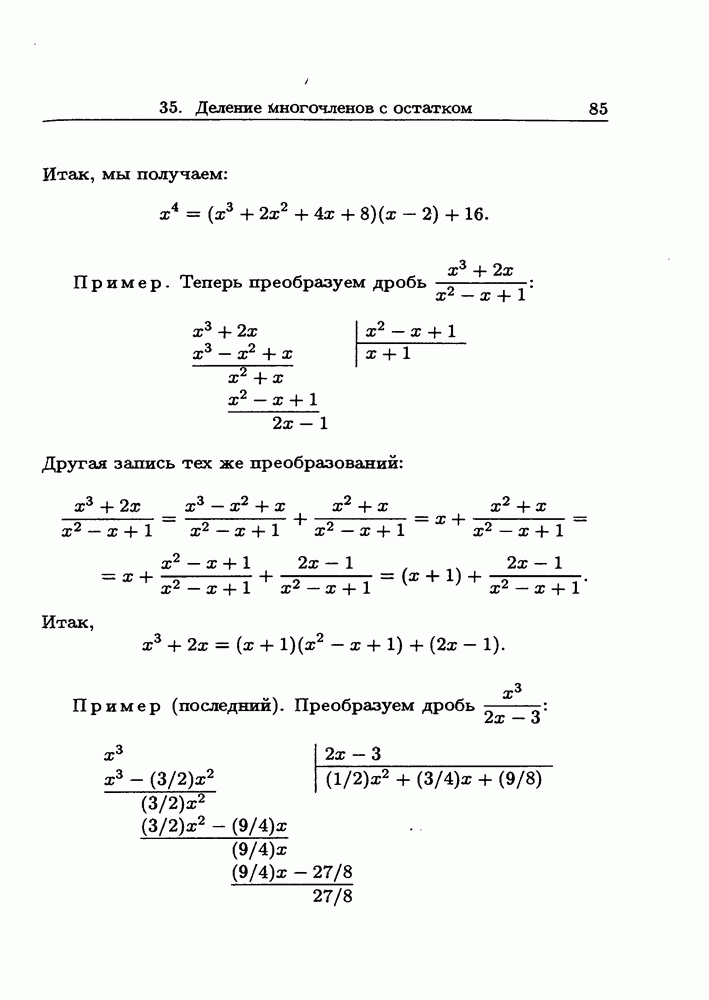| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
15. Действия с дробями
Бели Вас попросят сравнить дроби

то, конечно, Вы сразу скажете, что они равны:

Графически это равенство изображено на рис. 4.

Рис. 4
А что Вы скажете о дробях

Если бы Вы помнили наизусть таблицу умножения двузначных чисел, то сразу бы сказали, что они равны:

Но как быть, если мы не помним этой таблицы? Тогда надо привести дроби к общему знаменателю:

и сравнить числители

Так мы убедимся, что дроби равны — но так и не узнаем, что на самом деле обе они равны 13/23!
Задача 39. Что больше: 1/3 или 2/7?
Решение. 1/3 = 7/21, 2/7 = 6/21, т.е. 1/3 > 2/7.
Бытовая формулировка этой задачи («Что больше: бутылка на троих или две на семерых?») подсказывает другое решение: бутылка на троих — это две бутылки на шестерых, а не на семерых, т.е. 1/3 больше 2/7. Говоря научно, мы «привели дроби к одинаковому числителю»:

Задача 40. Что больше:  или
или 
Указание. Обе дроби меньше 1. На сколько?
Задача 41. Что больше:  или
или 

Рис. 5
Приведение к общему знаменателю — традиционная проблема при изучении арифметики. Классический вопрос: «Сколько торта останется мне, если брат съест половину торта, а сестра — треть торта?» Ответ (одна шестая) виден на рис. 5.
Мы уверены, что никто из наших читателей не складывает дроби, складывая отдельно числители и знаменатели:

Вместо суммы эта операция дает нечто среднее: 7/10 = 0,7 находится между 2/3 = 0,666 ... и 5/7 = 0,714285....
Это легко понять: если в одной компании было две бутылки на троих (по 2/3 на человека), а в другой компании было пять бутылок на семерых (по 5/7 на человека), то после встречи все выровняется, и будет семь бутылок на десятерых (7/10 на человека).
Задача 42. Назовем дроби  — целые положительные числа) соседними, если их разность
— целые положительные числа) соседними, если их разность  имеет числитель ±1, т. е. если
имеет числитель ±1, т. е. если 
1. Доказать, что в этом случае обе дроби несократимы.
2. Доказать, что если — и — соседние, то дробь  находится между ними и является соседней с обеими дробями
находится между ними и является соседней с обеими дробями 
3. Доказать, что в этом случае никакая дробь  с натуральными
с натуральными  , у которой
, у которой  не находится между
не находится между 
Задача 43. Метровый стержень разделили на 7 равных частей красными пометками и на 13 равных частей синими пометками. Затем его распилили на 20 равных частей. Докажите, что на всех этих частях (кроме крайних) будет ровно одна пометка — синяя или красная).
Решение. На крайних частях пометок не будет, так как — меньше, чем  Остается 18 частей. Достаточно доказать, что на каждой из них будет не более одной пометки. (Всего пометок также 18, поэтому ни одна часть не останется без пометки.) Красная пометка соответствует
Остается 18 частей. Достаточно доказать, что на каждой из них будет не более одной пометки. (Всего пометок также 18, поэтому ни одна часть не останется без пометки.) Красная пометка соответствует
числу  синяя — числу
синяя — числу  дробь
дробь

находится между ними. Следовательно, в ней будет проведен разрез, разделяющий  по разным частям.
по разным частям.
Задача 44. Что больше: пять процентов от семи миллионов или семь процентов от пяти миллионов? [«Вопрос мой прост и краток, — промолвил носорог, — Что больше: сорок пяток или пяток сорок?» — А. Милн. Винни-Пух и все-все-все. Пересказ Б. Заходера]
Задача 45. Как отрезать от шнура в  кусок в
кусок в  не имея метра?
не имея метра?
Решение. Кусок в  составляет три четверти от всего шнура:
составляет три четверти от всего шнура:

так что от шнура надо отрезать четверть (два раза сложив его пополам).
| << Предыдущий параграф | Следующий параграф >> |
- 1. Предисловие
- 2. Перемена мест слагаемых
- 3. Перемена мест сомножителей
- 4. Сложение столбиком
- 5. Таблица умножения. Умножение столбиком
- 6. Деление «уголком»
- 7. Двоичная система счисления
- 8. Коммутативность
- 9. Ассоциативность
- 10. Расстановки скобок
- 11. Дистрибутивность
- 12. Буквы в алгебре
- 13. Сложение отрицательных чисел
- 14. Умножение отрицательных чисел
- 15. Действия с дробями
- 16. Степени
- 17. Отрицательные степени
- 18. Как умножить a^m на a^n или почему наше определение удобно
- 19. Правило умножения степеней
- 20. Формулы сокращенного умножения. Квадрат суммы
- 21. Как объяснить формулу (a+b)^2=a^2+2ab+b^2 младшему брату или сестре
- 22. Квадрат разности
- 23. Разность квадратов
- 24. Куб суммы
- 25. Четвертая степень суммы
- 26. (a+b)^5, (a+b)^6 и треугольник Паскаля
- 27. Многочлены
- 28. Отступление: какие многочлены считать равными?
- 29. Сколько одночленов останется?
- 30. Коэффициенты и значения
- 31. Разложение на множители
- 32. Рациональные выражения
- 33. Преобразование рационального выражения в частное двух многочленов
- 34. Многочлены и рациональные дроби с одной переменной
- 35. Деление многочленов с остатком
- 36. Остаток при делении на х — а
- 37. Многочлены, значения, интерполяция
- 38. Арифметические прогрессии
- 39. Сумма арифметической прогрессии
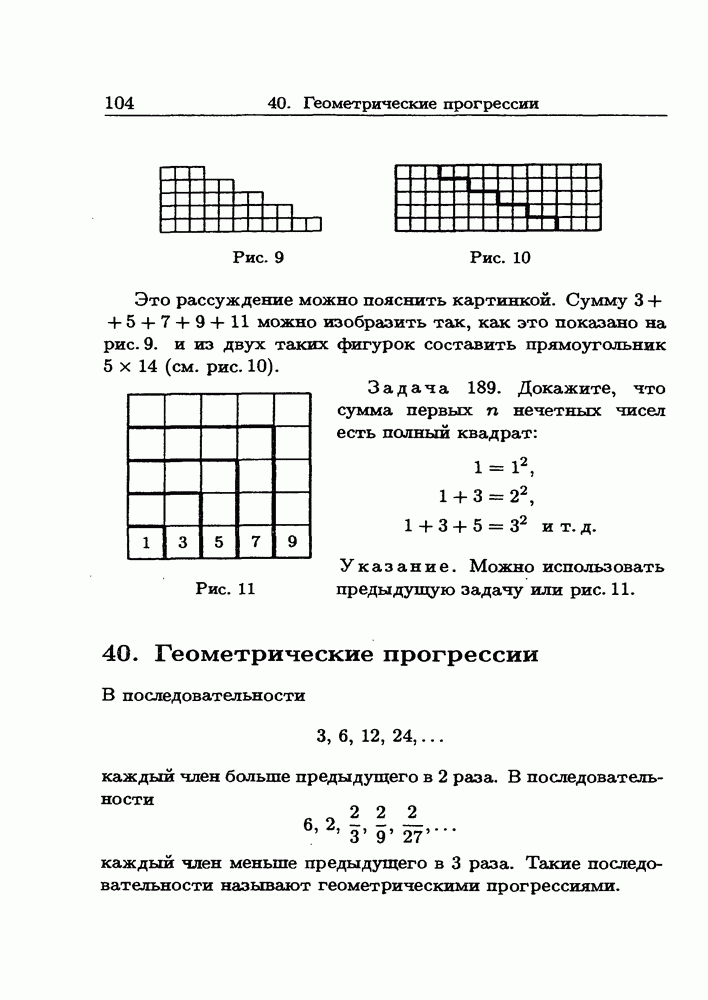
- 40. Геометрические прогрессии
- 41. Сумма геометрической прогрессии
- 42. Разные задачи о прогрессиях
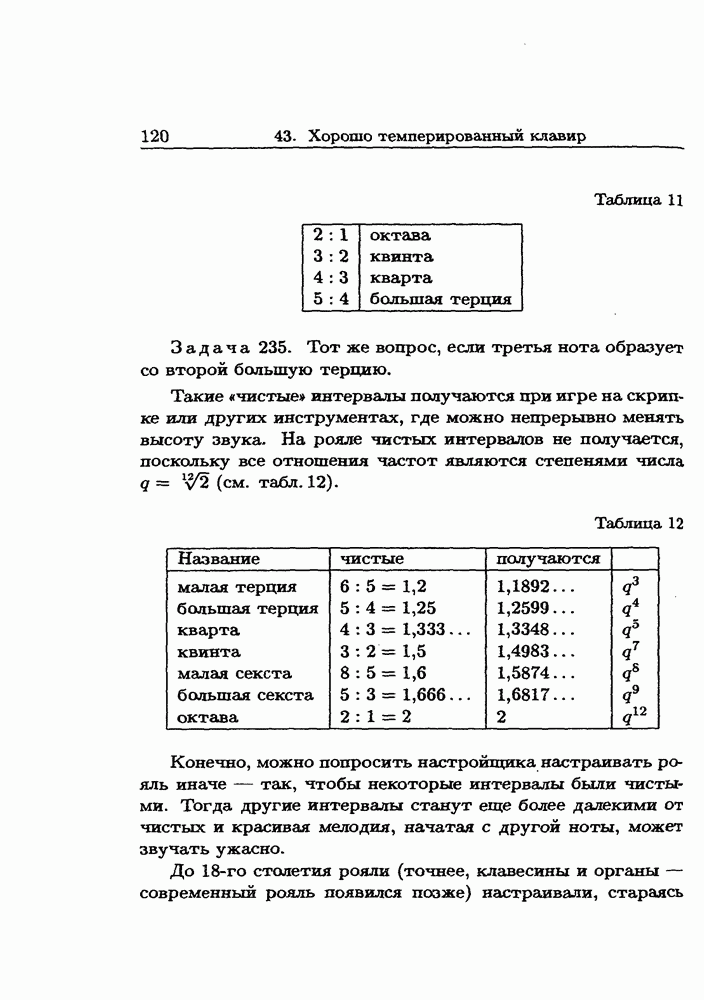
- 43. Хорошо темперированный клавир
- 44. Сумма бесконечной прогрессии
- 45. Уравнения
- 46. Квадратное уравнение
- 47. Случай p = 0. Квадратный корень
- 48. Свойства квадратных корней
- 49. Уравнение х^2 + рх + q = 0
- 50. Теорема Виета
- 51. Разложение квадратного трехчлена на множители
- 52. Формула для корней уравнения ах^2 + bх + c = 0
- 53. Бще одна формула корней квадратного уравнения
- 54. Квадратное уравнение становится линейным
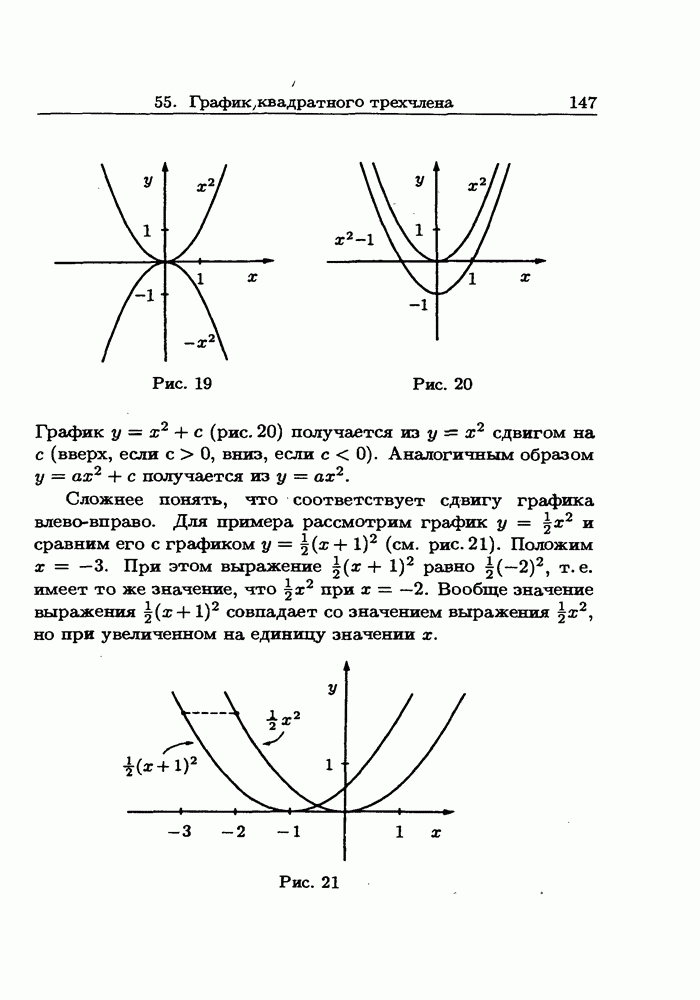
- 55. График квадратного трехчлена
- 56. Квадратные неравенства
- 57. Максимум и минимум квадратного трехчлена
- 58. Биквадратные уравнения
- 59. Возвратные уравнения
- 60. Как завалить на экзамене. Советы экзаменатору
- 61. Корни
- 62. Степень с дробным показателем
- 63. Доказательства числовых неравенств
- 64. Среднее арифметическое и среднее геометрическое
- 65. Среднее геометрическое не больше среднего арифметического
- 66. Задачи на максимум и минимум
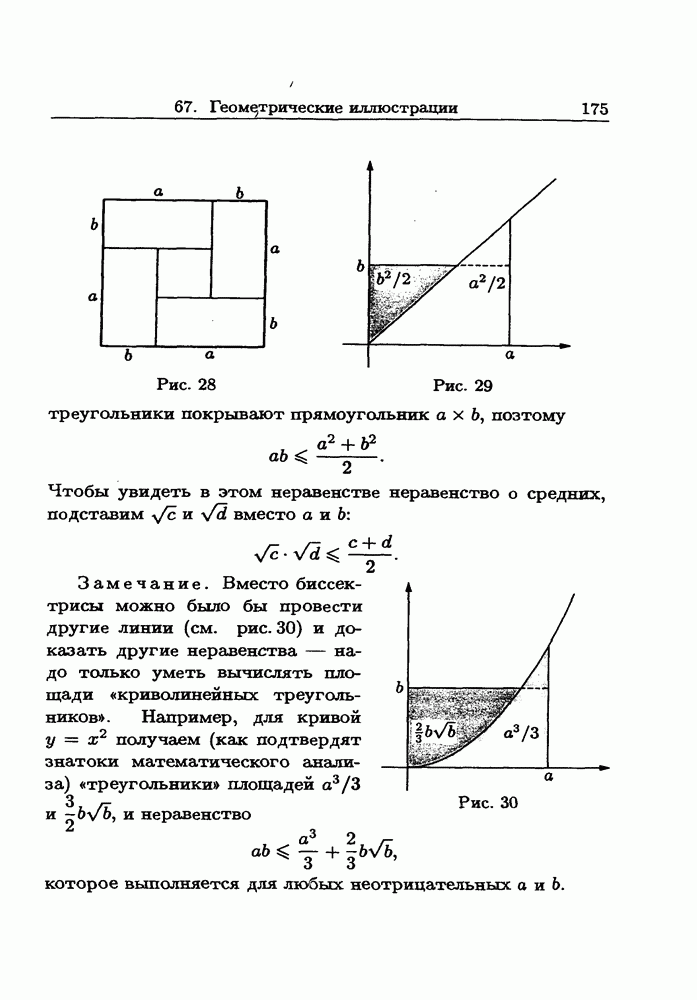
- 67. Геометрические иллюстрации
- 68. Средние многих чисел
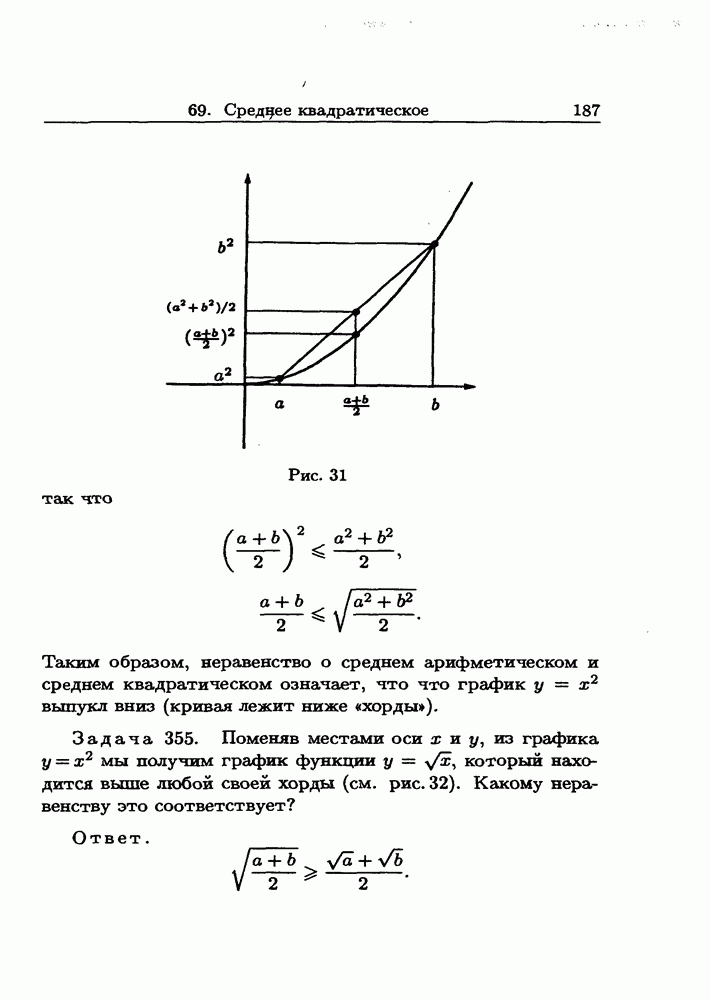
- 69. Среднее квадратическое
- 70. Среднее гармоническое
- 71. Книги для дальнейшего чтения