| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
23. Разность квадратов
Задача 69. Перемножить  .
.
Решение,  (
( сокращаются). Получаем формулу «разности квадратов»:
сокращаются). Получаем формулу «разности квадратов»:

Задача 70. Перемножить в уме 101 и 99.
Задача 71. Из квадрата со стороной а вырезан квадрат со стороной b (рис. 7). Разрезать получившуюся фигуру на части и сложить из них прямоугольник со сторонами  .
.

Рис. 7
Приведенные нами формулы (квадрат суммы, квадрат разности и разность квадратов) называют формулами сокращенного умножения.
Задача 72. Два целых числа, одно из которых на 2 больше другого, перемножили и к произведению прибавили 1.
Доказать, что получился точный квадрат (квадрат целого числа). Например,

Первое решение. Обозначим меньшее число через  . Тогда большее равно
. Тогда большее равно  . Их произведение равно
. Их произведение равно  Прибавив 1, получим
Прибавив 1, получим  (формула квадрата суммы).
(формула квадрата суммы).
Второе решение. Обозначим большее число через  . Тогда меньшее равно
. Тогда меньшее равно  Произведение равно
Произведение равно  . Прибавив 1, получим
. Прибавив 1, получим  (формула квадрата разности).
(формула квадрата разности).
Третье решение. Если мы не хотим отдавать предпочтение большему или меньшему из чисел, обозначим через  число между ними. Тогда меньшее число равно
число между ними. Тогда меньшее число равно  большее равно
большее равно  произведение равно
произведение равно  (формула разности квадратов), т.е. на единицу меньше точного квадрата.
(формула разности квадратов), т.е. на единицу меньше точного квадрата.
Задача 73. Напишем квадраты чисел 

и под каждыми двумя числами напишем их разность:

В нижнем ряду каждое число больше предыдущего на 2. Почему?
Решение. Соседние числа  имеют квадраты
имеют квадраты  . Разница квадратов равна
. Разница квадратов равна  и при увеличении
и при увеличении  на 1 она увеличивается на 2.
на 1 она увеличивается на 2.
Замечание. Последовательности чисел, в которых каждое следующее числю больше предыдущего на одну и ту же величину (как в 3,5,7,9,...), называют арифметическими прогрессиями. С ними мы еще встретимся.
Задача 74. Есть правило, позволяющее находить квадрат чисел, кончающихся на 5: «отбросьте последнюю цифру 5, останется число  ; умножьте
; умножьте  на
на  и к полученному числу допишите справа 25». Например:
и к полученному числу допишите справа 25». Например:

Обосновать это правило.
Задача 75. Вычислить


Рис. 8
Решение.

(см. рис. 8).
Задача 76. Вычислить 
Указание. Воспользуйтесь результатом предыдущей задачи.
Задача 77. Вычислить  .
.
Указание. Воспользуйтесь формулой разности квадратов.
Задача 78. Вычислить  .
.
Указание. И здесь полезна формула разности квадратов.
Задача 79. Вычислить  .
.
Указание. Даже здесь полезна формула разности квадратов.
Задача 80. Вычислить  Первое решение. Это равно
Первое решение. Это равно

Второе решение.

| << Предыдущий параграф | Следующий параграф >> |
- 1. Предисловие
- 2. Перемена мест слагаемых
- 3. Перемена мест сомножителей
- 4. Сложение столбиком
- 5. Таблица умножения. Умножение столбиком
- 6. Деление «уголком»
- 7. Двоичная система счисления
- 8. Коммутативность
- 9. Ассоциативность
- 10. Расстановки скобок
- 11. Дистрибутивность
- 12. Буквы в алгебре
- 13. Сложение отрицательных чисел
- 14. Умножение отрицательных чисел
- 15. Действия с дробями
- 16. Степени
- 17. Отрицательные степени
- 18. Как умножить a^m на a^n или почему наше определение удобно
- 19. Правило умножения степеней
- 20. Формулы сокращенного умножения. Квадрат суммы
- 21. Как объяснить формулу (a+b)^2=a^2+2ab+b^2 младшему брату или сестре
- 22. Квадрат разности
- 23. Разность квадратов
- 24. Куб суммы
- 25. Четвертая степень суммы
- 26. (a+b)^5, (a+b)^6 и треугольник Паскаля
- 27. Многочлены
- 28. Отступление: какие многочлены считать равными?
- 29. Сколько одночленов останется?
- 30. Коэффициенты и значения
- 31. Разложение на множители
- 32. Рациональные выражения
- 33. Преобразование рационального выражения в частное двух многочленов
- 34. Многочлены и рациональные дроби с одной переменной
- 35. Деление многочленов с остатком
- 36. Остаток при делении на х — а
- 37. Многочлены, значения, интерполяция
- 38. Арифметические прогрессии
- 39. Сумма арифметической прогрессии
- 40. Геометрические прогрессии
- 41. Сумма геометрической прогрессии
- 42. Разные задачи о прогрессиях
- 43. Хорошо темперированный клавир
- 44. Сумма бесконечной прогрессии
- 45. Уравнения
- 46. Квадратное уравнение
- 47. Случай p = 0. Квадратный корень
- 48. Свойства квадратных корней
- 49. Уравнение х^2 + рх + q = 0
- 50. Теорема Виета
- 51. Разложение квадратного трехчлена на множители
- 52. Формула для корней уравнения ах^2 + bх + c = 0
- 53. Бще одна формула корней квадратного уравнения
- 54. Квадратное уравнение становится линейным
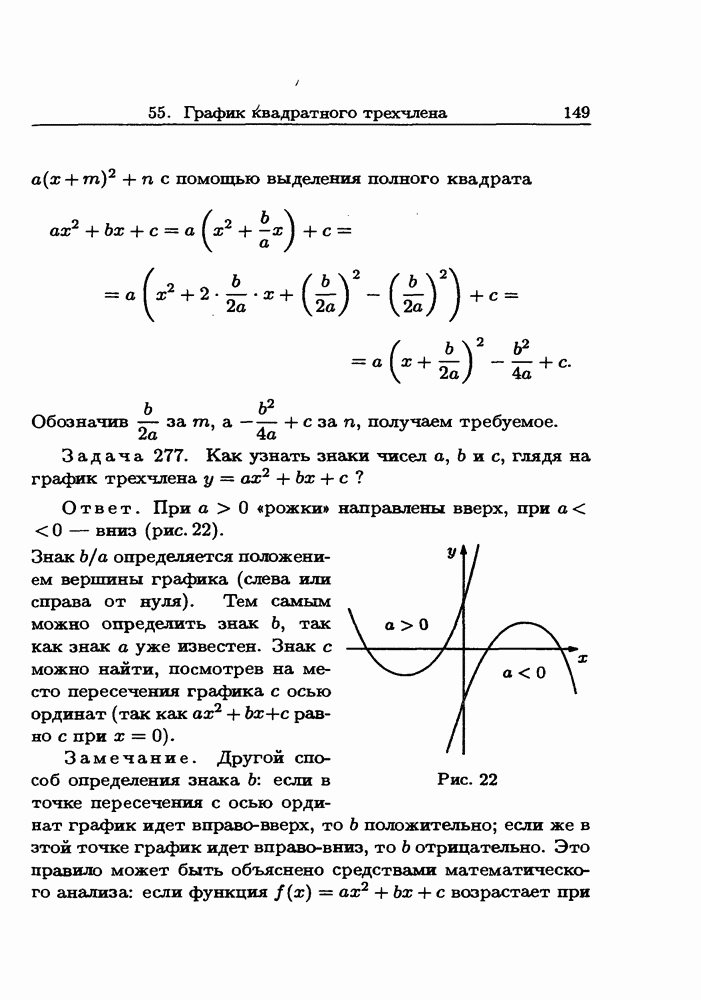
- 55. График квадратного трехчлена
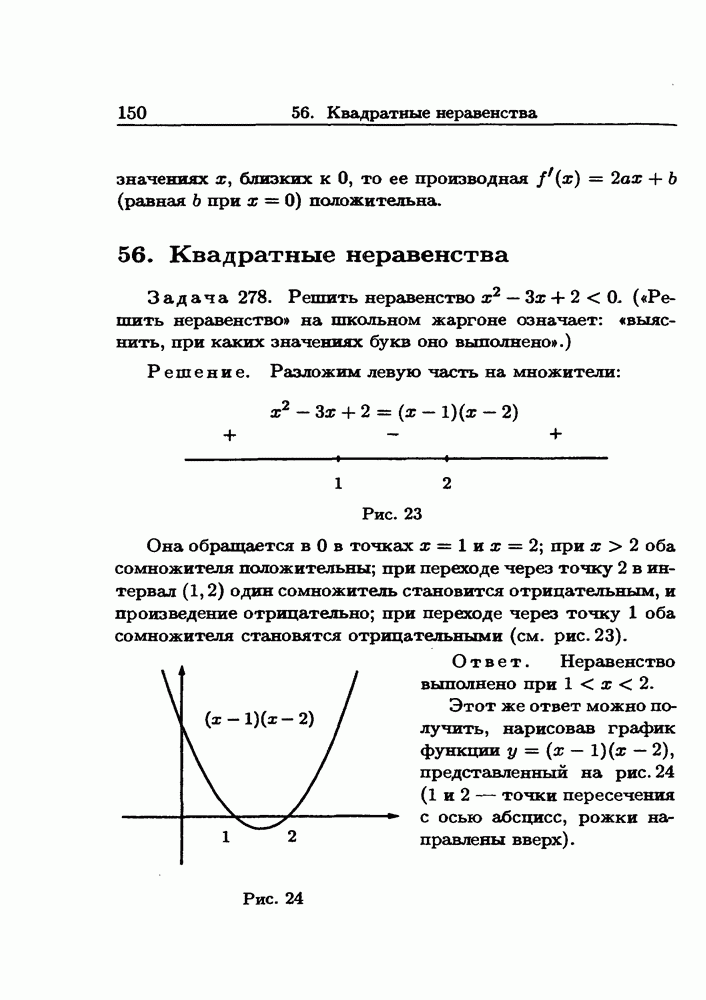
- 56. Квадратные неравенства
- 57. Максимум и минимум квадратного трехчлена
- 58. Биквадратные уравнения
- 59. Возвратные уравнения
- 60. Как завалить на экзамене. Советы экзаменатору
- 61. Корни
- 62. Степень с дробным показателем
- 63. Доказательства числовых неравенств
- 64. Среднее арифметическое и среднее геометрическое
- 65. Среднее геометрическое не больше среднего арифметического
- 66. Задачи на максимум и минимум
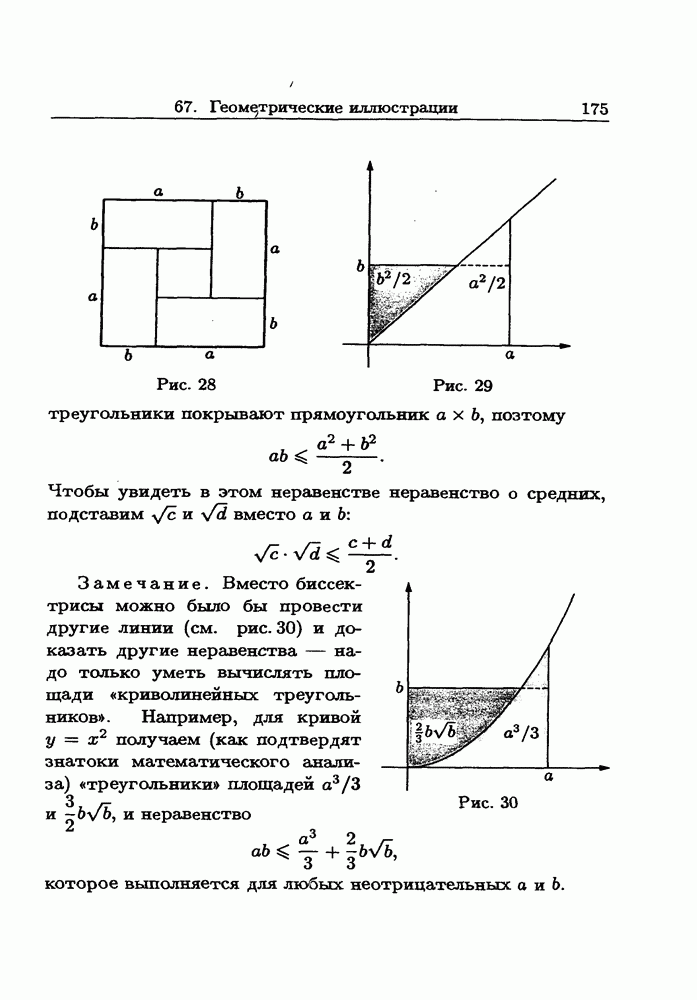
- 67. Геометрические иллюстрации
- 68. Средние многих чисел
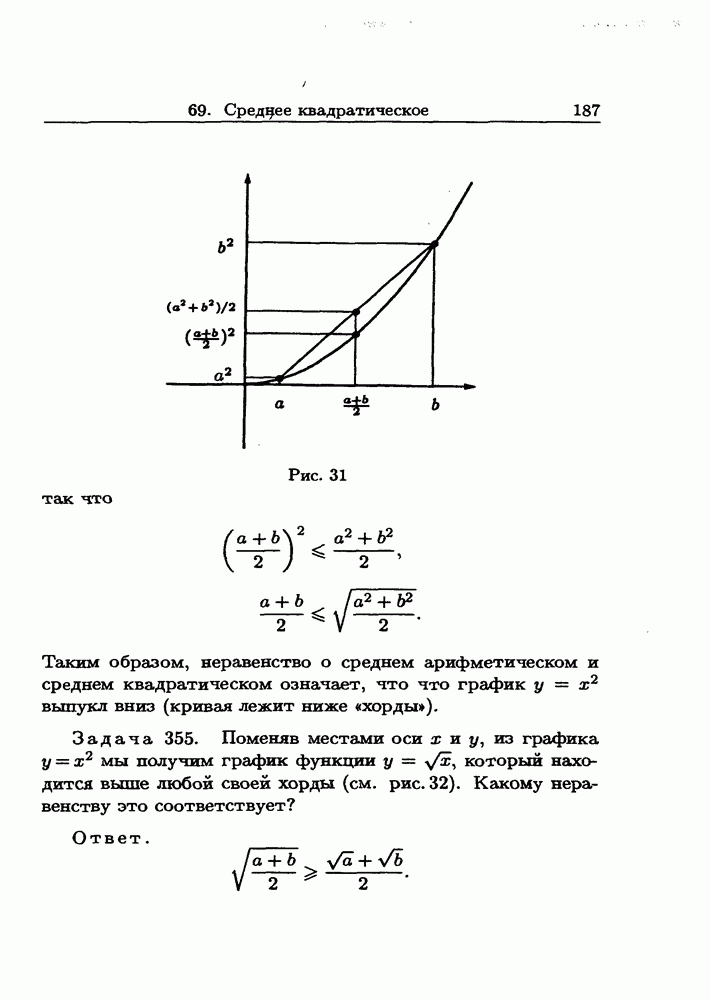
- 69. Среднее квадратическое
- 70. Среднее гармоническое
- 71. Книги для дальнейшего чтения