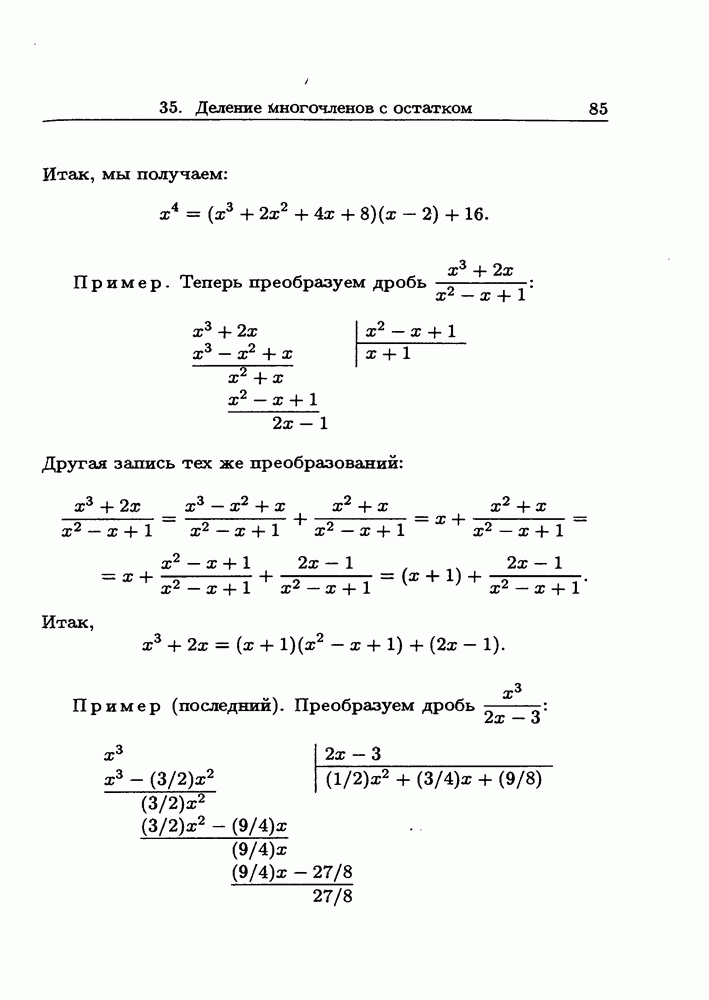| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
17. Отрицательные степени
Мы выписывали степени числа 2:

Попробуем, начиная с какого-либо числа (например, 128), записать эту последовательность в обратном порядке:

В первой последовательности каждое число было вдвое больше предыдущего, теперь — вдвое меньше. Продолжим эту последовательность:

У последовательности

было удобное краткое обозначение:

В обратном порядке:

Продолжая по аналогии, можно написать:

Эти обозначения широко используются. Таким образом,

Раньше, говоря о степенях, мы понимали  как «2, повторенное сомножителем 3 раза»,
как «2, повторенное сомножителем 3 раза»,  как «2, повторенное сомножителем 5 раз». Если еще можно, с некоторой натяжкой, сказать, что
как «2, повторенное сомножителем 5 раз». Если еще можно, с некоторой натяжкой, сказать, что  есть двойка, повторенная сомножителем один раз, то про
есть двойка, повторенная сомножителем один раз, то про  или
или  такое объяснение было бы смешным. Просто математики договорились считать, что (при положительных целых
такое объяснение было бы смешным. Просто математики договорились считать, что (при положительных целых  )
)  понимается как
понимается как 
Мы надеемся, что это соглашение не показалось Вам искусственным. Впоследствии мы увидим, насколько оно удобно и даже — в определенном смысле — неизбежно.
Задача 50. Запишите в виде десятичных дробей числа 
В табл. 10 приведено несколько «малых» чисел.
Деление чисел на большие и малые, как мы уже говорили, условно. При желании можно было бы включить в эту таблицу величины из предыдущей: например, радиус Земли  астрономических единиц.
астрономических единиц.
Задача 51. За какое время красный свет проходит расстояние, равное длине волны? (Это время называют периодом колебаний.)
Итак, запомните:
Определение. Для целых положительных 

Задача 52. Верно ли равенство  для отрицательных
для отрицательных  и для
и для 
Можно ли доказать, что  Нельзя, поскольку запись
Нельзя, поскольку запись  сама по себе, до принятия нашего соглашения (или, как говорят математики, определения) смысла не имеет. Если вдруг все математики мира почему-либо договорятся понимать
сама по себе, до принятия нашего соглашения (или, как говорят математики, определения) смысла не имеет. Если вдруг все математики мира почему-либо договорятся понимать  как-то иначе, то с этого момента равенство
как-то иначе, то с этого момента равенство  перестанет быть верным. Однако этого не произойдет — зачем менять привычное и удобное соглашение?! Нарушив его, мы чрезвычайно все усложним (см. следующий раздел).
перестанет быть верным. Однако этого не произойдет — зачем менять привычное и удобное соглашение?! Нарушив его, мы чрезвычайно все усложним (см. следующий раздел).
С помощью обозначений для степеней длинное выражение

Таблица 10

можно записать короче — как  , а
, а

как 
Задача 53. Записать с использованием показателей степени

Ответ,  .
.
Задача 54. Переписать, используя лишь положительные показатели степеней:

Ответ, 
| << Предыдущий параграф | Следующий параграф >> |
- 1. Предисловие
- 2. Перемена мест слагаемых
- 3. Перемена мест сомножителей
- 4. Сложение столбиком
- 5. Таблица умножения. Умножение столбиком
- 6. Деление «уголком»
- 7. Двоичная система счисления
- 8. Коммутативность
- 9. Ассоциативность
- 10. Расстановки скобок
- 11. Дистрибутивность
- 12. Буквы в алгебре
- 13. Сложение отрицательных чисел
- 14. Умножение отрицательных чисел
- 15. Действия с дробями
- 16. Степени
- 17. Отрицательные степени
- 18. Как умножить a^m на a^n или почему наше определение удобно
- 19. Правило умножения степеней
- 20. Формулы сокращенного умножения. Квадрат суммы
- 21. Как объяснить формулу (a+b)^2=a^2+2ab+b^2 младшему брату или сестре
- 22. Квадрат разности
- 23. Разность квадратов
- 24. Куб суммы
- 25. Четвертая степень суммы
- 26. (a+b)^5, (a+b)^6 и треугольник Паскаля
- 27. Многочлены
- 28. Отступление: какие многочлены считать равными?
- 29. Сколько одночленов останется?
- 30. Коэффициенты и значения
- 31. Разложение на множители
- 32. Рациональные выражения
- 33. Преобразование рационального выражения в частное двух многочленов
- 34. Многочлены и рациональные дроби с одной переменной
- 35. Деление многочленов с остатком
- 36. Остаток при делении на х — а
- 37. Многочлены, значения, интерполяция
- 38. Арифметические прогрессии
- 39. Сумма арифметической прогрессии
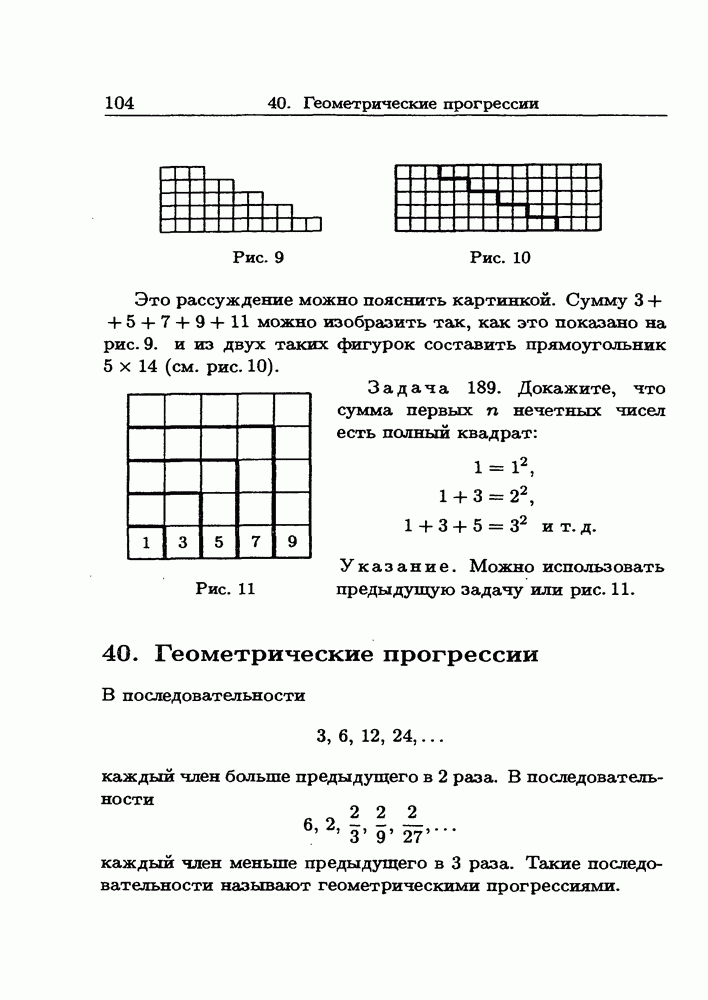
- 40. Геометрические прогрессии
- 41. Сумма геометрической прогрессии
- 42. Разные задачи о прогрессиях
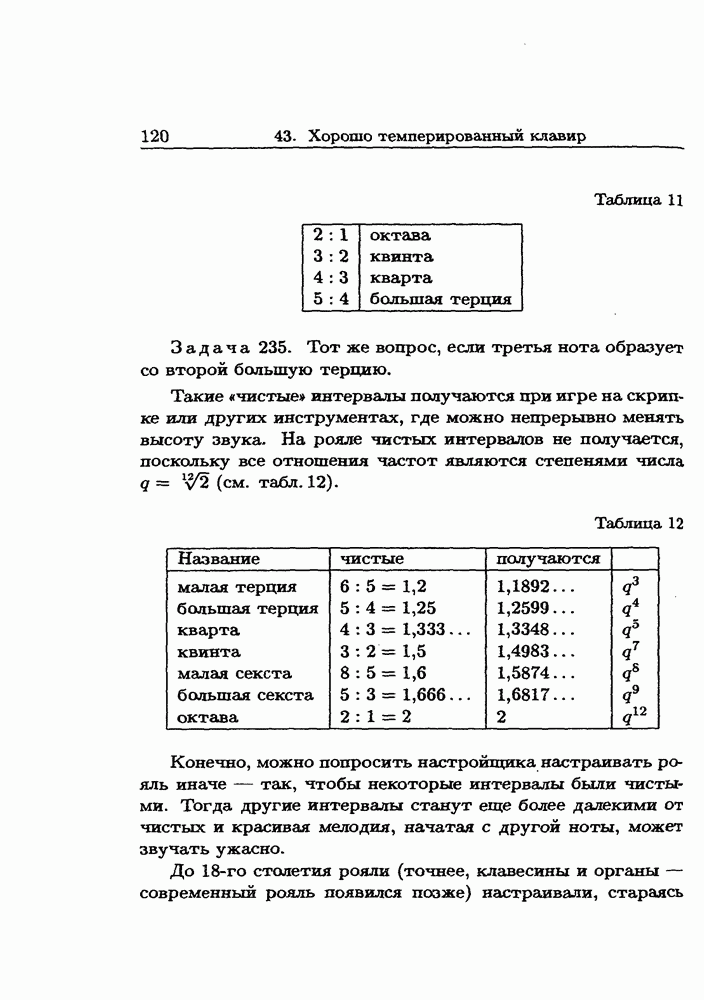
- 43. Хорошо темперированный клавир
- 44. Сумма бесконечной прогрессии
- 45. Уравнения
- 46. Квадратное уравнение
- 47. Случай p = 0. Квадратный корень
- 48. Свойства квадратных корней
- 49. Уравнение х^2 + рх + q = 0
- 50. Теорема Виета
- 51. Разложение квадратного трехчлена на множители
- 52. Формула для корней уравнения ах^2 + bх + c = 0
- 53. Бще одна формула корней квадратного уравнения
- 54. Квадратное уравнение становится линейным
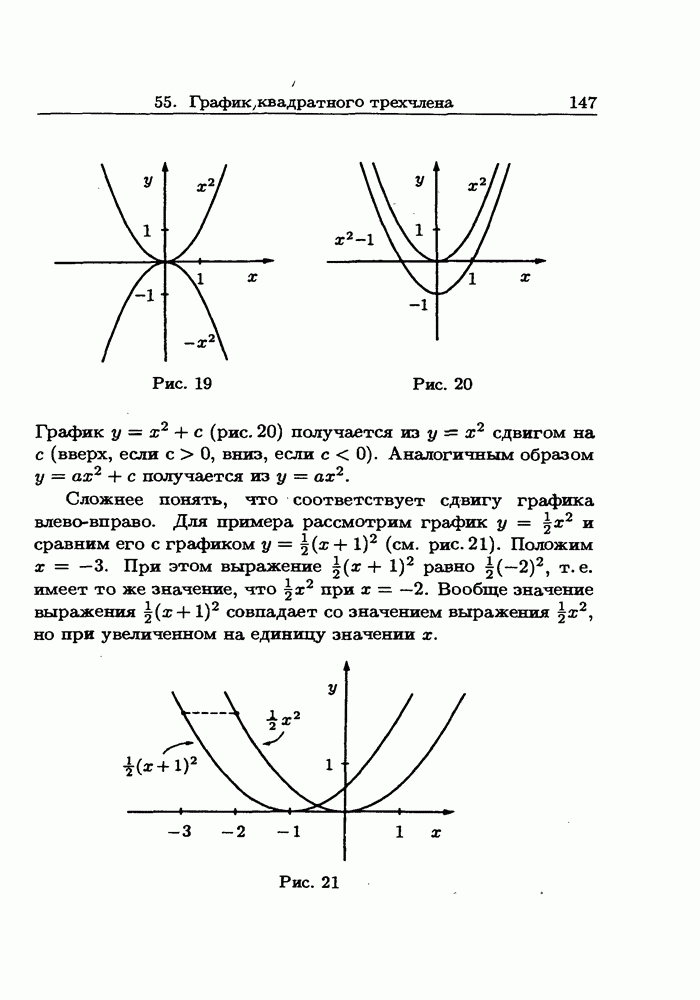
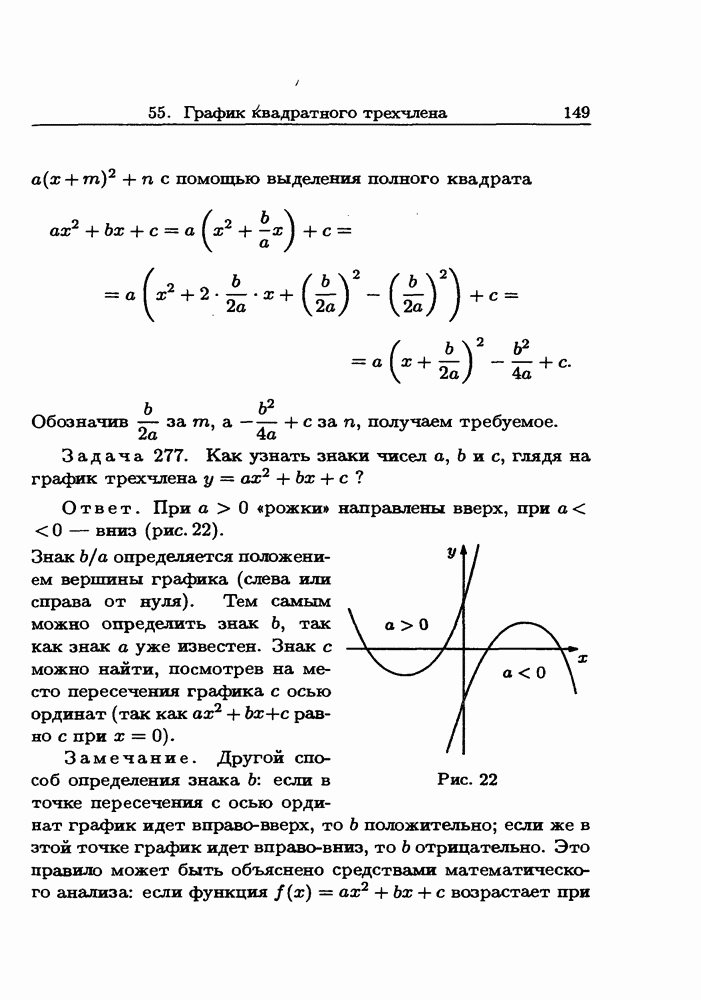
- 55. График квадратного трехчлена
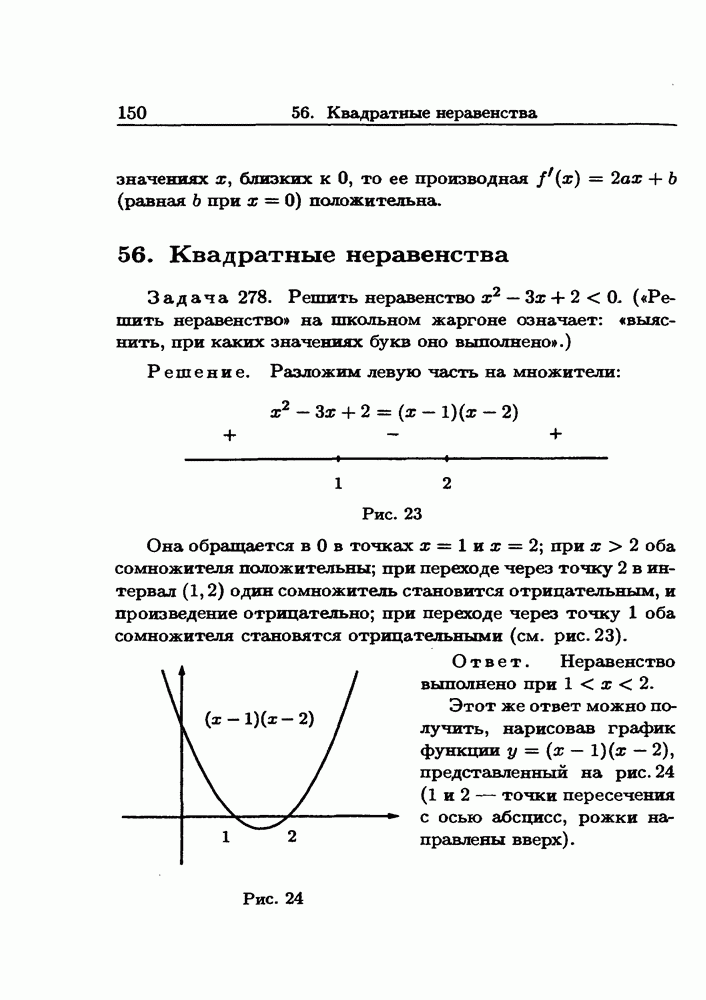
- 56. Квадратные неравенства
- 57. Максимум и минимум квадратного трехчлена
- 58. Биквадратные уравнения
- 59. Возвратные уравнения
- 60. Как завалить на экзамене. Советы экзаменатору
- 61. Корни
- 62. Степень с дробным показателем
- 63. Доказательства числовых неравенств
- 64. Среднее арифметическое и среднее геометрическое
- 65. Среднее геометрическое не больше среднего арифметического
- 66. Задачи на максимум и минимум
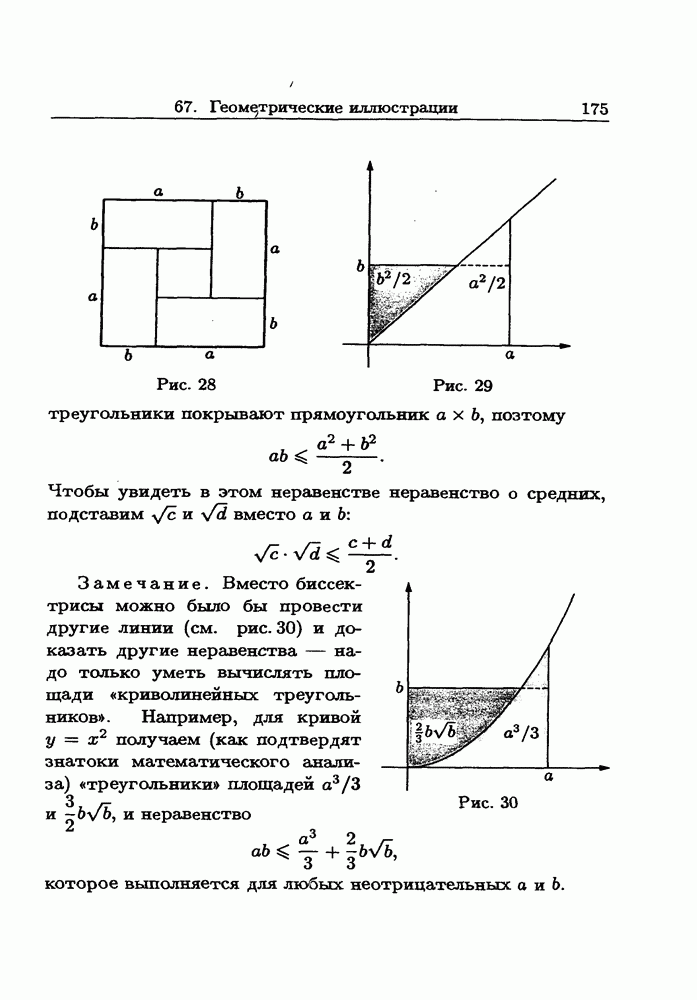
- 67. Геометрические иллюстрации
- 68. Средние многих чисел
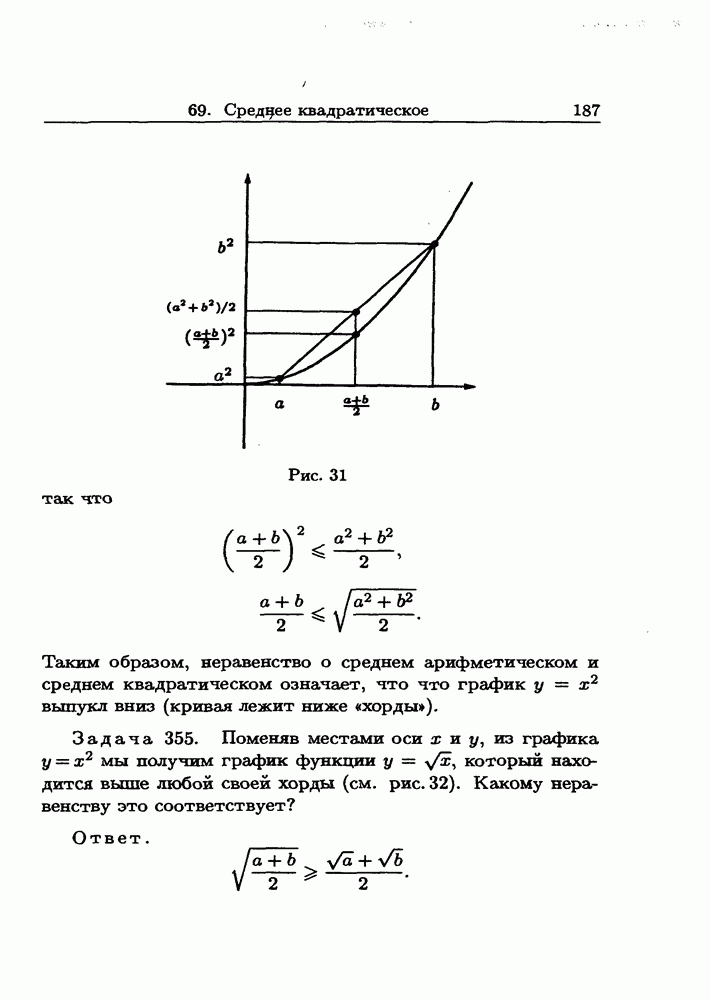
- 69. Среднее квадратическое
- 70. Среднее гармоническое
- 71. Книги для дальнейшего чтения