| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
66. Задачи на максимум и минимум
Задача 325. 1. Каково максимально возможное значение произведения двух неотрицательных чисел, сумма которых равна с? 2. Каково минимально возможное его значение?
Решение. 1. Среднее арифметическое их равно  , так что их среднее геометрическое не превосходит
, так что их среднее геометрическое не превосходит  , а его квадрат (т. е. произведение чисел) не превосходит
, а его квадрат (т. е. произведение чисел) не превосходит  — это максимально возможное значение достигается, когда числа равны.
— это максимально возможное значение достигается, когда числа равны.
2. Минимально возможное значение равно 0. Так будет, если одно из чисел равно 0, а другое равно с.
Задача 326. Каковы максимально и минимально возможные значения суммы двух неотрицательных чисел, произведение которых равно с > 0?
Решение. Среднее геометрическое этих чисел равно  поэтому их полусумма не меньше
поэтому их полусумма не меньше  а сумма не меньше
а сумма не меньше  (Это значение достигается, если числа равны.) Максимального значения не существует — сумма может быть сколь угодно велика, если одно число близко к нулю, а другое велико.
(Это значение достигается, если числа равны.) Максимального значения не существует — сумма может быть сколь угодно велика, если одно число близко к нулю, а другое велико.
Замечание. Как Вы помните, мы уже встречали две последние задачи, когда говорили о минимальном и максимальном значениях квадратичного многочлена.
Задача 327. Какова максимальная площадь прямоугольного участка, если длина забора 120 м?
Задача 328. Какова максимальная площадь прямоугольного участка пляжа, изображенного на рис. 26, если длина забора 120 м? (От моря пляж не отгорожен!)
Решение. Мысленно возведем симметричный забор в море (см. рис. 27). Периметр полученного прямоугольника будет 240, а площадь его будет максимальной, когда это квадрат со стороной 60, и равна 36002. Реальная площадь на берегу вдвое меньше и равна 18002, когда забор состоит из кусков длиной 30, 60 и 30.

Рис. 26

Рис. 27
Задача 329. Каково максимально возможное значение произведения ab, если a и b — неотрицательные числа, для которых а + 2b = 3?
Решение. Произведение чисел a и b максимально, когда максимально произведение чисел а и 2b — а оно максимально, когда эти числа равны, т.е.  Итак, максимальное значение произведения
Итак, максимальное значение произведения  равно
равно

| << Предыдущий параграф | Следующий параграф >> |
- 1. Предисловие
- 2. Перемена мест слагаемых
- 3. Перемена мест сомножителей
- 4. Сложение столбиком
- 5. Таблица умножения. Умножение столбиком
- 6. Деление «уголком»
- 7. Двоичная система счисления
- 8. Коммутативность
- 9. Ассоциативность
- 10. Расстановки скобок
- 11. Дистрибутивность
- 12. Буквы в алгебре
- 13. Сложение отрицательных чисел
- 14. Умножение отрицательных чисел
- 15. Действия с дробями
- 16. Степени
- 17. Отрицательные степени
- 18. Как умножить a^m на a^n или почему наше определение удобно
- 19. Правило умножения степеней
- 20. Формулы сокращенного умножения. Квадрат суммы
- 21. Как объяснить формулу (a+b)^2=a^2+2ab+b^2 младшему брату или сестре
- 22. Квадрат разности
- 23. Разность квадратов
- 24. Куб суммы
- 25. Четвертая степень суммы
- 26. (a+b)^5, (a+b)^6 и треугольник Паскаля
- 27. Многочлены
- 28. Отступление: какие многочлены считать равными?
- 29. Сколько одночленов останется?
- 30. Коэффициенты и значения
- 31. Разложение на множители
- 32. Рациональные выражения
- 33. Преобразование рационального выражения в частное двух многочленов
- 34. Многочлены и рациональные дроби с одной переменной
- 35. Деление многочленов с остатком
- 36. Остаток при делении на х — а
- 37. Многочлены, значения, интерполяция
- 38. Арифметические прогрессии
- 39. Сумма арифметической прогрессии
- 40. Геометрические прогрессии
- 41. Сумма геометрической прогрессии
- 42. Разные задачи о прогрессиях
- 43. Хорошо темперированный клавир
- 44. Сумма бесконечной прогрессии
- 45. Уравнения
- 46. Квадратное уравнение
- 47. Случай p = 0. Квадратный корень
- 48. Свойства квадратных корней
- 49. Уравнение х^2 + рх + q = 0
- 50. Теорема Виета
- 51. Разложение квадратного трехчлена на множители
- 52. Формула для корней уравнения ах^2 + bх + c = 0
- 53. Бще одна формула корней квадратного уравнения
- 54. Квадратное уравнение становится линейным
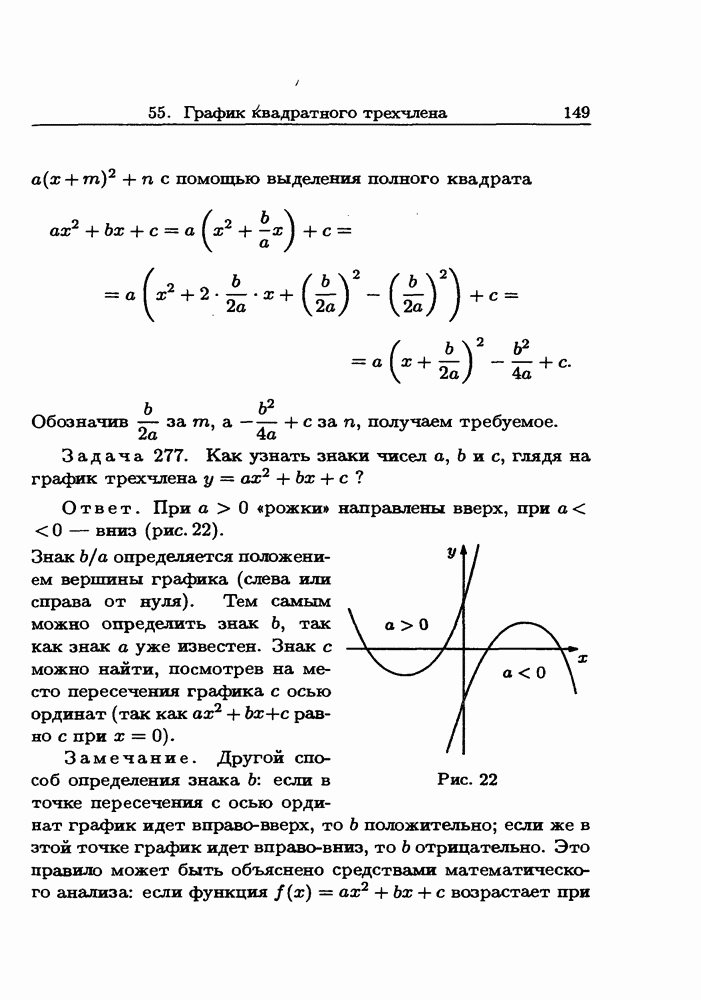
- 55. График квадратного трехчлена
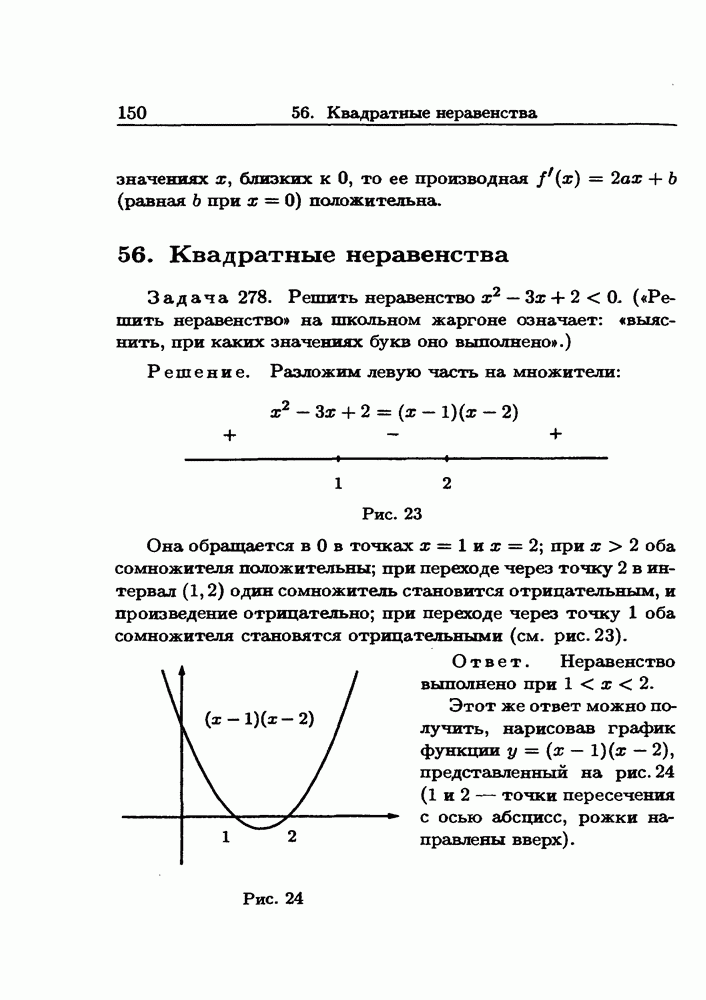
- 56. Квадратные неравенства
- 57. Максимум и минимум квадратного трехчлена
- 58. Биквадратные уравнения
- 59. Возвратные уравнения
- 60. Как завалить на экзамене. Советы экзаменатору
- 61. Корни
- 62. Степень с дробным показателем
- 63. Доказательства числовых неравенств
- 64. Среднее арифметическое и среднее геометрическое
- 65. Среднее геометрическое не больше среднего арифметического
- 66. Задачи на максимум и минимум
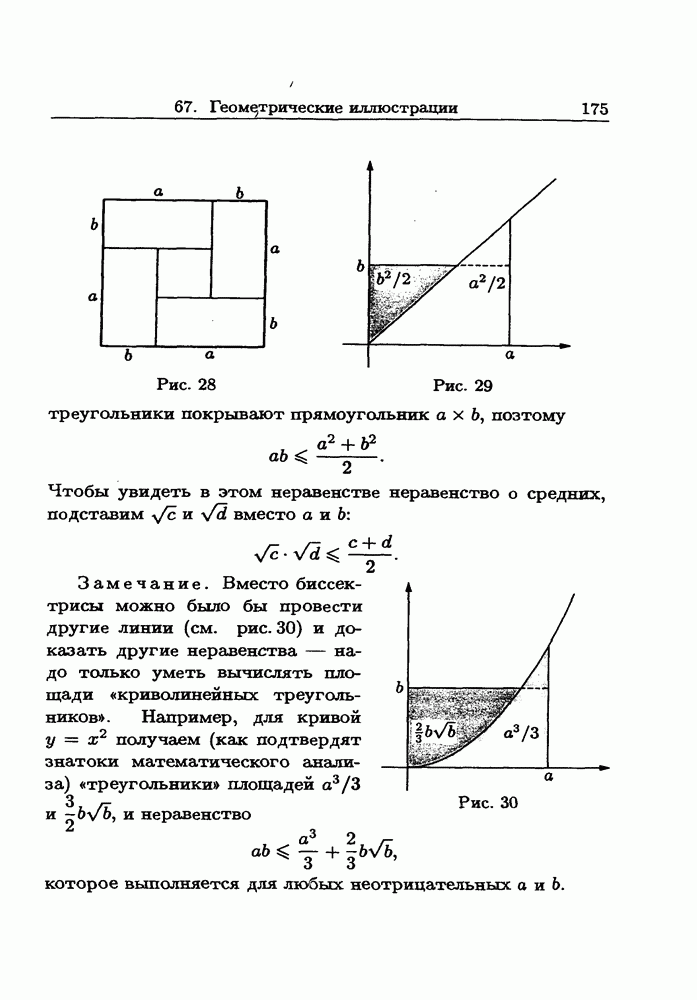
- 67. Геометрические иллюстрации
- 68. Средние многих чисел
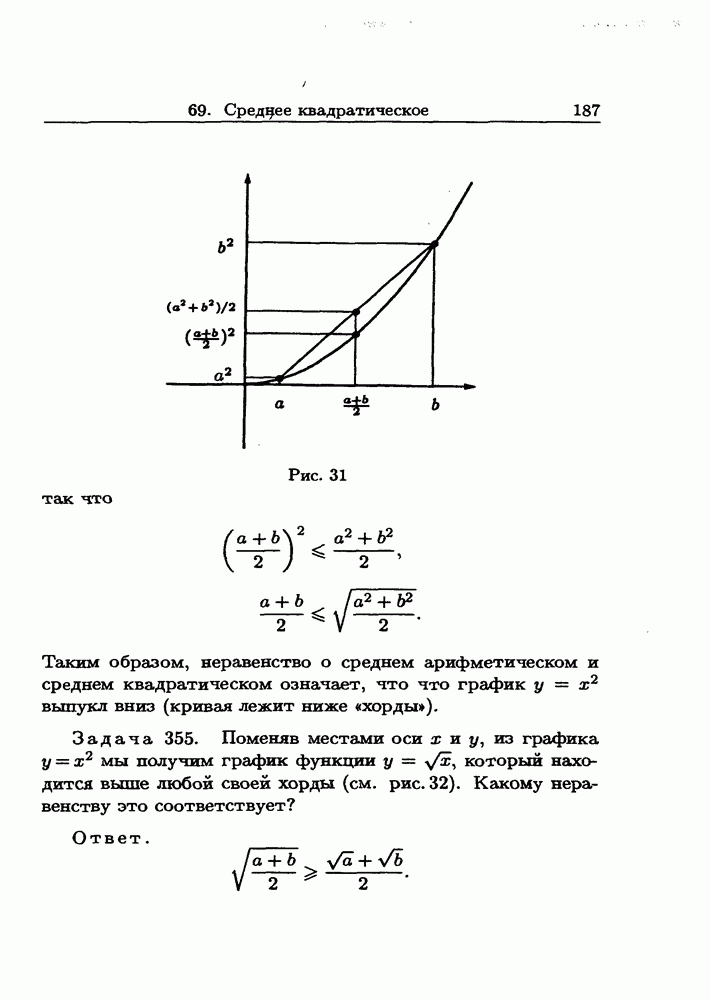
- 69. Среднее квадратическое
- 70. Среднее гармоническое
- 71. Книги для дальнейшего чтения