| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Сложение столбиком
Чтобы узнать, сколько будет 7+9, можно нарисовать 7 яблок, рядом 9 яблок (рис. 3) и сосчитать, сколько всего яблок: одно, два, три, четыре, ... пятнадцать, шестнадцать. Получим: 7 + 9 = 16. Таким способом можно складывать любые числа. Но чтобы сложить, к примеру, 137 и 268 таким способом, понадобится изрядное терпение. И математики изобрели другие способы. Один из них — сложение столбиком.

Рис. 3
В разное время и в разных странах люди записывали числа по-разному, и об этом написаны целые книги. Мы так привыкли с детства к записи чисел в десятичной системе с
помощью цифр 0,1,2,8,9, что с трудом можем представить себе, насколько ее изобретение облегчило вычисления. Даже сама возможность записывать сколь угодно большие числа — и при том достаточно коротко — для древних была вовсе не очевидной. Великий древнегреческий математик Архимед написал книгу «Псаммит, или исчисление песка» о том, что можно записать число, большее числа песчинок, заполняющих целиком сферу с радиусом, равным расстоянию от Земли до неподвижных звезд.
Сейчас десятичная система вне конкуренции, если не считать двоичной системы, которая распространена не среди людей, а среди компьютеров. В двоичной системе всего две цифры (0 и 1), числа записываются длиннее. Компьютеру это не страшно — лишь бы правила арифметических действий были простыми.
О двоичной системе мы еще поговорим, а пока вернемся к сложению чисел, записанных в десятичной системе. Их складывают «в столбик». Мы не будем объяснять Вам, как это делается — это Вы знаете сами. Попробуйте решить такую задачу.
Задача 1. В строку написано несколько восьмерок. Кое-где между ними вставлены знаки «+», причем полученная сумма равна 1000. Как так может быть? Привести пример с минимальным возможным числом слагаемых. (Например, расстановка 88 + 88 + 8 + 8 + 88 не подходит, так как получается не 1000, а всего лишь 280.)
Решение. Запишем сложение в столбик

Мы не знаем, сколько слагаемых и сколько восьмерок в каждом слагаемом. Известно, однако, что каждое слагаемое кончается на 8 и что в разряде единиц суммы стоит 0. Чтобы восьмерки дали нуль, нужно как минимум 5 слагаемых

При этом в уме остается 4, так как 8+8+8+8+8 = 40. Чтобы в разряде десятков получить 0, к этой четверке нужно добавить две восьмерки:

В уме остается 2, так что в разряде сотен нужна одна восьмерка

Ответ: 8 + 8 + 8 + 88 + 888 = 1000.
Задача 2. Какие цифры обозначены буквами А, Б и В в примере на сложение столбиком

(все буквы А обозначают одну и ту же цифру, буквы Б — другую, буквы В — третью)?
Решение. Цифра А равна единице — только единица может появиться при переносе из разряда сотен в разряд тысяч. Чтобы определить цифру Б, зададим себе такой вопрос: происходит ли перенос из разряда единиц в разряд десятков (при сложении А с Б)? Если бы он не происходил, то в разрядах единиц, десятков и сотен у суммы стояла бы одна и та же цифра — а это не так. Значит, перенос происходит. Поскольку А = 1, это возможно лишь в случае Б = 9. Получаем ответ: А = 1, Б = 1, В = 0.

| << Предыдущий параграф | Следующий параграф >> |
- 1. Предисловие
- 2. Перемена мест слагаемых
- 3. Перемена мест сомножителей
- 4. Сложение столбиком
- 5. Таблица умножения. Умножение столбиком
- 6. Деление «уголком»
- 7. Двоичная система счисления
- 8. Коммутативность
- 9. Ассоциативность
- 10. Расстановки скобок
- 11. Дистрибутивность
- 12. Буквы в алгебре
- 13. Сложение отрицательных чисел
- 14. Умножение отрицательных чисел
- 15. Действия с дробями
- 16. Степени
- 17. Отрицательные степени
- 18. Как умножить a^m на a^n или почему наше определение удобно
- 19. Правило умножения степеней
- 20. Формулы сокращенного умножения. Квадрат суммы
- 21. Как объяснить формулу (a+b)^2=a^2+2ab+b^2 младшему брату или сестре
- 22. Квадрат разности
- 23. Разность квадратов
- 24. Куб суммы
- 25. Четвертая степень суммы
- 26. (a+b)^5, (a+b)^6 и треугольник Паскаля
- 27. Многочлены
- 28. Отступление: какие многочлены считать равными?
- 29. Сколько одночленов останется?
- 30. Коэффициенты и значения
- 31. Разложение на множители
- 32. Рациональные выражения
- 33. Преобразование рационального выражения в частное двух многочленов
- 34. Многочлены и рациональные дроби с одной переменной
- 35. Деление многочленов с остатком
- 36. Остаток при делении на х — а
- 37. Многочлены, значения, интерполяция
- 38. Арифметические прогрессии
- 39. Сумма арифметической прогрессии
- 40. Геометрические прогрессии
- 41. Сумма геометрической прогрессии
- 42. Разные задачи о прогрессиях
- 43. Хорошо темперированный клавир
- 44. Сумма бесконечной прогрессии
- 45. Уравнения
- 46. Квадратное уравнение
- 47. Случай p = 0. Квадратный корень
- 48. Свойства квадратных корней
- 49. Уравнение х^2 + рх + q = 0
- 50. Теорема Виета
- 51. Разложение квадратного трехчлена на множители
- 52. Формула для корней уравнения ах^2 + bх + c = 0
- 53. Бще одна формула корней квадратного уравнения
- 54. Квадратное уравнение становится линейным
- 55. График квадратного трехчлена
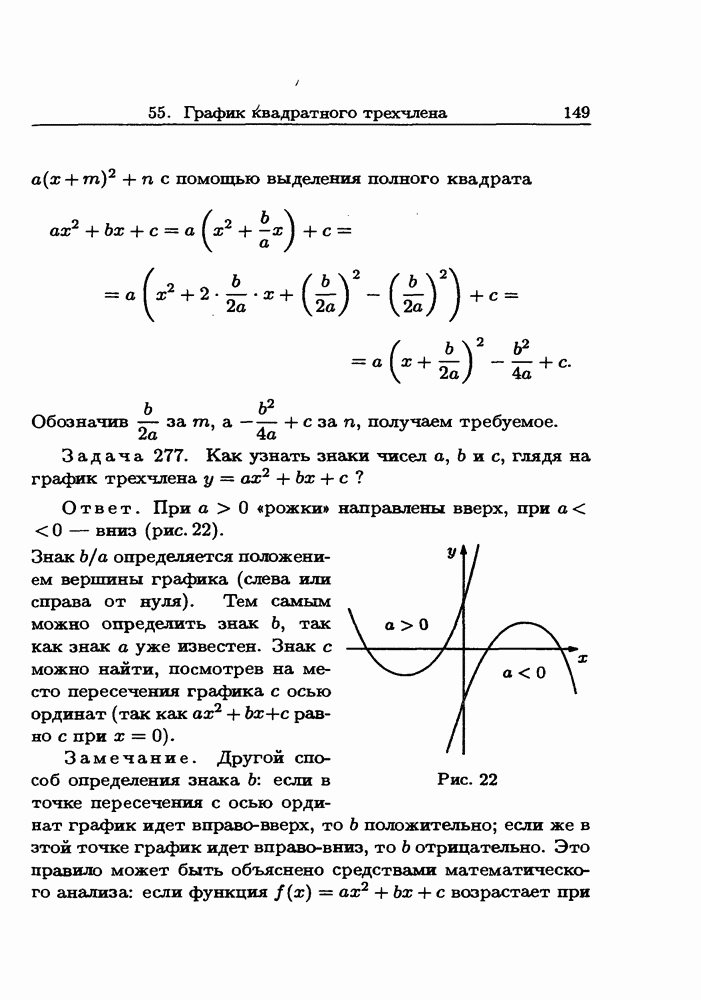
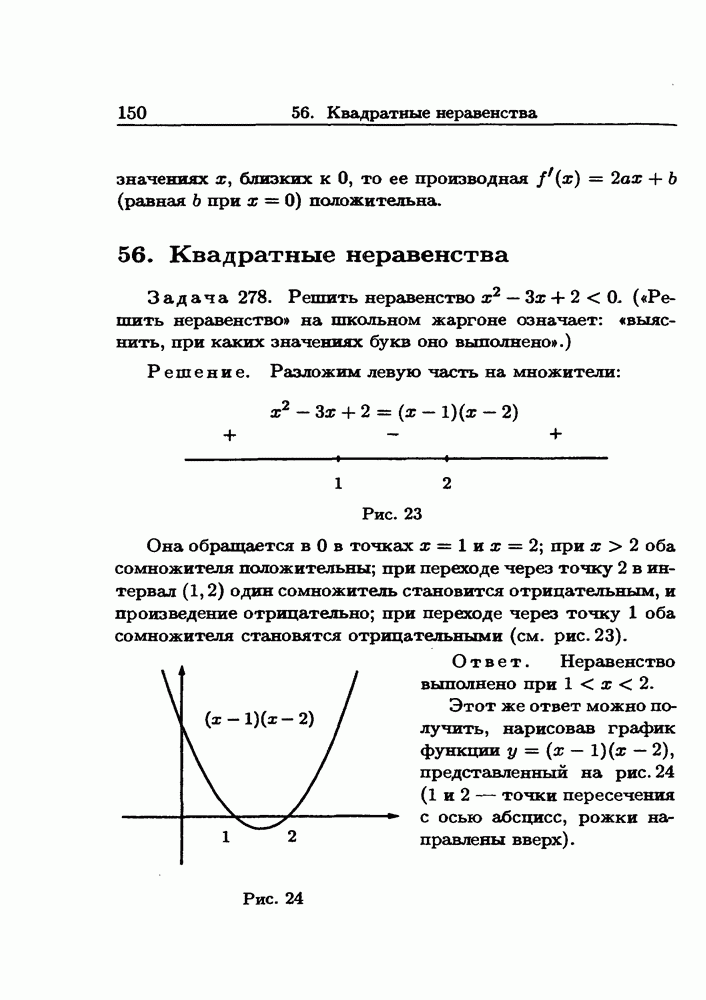
- 56. Квадратные неравенства
- 57. Максимум и минимум квадратного трехчлена
- 58. Биквадратные уравнения
- 59. Возвратные уравнения
- 60. Как завалить на экзамене. Советы экзаменатору
- 61. Корни
- 62. Степень с дробным показателем
- 63. Доказательства числовых неравенств
- 64. Среднее арифметическое и среднее геометрическое
- 65. Среднее геометрическое не больше среднего арифметического
- 66. Задачи на максимум и минимум
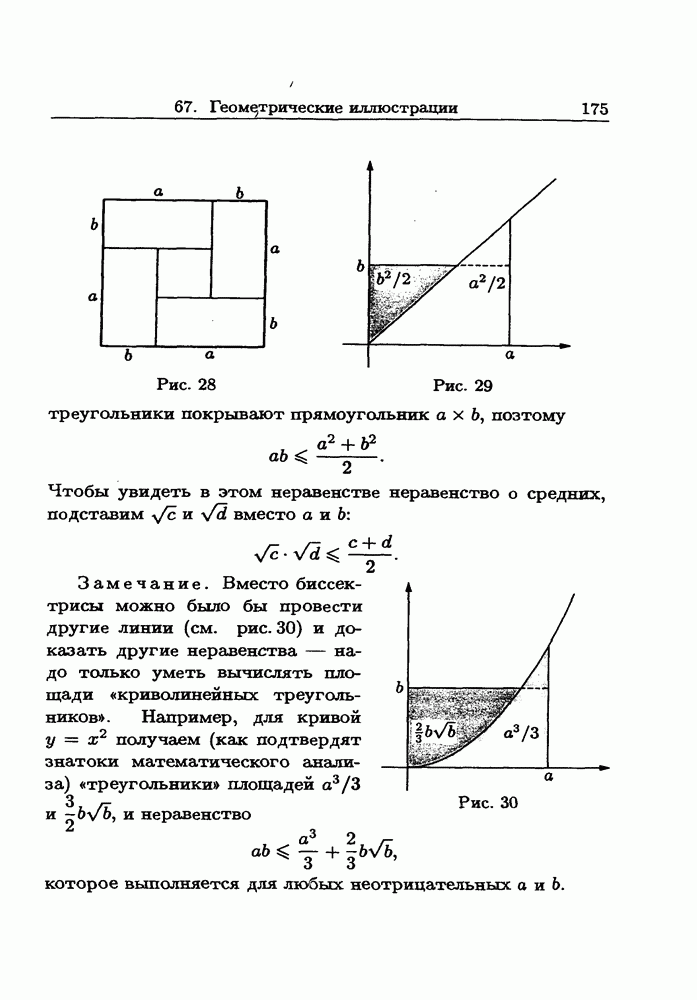
- 67. Геометрические иллюстрации
- 68. Средние многих чисел
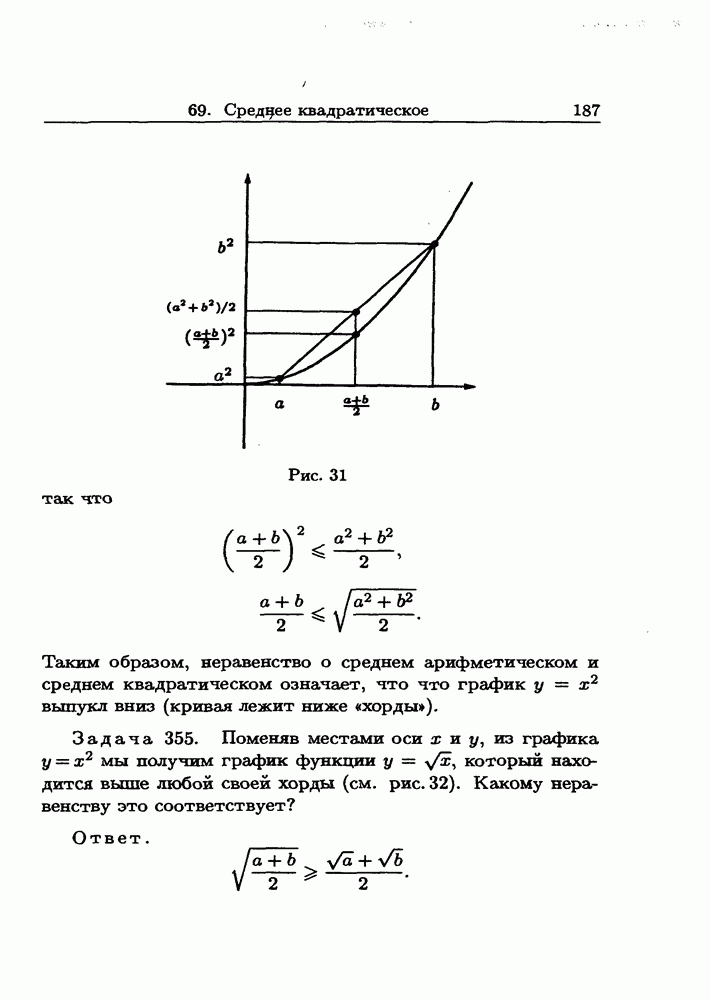
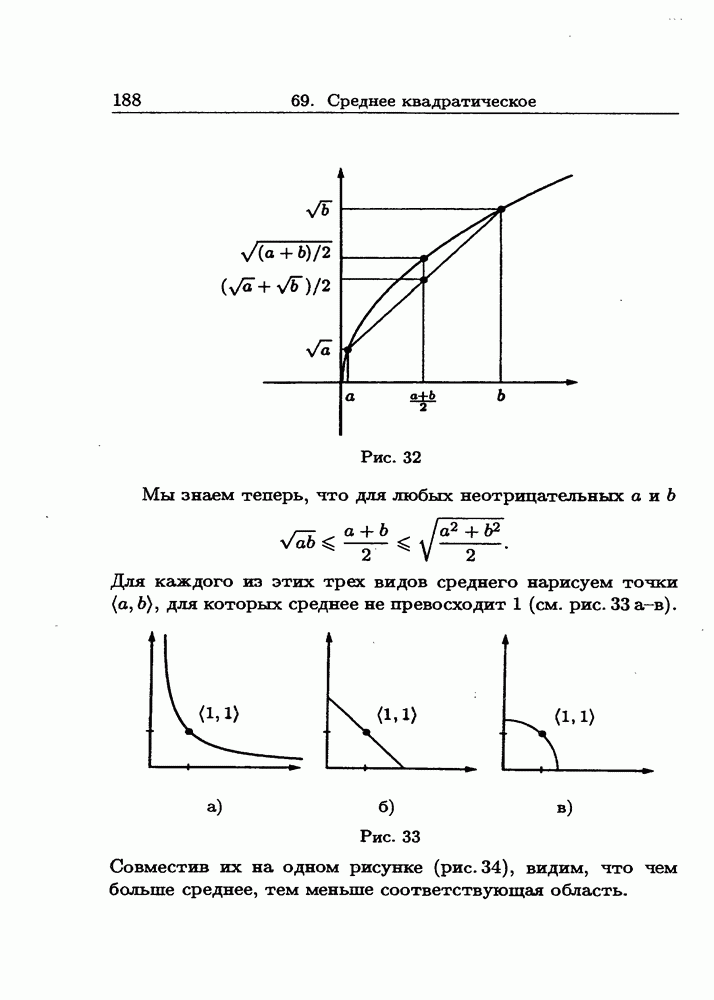
- 69. Среднее квадратическое
- 70. Среднее гармоническое
- 71. Книги для дальнейшего чтения