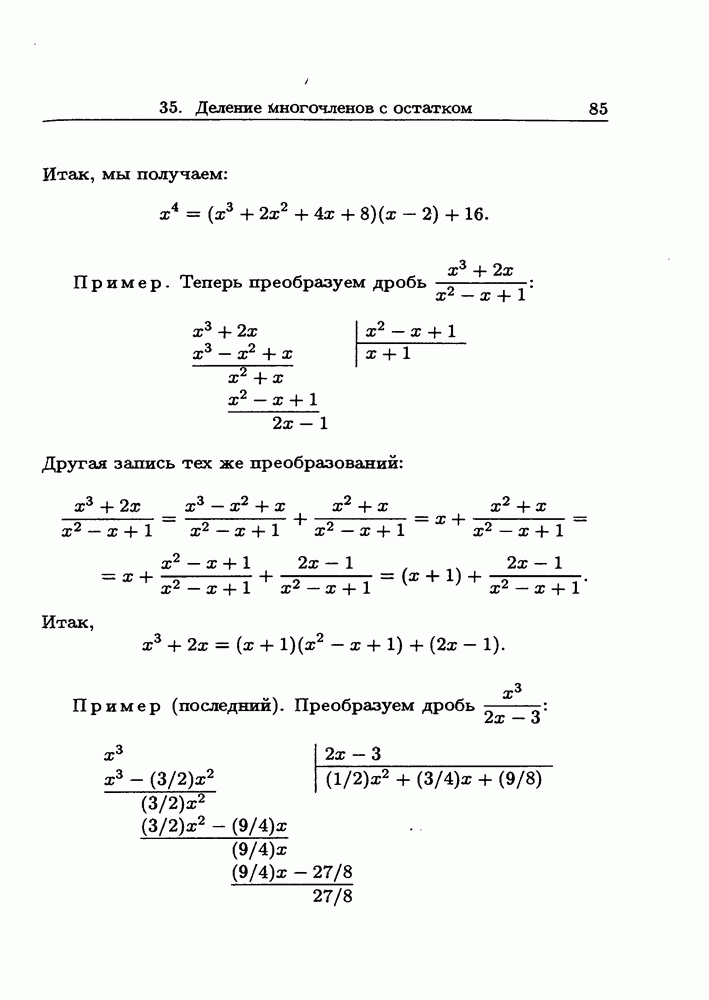| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
50. Теорема Виета
Теорема. Если квадратное уравнение  имеет два (различных) корня
имеет два (различных) корня  то
то

Другая формулировка: Если квадратное уравнение х^2 + рх + q имеет два различных корня а и Р, то

(Это — действительно другая запись того же утверждения, поскольку

а равенство многочленов  означает, что равны их коэффициенты.)
означает, что равны их коэффициенты.)
Доказательство. (Первый вариант). По формуле для корней квадратного уравнения

где  . (Или наоборот:
. (Или наоборот:

но это не важно.) Тогда

и

Что и требовалось.
(Второй вариант). Будем доказывать теорему Виета во второй из приведенный формулировок. Мы знаем, что если многочлен  имеет корни
имеет корни  , то его можно разложить на множители:
, то его можно разложить на множители:

В нашем случае, когда Р имеет степень 2, многочлен R может быть только числом (иначе правая часть имеет слишком большую степень), и число это равно 1, так как коэффициенты при  у многочленов
у многочленов  одинаковы. Значит,
одинаковы. Значит,

что и требовалось.
Задача 255. Как обобщить теорему Виета на случай уравнения, имеющего ровно один корень? Остаются ли в силе предложеные способы доказательства?
Задача 256. (Теорема Виета для кубического уравнения). Уравнение  имеет три корня
имеет три корня  . Доказать, что
. Доказать, что

Задача 257. Уравнение  имеет корни
имеет корни  Выразить
Выразить  через
через 
Решение. 
Задача 258. Уравнение  имеет корни
имеет корни  Выразить
Выразить  через
через 
Первое решение. 
Второе решение,  — разность между корнями; глядя на формулу, видим, что она равна
— разность между корнями; глядя на формулу, видим, что она равна  так что
так что

Задача 259. Уравнение  имеет корни
имеет корни  . Выразить
. Выразить

через  . (Этот многочлен от
. (Этот многочлен от  называется дискриминантом кубического уравнения. Как и в случае квадратного уравнения, он мал, если два корня близки друг к другу.)
называется дискриминантом кубического уравнения. Как и в случае квадратного уравнения, он мал, если два корня близки друг к другу.)
Задача 260. Уравнение  имеет корни
имеет корни  а уравнение
а уравнение  имеет корни
имеет корни  Выразить
Выразить

через  . (Этот многочлен называется результантом двух квадратных многочленов; он равен нулю, если у них есть общий корень.)
. (Этот многочлен называется результантом двух квадратных многочленов; он равен нулю, если у них есть общий корень.)
Теорема Виета позволяет составить квадратное уравнение с заданными корнями. Точнее, не теорема Виета, а обратная к ней: вот ее формулировка.
Теорема. Если  — любые числа, а
— любые числа, а  , то уравнение
, то уравнение  имеет корни
имеет корни 
Доказательство. Уравнение  очевидно, имеет корни
очевидно, имеет корни  . Раскрыв скобки, убеждаемся, что это и есть уравнение
. Раскрыв скобки, убеждаемся, что это и есть уравнение 
Задача 261. Составить квадратное уравнение с целыми коэффициентами, имеющее число  своим корнем.
своим корнем.
Указание. Второй корень равен 
Задача 262. Коэффициенты  квадратного уравнения
квадратного уравнения  (имеющего два корня) целые. Доказать, что
(имеющего два корня) целые. Доказать, что
(а) сумма квадратов его корней — целое число;
(б) сумма кубов его корней — целое число;
(в) сумма  степеней его корней при любом натуральном п — целое число.
степеней его корней при любом натуральном п — целое число.
Задача 263. 1. Доказать, что квадрат числа  — целые) также имеет вид к
— целые) также имеет вид к  для некоторых целых к, I.
для некоторых целых к, I.
2. То же для ( при любом целом
при любом целом 
3. Число  имеет вид к
имеет вид к  . Какой вид имеет число
. Какой вид имеет число  ?
?
4. Доказать, что существует бесконечно много целых чисел а, b, для которых 
Решение. 4. Равенство  выполнено при
выполнено при  поскольку
поскольку  . Перепишем это равенство так:
. Перепишем это равенство так:  . Возведем обе части в
. Возведем обе части в  степень:
степень:  Число
Число  равно к
равно к  при некоторых к и
при некоторых к и  в этом случае
в этом случае  равно к
равно к  Итак,
Итак,

т. е. к, I — решение уравнения.
Например,  Проверим:
Проверим: 
Задача 264. Доказать, что уравнение  имеет два корня разных знаков в том и только в том случае, когда
имеет два корня разных знаков в том и только в том случае, когда 
Решение. Если уравнение имеет корни разных знаков, то по теореме Виета коэффициент  , равный их произведению, меньше 0. Напротив, если произведение двух корней меньше 0, то корни будут разных знаков — если только корни есть. Убедиться в том, что корни есть, можно, вычислив дискриминант
, равный их произведению, меньше 0. Напротив, если произведение двух корней меньше 0, то корни будут разных знаков — если только корни есть. Убедиться в том, что корни есть, можно, вычислив дискриминант  : если
: если  , то
, то 
Другое объяснение: если  , то значение выражения
, то значение выражения  при
при  отрицательно. При больших
отрицательно. При больших  выражение становится положительным
выражение становится положительным  «перевешивает»
«перевешивает»  — значит, где-то в промежуточной точке оно обращается в нуль и уравнение имеет положительный корень. (Аналогично и для отрицательного корня.)
— значит, где-то в промежуточной точке оно обращается в нуль и уравнение имеет положительный корень. (Аналогично и для отрицательного корня.)
| << Предыдущий параграф | Следующий параграф >> |
- 1. Предисловие
- 2. Перемена мест слагаемых
- 3. Перемена мест сомножителей
- 4. Сложение столбиком
- 5. Таблица умножения. Умножение столбиком
- 6. Деление «уголком»
- 7. Двоичная система счисления
- 8. Коммутативность
- 9. Ассоциативность
- 10. Расстановки скобок
- 11. Дистрибутивность
- 12. Буквы в алгебре
- 13. Сложение отрицательных чисел
- 14. Умножение отрицательных чисел
- 15. Действия с дробями
- 16. Степени
- 17. Отрицательные степени
- 18. Как умножить a^m на a^n или почему наше определение удобно
- 19. Правило умножения степеней
- 20. Формулы сокращенного умножения. Квадрат суммы
- 21. Как объяснить формулу (a+b)^2=a^2+2ab+b^2 младшему брату или сестре
- 22. Квадрат разности
- 23. Разность квадратов
- 24. Куб суммы
- 25. Четвертая степень суммы
- 26. (a+b)^5, (a+b)^6 и треугольник Паскаля
- 27. Многочлены
- 28. Отступление: какие многочлены считать равными?
- 29. Сколько одночленов останется?
- 30. Коэффициенты и значения
- 31. Разложение на множители
- 32. Рациональные выражения
- 33. Преобразование рационального выражения в частное двух многочленов
- 34. Многочлены и рациональные дроби с одной переменной
- 35. Деление многочленов с остатком
- 36. Остаток при делении на х — а
- 37. Многочлены, значения, интерполяция
- 38. Арифметические прогрессии
- 39. Сумма арифметической прогрессии
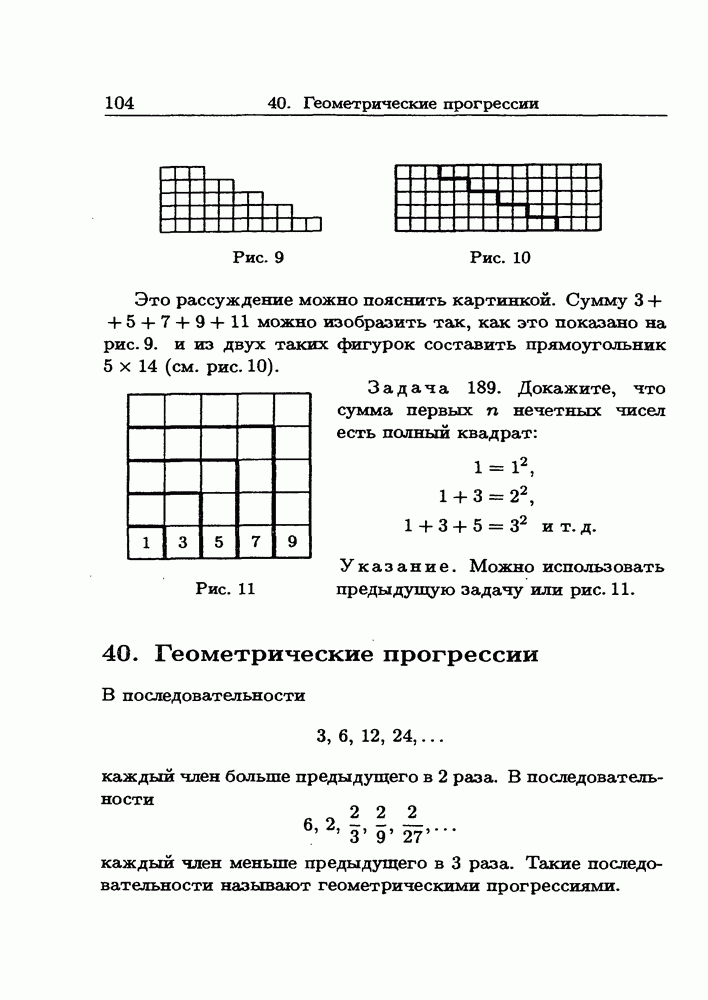
- 40. Геометрические прогрессии
- 41. Сумма геометрической прогрессии
- 42. Разные задачи о прогрессиях
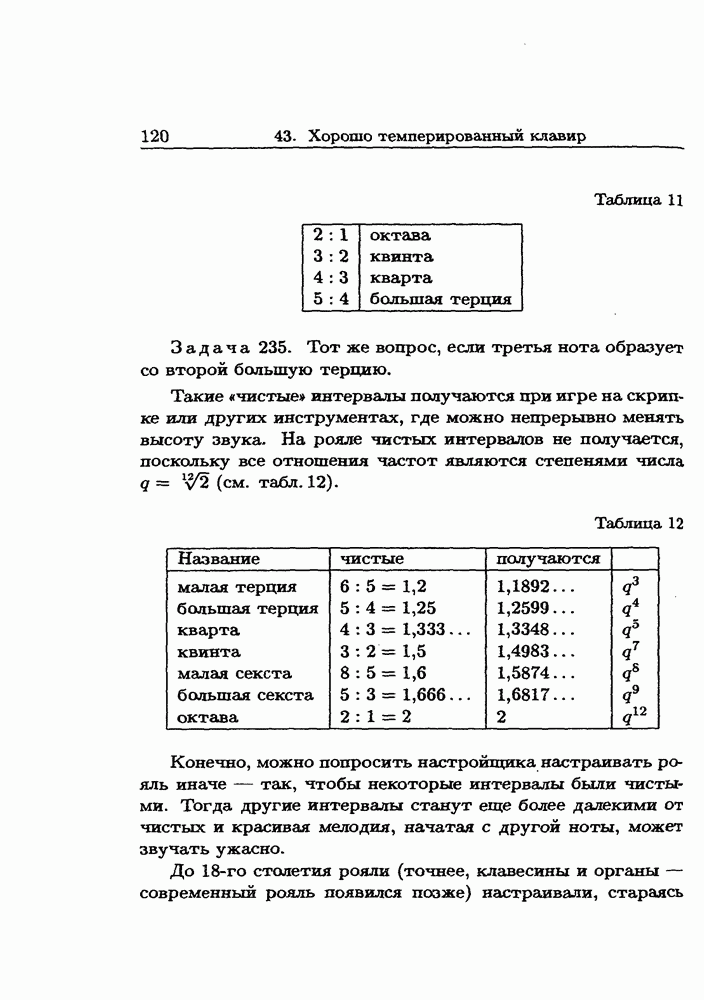
- 43. Хорошо темперированный клавир
- 44. Сумма бесконечной прогрессии
- 45. Уравнения
- 46. Квадратное уравнение
- 47. Случай p = 0. Квадратный корень
- 48. Свойства квадратных корней
- 49. Уравнение х^2 + рх + q = 0
- 50. Теорема Виета
- 51. Разложение квадратного трехчлена на множители
- 52. Формула для корней уравнения ах^2 + bх + c = 0
- 53. Бще одна формула корней квадратного уравнения
- 54. Квадратное уравнение становится линейным
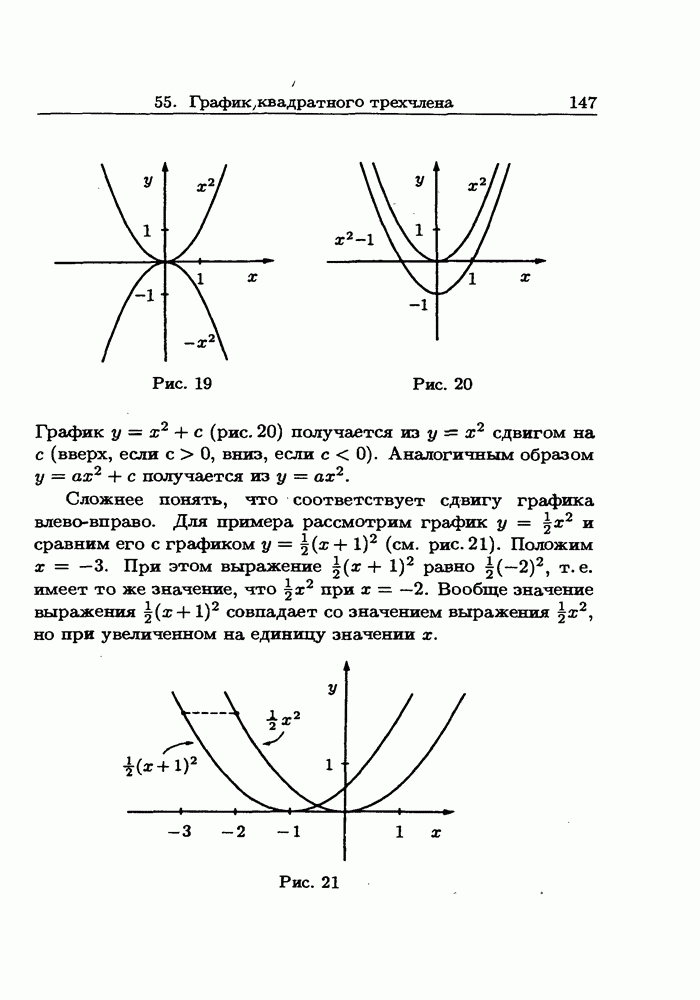
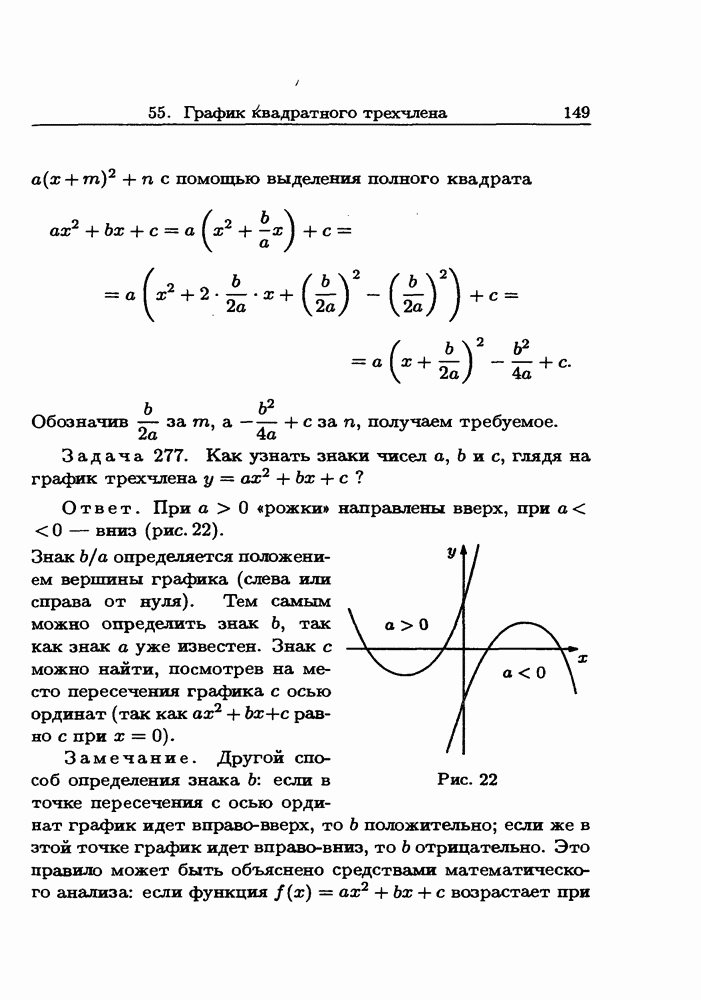
- 55. График квадратного трехчлена
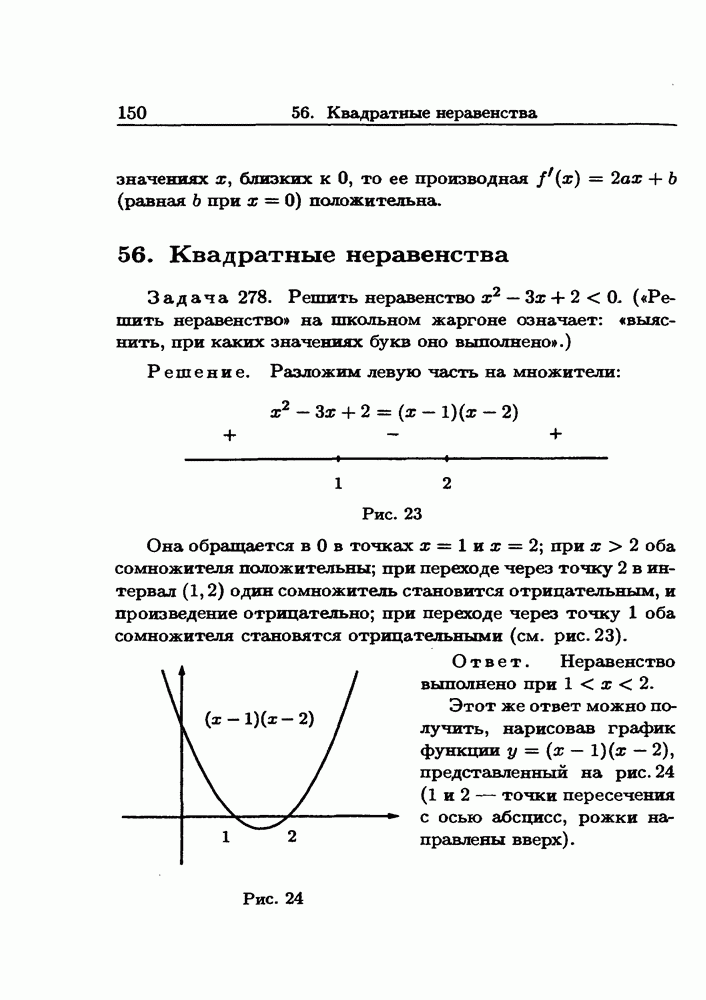
- 56. Квадратные неравенства
- 57. Максимум и минимум квадратного трехчлена
- 58. Биквадратные уравнения
- 59. Возвратные уравнения
- 60. Как завалить на экзамене. Советы экзаменатору
- 61. Корни
- 62. Степень с дробным показателем
- 63. Доказательства числовых неравенств
- 64. Среднее арифметическое и среднее геометрическое
- 65. Среднее геометрическое не больше среднего арифметического
- 66. Задачи на максимум и минимум
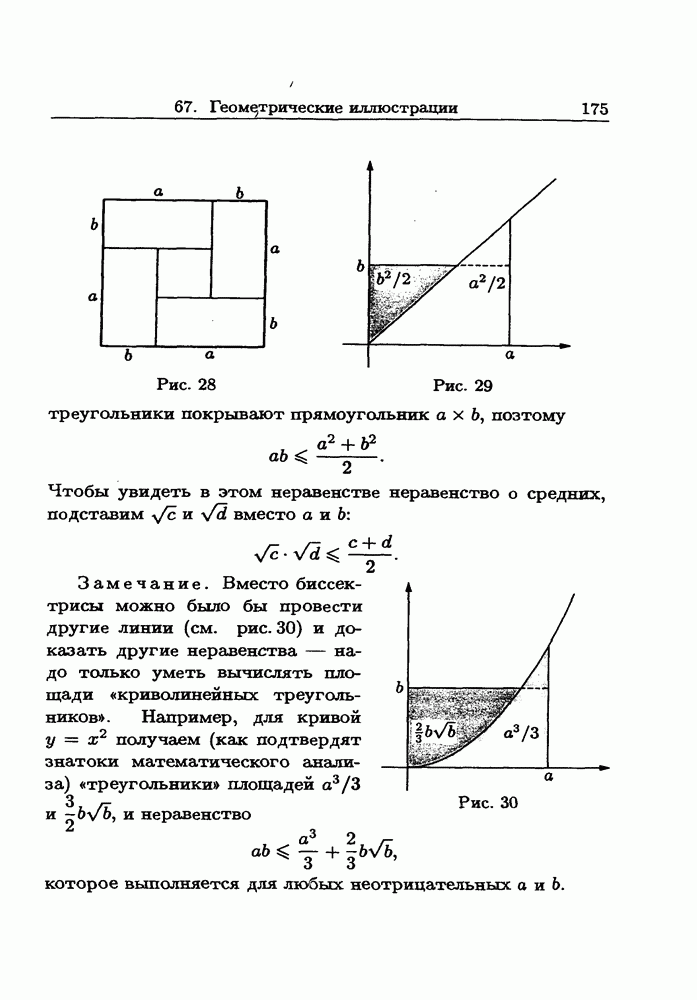
- 67. Геометрические иллюстрации
- 68. Средние многих чисел
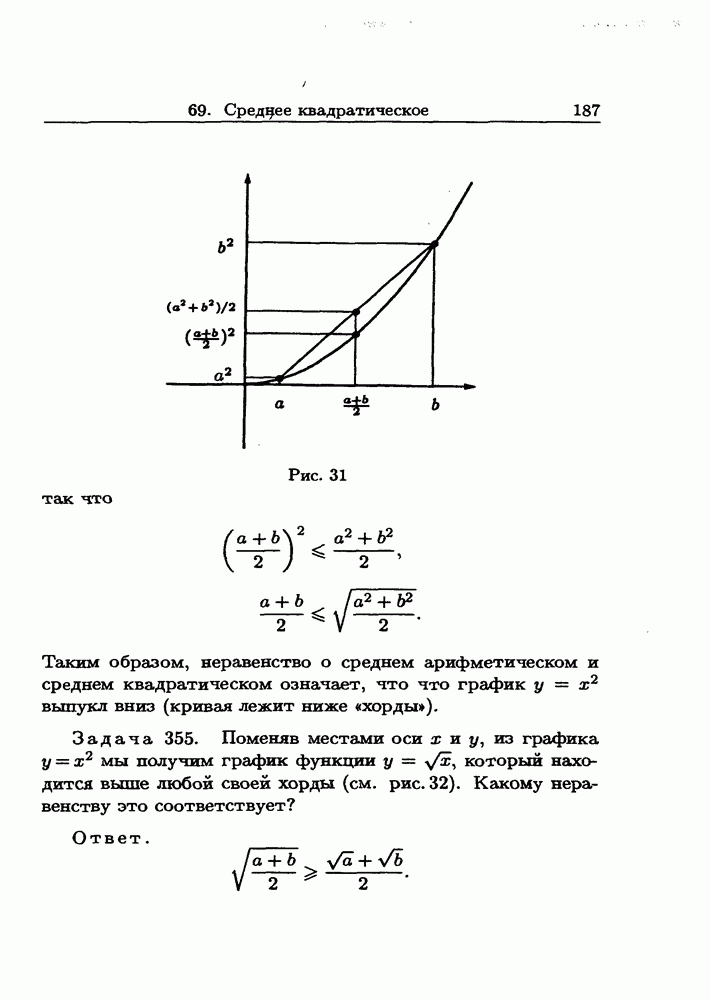
- 69. Среднее квадратическое
- 70. Среднее гармоническое
- 71. Книги для дальнейшего чтения