| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
62. Степень с дробным показателем
Следующее мнемоническое правило может помочь запомнить свойства корней: эти свойства (задачи 278-286) получаются из свойств степеней, если считать, что

Например, основное свойство корня (его определение)

теперь переписывается в виде

и становится частным случаем правила

при 
Свойство

теперь запишется в виде

и получается при 
Задача 303. Получите с помощью этого приема все указанные в задачах 294-302 свойства корней (используя свойства степеней).
Иметь дело с мнемоническими правилами всегда несколько унизительно, поэтому давайте поднимем его в ранге и будем считать его определением степени с показателем  (раньше мы рассматривали степени только с целым показателем).
(раньше мы рассматривали степени только с целым показателем).
Определение. При целом  полагаем
полагаем

Сразу же видно, что этого определения мало. Например, хотелось бы написать, что

(частный случай правила  при
при  . Но мы не знаем, что такое
. Но мы не знаем, что такое  . Чтобы восполнить этот пробел, определим
. Чтобы восполнить этот пробел, определим  как
как  и вообще
и вообще  как
как  или, другими словами, как
или, другими словами, как 
Определение. Для целого  и целого положительного
и целого положительного  определим
определим 

Внимательный читатель сразу же отметит подвох в этом определении. Например,

в то время как

Между тем  и тем самым
и тем самым  обязано равняться
обязано равняться  Чтобы наше определение было корректным, необходимо, чтобы
Чтобы наше определение было корректным, необходимо, чтобы

Задача 304. Проверьте это.
Решение.

Задача 305. Проверьте, что при сокращении общих множителей в дроби  значение выражения
значение выражения  согласно нашему определению не меняется.
согласно нашему определению не меняется.
Указание. См. предыдущую задачу, где в дроби 10/15 сократился общий множитель 5.
Теперь свойства степеней, которые мы знали для целых показателей, надо проверить для показателей, равных отношению двух целых чисел (рациональных показателей). Задача 306. Доказать, что

для любых дробей 
Решение. Пусть, например,  (в общем случае рассуждения аналогичны). Надо проверить, что
(в общем случае рассуждения аналогичны). Надо проверить, что

Приведем дроби 2/5 и 3/7 к общему знаменателю:

Мы уже знаем, что

поэтому

Задача 307. Доказать, что

Задача 308. Доказать, что

для любых рациональных показателей  .
.
Решение. Сначала пусть q — целое, 

Пусть теперь  при некотором целом k, а
при некотором целом k, а  . Тогда
. Тогда

Обозначив  через b, продолжим:
через b, продолжим:

Наконец, для произвольного  имеем
имеем

Сначала мы воспользовались тем, что

и затем использовали, что

(Эти два частных случая интересующего нас равенства мы разобрали заранее.)
Задача 309. Доказать, что при  значение
значение  увеличивается с ростом
увеличивается с ростом  , а при
, а при  значение
значение  уменьшается с ростом
уменьшается с ростом  .
.
Указание. Приведите сравниваемые значения показателя к общему знаменателю. Не забудьте, что  может быть и отрицательным (и в этом случае утверждение задачи остается верным).
может быть и отрицательным (и в этом случае утверждение задачи остается верным).
Эта задача открывает возможность определения  и для чисел
и для чисел  не являющихся отношениями двух целых. Например, число
не являющихся отношениями двух целых. Например, число

можно пытаться определить как число, большее всех чисел вида  и меньшее всех чисел вида
и меньшее всех чисел вида  при
при  (То, что такое число существует и единственно, доказывается в курсе математического анализа.)
(То, что такое число существует и единственно, доказывается в курсе математического анализа.)
Задача 310. Как бы Вы определили или 
Ответ. Естественно считать, что 
| << Предыдущий параграф | Следующий параграф >> |
- 1. Предисловие
- 2. Перемена мест слагаемых
- 3. Перемена мест сомножителей
- 4. Сложение столбиком
- 5. Таблица умножения. Умножение столбиком
- 6. Деление «уголком»
- 7. Двоичная система счисления
- 8. Коммутативность
- 9. Ассоциативность
- 10. Расстановки скобок
- 11. Дистрибутивность
- 12. Буквы в алгебре
- 13. Сложение отрицательных чисел
- 14. Умножение отрицательных чисел
- 15. Действия с дробями
- 16. Степени
- 17. Отрицательные степени
- 18. Как умножить a^m на a^n или почему наше определение удобно
- 19. Правило умножения степеней
- 20. Формулы сокращенного умножения. Квадрат суммы
- 21. Как объяснить формулу (a+b)^2=a^2+2ab+b^2 младшему брату или сестре
- 22. Квадрат разности
- 23. Разность квадратов
- 24. Куб суммы
- 25. Четвертая степень суммы
- 26. (a+b)^5, (a+b)^6 и треугольник Паскаля
- 27. Многочлены
- 28. Отступление: какие многочлены считать равными?
- 29. Сколько одночленов останется?
- 30. Коэффициенты и значения
- 31. Разложение на множители
- 32. Рациональные выражения
- 33. Преобразование рационального выражения в частное двух многочленов
- 34. Многочлены и рациональные дроби с одной переменной
- 35. Деление многочленов с остатком
- 36. Остаток при делении на х — а
- 37. Многочлены, значения, интерполяция
- 38. Арифметические прогрессии
- 39. Сумма арифметической прогрессии
- 40. Геометрические прогрессии
- 41. Сумма геометрической прогрессии
- 42. Разные задачи о прогрессиях
- 43. Хорошо темперированный клавир
- 44. Сумма бесконечной прогрессии
- 45. Уравнения
- 46. Квадратное уравнение
- 47. Случай p = 0. Квадратный корень
- 48. Свойства квадратных корней
- 49. Уравнение х^2 + рх + q = 0
- 50. Теорема Виета
- 51. Разложение квадратного трехчлена на множители
- 52. Формула для корней уравнения ах^2 + bх + c = 0
- 53. Бще одна формула корней квадратного уравнения
- 54. Квадратное уравнение становится линейным
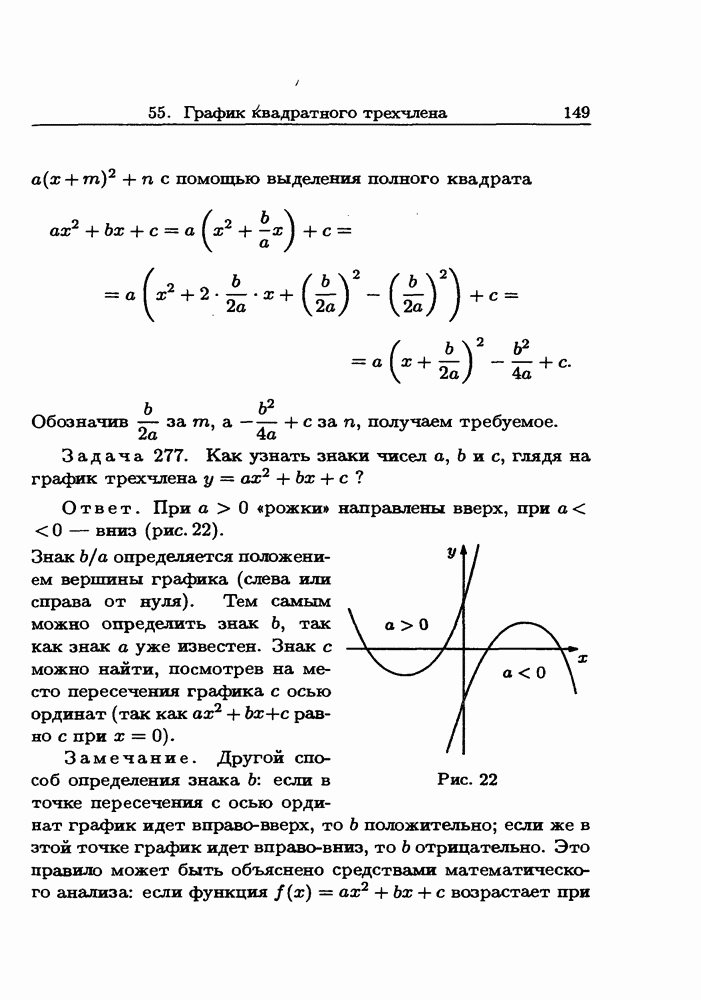
- 55. График квадратного трехчлена
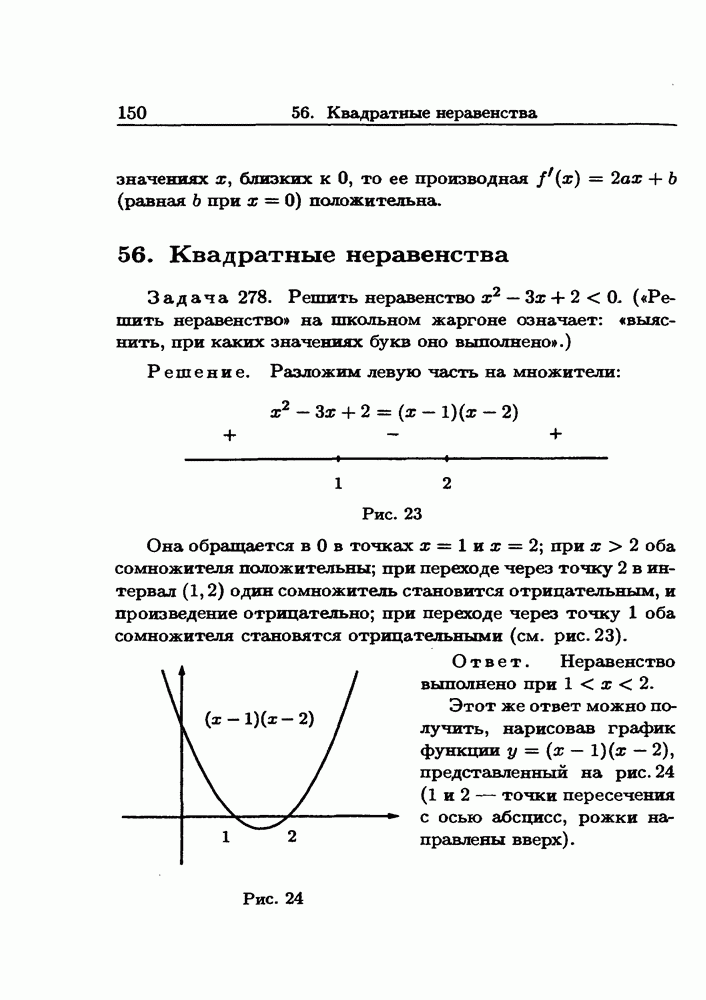
- 56. Квадратные неравенства
- 57. Максимум и минимум квадратного трехчлена
- 58. Биквадратные уравнения
- 59. Возвратные уравнения
- 60. Как завалить на экзамене. Советы экзаменатору
- 61. Корни
- 62. Степень с дробным показателем
- 63. Доказательства числовых неравенств
- 64. Среднее арифметическое и среднее геометрическое
- 65. Среднее геометрическое не больше среднего арифметического
- 66. Задачи на максимум и минимум
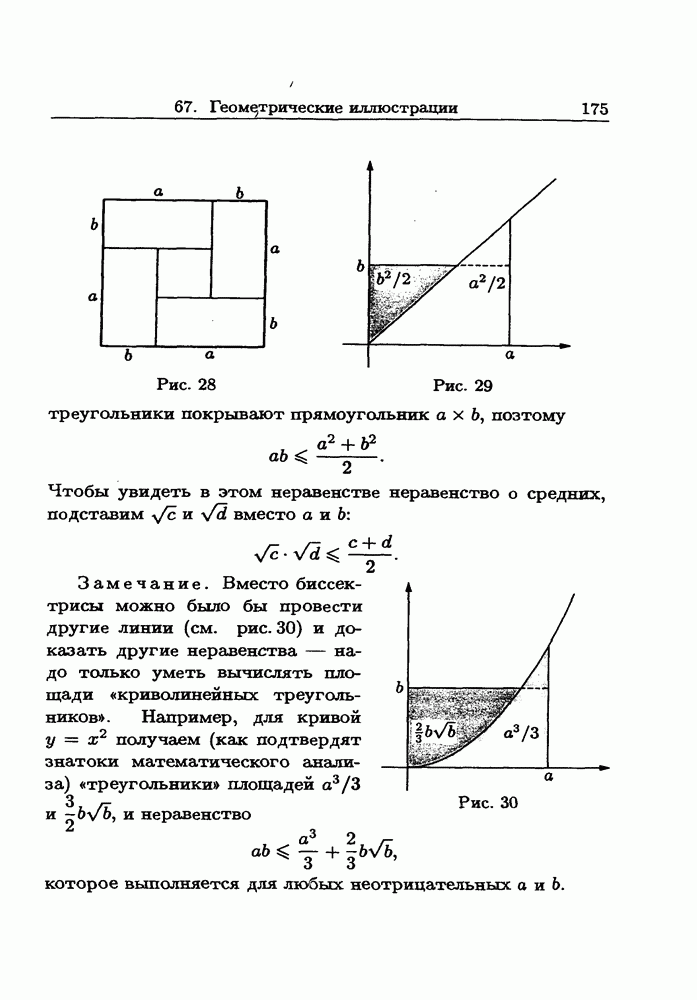
- 67. Геометрические иллюстрации
- 68. Средние многих чисел
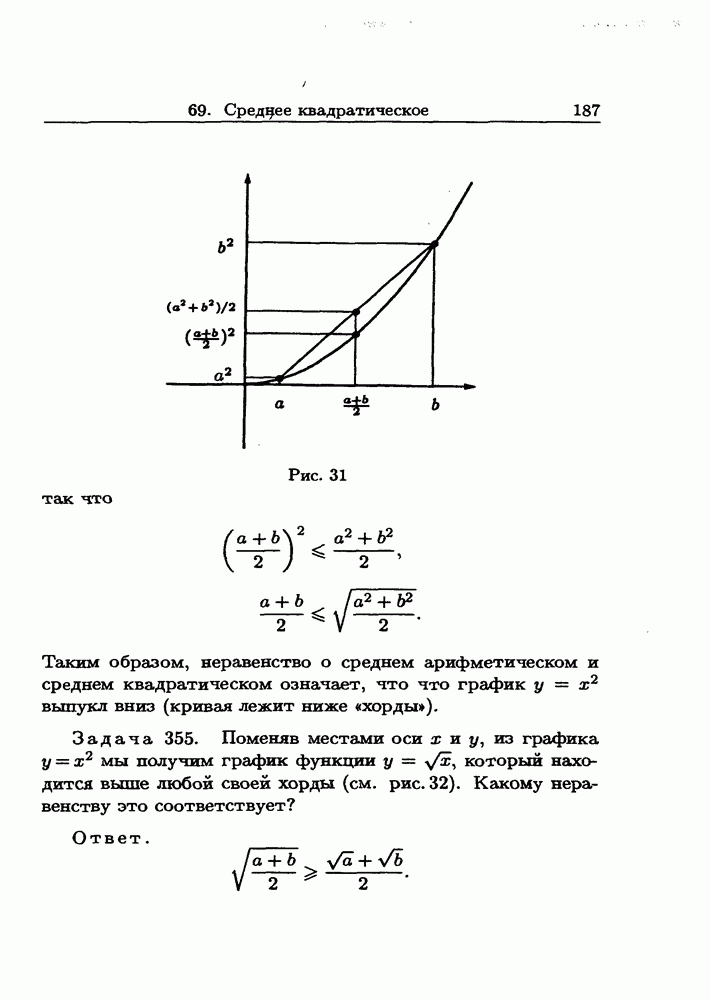
- 69. Среднее квадратическое
- 70. Среднее гармоническое
- 71. Книги для дальнейшего чтения