| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
44. Сумма бесконечной прогрессии
Один из «парадоксов Зенона» (древнегреческого философа) состоит в следующем (в изложении Льва Толстого в «Войне и мире», т. 3, ч. 3).
... Ахиллес никогда не догонит впереди идущую черепаху, несмотря на то, что Ахиллес идет в десять раз скорее черепахи: как только Ахиллес пройдет пространство, отделяющее его от черепахи, черепаха пройдет впереди его одну десятую этого пространства; Ахиллес пройдет эту десятую, черепаха пройдет одну сотую и т. д. до бесконечности. Задача эта представлялась древним неразрешимою.
Мы включили эту задачу в раздел о прогрессиях, поскольку отрезки, последовательно пробегаемые Ахиллесом, составляют геометрическую прогрессию

со знаменателем 1/10 (за единицу мы принимаем начальное расстояние между Ахиллесом и черепахой). Общее расстояние,
пройденное Ахиллесом до встречи с черепахой, есть «сумма бесконечного числа членов»

Педант заметил бы нам, что говорить о сумме бесконечного числа членов (не определяя эти понятия специально) не имеет смысла: прибавляя очередные члены, мы никогда не кончим. И он прав. Но мы все же не будем оправдываться, а вместо этого найдем эту сумму разными способами.
Способ 1. Обозначим сумму через S:

Тогда

откуда

Способ 2. Будем добавлять слагаемые по одному:

В итоге получится

что, как известно, равно  (так как 1/9 = 0,111...).
(так как 1/9 = 0,111...).
Способ 3. По формуле суммы геометрической прогрессии

В нашем случае q = 1/10, а  бесконечно (если можно так выразиться). Тогда
бесконечно (если можно так выразиться). Тогда  бесконечно мало (ведь с ростом
бесконечно мало (ведь с ростом  число
число  быстро убывает) и им можно пренебречь. Получаем формулу
быстро убывает) и им можно пренебречь. Получаем формулу

(мы изменили знаки в числителе и знаменателе). Вспомнив, что  получим ответ
получим ответ 
Способ 4. Вспомним, наконец, про Ахиллеса и черепаху. Здравый смысл подсказывает, что Ахиллес догонит черепаху, пробежав некоторое расстояние S. За это время черепаха, скорость которой в 10 раз меньше, проползет расстояние  и расстояние между ними уменьшится на
и расстояние между ними уменьшится на  . В начале оно равнялось 1, а в момент встречи стало нулевым, так что
. В начале оно равнялось 1, а в момент встречи стало нулевым, так что 
Пусть теперь Ахиллес стал бегать в 10 раз медленнее черепахи. Пока он пробегает расстояние до точки старта черепахи, черепаха уползает на вдесятеро большее расстояние. Когда Ахиллес добежит до этой точки, черепаха уползет на расстояние, в сто раз большее начального, и т. д. Получаем сумму

Разумеется, Ахиллес никогда не догонит черепаху. Но тем не менее в формулу

можно подставить  и получить «равенство»
и получить «равенство»

Задача 238. Можно ли придать явно нелепому утверждению «Ахиллес догонит черепаху, пробежав —1/9 метра» какой-то смысл?
Указание. Можно.
| << Предыдущий параграф | Следующий параграф >> |
- 1. Предисловие
- 2. Перемена мест слагаемых
- 3. Перемена мест сомножителей
- 4. Сложение столбиком
- 5. Таблица умножения. Умножение столбиком
- 6. Деление «уголком»
- 7. Двоичная система счисления
- 8. Коммутативность
- 9. Ассоциативность
- 10. Расстановки скобок
- 11. Дистрибутивность
- 12. Буквы в алгебре
- 13. Сложение отрицательных чисел
- 14. Умножение отрицательных чисел
- 15. Действия с дробями
- 16. Степени
- 17. Отрицательные степени
- 18. Как умножить a^m на a^n или почему наше определение удобно
- 19. Правило умножения степеней
- 20. Формулы сокращенного умножения. Квадрат суммы
- 21. Как объяснить формулу (a+b)^2=a^2+2ab+b^2 младшему брату или сестре
- 22. Квадрат разности
- 23. Разность квадратов
- 24. Куб суммы
- 25. Четвертая степень суммы
- 26. (a+b)^5, (a+b)^6 и треугольник Паскаля
- 27. Многочлены
- 28. Отступление: какие многочлены считать равными?
- 29. Сколько одночленов останется?
- 30. Коэффициенты и значения
- 31. Разложение на множители
- 32. Рациональные выражения
- 33. Преобразование рационального выражения в частное двух многочленов
- 34. Многочлены и рациональные дроби с одной переменной
- 35. Деление многочленов с остатком
- 36. Остаток при делении на х — а
- 37. Многочлены, значения, интерполяция
- 38. Арифметические прогрессии
- 39. Сумма арифметической прогрессии
- 40. Геометрические прогрессии
- 41. Сумма геометрической прогрессии
- 42. Разные задачи о прогрессиях
- 43. Хорошо темперированный клавир
- 44. Сумма бесконечной прогрессии
- 45. Уравнения
- 46. Квадратное уравнение
- 47. Случай p = 0. Квадратный корень
- 48. Свойства квадратных корней
- 49. Уравнение х^2 + рх + q = 0
- 50. Теорема Виета
- 51. Разложение квадратного трехчлена на множители
- 52. Формула для корней уравнения ах^2 + bх + c = 0
- 53. Бще одна формула корней квадратного уравнения
- 54. Квадратное уравнение становится линейным
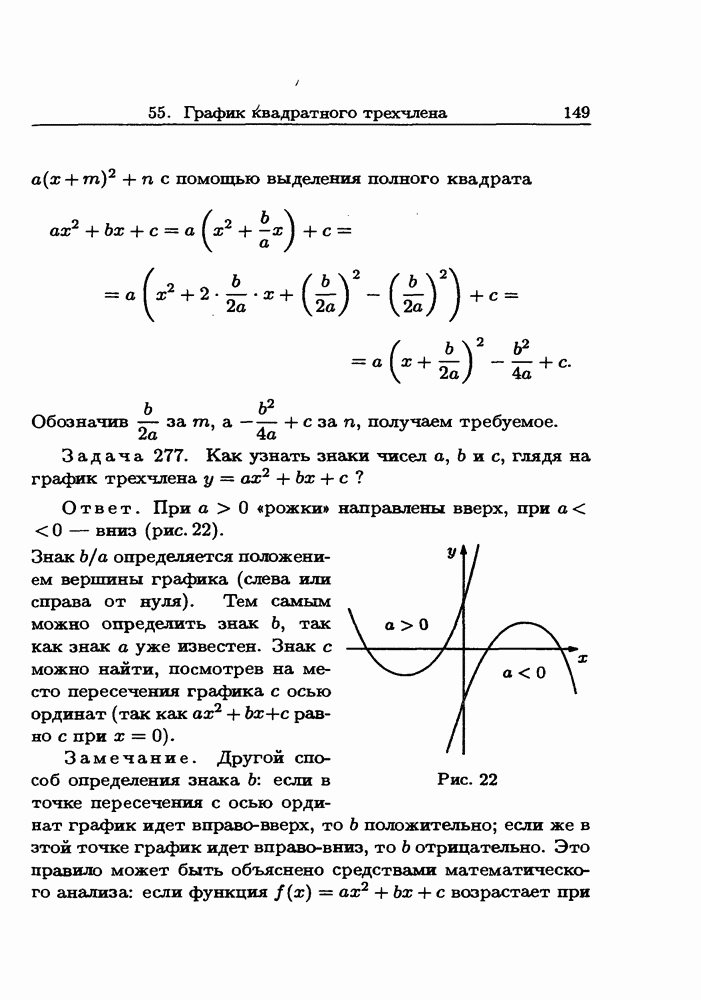
- 55. График квадратного трехчлена
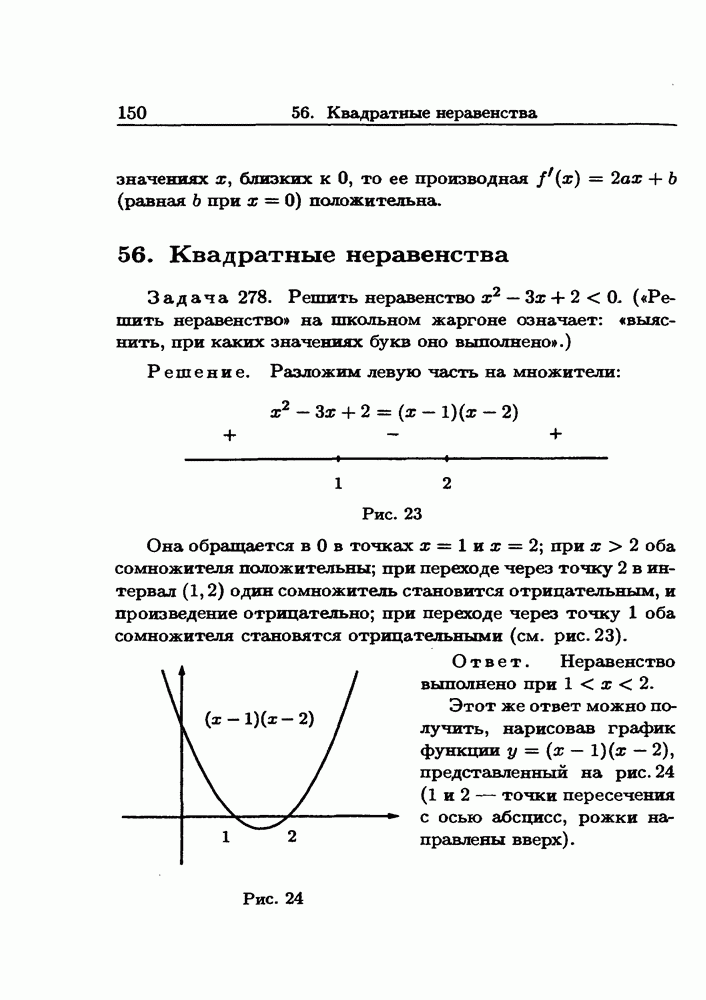
- 56. Квадратные неравенства
- 57. Максимум и минимум квадратного трехчлена
- 58. Биквадратные уравнения
- 59. Возвратные уравнения
- 60. Как завалить на экзамене. Советы экзаменатору
- 61. Корни
- 62. Степень с дробным показателем
- 63. Доказательства числовых неравенств
- 64. Среднее арифметическое и среднее геометрическое
- 65. Среднее геометрическое не больше среднего арифметического
- 66. Задачи на максимум и минимум
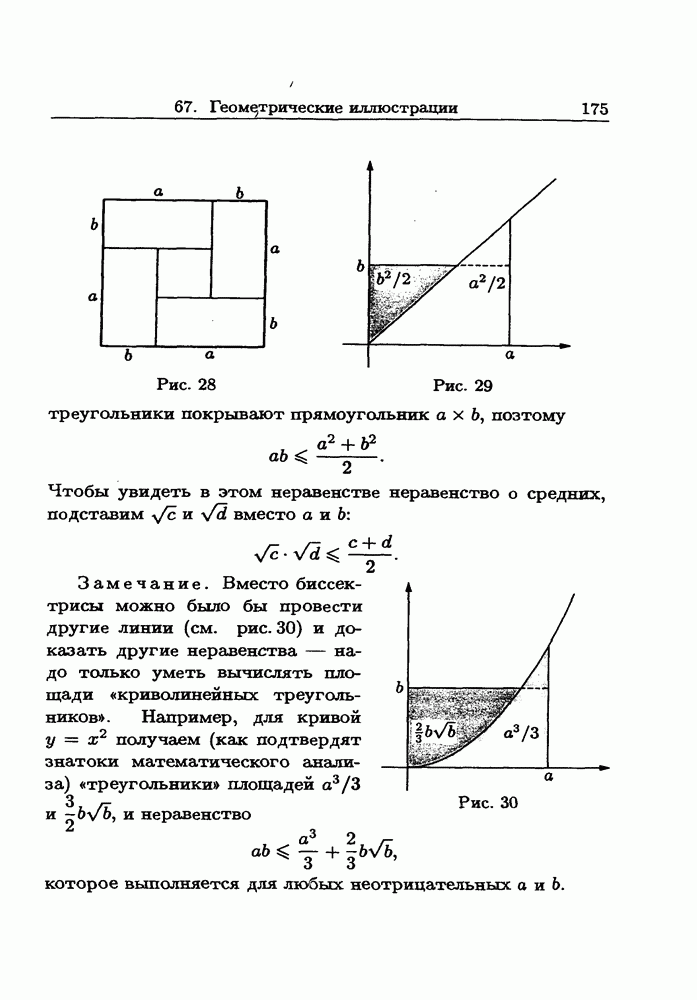
- 67. Геометрические иллюстрации
- 68. Средние многих чисел
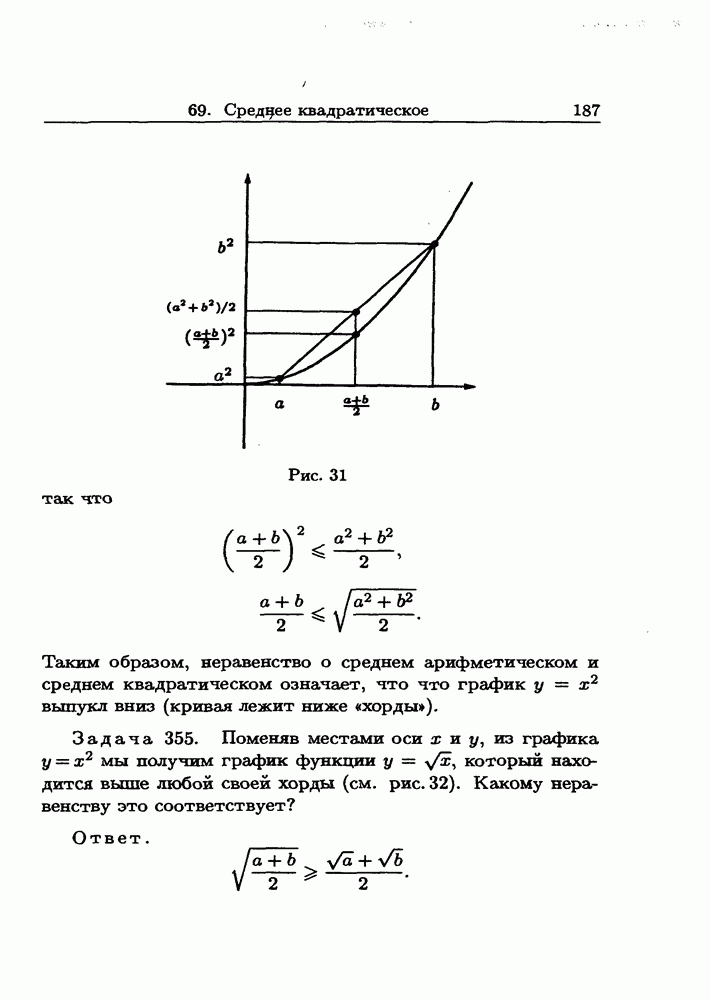
- 69. Среднее квадратическое
- 70. Среднее гармоническое
- 71. Книги для дальнейшего чтения