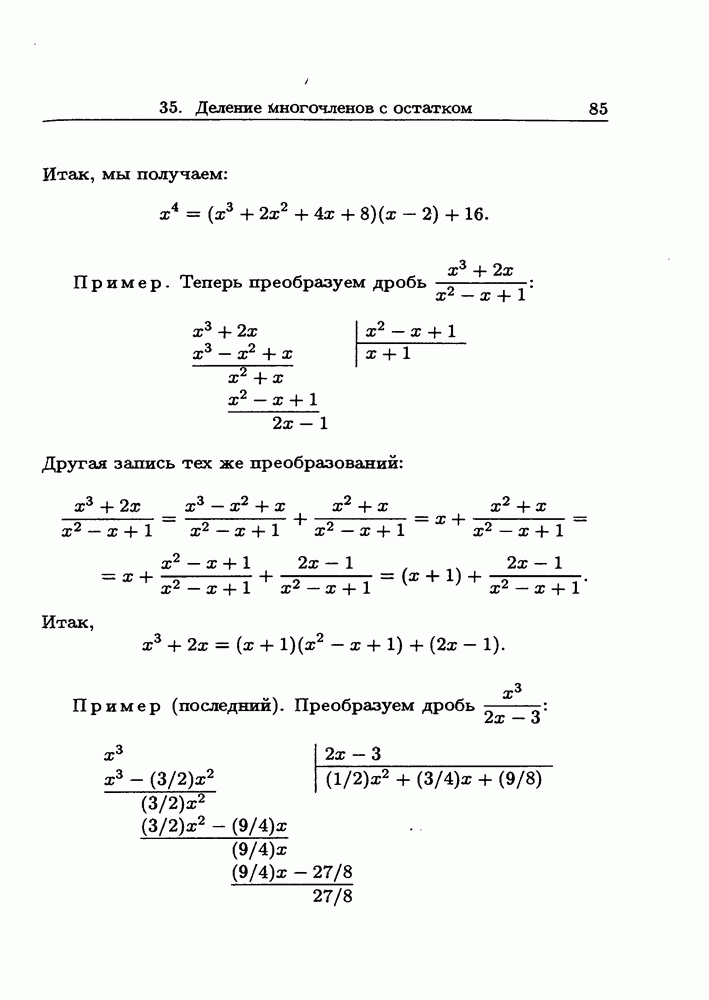| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
35. Деление многочленов с остатком
Обыкновенные дроби, числитель и знаменатель которых — целые положительные числа, бывают правильные и неправильные. Правильные — это те, у которых числитель меньше знаменателя. Например,  и
и  правильные дроби, а
правильные дроби, а  или
или  - неправильные.
- неправильные.
Из неправильной дроби можно выделить целую часть, разделив с остатком числитель на знаменатель; останется правильная дробь:

Сейчас мы научимся выполнять аналогичные преобразования для дробей, числитель и знаменатель которых — многочлены с одной переменной. Такая дробь считается правильной, если степень числителя меньше степени знаменателя. Например,  — правильные дроби,
— правильные дроби,  неправильные.
неправильные.
Всякая неправильная дробь может быть преобразовала к виду (многочлен)  (правильная дробь).
(правильная дробь).
Приведем несколько примеров преобразования неправильной дроби к такому виду.

(Когда мы говорили, что в многочленах не может быть деления, это не значило, что коэффициенты обязательно целые — они могут быть любыми, в том числе и дробными. Так, например, число 1/2 — вполне законный многочлен степени 0.)

Существует стандартный способ выделения многочлена из неправильной рациональной дроби, аналогичный обычному делению чисел «уголком». Покажем его на примерах:
Пример. Преобразуем неправильную дробь  :
:

Та же процедура может быть записана иначе:


Пример. Теперь преобразуем дробь 

Другая запись тех же преобразований:

Итак,

Пример (последний). Преобразуем дробь 

Те же преобразования:

Итак,


Задача 142. Каковы могут быть степени остатка и неполного частного при делении многочлена степени 7 на многочлен степени 3?
Ответ. Степень неполного частного равна 4, степень остатка может быть 0,1,2 или 3; кроме того, остатка может не быть вовсе (т. е. он может быть равен 0).
Задача 143. Доказать, что неполное частное и остаток (обладающие указанными в рамке свойствами) всегда существуют и единственны.
Решение. Метод нахождения неполного частного и остатка был продемонстрирован выше на примерах. Для доказательства единственности предположим, что при делении Р на S могут получиться два неполных частных  и два соответствующих остатка
и два соответствующих остатка  . Тогда мы имеем
. Тогда мы имеем

причем у обоих многочленов  степени меньше, чем у S. Тогда
степени меньше, чем у S. Тогда

и, следовательно,

Если получившийся многочлен  не равен нулю, то его степень меньше, чем у S (так как степени обоих многочленов
не равен нулю, то его степень меньше, чем у S (так как степени обоих многочленов  меньше, чем у S). Поэтому равенство
меньше, чем у S). Поэтому равенство  возможно в одном-единственном случае: если
возможно в одном-единственном случае: если 
Что считать остатком и частным, если степень делимого с самого начала меньше степени делителя? В этом случае полагают, что частное равно 0, а остаток равен делимому. Деление многочленов похоже на обычное деление:

В этом примере аналогия полная; чтобы убедиться в этом, достаточно подставить 10 вместо х. В других случаях, например,

аналогия неполная: подставив в последнее равенство  получим равенство
получим равенство  , которое, хотя и верно, но не означает, что при делении 1234 на 9 частное равно 136, а остаток равен 10 (на самом деле частное равно 137, а остаток равен 1).
, которое, хотя и верно, но не означает, что при делении 1234 на 9 частное равно 136, а остаток равен 10 (на самом деле частное равно 137, а остаток равен 1).
Задача 144.
1. Разделить  на
на  .
.
2. Разделить  на
на  .
.
3. Разделить  на
на  .
.
4. Разделить  на
на  .
.
5. Разделить  на
на  .
.
Пункты 1-3 являются частным случаем общей формулы

которую легко проверить делением уголком или просто перемножив  . На эту формулу можно смотреть как на способ суммирования ряда последовательных степеней некоторого числа х:
. На эту формулу можно смотреть как на способ суммирования ряда последовательных степеней некоторого числа х:

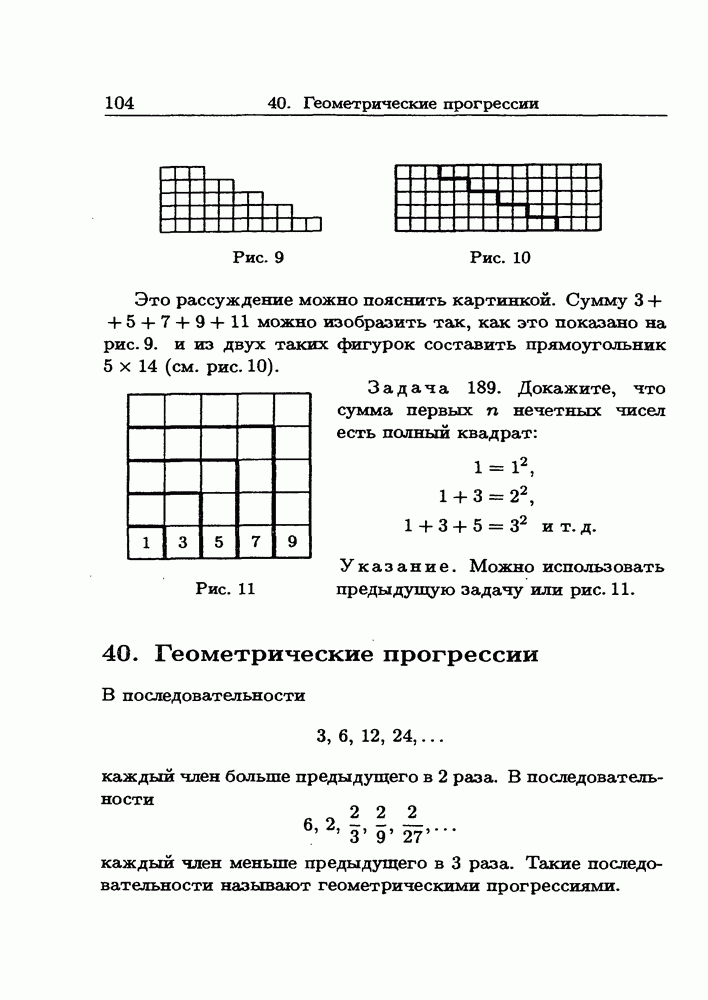
(она годится для всех х, кроме 1). См. ниже о сумме геометрической прогрессии.
Задача 145. Степени двойки

обладают таким свойством: сумма нескольких первых чисел этой последовательности на единицу меньше следующего числа:

и т. д. Объяснить наблюдаемую закономерность.
Решение. Подставим в равенство

значение х = 2. Получим

Возможно другое решение. Чтобы вычислить сумму 1 + 2 + 4 + 8 + 16, прибавим и вычтем 1:

Аналогично для других степеней.
| << Предыдущий параграф | Следующий параграф >> |
- 1. Предисловие
- 2. Перемена мест слагаемых
- 3. Перемена мест сомножителей
- 4. Сложение столбиком
- 5. Таблица умножения. Умножение столбиком
- 6. Деление «уголком»
- 7. Двоичная система счисления
- 8. Коммутативность
- 9. Ассоциативность
- 10. Расстановки скобок
- 11. Дистрибутивность
- 12. Буквы в алгебре
- 13. Сложение отрицательных чисел
- 14. Умножение отрицательных чисел
- 15. Действия с дробями
- 16. Степени
- 17. Отрицательные степени
- 18. Как умножить a^m на a^n или почему наше определение удобно
- 19. Правило умножения степеней
- 20. Формулы сокращенного умножения. Квадрат суммы
- 21. Как объяснить формулу (a+b)^2=a^2+2ab+b^2 младшему брату или сестре
- 22. Квадрат разности
- 23. Разность квадратов
- 24. Куб суммы
- 25. Четвертая степень суммы
- 26. (a+b)^5, (a+b)^6 и треугольник Паскаля
- 27. Многочлены
- 28. Отступление: какие многочлены считать равными?
- 29. Сколько одночленов останется?
- 30. Коэффициенты и значения
- 31. Разложение на множители
- 32. Рациональные выражения
- 33. Преобразование рационального выражения в частное двух многочленов
- 34. Многочлены и рациональные дроби с одной переменной
- 35. Деление многочленов с остатком
- 36. Остаток при делении на х — а
- 37. Многочлены, значения, интерполяция
- 38. Арифметические прогрессии
- 39. Сумма арифметической прогрессии
- 40. Геометрические прогрессии
- 41. Сумма геометрической прогрессии
- 42. Разные задачи о прогрессиях
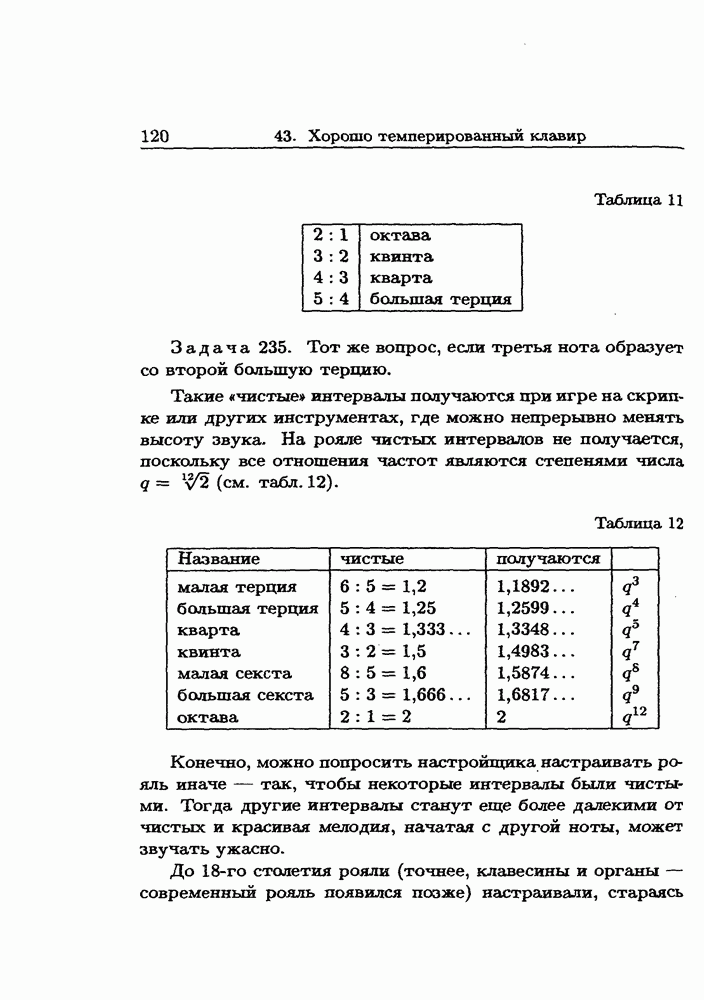
- 43. Хорошо темперированный клавир
- 44. Сумма бесконечной прогрессии
- 45. Уравнения
- 46. Квадратное уравнение
- 47. Случай p = 0. Квадратный корень
- 48. Свойства квадратных корней
- 49. Уравнение х^2 + рх + q = 0
- 50. Теорема Виета
- 51. Разложение квадратного трехчлена на множители
- 52. Формула для корней уравнения ах^2 + bх + c = 0
- 53. Бще одна формула корней квадратного уравнения
- 54. Квадратное уравнение становится линейным
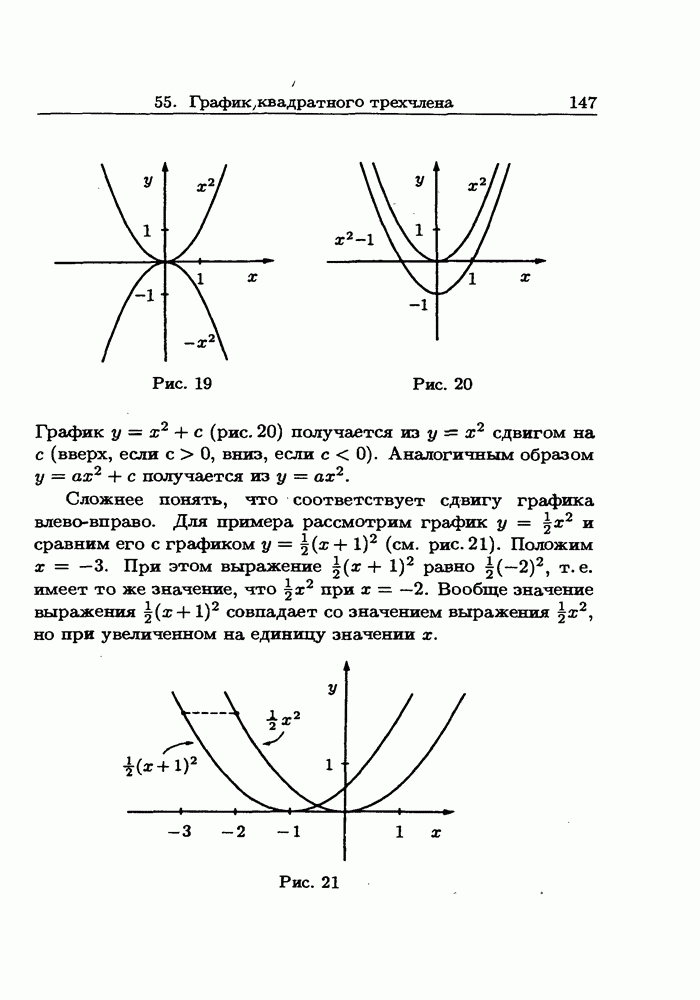
- 55. График квадратного трехчлена
- 56. Квадратные неравенства
- 57. Максимум и минимум квадратного трехчлена
- 58. Биквадратные уравнения
- 59. Возвратные уравнения
- 60. Как завалить на экзамене. Советы экзаменатору
- 61. Корни
- 62. Степень с дробным показателем
- 63. Доказательства числовых неравенств
- 64. Среднее арифметическое и среднее геометрическое
- 65. Среднее геометрическое не больше среднего арифметического
- 66. Задачи на максимум и минимум
- 67. Геометрические иллюстрации
- 68. Средние многих чисел
- 69. Среднее квадратическое
- 70. Среднее гармоническое
- 71. Книги для дальнейшего чтения