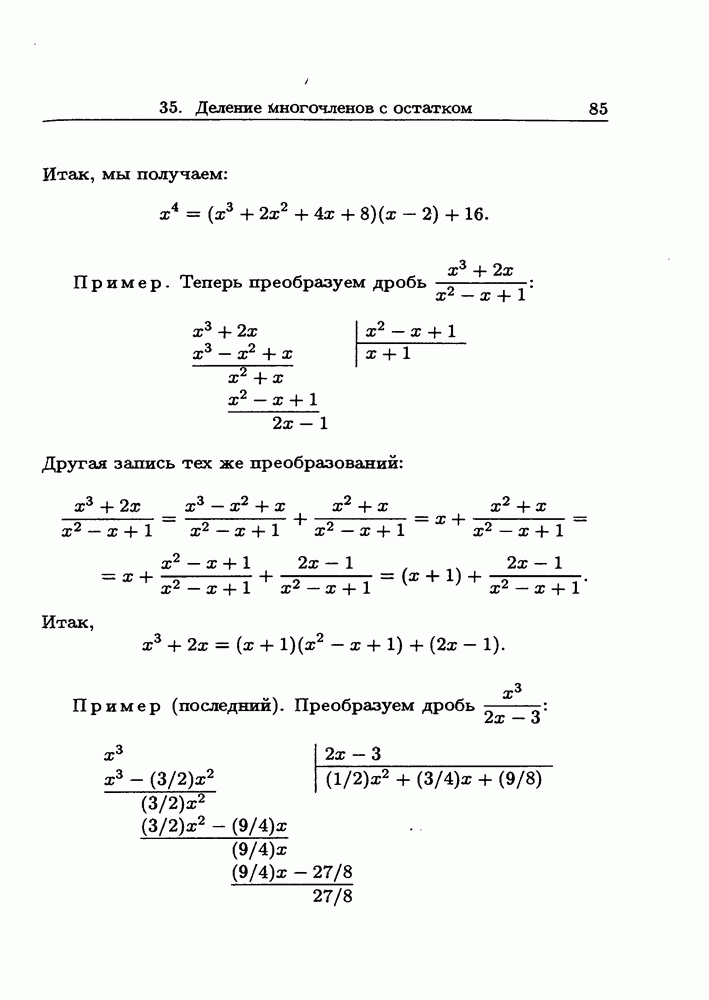| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
68. Средние многих чисел
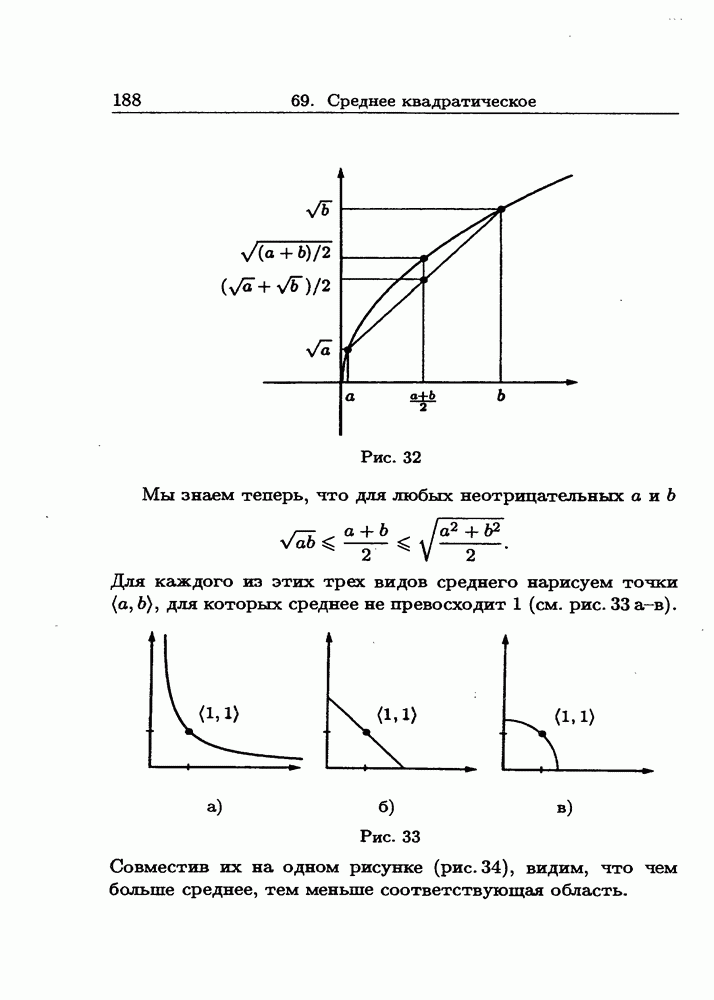
Среднее арифметическое трех чисел а, b, с определяется как  среднее геометрическое — как
среднее геометрическое — как  (мы вновь предполагаем, что
(мы вновь предполагаем, что  ). Аналогичные определения даются и для любого количества чисел: среднее арифметическое
). Аналогичные определения даются и для любого количества чисел: среднее арифметическое  чисел
чисел  определяется как
определяется как

среднее геометрическое неотрицательных чисел  — как
— как

Неравенство о среднем арифметическом и среднем геометрическом верно для любого количества чисел:

Как и в разобранном ранее случае двух чисел, равенство возможно, только если все числа равны.
Прежде чем доказывать неравенство, извлечем некоторые следствия.
Задача 331. Используя неравенство, доказать, что если  — неотрицательные числа, для которых
— неотрицательные числа, для которых

то

Решение.

В двух следующих задачах также предполагается использовать неравенство о среднем арифметическом и среднем геометрическом (без доказательства).
Задача 332. Доказать, что произведение  неотрицательных чисел с заданной суммой максимально, когда эти числа равны.
неотрицательных чисел с заданной суммой максимально, когда эти числа равны.
Задача 333. Доказать, что сумма  неотрицательных чисел с заданным произведением минимальна, когда эти числа равны.
неотрицательных чисел с заданным произведением минимальна, когда эти числа равны.
Существуют разные доказательства неравенства о средних арифметическом и геометрическом, но наиболее естественное использует математический анализ (понятие производной). Мы обойдемся без него — но поневоле это будет выглядеть как трюк.
Задача 334. Доказать неравенство о среднем арифметическом и среднем геометрическом для 
Решение. Нам даны 4 неотрицательных числа а, b, с, d. Будем менять их, сохраняя неизменной их сумму (и, следовательно, среднее арифметическое). При этом их произведение будет меняться — и мы будем следить за тем, как именно. Наше доказательство проходит в несколько этапов.
1. Заменим а и  на два числа, каждое из которых равно
на два числа, каждое из которых равно 

Сумма не изменится. Произведение возрастет (или останется прежним, если  сомножители с и d не меняются, а произведение двух чисел с заданной суммой
сомножители с и d не меняются, а произведение двух чисел с заданной суммой  максимально, когда числа равны.
максимально, когда числа равны.
2. То же самое сделаем с 

Сумма не изменится, произведение снова увеличится (или останется прежним, если  ).
).
3. Мы выравняли числа в первой паре и во второй паре, теперь будем выравнивать между парами:

4. Теперь осталось выравнять второе и четвертое числа:

В конечном итоге мы заменили числа

на числа

где  — среднее арифметическое, и их произведение возросло (или осталось прежним)
— среднее арифметическое, и их произведение возросло (или осталось прежним)

или

Что и требовалось.
Задача 335. Доказать, что неравенство между средним арифметическим и средним геометрическим для четырех чисел превращается в равенство, только если все числа равны.
Указание. Из решения предыдущей задачи видно, что равенство возможно лишь, если на всех стадиях описанного там процесса наши числа фактически не изменялись.
Задача 336. Как доказать неравенство о среднем арифметическом и геометрическом для  ?
?
Решение. Точно так же: сначала выравниваем числа в четырех парах, затем между парами — и получается две четверки, затем выравниваем все восемь.
Задача 337. Доказать неравенство о среднем арифметическом и геометрическом для 
Решение. Из трех чисел а, b, с сделаем четыре, добавив среднее геометрическое: получатся числа

к которым применим неравенство для четырех чисел:

Корень, стоящий в левой части неравенства, представляет собой не что иное, как  Чтобы убедиться в этом, возведем оба (неотрицательных) числа
Чтобы убедиться в этом, возведем оба (неотрицательных) числа  в четвертую степень: получим одно и то же:
в четвертую степень: получим одно и то же:

и

Итак,

Что и требовалось доказать.
Задача 338. Используя неравенство о средних для  доказать его для
доказать его для 
Задача 339. Доказать неравенство о средних для 
Указание. Воспользоваться предыдущими задачами.
Задача 340. Доказать неравенство о средних для всех целых 71 2.
Указание. Сначала доказываем для  , а затем спускаемся вниз.
, а затем спускаемся вниз.
Задача 341. Доказать, что неравенство между арифметическим и геометрическим средними обращается в равенство, только если все числа равны.
Неравенство о среднем арифметическом и геометрическом можно доказывать и по-другому.
Заметим прежде всего, что если все числа  увеличить в одно и то же число раз — например, в три раза — то и среднее арифметическое, и среднее геометрическое увеличатся в то же самое число раз. При этом их соотношение сохранится. Поэтому, желая доказать неравенство о среднем арифметическом и среднем геометрическом, можно изменить
увеличить в одно и то же число раз — например, в три раза — то и среднее арифметическое, и среднее геометрическое увеличатся в то же самое число раз. При этом их соотношение сохранится. Поэтому, желая доказать неравенство о среднем арифметическом и среднем геометрическом, можно изменить
все числа во столько раз, чтобы среднее арифметическое стало равно 1. Тем самым достаточно доказать:

Будем доказывать это для различных значений n.
1. Для  мы это уже знаем: если сумма двух чисел равна 2, то их можно записать как
мы это уже знаем: если сумма двух чисел равна 2, то их можно записать как  и их произведение равно
и их произведение равно 
2. Докажем это для  . Пусть сумма трех положительных чисел a, b, с равна 3. Если не все они равны 1, то среди них есть как числа, большие 1, так и числа, меньшие 1. Пусть например,
. Пусть сумма трех положительных чисел a, b, с равна 3. Если не все они равны 1, то среди них есть как числа, большие 1, так и числа, меньшие 1. Пусть например,  Тогда
Тогда  произведение
произведение

будет отрицательным, т. е.

Так как

то

или

Глядите-ка: мы имеем два числа  и с, их сумма меньше 2, а доказать надо, что их произведение не больше 1. А для двух чисел мы это уже знаем.
и с, их сумма меньше 2, а доказать надо, что их произведение не больше 1. А для двух чисел мы это уже знаем.
Внимательный читатель остановит нас: для двух чисел мы доказали, что если сумма равна 2, то произведение не
больше 1. А здесь сумма меньше 2. Но эта разница несущественна: увеличим одно из чисел, сделав сумму равной 2 — от этого произведение только возрастет.
3. Пусть теперь  мы должны доказать, что
мы должны доказать, что

Опять же одно из чисел (например, а) должно быть меньше 1, а другое (например, b) должно быть больше 1. Тогда

поэтому

И вновь осталось доказать, что если сумма трех (неотрицательных) чисел меньше 3, то их произведение не больше 1 — мы свели дело к доказанному ранее. И так далее.
Следующее доказательство неравенства о среднем арифметическом и геометрическом для трех чисел является, вероятно, самым коротким — но и самым загадочным.
Из тождества

которое легко проверить, раскрыв скобки, следует, что при неотрицательных о, 6, с его левая часть неотрицательна, то есть

Остается подставить вместо а, b и с кубические корни 

А вот еще одно обоснование неравенства о среднем арифметическом и геометрическом.
Нам нужно доказать, что произведение  неотрицательных чисел с заданной суммой максимально, когда числа равны. Пусть это не так и числа
неотрицательных чисел с заданной суммой максимально, когда числа равны. Пусть это не так и числа  для которых произведение максимально, не все равны между собой. Предположим, для примера, что
для которых произведение максимально, не все равны между собой. Предположим, для примера, что  . Будем менять
. Будем менять  оставляя
оставляя  неизменными, причем так, чтобы сумма
неизменными, причем так, чтобы сумма  оставалась постоянной. Произведение
оставалась постоянной. Произведение  а с ним и произведение
а с ним и произведение  будет меняться. Сделав
будет меняться. Сделав  равными, мы увеличим их произведение, поскольку произведение двух неотрицательных чисел с постоянной суммой максимально, когда числа равны. Тем самым увеличится и произведение
равными, мы увеличим их произведение, поскольку произведение двух неотрицательных чисел с постоянной суммой максимально, когда числа равны. Тем самым увеличится и произведение  значит, оно не было максимально возможным!
значит, оно не было максимально возможным!
Задача 342. Найти недостаток в этом рассуждении.
Ответ. Мы доказали, что максимум произведения  (при постоянной сумме) не может достигаться, если числа
(при постоянной сумме) не может достигаться, если числа  не равны. Но не доказали, что этот максимум вообще достигается. На самом деле этот факт следует из общих теорем математического анализа, так что пробел может быть восполнен. Кроме того, можно усложнить наше рассуждение, сближая
не равны. Но не доказали, что этот максимум вообще достигается. На самом деле этот факт следует из общих теорем математического анализа, так что пробел может быть восполнен. Кроме того, можно усложнить наше рассуждение, сближая  не до полного совпадения, а до тех пор, пока одно из них не станет равным среднему арифметическому чисел
не до полного совпадения, а до тех пор, пока одно из них не станет равным среднему арифметическому чисел  . Тогда в конце концов все числа станут равными среднему арифметическому.
. Тогда в конце концов все числа станут равными среднему арифметическому.
Задача 343. Числа  положительны; доказать, что
положительны; доказать, что

Задача 344. Доказать, что

при любых  .
.
Задана 345. Каково минимальное значение а  если
если  .
.
Задача 346. Доказать неравенство

для любых неотрицательных а, b и с.
Задача 347. Доказать неравенство

Задача 348. Доказать, что

Решение. Число  можно представить как произведение 11 сомножителей, из которых один равен 1, а все остальные равны
можно представить как произведение 11 сомножителей, из которых один равен 1, а все остальные равны  Сравнивая это произведение с
Сравнивая это произведение с  видим, что сумма сомножителей осталась неизменной, а все они стали равными. Следовательно, произведение выросло.
видим, что сумма сомножителей осталась неизменной, а все они стали равными. Следовательно, произведение выросло.
Задача 349. Доказать, что

Указание. Правую часть можно представить в виде произведения 11 сомножителей, один из которых равен

а остальные равны  . Левая часть есть произведение 11 одинаковых сомножителей. Достаточно убедиться, что сумма сомножителей левой части больше суммы сомножителей правой части и воспользоваться неравенством о среднем арифметическом и среднем геометрическом.
. Левая часть есть произведение 11 одинаковых сомножителей. Достаточно убедиться, что сумма сомножителей левой части больше суммы сомножителей правой части и воспользоваться неравенством о среднем арифметическом и среднем геометрическом.
Задача 350. Расположите 4 числа из двух предыдущих задач в порядке возрастания.
| << Предыдущий параграф | Следующий параграф >> |
- 1. Предисловие
- 2. Перемена мест слагаемых
- 3. Перемена мест сомножителей
- 4. Сложение столбиком
- 5. Таблица умножения. Умножение столбиком
- 6. Деление «уголком»
- 7. Двоичная система счисления
- 8. Коммутативность
- 9. Ассоциативность
- 10. Расстановки скобок
- 11. Дистрибутивность
- 12. Буквы в алгебре
- 13. Сложение отрицательных чисел
- 14. Умножение отрицательных чисел
- 15. Действия с дробями
- 16. Степени
- 17. Отрицательные степени
- 18. Как умножить a^m на a^n или почему наше определение удобно
- 19. Правило умножения степеней
- 20. Формулы сокращенного умножения. Квадрат суммы
- 21. Как объяснить формулу (a+b)^2=a^2+2ab+b^2 младшему брату или сестре
- 22. Квадрат разности
- 23. Разность квадратов
- 24. Куб суммы
- 25. Четвертая степень суммы
- 26. (a+b)^5, (a+b)^6 и треугольник Паскаля
- 27. Многочлены
- 28. Отступление: какие многочлены считать равными?
- 29. Сколько одночленов останется?
- 30. Коэффициенты и значения
- 31. Разложение на множители
- 32. Рациональные выражения
- 33. Преобразование рационального выражения в частное двух многочленов
- 34. Многочлены и рациональные дроби с одной переменной
- 35. Деление многочленов с остатком
- 36. Остаток при делении на х — а
- 37. Многочлены, значения, интерполяция
- 38. Арифметические прогрессии
- 39. Сумма арифметической прогрессии
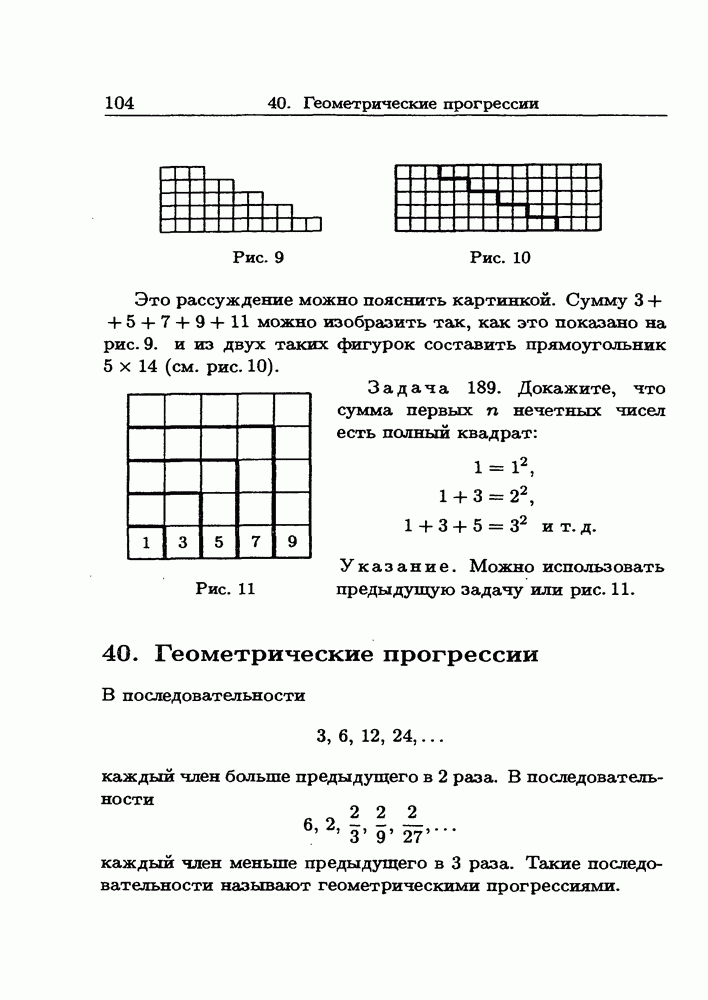
- 40. Геометрические прогрессии
- 41. Сумма геометрической прогрессии
- 42. Разные задачи о прогрессиях
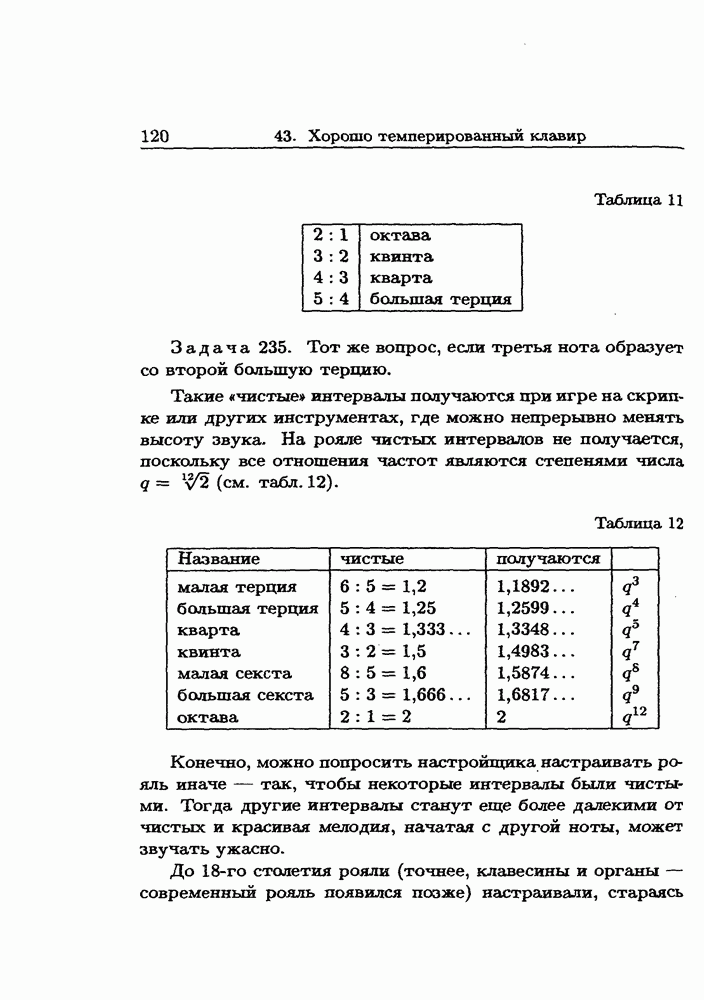
- 43. Хорошо темперированный клавир
- 44. Сумма бесконечной прогрессии
- 45. Уравнения
- 46. Квадратное уравнение
- 47. Случай p = 0. Квадратный корень
- 48. Свойства квадратных корней
- 49. Уравнение х^2 + рх + q = 0
- 50. Теорема Виета
- 51. Разложение квадратного трехчлена на множители
- 52. Формула для корней уравнения ах^2 + bх + c = 0
- 53. Бще одна формула корней квадратного уравнения
- 54. Квадратное уравнение становится линейным
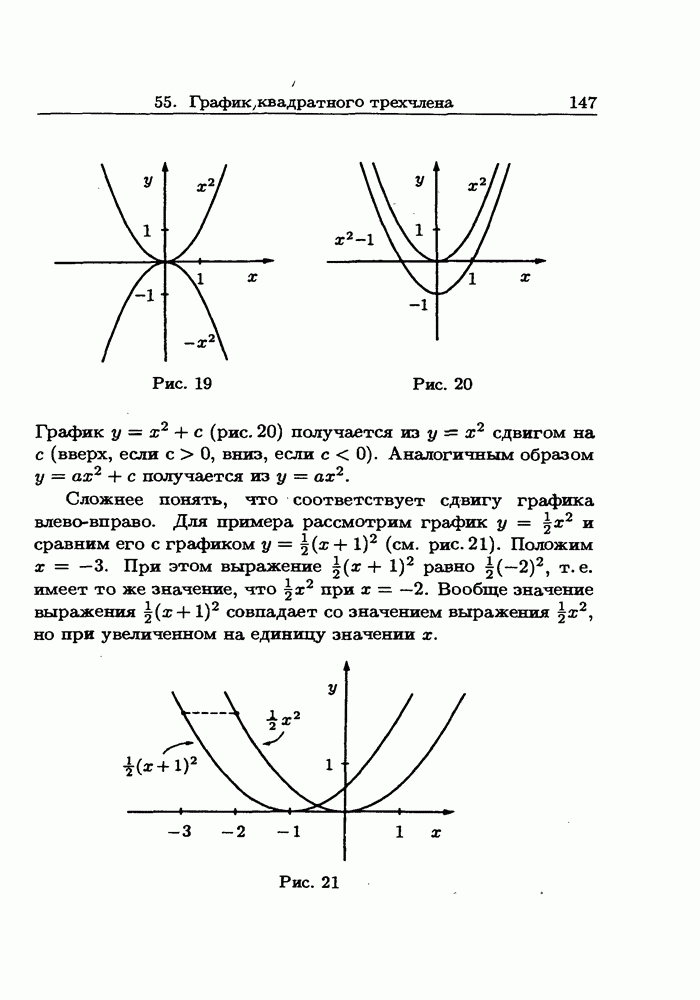
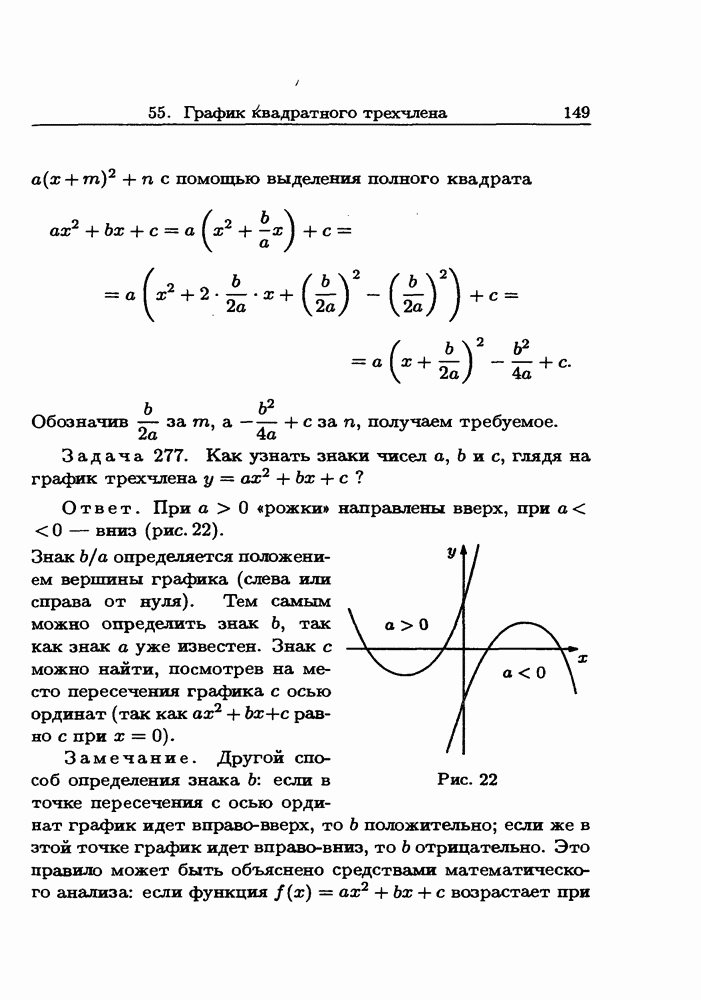
- 55. График квадратного трехчлена
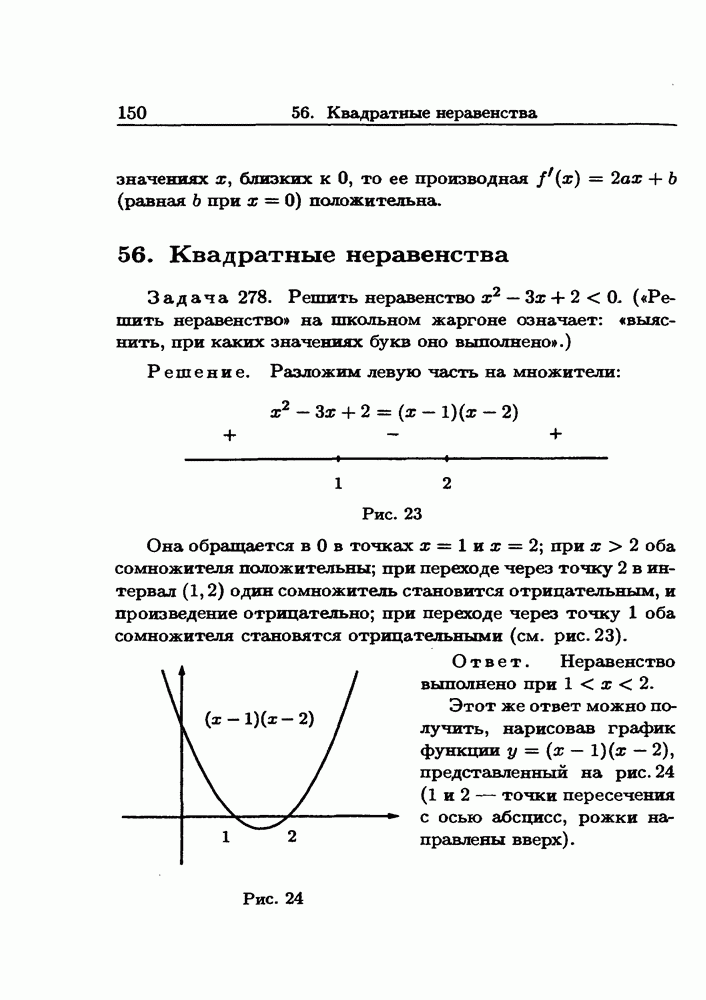
- 56. Квадратные неравенства
- 57. Максимум и минимум квадратного трехчлена
- 58. Биквадратные уравнения
- 59. Возвратные уравнения
- 60. Как завалить на экзамене. Советы экзаменатору
- 61. Корни
- 62. Степень с дробным показателем
- 63. Доказательства числовых неравенств
- 64. Среднее арифметическое и среднее геометрическое
- 65. Среднее геометрическое не больше среднего арифметического
- 66. Задачи на максимум и минимум
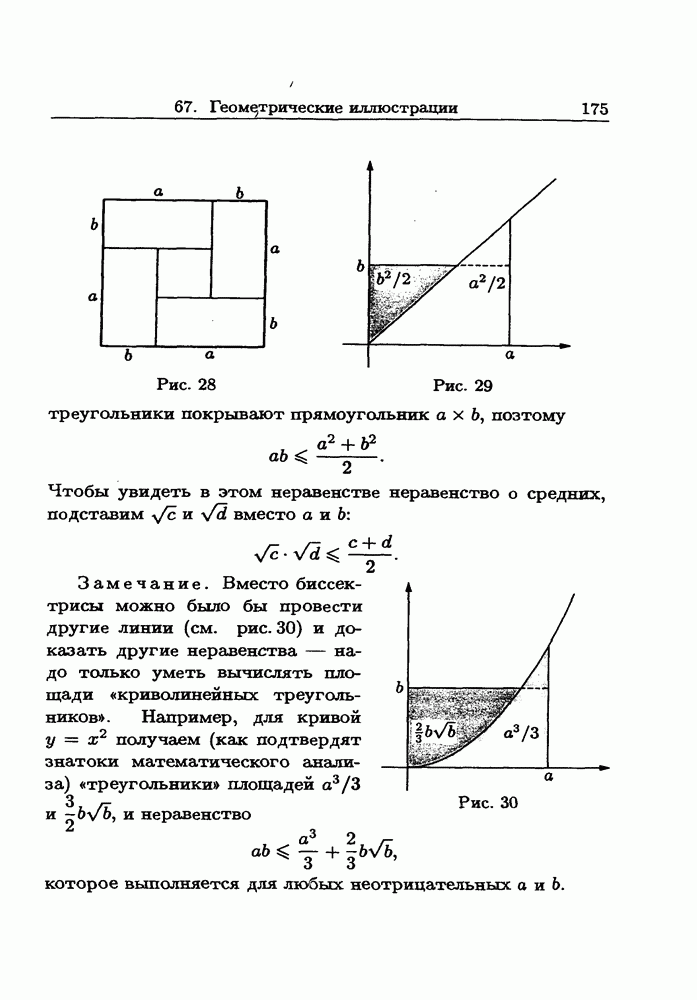
- 67. Геометрические иллюстрации
- 68. Средние многих чисел
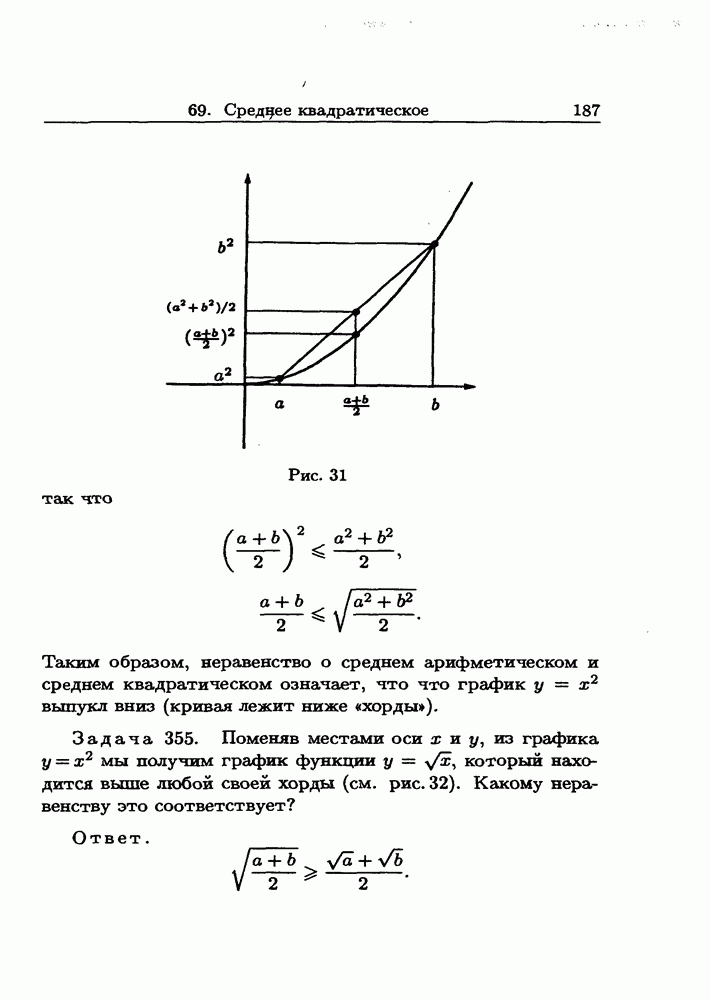
- 69. Среднее квадратическое
- 70. Среднее гармоническое
- 71. Книги для дальнейшего чтения