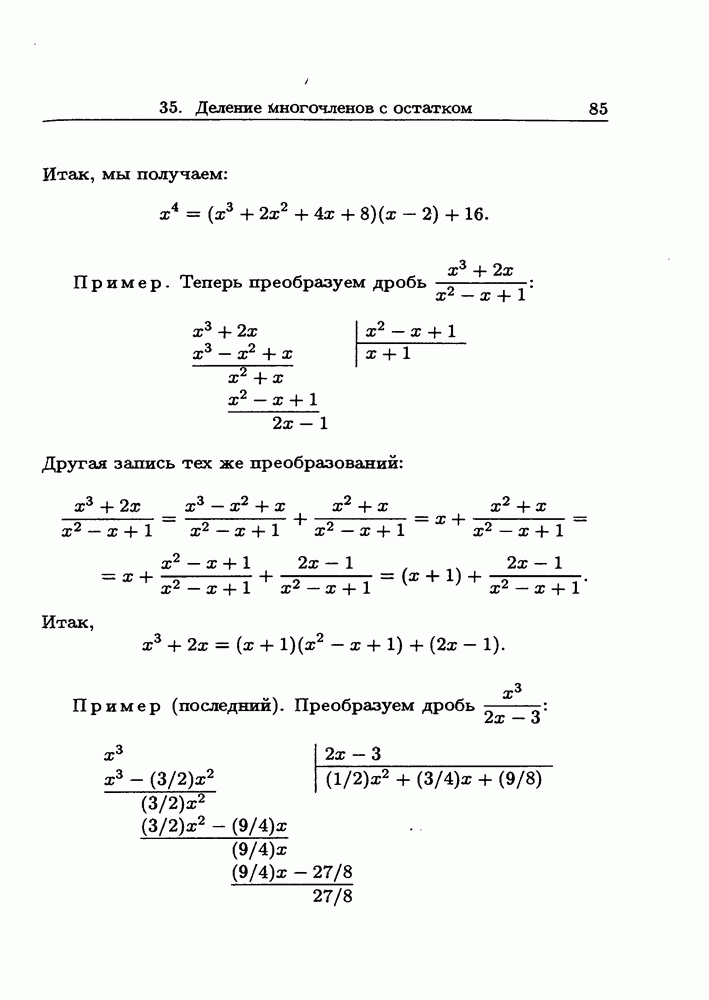| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
67. Геометрические иллюстрации
Некоторые из доказанных неравенств можно пояснить рисунками.
1. Неравенство

перепишем в виде

и, возведя в квадрат, получим

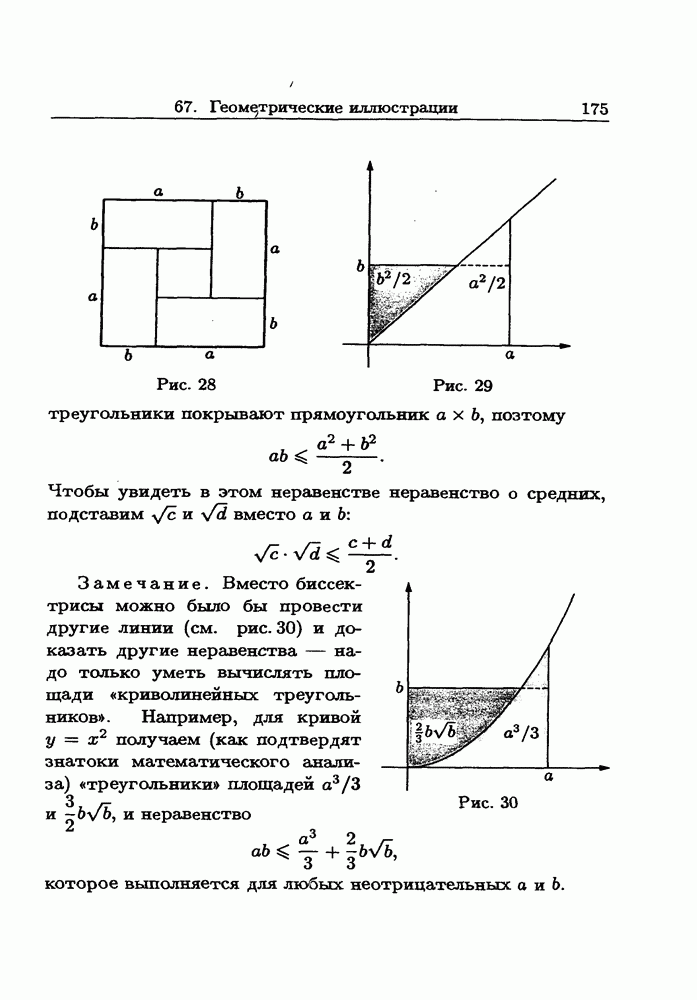
Это подтверждается тем, что четыре прямоугольника  можно поместить в квадрат со стороной а
можно поместить в квадрат со стороной а  и при этом еще останется свободное место в середине, если
и при этом еще останется свободное место в середине, если  (см. рис. 28).
(см. рис. 28).
Задача 330. Сколько останется места? Сравните результат с алгебраическим доказательством неравенства о средних.
2. Проведем биссектрису прямого угла и построим два равнобедренных прямоугольных треугольника с катетами a и b (см. рис. 29). Их площади равны  . Вместе эти
. Вместе эти

Рис. 28

Рис. 29
треугольники покрывают прямоугольник  , поэтому
, поэтому

Чтобы увидеть в этом неравенстве неравенство о средних, подставим  вместо а и b:
вместо а и b:


Рис. 30
Замечание. Вместо биссектрисы можно было бы провести другие линии (см. рис. 30) и доказать другие неравенства — надо только уметь вычислять площади «криволинейных треугольников». Например, для кривой  получаем (как подтвердят знатоки математического анализа) «треугольники» площадей
получаем (как подтвердят знатоки математического анализа) «треугольники» площадей  и неравенство
и неравенство

которое выполняется для любых неотрицательных а и b.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- 1. Предисловие
- 2. Перемена мест слагаемых
- 3. Перемена мест сомножителей
- 4. Сложение столбиком
- 5. Таблица умножения. Умножение столбиком
- 6. Деление «уголком»
- 7. Двоичная система счисления
- 8. Коммутативность
- 9. Ассоциативность
- 10. Расстановки скобок
- 11. Дистрибутивность
- 12. Буквы в алгебре
- 13. Сложение отрицательных чисел
- 14. Умножение отрицательных чисел
- 15. Действия с дробями
- 16. Степени
- 17. Отрицательные степени
- 18. Как умножить a^m на a^n или почему наше определение удобно
- 19. Правило умножения степеней
- 20. Формулы сокращенного умножения. Квадрат суммы
- 21. Как объяснить формулу (a+b)^2=a^2+2ab+b^2 младшему брату или сестре
- 22. Квадрат разности
- 23. Разность квадратов
- 24. Куб суммы
- 25. Четвертая степень суммы
- 26. (a+b)^5, (a+b)^6 и треугольник Паскаля
- 27. Многочлены
- 28. Отступление: какие многочлены считать равными?
- 29. Сколько одночленов останется?
- 30. Коэффициенты и значения
- 31. Разложение на множители
- 32. Рациональные выражения
- 33. Преобразование рационального выражения в частное двух многочленов
- 34. Многочлены и рациональные дроби с одной переменной
- 35. Деление многочленов с остатком
- 36. Остаток при делении на х — а
- 37. Многочлены, значения, интерполяция
- 38. Арифметические прогрессии
- 39. Сумма арифметической прогрессии
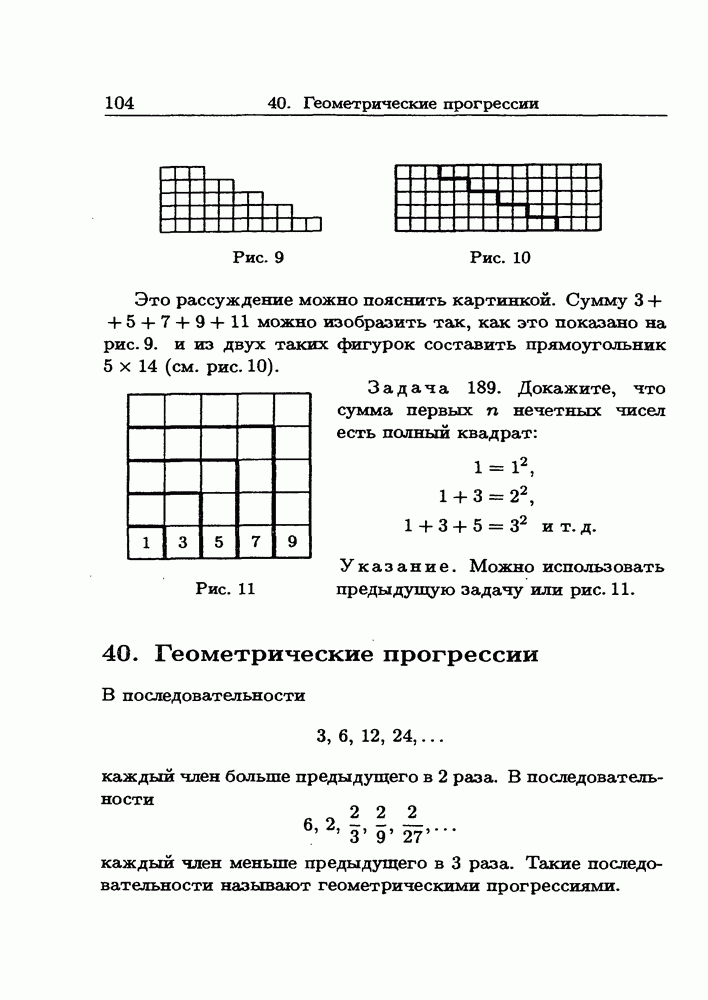
- 40. Геометрические прогрессии
- 41. Сумма геометрической прогрессии
- 42. Разные задачи о прогрессиях
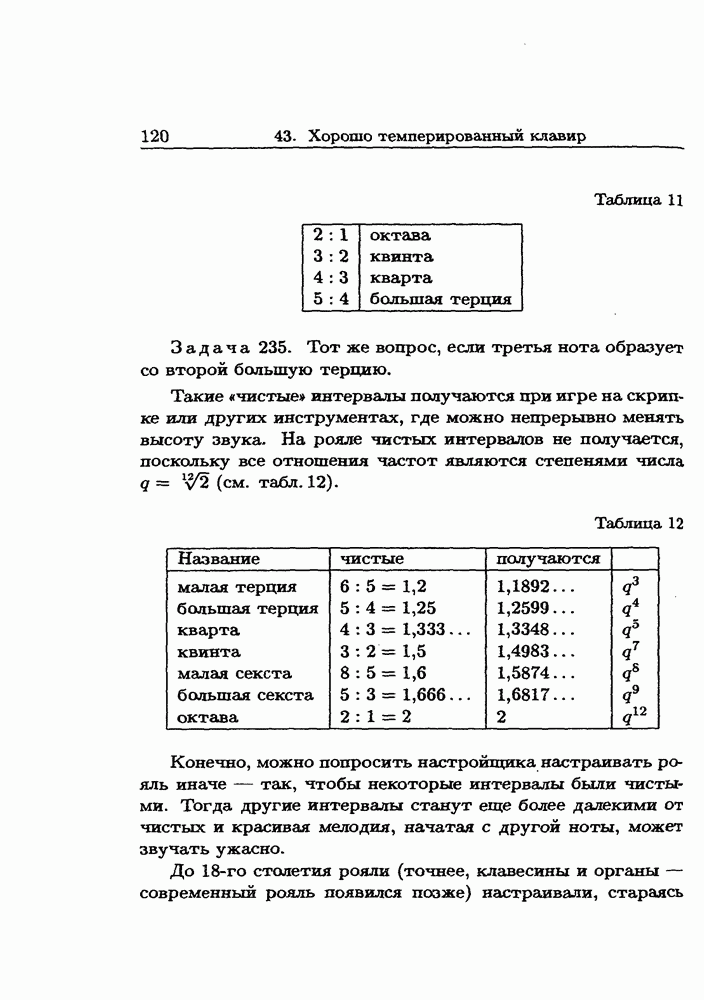
- 43. Хорошо темперированный клавир
- 44. Сумма бесконечной прогрессии
- 45. Уравнения
- 46. Квадратное уравнение
- 47. Случай p = 0. Квадратный корень
- 48. Свойства квадратных корней
- 49. Уравнение х^2 + рх + q = 0
- 50. Теорема Виета
- 51. Разложение квадратного трехчлена на множители
- 52. Формула для корней уравнения ах^2 + bх + c = 0
- 53. Бще одна формула корней квадратного уравнения
- 54. Квадратное уравнение становится линейным
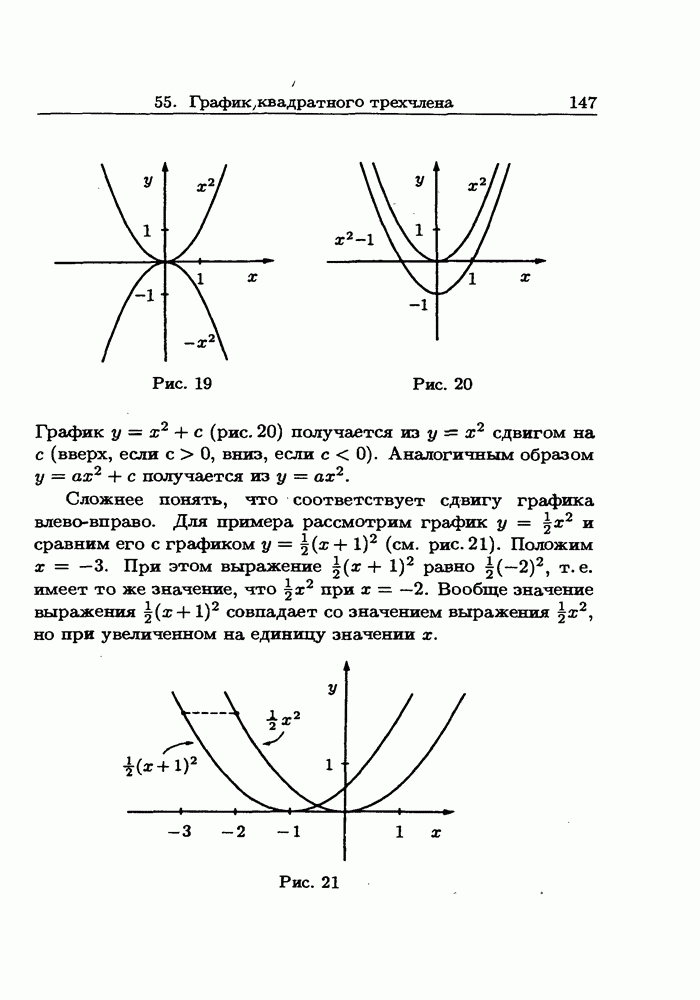
- 55. График квадратного трехчлена
- 56. Квадратные неравенства
- 57. Максимум и минимум квадратного трехчлена
- 58. Биквадратные уравнения
- 59. Возвратные уравнения
- 60. Как завалить на экзамене. Советы экзаменатору
- 61. Корни
- 62. Степень с дробным показателем
- 63. Доказательства числовых неравенств
- 64. Среднее арифметическое и среднее геометрическое
- 65. Среднее геометрическое не больше среднего арифметического
- 66. Задачи на максимум и минимум
- 67. Геометрические иллюстрации
- 68. Средние многих чисел
- 69. Среднее квадратическое
- 70. Среднее гармоническое
- 71. Книги для дальнейшего чтения