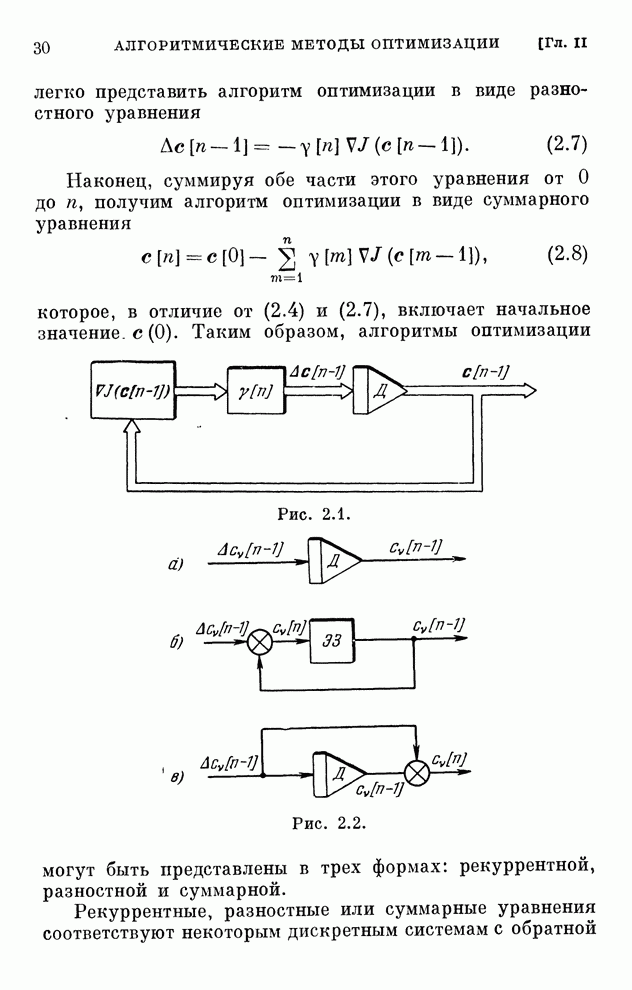
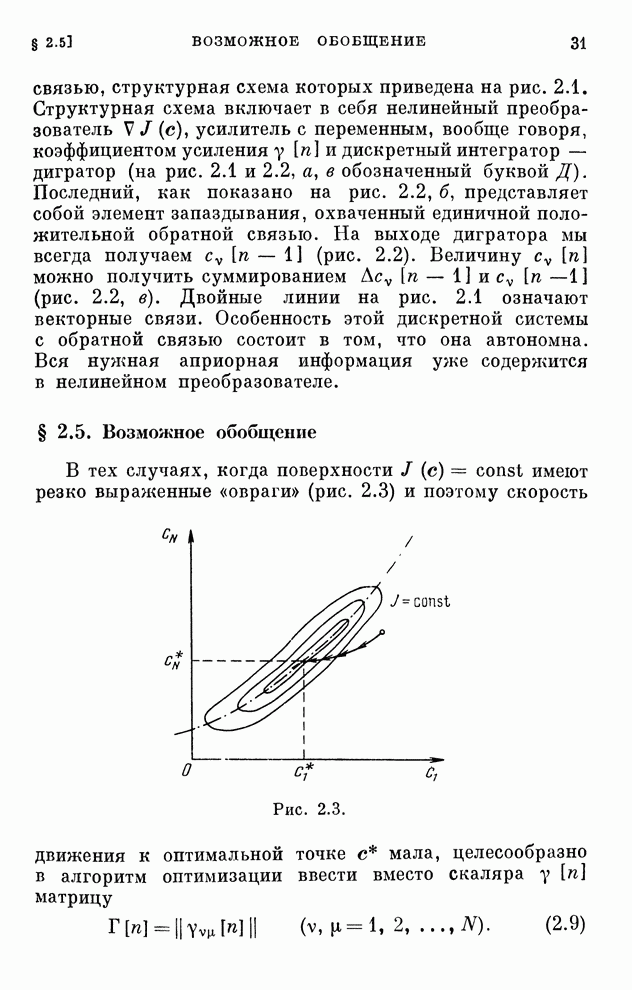
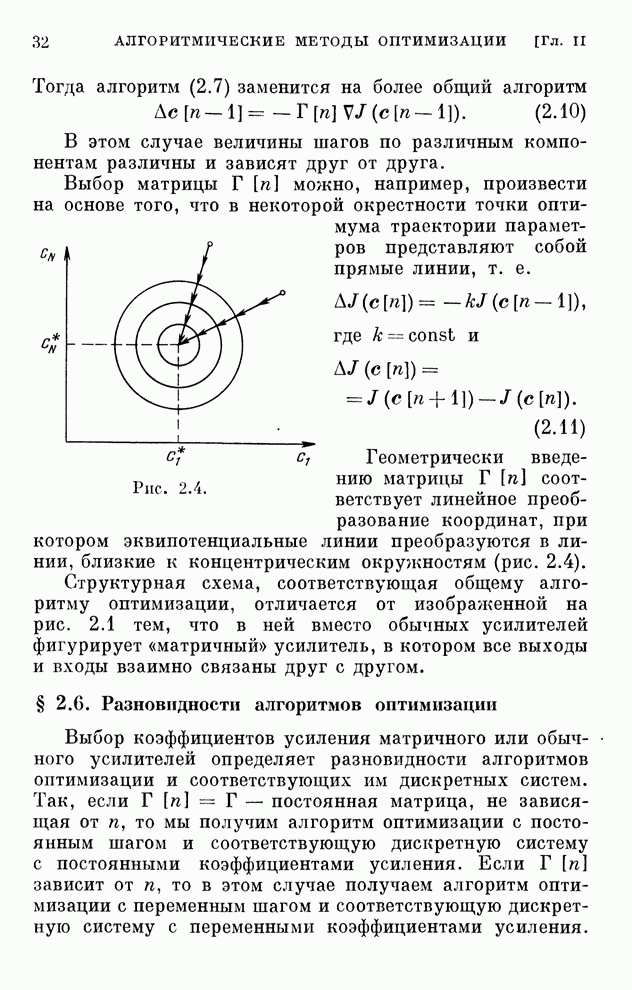
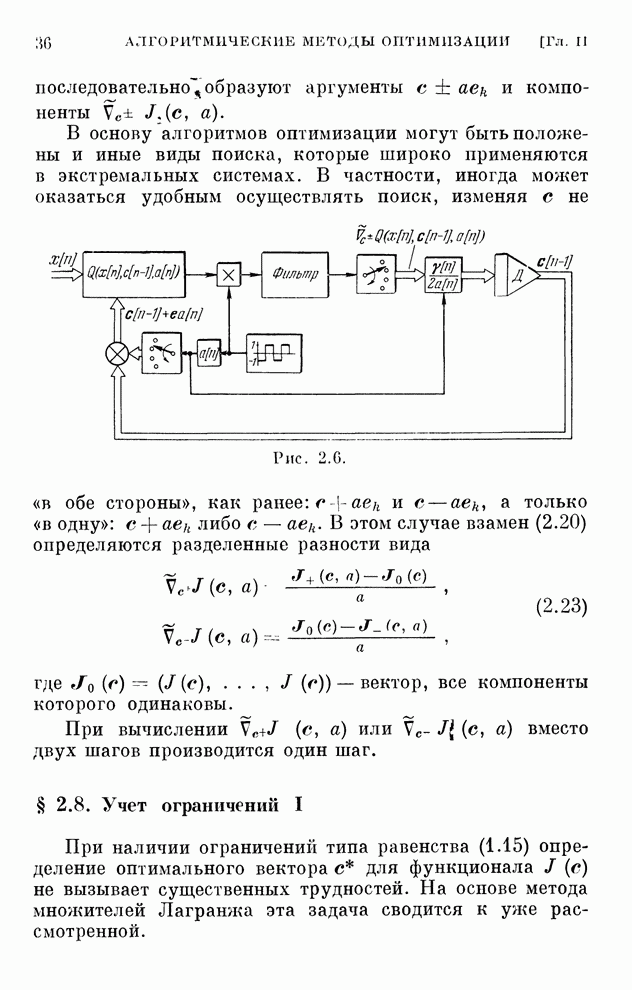
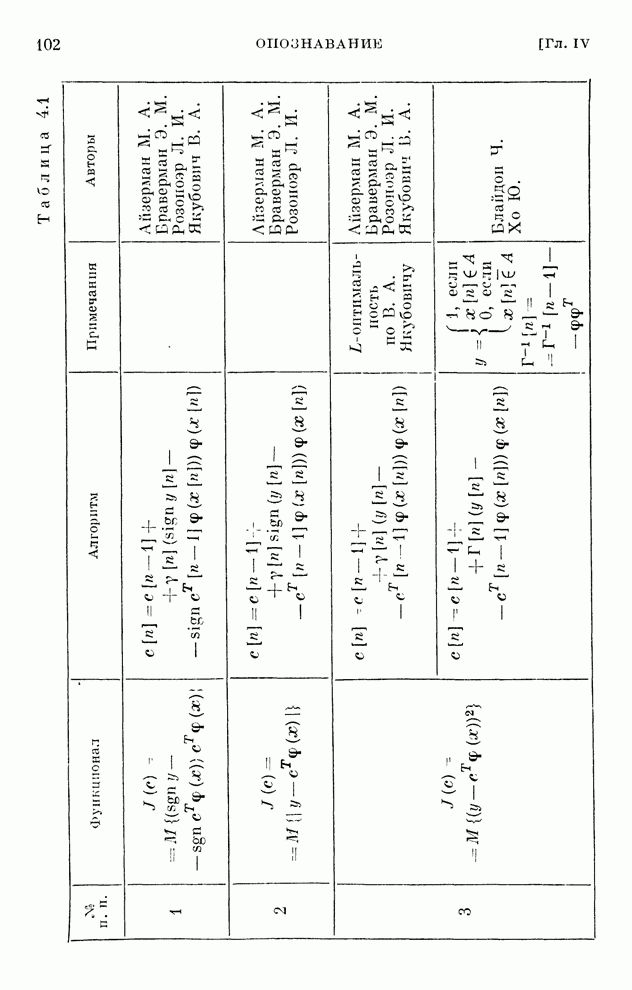
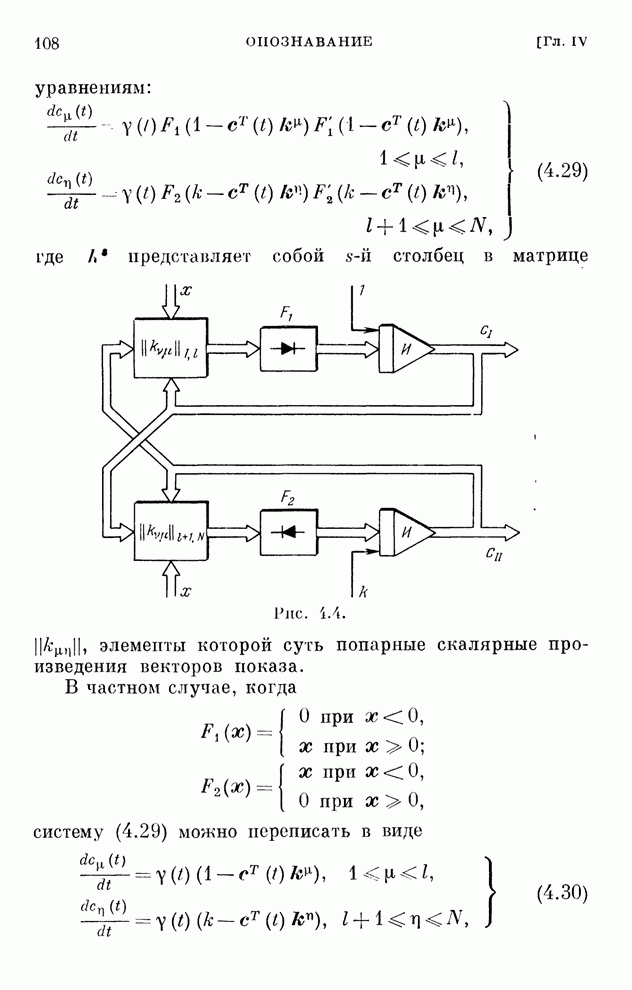
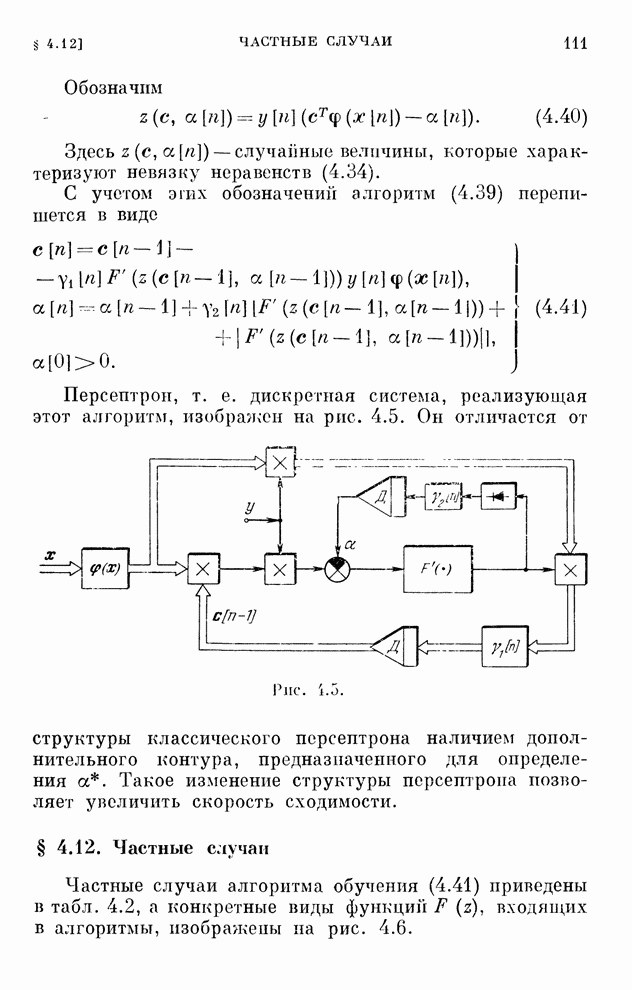
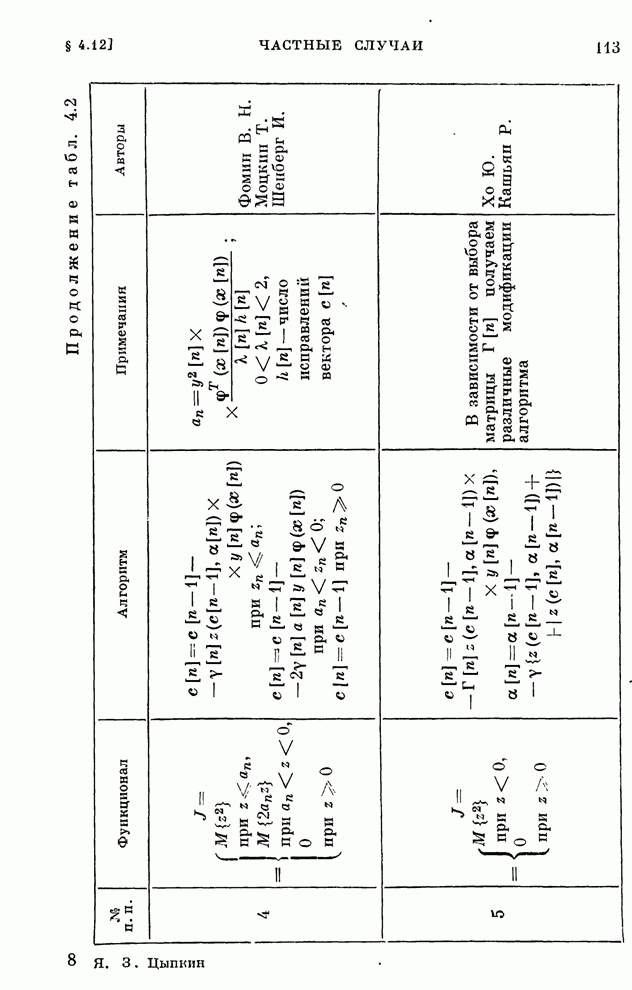
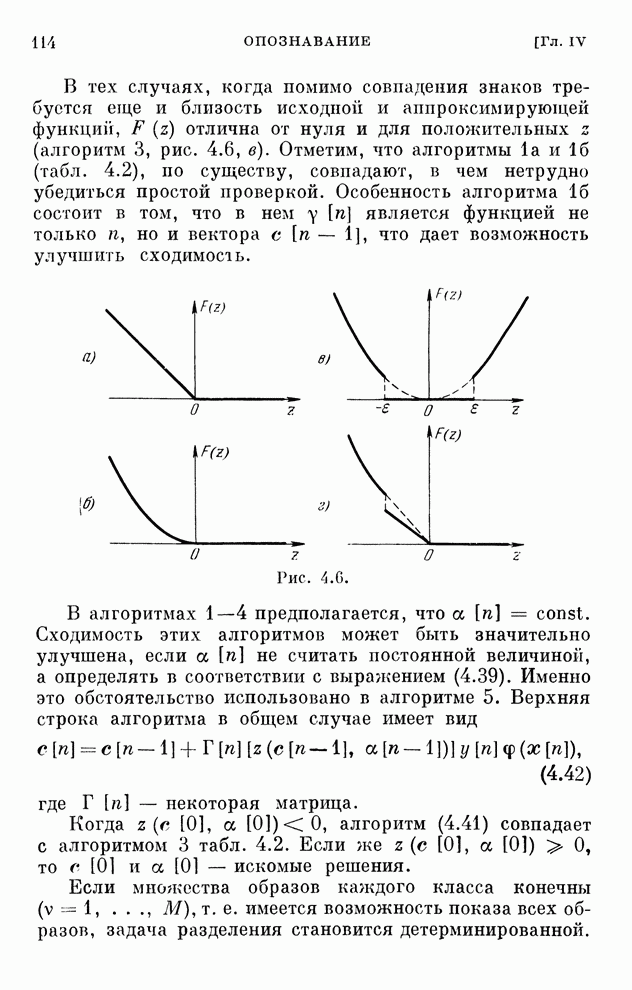
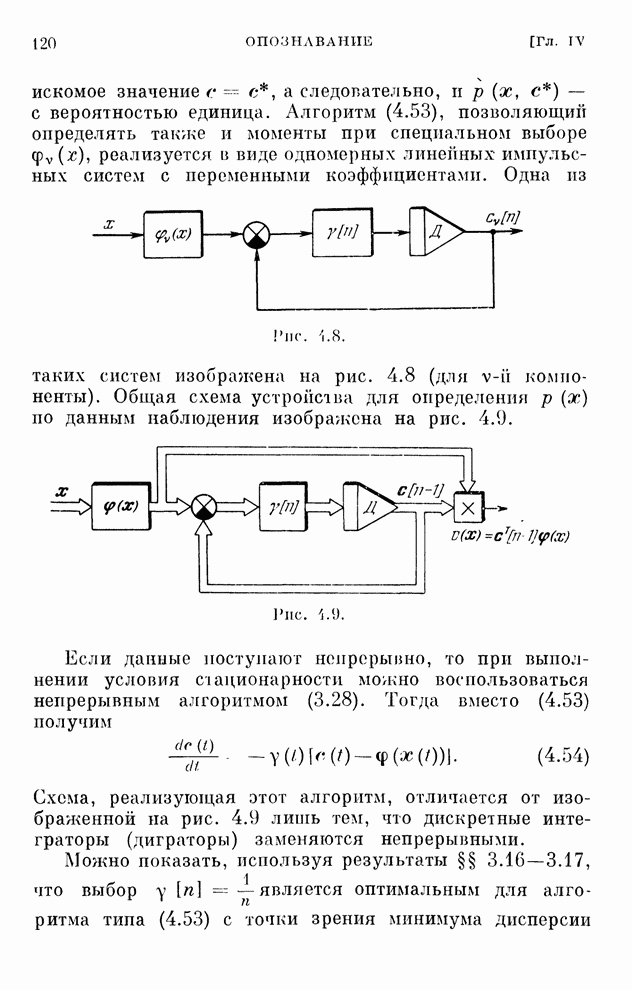
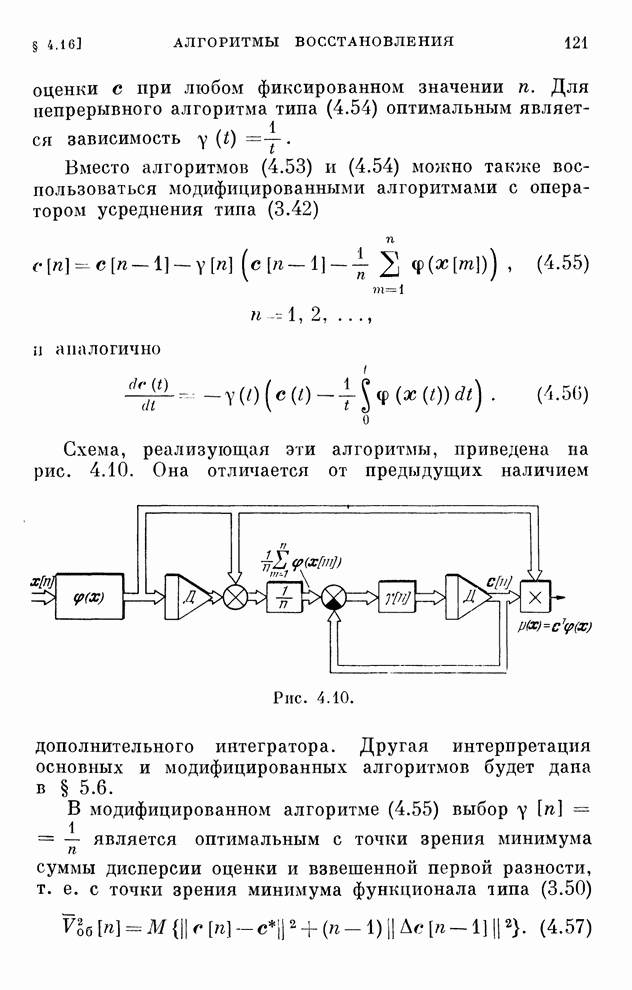
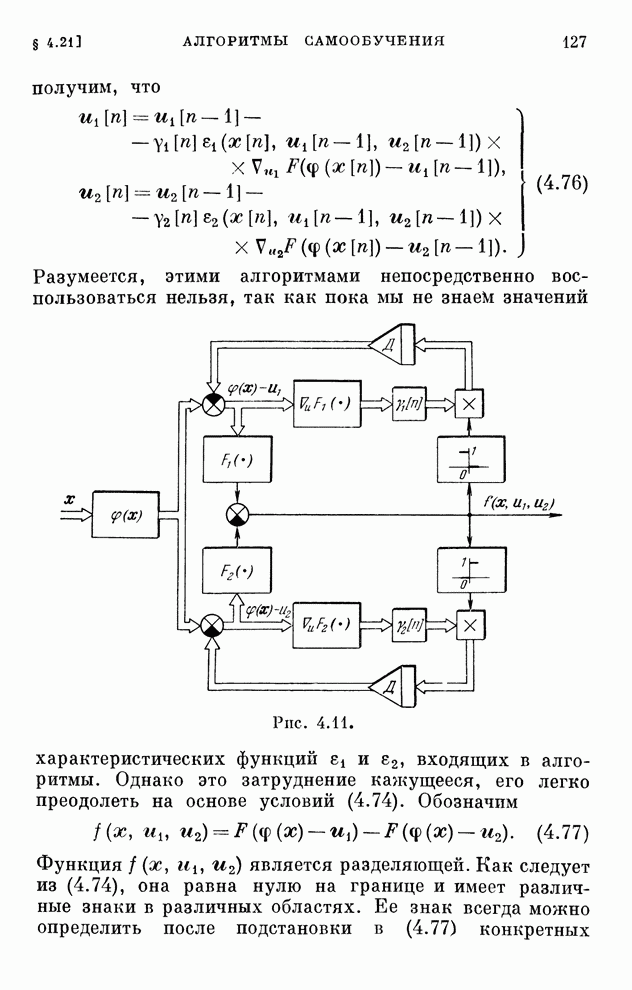
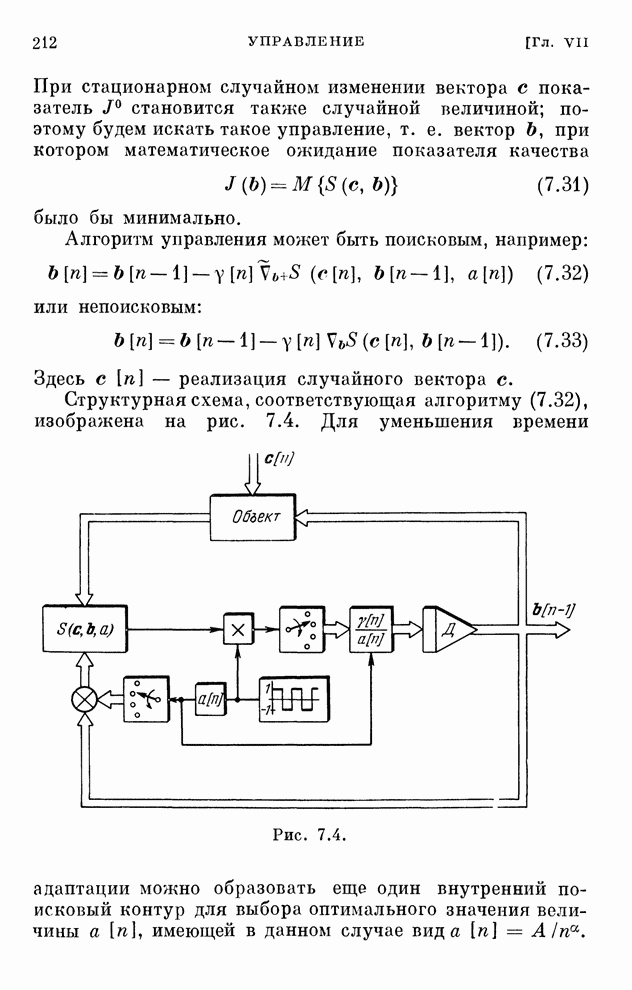
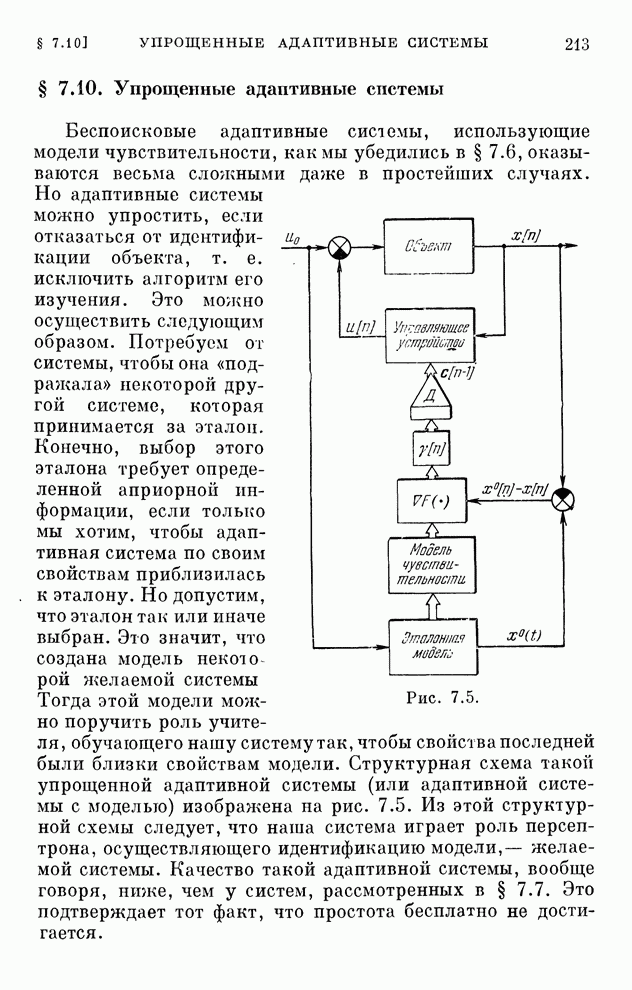
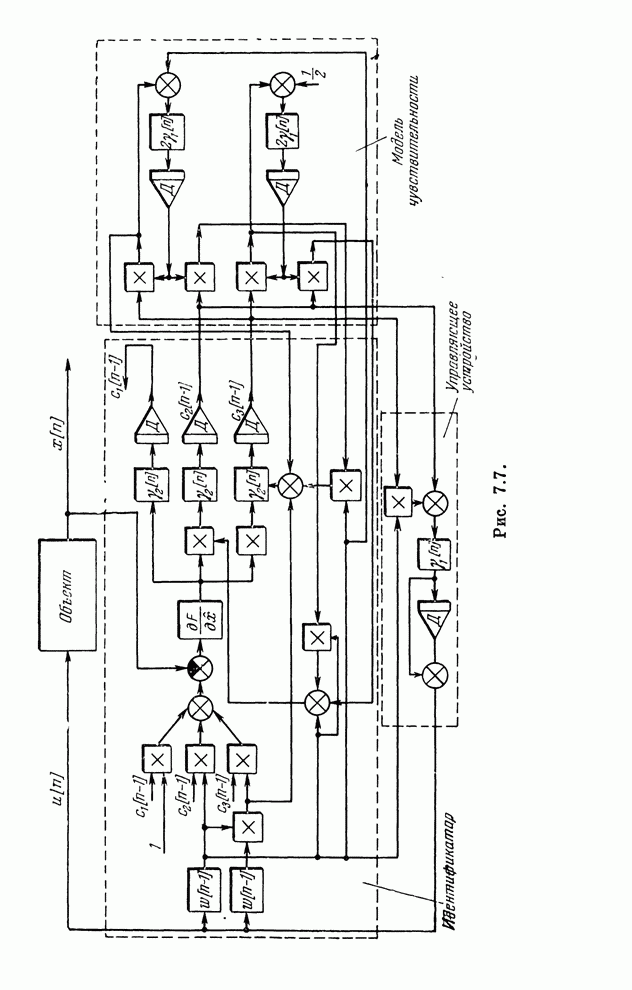
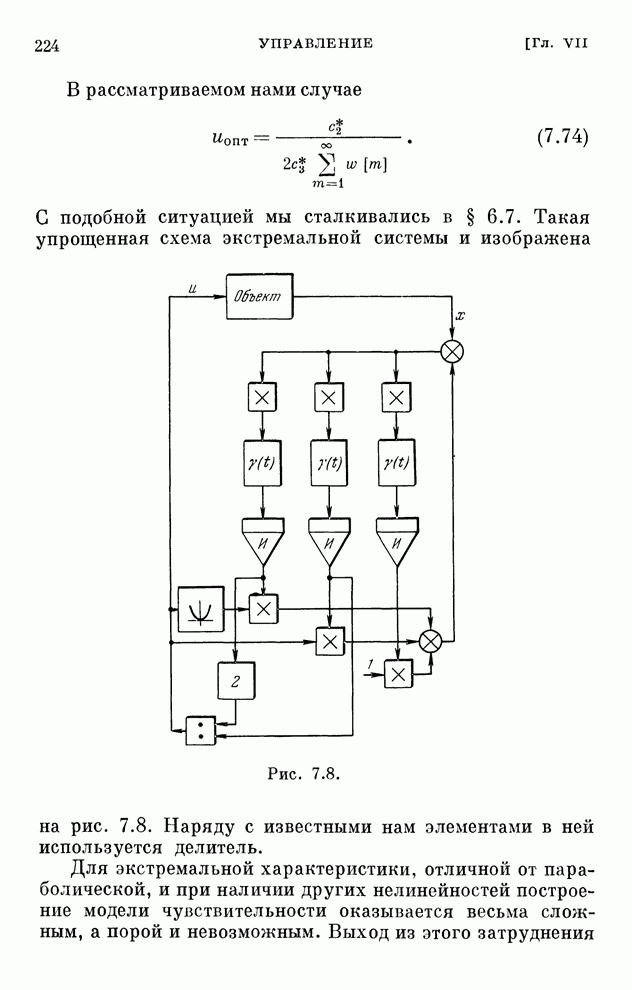
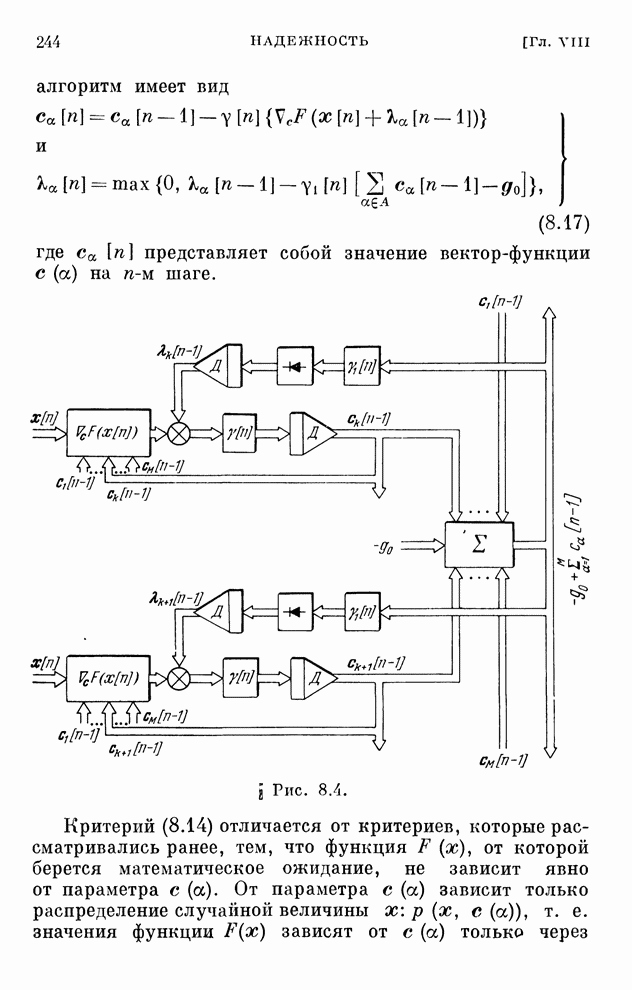
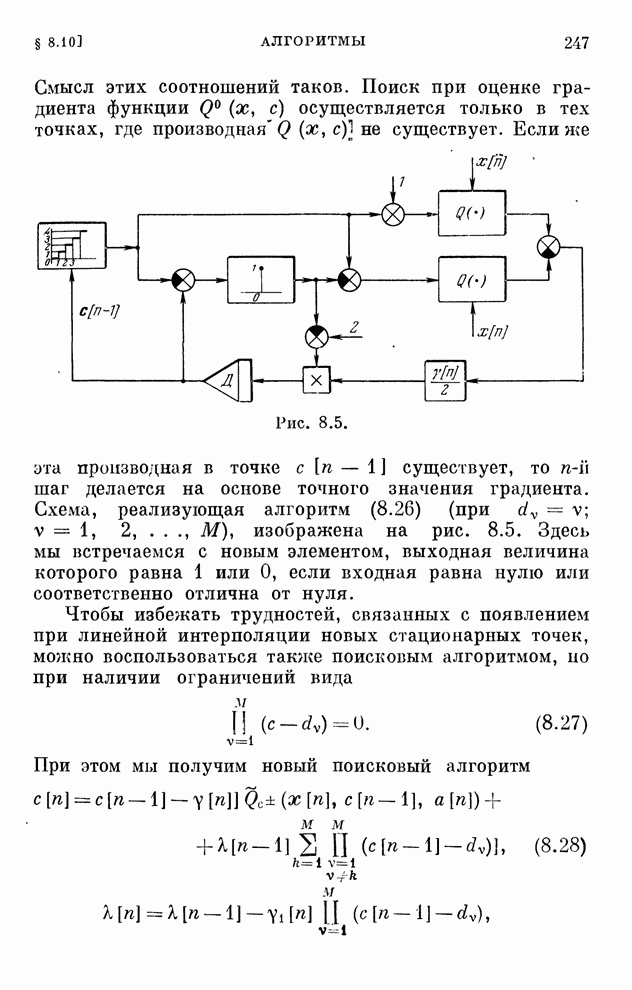
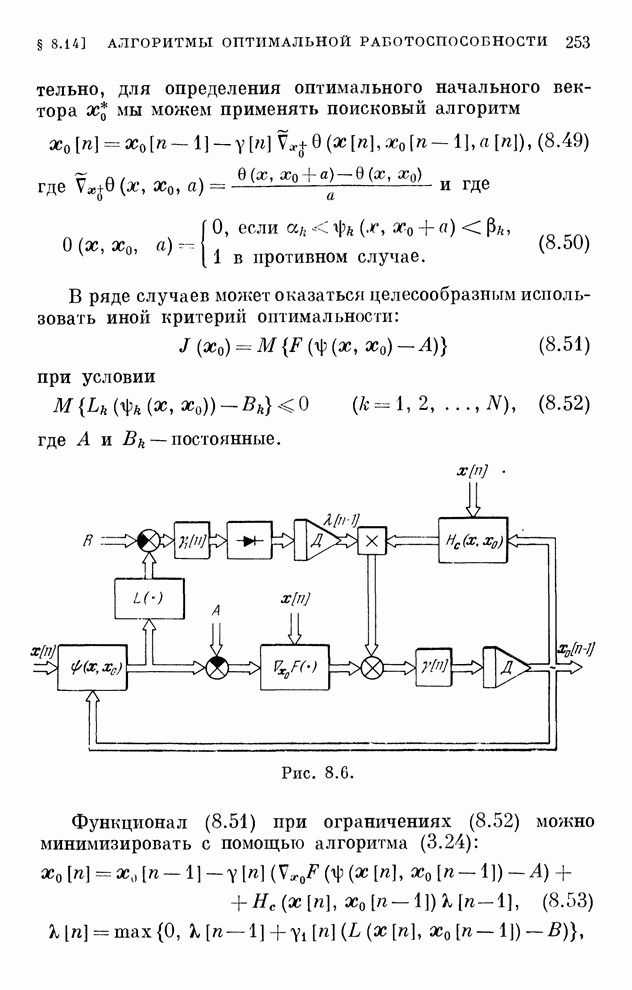
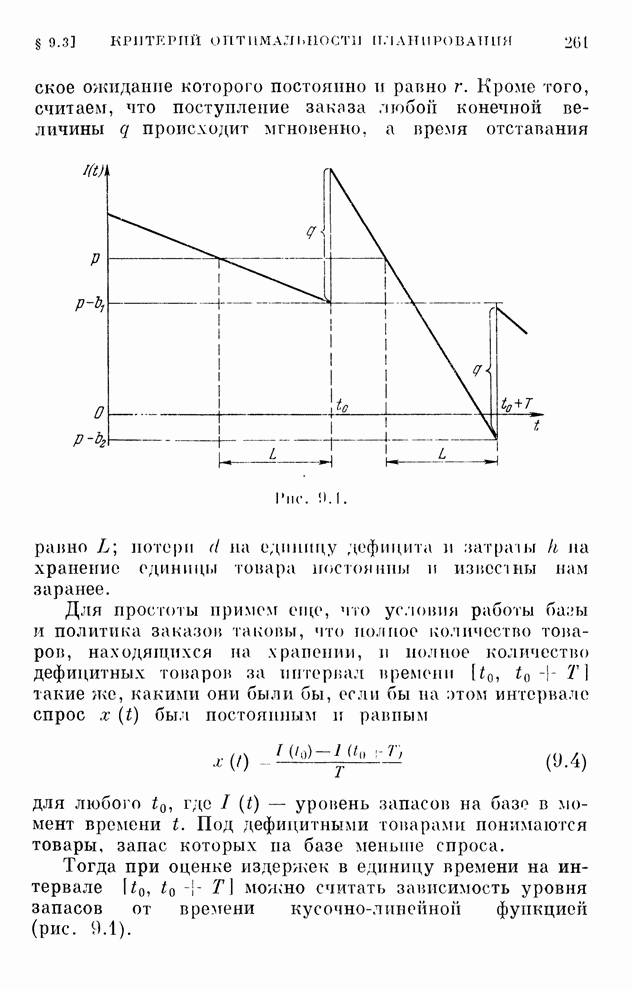
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Введение
В развитии теории автоматического управления можно выделить три наиболее характерных периода, которые удобно кратко назвать периодами детерминизма, стохастичности и адаптивности.
В счастливые времена детерминизма как уравнения, описывающие состояние управляемых объектов, так и внешние воздействия (задающие и возмущающие) предполагались известными. Такая полная определенность позволяла широко использовать классический аналитический аппарат для решения разнообразных проблем теории управления. Особенно это относится к линейным задачам, где безгранично господствующий принцип суперпозиции существенно облегчал решение задач и создавал полную иллюзию отсутствия принципиальных затруднений. Эти затруднения возникли, конечно, как только появилась необходимость в учете нелинейных факторов. Но и в области нелинейных задач, несмотря на отсутствие общих регулярных методов, были получены существенные результаты, относящиеся как к анализу, так и к синтезу автоматических систем.
Менее счастливое время наступило во второй период — период стохастичности, когда в связи с учетом более реальных условий работы автоматических систем было установлено, что внешние воздействия, задающие, а особенно возмущающие, непрерывно изменяются во времени и заранее не могут быть определены однозначно. Часто это относилось и к коэффициентам уравнений управляемых объектов. Поэтому возникла необходимость в привлечении иных подходов, учитывающих вероятностный характер внешних воздействий и уравнений. Эти подходы основаны на знании статистических характеристик случайных функций (которые тем или иным путем должны быть предварительно определены) и так же используют аналитические методы, как и в счастливые времена детерминизма.
Характерная особенность этих периодов развития теории автоматического управления состоит в том, что их методы и результаты непосредственно применимы к автоматическим системам с достаточной информацией, т. е. уравнения объекта и внешние воздействия либо их статистические характеристики должны быть известны.
В нынешнее «многострадальное» (с точки зрения теории автоматического управления) время с каждым днем мы все больше убеждаемся, что в современных сложных автоматических системах, работающих в самых разнообразных условиях, уравнения управляемых объектов и внешние воздействия (либо их статистические характеристики) не только неизвестны, но по различным причинам мы даже не имеем возможности заранее определить их экспериментальным путем. Иначе говоря, мы сталкиваемся с большей или меньшей начальной неопределенностью. Все это хотя и затрудняет управление такими объектами, но не делает это управление в принципе невозможным, свидетельствуя лишь о наступлении нового, третьего периода в теории управления — периода адаптивности. Возможность управления объектами при неполной и даже весьма малой априорной информации основана на применении адаптации и обучения в автоматических системах, которые уменьшают первоначальную неопределенность на основе использования информации, получаемой в течение процесса управления.
Не надо думать, что периоды детерминизма, стохастичности и адаптивности сменяли друг друга подобно кадрам в кино. Последующие периоды зарождались в недрах предшествующих, и мы являемся свидетелями сосуществования проблематики этих периодов.
На первой стадии каждого из перечисленных периодов основной задачей была задача анализа автоматических систем и выяснение их свойств. Затем возникли задачи синтеза автоматических систем, удовлетворяющих определенным требованиям. Естественно, появилось желание, а часто и необходимость осуществить синтез оптимальной в том или ином смысле системы.
Проблема оптимальности стала одной из центральных в автоматическом управлении. И если еще не достигнуты большие успехи в обосновании выбора и в формулировке показателей качества, то нас могут утешать блестящие результаты, связанные с проблемой оптимальности, которые сконцентрированы в принципе максимума Понтрягина и методе динамического программирования Беллмана. Хотя они и возникли на почве детерминистских задач, но с определенным успехом начинают завоевывать территорию стохастических и отчасти адаптивных задач.
Большим достижением периода стохастичности в этом же направлении являются методы Колмогорова — Винера и Калмана, которые в значительной мере исчерпали линейные задачи синтеза.
К сожалению, период адаптивности не может похвастаться столь блестящими результатами. Это объясняется тем, что проблема адаптации и связанные с ней проблемы обучения и самообучения еще очень молоды. Тем не менее мы все чаще и чаще обнаруживаем их в разнообразных задачах современной автоматики. Помимо основной, упомянутой уже выше задачи управления объектами в условиях неполной априорной информации или ее отсутствия, т. е. в условиях начальной неопределенности, задачи адаптации возникают при определении характеристик объектов и воздействий, при обучении опознаванию образов, ситуаций, при выработке и улучшении целей управления и т. п.
Термины «адаптация», «самообучение», «обучение» наиболее модны в современной теории автоматического управления. К сожалению, как правило, эти термины не имеют однозначного толкования, а зачастую не имеют просто никакого толкования. Это создает благоприятную почву для безудержных фантастических рассуждений, особенно часто бытующих в популярной литературе по кибернетике, а иногда проникающих и на страницы некоторых технических журналов.
Тем не менее, если исключить этот обильный, но мало содержательный поток «общих рассуждений», то можно указать на целый ряд интересных подходов и результатов, полученных в связи с решением перечисленных выше задач.
Следует, однако, заметить, что до последнего времени эти задачи рассматривались изолировано и независимо одна от другой. Связи между ними почти не замечались, хотя при более общем взгляде на проблемы адаптации, обучения и самообучения все эти задачи оказываются настолько тесно связанными, что приходится только удивляться тому, что эта связь не была подчеркнута ранее.
Основная наша цель состоит в обсуждении проблемы адаптации, обучения и самообучения с некоторой единой точки зрения, которая связала бы между собой задачи, казавшиеся ранее разрозненными, и которая позволила бы установить эффективные пути их решения.
Разумеется, на какое-либо осуществление этой цели можно надеяться лишь при выполнении хотя бы двух условий: наличия определенных, пусть условных, но содержательных понятий адаптации, обучения и самообучения и наличия некоторого математического аппарата, адекватного этим понятиям.
Первое условие находится если не в наших руках, то, по крайней мере, в руках комиссий по технической терминологии и поэтому из многочисленных, порой разноречивых определений мы надеемся либо выбрать более или менее подходящее для нашей книги, либо, в крайнем случае, прибавить еще одно определение. Что же касается второго условия, то обычно удовлетворить ему несоизмеримо труднее. Но, как это неоднократно случалось в истории науки, адекватный математический аппарат, хотя и в зародышевой форме, к счастью, существует. Он содержится, с одной стороны, в сформировавшейся к настоящему времени математической статистике, а с другой стороны, в интенсивно развивающейся новой математической дисциплине, известной под названием математического программирования.
Математическое программирование разрабатывает теорию и методы решения экстремальных задач и охватывает как специальные разделы (вариационное исчисление, принцип максимума Понтрягина, динамическое программирование Беллмана, линейное и нелинейное программирование), так и — как это можно понять сейчас — методы стохастической аппроксимации. Последние методы, к сожалению, мало использовавшиеся вне математической статистики, играют существенную роль в интересующей нас области.
Важно подчеркнуть, что математическое программирование не связано с необходимостью описания условий задачи в аналитическом, формульном виде, и поэтому может охватить значительно более широкий круг задач, чем те методы, с помощью которых пытаются получить решение в замкнутой аналитической форме. Алгоритмическая форма решения экстремальных задач дает возможность использовать средства современной вычислительной техники и не укладывать условия задачи в прокрустово ложе аналитического подхода, что обычно уводит нас далеко за пределы тех реальных задач, которые мы действительно хотели бы рассмотреть.
Алгоритмы обучения и адаптации должны позволить в условиях минимальной априорной информации достигнуть оптимума в том или ином смысле. Поэтому прежде всего мы должны познакомиться с проблемой оптимальности и алгоритмическими методами решения этой проблемы. Затем мы сможем обсудить понятия и методы, характерные для проблемы адаптации и обучения. И только после этого, вооружившись единой точкой зрения и подходом к интересующей нас проблеме, мы будем в состоянии приступить к решению разнообразных задач.
Именно такая последовательность и принята в настоящей книге.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- Глава I. Проблема оптимальности
- § 1.1. Введение
- § 1.2. Критерии оптимальности
- § 1.3. Еще о критериях оптимальности
- § 1.4. Ограничения
- § 1.5. Априорная и текущая информация
- § 1.6. Детерминированные и стохастические процессы
- § 1.7. Обычный и адаптивный подходы
- § 1.8. О методах решения проблемы оптимальности
- § 1.9. Заключение
- Глава II. Алгоритмические методы оптимизации
- § 2.1. Введение
- § 2.2. Условия оптимальности
- § 2.3. Регулярный итеративный метод
- § 2.4. Алгоритмы оптимизации
- § 2.5. Возможное обобщение
- § 2.6. Разновидности алгоритмов оптимизации
- § 2.7. Поисковые алгоритмы оптимизации
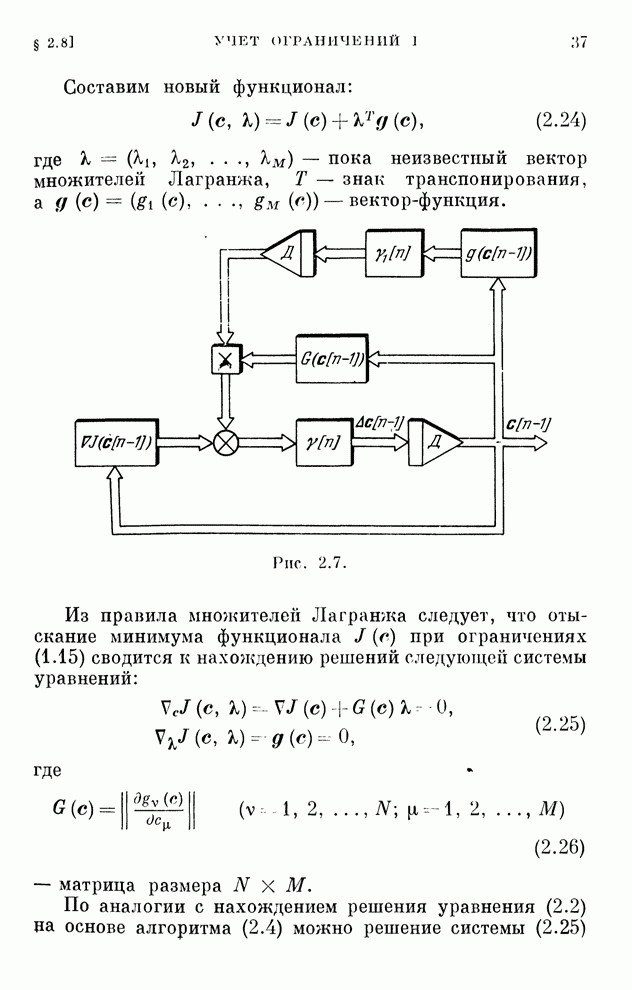
- § 2.8. Учет ограничений I
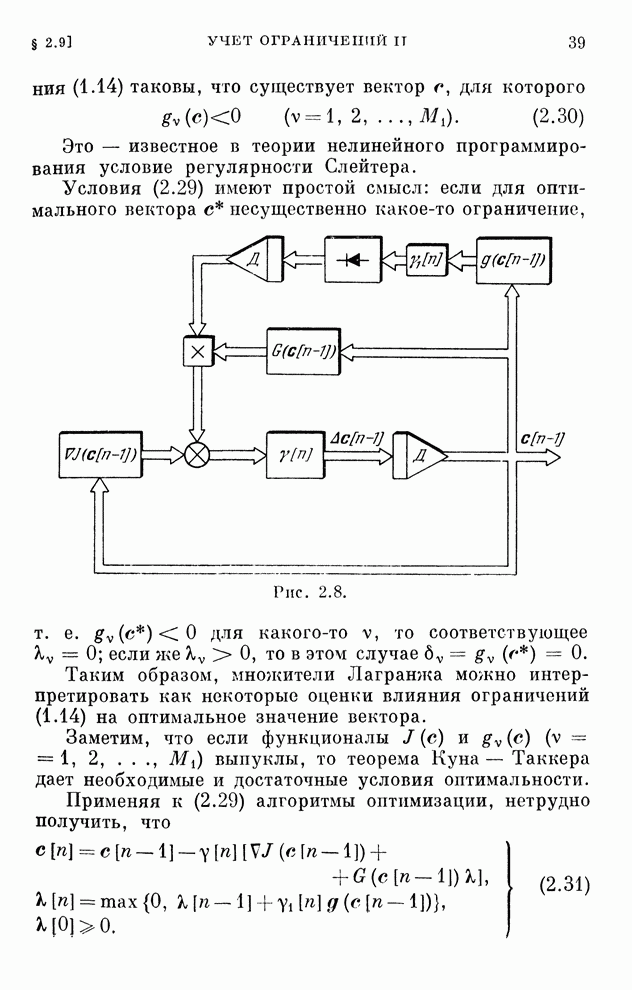
- § 2.9. Учет ограничений II
- § 2.10. Методы возможных направлений
- § 2.11. Обсуждение
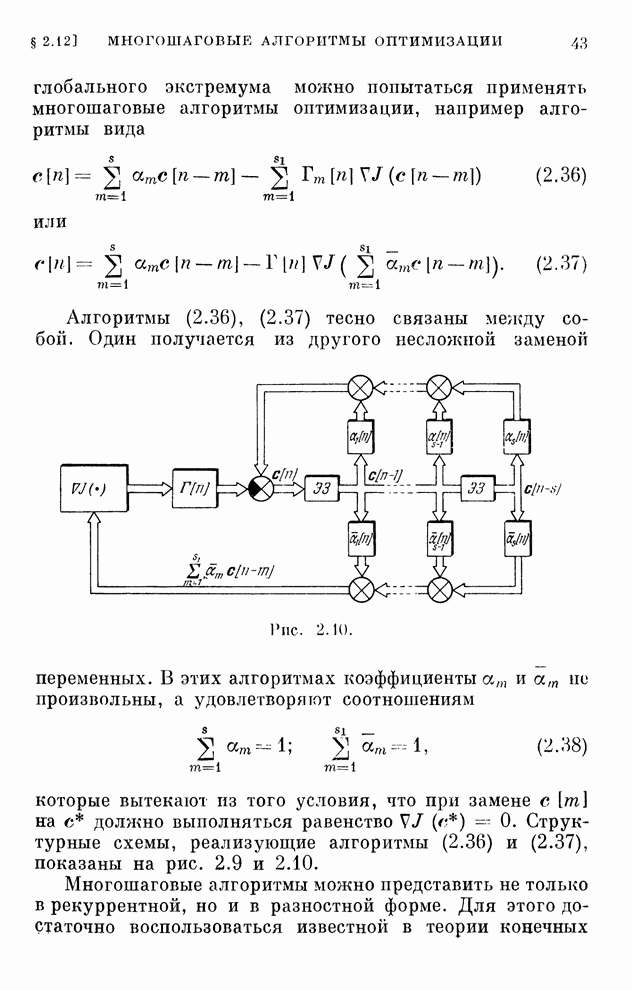
- § 2.12. Многошаговые алгоритмы оптимизации
- § 2.13. Непрерывные алгоритмы оптимизации
- § 2.14. Методы случайного поиска
- § 2.15. Сходимость и устойчивость
- § 2.16. Условия сходимости
- § 2.17. Об ускорении сходимости
- § 2.18. О наилучших алгоритмах
- § 2.19. Примеры
- § 2.20. Некоторые задачи
- § 2.21. Заключение
- Глава III. Адаптация и обучение
- § 3.1. Введение
- § 3.2. Понятия обучения, самообучения и адаптации
- § 3.3. Формулировка задачи
- § 3.4. Вероятностные итеративные методы
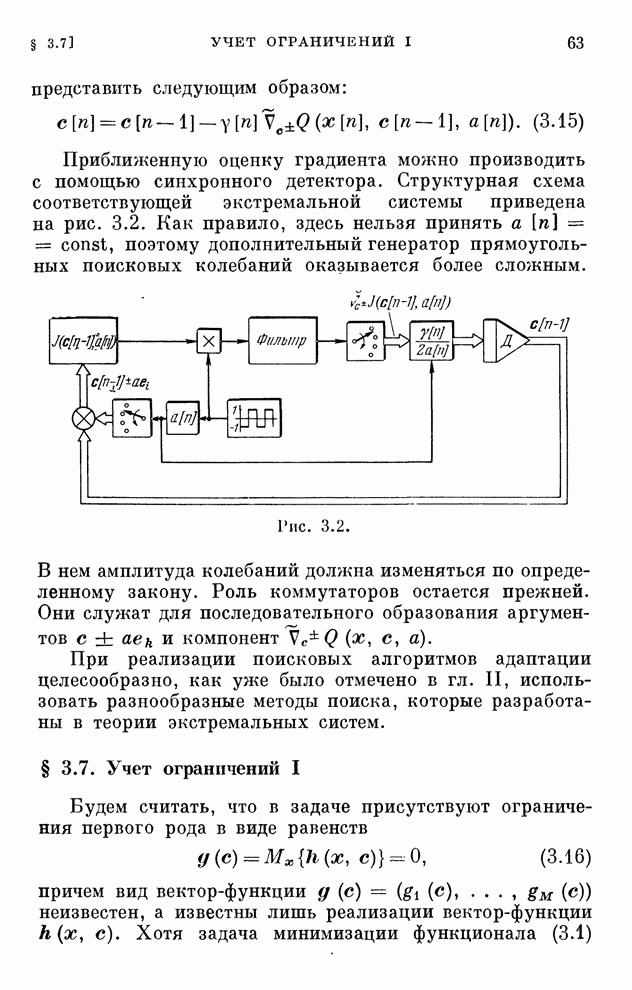
- § 3.5. Алгоритмы адаптации
- § 3.6. Поисковые алгоритмы адаптации
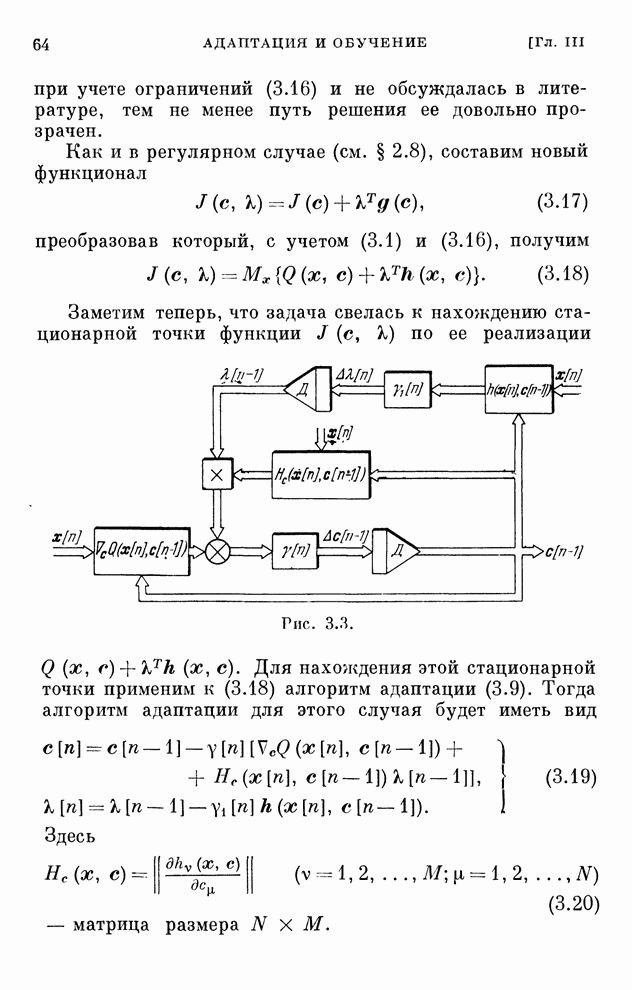
- § 3.7. Учет ограничений I
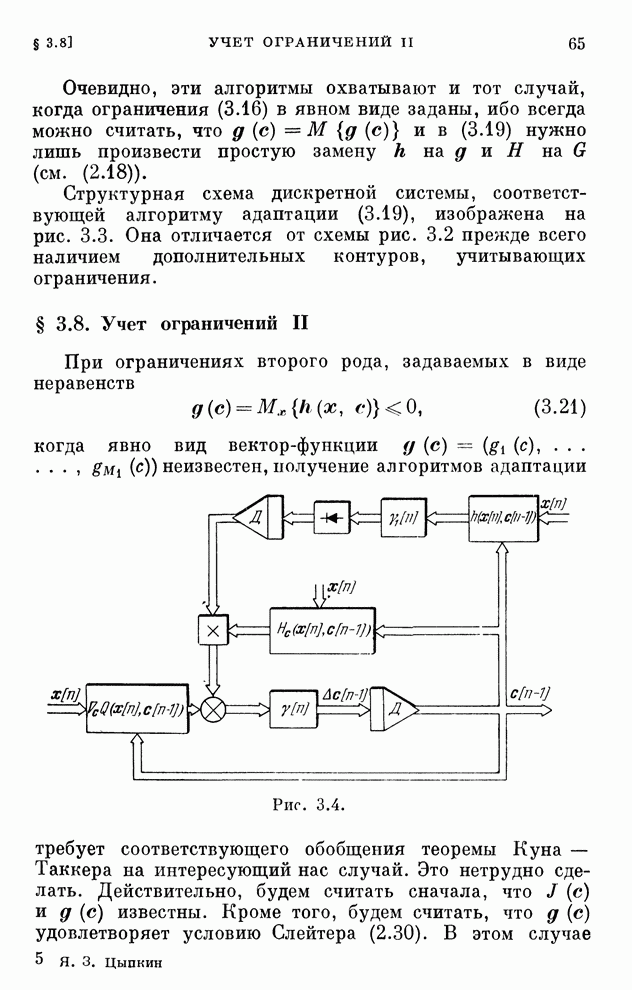
- § 3.8. Учет ограничений II
- § 3.9. Одно обобщение
- § 3.10. Многошаговые алгоритмы адаптации
- § 3.11. Непрерывные алгоритмы
- § 3.12. Вероятностная сходимость и устойчивость
- § 3.13. Условия сходимости
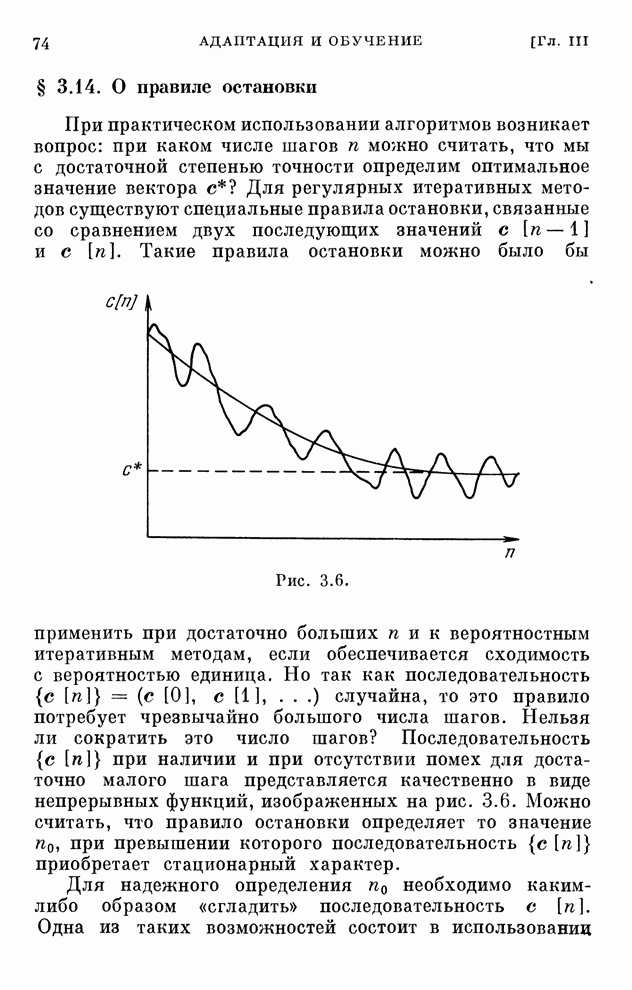
- § 3.14. О правиле остановки
- § 3.15. Об ускорении сходимости
- § 3.16. Мера качества алгоритмов
- § 3.17. Наилучшие алгоритмы
- § 3.18. Упрощенные наилучшие алгоритмы
- § 3.19. Частный случай
- § 3.20. Связь с методом наименьших квадратов
- § 3.21. Связь с байесовским методом
- § 3.22. Связь с методом максимального правдоподобия
- § 3.23. Обсуждение
- § 3.24. Некоторые задачи
- § 3.25. Заключение
- Глава IV. Опознавание
- § 4.1. Введение
- § 4.2. Обсуждение задачи опознавания
- § 4.3. Формулировка задачи
- § 4.4. Общие алгоритмы обучения
- § 4.5. Сходимость алгоритмов
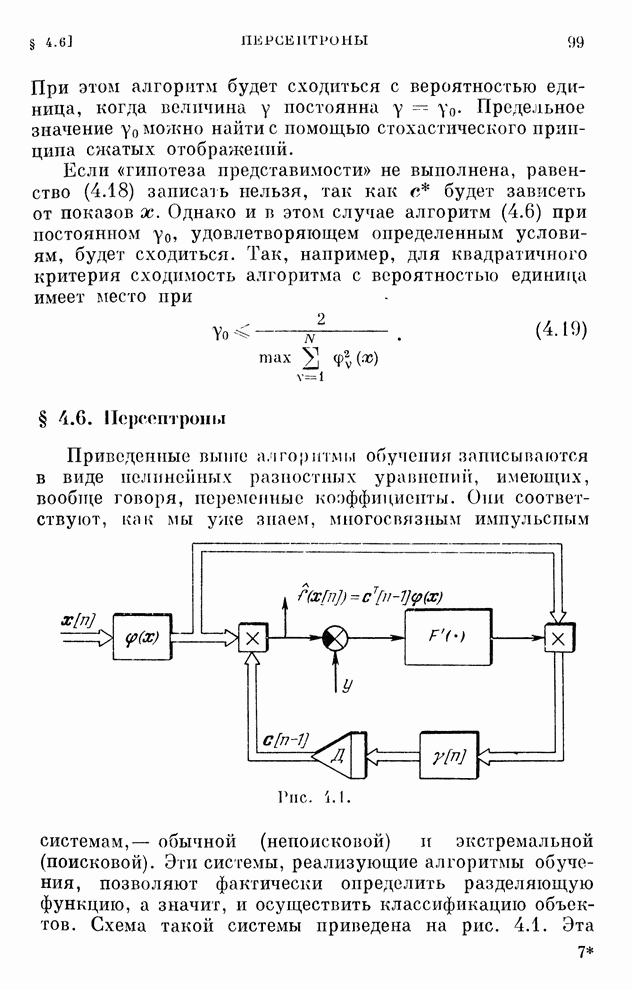
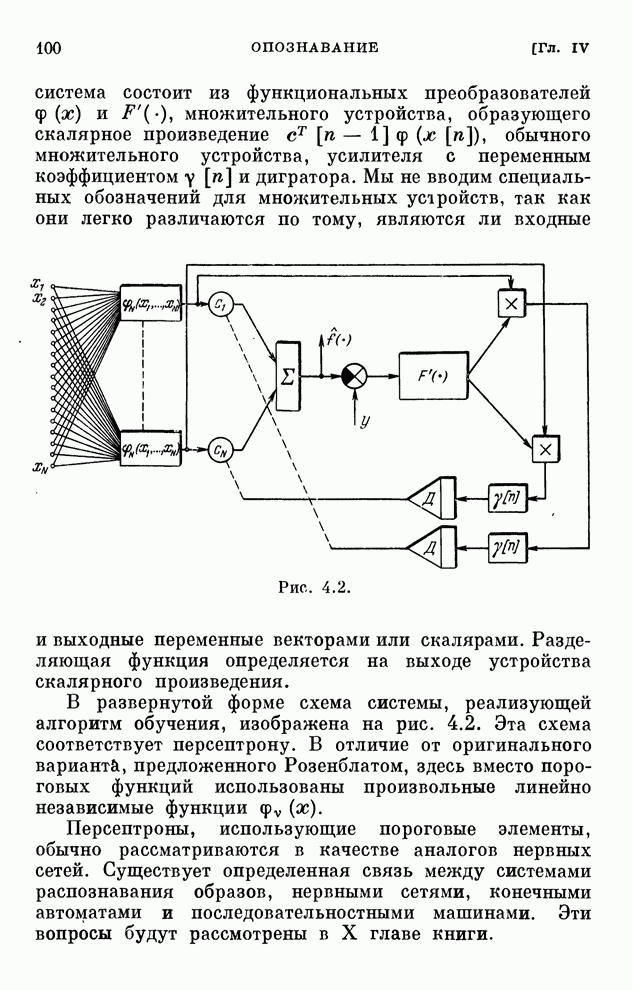
- § 4.6. Персептроны
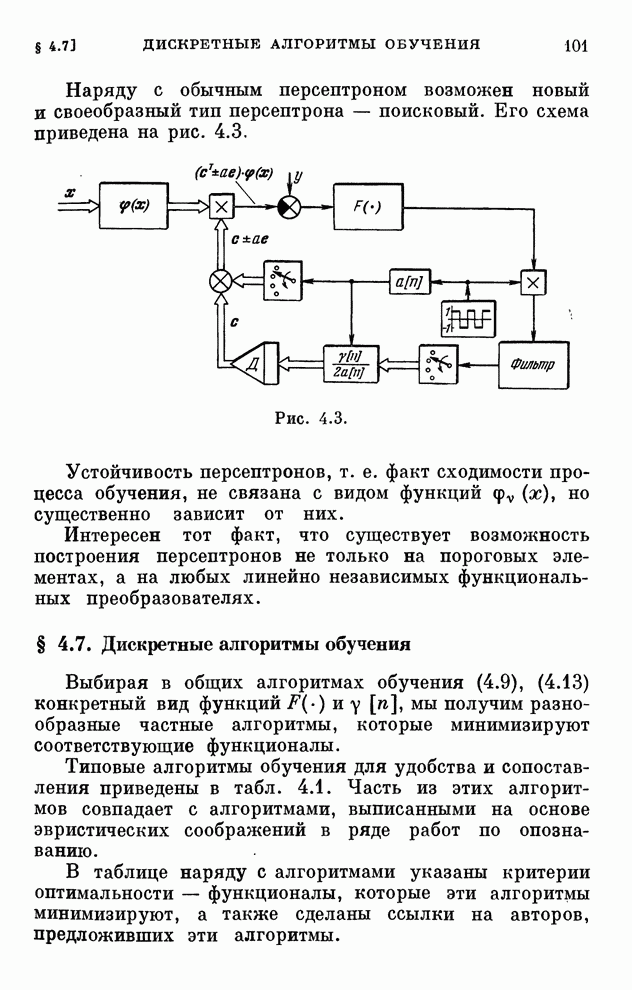
- § 4.7. Дискретные алгоритмы обучения
- § 4.8. Поисковые алгоритмы обучения
- § 4.9. Непрерывные алгоритмы обучения
- § 4.10. Замечания
- § 4.11. Еще об одном общем алгоритме обучения
- § 4.12. Частные случаи
- § 4.13. Обсуждение
- § 4.14. О самообучении
- § 4.15. О восстановлении плотности распределения и моментов
- § 4.10. Алгоритмы восстановления
- § 4.17. Принципы самообучения
- § 4.18. Средний риск
- § 4.19. Вариация среднего риска
- § 4.20. Условия минимума среднего риска
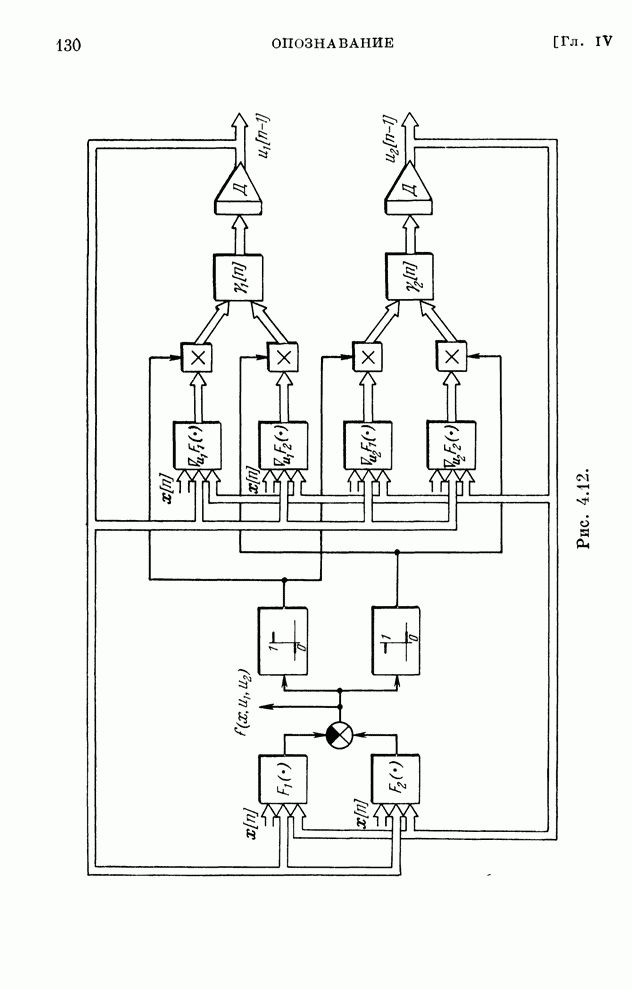
- § 4.21. Алгоритмы самообучения
- § 4.22. Обобщение
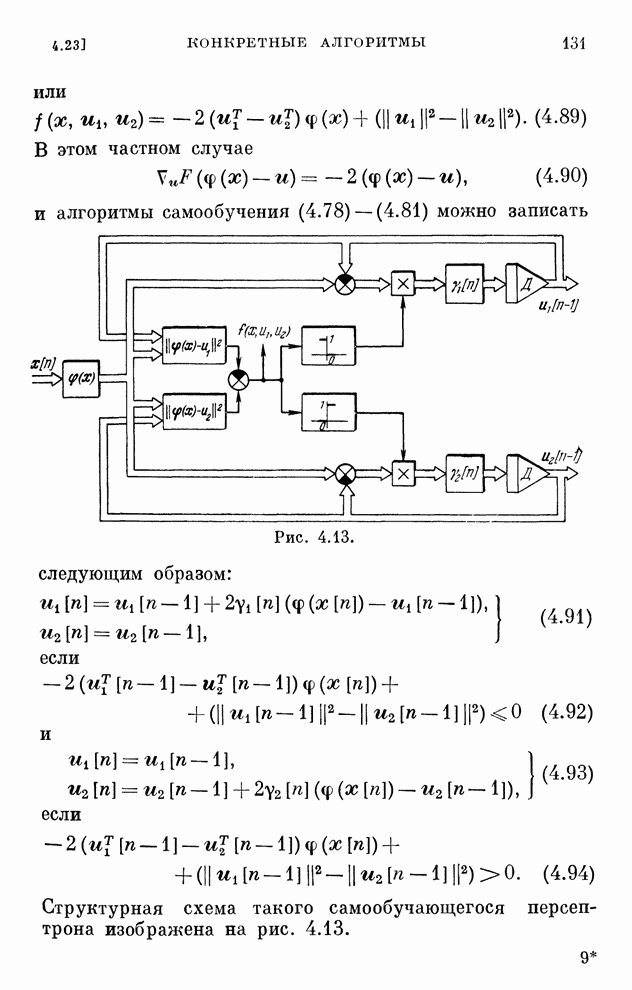
- § 4.23. Конкретные алгоритмы
- § 4.24. Поисковые алгоритмы самообучения
- § 4.25. Обсуждение
- § 4.26. Некоторые задачи
- § 4.27. Заключение
- Глава V. Идентификация
- § 5.1. Введение
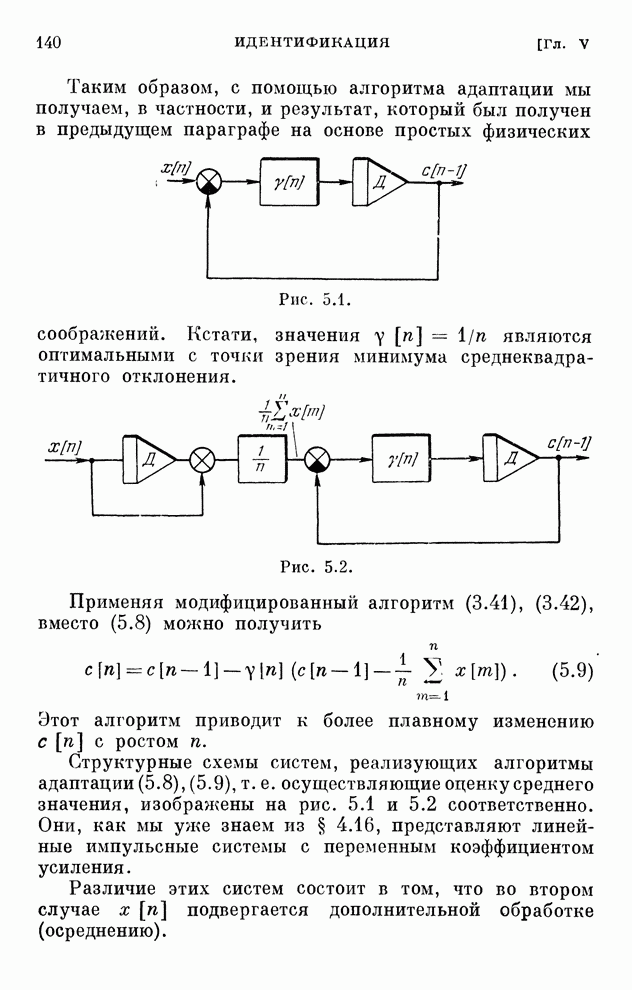
- § 5.2. Оценка среднего значения
- § 5.3. Другой подход
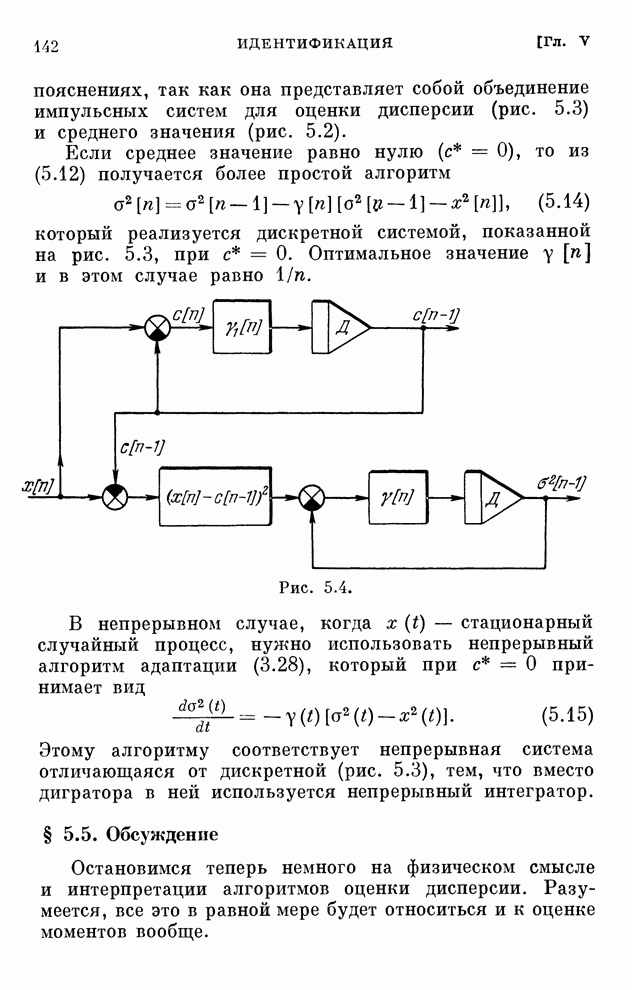
- § 5.4. Оценка дисперсии
- § 5.5. Обсуждение
- § 5.6. Оценка корреляционных функций
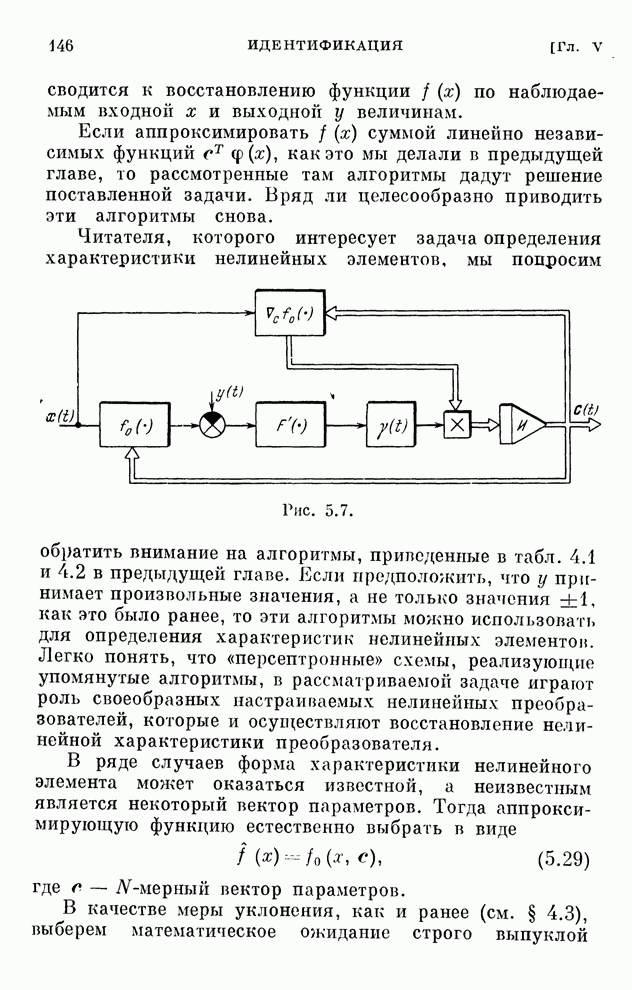
- § 5.7. Определение характеристик нелинейных элементов
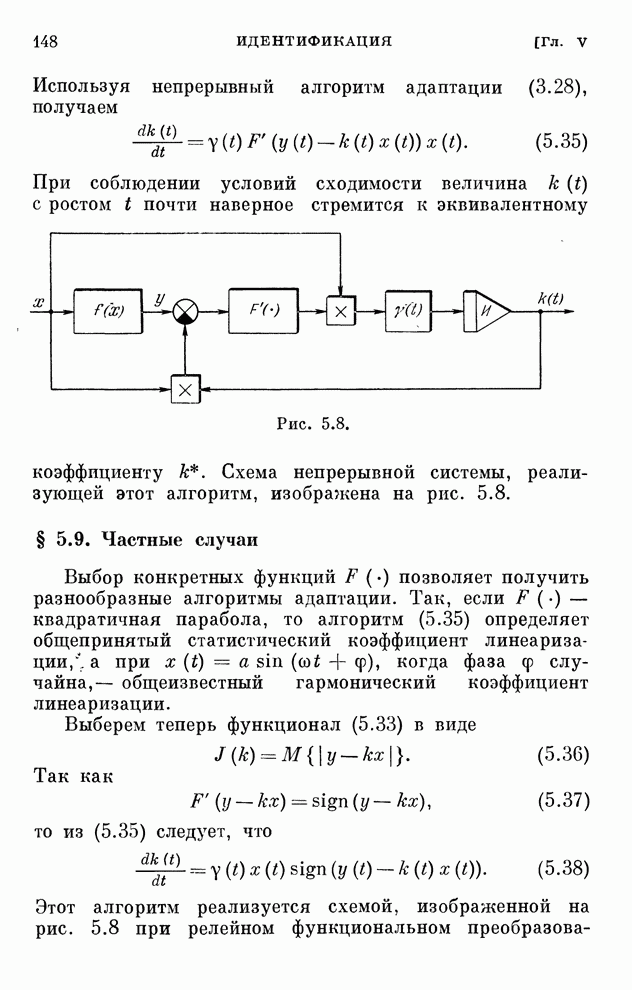
- § 5.8. Оценка коэффициента статистической линеаризации
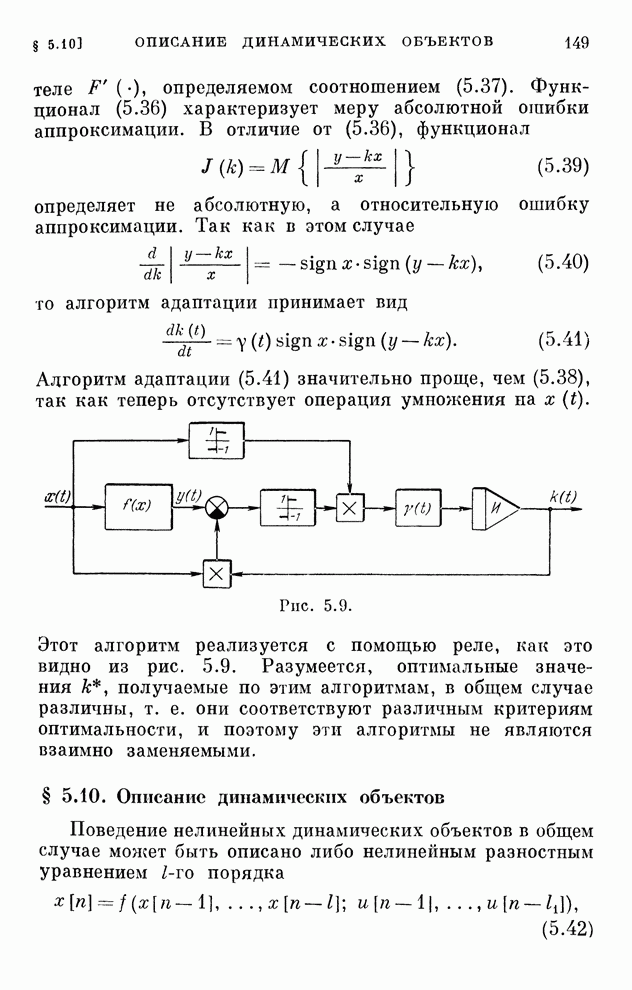
- § 5.9. Частные случаи
- § 5.10. Описание динамических объектов
- § 5.11. Идентификация нелинейных объектов I
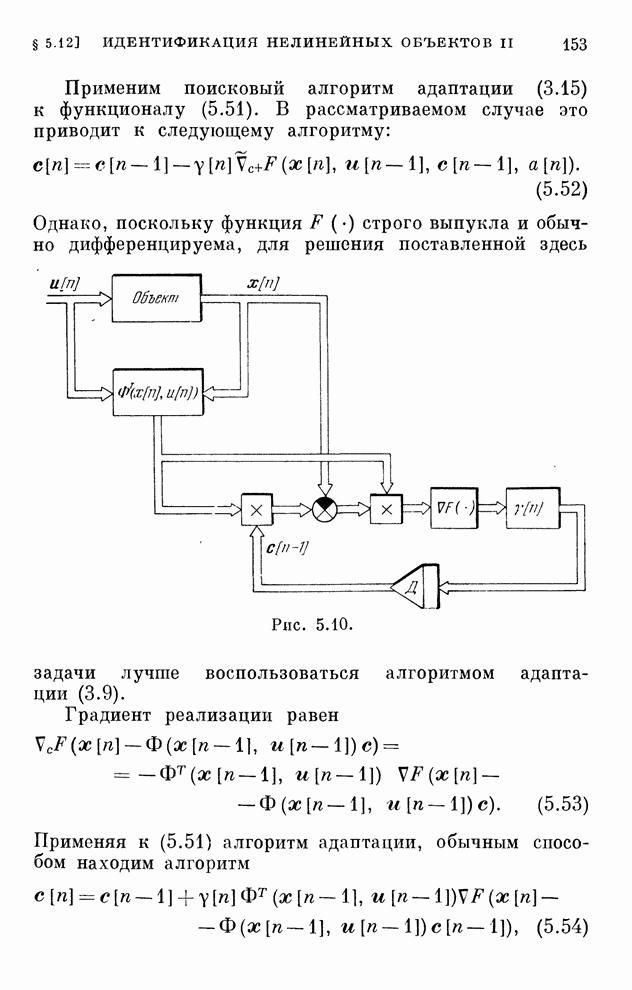
- § 5.12. Идентификация нелинейных объектов II
- § 5.13. Идентификация нелинейных объектов III
- § 5.14. Специальный случай
- § 5.15. Замечание
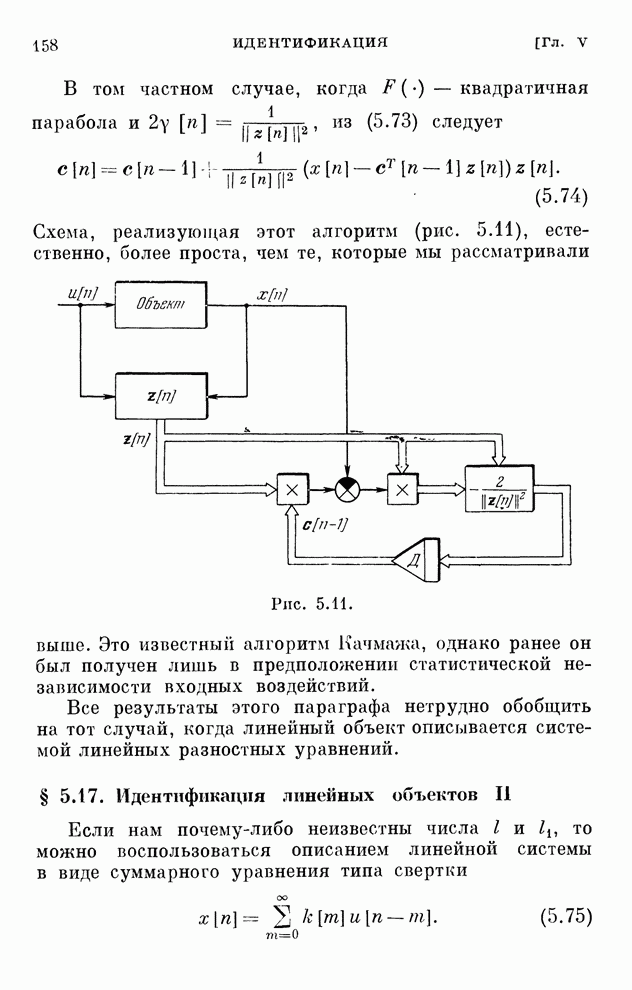
- § 5.16. Идентификация линейных объектов I
- § 5.17. Идентификация линейных объектов II
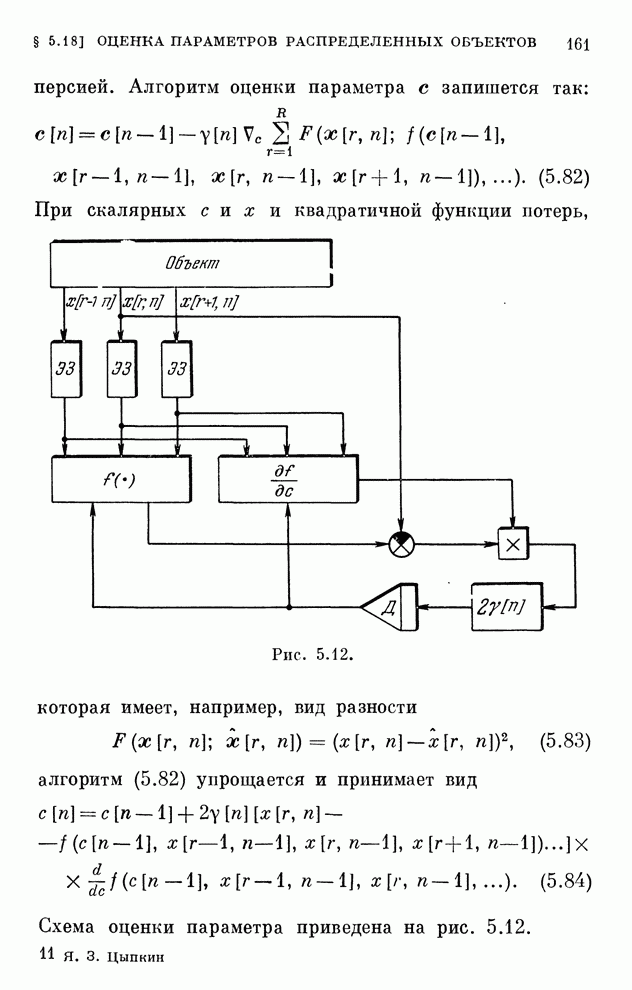
- § 5.18. Оценка параметров распределенных объектов
- § 5.19. Помехи
- § 5.20. Устранение влияния помех
- § 5.21. Некоторые задачи
- § 5.22. Заключение
- Глава VI. Фильтрация
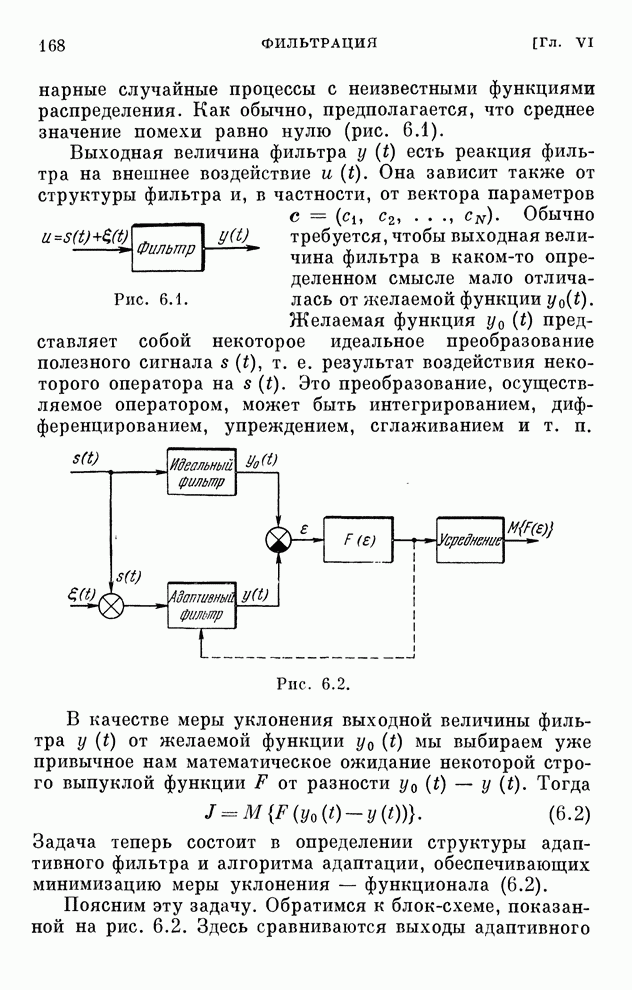
- § 6.1. Введение
- § 6.2. Критерий оптимальности
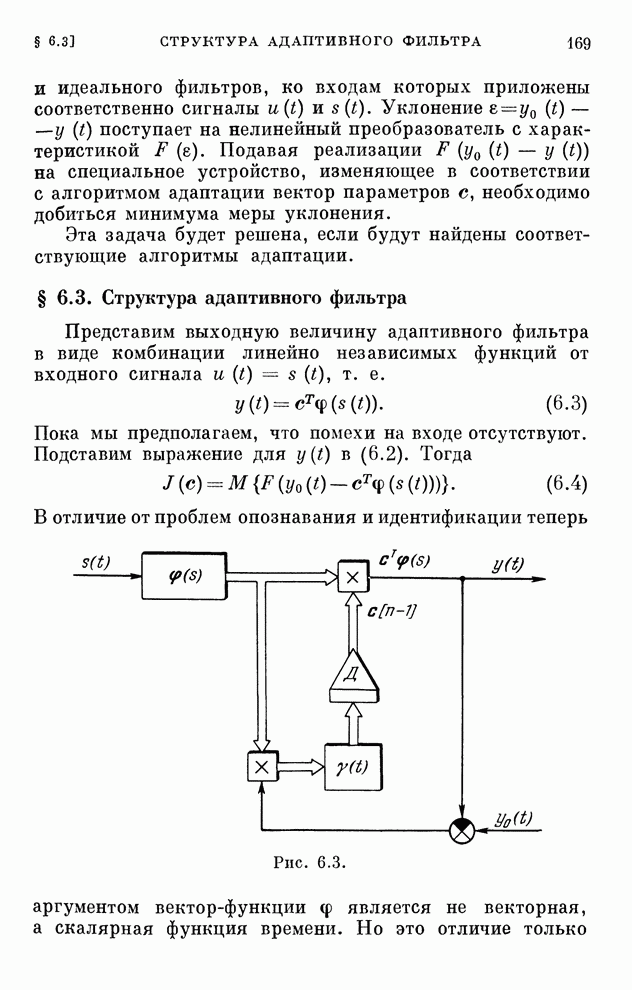
- § 6.3. Структура адаптивного фильтра
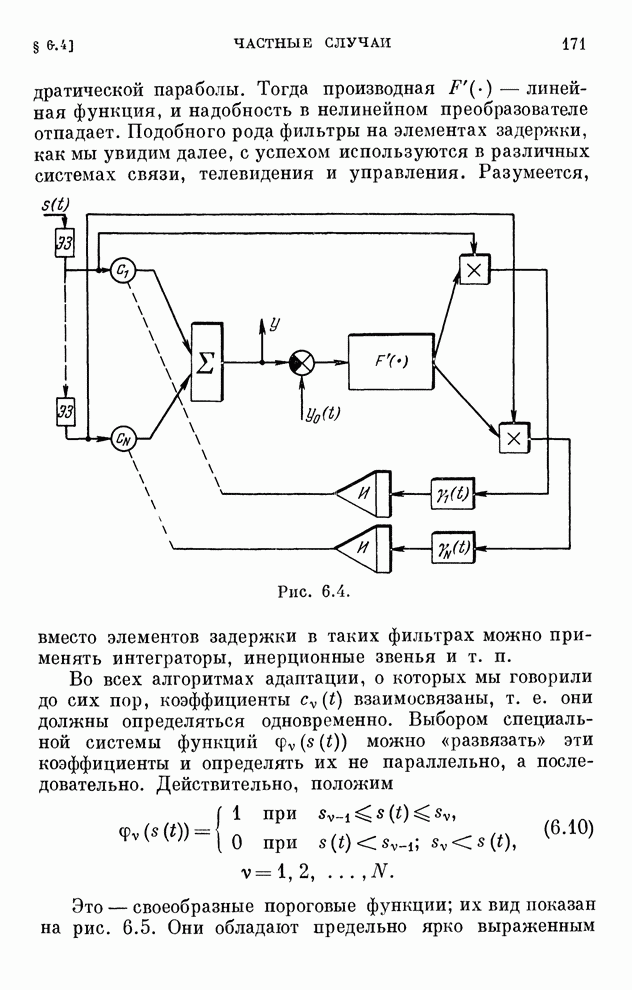
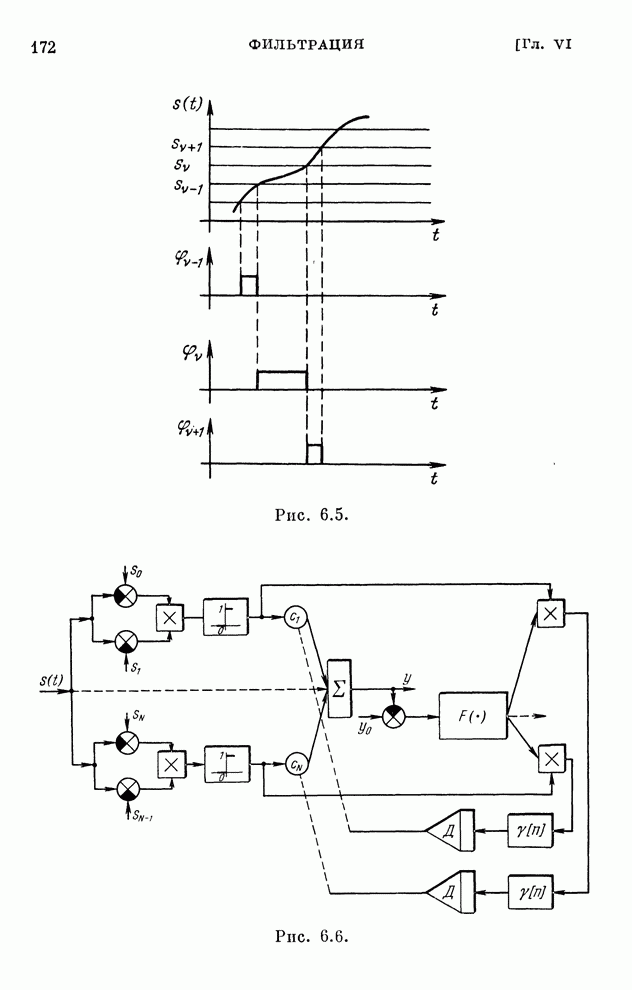
- § 6.4. Частные случаи
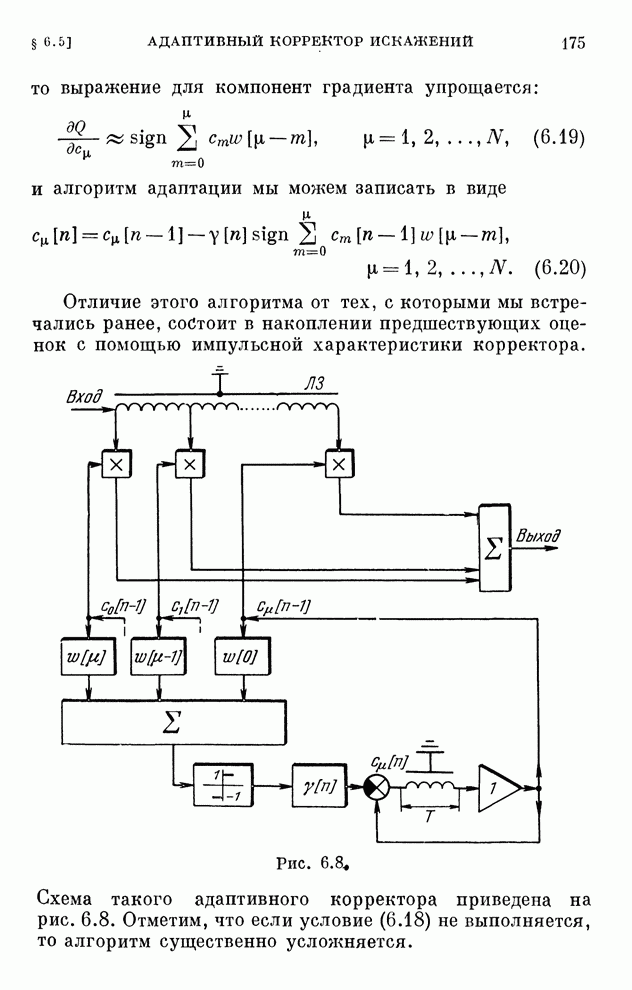
- § 6.5. Адаптивный корректор искажений
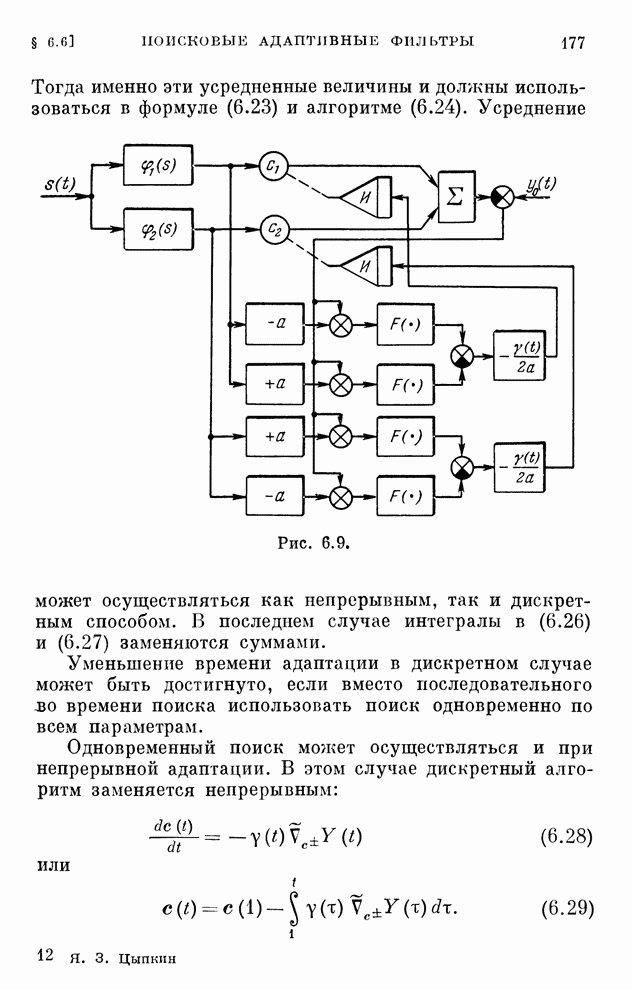
- § 6.6. Поисковые адаптивные фильтры
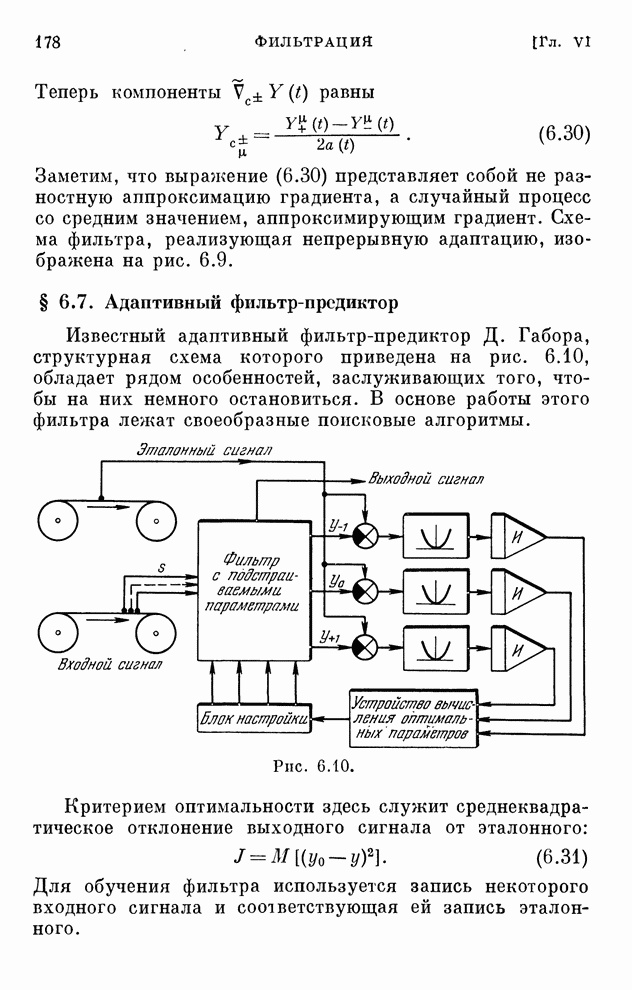
- § 6.7. Адаптивный фильтр-предиктор
- § 6.9. Статистическая теория приема
- § 6.10. Критерий оптимальности приема
- § 6.11. Определение решающего правила
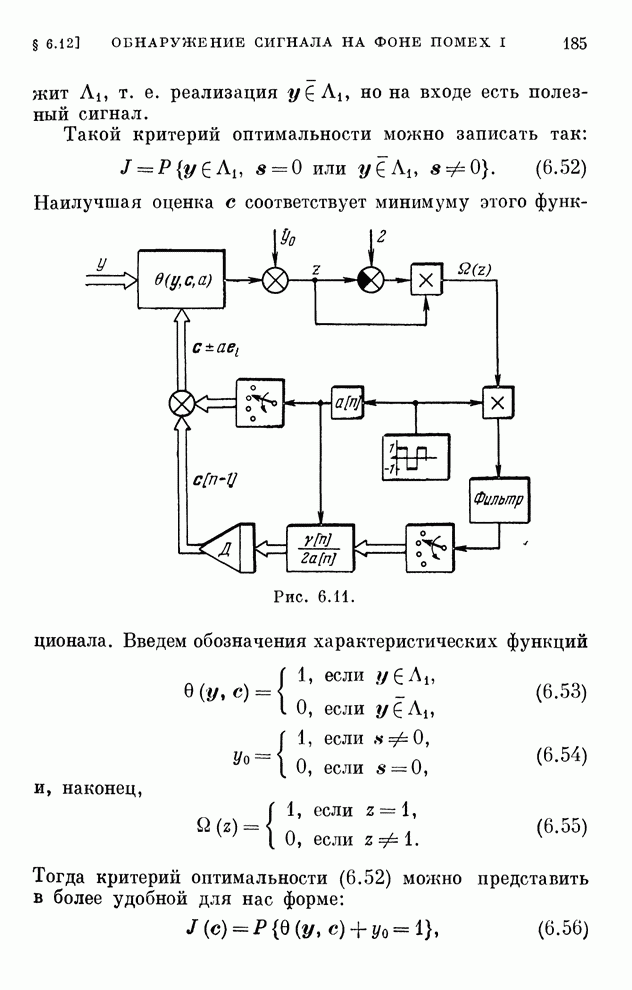
- § 6.12. Обнаружение сигнала на фоне помех I
- § 6.13. Обнаружение сигнала на фоне помех II
- § 6.14. Выделение сигнала на фоне помех
- § 6.15. Критерий оптимального выделения
- § 6.16. Алгоритм выделения
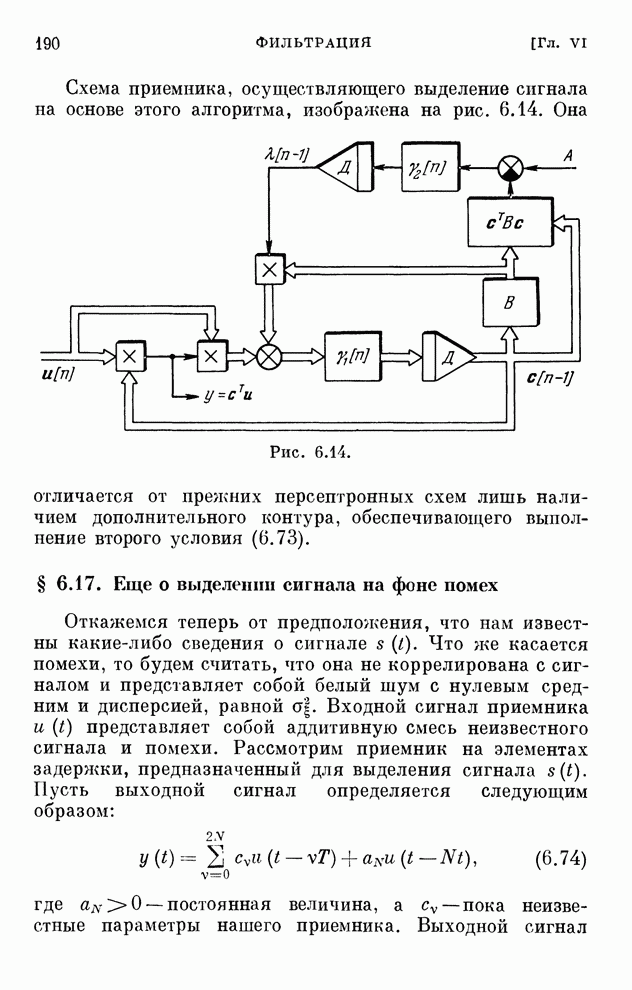
- § 6.17. Еще о выделении сигнала на фоне помех
- § 6.18. Другой критерий оптимальности
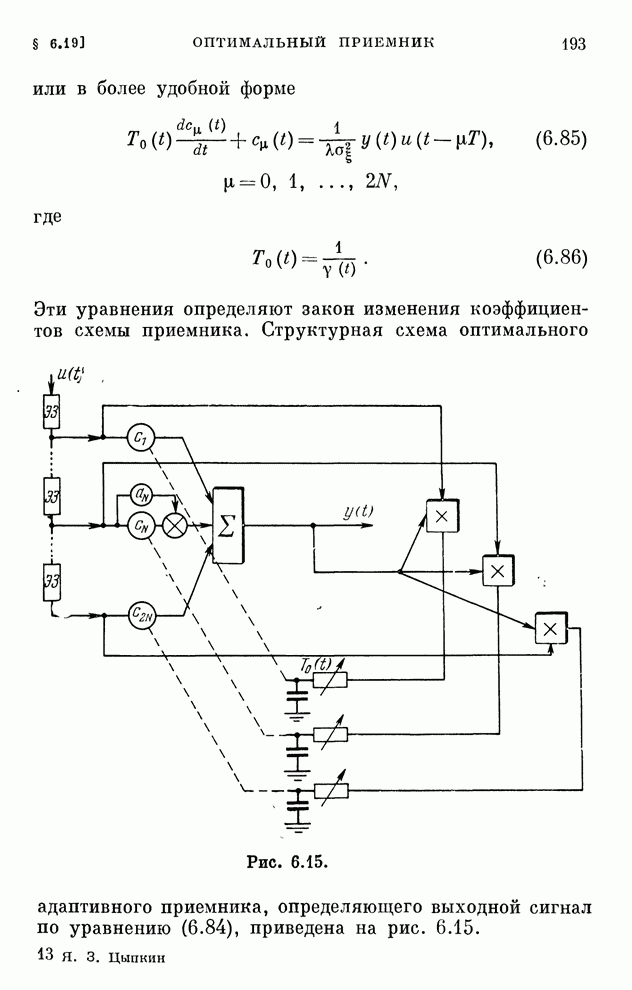
- § 6.19. Оптимальный приемник
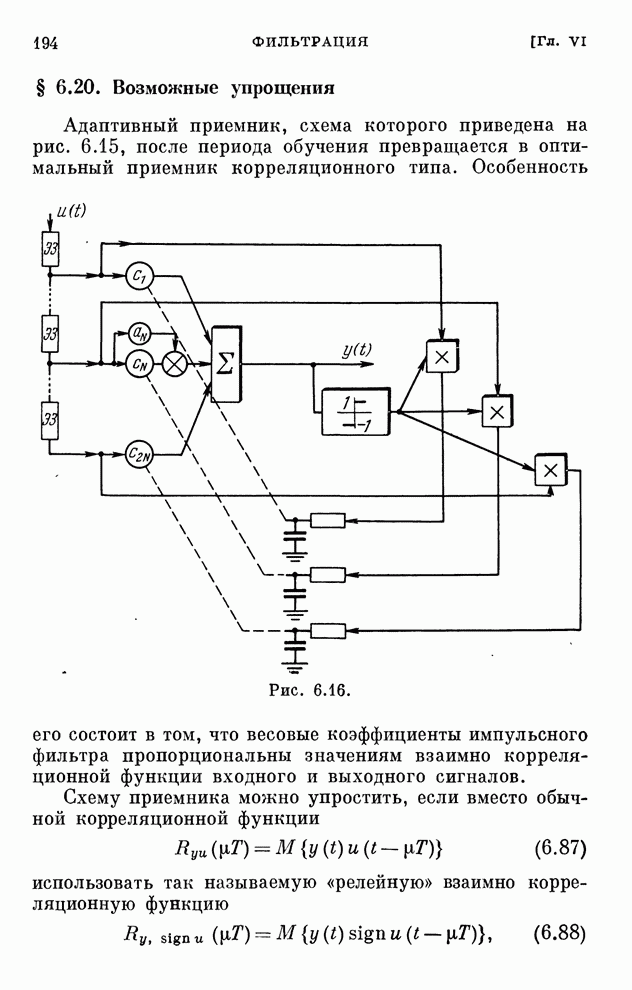
- § 6.20. Возможные упрощения
- § 6.21. Восстановление входных сигналов
- § 6.22. Алгоритмы восстановления
- § 6.23. О влиянии помех
- § 6.24. Некоторые задачи
- § 6.25. Заключение
- Глава VII. Управление
- § 7.1. Введение
- § 7.2. Когда нужна адаптация?
- § 7.3. Постановка задачи
- § 7.4. Дуальное управление
- § 7.5. Алгоритмы дуального управления
- § 7.6. Адаптивные системы управления I
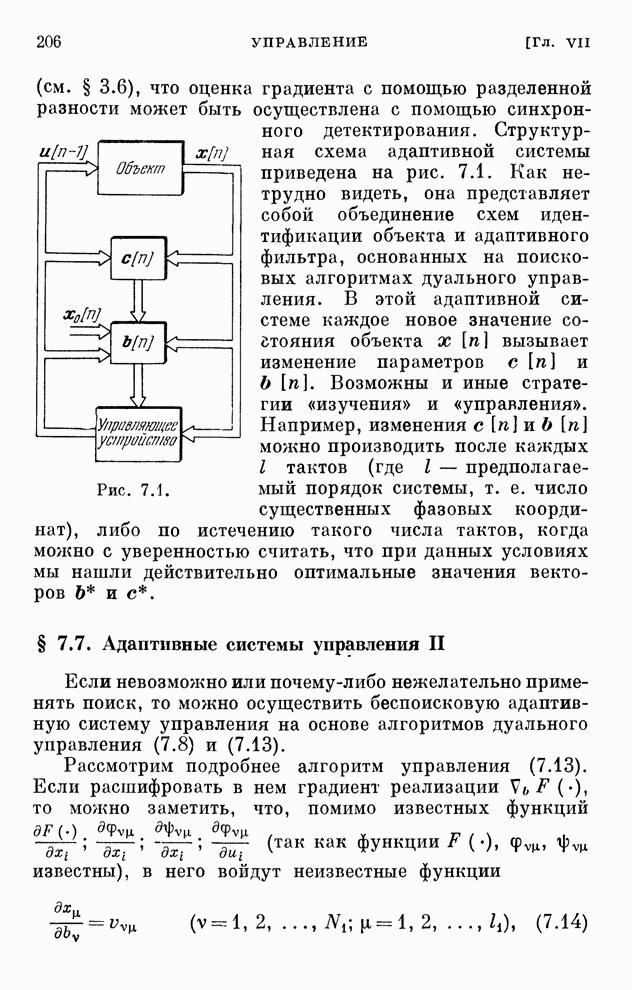
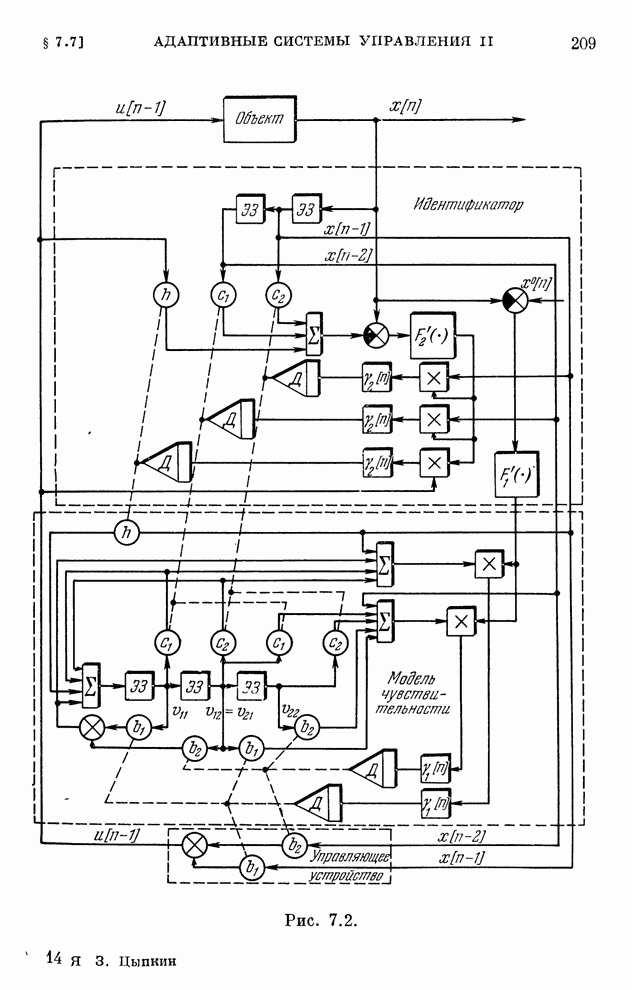
- § 7.7. Адаптивные системы управления II
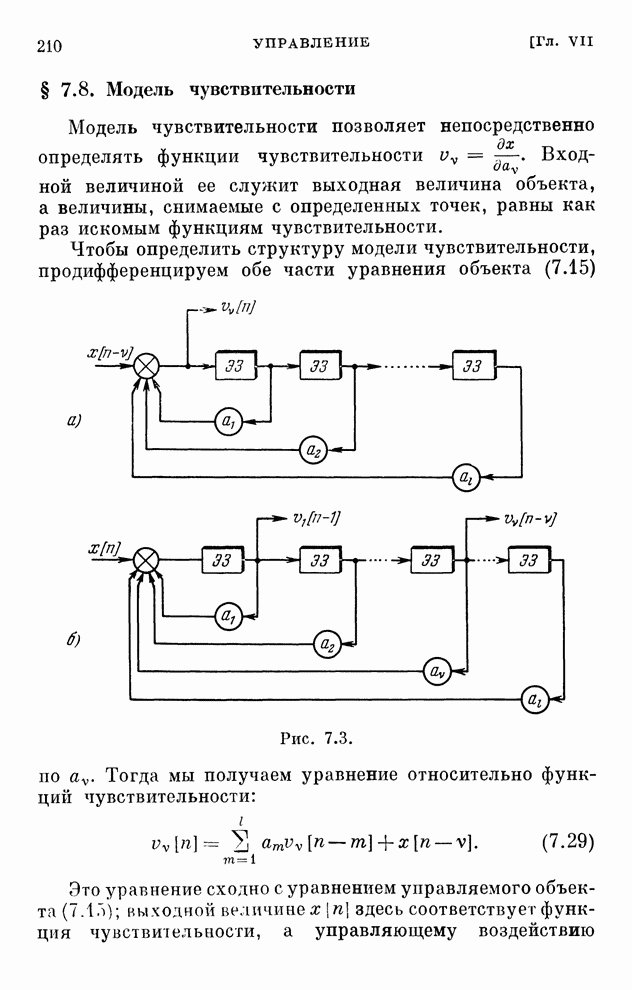
- § 7.8. Модель чувствительности
- § 7.9. Адаптивные системы управления III
- § 7.10. Упрощенные адаптивные системы
- § 7.11. Системы управления по возмущению
- § 7.12. Алгоритмы оптимального управления
- § 7.13. Еще одна возможность
- § 7.14. Экстремальные системы управления
- § 7.15. Алгоритмы экстремального управления
- § 7.16. Алгоритмы изучения
- § 7.17. Непрерывные алгоритмы
- § 7.18. Структурная схема
- § 7.19. Возможные упрощения
- § 7.20. О синтезе оптимальных систем
- § 7.21. Применение алгоритмов адаптации
- § 7.22. О синтезе оптимальных систем при наличии помех
- § 7.23. Управление и опознавание
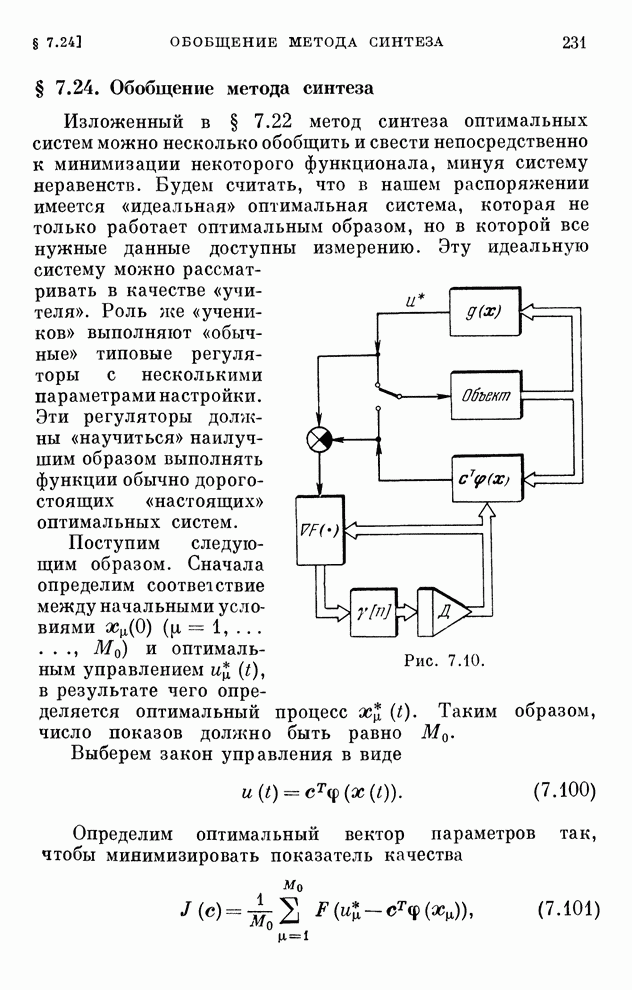
- § 7.24. Обобщение метода синтеза
- § 7.25. Некоторые задачи
- § 7.26. Заключение
- Глава VIII. Надежность
- § 8.1. Введение
- § 8.2. Понятие надежности
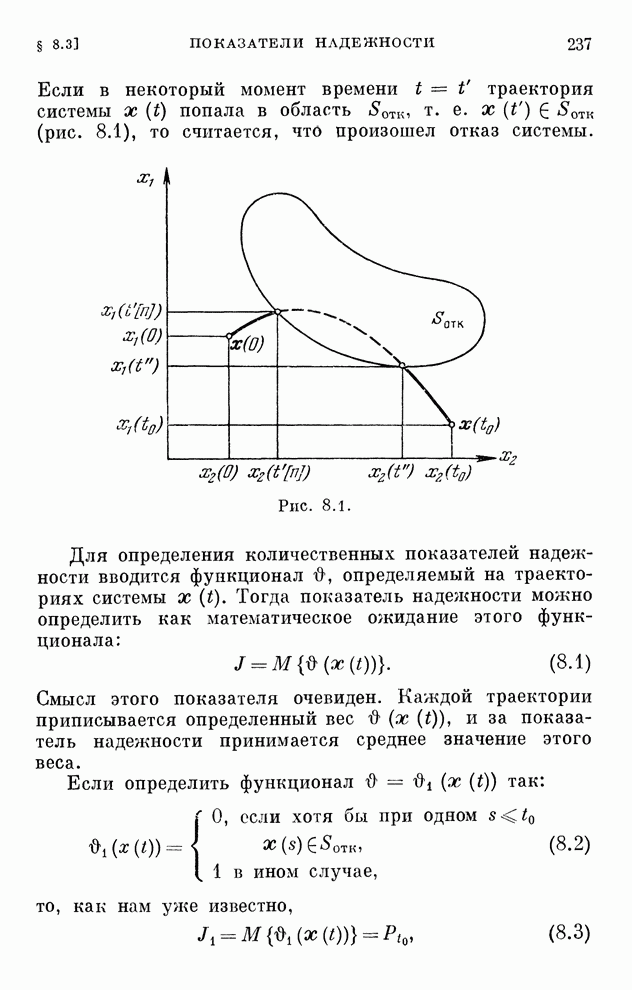
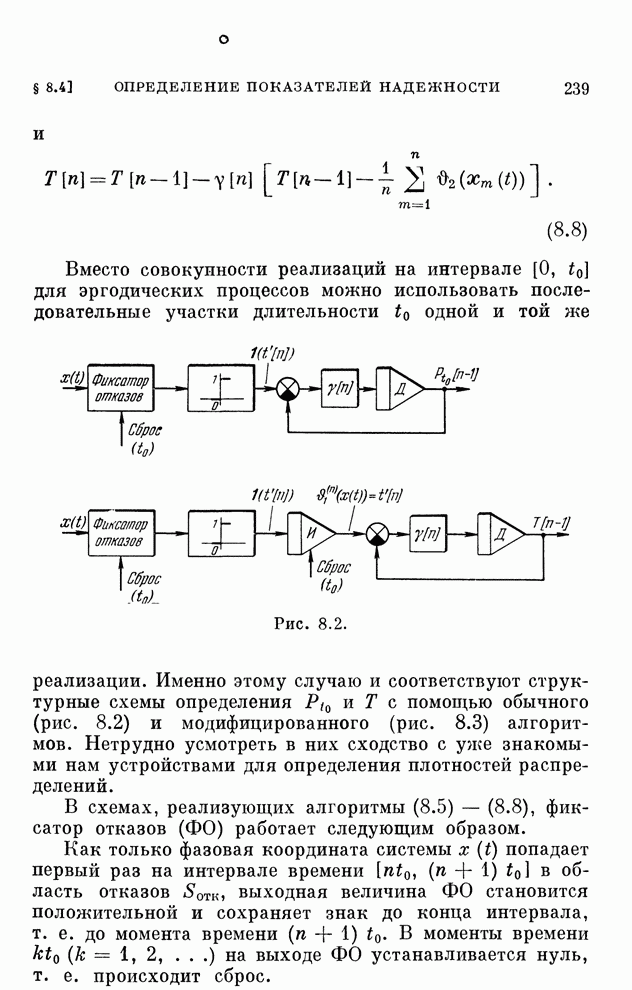
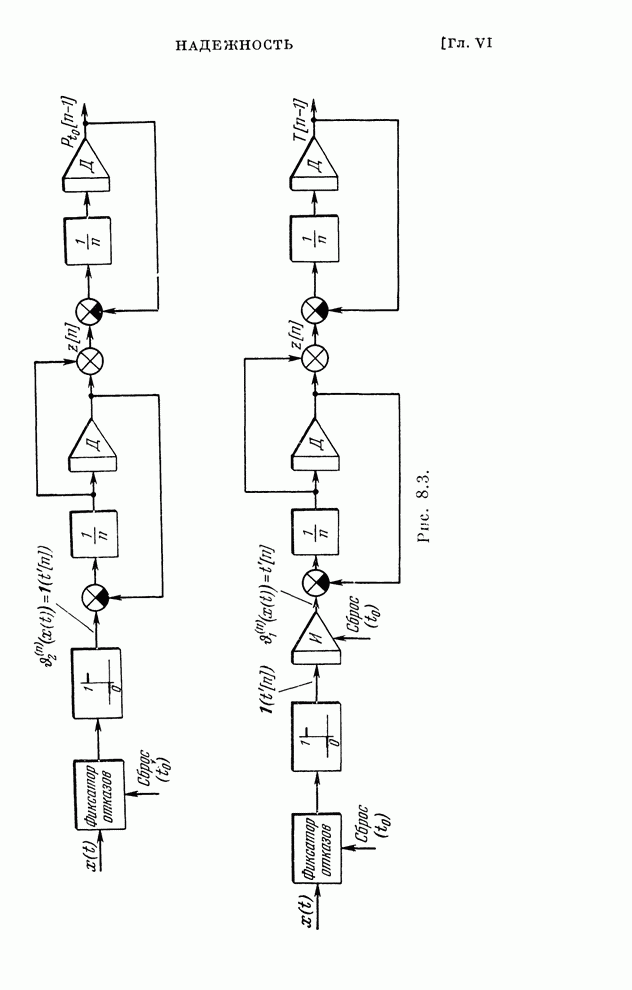
- § 8.4. Определение показателей надежности
- § 8.5. Минимизация эксплуатационных расходов
- § 8.6. Частный случай
- § 8.7. Минимизация стоимости, веса, объема
- § 8.8. Алгоритмы минимизации
- § 8.9. Особый случай
- § 8.10. Алгоритмы
- § 8.11. Повышение надежности путем резервирования
- § 8.12. Повышение надежности путем избыточности
- § 8.13. Проектирование сложных систем
- § 8.14. Алгоритмы оптимальной работоспособности
- § 8.15. О минимаксном критерии оптимизации
- § 8.16. Еще о проектировании сложных систем
- § 8.17. Замечание
- § 8.18. Некоторые задачи
- § 8.19. Заключение
- Глава IX. Исследование операций
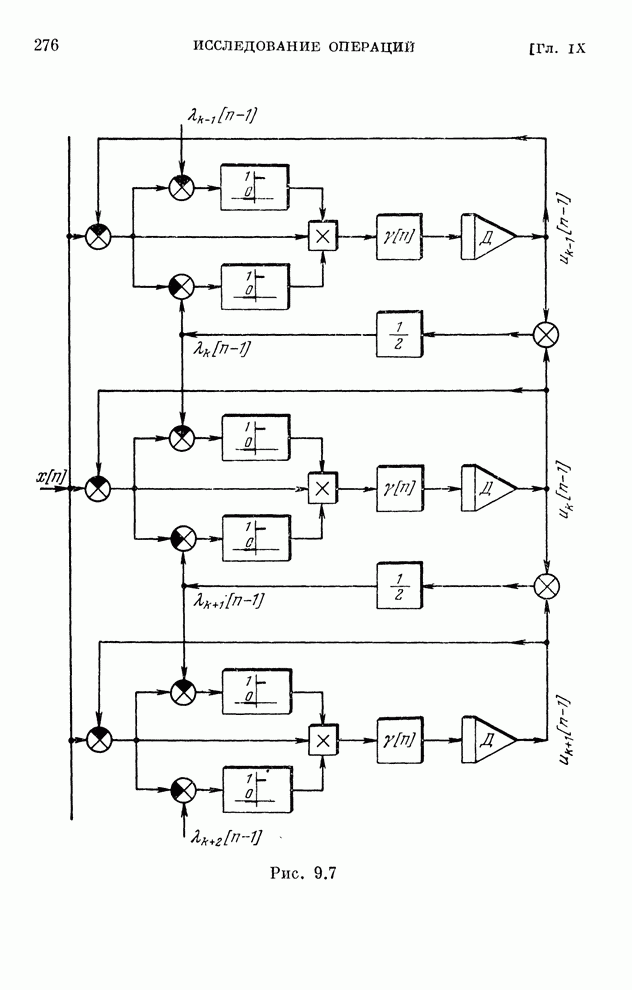
- § 9.1. Введение
- § 9.2. Планирование запасов
- § 9.3. Критерий оптимальности планирования
- § 9.4. Алгоритмы оптимального планировании
- § 9.5. Еще о планировании запасов
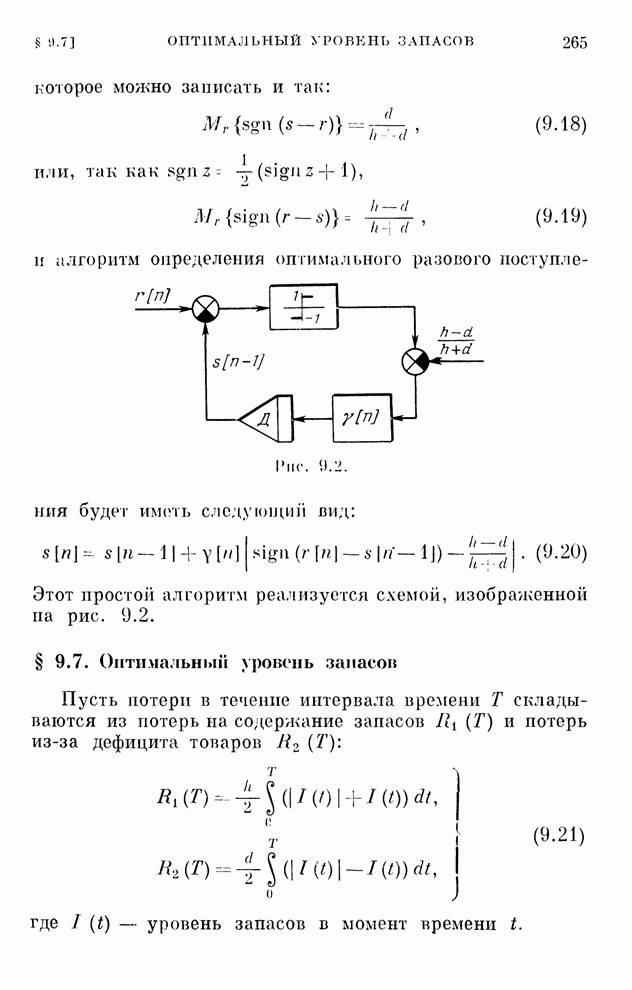
- § 9.6. Оптимальное разовое поступление
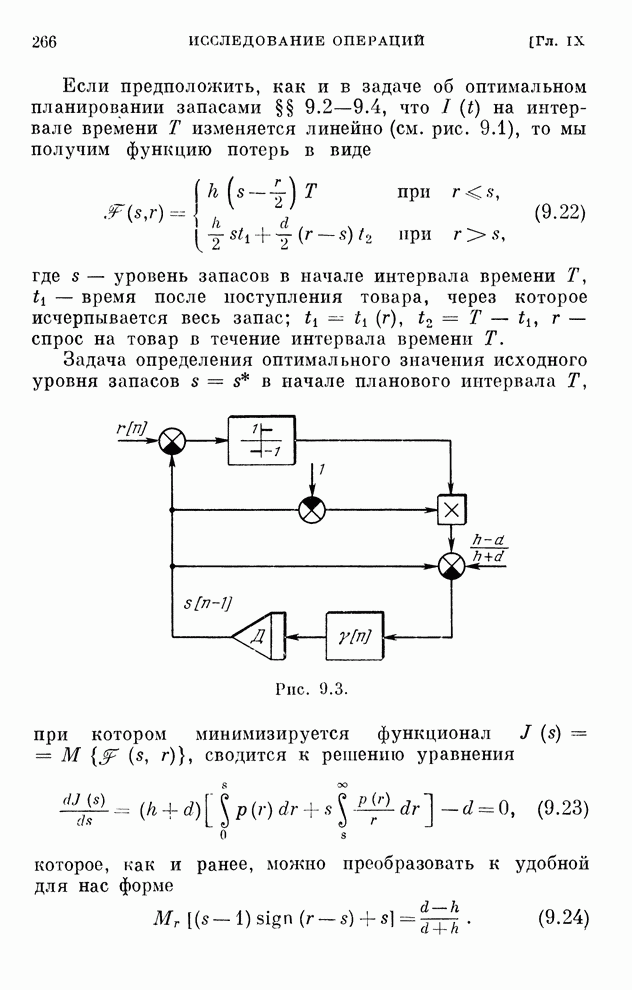
- § 9.7. Оптимальный уровень запасов
- § 9.8. Замечание
- § 9.9. Распределение производственных мощностей
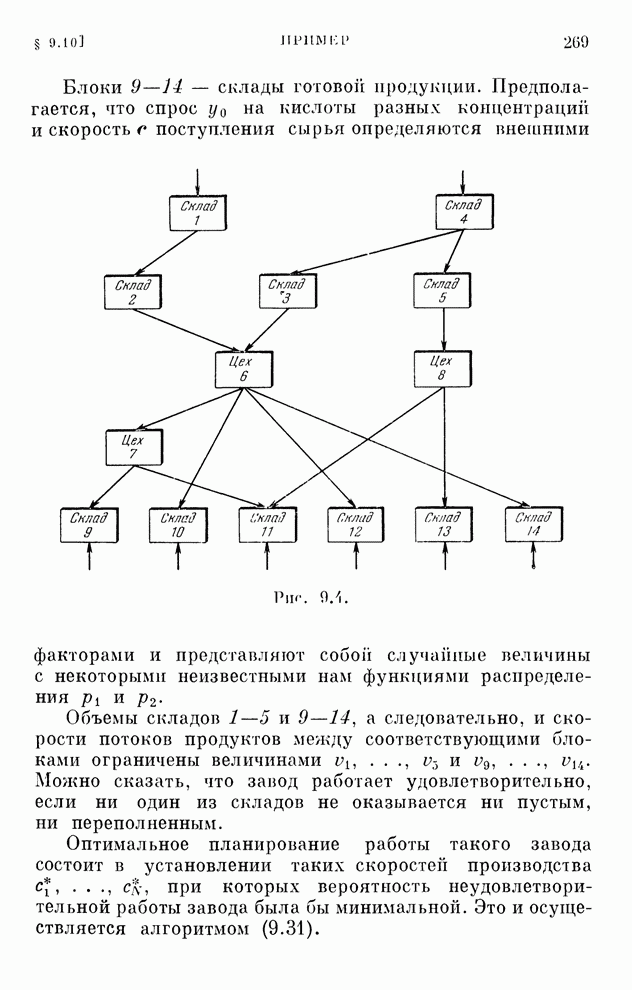
- § 9.10. Пример
- § 9.11. Распределение средств обнаружения
- § 9.12. Алгоритм оптимального распределения
- § 9.13. Распределение областей дискретизации
- § 9.14. Критерии оптимальности распределения
- § 9.15. Алгоритм оптимальных оценок
- § 9.16. Некоторые задачи
- § 9.17. Заключение
- Глава X. Игры и автоматы
- § 10.1. Введение
- § 10.2. Понятие игры
- § 10.3. Теорема о минимаксе
- § 10.4. Уравнения оптимальных стратегий
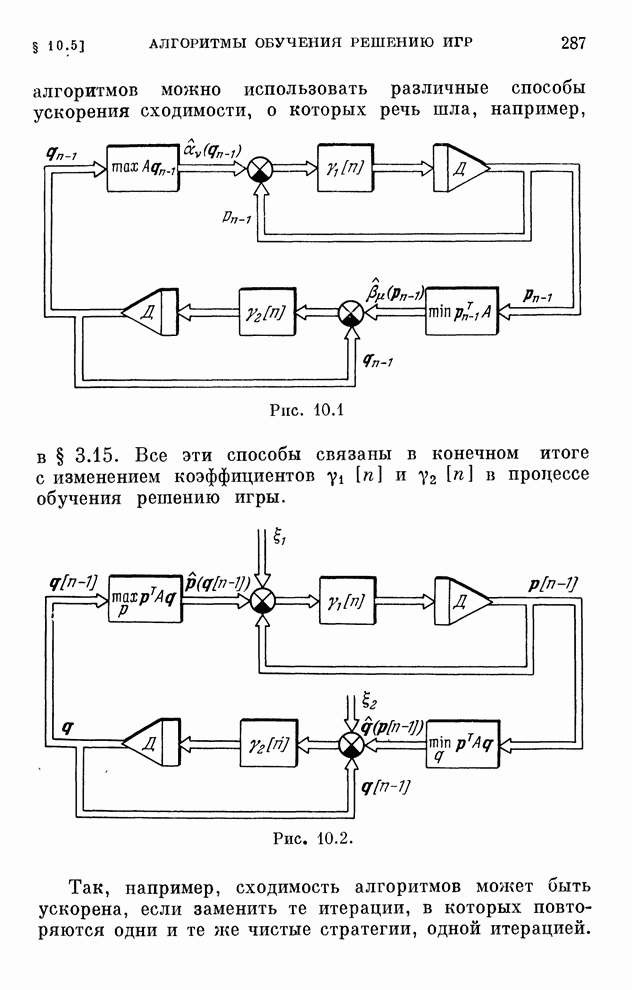
- § 10.5. Алгоритмы обучения решению игр
- § 10.6. Игры и линейное программирование
- § 10.7. Управление как игра
- § 10.8. Алгоритмы управления
- § 10.9. Одно обобщение
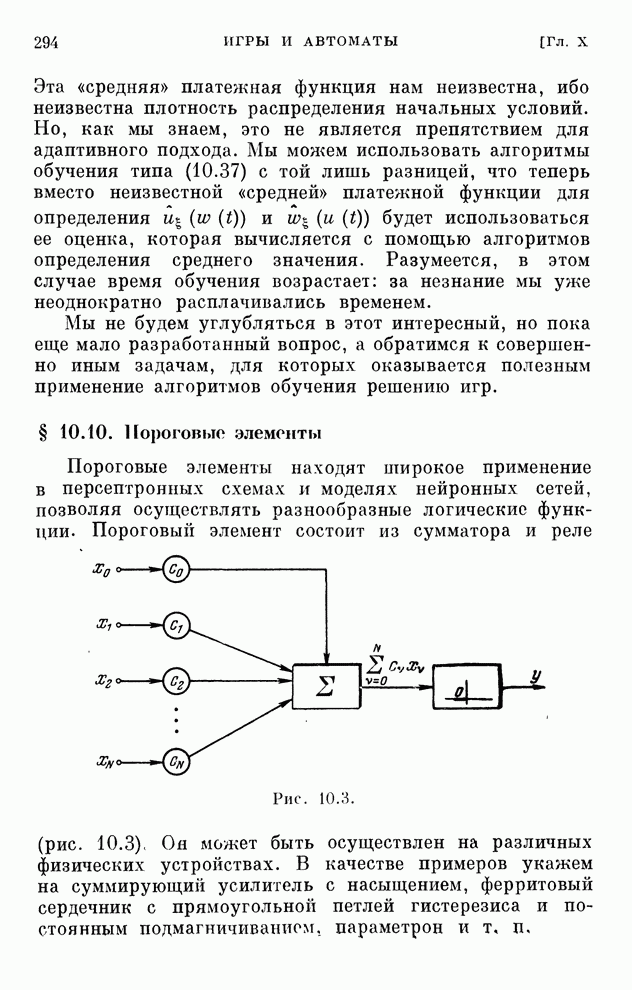
- § 10.10. Пороговые элементы
- § 10.11. О пороговой реализуемости логических функции
- § 10.12. Критерий реализуемости
- § 10.13. Алгоритмы реализуемости
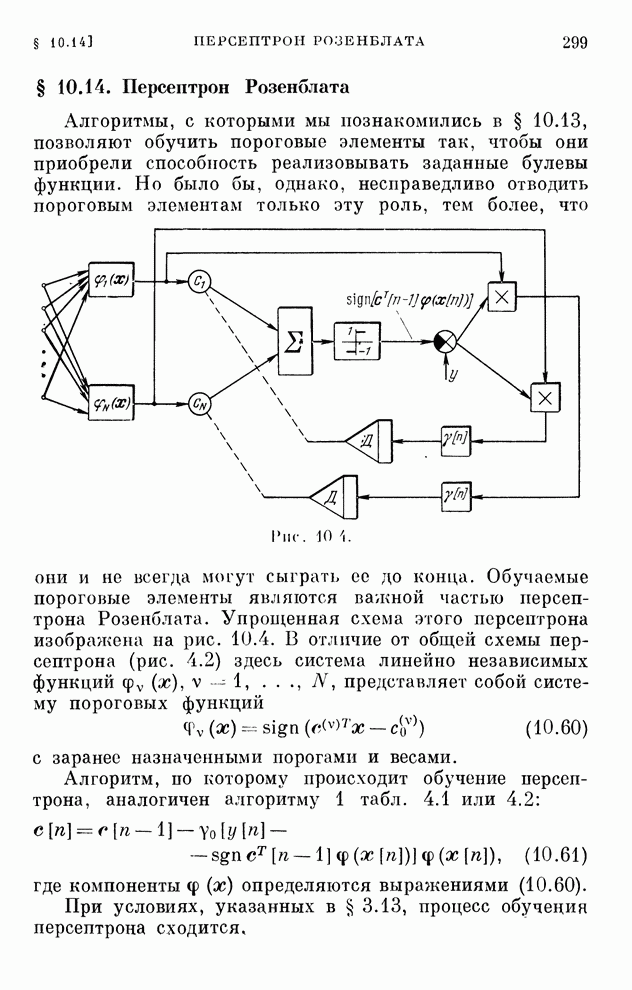
- § 10.14. Персептрон Розенблата
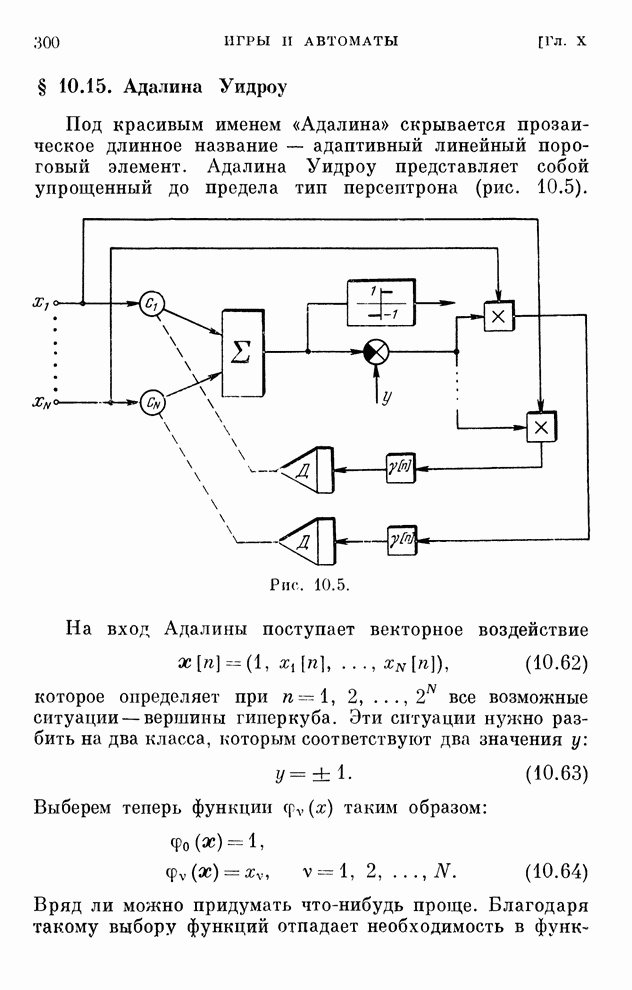
- § 10.15. Адалина Уидроу
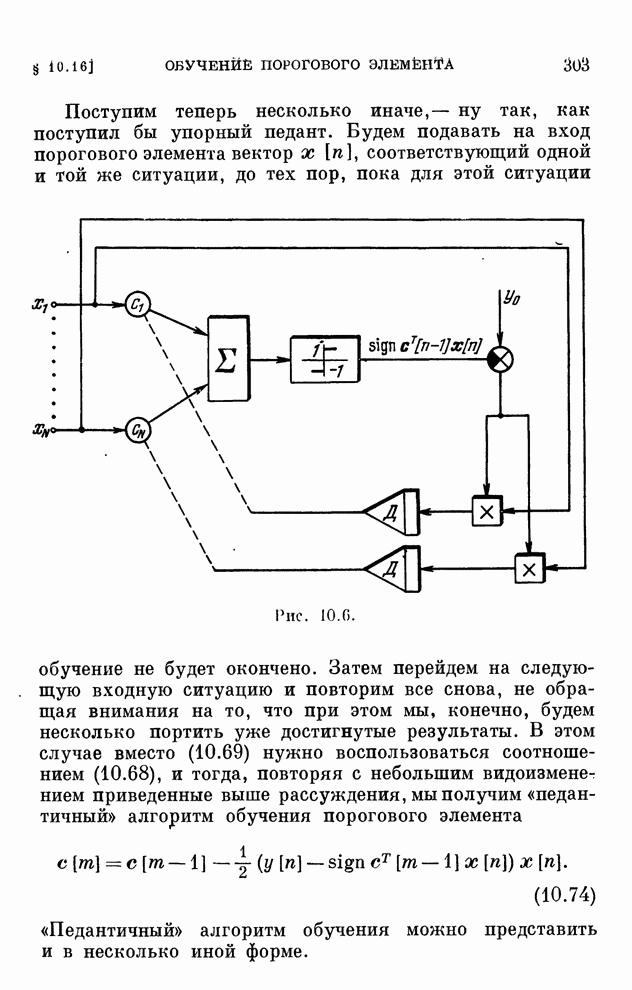
- § 10.16. Обучение порогового элемента
- § 10.17. Автоматы
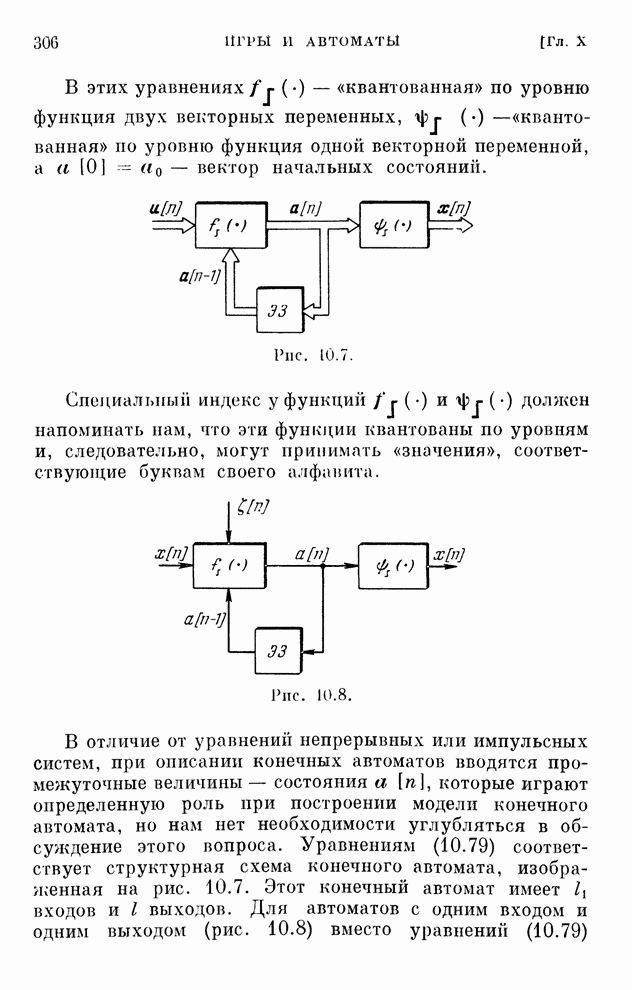
- § 10.18. Описание конечных автоматов
- § 10.19. Стохастические конечные автоматы
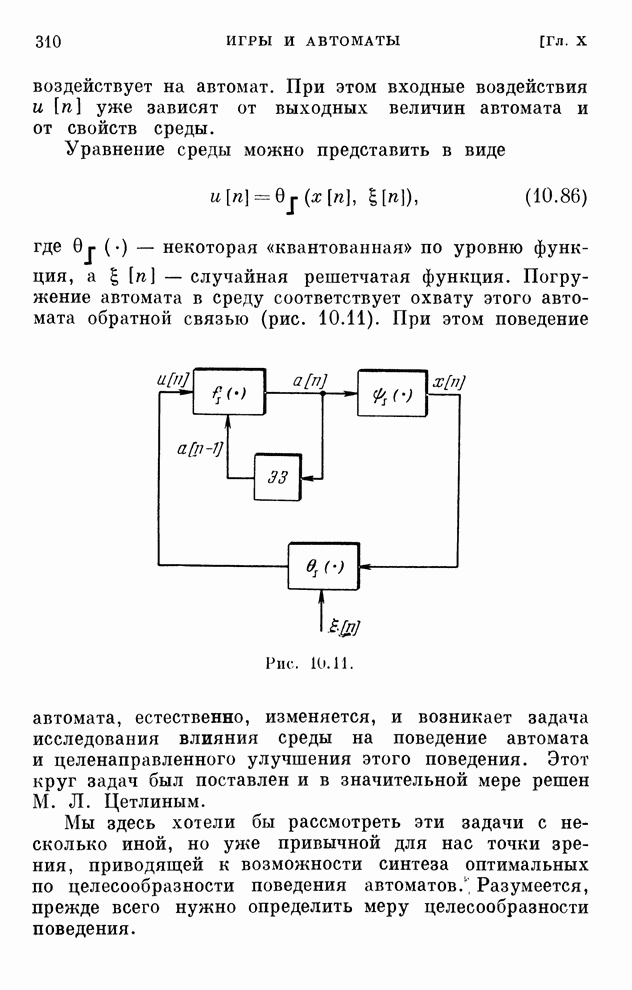
- § 10.20. Взаимодействие автомата со средой
- § 10.21. О мере целесообразности поведения
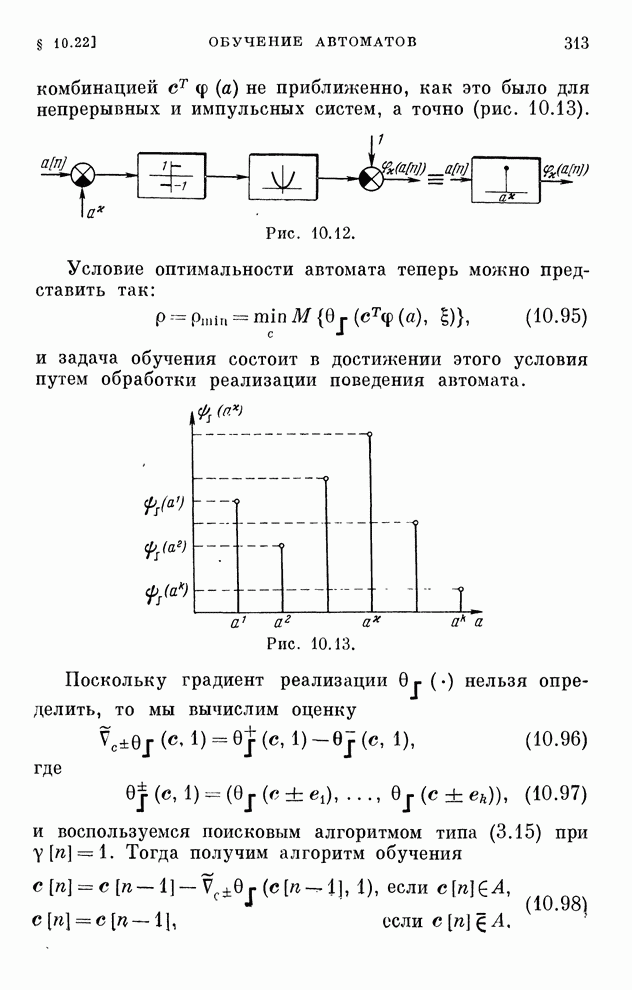
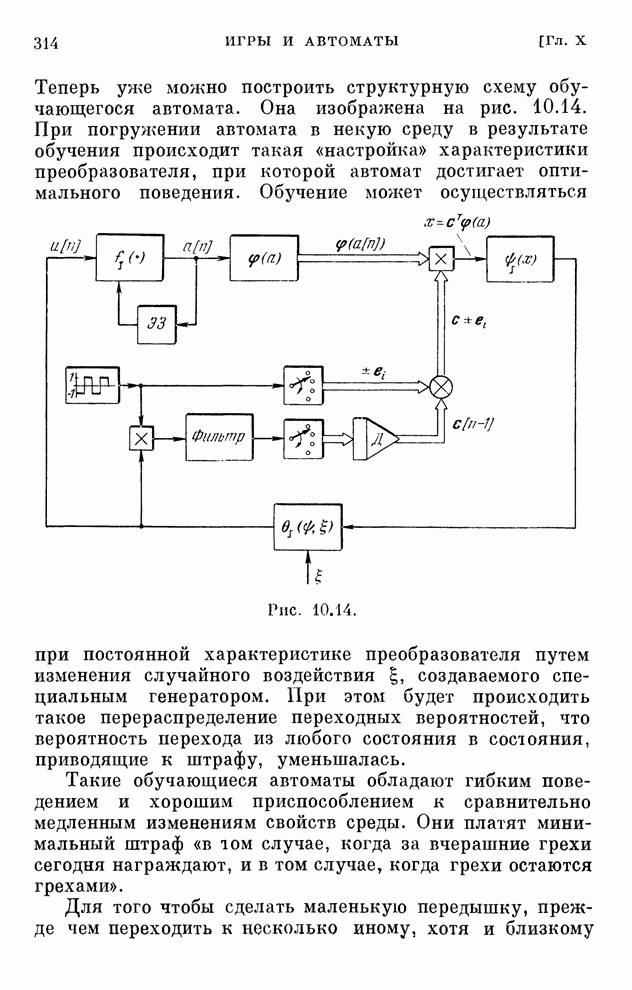
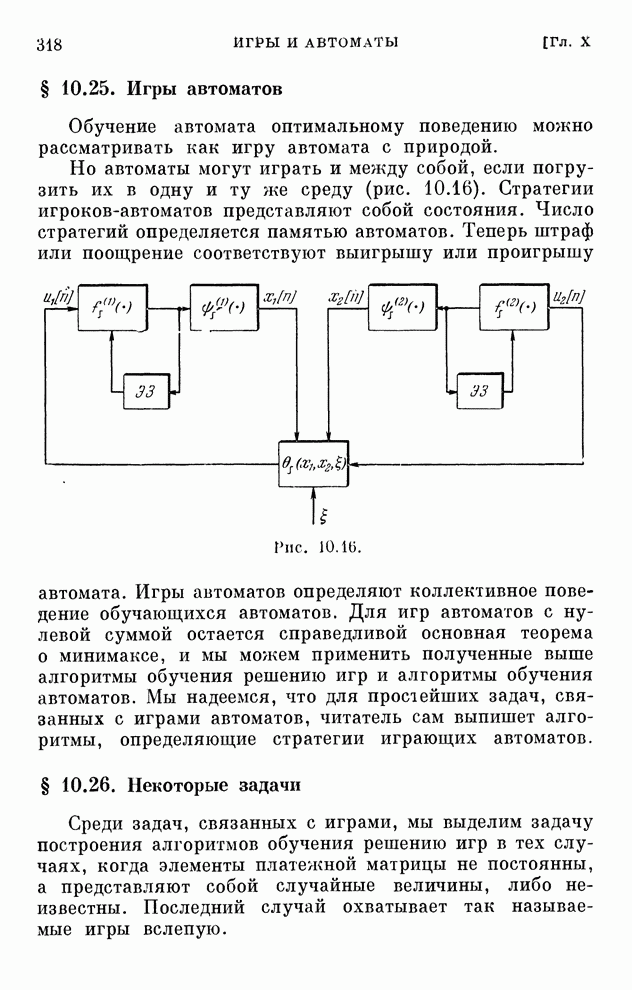
- § 10.22. Обучение автоматов
- § 10.23. О марковских цепях
- § 10.24. Марковское обучение
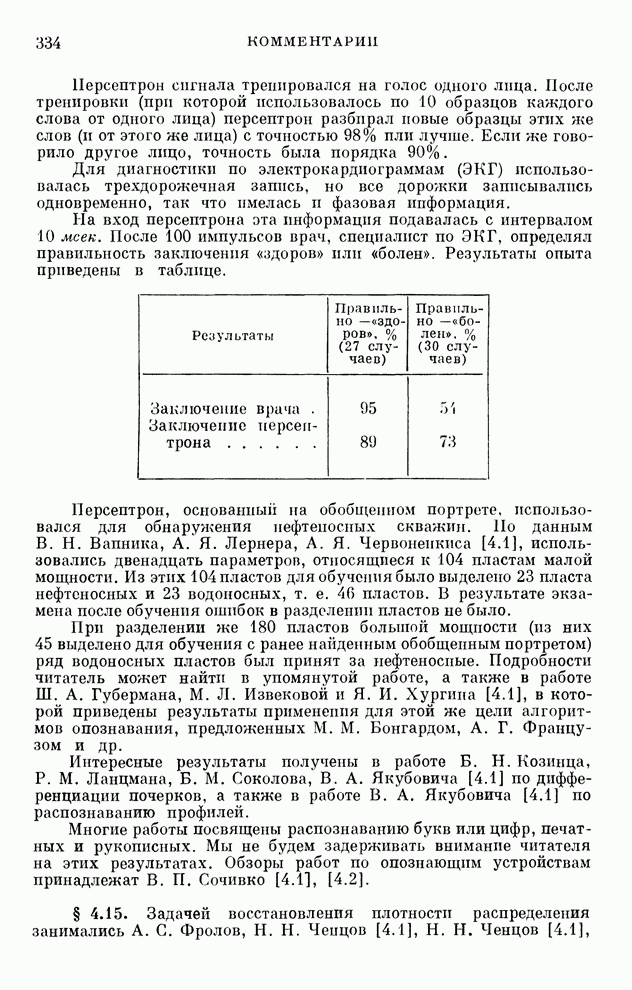
- § 10.25. Игры автоматов
- § 10.26. Некоторые задачи
- § 10.27. Заключение
- Послесловие
- Комментарии
- Литература