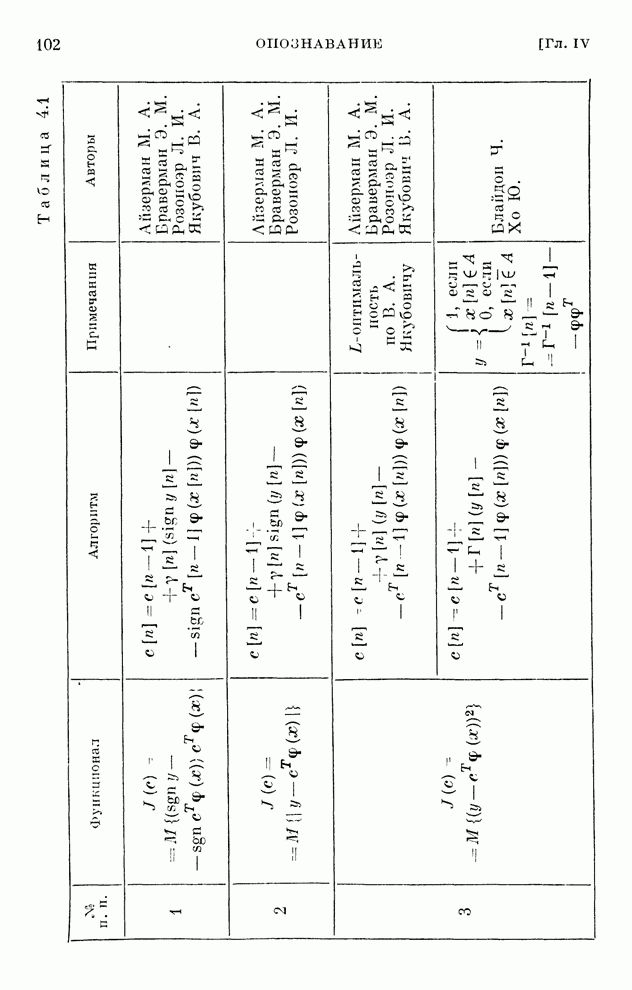
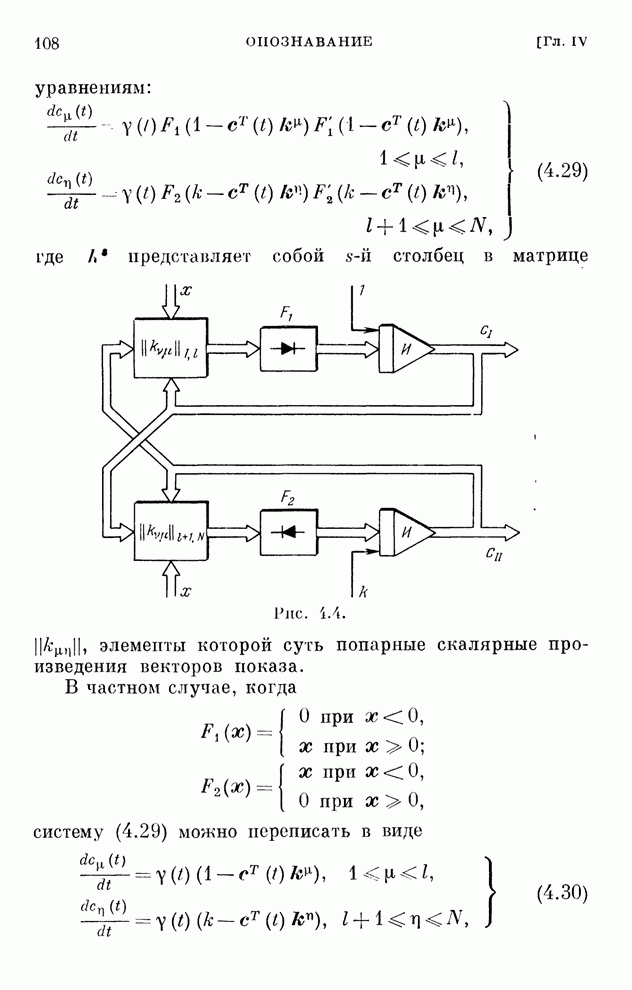
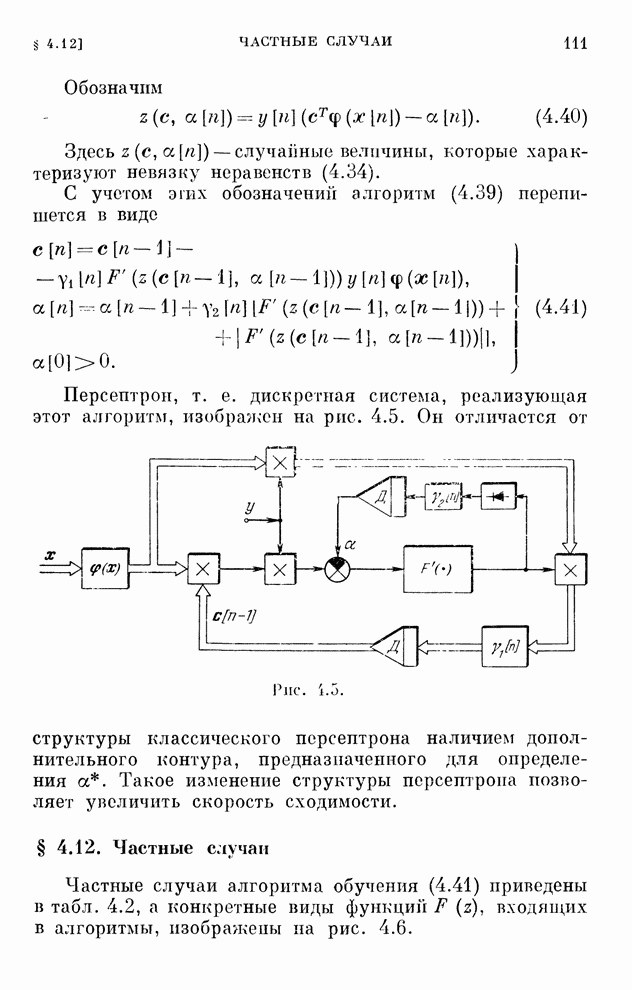
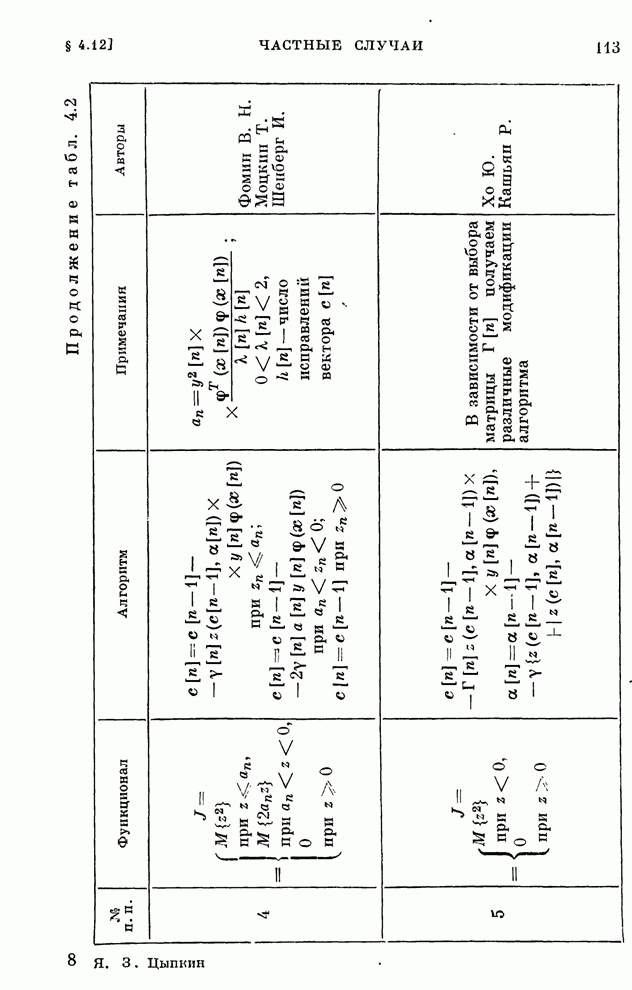
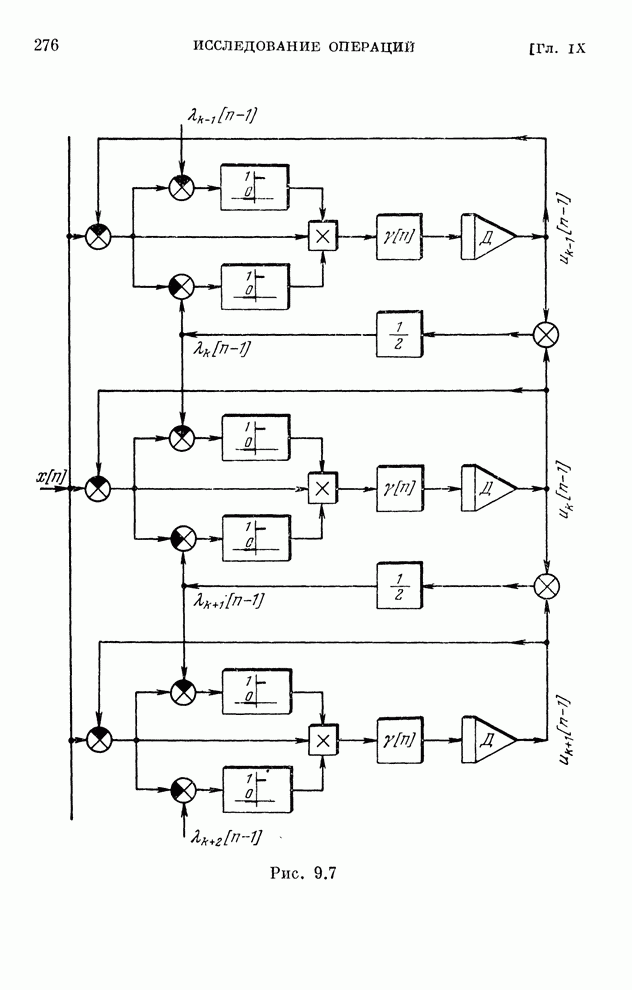
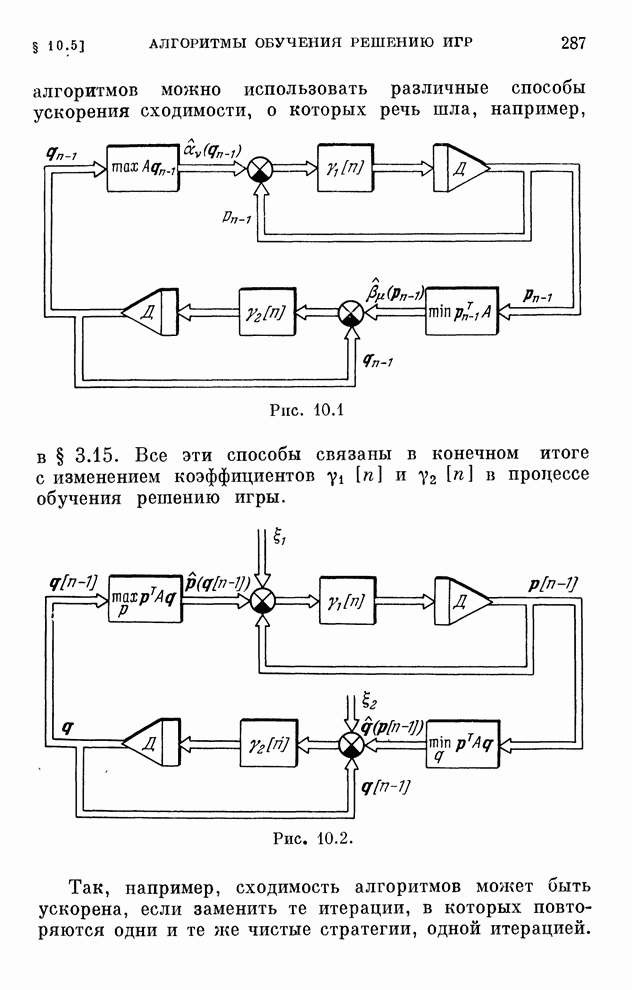
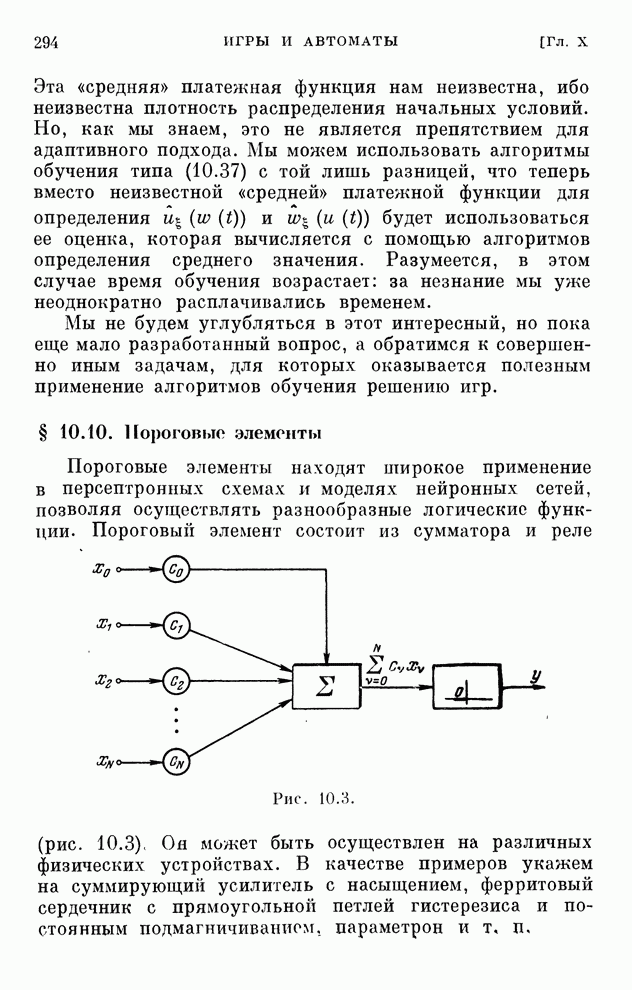
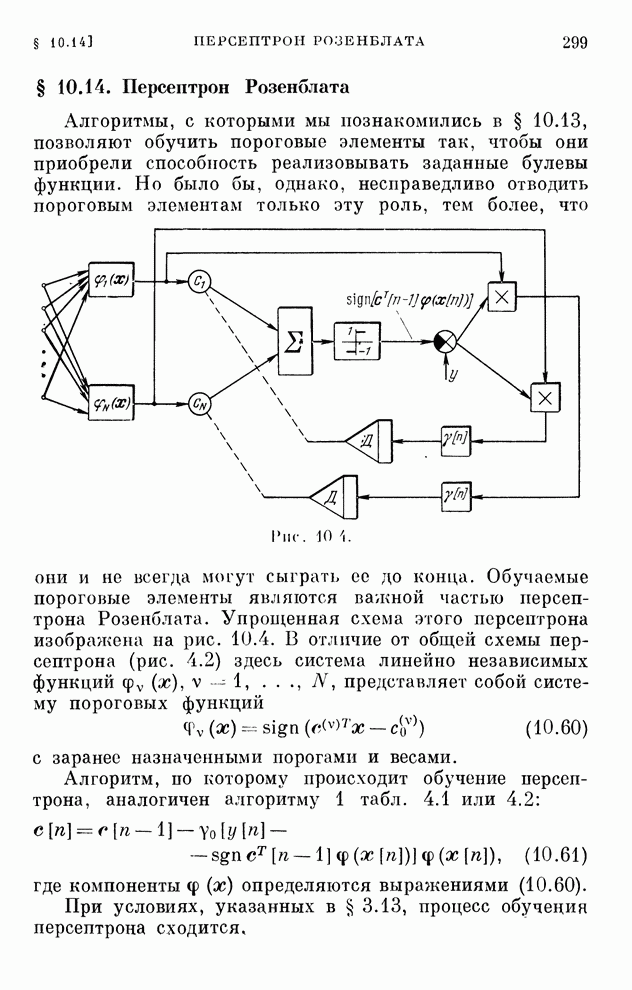
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
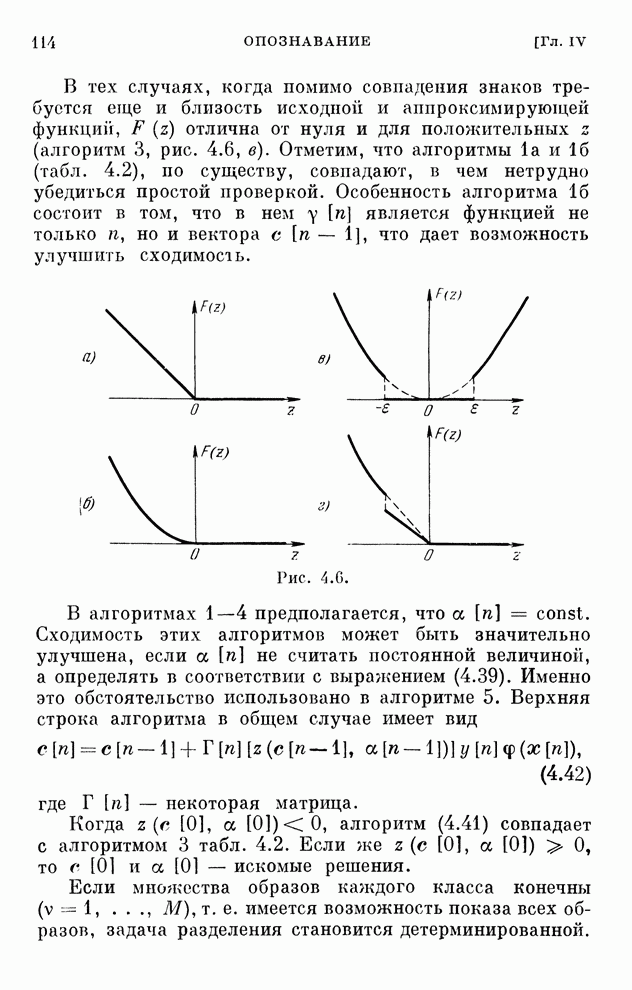
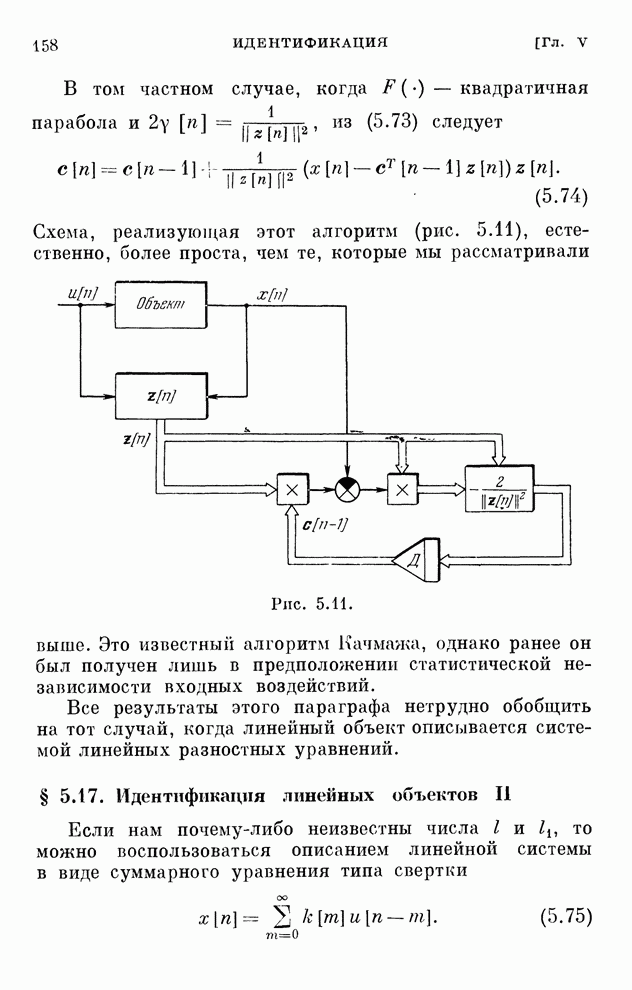
§ 2.15. Сходимость и устойчивость
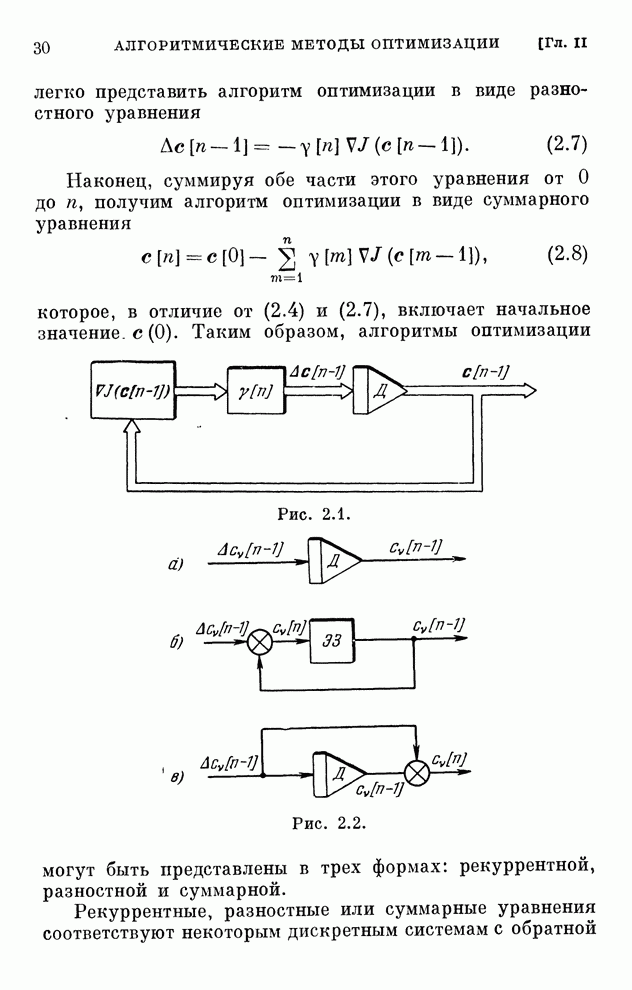
Алгоритмы оптимизации могут быть
реализованы, если они сходятся, т. е. если с течением времени ![]() в дискретных
алгоритмах и
в дискретных
алгоритмах и ![]() в
непрерывных алгоритмах стремятся к оптимальному значению вектора
в
непрерывных алгоритмах стремятся к оптимальному значению вектора ![]() . В связи с этим
установление сходимости приобретает важное значение. Только при
гарантированной сходимости можно рассчитывать на применение алгоритмов
оптимизации.
. В связи с этим
установление сходимости приобретает важное значение. Только при
гарантированной сходимости можно рассчитывать на применение алгоритмов
оптимизации.
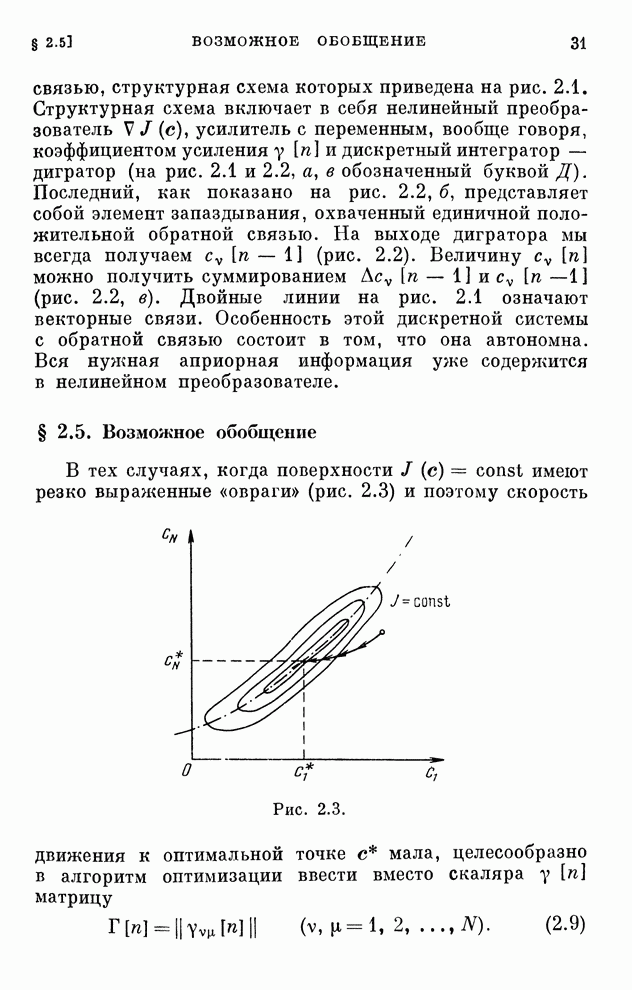
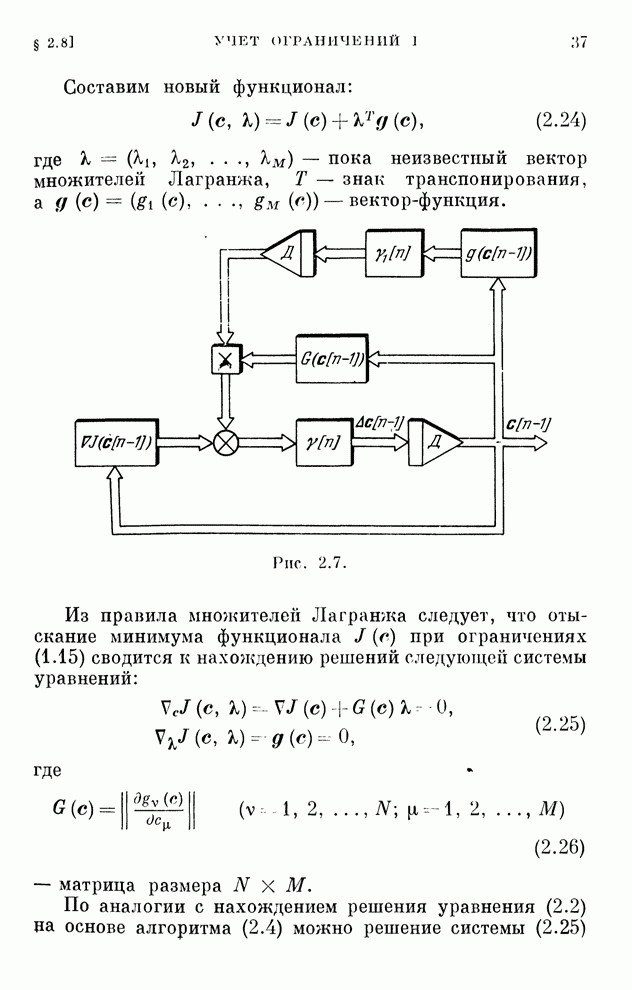
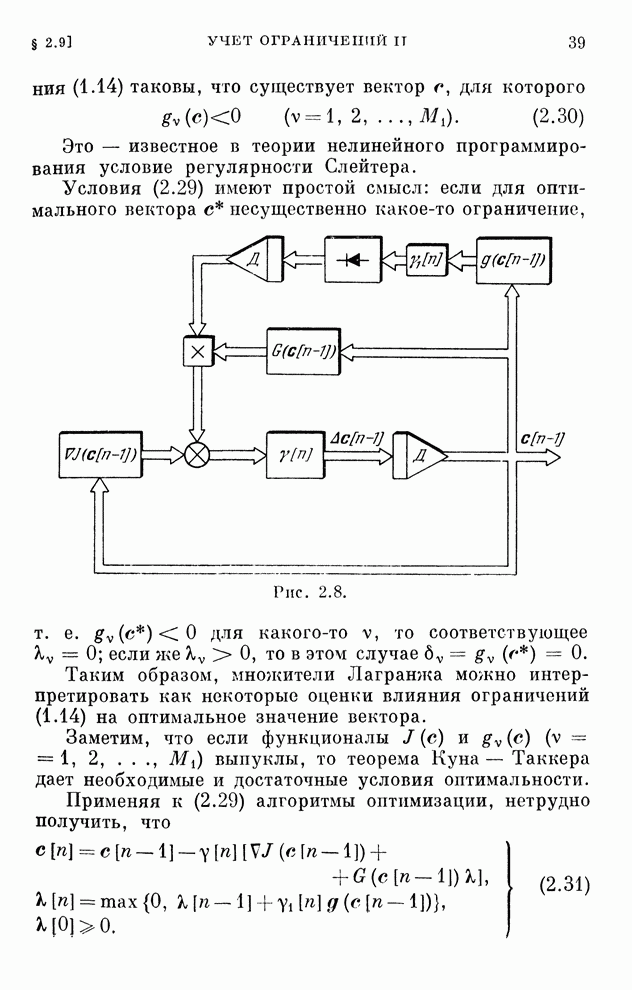
Поскольку каждому алгоритму оптимизации соответствует некоторая автономная система с обратной связью, то сходимость алгоритма, а значит и его реализуемость, эквивалентна устойчивости этой автономной системы.
Для исследования устойчивости можно использовать методы, довольно хорошо развитые в механике и теории автоматического управления.
Мы здесь схематически наметим некоторые возможности исследования устойчивости замкнутых дискретных систем особой структуры и, следовательно, сходимости алгоритмов оптимизации. Прежде всего воспользуемся подходом, аналогичным принятому в теории нелинейных систем, который можно трактовать как аналог метода Ляпунова для дискретных систем.
Составим уравнение в вариациях. Обозначим
![]() , (2.47)
, (2.47)
где ![]() — отклонение от оптимального вектора.
Подставляя это значение в рекуррентную форму алгоритма оптимизации (2.4),
легко получить
— отклонение от оптимального вектора.
Подставляя это значение в рекуррентную форму алгоритма оптимизации (2.4),
легко получить
![]() . (2.48)
. (2.48)
Это разностное уравнение имеет
тривиальное решение ![]() ,
так как для оптимального вектора
,
так как для оптимального вектора ![]() по определению
по определению ![]() . Устойчивость тривиального
решения уравнения (2.48) и соответствует сходимости алгоритма оптимизации
(2.4). Как известно, различают устойчивость в малом (когда все координаты
вектора
. Устойчивость тривиального
решения уравнения (2.48) и соответствует сходимости алгоритма оптимизации
(2.4). Как известно, различают устойчивость в малом (когда все координаты
вектора ![]() малы)
и в целом (при любых
малы)
и в целом (при любых ![]() ). Для исследования устойчивости в малом
нужно аппроксимировать
). Для исследования устойчивости в малом
нужно аппроксимировать ![]() линейным приближением и затем
рассмотреть устойчивость полученного линейного разностного уравнения. При
линейным приближением и затем
рассмотреть устойчивость полученного линейного разностного уравнения. При ![]() , т. е. в стационарном
случае, эта задача сводится к определению условий, при которых корни
соответствующего характеристического уравнения находятся внутри круга
единичного радиуса. Поскольку линейное приближение справедливо при достаточно
малых значениях
, т. е. в стационарном
случае, эта задача сводится к определению условий, при которых корни
соответствующего характеристического уравнения находятся внутри круга
единичного радиуса. Поскольку линейное приближение справедливо при достаточно
малых значениях ![]() ,
то устойчивость в малом соответствует сходимости алгоритмов оптимизации при
условии, что начальные значения векторов
,
то устойчивость в малом соответствует сходимости алгоритмов оптимизации при
условии, что начальные значения векторов ![]() принадлежат некоторой малой сфере с
неизвестным центром, что вряд ли полезно и интересно. Нас несоизмеримо больше
интересует устойчивость при любых начальных значениях
принадлежат некоторой малой сфере с
неизвестным центром, что вряд ли полезно и интересно. Нас несоизмеримо больше
интересует устойчивость при любых начальных значениях ![]() , т. е. устойчивость в целом.
Исследование этого типа устойчивости основано на применении аналога второго
метода Ляпунова.
, т. е. устойчивость в целом.
Исследование этого типа устойчивости основано на применении аналога второго
метода Ляпунова.
Выберем в качестве функции
Ляпунова норму вектора ![]() :
:
![]() . (2.49)
. (2.49)
Первая разность Ляпунова в силу уравнений (2.48) равна
![]() . (2.50)
. (2.50)
Условие устойчивости в целом требует, чтобы первая разность была отрицательна. После обычных и несложных преобразований получаем
![]() , (2.51)
, (2.51)
где ![]() — единичная матрица, а
— единичная матрица, а

![]() (2.52)
(2.52)
Фактически мы использовали здесь принцип сжатых отображений, который применительно к уравнению в вариациях, т. е. к случаю, когда неподвижная точка расположена в начале координат, тождествен прямому методу Ляпунова.
Принцип сжатых отображений может быть применен и непосредственно к алгоритму оптимизации в рекуррентной форме (2.4), для которого неподвижная точка соответствует значению оптимального вектора. Разумеется, при этом мы получим те же результаты, быть может, в несколько иной форме. Полученные таким образом условия являются, вообще говоря, лишь достаточными.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- Глава I. Проблема оптимальности
- § 1.1. Введение
- § 1.2. Критерии оптимальности
- § 1.3. Еще о критериях оптимальности
- § 1.4. Ограничения
- § 1.5. Априорная и текущая информация
- § 1.6. Детерминированные и стохастические процессы
- § 1.7. Обычный и адаптивный подходы
- § 1.8. О методах решения проблемы оптимальности
- § 1.9. Заключение
- Глава II. Алгоритмические методы оптимизации
- § 2.1. Введение
- § 2.2. Условия оптимальности
- § 2.3. Регулярный итеративный метод
- § 2.4. Алгоритмы оптимизации
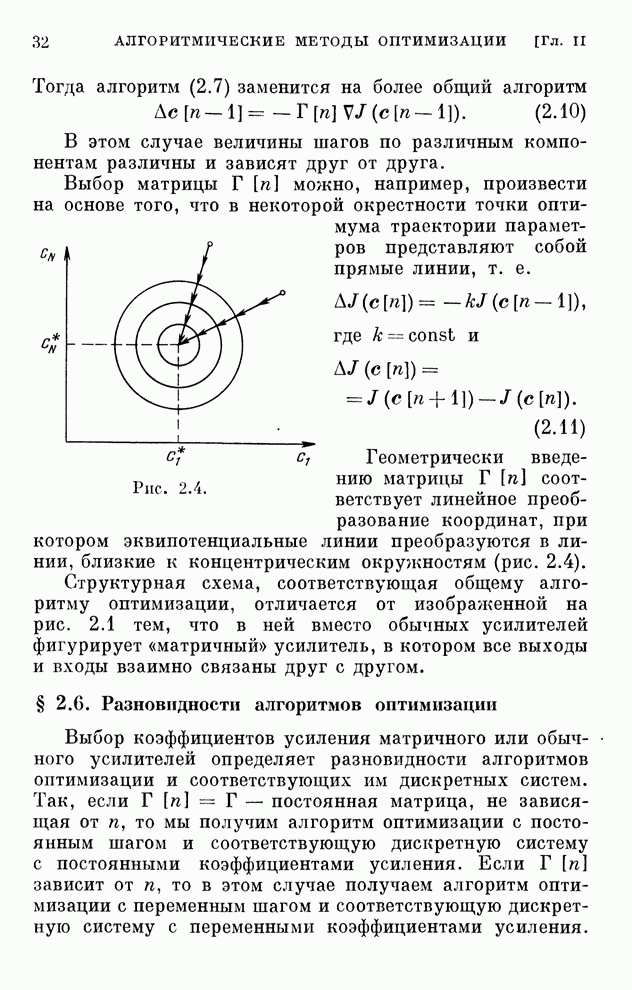
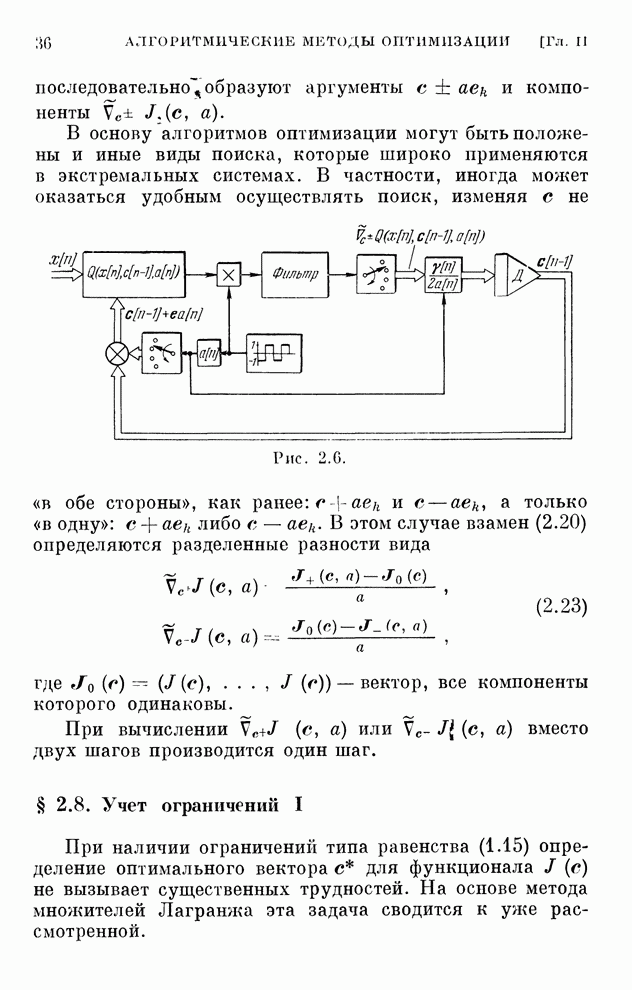
- § 2.5. Возможное обобщение
- § 2.6. Разновидности алгоритмов оптимизации
- § 2.7. Поисковые алгоритмы оптимизации
- § 2.8. Учет ограничений I
- § 2.9. Учет ограничений II
- § 2.10. Методы возможных направлений
- § 2.11. Обсуждение
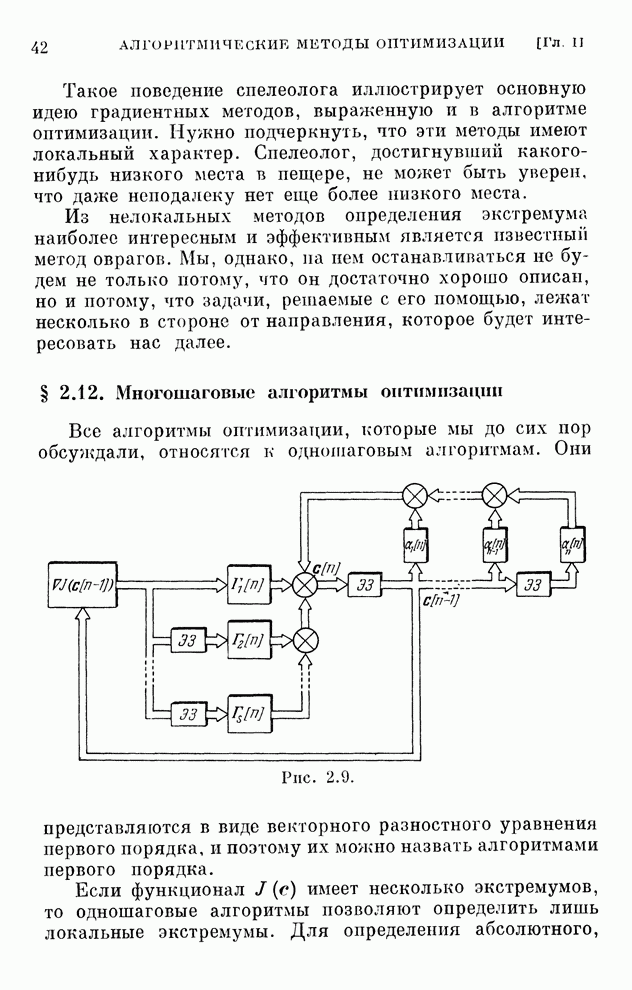
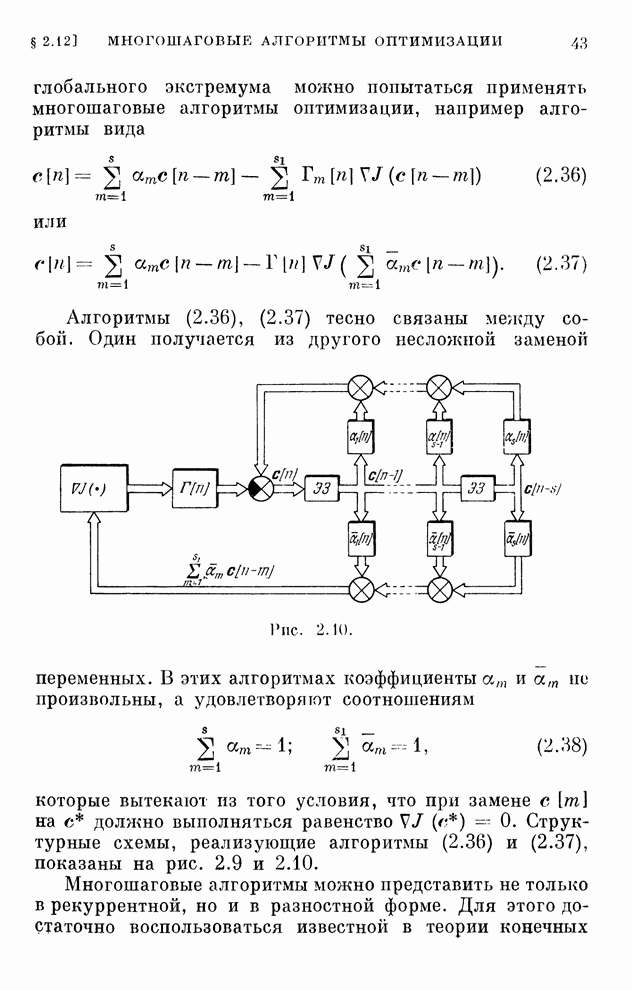
- § 2.12. Многошаговые алгоритмы оптимизации
- § 2.13. Непрерывные алгоритмы оптимизации
- § 2.14. Методы случайного поиска
- § 2.15. Сходимость и устойчивость
- § 2.16. Условия сходимости
- § 2.17. Об ускорении сходимости
- § 2.18. О наилучших алгоритмах
- § 2.19. Примеры
- § 2.20. Некоторые задачи
- § 2.21. Заключение
- Глава III. Адаптация и обучение
- § 3.1. Введение
- § 3.2. Понятия обучения, самообучения и адаптации
- § 3.3. Формулировка задачи
- § 3.4. Вероятностные итеративные методы
- § 3.5. Алгоритмы адаптации
- § 3.6. Поисковые алгоритмы адаптации
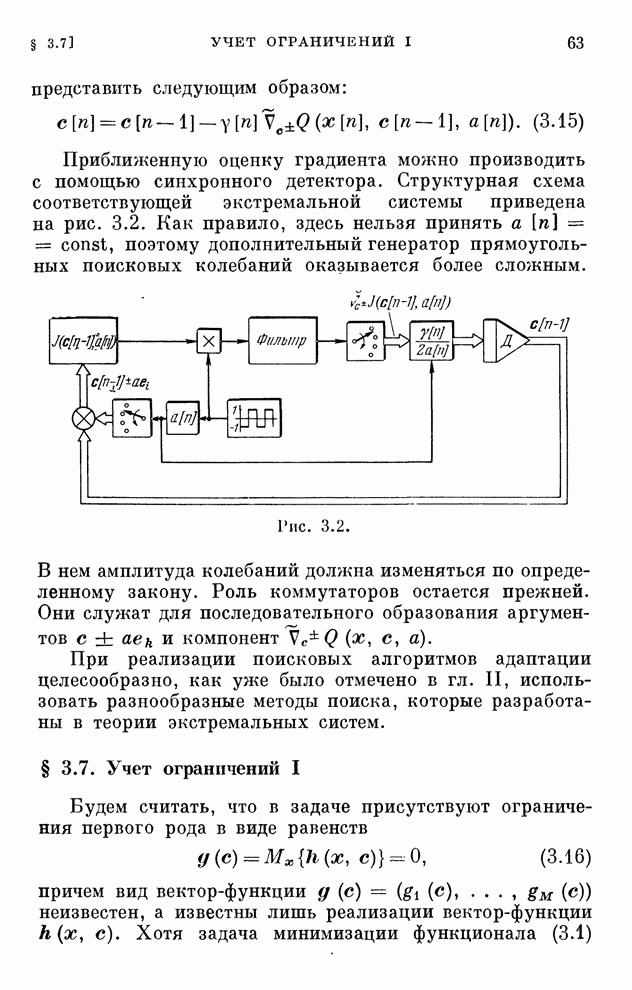
- § 3.7. Учет ограничений I
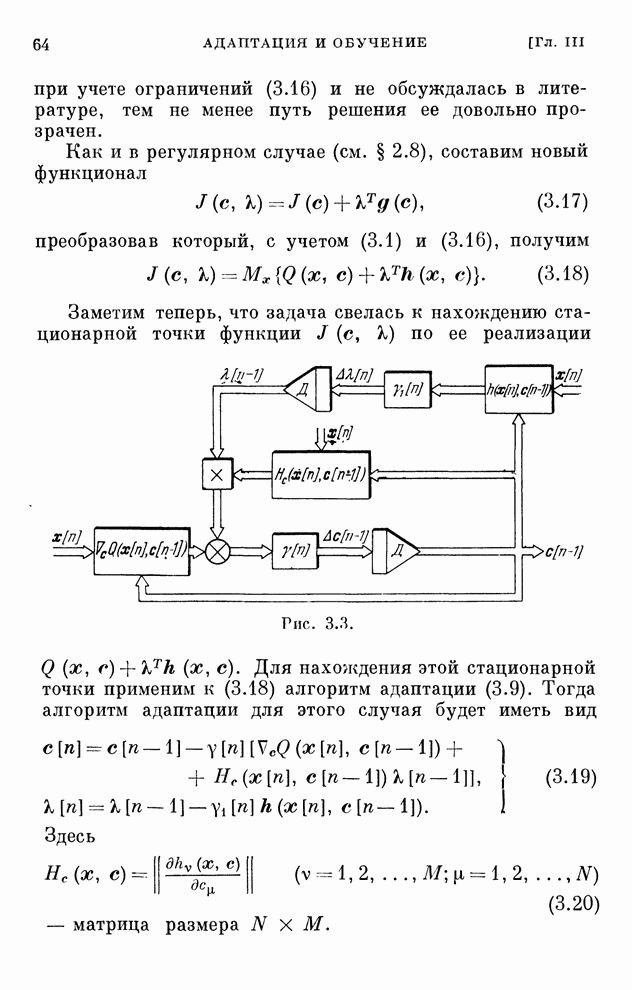
- § 3.8. Учет ограничений II
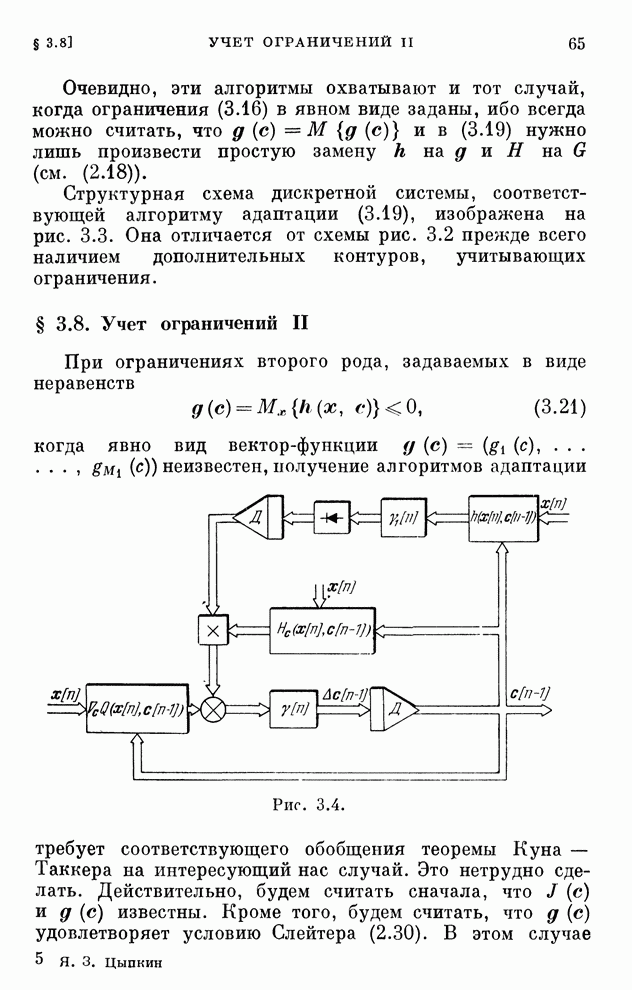
- § 3.9. Одно обобщение
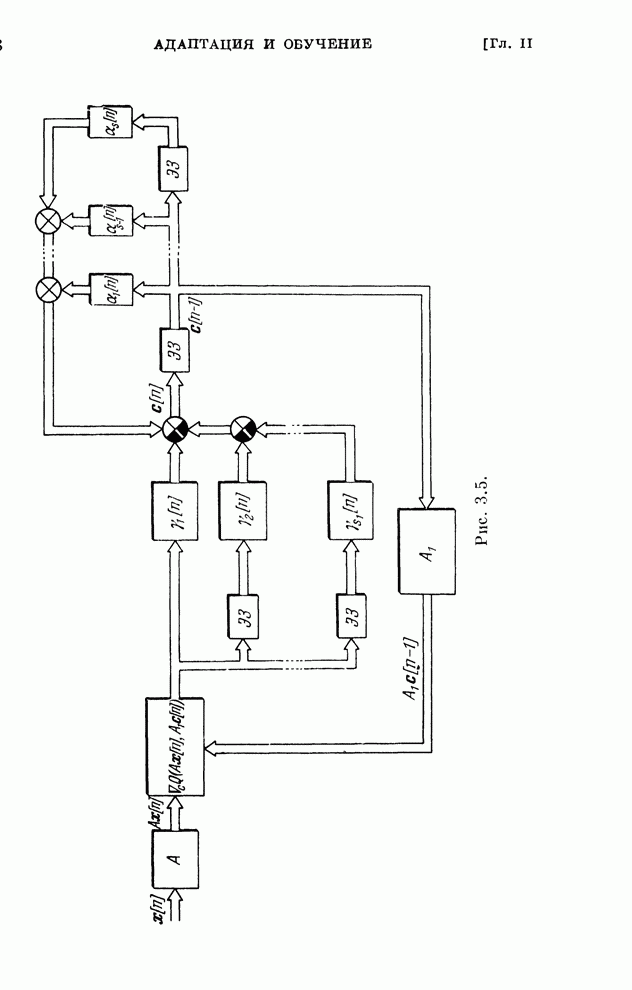
- § 3.10. Многошаговые алгоритмы адаптации
- § 3.11. Непрерывные алгоритмы
- § 3.12. Вероятностная сходимость и устойчивость
- § 3.13. Условия сходимости
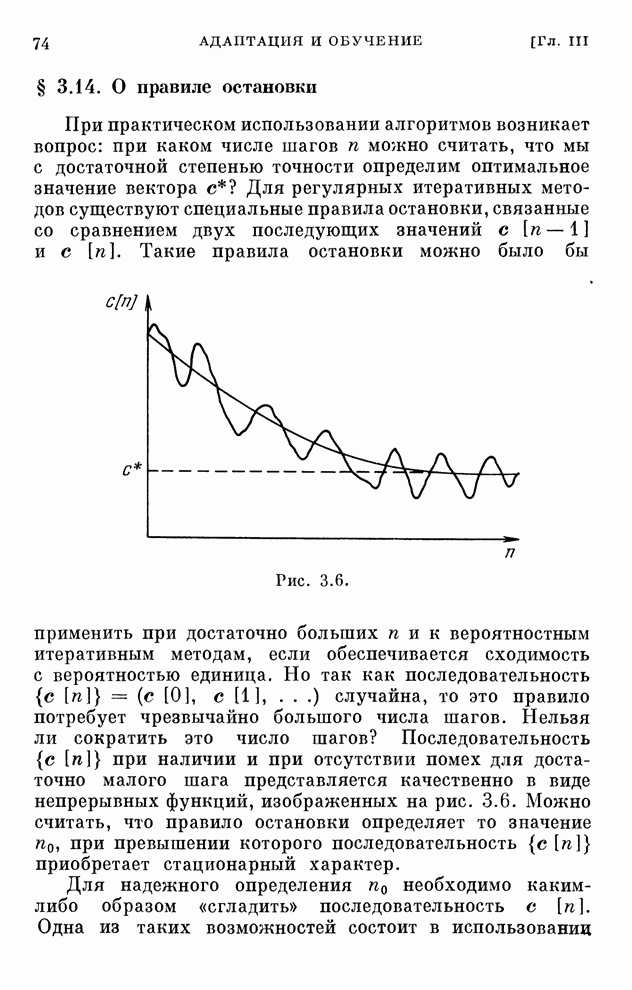
- § 3.14. О правиле остановки
- § 3.15. Об ускорении сходимости
- § 3.16. Мера качества алгоритмов
- § 3.17. Наилучшие алгоритмы
- § 3.18. Упрощенные наилучшие алгоритмы
- § 3.19. Частный случай
- § 3.20. Связь с методом наименьших квадратов
- § 3.21. Связь с байесовским методом
- § 3.22. Связь с методом максимального правдоподобия
- § 3.23. Обсуждение
- § 3.24. Некоторые задачи
- § 3.25. Заключение
- Глава IV. Опознавание
- § 4.1. Введение
- § 4.2. Обсуждение задачи опознавания
- § 4.3. Формулировка задачи
- § 4.4. Общие алгоритмы обучения
- § 4.5. Сходимость алгоритмов
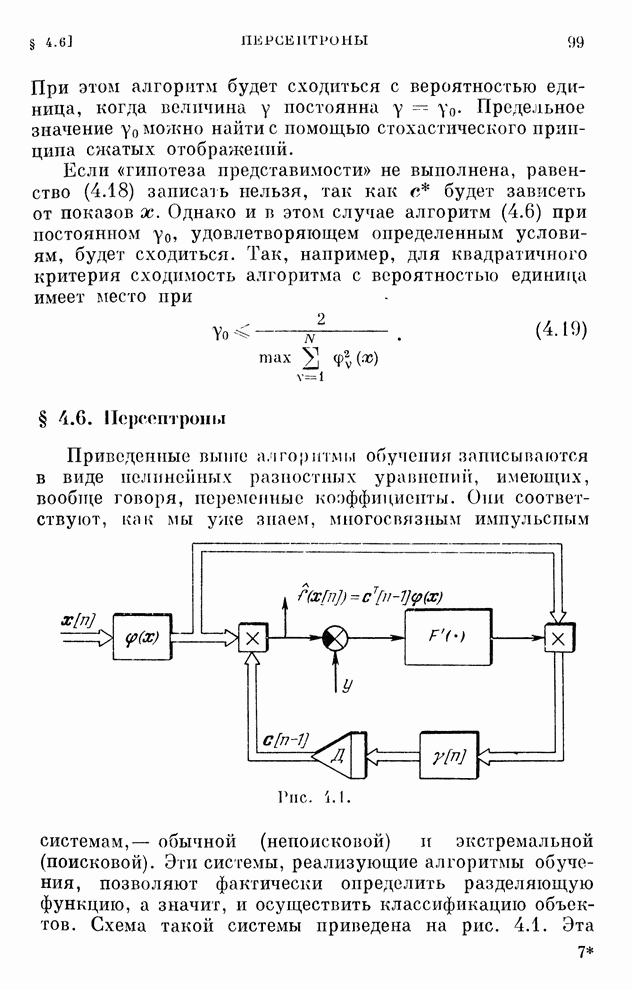
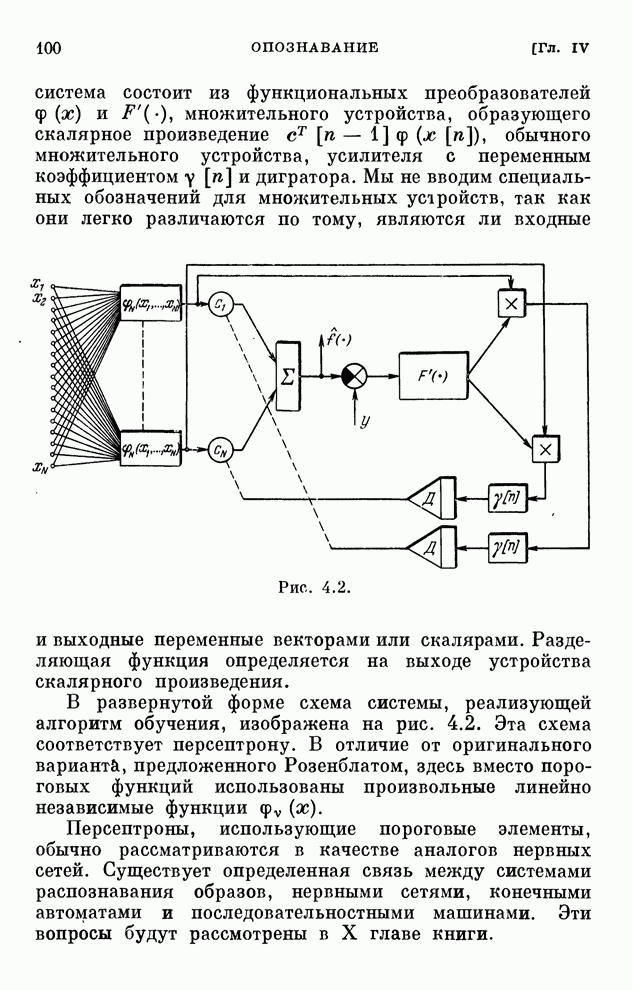
- § 4.6. Персептроны
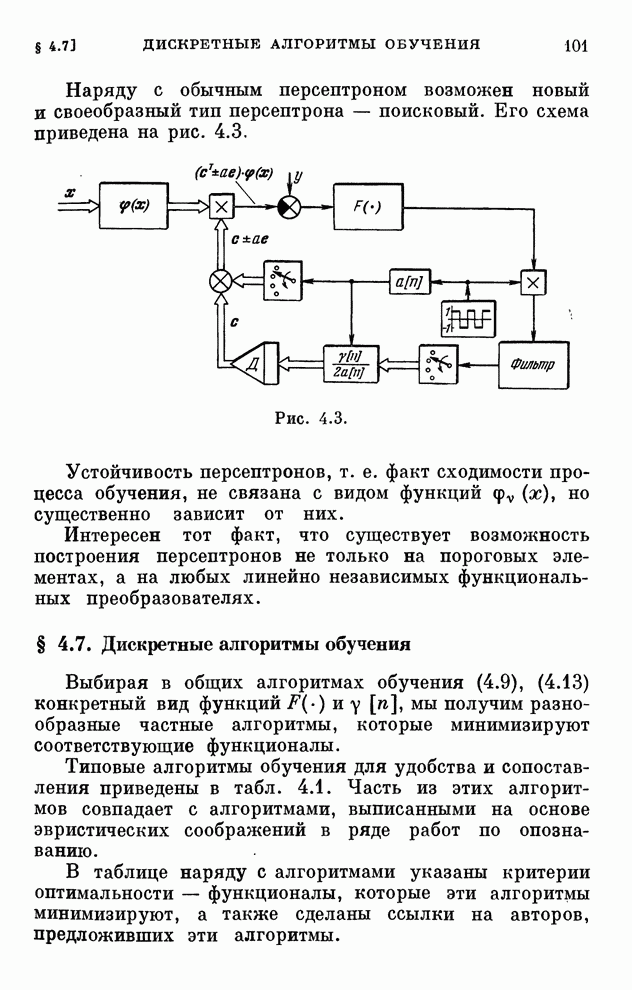
- § 4.7. Дискретные алгоритмы обучения
- § 4.8. Поисковые алгоритмы обучения
- § 4.9. Непрерывные алгоритмы обучения
- § 4.10. Замечания
- § 4.11. Еще об одном общем алгоритме обучения
- § 4.12. Частные случаи
- § 4.13. Обсуждение
- § 4.14. О самообучении
- § 4.15. О восстановлении плотности распределения и моментов
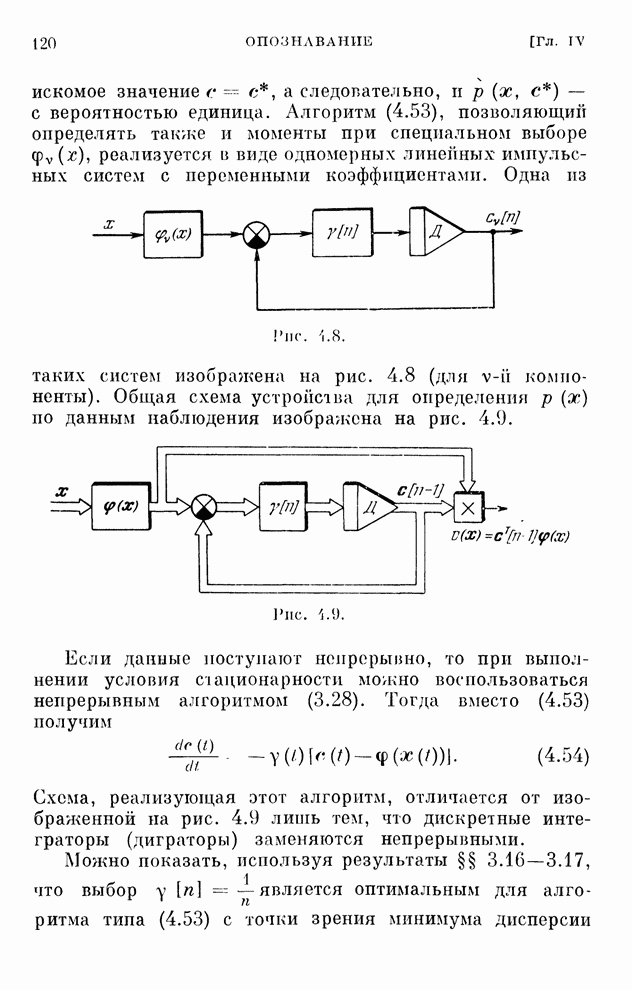
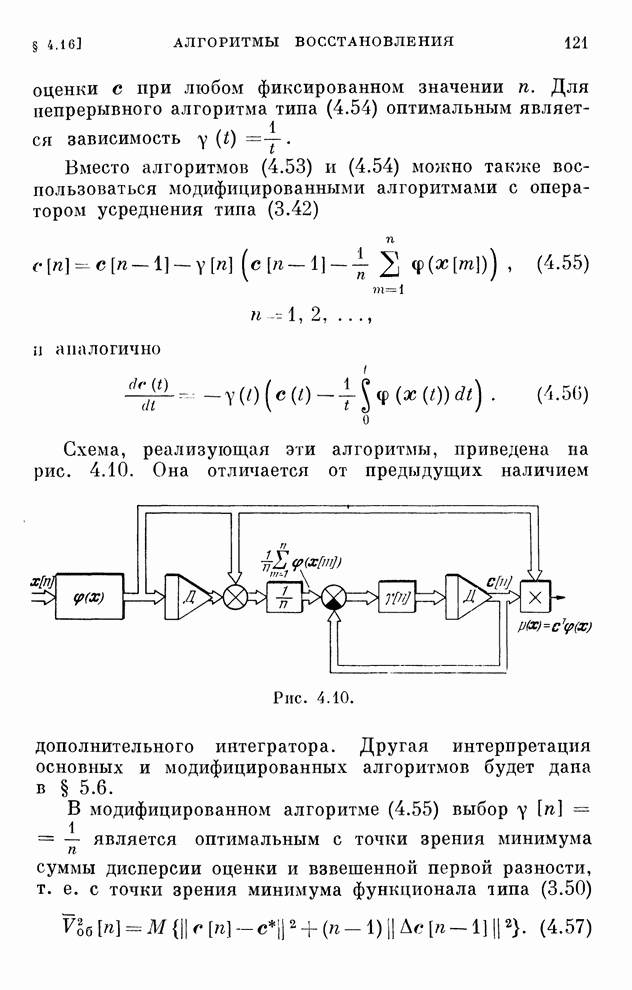
- § 4.10. Алгоритмы восстановления
- § 4.17. Принципы самообучения
- § 4.18. Средний риск
- § 4.19. Вариация среднего риска
- § 4.20. Условия минимума среднего риска
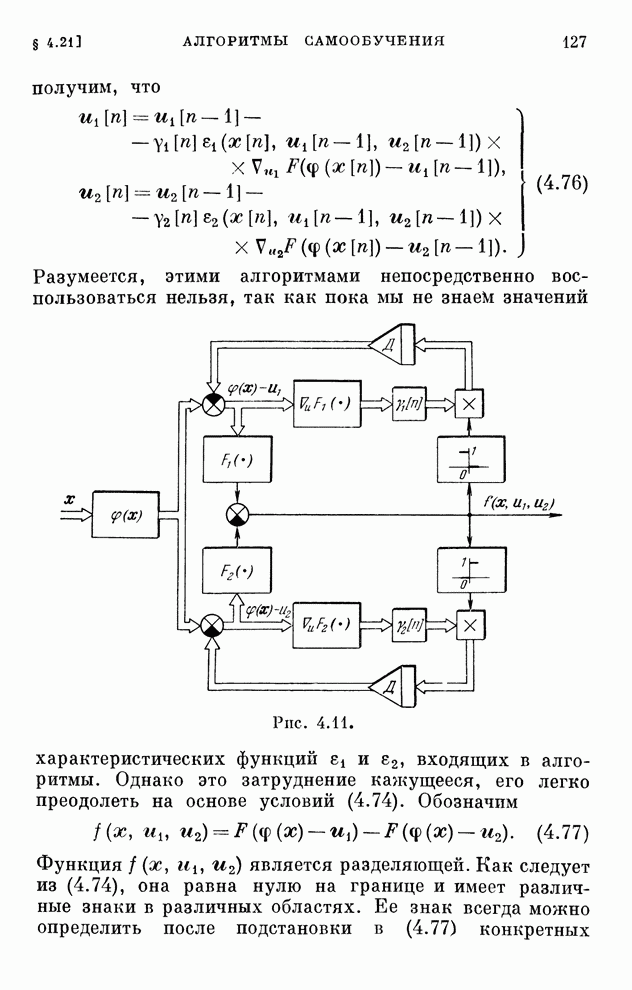
- § 4.21. Алгоритмы самообучения
- § 4.22. Обобщение
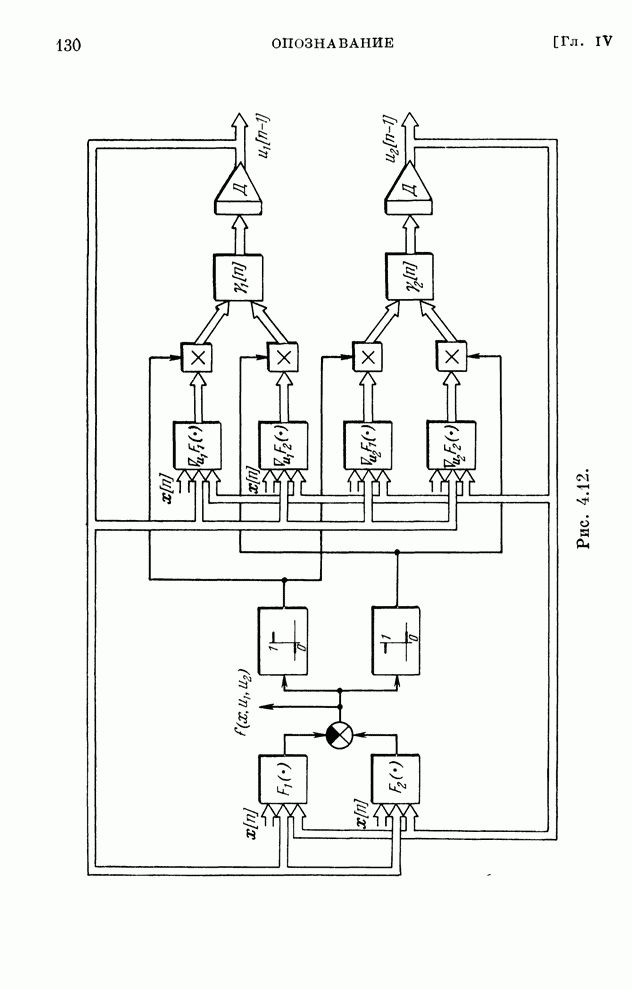
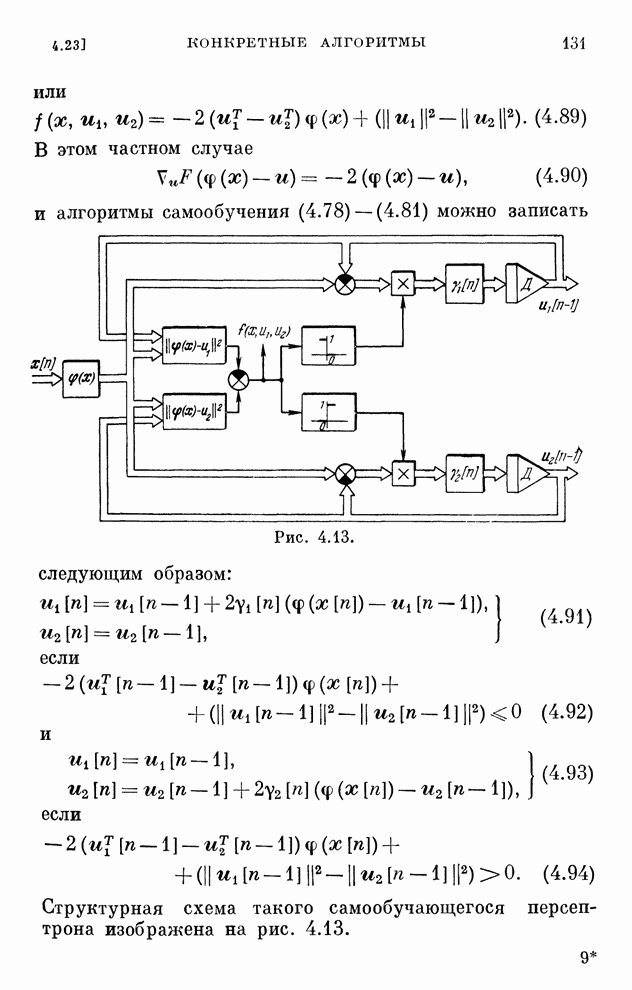
- § 4.23. Конкретные алгоритмы
- § 4.24. Поисковые алгоритмы самообучения
- § 4.25. Обсуждение
- § 4.26. Некоторые задачи
- § 4.27. Заключение
- Глава V. Идентификация
- § 5.1. Введение
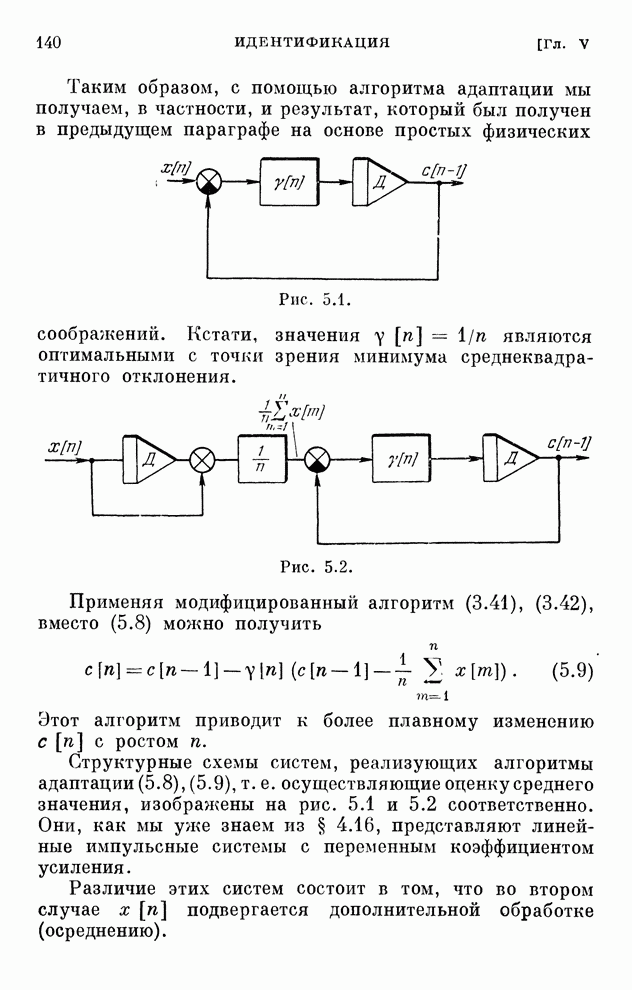
- § 5.2. Оценка среднего значения
- § 5.3. Другой подход
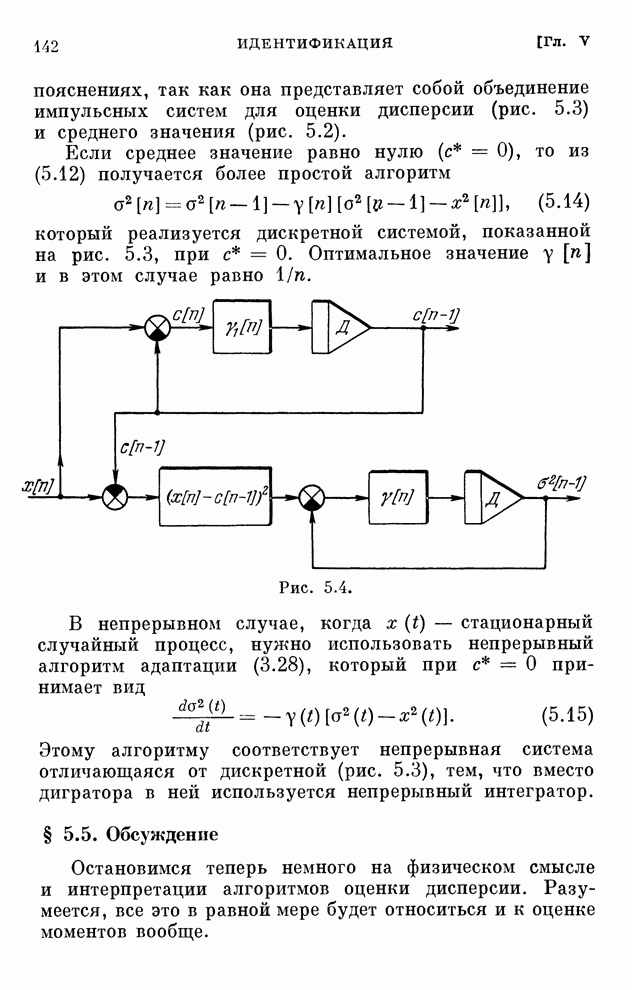
- § 5.4. Оценка дисперсии
- § 5.5. Обсуждение
- § 5.6. Оценка корреляционных функций
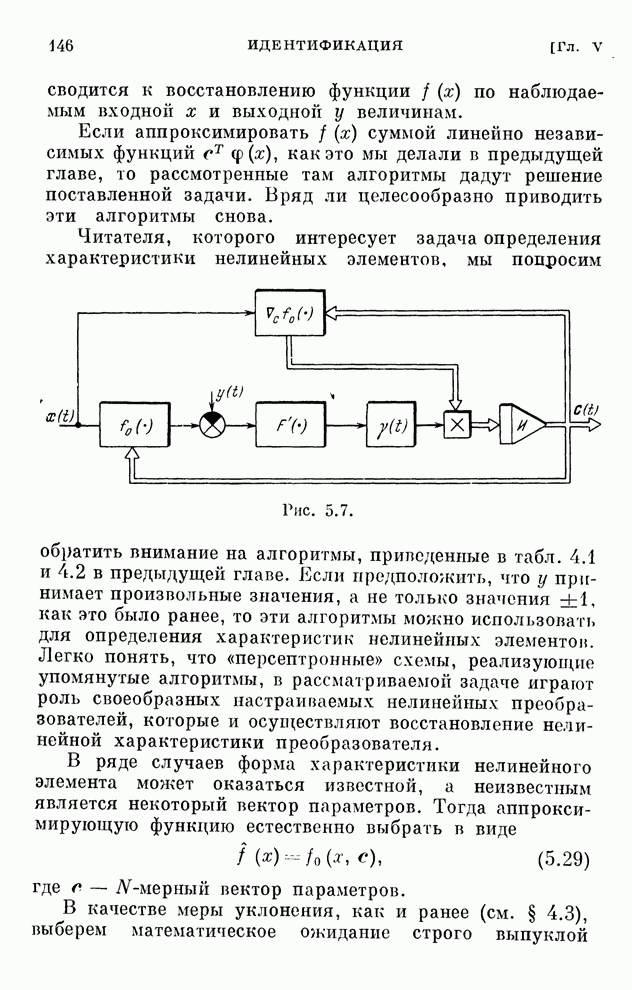
- § 5.7. Определение характеристик нелинейных элементов
- § 5.8. Оценка коэффициента статистической линеаризации
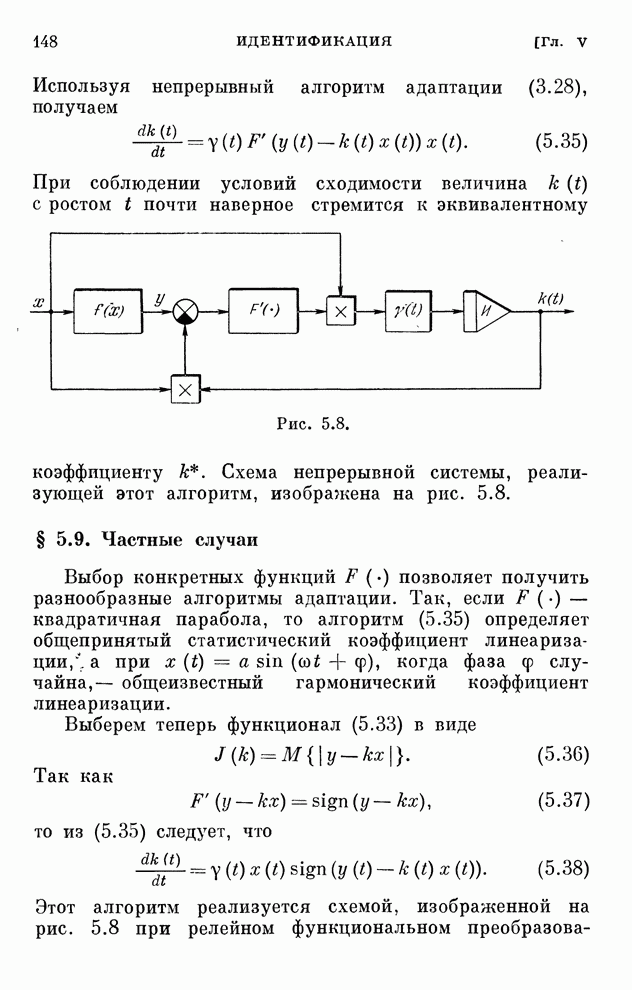
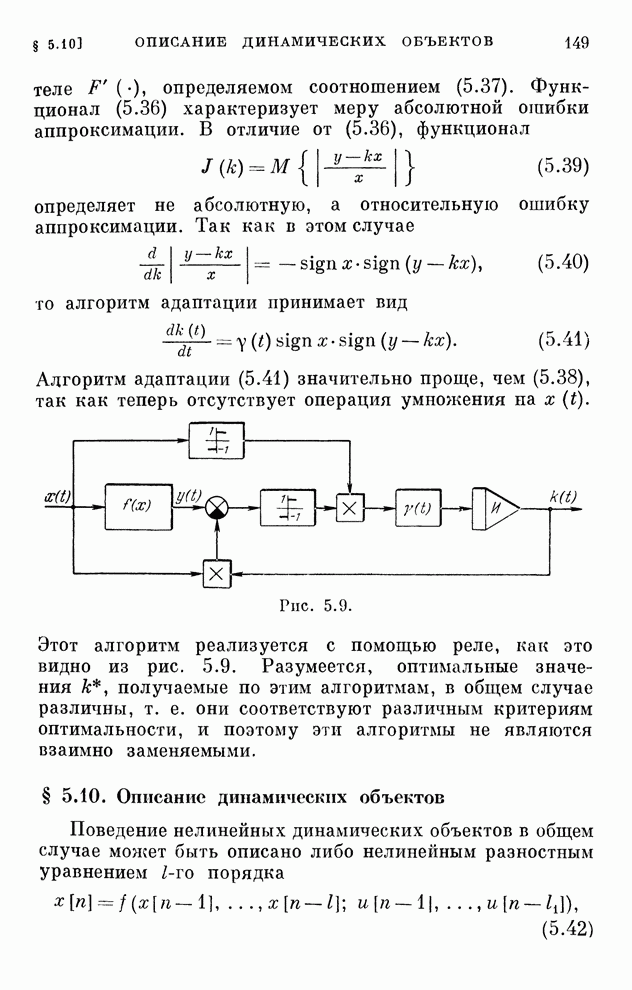
- § 5.9. Частные случаи
- § 5.10. Описание динамических объектов
- § 5.11. Идентификация нелинейных объектов I
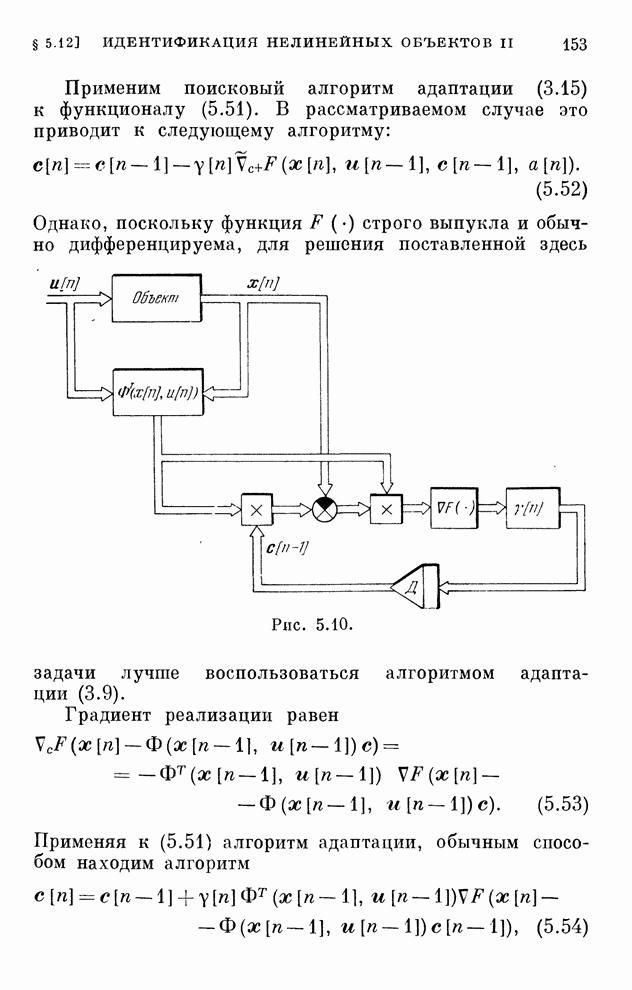
- § 5.12. Идентификация нелинейных объектов II
- § 5.13. Идентификация нелинейных объектов III
- § 5.14. Специальный случай
- § 5.15. Замечание
- § 5.16. Идентификация линейных объектов I
- § 5.17. Идентификация линейных объектов II
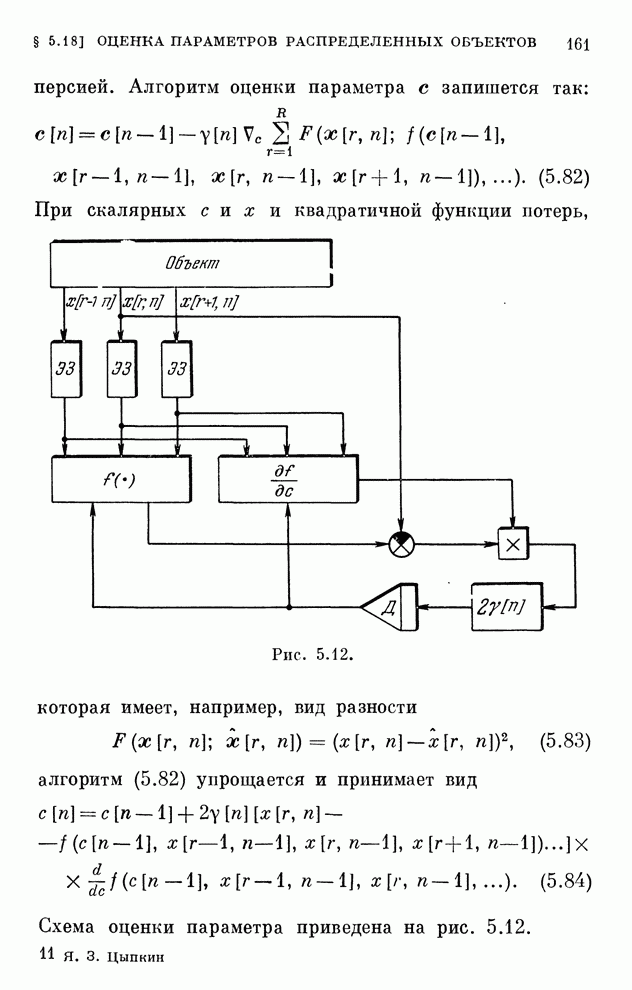
- § 5.18. Оценка параметров распределенных объектов
- § 5.19. Помехи
- § 5.20. Устранение влияния помех
- § 5.21. Некоторые задачи
- § 5.22. Заключение
- Глава VI. Фильтрация
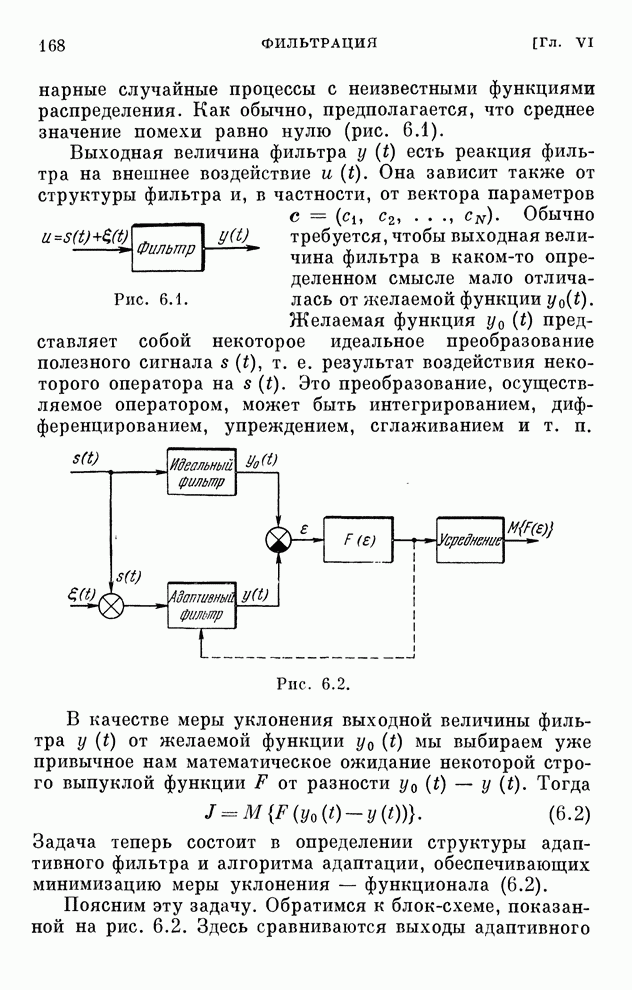
- § 6.1. Введение
- § 6.2. Критерий оптимальности
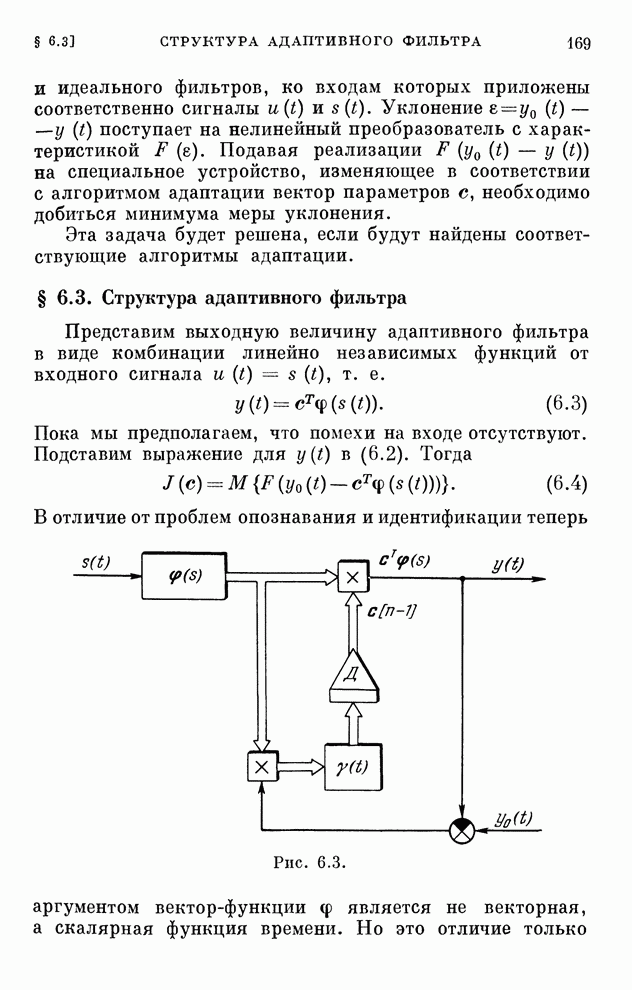
- § 6.3. Структура адаптивного фильтра
- § 6.4. Частные случаи
- § 6.5. Адаптивный корректор искажений
- § 6.6. Поисковые адаптивные фильтры
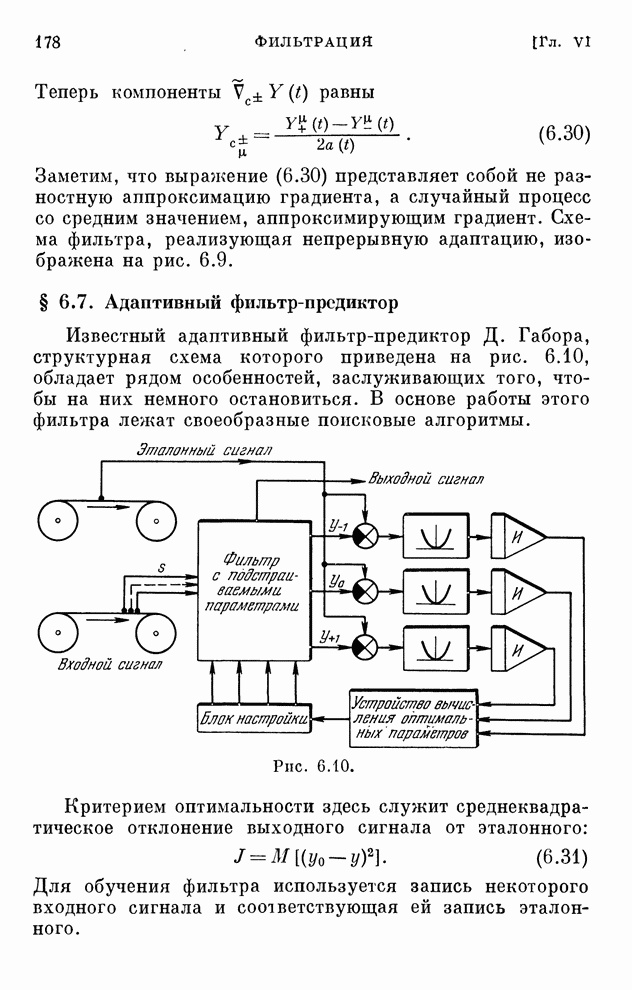
- § 6.7. Адаптивный фильтр-предиктор
- § 6.9. Статистическая теория приема
- § 6.10. Критерий оптимальности приема
- § 6.11. Определение решающего правила
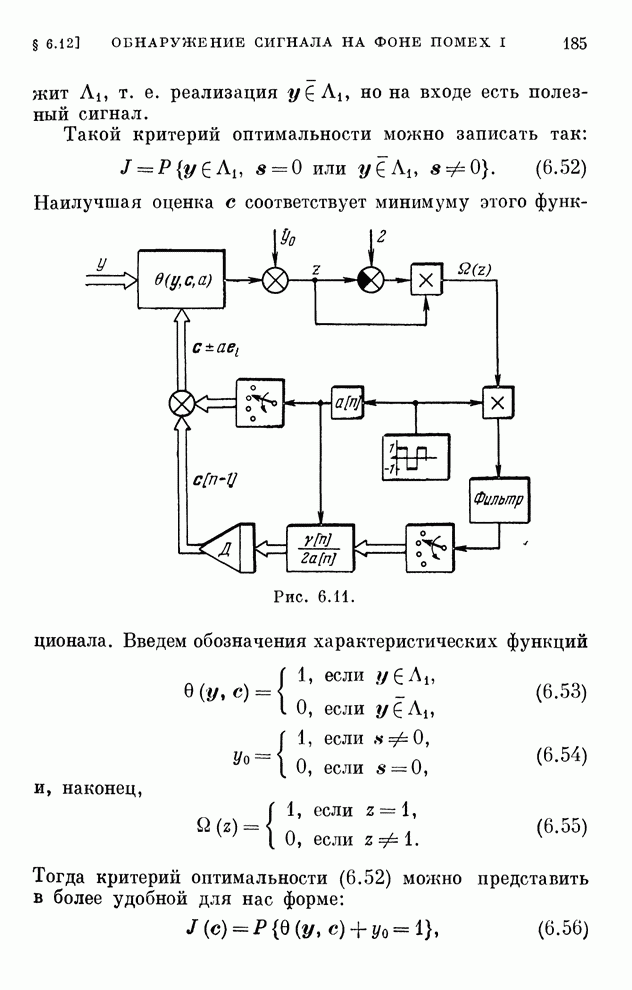
- § 6.12. Обнаружение сигнала на фоне помех I
- § 6.13. Обнаружение сигнала на фоне помех II
- § 6.14. Выделение сигнала на фоне помех
- § 6.15. Критерий оптимального выделения
- § 6.16. Алгоритм выделения
- § 6.17. Еще о выделении сигнала на фоне помех
- § 6.18. Другой критерий оптимальности
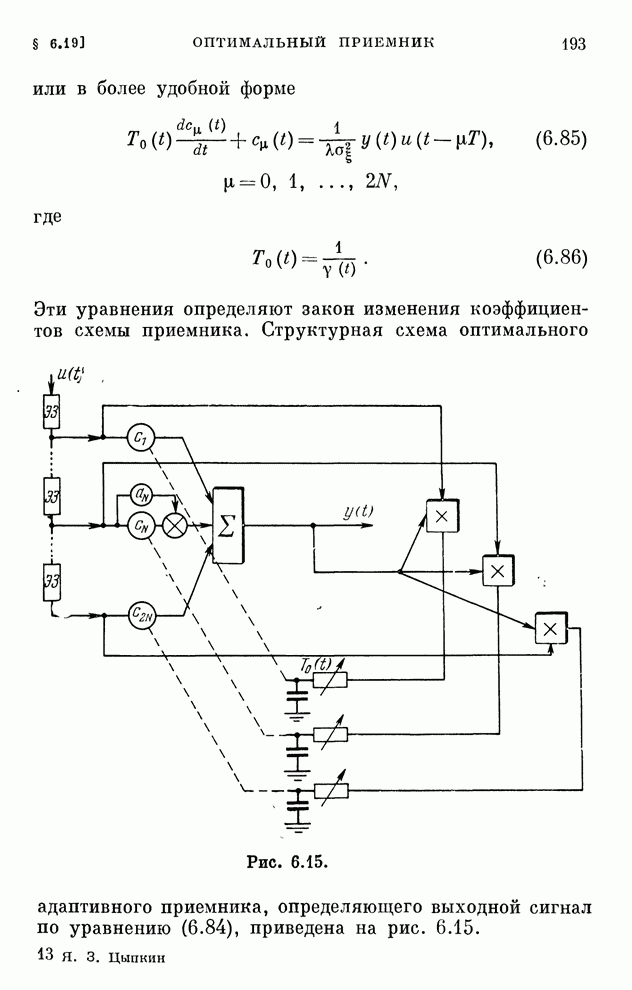
- § 6.19. Оптимальный приемник
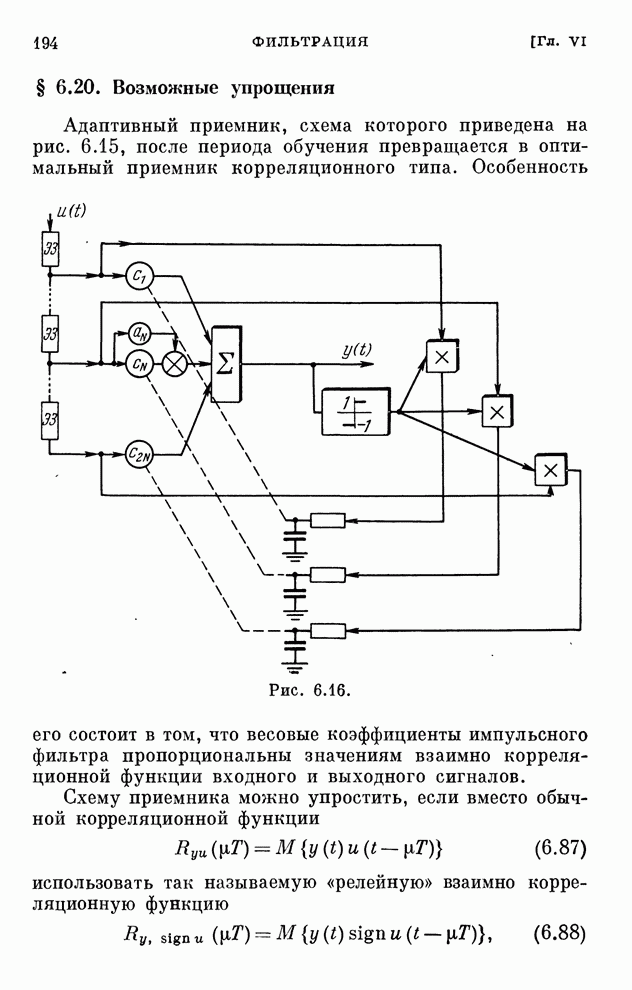
- § 6.20. Возможные упрощения
- § 6.21. Восстановление входных сигналов
- § 6.22. Алгоритмы восстановления
- § 6.23. О влиянии помех
- § 6.24. Некоторые задачи
- § 6.25. Заключение
- Глава VII. Управление
- § 7.1. Введение
- § 7.2. Когда нужна адаптация?
- § 7.3. Постановка задачи
- § 7.4. Дуальное управление
- § 7.5. Алгоритмы дуального управления
- § 7.6. Адаптивные системы управления I
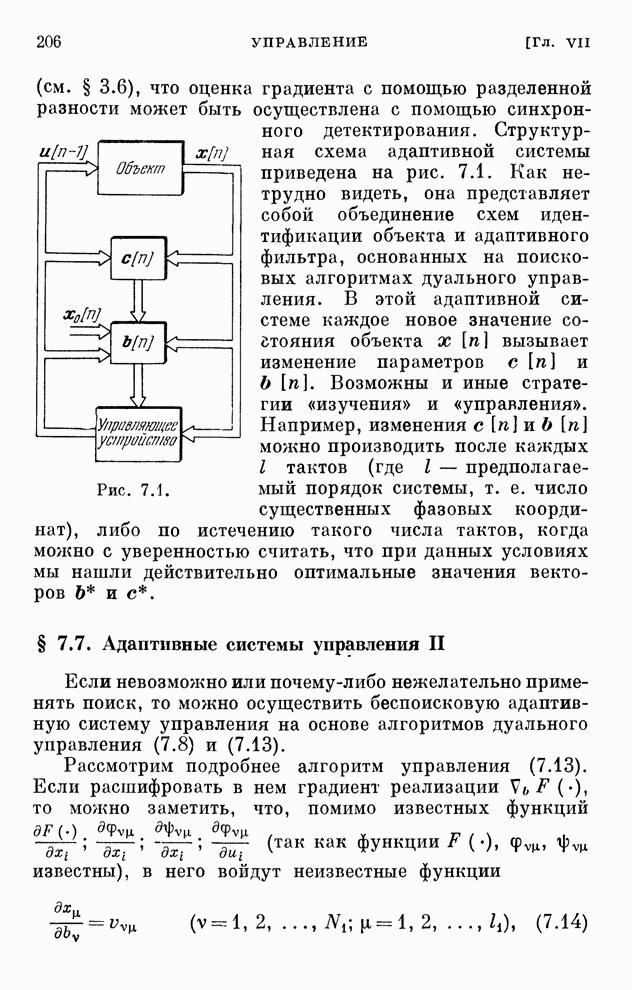
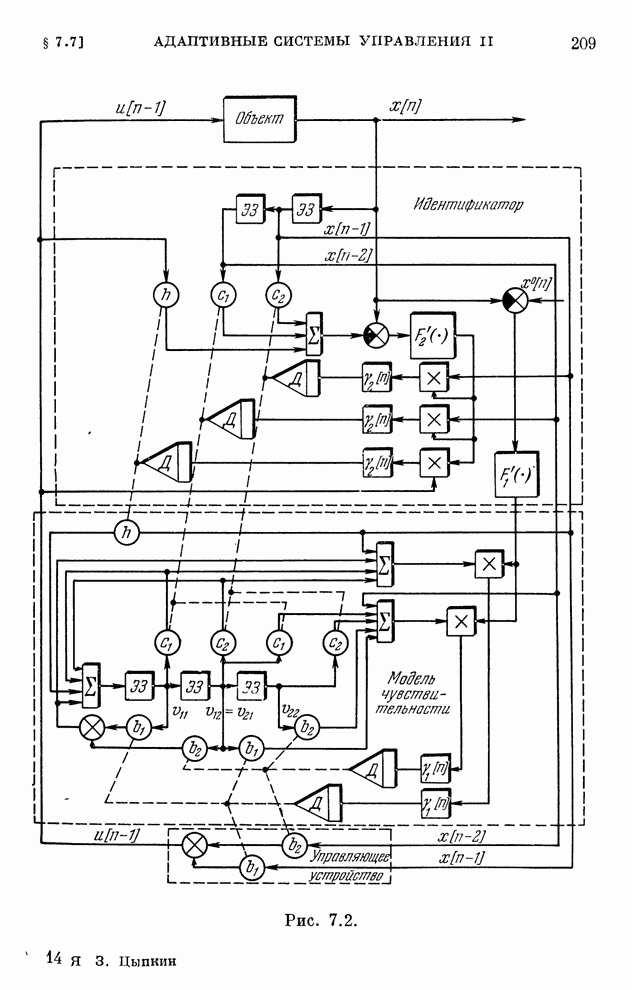
- § 7.7. Адаптивные системы управления II
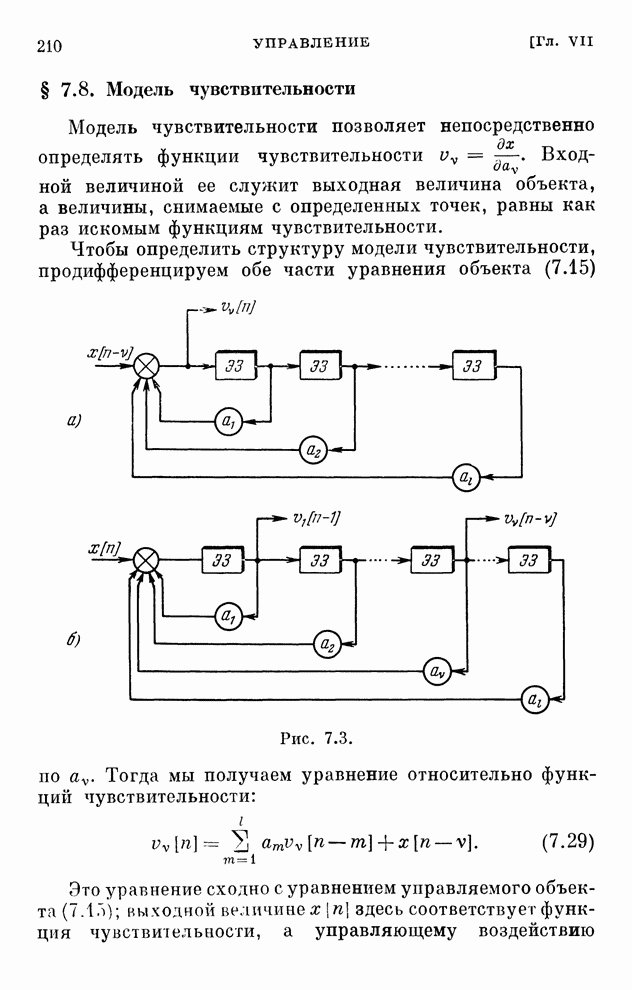
- § 7.8. Модель чувствительности
- § 7.9. Адаптивные системы управления III
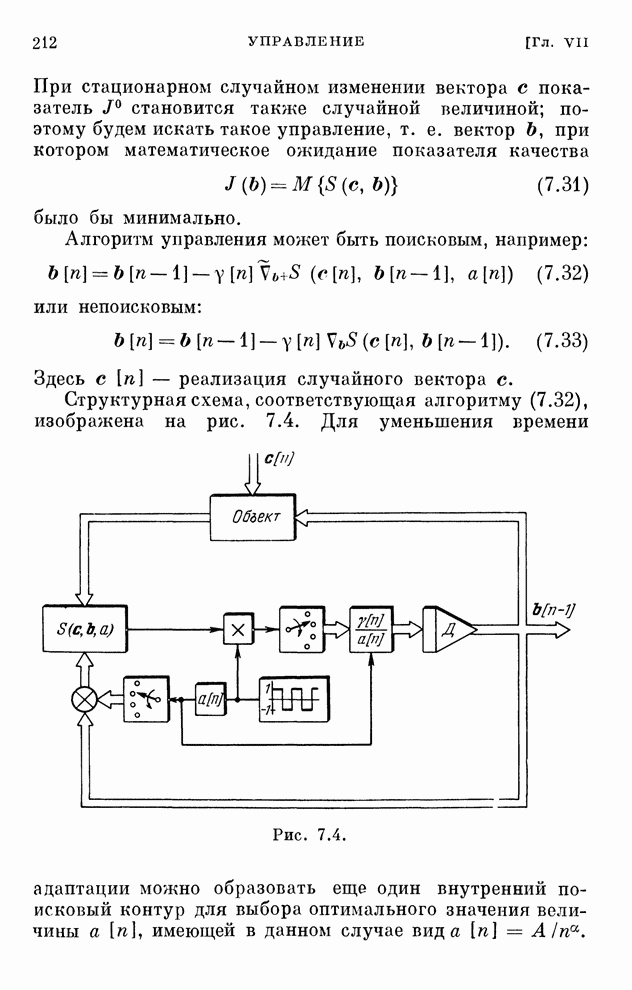
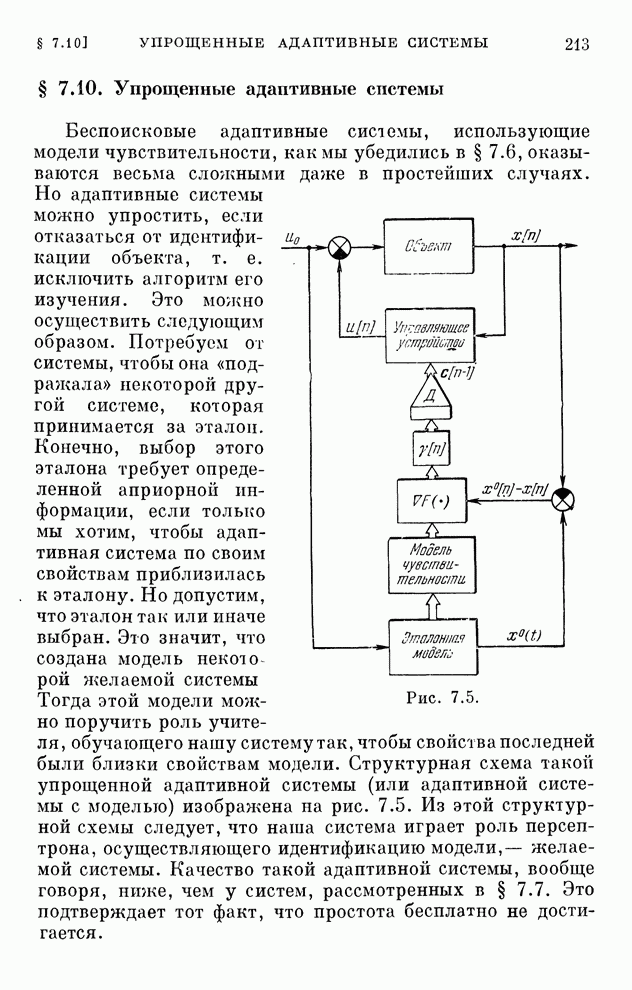
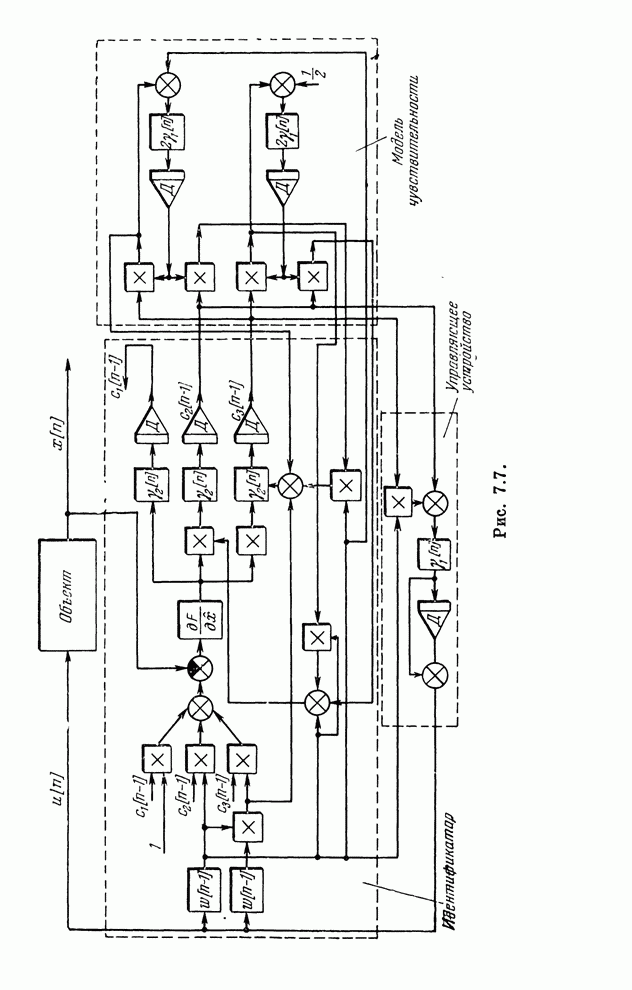
- § 7.10. Упрощенные адаптивные системы
- § 7.11. Системы управления по возмущению
- § 7.12. Алгоритмы оптимального управления
- § 7.13. Еще одна возможность
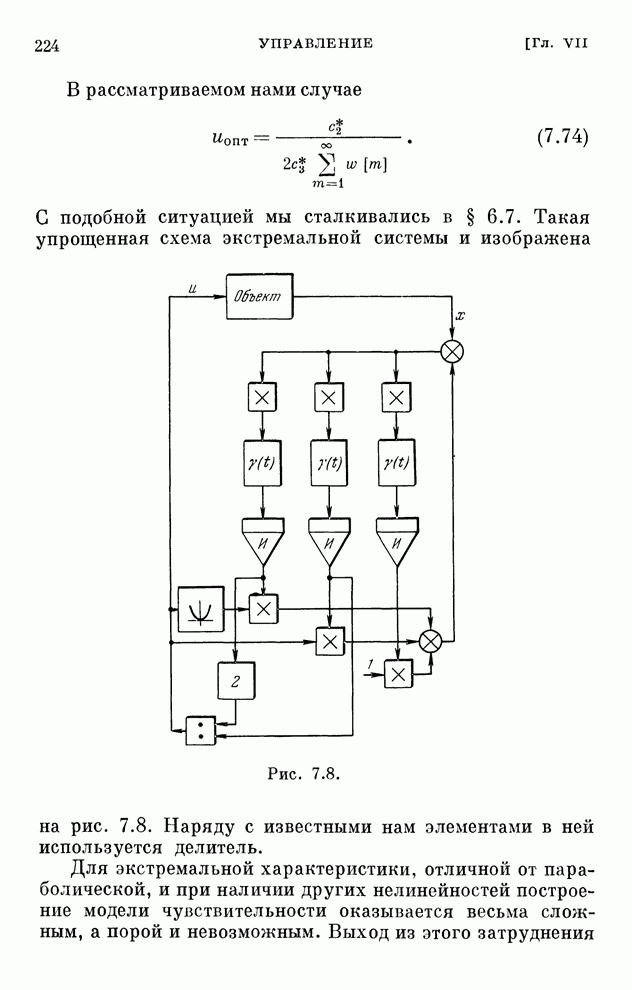
- § 7.14. Экстремальные системы управления
- § 7.15. Алгоритмы экстремального управления
- § 7.16. Алгоритмы изучения
- § 7.17. Непрерывные алгоритмы
- § 7.18. Структурная схема
- § 7.19. Возможные упрощения
- § 7.20. О синтезе оптимальных систем
- § 7.21. Применение алгоритмов адаптации
- § 7.22. О синтезе оптимальных систем при наличии помех
- § 7.23. Управление и опознавание
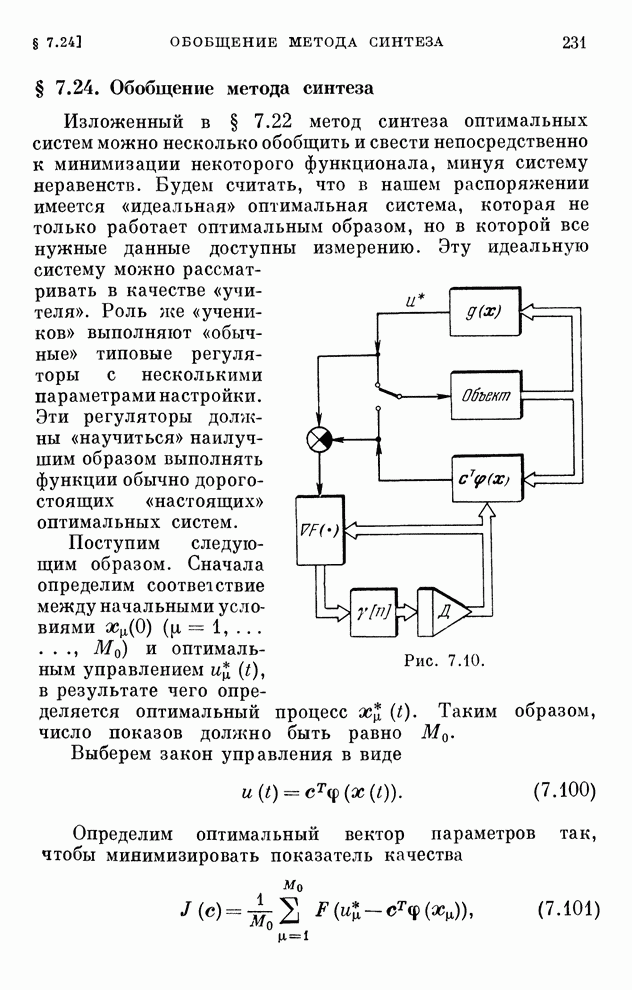
- § 7.24. Обобщение метода синтеза
- § 7.25. Некоторые задачи
- § 7.26. Заключение
- Глава VIII. Надежность
- § 8.1. Введение
- § 8.2. Понятие надежности
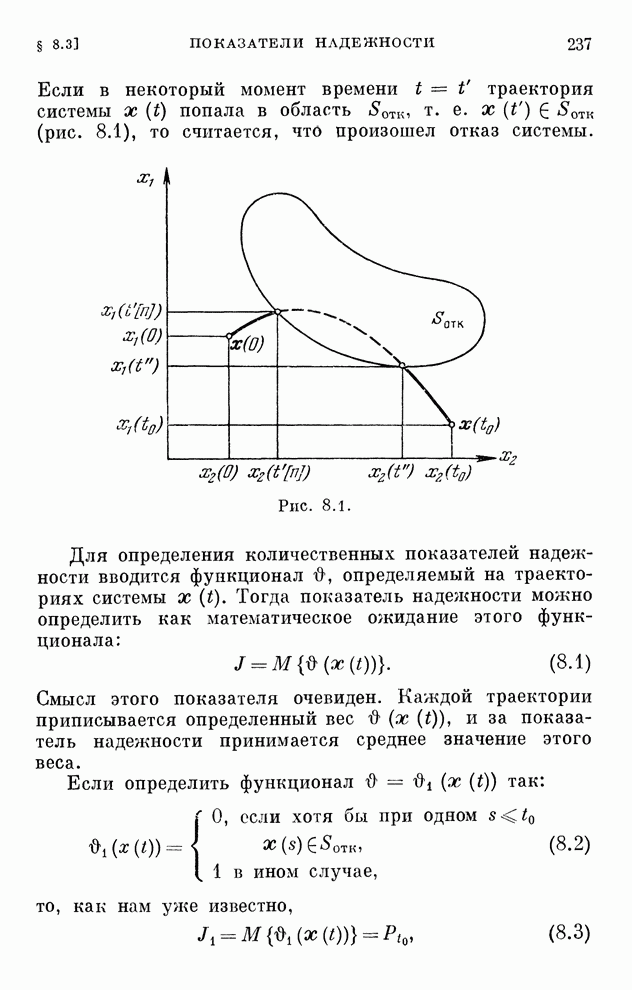
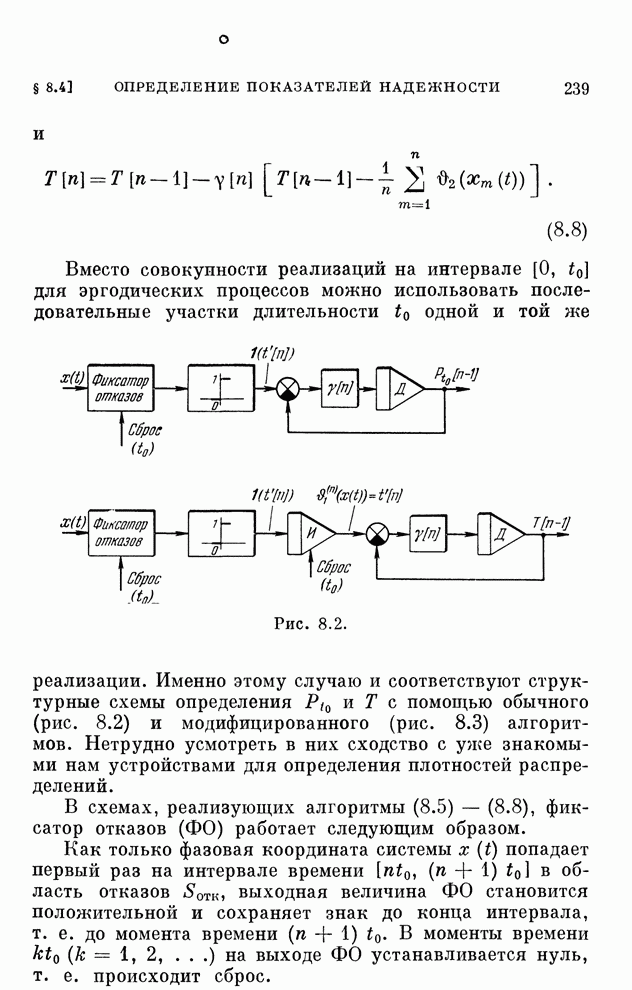
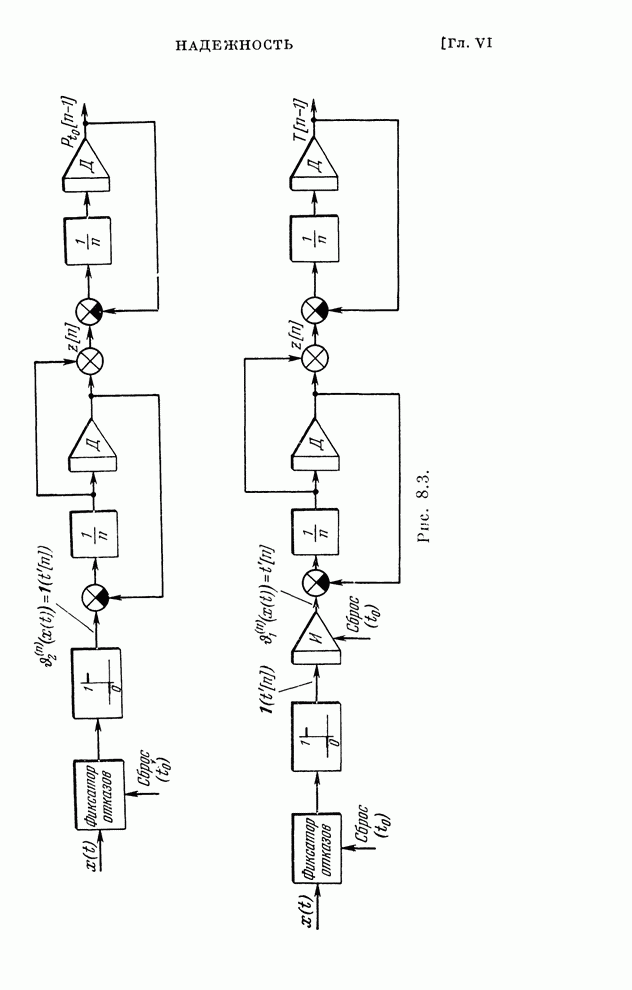
- § 8.4. Определение показателей надежности
- § 8.5. Минимизация эксплуатационных расходов
- § 8.6. Частный случай
- § 8.7. Минимизация стоимости, веса, объема
- § 8.8. Алгоритмы минимизации
- § 8.9. Особый случай
- § 8.10. Алгоритмы
- § 8.11. Повышение надежности путем резервирования
- § 8.12. Повышение надежности путем избыточности
- § 8.13. Проектирование сложных систем
- § 8.14. Алгоритмы оптимальной работоспособности
- § 8.15. О минимаксном критерии оптимизации
- § 8.16. Еще о проектировании сложных систем
- § 8.17. Замечание
- § 8.18. Некоторые задачи
- § 8.19. Заключение
- Глава IX. Исследование операций
- § 9.1. Введение
- § 9.2. Планирование запасов
- § 9.3. Критерий оптимальности планирования
- § 9.4. Алгоритмы оптимального планировании
- § 9.5. Еще о планировании запасов
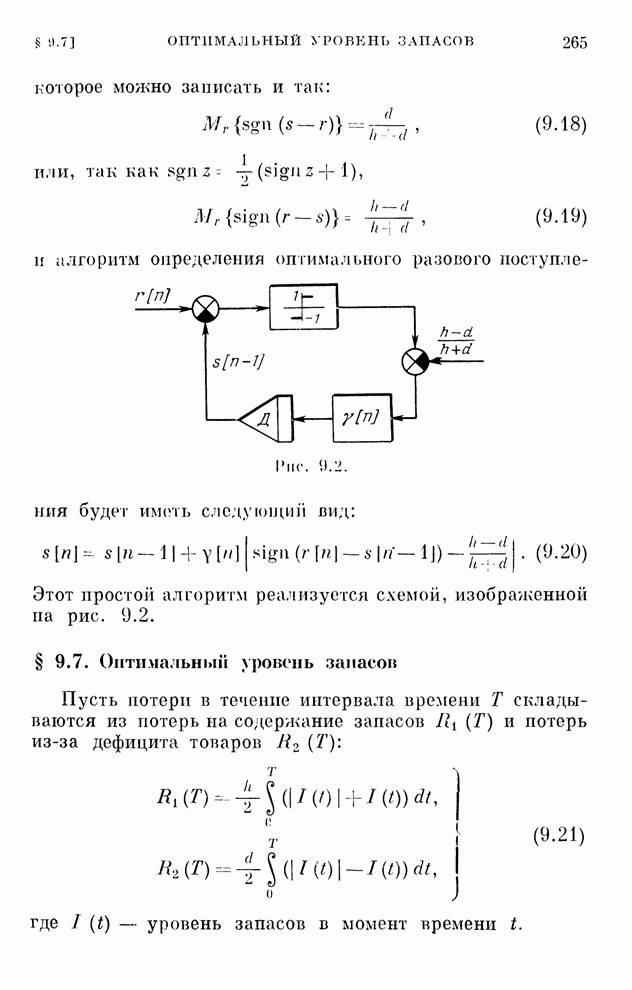
- § 9.6. Оптимальное разовое поступление
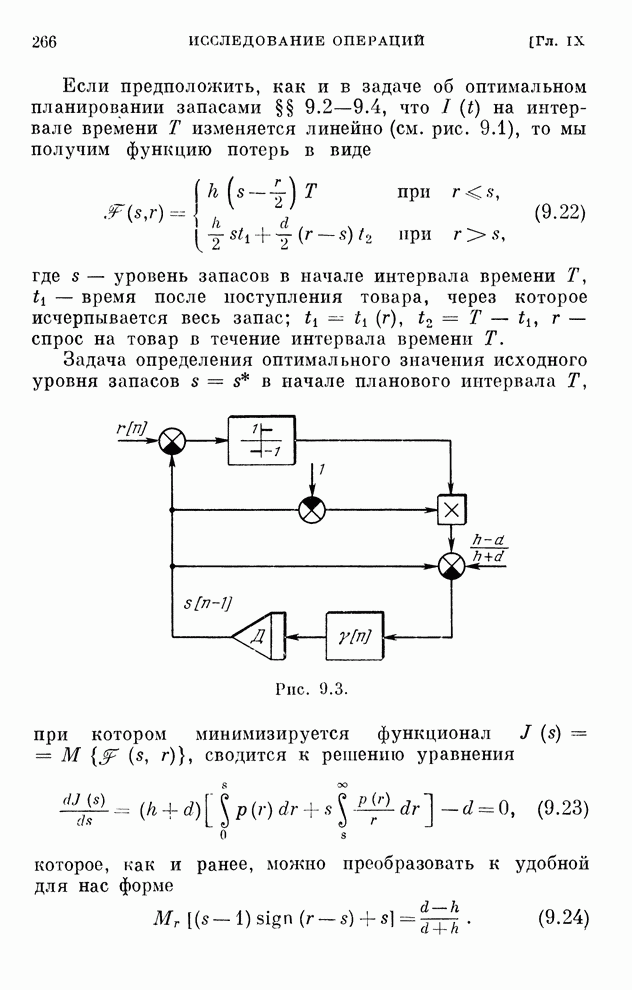
- § 9.7. Оптимальный уровень запасов
- § 9.8. Замечание
- § 9.9. Распределение производственных мощностей
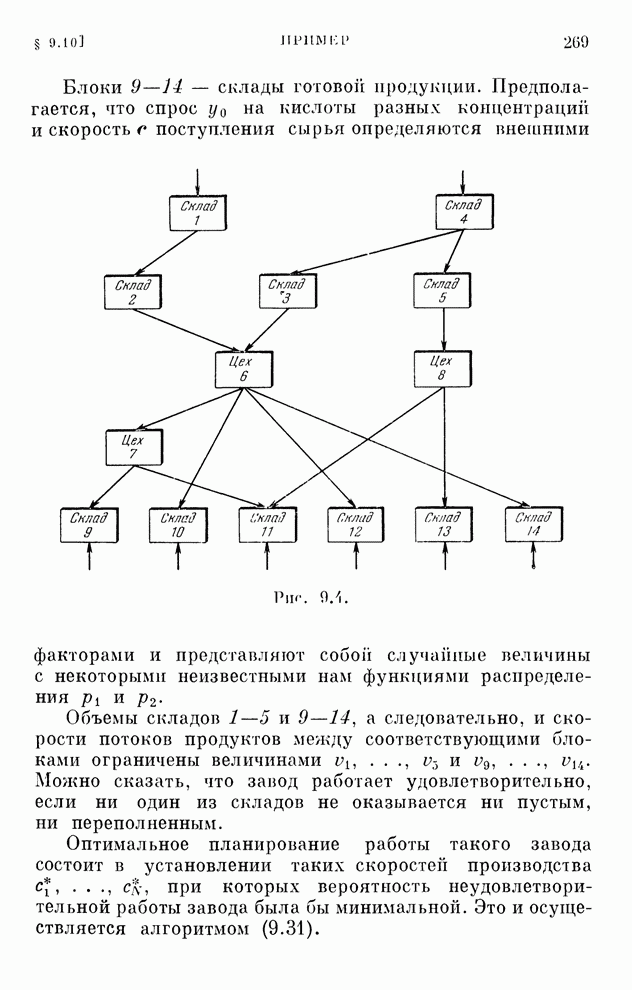
- § 9.10. Пример
- § 9.11. Распределение средств обнаружения
- § 9.12. Алгоритм оптимального распределения
- § 9.13. Распределение областей дискретизации
- § 9.14. Критерии оптимальности распределения
- § 9.15. Алгоритм оптимальных оценок
- § 9.16. Некоторые задачи
- § 9.17. Заключение
- Глава X. Игры и автоматы
- § 10.1. Введение
- § 10.2. Понятие игры
- § 10.3. Теорема о минимаксе
- § 10.4. Уравнения оптимальных стратегий
- § 10.5. Алгоритмы обучения решению игр
- § 10.6. Игры и линейное программирование
- § 10.7. Управление как игра
- § 10.8. Алгоритмы управления
- § 10.9. Одно обобщение
- § 10.10. Пороговые элементы
- § 10.11. О пороговой реализуемости логических функции
- § 10.12. Критерий реализуемости
- § 10.13. Алгоритмы реализуемости
- § 10.14. Персептрон Розенблата
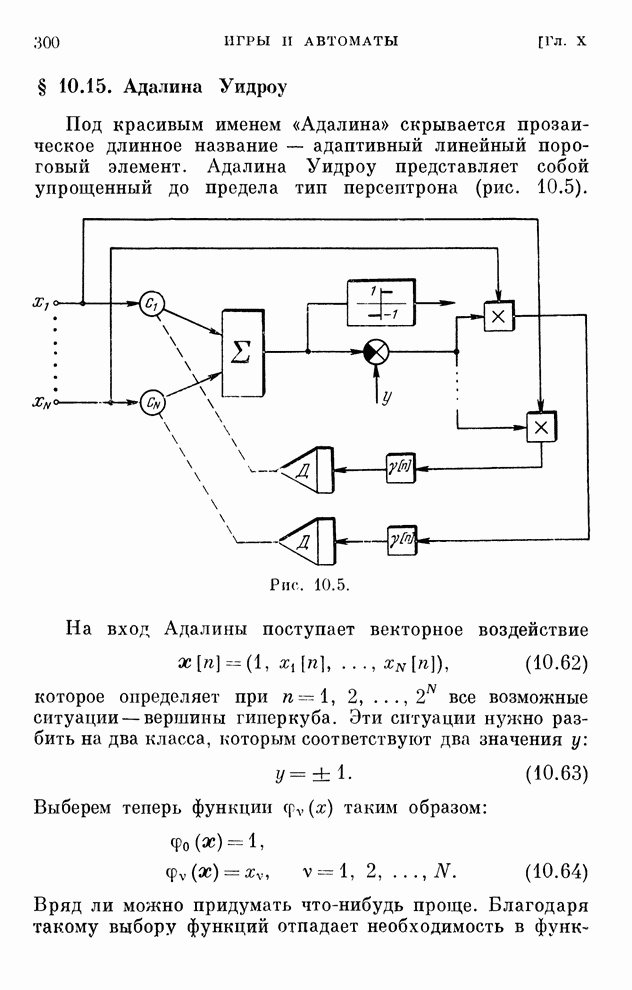
- § 10.15. Адалина Уидроу
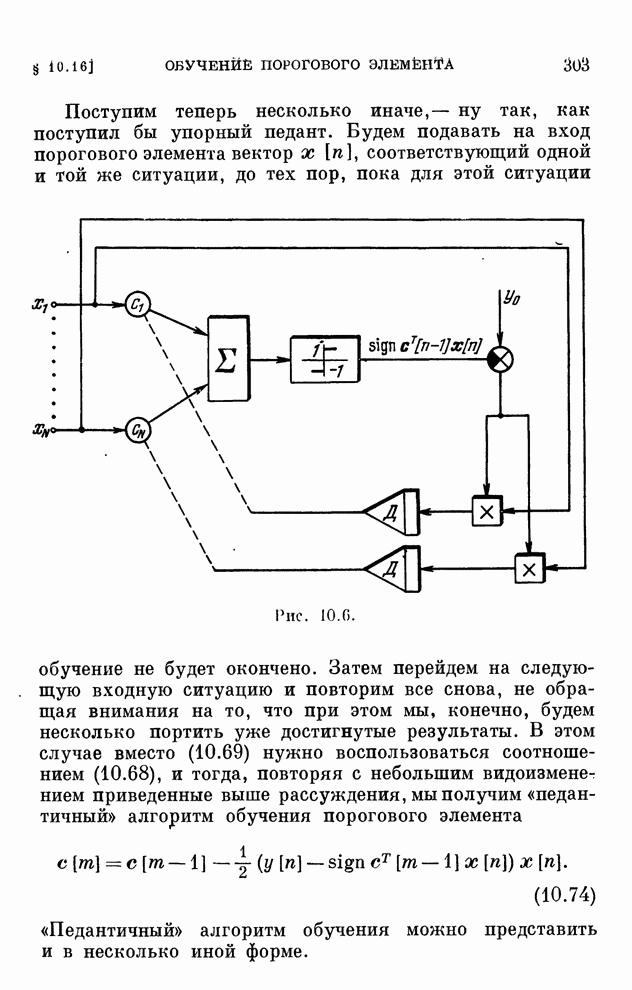
- § 10.16. Обучение порогового элемента
- § 10.17. Автоматы
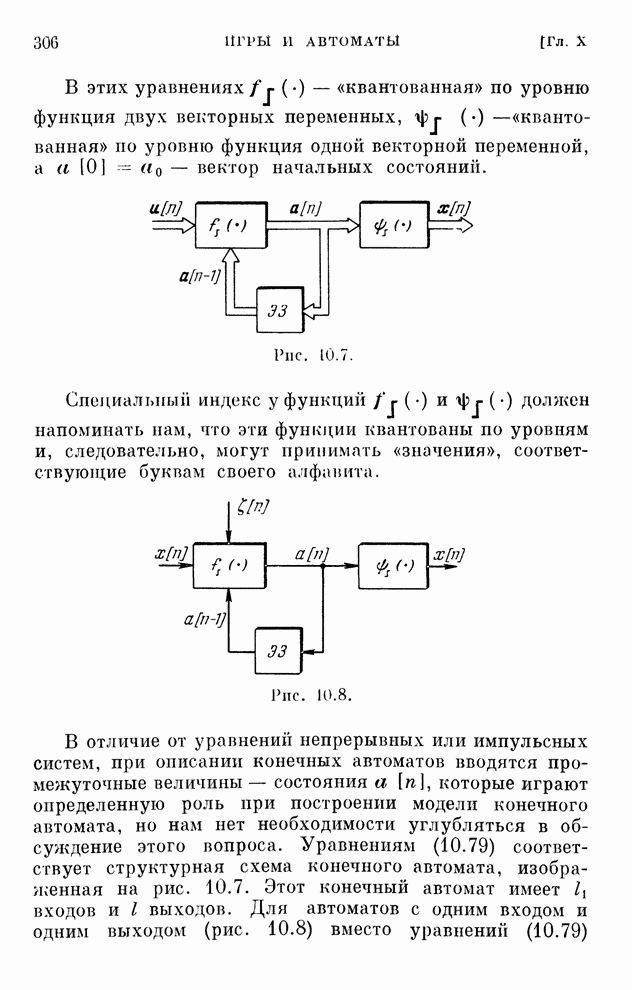
- § 10.18. Описание конечных автоматов
- § 10.19. Стохастические конечные автоматы
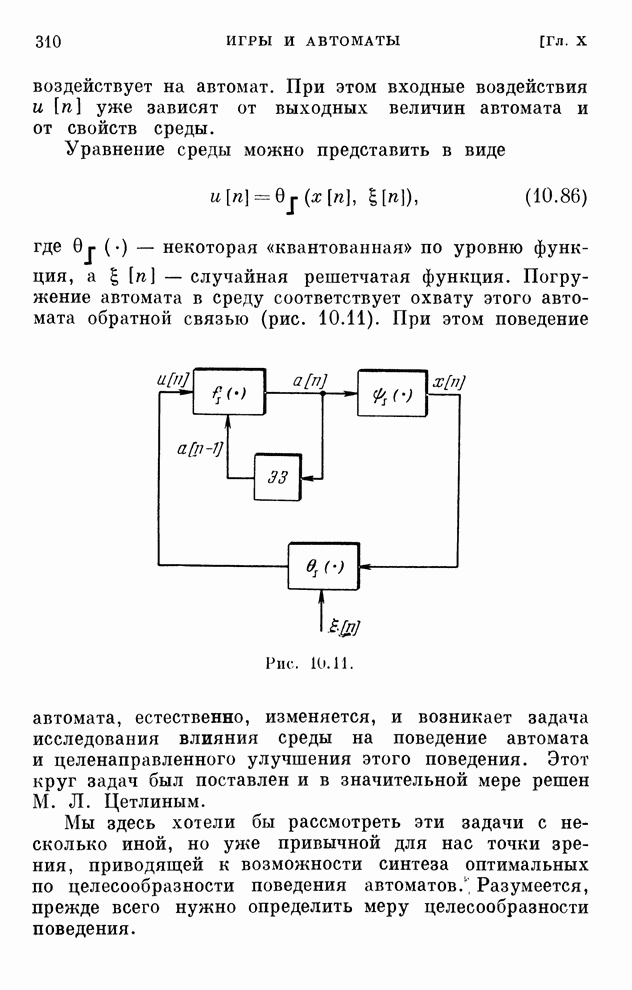
- § 10.20. Взаимодействие автомата со средой
- § 10.21. О мере целесообразности поведения
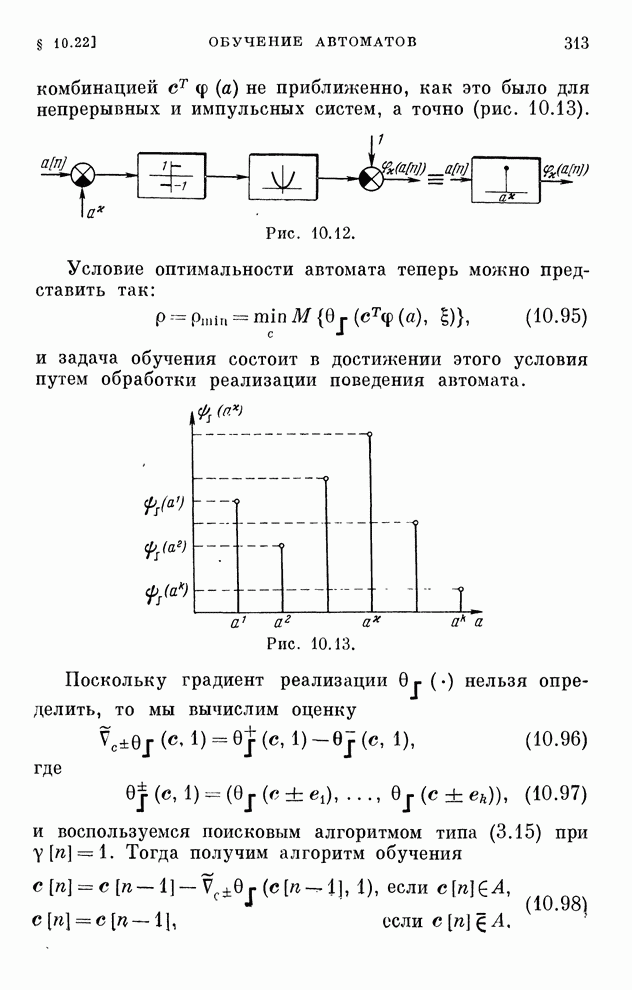
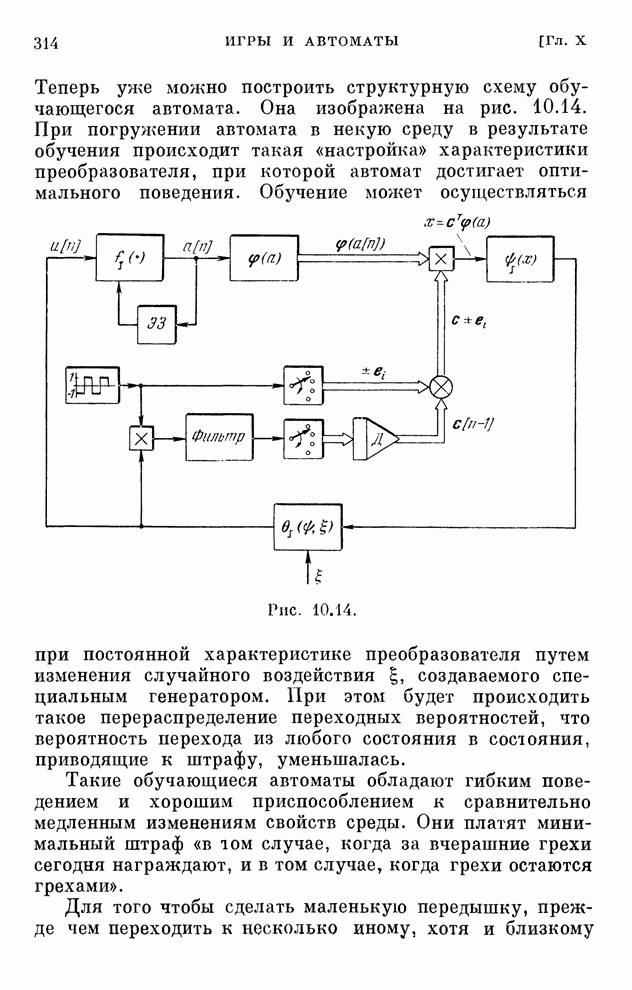
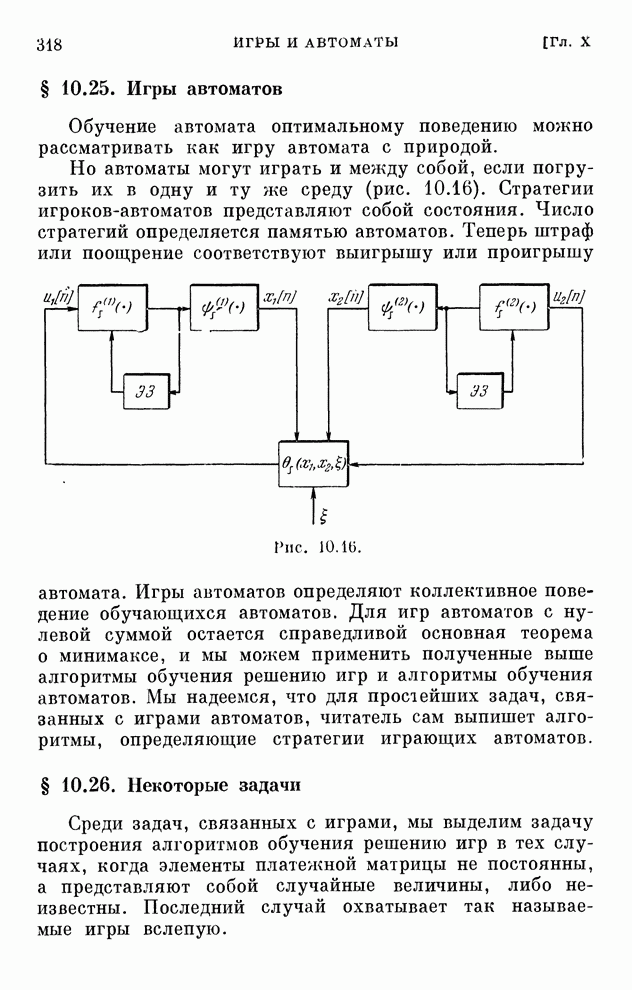
- § 10.22. Обучение автоматов
- § 10.23. О марковских цепях
- § 10.24. Марковское обучение
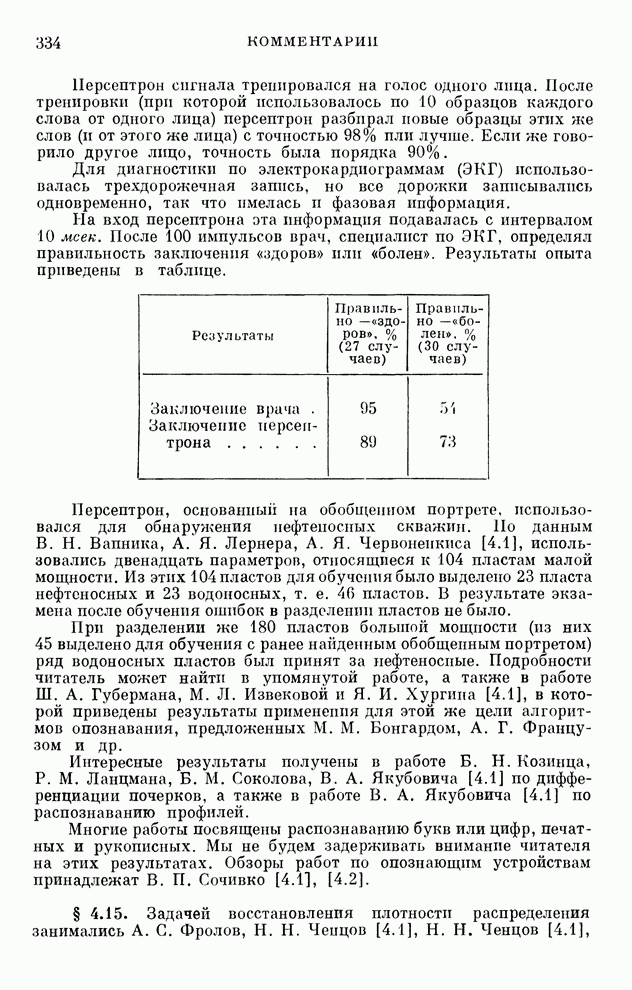
- § 10.25. Игры автоматов
- § 10.26. Некоторые задачи
- § 10.27. Заключение
- Послесловие
- Комментарии
- Литература