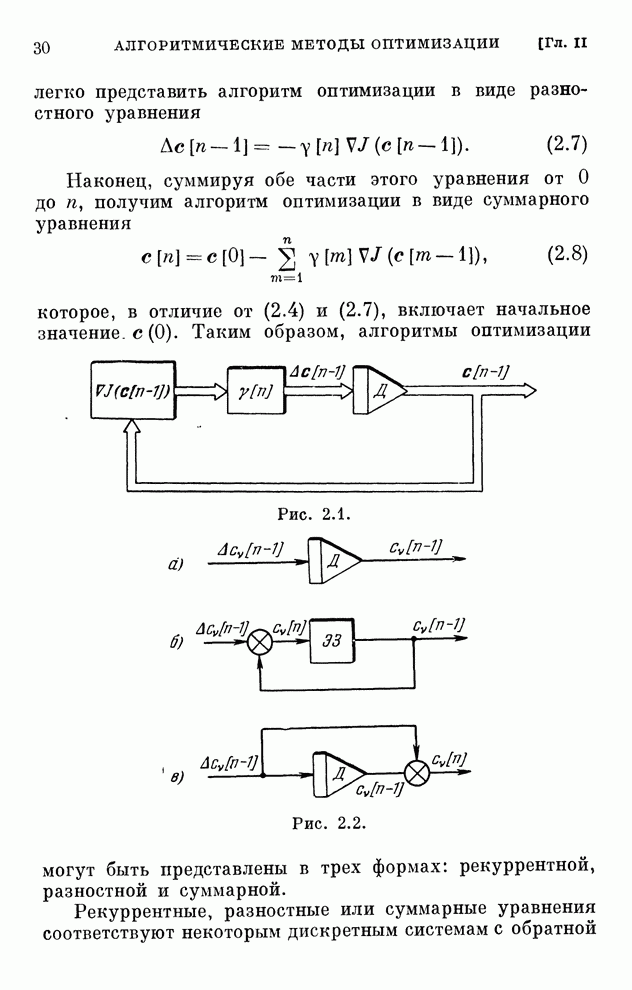
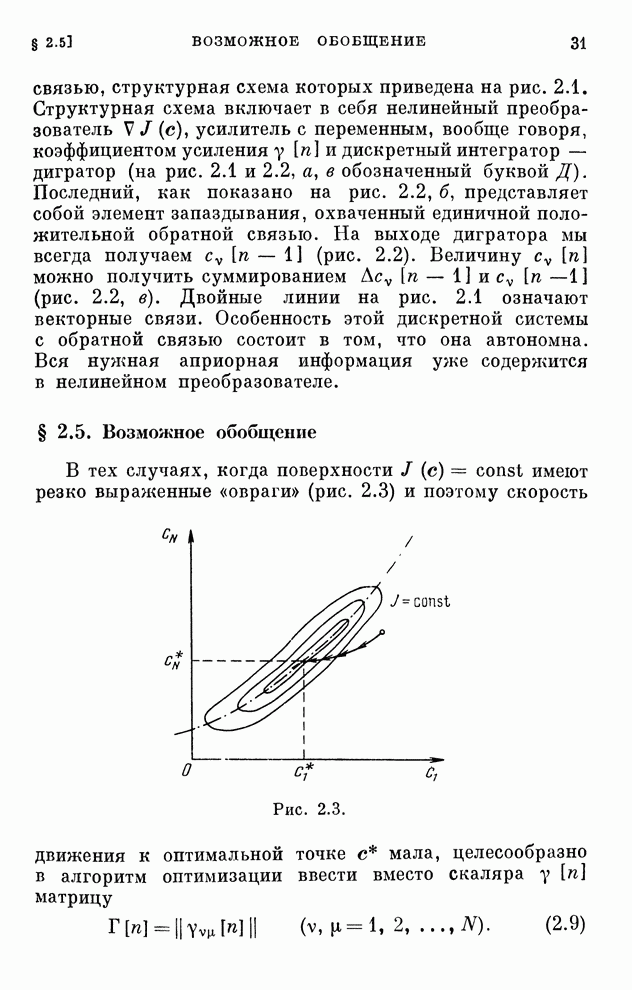
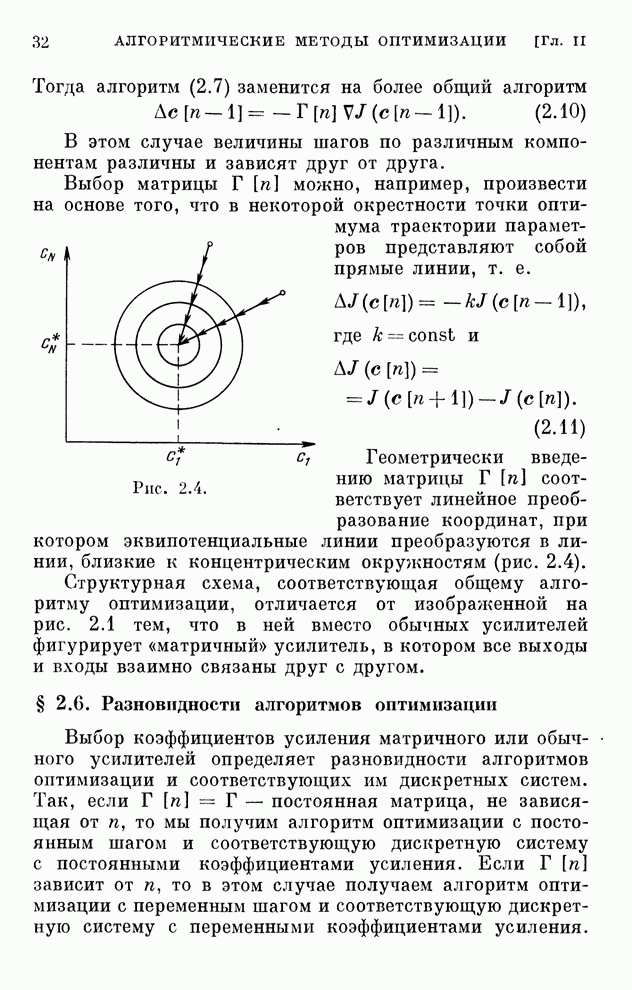
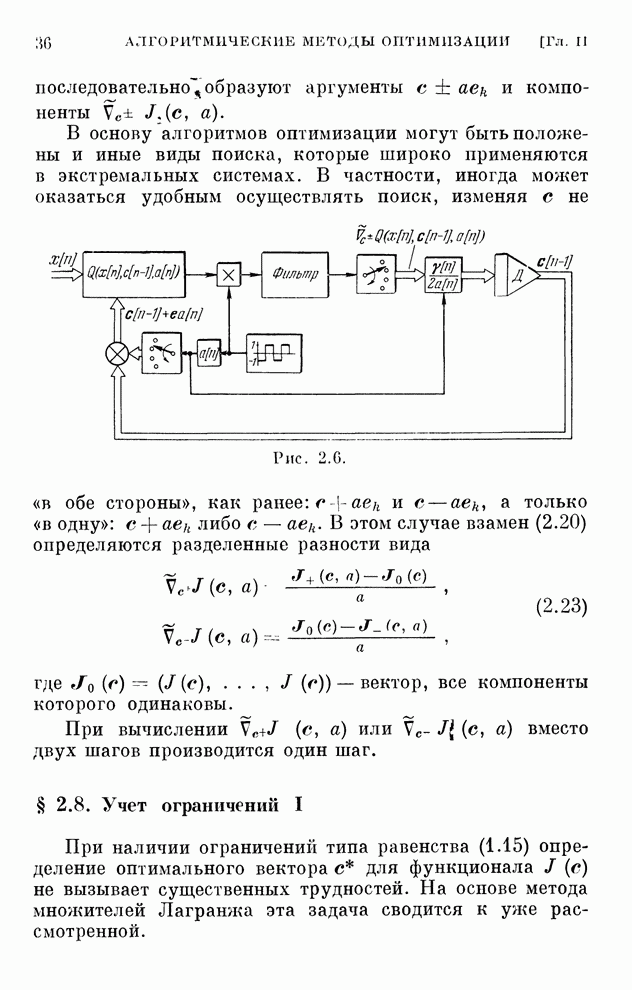
| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
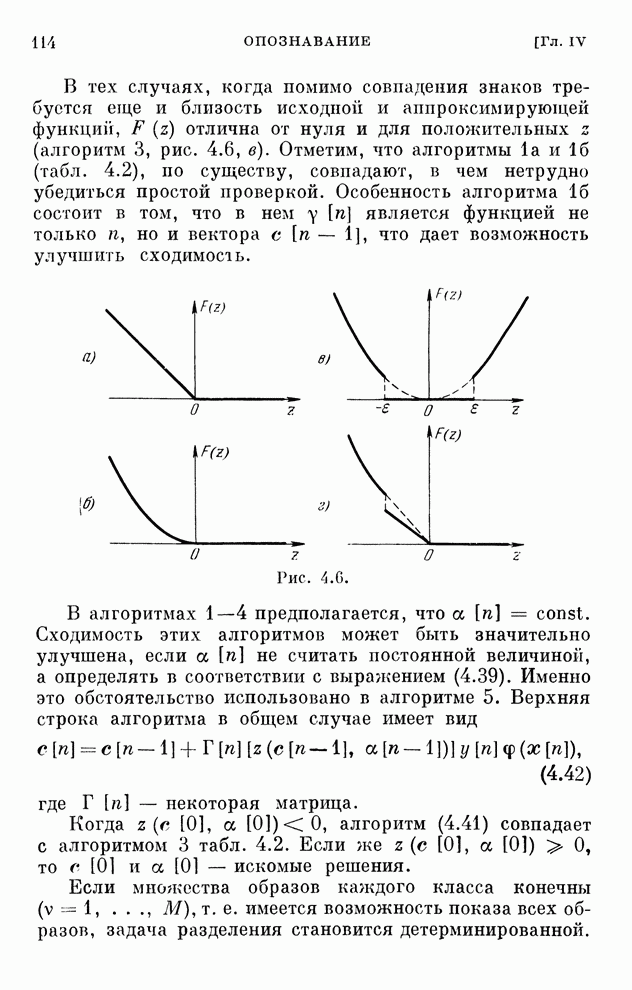
114
115
116
117
118
119
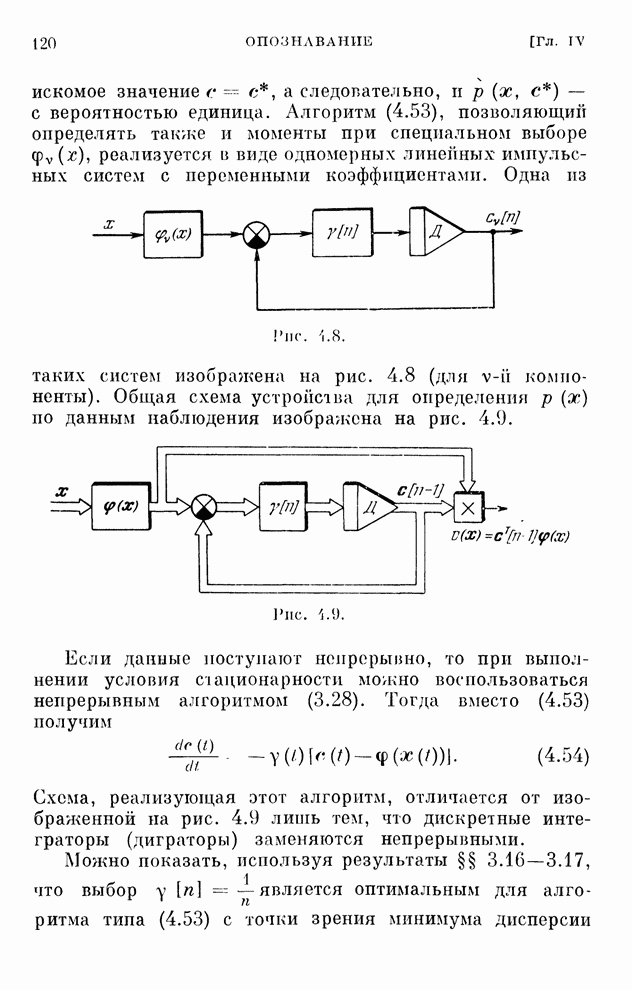
120
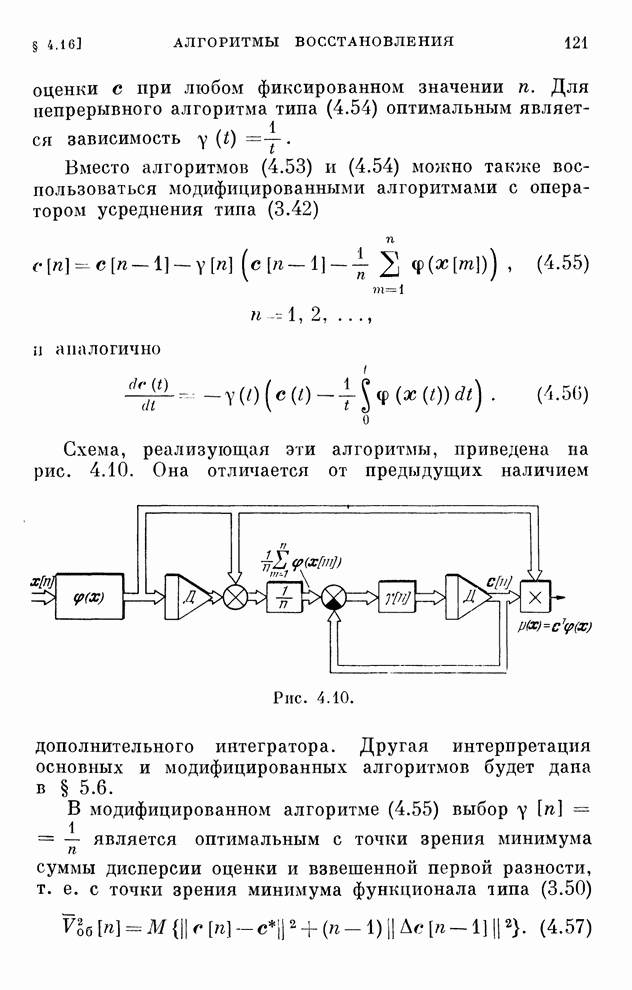
121
122
123
124
125
126
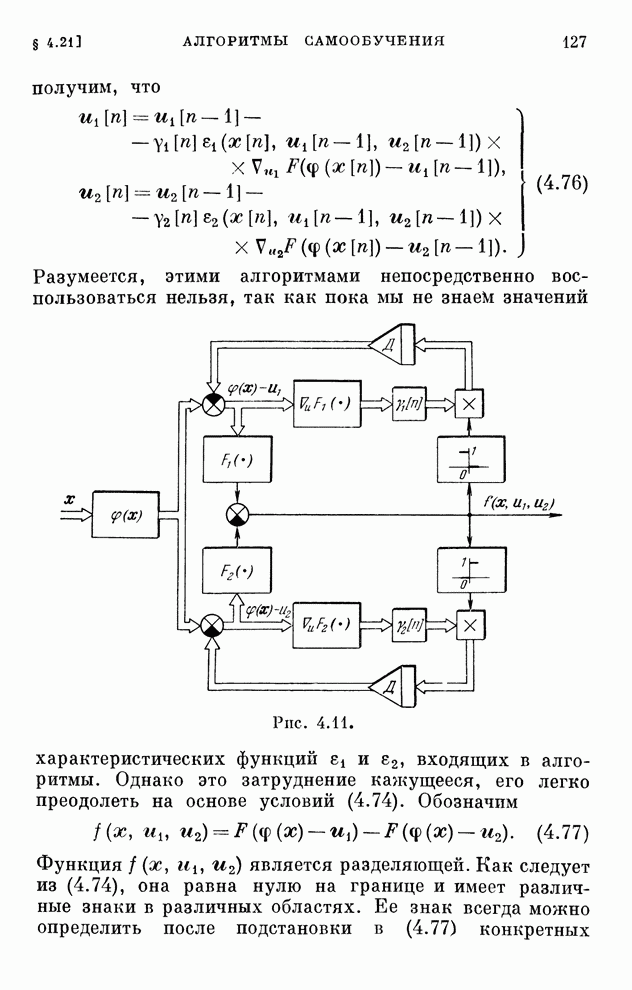
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
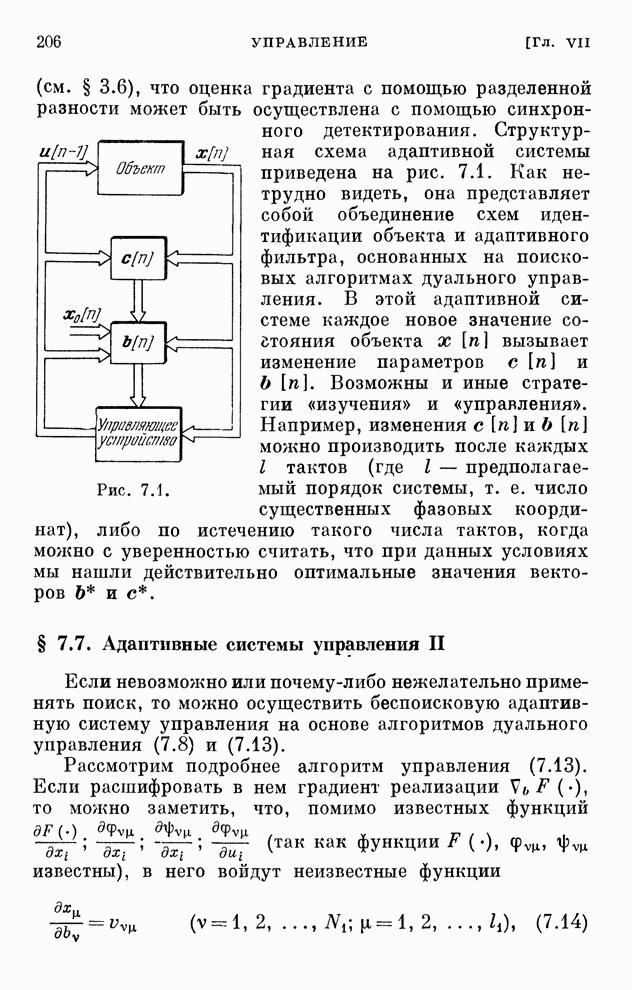
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
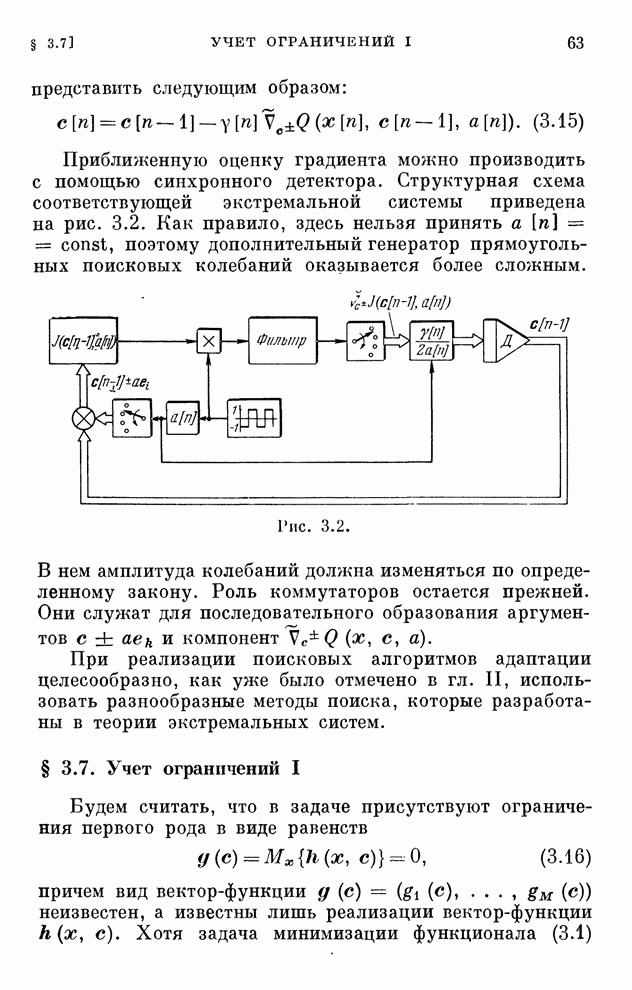
§ 2.17. Об ускорении сходимости
Мы уже упоминали в § 2.12, что
переход к многошаговым алгоритмам может привести к ускорению сходимости. Здесь
мы хотели бы на простейшем примере проиллюстрировать эту возможность.
Рассмотрим алгоритм (2.37) при ![]() ,
, ![]() ,
, ![]() .
.
Положим
![]() ;
;![]() ;
;![]() ;
; ![]() ,
, ![]() . (2.54)
. (2.54)
Тогда
![]() , (2.55)
, (2.55)
где
![]() .
.
При ![]() этот алгоритм сводится к обычному
алгоритму типа (2.4). В отличие от последнего в (2.55) аргументом градиента
является не просто
этот алгоритм сводится к обычному
алгоритму типа (2.4). В отличие от последнего в (2.55) аргументом градиента
является не просто ![]() ,
а средневзвешенное двух предшествующих значений,
,
а средневзвешенное двух предшествующих значений, ![]() и
и ![]() . Если это средневзвешенное ближе
к оптимальному значению
. Если это средневзвешенное ближе
к оптимальному значению ![]() , чем
, чем ![]() , то скорость сходимости увеличится.
Именно такая ситуация возникает, когда
, то скорость сходимости увеличится.
Именно такая ситуация возникает, когда ![]() стремится к
стремится к ![]() колебательным образом. Выбором
на каждом шаге
колебательным образом. Выбором
на каждом шаге ![]() можно
существенно ускорить сходимость. Легко себе представить, что при этом
можно
существенно ускорить сходимость. Легко себе представить, что при этом ![]() должно зависеть от
разностей
должно зависеть от
разностей ![]() . Приближенно
можно положить
. Приближенно
можно положить
 . (2.56)
. (2.56)

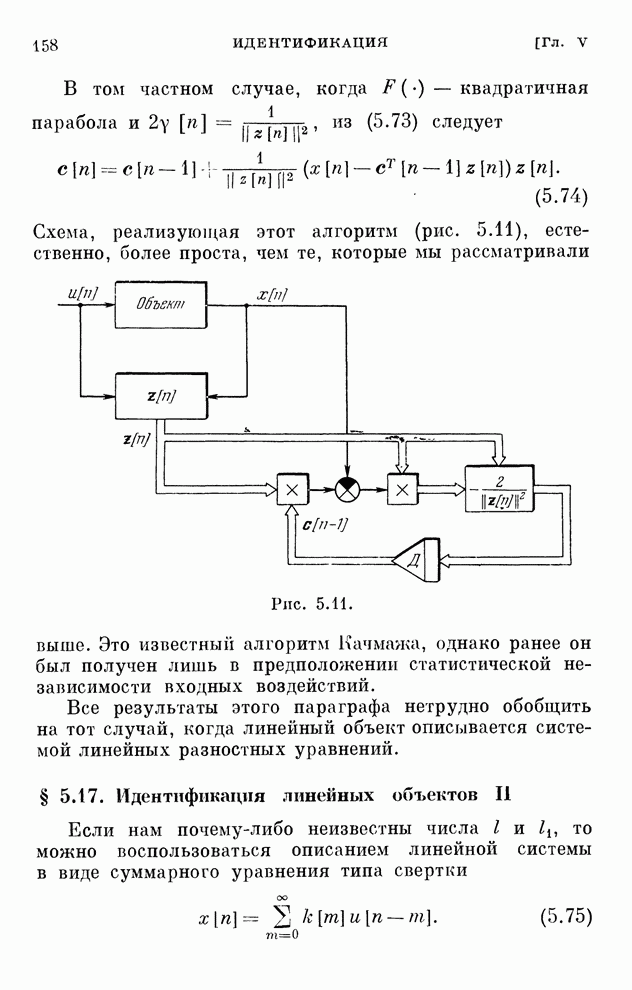
Рис. 2.11.
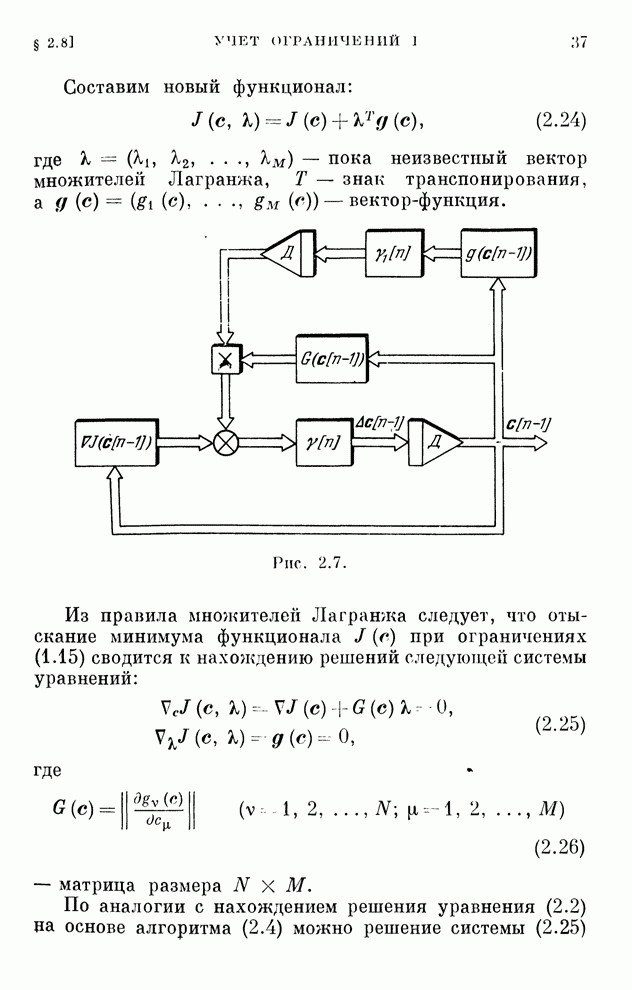
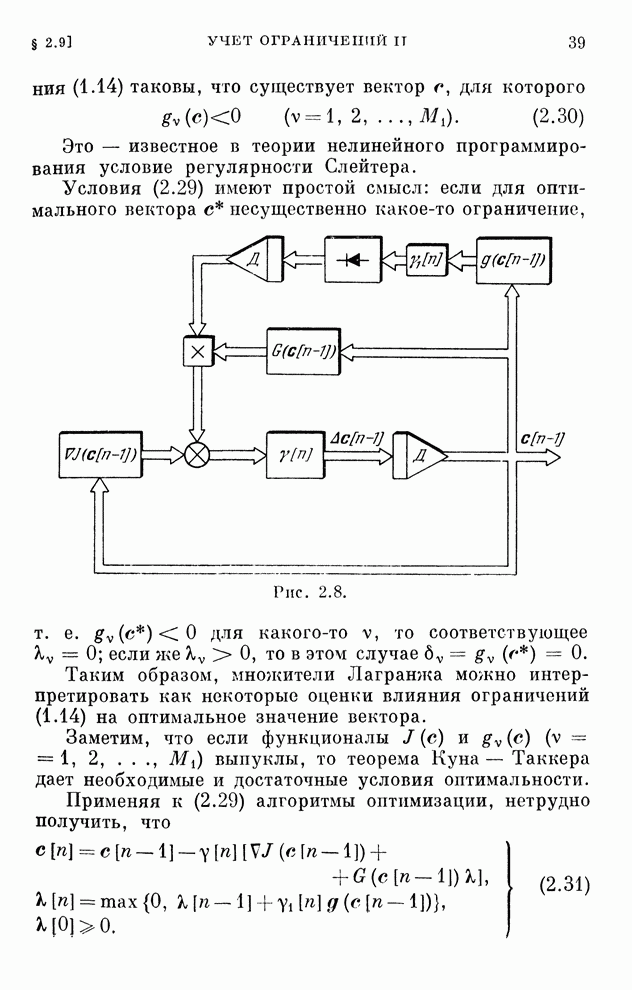
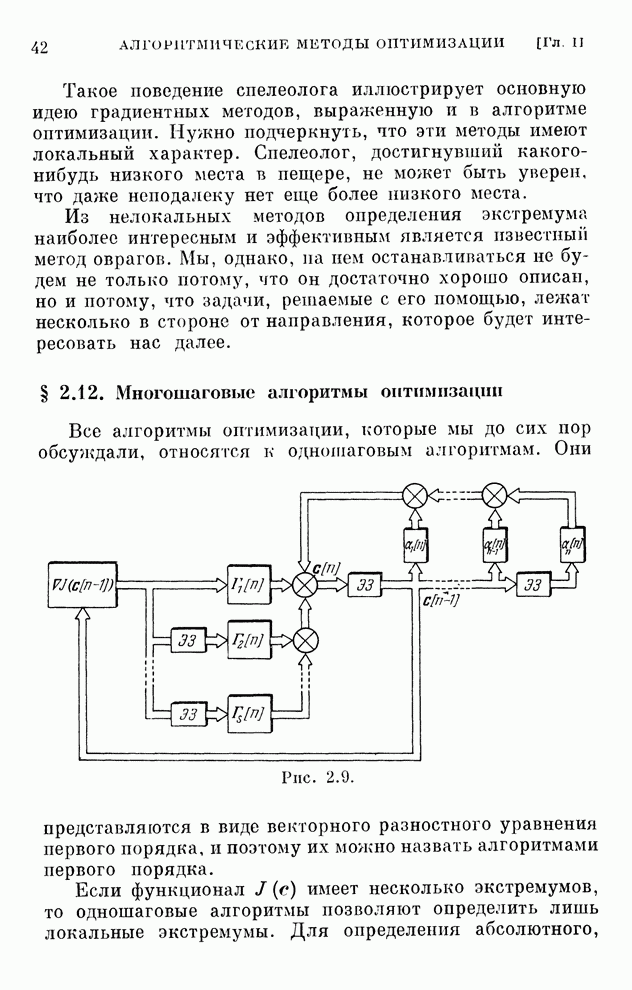
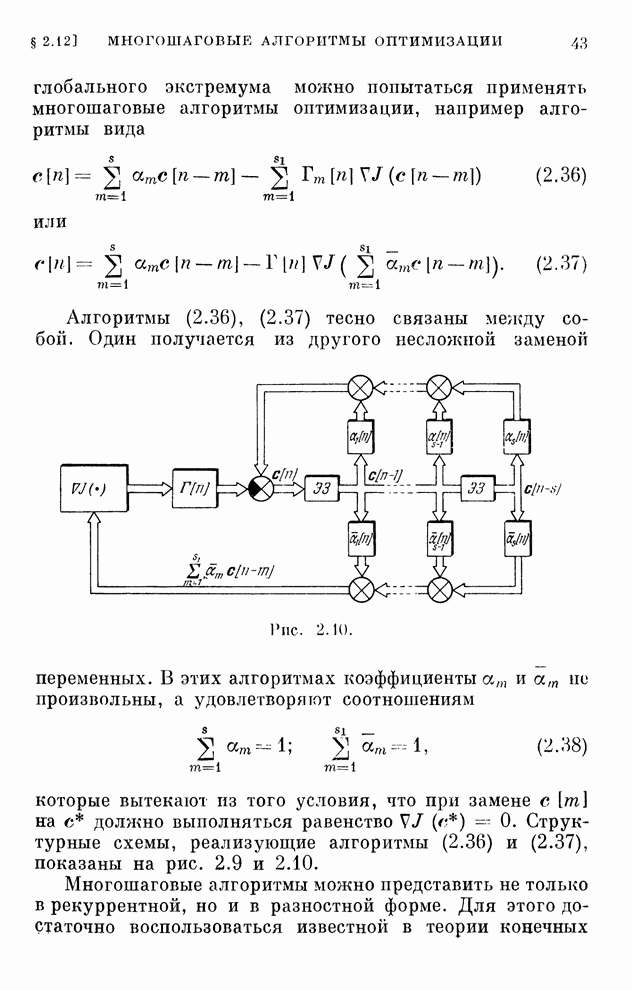
Структура системы, описываемая алгоритмом (2.55),
изображена на рис. 2.11. Существенная особенность ее состоит в том, что она
двухконтурна, а коэффициенты усиления
контуров зависят от текущего и предшествующего состояний. Вероятно, можно
усилить сходимость, если в зависимости от значений ![]() изменять соответственно
изменять соответственно ![]() .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- Глава I. Проблема оптимальности
- § 1.1. Введение
- § 1.2. Критерии оптимальности
- § 1.3. Еще о критериях оптимальности
- § 1.4. Ограничения
- § 1.5. Априорная и текущая информация
- § 1.6. Детерминированные и стохастические процессы
- § 1.7. Обычный и адаптивный подходы
- § 1.8. О методах решения проблемы оптимальности
- § 1.9. Заключение
- Глава II. Алгоритмические методы оптимизации
- § 2.1. Введение
- § 2.2. Условия оптимальности
- § 2.3. Регулярный итеративный метод
- § 2.4. Алгоритмы оптимизации
- § 2.5. Возможное обобщение
- § 2.6. Разновидности алгоритмов оптимизации
- § 2.7. Поисковые алгоритмы оптимизации
- § 2.8. Учет ограничений I
- § 2.9. Учет ограничений II
- § 2.10. Методы возможных направлений
- § 2.11. Обсуждение
- § 2.12. Многошаговые алгоритмы оптимизации
- § 2.13. Непрерывные алгоритмы оптимизации
- § 2.14. Методы случайного поиска
- § 2.15. Сходимость и устойчивость
- § 2.16. Условия сходимости
- § 2.17. Об ускорении сходимости
- § 2.18. О наилучших алгоритмах
- § 2.19. Примеры
- § 2.20. Некоторые задачи
- § 2.21. Заключение
- Глава III. Адаптация и обучение
- § 3.1. Введение
- § 3.2. Понятия обучения, самообучения и адаптации
- § 3.3. Формулировка задачи
- § 3.4. Вероятностные итеративные методы
- § 3.5. Алгоритмы адаптации
- § 3.6. Поисковые алгоритмы адаптации
- § 3.7. Учет ограничений I
- § 3.8. Учет ограничений II
- § 3.9. Одно обобщение
- § 3.10. Многошаговые алгоритмы адаптации
- § 3.11. Непрерывные алгоритмы
- § 3.12. Вероятностная сходимость и устойчивость
- § 3.13. Условия сходимости
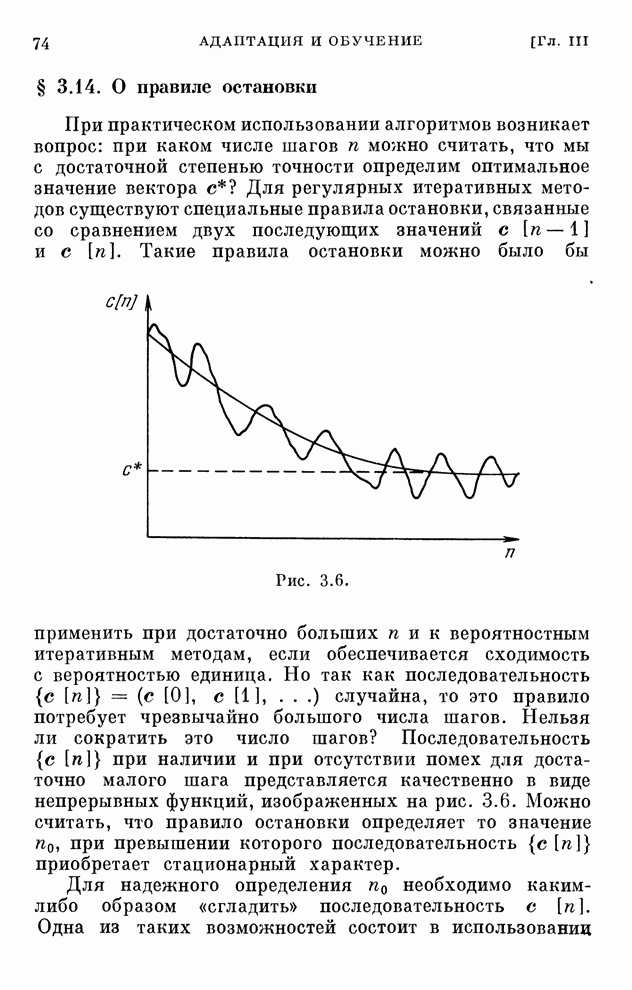
- § 3.14. О правиле остановки
- § 3.15. Об ускорении сходимости
- § 3.16. Мера качества алгоритмов
- § 3.17. Наилучшие алгоритмы
- § 3.18. Упрощенные наилучшие алгоритмы
- § 3.19. Частный случай
- § 3.20. Связь с методом наименьших квадратов
- § 3.21. Связь с байесовским методом
- § 3.22. Связь с методом максимального правдоподобия
- § 3.23. Обсуждение
- § 3.24. Некоторые задачи
- § 3.25. Заключение
- Глава IV. Опознавание
- § 4.1. Введение
- § 4.2. Обсуждение задачи опознавания
- § 4.3. Формулировка задачи
- § 4.4. Общие алгоритмы обучения
- § 4.5. Сходимость алгоритмов
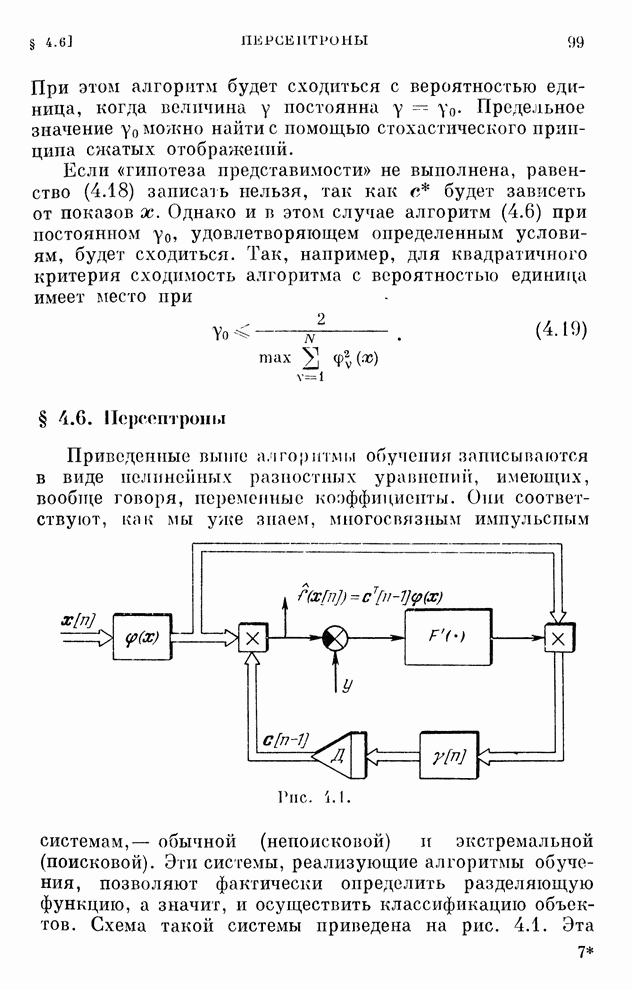
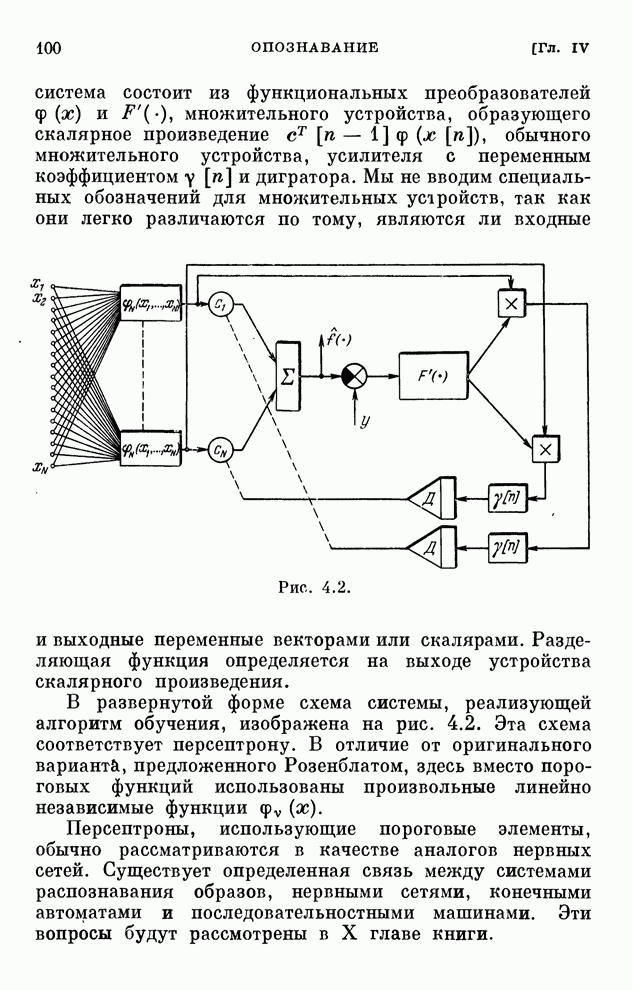
- § 4.6. Персептроны
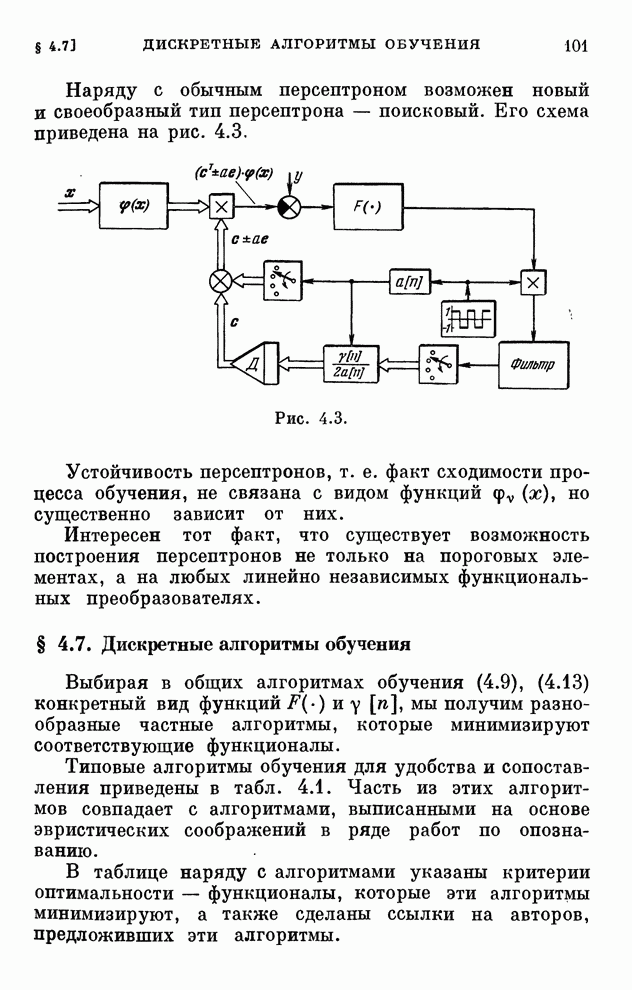
- § 4.7. Дискретные алгоритмы обучения
- § 4.8. Поисковые алгоритмы обучения
- § 4.9. Непрерывные алгоритмы обучения
- § 4.10. Замечания
- § 4.11. Еще об одном общем алгоритме обучения
- § 4.12. Частные случаи
- § 4.13. Обсуждение
- § 4.14. О самообучении
- § 4.15. О восстановлении плотности распределения и моментов
- § 4.10. Алгоритмы восстановления
- § 4.17. Принципы самообучения
- § 4.18. Средний риск
- § 4.19. Вариация среднего риска
- § 4.20. Условия минимума среднего риска
- § 4.21. Алгоритмы самообучения
- § 4.22. Обобщение
- § 4.23. Конкретные алгоритмы
- § 4.24. Поисковые алгоритмы самообучения
- § 4.25. Обсуждение
- § 4.26. Некоторые задачи
- § 4.27. Заключение
- Глава V. Идентификация
- § 5.1. Введение
- § 5.2. Оценка среднего значения
- § 5.3. Другой подход
- § 5.4. Оценка дисперсии
- § 5.5. Обсуждение
- § 5.6. Оценка корреляционных функций
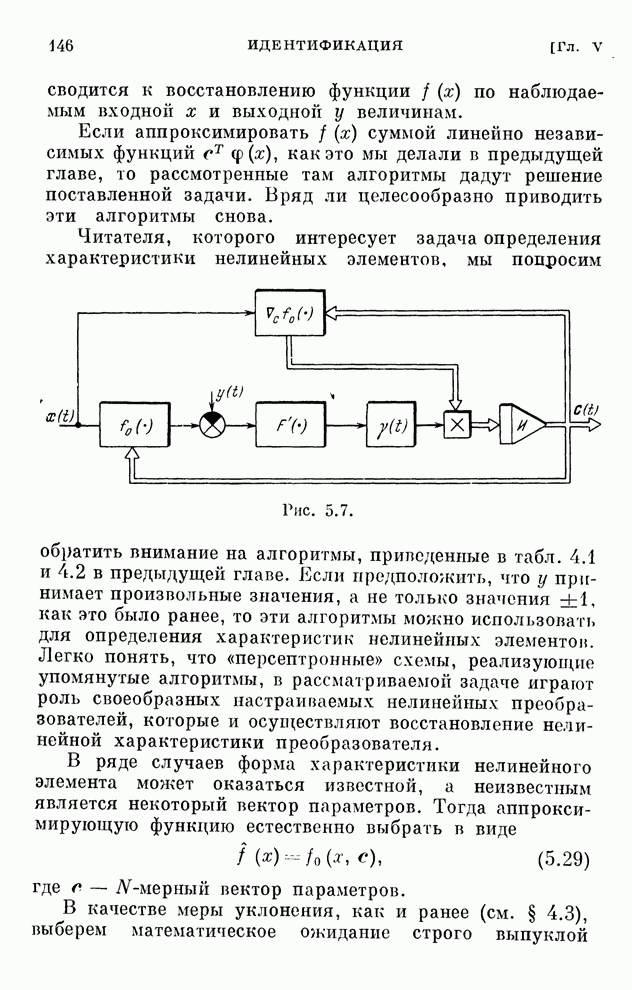
- § 5.7. Определение характеристик нелинейных элементов
- § 5.8. Оценка коэффициента статистической линеаризации
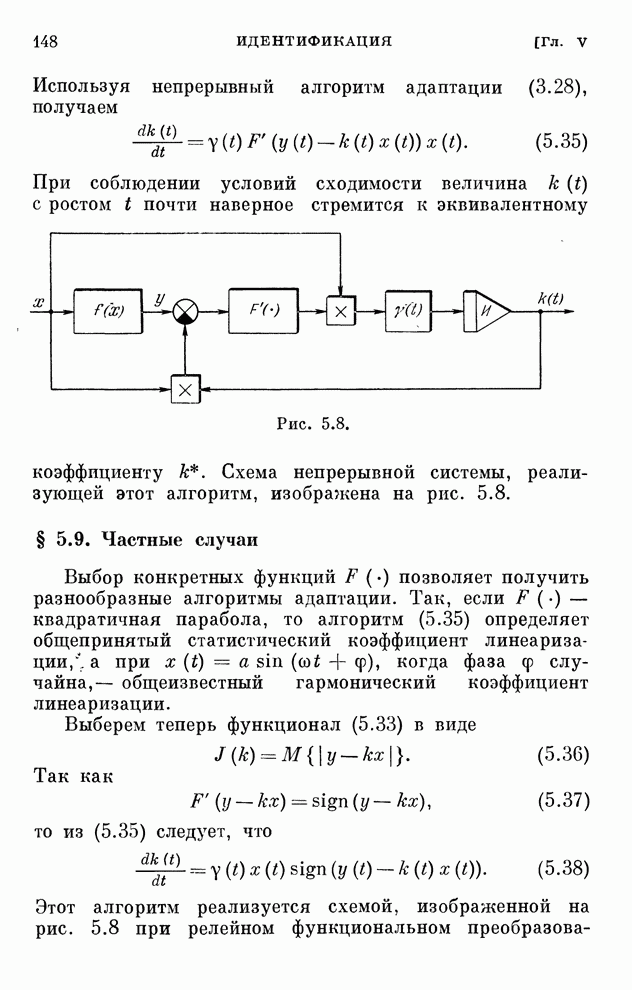
- § 5.9. Частные случаи
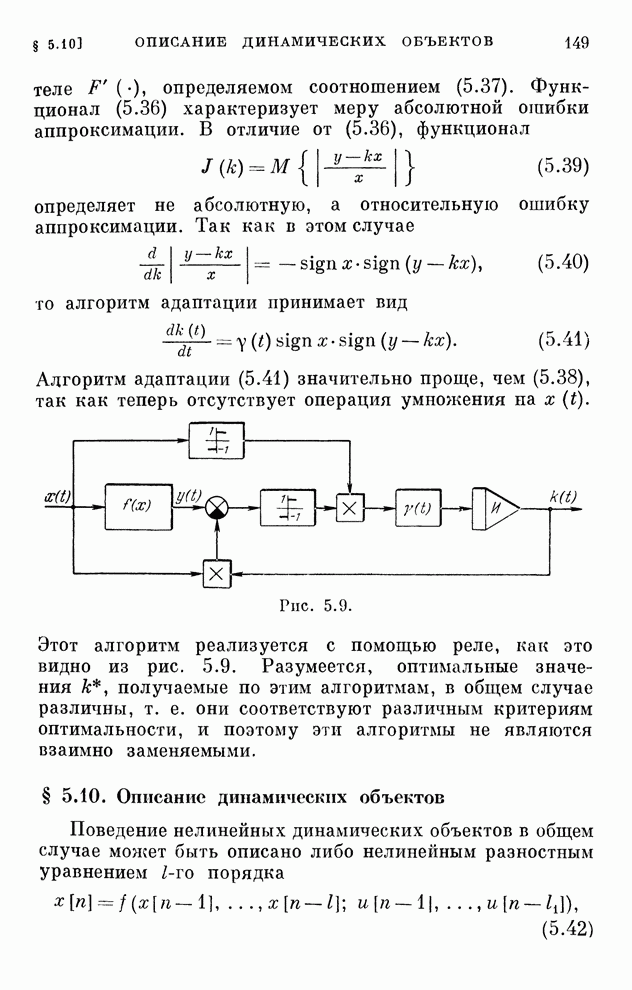
- § 5.10. Описание динамических объектов
- § 5.11. Идентификация нелинейных объектов I
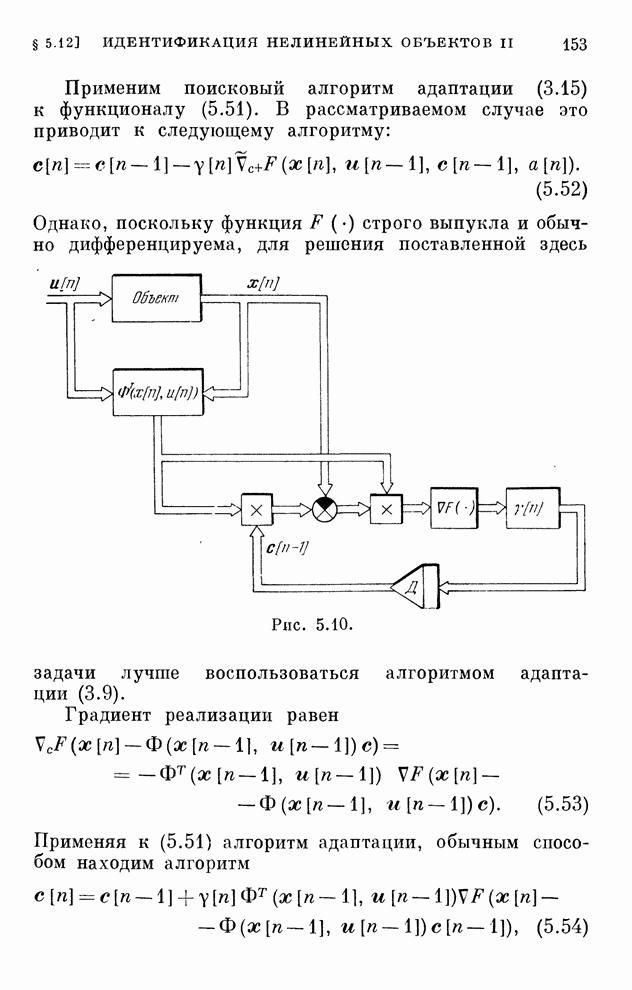
- § 5.12. Идентификация нелинейных объектов II
- § 5.13. Идентификация нелинейных объектов III
- § 5.14. Специальный случай
- § 5.15. Замечание
- § 5.16. Идентификация линейных объектов I
- § 5.17. Идентификация линейных объектов II
- § 5.18. Оценка параметров распределенных объектов
- § 5.19. Помехи
- § 5.20. Устранение влияния помех
- § 5.21. Некоторые задачи
- § 5.22. Заключение
- Глава VI. Фильтрация
- § 6.1. Введение
- § 6.2. Критерий оптимальности
- § 6.3. Структура адаптивного фильтра
- § 6.4. Частные случаи
- § 6.5. Адаптивный корректор искажений
- § 6.6. Поисковые адаптивные фильтры
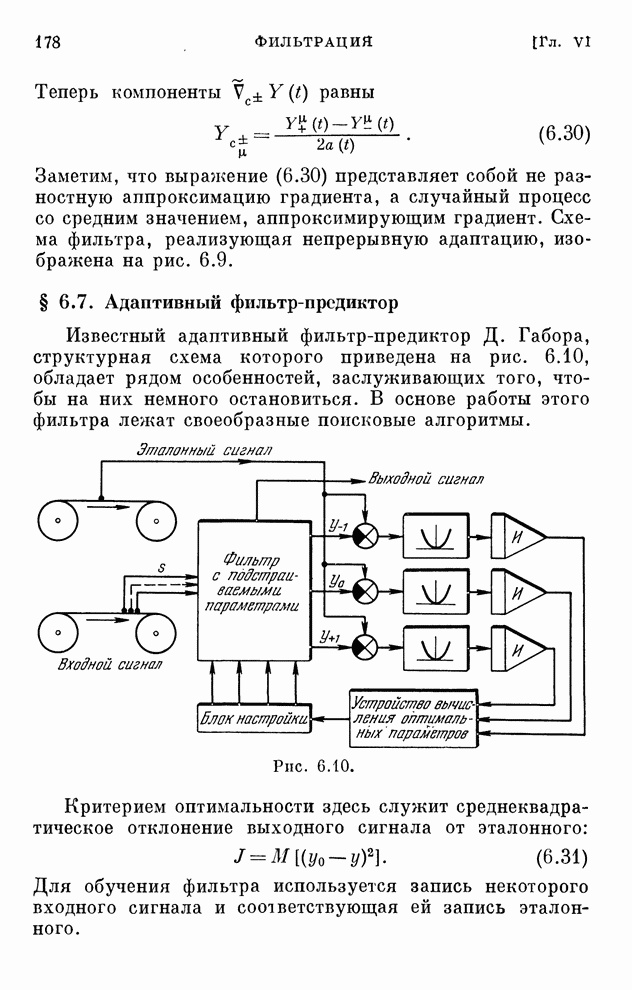
- § 6.7. Адаптивный фильтр-предиктор
- § 6.9. Статистическая теория приема
- § 6.10. Критерий оптимальности приема
- § 6.11. Определение решающего правила
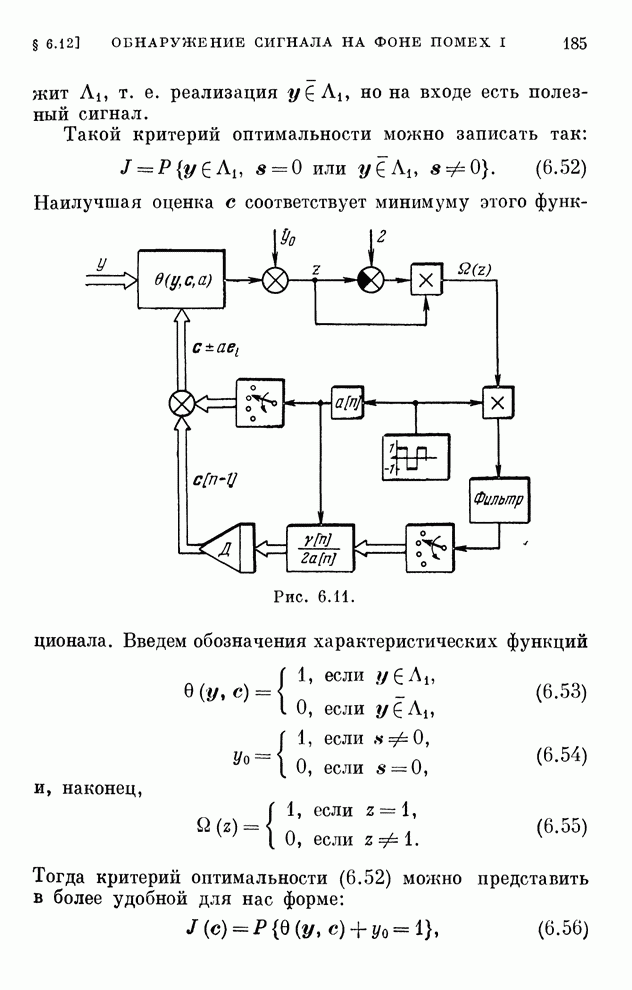
- § 6.12. Обнаружение сигнала на фоне помех I
- § 6.13. Обнаружение сигнала на фоне помех II
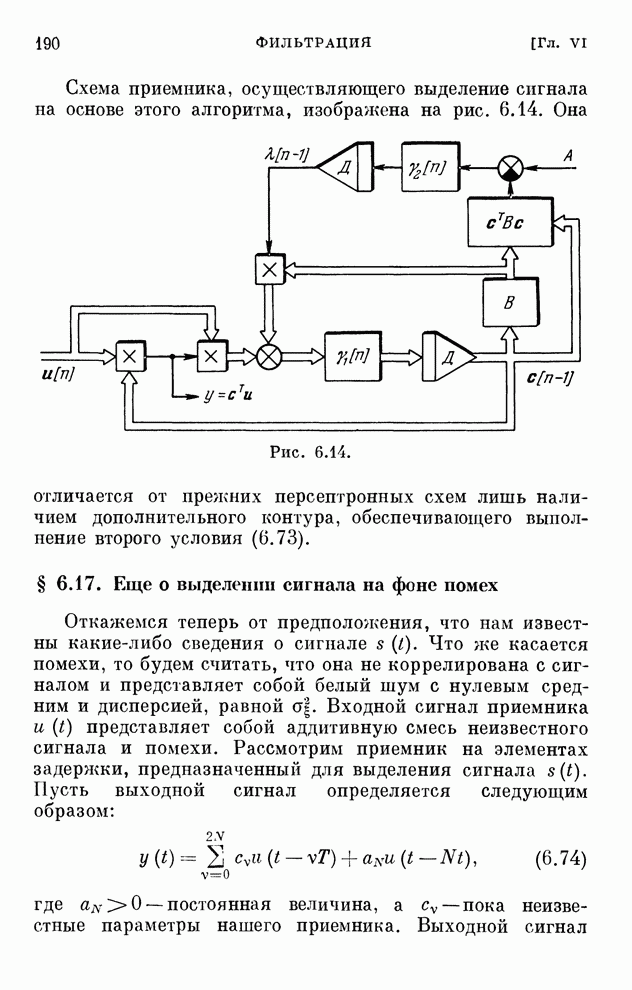
- § 6.14. Выделение сигнала на фоне помех
- § 6.15. Критерий оптимального выделения
- § 6.16. Алгоритм выделения
- § 6.17. Еще о выделении сигнала на фоне помех
- § 6.18. Другой критерий оптимальности
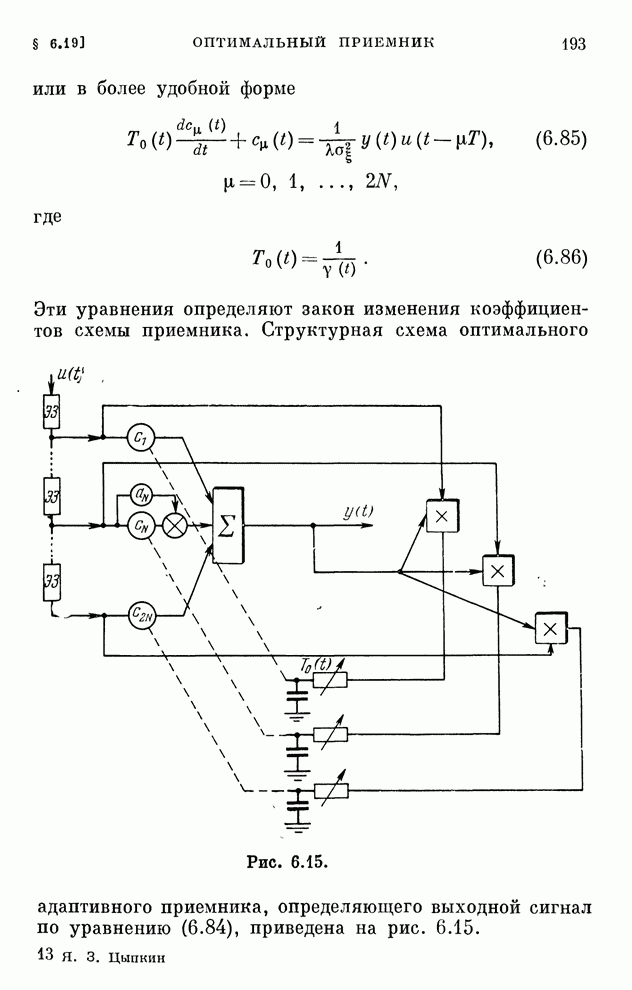
- § 6.19. Оптимальный приемник
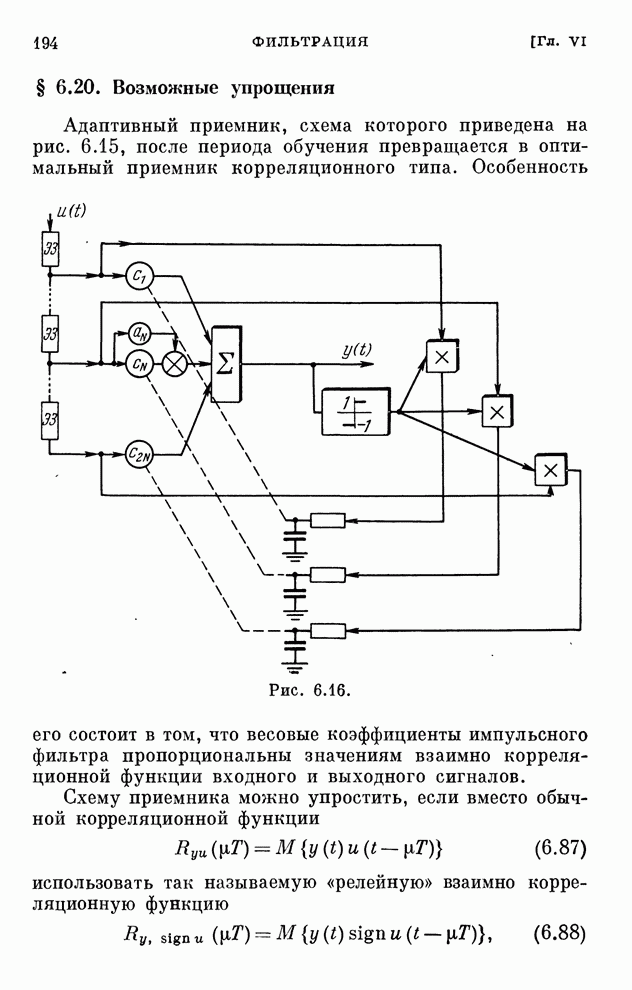
- § 6.20. Возможные упрощения
- § 6.21. Восстановление входных сигналов
- § 6.22. Алгоритмы восстановления
- § 6.23. О влиянии помех
- § 6.24. Некоторые задачи
- § 6.25. Заключение
- Глава VII. Управление
- § 7.1. Введение
- § 7.2. Когда нужна адаптация?
- § 7.3. Постановка задачи
- § 7.4. Дуальное управление
- § 7.5. Алгоритмы дуального управления
- § 7.6. Адаптивные системы управления I
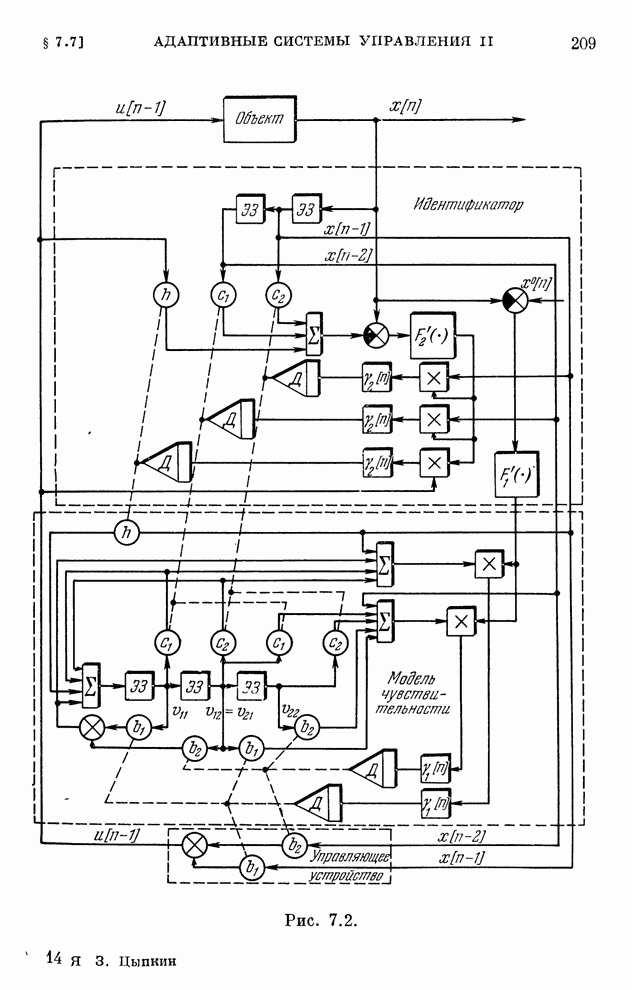
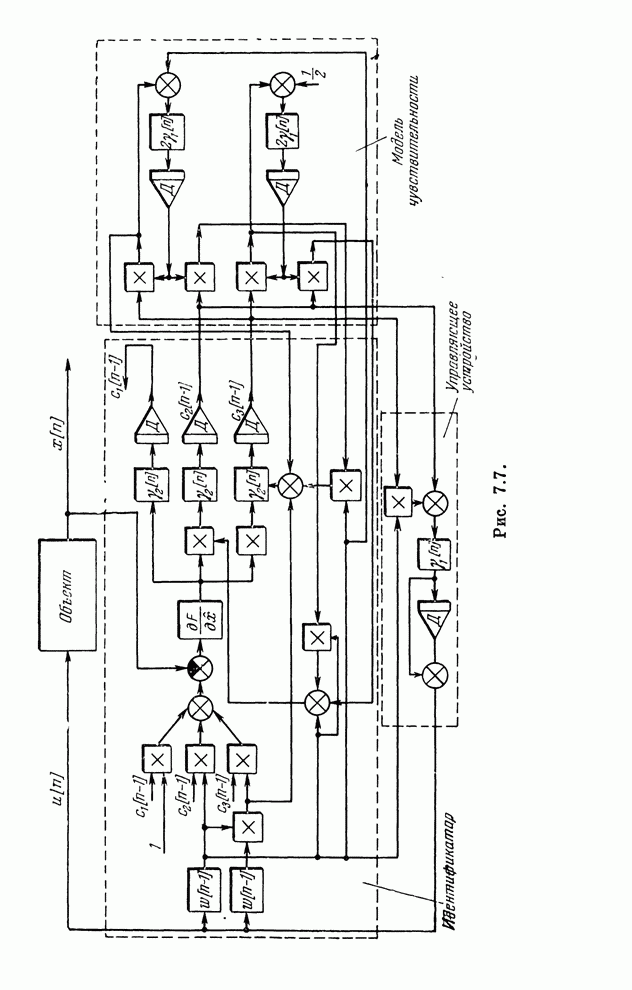
- § 7.7. Адаптивные системы управления II
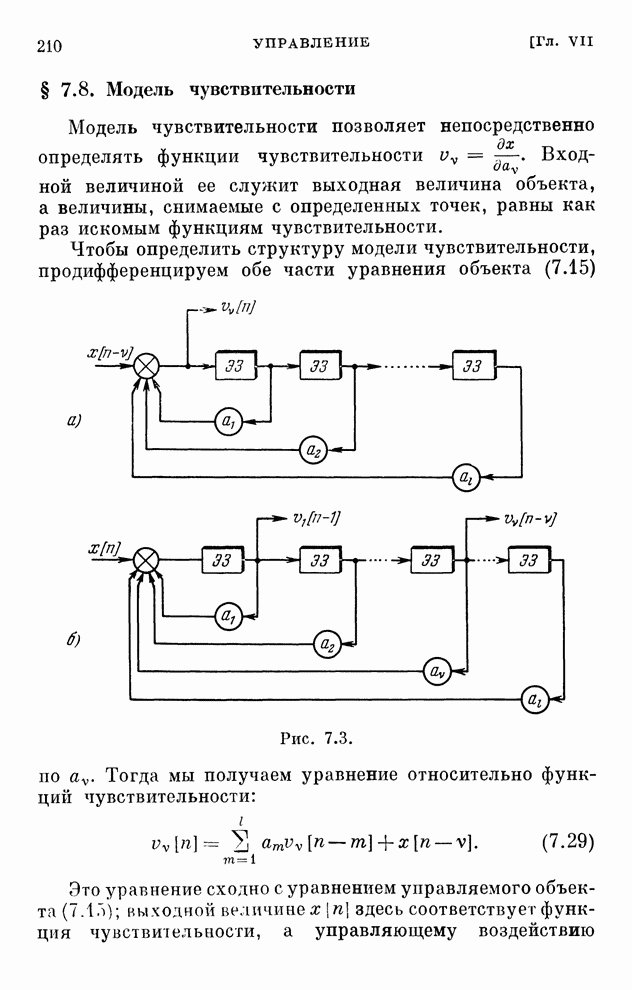
- § 7.8. Модель чувствительности
- § 7.9. Адаптивные системы управления III
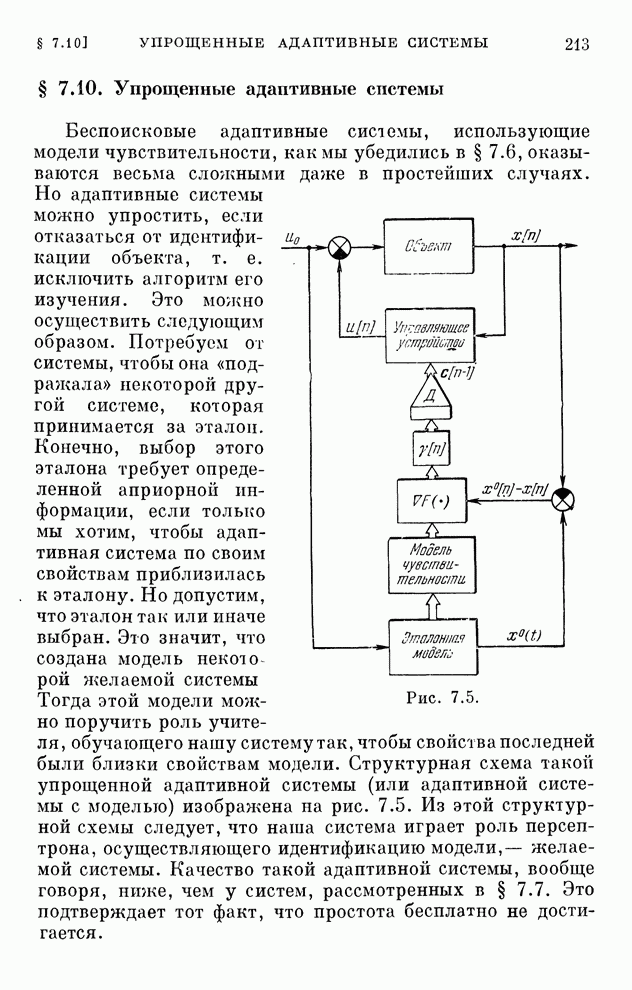
- § 7.10. Упрощенные адаптивные системы
- § 7.11. Системы управления по возмущению
- § 7.12. Алгоритмы оптимального управления
- § 7.13. Еще одна возможность
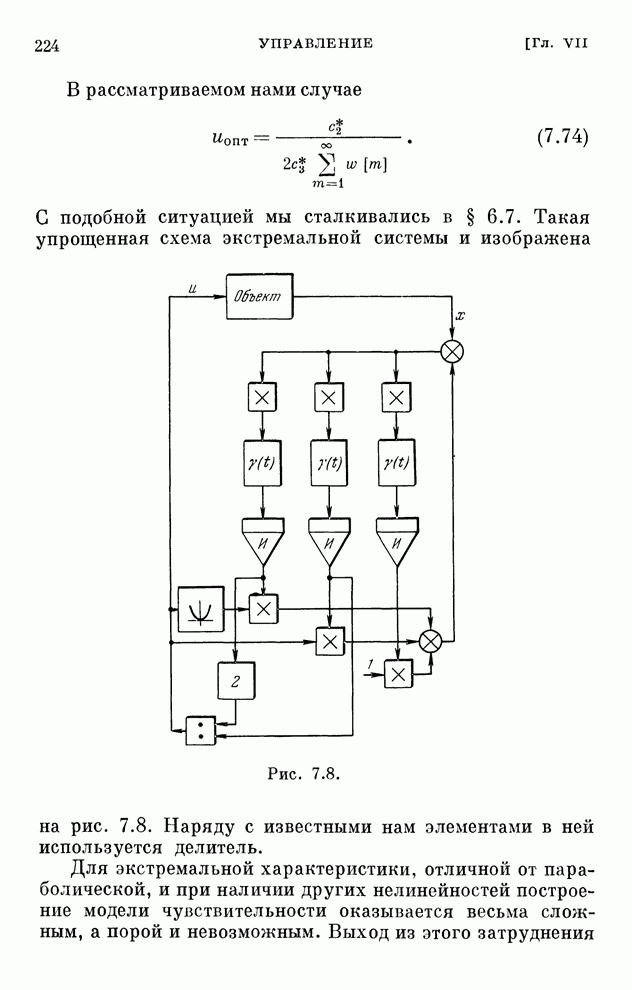
- § 7.14. Экстремальные системы управления
- § 7.15. Алгоритмы экстремального управления
- § 7.16. Алгоритмы изучения
- § 7.17. Непрерывные алгоритмы
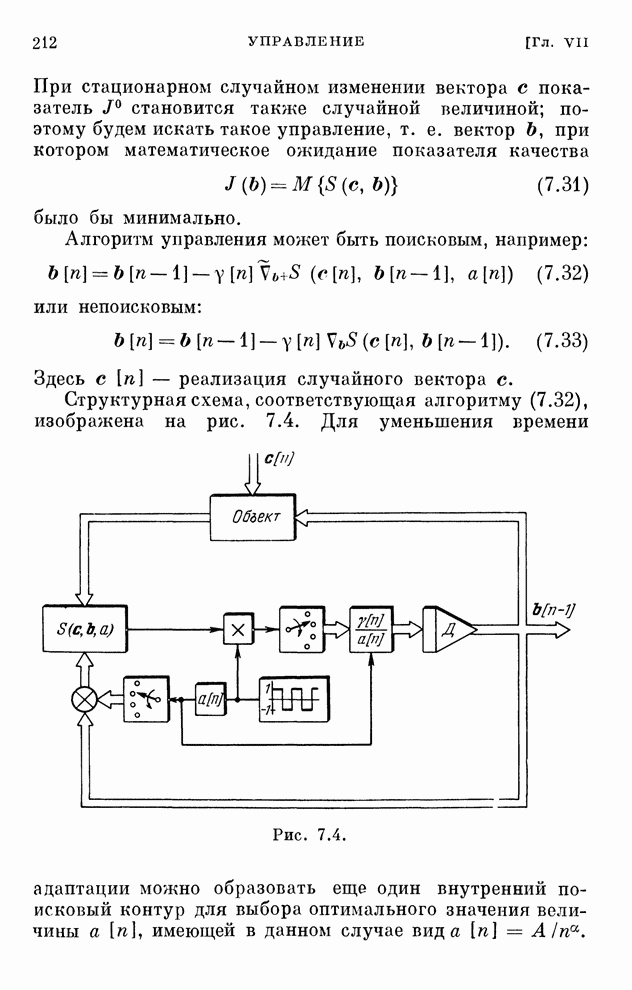
- § 7.18. Структурная схема
- § 7.19. Возможные упрощения
- § 7.20. О синтезе оптимальных систем
- § 7.21. Применение алгоритмов адаптации
- § 7.22. О синтезе оптимальных систем при наличии помех
- § 7.23. Управление и опознавание
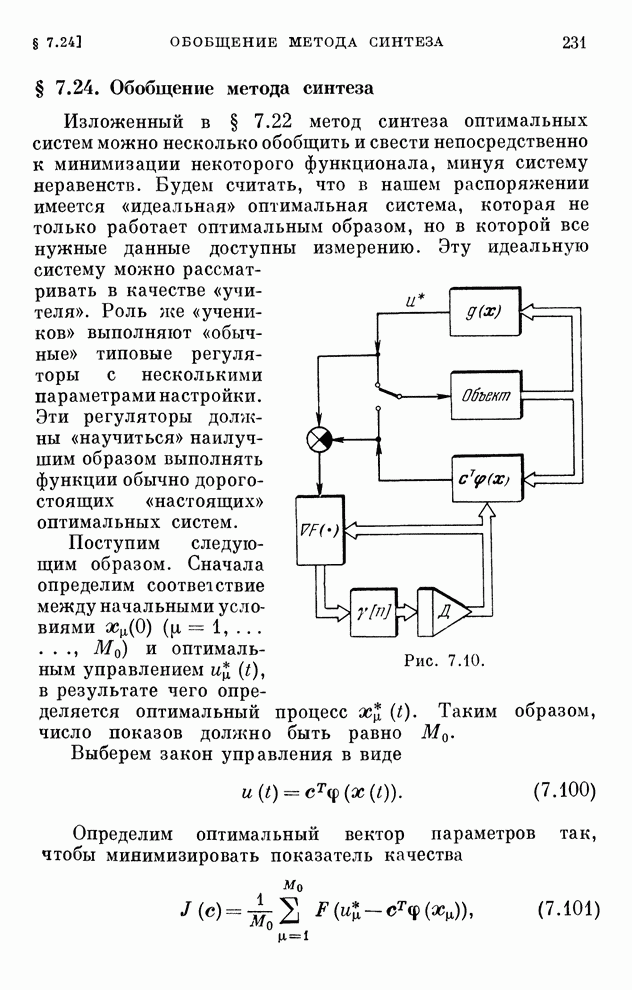
- § 7.24. Обобщение метода синтеза
- § 7.25. Некоторые задачи
- § 7.26. Заключение
- Глава VIII. Надежность
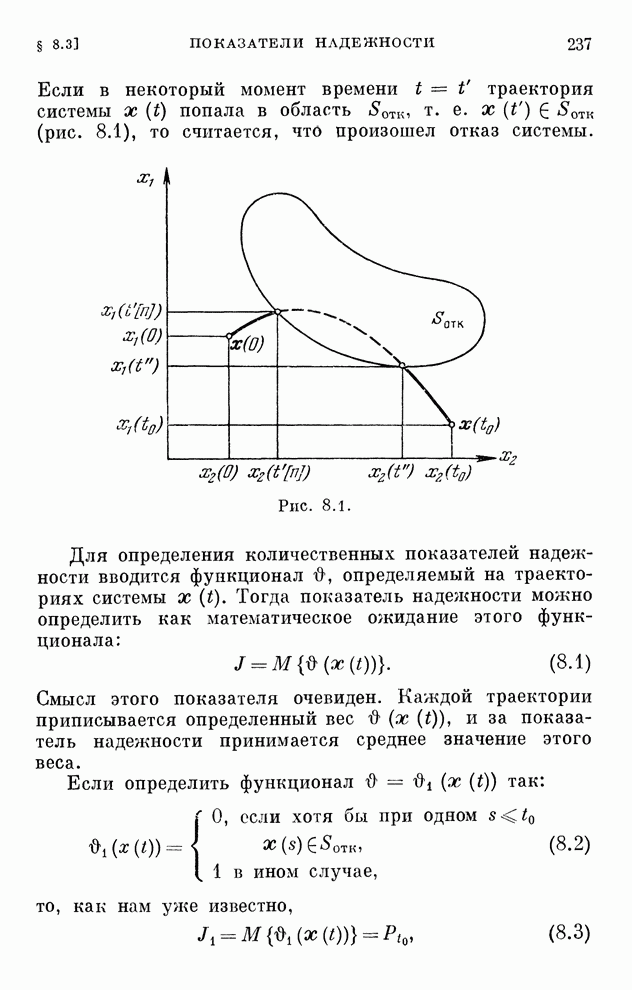
- § 8.1. Введение
- § 8.2. Понятие надежности
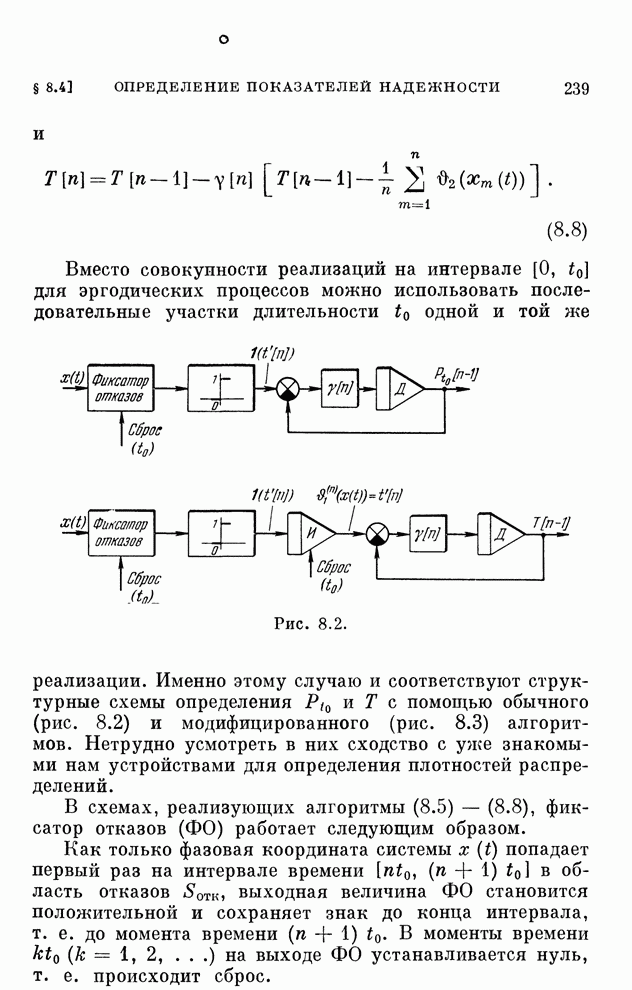
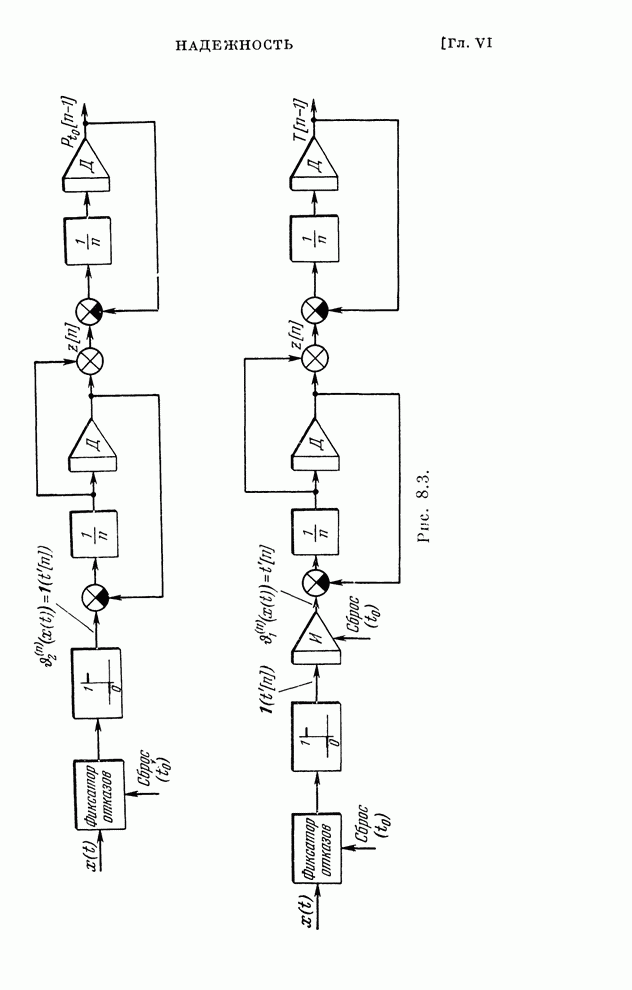
- § 8.4. Определение показателей надежности
- § 8.5. Минимизация эксплуатационных расходов
- § 8.6. Частный случай
- § 8.7. Минимизация стоимости, веса, объема
- § 8.8. Алгоритмы минимизации
- § 8.9. Особый случай
- § 8.10. Алгоритмы
- § 8.11. Повышение надежности путем резервирования
- § 8.12. Повышение надежности путем избыточности
- § 8.13. Проектирование сложных систем
- § 8.14. Алгоритмы оптимальной работоспособности
- § 8.15. О минимаксном критерии оптимизации
- § 8.16. Еще о проектировании сложных систем
- § 8.17. Замечание
- § 8.18. Некоторые задачи
- § 8.19. Заключение
- Глава IX. Исследование операций
- § 9.1. Введение
- § 9.2. Планирование запасов
- § 9.3. Критерий оптимальности планирования
- § 9.4. Алгоритмы оптимального планировании
- § 9.5. Еще о планировании запасов
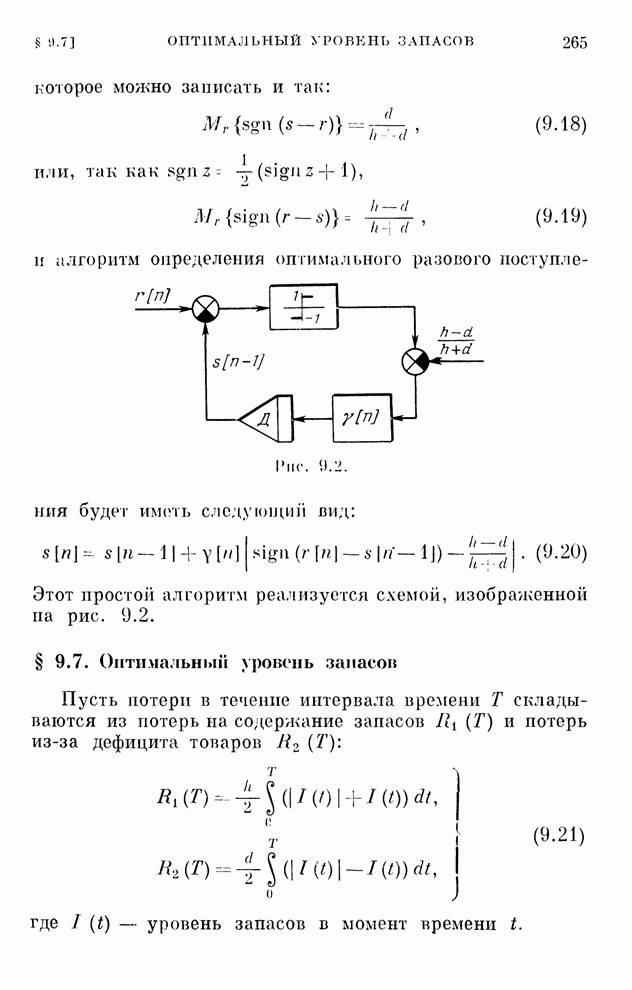
- § 9.6. Оптимальное разовое поступление
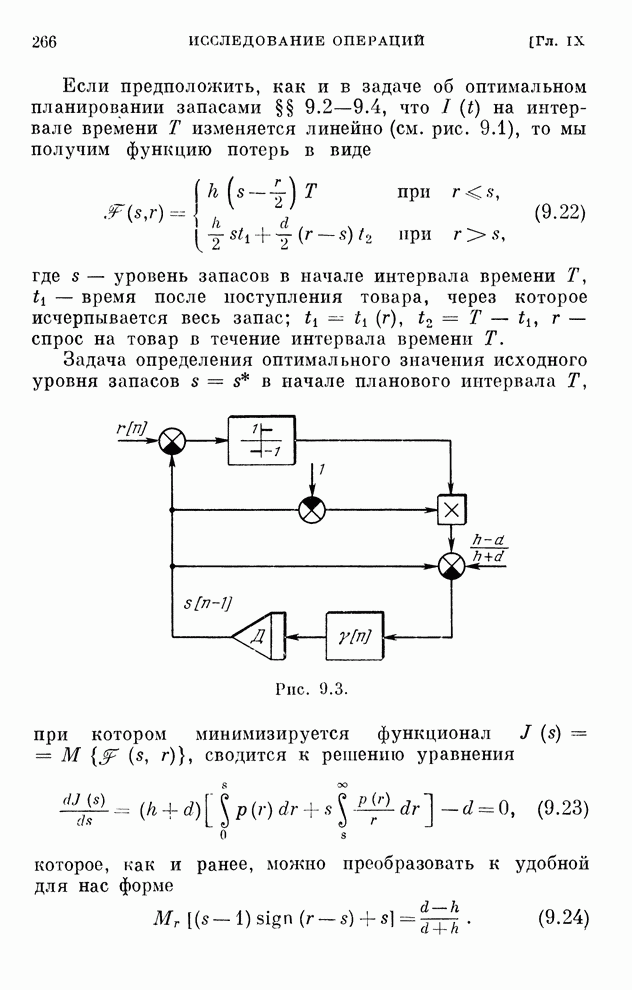
- § 9.7. Оптимальный уровень запасов
- § 9.8. Замечание
- § 9.9. Распределение производственных мощностей
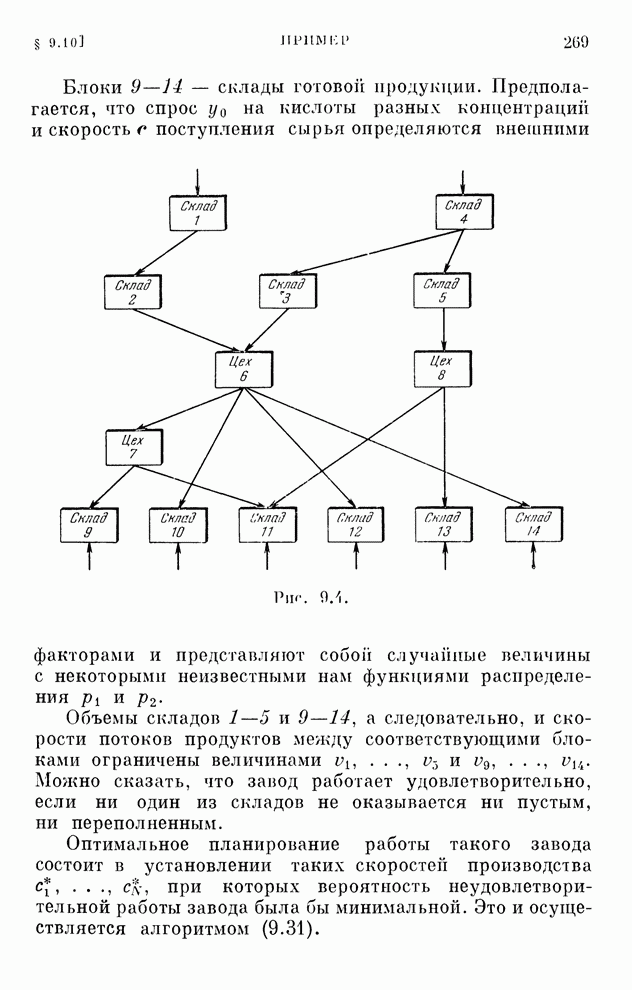
- § 9.10. Пример
- § 9.11. Распределение средств обнаружения
- § 9.12. Алгоритм оптимального распределения
- § 9.13. Распределение областей дискретизации
- § 9.14. Критерии оптимальности распределения
- § 9.15. Алгоритм оптимальных оценок
- § 9.16. Некоторые задачи
- § 9.17. Заключение
- Глава X. Игры и автоматы
- § 10.1. Введение
- § 10.2. Понятие игры
- § 10.3. Теорема о минимаксе
- § 10.4. Уравнения оптимальных стратегий
- § 10.5. Алгоритмы обучения решению игр
- § 10.6. Игры и линейное программирование
- § 10.7. Управление как игра
- § 10.8. Алгоритмы управления
- § 10.9. Одно обобщение
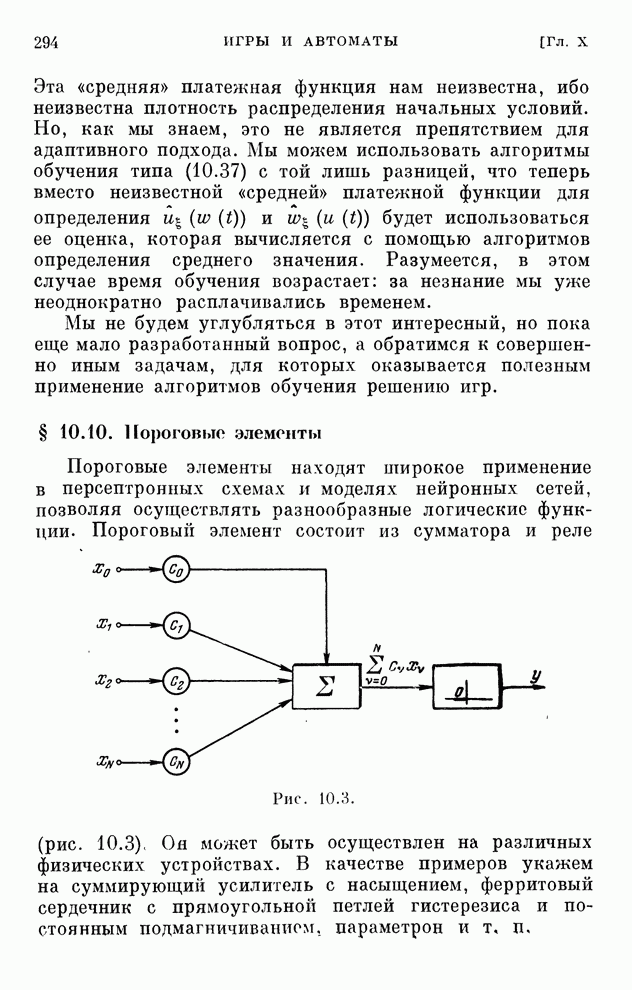
- § 10.10. Пороговые элементы
- § 10.11. О пороговой реализуемости логических функции
- § 10.12. Критерий реализуемости
- § 10.13. Алгоритмы реализуемости
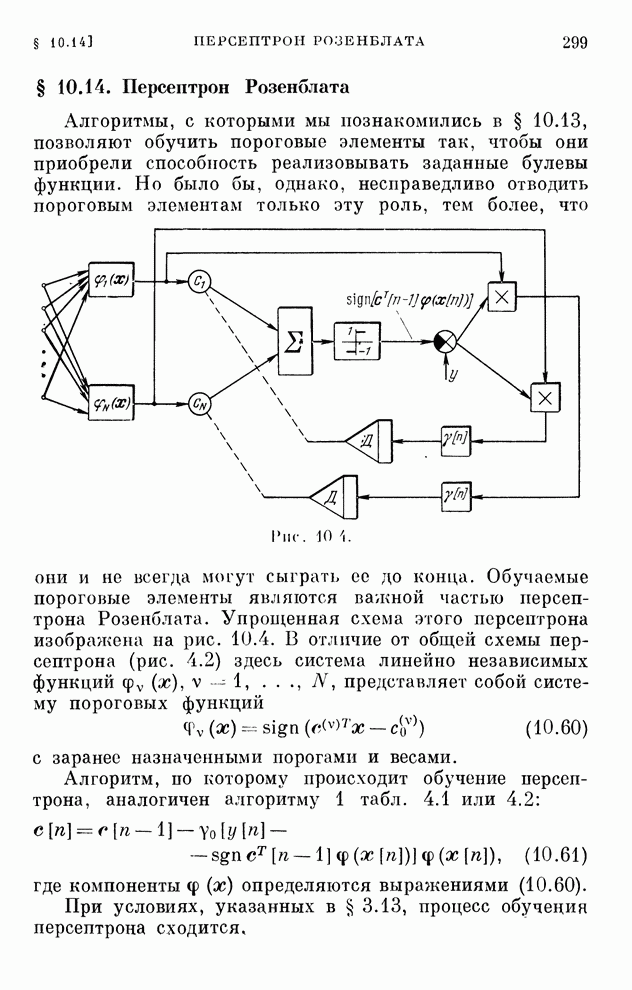
- § 10.14. Персептрон Розенблата
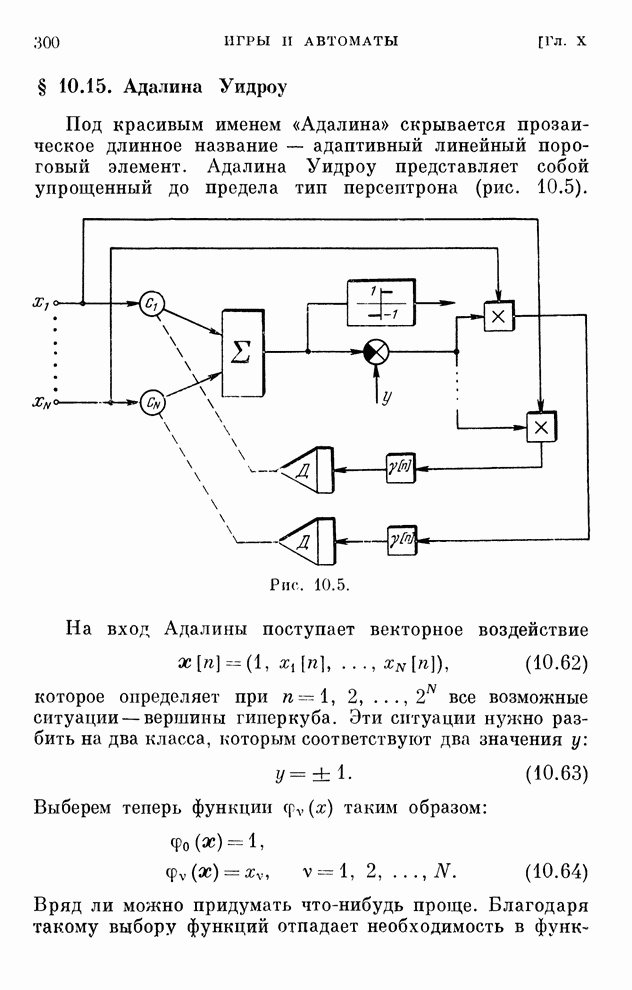
- § 10.15. Адалина Уидроу
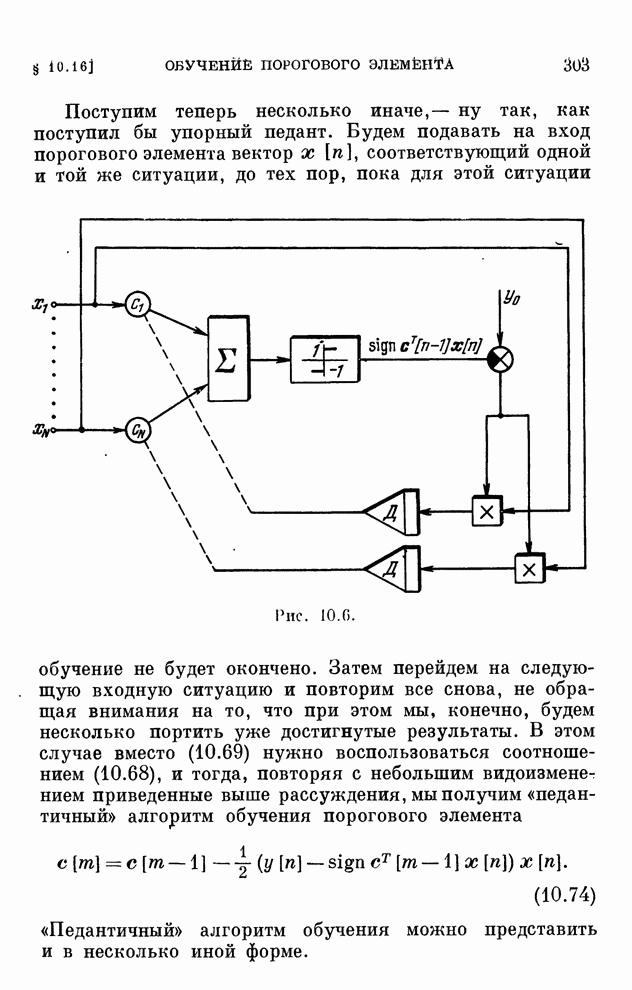
- § 10.16. Обучение порогового элемента
- § 10.17. Автоматы
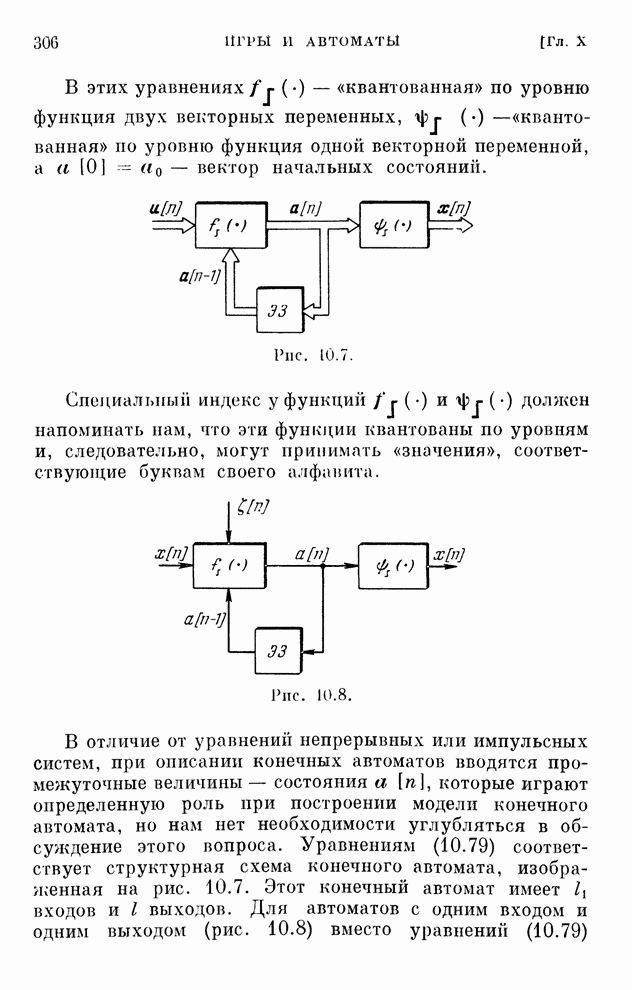
- § 10.18. Описание конечных автоматов
- § 10.19. Стохастические конечные автоматы
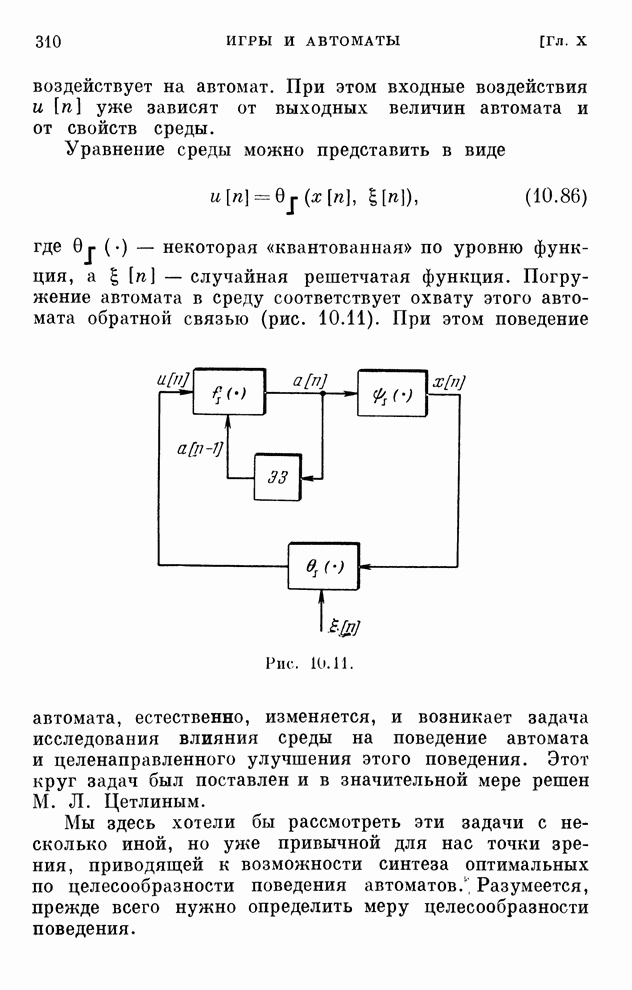
- § 10.20. Взаимодействие автомата со средой
- § 10.21. О мере целесообразности поведения
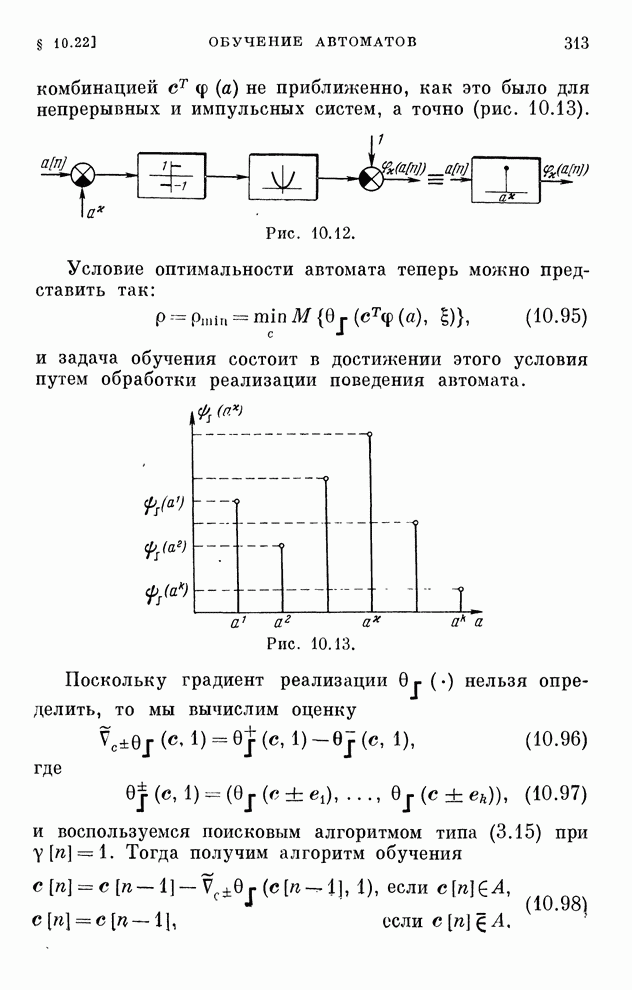
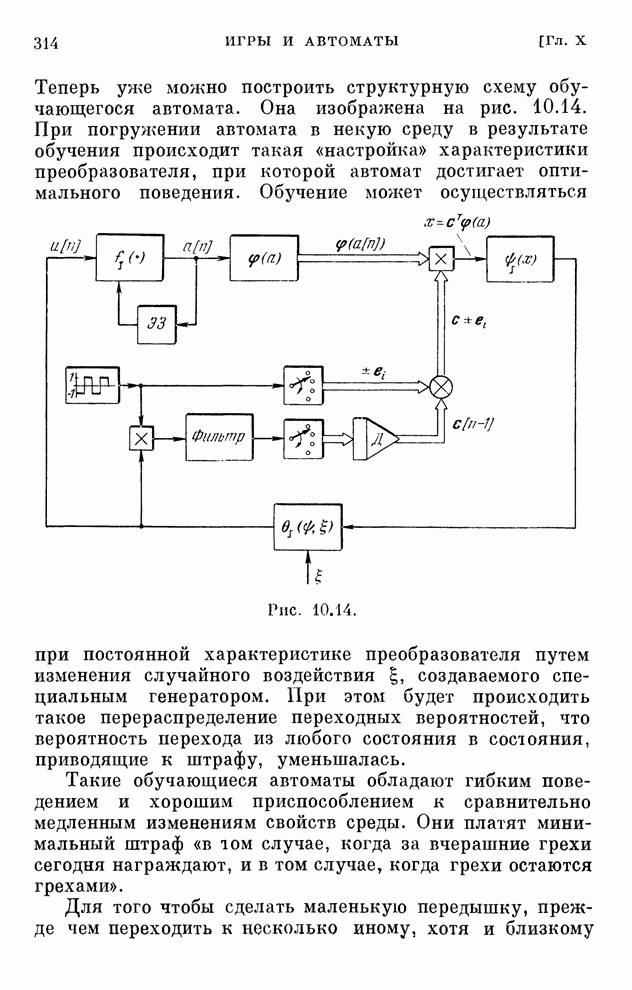
- § 10.22. Обучение автоматов
- § 10.23. О марковских цепях
- § 10.24. Марковское обучение
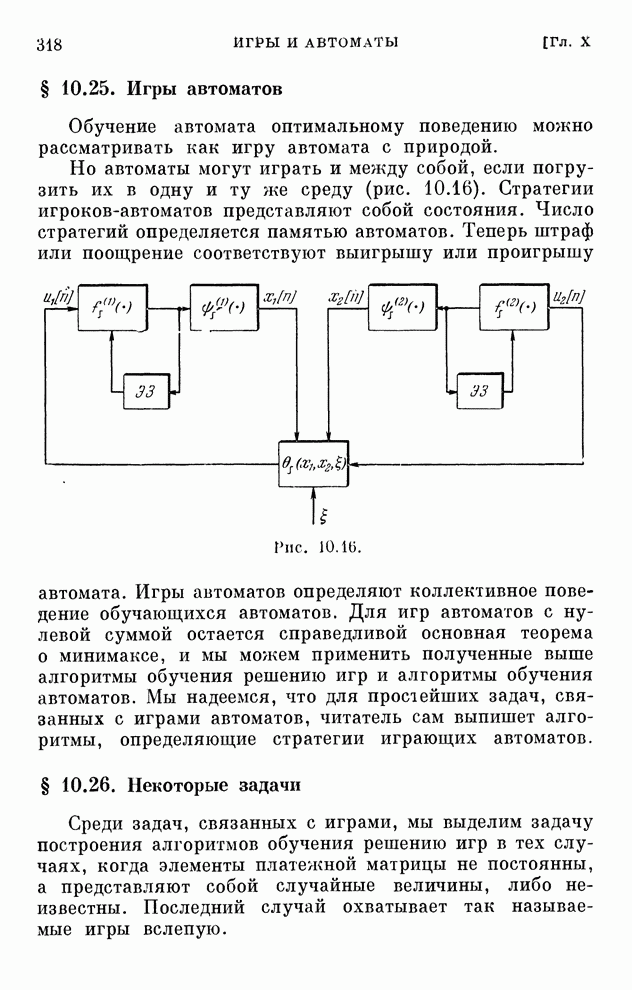
- § 10.25. Игры автоматов
- § 10.26. Некоторые задачи
- § 10.27. Заключение
- Послесловие
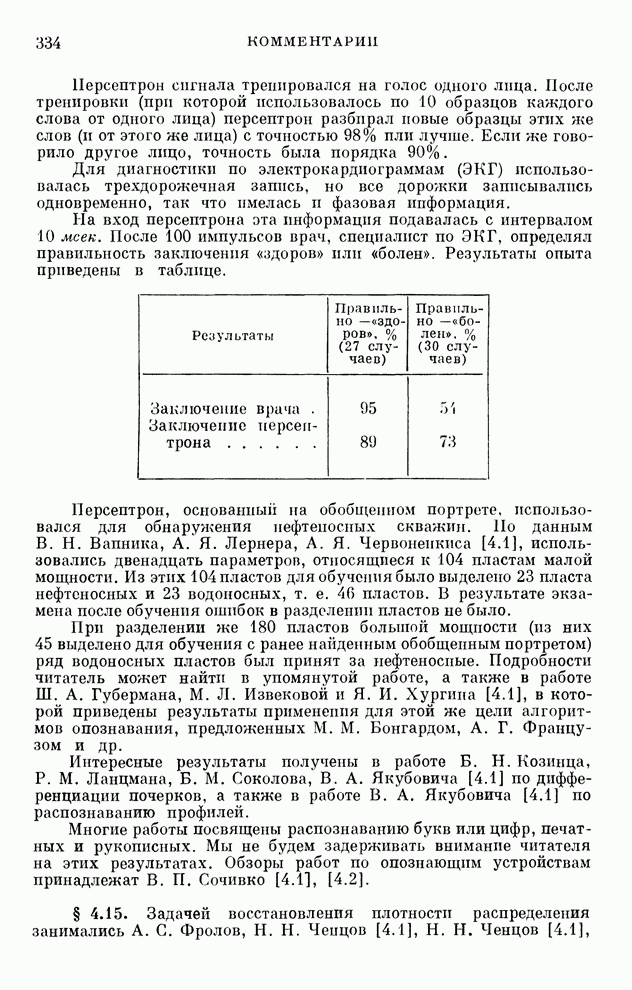
- Комментарии
- Литература