| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 2.9. Учет ограничений II
Ограничения типа неравенств не позволяют использовать классические подходы, которые мы до сих пор широко использовали. Для учета ограничений этого типа приходится прибегать к новому математическому аппарату — математическому программированию, возникшему сравнительно недавно.
Условия оптимальности в этом
случае даются теоремой Куна — Таккера, которая представляет собой обобщение
метода Лагранжа на случай ограничений типа неравенств. Теорема Куна — Таккера
утверждает, что оптимальный вектор ![]() удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
 (2.29)
(2.29)
Условия записаны в векторной
форме, ![]() ,
, ![]() ; неравенства
; неравенства ![]() ,
, ![]() означают, что все компоненты
этих векторов неотрицательны. Кроме того, предполагается, что ограничения
(1.14) таковы, что существует вектор
означают, что все компоненты
этих векторов неотрицательны. Кроме того, предполагается, что ограничения
(1.14) таковы, что существует вектор ![]() , для которого
, для которого
![]()
![]() . (2.30)
. (2.30)
Это — известное в теории нелинейного программирования условие регулярности Слейтера.
Условия (2.29) имеют простой
смысл: если для оптимального вектора ![]() несущественно какое-то ограничение, т.
е.
несущественно какое-то ограничение, т.
е. ![]() для
какого-то
для
какого-то ![]() ,
то соответствующее
,
то соответствующее ![]() ;
если же
;
если же ![]() , то
в этом случае
, то
в этом случае ![]() .
.

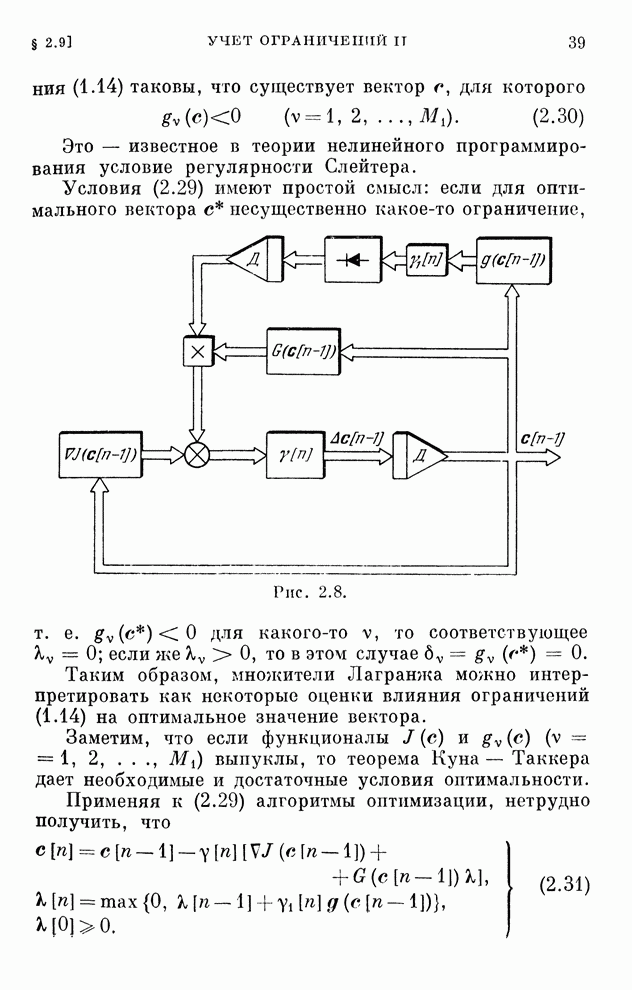
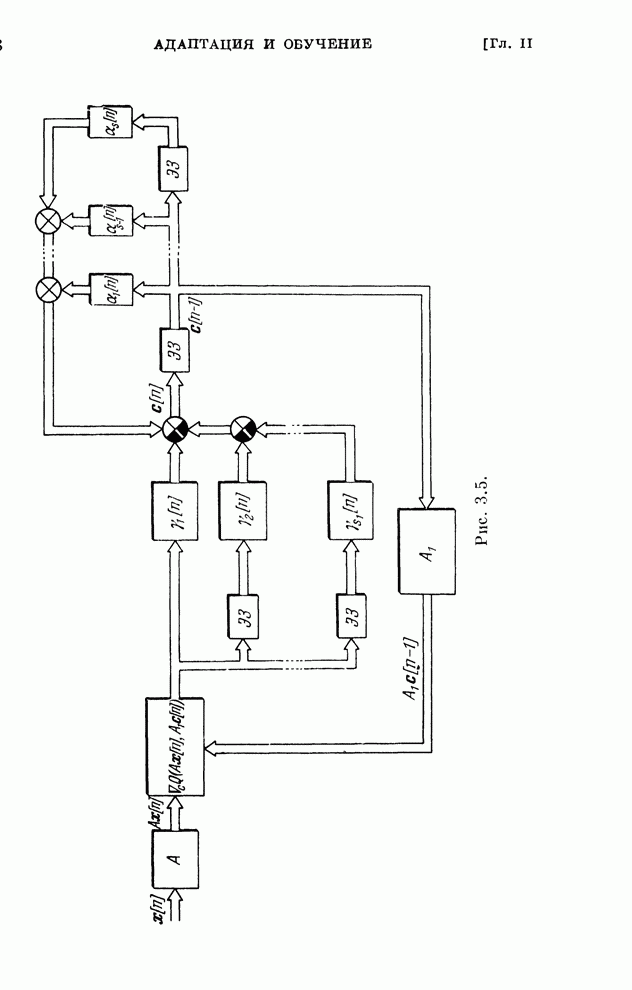
Рис. 2.8.
Таким образом, множители Лагранжа можно интерпретировать как некоторые оценки влияния ограничений (1.14) на оптимальное значение вектора.
Заметим, что если функционалы ![]() и
и ![]()
![]() выпуклы, то теорема Куна — Таккера дает
необходимые и достаточные условия оптимальности.
выпуклы, то теорема Куна — Таккера дает
необходимые и достаточные условия оптимальности.
Применяя к (2.29) алгоритмы оптимизации, нетрудно получить, что
 (2.31)
(2.31)
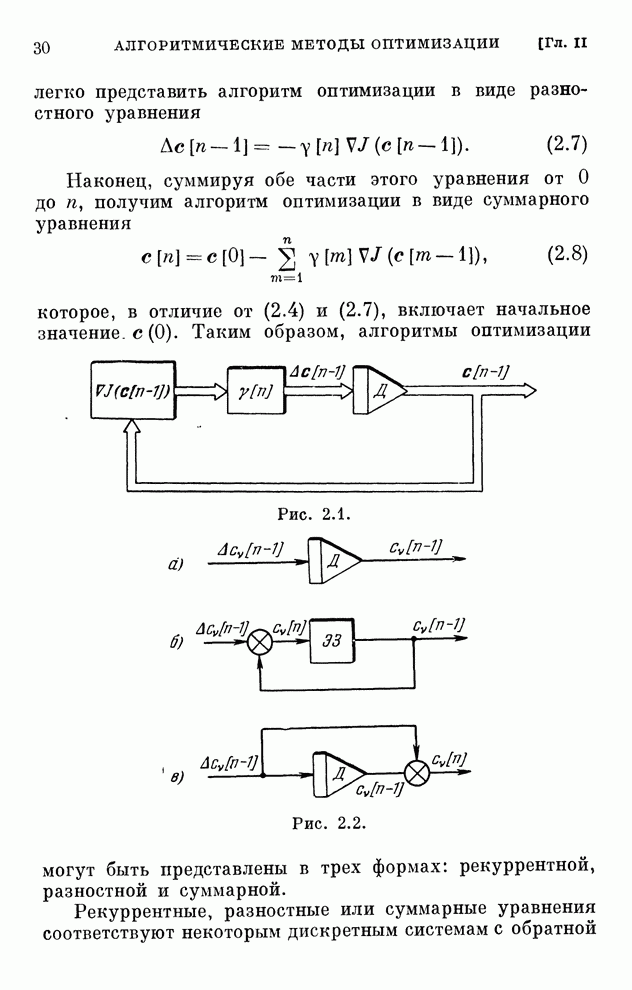
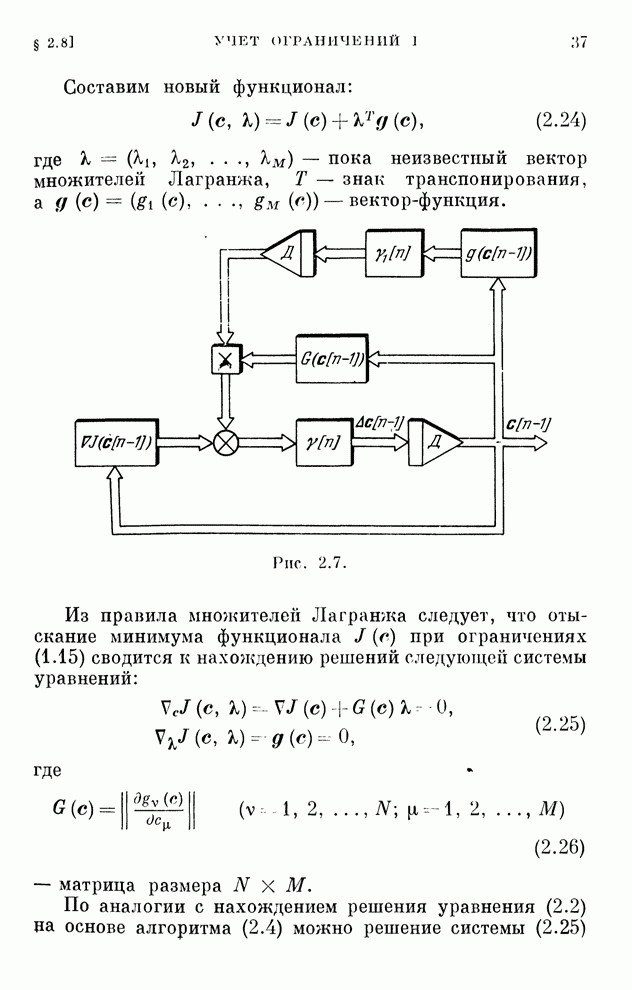
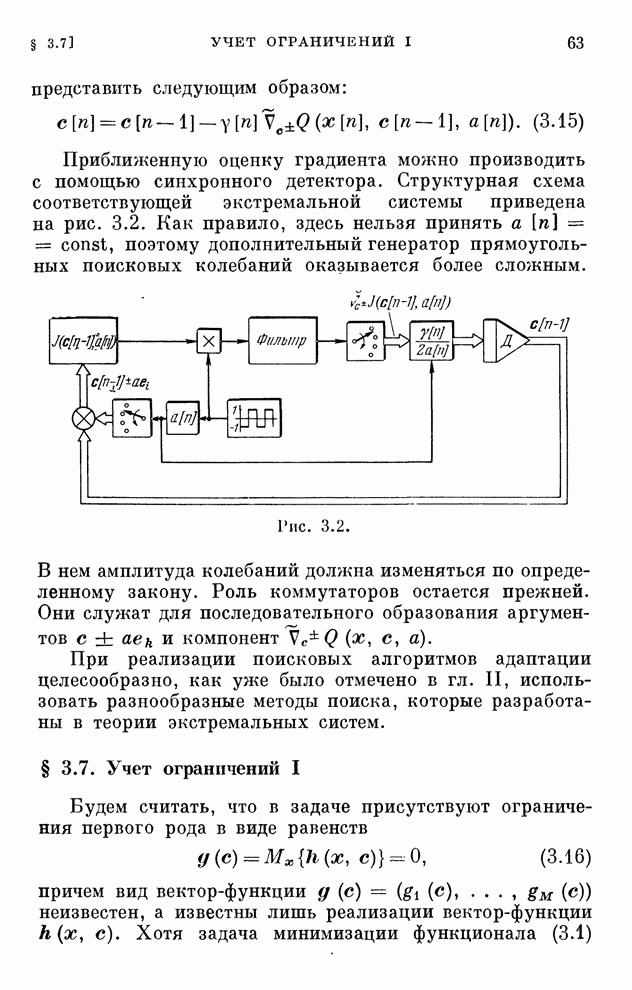
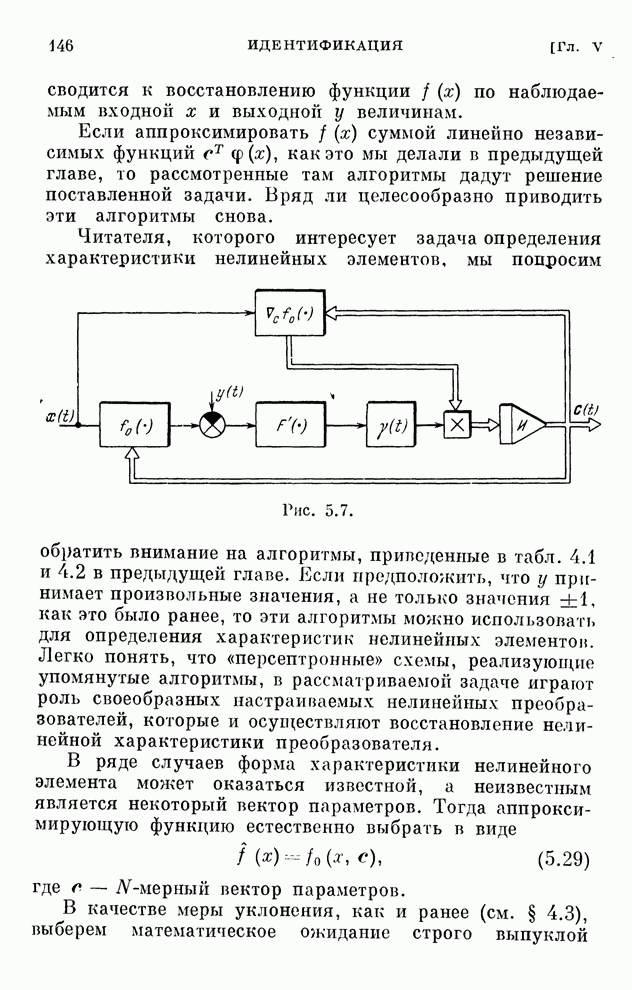
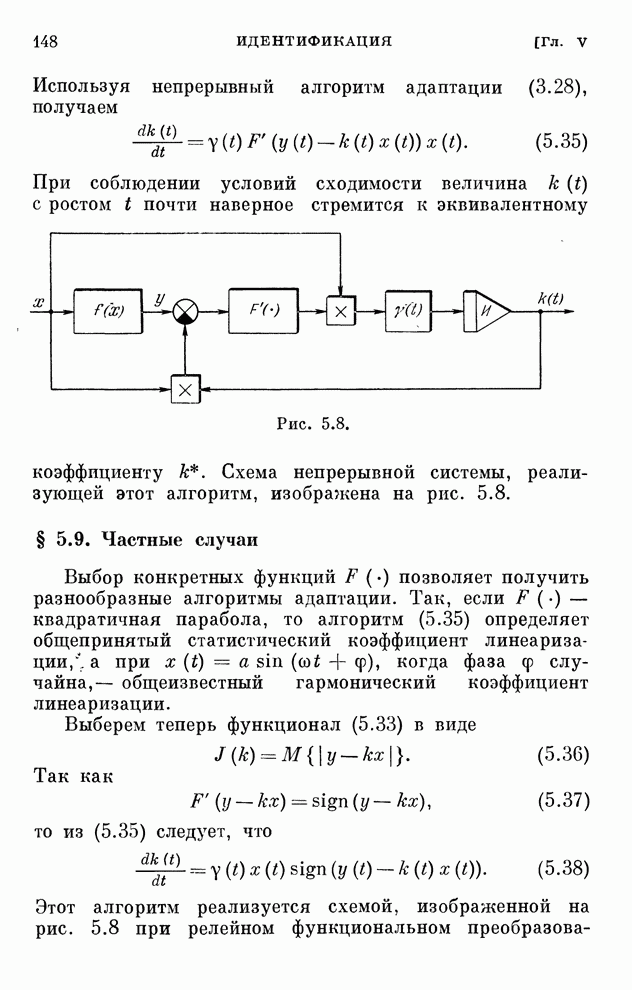
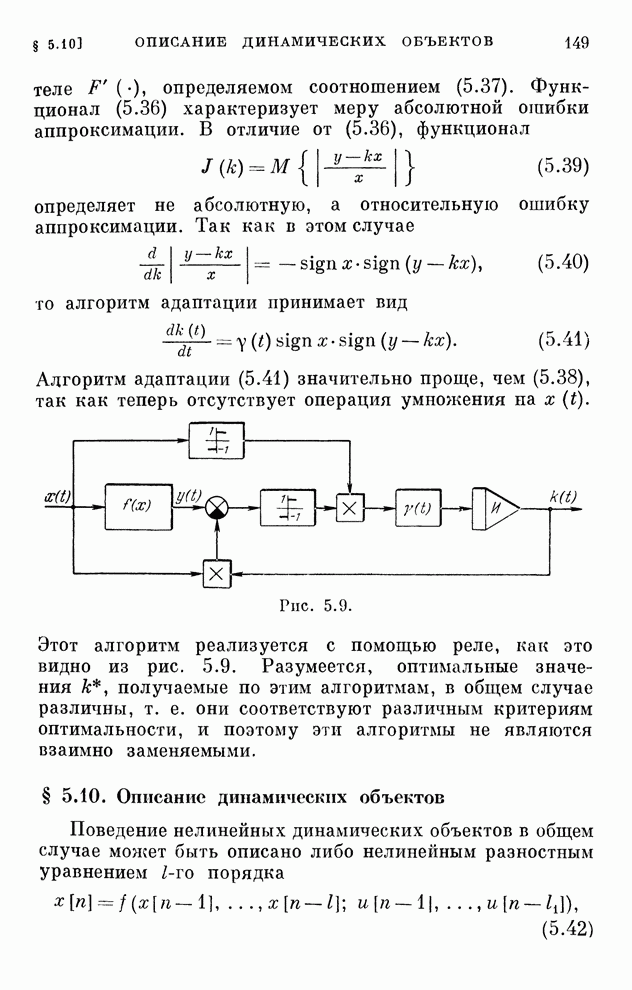
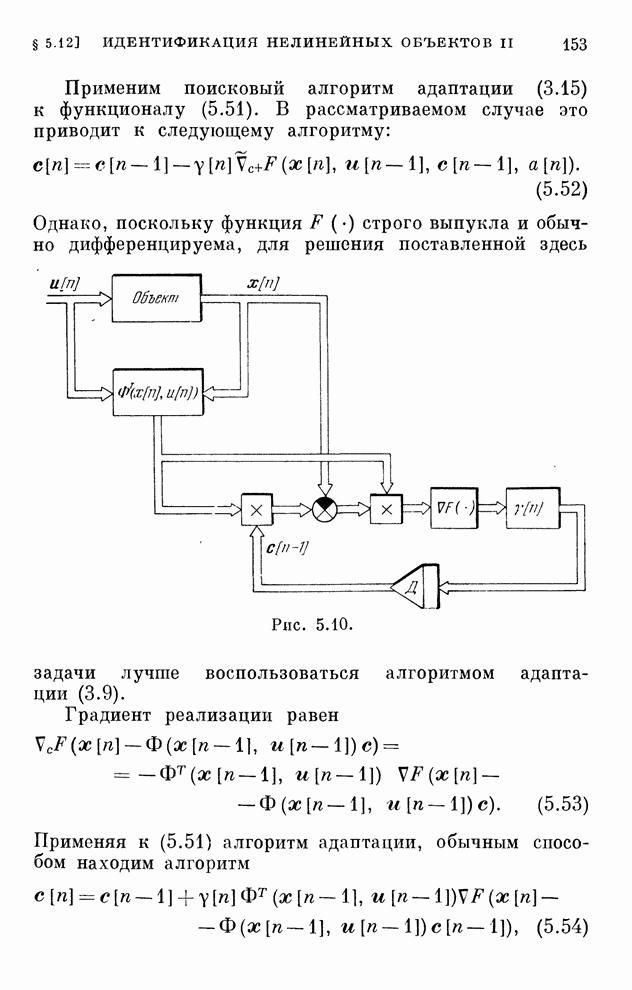
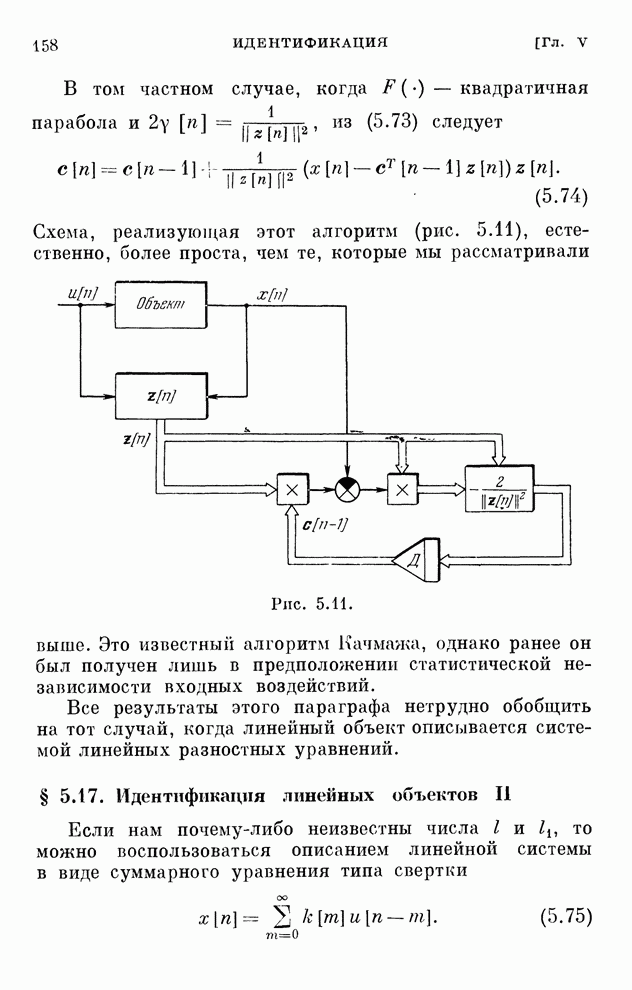
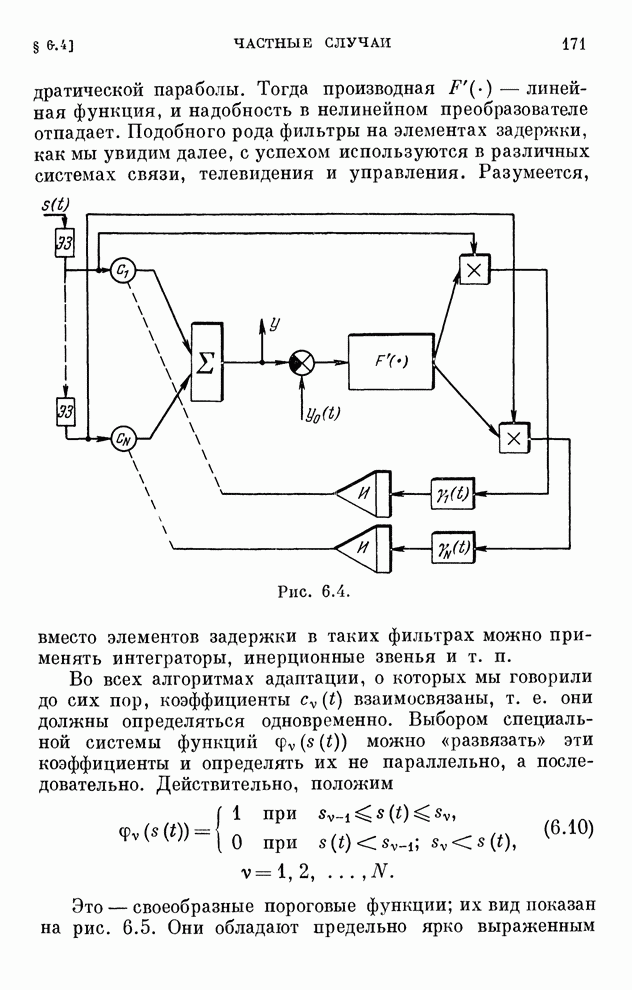
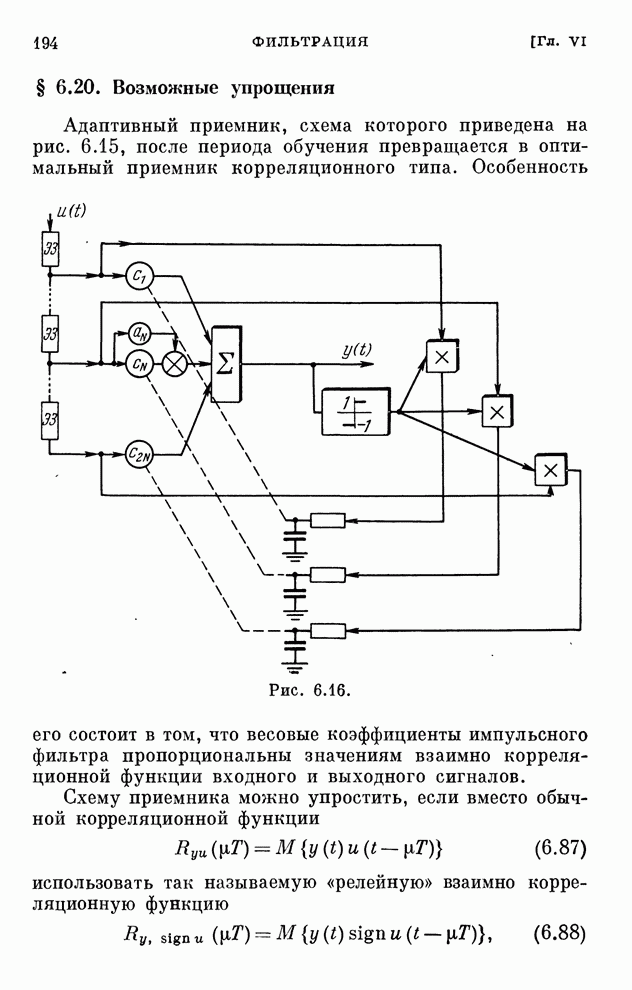
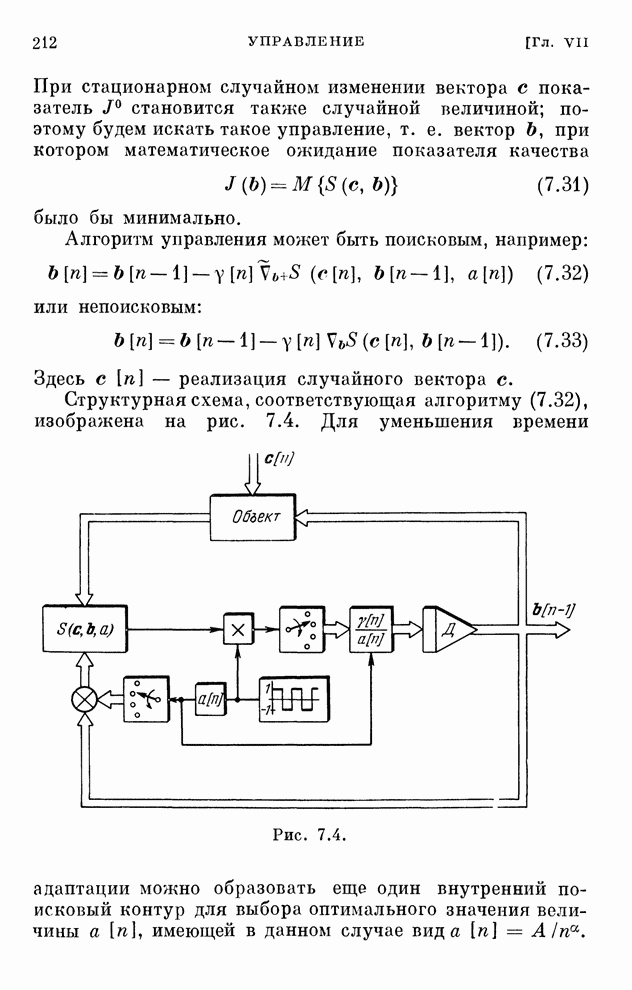
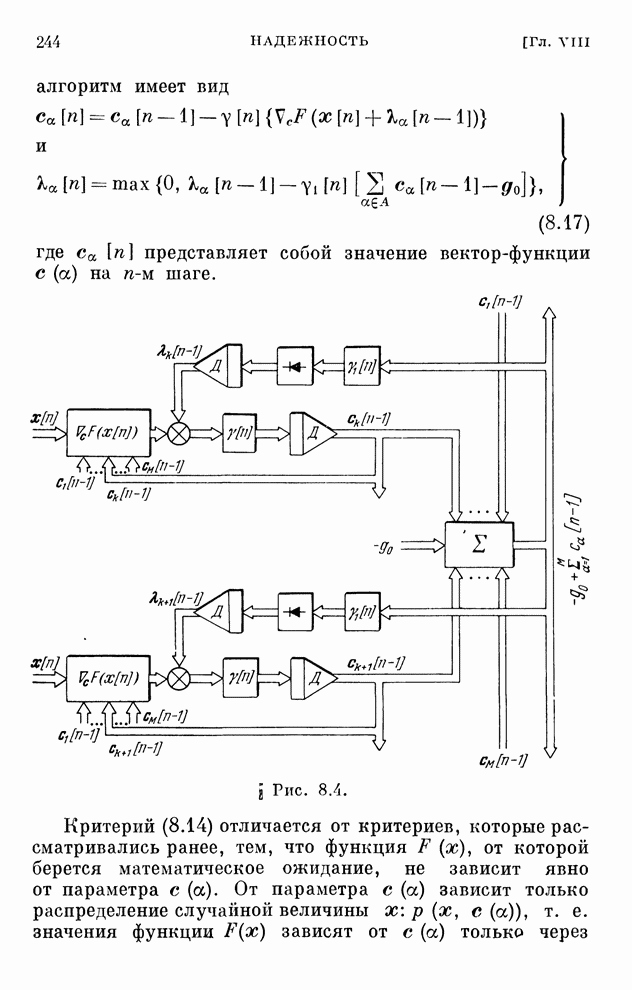
Структурная схема системы, соответствующая этому алгоритму, изображена на рис. 2.8. Она отличается от схемы рис. 2.7 только наличием однонаправленного устройства, которое обеспечивает учет ограничений в виде неравенств.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- Глава I. Проблема оптимальности
- § 1.1. Введение
- § 1.2. Критерии оптимальности
- § 1.3. Еще о критериях оптимальности
- § 1.4. Ограничения
- § 1.5. Априорная и текущая информация
- § 1.6. Детерминированные и стохастические процессы
- § 1.7. Обычный и адаптивный подходы
- § 1.8. О методах решения проблемы оптимальности
- § 1.9. Заключение
- Глава II. Алгоритмические методы оптимизации
- § 2.1. Введение
- § 2.2. Условия оптимальности
- § 2.3. Регулярный итеративный метод
- § 2.4. Алгоритмы оптимизации
- § 2.5. Возможное обобщение
- § 2.6. Разновидности алгоритмов оптимизации
- § 2.7. Поисковые алгоритмы оптимизации
- § 2.8. Учет ограничений I
- § 2.9. Учет ограничений II
- § 2.10. Методы возможных направлений
- § 2.11. Обсуждение
- § 2.12. Многошаговые алгоритмы оптимизации
- § 2.13. Непрерывные алгоритмы оптимизации
- § 2.14. Методы случайного поиска
- § 2.15. Сходимость и устойчивость
- § 2.16. Условия сходимости
- § 2.17. Об ускорении сходимости
- § 2.18. О наилучших алгоритмах
- § 2.19. Примеры
- § 2.20. Некоторые задачи
- § 2.21. Заключение
- Глава III. Адаптация и обучение
- § 3.1. Введение
- § 3.2. Понятия обучения, самообучения и адаптации
- § 3.3. Формулировка задачи
- § 3.4. Вероятностные итеративные методы
- § 3.5. Алгоритмы адаптации
- § 3.6. Поисковые алгоритмы адаптации
- § 3.7. Учет ограничений I
- § 3.8. Учет ограничений II
- § 3.9. Одно обобщение
- § 3.10. Многошаговые алгоритмы адаптации
- § 3.11. Непрерывные алгоритмы
- § 3.12. Вероятностная сходимость и устойчивость
- § 3.13. Условия сходимости
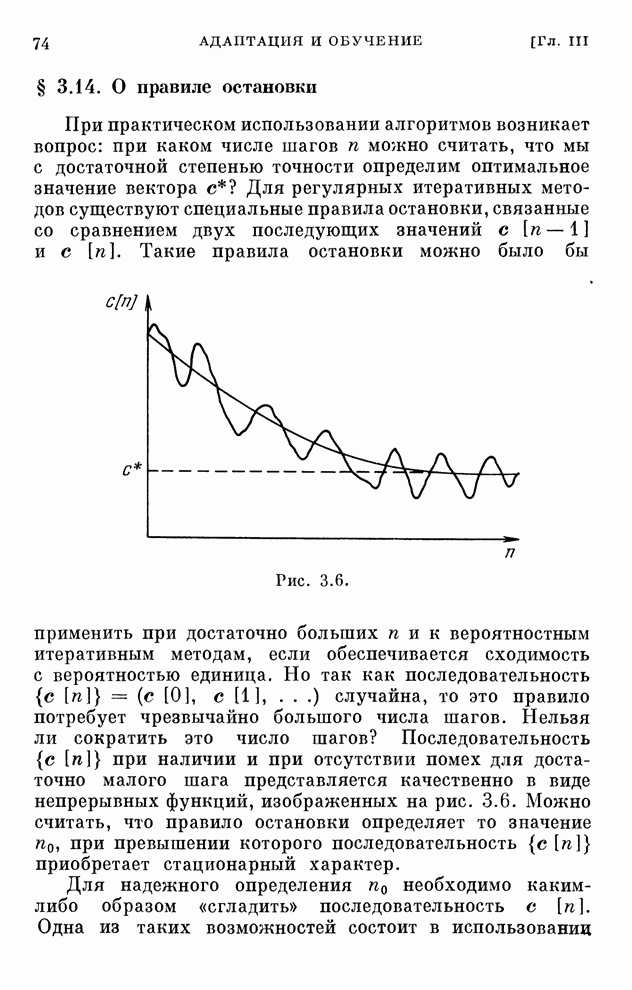
- § 3.14. О правиле остановки
- § 3.15. Об ускорении сходимости
- § 3.16. Мера качества алгоритмов
- § 3.17. Наилучшие алгоритмы
- § 3.18. Упрощенные наилучшие алгоритмы
- § 3.19. Частный случай
- § 3.20. Связь с методом наименьших квадратов
- § 3.21. Связь с байесовским методом
- § 3.22. Связь с методом максимального правдоподобия
- § 3.23. Обсуждение
- § 3.24. Некоторые задачи
- § 3.25. Заключение
- Глава IV. Опознавание
- § 4.1. Введение
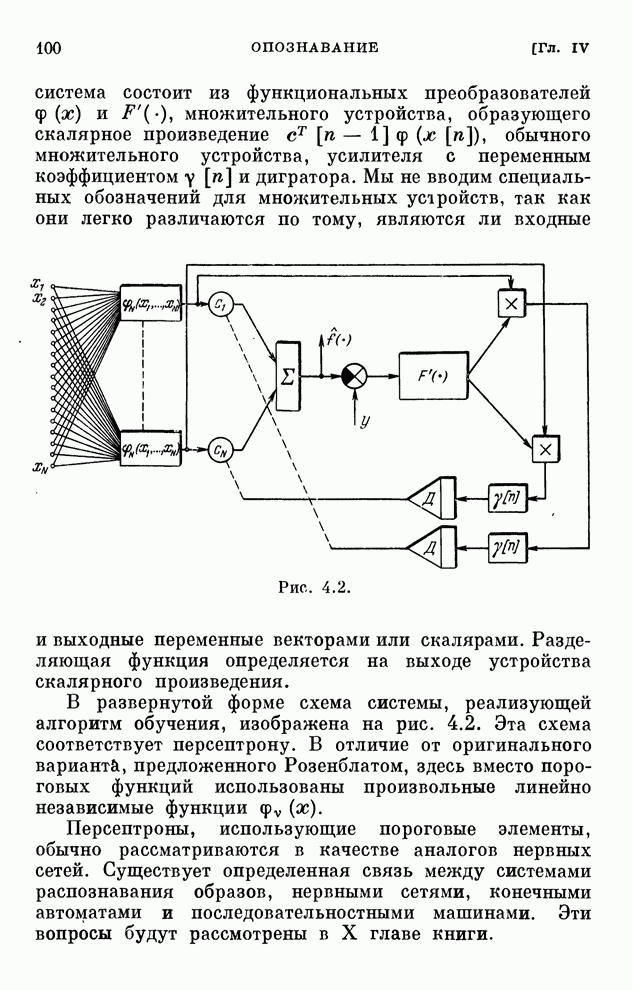
- § 4.2. Обсуждение задачи опознавания
- § 4.3. Формулировка задачи
- § 4.4. Общие алгоритмы обучения
- § 4.5. Сходимость алгоритмов
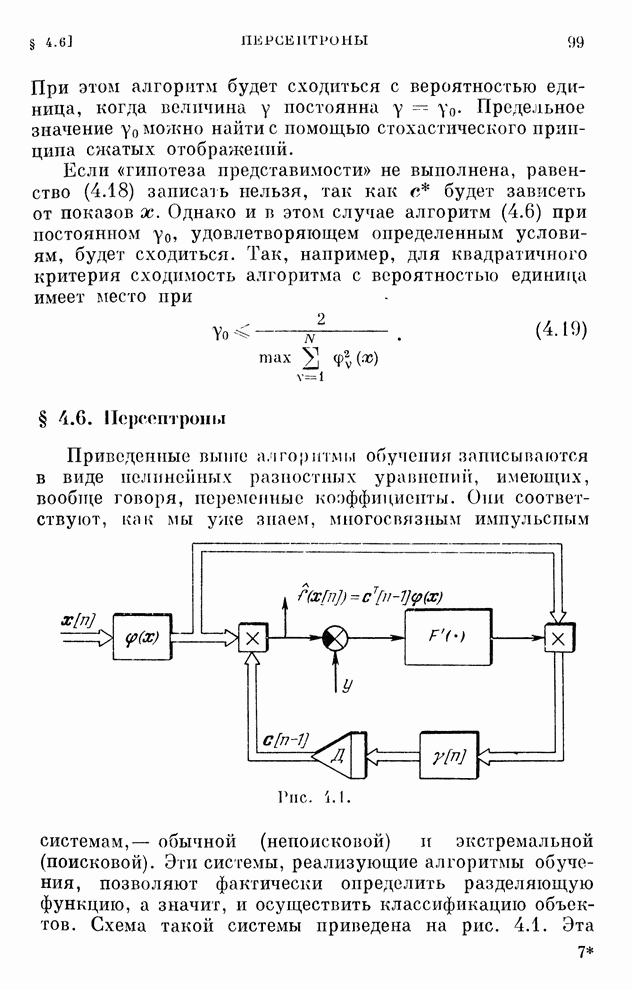
- § 4.6. Персептроны
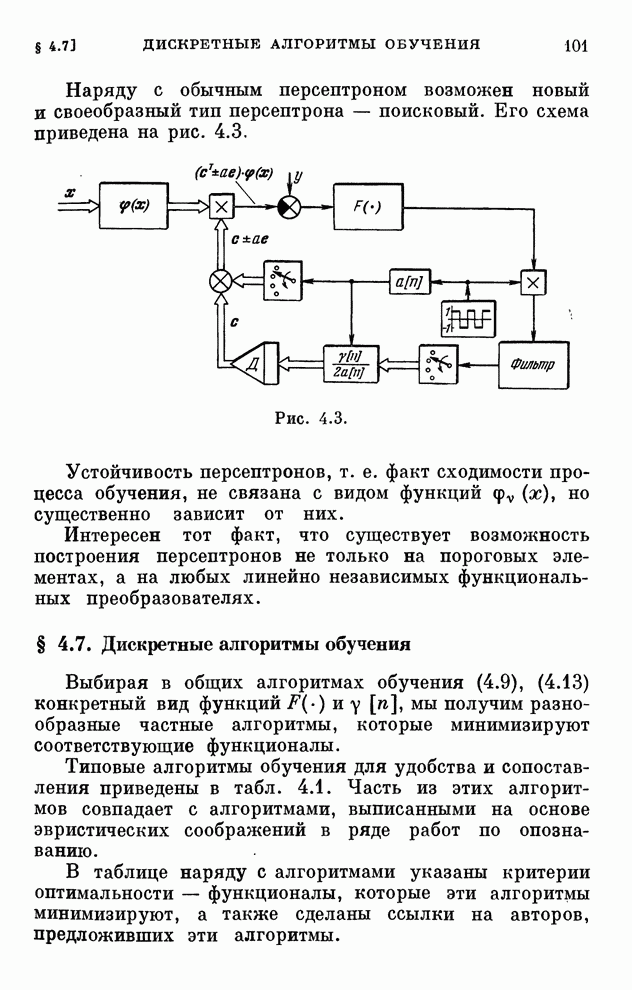
- § 4.7. Дискретные алгоритмы обучения
- § 4.8. Поисковые алгоритмы обучения
- § 4.9. Непрерывные алгоритмы обучения
- § 4.10. Замечания
- § 4.11. Еще об одном общем алгоритме обучения
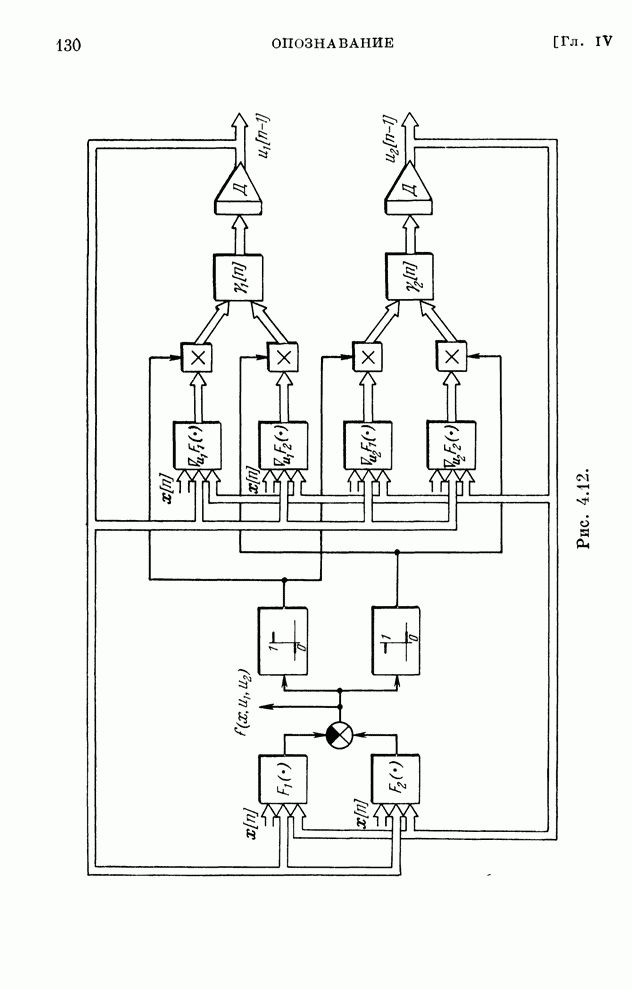
- § 4.12. Частные случаи
- § 4.13. Обсуждение
- § 4.14. О самообучении
- § 4.15. О восстановлении плотности распределения и моментов
- § 4.10. Алгоритмы восстановления
- § 4.17. Принципы самообучения
- § 4.18. Средний риск
- § 4.19. Вариация среднего риска
- § 4.20. Условия минимума среднего риска
- § 4.21. Алгоритмы самообучения
- § 4.22. Обобщение
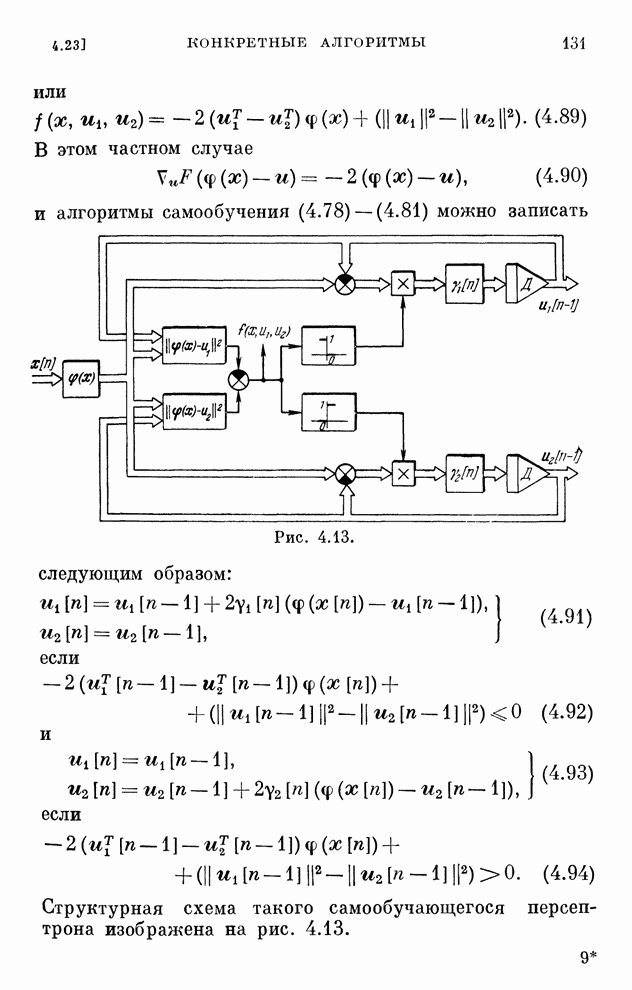
- § 4.23. Конкретные алгоритмы
- § 4.24. Поисковые алгоритмы самообучения
- § 4.25. Обсуждение
- § 4.26. Некоторые задачи
- § 4.27. Заключение
- Глава V. Идентификация
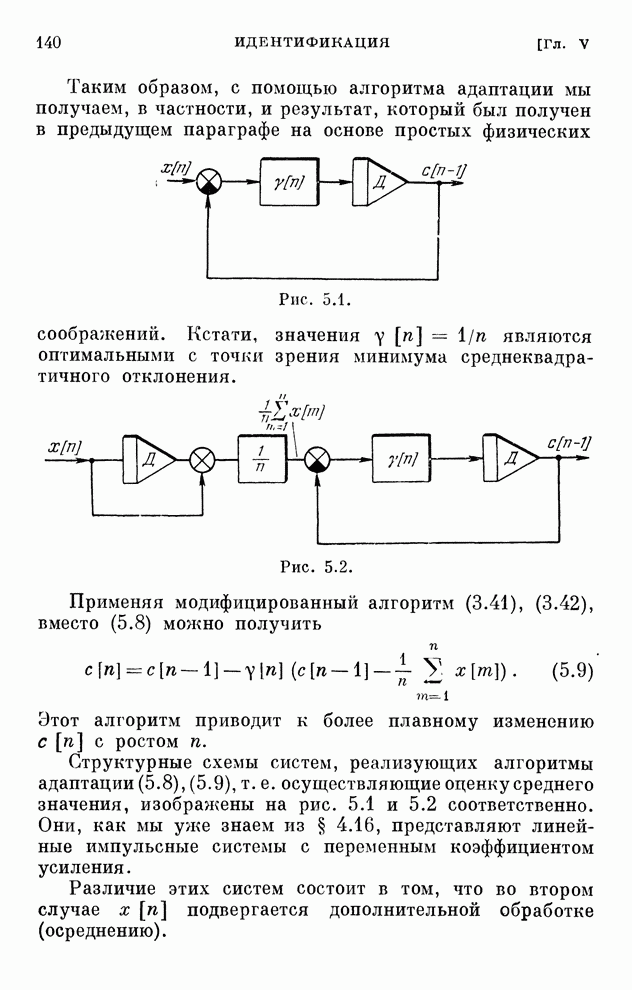
- § 5.1. Введение
- § 5.2. Оценка среднего значения
- § 5.3. Другой подход
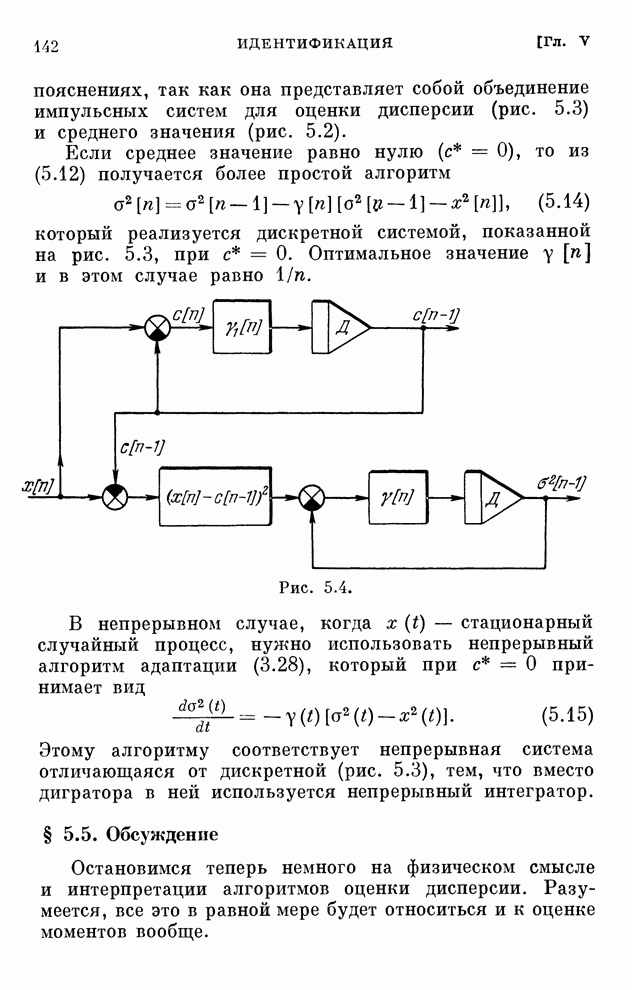
- § 5.4. Оценка дисперсии
- § 5.5. Обсуждение
- § 5.6. Оценка корреляционных функций
- § 5.7. Определение характеристик нелинейных элементов
- § 5.8. Оценка коэффициента статистической линеаризации
- § 5.9. Частные случаи
- § 5.10. Описание динамических объектов
- § 5.11. Идентификация нелинейных объектов I
- § 5.12. Идентификация нелинейных объектов II
- § 5.13. Идентификация нелинейных объектов III
- § 5.14. Специальный случай
- § 5.15. Замечание
- § 5.16. Идентификация линейных объектов I
- § 5.17. Идентификация линейных объектов II
- § 5.18. Оценка параметров распределенных объектов
- § 5.19. Помехи
- § 5.20. Устранение влияния помех
- § 5.21. Некоторые задачи
- § 5.22. Заключение
- Глава VI. Фильтрация
- § 6.1. Введение
- § 6.2. Критерий оптимальности
- § 6.3. Структура адаптивного фильтра
- § 6.4. Частные случаи
- § 6.5. Адаптивный корректор искажений
- § 6.6. Поисковые адаптивные фильтры
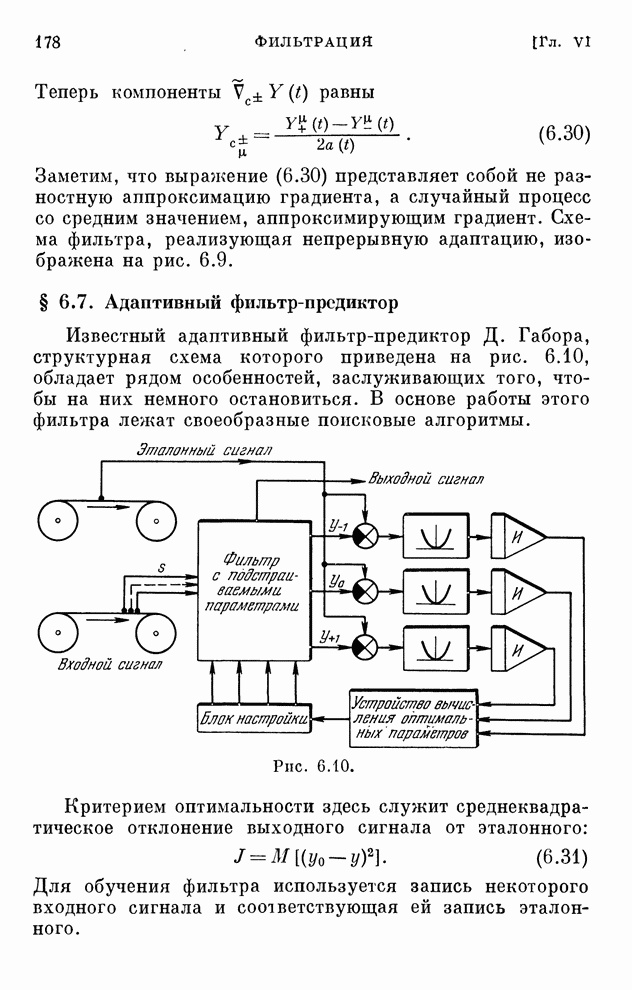
- § 6.7. Адаптивный фильтр-предиктор
- § 6.9. Статистическая теория приема
- § 6.10. Критерий оптимальности приема
- § 6.11. Определение решающего правила
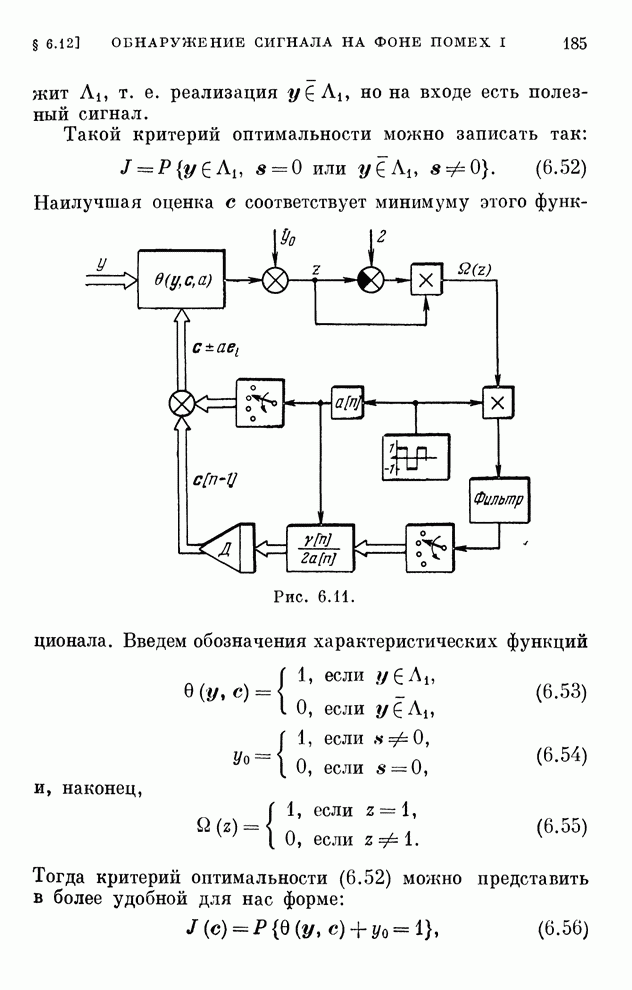
- § 6.12. Обнаружение сигнала на фоне помех I
- § 6.13. Обнаружение сигнала на фоне помех II
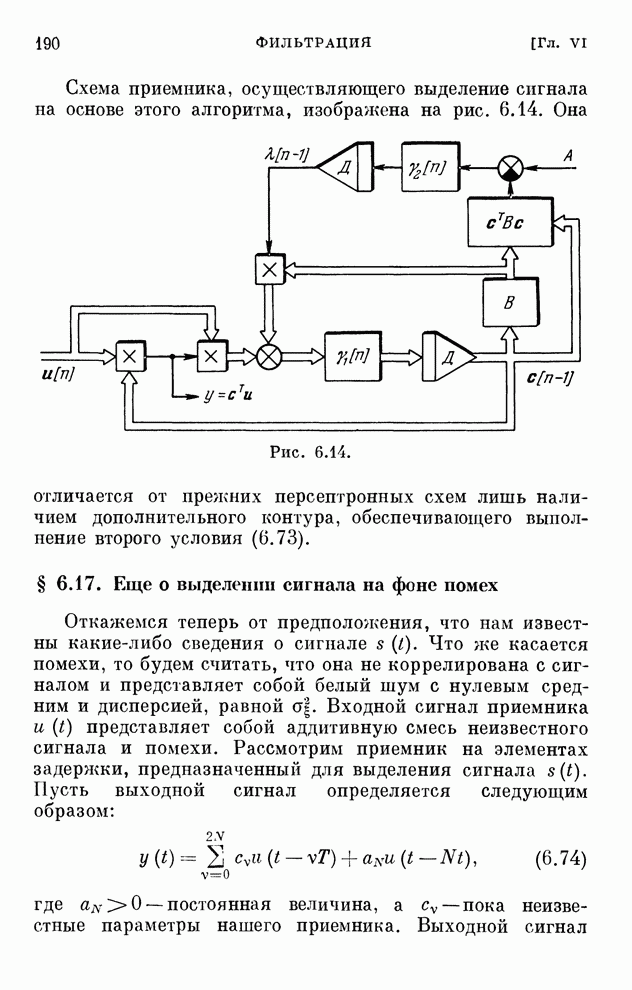
- § 6.14. Выделение сигнала на фоне помех
- § 6.15. Критерий оптимального выделения
- § 6.16. Алгоритм выделения
- § 6.17. Еще о выделении сигнала на фоне помех
- § 6.18. Другой критерий оптимальности
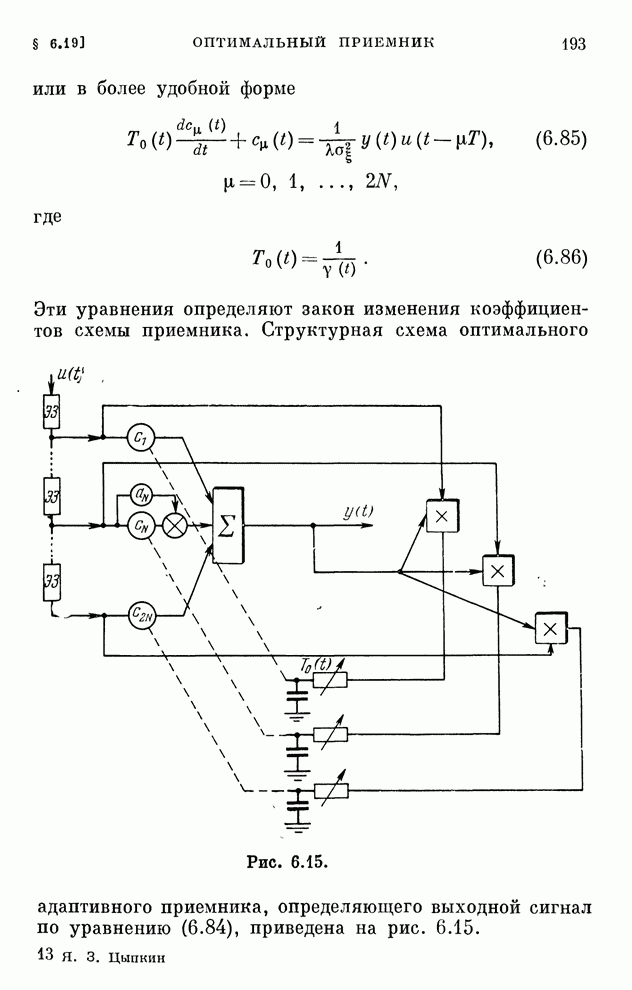
- § 6.19. Оптимальный приемник
- § 6.20. Возможные упрощения
- § 6.21. Восстановление входных сигналов
- § 6.22. Алгоритмы восстановления
- § 6.23. О влиянии помех
- § 6.24. Некоторые задачи
- § 6.25. Заключение
- Глава VII. Управление
- § 7.1. Введение
- § 7.2. Когда нужна адаптация?
- § 7.3. Постановка задачи
- § 7.4. Дуальное управление
- § 7.5. Алгоритмы дуального управления
- § 7.6. Адаптивные системы управления I
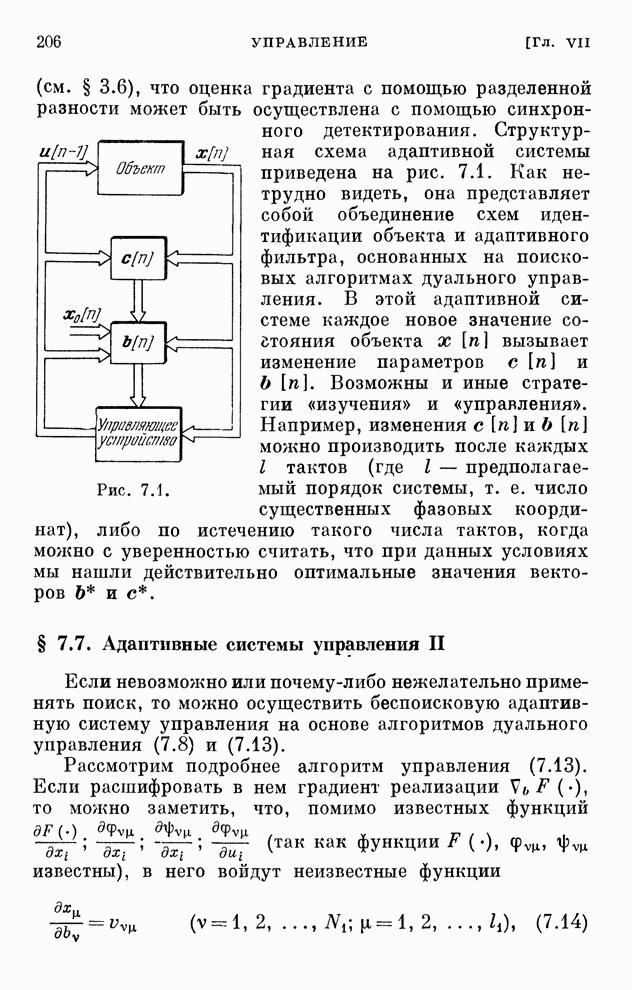
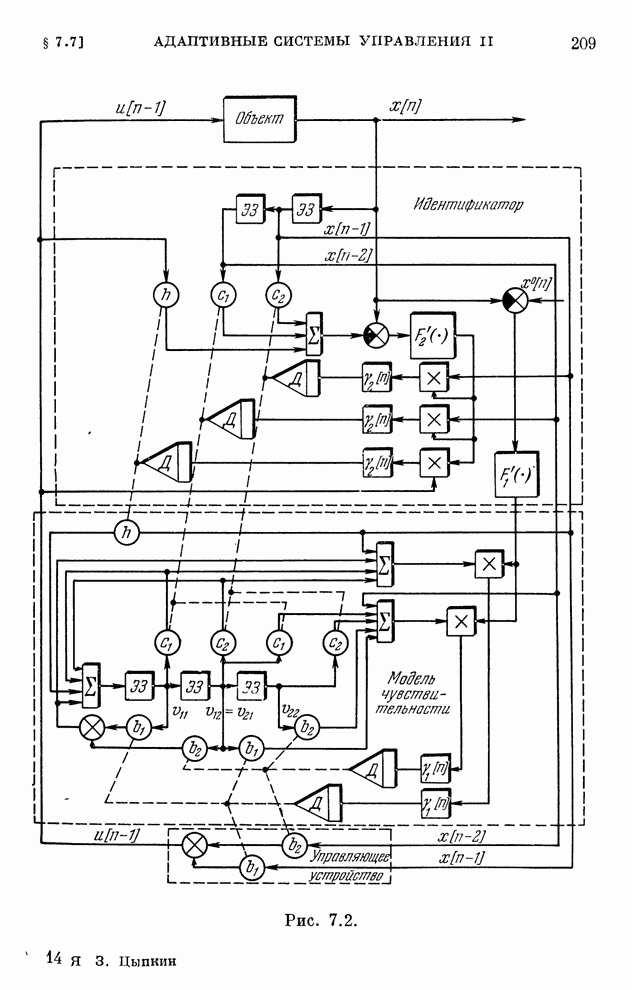
- § 7.7. Адаптивные системы управления II
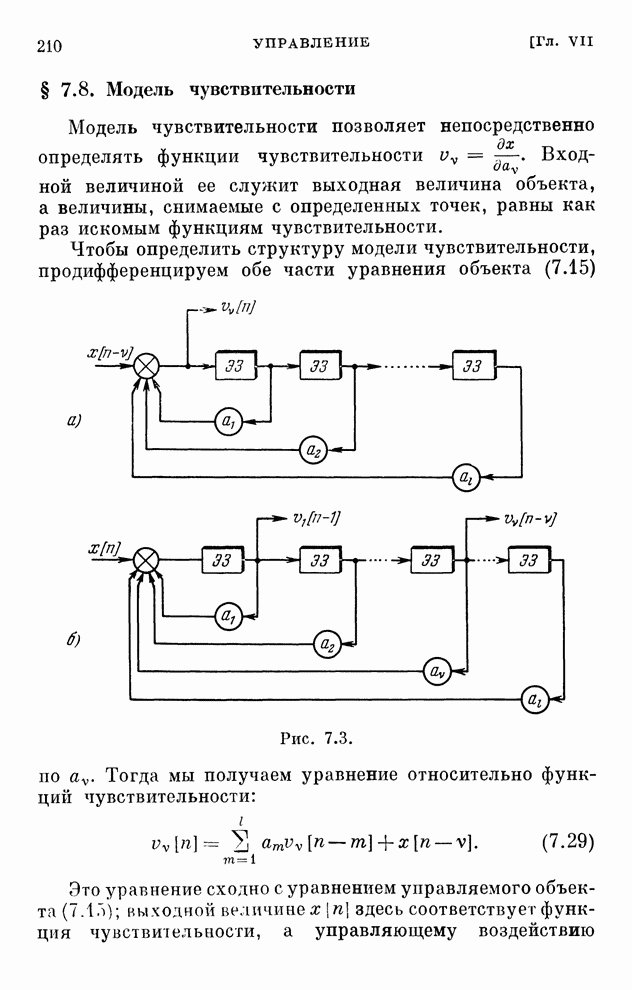
- § 7.8. Модель чувствительности
- § 7.9. Адаптивные системы управления III
- § 7.10. Упрощенные адаптивные системы
- § 7.11. Системы управления по возмущению
- § 7.12. Алгоритмы оптимального управления
- § 7.13. Еще одна возможность
- § 7.14. Экстремальные системы управления
- § 7.15. Алгоритмы экстремального управления
- § 7.16. Алгоритмы изучения
- § 7.17. Непрерывные алгоритмы
- § 7.18. Структурная схема
- § 7.19. Возможные упрощения
- § 7.20. О синтезе оптимальных систем
- § 7.21. Применение алгоритмов адаптации
- § 7.22. О синтезе оптимальных систем при наличии помех
- § 7.23. Управление и опознавание
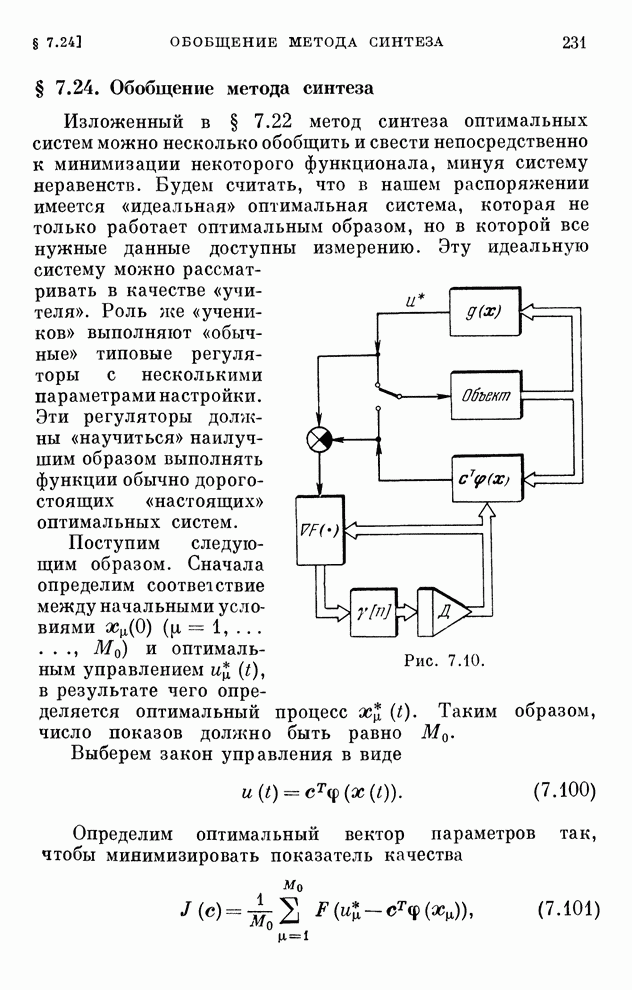
- § 7.24. Обобщение метода синтеза
- § 7.25. Некоторые задачи
- § 7.26. Заключение
- Глава VIII. Надежность
- § 8.1. Введение
- § 8.2. Понятие надежности
- § 8.4. Определение показателей надежности
- § 8.5. Минимизация эксплуатационных расходов
- § 8.6. Частный случай
- § 8.7. Минимизация стоимости, веса, объема
- § 8.8. Алгоритмы минимизации
- § 8.9. Особый случай
- § 8.10. Алгоритмы
- § 8.11. Повышение надежности путем резервирования
- § 8.12. Повышение надежности путем избыточности
- § 8.13. Проектирование сложных систем
- § 8.14. Алгоритмы оптимальной работоспособности
- § 8.15. О минимаксном критерии оптимизации
- § 8.16. Еще о проектировании сложных систем
- § 8.17. Замечание
- § 8.18. Некоторые задачи
- § 8.19. Заключение
- Глава IX. Исследование операций
- § 9.1. Введение
- § 9.2. Планирование запасов
- § 9.3. Критерий оптимальности планирования
- § 9.4. Алгоритмы оптимального планировании
- § 9.5. Еще о планировании запасов
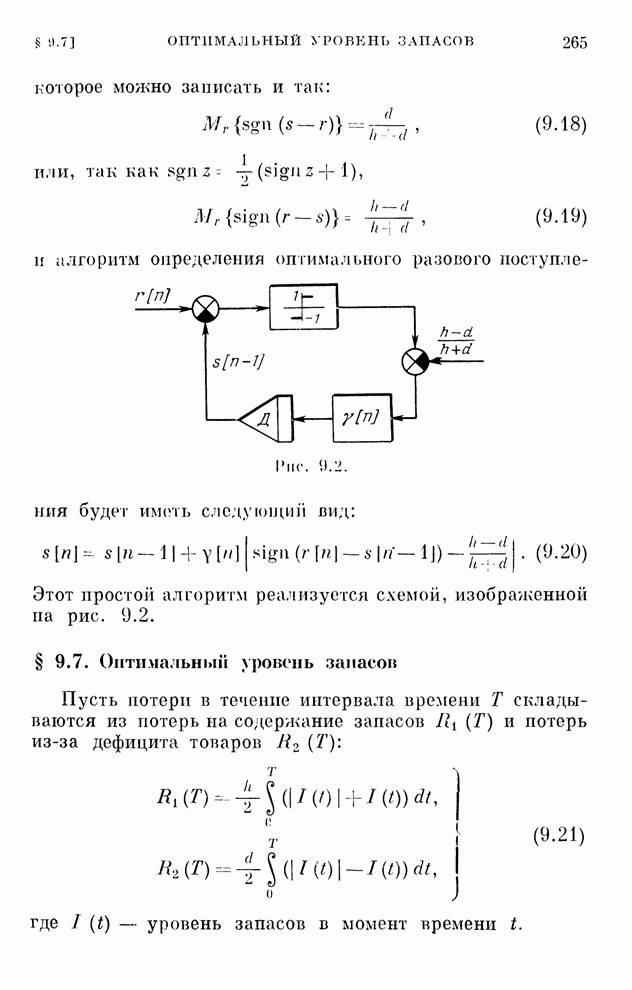
- § 9.6. Оптимальное разовое поступление
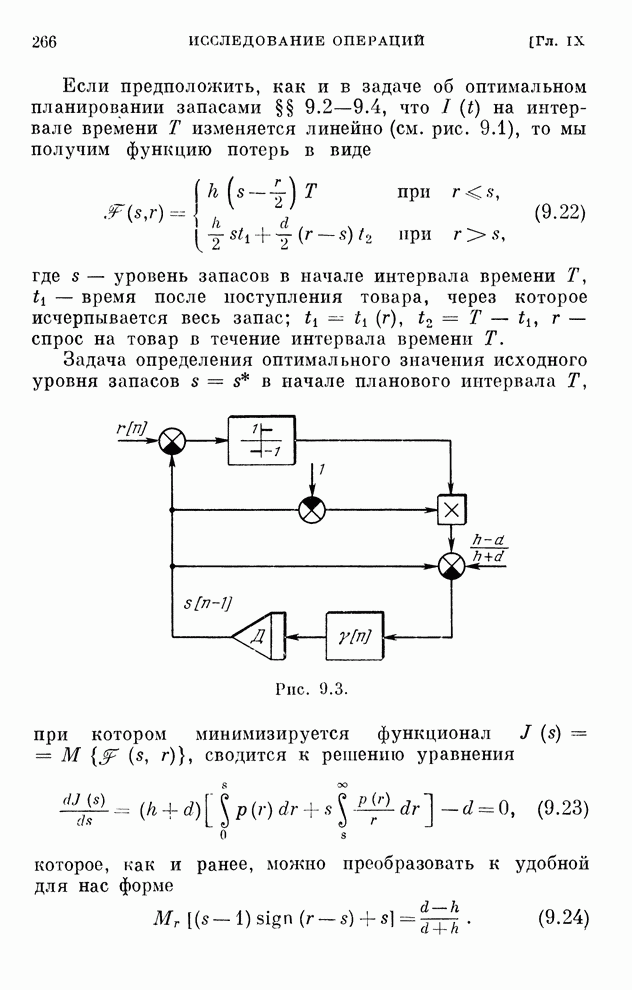
- § 9.7. Оптимальный уровень запасов
- § 9.8. Замечание
- § 9.9. Распределение производственных мощностей
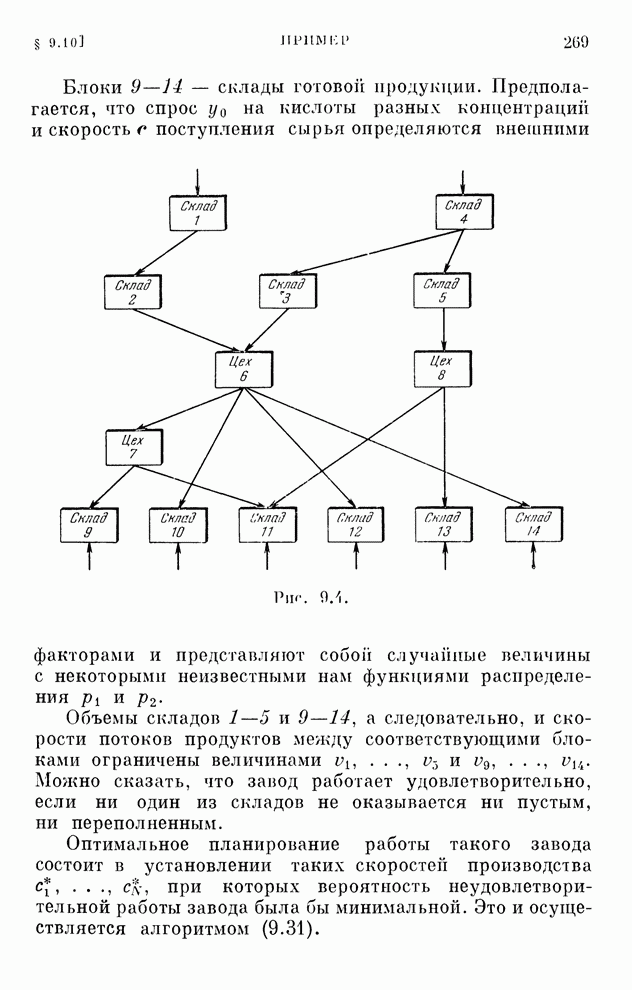
- § 9.10. Пример
- § 9.11. Распределение средств обнаружения
- § 9.12. Алгоритм оптимального распределения
- § 9.13. Распределение областей дискретизации
- § 9.14. Критерии оптимальности распределения
- § 9.15. Алгоритм оптимальных оценок
- § 9.16. Некоторые задачи
- § 9.17. Заключение
- Глава X. Игры и автоматы
- § 10.1. Введение
- § 10.2. Понятие игры
- § 10.3. Теорема о минимаксе
- § 10.4. Уравнения оптимальных стратегий
- § 10.5. Алгоритмы обучения решению игр
- § 10.6. Игры и линейное программирование
- § 10.7. Управление как игра
- § 10.8. Алгоритмы управления
- § 10.9. Одно обобщение
- § 10.10. Пороговые элементы
- § 10.11. О пороговой реализуемости логических функции
- § 10.12. Критерий реализуемости
- § 10.13. Алгоритмы реализуемости
- § 10.14. Персептрон Розенблата
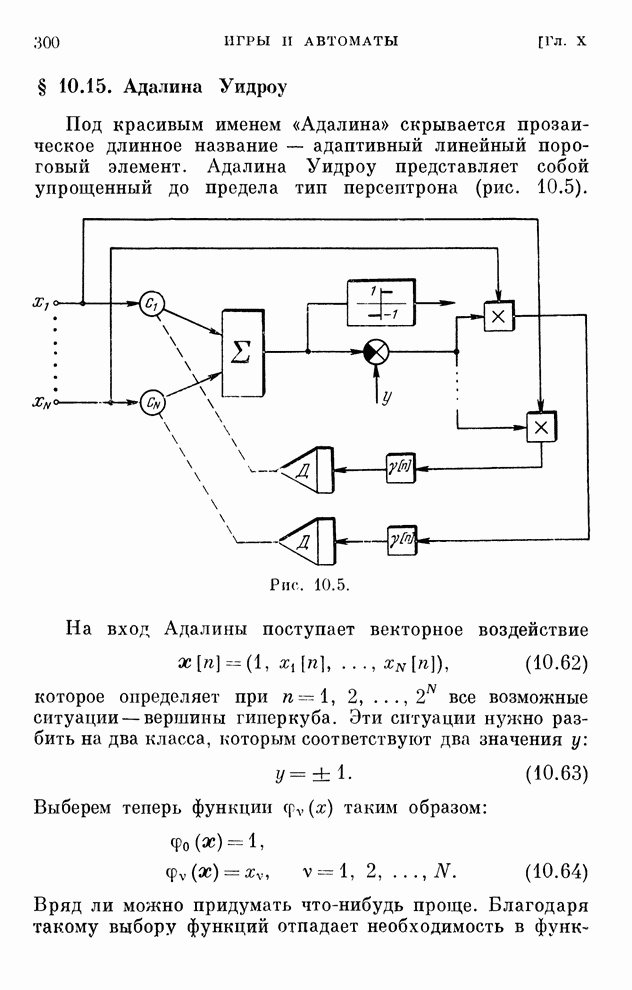
- § 10.15. Адалина Уидроу
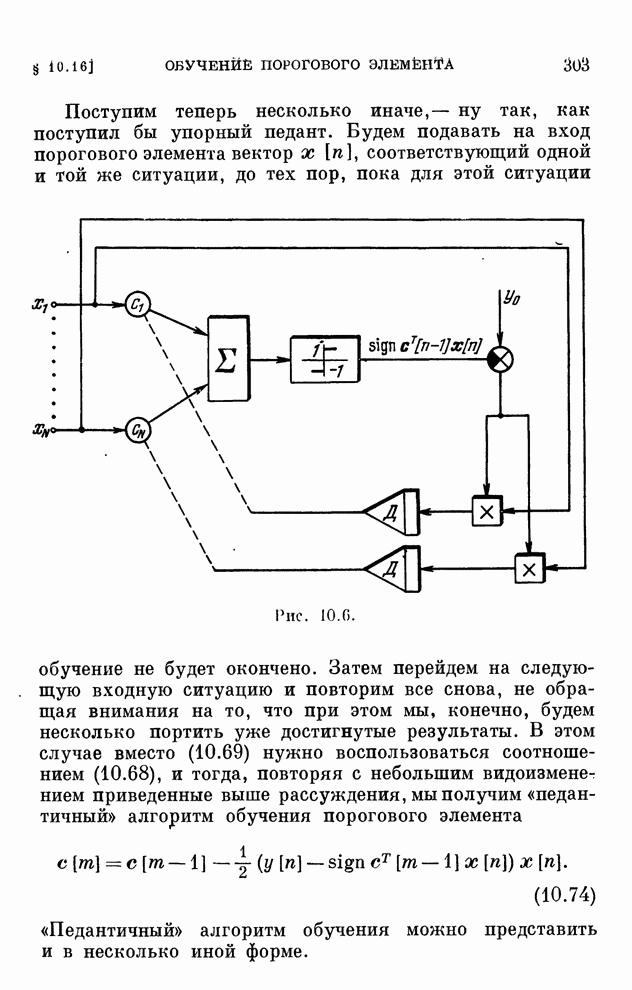
- § 10.16. Обучение порогового элемента
- § 10.17. Автоматы
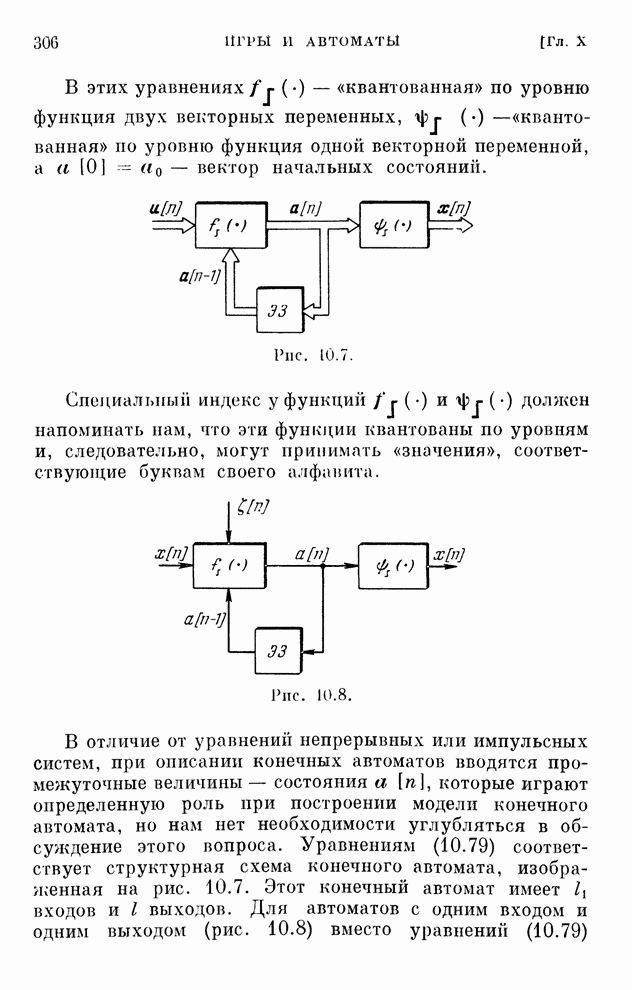
- § 10.18. Описание конечных автоматов
- § 10.19. Стохастические конечные автоматы
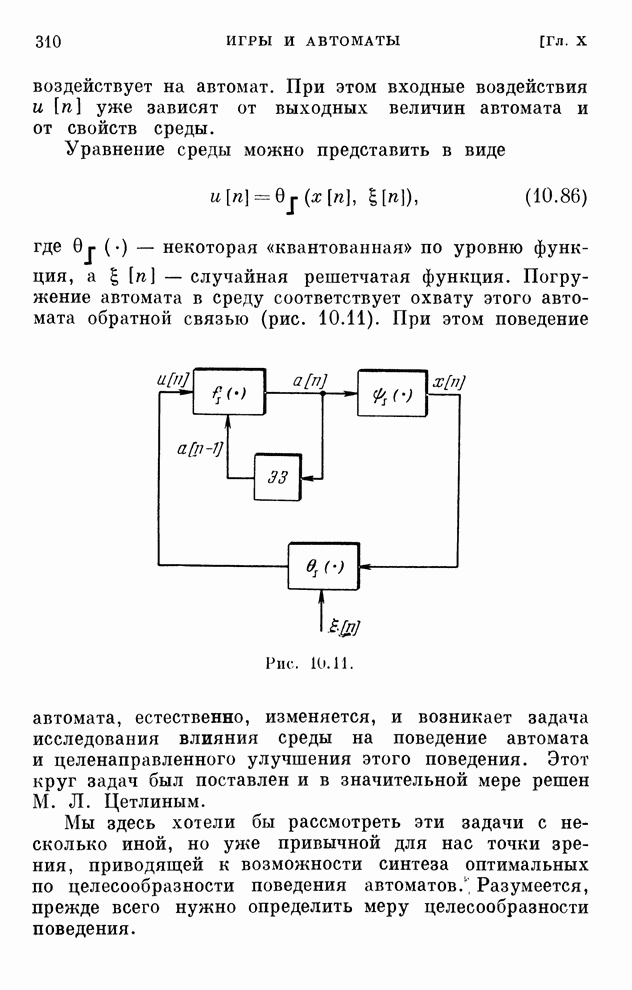
- § 10.20. Взаимодействие автомата со средой
- § 10.21. О мере целесообразности поведения
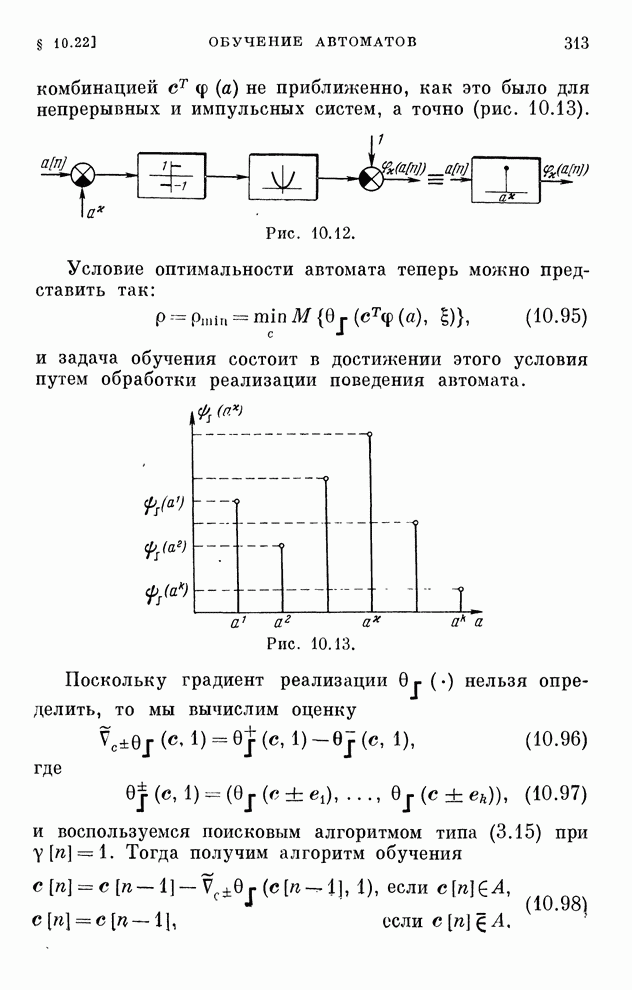
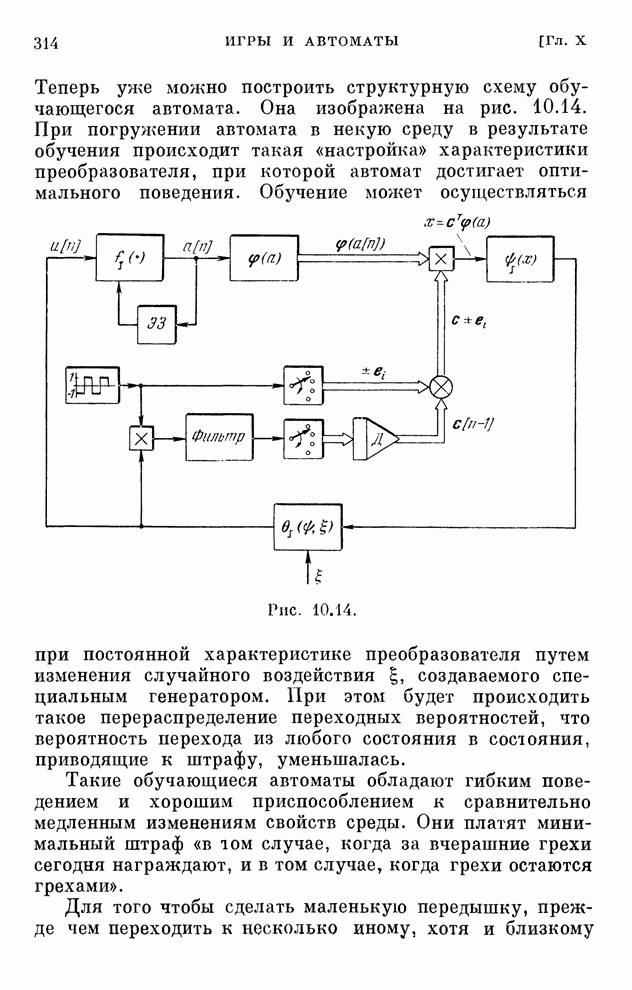
- § 10.22. Обучение автоматов
- § 10.23. О марковских цепях
- § 10.24. Марковское обучение
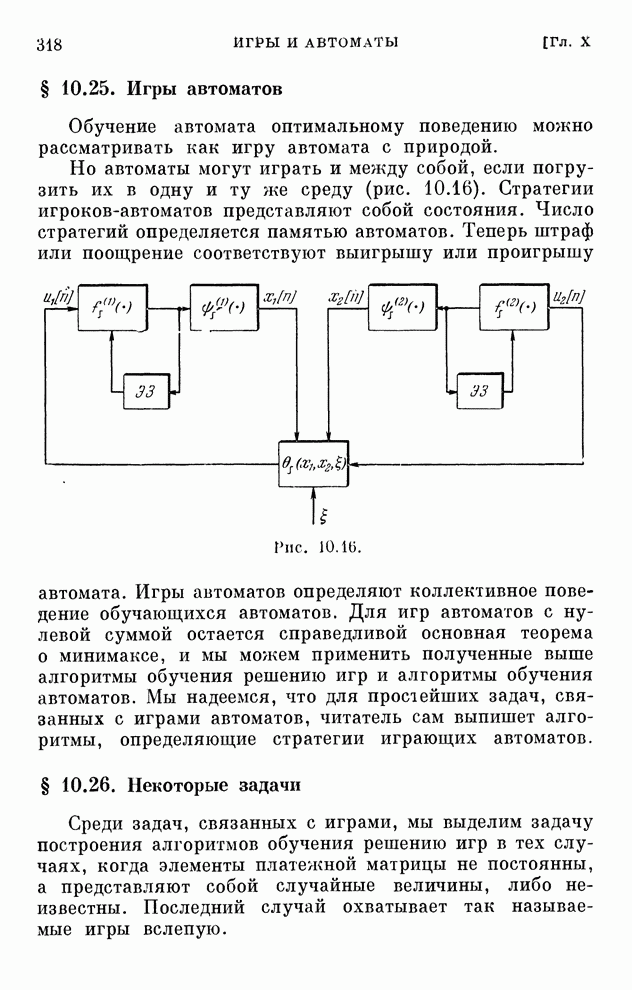
- § 10.25. Игры автоматов
- § 10.26. Некоторые задачи
- § 10.27. Заключение
- Послесловие
- Комментарии
- Литература