| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.5.7 Параметры состояния сети
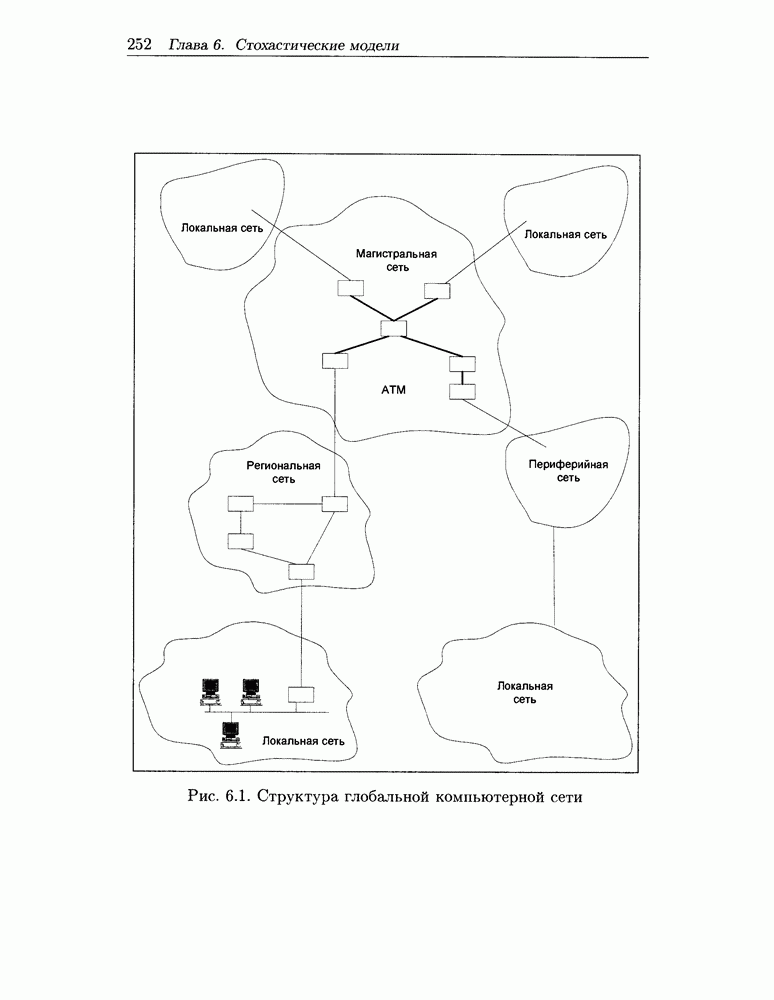
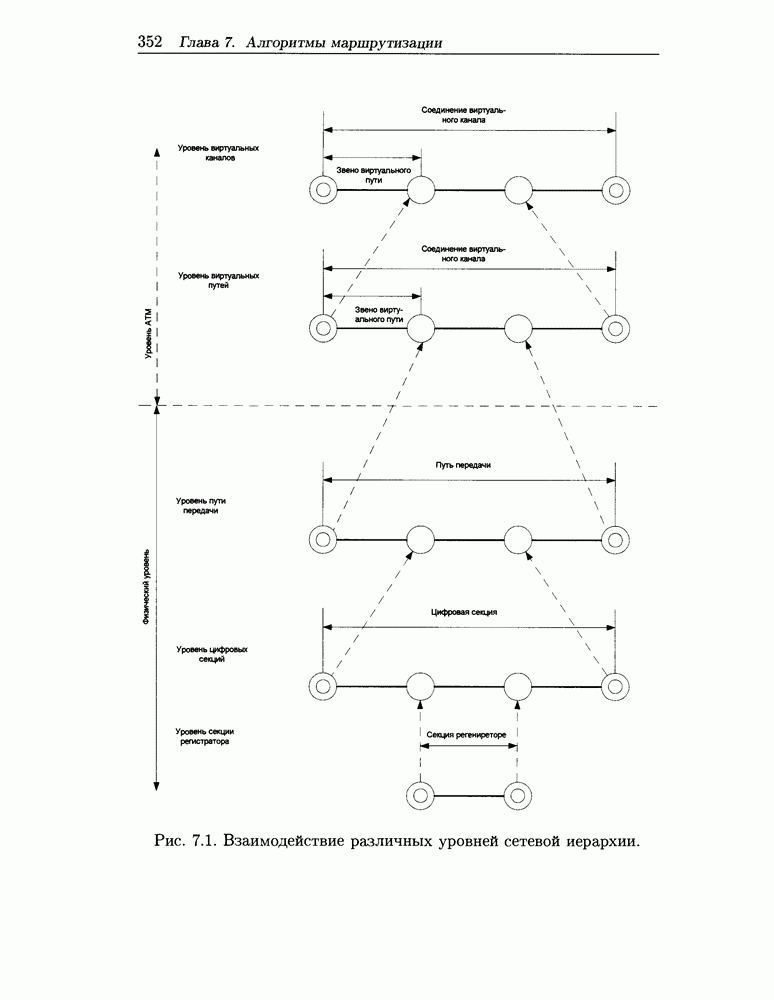
В отличие от параметров QoS и трафика заявки, состав параметров состояния сети не является столь же жестко заданным и во многом определяется принципами управления сети (распределенный -централизованный, сигналлинг - менеджмент). Рассмотрим состав этих параметров на примере PNNI [133] - протокола управления распределенной сетью на основе сигналлинга. В аспекте проблемы маршрутизации основными параметрами состояния сети являются Параметры линий. Линия ATM сети соединяет два порта соседних ATM узлов (т.е. между двумя узлами может быть проложено много отдельных линий) и служит для однонаправленной передачи ячеек между ними, физически же эта линия может быть реализована в виде участка (линейного или кольца) сети SDH/SONET (см. рис. 7.1). Значения параметров линий устанавливаются Менеджментом сети или являются результатом текущих вычислений алгоритма САС при установке-изменении-разъединении соединения. Еще раз подчеркнем, что значения этих параметров определяются отдельно для каждой из категорий обслуживания. В PNNI принята концепция выходящих (egress, outgoing) линий, согласно которой параметры линии вычисляются-модифицируются в узле, из которого она выходит. Параметры линий разделяются на два типа:
— параметр-атрибут, значения которого анализируются независимо (путем сопоставления с соответствующим параметром заявки) по всем линиям маршрута,
— параметр-метрика, значения которого определяют возможность использования маршрута для данной заявки (путем сопоставления с соответствующим параметром заявки) на основе совместного анализа по всем линиям маршрута. В простейшем варианте использование параметра-метрики по линиям маршрута является аддитивным.
С другой стороны, в соответствие с частотой изменения значений параметров их можно разделить на две группы:
• Квази-постоянные параметры.
• Динамические параметры.
В группе квази-постоянных параметрами-метриками являются:
(см. скан)
Рис. 7.1. Взаимодействие различных уровней сетевой иерархии.
- административный вес (AW- Administrative Weight) линии, характеризующий ее значимость в аспекте цены, физической протяженности, приоритетности и т.п.
- максимальный разброс в времени передачи ячеек по линии (Peak-to-Peak CDV), только для категорий обслуживания CBR и rt-VBR; в формулах для обозначения данного параметра будем применять CDV;
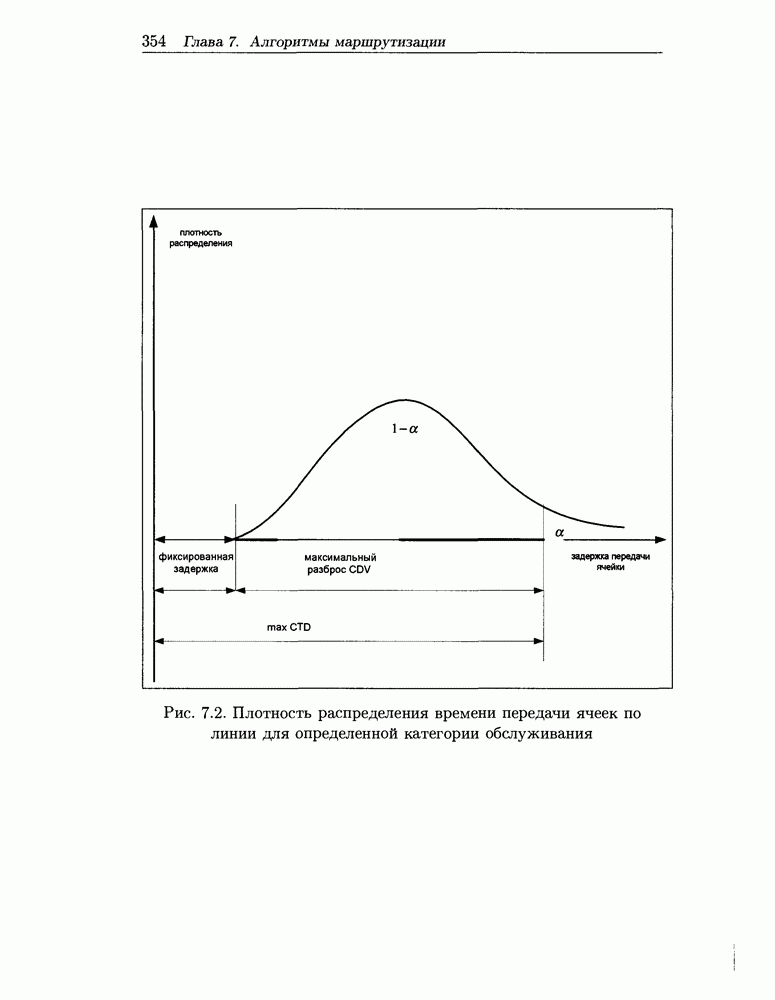
- максимальное время передачи ячейки по линии (MaxCTD), только для категорий обслуживания CBR и rt-VBR; в формулах для обозначения данного параметра будем применять MaxCTD; Аналогично QoS параметрам заявки, последние два параметра выражаются в квантилях. Взаимосвязь этих величин иллюстрируется на рис. 7.2.
Типовые значения параметра Peak-to-Peak CDV для линий различных видов приведены в таблице 7.6 [144].
Таблица 7.6.

Сопоставление QoS параметров заявки с соответствующими параметрами - метриками входящих в маршрут линий производится как на стадии выбора маршрута соединения, так и на стадии непосредственно его установки, в процессе передачи сообщения SETUP. Для такого сопоставления в настоящее время ATM Forum использует простейший аддитивный алгоритм, согласно которому интегральные параметры выбранного маршрута вычисляются по формулам:

где
I_CDV и I_MaxCTD - интегральные параметры маршрута соответственно в части параметров CDV и maxCTD,

Рис. 7.2. Плотность распределения времени передачи ячеек по линии для определенной категории обслуживания
CDV[i] и MaxCTD[i - соответствующие параметры-метрики  линии маршрута,
линии маршрута,
 - количество линий в составе маршрута.
- количество линий в составе маршрута.
Параметрами-атрибутами в группе квази-постоянных параметров являются:
— CLR (Cell Loss Ratio) - вероятность потери ячейки при передаче ее по данной линии,
— MCR (Maximum Cell Rate) - максимальная пропускная способность, выделенная по этой линии всем соединениям данной категории обслуживания,
— MNC (Maximum Number of Connections Supportable) - максимальное количество соединений, разрешенное для установки по данной линии.
Отметим, что в отличие от параметров CDV и MaxCTD, параметр заявки CLR проверяется не по всему маршруту (путем умножения или сложения соответствующих приведенных значений CLR входящих в него линий), а исключительно независимо по отдельным линиям. Возможность такого «выравнивания линий» для CLR определяется существенно большей его однородностью (как в части различных типов линий, так и в части различных заявок в пределах одной категории обслуживания) по сравнению с другими QoS параметрами заявки.
Динамическими параметрами линии являются следующие ее атрибуты:
- AvCR (Available Cell Rate) - доступная часть пропускной способности Линии для установки нового соединения данной категории обслуживания,
— CRM (Cell Rate Margin) - маргинальный параметр вариации эквивалентной пропускной способности соединения, применяемый в алгоритме GCAC (см. раздел 7.5.1), используется только для категорий rt-VBR и nrt-VBR,
— VF (Variance Factor) - Параметр Вариации, применяемый в алгоритме GCAC  используется только для категорий rt-VBR и nrt-VBR,
используется только для категорий rt-VBR и nrt-VBR,
— ANC (Actual Number of Connections) - Реальное Количество Соединений, установленных по данной линии.
Следует подчеркнуть, что в ATM сетях, в отличие от классических сетей типа SDH/SONET, все без исключения параметры линий являются не просто физическими параметрами или результатом измерений, а вычисляются или контролируются подсистемой САС. Так, например, при установке нового соединения САС вычисляет необходимую эквивалентную пропускную способность соединения для данной линии, которая должна обеспечить принятые для линии квази-постоянные параметры исходя из количества и параметров уже установленных соединений. Учитывая вероятностный характер поступления ячеек, эта величина должна быть больше значения PCR для категории обслуживания CBR и в то же время значительно меньше ее для категории VBR (вследствие природы статистического мультиплексирования ячеек, характерной для этого режима).
Выше были рассмотрены параметры линий, описанные в утвержденных стандартах ATM Forum. В целях повышения эффективности ATM сетей предпринимаются попытки расширить и видоизменить состав этих параметров. В первую очередь это касается параметров-метрик. Эти параметры имеют вероятностный, а не детерминированный характер, поэтому приведенные выше формулы определения их интегральных значений соответствуют наихудшему случаю (100%-й корреляции между случайными временами передачи по соседним линиям) и приводят к значительному завышению рассчитанных значений по сравнению с точными. В самом деле, например для квантиля, равного а и пути из двух линий имеем следующую формулу для случайных величин  соответствующих разбросу времени передачи ячейки по первой линии, по второй линии и по всему пути:
соответствующих разбросу времени передачи ячейки по первой линии, по второй линии и по всему пути:

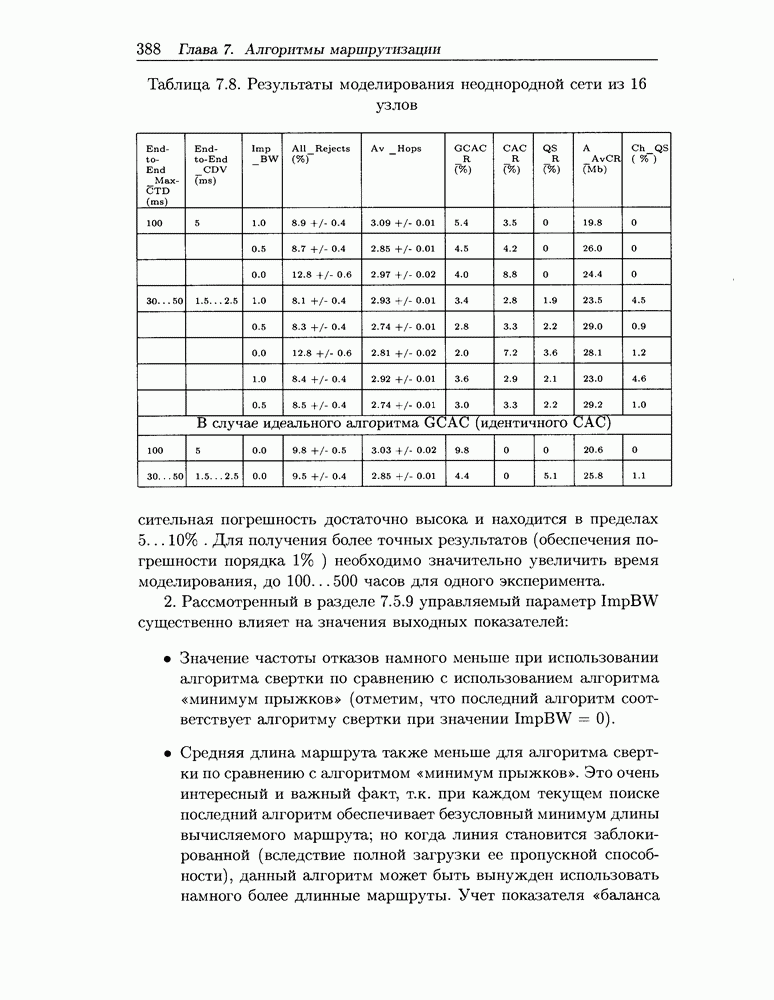
т.е. фактически для оценки величины I_CDV с квантилем а можно использовать не CDV[1]+CDV[2], а меньшее значение. Согласно приведенным в [137] результатам расчета (см. таблицу 7.7), завышение может достигать двух-пяти раз!
Прежде чем перейти к рассмотрению отдельных подходов, подчеркнем, что все они были специально разработаны не для использования в алгоритмах маршрутизации, а для повышения точности вычисления интегральных параметров I_CDV и I_MaxCTD непосредственно в ходе установки соединения процедурой Setup по уже выбранному маршруту.
Таблица 7.7. Результаты расчета параметра I_CDV в зависимости от количества линий в маршруте (N) и метода расчета,  .
.

Addtive - простейший аддитивный алгоритм, используемый в [132]; Asymptotic - асимптотический метод, предложенный в «Informative Appendix 4» документа [132];
Lucent - метод, предложенный в [137];
Exact - точный расчет.
В принципе разработанные подходы несложно приспособить и для использования в ходе вычисления маршрута, но такое приспособление, естественно, требует некоторых накладных расходов.
Предложенный в [132] (см. «Informative Appendix 4») алгоритм, получивший название «асимптотический», основан на использовании центральной предельной теоремы теории вероятностей. Для его применения каждая линия i вместо двух введенных ранее параметров CDV и MaxCTD должна характеризоваться четырьмя параметрами:
 - среднее значение разброса времени передачи;
- среднее значение разброса времени передачи;
 - дисперсия разброса времени передачи;
- дисперсия разброса времени передачи;
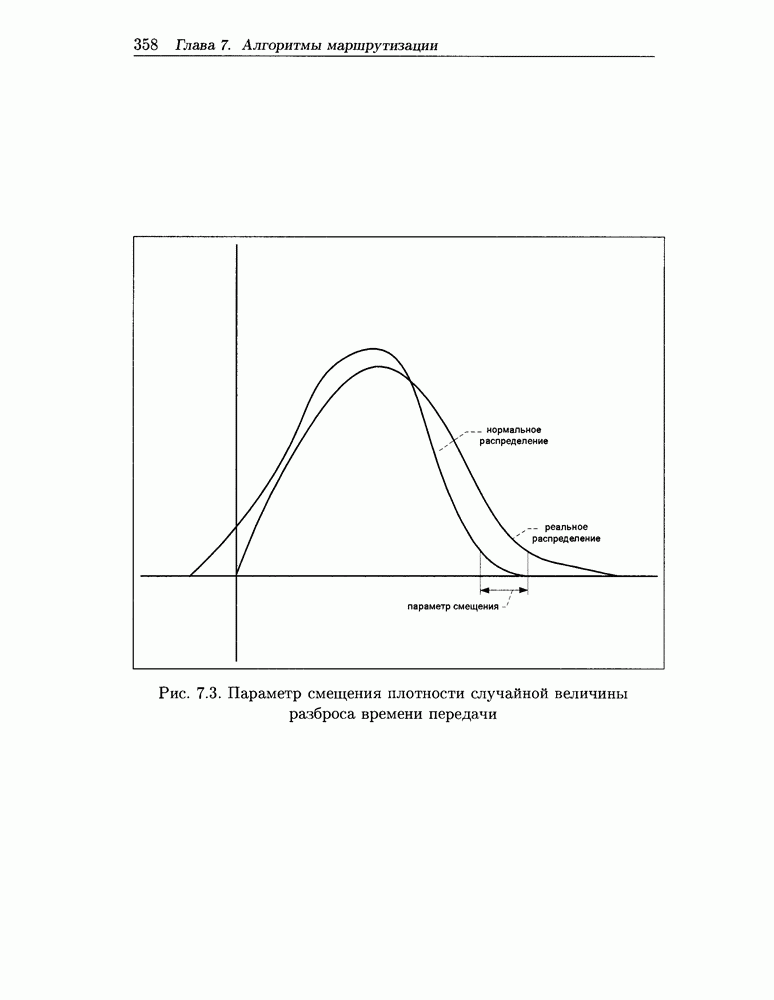
 - параметр смещения (Discrepancy) реального закона распределения разброса времени передачи от нормального закона с теми же значениями М и V (см. рис. 7.3);
- параметр смещения (Discrepancy) реального закона распределения разброса времени передачи от нормального закона с теми же значениями М и V (см. рис. 7.3);
 - фиксированная задержка в передаче.
- фиксированная задержка в передаче.
Интегральные параметры маршрута определяются по формулам:

Обозначим через  -
-  -квантиль стандартного нормального закона распределения с нулевым математическим ожиданием и единичной дисперсией. Тогда для вычисления интегральных характеристик справедливы формулы:
-квантиль стандартного нормального закона распределения с нулевым математическим ожиданием и единичной дисперсией. Тогда для вычисления интегральных характеристик справедливы формулы:

Рис. 7.3. Параметр смещения плотности случайной величины разброса времени передачи

Достоинством данного подхода, наряду с достаточно высокой точностью, является отсутствие каких-либо допущений (как и в случае простейшего аддитивного алгоритма) относительно вида функции распределения случайной величины времени передачи ячеек по линии. Наряду с этим следует указать и его недостатки:
• С точки зрения практического применения наиболее существенным, на наш взгляд, недостатком является существенное изменение и расширение состава учитываемых параметров линий. Это приводит как к несовместимости с разработанными к настоящему моменту алгоритмами САС (которые в процессе анализа текущей заявки должны обеспечивать для линии только значение параметра  , а не трех параметров
, а не трех параметров  , так и значительному их усложнению. Алгоритмы САС работают в процессе установки заявки, поэтому требования к скорости и, следовательно, простоте их работы являются очень важными [217].
, так и значительному их усложнению. Алгоритмы САС работают в процессе установки заявки, поэтому требования к скорости и, следовательно, простоте их работы являются очень важными [217].
• Недостатком данного похода является также его сложность как в аспекте самих вычислений, так и в аспекте объема хранимых в узлах параметрах линий.
• Основополагающим допущением данного подхода является независимость случайных величин разброса времени передачи, соответствующих различным линиям. В принципе такое допущение широко используется при вероятностном моделировании сетей передачи, но применительно к ATM сетям оно проявляется дифференцированно. Применительно к параметрам категории обслуживания CBR использование этого допущения вполне приемлемо, но применительно к категории VBR оно может привести к существенному занижению результатов расчета. Это связано с тем, что передача ячеек по соединению VBR, в отличие от передачи по соединению CBR, является существенно неоднородной по времени (периоды паузы и передачи) и эта неоднородность приводит к сильной корреляции состояния соединения по всем линиям его маршрута.
• Данный алгоритм в своем исходном виде практически применим только для оценки аккумулируемых величин ICDV и
I_MaxCTD непосредственно в ходе установки сообщения по выбранному маршруту. Применение же его в алгоритмах маршрутизации, основанных на методах поиска кратчайшего пути, весьма затруднительно, т.к. вышеприведенные выражения для интегральных характеристик маршрута не являются чисто аддитивными.
В [137] предлагается несколько другой подход к вычислению интегральных характеристик маршрута, в основе которого лежит применение неравенства Маркова (известного также как «обобщенное неравенство Чебышева») и основополагающего метода теории больших уклонений - метода Чернова. На основе аппроксимации случайной величины разброса времени передачи Гамма распределением в [137] разработано несколько вариантов алгоритма, отличающихся как точностью расчета, так и трудоемкостью. Рассмотрим кратко самый простой из предложенных алгоритмов, не останавливаясь на технических выкладках.
Для определения искомых величин I_CDV и I_MaxCTD в предложенном методе используются 3 параметра состояния сети по каждой из линий -  :
:
•  - логарифмический момент производящей функции случайной величины разброса времени передачи ячейки по линии ;
- логарифмический момент производящей функции случайной величины разброса времени передачи ячейки по линии ;
•  - заранее выбранный параметр, удовлетворяющий некоторому неравенству относительно плотности распределения времени задержки по линии ;
- заранее выбранный параметр, удовлетворяющий некоторому неравенству относительно плотности распределения времени задержки по линии ;
•  - фиксированная компонента в времени передачи по линии
- фиксированная компонента в времени передачи по линии 
Для определения этих величин случайное время передачи аппроксимируется Г-распределением с плотностью

где  - гамма-функция,
- гамма-функция,

Исходя из параметров Г-распределения для каждой конкретной линии j, несложно вычислить вспомогательные параметры по всем приемлемым для выбираемого маршрута линиям 

Для маршрута, состоящего из  линий
линий  искомые оценки вычисляются по формулам:
искомые оценки вычисляются по формулам:

По сравнению с «асимптотическим» методом преимуществом рассмотренного является то, что он использует меньшее количество параметров линий (три вместо четырех, необходимых в асимптотическом методе) и является более простым в аспекте реализации. Более того, он использует чисто аддитивные формулы для определения искомых величин, что весьма важно в аспекте применения алгоритмов кратчайшего пути. В то же время другие два недостатка асимптотического метода в полной мере присущи и ему. В [138] ставится вопрос о учете корреляции между линиями, но конкретных предложений и алгоритмов пока что не разработано. Кроме того, необходимость определения величины  заранее, до вычисления маршрута, по всем допустимым линиям, может сильно занизить значение этой величины по сравнению с использованием ее в ходе установки соединения (в последнем случае minimum берется только по линиям, входящим в маршрут) и тем самым увеличить искомое
заранее, до вычисления маршрута, по всем допустимым линиям, может сильно занизить значение этой величины по сравнению с использованием ее в ходе установки соединения (в последнем случае minimum берется только по линиям, входящим в маршрут) и тем самым увеличить искомое 
Отметим также, что на наш взгляд, требования как асимптотического метода, так и метода [137] по расширению состава учитываемых параметров линий в принципе могут свести на нет их преимущества в части точности расчета. В самом деле, если при использовании простейшего аддитивного метода заявка может получить отказ при установке вследствие некорректного сопоставления ее  параметра с завышенной интегральной оценкой маршрута, то при использовании двух последних методов отказы при установке могут появляться ввиду невозможности алгоритмом САС гарантировать значения сразу нескольких параметров линии.
параметра с завышенной интегральной оценкой маршрута, то при использовании двух последних методов отказы при установке могут появляться ввиду невозможности алгоритмом САС гарантировать значения сразу нескольких параметров линии.
Безусловно, эти чисто качественные соображения нуждаются в количественном анализе.
Существуют также и другие подходы к расчету интегральных параметров маршрута в части CDV и MaxCTD (например, в [139] делается попытка учесть параметры шейпинга в отдельных узлах маршрута), но недостаток места не позволяет рассмотреть их более подробно.
Другим возможным направлением расширения состава параметров линий является учет их не только в части выходного узла (как это принято в [133]), но и в части входного узла. Практическая возможность такого учета обусловлена следующим:
• Во-первых тем, что большинство параметров линий вычисляется и-или контролируется алгоритмом САС, а в разных узлах эти алгоритмы работают независимо;
• Во-вторых тем, что фактически в каждом узле при установке текущего соединения САС работает четыре раза, проверяя как для соединения в прямом направлении, так и в обратном, и входную, и выходную линию.
Для квази-постоянных параметров линий такое расширение внешне не является заметным, т. к. имея, например, параметры CDVf [выходящая линия j] и СDV [входящая линия j] (эти данные используются алгоритмом САС как исходные для прогнозирования функционирования сети при установке текущего соединения соответственно в выходном узле  линии и входном ее узле), алгоритм маршрутизации может использовать в качестве исходных величину CDV[j] = СБУ [выходящая линия j] + СБУ[входящая линия j]. Для динамических параметров (в первую очередь AvCR) такое расширение оборачивается необходимостью распространять по сети двойной объем информации (см. рис. 7.4).
линии и входном ее узле), алгоритм маршрутизации может использовать в качестве исходных величину CDV[j] = СБУ [выходящая линия j] + СБУ[входящая линия j]. Для динамических параметров (в первую очередь AvCR) такое расширение оборачивается необходимостью распространять по сети двойной объем информации (см. рис. 7.4).
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
- 6.1.1 Структура компьютерных сетей
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
- 6.3 Управление потоками в сети пакетной коммутации
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
- 6.3.3 Локальное управление буферами
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
- 7.4.2 Анализ развития СПД «Сирена»
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
- 7.5.4 Классификация алгоритмов маршрутизации
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
- 7.5.8 Показатели качества маршрутизации
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
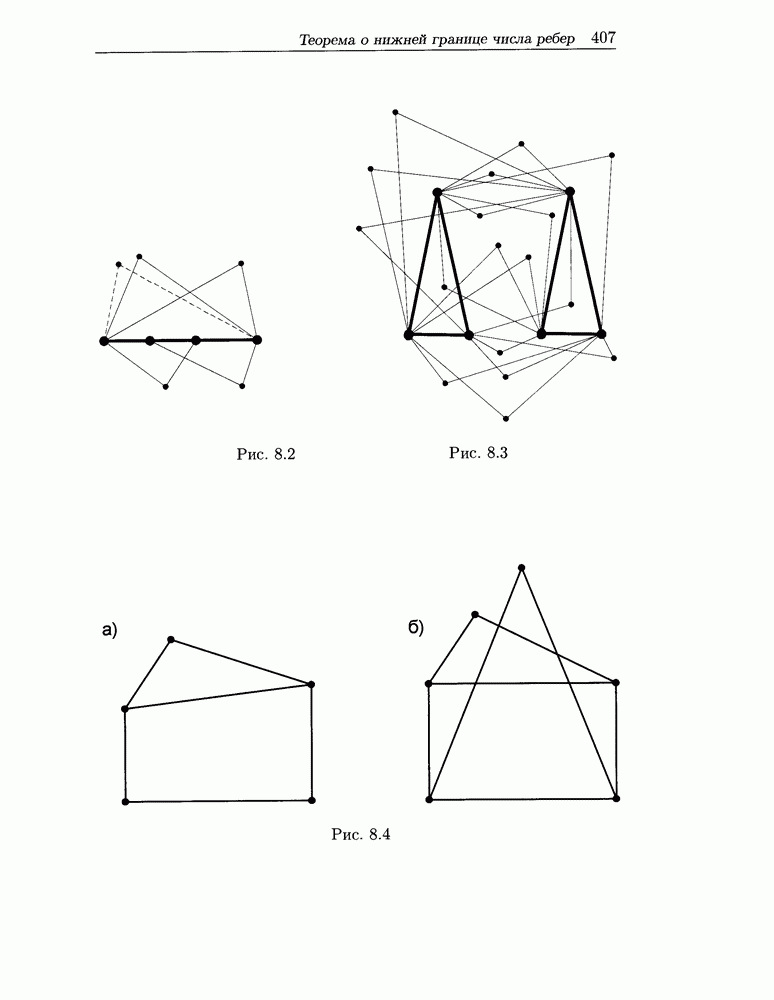
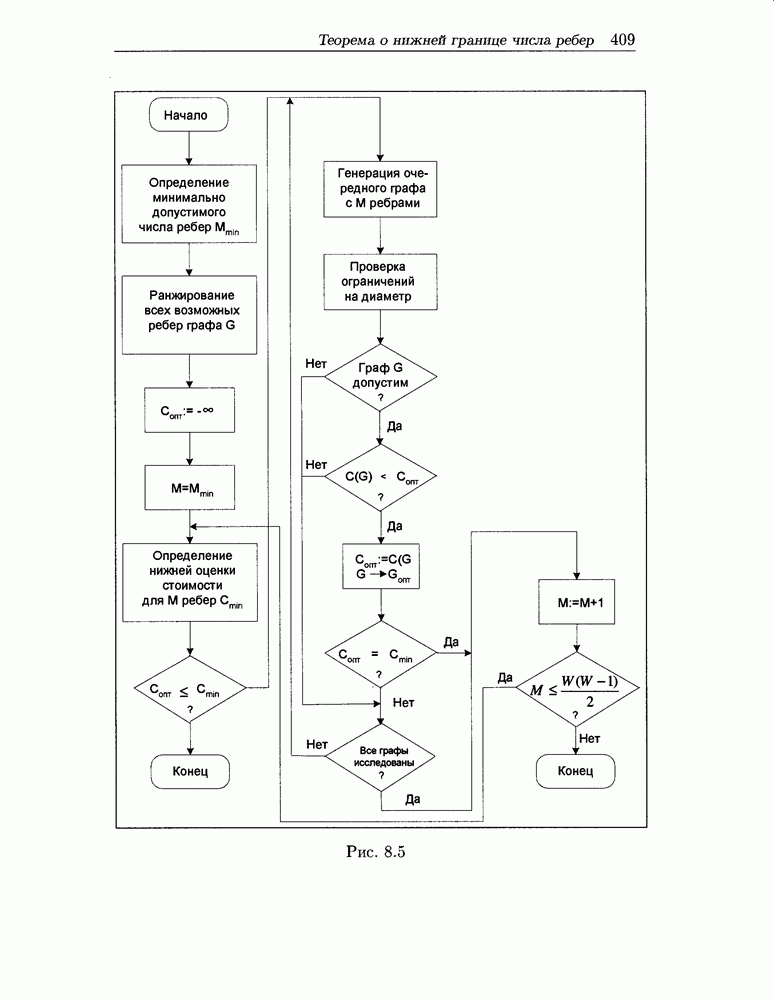
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
- 9.1 Состояние и перспективы развития беспроводных радиосетей
- 9.2 Схема распределенного управления
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
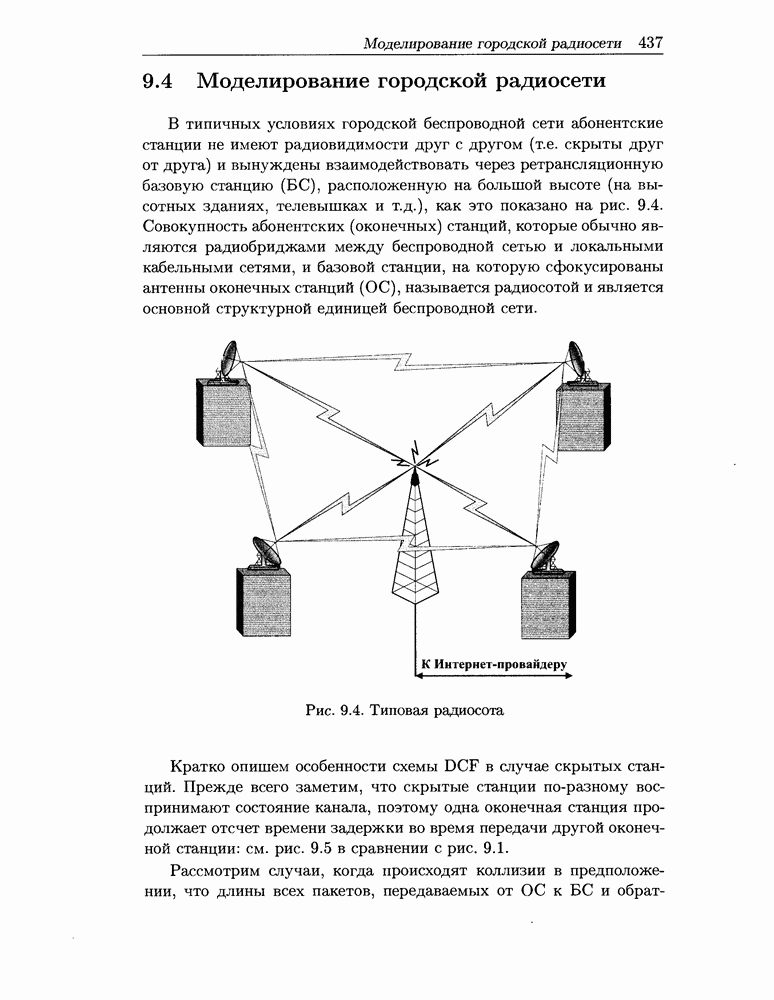
- 9.4 Моделирование городской радиосети
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
- 9.5 Численные результаты исследования городской радиосоты
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература