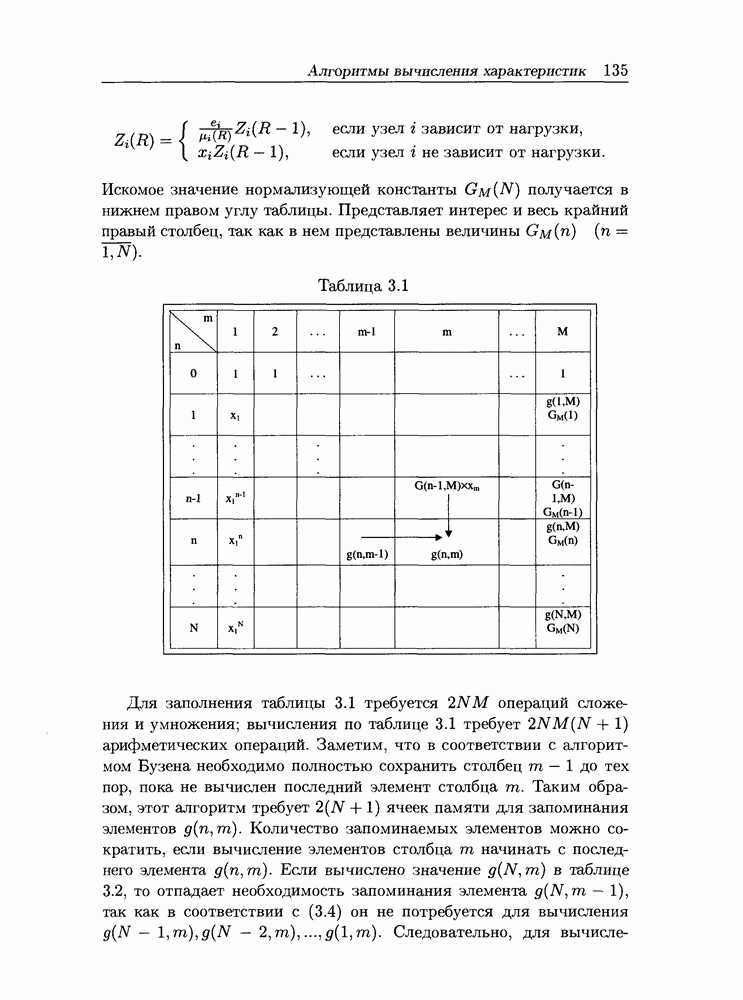
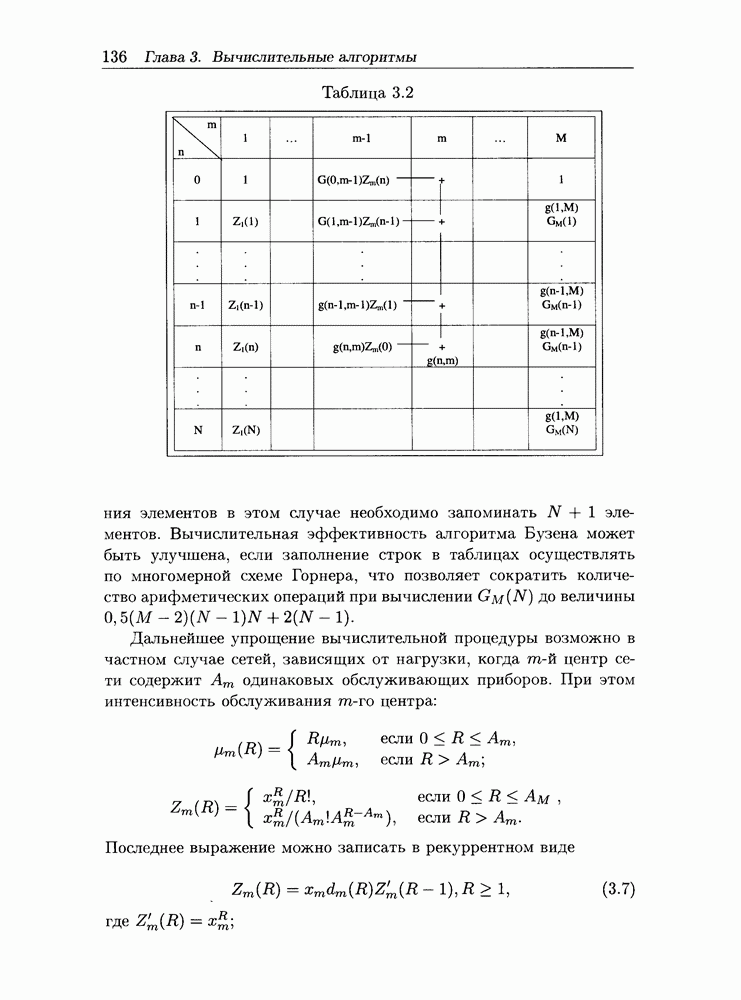
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2.5.3 Пример расчета
Рассмотрим применение методов синтеза сетей МО для решения задачи оптимизации производительности вычислительной системы, модель которой представлена на рисунке 2.1. В соответствии с рисунком 2.1 первый центр обслуживания представляет собой центральный процессор, а остальные центры с номерами  моделируют работу
моделируют работу  внешних устройств. Пребывание любого задания (программы) в первом центре соответствует выполнению последовательности команд между двумя следующими друг за другом обращениями к внешним устройствам. Вероятность обращения к
внешних устройств. Пребывание любого задания (программы) в первом центре соответствует выполнению последовательности команд между двумя следующими друг за другом обращениями к внешним устройствам. Вероятность обращения к  ВУ равна
ВУ равна  ; величина
; величина  представляет собой вероятность завершения задания. В этом случае через ветвь, обозначенную на рис. 2.1 «Ввод нового задания», в систему поступает новое задание. Таким образом, число заданий в сети остается постоянным, равным уровню мультипрограммирования
представляет собой вероятность завершения задания. В этом случае через ветвь, обозначенную на рис. 2.1 «Ввод нового задания», в систему поступает новое задание. Таким образом, число заданий в сети остается постоянным, равным уровню мультипрограммирования 
Предполагается, что все задания, решаемые системой, принадлежат одному классу и объем памяти пользователей поровну разделен между N статистически идентичными заданиями. Так как все задания требуют равные объемы памяти, емкость оперативной памяти является линейной функцией N. Среднее время обслуживания требования в  узле
узле 
Под стоимостью ВС в дальнейшем будем понимать стоимость ее вычислительного ядра, включающего процессор, оперативную и внешнюю память. Общая стоимость ВС  и стоимость вычислительного ядра
и стоимость вычислительного ядра  связаны соотношением
связаны соотношением  где
где  - стоимость периферийного оборудования ВС, включающего устройства печати, видеотерминалы, мультиплексоры передачи данных и другие устройства ВС, необходимые для организации вычислительного процессора.
- стоимость периферийного оборудования ВС, включающего устройства печати, видеотерминалы, мультиплексоры передачи данных и другие устройства ВС, необходимые для организации вычислительного процессора.
Исходными параметрами для решения задачи синтеза являются следующие величины: М - число узлов; N - число заданий;  - переходные вероятности
- переходные вероятности  ;
;  - среднее число команд, выполняемых в процессоре на каждое обращение;
- среднее число команд, выполняемых в процессоре на каждое обращение;  - среднее число передаваемых слов на операцию ввода-вывода в
- среднее число передаваемых слов на операцию ввода-вывода в  внешнем устройстве
внешнем устройстве  ;
;  - стоимостной коэффициент в узле
- стоимостной коэффициент в узле  ; а - коэффициент нелинейности в узле
; а - коэффициент нелинейности в узле  ;
;  - стоимость раздела оперативной памяти; S - ограничение на стоимость ВС (используется при решении задачи синтеза в постановке 1); А - ограничение на производительность ВС (используется при решении задачи синтеза в постановке 2).
- стоимость раздела оперативной памяти; S - ограничение на стоимость ВС (используется при решении задачи синтеза в постановке 1); А - ограничение на производительность ВС (используется при решении задачи синтеза в постановке 2).
Критерием оптимальности при решении задачи синтеза в постановке 1 является обеспечение максимальной производительности ВС, измеряемой в количестве выполненных в единицу времени заданий, при наличии ограничений на стоимость ВС. Эта стоимость, как уже отмечалось, не включает стоимости вспомогательного оборудования, установки, эксплуатационных расходов.
Определим стоимость ВС следующим образом:

где  - стоимостные коэффициенты в узле
- стоимостные коэффициенты в узле  ;
;  -быстродействие устройства в
-быстродействие устройства в  узле;
узле;  - интенсивность обслуживания в
- интенсивность обслуживания в  узле; а - относительные величины средних частот обращений к узлам;
узле; а - относительные величины средних частот обращений к узлам;  - общее число требований к обработке, необходимых для одного задания в узле
- общее число требований к обработке, необходимых для одного задания в узле  ;
;  - стоимость оперативной памяти в зависимости от уровня мультипрограммирования.
- стоимость оперативной памяти в зависимости от уровня мультипрограммирования.
Среднее число требований к обработке на одно обращение к  узлу определяется по формуле
узлу определяется по формуле

где
Взаимосвязь между интенсивностью обслуживания  и быстродействием устройства
и быстродействием устройства  будет
будет

Задача оптимизации структуры ВС может быть сформулирована в одной из следующих постановок.
Постановка 1. Найти

при ограничении

Постановка 2. Найти

при ограничении

где  - нормализующая константа замкнутой сети.
- нормализующая константа замкнутой сети.
Решение ищется на множестве значений интенсивностей обслуживания  и N, где N - уровень мультипрограммирования.
и N, где N - уровень мультипрограммирования.
Вектор обращений  и вектор требований к обработке заданий
и вектор требований к обработке заданий  определяют параметры рабочей нагрузки. Уровень мультипрограммирования N и вектор быстродействия устройств
определяют параметры рабочей нагрузки. Уровень мультипрограммирования N и вектор быстродействия устройств  составляют
составляют  переменных. Отметим, что, решив задачу оптимизации относительно
переменных. Отметим, что, решив задачу оптимизации относительно  переход к параметрам b осуществляется с помощью формулы (2.65).
переход к параметрам b осуществляется с помощью формулы (2.65).
Уровень мультипрограммирования обычно ограничен относительно малыми положительными числами, поэтому выбор оптимального N может быть определен путем дискретного поиска. Для каждого значения  решается задача оптимизации производительности ВС при ограничении на стоимость и вычисляется значение целевой функции. Оптимальный уровень мультипрограммирования N соответствует наибольшему значению целевой функции.
решается задача оптимизации производительности ВС при ограничении на стоимость и вычисляется значение целевой функции. Оптимальный уровень мультипрограммирования N соответствует наибольшему значению целевой функции.
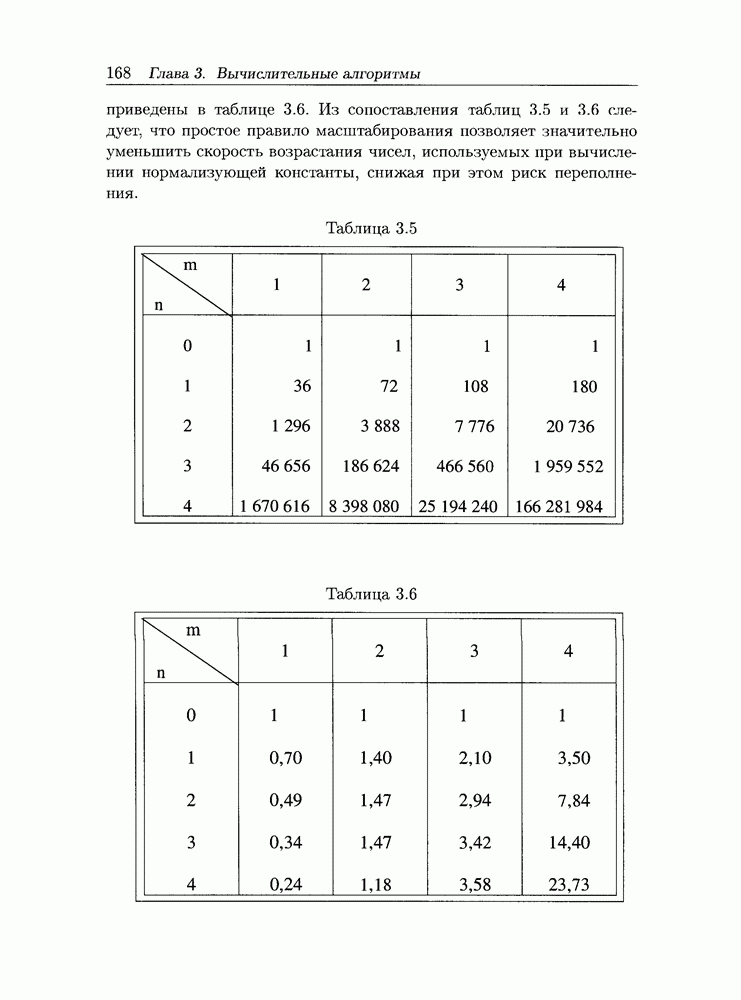
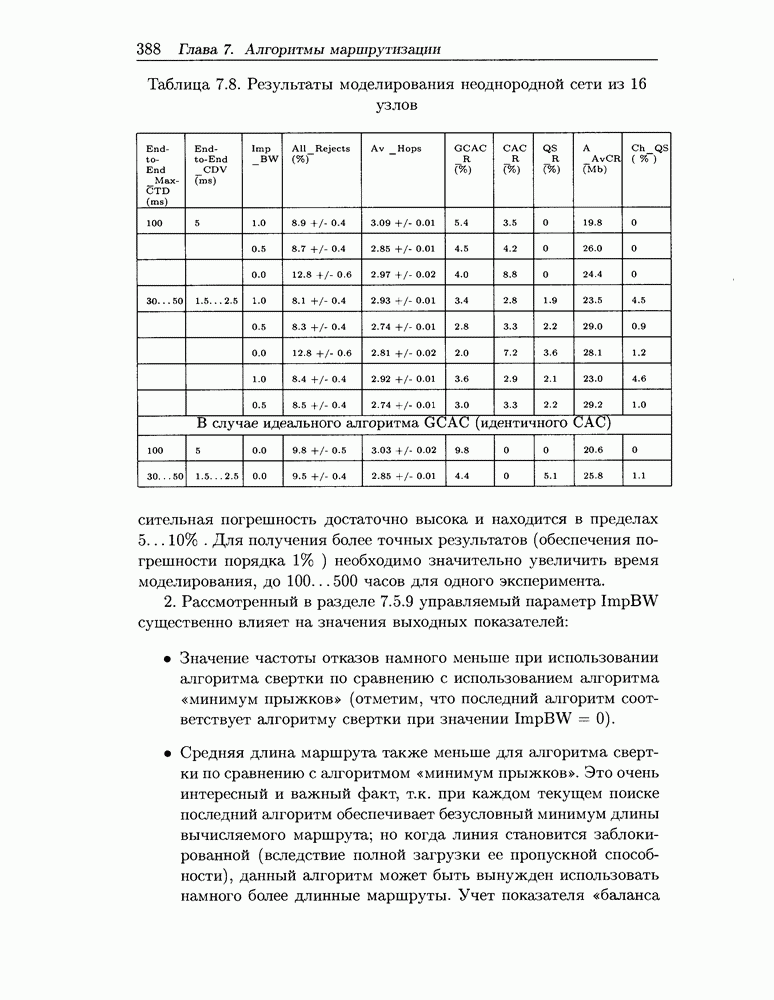
В таблицах 2.1 и 2.2 для модели, определенной на рисунке 2.1, приведены параметры рабочей нагрузки и оценки стоимости устройств (величина  указана в миллионах операций,
указана в миллионах операций,  - в миллионах слов,
- в миллионах слов,  . Быстродействие устройств ввода-вывода определялось в миллионах слов, передаваемых в секунду (с учетом времени установки головок, поиска записи на дорожке и передачи данных, которое находилось для емкости блока в 1000 слов).
. Быстродействие устройств ввода-вывода определялось в миллионах слов, передаваемых в секунду (с учетом времени установки головок, поиска записи на дорожке и передачи данных, которое находилось для емкости блока в 1000 слов).
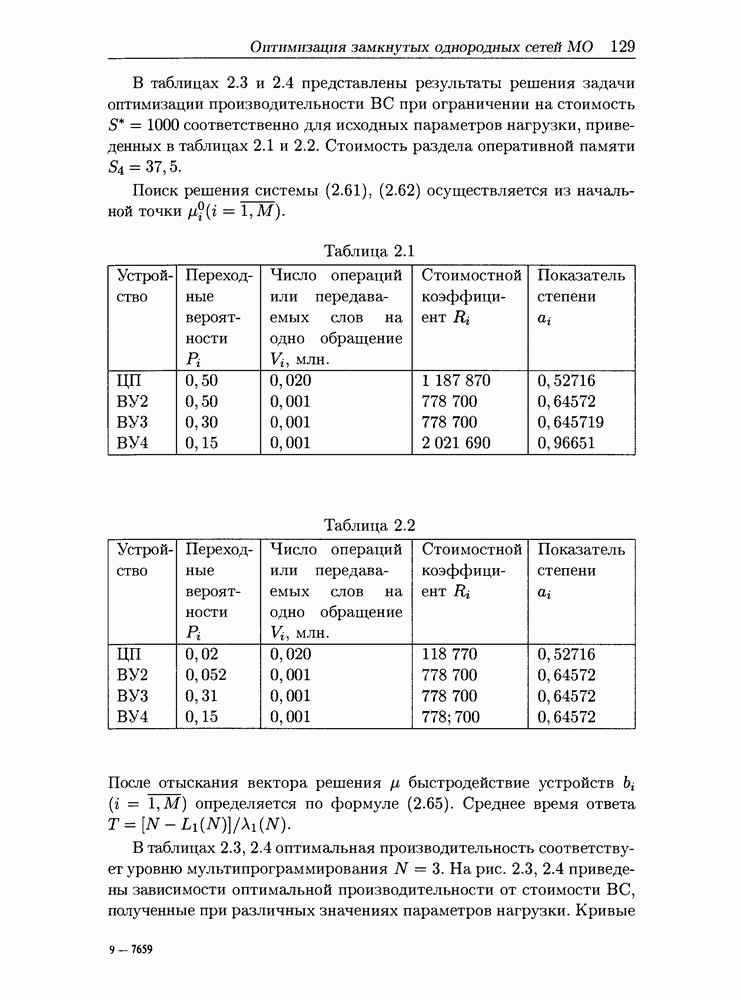
В таблицах 2.3 и 2.4 представлены результаты решения задачи оптимизации производительности ВС при ограничении на стоимость  соответственно для исходных параметров нагрузки, приведенных в таблицах 2.1 и 2.2. Стоимость раздела оперативной памяти
соответственно для исходных параметров нагрузки, приведенных в таблицах 2.1 и 2.2. Стоимость раздела оперативной памяти 
Поиск решения системы (2.61), (2.62) осуществляется из начальной точки  .
.
Таблица 2.1

Таблица 2.2

После отыскания вектора решения Ц быстродействие устройств  определяется по формуле (2.65). Среднее время ответа
определяется по формуле (2.65). Среднее время ответа 
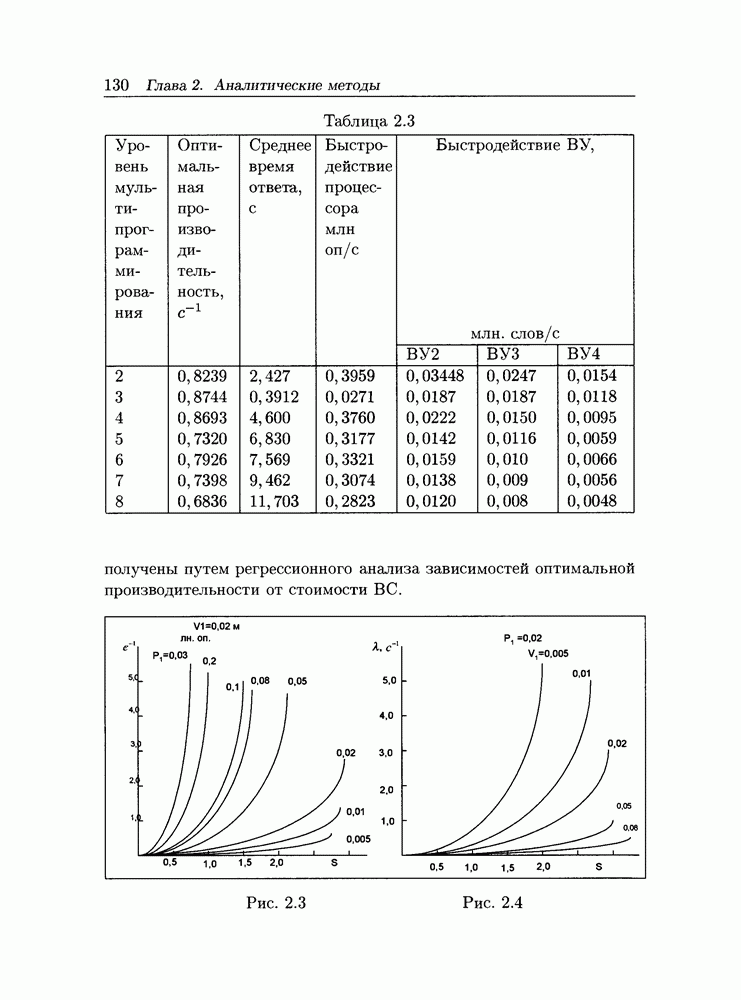
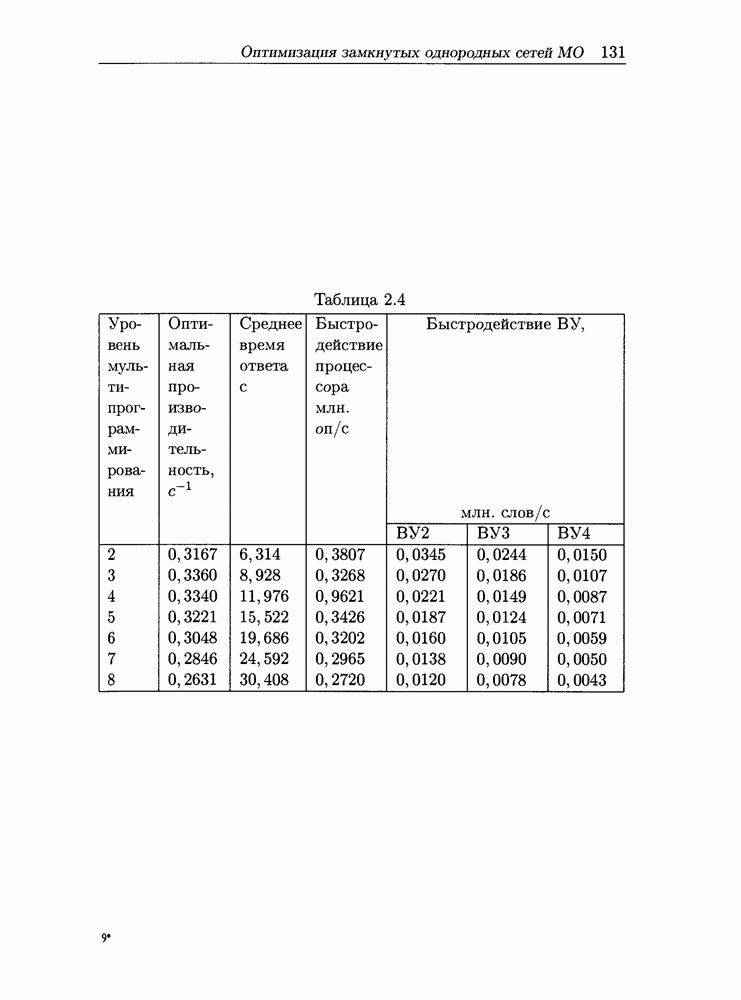
В таблицах 2.3, 2.4 оптимальная производительность соответствует уровню мультипрограммирования  На рис. 2.3, 2.4 приведены зависимости оптимальной производительности от стоимости ВС, полученные при различных значениях параметров нагрузки.
На рис. 2.3, 2.4 приведены зависимости оптимальной производительности от стоимости ВС, полученные при различных значениях параметров нагрузки.
Таблица 2.3

Кривые получены путем регрессионного анализа зависимостей оптимальной производительности от стоимости ВС.

Рис. 2.3

Рис. 2.4
Таблица 2.4

| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
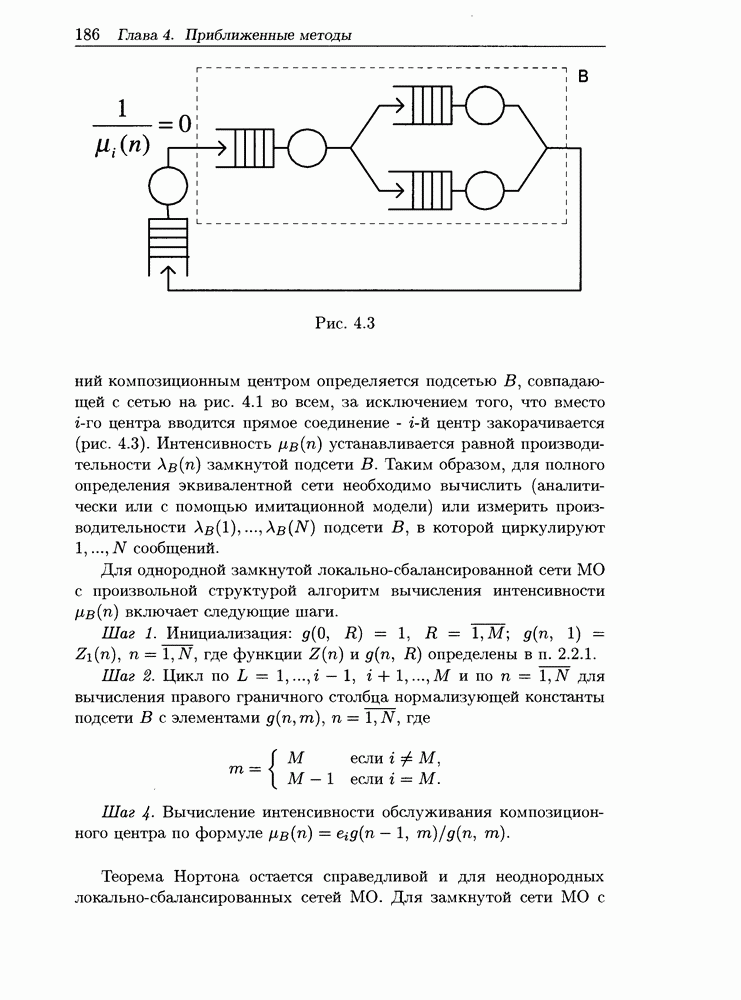
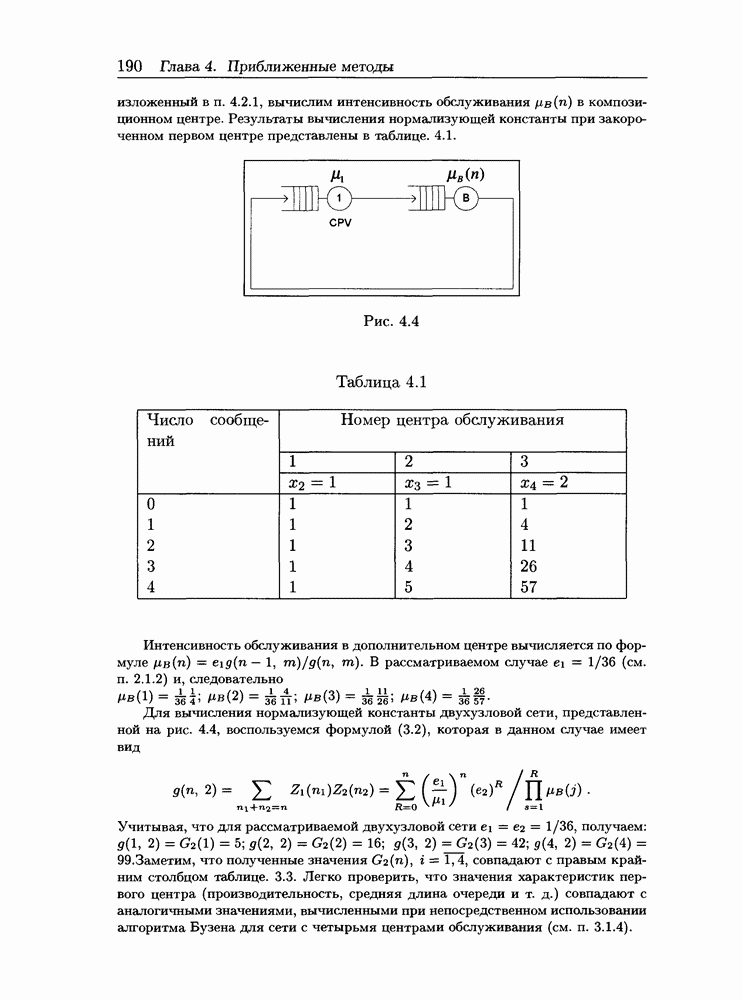
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
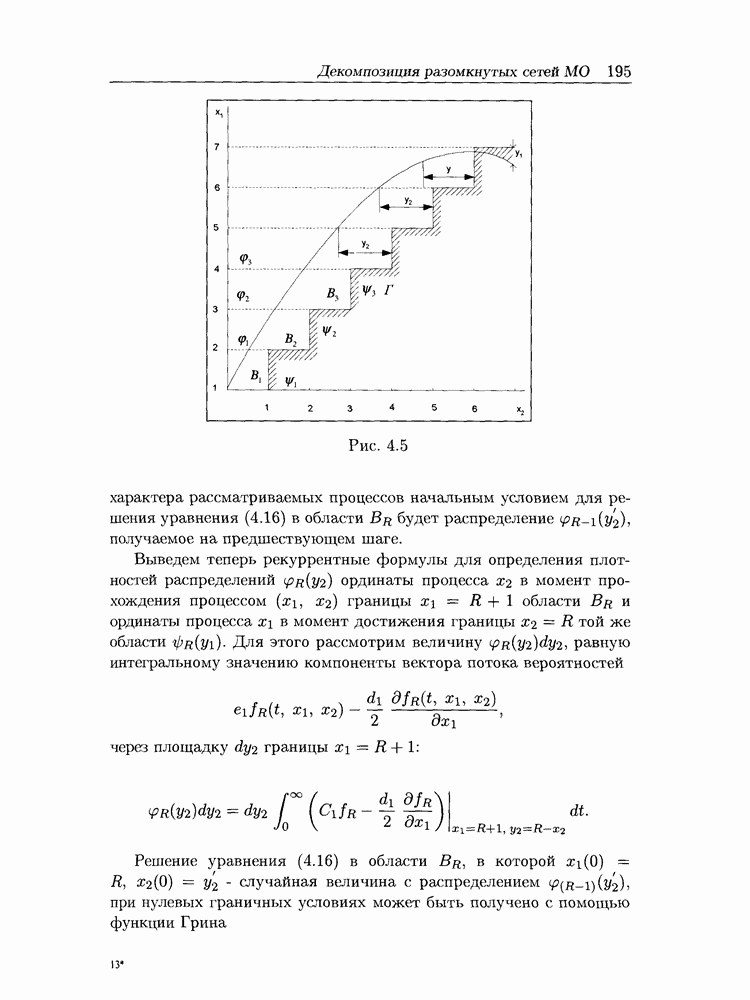
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
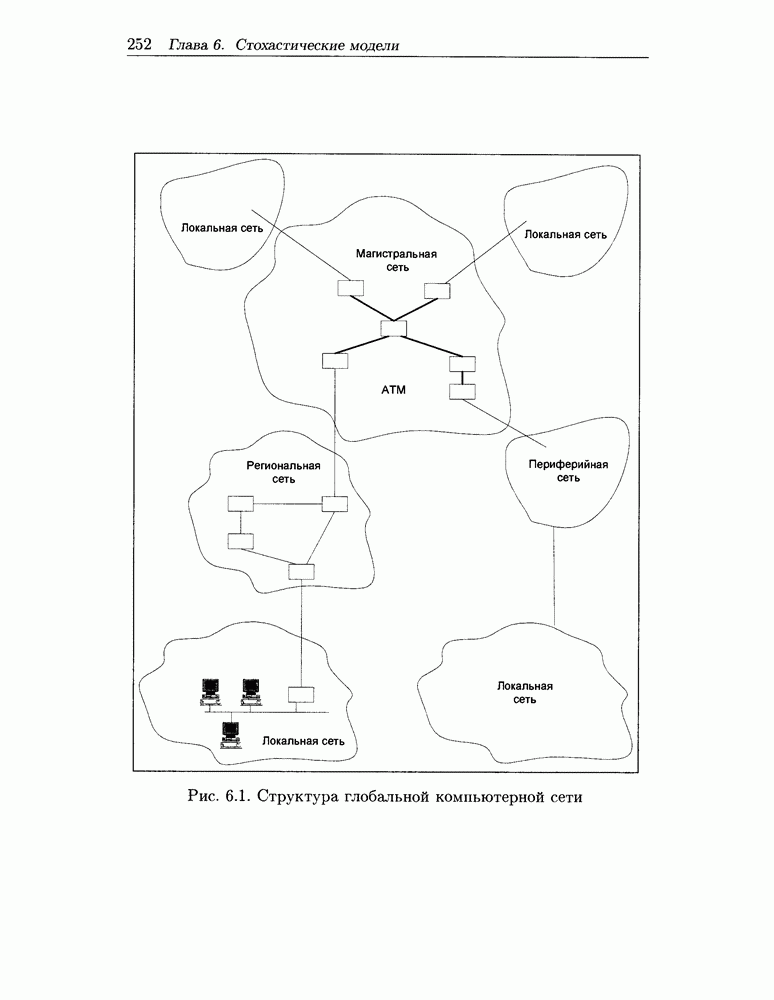
- 6.1.1 Структура компьютерных сетей
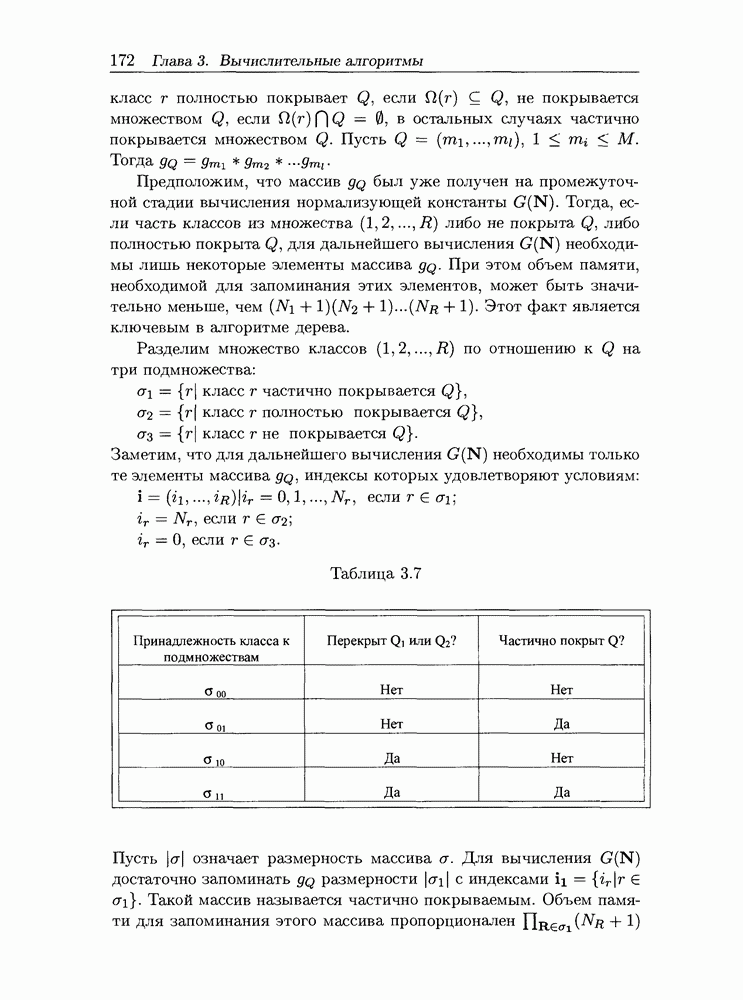
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
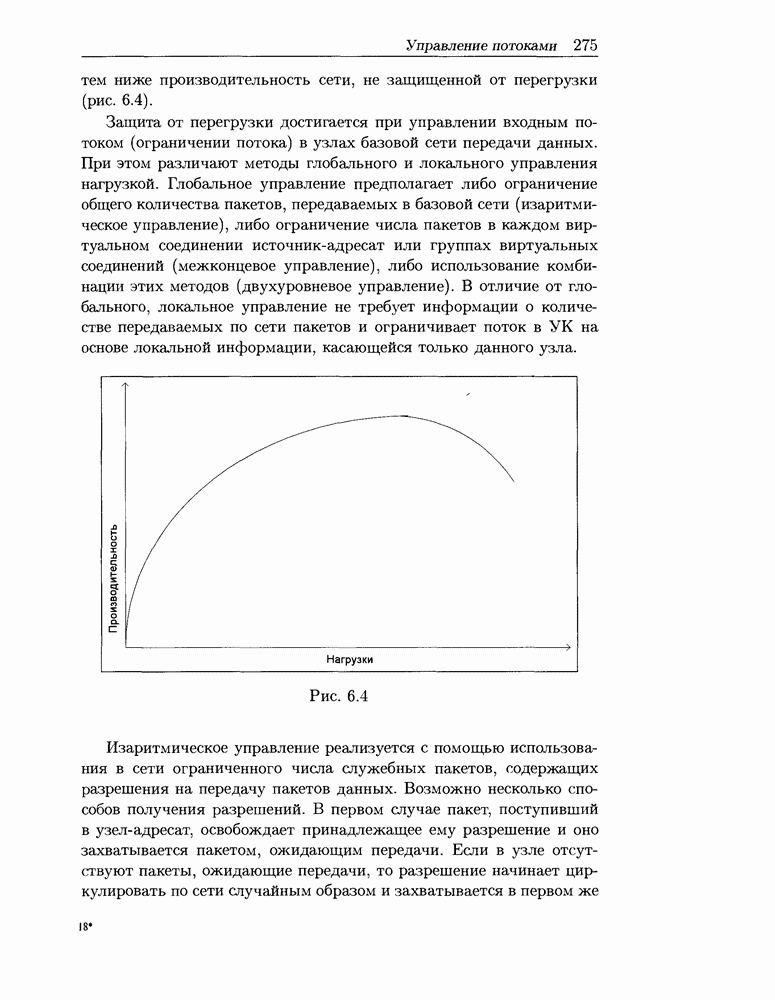
- 6.3 Управление потоками в сети пакетной коммутации
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
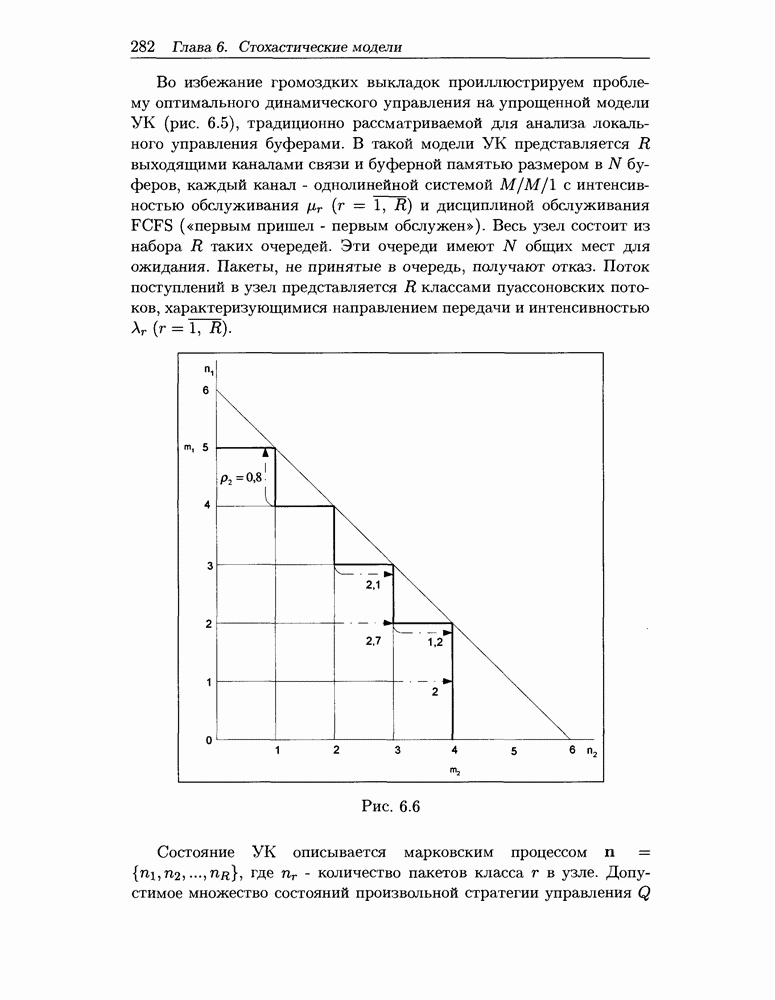
- 6.3.3 Локальное управление буферами
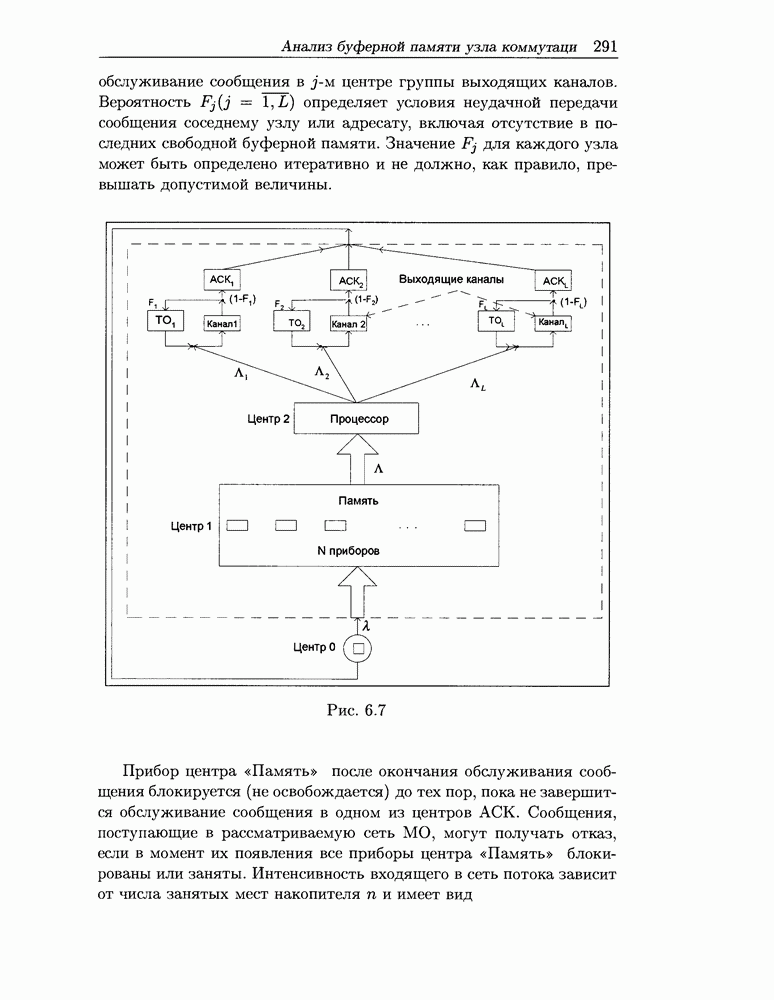
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
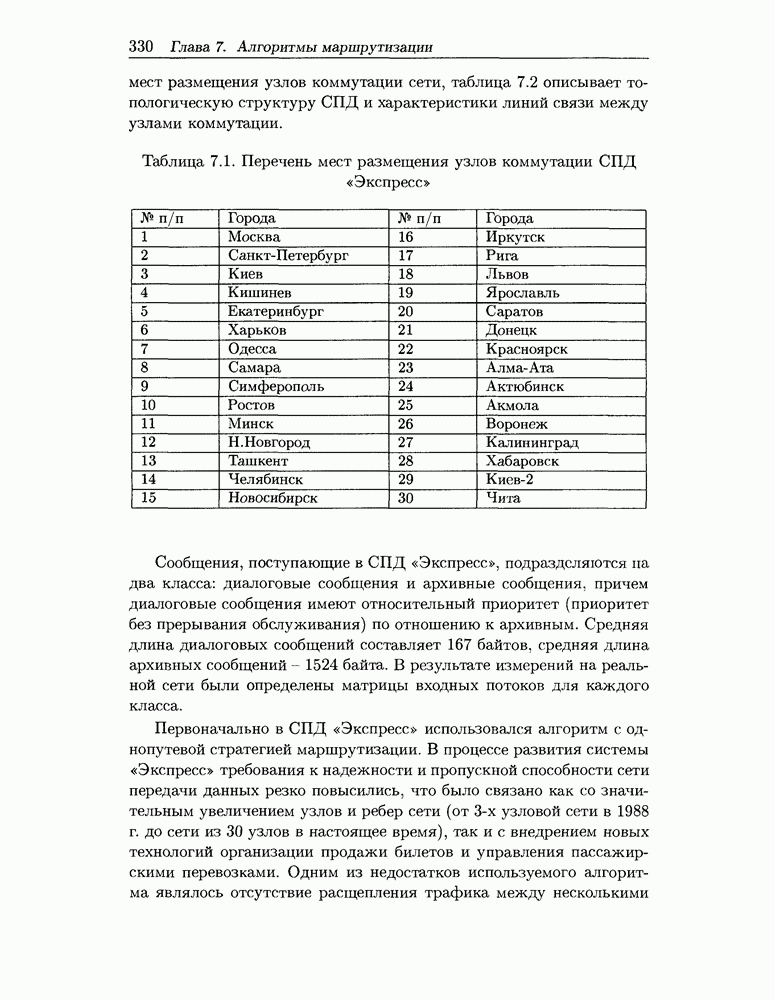
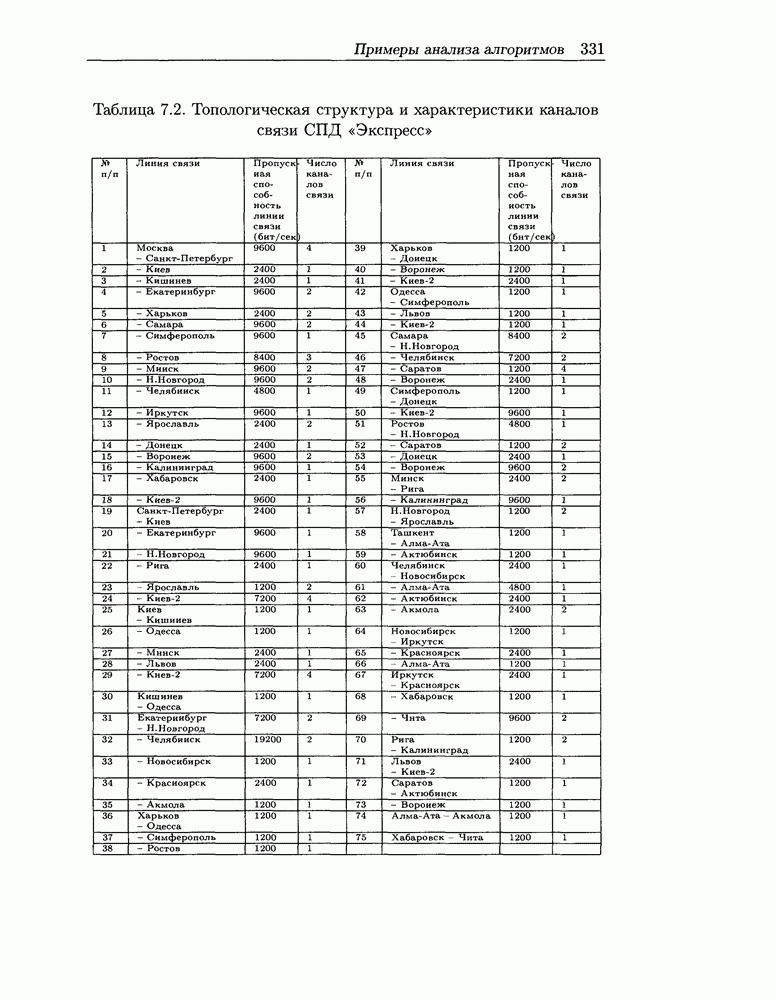
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
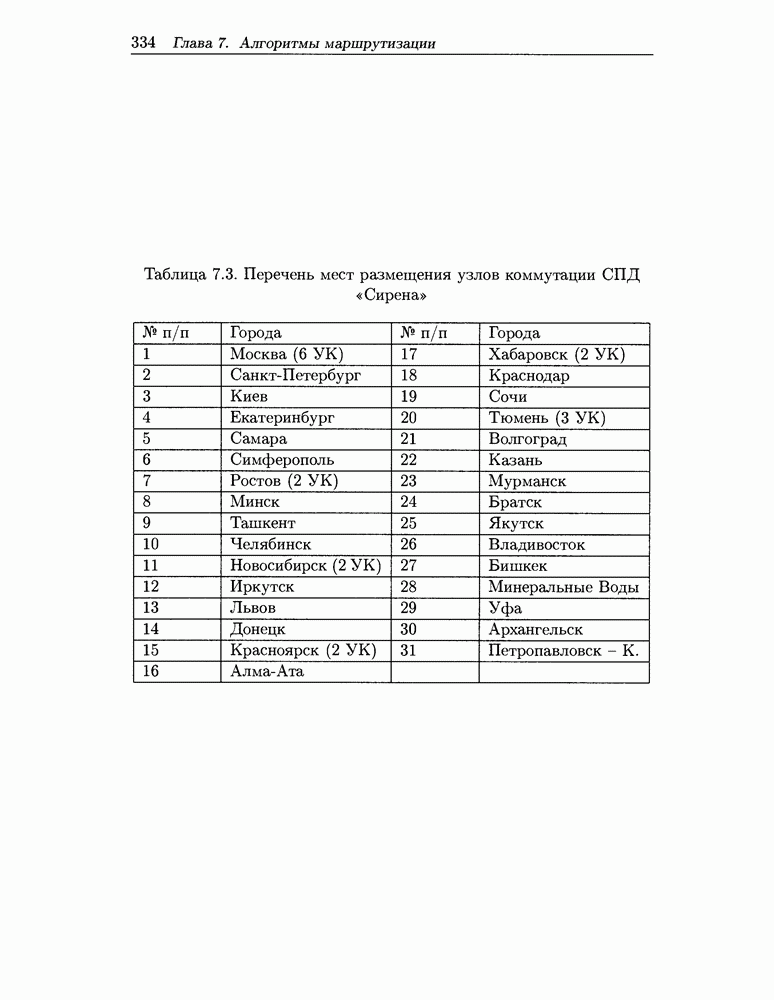
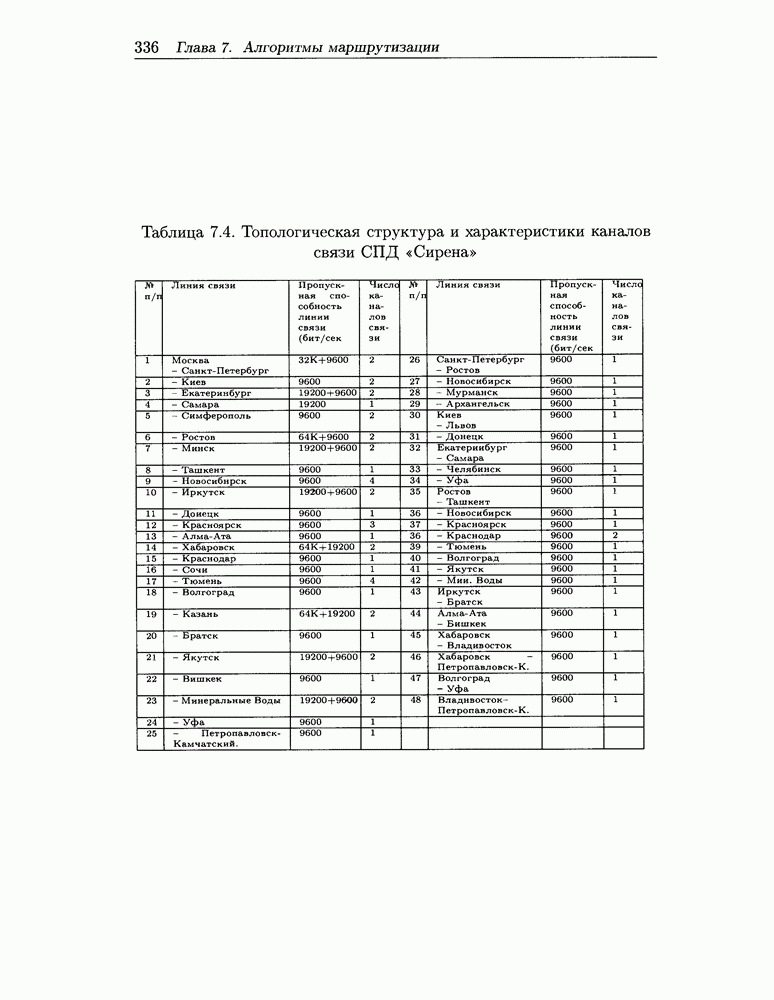
- 7.4.2 Анализ развития СПД «Сирена»
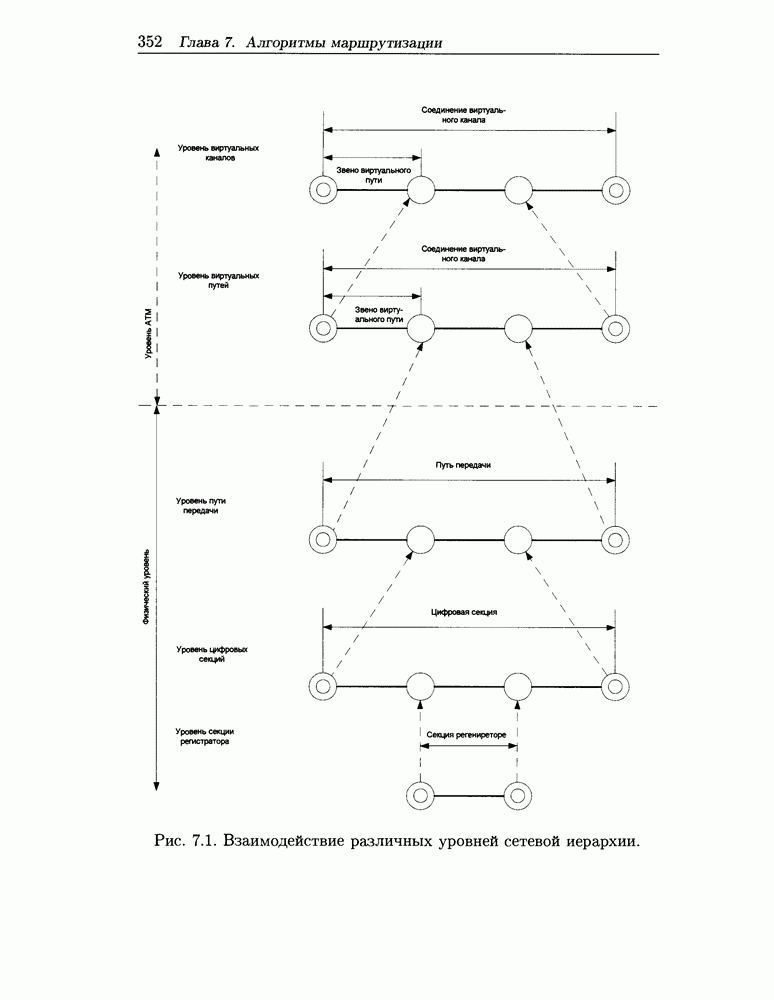
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
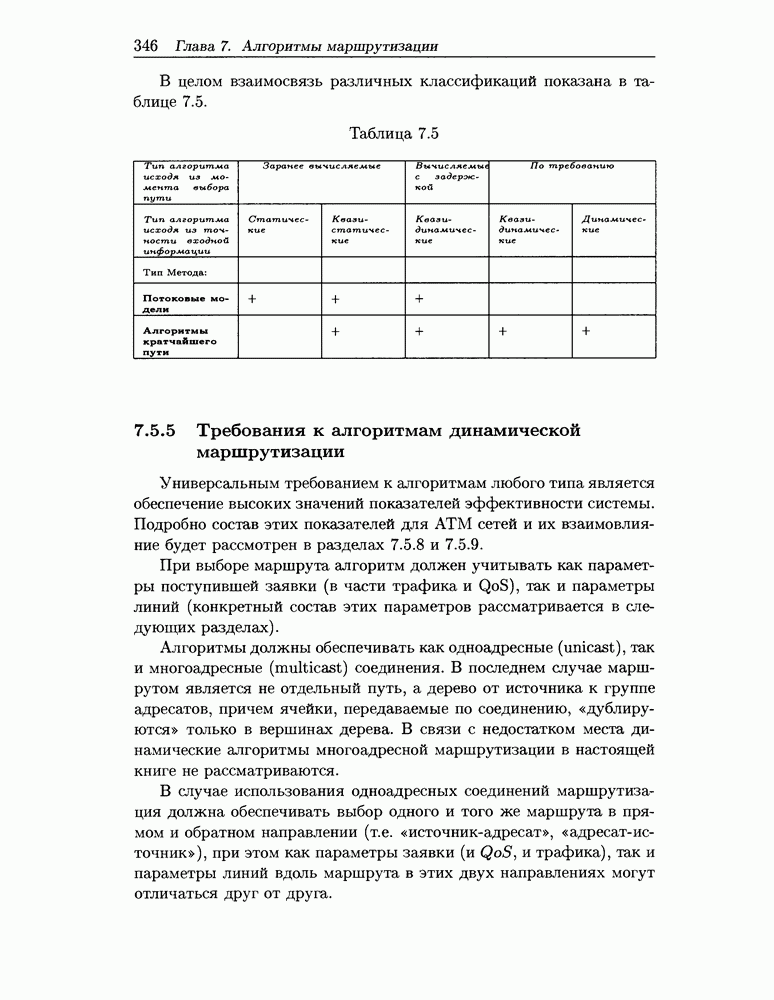
- 7.5.4 Классификация алгоритмов маршрутизации
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
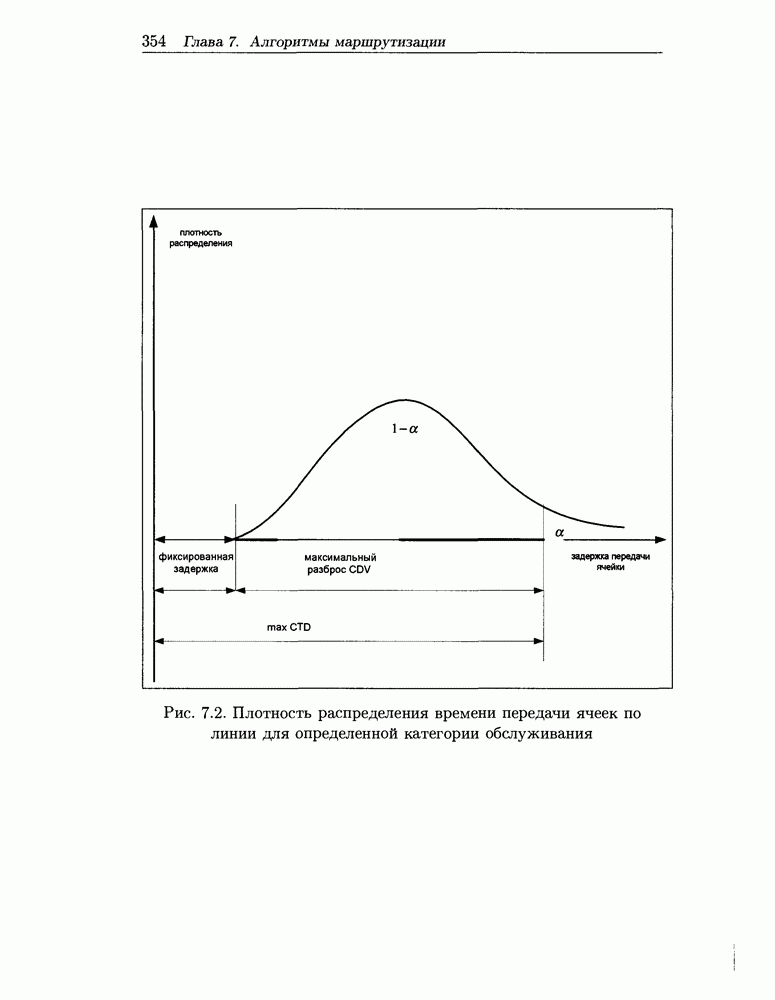
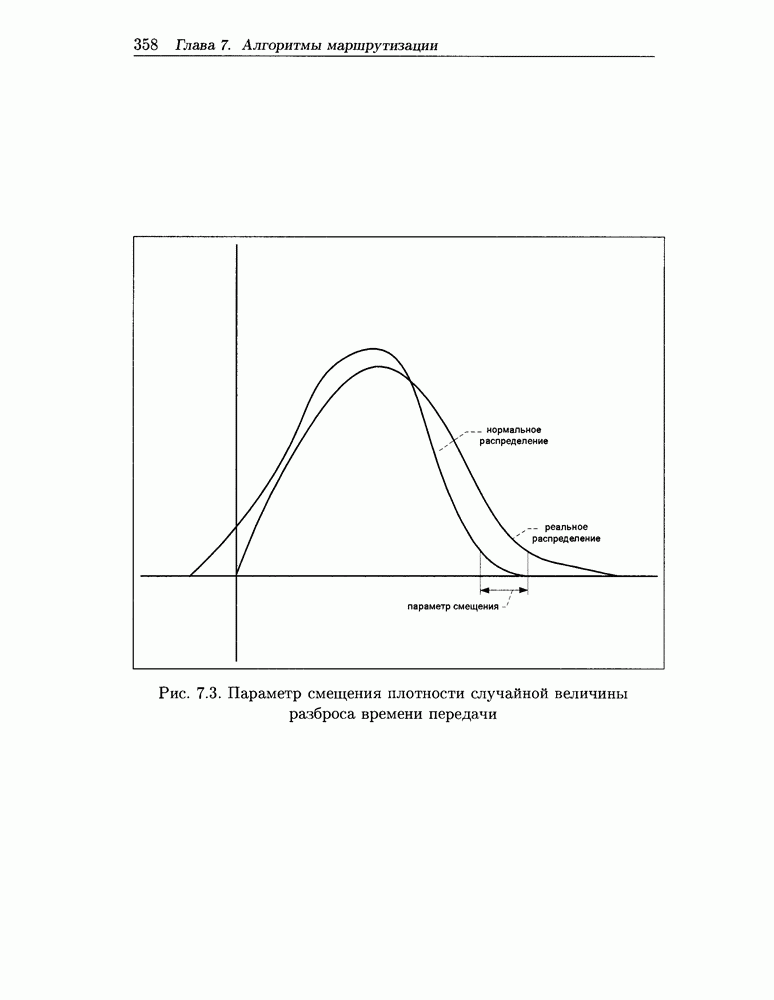
- 7.5.8 Показатели качества маршрутизации
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
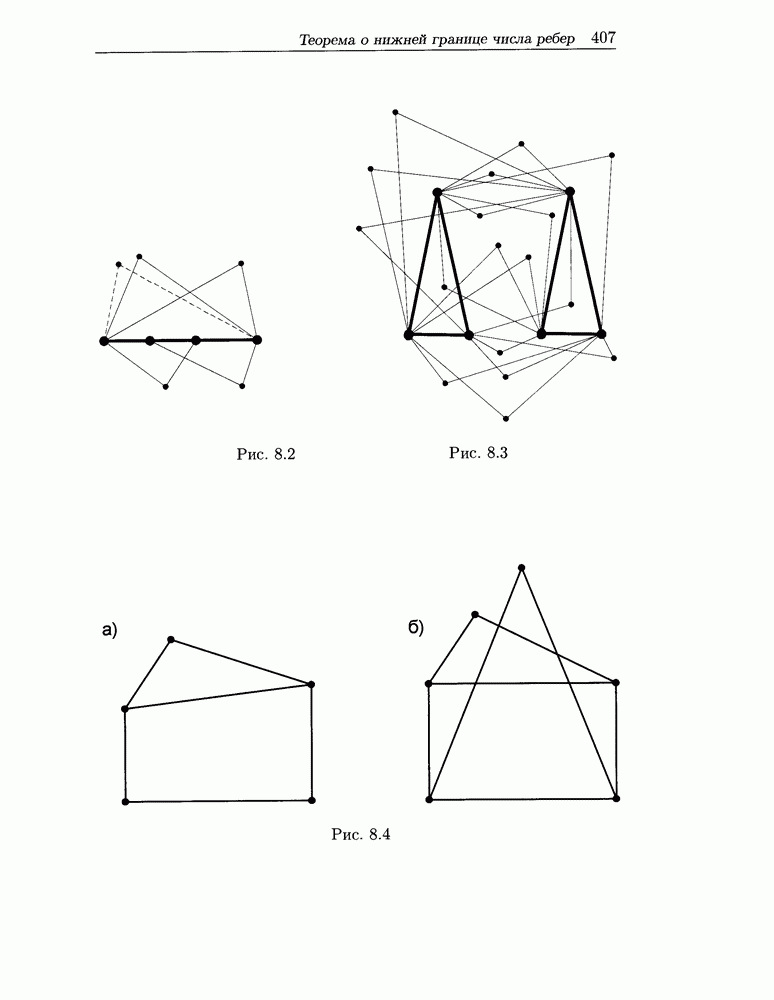
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
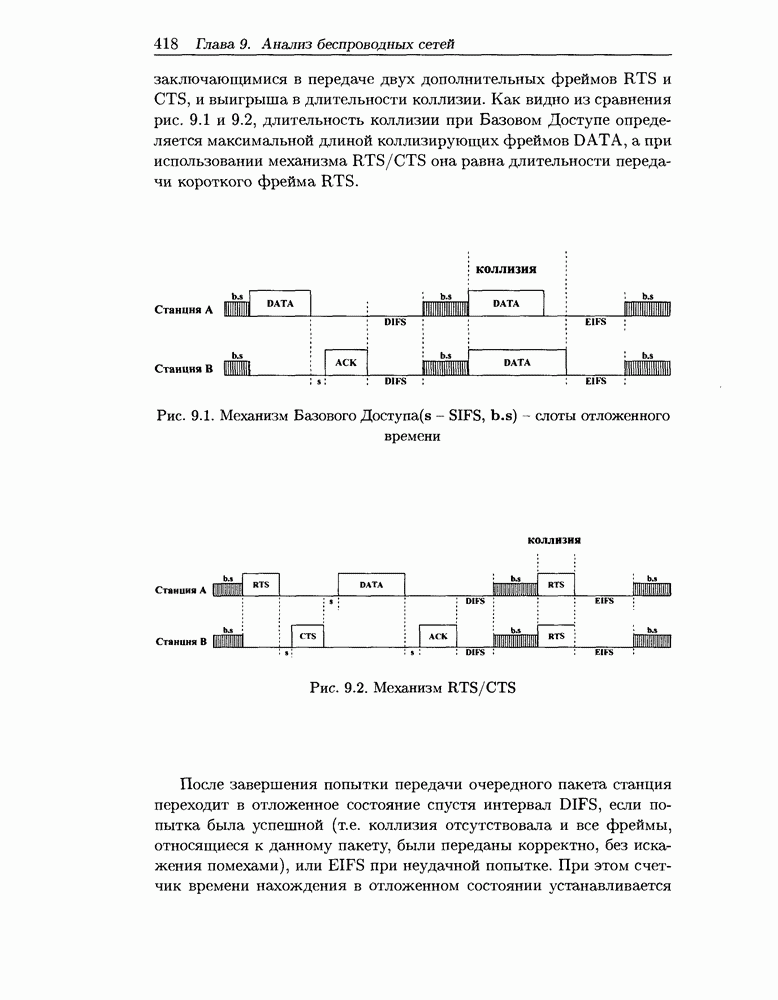
- 9.1 Состояние и перспективы развития беспроводных радиосетей
- 9.2 Схема распределенного управления
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
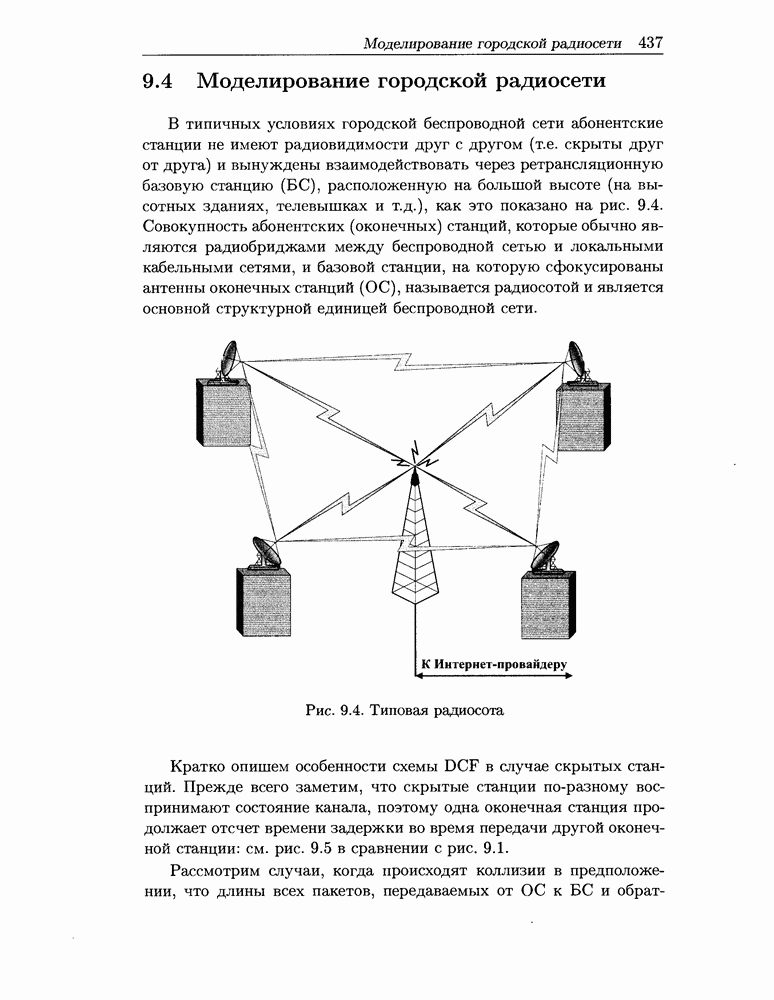
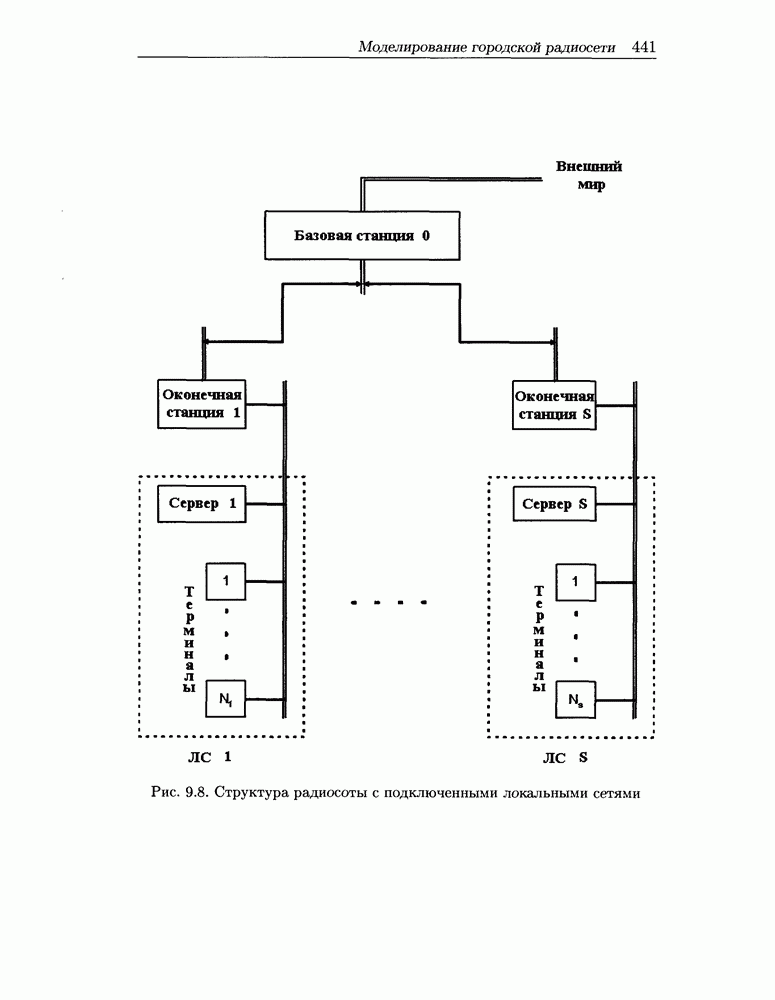
- 9.4 Моделирование городской радиосети
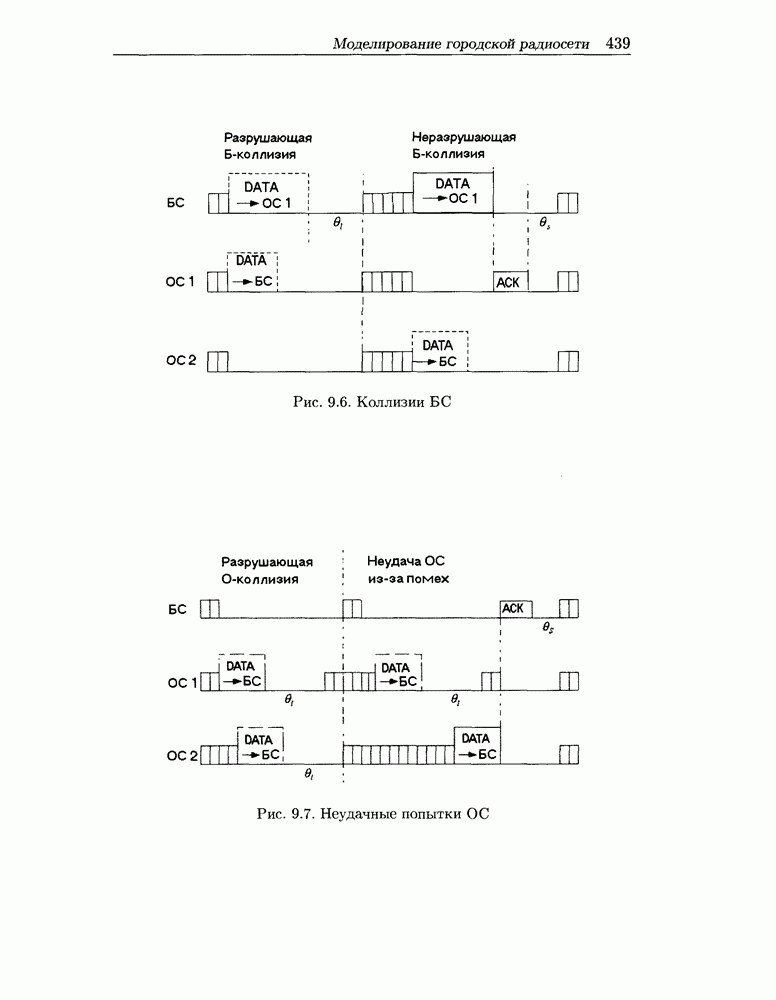
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
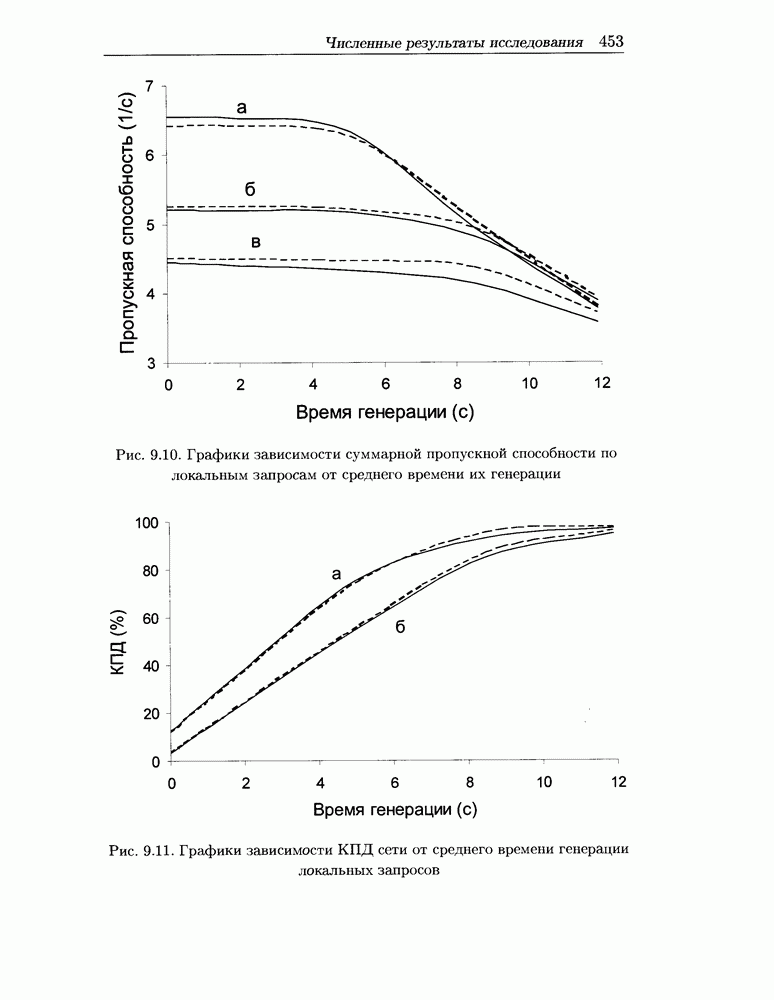
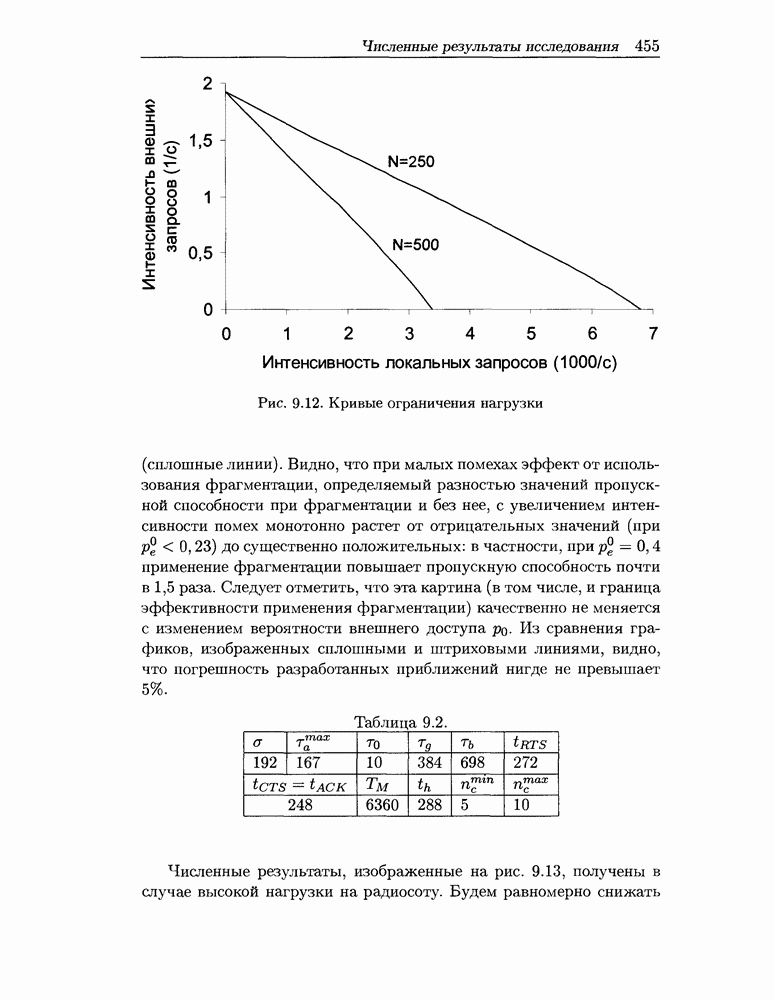
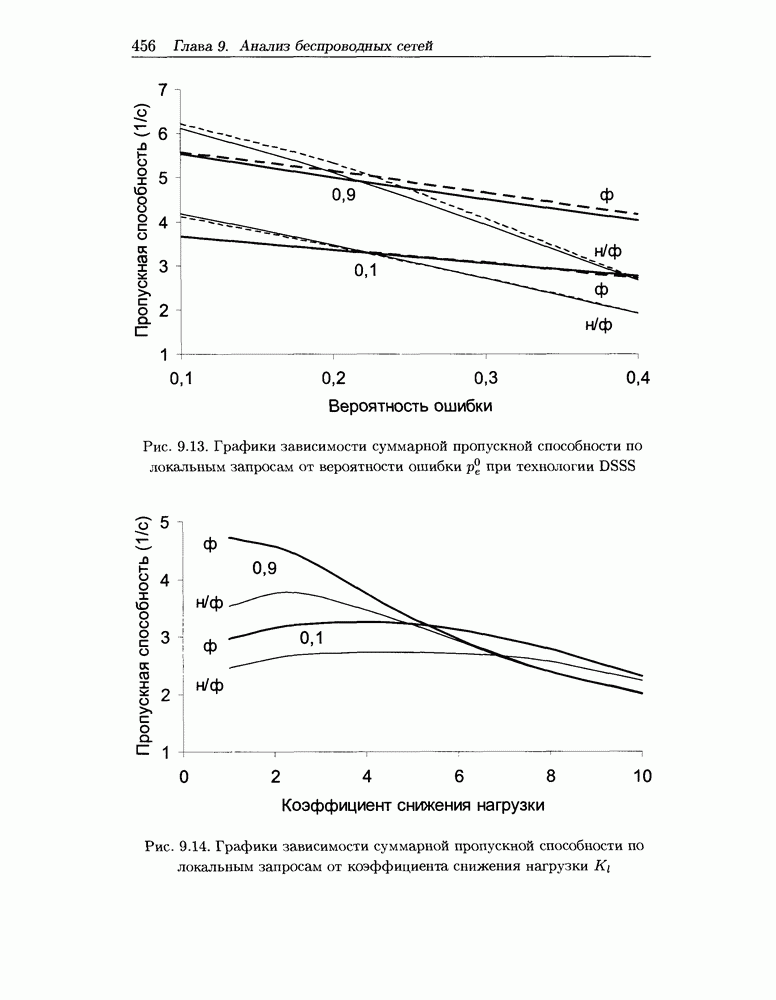
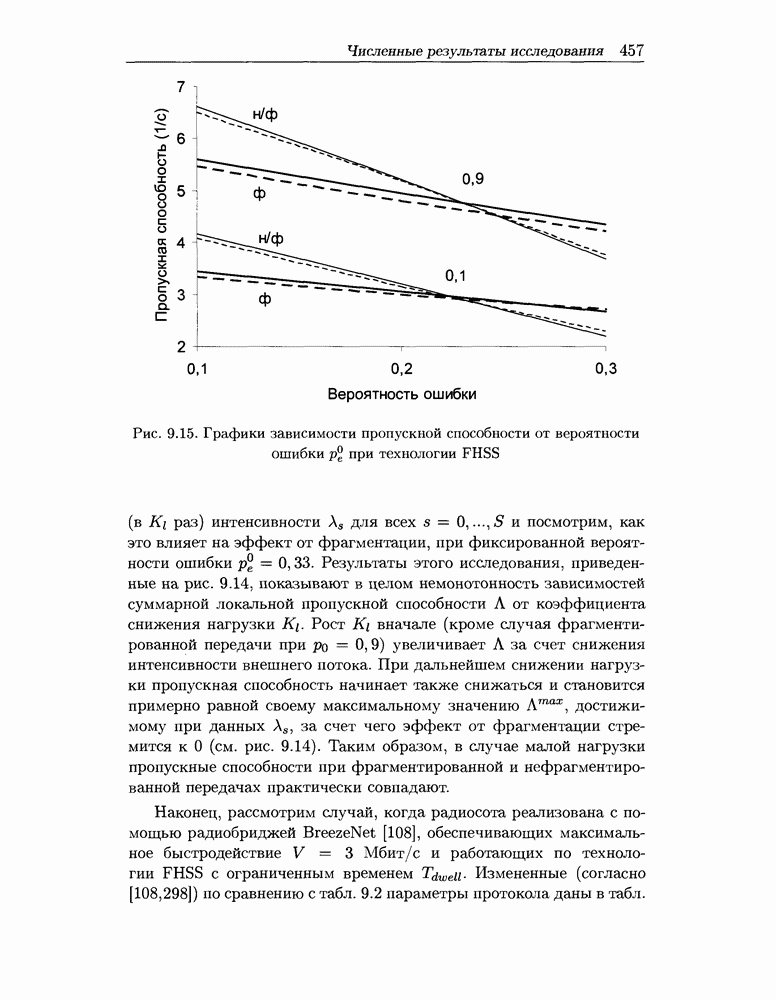
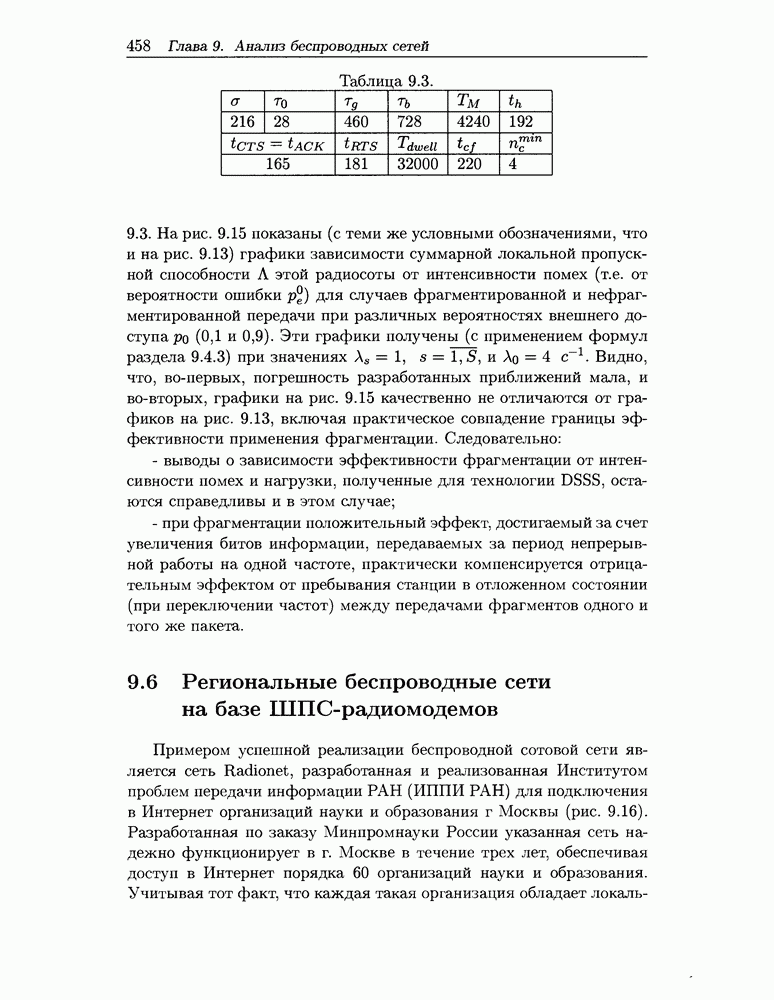
- 9.5 Численные результаты исследования городской радиосоты
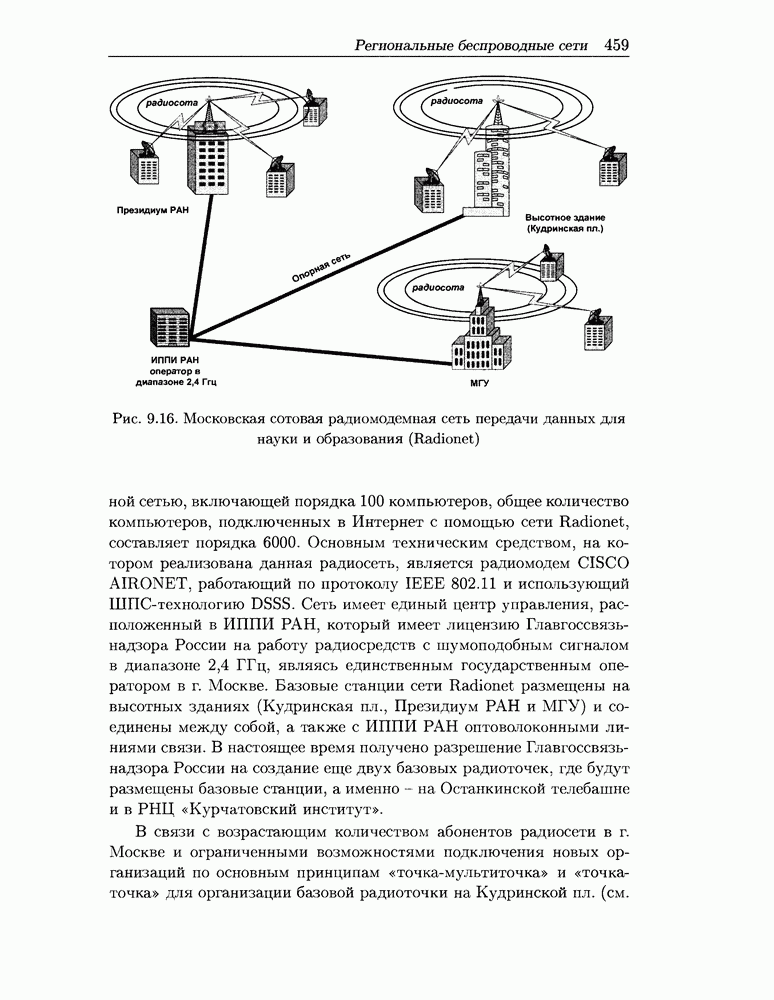
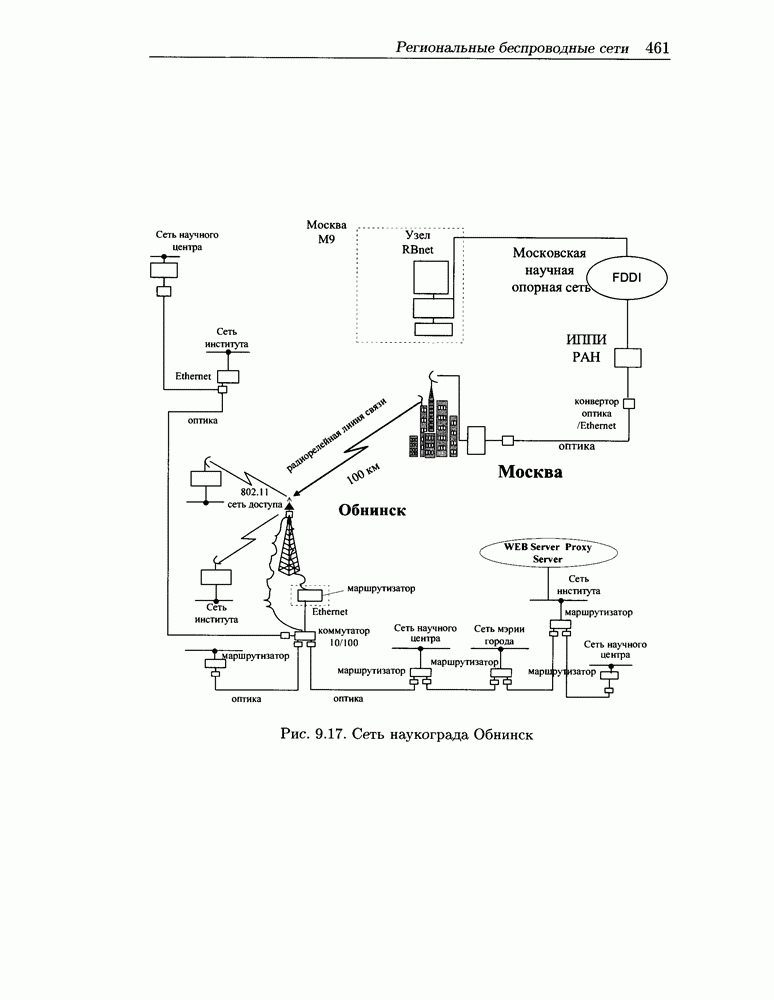
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
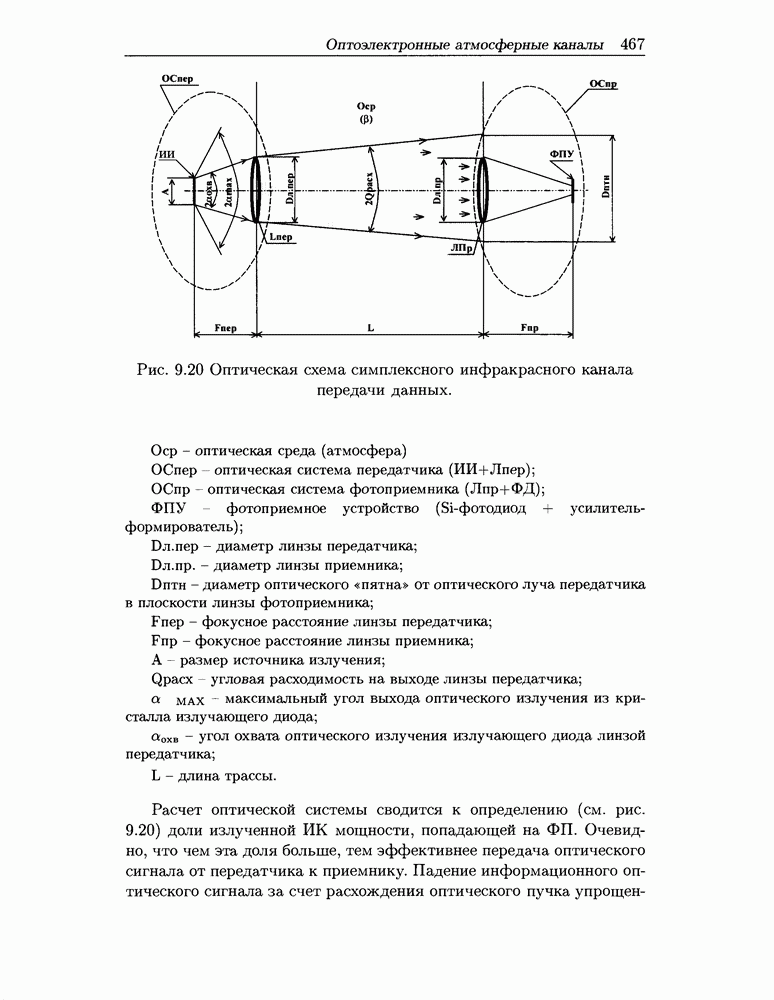
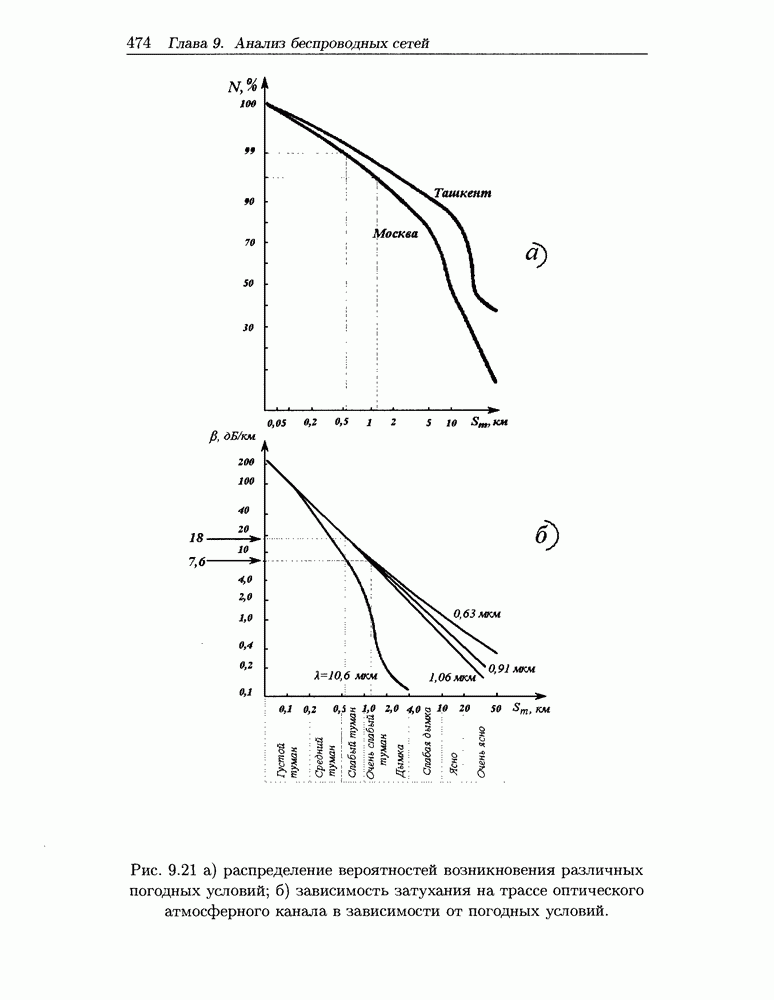
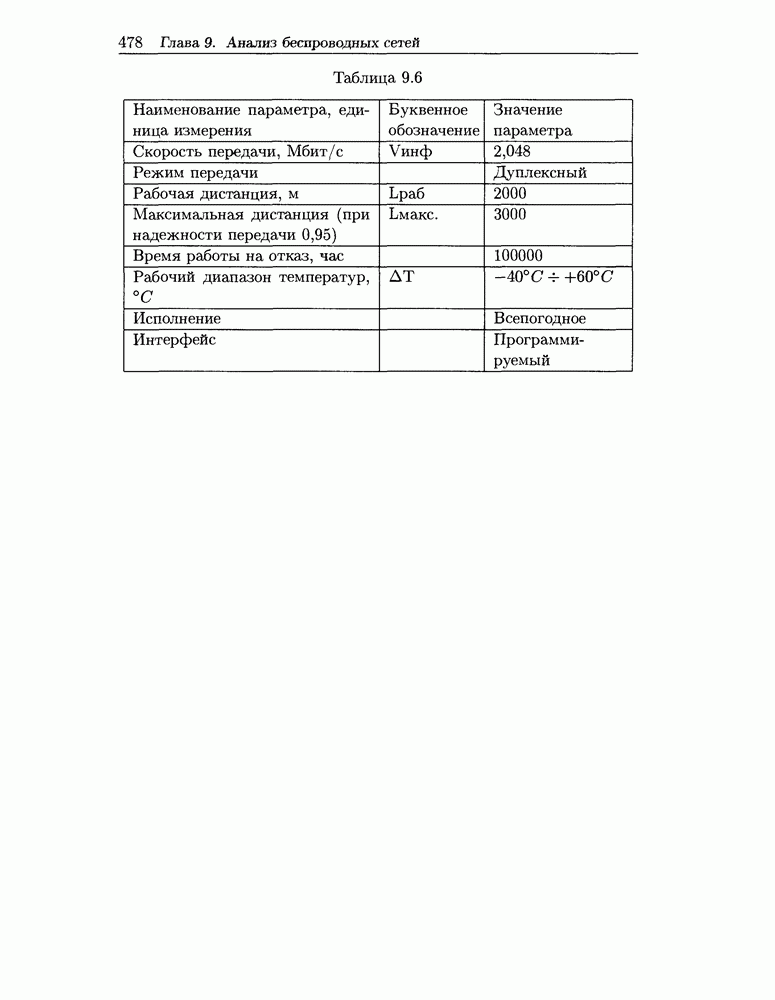
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература