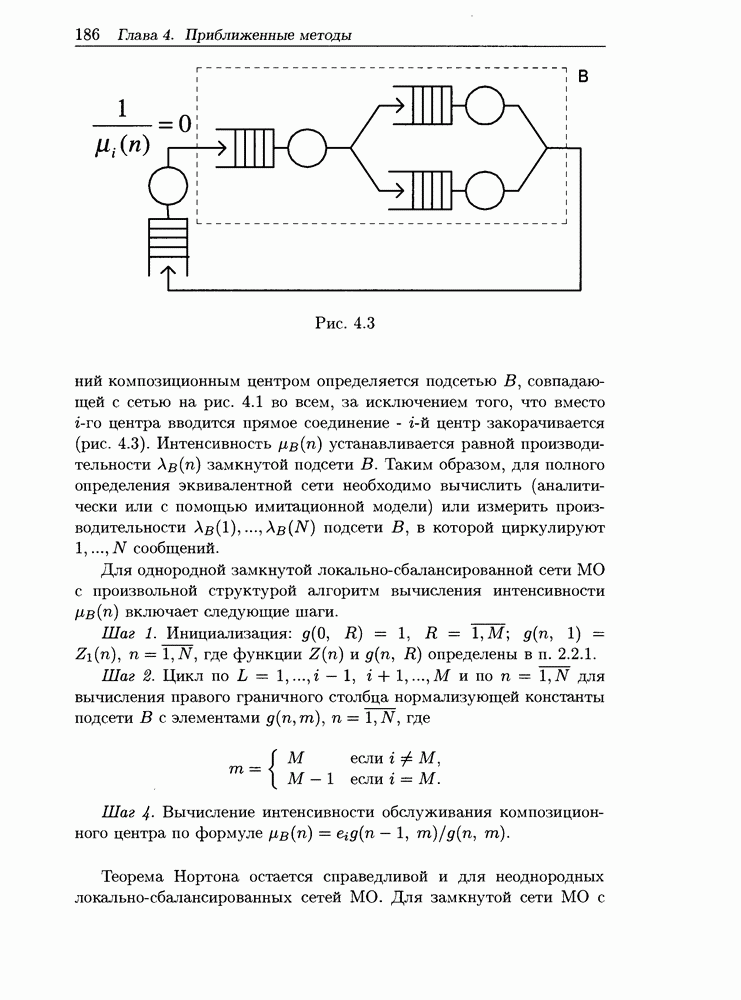
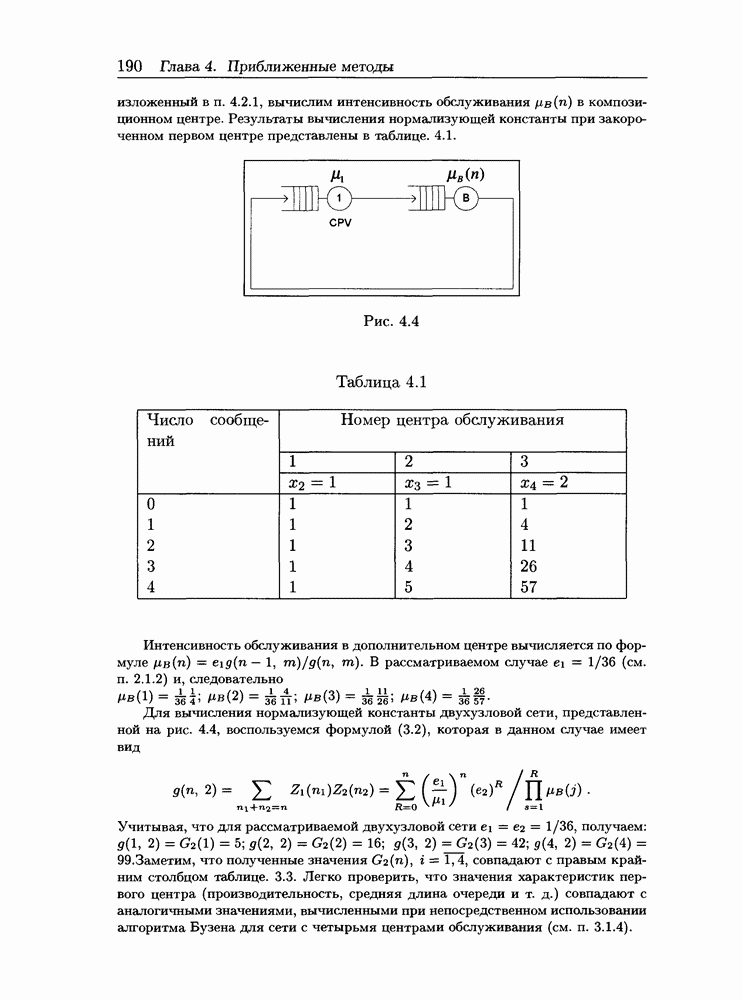
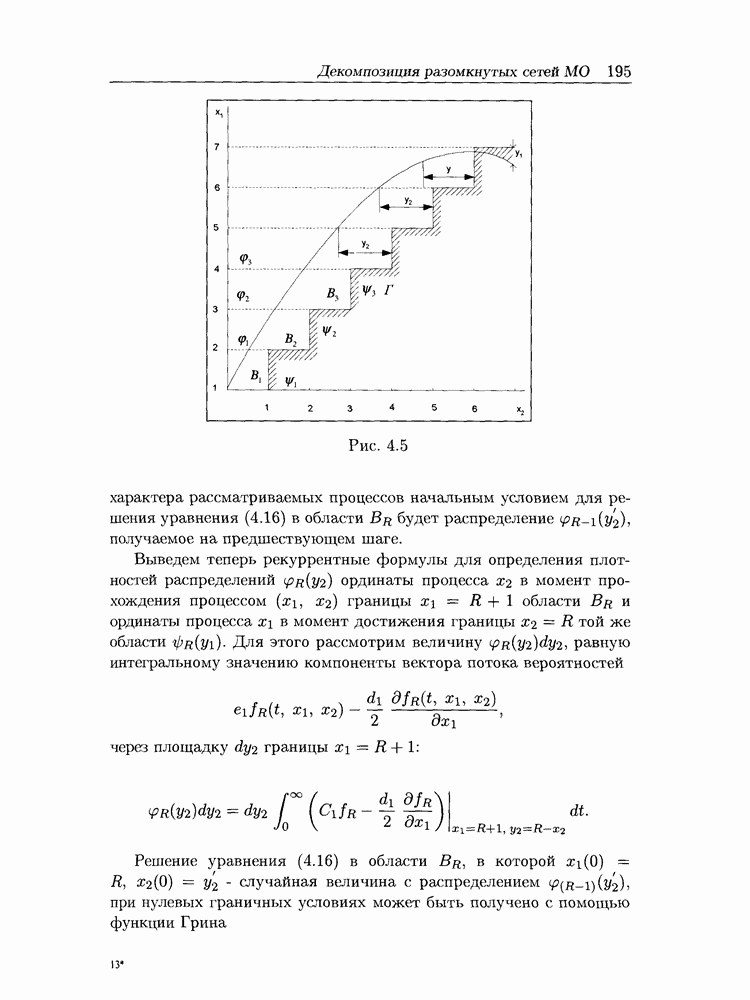
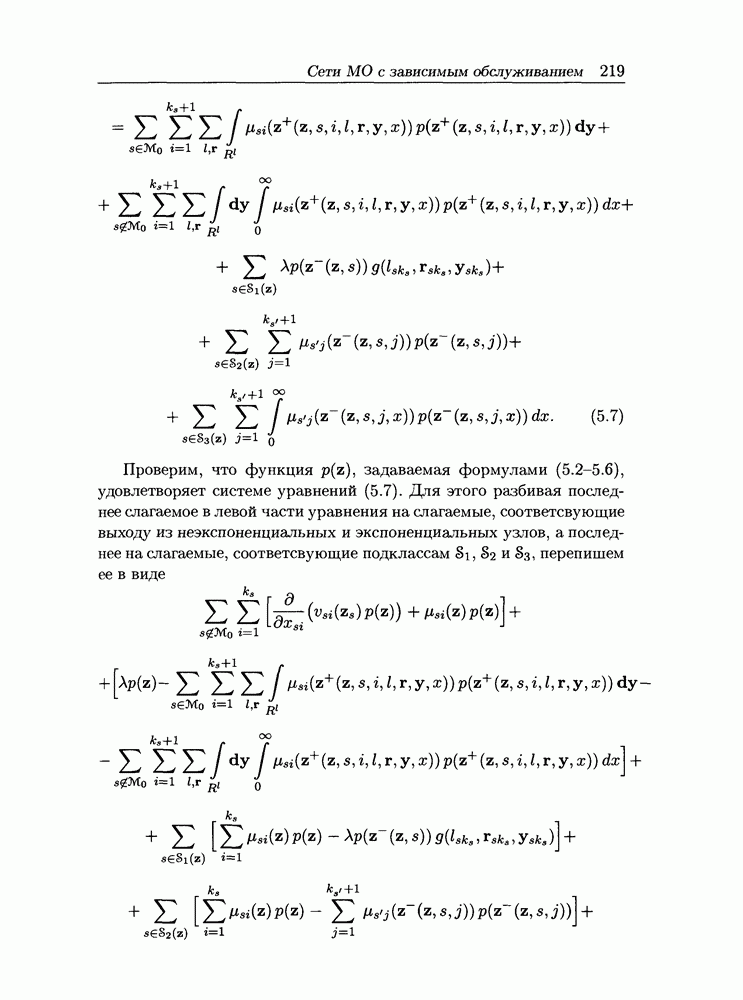| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
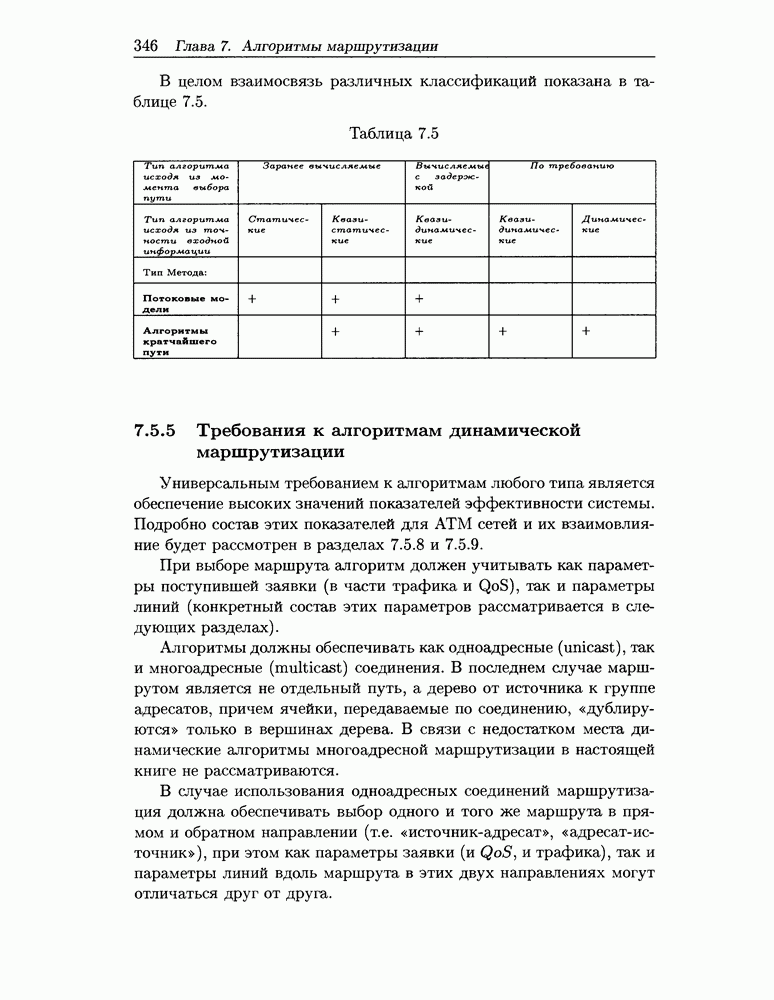
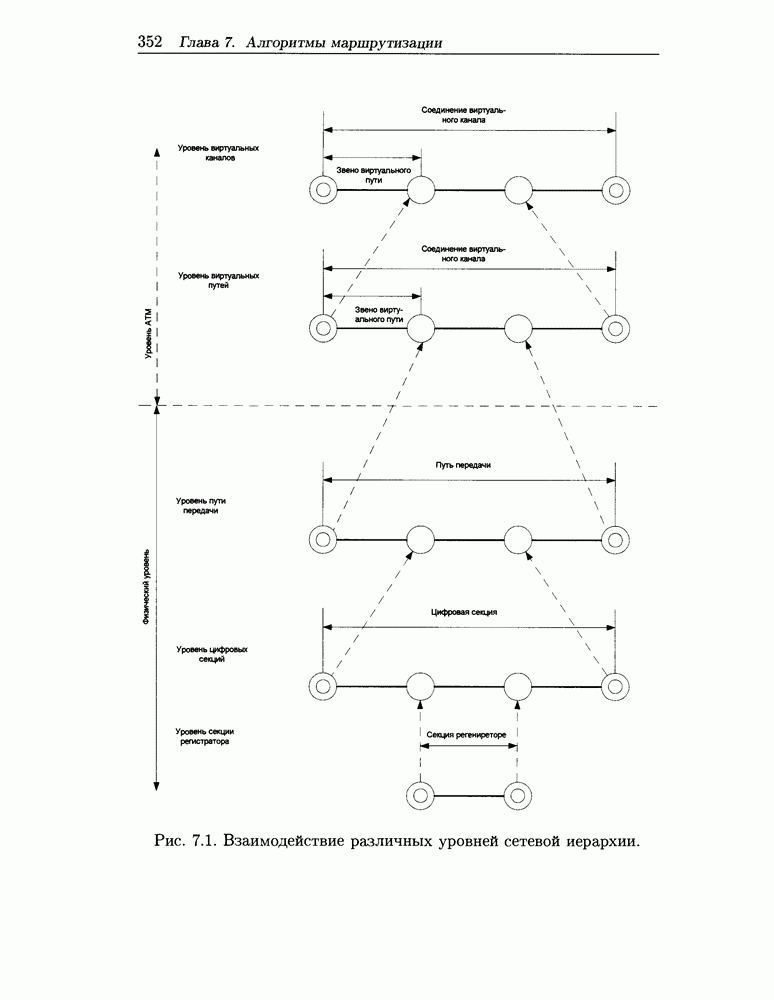
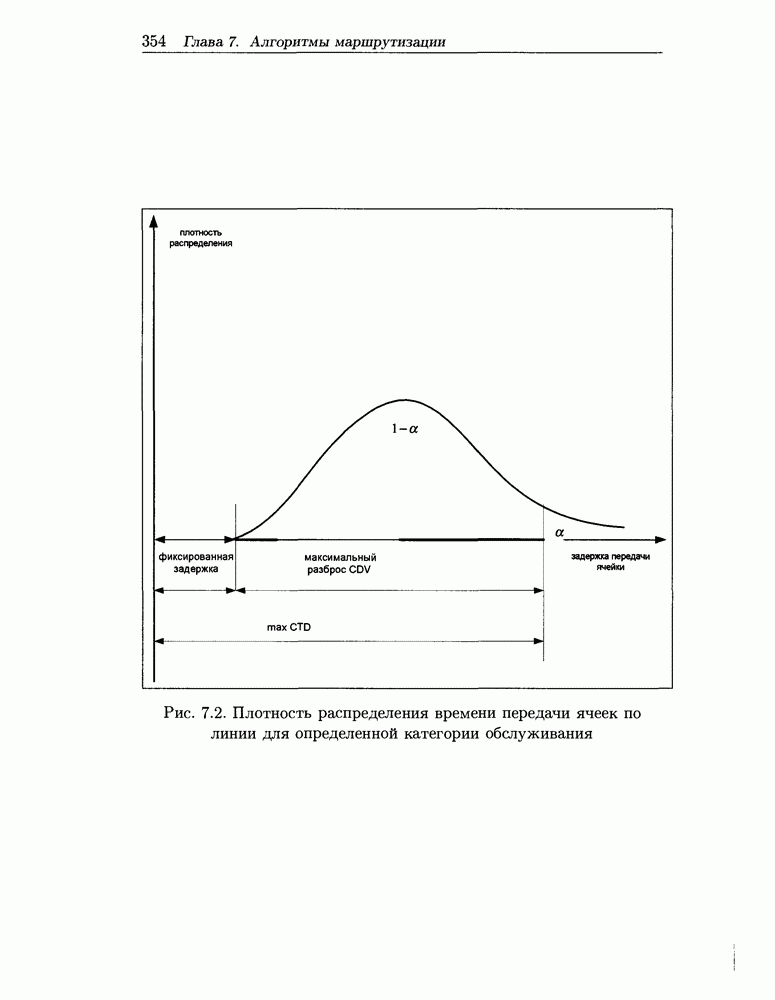
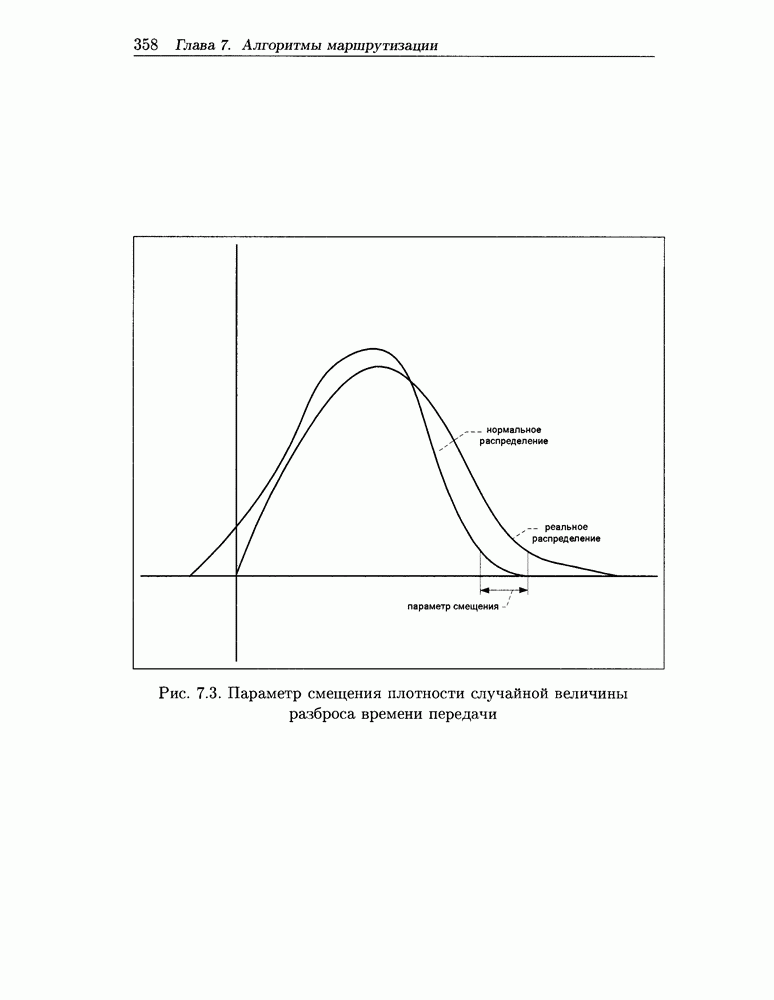
5.2.5 Частные случаи
Приведем теперь некоторые следствия и частные случаи полученного общего результата
Следствие 1. Для вероятностей состояний изолированных узлов рассматриваемых типов справедливы представления (5.3-5.6), где нагрузка изолированного узла  определяется теперь формулой
определяется теперь формулой  а величина
а величина  представляет собой среднюю длительность обслуживания заявок в этом узле.
представляет собой среднюю длительность обслуживания заявок в этом узле.
Доказательство очевидно.
Следствие 2. Для вероятностей макросостояний рассматриваемой сети справедливо мультипликативное представление

где  - вероятность наличия
- вероятность наличия  заявок в сети,
заявок в сети,  - соответствующая вероятность для
- соответствующая вероятность для  узла, причем последние вероятности определяются соотношениями для узлов s типа 0
узла, причем последние вероятности определяются соотношениями для узлов s типа 0

с

для узлов s типа 1

для узлов s типов 2 или 3

Доказательство получается простым интегрированием соответсвующих выражений (5.2-5.6) для вероятностей микросотояний по дополнительным переменным.
Рассмотрим теперь сеть, в которую поступают несколько J классов заявок, для различения которых используем их объемы  так что характеристика заявки имеет вид
так что характеристика заявки имеет вид  . Обозначим через
. Обозначим через  загрузку
загрузку  узла заявками
узла заявками  класса. Справедливо
класса. Справедливо
Следствие 3. Для вероятностей макросостояний сети рассматриваемого типа с несколькими классами заявок справедливо мультипликативное представление (5.14), где вероятности состояний узлов типа 0 имеют вид

с

а в формулах (5.17, 5.18) для вероятностей состояний узлов типов  следует заменить на
следует заменить на

Доказательство получается путем интегрирования в исходных формулах (5.3, 5.5, 5.6) с учетом разбиения заявок на классы.
Приведем теперь результаты для рассмотренных в разделе 3 частных случаев
Сеть Келли
Так как в сети Келли все узлы экпоненциальные, а объемы заявок постоянны и принимают одно из к возможных значений, то для сети Келли справедливо мультипликативное представление (5.14), где для распределения вероятностей состояний узлов имеет место
Следствие 4. Распределения вероятностей состояний узлов в сети Келли задается формулами (5.15, 5.16) с  где теперь в отличие от того, как было указано ранее
где теперь в отличие от того, как было указано ранее

среднее число посещений s-oгo узла заявками i-ого потока.
Доказательство очевидно.
Сеть Джексона
Следствие 5. Распределение вероятностей состояний сети Джексона имеет вид (5.14-5.16), где величина загрузки узлов определяется как и в сети Келли, а среднее число посещений  узла
узла  определяется теперь соотношением
определяется теперь соотношением

где  вектор средних чисел посещения состояний до поглощения.
вектор средних чисел посещения состояний до поглощения.
Для доказательства достаточно заметить, что согласно теории обрывающихся марковских цепей формула (5.21) определяет среднее число посещений различных состояний поглощающей марковской цепью с начальным распределением до поглощения ее поглощающим состоянием.
ВСМР-сеть
Аналогичный результат справедлив и для ВСМР-сетей
Следствие 6. Для распределения вероятностей состояний ВСМР-сети справедливо мультипликативное представление (5.14) с распределениями вероятностей состояний для узлов вида (5.15-5.18), где величина загрузки узлов определяется соотношением

где  — средняя длительность обслуживания заявок
— средняя длительность обслуживания заявок  потока в
потока в  узле, а среднее число посещений
узле, а среднее число посещений  узла заявками
узла заявками  потока
потока  как и прежде, означает среднее число посещений
как и прежде, означает среднее число посещений  узла заявками
узла заявками  потока и вычисляется по формуле (5.21).
потока и вычисляется по формуле (5.21).
Доказательство получается подстановкой характеристик ВСМР-сети в общие формулы.
Зависимое обслуживание
При моделировании зависимого обслуживания для неэкспоненциальных узлов положим

Тогда  справедливо
справедливо
Следствие 7. Для распределения вероятностей состояний сети с зависимым обслуживанием заявок справедливо мультипликативное представление, для макросостояний определяемой формулами (5.14-5.18).
Доказательство как и ранее получается подстановкой характеристик такой сети в общие формулы (5.2-5.6).
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
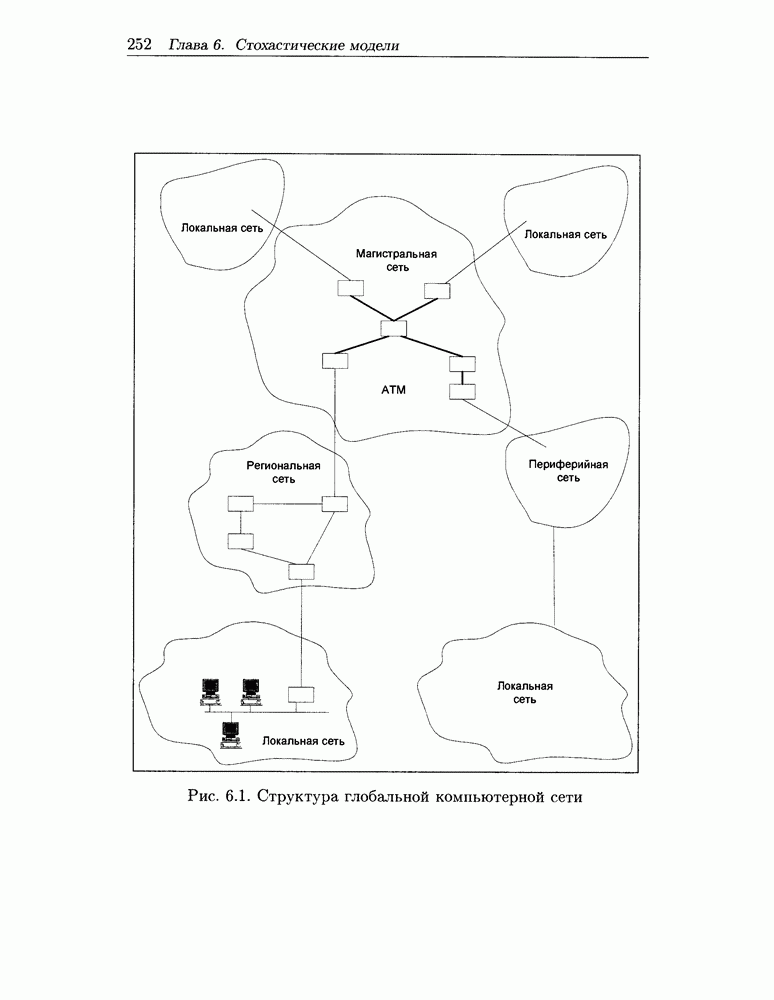
- 6.1.1 Структура компьютерных сетей
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
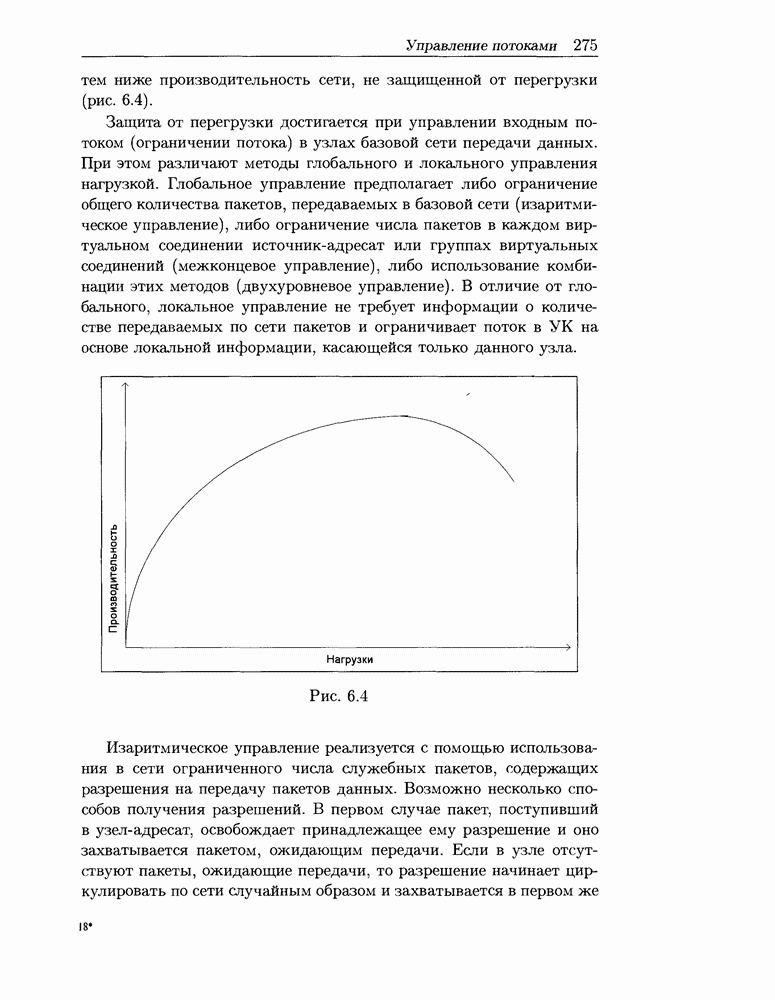
- 6.3 Управление потоками в сети пакетной коммутации
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
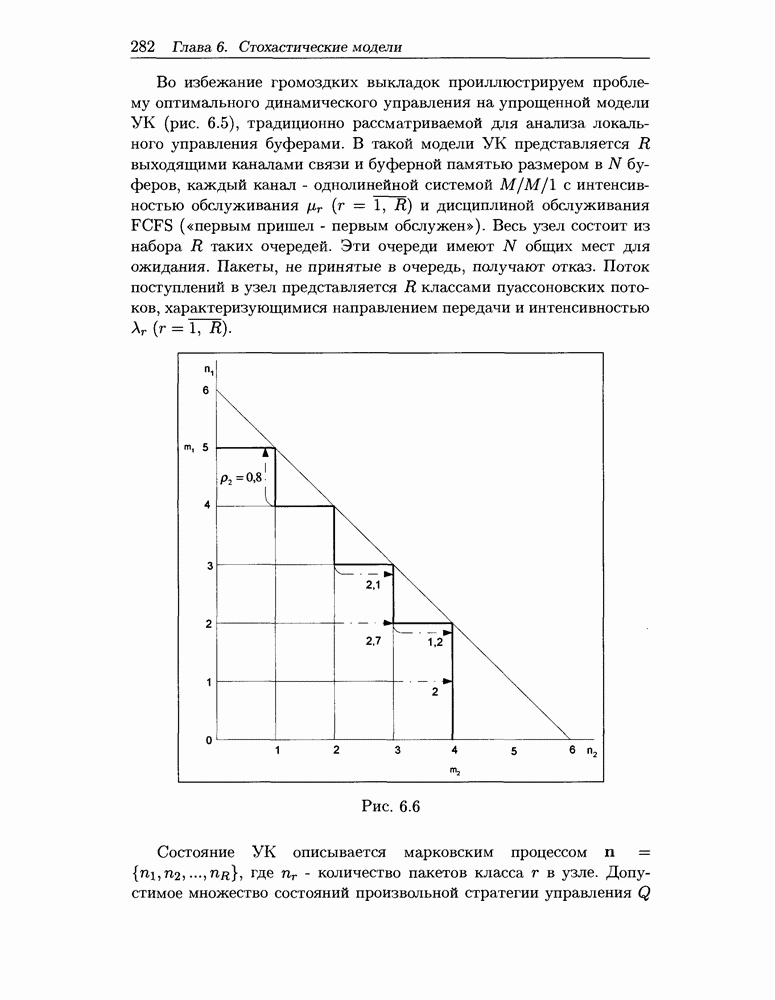
- 6.3.3 Локальное управление буферами
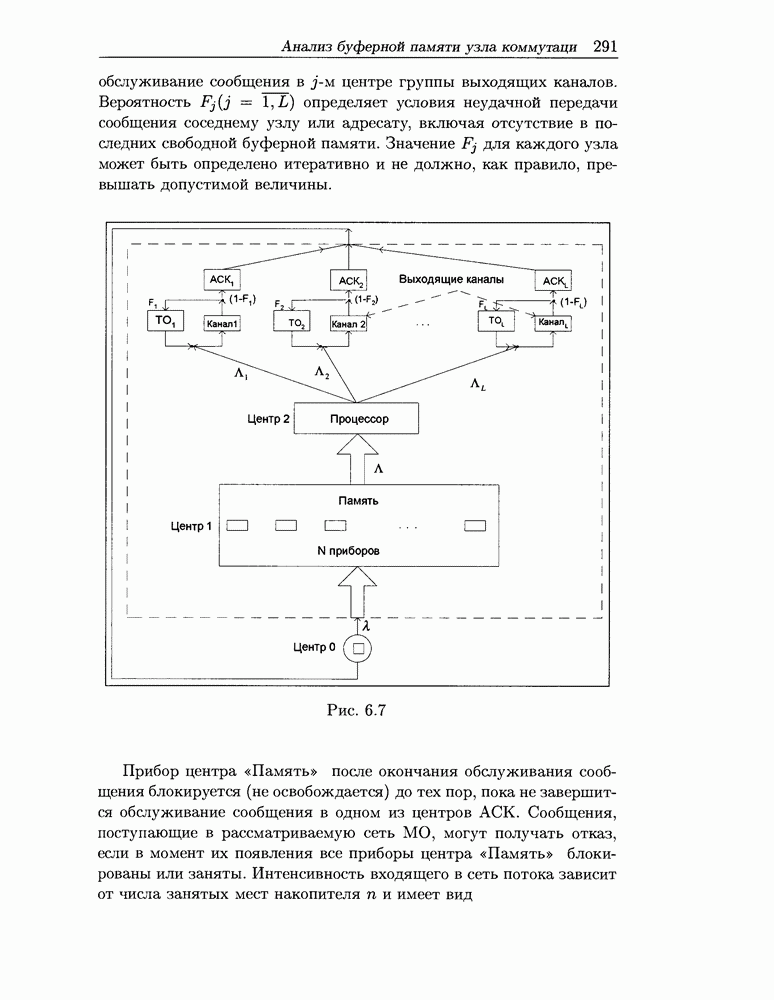
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
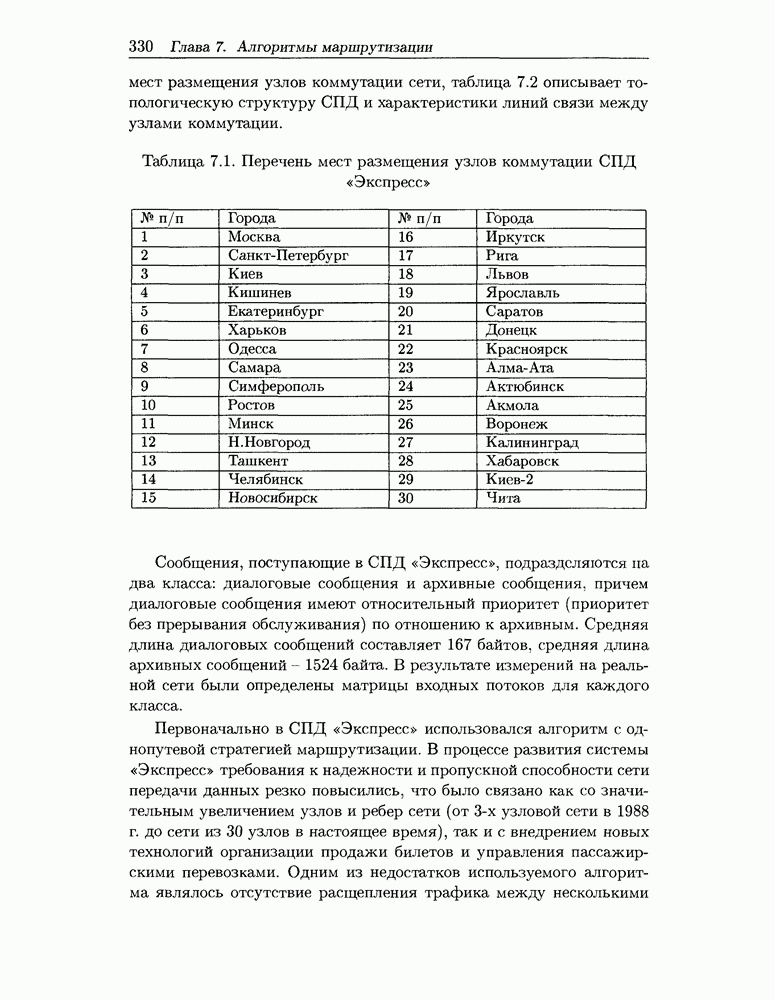
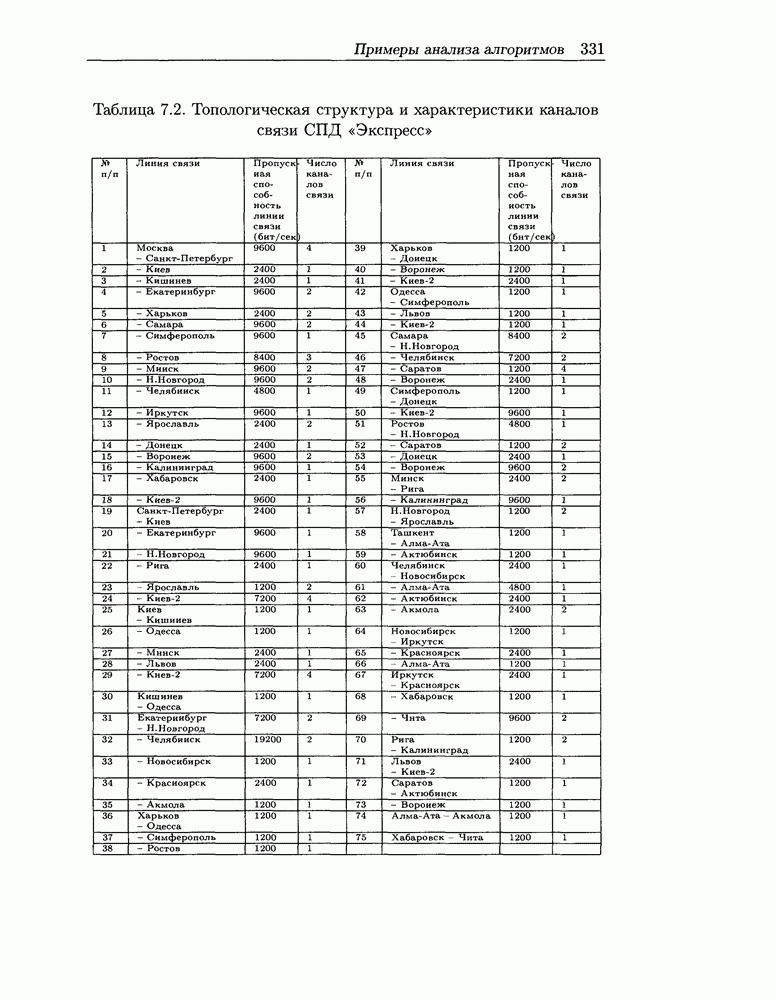
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
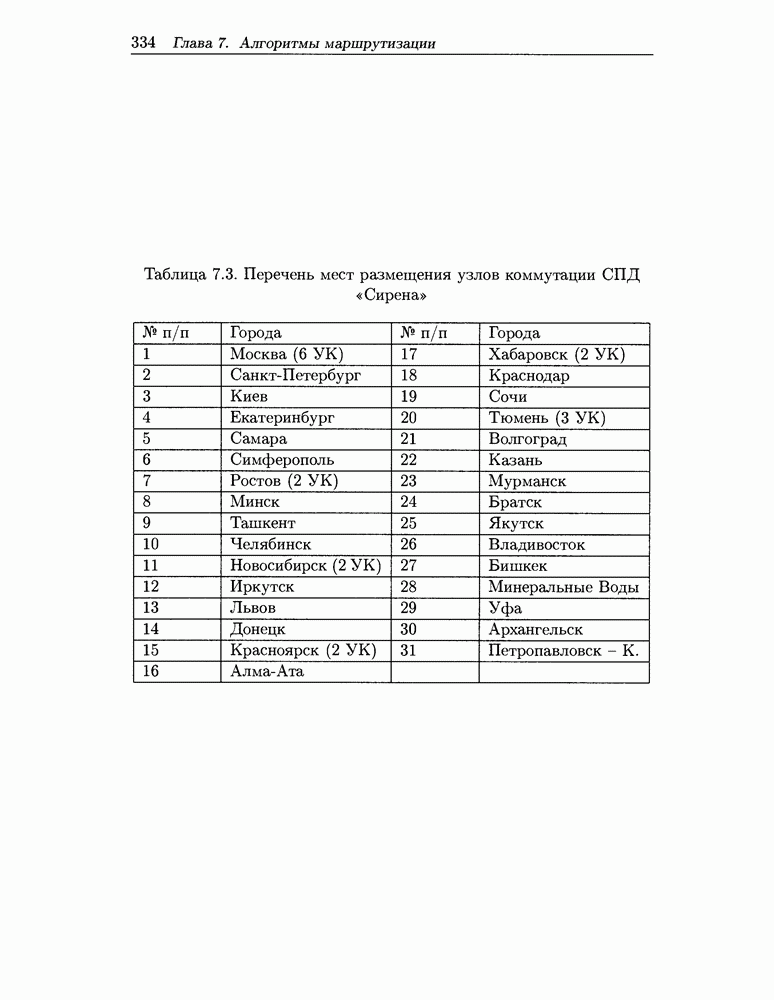
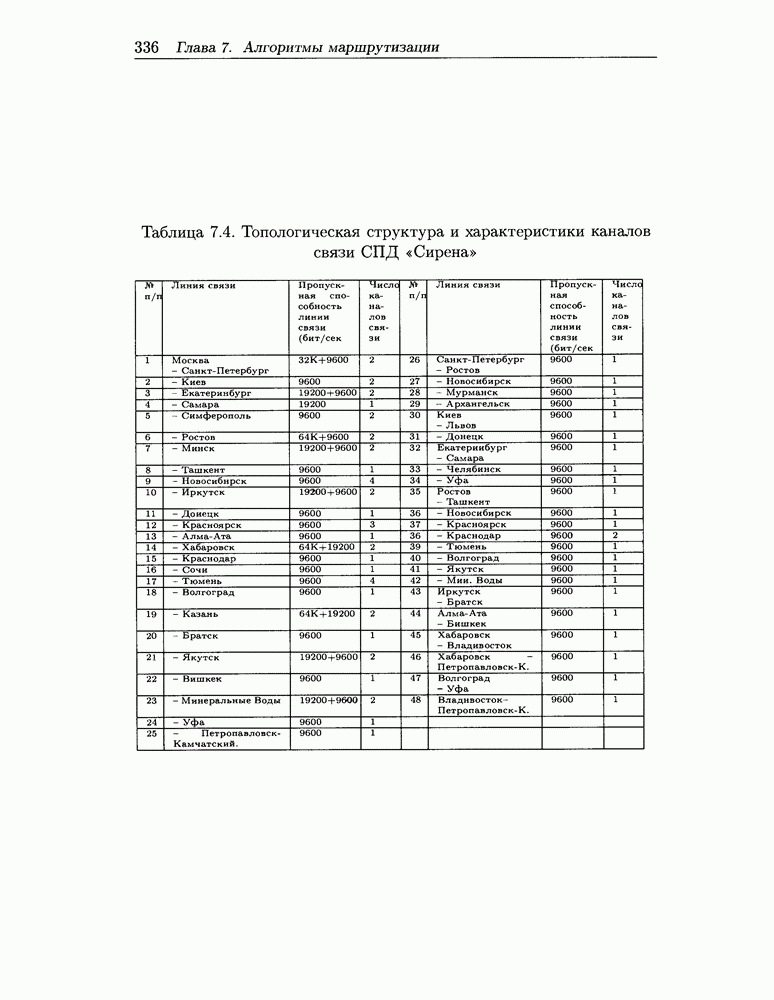
- 7.4.2 Анализ развития СПД «Сирена»
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
- 7.5.4 Классификация алгоритмов маршрутизации
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
- 7.5.8 Показатели качества маршрутизации
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
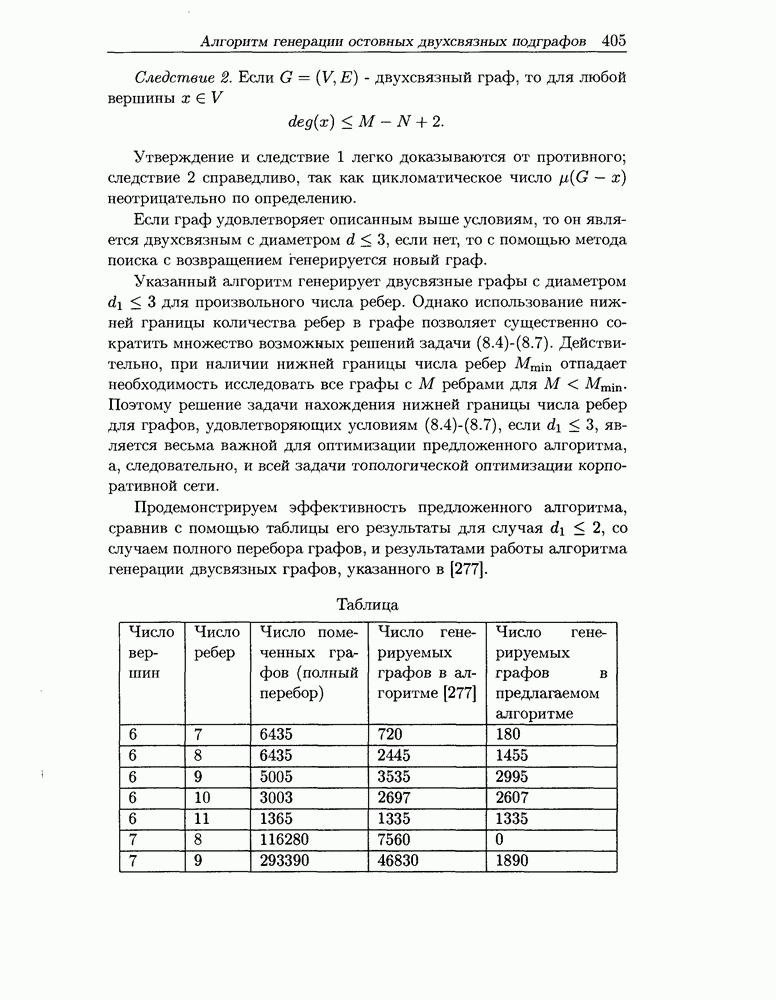
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
- 9.1 Состояние и перспективы развития беспроводных радиосетей
- 9.2 Схема распределенного управления
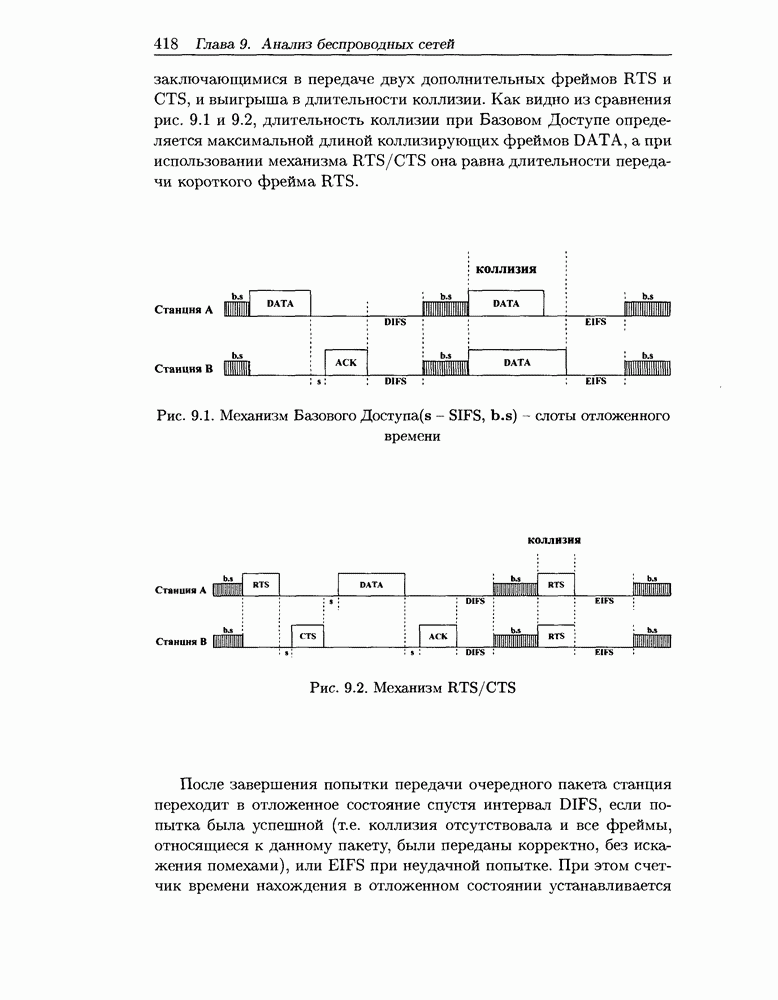
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
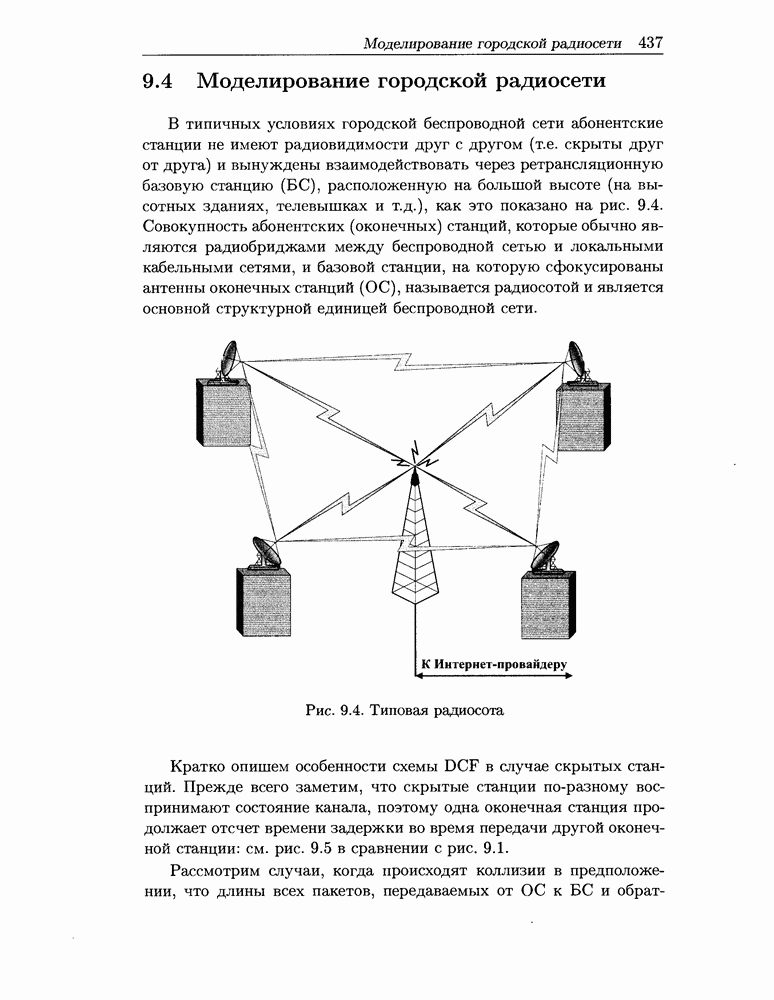
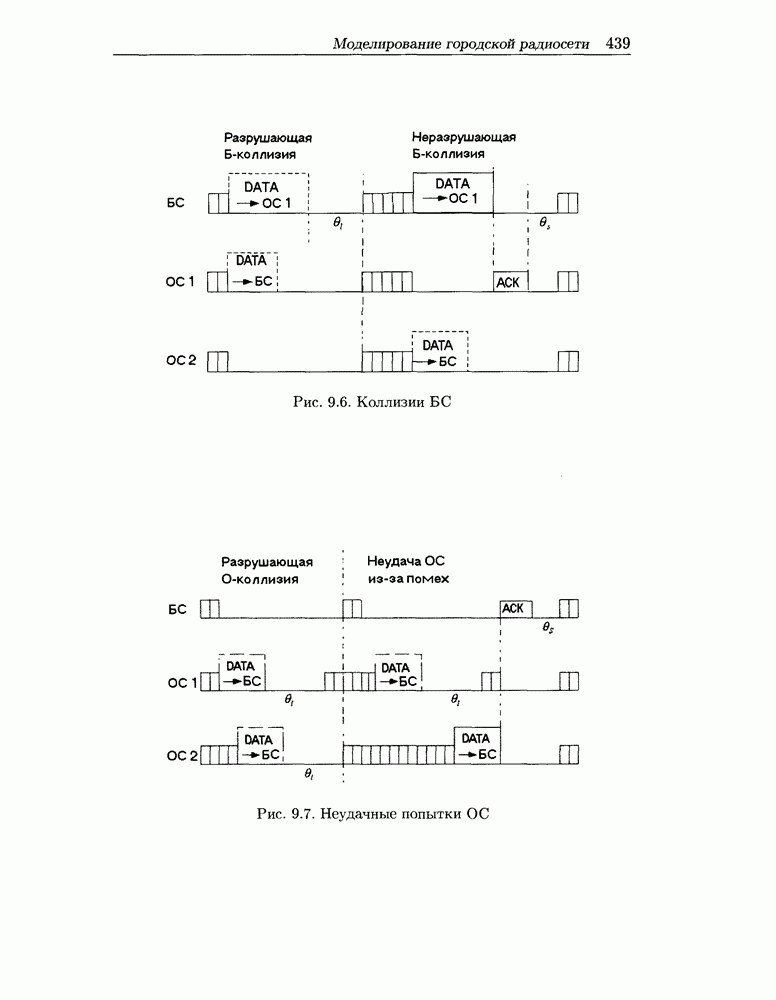
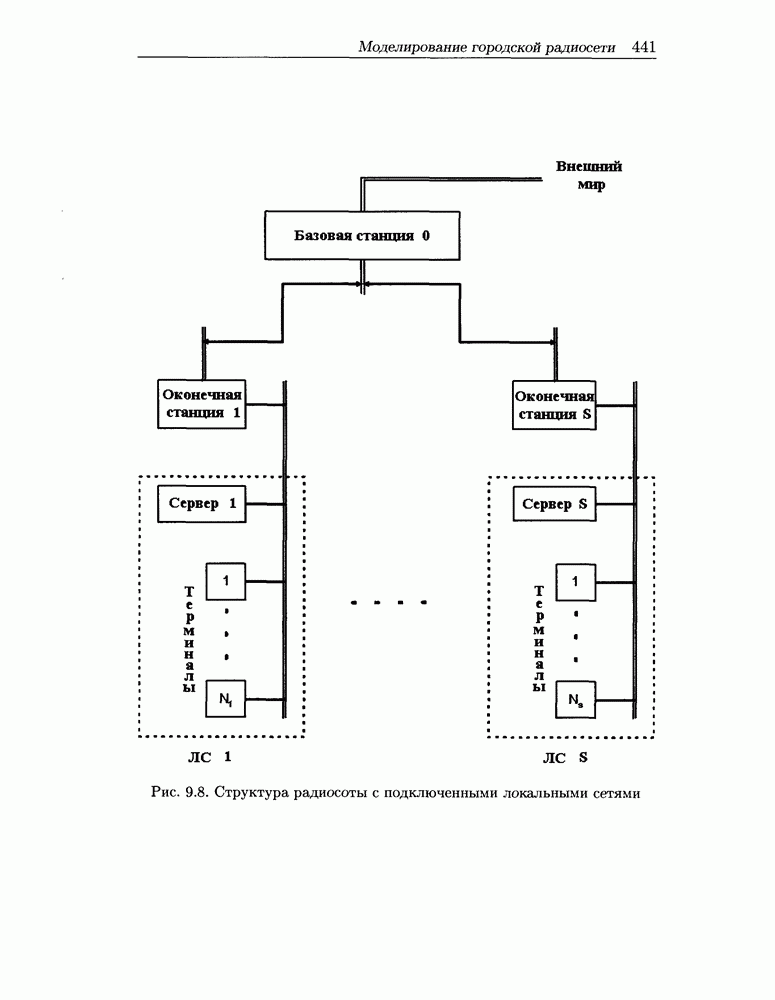
- 9.4 Моделирование городской радиосети
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
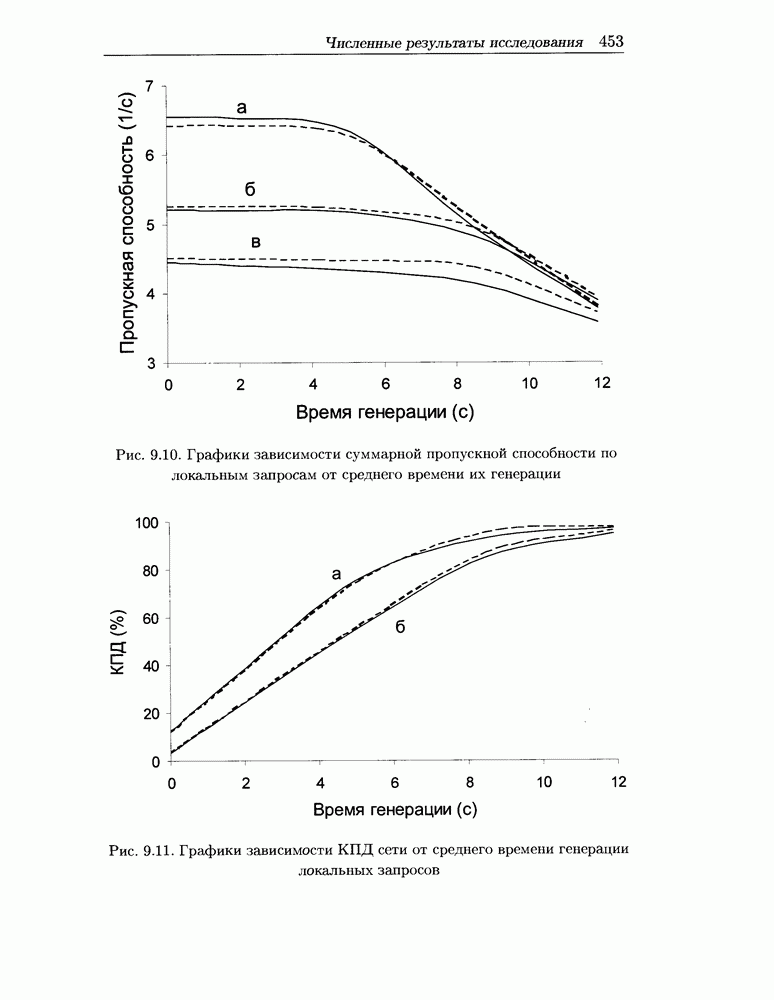
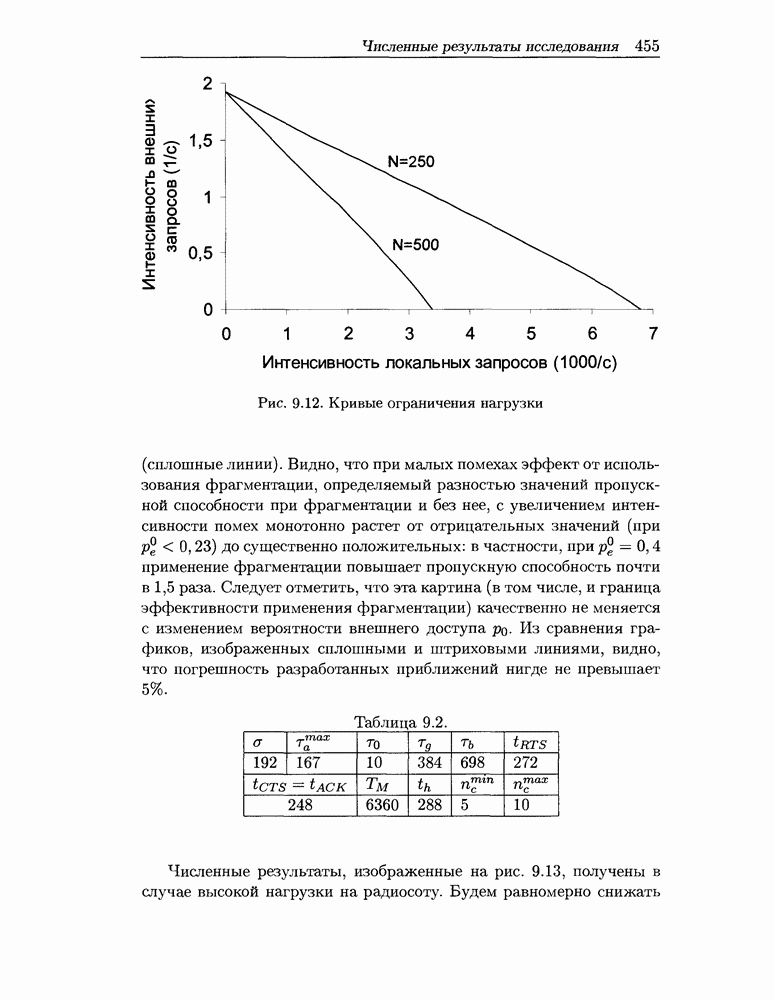
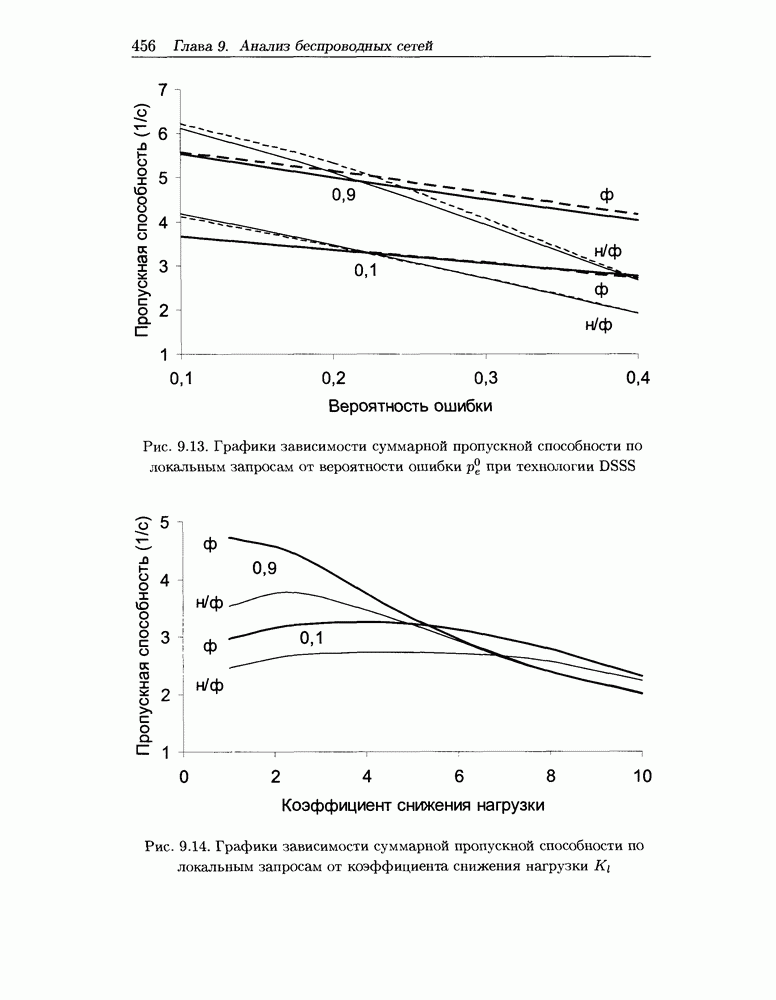
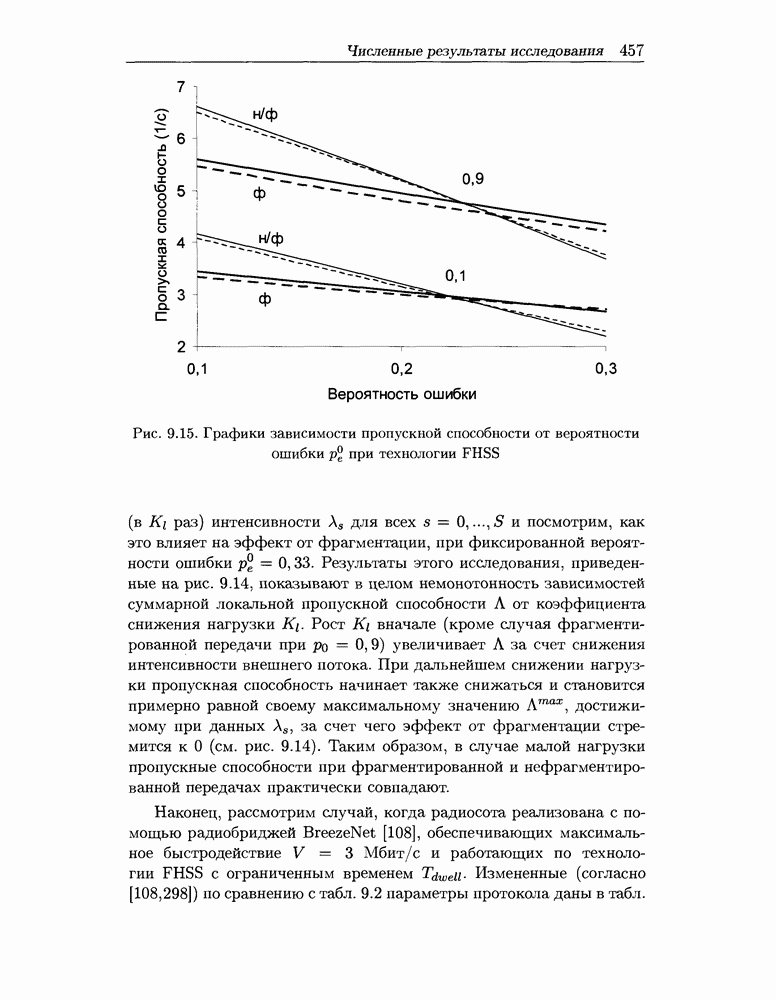
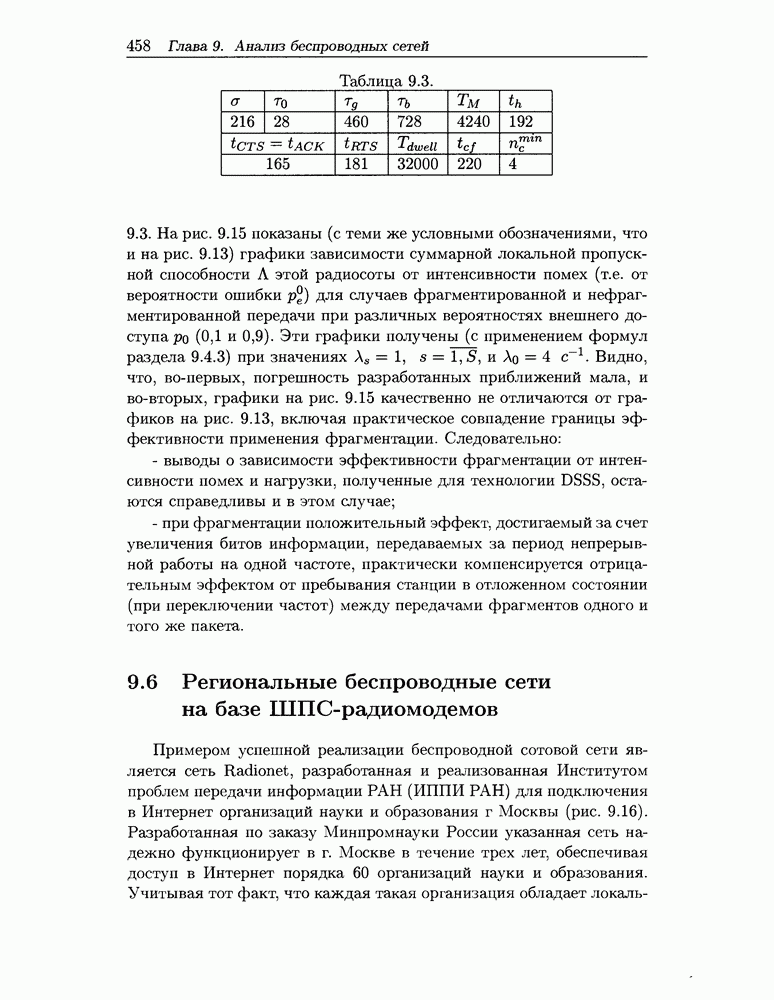
- 9.5 Численные результаты исследования городской радиосоты
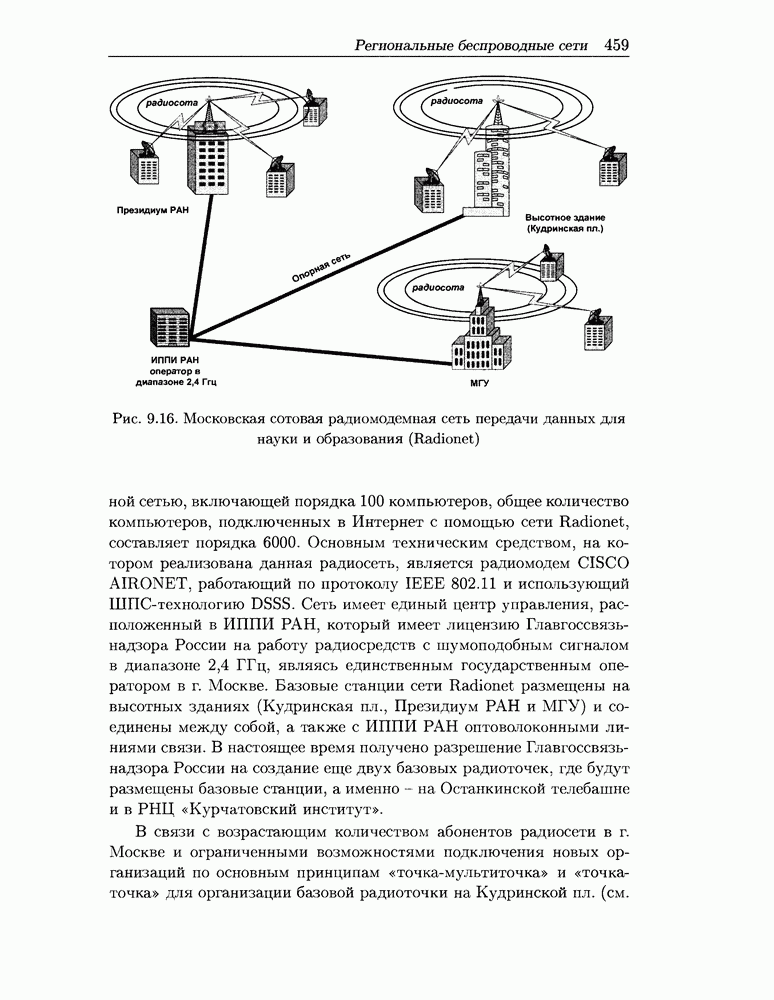
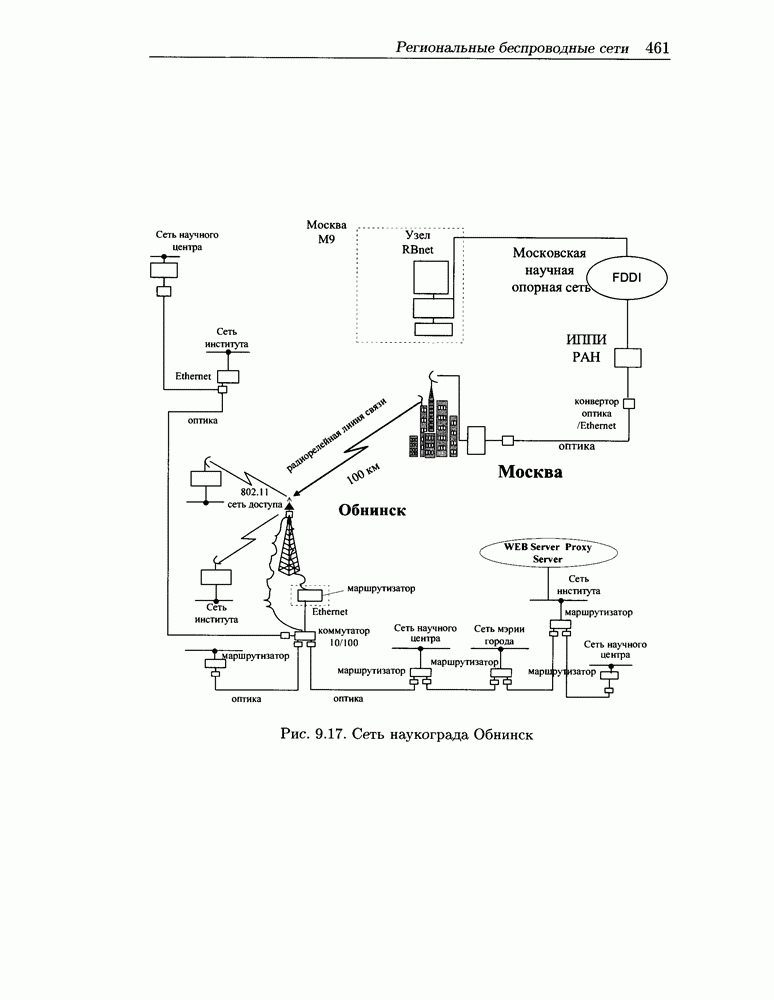
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
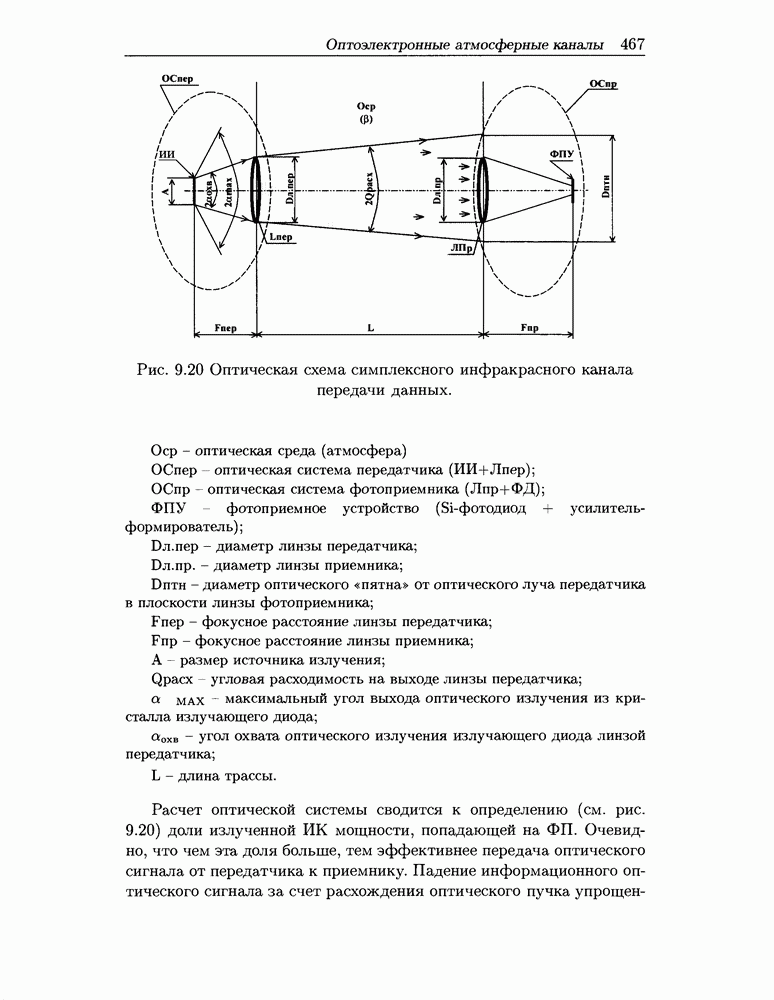
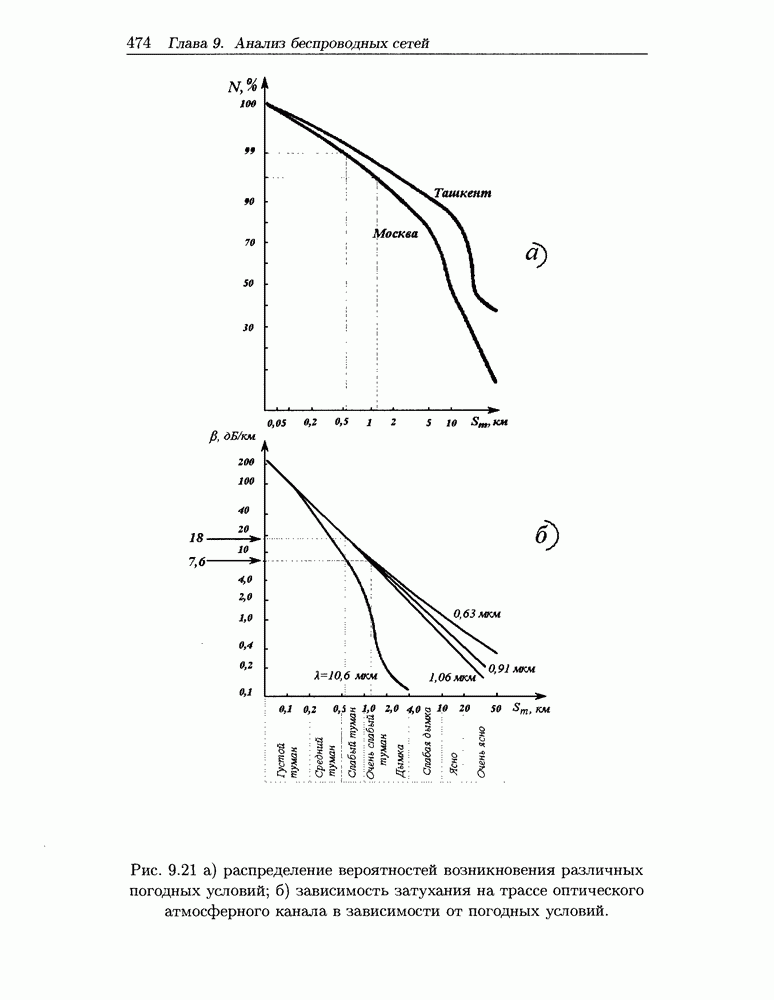
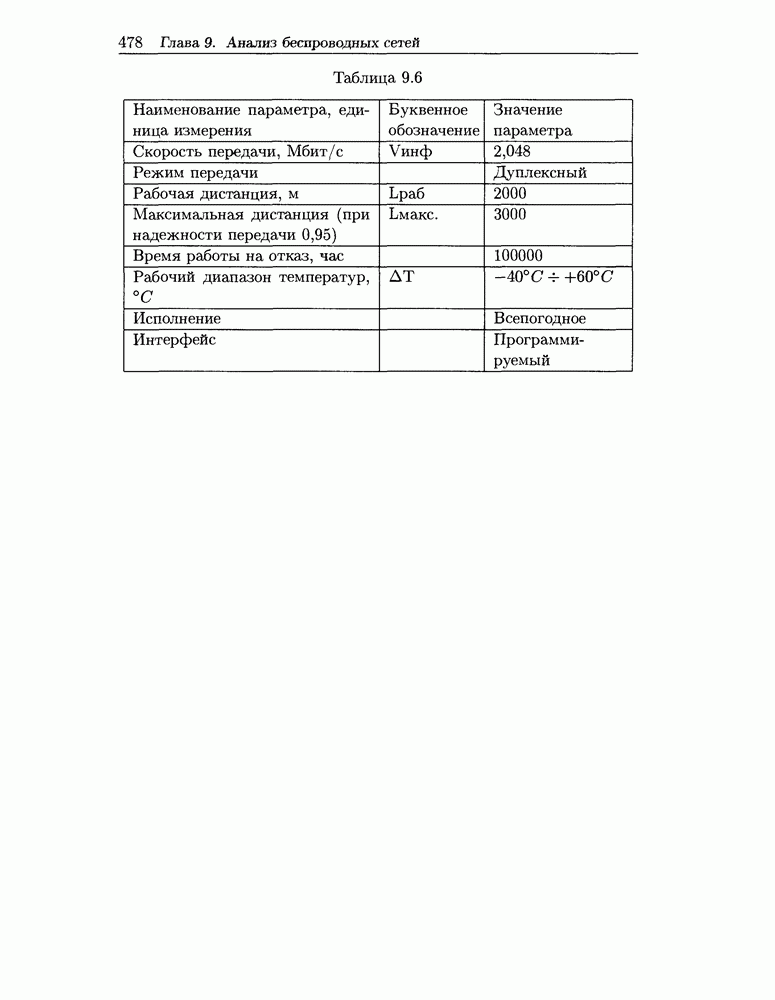
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература