| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.6.4 Метод введения дополнительного события
Этот метод, предложенный Данцигом, Кестеном и Ранненбергом (метод коллективных меток - method of collective marks) и развитый затем Г.П. Климовым (метод «катастроф»), позволяет легко получить аналитические результаты в ситуациях, когда другие известные методы приводят к трудоемким выкладкам. Особенно эффективен он оказался при анализе ненадежных и приоритетных систем массового обслуживания.
Сущность этого метода заключается в следующем. Пусть требуется найти некоторое распределение, характеризующее функционирование СМО. Производящей функции этого распределения (если распределение дискретное) или его преобразованию Лапласа - Стилтьеса придается вероятностный смысл за счет «раскрашивания» запросов или введения в рассмотрение потока «катастроф». Затем вводится в рассмотрение некоторое (дополнительное) случайное событие и вероятность его подсчитывается в терминах производящей функции или преобразованию Лапласа - Стилтьеса искомого распределения двумя различными способами. В результате получается уравнение, решением которого является функция, которая интересует исследователя.
Проиллюстрируем этот метод, применив его для нахождения вероятностных характеристик системы MG1. Важной характеристикой производительности многих реальных систем является распределение периода занятости системы. Период занятости есть интервал времени с момента поступления запроса в пустую систему до момента, когда система впервые вновь окажется пустой. Знание периода занятости позволяет решать задачи, связанные, например, с планированием проведения в системе профилактических работ, исследованием возможности дополнительной загрузки прибора выполнением некоторой второстепенной «фоновой» работы и т.д.
Обозначим  функцию стационарного распределения длины периода занятости в рассматриваемой системе,
функцию стационарного распределения длины периода занятости в рассматриваемой системе,  -ее преобразование Лапласа - Стилтьеса.
-ее преобразование Лапласа - Стилтьеса.
Считаем, что выполняется условие:

гарантирующее существование стационарного распределения длины периода занятости рассматриваемой СМО.
Утверждение 13.
Преобразование  Лапласа - Стилтьеса распределения длины периода занятости рассматриваемой СМО удовлетворяет следующему функциональному уравнению:
Лапласа - Стилтьеса распределения длины периода занятости рассматриваемой СМО удовлетворяет следующему функциональному уравнению:

Доказательство. Легко видеть, что распределение длины периода занятости системы не зависит от того, в каком порядке обслуживаются запросы. Для облегчения анализа структуры периода занятости предположим, что запросы обслуживаются в инверсионном порядке, то есть на обслуживание всегда выбирается запрос, пришедший в систему последним. Такая дисциплина выбора из очереди кодируется как LIFO (Last In - First Out) или LCFS (Last Came - First Served). При такой дисциплине выбора из очереди каждый запрос как бы порождает период занятости системы запросами, пришедшими в систему после него. Причем структура и, следовательно, распределение длины периода занятости, порожденного некоторым запросом, такие же, как структура и распределение длины периода занятости системы. Используя эти рассуждения, мы приходим к пониманию того, что период занятости системы состоит из времени обслуживания первого запроса, с которого начался период занятости, и случайного числа периодов занятости, порожденных запросами, пришедшими в систему за время обслуживания первого запроса.
Теперь предположим, что независимо от функционирования данной системы поступает простейший поток катастроф интенсивности s. Введем в рассмотрение (дополнительное) событие А, состоящее в том, что за данный период занятости не поступили катастрофы.
Напомним, что согласно вероятностной трактовке преобразования Лапласа - Стилтьеса, величина  есть вероятность того, что не произойдет ни одной катастрофы за случайное время, имеющее функцию распределения H(t). Поэтому легко понять, что вероятность события А определяется следующим образом:
есть вероятность того, что не произойдет ни одной катастрофы за случайное время, имеющее функцию распределения H(t). Поэтому легко понять, что вероятность события А определяется следующим образом:

Найдем теперь вероятность этого же события иначе. Назовем произвольный запрос «плохим», если за период занятости, порожденный им, наступает катастрофа. Используя достигнутое нами понимание структуры периода занятости, нетрудно убедиться, что для того, чтобы запрос, с которого начался период занятости, был неплохим (вероятность этого есть Р(А)), необходимо и достаточно, чтобы за время его обслуживания не поступили события из суммарного потока катастроф и потока плохих запросов.
Поток катастроф является простейшим потока интенсивности s. Поток плохих запросов получается из исходного простейшего потока интенсивности  в результате применения простейшей процедуры рекуррентного просеивания (произвольный запрос включается в просеянный поток с вероятностью
в результате применения простейшей процедуры рекуррентного просеивания (произвольный запрос включается в просеянный поток с вероятностью  независимо от других запросов). Поэтому, согласно Утверждению 6, просеянный поток является простейшим потоком интенсивности
независимо от других запросов). Поэтому, согласно Утверждению 6, просеянный поток является простейшим потоком интенсивности  Согласно Утверждению 5, суммарный поток катастроф и плохих запросов является простейшим потоком интенсивности
Согласно Утверждению 5, суммарный поток катастроф и плохих запросов является простейшим потоком интенсивности 
Таким образом, используя еще раз вероятностную трактовку преобразования Лапласа - Стилтьеса мы получаем следующую формулу для вероятности события  :
:

Сравнивая выражения (1.83) и (1.84), мы убеждаемся в справедливости формулы (1.82). Утверждение 13 доказано.
Уравнение (1.82), полученное Дж. Кендаллом в 1951 году, имеет единственное решение в области Res > 0, такое, что 
В случае, если распределение времени обслуживания показательное,  рассматриваемая система есть М|М|1 и преобразование Лапласа - Стилтьеса распределения времени обслуживания
рассматриваемая система есть М|М|1 и преобразование Лапласа - Стилтьеса распределения времени обслуживания  имеет вид:
имеет вид:  При этом функциональное уравнение (1.82) переходит в квадратное уравнение для неизвестного преобразования Лапласа - Стилтьеса
При этом функциональное уравнение (1.82) переходит в квадратное уравнение для неизвестного преобразования Лапласа - Стилтьеса 

Решая уравнение (1.85), получаем:

В этой формуле выбираем только знак  чтобы полученное решение удовлетворяло условию
чтобы полученное решение удовлетворяло условию  Обращая теперь преобразование Лапласа - Стилтьеса
Обращая теперь преобразование Лапласа - Стилтьеса  получаем следующее выражение для производной функции
получаем следующее выражение для производной функции  распределения длины периода занятости системы М|М|1 :
распределения длины периода занятости системы М|М|1 :

где функция  есть модифицированная функция Бесселя первого рода.
есть модифицированная функция Бесселя первого рода.
В общем случае уравнение (1.82) можно решать методом итераций, снабдив функцию  индексом
индексом  в левой части уравнения и индексом
в левой части уравнения и индексом  в правой части. Эта процедура имеет геометрическую скорость сходимости последовательности
в правой части. Эта процедура имеет геометрическую скорость сходимости последовательности  к значению
к значению  при фиксированном значении аргумента
при фиксированном значении аргумента 
Кроме того, путем последовательного дифференцирования уравнения (1.82) с последующей подстановкой аргумента  и учета свойства 5 преобразования Лапласа - Стилтьеса, можно получить рекуррентную последовательность формул для вычисления начальных моментов распределения длины периода занятости. Так, среднее значение
и учета свойства 5 преобразования Лапласа - Стилтьеса, можно получить рекуррентную последовательность формул для вычисления начальных моментов распределения длины периода занятости. Так, среднее значение  длины периода занятости и второй начальный момент
длины периода занятости и второй начальный момент  ее распределения определяются формулой:
ее распределения определяются формулой:

Как и следовало ожидать, с ростом коэффициента загрузки  и приближением его значения к единице среднее значение периода занятости стремится к бесконечности.
и приближением его значения к единице среднее значение периода занятости стремится к бесконечности.
Рассмотрим теперь другую характеристику функционирования системы MG1 - число  запросов, обслуженных за период занятости. Обозначим
запросов, обслуженных за период занятости. Обозначим 
Утверждение 14. Производящая функция  удовлетворяет следующему функциональному уравнению:
удовлетворяет следующему функциональному уравнению:

Доказательство. Производящей функции  придадим вероятностный смысл следующим образом. Каждый из запросов независимо от других назовем красным с вероятностью z и синим с дополнительной вероятностью. Произвольный запрос назовем темнокрасным, если он сам красный и за период занятости, порожденный им, в системе обслуживались только красные запросы. Введем событие А, состоящее в том, что запрос, с которого начинается период занятости, является темно-красным. Найдем вероятность этого события. С одной стороны, очевидно, что
придадим вероятностный смысл следующим образом. Каждый из запросов независимо от других назовем красным с вероятностью z и синим с дополнительной вероятностью. Произвольный запрос назовем темнокрасным, если он сам красный и за период занятости, порожденный им, в системе обслуживались только красные запросы. Введем событие А, состоящее в том, что запрос, с которого начинается период занятости, является темно-красным. Найдем вероятность этого события. С одной стороны, очевидно, что

С другой стороны, из проделанного выше анализа структуры периода занятости ясно, что для того, чтобы запрос был темно-красным, необходимо и достаточно, чтобы он сам был красным (вероятность этого равна z) и за время его обслуживания могли поступать только темно-красные запросы.
Так как поток запросов - простейший с параметром  , а произвольный запрос является темно-красным с вероятностью
, а произвольный запрос является темно-красным с вероятностью  , то поток нетемно-красных вызовов (как это следует из Утверждения 6) является простейшим с параметром
, то поток нетемно-красных вызовов (как это следует из Утверждения 6) является простейшим с параметром  Вспоминая вероятностную интерпретацию преобразования Лапласа - Стилтьеса, из приведенных рассуждений выводим следующую альтернативную формулу для вероятности события
Вспоминая вероятностную интерпретацию преобразования Лапласа - Стилтьеса, из приведенных рассуждений выводим следующую альтернативную формулу для вероятности события 

Сравнивая формулы (1.90) и (1.91), убеждаемся в справедливости (1.89). Утверждение 14 доказано.
Уравнение (1.89) определяет единственную аналитическую в области  функцию, такую, что
функцию, такую, что 
Следствие. Среднее число запросов, обслуженных в системе MG1 за один период занятости, задается формулой:

Приведем еще одно доказательство формулы Поллячека-Хинчина для производящей функции распределения вероятностей числа запросов в системе MG1 в моменты окончания обслуживания. Каждый из запросов, приходящих в систему, независимо от других назовем красным с вероятностью 2 и синим с дополнительной вероятностью. Введем событие А, состоящее в том  что запрос, уходящий в данный момент окончания обслуживания из системы, сам красный и все запросы, остающиеся в системе в этот момент, тоже красные.
что запрос, уходящий в данный момент окончания обслуживания из системы, сам красный и все запросы, остающиеся в системе в этот момент, тоже красные.
Из вероятностной интерпретации производящей функции очевидно следует, что:

где  есть искомая производящая функция распределения вероятностей числа запросов в системе
есть искомая производящая функция распределения вероятностей числа запросов в системе  в моменты окончания обслуживания.
в моменты окончания обслуживания.
С другой стороны, для того, чтобы произошло событие А, необходимо и достаточно, чтобы все запросы, которые находились в системе в предыдущий момент окончания обслуживания (если система была непуста), были красными и за время обслуживания не пришли синие запросы, а если система была пуста, то первый пришедший запрос должен быть красным и за время его обслуживания не пришли синие запросы.
Из этих рассуждений следует, что:

Из соотношений этого соотношения и (1.92) очевидным образом следует формула Поллячека - Хинчина:

полученная нами ранее с помощью метода вложенных цепей Маркова.
В заключение подраздела найдем характеристики системы MG1 с дисциплиной LIFO.
Выше отмечалось, что распределение периода занятости системы M|G|1 не зависит от дисциплины обслуживания. Поэтому уравнение (1.82) определяет преобразование Лапласа - Стилтьеса распределения периода занятости для всех дисциплин. Кроме того, несложно видеть, что и распределения числа запросов в системе MG1 при дисциплинах FIFO и LIFO совпадают и задаются формулой (1.81).
Распределение времени ожидания запроса при дисциплинах FIFO и LIFO различно. При дисциплине FIFO преобразование Лапласа - Стилтьеса  стационарного распределения времени ожидания задается формулой (1.52).
стационарного распределения времени ожидания задается формулой (1.52).
Утверждение 15. При дисциплине LIFO преобразование Лапласа - Стилтьеса  имеет следующий вид:
имеет следующий вид:

где функция  является решением уравнения (1.82).
является решением уравнения (1.82).
Доказательство. Введем поток катастроф и понятие «плохого» запроса, как это было сделано при доказательстве Утверждения 13. При этом функция  есть вероятность того, что за время ожидания данного запроса не наступит катастрофа, а функция
есть вероятность того, что за время ожидания данного запроса не наступит катастрофа, а функция  есть вероятность того, что произвольный запрос не является «плохим», то есть катастрофа не наступает за период занятости, порожденный этим запросом.
есть вероятность того, что произвольный запрос не является «плохим», то есть катастрофа не наступает за период занятости, порожденный этим запросом.
Учитывая сущность дисциплины LIFO и рассуждения, использованные при доказательстве Утверждения 13, получаем формулу:

где  есть преобразование Лапласа - Стилтьеса распределения остаточного (после момента поступления запроса, время ожидания которого мы исследуем) времени обслуживания запроса, находящегося на приборе.
есть преобразование Лапласа - Стилтьеса распределения остаточного (после момента поступления запроса, время ожидания которого мы исследуем) времени обслуживания запроса, находящегося на приборе.
По аналогии с функцией распределения F(t) остаточного времени до момента поступления запроса в рекуррентном потоке, приведенной в разделе 2, для функции распределения B(t) остаточного времени обслуживания имеем формулу:

Отметим, что эта функция уже использовалась в формуле Бенеша (1.54). Легко видеть, что преобразование Лапласа - Стилтьеса этой функции имеет вид:

Учитывая это, а также уравнение (1.82) и формулу  из (1.94) получаем соотношение (1.93). Утверждение 15 доказано.
из (1.94) получаем соотношение (1.93). Утверждение 15 доказано.
Замечание. Сравнивая формулы (1.52) и (1.93), заключаем, что распределения времени ожидания в системах с дисциплинами FIFO и LIFO - различные. При этом средние времена ожидания совпадают.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
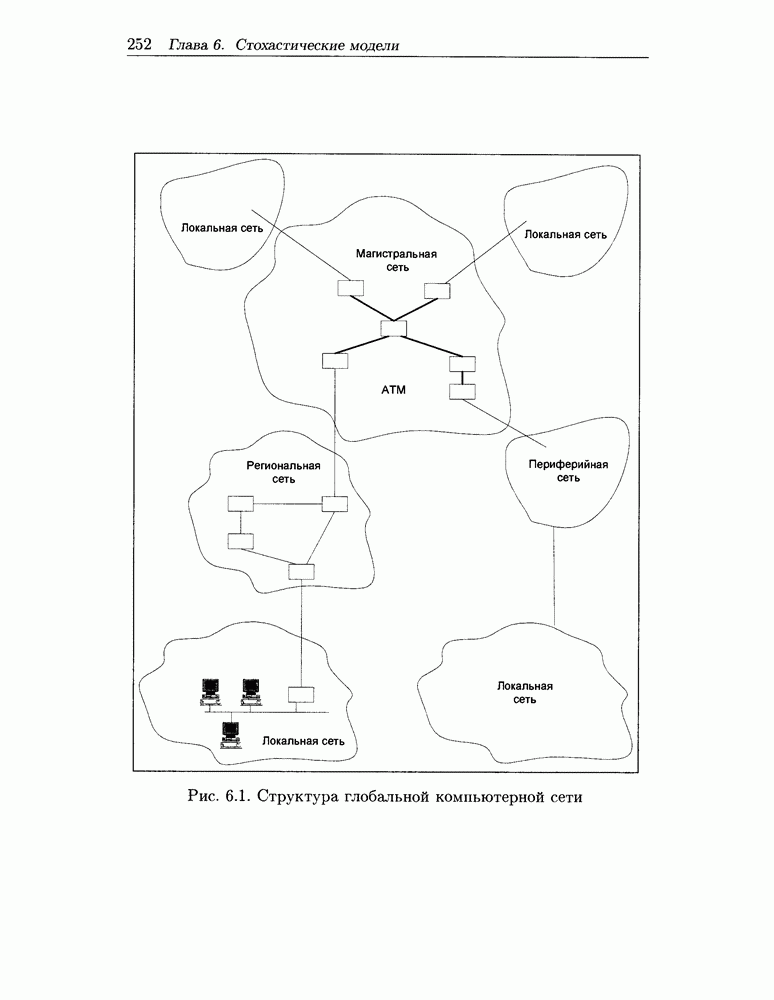
- 6.1.1 Структура компьютерных сетей
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
- 6.3 Управление потоками в сети пакетной коммутации
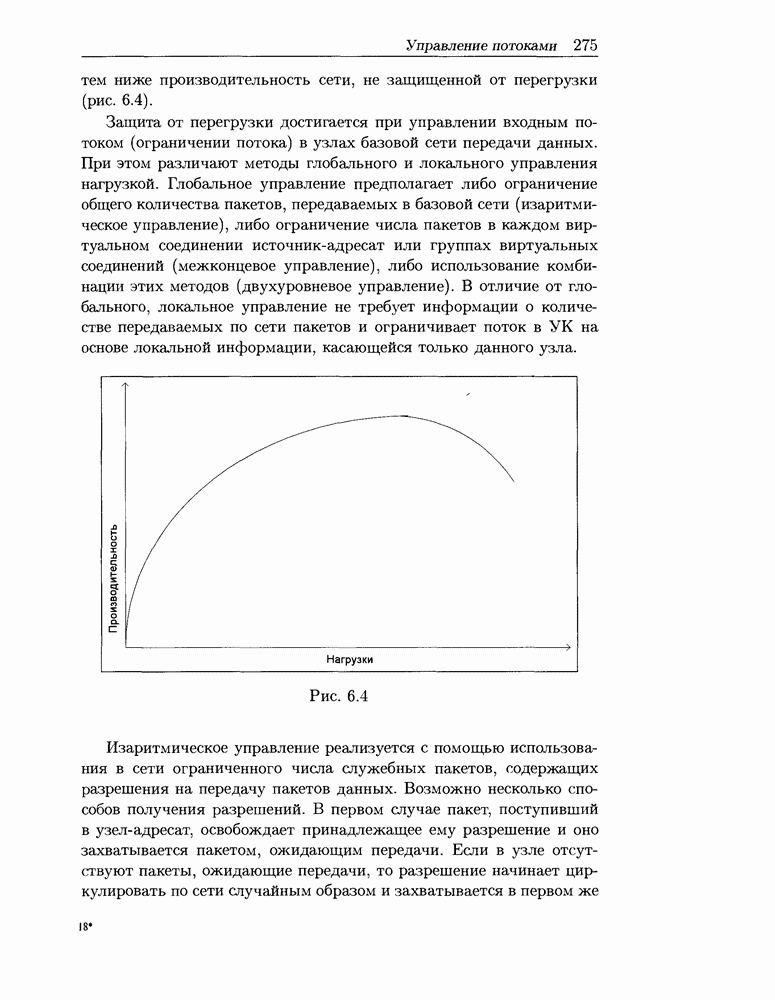
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
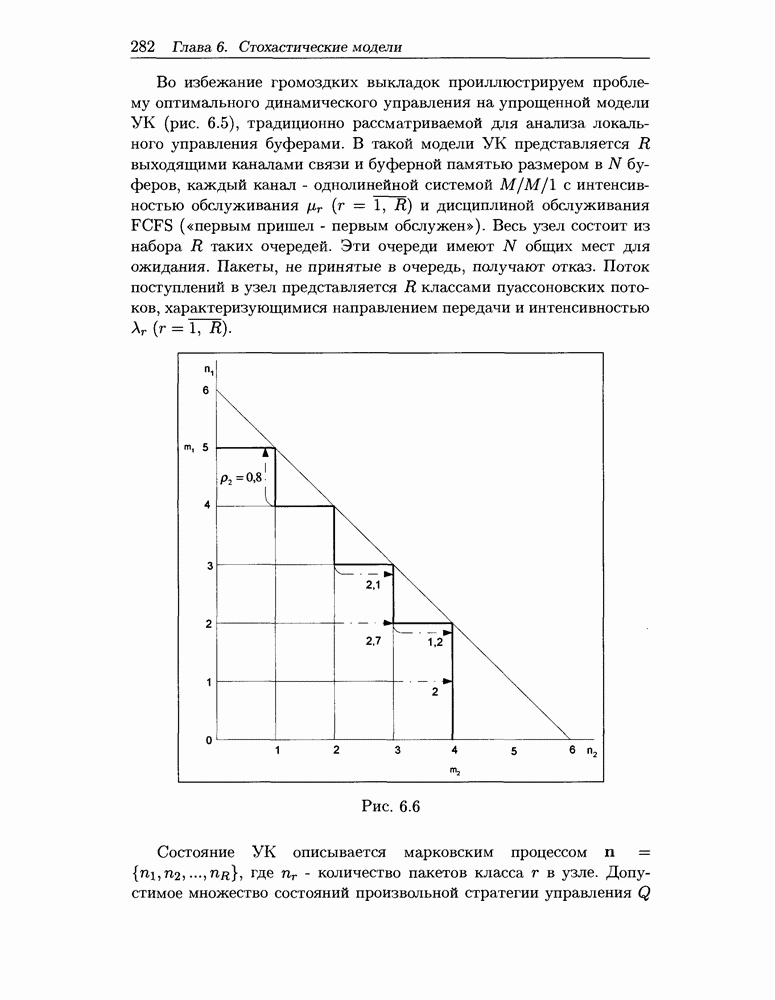
- 6.3.3 Локальное управление буферами
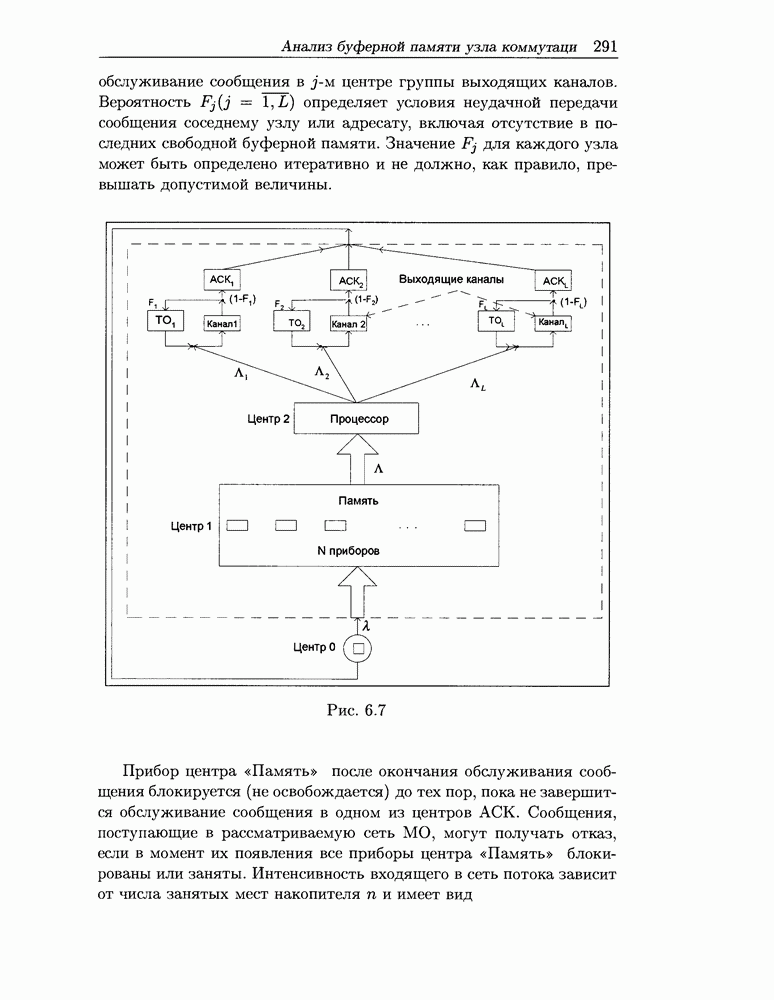
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
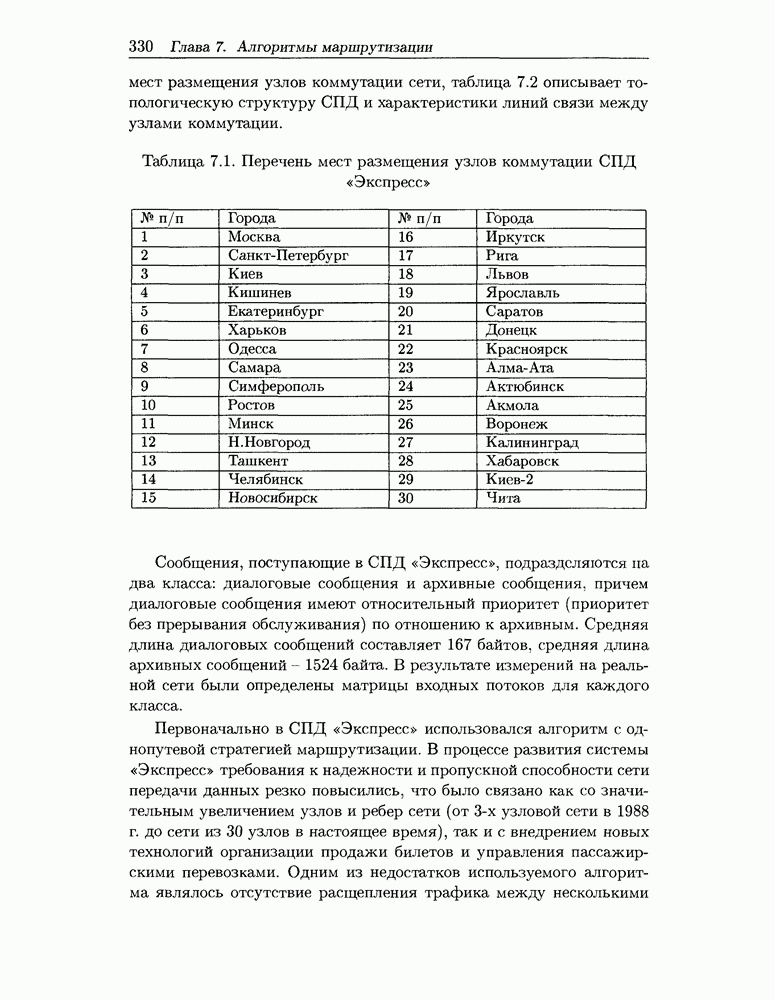
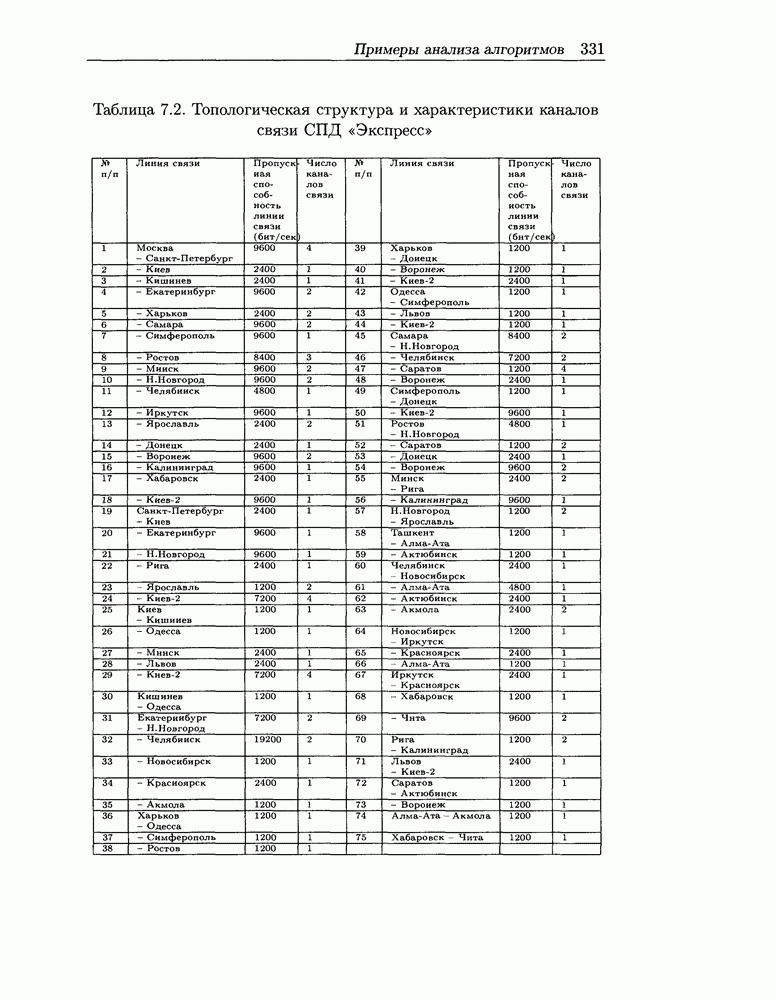
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
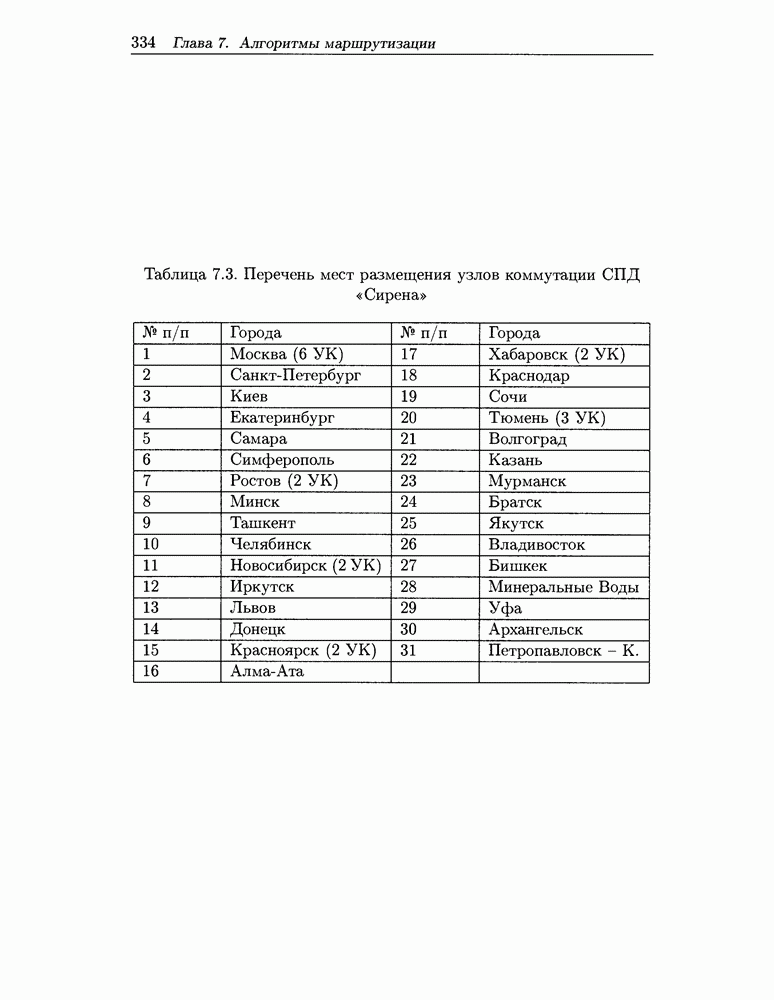
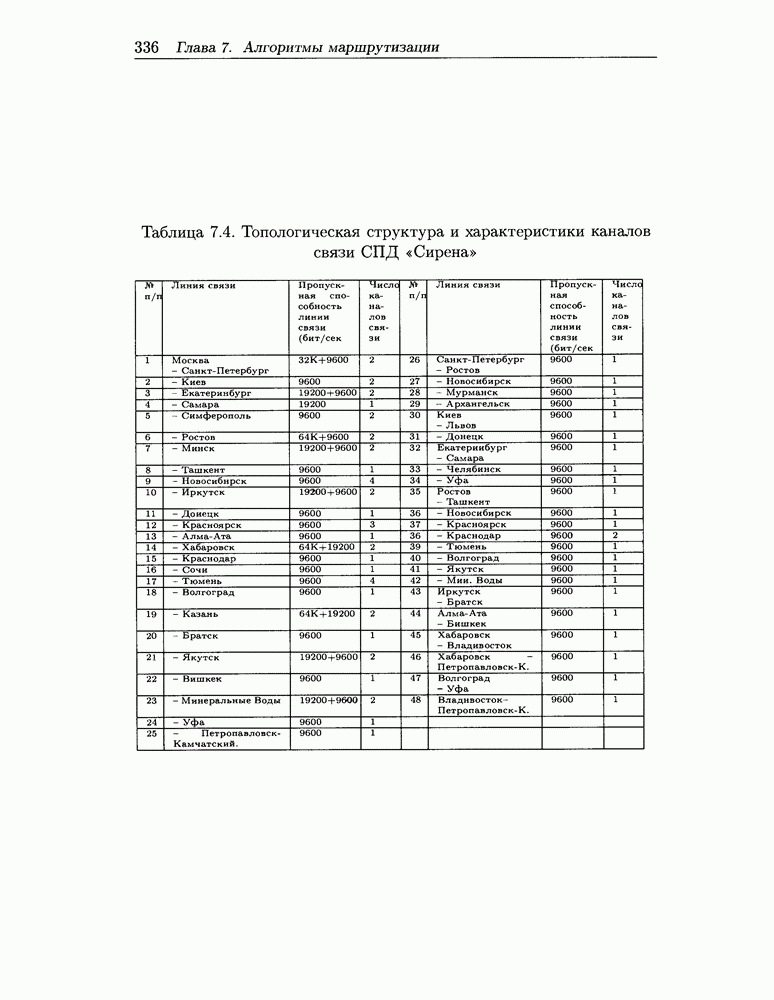
- 7.4.2 Анализ развития СПД «Сирена»
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
- 7.5.4 Классификация алгоритмов маршрутизации
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
- 7.5.8 Показатели качества маршрутизации
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
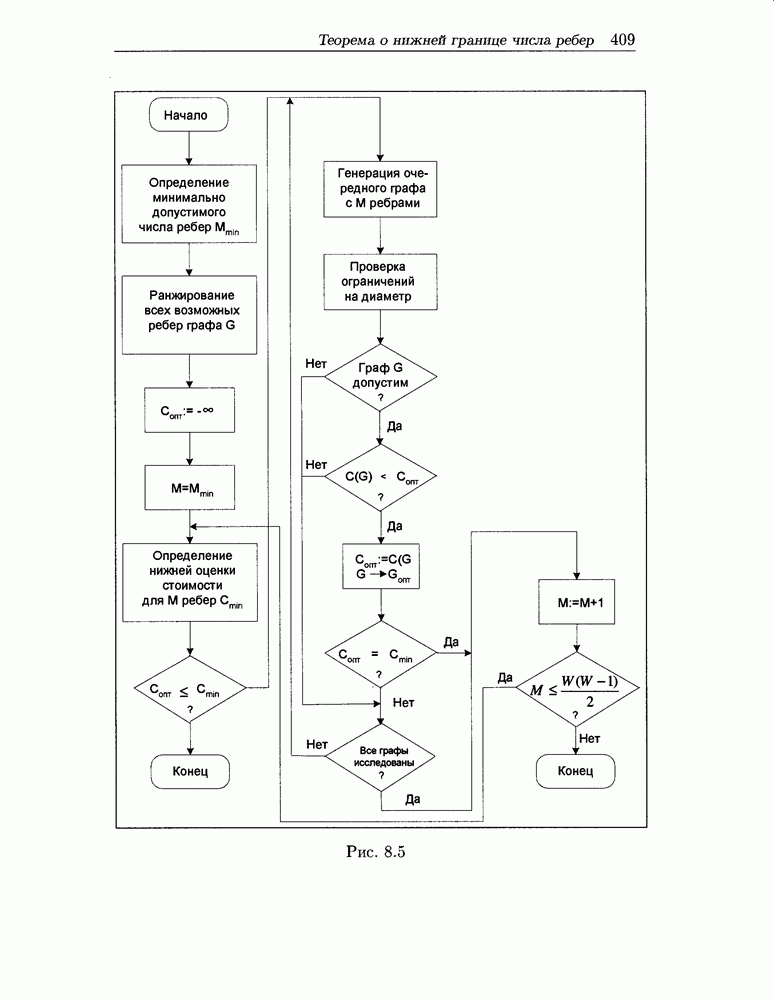
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
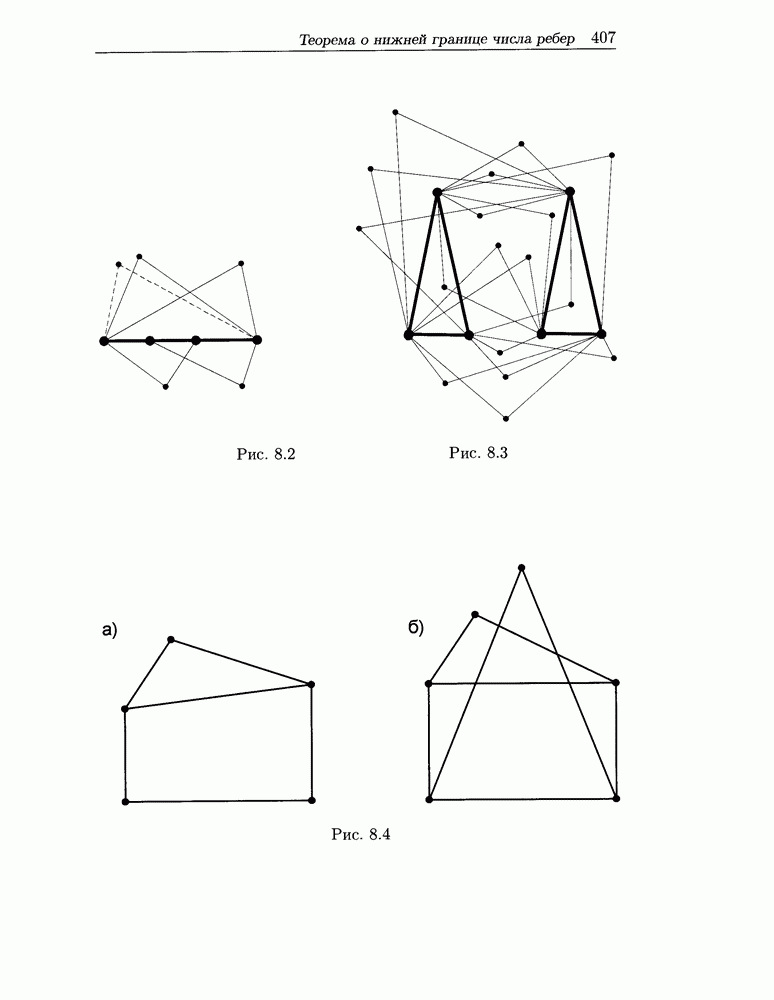
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
- 9.1 Состояние и перспективы развития беспроводных радиосетей
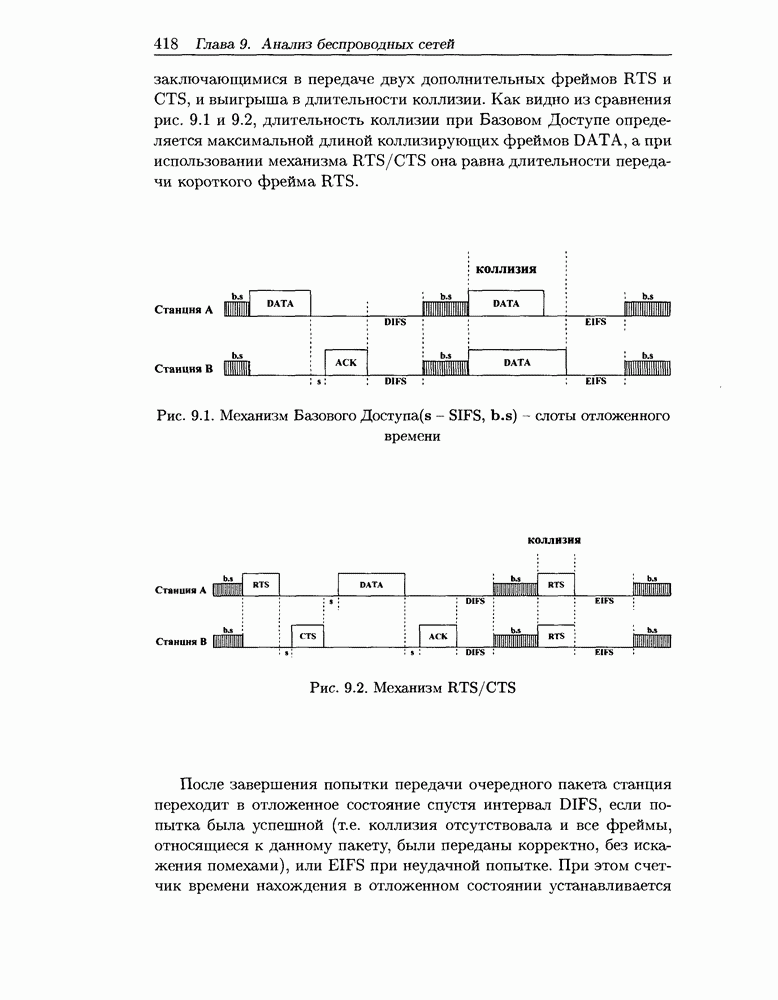
- 9.2 Схема распределенного управления
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
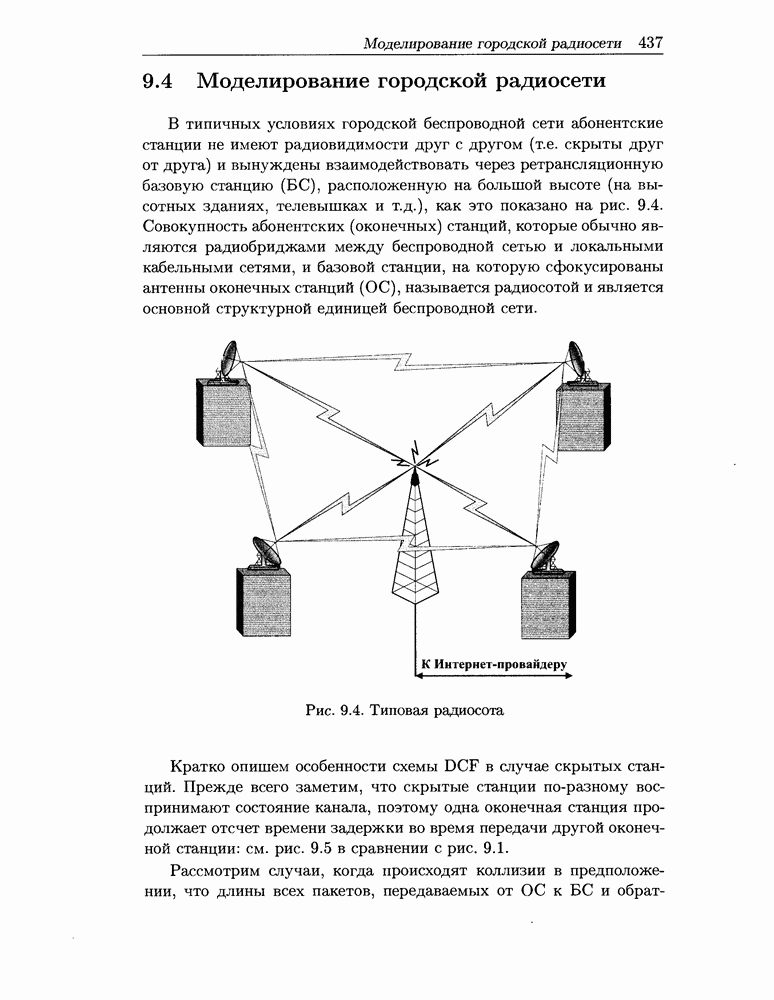
- 9.4 Моделирование городской радиосети
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
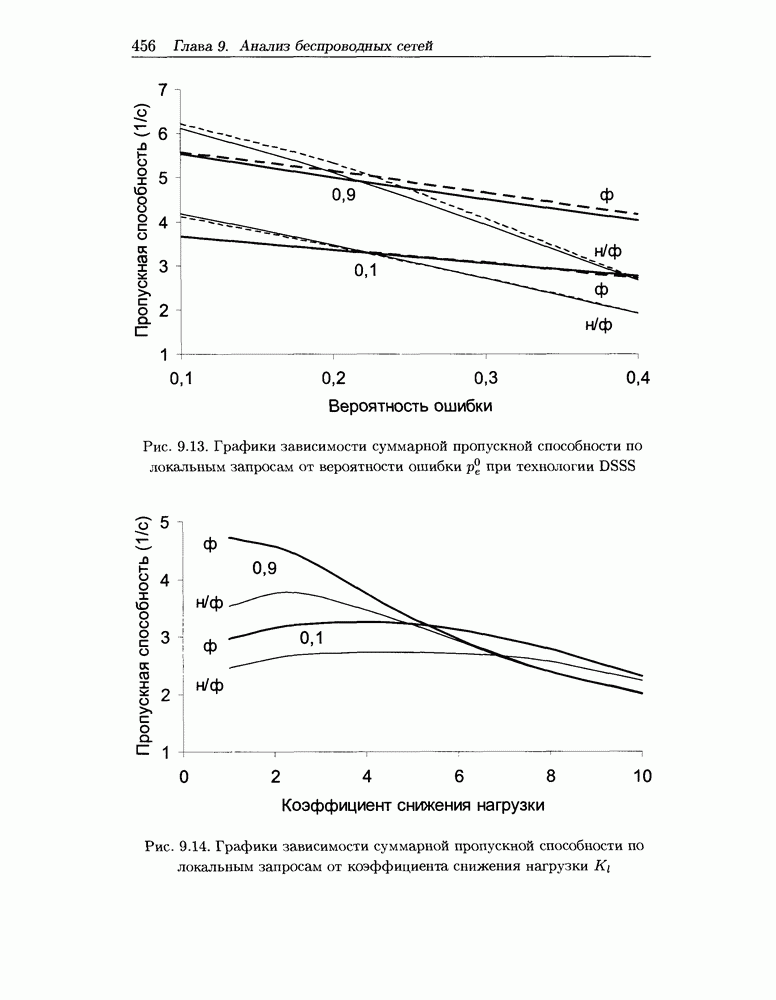
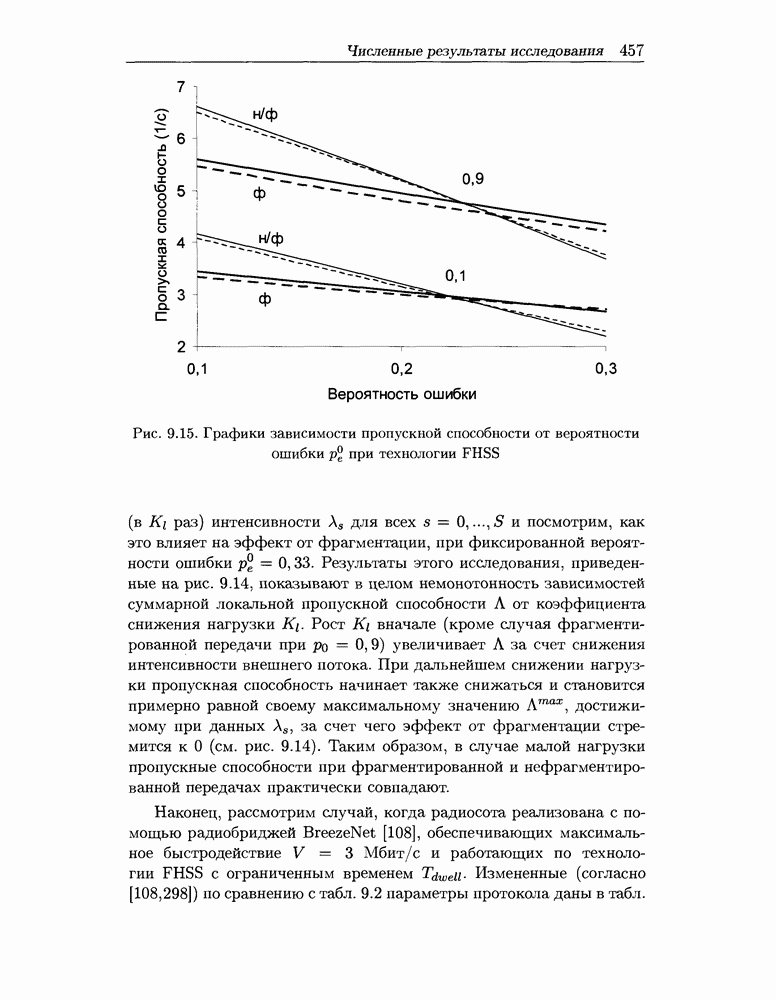
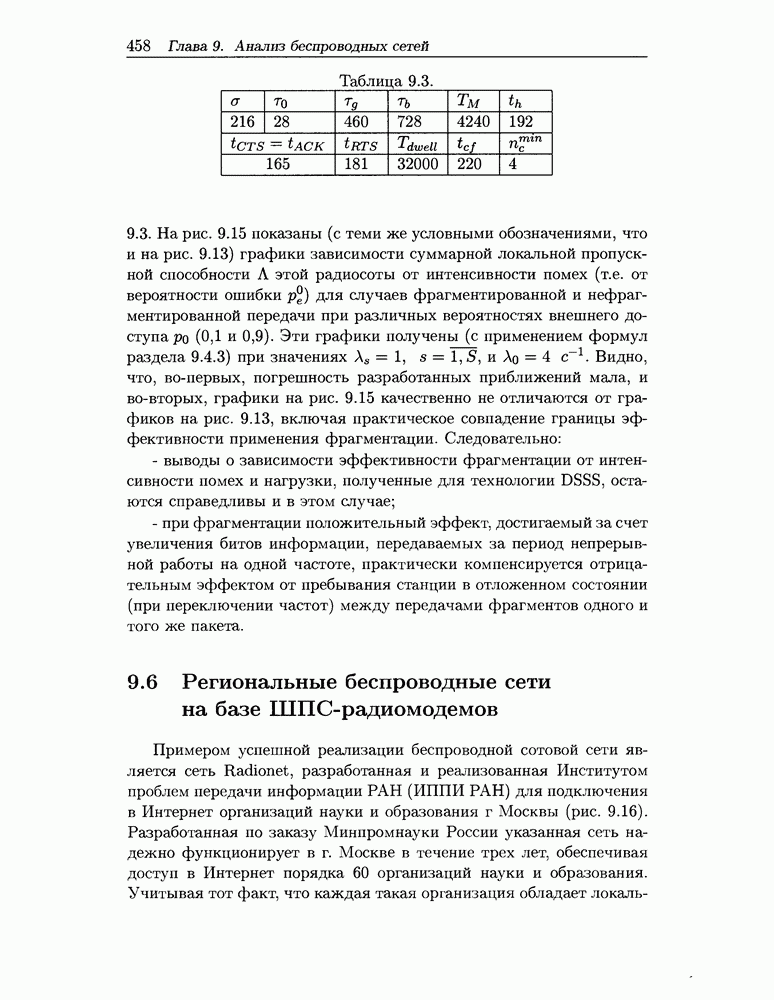
- 9.5 Численные результаты исследования городской радиосоты
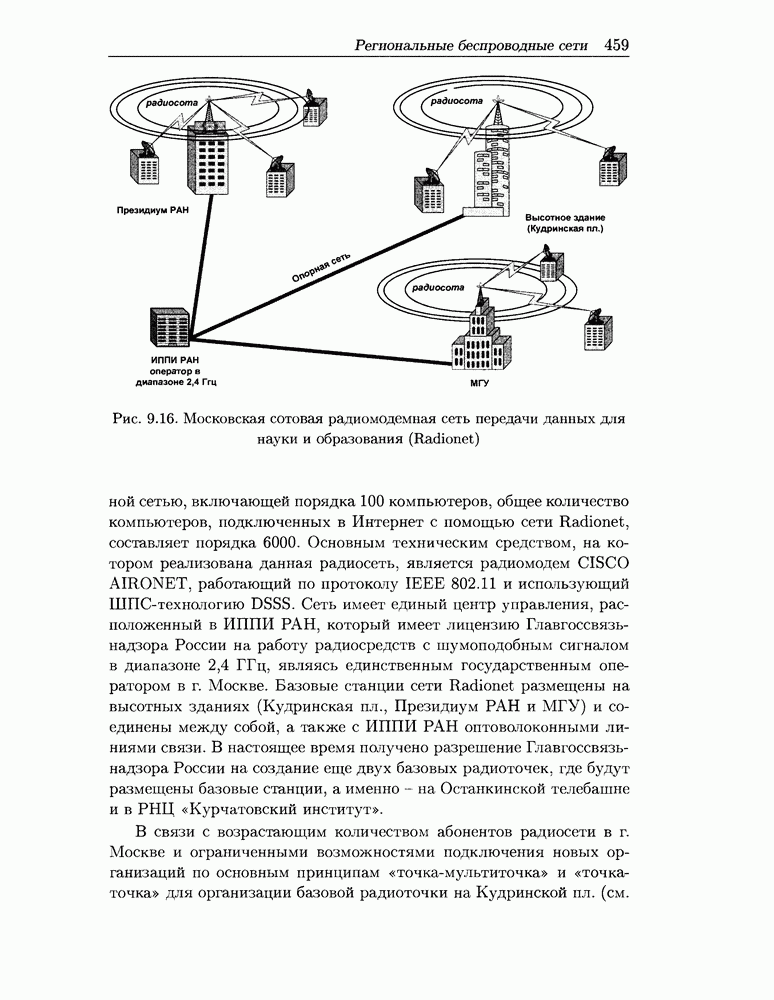
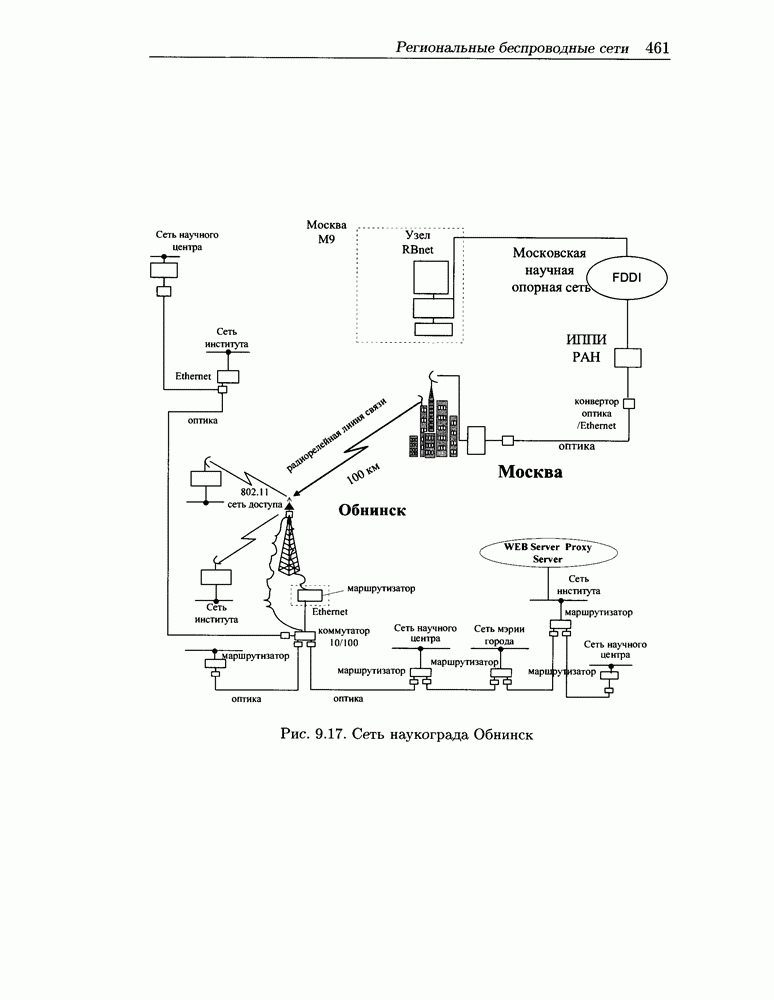
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
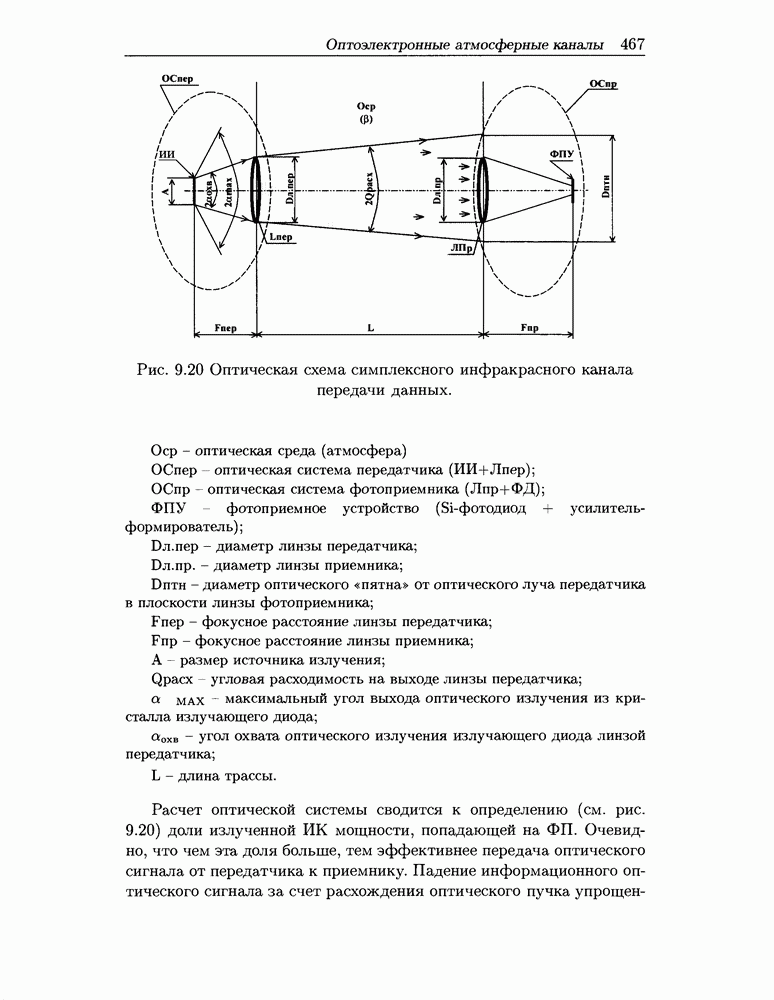
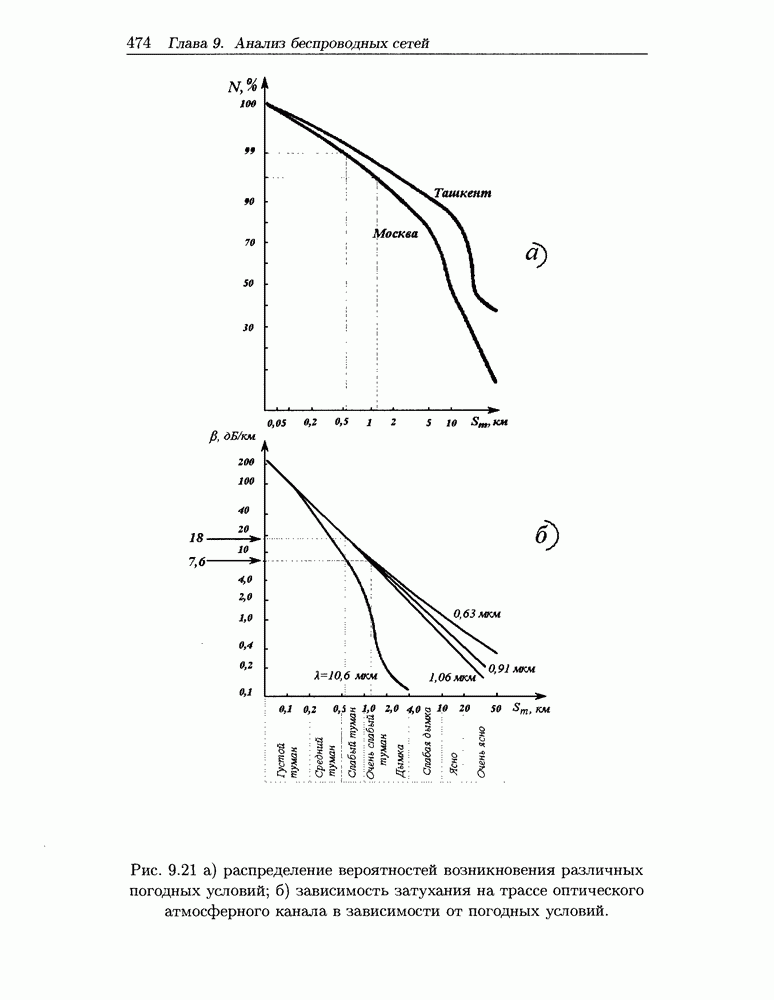
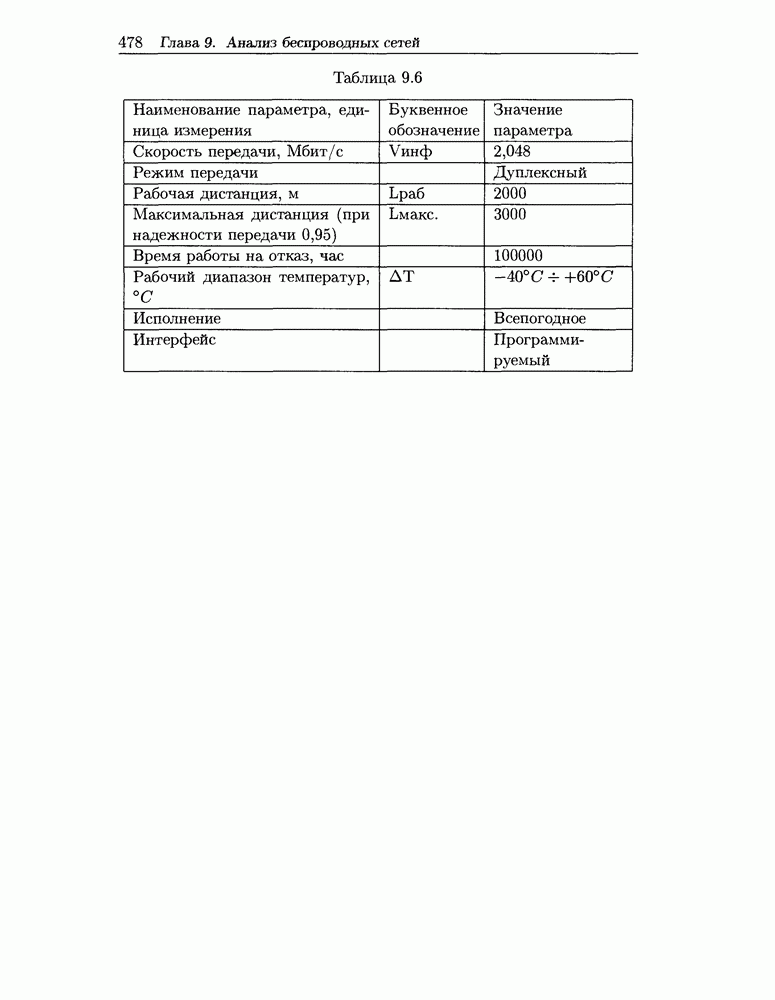
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература