| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9.5 Численные результаты исследования городской радиосоты
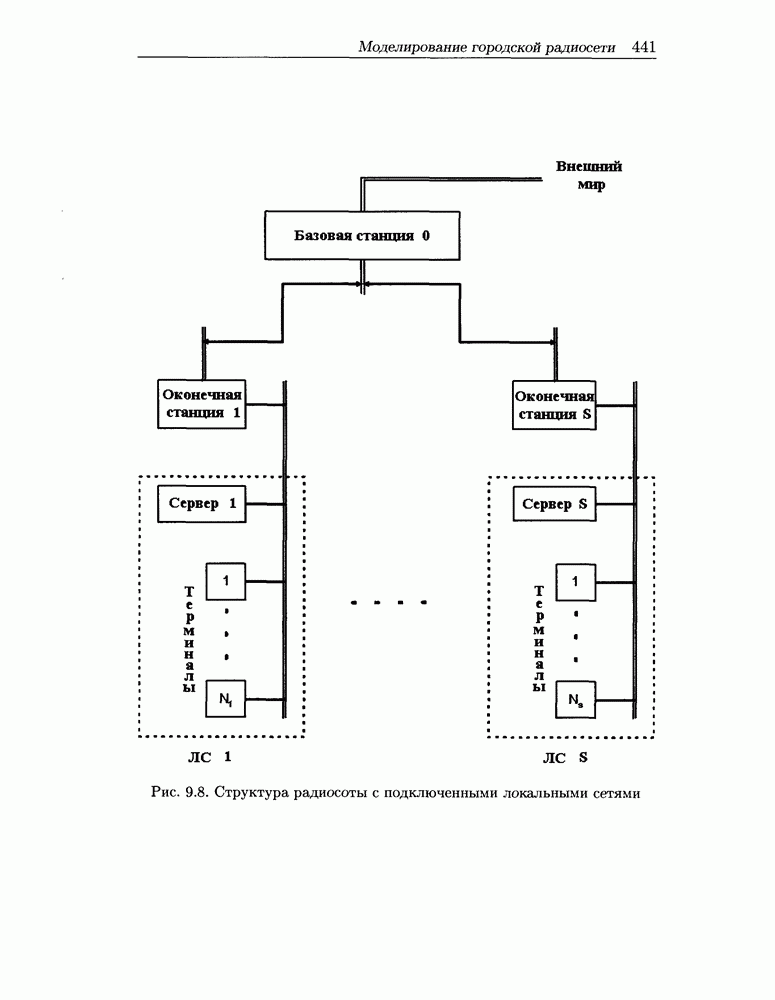
Рассмотрим радиосоту, объединяющую  оконечных станций со статистически однородными локальными сетями, т.е. для каждого
оконечных станций со статистически однородными локальными сетями, т.е. для каждого 

(значение  соответствует расстоянию в 5 километров). Кроме того: средние количества пакетов-ответов
соответствует расстоянию в 5 километров). Кроме того: средние количества пакетов-ответов  для всех серверов
для всех серверов  ; после обслуживания любого запроса в любом из локальных серверов
; после обслуживания любого запроса в любом из локальных серверов  с одинаковой интенсивностью
с одинаковой интенсивностью  пакеты ответа поступают в среднем через 0,002 с; при обслуживании во «внешнем мире» эти величины равны, соответственно,
пакеты ответа поступают в среднем через 0,002 с; при обслуживании во «внешнем мире» эти величины равны, соответственно,  и 0,02 с. Значение
и 0,02 с. Значение  выбрано из расчета максимально возможного расстояния между станциями, равного 50 километров, а предел длины пакета
выбрано из расчета максимально возможного расстояния между станциями, равного 50 километров, а предел длины пакета  байт.
байт.

Начнем со случая, когда радиосота реализована по технологии FHSS с быстродействием V = 2 Мбит/с, достаточно большим временем  (что позволяет ограничиться формулами раздела 9.4.2) и фрагментация не используется, т.е.
(что позволяет ограничиться формулами раздела 9.4.2) и фрагментация не используется, т.е.  байт. Соответствующие параметры протокола Radio-Ethernet, полученные на основе данных из [298], приведены в
байт. Соответствующие параметры протокола Radio-Ethernet, полученные на основе данных из [298], приведены в  (временные параметры даны в микросекундах). Вероятность помех при передаче пакета равна
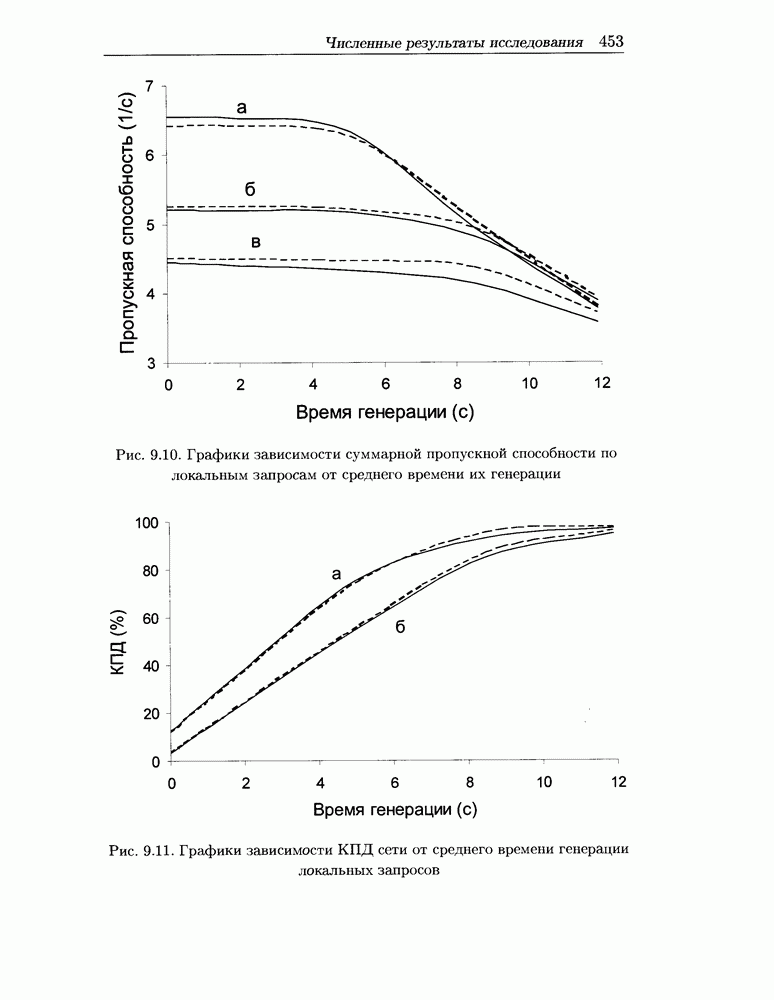
(временные параметры даны в микросекундах). Вероятность помех при передаче пакета равна  На рис. 9.10 показаны зависимости суммарной локальной пропускной способности
На рис. 9.10 показаны зависимости суммарной локальной пропускной способности  этой радиосоты от среднего времени генерации запроса
этой радиосоты от среднего времени генерации запроса 
Эти зависимости получены при  с помощью имитационного моделирования (сплошные линии) и аналитических методов раздела 9.4.2 (штриховые линии) для следующих случаев, отличающихся вероятностями внешнего доступа
с помощью имитационного моделирования (сплошные линии) и аналитических методов раздела 9.4.2 (штриховые линии) для следующих случаев, отличающихся вероятностями внешнего доступа  и интенсивности потока внешних запросов
и интенсивности потока внешних запросов  Видно, что при уменьшении
Видно, что при уменьшении  кривые входят в область насыщения, т.е. пропускная способность полностью определяется интенсивностью обслуживания в «узком месте», которым является базовая станция (кривые (а) и
кривые входят в область насыщения, т.е. пропускная способность полностью определяется интенсивностью обслуживания в «узком месте», которым является базовая станция (кривые (а) и  , а в случае (в) - все станции.
, а в случае (в) - все станции.

Рис. 9.10. Графики зависимости суммарной пропускной способности по локальным запросам от среднего времени их генерации

Рис. 9.11. Графики зависимости КПД сети от среднего времени генерации локальных запросов
При больших  пропускная способность примерно равна своему максимальному значению
пропускная способность примерно равна своему максимальному значению  , достижимому при данном
, достижимому при данном  и определяемому (из расчета нулевой задержки передачи) из формулы:
и определяемому (из расчета нулевой задержки передачи) из формулы:

Поэтому используем в качестве показателя эффективности работы радиосоты ее коэффициент полезного действия (КПД), равный проценту, который  составляет от Атах. Графики зависимости КПД от
составляет от Атах. Графики зависимости КПД от  показаны на рис. 9.11 для случаев (а) и (б) (график для случая (в) не приведен ввиду его практического совпадения со случаем (б)).
показаны на рис. 9.11 для случаев (а) и (б) (график для случая (в) не приведен ввиду его практического совпадения со случаем (б)).
Как видно из рис. 9.10 и 9.11, погрешность разработанных приближений нигде не превышает 5%, поэтому данный метод вполне применим для оценки пропускной способности радиосети, причем в отличие от имитационного моделирования может эффективно использоваться при решении поисковых задач проектирования сетей с сотнями и тысячами клиентов. В качестве примера найдем область значений интенсивностей  где КПД сети не меньше 80%. При этом установим следующие (более реальные) параметры сети:
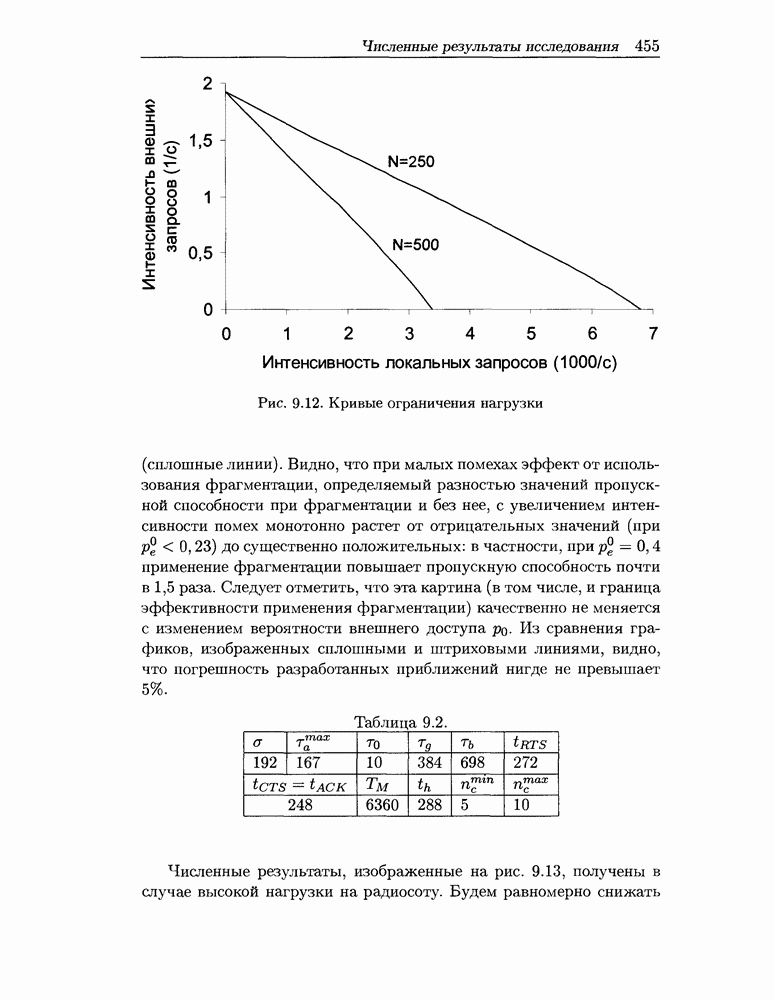
где КПД сети не меньше 80%. При этом установим следующие (более реальные) параметры сети:  а N принимает два значения - 250 и 500. При имитационном моделировании на решение этой задачи потребовались бы недели, в то время как разработанный метод позволил в течение часа получить следующие результаты: рис. 9.12. Кривые на этом рисунке ограничивают сверху искомую область значений.
а N принимает два значения - 250 и 500. При имитационном моделировании на решение этой задачи потребовались бы недели, в то время как разработанный метод позволил в течение часа получить следующие результаты: рис. 9.12. Кривые на этом рисунке ограничивают сверху искомую область значений.
Перейдем к исследованию эффективности использования фрагментации. Рассмотрим случай, когда радиосота реализована по технологии DSSS с быстродействием  Мбит/с и
Мбит/с и  байт. Соответствующие параметры протокола [298] даны в табл. 9.2. Кроме того,
байт. Соответствующие параметры протокола [298] даны в табл. 9.2. Кроме того,  На рис. 9.13 показаны графики суммарной локальной пропускной способности
На рис. 9.13 показаны графики суммарной локальной пропускной способности  этой радиосоты в зависимости от интенсивности помех, характеризуемой вероятностью ошибки
этой радиосоты в зависимости от интенсивности помех, характеризуемой вероятностью ошибки  из-за помех при передаче фрейма DATA с нефрагментированным пакетом ответа. Эти графики, образующие два семейства, отличающихся вероятностью внешнего доступа
из-за помех при передаче фрейма DATA с нефрагментированным пакетом ответа. Эти графики, образующие два семейства, отличающихся вероятностью внешнего доступа  и 0,9), получены при фрагментированной (толстые линии с меткой «ф») и нефрагментированной (тонкие линии с меткой «н/ф») передаче пакетов с помощью имитационного моделирования (штриховые линии) и разработанных приближений (сплошные линии).
и 0,9), получены при фрагментированной (толстые линии с меткой «ф») и нефрагментированной (тонкие линии с меткой «н/ф») передаче пакетов с помощью имитационного моделирования (штриховые линии) и разработанных приближений (сплошные линии).

Рис. 9.12. Кривые ограничения нагрузки
Видно, что при малых помехах эффект от использования фрагментации, определяемый разностью значений пропускной способности при фрагментации и без нее, с увеличением интенсивности помех монотонно растет от отрицательных значений (при  ) до существенно положительных: в частности, при
) до существенно положительных: в частности, при  применение фрагментации повышает пропускную способность почти в 1,5 раза. Следует отметить, что эта картина (в том числе, и граница эффективности применения фрагментации) качественно не меняется с изменением вероятности внешнего доступа
применение фрагментации повышает пропускную способность почти в 1,5 раза. Следует отметить, что эта картина (в том числе, и граница эффективности применения фрагментации) качественно не меняется с изменением вероятности внешнего доступа  . Из сравнения графиков, изображенных сплошными и штриховыми линиями, видно, что погрешность разработанных приближений нигде не превышает 5%.
. Из сравнения графиков, изображенных сплошными и штриховыми линиями, видно, что погрешность разработанных приближений нигде не превышает 5%.
Таблица 9.2.

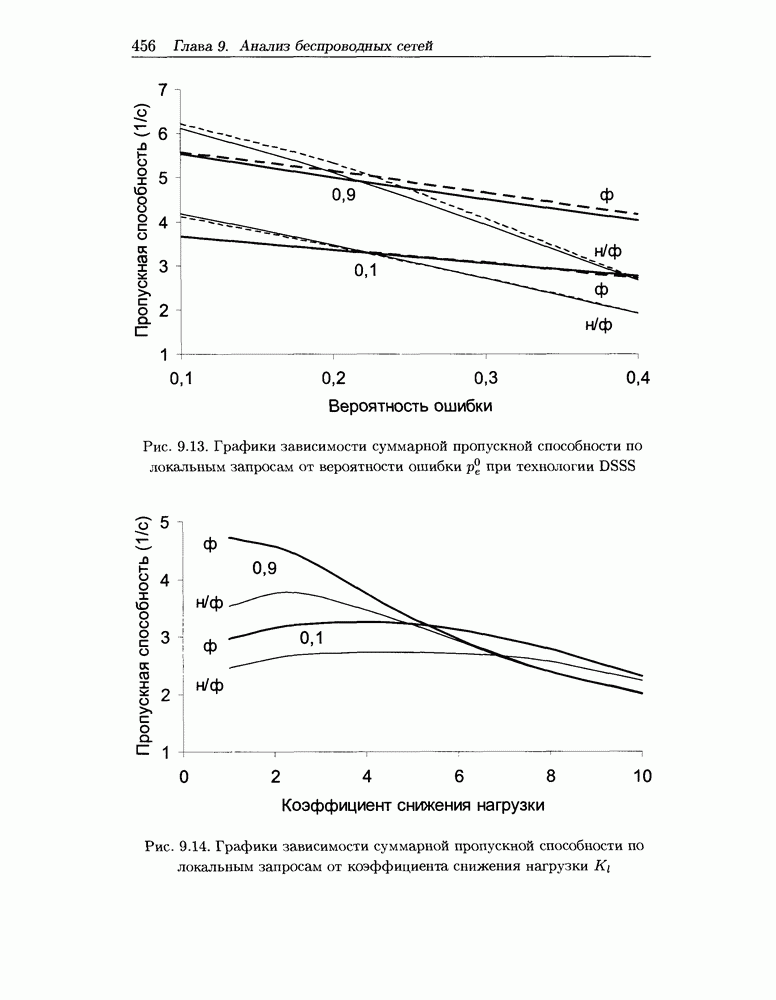
Численные результаты, изображенные на рис. 9.13, получены в случае высокой нагрузки на радиосоту.

Рис. 9.13. Графики зависимости суммарной пропускной способности по локальным запросам от вероятности ошибки при технологии DSSS

Рис. 9.14. Графики зависимости суммарной пропускной способности по локальным запросам от коэффициента снижения нагрузки 

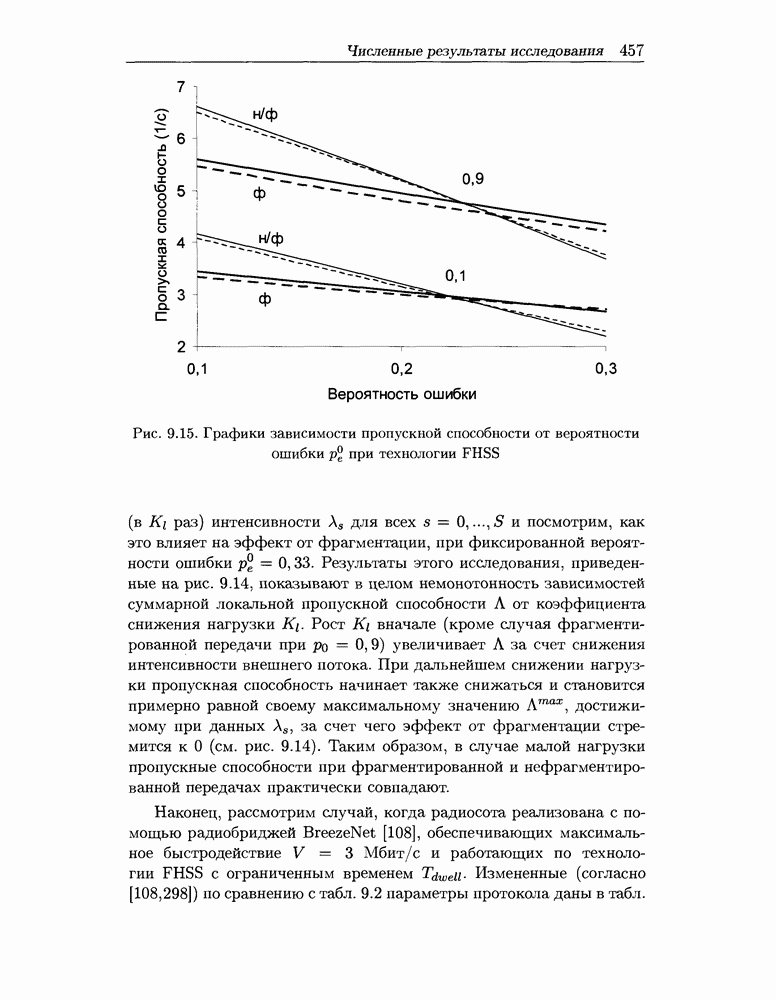
Рис. 9.15. Графики зависимости пропускной способности от вероятности ошибки при технологии FHSS
Будем равномерно снижать (в  раз) интенсивности
раз) интенсивности  для всех
для всех  и посмотрим, как это влияет на эффект от фрагментации, при фиксированной вероятности ошибки
и посмотрим, как это влияет на эффект от фрагментации, при фиксированной вероятности ошибки  Результаты этого исследования, приведенные на рис. 9.14, показывают в целом немонотонность зависимостей суммарной локальной пропускной способности
Результаты этого исследования, приведенные на рис. 9.14, показывают в целом немонотонность зависимостей суммарной локальной пропускной способности  от коэффициента снижения нагрузки
от коэффициента снижения нагрузки  вначале (кроме случая фрагментированной передачи при
вначале (кроме случая фрагментированной передачи при  увеличивает
увеличивает  за счет снижения интенсивности внешнего потока. При дальнейшем снижении нагрузки пропускная способность начинает также снижаться и становится примерно равной своему максимальному значению Атах, достижимому при данных
за счет снижения интенсивности внешнего потока. При дальнейшем снижении нагрузки пропускная способность начинает также снижаться и становится примерно равной своему максимальному значению Атах, достижимому при данных  за счет чего эффект от фрагментации стремится к 0 (см. рис. 9.14). Таким образом, в случае малой нагрузки пропускные способности при фрагментированной и нефрагментированной передачах практически совпадают.
за счет чего эффект от фрагментации стремится к 0 (см. рис. 9.14). Таким образом, в случае малой нагрузки пропускные способности при фрагментированной и нефрагментированной передачах практически совпадают.
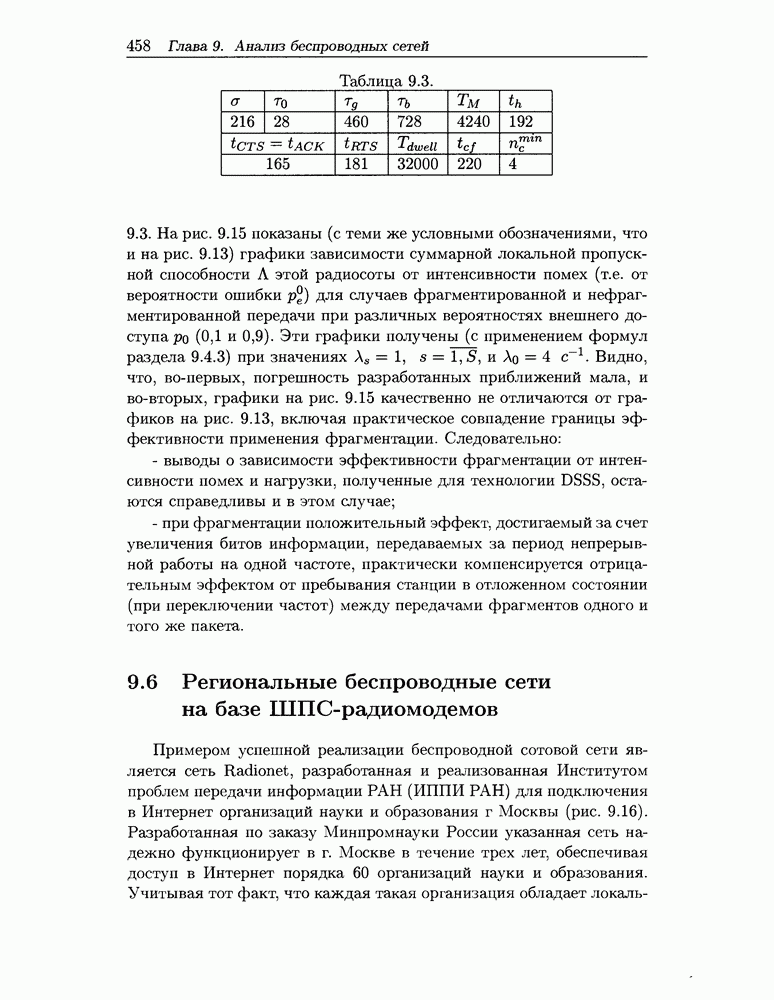
Наконец, рассмотрим случай, когда радиосота реализована с помощью радиобриджей BreezeNet [108], обеспечивающих максимальное быстродействие V = 3 Мбит/с и работающих по технологии FHSS с ограниченным временем  . Измененные (согласно [108,298]) по сравнению с табл. 9.2 параметры протокола даны в табл. 9.3.
. Измененные (согласно [108,298]) по сравнению с табл. 9.2 параметры протокола даны в табл. 9.3.
Таблица 9.3.

На рис. 9.15 показаны (с теми же условными обозначениями, что и на рис. 9.13) графики зависимости суммарной локальной пропускной способности  этой радиосоты от интенсивности помех (т.е. от вероятности ошибки
этой радиосоты от интенсивности помех (т.е. от вероятности ошибки  ) для случаев фрагментированной и нефрагментированной передачи при различных вероятностях внешнего доступа
) для случаев фрагментированной и нефрагментированной передачи при различных вероятностях внешнего доступа  (0,1 и 0,9). Эти графики получены (с применением формул раздела 9.4.3) при значениях
(0,1 и 0,9). Эти графики получены (с применением формул раздела 9.4.3) при значениях  Видно, что, во-первых, погрешность разработанных приближений мала, и во-вторых, графики на рис. 9.15 качественно не отличаются от графиков на рис. 9.13, включая практическое совпадение границы эффективности применения фрагментации. Следовательно:
Видно, что, во-первых, погрешность разработанных приближений мала, и во-вторых, графики на рис. 9.15 качественно не отличаются от графиков на рис. 9.13, включая практическое совпадение границы эффективности применения фрагментации. Следовательно:
- выводы о зависимости эффективности фрагментации от интенсивности помех и нагрузки, полученные для технологии DSSS, остаются справедливы и в этом случае;
- при фрагментации положительный эффект, достигаемый за счет увеличения битов информации, передаваемых за период непрерывной работы на одной частоте, практически компенсируется отрицательным эффектом от пребывания станции в отложенном состоянии (при переключении частот) между передачами фрагментов одного и того же пакета.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
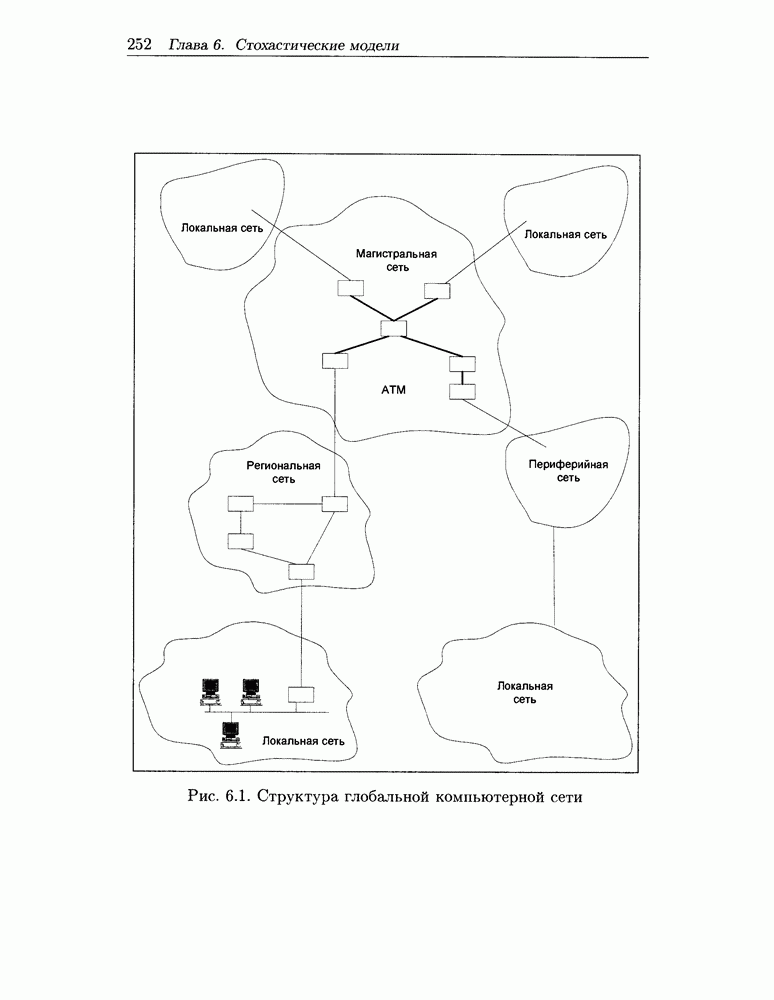
- 6.1.1 Структура компьютерных сетей
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
- 6.3 Управление потоками в сети пакетной коммутации
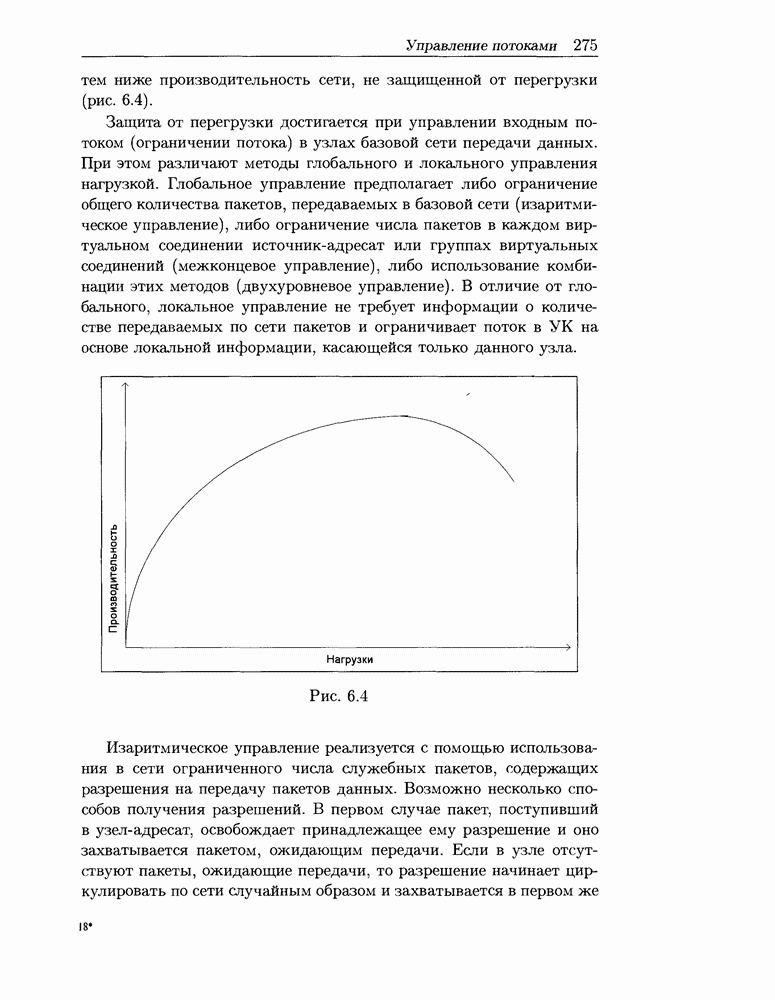
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
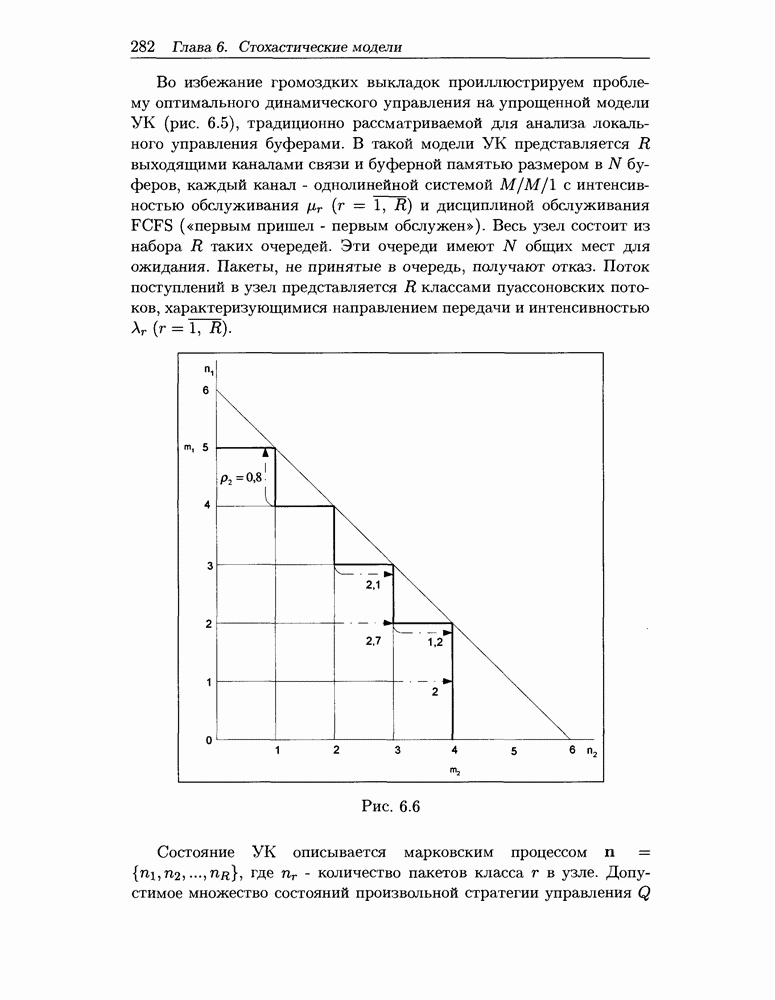
- 6.3.3 Локальное управление буферами
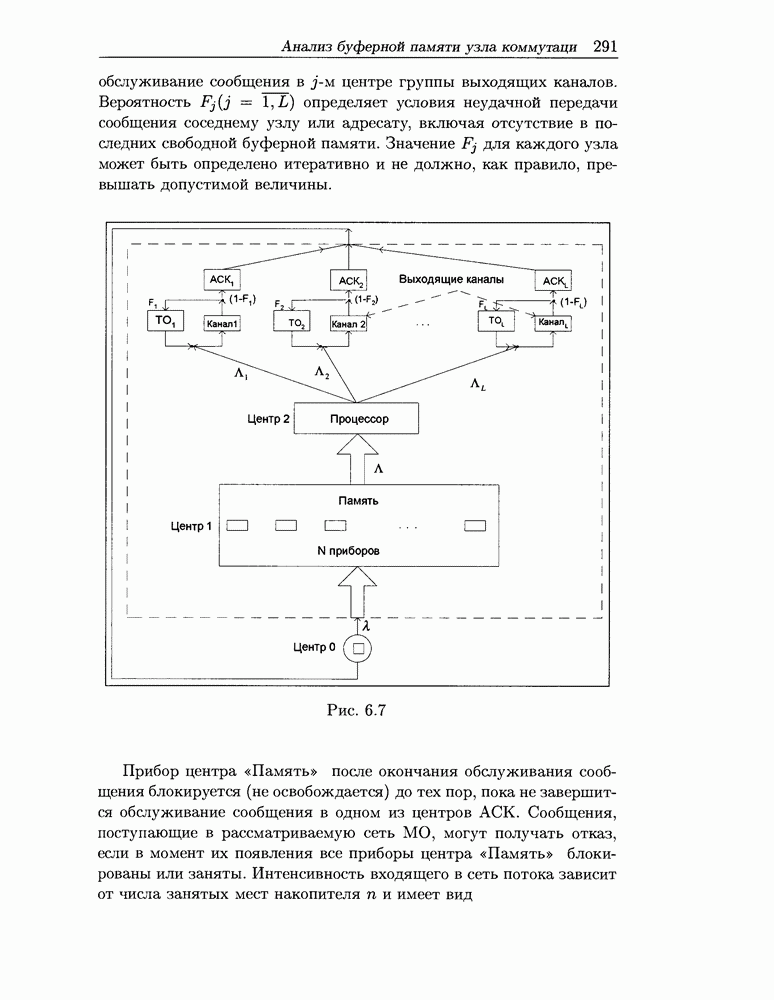
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
- 7.4.2 Анализ развития СПД «Сирена»
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
- 7.5.4 Классификация алгоритмов маршрутизации
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
- 7.5.8 Показатели качества маршрутизации
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
- 9.1 Состояние и перспективы развития беспроводных радиосетей
- 9.2 Схема распределенного управления
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
- 9.4 Моделирование городской радиосети
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
- 9.5 Численные результаты исследования городской радиосоты
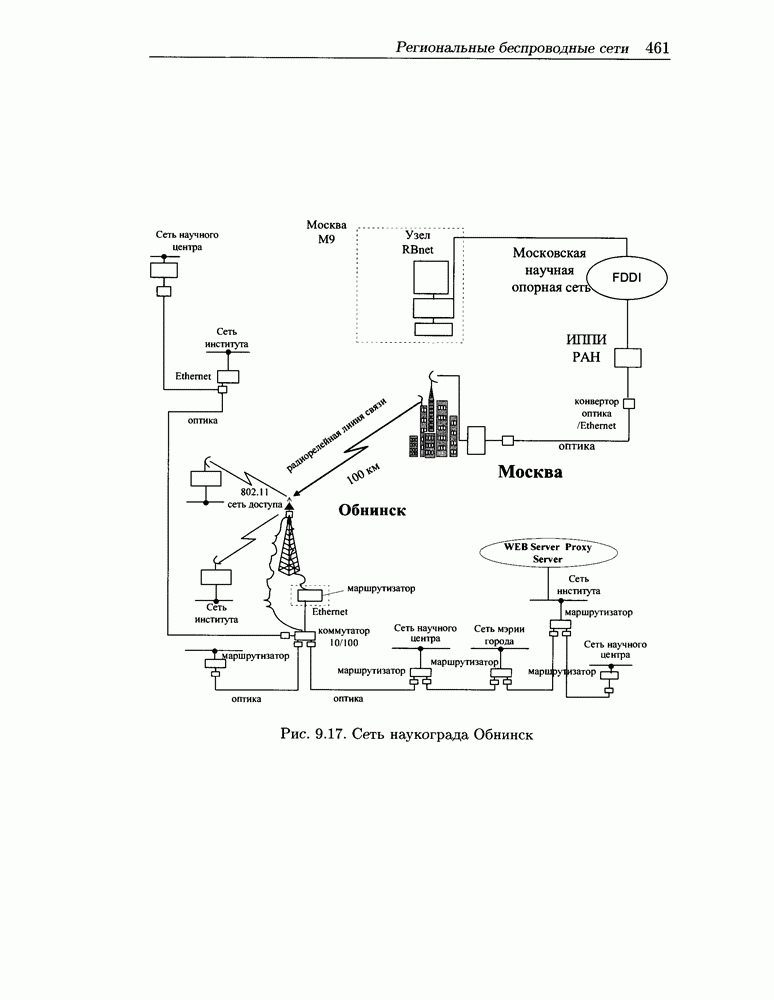
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
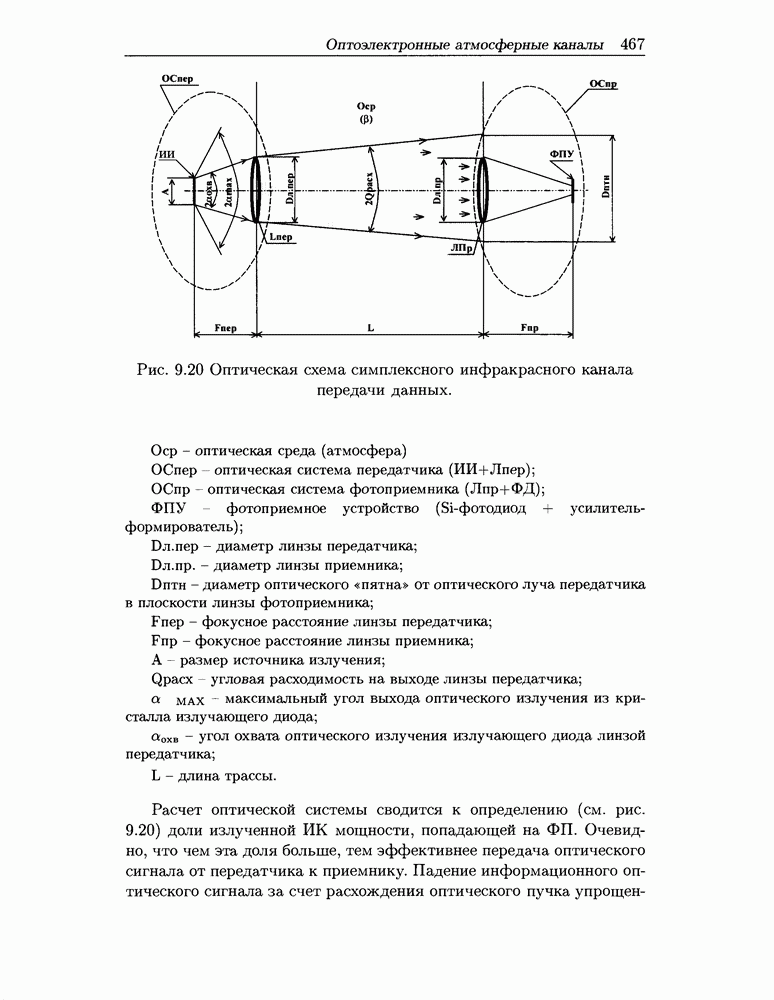
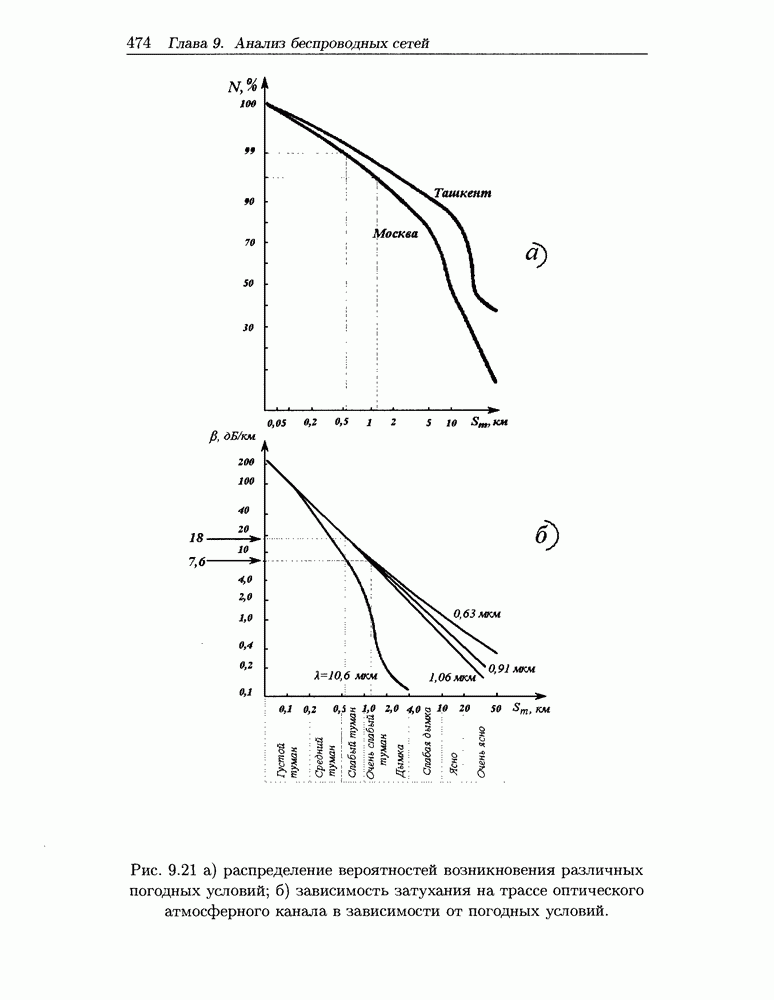
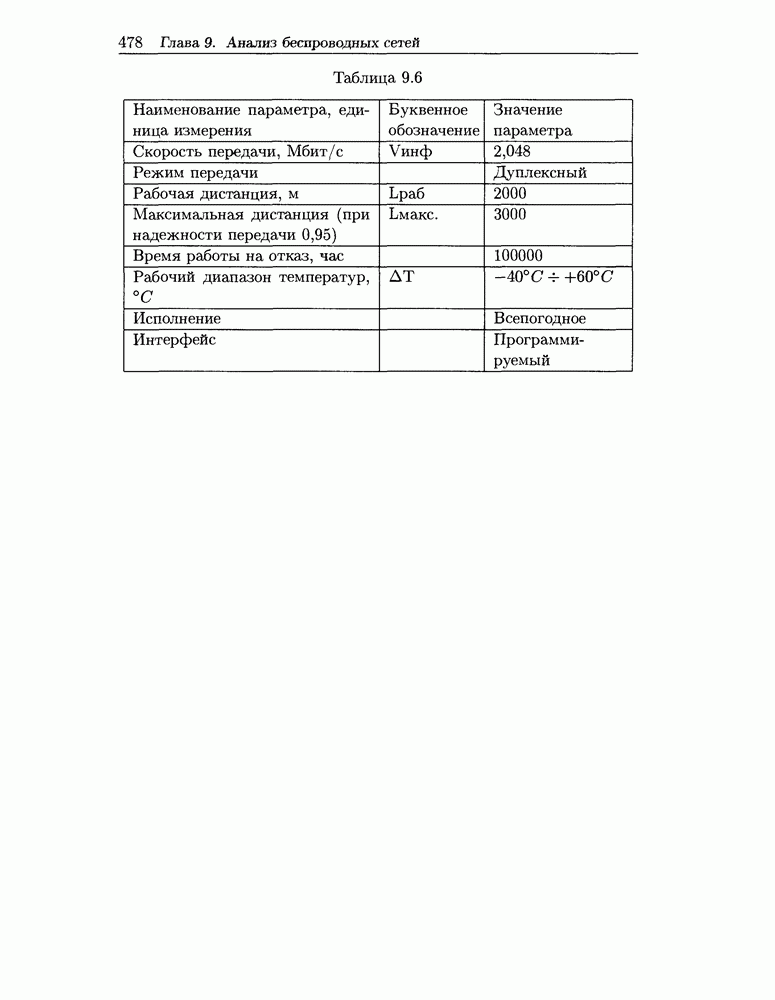
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература