| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.9 Многофазные системы
В рассмотренных выше разделах были рассмотрены модели СМО, в которых обслуживание запросов производится одним прибором либо одним из нескольких параллельных идентичных приборов. Вместе с тем, процесс обработки запросов во многих реальных системах состоит из их последовательной обработки в нескольких обслуживающих устройствах. Системы обслуживания такого вида явились прототипом сетей массового обслуживания и получили название многофазных СМО.
Многофазные СМО принято кодировать в виде последовательности символов типа:

Здесь символ  описывает входящий поток на вход цепочки из
описывает входящий поток на вход цепочки из  последовательных обслуживающих устройств, символы
последовательных обслуживающих устройств, символы  описывают соответственно распределение времени обслуживания, число параллельных каналов и число мест в буфере для ожидания в
описывают соответственно распределение времени обслуживания, число параллельных каналов и число мест в буфере для ожидания в  звене цепочки. Символы
звене цепочки. Символы  принимают значение в тех же множествах, как и соответствующие символы в описании однофазных систем, изученных нами выше. Символ
принимают значение в тех же множествах, как и соответствующие символы в описании однофазных систем, изученных нами выше. Символ  означает переход запроса на вход следующего обслуживающего устройства по окончании его обслуживания в предыдущем.
означает переход запроса на вход следующего обслуживающего устройства по окончании его обслуживания в предыдущем.
В некотором смысле этот символ является заменителем символа, задающего вид входящего потока в соответствующую систему обслуживания, поскольку входящий поток в данную СМО определяется выходящим потоком запросов из предыдущей СМО.
Если какой - либо символ принимает конечное значение, то возникает вопрос о поведении многофазной СМО в ситуации, когда буфер перед соответствующей однофазной СМО уже полон, а на вход этой СМО поступает следующий запрос. Обычно рассматриваются два варианта: поступающий запрос теряется и поступающий запрос остается на приборе, где он закончил обслуживание, временно блокируя дальнейшую работу этого прибора.
Известные результаты для широкого круга многофазных СМО довольно исчерпывающе описаны в справочнике [210]. Здесь мы кратко коснемся трех простых многофазных СМО.
Первая из них - это многофазная СМО с бесконечным буфером перед первой фазой, на вход которой поступает простейший поток интенсивности  , а время обслуживания в каждой из
, а время обслуживания в каждой из  фаз имеет показательное распределение с параметром
фаз имеет показательное распределение с параметром  Предполагается, что одновременно в системе может обслуживаться только один запрос. Только по завершении прохождения запросом всей цепочки приборов на обслуживание может быть выбран следующий запрос.
Предполагается, что одновременно в системе может обслуживаться только один запрос. Только по завершении прохождения запросом всей цепочки приборов на обслуживание может быть выбран следующий запрос.
Вспоминая, что эрганговская случайная величина с параметрами  есть сумма
есть сумма  независимых случайных величин с параметром
независимых случайных величин с параметром  приходим к выводу, что все характеристики рассматриваемой СМО легко получить из характеристик соответствующей однофазной СМО типа
приходим к выводу, что все характеристики рассматриваемой СМО легко получить из характеристик соответствующей однофазной СМО типа  Анализ такой СМО можно провести с использованием так называемого метода фаз Эрланга. Соответствующие результаты можно получить также из формул для системы
Анализ такой СМО можно провести с использованием так называемого метода фаз Эрланга. Соответствующие результаты можно получить также из формул для системы 
Так, для производящей функции  распределения
распределения  числа запросов в системе из формулы Поллячека - Хинчина см., например, формулу (1.45), с учетом равенства:
числа запросов в системе из формулы Поллячека - Хинчина см., например, формулу (1.45), с учетом равенства:  получаем:
получаем:
 (1.122)
(1.122)
где коэффициент загрузки  определяется как
определяется как 
Обозначим  - корни уравнения
- корни уравнения
 (1.123)
(1.123)
по модулю большие единицы.
Разлагая правую часть уравнения (1.122) на простые дроби и используя свойства производящей функции получаем:
 (1.124)
(1.124)
где коэффициенты  определяются следующим образом:
определяются следующим образом:
 (1.126)
(1.126)
Рассмотрим теперь следующую многофазную СМО:

то есть, многофазную СМО, состоящую из  последовательных многоканальных СМО с бесконечным буфером. Пусть
последовательных многоканальных СМО с бесконечным буфером. Пусть  - интенсивность входящего потока,
- интенсивность входящего потока,  - интенсивность обслуживания в каждом из этих каналов
- интенсивность обслуживания в каждом из этих каналов  системы,
системы,  .
.
Обозначим  число запросов в
число запросов в  системе в момент времени
системе в момент времени  - стационарную вероятность состояния
- стационарную вероятность состояния  рассматриваемой СМО, то есть
рассматриваемой СМО, то есть
 (1.127)
(1.127)
Можно показать, что условием существования пределов (1.127) является выполнение неравенств
 (1.128)
(1.128)
Далее считаем эти неравенства выполненными.
Используя  - метод», можно получить систему дифференциальных уравнений для вероятностей
- метод», можно получить систему дифференциальных уравнений для вероятностей  откуда, переходя к пределу при
откуда, переходя к пределу при  получим следующую систему уравнений для стационарных вероятностей
получим следующую систему уравнений для стационарных вероятностей 

где

Непосредственной подстановкой несложно убедиться, что решение системы (1.129) имеет следующий вид:
 (1.130)
(1.130)
где

Вероятность  находится из условия нормировки:
находится из условия нормировки:
 (1.131)
(1.131)
и имеет вид
 (1.132)
(1.132)
Из (1.130), (1.131) и формул  видим, что стационарные вероятности
видим, что стационарные вероятности  рассматриваемой СМО представимы в мультипликативном виде:
рассматриваемой СМО представимы в мультипликативном виде:
 (1.133)
(1.133)
то есть, совместная вероятность того, что в произвольный момент времени на к-й фазе находится  запросов,
запросов,  , равна произведению вероятностей того, что
, равна произведению вероятностей того, что  запросов в данный момент находится на
запросов в данный момент находится на  фазе независимо от числа запросов на других фазах,
фазе независимо от числа запросов на других фазах, 
Этот факт, позволяющий рассчитывать распределение вероятностей состояний многофазной системы как произведение вероятностей состояний однофазных СМО, образующих данную СМО, следует из теоремы Берка ([154]), которая формулируется следующим образом.
Теорема. В системе с с параллельными каналами, простейшим входящим потоком интенсивности  и одинаковым для каждого канала показательным распределением времени обслуживания с параметром
и одинаковым для каждого канала показательным распределением времени обслуживания с параметром  в стационарном состоянии выходящий поток является простейшим потоком интенсивности
в стационарном состоянии выходящий поток является простейшим потоком интенсивности  .
.
Таким образом, обслуживание простейшего потока запросов на каждой фазе многофазной СМО с показательным распределением времени обслуживания не изменяет характера потока и в результате совместное распределение вероятностей числа запросов в соответствующей многофазной системе имеет мультипликативный вид.
В заключение раздела кратко рассмотрим многофазную СМО типа 
Интенсивность входящего потока обозначим  , функцию распределения времени обслуживания -
, функцию распределения времени обслуживания -  интенсивность обслуживания любым прибором на второй фазе обозначим
интенсивность обслуживания любым прибором на второй фазе обозначим  .
.
Предполагаем, что в случае занятости всех приборов на второй фазе в момент окончания обслуживания запроса на первой фазе с вероятностью  запрос уходит из системы недообслуженным (теряется), а с дополнительной вероятностью первый прибор блокируется и не обслуживает следующий запрос, пока не освободится прибор на второй фазе. Как крайние случаи при
запрос уходит из системы недообслуженным (теряется), а с дополнительной вероятностью первый прибор блокируется и не обслуживает следующий запрос, пока не освободится прибор на второй фазе. Как крайние случаи при  мы имеем систему с блокировкой прибора, при
мы имеем систему с блокировкой прибора, при  - систему с потерями.
- систему с потерями.
Будем рассматривать двумерный процесс  где
где  есть
есть  момент окончания обслуживания запроса на первой фазе,
момент окончания обслуживания запроса на первой фазе,  - число запросов на первой фазе,
- число запросов на первой фазе,  - число запросов на второй фазе в момент времени
- число запросов на второй фазе в момент времени  Несложно видеть, что этот процесс является двумерной цепью Маркова с дискретным временем.
Несложно видеть, что этот процесс является двумерной цепью Маркова с дискретным временем.
Обозначим одношаговые вероятности переходов этой цепи

Введем производящую функцию

Аналогично вложенной цепи для системы MG1, изученной в разделе 6, вероятности переходов  зависят от значения
зависят от значения  , но не зависят от
, но не зависят от  и I отдельно. Это делает введенное определение производящей функции
и I отдельно. Это делает введенное определение производящей функции  корректным.
корректным.
Анализируя переходы двумерной цепи Маркова, можно убедиться, что производящие функции  определяются следующим образом:
определяются следующим образом:

где

Составим из производящих функций  матричную производящую функцию R(z) и введем в рассмотрение матрицу
матричную производящую функцию R(z) и введем в рассмотрение матрицу  , состоящую из элементов
, состоящую из элементов

Матрица  характеризует вероятности переходов числа занятых каналов на второй фазе системы за время, когда прибор на первой фазе простаивает, ожидая прихода запроса.
характеризует вероятности переходов числа занятых каналов на второй фазе системы за время, когда прибор на первой фазе простаивает, ожидая прихода запроса.
Обозначим
 (1.134)
(1.134)
Утверждение 22. Векторная производящая функция  удовлетворяет матричному функциональному уравнению:
удовлетворяет матричному функциональному уравнению:
 (1.135)
(1.135)
Здесь I - тождественная матрица.
Условия существования пределов (1.134) и алгоритмы решения уравнения (1.135) можно найти, например, в [71], [252].
Распределение вероятностей состояний системы в произвольные моменты времени можно найти, используя теорию процессов марковского восстановления по аналогии с тем, как это сделано в подпункте 1.6.1.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
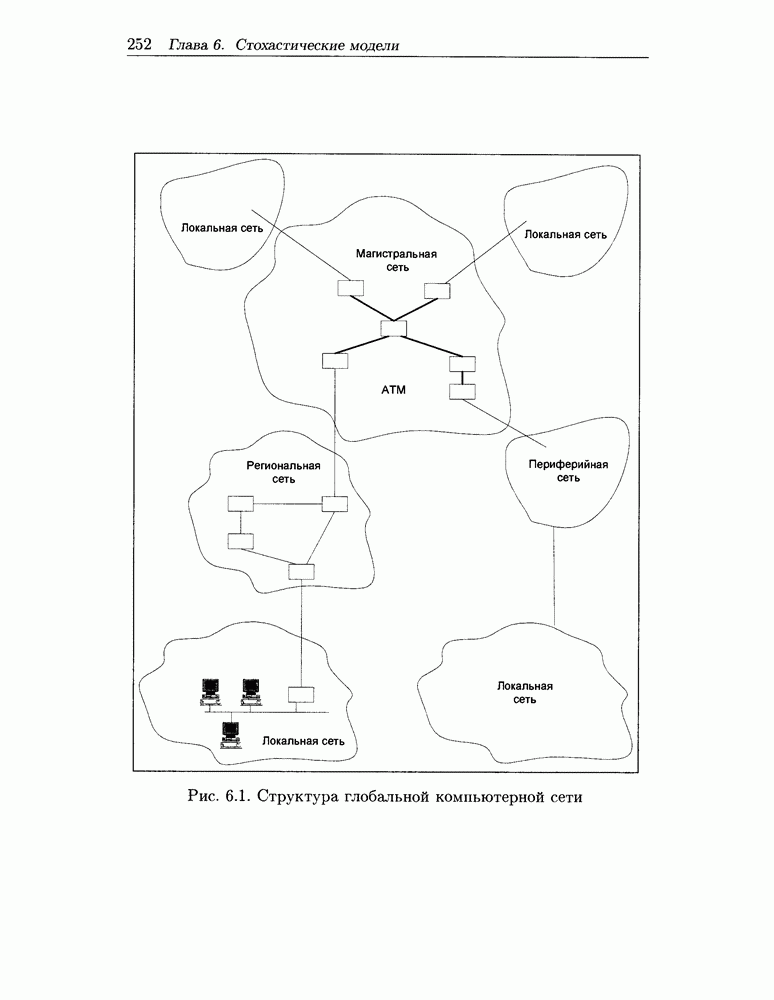
- 6.1.1 Структура компьютерных сетей
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
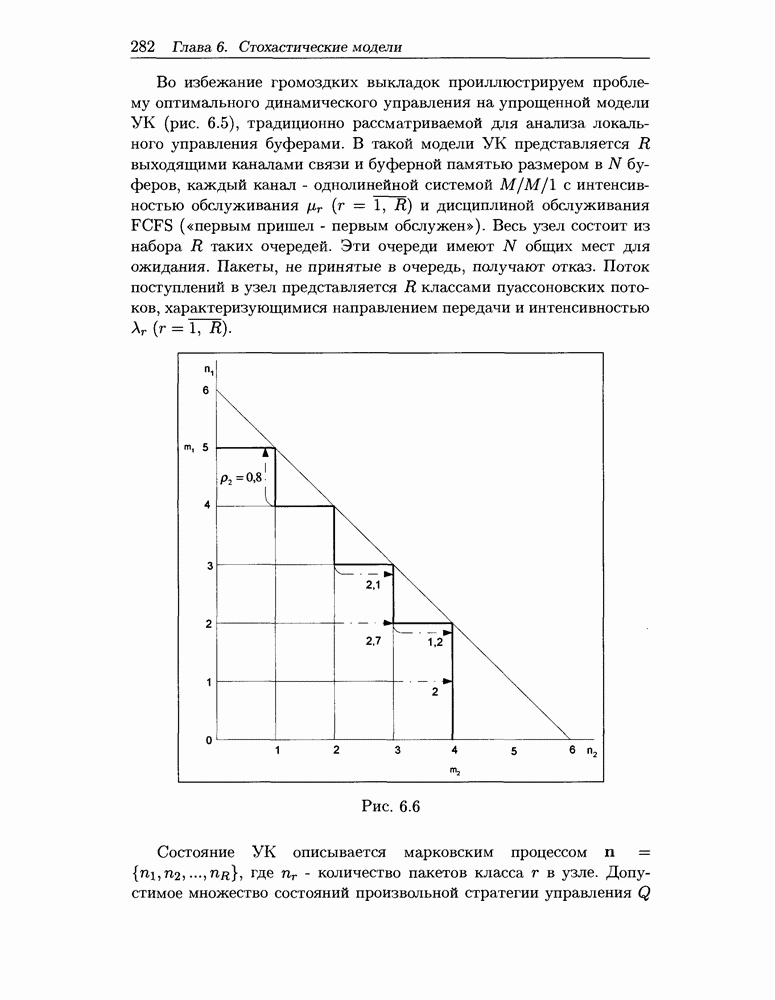
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
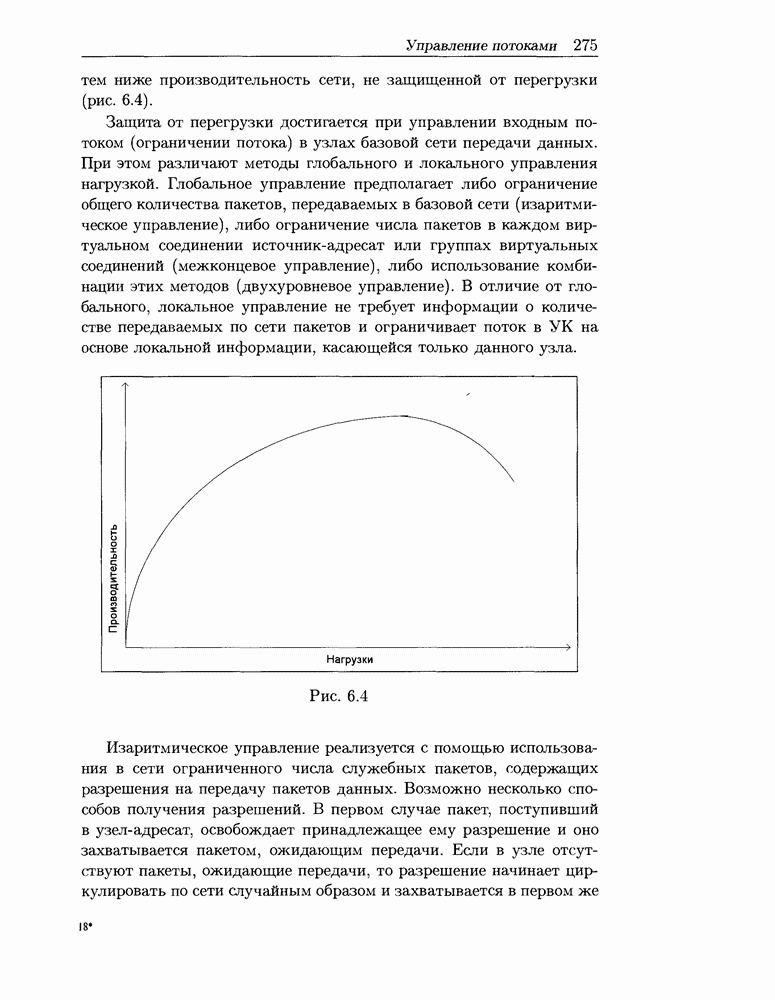
- 6.3 Управление потоками в сети пакетной коммутации
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
- 6.3.3 Локальное управление буферами
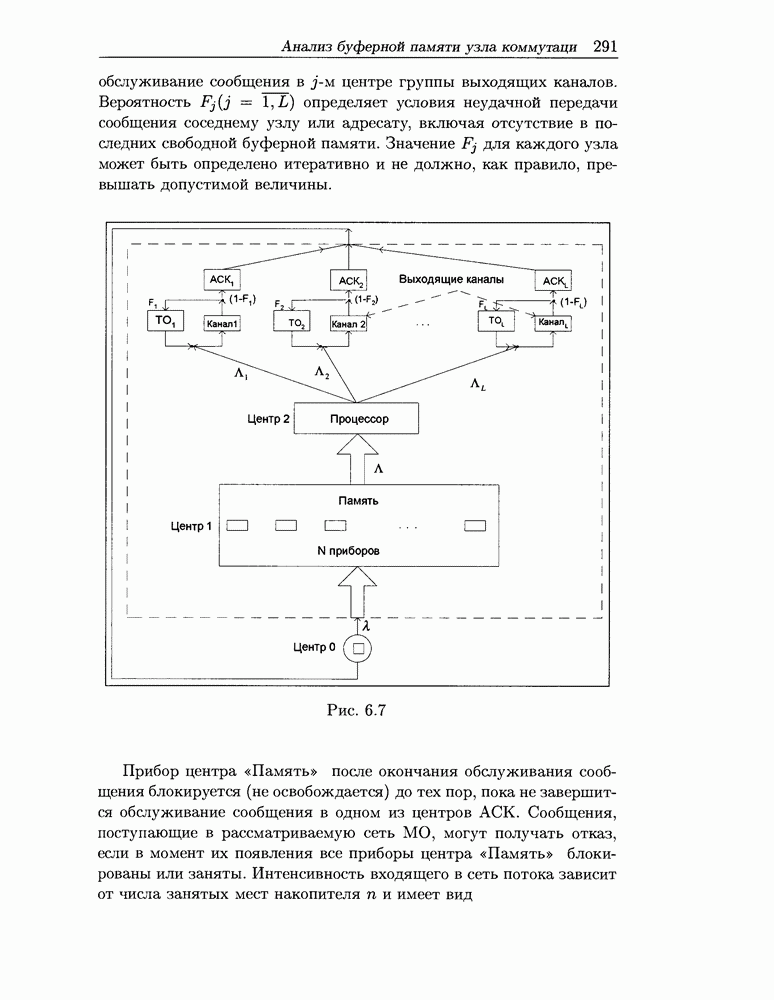
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
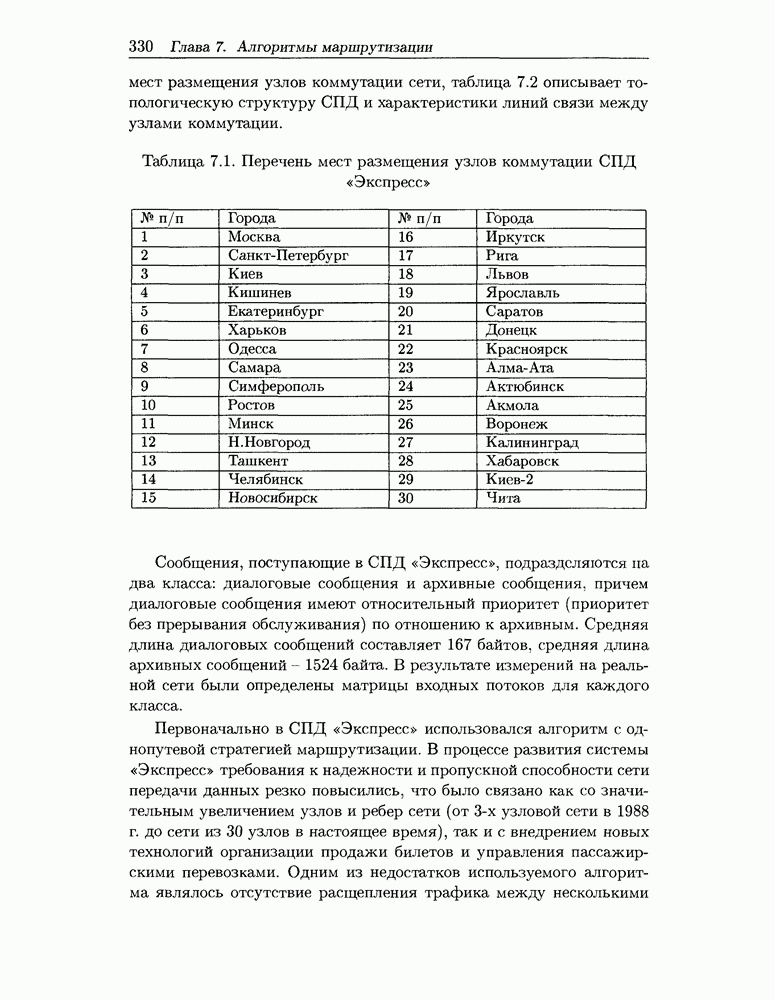
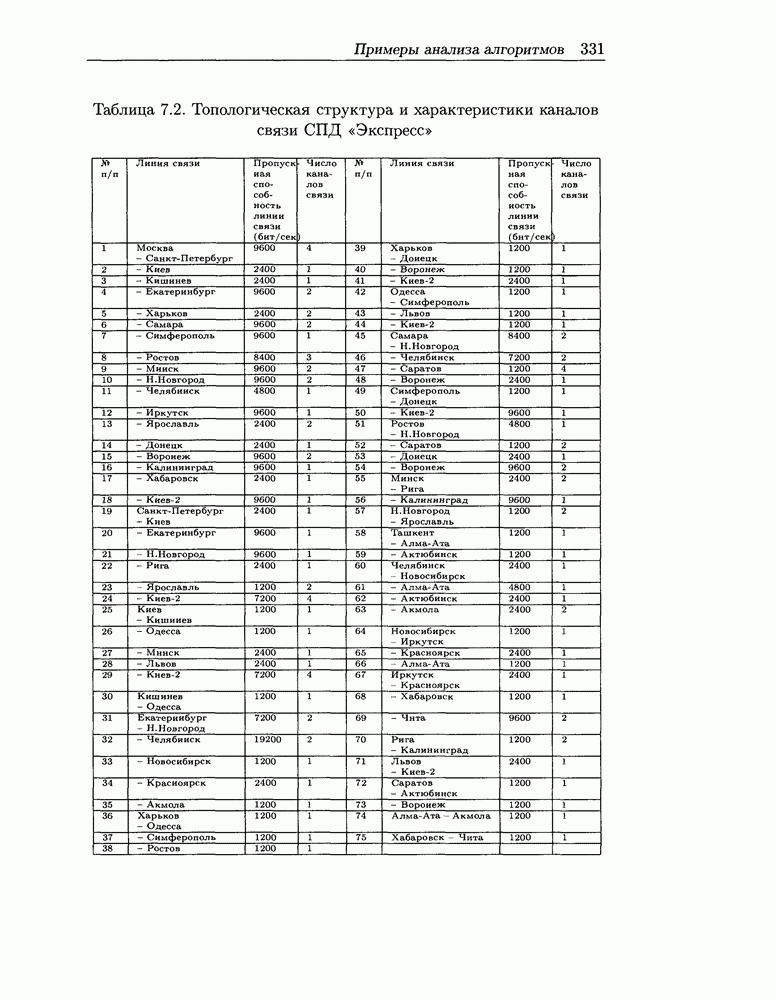
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
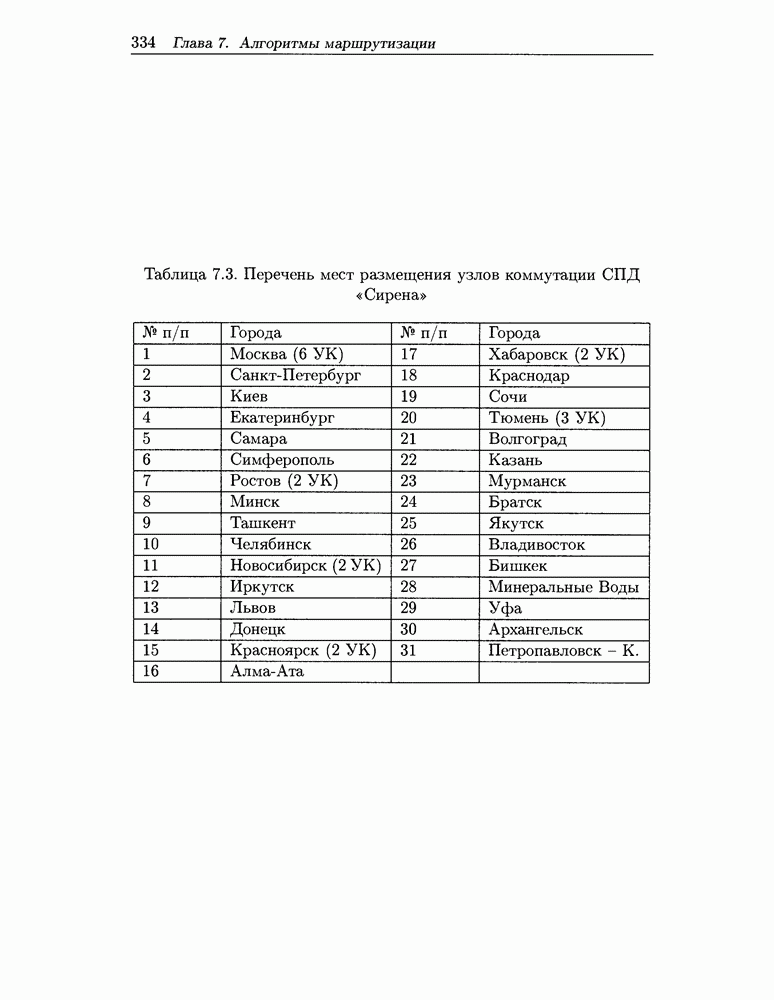
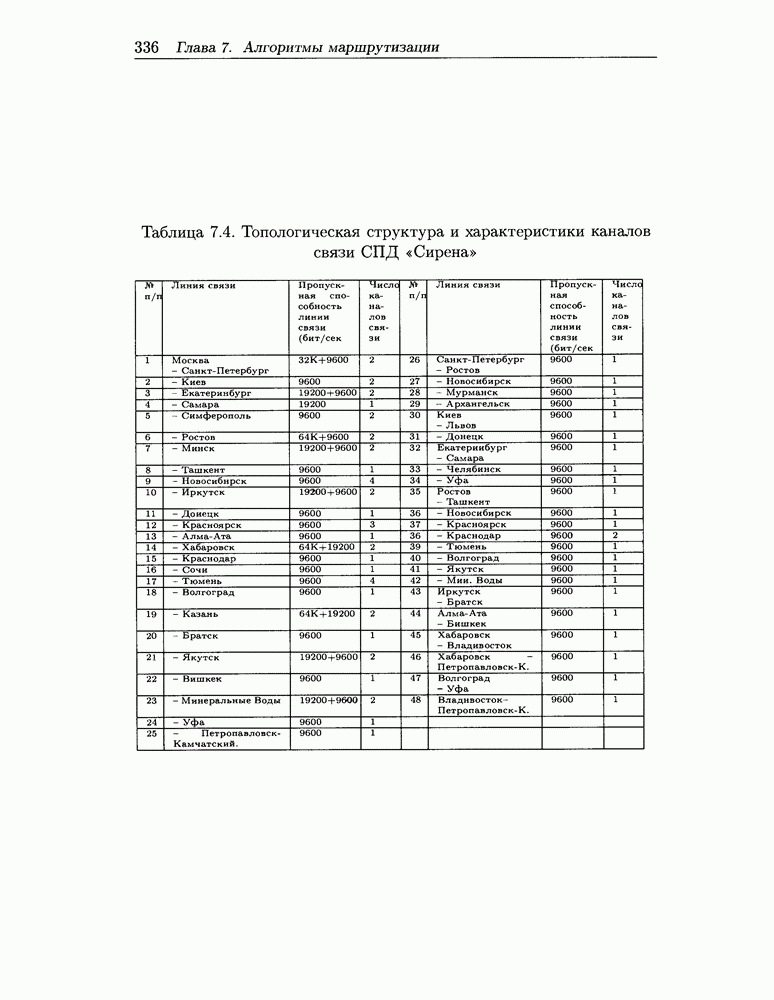
- 7.4.2 Анализ развития СПД «Сирена»
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
- 7.5.4 Классификация алгоритмов маршрутизации
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
- 7.5.8 Показатели качества маршрутизации
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
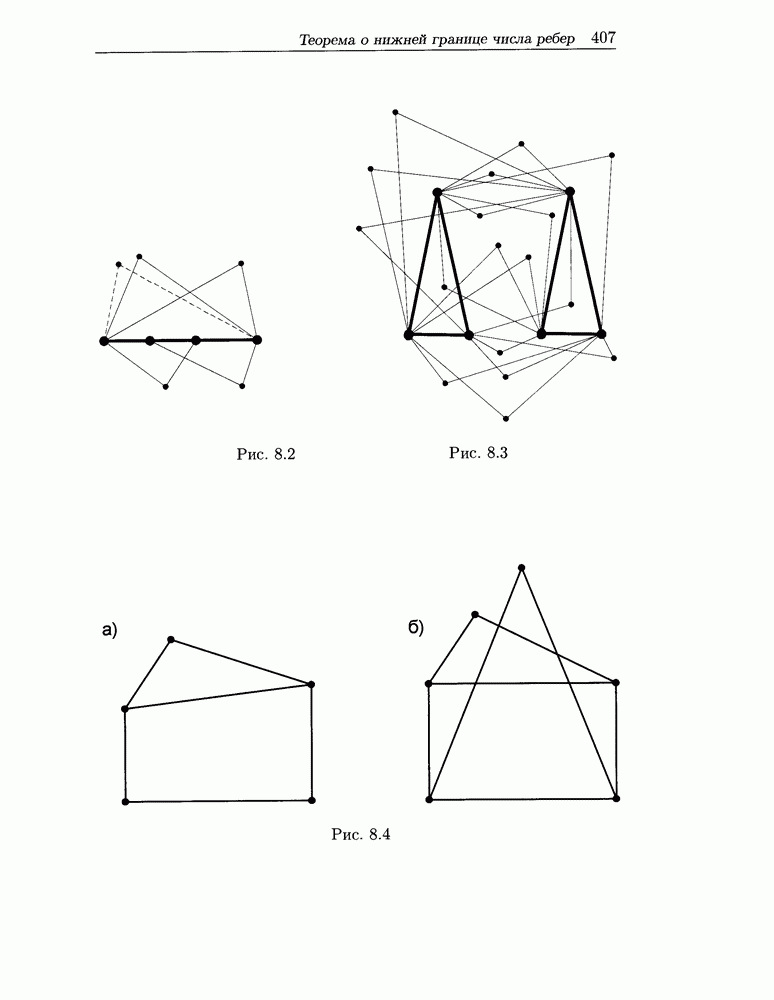
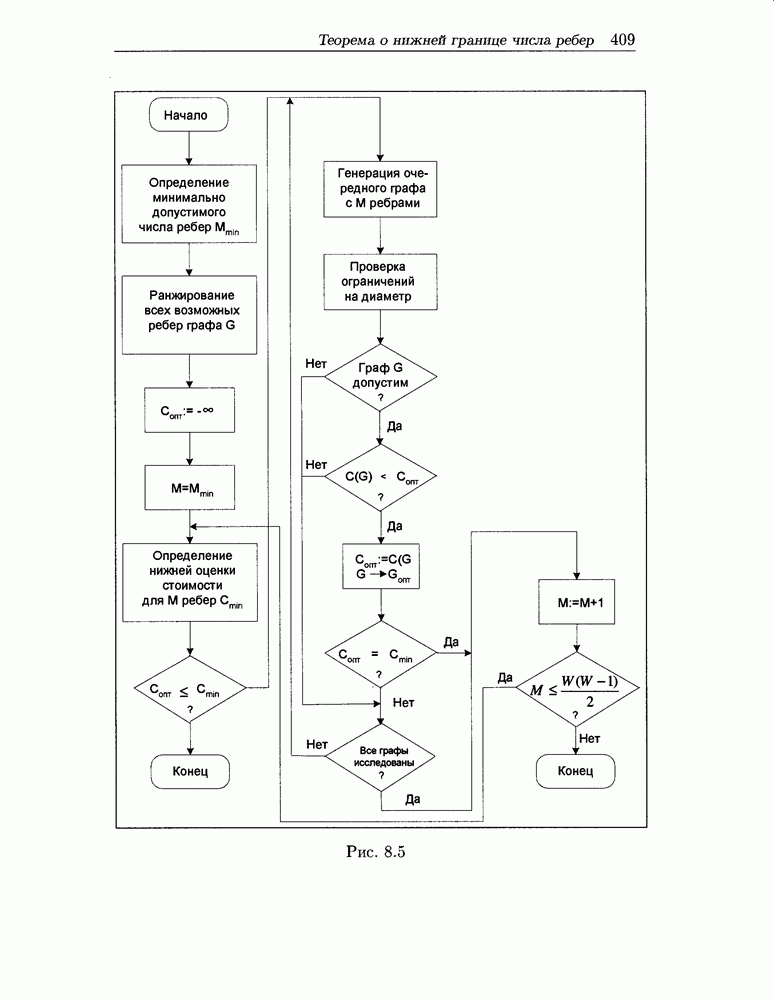
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
- 9.1 Состояние и перспективы развития беспроводных радиосетей
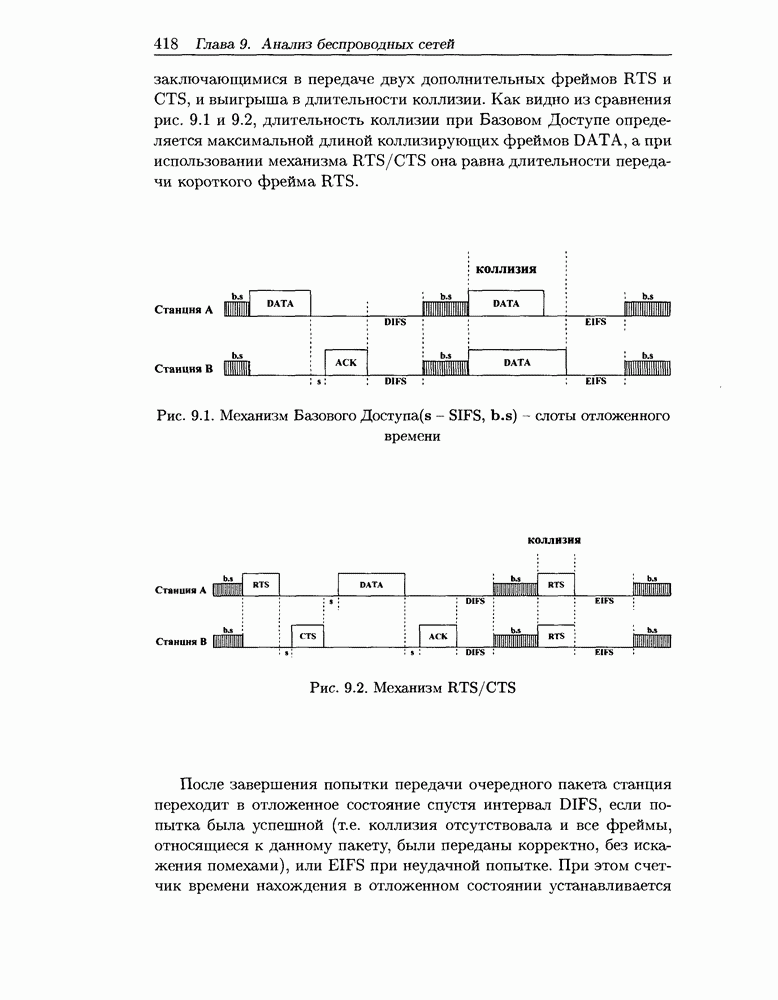
- 9.2 Схема распределенного управления
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
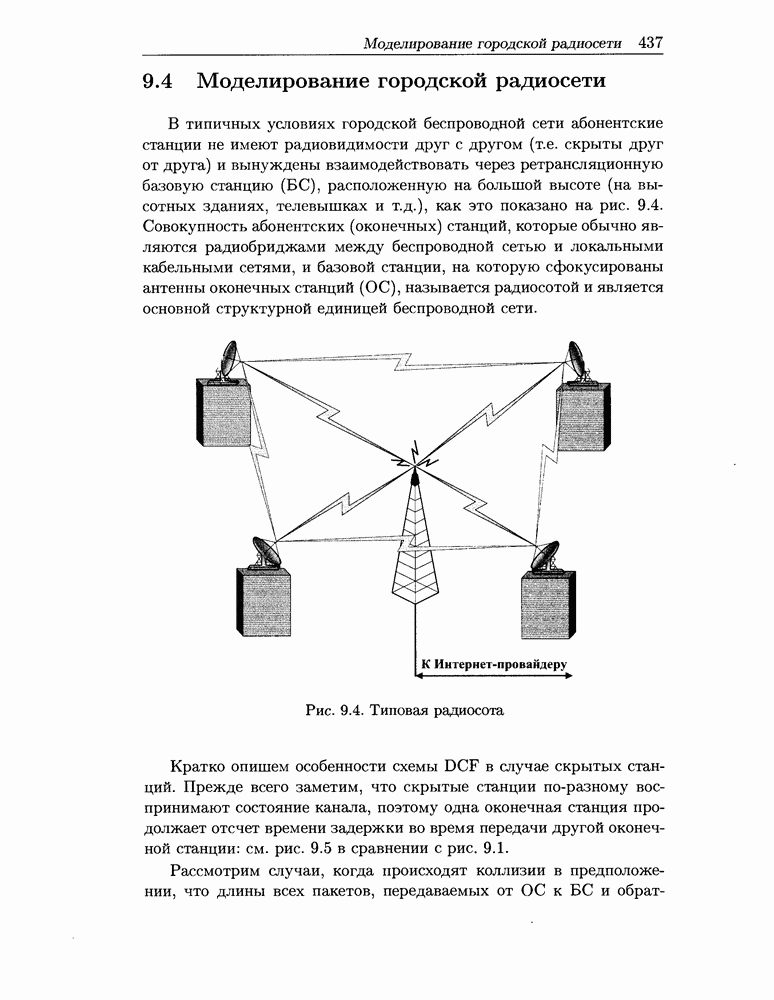
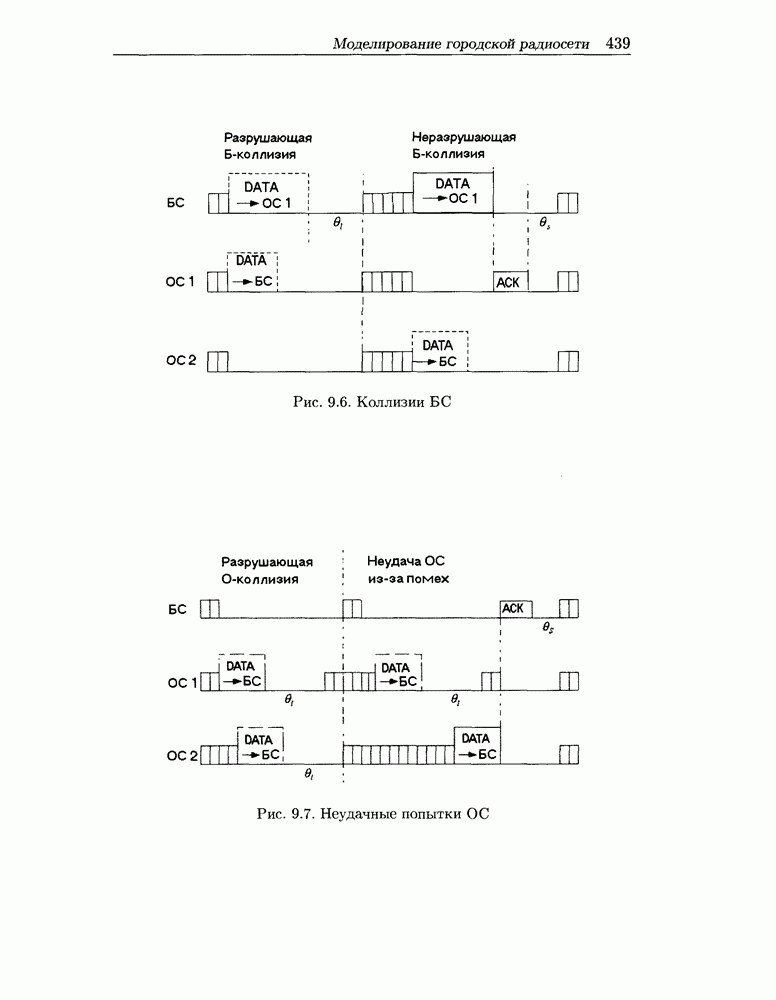
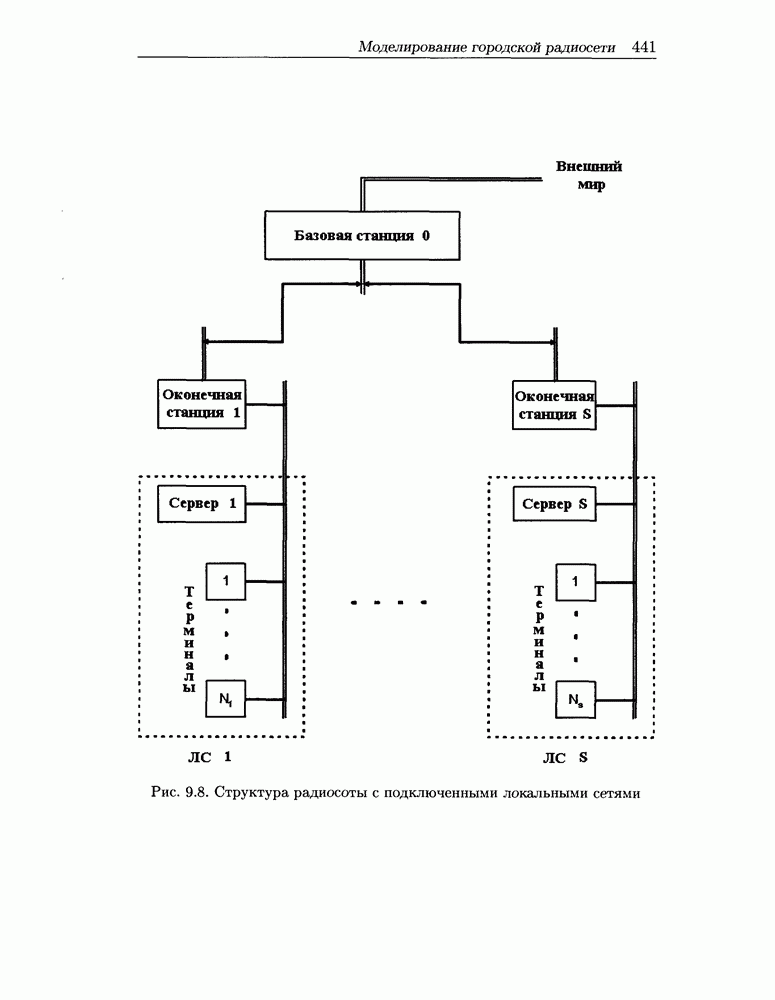
- 9.4 Моделирование городской радиосети
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
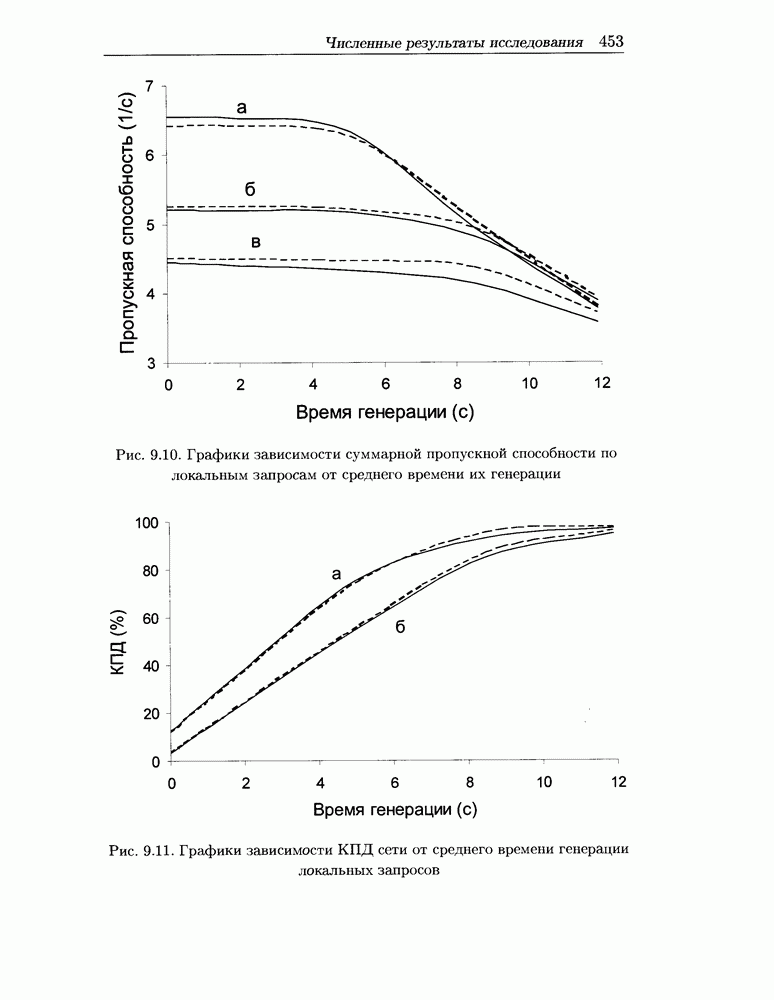
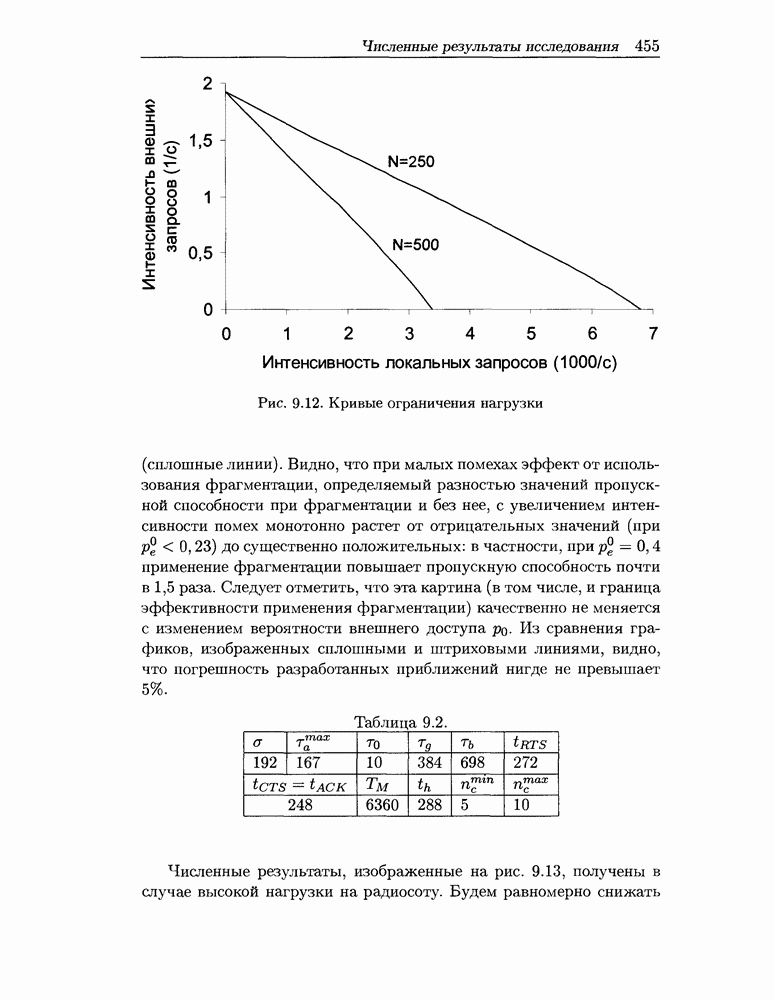
- 9.5 Численные результаты исследования городской радиосоты
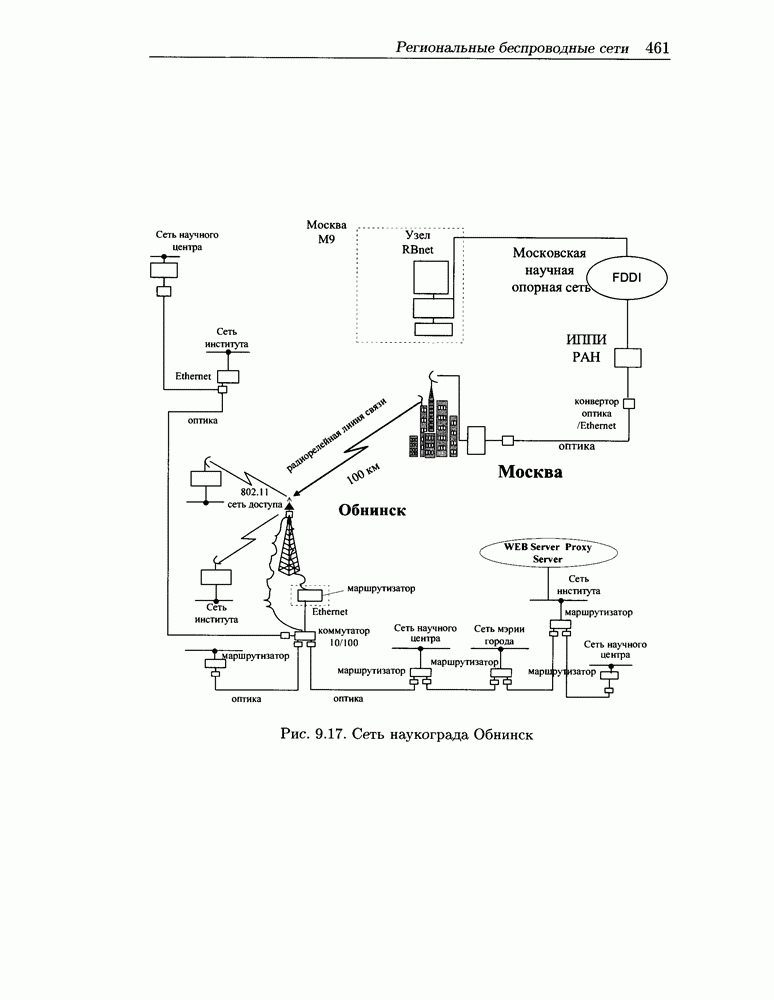
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
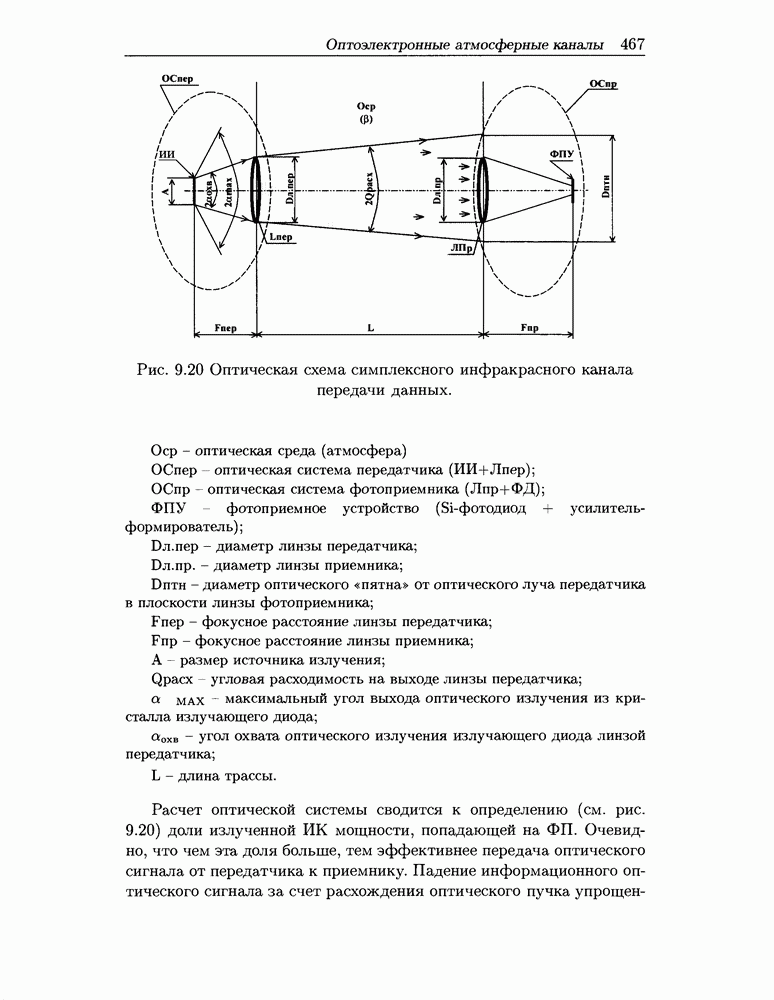
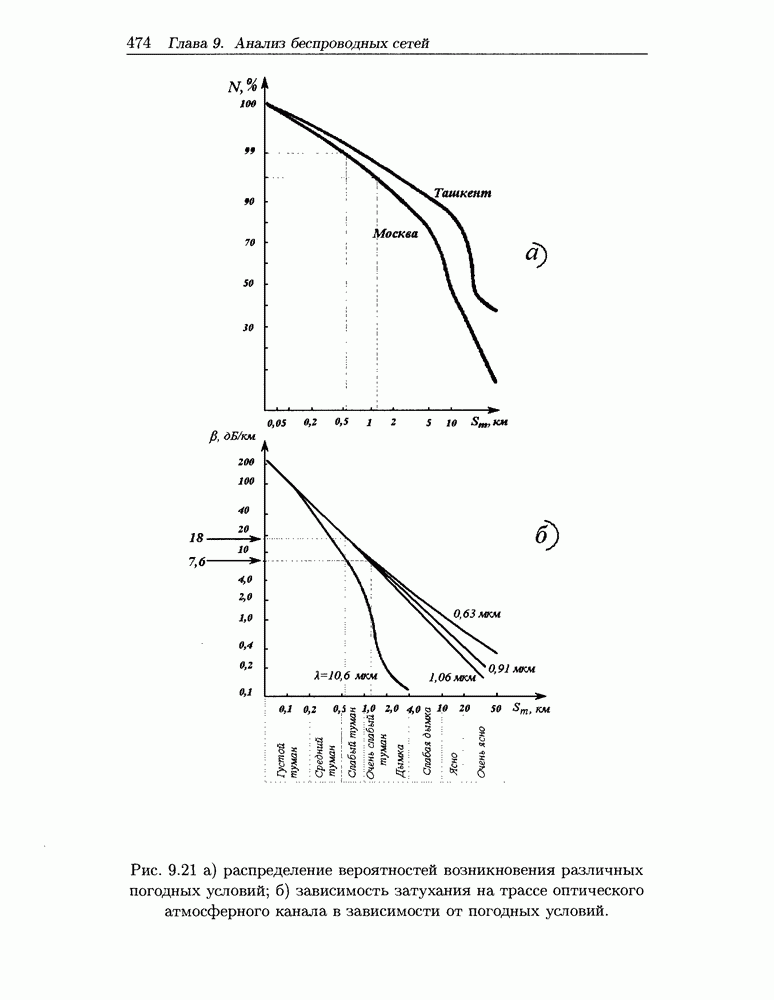
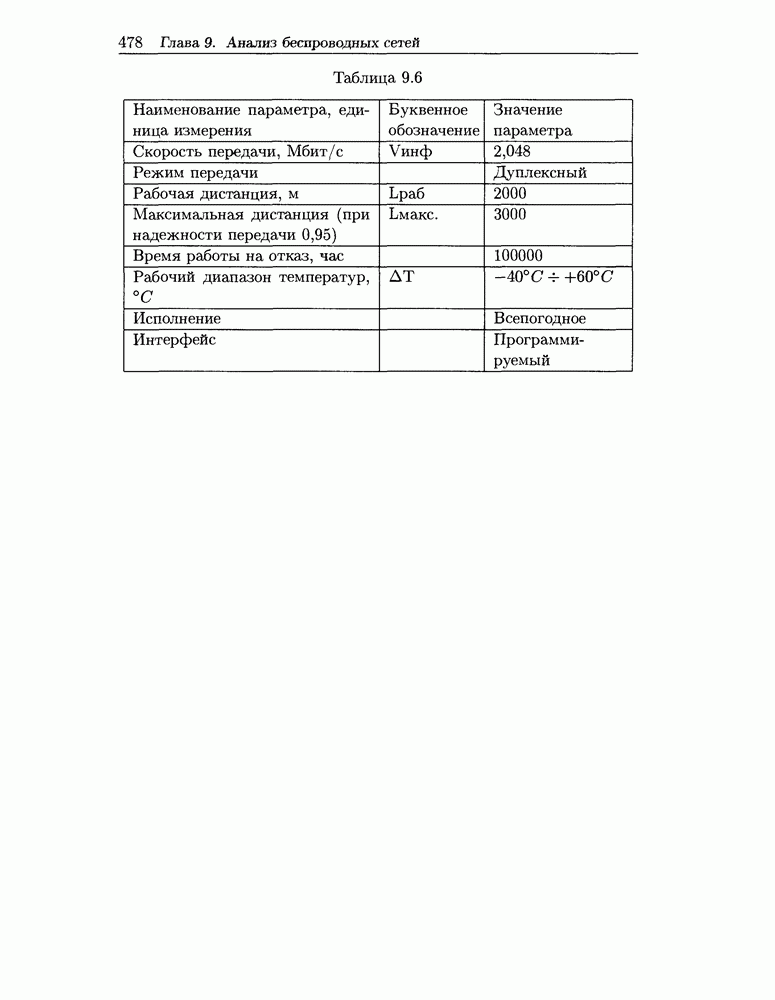
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература