| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
Описанные в п. 3.4.2 методы реконфигурации сети МО позволяют лишь частично снизить затраты времени счета и памяти, но, очевидно, не могут решить проблему точного расчета сетей МО большой размерности. Действительно, анализ базовой сети передачи данных средних размеров требует исследования модели сети МО, включающей до М = 50 центров обслуживания,  классов с числом сообщений
классов с числом сообщений  в каждом. Формулы (3.46) - (3.48) показывают, что затраты ресурсов ЭВМ, необходимые для расчета таких сетей МО, превышают возможности современных ЭВМ.
в каждом. Формулы (3.46) - (3.48) показывают, что затраты ресурсов ЭВМ, необходимые для расчета таких сетей МО, превышают возможности современных ЭВМ.
Поэтому в настоящем разделе описывается новый вычислительный алгоритм свертки в виде дерева (или просто алгоритм дерева), частичный случай которого для расчета сетей древовидной структуры приведен в [41], а общий случай разработан в [242]. В отличие от традиционного алгоритма свертки (алгоритма последовательной свертки) и метода средних значений, алгоритм дерева использует информацию о маршрутах сообщений каждого класса. Использование этой информации позволяет существенно сократить затраты времени и памяти при расчете сетей МО с большим числом центров обслуживания и классов сообщений, в которых сообщения каждого класса в среднем посещают лишь небольшую долю от имеющихся в сети центров обслуживания (свойство разряженности сети.
Если в сети, обладающей свойством разряженности, отдельные классы сообщений группируются в некоторых частях сети (свойство локализации), то сокращение времени счета и затрат памяти для реализации вычислительного алгоритма может быть еще более значительным.
Алгоритм дерева, являющийся обобщением традиционного алгоритма последовательной свертки, реализуется для замкнутых сетей МО с мультипликативной формой вероятностей состояний (3.22)

где  - нормализующая константа;
- нормализующая константа;

Нормализующая константа отыскивается с помощью вспомогательной функции  [см. формулу (3.23)], определяющей соотношение свертки
[см. формулу (3.23)], определяющей соотношение свертки

В отличие от алгоритма последовательной свертки, предусматривающего использование операции свертки (3.49) последовательно для номеров  от 1 до М, в алгоритме дерева операция свертки осуществляется с помощью бинарного дерева, для построения которого используется информация о маршрутах сообщений каждого класса. В результате этого в операции свертки участвуют множества, размерность которых меньше размерности R множеств, используемых в алгоритме последовательной свертки.
от 1 до М, в алгоритме дерева операция свертки осуществляется с помощью бинарного дерева, для построения которого используется информация о маршрутах сообщений каждого класса. В результате этого в операции свертки участвуют множества, размерность которых меньше размерности R множеств, используемых в алгоритме последовательной свертки.
Обозначим  массив номеров обслуживающих центров, которые могут посещаться сообщениями класса
массив номеров обслуживающих центров, которые могут посещаться сообщениями класса  , a Q - подмножество номеров всех обслуживающих центров сети.
, a Q - подмножество номеров всех обслуживающих центров сети.
Будем говорить, что класс  полностью покрывает Q, если
полностью покрывает Q, если  , не покрывается множеством Q, если
, не покрывается множеством Q, если  в остальных случаях частично покрывается множеством Q. Пусть
в остальных случаях частично покрывается множеством Q. Пусть  Тогда
Тогда 
Предположим, что массив  был уже получен на промежуточной стадии вычисления нормализующей константы
был уже получен на промежуточной стадии вычисления нормализующей константы  . Тогда, если часть классов из множества (1,2, либо не покрыта Q, либо полностью покрыта Q, для дальнейшего вычисления
. Тогда, если часть классов из множества (1,2, либо не покрыта Q, либо полностью покрыта Q, для дальнейшего вычисления  необходимы лишь некоторые элементы массива
необходимы лишь некоторые элементы массива  При этом объем памяти, необходимой для запоминания этих элементов, может быть значительно меньше, чем
При этом объем памяти, необходимой для запоминания этих элементов, может быть значительно меньше, чем  . Этот факт является ключевым в алгоритме дерева.
. Этот факт является ключевым в алгоритме дерева.
Разделим множество классов  по отношению к Q на три подмножества:
по отношению к Q на три подмножества:

Заметим, что для дальнейшего вычисления  необходимы только те элементы массива
необходимы только те элементы массива  индексы которых удовлетворяют условиям:
индексы которых удовлетворяют условиям:

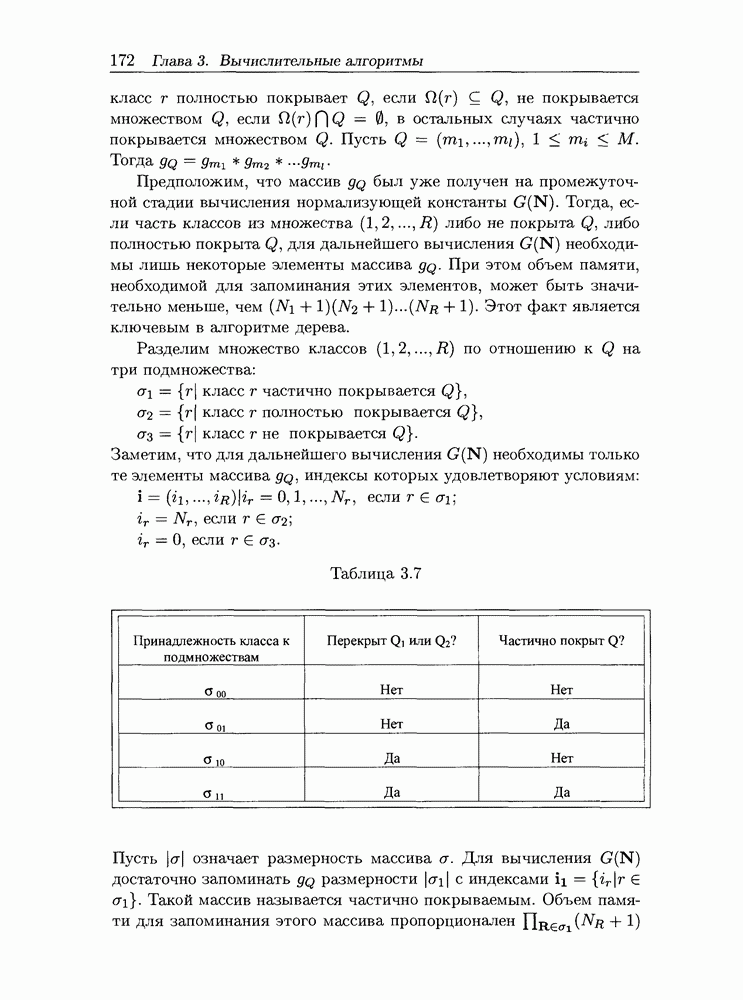
Таблица 3.7

Пусть  означает размерность массива а. Для вычисления
означает размерность массива а. Для вычисления  достаточно запоминать
достаточно запоминать  размерности
размерности  с индексами
с индексами  . Такой массив называется частично покрываемым. Объем памяти для запоминания этого массива пропорционален
. Такой массив называется частично покрываемым. Объем памяти для запоминания этого массива пропорционален  (дополнительно небольшой объем памяти требуется для запоминания элементов множества
(дополнительно небольшой объем памяти требуется для запоминания элементов множества  ).
).
Для сетей МО, обладающих свойством разряженности, экономия памяти при использовании частично покрываемых массивов вместо массивов размерности R может быть очень существенной. Языки программирования, допускающие динамическое распределение памяти (такие, как  ), позволяют эффективно использовать частично покрываемые массивы. Однако экономия памяти возможна даже при статическом распределении памяти.
), позволяют эффективно использовать частично покрываемые массивы. Однако экономия памяти возможна даже при статическом распределении памяти.
Пусть Q распадается на два подмножества:  Тогда
Тогда

Говорят, что класс  перекрыт, если он частично покрыт и
перекрыт, если он частично покрыт и  Разобьем множество классов
Разобьем множество классов  на четыре подмножества:
на четыре подмножества:  Принадлежность класса к одному из подмножеств в зависимости от его отношения к Q (частично перекрыт или нет), а также к
Принадлежность класса к одному из подмножеств в зависимости от его отношения к Q (частично перекрыт или нет), а также к  (перекрыт или нет) определяется по таблице 3.7. Для выполнения операции (3.50) необходимо
(перекрыт или нет) определяется по таблице 3.7. Для выполнения операции (3.50) необходимо

операций умножения и почти такое же количество операций сложения: количество операций сложения меньше, чем умножений, на величину 
Выражение (3.51) может использоваться как мера времени для реализации операции свертки по формуле (3.50). Таким образом, при частично покрываемых массивах операция свертки (3.50) может быть выполнена с существенной экономией памяти и времени, если имеется несколько частично покрытых классов в  .
.
При применении описанных выше соображений в алгоритме последовательной свертки можно также достигнуть некоторой экономии памяти и времени. В этом случае алгоритм начинается с подсети 1, состоящей из обслуживающего центра с номером 1, а затем последовательно «сливает» эту подсеть с другими центрами обслуживания. Когда все центры будут соединены, алгоритм заканчивает работу. Основная цель алгоритма дерева отыскать последовательность сверток («слияния»), минимизирующую число частично покрываемых классов в промежуточных подсетях, используя информацию о маршрутах сообщений. Для реализации этой цели служит бинарное дерево (рис. 3.1).

Рис. 3.1

Рис. 3.2
Обслуживающие центры сети МО размещаются в листьях бинарного дерева. Каждый узел дерева соответствует подмножеству центров обслуживания (подсети), которые сходятся к этому узлу. Таким образом, корень дерева соответствует сети в целом. Осуществим обход всех узлов дерева в соответствии с некоторым правилом. Корень дерева посещается в последнюю очередь. Промежуточный узел посещается только после обхода всех узлов нижнего уровня, сходящихся к нему. Посещение узла соответствует вычислению массива g по формуле (3.50) исходя из известных массивов g узлов нижнего уровня. При достижении корневого узла находится нормализующая константа  сети.
сети.
Заметим, что алгоритм последовательной свертки является частным случаем алгоритма дерева и соответствует дереву, представленному на рис. 3.2.
Пусть  означает подсеть, состоящую только из центра с номером
означает подсеть, состоящую только из центра с номером  - множество его частично покрываемых классов;
- множество его частично покрываемых классов;  - множество его полностью покрываемых классов. Тогда массив g подсети
- множество его полностью покрываемых классов. Тогда массив g подсети  имеет вид
имеет вид

где 
Если  то последнее произведение в (3.52) равно 1. Расчет по формуле (3.52) требует порядка
то последнее произведение в (3.52) равно 1. Расчет по формуле (3.52) требует порядка  операций умножения.
операций умножения.
Затраты времени и памяти ЭВМ, необходимые для вычисления нормализующей константы  по алгоритму дерева, зависят от последовательности слияния подсетей, которая определяется конфигурацией дерева, расположением обслуживающих центров в листьях дерева и порядком обхода дерева.
по алгоритму дерева, зависят от последовательности слияния подсетей, которая определяется конфигурацией дерева, расположением обслуживающих центров в листьях дерева и порядком обхода дерева.
В настоящее время не решена задача оптимального построения дерева, минимизирующего затраты памяти и времени ЭВМ. Однако найдены эффективные эвристические подходы для решения этой задачи.
Алгоритм дерева использует две процедуры. Первая из них, называемая препроцессором, применяется для построения дерева; вторая реализует основные функции алгоритма - обход дерева и свертку массивов. Процедура построения дерева требует значительно меньше памяти и времени ЭВМ, чем реализация операций свертки. Препроцессор позволяет получить точные априорные оценки объема памяти и времени, необходимые для расчета конкретной сети МО. Указанные оценки позволяют осуществлять сравнение с другими вычислительными алгоритмами и, что не менее важно, определять возможность использования данного класса ЭВМ для реализации алгоритма (не превышают ли требования алгоритма, например, объемов оперативной памяти ЭВМ).
Как уже отмечалось, возможны различные способы построения бинарного дерева. Однако все эти способы имеют общие черты, основанные на следующем базовом алгоритме.
Алгоритм 1. Основная процедура построения дерева.
Инициализация.
Делать, пока существуют две подсети:
выполнить слияние;
отсортировать подсети согласно критерию размера;
выделить две подсети для слияния по критерию стоимости; слить две подсети в одну;
Конец;
Конец.
Первоначально имеется М подсетей, каждая из которых соответствует центру обслуживания. Алгоритм определения последовательности слияния состоит в следующем. Во-первых, определяются отношения между подсетями.
Такое отношение существует, если множество частично покрываемых классов одной подсети принадлежит множеству частично покрываемых классов другой подсети. Подсети, между которыми существует такое отношение, сливаются. В противном случае для слияния выбираются две подсети на основании критерия, условно названного стоимостью. Выбор облегчается первичной сортировкой в соответствии с критерием размера. Указанный критерий определяется следующим образом.
Пусть Q - массив подмножества номеров центров обслуживания;  - множество его частично покрываемых классов. Тогда вес Q определяется выражением
- множество его частично покрываемых классов. Тогда вес Q определяется выражением

где  определяет число элементов, имеющихся в множестве А, но отсутствующих в В. Первый кандидат для слияния выбирается по минимальному весу, следующий - по критерию стоимости. Стоимость слияния двух подсетей А и В вычисляется следующим образом. Для любого
определяет число элементов, имеющихся в множестве А, но отсутствующих в В. Первый кандидат для слияния выбирается по минимальному весу, следующий - по критерию стоимости. Стоимость слияния двух подсетей А и В вычисляется следующим образом. Для любого  если
если  то цена класса равна
то цена класса равна  если
если  , то цена класса равна -2, если
, то цена класса равна -2, если  то цена класса равна -1. Очевидно, что выбор подсети меньшей стоимости делает алгоритм слияния более эффективным.
то цена класса равна -1. Очевидно, что выбор подсети меньшей стоимости делает алгоритм слияния более эффективным.
Далее рассмотрим один из возможных конкретных алгоритмов построения дерева, в соответствии с которым первоначально каждый центр обслуживания представляет собой подсеть нижнего уровня дерева и осуществляется наращивание дерева по одному уровню за каждый шаг.
Алгоритм 2.
Инициализация.
Для каждого уровня дерева от листьев к корню делать: сортировать подсети по весу в порядке убывания; пометить все подсети;
Делать пока остались помеченные подсети:
выбрать подсеть с максимальным весом в качестве первого кандидата к слиянию;
выбрать из оставшихся помеченных подсетей другого кандидата для слияния с минимальной стоимостью;
осуществить процедуру слияния выбранных двух подсетей.
Конец.
Конец.
Конец.
Для построенного дерева препроцессор вычисляет необходимые объемы памяти и времени. Время вычисления  складывается из времени расчета массива
складывается из времени расчета массива  для листьев дерева и времени реализации
для листьев дерева и времени реализации  слияний. Объем памяти для расчета
слияний. Объем памяти для расчета  совпадает с объемом памяти, необходимой для запоминания массивов
совпадает с объемом памяти, необходимой для запоминания массивов  . Число массивов
. Число массивов  , одновременно сохраняемых при расчете
, одновременно сохраняемых при расчете  зависит от порядка обхода дерева. Например, при использовании алгоритма 2 максимальное число одновременно запоминаемых массивов равно
зависит от порядка обхода дерева. Например, при использовании алгоритма 2 максимальное число одновременно запоминаемых массивов равно  . Однако заметим, что массивы имеют различные размеры, поэтому число одновременно запоминаемых массивов неоднозначно определяет требуемый объем памяти.
. Однако заметим, что массивы имеют различные размеры, поэтому число одновременно запоминаемых массивов неоднозначно определяет требуемый объем памяти.
После того как вычислена нормализующая константа, можно перейти к расчету других характеристик сети. Например, пропускная способность центра  для сообщений класса
для сообщений класса  в соответствии с (3.32) имеет вид
в соответствии с (3.32) имеет вид

Для расчета средней длины очереди сообщений  класса в
класса в  центре по формуле (3.35) необходимо предварительно рассчитывать маргинальные вероятности
центре по формуле (3.35) необходимо предварительно рассчитывать маргинальные вероятности  определяемые из (3.29) как
определяемые из (3.29) как

Нормализующие константы  входящие в последние выражения, вычисляются с помощью соответствующих модификаций бинарного дерева [242]. В частности,
входящие в последние выражения, вычисляются с помощью соответствующих модификаций бинарного дерева [242]. В частности,  отыскивается из исходного дерева для сети МО с числом сообщений, определяемым вектором
отыскивается из исходного дерева для сети МО с числом сообщений, определяемым вектором  , а для расчета
, а для расчета  используется бинарное дерево, отличающееся от исходного отсутствием центра обслуживания с номером
используется бинарное дерево, отличающееся от исходного отсутствием центра обслуживания с номером  .
.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
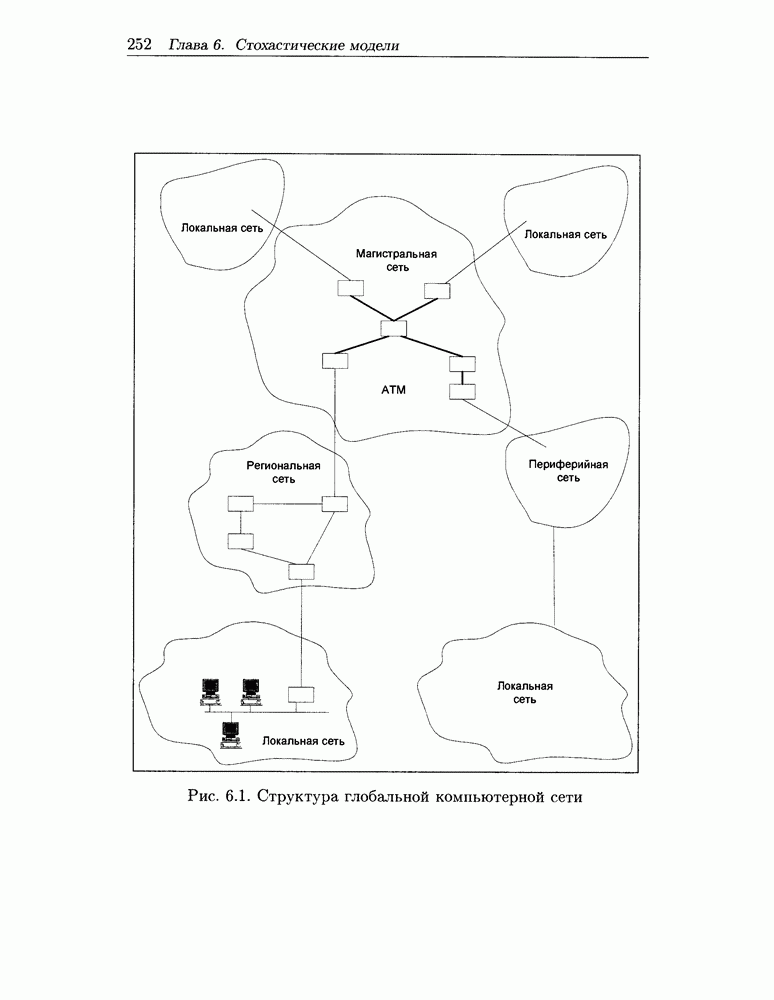
- 6.1.1 Структура компьютерных сетей
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
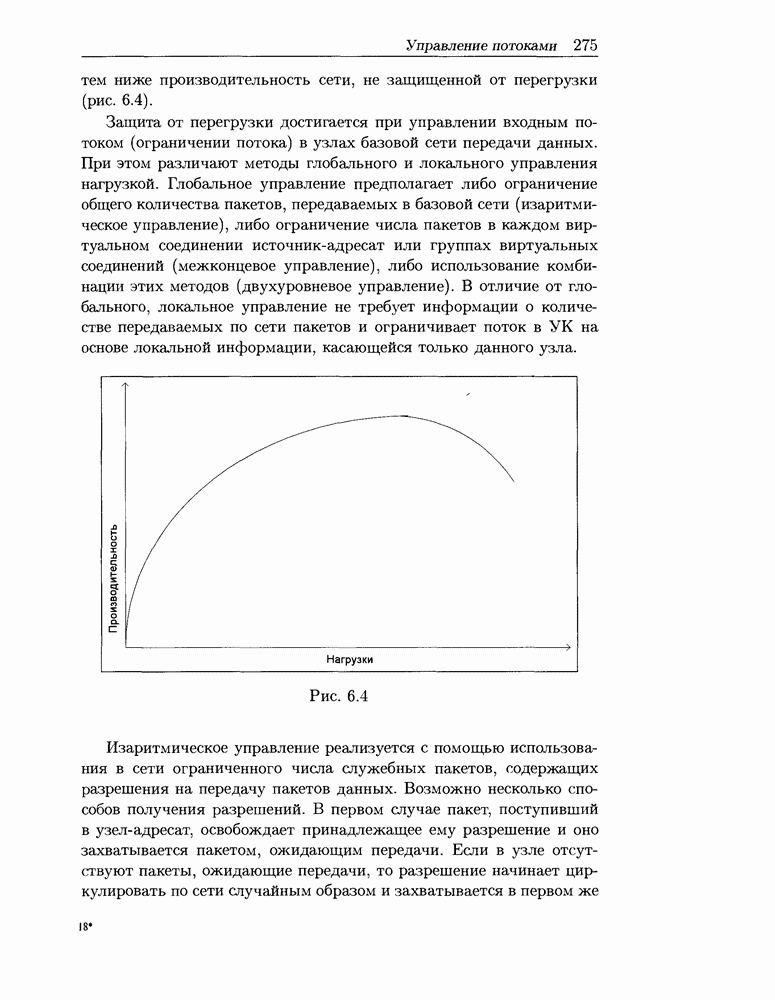
- 6.3 Управление потоками в сети пакетной коммутации
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
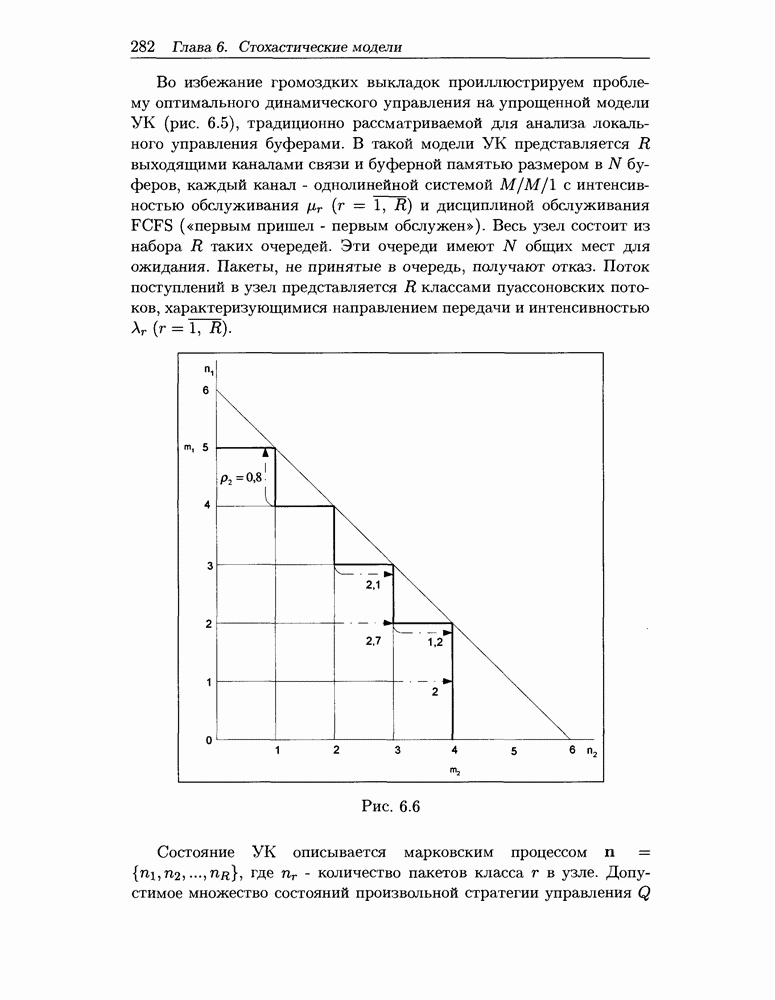
- 6.3.3 Локальное управление буферами
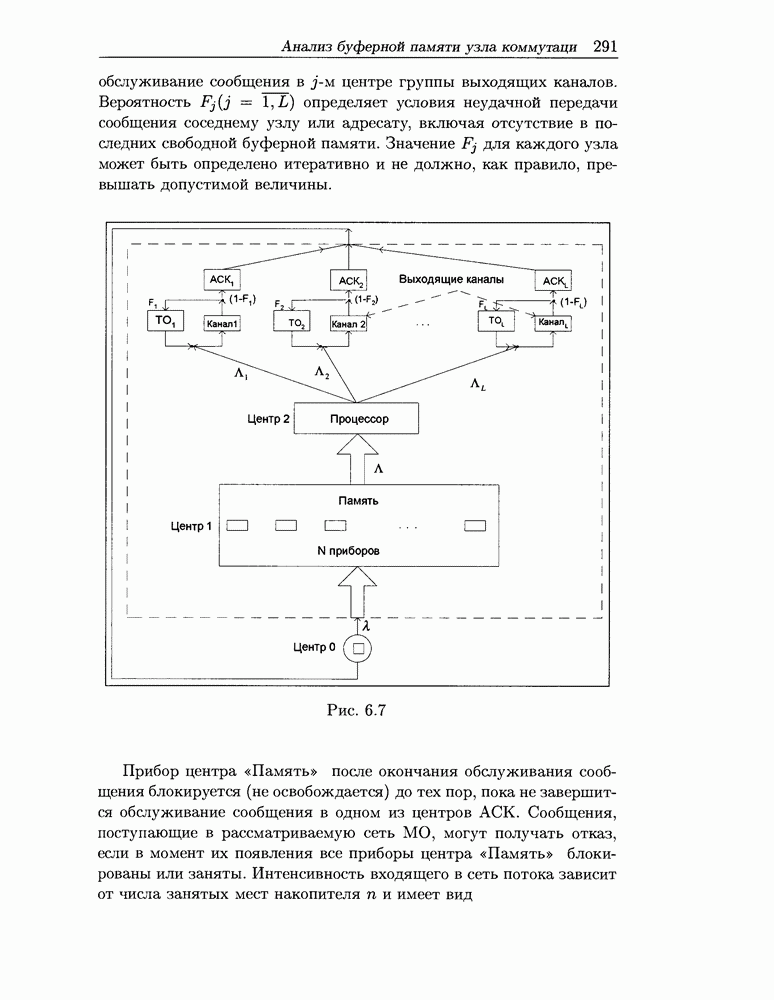
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
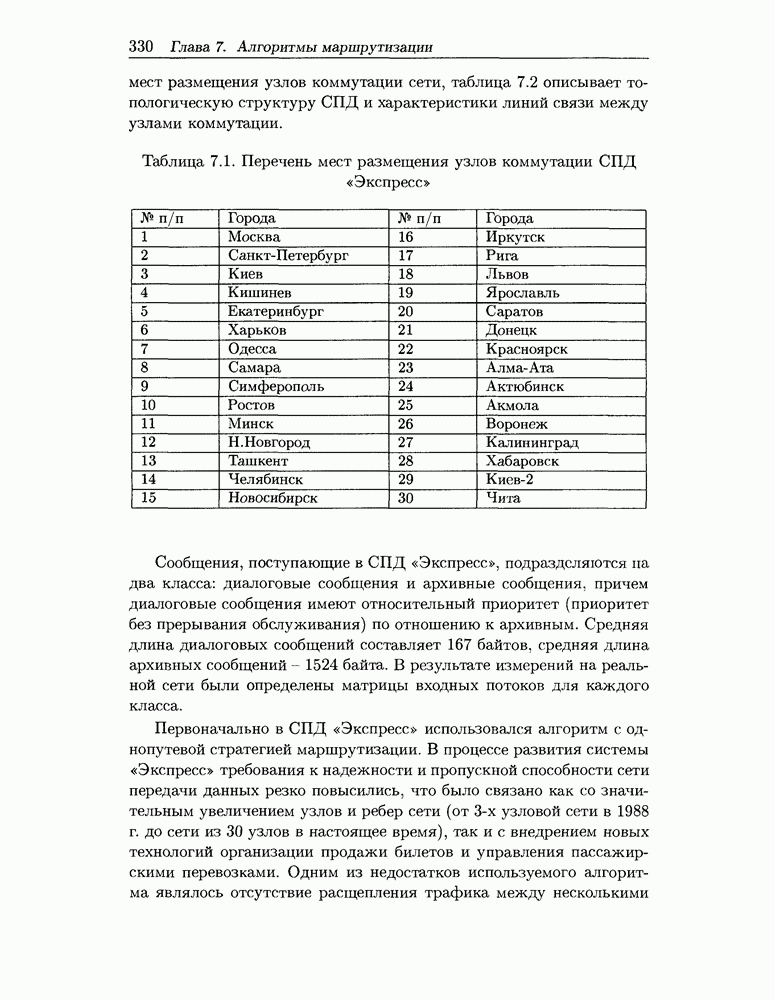
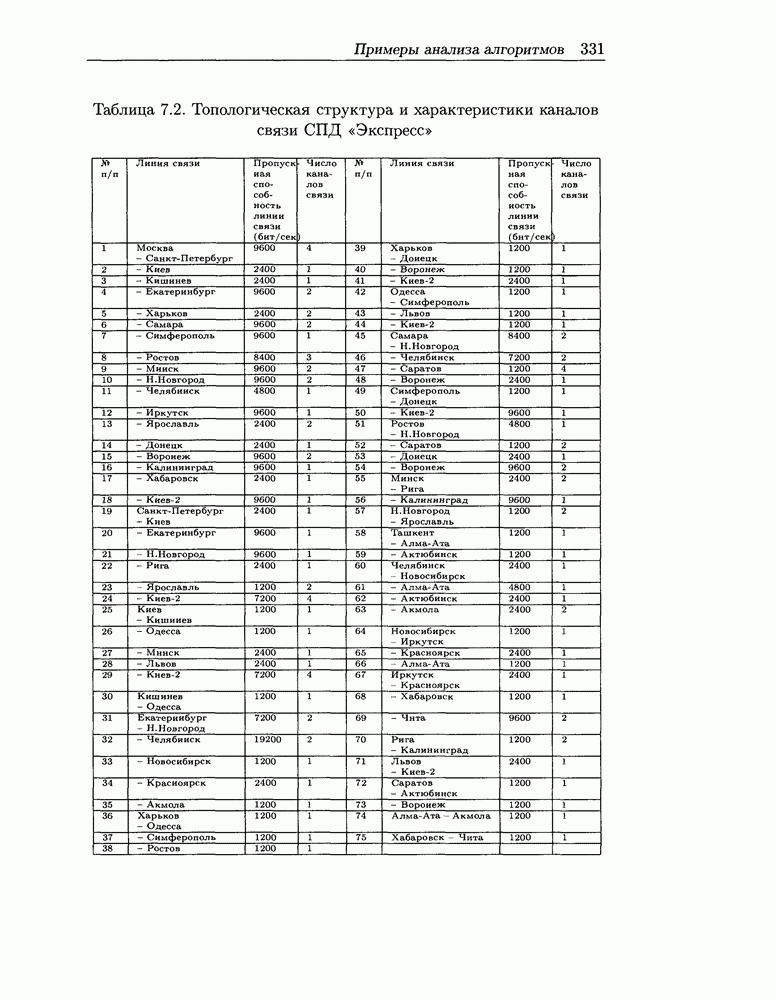
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
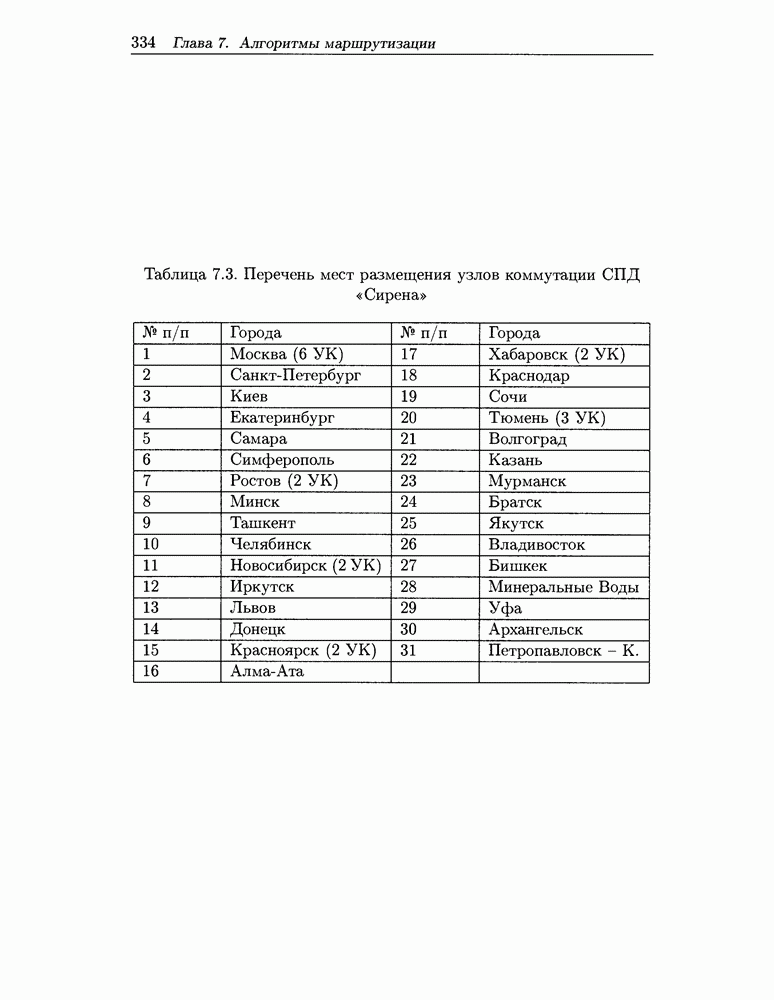
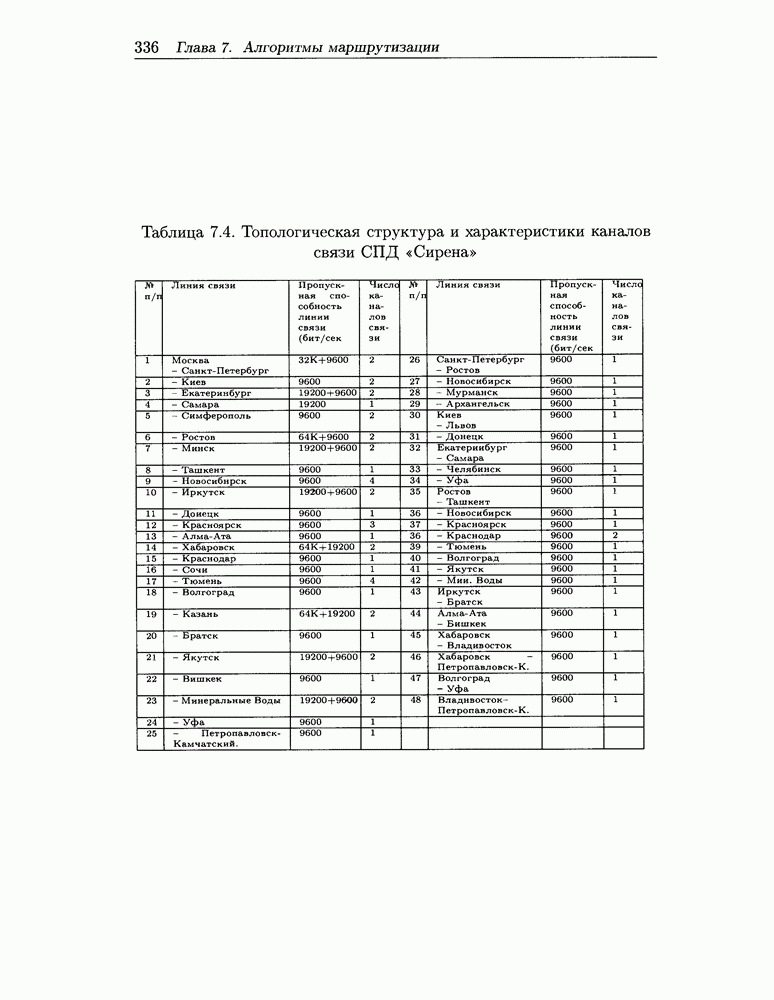
- 7.4.2 Анализ развития СПД «Сирена»
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
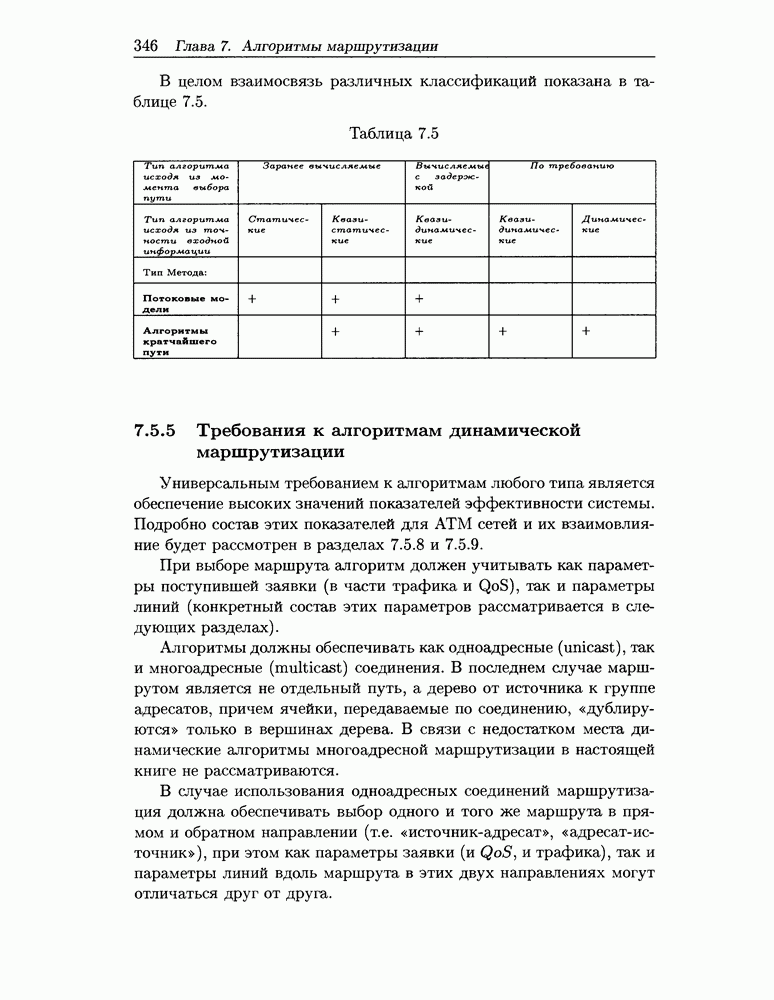
- 7.5.4 Классификация алгоритмов маршрутизации
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
- 7.5.8 Показатели качества маршрутизации
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
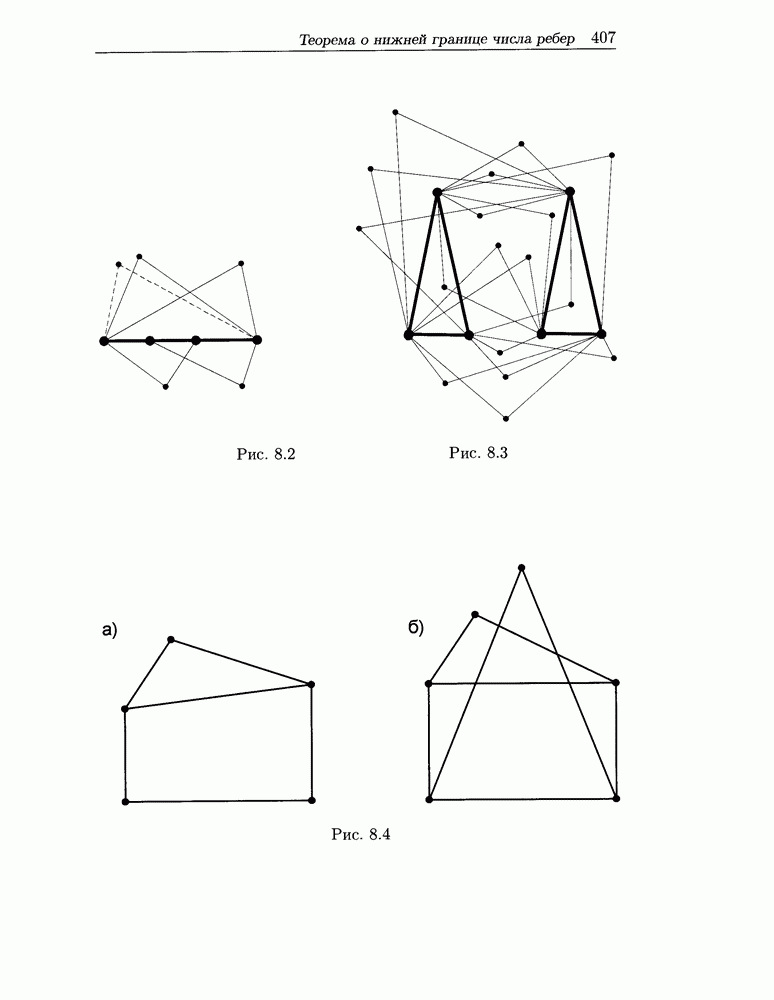
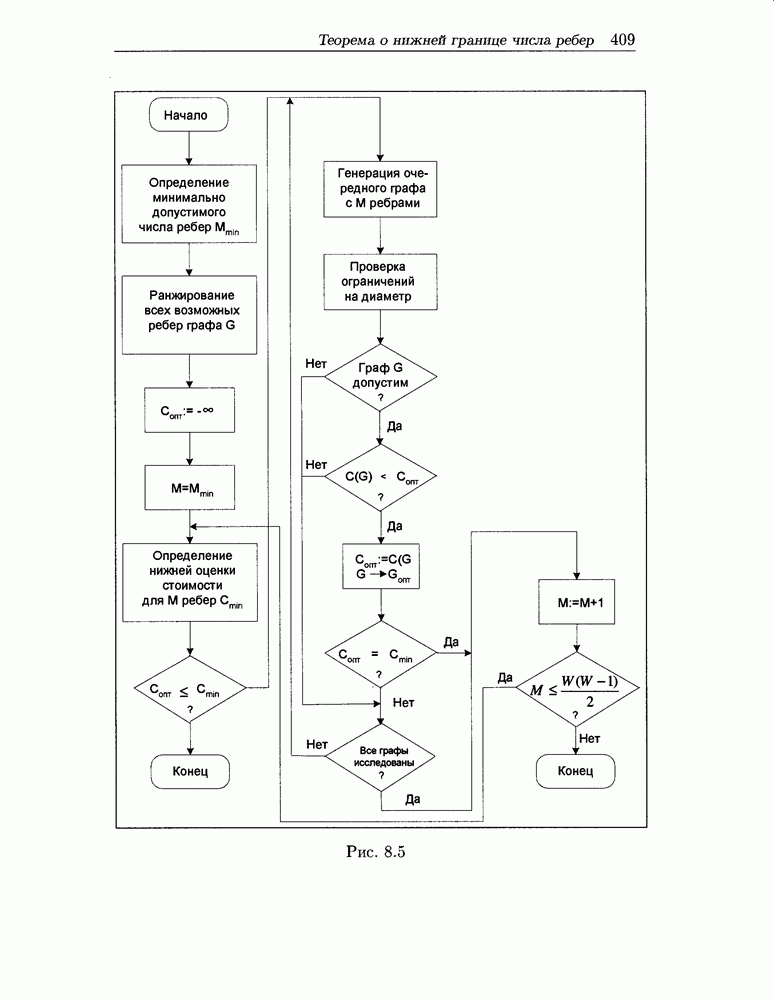
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
- 9.1 Состояние и перспективы развития беспроводных радиосетей
- 9.2 Схема распределенного управления
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
- 9.4 Моделирование городской радиосети
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
- 9.5 Численные результаты исследования городской радиосоты
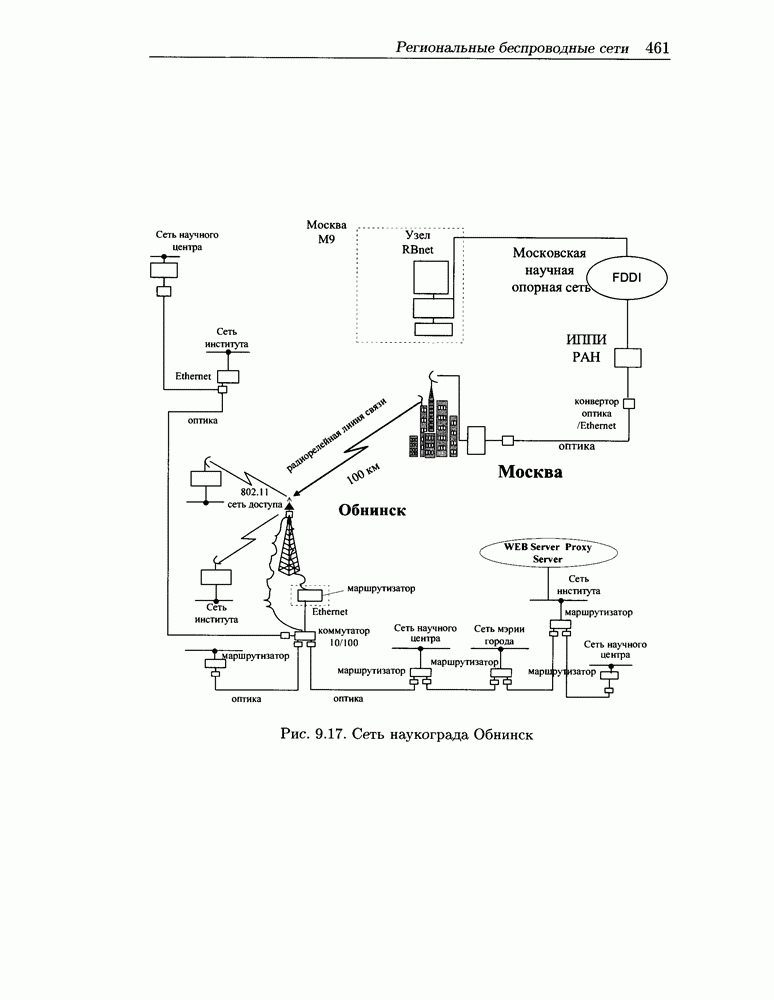
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
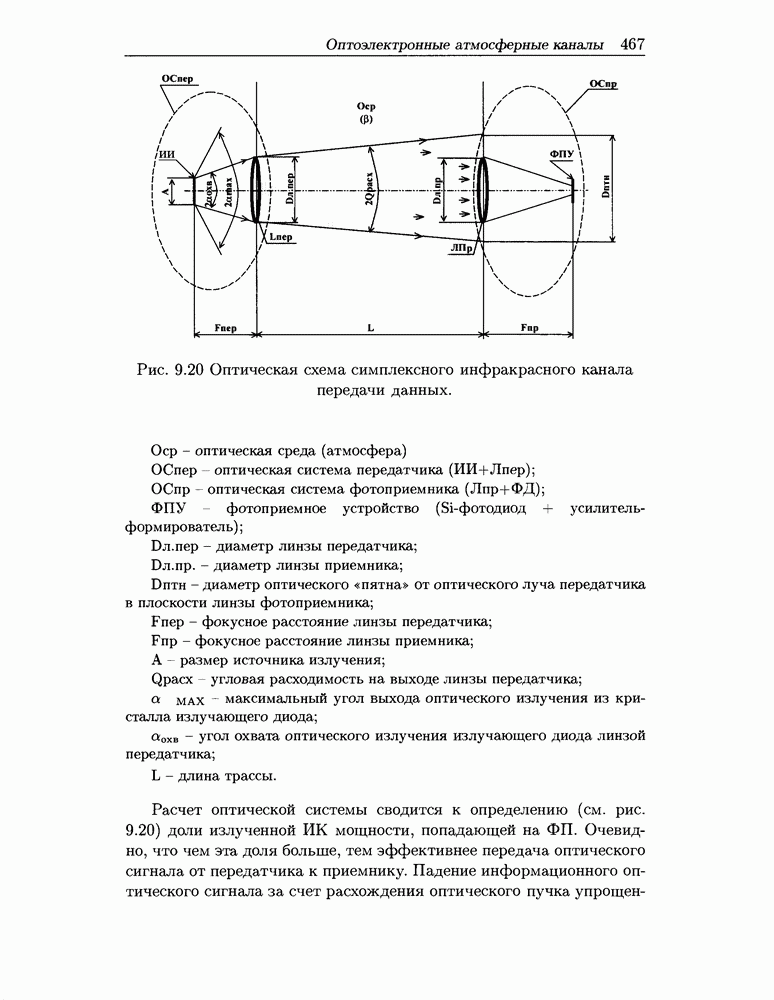
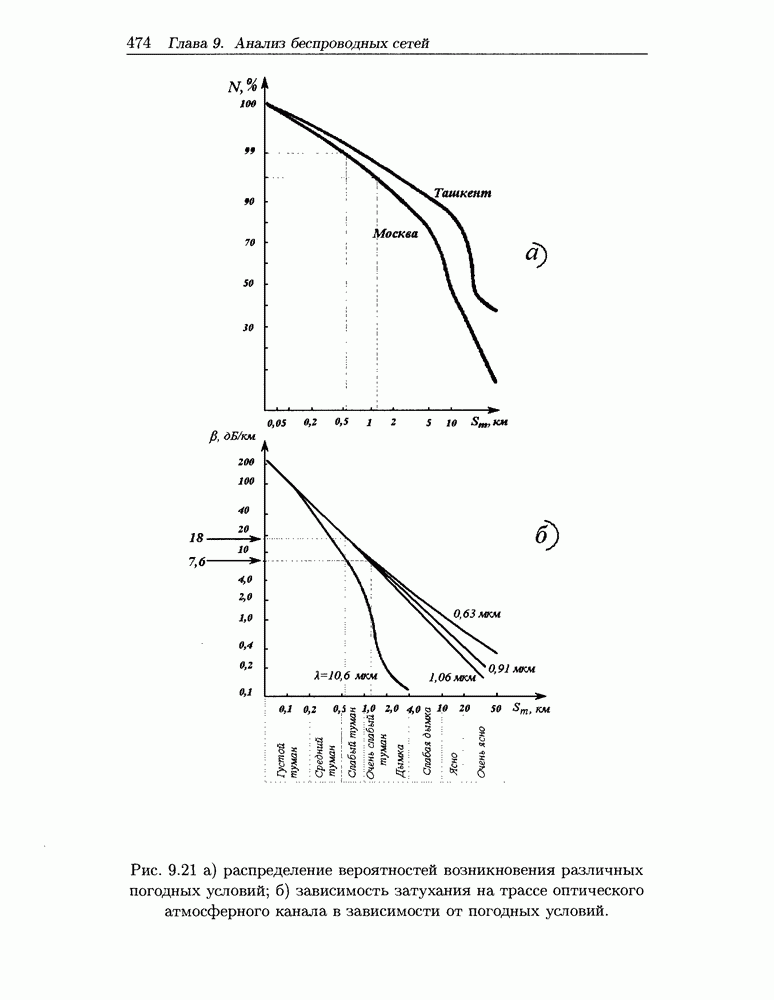
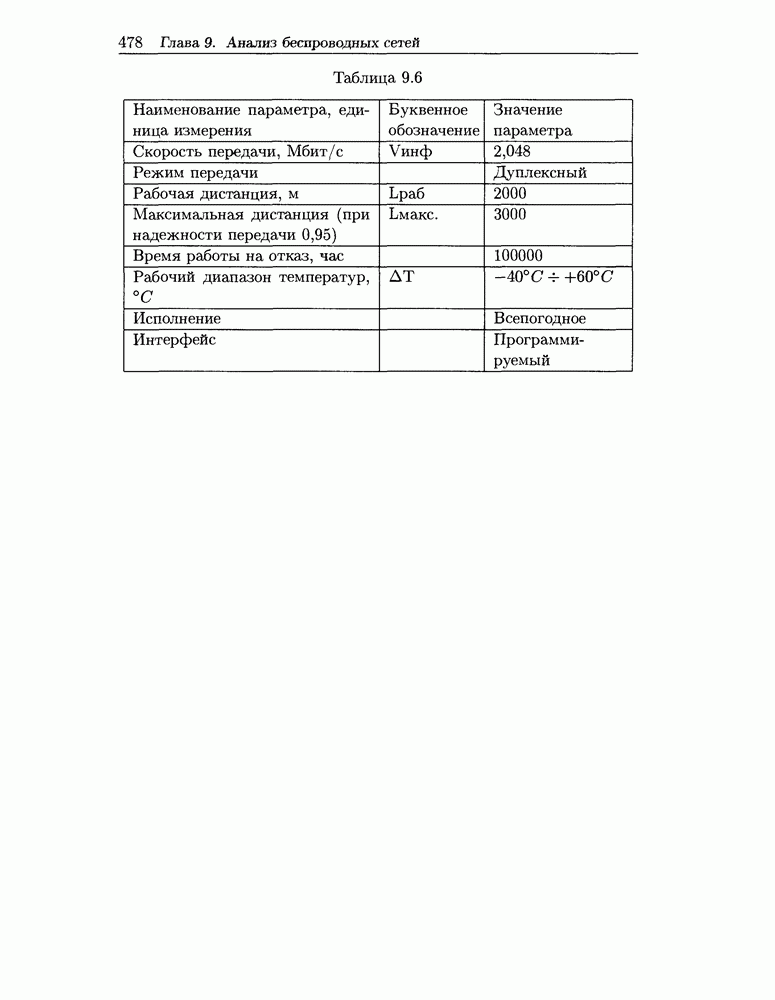
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература