| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
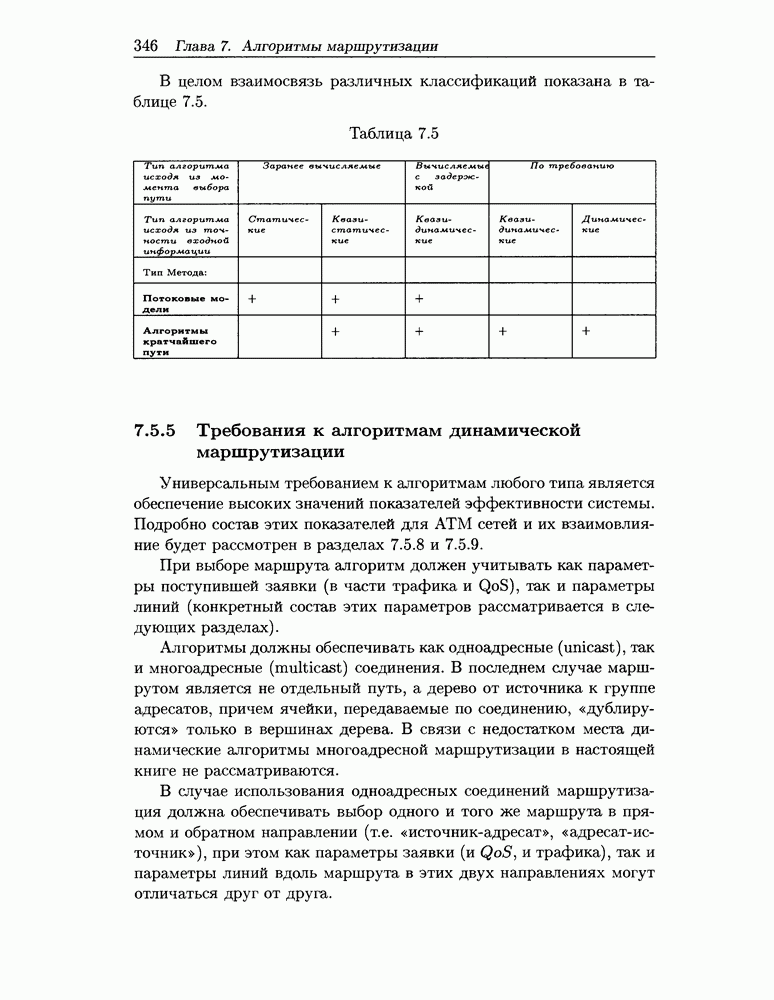
9.4.2 Аналитический метод оценки пропускной способности
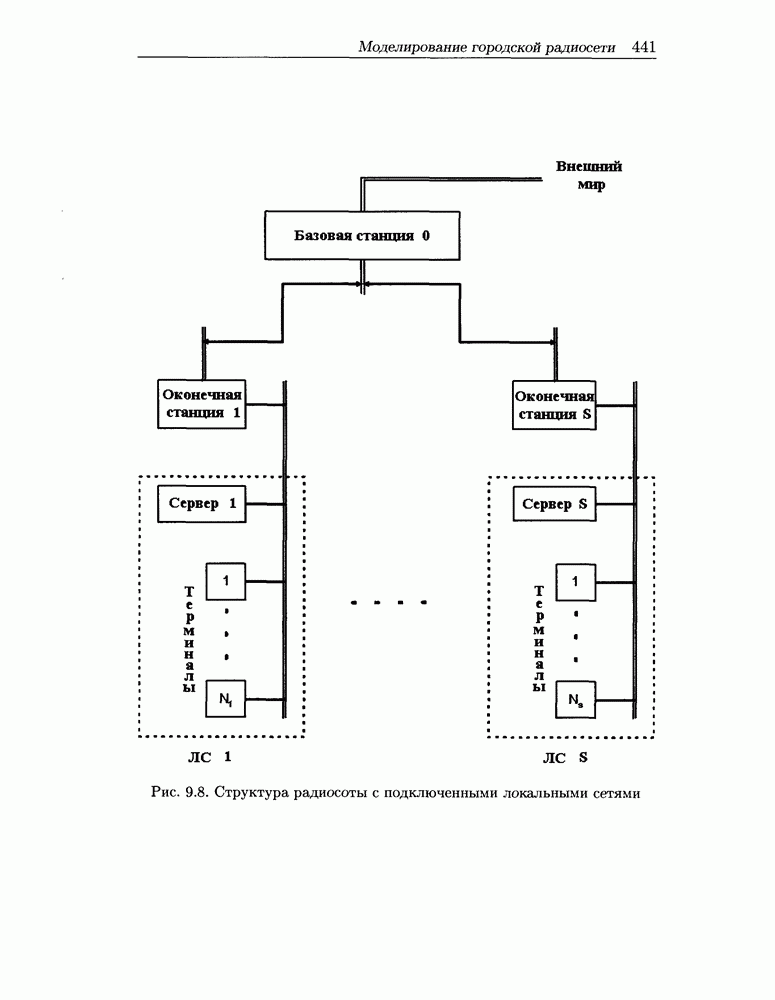
Итак, рассмотрим радиосоту на рис. 9.8. Так как число терминалов в каждой локальной сети обычно велико [8,244], применим вывод из [98] о том, что при оценке пропускных способностей можно заменить конвейерную передачу (через оконечную и базовую станции) файлов-ответов на последовательную.
Тогда, пренебрегая интервалами  между поступлениями последовательных пакетов ответов (эти интервалы достаточно малы и «накладываются» на время ожидания в очереди), получаем замкнутую экспоненциальную модель, изображенную на рис. 9.9.
между поступлениями последовательных пакетов ответов (эти интервалы достаточно малы и «накладываются» на время ожидания в очереди), получаем замкнутую экспоненциальную модель, изображенную на рис. 9.9.

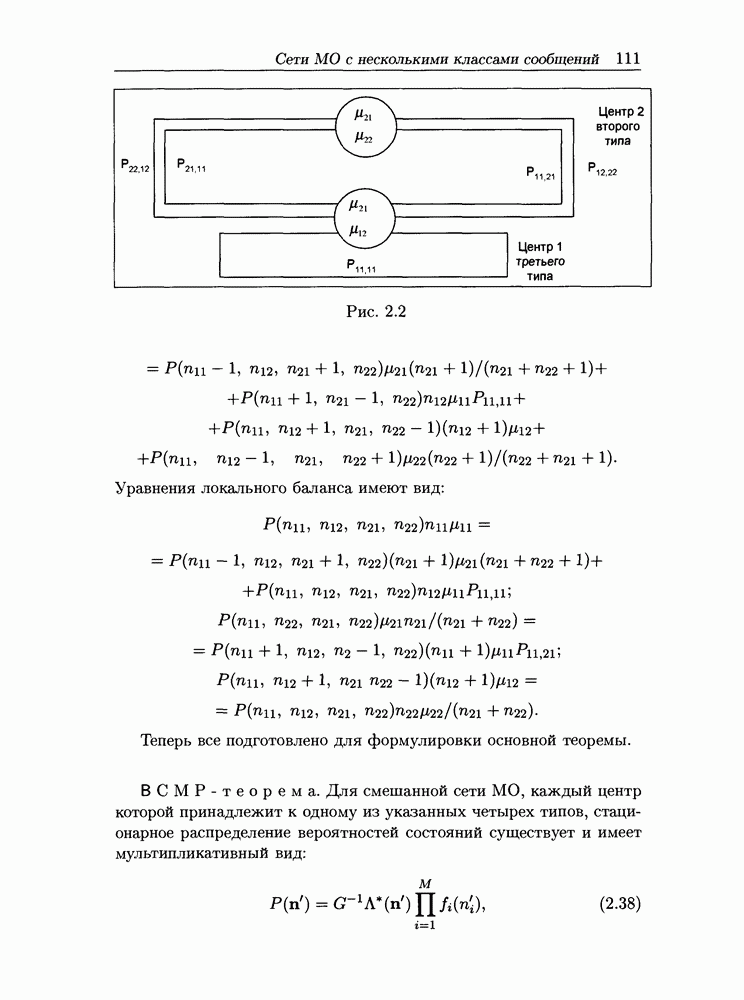
Рис. 9.9. Модель радиосоты
В этой модели циркулируют заявки  классов, разбитых на
классов, разбитых на  укрупненных классов. Из
укрупненных классов. Из  -станции
-станции  , моделирующей работу терминалов локальной сети s, исходят заявки класса
, моделирующей работу терминалов локальной сети s, исходят заявки класса  - это запросы «внешнего мира», генерация которых, согласно
- это запросы «внешнего мира», генерация которых, согласно  моделируется одноканальным устройством ОУЗ), которые после прохождения через одноканальные устройства (ОУ
моделируется одноканальным устройством ОУЗ), которые после прохождения через одноканальные устройства (ОУ  ) Омоделирующие станции, и обслуживания в требуемом сервере
) Омоделирующие станции, и обслуживания в требуемом сервере  (также
(также  -станции
-станции  ) меняют свой класс на
) меняют свой класс на  Общее число заявок укрупненного класса s (включающего классы
Общее число заявок укрупненного класса s (включающего классы  ) фиксировано и равно
) фиксировано и равно  . Ненулевые вероятности переходов между узлами модели на рис. 9.9 имеют вид: для заявок класса
. Ненулевые вероятности переходов между узлами модели на рис. 9.9 имеют вид: для заявок класса  при
при 

для заявок класса  при
при 


для заявок класса 

для заявок класса  при
при 

В этих выражениях  Для всех
Для всех 
Предположив известными средние времена передачи пакета  каждой станцией
каждой станцией  из этой модели с помощью метода, изложенного в
из этой модели с помощью метода, изложенного в  находим для каждой станции s: искомые пропускные способности
находим для каждой станции s: искомые пропускные способности  по запросам из каждой локальной сети
по запросам из каждой локальной сети  и по внешним запросам
и по внешним запросам  а также вероятности
а также вероятности  отсутствия очередей к каждой из станций
отсутствия очередей к каждой из станций  При большом числе терминалов
При большом числе терминалов  точные методы оказываются чрезмерно ресурсоемкими и значения этих показателей целесообразно определять из следующих асимптотических приближений [9,236]:
точные методы оказываются чрезмерно ресурсоемкими и значения этих показателей целесообразно определять из следующих асимптотических приближений [9,236]:

где коэффициенты посещения  имеют вид:
имеют вид:

а значения  находятся из системы уравнений
находятся из системы уравнений

с ограничениями  для всех s.
для всех s.
Кроме того, из значений  имеем [40] интенсивности поступления пакетов для передачи на станцию
имеем [40] интенсивности поступления пакетов для передачи на станцию  , где
, где  - интенсивности поступления соответственно пакетов-запросов и пакетов-ответов, определяемые выражениями
- интенсивности поступления соответственно пакетов-запросов и пакетов-ответов, определяемые выражениями

Теперь на основе этих показателей будем искать значения Та. Предположим:
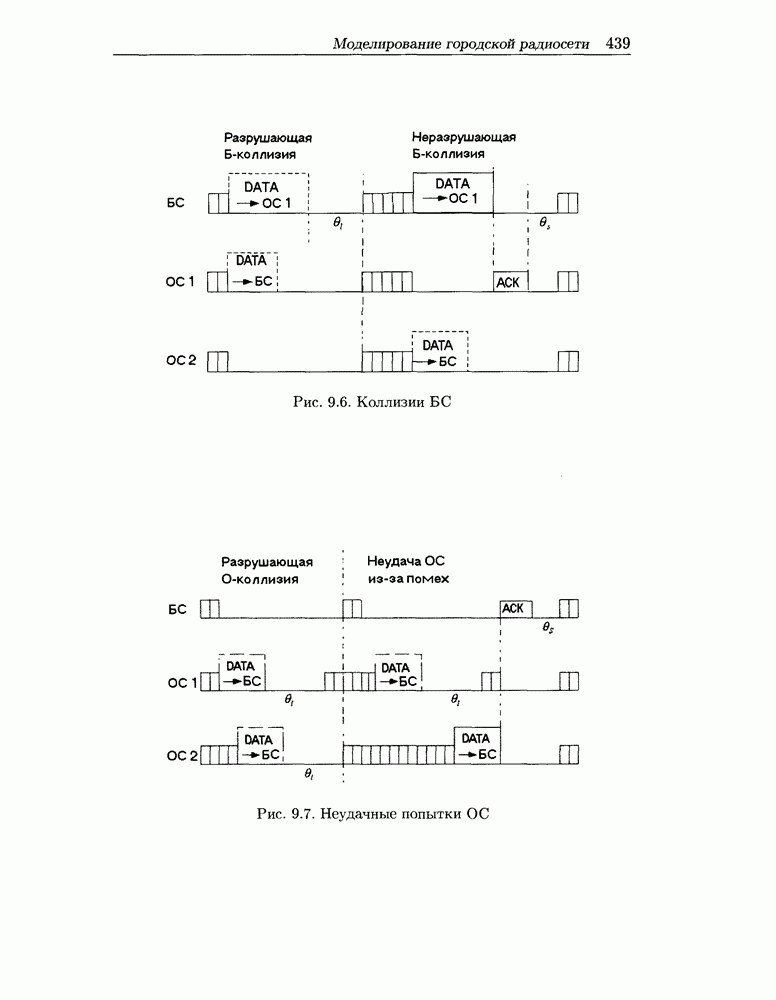
1) механизм слежения за эфиром абсолютно надежен;
2) длина всех пакетов одинакова, так что каждый из них состоит из  фрагментов, а время передачи любого фрейма DATA
фрагментов, а время передачи любого фрейма DATA  и вероятность его искажения помехами соответственно равны
и вероятность его искажения помехами соответственно равны

3) для передачи всех пакетов используются фреймы RTS и CTS (что рекомендуется стандартом IEEE 802.11 в случае «скрытых» станций), так что отсутствуют коллизии фреймов DATA;
4) число попыток передачи пакета не ограничено;
5) при подсчете тайм-аутов и  используются (вместо
используются (вместо  ) реальные значения
) реальные значения  времени распространения сигнала между оконечной станцией s и базовой станцией.
времени распространения сигнала между оконечной станцией s и базовой станцией.
Кроме того, не будем учитывать потери от коллизирующих фреймов RTS в части бесполезного занятия эфира. Обозначим: то  .
.
Передача пакета может начаться только в те моменты времени, когда эфир свободен и с момента занятости эфира прошло, по крайней мере, время  или
или  Пренебрегая потерями от коллизирующих фреймов RTS в части бесполезного занятия эфира (включая интервалы
Пренебрегая потерями от коллизирующих фреймов RTS в части бесполезного занятия эфира (включая интервалы  ), долю U этих моментов времени можно приближенно оценить выражением
), долю U этих моментов времени можно приближенно оценить выражением  где доля моментов
где доля моментов  когда эфир занят передачей пакета от станции s, определяется по формулам:
когда эфир занят передачей пакета от станции s, определяется по формулам:

В этих формулах

 времена передачи соответствующих фреймов, а
времена передачи соответствующих фреймов, а  вероятности искажения помехами соответственно одного из последовательных фреймов RTS и CTS и фрейма АСК.
вероятности искажения помехами соответственно одного из последовательных фреймов RTS и CTS и фрейма АСК.
Вероятность неуспешной попытки передачи пакета от станции s равна:

где  - вероятность коллизии при передаче RTS. Найдем эту величину. Пусть передача RTS от оконечной станции s началась в момент
- вероятность коллизии при передаче RTS. Найдем эту величину. Пусть передача RTS от оконечной станции s началась в момент  Тогда коллизия с RTS от другой оконечной станции i произойдет в случае, если та начала передачу в интервале
Тогда коллизия с RTS от другой оконечной станции i произойдет в случае, если та начала передачу в интервале  для
для  (коллизия с базовой станцией) этот интервал равен
(коллизия с базовой станцией) этот интервал равен  Следовательно, предполагая (здесь и далее) пуассоновский характер распределения моментов начала передачи на интервалах свободного эфира, имеем:
Следовательно, предполагая (здесь и далее) пуассоновский характер распределения моментов начала передачи на интервалах свободного эфира, имеем:

где

Решая систему уравнений  находим
находим 
Определим среднее время пребывания станции s в состоянии отложенной передачи в расчете на один пакет, включая время возможного ожидания освобождения канала. Рассмотрим случай 1 передачи пакета, поступившего в непустую очередь. Учитывая, что очередь может быть пуста только при поступлении пакета-запроса или первого из пакетов-ответов, находим вероятность этого случая:

Исходя из (9.1), среднее отложенное время определяется по формуле

с коэффициентом  , где
, где  - суммарное отложенное время при j неудачных попытках передачи пакета, т.е.
- суммарное отложенное время при j неудачных попытках передачи пакета, т.е.

где

а вероятность того, что произошло ровно j неудачных попыток, равна

где

наконец, делитель  в (9.48) отражает тот факт, что отсчет отложенного времени ведется только при свободном эфире. Для удобства вычисления формулу (9.48) можно представить в виде:
в (9.48) отражает тот факт, что отсчет отложенного времени ведется только при свободном эфире. Для удобства вычисления формулу (9.48) можно представить в виде:

где

Рассмотрим теперь различные случаи поступления пакета в пустую очередь. Формулы (9.48) и (9.49) остаются справедливыми и в этих случаях, но с заменой коэффициента  на
на  , где
, где  - номер случая.
- номер случая.
Случай 2: станция s находится в состоянии отложенной передачи (включая интервал задержки) после своей последней передачи. Вероятность этого случая -  где
где

а коэффициент -  . В остальных случаях станция s не находится в состоянии отложенной передачи.
. В остальных случаях станция s не находится в состоянии отложенной передачи.
Случай 3: при поступлении Пакета либо эфир занят, либо не истек интервал задержки после передачи другой станции. Вероятность -

коэффициент -

Случай 4: при поступлении пакета эфир свободен и истек интервал задержки. Вероятность -  коэффициент
коэффициент 
Суммируя (с соответствующими вероятностями средние отложенные времена Та для всех случаев и учитывая (из (9.44)), что фактическое среднее время занятости эфира при передаче одного пакета станцией s примерно равно

- потери станции s из-за коллизий, находим искомое среднее время передачи пакета:

где Та определяется так же, как  но с заменой
но с заменой  на усредненный коэффициент
на усредненный коэффициент  Подставляя значения Ts в (9.39) -(9.42), получаем искомые пропускные способности.
Подставляя значения Ts в (9.39) -(9.42), получаем искомые пропускные способности.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
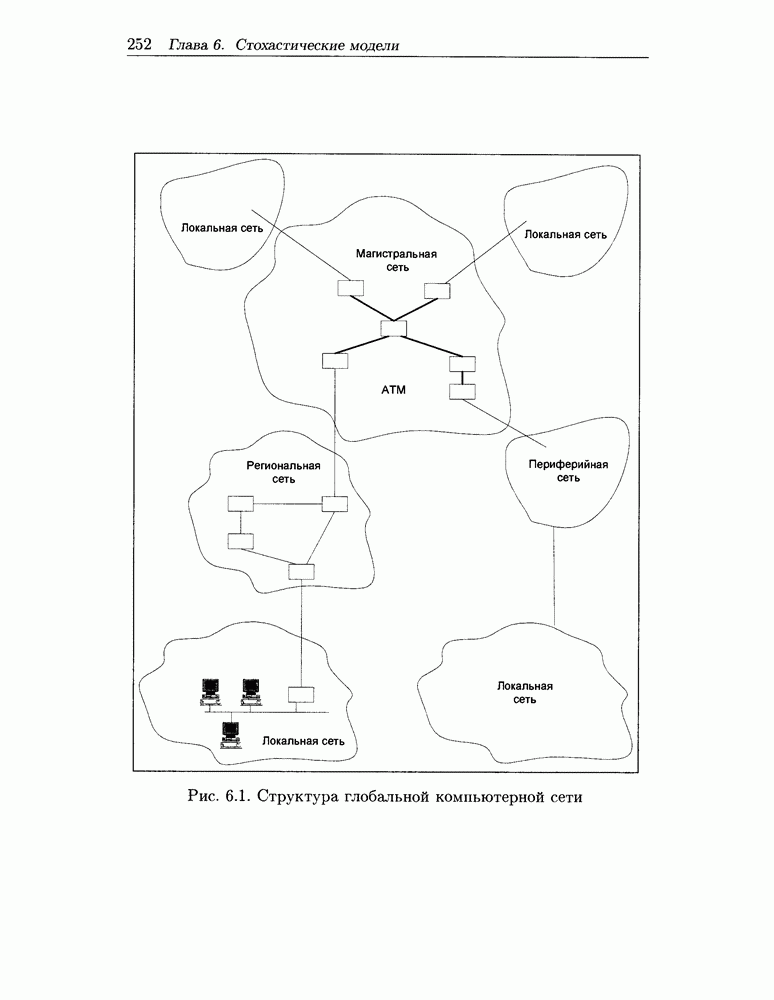
- 6.1.1 Структура компьютерных сетей
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
- 6.3 Управление потоками в сети пакетной коммутации
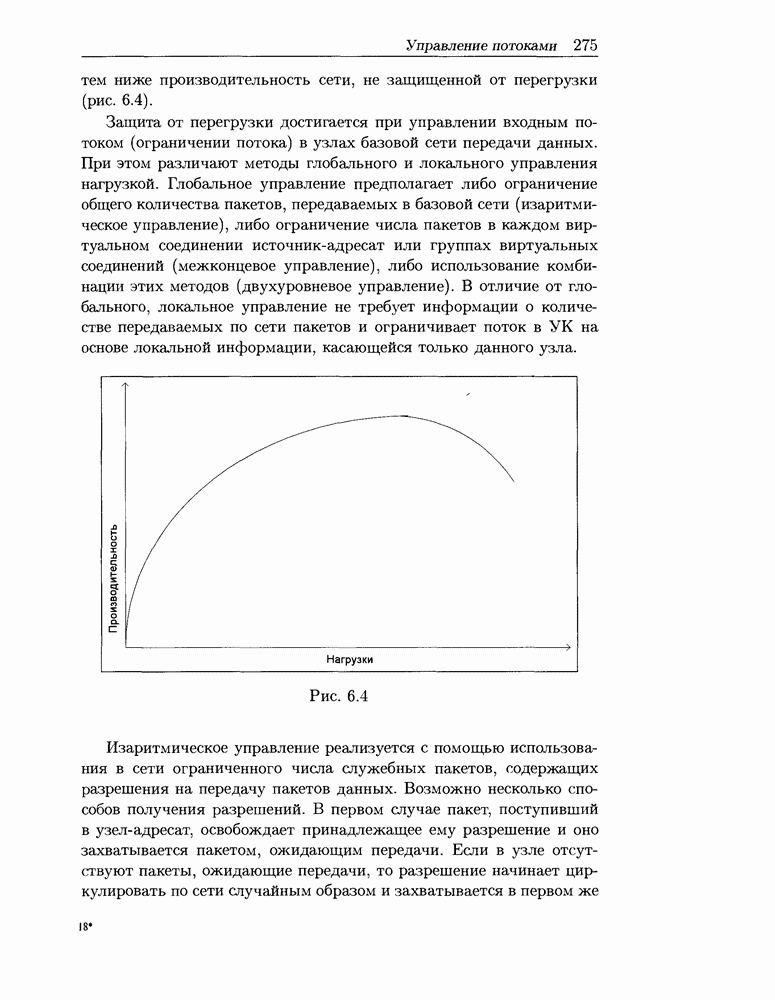
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
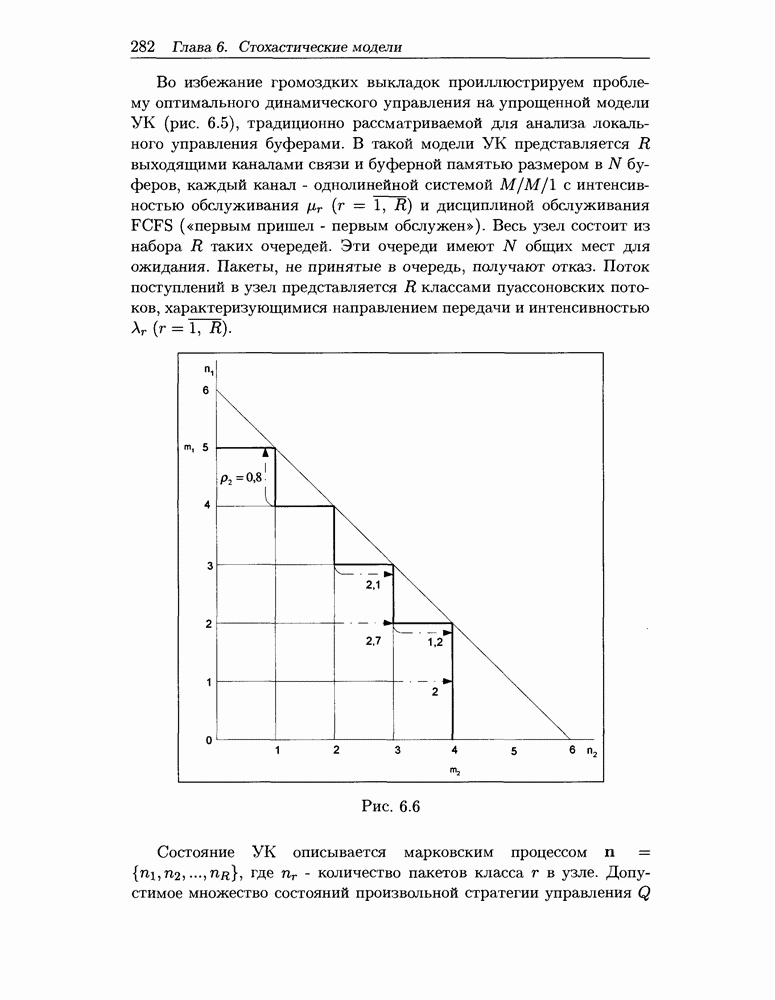
- 6.3.3 Локальное управление буферами
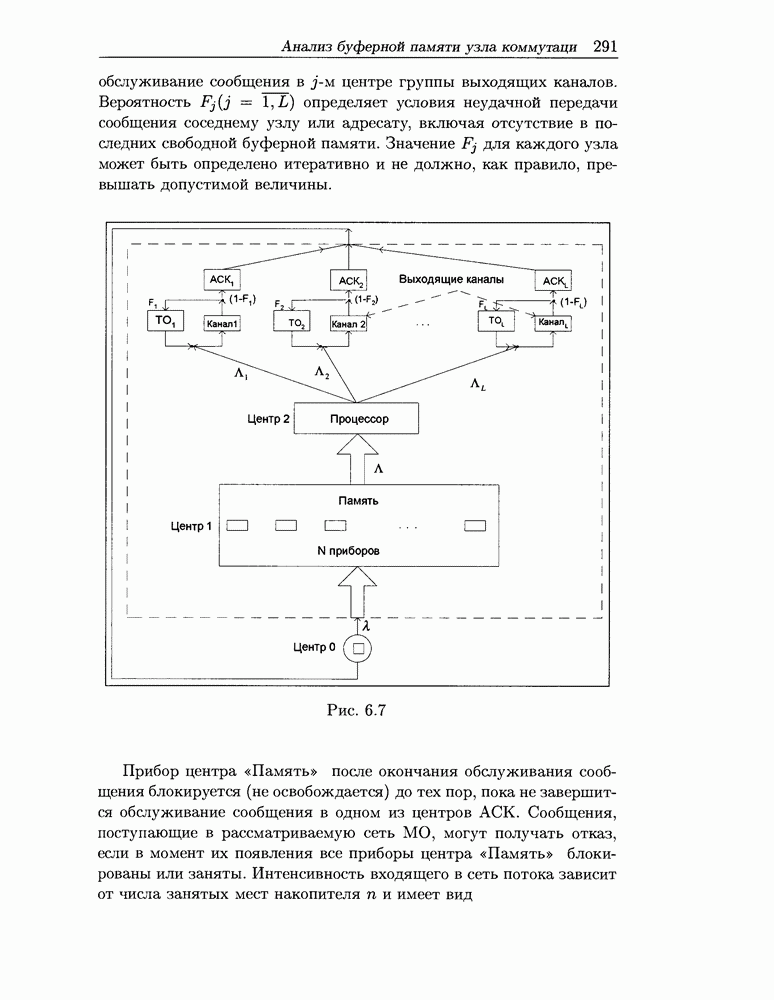
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
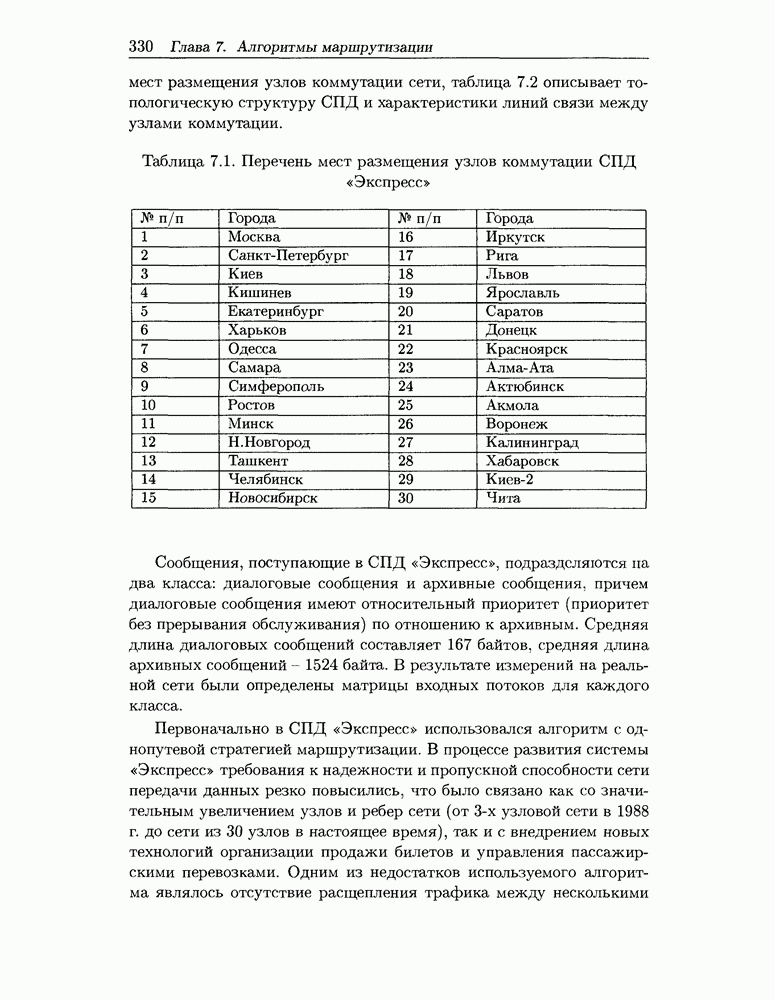
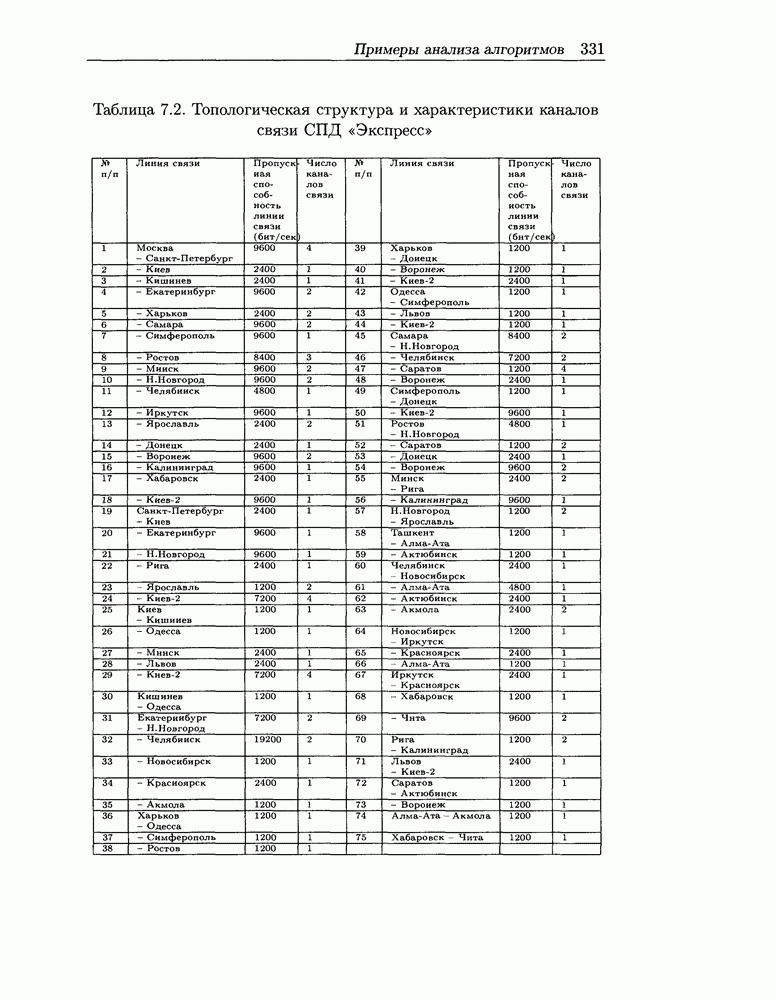
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
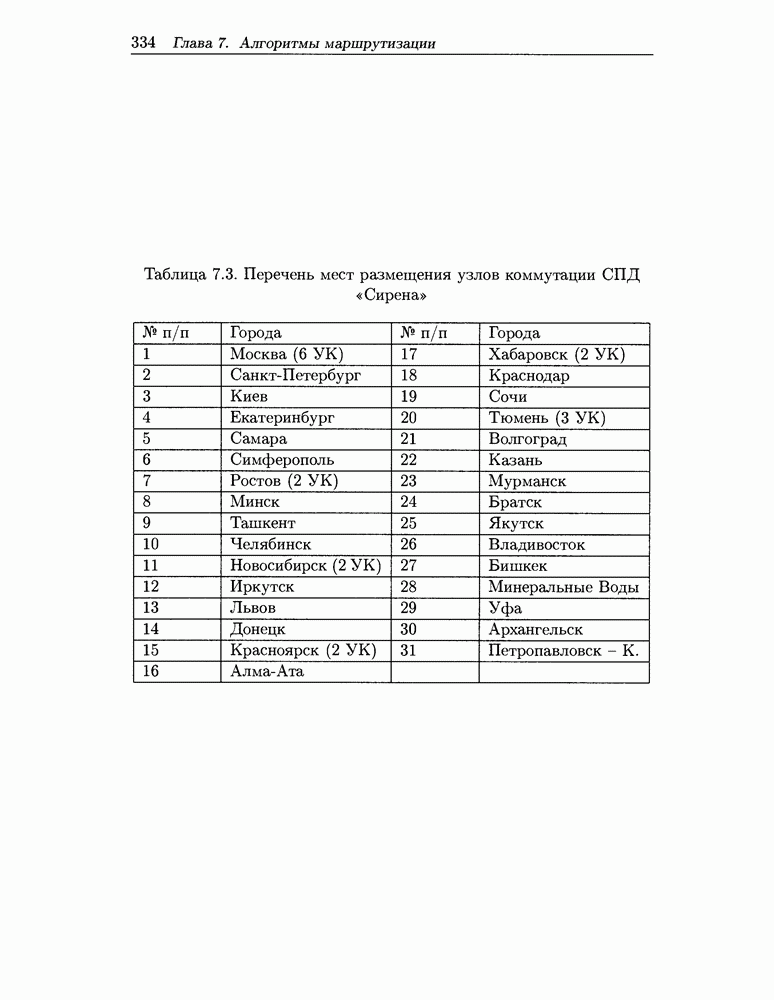
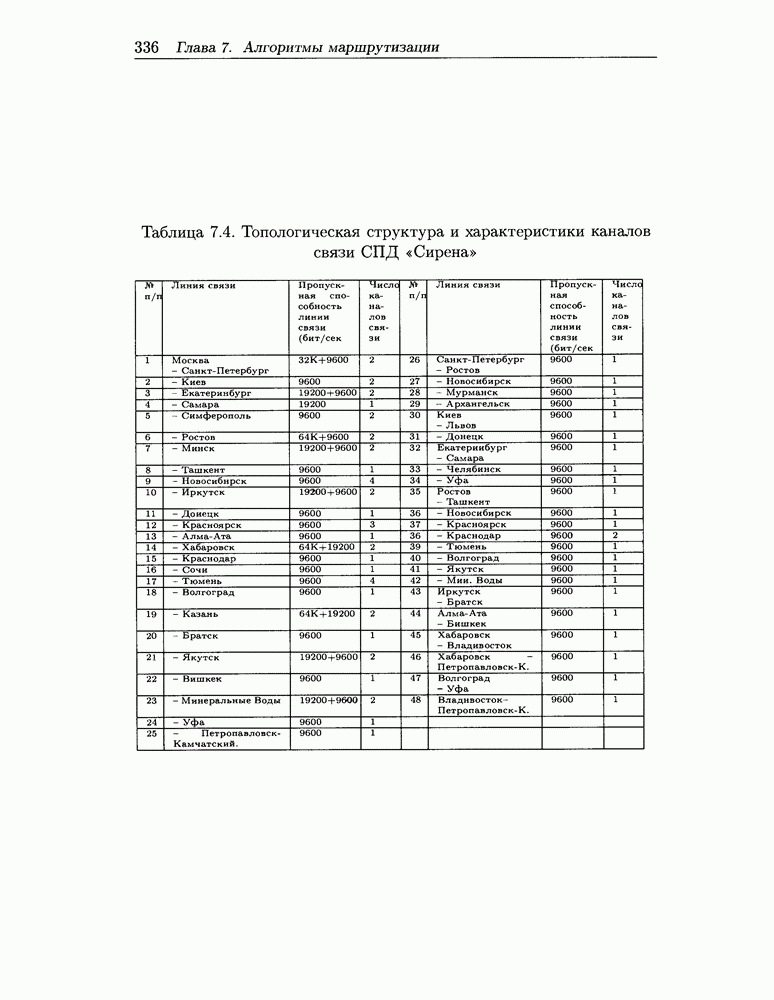
- 7.4.2 Анализ развития СПД «Сирена»
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
- 7.5.4 Классификация алгоритмов маршрутизации
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
- 7.5.8 Показатели качества маршрутизации
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
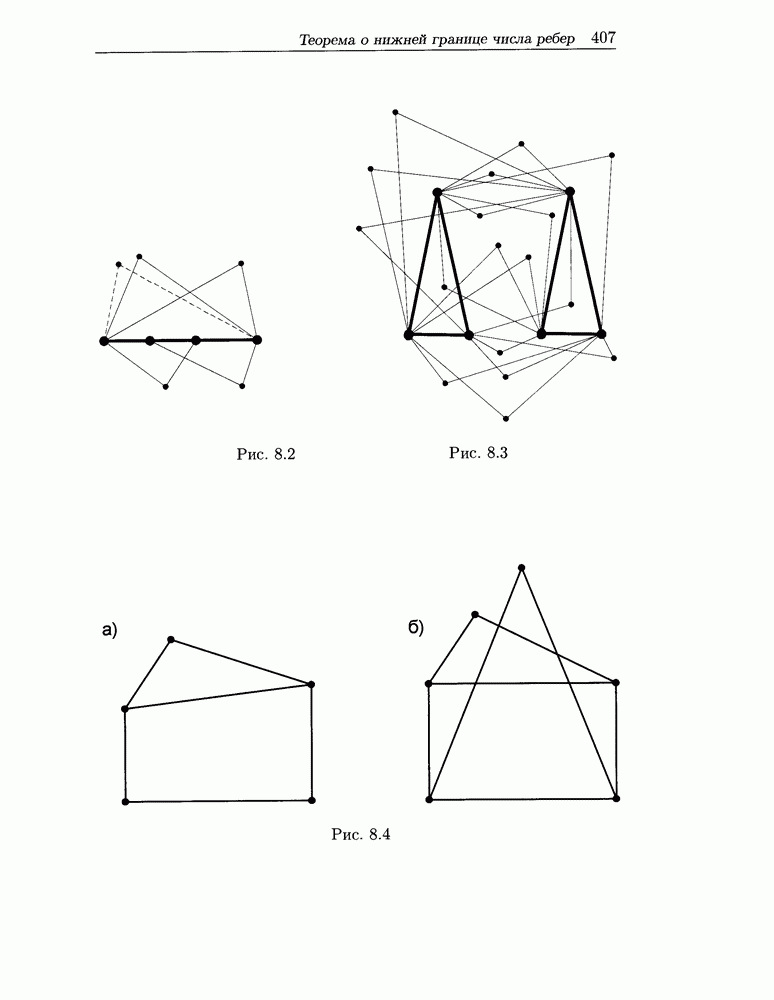
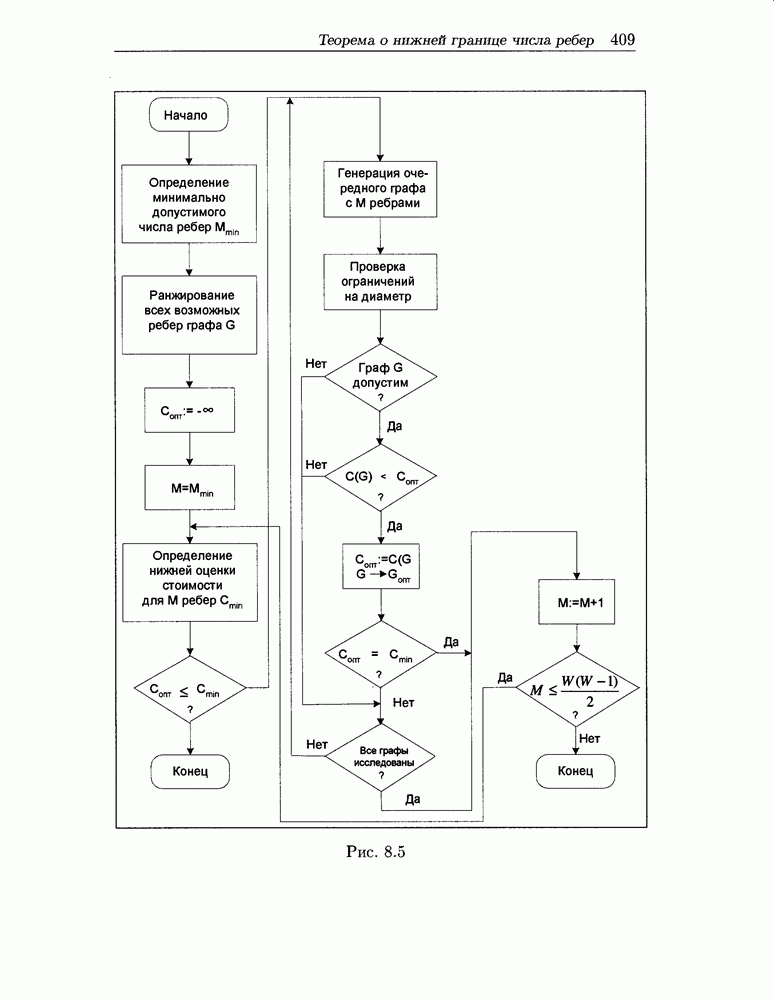
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
- 9.1 Состояние и перспективы развития беспроводных радиосетей
- 9.2 Схема распределенного управления
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
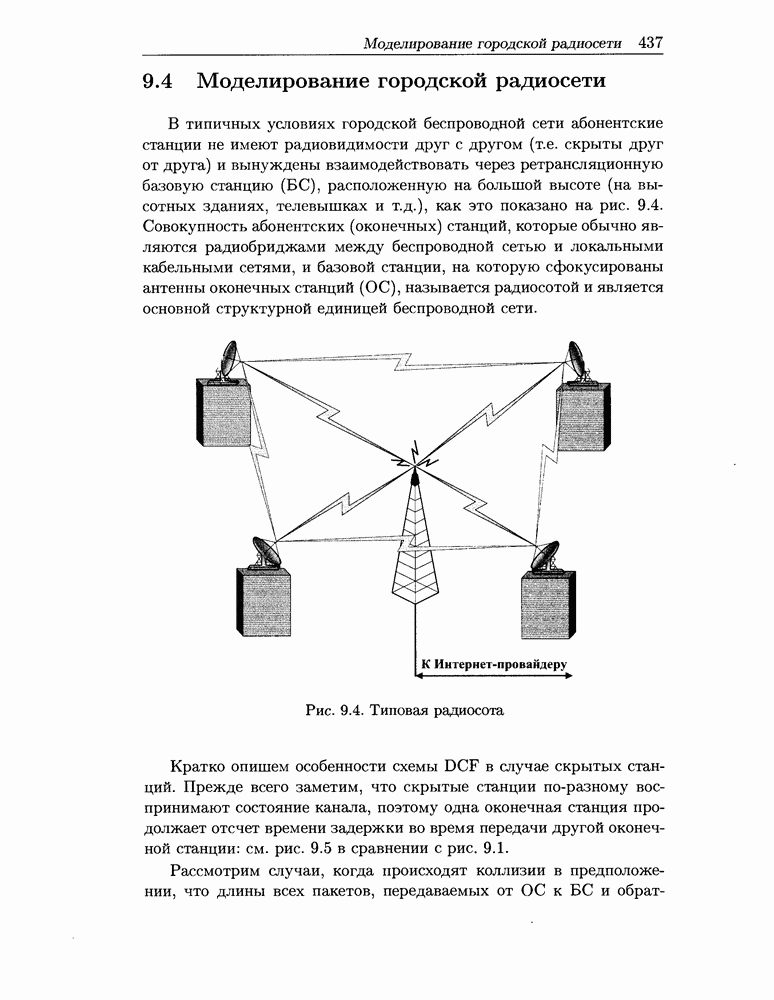
- 9.4 Моделирование городской радиосети
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
- 9.5 Численные результаты исследования городской радиосоты
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература