| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.3.2 Фиксированная (однопутевая) маршрутизация
По сравнению с альтернативной маршрутизацией задача поиска единственного оптимального пути является гораздо более сложной.
Дело в том, что ограничение (7.15 а) является требованием целочисленности переменных  которое переводит задачу в класс задач целочисленного нелинейного программирования, идентичных задаче «о рюкзаке». Известно [194], что такие задачи являются NP-полными, то есть для их решения не известны алгоритмы с полиномиальной сложностью. В работах [64, 89, 173] приводятся эвристические алгоритмы, которые позволяют получить приближенное решение задачи с небольшими вычислительными затратами. Одним из основных недостатков эвристических алгоритмов является невозможность оценки погрешности получаемых решений.
которое переводит задачу в класс задач целочисленного нелинейного программирования, идентичных задаче «о рюкзаке». Известно [194], что такие задачи являются NP-полными, то есть для их решения не известны алгоритмы с полиномиальной сложностью. В работах [64, 89, 173] приводятся эвристические алгоритмы, которые позволяют получить приближенное решение задачи с небольшими вычислительными затратами. Одним из основных недостатков эвристических алгоритмов является невозможность оценки погрешности получаемых решений.
В настоящей работе предлагается подход, который позволяет получить точную нижнюю оценку задачи. Данный подход строится на методе релаксации (ослаблении) Лагранжа. Метод состоит в том, что вместо исходной задачи решается двойственная задача, в которой некоторые ограничения включаются в функцию Лагранжа с соответствующими неопределенными множителями (подвергаются лагранжеву ослаблению). Практика показывает [101], что для многих задач целочисленной оптимизации:
- двойственная функция хорошо обусловлена, что позволяет получить удовлетворительную скорость сходимости;
- скачки двойственности (разности между целочисленным оптимумом и оптимумом двойственной задачи) очень малы или могут отсутствовать вовсе.
Таким образом, получение хорошей нижней оценки позволяет:
- оценить качество решений, получаемых эвристическими алгоритмами (и останавливаться на них, если эти решения будут откланяться от нижней оценки не более чем на заданную величину);
- строить алгоритмы типа «ветвей и границ», чтобы получать оптимальные решения или решения с заданной точностью.
Использование метода релаксации Лагранжа для решения задачи фиксированной маршрутизации впервые было использовано в работе [194]. Предлагаемый здесь подход использует ослабление меньшего числа ограничений, что повышает точность решения задачи.
Для использования метода релаксации переформулируем исходную задачу. Введем следующее обозначение:  для всех
для всех  . Величина
. Величина  называется загрузкой линии связи
называется загрузкой линии связи  и представляет собой одну из наиболее важных характеристик качества функционирования сети передачи данных. Из ограничения (7.13) следует, что
и представляет собой одну из наиболее важных характеристик качества функционирования сети передачи данных. Из ограничения (7.13) следует, что  Итак:
Итак:
Требуется найти:
1) Переменные и загрузки линий связи  такие, что:
такие, что:

при выполнении ограничений:

Заметим, что целевая функция в (7.22) является строго возрастающей функцией от  .
.
Используя этот факт легко доказать, что равенство (7.23) можно заменить на неравенство
 (7.23а)
(7.23а)
Теперь исходная задача подготовлена к лагранжеву ослаблению. Избавимся от ограничений (7.23а), умножив их на неопределенные множители Лагранжа  и переходим к функции Лагранжа:
и переходим к функции Лагранжа:

Таким образом, решается следующая задача:

при выполнении ограничений:


Множество допустимых решений для задачи (7.27) - (7.31) является подмножеством всех допустимых решений задачи (7.22) - (7.26).
Условия (7.31) и (7.23 а) гарантируют, что для любого допустимого решения задачи (7.22) - (7.26) выражение:  меньше или равно нулю. Таким образом, решение задачи (7.27) - (7.31) для произвольных значений переменных
меньше или равно нулю. Таким образом, решение задачи (7.27) - (7.31) для произвольных значений переменных  дает возможность определить нижнюю оценку задачи (7.22) - (7.26). Тогда,
дает возможность определить нижнюю оценку задачи (7.22) - (7.26). Тогда,  также является нижней оценкой задачи (7.22) -(7.26).
также является нижней оценкой задачи (7.22) -(7.26).
Предположим, что значения переменных  известны. Перепишем целевую функцию
известны. Перепишем целевую функцию  в следующем виде:
в следующем виде:

Данный вид целевой функции позволяет разделить исходную задачу на две независимые подзадачи.
Подзадача 1.

при выполнении ограничений:

Подзадача 2.

при выполнении ограничений:

Подзадача 1 может быть разделена на М независимых подзадач (по одной на каждую линию связи):

при ограничении: 
Решение данной подзадачи имеет следующий вид:

Подзадача 2 может быть разделена на  независимых подзадач (по одной на каждую пару «источник
независимых подзадач (по одной на каждую пару «источник  - адресат
- адресат 

при выполнении ограничений:

Легко заметить, что задача (7.40) - (7.42) представляет собой задачу выбора кратчайших маршрутов между заданной парой узлов  если в качестве «весов» ребер рассматривать величины
если в качестве «весов» ребер рассматривать величины  .
.
Так как подзадачи (7.40) - (7.42) независимы, то для решения подзадачи 2 можно использовать алгоритм поиска кратчайших путей между всеми парами узлов, например, алгоритм Флойда.
Теперь рассмотрим процедуру поиска множителей Лагранжа о  Функция
Функция  является вогнутой, не всюду дифференцируемой функцией от а [101]. Для данной функции легко вычислить субградиент в точке а:
является вогнутой, не всюду дифференцируемой функцией от а [101]. Для данной функции легко вычислить субградиент в точке а:

Тогда, для поиска минимума функции  можно использовать субградиентный алгоритм [112], в соответствии с которым множители Лагранжа
можно использовать субградиентный алгоритм [112], в соответствии с которым множители Лагранжа  вычисляются по следующей итеративной формуле:
вычисляются по следующей итеративной формуле:

Существует несколько методов выбора параметров перемещения  в частности:
в частности:
- метод с постоянным шагом -  ;
;
- метод сходящегося ряда - 
- метод релаксации -  , где Т - оценка оптимального решения задачи (7.22) - (7.26) и, следовательно, функции
, где Т - оценка оптимального решения задачи (7.22) - (7.26) и, следовательно, функции  коэффициент релаксации S удовлетворяет условию:
коэффициент релаксации S удовлетворяет условию: 
Аналогично [194] остановимся на методе релаксации, который состоит из следующих основных шагов.
Шаг 1. Инициализация:
1) Используя любой приближенный алгоритм, найти верхнюю оценку решения задачи (7.22) - (7.26) - Т.
2) Выбрать начальные значения множителей Лагранжа - 
3) Установить:
 (
( — номер итерации);
— номер итерации);
 (
( — счетчик «безрезультатных» итераций);
— счетчик «безрезультатных» итераций);
 (коэффициент релаксации);
(коэффициент релаксации);
 (текущее значение оптимального решения).
(текущее значение оптимального решения).
Шаг 2. Решение задачи Лагранжа:
Используя значения  решить подзадачи 1 и 2. В результате решения будут получены:
решить подзадачи 1 и 2. В результате решения будут получены: 
Шаг 3. Оценка полученного решения и проверка условий прекращения поиска:
1) Если  , то положить:
, то положить:
а) 
b)  (множители Лагранжа, соответствующие текущему оптимальному решению);
(множители Лагранжа, соответствующие текущему оптимальному решению); 
с) 
2) Если  являются допустимыми решениями задачи
являются допустимыми решениями задачи  то вычислить среднее значение задержки сообщения Т, соответствующее переменным
то вычислить среднее значение задержки сообщения Т, соответствующее переменным  и, если,
и, если,  то запомнить данную величину в качестве оптимального решения:
то запомнить данную величину в качестве оптимального решения:  .
.
3) Положить  Если
Если  заданного значения
заданного значения  , то:
, то:
а) 
b) 
c) 
d) 
e) перейти к шагу 2.
4) Если  заданного значения гтах, или
заданного значения гтах, или  или
или  заданной погрешности вычислений
заданной погрешности вычислений  , то STOP: найдено оптимальное решение.
, то STOP: найдено оптимальное решение.
Шаг 4. Вычисление множителей Лагранжа:
1) Вычисляется новое значение субградиента:

2) Вычисляется параметр перемещения 

3) Вычисляются новые множители Лагранжа:

4) 
5) Переход к шагу 2.
Как уже отмечалось выше, получение точной нижней оценки для задачи поиска единственного оптимального пути представляет собой очень важную задачу, однако, в общем случае решение данной задачи может не удовлетворять требуемым ограничениям.
В тех случаях, когда в результате решения задачи необходимо получить оптимальные пути между каждой парой узлов «источник - адресат». Для этой цели необходимо использовать приближенные методы, один из которых описывается ниже. Заметим также, что решение, полученное с помощью данного алгоритма, может быть использовано на шаге 1 предыдущего алгоритма.
Шаг 1. Инициализация:
1) Упорядочить множество пар «источник  - адресат
- адресат  по убыванию величин
по убыванию величин  Полученное множество пар обозначим через
Полученное множество пар обозначим через  .
.
2) Положить 
Шаг 2. Поиск допустимого решения:
1) Для V пары «источник  - адресат
- адресат  выполнить следующие действия:
выполнить следующие действия:
a) найти «наименее загруженный» маршрут  (под загрузкой маршрута
(под загрузкой маршрута  понимается величина
понимается величина  если таких маршрутов несколько, выбрать среди них маршрут с наименьшим числом промежуточных узлов;
если таких маршрутов несколько, выбрать среди них маршрут с наименьшим числом промежуточных узлов;
b) распределить потоки по выбранному маршруту:

если  то STOP (допустимого решения не существует).
то STOP (допустимого решения не существует).
2) Вычислить задержки Z между каждой парой узлов «источник  - адресат
- адресат 
Шаг 3. Поиск «оптимального» решения:
1) Упорядочить множество пар «источник  - адресат
- адресат  по убыванию величин
по убыванию величин  Полученное множество пар обозначим через
Полученное множество пар обозначим через 
2) Для V пары «источник  - адресат
- адресат  выполнить следующие действия:
выполнить следующие действия:
a) найти маршрут  такой, что отклонение всего потока 7 на этот маршрут приведет к максимальному уменьшению величины
такой, что отклонение всего потока 7 на этот маршрут приведет к максимальному уменьшению величины  (алгоритм определения такого маршрута будет описан ниже);
(алгоритм определения такого маршрута будет описан ниже);
b) распределить потоки по выбранному маршруту:

3) Вычислить: 
Остановимся подробнее на следующих шагах приближенного алгоритма: определение «наименее загруженного» маршрута (шаг 2.1 а) и определение «оптимального» маршрута (шаг 3.2 а).
«Наименее загруженный» маршрут можно найти с помощью модификации алгоритма Дейкстры [177].
Для определения «оптимального» маршрута можно использовать следующий простой алгоритм (напомним, что определение такого маршрута выполняется для заданной пары узлов  ).
).
Шаг 1. Удалить поток из «наименее загруженного» маршрута  (предполагается, что все маршруты
(предполагается, что все маршруты  были сохранены):
были сохранены):

Шаг 2. Добавить поток  во все линии связи
во все линии связи  :
:

Шаг 3. Вычислить «веса» линий связи 
если  положить:
положить:  , иначе:
, иначе: 
Шаг 4. Используя «веса»  определить кратчайший путь между парой узлов
определить кратчайший путь между парой узлов  Для этой цели вновь можно использовать алгоритм Дейкстры.
Для этой цели вновь можно использовать алгоритм Дейкстры.
Шаг 5. Удалить поток  из всех линии связи
из всех линии связи 

Шаг 6. Конец работы алгоритма.
Теоретическая сложность приближенного алгоритма определяется шагами 2.1 а и 3.2 а и составляет 
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Введение
- ГЛАВА 1. Математические методы теории очередей
- 1.2 Входящий поток, время обслуживания
- 1.3 Марковские случайные процессы
- 1.3.1 Процессы гибели и размножения
- 1.3.2 Метод диаграмм интенсивностей переходов
- 1.3.3 Цепи Маркова с дискретным временем
- 1.4 Преобразования Лапласа и Лапласа — Стилтьеса. Производящая функция
- 1.5 Однолинейные марковские системы массового обслуживания
- 1.5.2 Система типа М\М\1\n
- 1.5.3 Система с конечным числом источников
- 1.6 Полумарковские однолинейные системы и методы их анализа
- 1.6.1 Метод вложенных цепей Маркова в приложении для системы M\G\1
- 1.6.2 Метод вложенных цепей Маркова в приложении для системы GI\M\1
- 1.6.3 Метод введения дополнительной переменной
- 1.6.4 Метод введения дополнительного события
- 1.7 Многолинейные системы массового обслуживания
- 1.7.2 Многоканальные системы без буфера для ожидания
- 1.7.3 Система М\М\оо
- 1.7.4 Система M\G\1 с дисциплиной равномерного распределения процессора и дисциплиной LIFO с прерыванием обслуживания
- 1.8 Приоритетные системы массового обслуживания
- 1.9 Многофазные системы
- 1.10 Перспективные направления исследований в теории очередей
- ГЛАВА 2. Аналитические методы теории сетей очередей
- 2.1.1 Маршрутная матрица и потоки в сетях
- 2.1.2 Другие определения
- 2.2 Однородные экспоненциальные сети
- 2.2.1 Уравнения глобального баланса для замкнутых цепей
- 2.2.2 Вид решения в мультипликативной форме
- 2.2.3 Сети, зависящие от нагрузки
- 2.2.4 Показатели качества функционирования однородных сетей
- 2.3 Сети массового обслуживания с несколькими классами сообщений
- 2.3.2 Теорема ВСМР
- 2.3.3 Открытые сети МО с несколькими классами
- 2.4 Итерационный метод анализа средних значений
- 2.4.1 Общее описание метода
- 2.4.2 Однородная замкнутая сеть МО, зависящая от нагрузки
- 2.5 Оптимизация замкнутых однородных сетей массового обслуживания
- 2.5.1 Некоторые свойства характеристик замкнутых однородных сетей МО
- 2.5.2 Постановка и решение задачи оптимизации
- 2.5.3 Пример расчета
- ГЛАВА 3. Вычислительные алгоритмы (методы вычислений характеристик сетей очередей)
- 3.1 Алгоритмы вычисления характеристик однородных замкнутых экспоненциальных сетей массового обслуживания
- 3.1.2 Вычисление характеристик сети
- 3.1.3 Аналитическое представление нормализующей константы
- 3.1.4 Пример расчета
- 3.2 Расчет сетей с несколькими классами сообщений
- 3.2.2 Маргинальное распределение длины очереди и пропускная способность
- 3.2.3 Расчет среднего времени ожидания и средней длины очереди
- 3.2.4 Алгоритм расчета замкнутой сети МО, допускающей изменение класса сообщений
- 3.3 Вычислительные аспекты метода анализа средних значений
- 3.3.1 Основные соотношения
- 3.3.2 Оценка эффективности вычислительного алгоритма
- 3.3.3 Расширение метода
- 3.4 Практические аспекты реализации алгоритмов расчета сетей массового обслуживания большой размерности
- 3.4.2 Реконфигурация сети МО
- 3.4.3 Обобщенный алгоритм свертки в виде дерева для расчета сетей МО
- ГЛАВА 4. Приближенные методы исследования сетей очередей
- 4.1 Область применения и краткий анализ приближенных методов
- 4.1.1 Аппроксимация функций распределения
- 4.1.2 Диффузионная и декомпозиционная аппроксимации
- 4.2 Декомпозиционные методы на основе теоремы Нортона
- 4.2.2 Приближенный декомпозиционный алгоритм
- 4.2.3 Пример расчета
- 4.3 Декомпозиция разомкнутых сетей массового обслуживания на уровне первых моментов
- 4.3.2 Диффузионная аппроксимация системы МО GI/G/1
- 4.4 Полиномиальная аппроксимация
- 4.4.2 Оценка вычислительной сложности метода
- 4.4.3 Пример расчета
- ГЛАВА 5. Развитие теории мультипликативных сетей очередей
- 5.1 Основные направления развития теории мультипликативных сетей
- 5.2 Сети массового обслуживания с зависимым обслуживанием
- 5.2.2 Частные случаи
- 5.2.3 Марковский процесс, описывающий функционирование сети
- 5.2.4 Основная теорема о мультипликативности сети
- 5.2.5 Частные случаи
- 5.3 G-сеть с отрицательными заявками
- 5.3.1 G-сеть с отрицательными заявками и групповыми удалениями положительных заявок
- 5.3.2 G-сеть с отрицательными заявками и триггерами
- 5.4 Решение уравнений баланса для интенсивности потоков и устойчивости G-сетей
- 5.5 G-сеть со случайным временем активизации сигналов
- 5.5.1 Однолинейные узлы
- 5.5.2 Симметричная G-сеть
- 5.5.3 Обсуждение результатов
- 5.6 G-сети с несколькими классами положительных заявок и сигналов
- 5.7 Другие модели и методы анализа G-сетей
- ГЛАВА 6. Стохастические модели компьютерных сетей
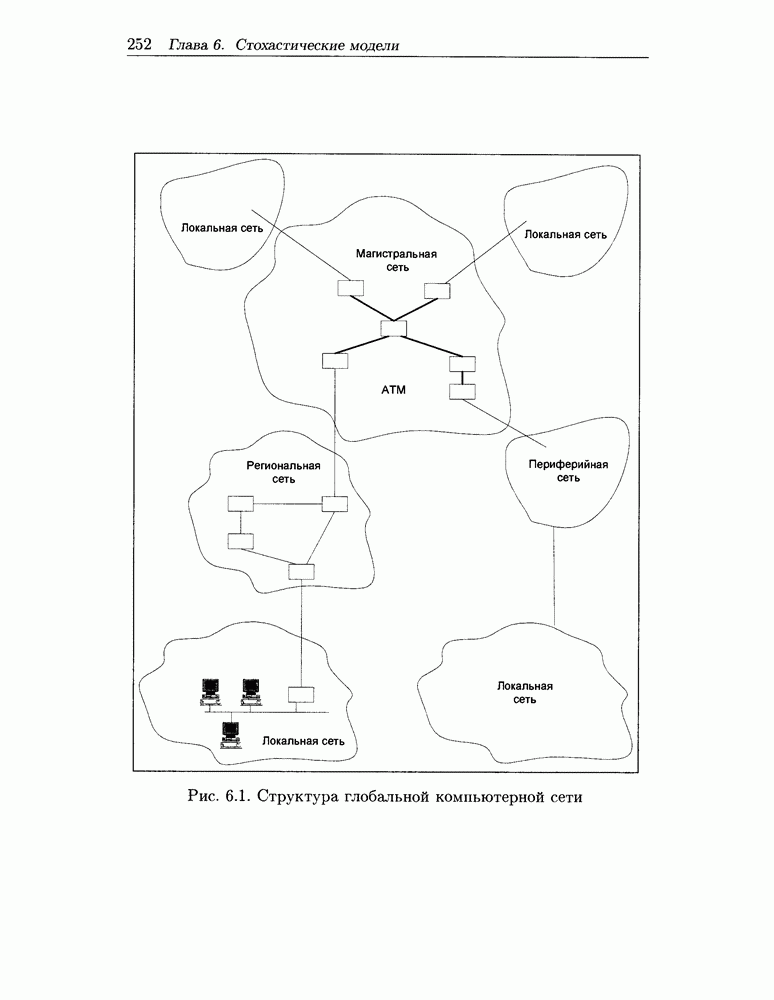
- 6.1.1 Структура компьютерных сетей
- 6.1.2 Сетевые протоколы
- 6.1.3 Использование теории сетей МО для исследования компьютерных сетей
- 6.2 Методы расчета характеристик сети пакетной коммутации
- 6.2.1 Анализ межконцевых задержек
- 6.2.2 Оптимизация пропускной способности и выбор маршрутов
- 6.2.3 Модель сети с ограниченной буферной памятью в узлах коммутации пакетов
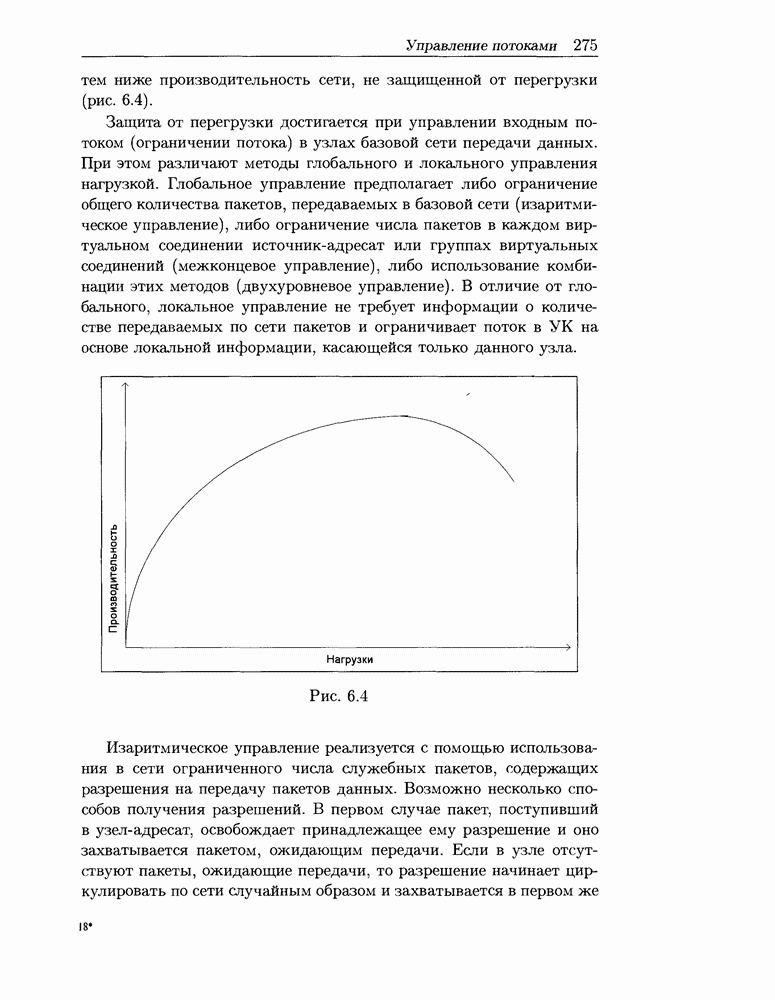
- 6.3 Управление потоками в сети пакетной коммутации
- 6.3.1 Методы управления потоками
- 6.3.2 Сетевая модель глобального управления
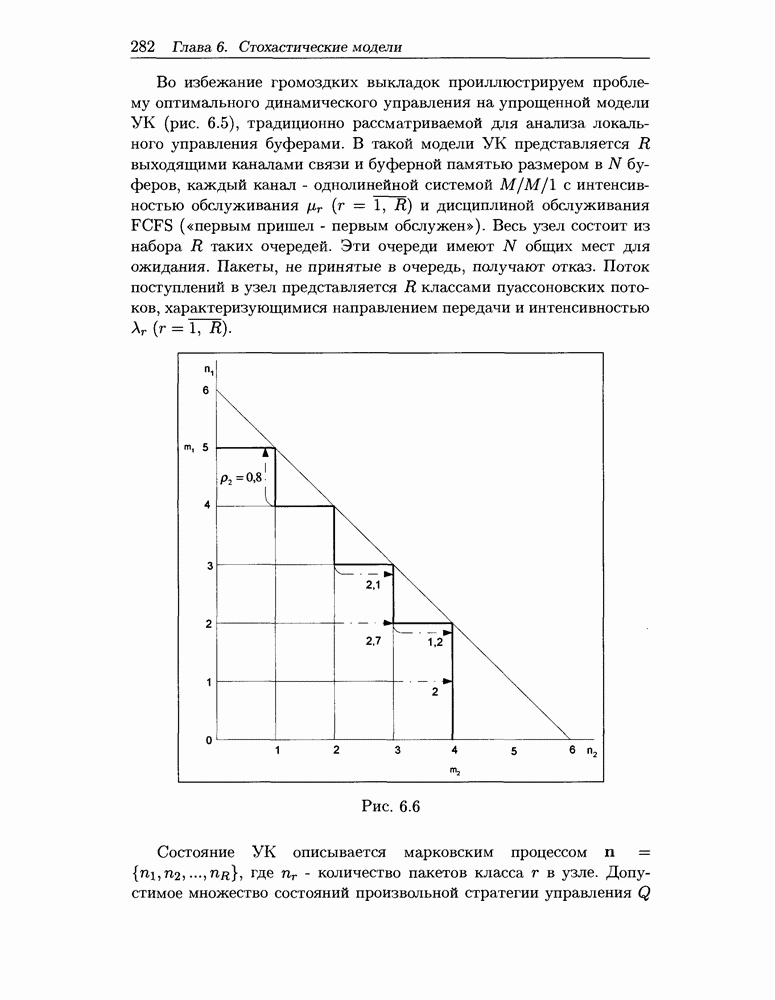
- 6.3.3 Локальное управление буферами
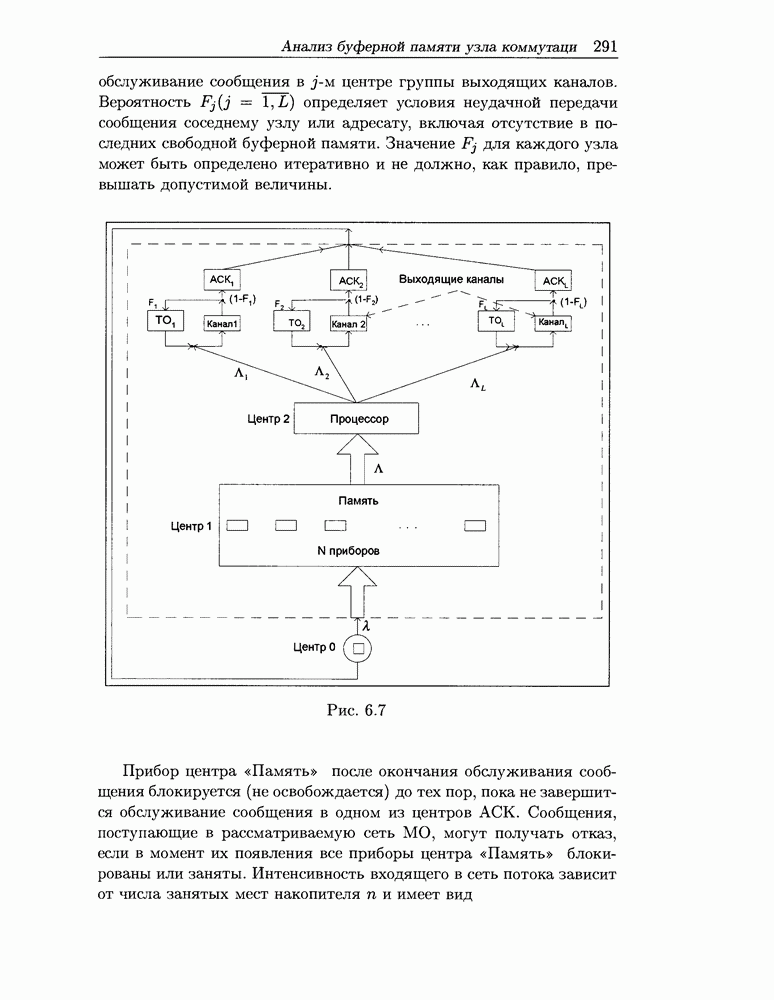
- 6.4 Анализ буферной памяти узла коммутаци
- 6.4.1 Процесс буферизации в узле коммутации и схемы организации буферной памяти
- 6.4.2 Анализ однородного пула равнодоступных буферов
- 6.4.3 Сетевая модель памяти секционной структуры
- 6.4.4 Анализ динамической памяти с цепочкой буферов
- ГЛАВА 7. Математические модели исследования алгоритмов маршрутизации
- 7.2 Постановка задачи
- 7.3 Алгоритмы решения задачи выбора оптимальных потоков в сети
- 7.3.1 Альтернативная маршрутизация
- 7.3.2 Фиксированная (однопутевая) маршрутизация
- 7.3.3 К-путевая маршрутизация
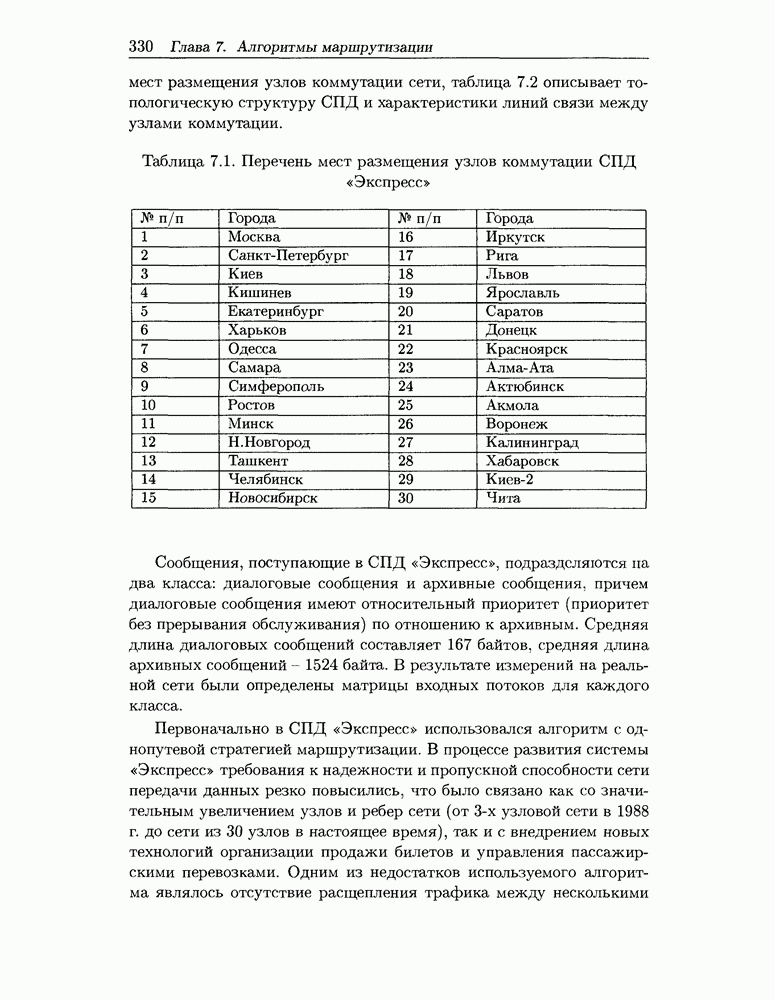
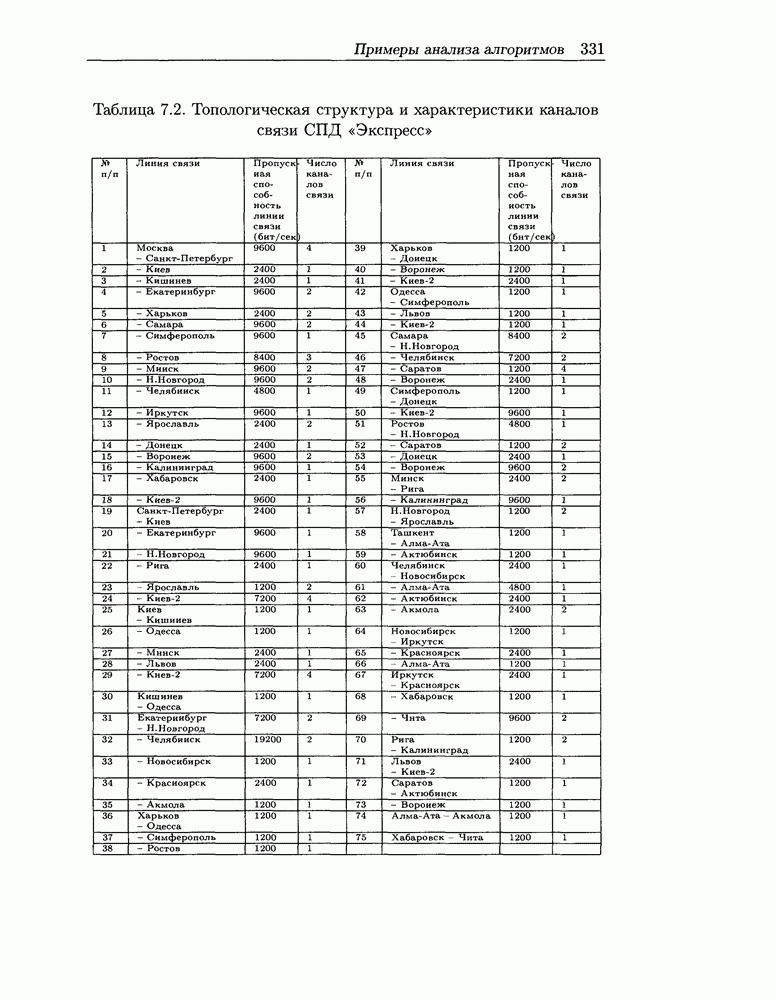
- 7.4 Примеры анализа алгоритмов маршрутизации в сетях передачи данных
- 7.4.1 Анализ различных вариантов алгоритмов маршрутизации для СПД «Экспресс»
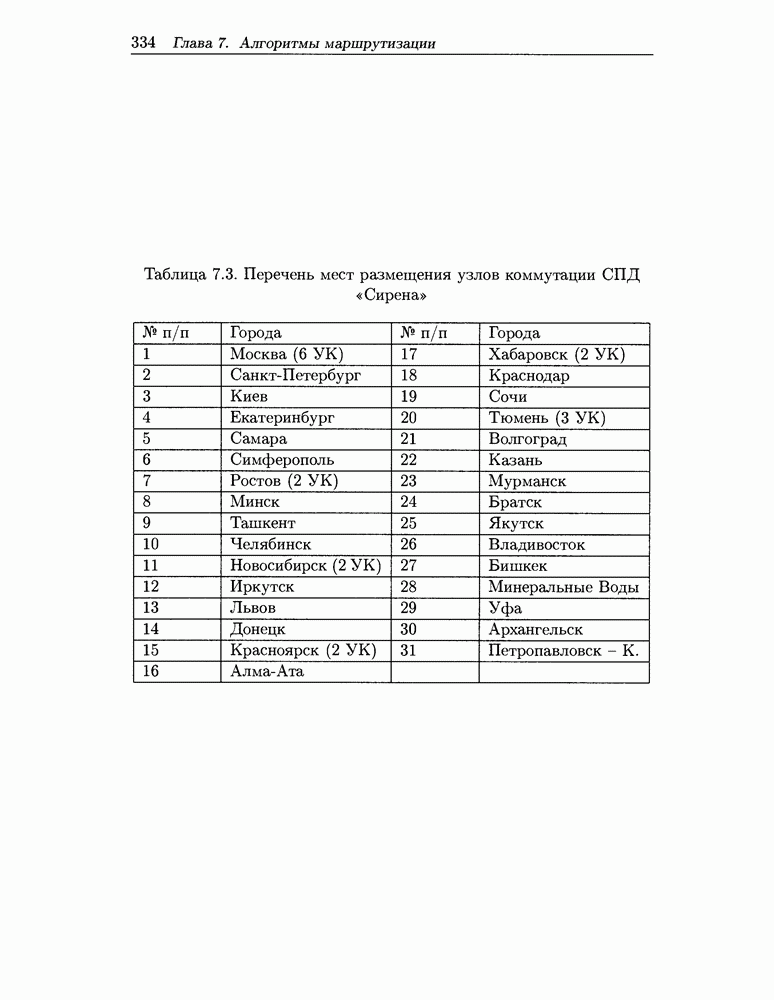
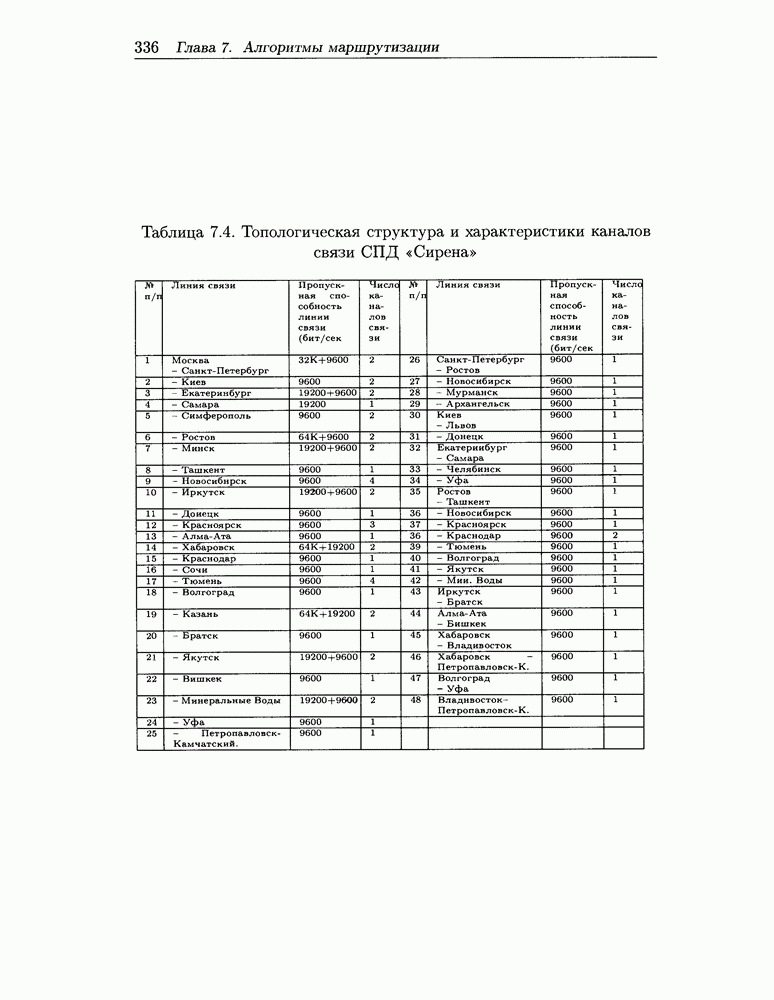
- 7.4.2 Анализ развития СПД «Сирена»
- 7.5 Динамическая маршрутизация в ATM сетях
- 7.5.1 Характерные особенности ATM сетей
- 7.5.2 Основные понятия маршрутизации для ATM сетей
- 7.5.3 Взаимосвязь с подсистемой установки соединения
- 7.5.4 Классификация алгоритмов маршрутизации
- 7.5.5 Требования к алгоритмам динамической маршрутизации
- 7.5.6 Входные параметры заявки.
- 7.5.7 Параметры состояния сети
- 7.5.8 Показатели качества маршрутизации
- 7.5.9 Анализ подходов к реализации общих требований
- 7.5.10 Маршрутизация запасных соединений
- 7.5.11 Выбор оптимального алгоритма и значений его параметров
- ГЛАВА 8. Оптимизация топологической структуры компьютерной сети
- 8.1 Принципы топологического проектирования сетей передачи информации
- 8.2 Описание задачи синтеза топологии; исходные данные
- 8.3 Комбинаторный алгоритм топологической оптимизации сети передачи информации
- 8.4 Оптимизация топологической структуры по критериям стоимости и надежности
- 8.5 Алгоритм генерации остовных двухсвязных подграфов заданного графа
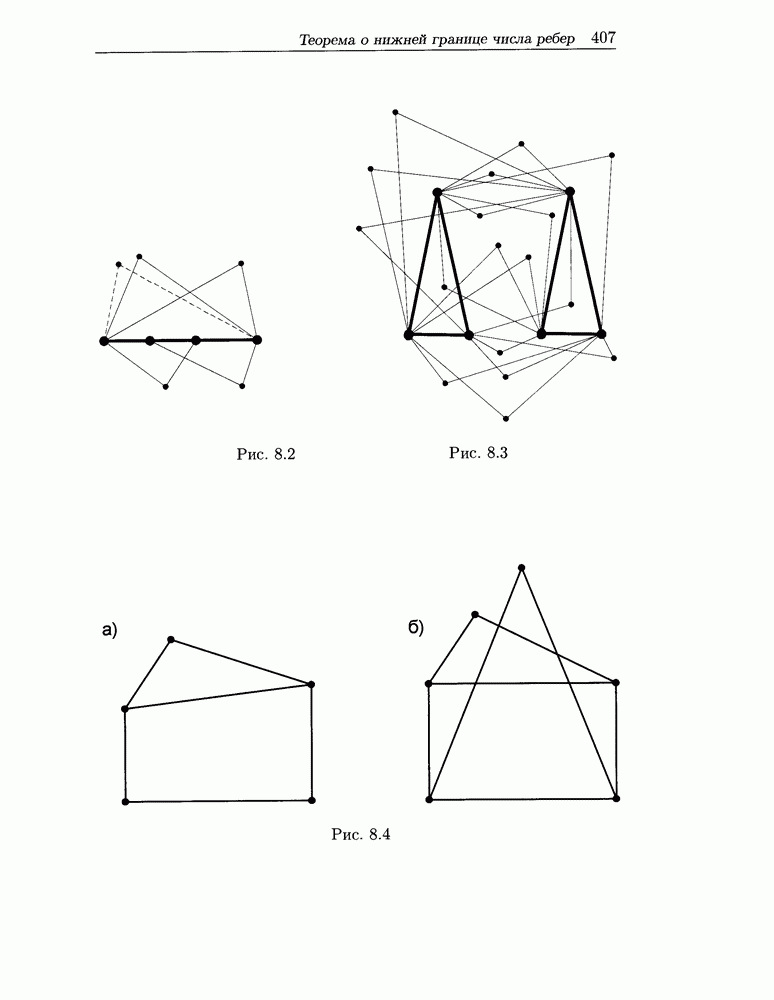
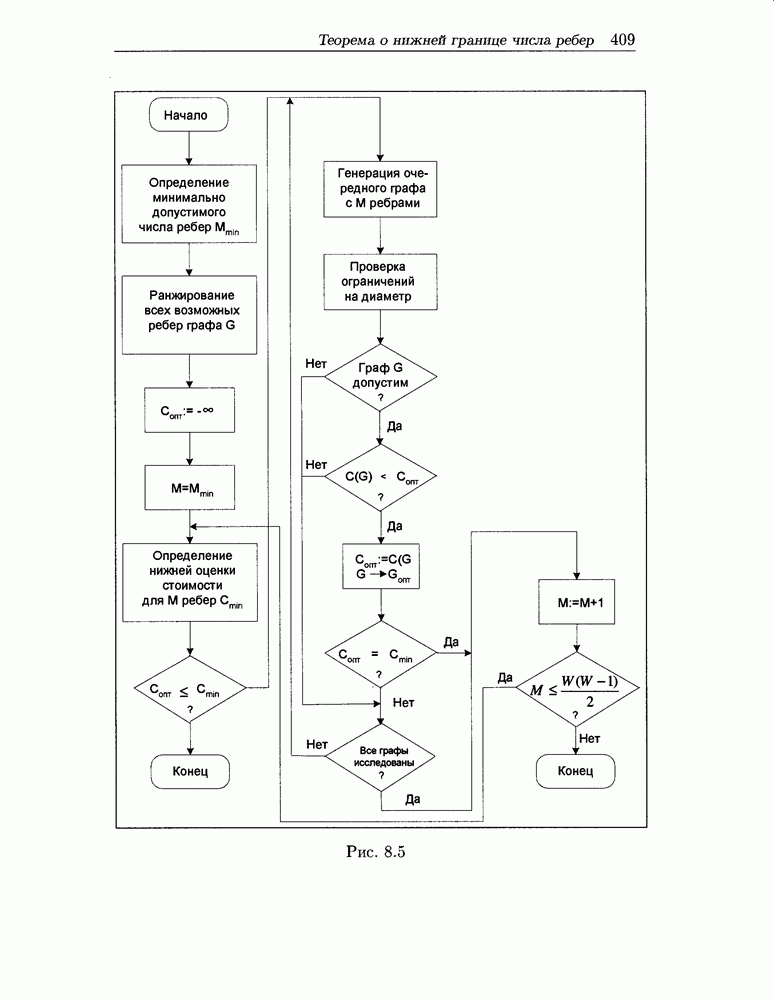
- 8.6 Характеристики некоторых экстремальных графов. Теорема о нижней границе числа ребер
- 8.7 Общая задача топологического синтеза компьютерной сети
- ГЛАВА 9. Методы анализа беспроводных компьютерных сетей
- 9.1 Состояние и перспективы развития беспроводных радиосетей
- 9.2 Схема распределенного управления
- 9.3 Моделирование беспроводной локальной сети в условиях высокой нагрузки
- 9.3.1 Оценка пропускной способности
- 9.3.2 Оценка вероятности передачи
- 9.3.3 Случай фрагментации пакетов
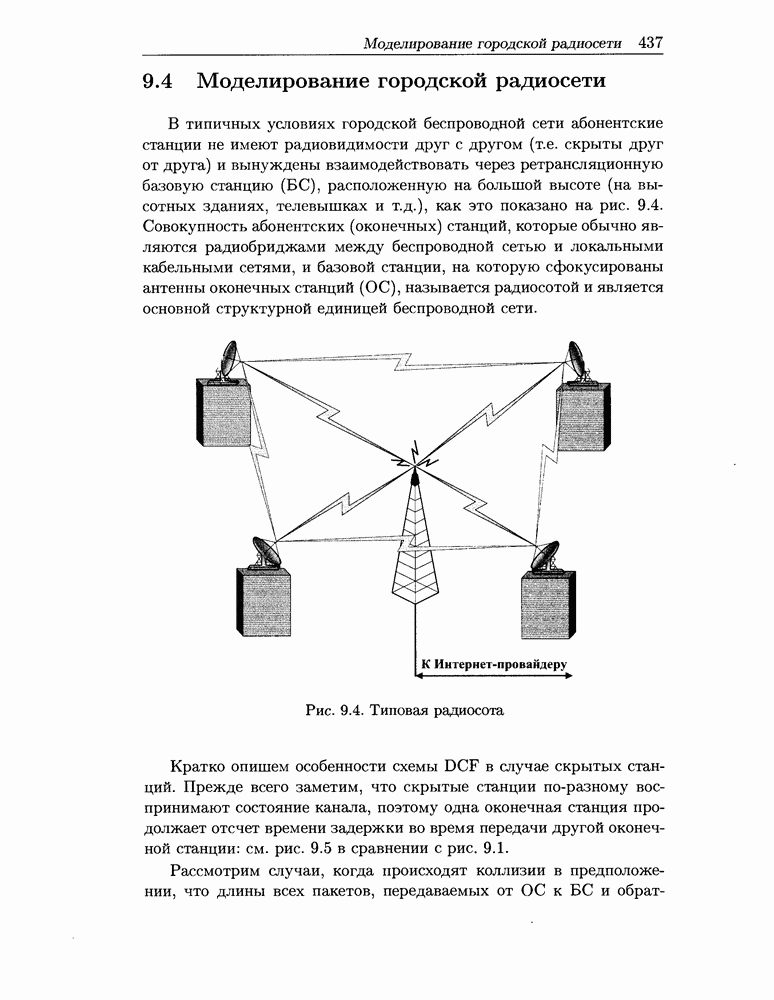
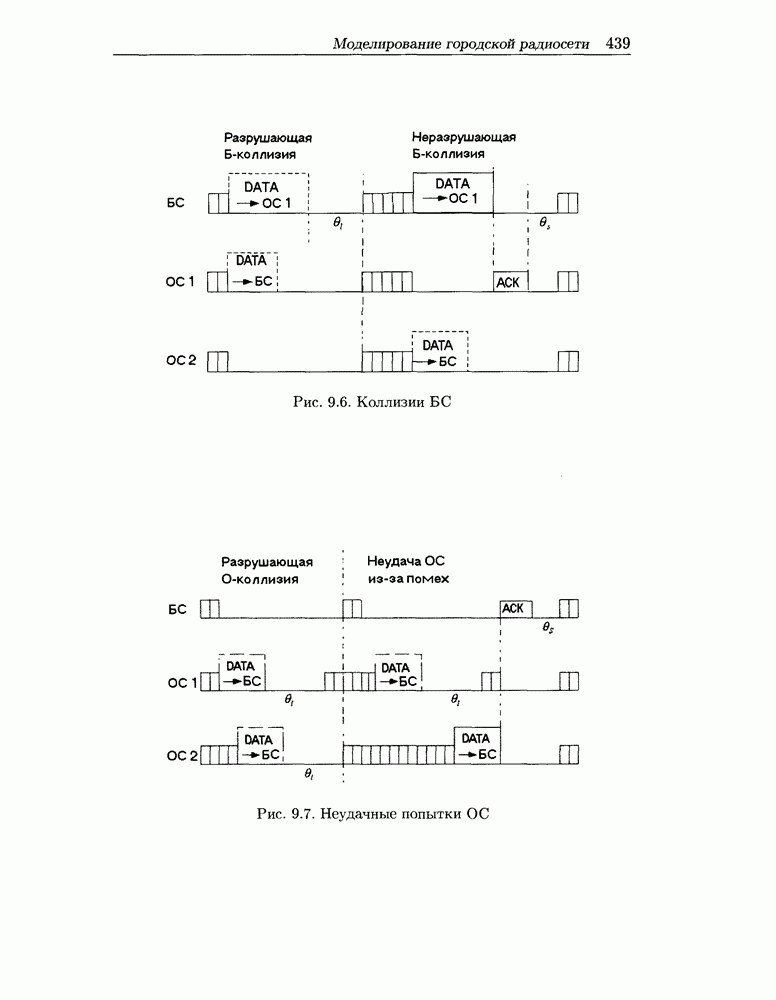
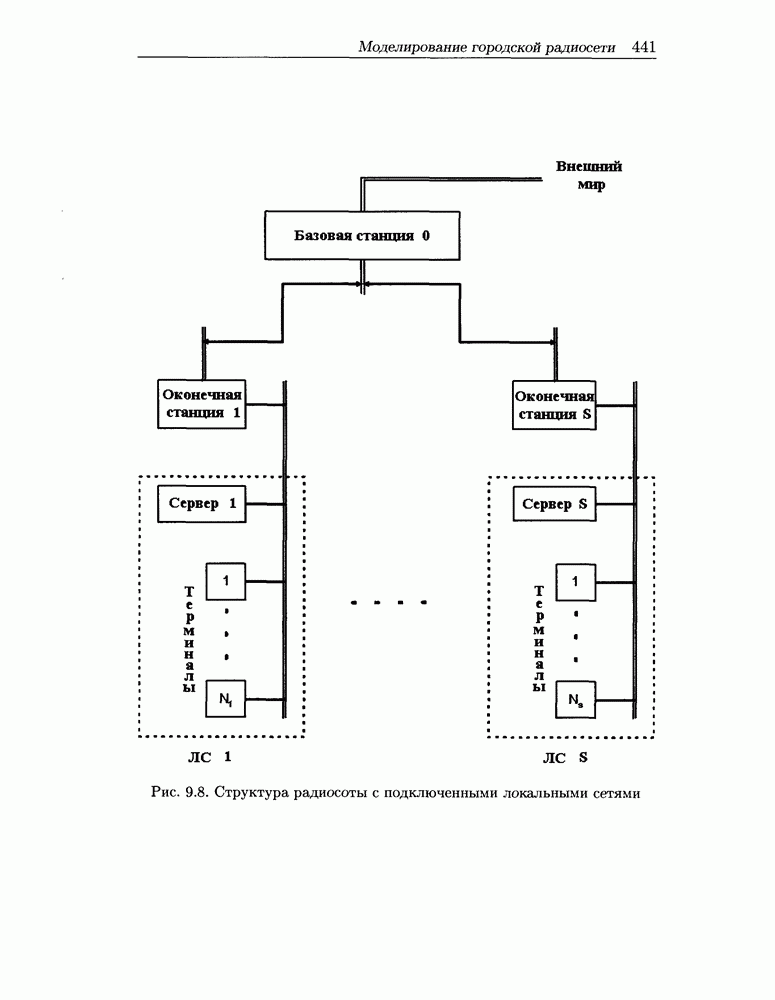
- 9.4 Моделирование городской радиосети
- 9.4.1 Имитационное моделирование радиосоты
- 9.4.2 Аналитический метод оценки пропускной способности
- 9.4.3 Метод оценки пропускной способности при технологии FHSS
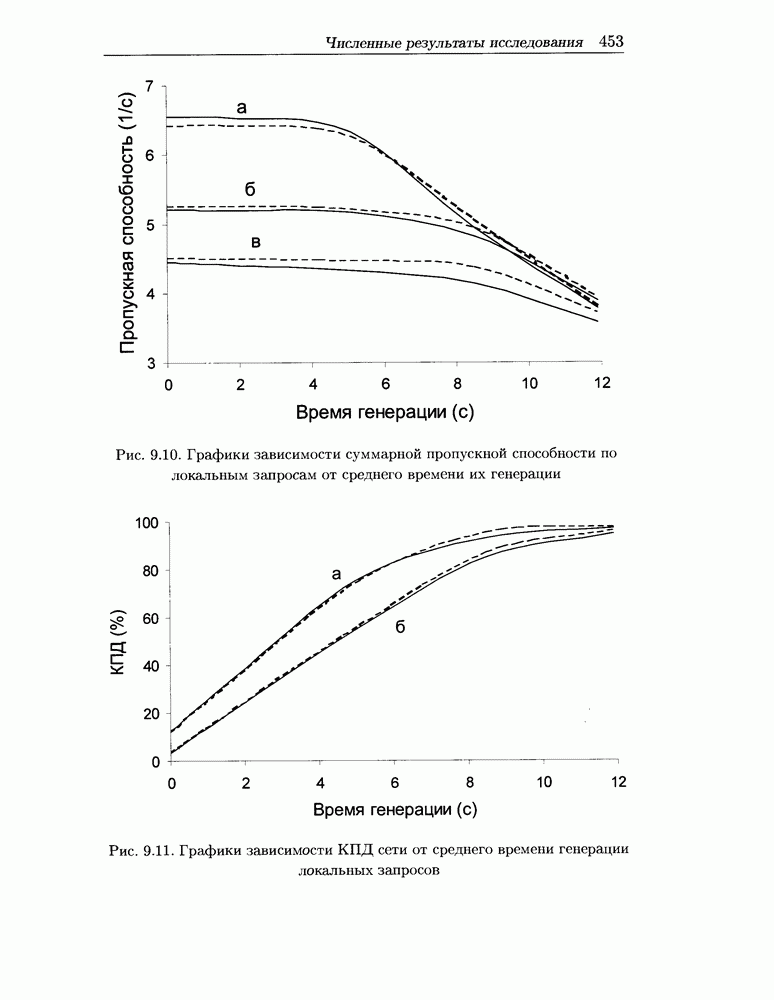
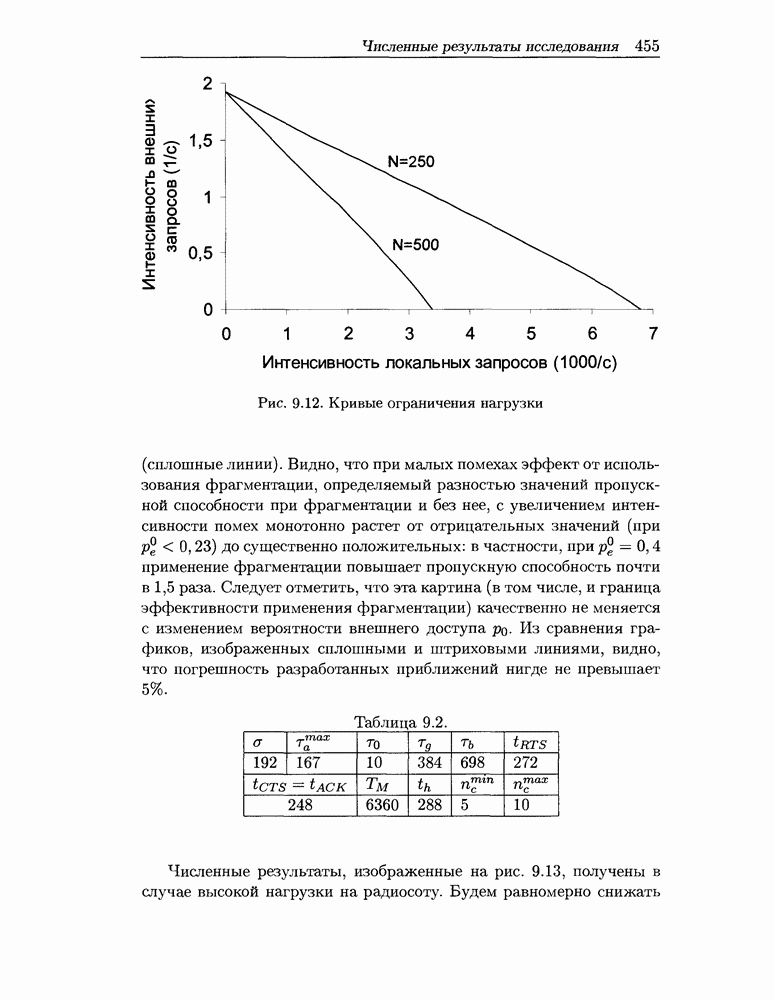
- 9.5 Численные результаты исследования городской радиосоты
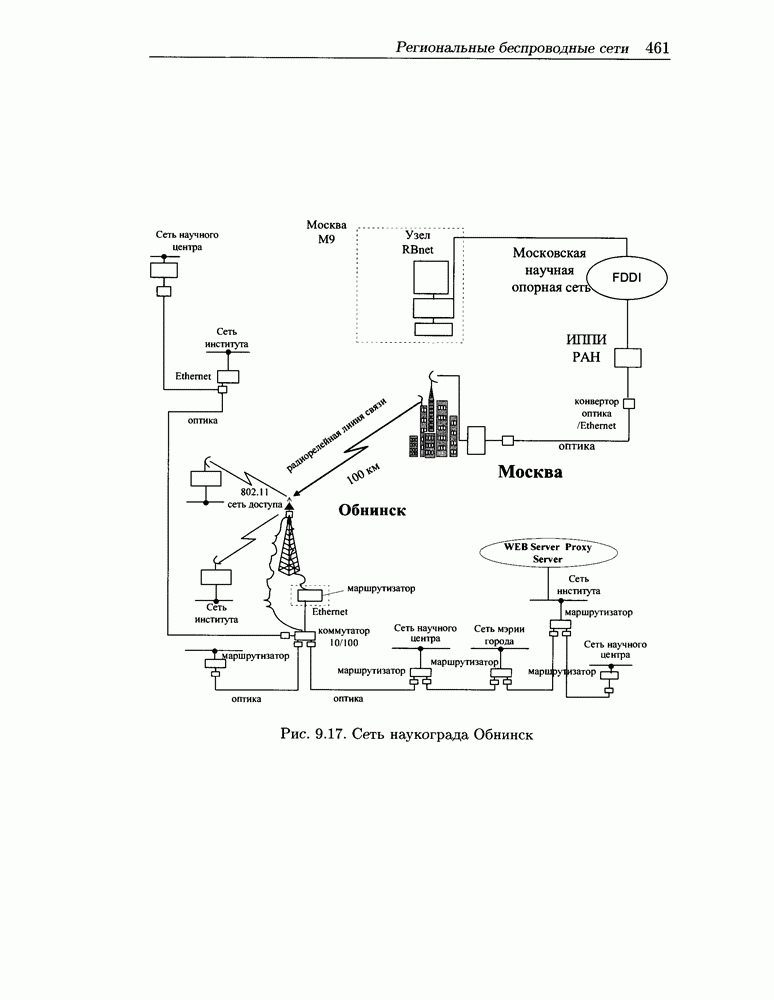
- 9.6 Региональные беспроводные сети на базе ШПС-радиомодемов
- 9.7 Аэростатная беспроводная сеть
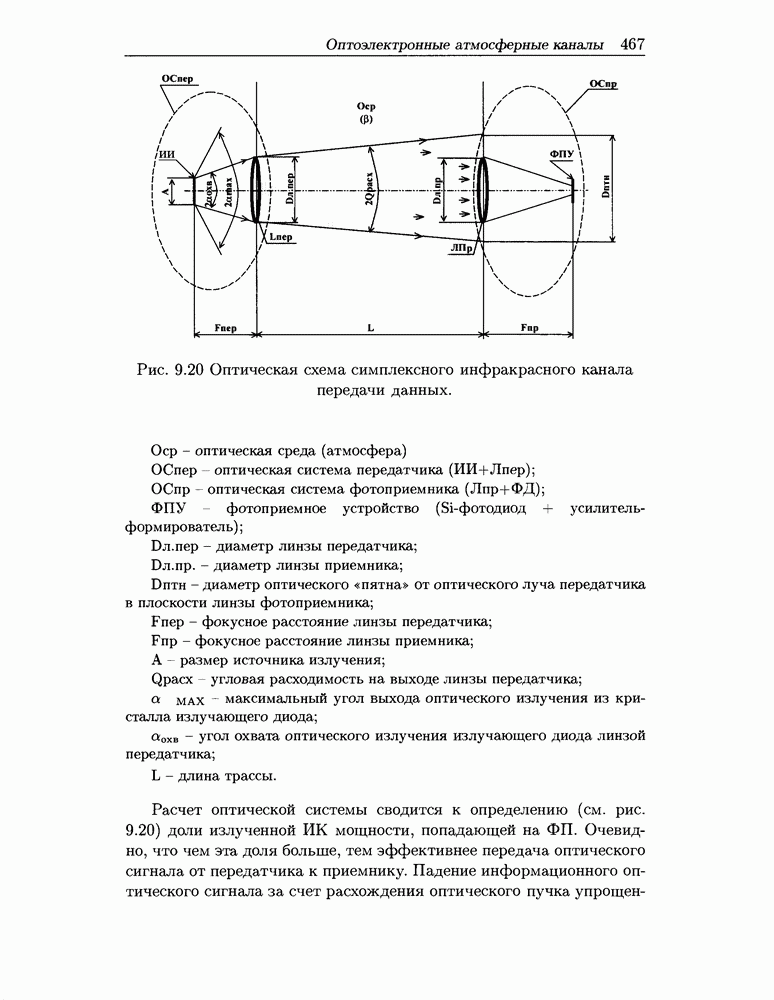
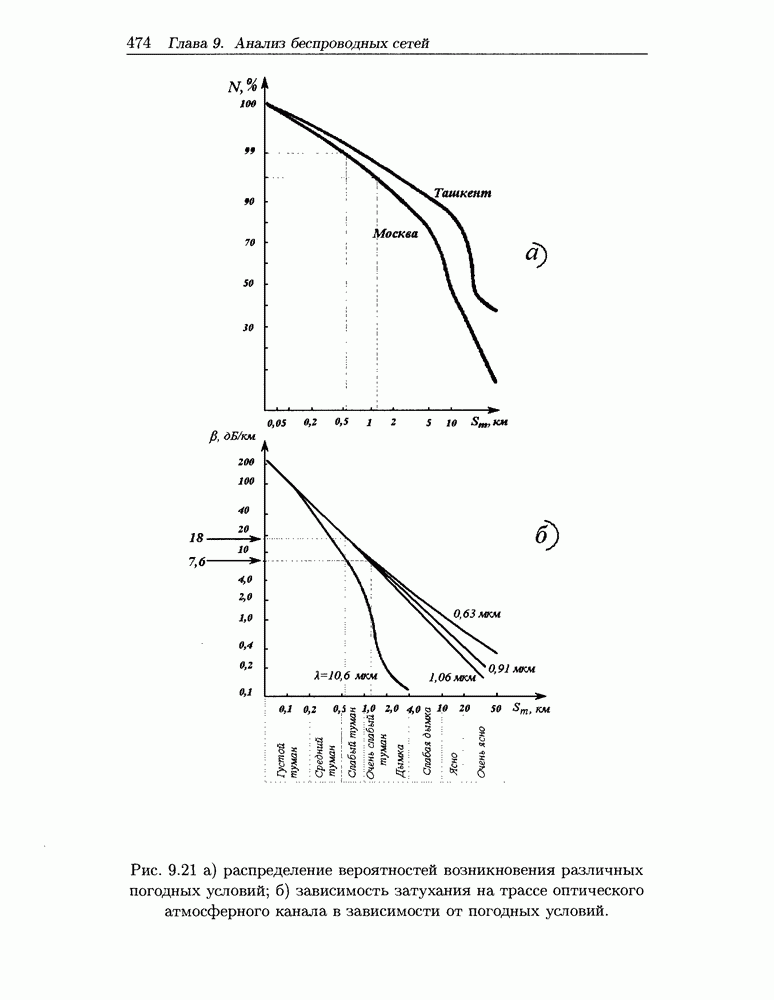
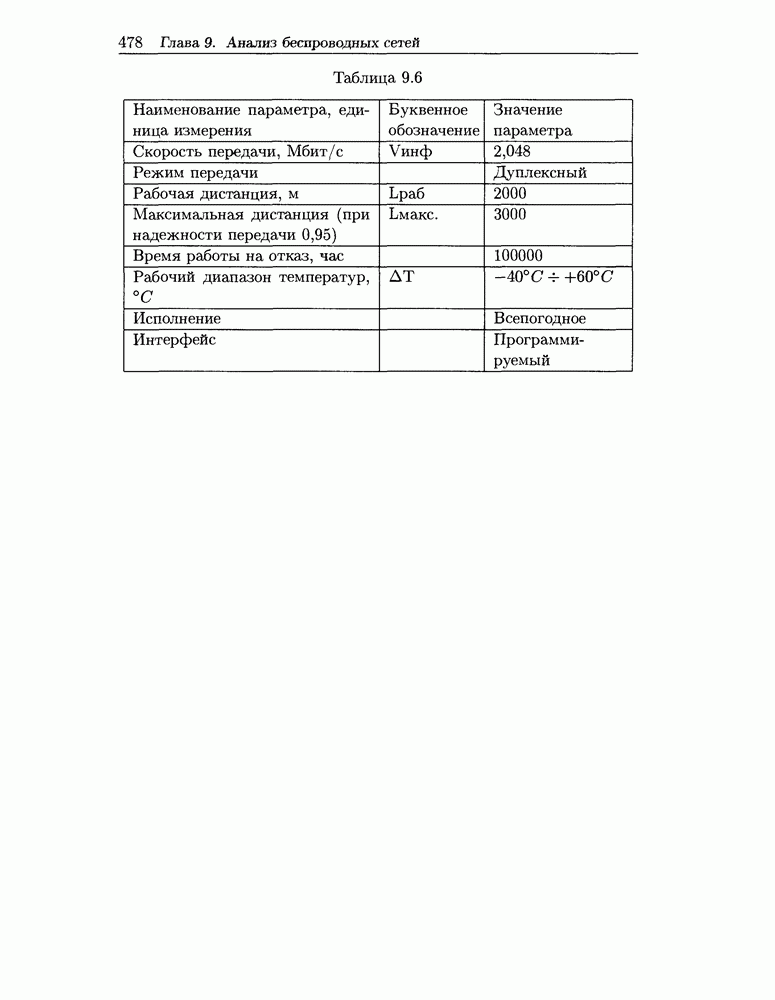
- 9.8 Оптоэлектронные атмосферные каналы передачи данных в компьютерных сетях
- Литература